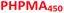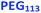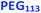Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enthalpic incompatibility between two steric stabilizer blocks provides control over the vesicle size distribution during polymerization-induced self-assembly in aqueous media†
Deborah L.
Beattie
,
Oleksandr O.
Mykhaylyk
 * and
Steven P.
Armes
* and
Steven P.
Armes
 *
*
Department of Chemistry, University of Sheffield, Dainton Building, Brook Hill, Sheffield, South Yorkshire, S3 7HF, UK. E-mail: s.p.armes@shef.ac.uk; o.mykhaylyk@sheffield.ac.uk
First published on 29th June 2020
Abstract
Over the past two decades, block copolymer vesicles have been widely used by many research groups to encapsulate small molecule drugs, genetic material, nanoparticles or enzymes. They have also been used to design examples of autonomous self-propelled nanoparticles. Traditionally, such vesicles are prepared via post-polymerization processing using a water-miscible co-solvent such as DMF or THF. However, such protocols are invariably conducted in dilute solution, which is a significant disadvantage. In addition, the vesicle size distribution is often quite broad, whereas aqueous dispersions of relatively small vesicles with narrow size distributions are highly desirable for potential biomedical applications. Alternatively, concentrated dispersions of block copolymer vesicles can be directly prepared via polymerization-induced self-assembly (PISA). Moreover, using a binary mixture of a relatively long and a relatively short steric stabilizer block enables the convenient PISA synthesis of relatively small vesicles with reasonably narrow size distributions in alcoholic media (C. Gonzato et al., JACS, 2014, 136, 11100–11106). Unfortunately, this approach has not yet been demonstrated for aqueous media, which would be much more attractive for commercial applications. Herein we show that this important technical objective can be achieved by judicious use of two chemically distinct, enthalpically incompatible steric stabilizer blocks, which ensures the desired microphase separation across the vesicle membrane. This leads to the formation of well-defined vesicles of around 200 nm diameter (size polydispersity = 13–16%) in aqueous media at 10% w/w solids as judged by transmission electron microscopy, dynamic light scattering and small-angle X-ray scattering.
Introduction
Over the past decade or so, polymerization-induced self-assembly (PISA) has become widely recognized as a highly efficient and versatile technique for the rational synthesis of a wide range of block copolymer nano-objects in concentrated solution.1,2 Systematic variation of the relative volume fractions of the solvophilic and solvophobic blocks allows convenient access to sterically-stabilized spheres, worms and vesicles using many different monomers.3–11 In principle, various types of controlled/living polymerization techniques can be used for such PISA syntheses but reversible addition–fragmentation chain transfer (RAFT) polymerization is most commonly reported in the literature.12RAFT-mediated PISA can be conducted in a wide range of solvents.13–20 In practice, water is the most cost-effective, environmentally-friendly and is also best suited for potential biomedical applications. Of particular relevance to the present study, RAFT aqueous dispersion polymerization2,21,22 involves chain extension of a water-soluble homopolymer with a water-miscible monomer such as 2-hydroxypropyl methacrylate (HPMA),23–26 diacetone acrylamide (DAAM),27–29N-isopropyl acrylamide (NIPAM)30 or 2-methoxyethyl acrylate (MEA).31,32 This growing second block eventually becomes insoluble at some critical degree of polymerization (DP), thus triggering in situ self-assembly to form diblock copolymer nanoparticles.
Two of the earliest RAFT aqueous dispersion polymerization formulations involved the use of poly(glycerol monomethacrylate) (PGMA) or poly(2-(methacryloyloxy)ethyl phosphorylcholine) (PMPC) as the water-soluble precursor block to grow a hydrophobic structure-directing PHPMA block.23,33–36 Numerous studies have indicated that PGMA and PMPC are highly attractive building blocks for the rational design of nanobiomaterials owing to their proven biocompatibility.37–47 Similarly, poly(ethylene glycol) (PEG) is a well-known biocompatible polymer that can be utilized as a hydrophilic steric stabilizer.6,26,48–55 In particular, PISA enables PEG-PHPMA thermoresponsive worms and vesicles to be readily prepared directly in aqueous solution.8,48,49,54 The worms form soft, free-standing physical gels that can be used for 3D cell culture but the vesicles tend to be relatively large and rather polydisperse in terms of their size distribution.38,48,55–58 Controlling the particle size distribution of block copolymer vesicles is an important and long-standing scientific problem, with various ingenious strategies being reported in the literature.59–69
For example, Luo and Eisenberg reported that judicious use of a binary mixture of two AB diblock copolymers enabled the preparation of low-dispersity vesicles.61,70,71 More specifically, using a relatively long and a relatively short poly(acrylic acid) (PAA) stabilizer block in combination with a common hydrophobic polystyrene (PS) block led to spatial segregation across the vesicle membrane. The longer PAA chains were preferentially expressed at the outer leaflet, while the shorter chains were located within the more sterically-congested inner leaflet, with this configuration lowering the free energy for the vesicle morphology. Luo and Eisenberg later demonstrated that the same principle was also applicable for spatial segregation of two chemically distinct corona blocks – PAA and poly(4-vinylpyridine) – across a PS membrane.72 However, these studies utilized a traditional post-polymerization processing route that required a water-miscible co-solvent and a relatively low copolymer concentration. Thus, it does not provide a scalable route to well-defined vesicles. Subsequently, Gonzato et al. showed that this ‘binary mixture of steric stabilizers’ concept was also valid for PISA formulations by demonstrating the synthesis of relatively small, low polydispersity vesicles using RAFT alcoholic dispersion polymerization.73 Both dynamic light scattering and small-angle X-ray scattering (SAXS) studies indicated a significant reduction in the width of the vesicle size distribution. However, as far as we are aware, this approach has not yet been reported for any aqueous PISA formulations. This omission is perhaps surprising given the strong interest in using block copolymer vesicles for a wide range of biomedical applications, including intracellular delivery of drugs,74–76 genes77–79 or antibodies,80 antibacterial agents81,82 for autonomous locomotion83 or chemotaxis84 and for encapsulation of therapeutic enzymes.51,57,58,85
Herein, we report the rational synthesis of relatively small diblock copolymer vesicles with narrow size distributions directly at 10% w/w solids using an aqueous PISA formulation. This is achieved by employing two chemically dissimilar stabilizer blocks of differing degrees of polymerization (see Scheme 1). These two stabilizers are non-ionic PEG and zwitterionic PMPC, whose mutual enthalpic incompatibility has been previously reported by Blanazs and co-workers.86 We use SAXS analysis to demonstrate that using such a binary mixture of enthalpically incompatible stabilizers is essential to exert the desired control over the vesicle size distribution during aqueous PISA. In contrast, a binary mixture of chemically identical stabilizers appears to reduce the breadth of the vesicle size distribution but only produces relatively large vesicles, which are considered to be less useful for many potential biomedical application.
Results and discussion
Targeting the vesicle morphology
It is well known in the block copolymer literature that asymmetric diblock copolymer compositions must be targeted to access vesicle phase space. This was originally established by Eisenberg and co-workers using traditional post-polymerization processing via a solvent switch in dilute solution87,88 but it is equally valid for PISA syntheses.33,35 This design rule can be explained in terms of the geometric packing parameter P introduced by Israelachvili and co-workers to account for surfactant self-assembly,89 which has been subsequently validated for the self-assembly of amphiphilic diblock copolymers.90 If P is greater than 0.50, then vesicles are favored unless there are other constraints, in which case kinetically-trapped spheres may be formed.91Vesicle synthesis strategy
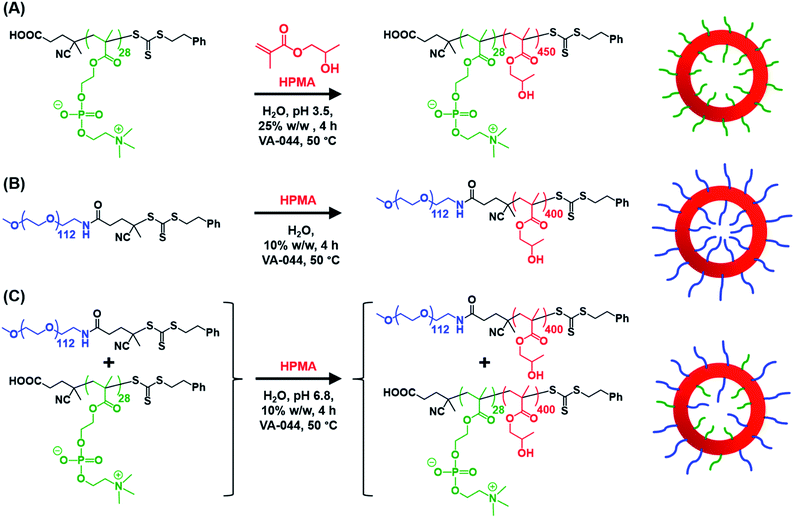
Informed by this design rule, Sugihara and co-workers reported that targeting PMPC25–PHPMA400via aqueous PISA at 25% w/w solids produced a rather polydisperse vesicular morphology at 70 °C.34 In the present study, a closely-related aqueous PISA formulation was used to produce PMPC28–PHPMA450 vesicles (Scheme 1a) by targeting the same relatively high copolymer concentration and a slightly longer structure-directing PHPMA block. A lower reaction temperature of 50 °C was also employed but the most important difference is that a carboxylic acid-functionalized RAFT agent was used to prepare the PMPC precursor block. This was a deliberate choice because this ionizable end-group is known to influence the electrophoretic behavior of block copolymer nano-objects,92,93 which was expected to aid discrimination between the three types of vesicles shown in Scheme 1. To ensure the formation of pure PMPC28–PHPMA450 vesicles, PISA syntheses were conducted at low pH to prevent end-group ionization reducing the packing parameter, which would inevitably lead to kinetically-trapped spheres.92,93 The HPMA polymerization proceeded to more than 99% conversion within 4 h and GPC studies (refractive index detector, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 chloroform/methanol eluent) indicated a relatively high blocking efficiency (see Fig. S2†). A relatively broad molecular weight distribution was obtained (see Table S1†) but this was not unexpected given the known contamination of the HPMA monomer with a dimethacrylate impurity, which inevitably leads to branching when targeting a relatively high degree of polymerization (DP).33 Indeed, a relatively high dispersity was also reported by Sugihara et al.34
1 chloroform/methanol eluent) indicated a relatively high blocking efficiency (see Fig. S2†). A relatively broad molecular weight distribution was obtained (see Table S1†) but this was not unexpected given the known contamination of the HPMA monomer with a dimethacrylate impurity, which inevitably leads to branching when targeting a relatively high degree of polymerization (DP).33 Indeed, a relatively high dispersity was also reported by Sugihara et al.34
Similarly, the PEG113–PHPMA400 formulation outlined in Scheme 1b has already been reported by Warren et al., who obtained relatively large polydisperse vesicles when conducting such aqueous PISA syntheses at 10% w/w solids.48 In the present study, a HPMA conversion of more than 99% was achieved within 4 h at 50 °C, while 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 chloroform/methanol GPC studies indicated an Mn of 45
1 chloroform/methanol GPC studies indicated an Mn of 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 g mol−1 and an Mw/Mn of 1.45 for the PEG113–PHPMA400 chains (see Fig. S2 and Table S1†). These GPC data are similar to that reported by Warren and co-workers.48
400 g mol−1 and an Mw/Mn of 1.45 for the PEG113–PHPMA400 chains (see Fig. S2 and Table S1†). These GPC data are similar to that reported by Warren and co-workers.48
Bearing in mind the earlier PISA studies by Gonzato et al.,73 we hypothesized that using a judicious binary mixture of a relatively long PEG113 stabilizer and a relatively short PEG45 stabilizer while targeting a sufficiently long structure-directing PHPMA block should yield small vesicles with a relatively narrow size distribution. However, this strategy proved fruitless, as summarized in Fig. S3 and S4.† Regardless of the PEG113 mole fraction employed, only relatively large and/or polydisperse vesicles (or even less well-defined structures) could be obtained.94 To address this unexpected problem, we speculated that a binary mixture of a pair of chemically dissimilar stabilizer blocks should enhance the apparently weak segregation of the long and short chains across the vesicle membrane and ideally also simultaneously reduce the vesicle size. According to Blanazs and co-workers, PEG114 and PMPC50 homopolymers are sufficiently enthalpically incompatible to form an aqueous biphasic solution, while PEG114–PMPC23 diblock copolymers forms a range of structures exhibiting long-range order in concentrated aqueous solution.86 Thus we explored the synthesis of hybrid vesicles using the PISA formulation outlined in Scheme 1c. Based on the prior studies by Eisenberg et al.,72 this strategy should result in the relatively long PEG113 stabilizer chains being preferentially expressed at the outer leaflet of the vesicle membrane, while the relatively short PMPC28 chains should be located within the vesicle lumen. The PEG113 mole fraction was systematically varied when preparing a series of [xPEG113 + (1 − x) PMPC28] − PHPMA400 nano-objects. Given the well-known tendency for the PEG113 stabilizer block to produce either oligolamellar vesicles or insoluble precipitates when targeting longer PHPMA blocks at high solids,48 these PISA syntheses were conducted at 10% w/w solids to ensure formation of unilamellar vesicles. More than 99% HPMA conversion was achieved within 4 h and a high blocking efficiency was obtained for each of these aqueous PISA syntheses (see Fig. S2 and Table S1†).
Kinetic studies of the synthesis of [xPEG113 + (1 − x) PMPC28] − PHPMA400 diblock copolymer nanoparticles
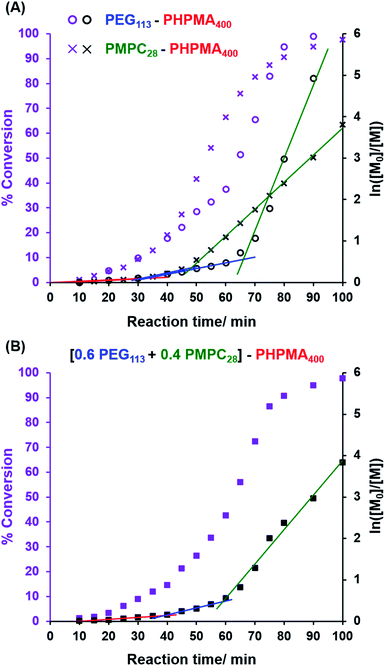
For the synthesis of small vesicles with a relatively narrow size distribution, Gonzato et al. employed a binary mixture of a relatively long and a relatively short poly(methacrylic acid) (PMAA) precursor for the RAFT dispersion polymerization of benzyl methacrylate (BzMA) in ethanol.73 Both stabilizer blocks were prepared using the same trithiocarbonate-based RAFT agent and it was implicitly assumed that the structure-directing poly(benzyl methacrylate) (PBzMA) chains grown from each of these PMAA stabilizers would have the same mean DP. However, this may not necessarily be the case. This is because the critical PBzMA DP required for micellar nucleation actually depends on the DP of the PMAA stabilizer block. Thus, nucleation should commence at a significantly lower critical PBzMA DP when using the shorter PMAA62 block compared to when utilising the PMAA171 block. In principle, this could be important, because the nascent nuclei quickly become swollen with unreacted BzMA and the ensuing high local monomer concentration leads to a substantial increase in the rate of polymerization.12,35,95 Thus if micellar nucleation is delayed for the PMAA171 block, the PBzMA chains grown from this precursor are likely to be shorter than those grown from the PMAA62 block. Moreover, this suggests that the membranes of the resulting vesicles might comprise a bimodal distribution of PBzMA chain lengths. However, it is perhaps also worth bearing in mind that block copolymer self-assembly can be remarkably tolerant of dispersity effects.70,96–98In the present study, we undertook kinetic experiments in order to assess to what extent the critical DP required for micellar nucleation differs for the PMPC28 and PEG113 precursors. The conversion vs. time curves and corresponding semilogarithmic plots obtained from 1H NMR studies are shown in Fig. 1A when using each of these stabilizer blocks in turn for the RAFT aqueous dispersion polymerization of HPMA. As previously reported by Cornel and co-workers,99 three distinct stages are observed for each polymerization, with the second inflection point being assigned to micellar nucleation. As expected, this event occurs at a significantly earlier stage when using the PMPC28 precursor. In this case, an eight-fold increase in the rate of polymerization of HPMA occurs after 48 min, which corresponds to an instantaneous conversion of 30% and hence a critical PHPMA DP of 120. In contrast, a rate acceleration is not observed until 66 min when using the PEG113 precursor, which corresponds to an instantaneous conversion of 42% and a critical PHPMA DP of 168. Interestingly, a 31-fold rate enhancement is observed in this case, which might be expected to mitigate the anticipated bimodal distribution of PHPMA chain lengths when using a binary mixture of PMPC28 and PEG113 stabilizers. Indeed, GPC analyses of nominal binary mixtures of PEG113–PHPMA400 plus PMPC28–PHPMA400 do not provide any evidence for a bimodal molecular weight distribution (see Fig. S2†).
The kinetic data obtained when employing a binary mixture of 0.60 PEG113 and 0.40 PMPC28 stabilizer blocks are shown in Fig. 1B. Perhaps surprisingly, only a single micellar nucleation event is observed for this latter formulation: a nine-fold rate enhancement occurs after 59 min, which corresponds to 38% conversion and hence a critical PHPMA DP of 152. Thus, micellar nucleation occurs at a time point (and a critical PHPMA DP) that is intermediate between those observed in Fig. 1A. This suggests that these nascent micelles actually comprise a binary mixture of PEG113–PHPMA152 and PMPC28–PHPMA152 chains owing to entropic mixing of the growing amphiphilic copolymer chains during PISA. This interpretation is consistent with the corresponding aqueous electrophoresis data (see later) obtained for the three types of vesicles described in Scheme 1. Thus, our initial concern regarding the potential problem of a bimodal distribution of PHPMA chain lengths being generated during such PISA syntheses appears to be unfounded.
Structural characterization of [xPEG113 + (1 − x) PMPC28] − PHPMA400 diblock copolymer nano-objects
The TEM images shown in Fig. 2 were used to assign the predominant copolymer morphology and this information was combined with DLS data to construct Fig. 3. This phase diagram is strikingly similar to that reported by Gonzato et al.,73 but differs markedly from that shown in Fig. S3† for the synthesis of [xPEG113 + (1 − x) PEG45] − PHPMA400 nano-objects.For PISA syntheses conducted using relatively low levels of PEG113 stabilizer (i.e. for either pure PMPC28 or PMPC28-rich formulations), only kinetically-trapped spheres could be obtained at 10% w/w solids. Moreover, using a PEG113 mole fraction of either 0.4 or 0.5 merely produced mixed phases comprising spheres and vesicles. However, a pure vesicle morphology was observed when employing PEG113-rich PISA formulations (see Fig. 2). Furthermore, using PEG113 mole fractions of either 0.6 or 0.7 clearly afforded the smallest vesicles with the narrowest size distributions (lowest DLS polydispersities). However, in our experience, the polydispersity reported by DLS is a rather crude measure of the breadth of a size distribution. For example, the relatively low DLS polydispersities (<0.10) obtained for [xPEG113 + (1 − x) PEG45] − PHPMA400 vesicles when x = 0.7 or 0.8 (Fig. S3†) are clearly inconsistent with the corresponding TEM images (Fig. S4†) since the latter suggest a rather broad size range. Hence we followed the strategy adopted by Gonzato and co-workers,73 who utilized small-angle X-ray scattering (SAXS) to compare vesicle size distributions. Accordingly, SAXS patterns were recorded for each of the aqueous PISA formulations reported in Fig. 1 and 2 (see Fig. 4). One striking observation is that the two vesicle dispersions identified by DLS as possessing relatively low polydispersities (i.e. x = 0.6 and 0.7) exhibit multiple fringes at intermediate q. This is a well-known signature for particles with relatively narrow size distributions since minima arising from the particle form factor are only partially smeared by the particle size distribution. Moreover, the large polydisperse vesicles formed at higher PEG113 mole fractions according to DLS (see Fig. 3) are characterized by SAXS patterns with substantially attenuated minima (see Fig. 4). Thus, these two sizing techniques are in rather good agreement.
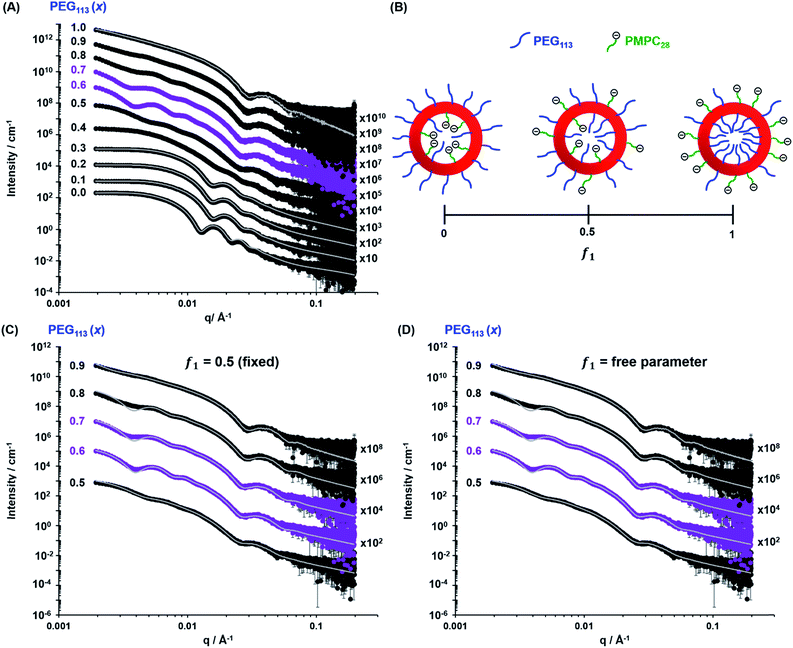 | ||
| Fig. 4 (A) Experimental SAXS patterns (symbols) and corresponding data fits (grey lines) obtained for 1.0% w/w aqueous dispersions of [xPEG113 + (1 − x) PMPC28] − PHPMA400 nano-objects originally prepared at 10% w/w solids, where the mole fraction (x) ranges from 0.0 (PMPC28–PHPMA400) to 1.0 (PEG113–PHPMA400). Scattering curves obtained for nano-objects prepared using a PEG mole fraction of 0.1–0.3 could be satisfactorily fitted using the blob-modified spherical micelle model, while the scattering patterns obtained for PMPC28–PHPMA400 spheres were fitted using a well-known spherical micelle model.100 A well-established vesicle model101 was employed to fit the scattering pattern recorded for PEG113–PHPMA400 vesicles obtained when x = 1.0. (B) Schematic representation of the segregation fitting parameter f1, which indicates the mole fraction of PMPC28 chains occupying the outer leaflet of the vesicles. (C) Experimental SAXS patterns [same symbols as shown in (A)] recorded for the sub-set of [xPEG113 + (1 − x) PMPC28] − PHPMA400 vesicles obtained for x = 0.50–0.90. These patterns were fitted using a refined vesicle model that takes account of the binary mixture of diblock copolymer chains [eqn (16)] using a fixed segregation parameter f1 of 0.50 (which corresponds to a purely statistical mixture of PEG and PMPC stabilizer chains occupying the outer corona). The grey lines indicate the data fits obtained using this more sophisticated scattering model. In contrast, (D) shows the data fits obtained when f1 is allowed to vary as a free parameter. | ||
While DLS provides information regarding the vesicle size distribution, SAXS provides additional structural information. However, an appropriate scattering model is required to fit SAXS patterns to determine the overall vesicle diameter, size polydispersity, membrane thickness, mean aggregation number, radius of gyration of the stabilizer chains and the solvent volume fraction within the vesicle membrane. TEM analysis (Fig. 2) indicates the presence of two copolymer morphologies: spheres and vesicles. There are well-developed SAXS models for analysing scattering patterns for both types of diblock copolymer nano-objects.100,101 However, as the current system comprises two types of diblock copolymer chains bearing enthalpically incompatible stabilizer blocks, their spatial distribution within the coronal layer must also be considered. For a vesicle morphology, the PEG113 and PMPC28 stabilizer chains could be either randomly distributed or spatially segregated between the inner and outer vesicle leaflets. Thus, the well-established scattering model for vesicles101 requires further refinement. Similarly, adjustment must be made to the scattering model for spheres if this morphology is obtained.100
Small angle X-ray scattering (SAXS) models
In general, the X-ray scattering intensity, I(q), from a dispersion of uniform nano-objects can be expressed as: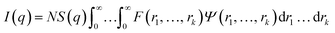 | (1) |
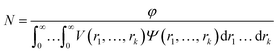 | (2) |
Fmic(q, r1) = Ns2βs2As2(q, r1) + Nsβc2Fc(q, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g) + Ns(Ns − 1) × βc2Fco(q, r1) + 2Ns2βsβcAs(q, r1)Aco(q, r1)ψ(q, Rgblob) g) + Ns(Ns − 1) × βc2Fco(q, r1) + 2Ns2βsβcAs(q, r1)Aco(q, r1)ψ(q, Rgblob) | (3) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g is the averaged radius of gyration of the corona blocks. To model spherical micelles comprising a binary mixture of PEG113 and PMPC28 blocks, the
g is the averaged radius of gyration of the corona blocks. To model spherical micelles comprising a binary mixture of PEG113 and PMPC28 blocks, the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g was calculated based on their relative volume fractions using an approximate radius of gyration for each pure block [RgPEG = 2.6 nm and RgPMPC = 1.4 nm]. These Rg values were estimated assuming that the repeat unit length of PMPC is 0.255 nm (the length of two C–C bonds in a trans conformation). Thus, the total contour length of a PMPC28 block is LPMPC28 = 28 × 0.255 nm = 7.15 nm. Similarly, the contour length of an ethylene glycol repeat unit is 0.37 nm (estimated from the known crystal structure of PEG homopolymer),103 hence the total contour length of a PEG113 block is LPEG113 = 113 × 0.37 nm = 41.81 nm. Assuming a mean PMPC Kuhn length of 1.53 nm (based on the known literature value for PMMA)104 and a mean PEG Kuhn length of 1.0 nm,105 the estimated unperturbed radius of gyration for each block was determined using Rg(PEG or PMPC) = (contour length × Kuhn length/6)0.5. The self-correlation term for the corona blocks is given by the Debye function:
g was calculated based on their relative volume fractions using an approximate radius of gyration for each pure block [RgPEG = 2.6 nm and RgPMPC = 1.4 nm]. These Rg values were estimated assuming that the repeat unit length of PMPC is 0.255 nm (the length of two C–C bonds in a trans conformation). Thus, the total contour length of a PMPC28 block is LPMPC28 = 28 × 0.255 nm = 7.15 nm. Similarly, the contour length of an ethylene glycol repeat unit is 0.37 nm (estimated from the known crystal structure of PEG homopolymer),103 hence the total contour length of a PEG113 block is LPEG113 = 113 × 0.37 nm = 41.81 nm. Assuming a mean PMPC Kuhn length of 1.53 nm (based on the known literature value for PMMA)104 and a mean PEG Kuhn length of 1.0 nm,105 the estimated unperturbed radius of gyration for each block was determined using Rg(PEG or PMPC) = (contour length × Kuhn length/6)0.5. The self-correlation term for the corona blocks is given by the Debye function: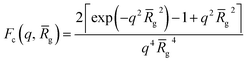 | (4) |
The core and corona block X-ray scattering contrast is given by βs = Vs(ξs − ξsol) and βc = ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) c(
c(![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) c − ξsol), respectively. ξs,
c − ξsol), respectively. ξs, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) c, and ξsol are the scattering length density (SLD) of the core block (ξHPMA = 11.11 × 1010 cm−2), the mean SLD of the corona blocks (ξPMPC = 11.6 × 1010 cm−2 and/or ξPEG = 10.85 × 1010 cm−2) and the SLD of the solvent (ξwater = 9.42 × 1010 cm−2), respectively. The mean SLD of the corona formed when using binary mixtures of PEG113 and PMPC28 stabilizer blocks was calculated based on the relative volume fractions of these two components. Vs is the volume of the core block and
c, and ξsol are the scattering length density (SLD) of the core block (ξHPMA = 11.11 × 1010 cm−2), the mean SLD of the corona blocks (ξPMPC = 11.6 × 1010 cm−2 and/or ξPEG = 10.85 × 1010 cm−2) and the SLD of the solvent (ξwater = 9.42 × 1010 cm−2), respectively. The mean SLD of the corona formed when using binary mixtures of PEG113 and PMPC28 stabilizer blocks was calculated based on the relative volume fractions of these two components. Vs is the volume of the core block and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) c is the mean volume of the corona block calculated from the PEG113 and PMPC28 block volumes (VPEG and VPMPC, respectively) using their relative volume fractions. Block copolymer volumes were obtained from the relation
c is the mean volume of the corona block calculated from the PEG113 and PMPC28 block volumes (VPEG and VPMPC, respectively) using their relative volume fractions. Block copolymer volumes were obtained from the relation 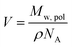 using the following densities: ρPMPC = 1.28 g cm−3, ρPEG = 1.17 g cm−3 and ρHPMA = 1.21 g cm−3 (see ESI for further details†). Here Mw,pol is the mean molecular weight of the stabilizer block (PEG113 or PMPC28) as determined by 1H NMR spectroscopy and NA is Avogadro's constant. The amplitude of the sphere form factor is used for that of the core self-term:
using the following densities: ρPMPC = 1.28 g cm−3, ρPEG = 1.17 g cm−3 and ρHPMA = 1.21 g cm−3 (see ESI for further details†). Here Mw,pol is the mean molecular weight of the stabilizer block (PEG113 or PMPC28) as determined by 1H NMR spectroscopy and NA is Avogadro's constant. The amplitude of the sphere form factor is used for that of the core self-term:
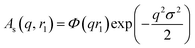 | (5) |
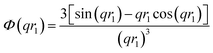 | (6) |
A sigmoidal interface between the two blocks was assumed for the spherical micelle form factor [eqn (3)]. This is described by the exponent term in eqn (5) with a width, σ, to account for the decaying scattering length density at the core–shell interface. The σ value was fixed at 2.5 Å during fitting. The form factor amplitude for the spherical micelle corona is given by:
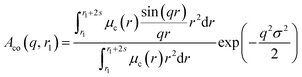 | (7) |
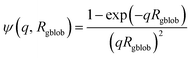 | (8) |
| Fco(q, r1) = [nblob(nblob − 1)ψ2(q, Rgblob)Aco2(q, r1) + nblobFc(q, Rgblob)]/nblob2 | (9) |
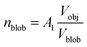 , A1 is a fitting parameter related to the number of ‘blobs’ formed in the studied nano-object, the ‘blob’ volume is given by
, A1 is a fitting parameter related to the number of ‘blobs’ formed in the studied nano-object, the ‘blob’ volume is given by 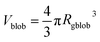 and Vobj is equal to the spherical micelle corona volume
and Vobj is equal to the spherical micelle corona volume 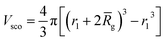 . Fc(q, Rgblob) is expressed using a function analogous to that given in eqn (4). The mean aggregation number for the spherical micelles is given by:
. Fc(q, Rgblob) is expressed using a function analogous to that given in eqn (4). The mean aggregation number for the spherical micelles is given by: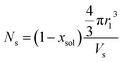 | (10) |
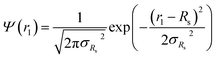 | (11) |
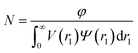 | (12) |
V(r1) = (Vs + ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) c)Ns(r1) c)Ns(r1) | (13) |
A structure factor, S(q), was included in this model to account for the repulsive interactions arising from the anionic carboxylate end-group on each PMPC28 stabilizer chain. Since the micelles are not perfectly centrosymmetric, eqn (1) should be rewritten as:108
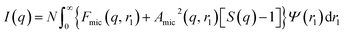 | (14) |
| Amic(q, r1) = NsβsAs(q, r1) + NsβcAco(q, r1)ψ(q, Rgblob) | (15) |
A hard-sphere structure factor, S(q) = SPY(q, RPY, fPY), (solved using the Percus–Yevick closure relation) was introduced to account for interactions between spherical micelles,108 where RPY is the effective interparticle correlation radius and fPY is the effective volume fraction. Although this structure factor is not strictly correct in this case, it nevertheless provides a useful analytical expression.109
For vesicles, the form factor in eqn (1) is given as
| Fv(q, r1, r2) = Nv2βs2Am2(q, r1, r2) + Nv(Nv − 1)Fvc(q, r1, r2) + 2Nv2βsAm(q, r1, r2)Avc(q, r1, r2)ψ(q, Rgblob) + Nv[fPEGβPEG2Fc(q, RgPEG) + fPMPCβPMPC2Fc(q, RgPMPC)] | (16) |
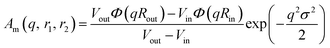 | (17) |
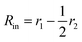 is the inner radius of the membrane,
is the inner radius of the membrane, 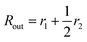 is the outer radius of the membrane (in this case, r1 is the radius from the centre of the vesicle to the middle of its membrane and r2 is the thickness of the hydrophobic part of the membrane),
is the outer radius of the membrane (in this case, r1 is the radius from the centre of the vesicle to the middle of its membrane and r2 is the thickness of the hydrophobic part of the membrane), 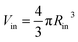 , and
, and 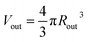 . Φ(qRout) and Φ(qRin) are defined by expressions that are analogous to those used in eqn (6). The mean vesicle aggregation number, Nv(r1, r2), is given by:
. Φ(qRout) and Φ(qRin) are defined by expressions that are analogous to those used in eqn (6). The mean vesicle aggregation number, Nv(r1, r2), is given by: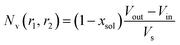 | (18) |
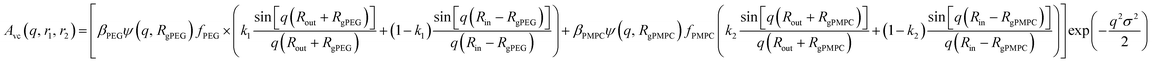 | (19) |
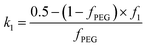 and k2 = f1, respectively. f1 is a fitting parameter such that 0 ≤ f1 ≤ 1, where f1 = 0.5 corresponds to a random distribution of the PEG113 and PMPC28 stabilizer chains between the outer and the inner vesicle leaflets. Importantly, an f1 value of zero indicates that all PMPC28 stabilizer chains are preferentially located in the inner vesicle leaflet, i.e. within the vesicle lumen. In contrast, an f1 value of unity indicates that these stabilizer chains are exclusively located in the outer vesicle leaflet (Fig. 4B). The form factor for the inner and outer vesicle corona is described as:
and k2 = f1, respectively. f1 is a fitting parameter such that 0 ≤ f1 ≤ 1, where f1 = 0.5 corresponds to a random distribution of the PEG113 and PMPC28 stabilizer chains between the outer and the inner vesicle leaflets. Importantly, an f1 value of zero indicates that all PMPC28 stabilizer chains are preferentially located in the inner vesicle leaflet, i.e. within the vesicle lumen. In contrast, an f1 value of unity indicates that these stabilizer chains are exclusively located in the outer vesicle leaflet (Fig. 4B). The form factor for the inner and outer vesicle corona is described as:| Fvc(q, r1, r2) = [nblob(nblob − 1)ψ2(q, Rgblob) × Avc2(q, r1, r2) + nblobFc(q, Rgblob)]/nblob2 | (20) |
For such nblob calculations, Vobj is equal to the vesicle corona volume 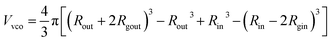 . Herein, the mean thickness of the outer and inner vesicle corona were calculated as the average diameter of the outer and inner corona block, 2Rgout = 2(fPEG × k1 × RgPEG3 + fPMPC × k2 × RgPMPC3)1/3 and 2Rgin = 2[fPEG(1 − k1) × RgPEG3 + fPMPC(1 − k2) × RgPMPC3]1/3, respectively.
. Herein, the mean thickness of the outer and inner vesicle corona were calculated as the average diameter of the outer and inner corona block, 2Rgout = 2(fPEG × k1 × RgPEG3 + fPMPC × k2 × RgPMPC3)1/3 and 2Rgin = 2[fPEG(1 − k1) × RgPEG3 + fPMPC(1 − k2) × RgPMPC3]1/3, respectively.
For the vesicle model, it was assumed that Rv (the mean radius from the centre of the vesicle to the middle of the membrane) and Tm (the mean vesicle membrane thickness) have finite polydispersity. Assuming that each parameter has a Gaussian distribution, the polydispersity function in eqn (1) can be expressed as:
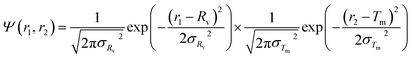 | (21) |
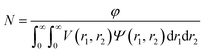 | (22) |
| V(r1, r2) = (Vs + fPEGVPEG + fPMPCVPMPC)Nv(r1, r2) | (23) |
Since the vesicles are significantly larger than spherical micelles, the structure factor for vesicle interactions only makes a significant contribution at low q. Unfortunately, this region was not well-resolved in our synchrotron SAXS experiments. Thus, it was assumed for SAXS analysis of the vesicles that the structure factor is close to unity [S(q) = 1 in eqn (1)]. The programming tools available within Irena SAS macros for Igor Pro were used to implement the scattering models.110 Model fittings were performed using the least-squares method.
SAXS analysis
The above structural models for spheres and vesicles produced reasonably good fits to the corresponding experimental SAXS patterns (Fig. 4). Unfortunately, the first minimum in the form factor at q < 0.004 Å−1 corresponding to the overall vesicle diameter is not sufficiently resolved to observe the associated secondary minimum at q ∼ 0.008 Å−1 (Fig. 4). This is likely to be the result of smearing at low q (close to the beamstop) caused by the finite X-ray beam cross-section and the pixel size of the X-ray detector. This technical problem has some repercussions for the data fits. To overcome this problem, the most affected data points close to the beamstop (including the first minimum and below) were excluded from the fitting range. The resulting structural parameters were then used to recalculate scattering patterns over the entire experimental q range (Fig. 4). A summary of the structural parameters derived from data fits to the SAXS patterns shown in Fig. 4 is provided in Table 1.| PEG113 (x) | TEM | DLS | SAXS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Morphology assignment | D z/nm | PDI | R s ± σRs/nm | R v ± σRv/nm | σ R v /Rv/% | T m ± σTm/nm | σ T m /Tm/% | D s or Dv/nm | R gblob/nm | f 1 | |
| a R s is the spherical micelle core radius, Rv is the distance from the centre of the vesicle to the middle of the vesicle membrane and σR denotes the corresponding standard deviations for these two parameters. Tm is the vesicle membrane thickness and σTm denotes the standard deviation of this parameter. Ds or Dv are the sphere or vesicle diameter respectively. Rgblob is the radius of gyration of the inhomogeneous ‘blobs’ within the coronal layer of stabilizer chains. f1 is the segregation parameter which indicates the fraction of PMPC stabilizer chains located within the outer corona, and an asterisk (*) indicates when f1 was fixed at 0.50 during fitting (N.B. ‘n.d.’ denotes ‘not determined’). | |||||||||||
| 0 | Spheres | 82 | 0.02 | 34.0 ± 3.0 | — | — | — | — | 73.3 | — | — |
| 0.1 | Spheres | 69 | 0.01 | 27.9 ± 2.9 | — | — | — | — | 61.6 | 4.2 | — |
| 0.2 | Spheres | 69 | 0.03 | 28.2 ± 3.1 | — | — | — | — | 62.6 | 3.9 | — |
| 0.3 | Spheres | 71 | 0.03 | 28.4 ± 3.3 | — | — | — | — | 63.4 | 4.1 | — |
| 0.4 | Spheres & vesicles | 92 | 0.07 | n.d. | n.d. | n.d | n.d. | n.d. | n.d. | n.d. | n.d. |
| 0.5 | Spheres & vesicles | 146 | 0.08 | — | 60.9 ± 18.8 | 31 | 23.9 ± 3.6 | 15 | 156 | 4.2 | 0.5* |
| 61.5 ± 18.8 | 31 | 23.7 ± 3.6 | 15 | 157 | 0.14 | ||||||
| 0.6 | Vesicles | 189 | 0.08 | — | 79.6 ± 10.6 | 13 | 22.3 ± 2.8 | 13 | 192 | 2.8 | 0.5* |
| 80.1 ± 10.6 | 13 | 22.1 ± 2.8 | 13 | 193 | ∼0 | ||||||
| 0.7 | Vesicles | 200 | 0.07 | — | 81.7 ± 12.6 | 15 | 22.1 ± 2.7 | 12 | 196 | 2.9 | 0.5* |
| 82.1 ± 12.6 | 15 | 21.9 ± 2.7 | 12 | 197 | ∼0 | ||||||
| 0.8 | Vesicles | 228 | 0.13 | — | 81.8 ± 13.1 | 16 | 21.5 ± 2.6 | 12 | 196 | 3.3 | 0.5* |
| 82.1 ± 13.1 | 16 | 21.5 ± 2.6 | 12 | 196 | ∼0 | ||||||
| 0.9 | Vesicles | 331 | 0.17 | — | 98.5 ± 35.1 | 36 | 21.0 ± 2.4 | 11 | 228 | 3.0 | 0.5* |
| 98.7 ± 35.1 | 36 | 20.9 ± 2.4 | 12 | 229 | ∼0 | ||||||
| 1.0 | Vesicles | 462 | 0.18 | — | 185 ± 54 | 29 | 20.4 ± 2.8 | 14 | 402 | — | — |
The initial morphology assignment by TEM informed our choice of scattering model, with satisfactory data fits being achieved in all but one case (x = 0.40). Data fits to the experimental SAXS patterns of the kinetically-trapped spheres obtained using a relatively high proportion of PMPC28 stabilizer chains could be achieved using the blob-modified spherical micelle model (Fig. 4A). Exceptionally, the scattering pattern recorded for the PMPC28–PHPMA400 spheres (which would not be expected to exhibit SLD variations across the sphere corona) was fitted using the classic spherical micelle model.100 For spheres obtained when using a PEG113 mole fraction (x) of 0.10–0.30, the structural information derived from such data fits was consistent with DLS studies, suggesting that all three formulations produced spheres with comparable micelle core radii and overall diameters [calculated using Ds = 2(Rs + 2![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g)] with relatively low polydispersities of 10–12%. Furthermore, Rgblob values were comparable to the radii of gyration of the stabilizer chains, indicating that similar inhomogeneous blobs were generated across the sphere coronas.
g)] with relatively low polydispersities of 10–12%. Furthermore, Rgblob values were comparable to the radii of gyration of the stabilizer chains, indicating that similar inhomogeneous blobs were generated across the sphere coronas.
When fitting vesicles comprising a binary mixture of PEG113 and PMPC28 stabilizer chains, two scenarios were considered when assessing the spatial distribution of these stabilizer chains across the inner and outer vesicle leaflets. Initially, SAXS patterns were fitted assuming a statistical distribution (f1 = 0.5) of PEG113 and PMPC28 stabilizer chains across the inner and outer leaflets (see Fig. 4C and the upper row of each PEG113 mol fraction between 0.5 and 0.9 in Table 1 for fitting results). Owing to the large number of parameters, RgPEG and RgPMPC were fixed at their estimated values of 2.6 nm and 1.4 nm, respectively. The second scenario involved fitting the segregation parameter, f1, using the data fit obtained in the first scenario as a starting point (see Fig. 4D and the lower row of each PEG113 mole fraction between 0.5 and 0.9 in Table 1 for fitting results). This conservative approach was adopted owing to the large number of parameters involved in the refined vesicle model. In addition, Rgblob and its related fitting parameter were fixed when fitting f1.
Clearly, the data fits achieved for both the first and second scenarios appear to be very similar (compare Fig. 4C and D). However, it is emphasized that the minimized chi-squared value was always reduced by about 5% in the latter case, with the vesicle radius (Rv), membrane thickness (Tm) and their associated polydispersities (σRv and σTm) varying very little when fitting f1 (Table 1). Given that the main contribution to the overall X-ray scattering comes from the hydrophobic PHPMA chains within the vesicle membranes rather than the hydrophilic PEG113 and PMPC28 stabilizer chains, this apparently modest reduction in the chi-squared value is considered to be significant. Thus, fitting f1 simply provides a statistically better fit, rather than revealing any new structural features arising from the microphase separation of the PEG113 and PMPC28 stabilizer chains across the vesicle membrane. Typically, f1 tended towards zero whenever this parameter was not constrained. According to Fig. 4B and Table 1, these very low f1 values determined for x = 0.6–0.9 indicate that the majority of the PMPC28 chains are located within the vesicle inner leaflet, suggesting substantial enthalpic incompatibility between the PEG113 and PMPC28 blocks. In the case of the (0.5 PEG113 + 0.5 PMPC28) − PHPMA400 formulation (i.e. x = 0.5 in Table 1, for which f1 = 0.14), a plausible explanation is that there are more PMPC28 chains than can be accommodated within the inner leaflet, causing some of these chains to occupy the outer leaflet despite the presence of the PEG113 chains. Alternatively, TEM analysis indicated that a minor population of spheres are also present in this case (Fig. 2), which might be expected to affect the f1 value [N.B. A satisfactory data fit could nevertheless be obtained using the modified vesicle model simply because the much smaller spheres make a negligible contribution to the X-ray scattering].
According to TEM analysis, the first pure vesicle phase is formed by the (0.6 PEG113 + 0.4 PMPC28) − PHPMA400 formulation. Interestingly, these vesicles also exhibit the lowest standard deviation (σRv) for the mean vesicle radius (Rv). In this case, the size polydispersity (which is calculated as a variance, i.e. σRv/Rv × 100%) is 13%. SAXS analysis indicates higher polydispersities as the PEG113 mole fraction is increased up to 0.9. Moreover, the f1 data fits suggest that optimum microphase separation is achieved for the (0.6 PEG113 + 0.4 PMPC28) − PHPMA400 formulation, which corresponds to the formation of vesicles with the lowest polydispersity. Thus, the above suggestion that the x = 0.5 formulation simply contains too many PMPC28 stabilizer chains to be accommodated within the inner leaflet of the vesicles seems to be physically reasonable. Conversely, the x = 0.7 formulation contains too few PMPC28 chains to fully occupy the inner leaflet, thus requiring some PEG113 chains to be co-located within the vesicle lumen. As the PEG113 mole fraction is increased, the PEG113 and PMPC28 chains are increasingly unable to maintain complete microphase separation across the membrane, despite the majority of the PMPC28 chains being located within the vesicle lumen. This suggests that the enthalpic incompatibility between the PEG113 and PMPC28 chains drives the formation of relatively small, low polydispersity vesicles.
The fitted Rgblob values for vesicles comprising both PEG113 and PMPC28 stabilizer blocks were comparable when assuming f1 = 0.5. These values are also similar to those determined for the spheres, indicating that similar inhomogeneous ‘blobs’ are produced within both types of coronal layers. In addition to confirming the formation of larger, more polydisperse vesicles when using higher PEG113 mole fractions (x > 0.7), SAXS analysis also indicated a monotonic (albeit modest) reduction in vesicle membrane thickness with increasing PEG113 mole fraction. The overall vesicle diameter was calculated using Dv = 2(Rv + 0.5Tm + 2RgPEG). RgPEG was used as the f1 data fits suggest that, in most cases, the vesicle outer leaflet contains solely PEG113 chains. Allowing for the effect of polydispersity, these SAXS-derived volume-average diameters are in reasonably good agreement with the z-average diameters reported by DLS (Table 1). As expected, the biggest deviations are observed for relatively large polydisperse vesicles, because DLS is more biased towards larger nano-objects.
Effect of pH and salt on colloidal stability of vesicles
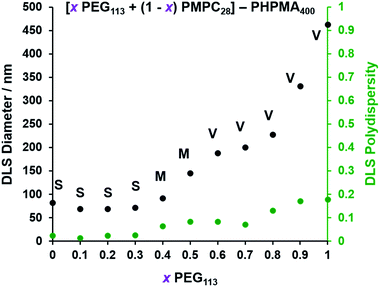
Electrophoretic mobility distributions (determined at pH 7.0) are shown for the PEG113–PHPMA400 vesicles, [0.6 PEG113 + 0.4 PMPC28] − PHPMA400 vesicles and PMPC28–PHPMA450 vesicles in Fig. 5A. The former vesicles have a relatively low mobility that lies close to zero (see blue distribution). In contrast, the latter vesicles exhibit a distinctly negative mobility owing to ionization of the terminal carboxylic acid group at pH 7.0 (see green distribution). Finally, the [0.6 PEG113 + 0.4 PMPC28] − PHPMA400 vesicles exhibit intermediate behavior, with a mobility closer to that of the PEG113–PHPMA400 vesicles (see red distribution). It is perhaps also worth emphasizing that the unimodal nature of this latter distribution is consistent with entropic mixing of the PEG113–PHPMA400 and PMPC28–PHPMA400 chains to form hybrid vesicles, rather than the formation of two distinct populations of PEG113–PHPMA400 and PMPC28–PHPMA400 nano-objects. Similar observations were reported by Semsarilar and co-workers when preparing hybrid vesicles using binary mixtures of polyelectrolytic and non-ionic steric stabilizers.111,112The corresponding zeta potential vs. pH curves determined for each type of vesicle are shown in Fig. 5B. These three curves are consistent with the mobility data. Thus, the PEG113–PHPMA400 vesicles exhibit zeta potentials close to zero, as expected for the non-ionic PEG chains. In contrast, the PMPC28–PHPMA450 vesicles exhibit quite strongly negative zeta potentials (e.g. −33 mV at pH 9) owing to ionization of the carboxylic acid end-group (pKa ∼ 4.7)92 on the PMPC chains. Finally, the hybrid [0.6 PEG113 + 0.4 PMPC28] − PHPMA400 vesicles exhibit only weakly negative zeta potentials (−16 mV at pH 9). This is consistent with most of the PMPC chains being preferentially located within the lumen, rather than being expressed at the outer leaflet of such vesicles.
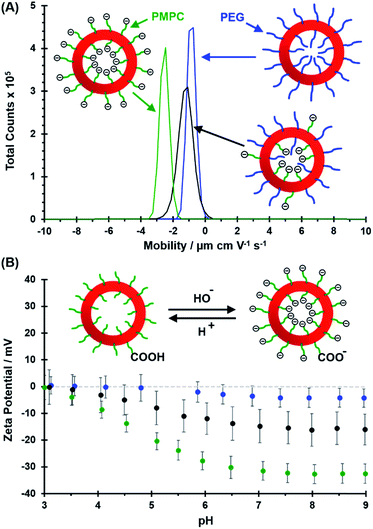
Fig. 6 shows the relative change in intensity-average diameter with added salt (up to 3.0 M ammonium sulfate) for PEG113–PHPMA400 vesicles (blue curve), [0.6 PEG113 + 0.4 PMPC28] − PHPMA400 vesicles (red curve), and PMPC28–PHPMA450 vesicles (green curve). All data are normalized to the intensity-average diameter of each type of vesicle as determined in deionized water. It is well known that PEG can be readily salted out in the presence of sulfate anions,113 whereas PMPC is highly tolerant to added salt up to 5 M.114,115 Thus the addition of just 0.50 M ammonium sulfate leads to a substantial increase in the apparent size of the PEG113–PHPMA400 vesicles, indicating significant flocculation. In contrast, the PMPC28–PHPMA450 vesicles remain colloidally stable even in the presence of 3.0 M ammonium sulfate. Importantly, the [0.6 PEG113 + 0.4 PMPC28] − PHPMA400 vesicles undergo incipient flocculation in the presence of 2.0 M ammonium sulfate. This suggests that most of the PEG chains are expressed at the outer leaflet of the vesicle membrane, which is consistent with the aqueous electrophoresis data shown in Fig. 5.
Conclusions
In summary, judicious use of a binary mixture of a relatively long non-ionic PEG steric stabilizer and a relatively short zwitterionic PMPC steric stabilizer enables the rational synthesis of rather small (<200 nm diameter) hybrid diblock copolymer vesicles with a relatively narrow size distribution (size polydispersity = 13–16%) at 10% w/w solids in aqueous solution via polymerization-induced self-assembly. Aqueous electrophoresis and salt-induced flocculation studies provide evidence for the relatively long PEG chains being preferentially expressed at the outer leaflet of the vesicle membrane. SAXS studies confirm that systematic variation of the relative proportions of the zwitterionic and non-ionic steric stabilizers is required to achieve optimal control over the vesicle size distribution. SAXS analysis also provides further evidence for confinement of most of the PMPC chains to the inner leaflet of the vesicles. Importantly, control experiments conducted using a binary mixture of chemically identical long and short PEG stabilizer blocks only produced relatively large vesicles which are less useful for potential biomedical applications. Thus, enthalpic incompatibility between the two types of steric stabilizers appears to offer a decisive advantage in this context. We anticipate that the reproducible and scalable synthesis of highly biocompatible small vesicles with relatively narrow size distributions reported herein will drive new developments in the field of nanobiotechnology.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. P. A. thanks EPSRC for an Established Career Particle Technology Fellowship (EP/R003009). S. P. A. and O. O. M. thank the University of Sheffield for an EPSRC DTA PhD studentship to support D. L. B. The authors are grateful to Diamond Light Source (Didcot, UK) for providing SAXS beam time (SM 21776-1) and the personnel of I22 station are thanked for their assistance. Dr N. J. W. Penfold is thanked for providing the PEG113 macro-CTA.Notes and references
- B. Charleux, G. Delaittre, J. Rieger and F. D'Agosto, Macromolecules, 2012, 45, 6753–6765 CrossRef CAS.
- N. J. Warren and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 10174–10185 CrossRef CAS PubMed.
- X. Wang and Z. An, Macromol. Rapid Commun., 2019, 40, 1800325 CrossRef PubMed.
- J. Tan, X. Li, R. Zeng, D. Liu, Q. Xu, J. He, Y. Zhang, X. Dai, L. Yu, Z. Zeng and L. Zhang, ACS Macro Lett., 2018, 7, 255–262 CrossRef CAS.
- B. Zhang, X. Lv, A. Zhu, J. Zheng, Y. Yang and Z. An, Macromolecules, 2018, 51, 2776–2784 CrossRef CAS.
- J. Tan, Q. Xu, X. Li, J. He, Y. Zhang, X. Dai, L. Yu, R. Zeng and L. Zhang, Macromol. Rapid Commun., 2018, 39, 1700871 CrossRef PubMed.
- Y. Zhang, Z. Wang, K. Matyjaszewski and J. Pietrasik, Macromol. Rapid Commun., 2019, 40, 1800331 CrossRef PubMed.
- J. Tan, H. Sun, M. Yu, B. S. Sumerlin and L. Zhang, ACS Macro Lett., 2015, 4, 1249–1253 CrossRef CAS.
- B. Karagoz, L. Esser, H. T. Duong, J. S. Basuki, C. Boyer and T. P. Davis, Polym. Chem., 2014, 5, 350–355 RSC.
- J. Yeow, O. R. Sugita and C. Boyer, ACS Macro Lett., 2016, 5, 558–564 CrossRef CAS.
- J. Rieger, Macromol. Rapid Commun., 2015, 36, 1458–1471 CrossRef CAS PubMed.
- S. L. Canning, G. N. Smith and S. P. Armes, Macromolecules, 2016, 49, 1985–2001 CrossRef CAS PubMed.
- Y. Pei, L. Thurairajah, O. R. Sugita and A. B. Lowe, Macromolecules, 2015, 48, 236–244 CrossRef CAS.
- L. A. Fielding, J. A. Lane, M. J. Derry, O. O. Mykhaylyk and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 5790–5798 CrossRef CAS PubMed.
- J. Tan, J. He, X. Li, Q. Xu, C. Huang, D. Liu and L. Zhang, Polym. Chem., 2017, 8, 6853–6864 RSC.
- A. B. Lowe, Polymer, 2016, 106, 161–181 CrossRef CAS.
- G. Mellot, P. Beaunier, J. M. Guigner, L. Bouteiller, J. Rieger and F. Stoffelbach, Macromol. Rapid Commun., 2019, 40, 1800315 CrossRef PubMed.
- P. Gurnani, C. P. Bray, R. A. E. Richardson, R. Peltier and S. Perrier, Macromol. Rapid Commun., 2019, 40, 1800314 CrossRef PubMed.
- Q. Zhang and S. Zhu, ACS Macro Lett., 2015, 4, 755–758 CrossRef CAS.
- C. Gao, H. Zhou, Y. Qu, W. Wang, H. Khan and W. Zhang, Macromolecules, 2016, 49, 3789–3798 CrossRef CAS.
- Z. An, Q. Shi, W. Tang, C. K. Tsung, C. J. Hawker and G. D. Stucky, J. Am. Chem. Soc., 2007, 129, 14493–14499 CrossRef CAS PubMed.
- J. Rieger, C. Grazon, B. Charleux, D. Alaimo and C. Jérôme, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 2373–2390 CrossRef CAS.
- S. Sugihara, S. P. Armes, A. Blanazs and A. L. Lewis, Soft Matter, 2011, 7, 10787–10793 RSC.
- Q. Xu, Y. Zhang, X. Li, J. He, J. Tan and L. Zhang, Polym. Chem., 2018, 9, 4908–4916 RSC.
- J. Tan, D. Liu, Y. Bai, C. Huang, X. Li, J. He, Q. Xu, X. Zhang and L. Zhang, Polym. Chem., 2017, 8, 1315–1327 RSC.
- L. D. Blackman, K. E. B. Doncom, M. I. Gibson and R. K. O'Reilly, Polym. Chem., 2017, 8, 2860–2871 RSC.
- X. Wang, J. Zhou, X. Lv, B. Zhang and Z. An, Macromolecules, 2017, 50, 7222–7232 CrossRef CAS.
- W. Zhou, Q. Qu, Y. Xu and Z. An, ACS Macro Lett., 2015, 4, 495–499 CrossRef CAS.
- C. A. Figg, R. N. Carmean, K. C. Bentz, S. Mukherjee, D. A. Savin and B. S. Sumerlin, Macromolecules, 2017, 50, 935–943 CrossRef CAS.
- C. A. Figg, A. Simula, K. A. Gebre, B. S. Tucker, D. M. Haddleton and B. S. Sumerlin, Chem. Sci., 2015, 6, 1230–1236 RSC.
- G. Liu, Q. Qiu, W. Shen and Z. An, Macromolecules, 2011, 44, 5237–5245 CrossRef CAS.
- G. Mellot, J. M. Guigner, L. Bouteiller, F. Stoffelbach and J. Rieger, Angew. Chem., Int. Ed., 2019, 58, 3173–3177 CrossRef CAS PubMed.
- Y. Li and S. P. Armes, Angew. Chem., Int. Ed., 2010, 49, 4042–4046 CrossRef CAS PubMed.
- S. Sugihara, A. Blanazs, S. P. Armes, A. J. Ryan and A. L. Lewis, J. Am. Chem. Soc., 2011, 133, 15707–15713 CrossRef CAS PubMed.
- A. Blanazs, J. Madsen, G. Battaglia, A. J. Ryan and S. P. Armes, J. Am. Chem. Soc., 2011, 133, 16581–16587 CrossRef CAS PubMed.
- P. Chambon, A. Blanazs, G. Battaglia and S. P. Armes, Macromolecules, 2012, 45, 5081–5090 CrossRef CAS.
- I. Canton, N. J. Warren, A. Chahal, K. Amps, A. Wood, R. Weightman, E. Wang, H. Moore and S. P. Armes, ACS Cent. Sci., 2016, 2, 65–74 CrossRef CAS PubMed.
- D. E. Mitchell, J. R. Lovett, S. P. Armes and M. I. Gibson, Angew. Chem., Int. Ed., 2016, 55, 2801–2804 CrossRef CAS PubMed.
- S. Monge, B. Canniccioni, A. Graillot and J. J. Robin, Biomacromolecules, 2011, 12, 1973–1982 CrossRef CAS PubMed.
- J. Madsen, S. P. Armes, K. Bertal, H. Lomas, S. MacNeil and A. L. Lewis, Biomacromolecules, 2008, 9, 2265–2275 CrossRef CAS PubMed.
- A. Blanazs, R. Verber, O. O. Mykhaylyk, A. J. Ryan, J. Z. Heath, C. W. I. Douglas and S. P. Armes, J. Am. Chem. Soc., 2012, 134, 9741–9748 CrossRef CAS PubMed.
- T. Ueda, H. Oshida, K. Kurita, K. Ishihara and N. Nakabayashi, Polym. J., 1992, 24, 1259–1269 CrossRef CAS.
- K. Ishihara, J. Biomed. Mater. Res., Part A, 2019, 107, 933–943 CrossRef CAS PubMed.
- S. I. Yusa, K. Fukuda, T. Yamamoto, K. Ishihara and Y. Morishima, Biomacromolecules, 2005, 6, 663–670 CrossRef CAS PubMed.
- Y. Iwasaki and K. Ishihara, Anal. Bioanal. Chem., 2005, 381, 534–546 CrossRef CAS PubMed.
- A. L. Lewis, Colloids Surf., B, 2000, 18, 261–275 CrossRef CAS PubMed.
- K. Ishihara, H. Nomura, T. Mihara, K. Kurita, Y. Iwasaki and N. Nakabayashi, J. Biomed. Mater. Res., 1998, 39, 323–330 CrossRef CAS PubMed.
- N. J. Warren, O. O. Mykhaylyk, D. Mahmood, A. J. Ryan and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 1023–1033 CrossRef CAS PubMed.
- N. J. W. Penfold, J. R. Whatley and S. P. Armes, Macromolecules, 2019, 52, 1653–1662 CrossRef CAS.
- S. Varlas, J. C. Foster, P. G. Georgiou, R. Keogh, J. T. Husband, D. S. Williams and R. K. O'Reilly, Nanoscale, 2019, 11, 12643–12654 RSC.
- L. D. Blackman, S. Varlas, M. C. Arno, A. Fayter, M. I. Gibson and R. K. O'Reilly, ACS Macro Lett., 2017, 6, 1263–1267 CrossRef CAS PubMed.
- Y. Zhang, J. He, X. Dai, L. Yu, J. Tan and L. Zhang, Polym. Chem., 2019, 10, 3902–3911 RSC.
- S. Sugihara, A. H. Ma'Radzi, S. Ida, S. Irie, T. Kikukawa and Y. Maeda, Polymer, 2015, 76, 17–24 CrossRef CAS.
- K. Ren and J. Perez-Mercader, Polym. Chem., 2017, 8, 3548–3552 RSC.
- N. Zaquen, J. Yeow, T. Junkers, C. Boyer and P. B. Zetterlund, Macromolecules, 2018, 51, 5165–5172 CrossRef CAS.
- J. Tan, D. Liu, X. Zhang, C. Huang, J. He, Q. Xu, X. Li and L. Zhang, RSC Adv., 2017, 7, 23114–23121 RSC.
- L. D. Blackman, S. Varlas, M. C. Arno, Z. H. Houston, N. L. Fletcher, K. J. Thurecht, M. Hasan, M. I. Gibson and R. K. O'Reilly, ACS Cent. Sci., 2018, 4, 718–723 CrossRef CAS PubMed.
- S. Varlas, L. D. Blackman, H. E. Findlay, E. Reading, P. J. Booth, M. I. Gibson and R. K. O'Reilly, Macromolecules, 2018, 51, 6190–6201 CrossRef CAS.
- J. R. Howse, R. A. L. Jones, G. Battaglia, R. E. Ducker, G. J. Leggett and A. J. Ryan, Nat. Mater., 2009, 8, 507–511 CrossRef CAS PubMed.
- C. S. Ho, J. W. Kim and D. A. Weitz, J. Am. Chem. Soc., 2008, 130, 9543–9549 CrossRef PubMed.
- L. Luo and A. Eisenberg, J. Am. Chem. Soc., 2001, 123, 1012–1013 CrossRef CAS PubMed.
- F. Liu and A. Eisenberg, J. Am. Chem. Soc., 2003, 125, 15059–15064 CrossRef CAS PubMed.
- A. Blanazs, M. Massignani, G. Battaglia, S. P. Armes and A. J. Ryan, Adv. Funct. Mater., 2009, 19, 2906–2914 CrossRef CAS.
- M. Huo, Z. Xu, M. Zeng, P. Chen, L. Liu, L. T. Yan, Y. Wei and J. Yuan, Macromolecules, 2017, 50, 9750–9759 CrossRef CAS.
- R. Stoenescu and W. Meier, Chem. Commun., 2002, 8, 3016–3017 RSC.
- A. Rank, S. Hauschild, S. Förster and R. Schubert, Langmuir, 2009, 25, 1338–1344 CrossRef PubMed.
- S. Hauschild, U. Lipprandt, A. Rumplecker, U. Borchert, A. Rank, R. Schubert and S. Förster, Small, 2005, 1, 1177–1180 CrossRef CAS PubMed.
- F. Li, S. Prévost, R. Schweins, A. T. M. Marcelis, F. A. M. Leermakers, M. A. Cohen Stuart and E. J. R. Sudhölter, Soft Matter, 2009, 5, 4169–4172 RSC.
- A. K. Brannan and F. S. Bates, Macromolecules, 2004, 37, 8816–8819 CrossRef CAS.
- O. Terreau, L. Luo and A. Eisenberg, Langmuir, 2003, 19, 5601–5607 CrossRef CAS.
- L. Luo and A. Eisenberg, Langmuir, 2001, 17, 6804–6811 CrossRef CAS.
- L. Luo and A. Eisenberg, Angew. Chem., Int. Ed., 2002, 41, 1001–1004 CrossRef CAS PubMed.
- C. Gonzato, M. Semsarilar, E. R. Jones, F. Li, G. J. P. Krooshof, P. Wyman, O. O. Mykhaylyk, R. Tuinier and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 11100–11106 CrossRef CAS PubMed.
- J. Du, Y. Tang, A. L. Lewis and S. P. Armes, J. Am. Chem. Soc., 2005, 127, 17982–17983 CrossRef CAS PubMed.
- J. Du, L. Fan and Q. Liu, Macromolecules, 2012, 45, 8275–8283 CrossRef CAS.
- K. K. Upadhyay, A. N. Bhatt, A. K. Mishra, B. S. Dwarakanath, S. Jain, C. Schatz, J. F. Le Meins, A. Farooque, G. Chandraiah, A. K. Jain, A. Misra and S. Lecommandoux, Biomaterials, 2010, 31, 2882–2892 CrossRef CAS PubMed.
- O. Onaca, R. Enea, D. W. Hughes and W. Meier, Macromol. Biosci., 2009, 9, 129–139 CrossRef CAS PubMed.
- H. Lomas, I. Canton, S. MacNeil, J. Du, S. P. Armes, A. J. Ryan, A. L. Lewis and G. Battaglia, Adv. Mater., 2007, 19, 4238–4243 CrossRef CAS.
- H. Lomas, J. Du, I. Canton, J. Madsen, N. J. Warren, S. P. Armes, A. L. Lewis and G. Battaglia, Macromol. Biosci., 2010, 10, 513–530 CrossRef CAS PubMed.
- I. Canton, M. Massignani, N. Patikarnmonthon, L. Chierico, J. Robertson, S. A. Renshaw, N. J. Warren, J. P. Madsen, S. P. Armes, A. L. Lewis and G. Battaglia, FASEB J., 2013, 27, 98–108 CrossRef CAS PubMed.
- Y. Xi, Y. Wang, J. Gao, Y. Xiao and J. Du, ACS Nano, 2019, 13, 13645–13657 CrossRef CAS PubMed.
- C. Zhang, Y. Zhu, C. Zhou, W. Yuan and J. Du, Polym. Chem., 2013, 4, 255–259 RSC.
- D. A. Wilson, R. J. M. Nolte and J. C. M. Van Hest, Nat. Chem., 2012, 4, 268–274 CrossRef CAS PubMed.
- A. Joseph, C. Contini, D. Cecchin, S. Nyberg, L. Ruiz-Perez, J. Gaitzsch, G. Fullstone, X. Tian, J. Azizi, J. Preston, G. Volpe and G. Battaglia, Sci. Adv., 2017, 3, e1700362 CrossRef PubMed.
- K. T. Kim, J. J. L. M. Cornelissen, R. J. M. Nolte and J. C. M. Van Hest, Adv. Mater., 2009, 21, 2787–2791 CrossRef CAS.
- A. Blanazs, N. J. Warren, A. L. Lewis, S. P. Armes and A. J. Ryan, Soft Matter, 2011, 7, 6399–6403 RSC.
- D. E. Discher and A. Eisenberg, Science, 2002, 297, 967–973 CrossRef CAS PubMed.
- Y. Mai and A. Eisenberg, Chem. Soc. Rev., 2012, 41, 5969–5985 RSC.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568 RSC.
- A. Blanazs, S. P. Armes and A. J. Ryan, Macromol. Rapid Commun., 2009, 30, 267–277 CrossRef CAS PubMed.
- A. Blanazs, A. J. Ryan and S. P. Armes, Macromolecules, 2012, 45, 5099–5107 CrossRef CAS.
- J. R. Lovett, N. J. Warren, L. P. D. Ratcliffe, M. K. Kocik and S. P. Armes, Angew. Chem., Int. Ed., 2015, 54, 1279–1283 CrossRef CAS PubMed.
- J. R. Lovett, N. J. Warren, S. P. Armes, M. J. Smallridge and R. B. Cracknell, Macromolecules, 2016, 49, 1016–1025 CrossRef CAS PubMed.
- When using a PEG113 mole fraction of 0.7 to 0.9, relatively narrow vesicle size distributions were obtained (i.e., DLS polydispersities were below 0.10). However, the mean vesicle diameter ranged from 600 nm to more than 1 μm, which is too large for certain biomedical applications such as intracellular delivery, see I. Canton and G. Battaglia, Chem. Soc. Rev., 2012, 41, 2718–2739 RSC.
- E. R. Jones, M. Semsarilar, P. Wyman, M. Boerakker and S. P. Armes, Polym. Chem., 2016, 7, 851–859 RSC.
- W. Sriprom, M. James, S. Perrier and C. Neto, Macromolecules, 2009, 42, 3138–3146 CrossRef CAS.
- N. A. Lynd and M. A. Hillmyer, Macromolecules, 2005, 38, 8803–8810 CrossRef CAS.
- S. J. Holder, R. C. Hiorns, N. A. J. M. Sommerdijk, S. J. Williams, R. G. Jones and R. J. M. Nolte, Chem. Commun., 1998, 14, 1445–1446 RSC.
- E. J. Cornel, S. Van Meurs, T. Smith, P. S. O'Hora and S. P. Armes, J. Am. Chem. Soc., 2018, 140, 12980–12988 CrossRef CAS PubMed.
- J. S. Pedersen, J. Appl. Crystallogr., 2000, 33, 637–640 CrossRef CAS.
- J. Bang, S. Jain, Z. Li, T. P. Lodge, J. S. Pedersen, E. Kesselman and Y. Talmon, Macromolecules, 2006, 39, 1199–1208 CrossRef CAS.
- J. S. Pedersen, I. W. Hamley, C. Y. Ryu and T. P. Lodge, Macromolecules, 2000, 33, 542–550 CrossRef CAS.
- Y. Takahashi and H. Tadokoro, Macromolecules, 1973, 6, 672–675 CrossRef CAS.
- L. J. Fetters, D. J. Lohsey and R. H. Colby, Physical Properties of Polymers Handbook, Springer, New York, 2nd edn, 2007 Search PubMed.
- L. J. Fetters, D. J. Lohse, D. Richter, T. A. Witten and A. Zirkel, Macromolecules, 1994, 27, 4639–4647 CrossRef CAS.
- J. S. Pedersen and M. C. Gerstenberg, Colloids Surf., A, 2003, 213, 175–187 CrossRef CAS.
- J. S. Pedersen, C. Svaneborg, K. Almdal, I. W. Hamley and R. N. Young, Macromolecules, 2003, 36, 416–433 CrossRef CAS.
- J. S. Pedersen, J. Chem. Phys., 2001, 114, 2839 CrossRef CAS.
- T. J. Neal, D. L. Beattie, S. J. Byard, G. N. Smith, M. W. Murray, N. S. J. Williams, S. N. Emmett, S. P. Armes, S. G. Spain and O. O. Mykhaylyk, Macromolecules, 2018, 51, 1474–1487 CrossRef CAS.
- J. Ilavsky and P. R. Jemian, J. Appl. Crystallogr., 2009, 42, 347–353 CrossRef CAS.
- M. Semsarilar, V. Ladmiral, A. Blanazs and S. P. Armes, Langmuir, 2012, 28, 914–922 CrossRef CAS PubMed.
- M. Semsarilar, V. Ladmiral, A. Blanazs and S. P. Armes, Langmuir, 2013, 29, 7416–7424 CrossRef CAS PubMed.
- F. E. Bailey and R. W. Callard, J. Appl. Polym. Sci., 1959, 1, 56–62 CrossRef CAS.
- K. Ishihara, M. Mu, T. Konno, Y. Inoue and K. Fukazawa, J. Biomater. Sci., Polym. Ed., 2017, 28, 884–899 CrossRef CAS.
- Z. J. Zhang, J. Madsen, N. J. Warren, M. Mears, G. J. Leggett, A. L. Lewis and M. Geoghegan, Eur. Polym. J., 2017, 87, 449–457 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, copolymer characterization techniques, supporting figures: assigned 1H NMR spectra, GPC curves, tabulated GPC data, DLS phase diagram for [xPEG113 + (1 − x) PEG45] − PHPMA400 nano-objects, TEM images for [xPEG113 + (1 − x) PEG45] − PHPMA400 vesicles and tabulated ammonium sulfate solution viscosities. See DOI: 10.1039/d0sc01320j |
| This journal is © The Royal Society of Chemistry 2020 |