Open Access Article
Open Access ArticleDemonstration of green hydrogen production using solar energy at 28% efficiency and evaluation of its economic viability†
M. A.
Khan
 *,
I.
Al-Shankiti
,
A.
Ziani
and
H.
Idriss
*,
I.
Al-Shankiti
,
A.
Ziani
and
H.
Idriss
 *
*
Hydrogen Platform, SABIC-CRD, King Abdullah University of Science and Technology (KAUST), Thuwal 23955, Saudi Arabia. E-mail: mohd.khan1@ucalgary.ca; IdrissH@SABIC.com
First published on 6th January 2021
Abstract
The solar to hydrogen (STH) efficiency of photovoltaic-electrolysis (PV-E) setups is a key parameter to lower the cost of green hydrogen produced. Commercial c-Si solar cells have neared saturation with respect to their efficiency, which warrants the need to look at alternative technologies. In this work, we report a concentrator photovoltaic-electrolysis (CPV-E) setup with a STH efficiency of 28% at 41 suns (without the use of Fresnel lenses), the highest reported efficiency using an alkaline system to date. Using this as a base case, we carried out a detailed techno-economic (TEA) analysis, which showed that despite the high cost associated with CPV cells, the levelized cost of hydrogen (LCOH) is at $5.9 kg−1, close to that from c-Si solar farms ($4.9 kg−1), primarily due to the high STH efficiency. We also report sensitivity analysis of factors affecting both CPV and alkaline electrolyser systems such as the CPV module efficiency and installed capacity, electrolyser stack lifetime, operating current density, and working hours. Our results indicate that in a scenario where the installed capacity of CPV technology matches that of silicon and with an electrolyser operating current density of ∼0.7 A cm−2, the LCOH from CPV-electrolysis systems can be <$2 kg−1. These results demonstrate the potential of CPV technology for large-scale green hydrogen production to replace that obtained from fossil fuels.
1. Introduction
Molecular hydrogen as an energy vector helps in decarbonizing our energy system in order to achieve the emission reduction goals, for example as stated in the Paris Agreement. To make a meaningful difference and achieve net zero emissions, hydrogen will have to be produced via water splitting using renewable electricity. Solar photovoltaic (PV) power represents one of the cheapest and most widely deployed sources of renewable electricity with over 520 GW of cumulative installed capacity worldwide as of 2018.1,2 For that reason, it is considered as the prime vector of energy to power green hydrogen production. While there are other methods of solar hydrogen production such as photocatalytic reactions3 and direct photo-electrochemical water splitting,4,5 present day technology is only available for decoupled PV-electrolysis (PV-E) systems. Silicon based PV cells dominate the market with ∼95% share of current production,1 and have seen their cost dropping significantly in the last few years. Nonetheless, the estimated cost of green H2 from silicon-based PV-E is still very high for sustainable production. It varies widely depending on the nature and level of studies: $3–17 kg−1,6 $12 kg−1,7 and $12–16 kg−1,8,9 among others. The cost of green H2 produced depends on several factors such as module and tracker cost, electrolyser stack cost, balance of system (BOS) and balance of plant (BOP) cost, operation and maintenance (O & M) cost and system efficiency.7,10,11 Out of all these factors the system efficiency or in other words the solar to hydrogen (STH) efficiency directly influences all the other factors and can lead to significant reduction in size of PV and electrolyser plants.10 Silicon PV cells are close to reaching their theoretical efficiencies of ∼30% which means that there is not much scope of increasing the STH efficiency with silicon PV.12 Unlike silicon PV, concentrator photovoltaic cells (CPV) based on III–V group elements have already reached a much higher efficiency of ∼47% (4J cell)13 and theoretically can reach over 80% efficiency.14–16 At a modular level, 43.4%16 and 43%17 efficient CPV modules have been demonstrated with a projected modular efficiency of 47% by 2035.16–18 Moreover they can operate at high light concentrations (>1000 suns) largely compensating for the higher manufacturing cost.16The high efficiency of CPV cells has encouraged researchers to explore CPV-electrolysis (CPV-E) setups in recent years. For instance, Chang and co-workers reported a STH efficiency of ∼20.6% using a single junction GaAs PV cell coupled to a proton-exchange-membrane (PEM) electrolyser using a DC–DC convertor.19 Nakamura and co-workers reported a STH efficiency of 24.4% using a CPV-E system, without the use of power electronics.20 The power matching was done by optimizing the ratio of the number of electrolysers to CPV cells. The highest STH efficiency (∼31%) was reported on a laboratory scale through direct coupling of two PEM electrolysers with one CPV cell, operating at 42 suns.21 All these previous reports coupled CPV cells with PEM electrolysers which are expensive with high stack and BOP costs.11,22 Moreover, there are no reports on techno-economic analysis (TEA) of CPV-E systems, to investigate the effect of using high efficiency CPV cells on the cost of H2 produced, which was the primary motivation to move away from silicon solar cells.
In this work, we give experimental evidence of the potential of CPV cells for achieving high STH efficiency and subsequently analyse the effect of efficiency and economy of scale on H2 cost.
(1) Specifically, we used triple junction (3J) InGaP/InGaAs/Ge CPV cells connected to alkaline electrolysers. With appropriate power matching, and without a DC–DC converter, it was possible to achieve a STH efficiency of 28% under 41 suns, which is the highest efficiency reported to date for PV cells coupled with alkaline electrolysers.
(2) Using this as a base case, we carried out a TEA analysis of cost of H2 produced assuming a commercial CPV farm (module efficiency ∼41%) coupled with an alkaline electrolyser plant (electrolyser efficiency ∼70%), thus operating at 28% plant or STH efficiency. The levelized cost of H2 under these base case conditions was ∼5.9 $ kg−1 and expected to go down to 5.6 $ kg−1, at a STH efficiency of 31.5%. In comparison, the cost of hydrogen when using silicon PV modules (module efficiency ∼17.5%) was calculated to be ∼4.9 $ kg−1.
(3) We have also projected the cost of CPV modules, trackers and associated H2 as a function of cumulative installed capacity. At a learning rate of 18%, the cost of H2 from CPV-E setups could go down to 2.65 $ kg−1 if the cumulative installed capacity exceeds >100 GW in a range like silicon PV cells.
We hope that the experimental results obtained (STH efficiency = 28%), stable performance, followed by TEA, will encourage researchers, governments, and companies to explore CPV-E setups for large-scale green H2 production.
2. Methodology
a. PV-E setup
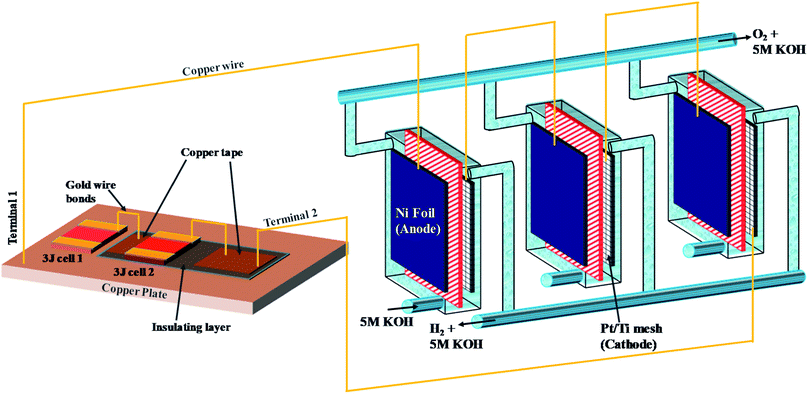
The PV-E experimental setup was designed as shown in Scheme 1. Alkaline electrolysers were fabricated using poly(methyl methacrylate) (PMMA) sheets, ideal for use under alkaline conditions. An alkaline anion exchange membrane (Sustainion® 37–50) with area ∼12.25 cm2 was used for ion transfer and gas separation, Nickel foil (Alfa Aesar, 99.5% purity, 0.25 mm thick) was used as the anode. A platinum film (Kurt J. Lesker, 99.99% pure target, 10 nm thick) was sputtered onto both sides of a porous titanium mesh used as the cathode. The geometric area of the anode and cathode was the same as that of the anion exchange membrane. Triple junction (3J) GaInP/GaInAs/Ge CPV cells (3.0 × 3.0 mm2) from Azure Space (type 3C44C) were used as the photoabsorbers. The first CPV cell was mounted onto an air-cooled copper plate using silver paste (High Purity Silver paint, SPI-Paint, 43% Ag solid, bulk resistivity 3 × 10−7 Ω m) due to its high thermal and electrical conductivity. The silver paste was dried in an oven at 70 °C for 2 hours. To make a series connection, the second CPV cell was insulated from the copper plate using a polyimide tape. The electrical connections as shown in the schematic were realised using ball wire bonding with 25 μm gold wire (HB16, TPT Wire Bonder GmbH & Co). The two CPV cells are coupled with three alkaline electrolysers connected in series using copper wires. The electrolyte (5 M KOH) flow was split between the three electrolysers and H2/O2 gases were collected and measured volumetrically (their purity was independently confirmed with gas chromatography (GC) as a routine check).b. Techno-economic analysis
To estimate the return on capital investment for the development of a CPV-E facility, a discounted cash flow spreadsheet was developed to calculate the capital expenditure (CAPEX), annual operating expenditure (OPEX) and revenue over the project lifetime (see ESI† tables). It was assumed that land acquisition, CAPEX allocation and construction of the plant were completed in the first three years, with plant operation beginning in the fourth year. A nominal interest rate (NIR) of 12% was used in the study, while the working capital was assumed to be 15% of the capital investment. A plant lifetime of 20 years was taken based on the typical lifetime of PV cells while the cost of storage and transportation of hydrogen was not considered in this study.7,23 The analysis was designed for a plant based in the city of Tabuk in Saudi Arabia, operating for 9.1 hours per day without grid support and for a production capacity of 50 ton H2 per day at a pressure of 20 bars. The region of Tabuk was chosen for its high daily average sunshine (9.1 hours),24 a low population density (6 km−2), and high direct normal irradiance (DNI) of ∼7.37 kW h m−2.25 The electricity price needed to run pumps, power electronics and other utilities was taken at 0.05 $ kW−1 h−1 (unless otherwise stated). The process contingency in this analysis uses 20% of direct costs due to the greater uncertainties in the system configuration.26 The indicated process and economic assumptions are summarized in Table 1 (more details are given in the ESI† tables). The capital and utility costs of compressors and pumps were modelled using Aspen Plus. The levelized cost of hydrogen (LCOH) also known as the minimum selling price (MSP) was calculated by adjusting its value such that the net present value (NPV) of the capital and operating expenses and product revenue are summed to zero (eqn (1)–(3)). | (1) |
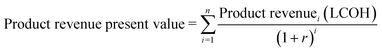 | (2) |
| NPV = 0 = product revenue PV − (operating cost PV + capital expenses) | (3) |
| Location | Tabuk, KSA |
|---|---|
| Process parameters | |
| Total production (ton per day) | 50 |
| Sunshine hours (hours per day)24 | 9.1 |
| H2 production rate (ton per h) | 5.49 |
| Annual working days (days per year) | 333 |
| H2 production rate (ton per year) | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 650 |
| Solar irradiation (kW h m−2)25 | 7.37 |
| Energy per kg of H2 (kW h kg(H2)−1) – LHV | 32.66 |
| Required electricity for utilities (kW h per ton H2) | 161 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Economic parameters | |
| Plant lifetime (years)7,23 | 20 |
| Discount rate (r) (%) | 12 |
| Land cost ($ km−2)26 | $123![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 497.00 497.00 |
| CO2 credit ($ per ton CO2)11,28,29 | 50 |
| O2 credit ($ per ton O2)30 | 40 |
| Electricity price ($ kW−1 h−1) | 0.05 |
| Contingency | 20% |
3. Results and discussion
a. Experimental results
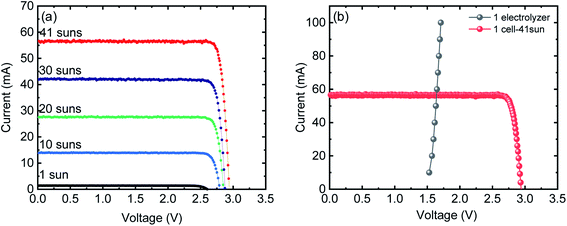
Fig. 1(a) shows the current–voltage (I–V) characteristics of the InGaP/InGaAs/Ge 3J CPV cell (3 × 3 mm2) from Azur Space under one and multiple suns up to 41-sun illumination. The cell was mounted onto an air-cooled copper plate, maintaining the temperature at ∼25 °C. An Asahi Spectra 320 W solar simulator (350–1800 nm) was used as the light source and the irradiation was adjusted by the distance to the device and the power of the solar simulator. The one sun light flux was verified using a pre-calibrated monocrystalline silicon reference cell (Newport, 91150-KG5). Following a standard method for characterizing CPV cells, we used the ratio of the short circuit currents to confirm that the cell was illuminated with 41 suns. Under 41 suns (obtained directly from solar simulation without the use of external light concentrators such as Fresnel lenses), the short circuit current and open-circuit voltage (Voc) were 56.50 mA and 2.93 V, respectively. At the maximum power point (MPP), the voltage (VMPP) and current (IMPP) were 2.70 V and 55.62 mA, respectively. The calculated fill factor (FF) and solar-to-electricity or PV cell efficiency was 0.90 and 40.7% under these operating conditions. More information on the Azur space cells is given in Fig. S1 and S2 of the ESI.† We have opted not to use Fresnel lenses in this work to minimize losses, and therefore the highest possible sun concentration obtained directly from the solar simulator was 41 suns. To increase the sun light flux the use of Fresnel lenses is needed and with them associated losses which depend very much on their materials nature (quality) and configuration.27 We have previously observed that the use of Fresnel lenses as light concentrators led to additional optical losses up to 30%5 without optimization, although further improvement was made possible, dropping the loss to ca. 15%.4Fig. 1(b) overlaps the I–V characteristics of a single alkaline electrolyser and the CPV cell. The I–V curve of the electrolyser was generated using chrono-potentiometry (CP) measurements performed at different current densities. The cross-point of the electrolyser I–V curve and the solar cell I–V curve is the system coupling point and specifies the operating voltage (VOP) and current (IOP) of the system, which was ∼1.66 V and 56.3 mA respectively. Since the VMP of the CPV cell under 41 suns is ∼2.70 V, there is an additional 1.04 V that results in energy wasted as heat rather than stored in H2 chemical bonds. Based on the operating current (IOP), the maximum STH efficiency of the system calculated using eqn (4) was found to be ∼18.7% based on 100% faradaic efficiency (ηF).
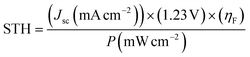 | (4) |
While the additional 1.04 V is not enough to run another electrolyser, the limitation can be overcome by coupling multiple PV and/or electrolyser units connected in series, to match the voltage characteristics of the components.20
Fig. 2(a) shows the I–V characteristics of two InGaP/InGaAs/Ge 3J CPV cells (3 × 3 mm2) connected in series, under 41-sun illumination. As expected upon using two cells in series, the current remained unchanged, but the total voltage increased. At the MPP, the VMPP and IMPP were 5.29 V and 55.18 mA, respectively. The configuration of the three electrolysers in terms of electro-catalysts, membranes and electrolyte conductivity was designed to match the characteristics of the two cells. Overlapping with the I–V curves of the three alkaline electrolysers connected in series resulted in a VOP and IOP of 5.02 V and 56.21 mA, respectively. Thus, it is possible to utilize the extra voltage from the two cells and run a third electrolyser. Fig. 2(b) shows the H2 and O2 production rates from the system, presented in Scheme 1, under 41 sun-illumination. There was stoichiometric production of H2 and O2 in 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio at a STH efficiency of ∼28%, which was calculated using eqn (5):
1 ratio at a STH efficiency of ∼28%, which was calculated using eqn (5):
 | (5) |
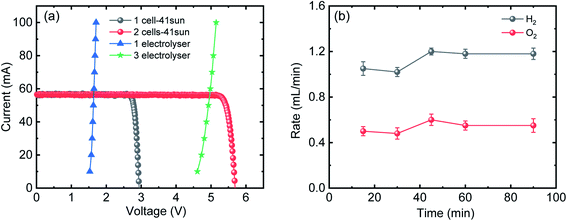 | ||
| Fig. 2 (a) I–V curves of one (grey) and two 3J CPV cells (red) connected in series under 41-sun illumination overlapped with I–V curves of single (blue) and three (green) alkaline electrolysers connected in series. (b) H2 and O2 production rates from three alkaline electrolysers connected in series. Power is supplied from two CPV 3J cells connected in series under 41-sun illumination (without the use of Fresnel lenses to minimize further losses) as shown in Scheme 1. | ||
b. TEA results for the base case
A STH efficiency of 28% is the highest reported for PV cells coupled to alkaline electrolysers. As mentioned earlier, the STH efficiency is an important driver for researchers and directly affects H2 cost. Using this as a base case, we have conducted TEA for green hydrogen production using a CPV-E system working at an STH efficiency of 28.7%. As a reference, the same analysis was done for H2 produced using conventional c-Si PV technology. The process and economic parameters were identical in both cases; these are summarized in Table 1.Table 2 shows the CPV farm and electrolyser plant parameters used for the base case study. Based on a H2 production capacity of 50 ton per day, the PV farm and electrolyser plant were sized at ∼256.3 MW based on an electrolysis efficiency of 70%, and 9.1 hours daily operation, using eqn (6).
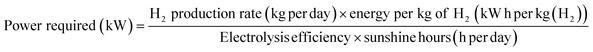 | (6) |
| PV parameters | CPV | Silicon |
|---|---|---|
| Power needed for solar farm (kW) | 256![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 357.92 357.92 |
256![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 357.92 357.92 |
| Module efficiency (%) | 41 | 12% (17.5 × 0.685) |
| Sunlight concentration | 820 | 1 |
| Tracker | Dual axis | Single axis |
| Land or PV packing factor31 | 4 | 3 |
| Module and tracker cost ($ W−1) | 0.72 (ref. 32) | 0.50 (ref. 33 and 34) |
| Design, labour, permitting and installation ($ W−1) | 0.43 | 0.30 |
| PV inverter cost ($ W−1)34 | 0.08 | 0.07 |
| PV O & M cost (USD per kW h)34 | 0.008 | 0.008 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Electrolyser plant parameters | ||
| Electrolyser plant size (kW) | 256![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 357.92 357.92 |
|
| Electrolyser efficiency (%)9,11 | 70% | |
| Electrolyser O & M (% of total uninstalled CAPEX)7,23 | 3% | |
| Stack cost ($ kW−1)22 | 272 | |
| Balance of plant (BOP) capital cost ($ kW−1)11,22 | 272 | |
| H2 loss due to separation | 3.0% | |
| Electrolyser installation factor35 | 12.0% | |
| Electrolyte needed (ton per ton H2) | 10 | |
| Electrolyser replacement factor7,35 | 1.5% | |
The CPV module cost as a function of efficiency was taken from an analysis performed by the National Renewable Energy Laboratory (NREL) in 2015,32 operating at high concentrations of ∼830× and was further verified with industrial input/private communication from CPV module manufactures (BSQ, Spain).32,36 The cost of the dual axis tracker needed for CPV modules was taken at ∼50% of the module cost, based on industrial input/private communication (BSQ, Spain).36 The cost of labour, design, permitting and interconnection of the PV solar farm was taken as an average from various reported installed projects.37 At a module efficiency of 41%, the CPV module cost would be ∼0.48 $ W−1 with a dual axis tracker cost of 0.24 $ W−1.32 In contrast highly efficient (17.5%) c-Si modules are much cheaper with module costs at 0.3 $ W−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 and tracker costs of 0.2 $ W−1.33,34 It is important to note here that CPV modules are known to maintain >90% of their efficiency throughout the day while c-Si modules with single axis tracking only maintain their efficiency of ∼60–70% of the day.38,39 Moreover, silicon PV cells are temperature-sensitive with a temperature coefficient of about −0.5% per °C, which means that for every degree above 25° it loses 0.5% of performance.40,41 Thus, for accuracy, the average module efficiency of c-Si was taken as 12% (17.5 × 0.685). The average packing factor or land factor was taken as 4, which is the standard for CPV farms with dual axis trackers and 3 for c-Si farms with single axis tracking.31 This land factor is the ratio of actual land area to PV array area and encompasses space requirements for pumps, compressors, heat exchangers, a control room, and access roads.
33 and tracker costs of 0.2 $ W−1.33,34 It is important to note here that CPV modules are known to maintain >90% of their efficiency throughout the day while c-Si modules with single axis tracking only maintain their efficiency of ∼60–70% of the day.38,39 Moreover, silicon PV cells are temperature-sensitive with a temperature coefficient of about −0.5% per °C, which means that for every degree above 25° it loses 0.5% of performance.40,41 Thus, for accuracy, the average module efficiency of c-Si was taken as 12% (17.5 × 0.685). The average packing factor or land factor was taken as 4, which is the standard for CPV farms with dual axis trackers and 3 for c-Si farms with single axis tracking.31 This land factor is the ratio of actual land area to PV array area and encompasses space requirements for pumps, compressors, heat exchangers, a control room, and access roads.
The total CAPEX of alkaline electrolysers was taken at ∼544 $ kW−1, considering multi stack systems operating at full load hours.22 The stack cost contributes ∼50% to the electrolyser CAPEX, while 50% is for BOP which consists of a gas management system, electrolyte delivery system, thermal management and power electronics.11 For the base case scenario, the electrolyser replacement factor was calculated assuming a change of the electrolyser stack every 7 years, which means two changes throughout a plant lifetime of 20 years.7,35 The stack replacement cost is taken as 15% of the total electrolyser CAPEX; an annual electrolyser replacement factor of ∼1.5%.7
Table 3 and Fig. 3 present the base case results of the TEA analysis following the assumptions listed in Table 2. The total CAPEX of the CPV and electrolyser plants was $571![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 439
439![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525.79, with the CPV solar farm cost being the dominant factor (55.27%) due to the current high costs of CPV modules. The CAPEX costs for the c-Si solar farm were less at $464
525.79, with the CPV solar farm cost being the dominant factor (55.27%) due to the current high costs of CPV modules. The CAPEX costs for the c-Si solar farm were less at $464![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 326
326![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 667.85 primarily due to cheaper modules. The module cost is determined by several factors out of which the dominant ones are the module efficiency, cell costs ($ m−2), manufacturing yield, assembly costs and scale of manufacturing.32 While CPV cells are twice efficient compared to silicon cells, they are more expensive (∼12
667.85 primarily due to cheaper modules. The module cost is determined by several factors out of which the dominant ones are the module efficiency, cell costs ($ m−2), manufacturing yield, assembly costs and scale of manufacturing.32 While CPV cells are twice efficient compared to silicon cells, they are more expensive (∼12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 $ m−2versus ∼70–80 $ m−2).32,42 In recent years with the commercialization of high concentration technology (>800 suns), the effect of CPV cell cost has diminished. Currently the biggest hurdle for CPV modules is the scale of manufacturing which will also reduce assembly costs. The role of economy of scale will be discussed in Fig. 4. Another major difference in CAPEX costs is the land costs of ∼$381,375.86 for a CPV farm versus $977
000 $ m−2versus ∼70–80 $ m−2).32,42 In recent years with the commercialization of high concentration technology (>800 suns), the effect of CPV cell cost has diminished. Currently the biggest hurdle for CPV modules is the scale of manufacturing which will also reduce assembly costs. The role of economy of scale will be discussed in Fig. 4. Another major difference in CAPEX costs is the land costs of ∼$381,375.86 for a CPV farm versus $977![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 275.64 for a c-Si farm, arising due to the lower efficiency c-Si modules. Since the land is very cheap, because of the location (Table 1), the total land cost is a very small fraction (<1%) of the total CAPEX for both technologies and does not affect the final cost of H2 a great deal. However, the availability of land and its cost in other locations might be a critical factor, in densely populated areas, with the c-Si solar farm needing about 2.5 times more land area than the CPV farm.
275.64 for a c-Si farm, arising due to the lower efficiency c-Si modules. Since the land is very cheap, because of the location (Table 1), the total land cost is a very small fraction (<1%) of the total CAPEX for both technologies and does not affect the final cost of H2 a great deal. However, the availability of land and its cost in other locations might be a critical factor, in densely populated areas, with the c-Si solar farm needing about 2.5 times more land area than the CPV farm.
| CAPEX | CPV | Silicon PV |
|---|---|---|
| Total PV cost ($) | $315![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 832![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967.03 967.03 |
$225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 594 594![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976.45 976.45 |
| Total electrolyser capital ($) | $156![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 193 193![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 758.24 758.24 |
$156![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 193 193![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 758.24 758.24 |
| Gas processing ($) | $4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 143 143![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572.97 572.97 |
$4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 143 143![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572.97 572.97 |
| Electrolyte processing ($) | $29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306.58 306.58 |
$29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306.58 306.58 |
| Land cost ($) | $381![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375.86 375.86 |
$977![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 275.64 275.64 |
| Contingency (%) | $94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 858 858![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545.11 545.11 |
$77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 387 387![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 777.97 777.97 |
| Total CAPEX ($) | $571![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 439 439![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525.79 525.79 |
$464![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 326 326![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 667.85 667.85 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| OPEX | ||
| Annual PV maintenance ($ per year) | $18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662.86 662.86 |
|
| Compressor ($ per year) | $393![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477.73 477.73 |
|
| Water pump ($ per year) | $20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755.22 755.22 |
|
| Annual water cost ($ per year) | $216![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450.00 450.00 |
|
| O & M of electrolyser ($ per year) | $4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 183 183![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761.38 761.38 |
|
| Annual electrolyser replacement ($ per year) | $2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342 342![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 906.37 906.37 |
|
| Annual electricity cost for utilities ($ per year) | $134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032.50 032.50 |
|
| Annual staff cost ($ per year) | $1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 598 598![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400.00 400.00 |
|
| Total OPEX ($ per year) | $8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 908 908![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 446.06 446.06 |
|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| LCOH ($ per kg) | $5.9 | $4.9 |
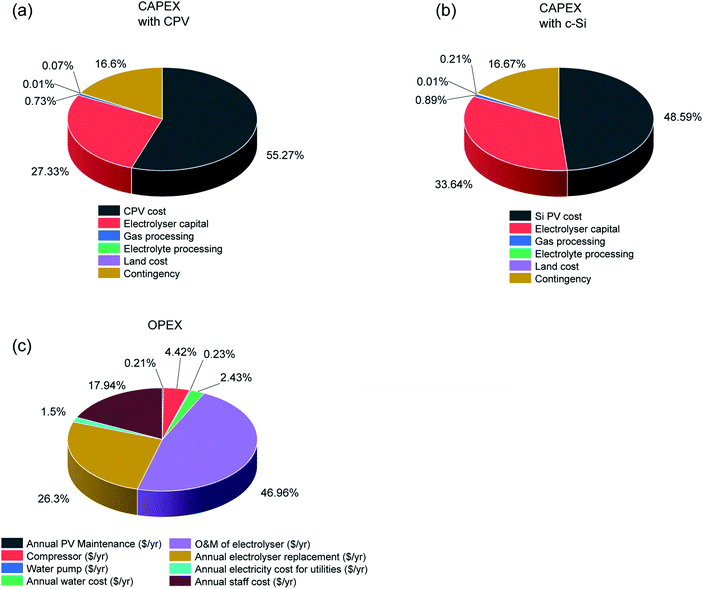 | ||
| Fig. 3 Breakdown of total capex for a CPV (a) and c-Si PV (b) powered electrolysis process to produce 50 tons H2 per day using the assumptions listed in Tables 1 and 2. (c) Annual OPEX for both technologies i.e. CPV-E and c-Si PV-E. | ||
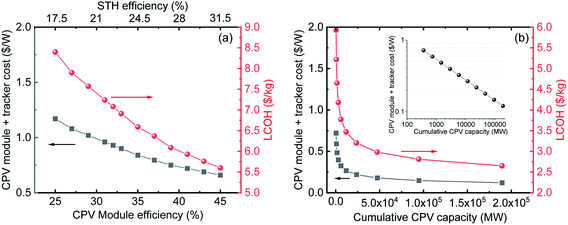 | ||
| Fig. 4 (a) Module + tracker costs (left) and cost of H2 (right) as a function of CPV module efficiency (bottom) and STH efficiency (top). (b) Module + tracker costs (left) and cost of H2 (right) as a function of projected cumulative CPV capacity (bottom). For both projections, the electrolyser efficiency, CAPEX and OPEX were kept constant as mentioned in Tables 2 and 3. | ||
The annual OPEX of $8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 908
908![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 446 is identical for both systems; with electrolyser O & M and electrode replacement cost the dominant factors at 46.96% and 26.3%, respectively. Currently, the electrolyser market is also relatively small with total worldwide installed capacity in the MW scale.11 With increase in production and global cumulative installations, the electrolyser O & M costs are expected to drop.11 The electrode replacement costs will come down with development of catalysts with improved stability and efficiency. The effect of catalyst lifetime on the H2 price is discussed in Fig. 5. The revenue stream mainly consists of income from H2 (∼91%) with a small fraction from O2 and CO2 credit (∼9%) (the CO2 credit is based on the CO2 released while making hydrogen from methane (5.5 times the amount of hydrogen per weight) without considering process energy consumption as per the equation: CH4 + 2H2O → 4H2 + CO2). After calculating the CAPEX, OPEX and revenue, we determined the LCOH using a discounted cash flow method and the economic assumptions and parameters listed in Table 1. The LCOH at which the NPV is zero was ∼5.9 $ kg−1 for the CPV-E process and ∼4.9 $ kg−1 for the c-Si PV-E setup (Table 3).
446 is identical for both systems; with electrolyser O & M and electrode replacement cost the dominant factors at 46.96% and 26.3%, respectively. Currently, the electrolyser market is also relatively small with total worldwide installed capacity in the MW scale.11 With increase in production and global cumulative installations, the electrolyser O & M costs are expected to drop.11 The electrode replacement costs will come down with development of catalysts with improved stability and efficiency. The effect of catalyst lifetime on the H2 price is discussed in Fig. 5. The revenue stream mainly consists of income from H2 (∼91%) with a small fraction from O2 and CO2 credit (∼9%) (the CO2 credit is based on the CO2 released while making hydrogen from methane (5.5 times the amount of hydrogen per weight) without considering process energy consumption as per the equation: CH4 + 2H2O → 4H2 + CO2). After calculating the CAPEX, OPEX and revenue, we determined the LCOH using a discounted cash flow method and the economic assumptions and parameters listed in Table 1. The LCOH at which the NPV is zero was ∼5.9 $ kg−1 for the CPV-E process and ∼4.9 $ kg−1 for the c-Si PV-E setup (Table 3).
c. Sensitivity analysis
To understand the effect of various parameters on the LCOH, a sensitivity analysis was performed. We first analysed the effect of two factors critical for CPV technology. These are (i) CPV module efficiency and (ii) economy of scale or cumulative installed capacity. As mentioned earlier, CPV cells have the potential to reach a theoretical efficiency of over 80%; and 60% cell efficiency is a real possibility in the next few years. The analysis is for CPV module efficiencies ranging from 25 to 45% as 43.4%16 and 43%17 efficient modules have already been demonstrated on a laboratory scale with projections of a 47% efficient module commercially available by 2035.16–18 A higher efficiency means higher output power per unit area which directly translates into lower cost ($ W−1) or in other words, a smaller cell area is needed to reach the same output power. Therefore, it is important to analyse the effect of increase in CPV module efficiency on the levelized cost of H2. Using an analysis by NREL on the effect of efficiency on CPV module costs, we calculated the cost of H2 at different module efficiencies or STH efficiencies.28 For these calculations, we have assumed a fixed electrolyser efficiency of 70% and costs, as listed in Table 2. Fig. 4(a) shows the dependence of the “CPV module plus tracker cost” as well as the “LCOH” (y-axes) on the “CPV module efficiency” and “STH efficiency” (x-axes). We notice that the efficiency of the system reduces the total CAPEX in different ways. In addition to the expected reduction in modular costs a noticeable reduction in trackers cost, labour, installation, maintenance and of the land costs occurs. This results in reduction in the cost of H2 from ∼8.4 $ kg−1 at a STH efficiency of 17.5% to ∼5.6 $ kg−1 at 31.5% STH efficiency as seen in Fig. 4(a).The analysis in Fig. 4(a) is based on the effect of increasing efficiency on lowering module cost and LCOH. The decrease of the CPV module + tracker cost with increasing the CPV module efficiency is primarily due to the use of fewer materials, as indicated above. With further momentum on the use of CPV technology, significant cost reductions can be expected due to the economy of scale. As an example, in the last 40 years c-Si technology has seen prices going down from ∼80 $ W−1 to ∼0.3 $ W−1 as cumulative capacity increased from ∼5 MW to 500 GW, leading to a learning rate (LR) of ∼28%.33 In the last year, Si-PV module prices have reached a plateau while CPV has still a very large price drop potential. CPV systems have seen a LR of ∼18% which can be used to project module costs as cumulative capacity increases.43 Currently, the cumulative capacity of CPV farms is only around 370 MW,16 with module and tracker costs of ∼0.72 $ W−1. Using this as a starting point and LR of 18% we have projected prices to go down to ∼0.12 $ W−1 if the cumulative capacity increases up to ∼189 GW (see Table 4 and inset of Fig. 4(b)). The CPV modules were kept constant for these projections. Based on these projected costs, we have also calculated the LCOH as shown in Fig. 4(b). We observe a significant reduction in LCOH from 5.9 $ kg−1 currently to ∼2.6 $ kg−1 when module prices go down to ∼0.12 $ W−1. It is important to note that the projections presented in Fig. 4 are based solely on reduction in CPV module prices without considering the foreseen drop in electrolyser costs. The combined effect of improvement in CPV and electrolyser performance on LCOH is analysed in the next section.
| Projected CPV cumulative capacity (MW) | Projected CPV module + tracker cost ($ W−1) |
|---|---|
| 370 (current – 2020) | 0.72 |
| 740 | 0.59 |
| 1480 | 0.48 |
| 2960 | 0.40 |
| 5920 | 0.32 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
0.27 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680 680 |
0.22 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
0.18 |
94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 720 |
0.15 |
189![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 440 |
0.12 |
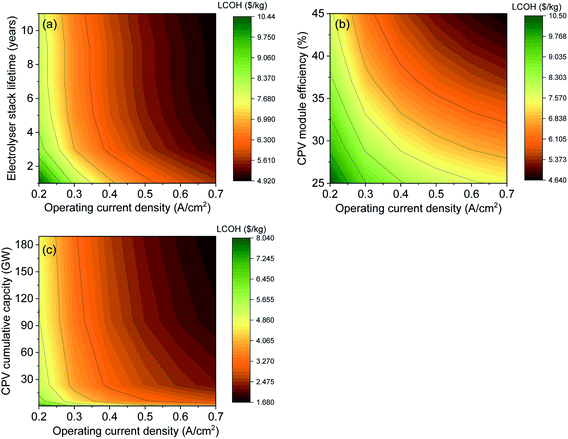
To analyse the sensitivity to electrolyser CAPEX cost, we have changed the model to be sensitive to operating current density by determining the electrolyser stack cost per unit area. This is calculated using a reference stack cost of 272 $ kW−1, operating conditions at 0.4 A cm−2 and 1.7 V (the base case) corresponding to an installed cost of $1850 m−2.44 Depending on the operating current density and the electrolyser area, the capital cost of the electrolyser changes. Fig. 5(a) shows the effect of LCOH as a function of electrolyser stack lifetime and electrolyser operating current density at 41% CPV module efficiency. The stack lifetime affects the electrolyser OPEX while the operating current density affects the electrolyser CAPEX. The results show that LCOH is sensitive to both operating current density and stack lifetime when the lifetime is below 3 years. The impact of stack lifetime on the LCOH is less pronounced after 4 years, where it is more affected by the change in current density or in other words the size of the electrolyser. Moreover, the effect of changing the performance of both the CPV solar farm and the electrolyser on the LCOH is given in Fig. 5(b). Both parameters have almost an equal impact on the LCOH, where the cost drops to 4.64 $ kg−1 when the CPV module efficiency and the operating current density are at 45% and 0.7 A cm−2, respectively. Finally, the effect of CPV installed cumulative capacity and stack current density on the LCOH is shown in Fig. 5(c). The graph summarizes the importance of both CPV and electrolyser CAPEX on H2 cost. When the cost of CPV modules keeps decreasing at a LR of ∼18%, LCOH can be <2 $ kg−1 at an installed CPV cumulative capacity of >180 GW and an operating current density of 0.7 A cm−2. The effect of grid electricity cost for 24 hours operation on the LCOH is given in the ESI.†
4. Conclusions and outlook
The present experimental work shows that a stable system with a STH efficiency of 28% can be obtained upon optimising the configuration of CPV cells (40.7% efficient) and available alkaline electrolysers (70% efficient). Detailed TEA analysis showed that despite the high cost of these CPV cells, the LCOH with CPV solar farms, today, can approach that obtained using c-Si solar farms. Because commercial c-Si solar cells have neared saturation, we have carried out a sensitivity analysis of several factors affecting both CPV and alkaline electrolyser systems. These included the CPV module efficiency, installed capacity, electrolyser stack lifetime and operating current density. Results indicate that when the installed capacity of CPV technology matches that of silicon and when electrolyser's operating current density reaches ∼0.7 A cm−2, the levelized cost of H2 from CPV-electrolysis systems can drop below $2 kg−1. The present cost of hydrogen from steam methane reformers with CO2 sequestration is between $1.2 and $2.8 kg−1.6Hydrogen can be produced from water with high efficiency and production rates. The considerable increase in efficiency as seen in this work puts STH efficiency at par with other practical engines. Like any technology, the one presented here will see its cost dropping down with time once in use and like any breakthrough technology; it can only be brought to life with strong incentives. In recent years, the silicon PV industry experienced a large price drop of more than 80% mostly from subsidized industries that could sell products with little to no profit. On the other hand, CPV has suffered from a lack of a dedicated supply chain, which has forced many companies to develop and produce most of the components (trackers, modules, etc.) themselves. We hope that these results and cost analysis will encourage researchers, governments, and companies to explore CPV-electrolysis for commercial H2 production. The main incentive, in the short term, may not be wealth but the environment; and this would bring with time the needed ingredients for progress and prosperity.
List of abbreviations
| IRR | Internal rate of return |
| OPEX | Operating expenditure |
| CAPEX | Capital expenditure |
| PV | Photovoltaic |
| CPV | Concentrated photovoltaic |
| LCOH | Levelized cost of hydrogen |
| BOS | Balance of system |
| BOP | Balance of plant |
| DI | De-ionized water |
| O & M | Operation and maintenance |
| PEM | Polymer electrolyte membrane |
| STH | Solar to hydrogen efficiency |
| NPV | Net present value |
| MSP | Minimum selling price |
| FF | Fill factor |
| PMMA | Poly(methyl methacrylate) |
| GC | Gas chromatography |
| DNI | Direct normal irradiance |
| η F | Faradaic efficiency |
| V OP | Operating voltage |
| I OP | Operating current |
| V MMP | Voltage at maximum power point |
| I MMP | Current at maximum power point |
| 3J | Triple junction |
| NREL | National renewable energy laboratory |
Conflicts of interest
There are no conflicts to declare.References
- A. Jaeger-Waldau, PV Status Report 2019, EUR 29938 EN, Publications Office of the European Union, Luxembourg, 2019, DOI:10.2760/326629.
- M. Taylor, P. Ralon, H. Anuta and S. Al-Zoghoul, Renewable power, generation cost, International Renewable Energy Agency, Abu Dhabi, 2020 Search PubMed.
- H. Idriss, Hydrogen production from water: past and present, Curr. Opin. Chem. Eng., 2020, 29, 74–82 CrossRef.
- A. Ziani, I. Al-Shankiti, M. A. Khan and H. Idriss, Integrated Photo-Electrocatalytic (PEC) Systems for Water Splitting to Hydrogen and Oxygen under Concentrated Sunlight: Effect of Internal Parameters on Performance, Energy Fuels, 2020, 34(10), 13179–13185 CrossRef CAS.
- M. Khan, I. Shankiti, A. Ziani, N. Wehbe and H. Idriss, A Stable Integrated Photoelectrochemical Reactor for H2 Production from Water Attains a Solar-to-Hydrogen Efficiency of 18% at 15 Suns and 13% at 207 Suns, Angew. Chem., 2020, 59, 14802–14808 CrossRef CAS PubMed.
- B. Parkinson, P. Balcombe, J. Speirs, A. Hawkes and K. Hellgardt, Levelized cost of CO2 mitigation from hydrogen production routes, Energy Environ. Sci., 2019, 12(1), 19–40 RSC.
- M. R. Shaner, H. A. Atwater, N. S. Lewis and E. W. McFarland, A comparative technoeconomic analysis of renewable hydrogen production using solar energy, Energy Environ. Sci., 2016, 9(7), 2354–2371 RSC.
- D. Yadav and R. Banerjee, Net energy and carbon footprint analysis of solar hydrogen production from the high-temperature electrolysis process, Appl. Energy, 2020, 262, 114503 CrossRef CAS.
- J. Hinkley, J. Hayward, R. McNaughton, R. Gillespie, A. Matsumoto, M. Watt and K. Lovegrove, Cost assessment of hydrogen production from PV and electrolysis, Report to ARENA as Part of Solar Fuels Roadmap, Project A-3018, 2016, pp. 1–4 Search PubMed.
- S. Alsayegh, R. Varjian, Y. Alsalik, K. Katsiev, T. Isimjan and H. Idriss, Methanol Production Using Ultrahigh Concentrated Solar Cells: Hybrid Electrolysis and CO2 Capture, ACS Energy Lett., 2020, 5(2), 540–544 CrossRef CAS.
- IEA, The Future of Hydrogen: Seizing Today's Opportunities, 2019, https://www.iea.org/reports/the-future-of-hydrogen Search PubMed.
- L. C. Andreani, A. Bozzola, P. Kowalczewski, M. Liscidini and L. Redorici, Silicon solar cells: toward the efficiency limits, Adv. Phys., 2019, 4(1), 1548305 CAS.
- M. A. Green, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger, M. Yoshita and A.W.Y. Ho-Baillie, Solar cell efficiency tables (version 54), Prog. Photovolt: Res. Appl., 2019, 27(7), 565–575 CrossRef.
- F. Dimroth, T. N. Tibbits, M. Niemeyer, F. Predan, P. Beutel, C. Karcher, E. Oliva, G. Siefer, D. Lackner and P. Fuß-Kailuweit, Four-junction wafer-bonded concentrator solar cells, IEEE Journal of Photovoltaics, 2015, 6(1), 343–349 Search PubMed.
- M. A. Green, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger, M. Yoshita and A. W. Ho-Baillie, Solar cell efficiency tables (version 54), Prog. Photovoltaics, 2019, 27(7), 565–575 Search PubMed.
- M. Wiesenfarth, S. Philipps, A. Bett, K. Horowitz and S. Kurtz, Current status of concentrator photovoltaic (CPV) technology Version 1.3, Fraunhofer Inst. Sol. Energy Syst. ISE, Nat. Renewable Energy Lab., 2017 Search PubMed.
- M. Steiner, G. Siefer, T. Schmidt, M. Wiesenfarth, F. Dimroth and A. W. Bett, 43% sunlight to electricity conversion efficiency using CPV, IEEE Journal of Photovoltaics, 2016, 6(4), 1020–1024 Search PubMed.
- M. Wiesenfarth, I. Anton and A. Bett, Challenges in the design of concentrator photovoltaic (CPV) modules to achieve highest efficiencies, Appl. Phys. Rev., 2018, 5(4), 041601 Search PubMed.
- W. J. Chang, K.-H. Lee, H. Ha, K. Jin, G. Kim, S.-T. Hwang, H.-m. Lee, S.-W. Ahn, W. Yoon and H. Seo, Design principle and loss engineering for photovoltaic–electrolysis cell system, ACS Omega, 2017, 2(3), 1009–1018 CrossRef CAS PubMed.
- A. Nakamura, Y. Ota, K. Koike, Y. Hidaka, K. Nishioka, M. Sugiyama and K. Fujii, A 24.4% solar to hydrogen energy conversion efficiency by combining concentrator photovoltaic modules and electrochemical cells, Appl. Phys. Express, 2015, 8(10), 107101 CrossRef.
- J. Jia, L. C. Seitz, J. D. Benck, Y. Huo, Y. Chen, J. W. D. Ng, T. Bilir, J. S. Harris and T. F. Jaramillo, Solar water splitting by photovoltaic-electrolysis with a solar-to-hydrogen efficiency over 30%, Nat. Commun., 2016, 7(1), 1–6 Search PubMed.
- J. Proost, State-of-the art CAPEX data for water electrolysers, and their impact on renewable hydrogen price settings, Int. J. Hydrogen Energy, 2019, 44(9), 4406–4413 CrossRef CAS.
- W. G. Colella, B. James and J. M. Moton, Hydrogen Pathways Analysis for Polymer Electrolyte Membrane (PEM) Electrolysis, Strategic Analysis Inc, 2014 Search PubMed.
- S. Rehman, Solar radiation over Saudi Arabia and comparisons with empirical models, Energy, 1998, 23(12), 1077–1082 CrossRef.
- E. Zell, S. Gasim, S. Wilcox, S. Katamoura, T. Stoffel, H. Shibli, J. Engel-Cox and M. Al Subie, Assessment of solar radiation resources in Saudi Arabia, Sol. Energy, 2015, 119, 422–438 CrossRef.
- B. D. James, G. N. Baum, J. Perez and K. N. Baum, Technoeconomic Analysis of Photoelectrochemical (PEC) Hydrogen Production, DOE report, 2009 Search PubMed.
- V. D. Rumyantsev, V. M. Andreev, A. W. Bett, F. Dimroth, M. Hein, G. Lange, M. Z. Shvarts and O. V. Sulima, Progress in development of all-glass terrestrial concentrator modules based on composite Fresnel lenses and III-V solar cells, Conference Record of the Twenty-Eighth IEEE Photovoltaic Specialists Conference, Anchorage, AK, US, 2000, DOI:10.1109/PVSC.2000.916096.
- S. Restrepo-Valencia and A. Walter, Techno-Economic Assessment of Bio-Energy with Carbon Capture and Storage Systems in a Typical Sugarcane Mill in Brazil, Energies, 2019, 12(6), 1129 CrossRef CAS.
- D. McIlveen-Wright, Y. Huang, S. Rezvani, J. D. Mondol, D. Redpath, M. Anderson, N. Hewitt and B. Williams, A techno-economic assessment of the reduction of carbon dioxide emissions through the use of biomass co-combustion, Fuel, 2011, 90(1), 11–18 CrossRef CAS.
- M. Steinberg and H. C. Cheng, Modern and prospective technologies for hydrogen production from fossil fuels, Int. J. Hydrogen Energy, 1989, 14(11), 797–820 CrossRef CAS.
- S. Ong, C. Campbell, P. Denholm, R. Margolis and G. Heath, Land-use Requirements for Solar Power Plants in the United States, National Renewable Energy Lab. (NREL), Golden, CO, United States, 2013 Search PubMed.
- K. Horowitz, M. Woodhouse, H. Lee and G. Smestad, Bottom-Up Cost Analysis of a High Concentration PV Module, National Renewable Energy Lab. (NREL), Golden, CO, United States, 2015 Search PubMed.
- X. Wang and A. Barnett, The evolving value of photovoltaic module efficiency, Appl. Sci., 2019, 9(6), 1227 CrossRef CAS.
- M. Bolinger, J. Seel and D. Robson, Utility-Scale Solar: Empirical Trends in Project Technology, Cost, Performance, and PPA Pricing in the United States–2019 Edition, 2019 Search PubMed.
- B. D. James, D. A. DeSantis and G. Saur, Hydrogen Production Pathways Cost Analysis (2013–2016), Strategic Analysis Inc., Arlington, VA, United States, 2016 Search PubMed.
- Quoted by BSQ Solarin Madrid, S., https://www.bsqsolar.com/.
- M. Bolinger and J. Seel, Utility-scale Solar: Empirical Trends in Project Technology, Cost, Performance, and PPA Pricing in the United States, LBNL, 2018 Search PubMed.
- M. Renzi, M. Santolini and G. Comodi, Performance analysis of a 3.5 kWp CPV system with two-axis tracker, Energy Procedia, 2014, 61, 220–224 CrossRef.
- R. Mikami, M. Inagaki, M. Moriguchi, K.-i. Kitayama, H. Konaka and T. Iwasaki, Advantages of Concentrator Photovoltaic System in High Solar Radiation Region, SEI Tech. Rev., 2016,(82), 137 Search PubMed.
- S. Ponce-Alcántara, J. P. Connolly, G. Sánchez, J. M. Míguez, V. Hoffmann and R. Ordás, A statistical analysis of the temperature coefficients of industrial silicon solar cells, Energy Procedia, 2014, 55, 578–588 CrossRef.
- M. Khalis, R. Masrour, G. Khrypunov, M. Kirichenko, D. Kudiy and M. Zazoui, In Effects of temperature and concentration mono and polycrystalline silicon solar cells: extraction parameters, J. Phys.: Conf. Ser., 2016, 012001 CrossRef.
- D. C. Bobela, L. Gedvilas, M. Woodhouse, K. A. Horowitz and P. A. Basore, Economic competitiveness of III–V on silicon tandem one-sun photovoltaic solar modules in favorable future scenarios, Prog. Photovoltaics, 2017, 25(1), 41–48 Search PubMed.
- J. E. Haysom, O. Jafarieh, H. Anis, K. Hinzer and D. Wright, Learning curve analysis of concentrated photovoltaic systems, Prog. Photovoltaics, 2015, 23(11), 1678–1686 Search PubMed.
- D. Stolten and B. Emonts, Hydrogen Science and Engineering, 2 Volume Set: Materials, Processes, Systems, and Technology, John Wiley & Sons, 2016, vol. 1 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0se01761b |
| This journal is © The Royal Society of Chemistry 2021 |