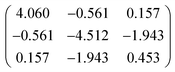Increasing ion yield circular dichroism in femtosecond photoionisation using optimal control theory
Received
15th November 2021
, Accepted 17th February 2022
First published on 12th April 2022
Abstract
We investigate how optimal control theory can be used to improve Circular Dichroism (CD) signals for the A-band of fenchone measured via the photoionization yield upon further excitation. These transitions are electric dipole forbidden to first order, which translates into low population transfer to the excited state but allows for a clearer interplay between electric and magnetic transition dipole moments, which are of the same order of magnitude. Using a model including the electronic ground and excited A state as well as all permanent and transition multipole moments up to the electric quadrupole, we find that the absolute CD signal of randomly oriented molecules can be increased by a factor of 2.5 when using shaped laser pulses, with the anisotropy parameter g increasing from 0.06 to 1. We find that this effect is caused by the interference between the excitation pathways prompted by the different multipole moments of the molecule.
1 Introduction
Chirality is the property of an object to not be superimposable with its mirror image through a combination of translations and rotations. In molecular systems, the mirrored forms, called enantiomers, have almost entirely identical physical properties and interact indistinguishably with non-chiral probes. At the same time, enantiomers can behave very differently in their interaction with other chiral objects, as evidenced by the role of chirality in many biochemical and medical processes. The development of better techniques for chiral discrimination is therefore a very active field of research both from a theoretical and experimental point of view.
Characterisation of chirality can be achieved via chiral observables, i.e. properties which take on different values for each enantiomer. These techniques either rely on the interaction of the sample with a chiral probe or on the construction of a chiral setup to record the response.1 A prototypical chiral observables is circular dichroism (CD), which has been the subject of many theoretical2–8 and experimental9–13 studies. It is defined as the difference in absorption of circularly polarised light (acting as the chiral probe) by the two enantiomeric forms of a chiral molecule. To leading order, circular dichroism is formed by the interplay between electric dipole and magnetic dipole transitions. Due to the generally low magnitude of magnetic dipole transition moments, CD is a comparatively weak effect, amounting to less than 1% of the total absorption signal. In recent years a lot of effort has been invested in the description and measurement of chiral observables which do not require involvement of the weak magnetic transition dipole moments, two notable examples being the photoelectron circular dichroism (PECD) and rotational spectroscopy with microwave three-wave mixing (M3WM). The enantiomeric contrast obtained with these techniques reaches values of several percent even with transform-limited pulses. Recently, it has been shown that optimal control theory can be used to increase this value even further by exploiting interference between various photoionization pathways.14 For instance, perfect anisotropy in the photoelectron angular distribution of a randomly oriented ensemble can be generated by exploiting interferences between single-photon pathways and a manifold of resonantly enhanced two-photon pathways.15 Prospects for control are even more promising for M3WM where complete enantiomer-specific population transfer is possible if a suitable combination of frequencies and polarization for the electric fields driving the three-wave mixing process is chosen.16 These recent successes in enhancing chiral signatures with shaped pulses strongly suggest that interference between different excitation pathways may be a promising avenue to increase the contrast also in CD experiments. However, PECD and M3WM are pure electric dipole effects to first order, which leads to strong transitions and the possibility to attain high contrast with moderate laser intensities. Conversely, CD relies on small magnetic dipole transition moments. This raises the question whether interference effects between different excitation paths can also be exploited to increase the contrast of the overall much weaker CD signals. In the pursuit of understanding how to maximise the dichroic signal, the magnitude of CD both as a function of laser pulse frequency,7,8 as well as duration and envelope5 have been theoretically investigated. The majority of these studies focused on the leading-order contribution to CD which involves only the electric dipole and magnetic dipole transition moment in the absorption process. However, it has long been established that all multipolar terms in the light–matter interaction contribute to CD.17 Indeed, the electric quadrupole has a noticeable effect in the absorption signatures for the 1,2-propylene oxide molecule when multiphoton excitations are considered.8 Even beyond chiral observables, there is recent interest in the study of nondipole effect for many different physical processes, for example in photoionisation18–21 and high-harmonic generation.22,23
When attempting to increase the CD signal in an experiment, the final puzzle piece is to transfer the optimal pulses from theory to the lab. This step requires to disentangle the physically relevant pulse properties from purely numerical features that are often introduced by optimisation algorithms. It also relies on an appropriate correspondence between the theoretical figure of merit used in the optimization and the experimentally measured quantity. Although experimental determination of absorption CD in the liquid phase is well-established,24 optimal control of chiral signatures for molecules in the gas phases presents a more adequate framework to compare theory and experiment. This is because emerging gas phase techniques allow for measurements under collision- and interaction-free conditions25,26 also in table-top setups, which therefore serve as the focal point of our investigations. One way to assess CD is mapping into the ionisation continuum: by using resonance enhanced mulitphoton ionisation (REMPI), the helicity-dependent population of the optically active electronic state is translated into ion yields.10,11 In combination with time-of-flight laser mass spectrometry it is possible not only to measure the CD of the parent ion but also of the fragment ions. Successful experiments have recently been reported for several chiral molecules7,27,28 exploiting the advent of advanced techniques such as the measurement of differential photoion CD29 or twin-peak setups for improved statistics adapted to femtosecond laser pulses.30 For resonant processes, ion-yield CD and absorption CD are closely connected with the normalised difference in ion yields which for a specific resonance is equal to the normalised CD in extinction.27
In this paper we investigate, for the first time, in how far optimal control can exploit the interaction of the molecule with light via the transition electric dipole, magnetic dipole, and electric quadrupole as well as permanent electric dipole and quadrupole moments to enhance circular dichroism. In order to avoid concealment of the magnetic-dipole dependent CD signal by strong electric dipole transitions, we focus on the A-band n → π* transition in fenchone. This transition is electric dipole-forbidden to first order9 which allows multipolar signatures to come to the forefront. By using an effective two-level description together with a physically motivated parametrisation of the laser pulse, we are able to elucidate the role of different multipole orders in the optimised protocols. Moreover, we examine how the optimised pulses address different molecular orientations when maximising CD for an orientationally averaged ensemble. To stay close to experimental realisation, we also ensure that the pulse parameters are feasible in state-of-the-art table-top experiments in the femtosecond regime.
This paper is organised as follows: Section 2 introduces the theoretical model of fenchone and the molecule's interaction with a laser pulse as well as the control functional and algorithm. Section 3 presents the results from our optimisations with a particular focus on the role of the permanent electric dipole and electric quadrupole transition moments for the control protocols. Finally, Section 4 concludes and presents an outlook for future investigations.
2 Theoretical framework
Setting the stage for an optimal control problem can be condensed to three main questions: How do we represent the relevant physical states and model dynamics of the molecule under study? How do we encode the physical control target in a mathematical functional? And finally, which algorithm do we use to minimise, respectively maximise, the target functional? We begin by addressing the question of representation and dynamics. To this end, in Section 2.1 we introduce the description of the light–matter interaction of a laser field with a chiral molecule beyond the electric dipole approximation.31,32 Then, we discuss the most important features of the A-band transition in fenchone9 in Section 2.2, which allows us to employ a minimal description for the molecule that still contains all of the relevant physics. Specifically, we motivate a model involving only two electronic states (the ground state and the first excited state) and neglecting any additional degrees of freedom. Such a two-level description does not account for continuum dynamics, but the absorption step serves as an important first step towards optimising ion-yield CD experiments – a high contrast during the absorption step will lead to high contrast in the ion yield. Finally in Section 2.3 we detail how to account for orientational averaging in optimisations,33 introduce an optimisation functional specifically adapted to the task of maximising CD, and discuss which algorithm is particularly suitable for computing optimised pulses.
2.1 Light–matter interaction in chiral molecules
Within the Born–Oppenheimer approximation, the Hamiltonian describing the interaction of a molecule with an electromagnetic field using minimum coupling is given by,17,31,32,34| | 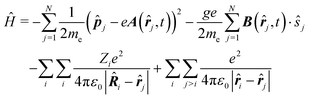 | (1) |
| | 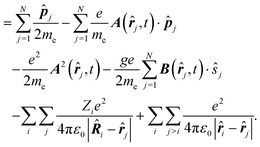 | (2) |
In eqn (2), ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) j,
j, ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) j and ŝj are the momentum, position and spin operators for the jth electron,
j and ŝj are the momentum, position and spin operators for the jth electron, ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) i and Zi are the position operator and nuclear charge for the ith nuclei, A(
i and Zi are the position operator and nuclear charge for the ith nuclei, A(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) j,t) is the vector potential, and B(
j,t) is the vector potential, and B(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) j,t) the magnetic field. Moreover, the constants e, me, g and ε0 correspond to the charge and mass of the electron, the spin g-factor and the vacuum permittivity. The terms containing squares of the vector potential A can be safely neglected outside the strong-field regime. More specifically, for optical or near UV wavelengths, this approximation is well-motivated for intensities I < 1018 W cm−2.35 Introducing the expansion of the electric field (see eqn (19) and (23) in Appendix A), and performing a suitable gauge transformation, the multipolar form of the light–matter interaction Hamiltonian becomes32,36 for an incident light field propagating in z direction,
j,t) the magnetic field. Moreover, the constants e, me, g and ε0 correspond to the charge and mass of the electron, the spin g-factor and the vacuum permittivity. The terms containing squares of the vector potential A can be safely neglected outside the strong-field regime. More specifically, for optical or near UV wavelengths, this approximation is well-motivated for intensities I < 1018 W cm−2.35 Introducing the expansion of the electric field (see eqn (19) and (23) in Appendix A), and performing a suitable gauge transformation, the multipolar form of the light–matter interaction Hamiltonian becomes32,36 for an incident light field propagating in z direction,| | 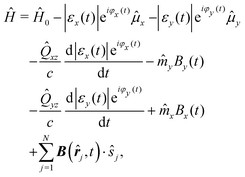 | (3) |
where we collected the field-free terms into the time-independent Hamiltonian Ĥ0, and used the definitions,| | 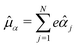 | (4) |
| | 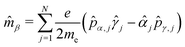 | (5) |
| | 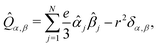 | (6) |
for electric dipole, magnetic dipole, and electric quadrupole operators with α,β,γ ∈ {x,y,z} The first line in eqn (3) corresponds to the well-known dipole approximation. It is equivalent to neglecting the spatial dependence of the electric field entirely, such that only a function of time remains. Note that the dipole approximation removes any information concerning the direction of propagation, k, hence the handedness of circularly polarised light is lost in such a model. As such, the only spatial information encoded in the dipole approximation is the transition dipole moment μ (a molecular vector) and the plane of polarisation of light (a field pseudovector). In order to get a chiral observable in the dipole approximation it is necessary to introduce another vector in the process, so that we can define a pseudoscalar that codifies the handedness of the molecule.1 For instance, the photoelectron angular distribution of a randomly oriented sample of chiral molecules presents a forward–backward asymmetry, known as Photoelectron Circular Dichroism (PECD).37 The high contrast of the signal (up to 10% between both enantiomers) has motivated extensive theoretical and experimental studies. Although PECD measurements provide comparatively high signal strengths, the description of the corresponding observable is more complex than CD from a theoretical point of view due to the necessity to describe the electronic continuum. Conversely, chiral signatures from light absorption – (conventional) CD and ion-yield CD – primarily rely on bound-state electronic properties. Nevertheless, a chiral signature due to CD requires the helicity of light to explicitly enter the interaction via the propagation vector k. For this reason our model includes the next-higher order term of the multipole expansion beyond the electric dipole, cf. the second and third line of eqn (3).
2.2 System under study: a-band of fenchone
Electric dipole transitions are typically much stronger than the corresponding magnetic dipole transitions. As a result, CD signatures can easily be concealed by the electric dipole, leading to low-contrast signals in experiments. In order to avoid such concealment, we focus on the A-band of fenchone. This transition is electric dipole forbidden to first order, since its main component is a symmetry forbidden n → π* transition,9 and therefore features electric and magnetic transition dipole moments of the same order of magnitude.
We seek to optimise laser pulses as used in table-top experiments, i.e. pulse lengths of the order of 100 fs and laser wavelengths of 300 nm. This timescale is significantly shorter than the rotational periods of fenchone, which are of the order of 1 ns.38 Therefore we can safely assume that the molecule remains at a single fixed orientation during the full length of the pulse. Conversely, the main vibrational modes of the fenchone molecule have periods of the order of 50 fs. These short amplitude motions, however, correspond to individual C–H and C–C bonds in the molecular backbone, and are not expected to play a significant role in the electronic dynamics.39 Therefore, we will restrict the modeling to the electronic degree of freedom.
Representing the Hamiltonian, eqn (3), in the basis of electronic eigenstates of fenchone, |Ψn〉 = |n〉, we obtain the expression
| | 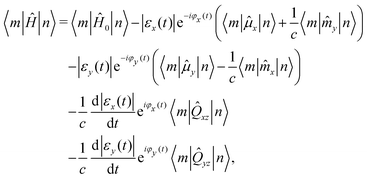 | (7) |
where we have used the fact that, for symmetry reasons, any contribution due to spin vanishes for real-valued wave functions of singlet states.
31,34 In
eqn (7), |
εα(
t)|e
−iφα(t) is the
α component of the complex-valued Fourier transform of the electric field, and we have represented the magnetic field
B(
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
,
t) in terms of the electric field
via the Fourier space Maxwell equation
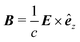
(see Appendix A for details on the expansion of the electric field).
We have calculated electronic state energies as well as permanent and transition moments with the DALTON 2020 software package40,41 at Coupled Cluster Singles Doubles (CCSD) level with a 6-31G basis set, employing the Linear Response theory implementations described in ref. 42–44. Due to the localised nature of the two states involved in the A-band transition (the ground and the first electronic excited state), a more extended basis set describing the strong Rydberg nature of higher excited states,45 was not necessary. Furthermore, in order to guarantee a good representation of the two states in this minimal model, we included up to the fifth electronic excited state when calculating electronic energies and multipole moments. All computed quantities relevant for the optimisations are provided in Table 1. Note that the permanent magnetic dipole moment is neglected due to the singlet nature of the electronic states considered.
Table 1 Energies, permanent electric dipole and transition multipole moments for the ground and first electronic excited state of fenchone obtained at CCSD/6-31G level with DALTON2020.0
|
|
|0〉 |
|1〉 |
| Energy eV |
El. dip. ea0 |
Mag. dip. eħme−1 |
El. quad. ea02 |
Energy eV |
El. dip. ea0 |
Mag. dip. eħme−1 |
El. quad. ea02 |
| 〈0| |
0 |

|
|

|
|

|

|
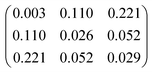
|
| 〈1| |
|

|

|
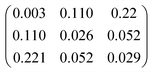
|
4.01 |

|
|
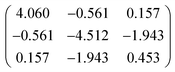
|
2.3 Optimal control of circular dichroism
Since we neglect rotational motion, the Hamiltonian (eqn (3) and (7)) only describes a single orientation of the chiral molecule with respect to the light pulse. However, experiments are typically carried out with a statistical ensemble of randomly oriented molecules which have to be accounted for in the model. Averaging over all Euler angles, defined with respect to the orientation shown in Fig. 1 in the y–z–y convention, we obtain for the excited state population of a single enantiomer| | 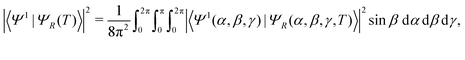 | (8) |
with |Ψ1(α,β,γ)〉 the excited state electronic eigenfunction, and |ΨR(α,βγ,T)〉 the state of the R enantiomer wave function at time T.
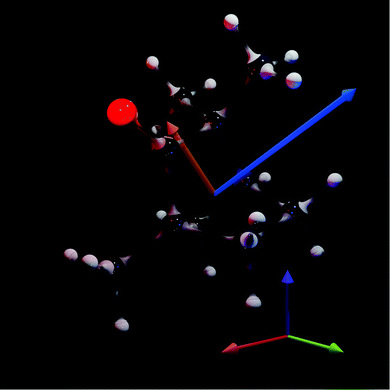 |
| | Fig. 1 Reference geometry of fenchone, as obtained after optimisation at CCSD/6-31G level with DALTON2020.0, superimposed with the transition electric dipole moment (scaled ×400, orange) and transition magnetic dipole (scaled ×4, blue). The coordinate system indicates the orientation of the molecular frame, with the RGB axes corresponding to the x, y, z Cartesian coordinates. | |
With this final puzzle piece on the question of representation in place, we can now turn to address the description of the system dynamics. To this end, we employ the time–dependent Schrödinger equation,
| | 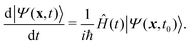 | (9) |
Although this equation of motion only describes coherent dynamics, such a treatment is justified by the fact that any decoherence or decay is expected to occur on much longer time scales than the fs pulse durations. As it is commonly done in the field of optimal control, we have separated the Hamiltonian in
eqn (3) into a field-free, time-independent system Hamiltonian,
Ĥ0, (the so-called drift) and the time-dependent Hamiltonian due to the interaction of the chiral molecule with the electric field (the so-called control
ε),
| | 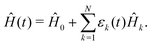 | (10) |
The coupling to an external field provides a means to steer the dynamics of the system towards a specific target, in our case by shaping an incident electromagnetic pulse containing both AC and DC components.
Next, we address the question of how to encode the physical target in terms of a functional, JT. This functional quantifies how well the control pulses implement the optimisation goal. Here we target a high contrast in electronic state populations of the two enantiomers of fenchone. This will serve as a precursor for getting high-contrast in ion-yield CD signals: such experiments measure the number of ions obtained after absorption and subsequent ionisation, and therefore a high difference in the absorption step is expected to yield strong contrast in the ionisation step. As seen in the previous section, the two enantiomeric forms share the same drift Hamiltonian, however, they feature a different relation between the electric and magnetic dipole transition moments: for one enantiomer the product of both quantities is positive, while for the other it is negative. This relative arrangement of the multipole moments in the light–matter interaction term is the source of the different dynamics in a given enantiomer when exposed to a light source with different helicity, and thus the origin of circular dichroism. Note that in this work we use a complementary (and equivalent) point of view to evaluate the CD: instead of changing the helicity of the pulse, we consider how a specific light field interacts with each of the enantiomers. Therefore, starting from chiral molecules in the ground state, we seek a pulse which selectively excites one of the enantiomers while leaving the opposite form in the ground state. Once a difference in electronic state population between the two enantiomers is established, a second pulse can be used to selectively ionise from the higher energy level, thus obtaining an increased ionisation CD signal. For a single orientation this goal can be encoded by a so-called state-to-state optimisation via the following functional,
| | 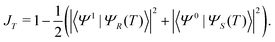 | (11) |
Similar functionals aiming to increase the distinguishability of two systems with a single control are also prominent,
e.g., in quantum discrimination of magnetic fields.
46–48 In
eqn (11),
Ψ0 and
Ψ1 refer respectively to the ground and electronic excited state of the chiral molecule.
ΨR(
T) (
ΨS(
T)) denotes the state of the
R(
S) enantiomer at final time
T. This functional takes on its minimal value 0 when the
R enantiomer is completely excited and the
S enantiomer remains entirely in the ground state, and its maximal value 1 in the opposite scenario. Note that both extrema correspond to perfect distinguishability, while a vanishing chiral signal corresponds to a functional value of 0.5. Thus, increasing the distance to this middle point, which can be achieved by either minimisation or maximisation, improves the realisation of our physical goal.
The linearly polarised components of the electric field, Ex(t) and Ey(t), can be represented as two different control pulses which are optimised independently allowing for arbitrary elliptical polarisation. Moreover, due to the small absorption amplitude in the A-band transition of fenchone, we can use perturbation theory to predict which light–matter interaction terms will be the most relevant in this system.17 Specifically, we expect three main contributions for each control field: DC components (E(0)x/y), which primarily couple to the permanent dipole, one-photon excitation components (E(1)x/y) with frequency ω(1), which primarily couple to the electric and magnetic dipole transitions, and two-photon excitation components (E(2)x/y) with frequency ω(2) which primarily couple to the electric quadrupole moments.17 The interference between the one and two photon excitation pathways, together with the coupling to the DC field component, will be the main resource exploited by the optimised pulses. This physical intuition suggests to employ a parametrisation for the control pulses, which allows to reduce the dimensionality of the optimisation landscape. Therefore we will represent the control field as a superposition of the three aforementioned contributions,
| | | Ex = s(t)(E(0)x + E(1)xsin(ω(1)t) + E(2)xsin(ω(2)t)) | (12) |
| | | Ey = s(t)(E(0)y + E(1)ysin(ω(1)t + φ) + E(2)ysin(ω(2)t + φ)), | (13) |
with
φ the relative phase between the
x and
y components of the electric field. In
eqn (12) and (13)s(
t) is an envelope function ensuring that the pulse is smoothly turned on and off. Here we choose a squared sine as a good approximation to experimental pulse shapes,
49| | 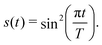 | (14) |
Note that we keep ω(1) as an optimisation parameter and do not fix it to the resonant frequency of the electronic excitation (ωr = 4.01 eV). This is done to allow for non-resonant processes in the optimal solutions and permits flexibility in view of potential DC and AC Stark shifts. Conversely, we keep the frequency for the two-photon pathway to the excited state fixed at ω(2) = ω(1)/2 to explicitly target a bichromatic control mechanism using interference between a one- and two-photon pathway.
To account for orientational averaging we perform an ensemble optimisation:33 We propagate a set of differently orientated molecules, each described by its own Hamiltonian, under the effect of the same control pulses, and minimise the averaged functional,
| | 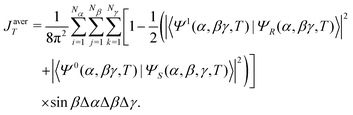 | (15) |
Note that we have replaced the integrals from
eqn (8) by sums, discretising the set of orientations. We have chosen
Nα =
Nγ = 2
Nβ = 14 to sample the orientations equidistantly and with identical spacing for all three Euler angles,
i.e., Δ = Δ
α = Δ
β = Δ
γ.
Since we can describe the control field with very few parameters, cf.eqn (12) and (13), gradient-free optimisation methods are particularly suitable. We have used a combination of the Multi–Level Single Linkage (MLSL) approach50–52 and the generalised simplex (or Nelder-Mead)53–55 algorithm as implemented in the python NLopt library.56 The MLSL algorithm stochastically samples the parameter space of the optimisation. This global scan of the optimisation landscape complements the local nature of the generalised simplex method and allows to find the optimal solution even when several local minima are present. All propagations have been performed using the QDYN library.57 Optimal control algorithms per se do not impose any restriction on the calculated pulses. However, in gradient free methods it is easily possible to restrict the domain of the parameters to be optimised. These constraints should be chosen in order to obtain control pulses apt for experimental applications, which are usually limited by the total pulse duration, and the maximum field strength that can be generated. In table-top setups, pulses with 30–40 fs duration and peak electric field strengths of the order of GV m−1 can be routinely obtained. However, due to the small transition moments of the A-band of fenchone, such pulses result in populations of the excited state of around 1%. These low values are insufficient to increase the contrast in the CD signal with a high signal to noise ratio. Preliminary simulations showed that we can obtain population transfer of ≈10% by using pulses of 100 fs total duration and peak electric field strength of 25.7 GV m−1 (corresponding to a value of 0.05 atomic units). Fields of such intensity (≈1014 W cm−2) result in comparatively weak light–matter interaction for the A-band transitions, so the pulses can still be considered to be below the strong field regime. These conditions are at the upper limit of experimental feasibility in table top setups but are still possible, albeit challenging, to implement. It should be noted that a more complex model beyond a two-level description would increase the dimension of the parameter space, where gradient-based methods show their strengths. A more detailed discussion on which optimisation algorithm is most suitable to a particular problem can be found for example in ref. 58.
3 Results and discussion
3.1 Circular dichroism of randomly oriented ensembles
As a guess for the optimisation we choose a 100 fs duration circularly polarised pulse with a single-frequency component at ω = 4.01 eV and E(1)x = E(1)y = 25.7 GV m−1. Due to the electric dipole forbidden nature of the transition, population transfer to the excited state with this pulse reaches maximum values of 8%, with a difference in excited state population between the R and S enantiomers around 0.5%. We can quantify the dichroic signal with the anisotropy factor g, defined as the ratio between the difference in absorption of circularly polarised light between the left and right enantiomers over the absorption of non-polarised light for that band, taken as the average absorption of both enantiomers:59| | 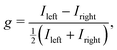 | (16) |
where Ileft and Iright refer to the absorption of a given enantiomer, which here corresponds to to the excited state populations. In the case of a guess circularly polarised pulse we obtain g = 6.25 × 10−2, which compares very well with the 5 × 10−2 value reported in the literature.9 This result supports the choice of a two-state model to represent the system. The generalised simplex (or Nelder-Mead) algorithm minimises the value of the rotationally averaged functional JaverT (cf.eqn (15)) by independently varying the different components of the pulse: the intensity of the DC component (E(0)x/y, coupling primarily to the permanent electric dipole moment), the one-photon component (E(1)x/y, coupling primarily to the electric and magnetic dipole transitions), the two-photon component (E(2)x/y, coupling primarily to electric quadrupole moment), as well as the frequency ω(1). The optimised pulses in time and frequency domain as well as the resulting population dynamics are displayed in Fig. 2. The optimised values for the pulse parameters, cf.eqn (12) and (13), are shown in Table 2.
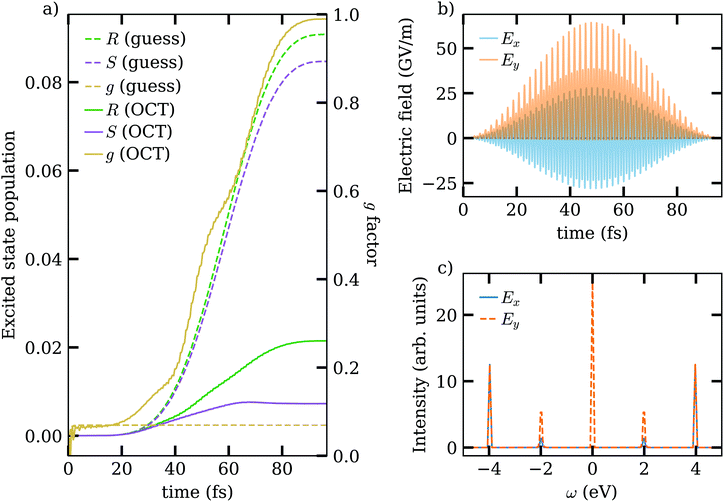 |
| | Fig. 2 Results for the optimisation of circular dichroism of a rotational ensemble for the A-band transition of fenchone. (a) Evolution of the excited state population as a function of time for the R (green) and S (purple) enantiomer of fenchone, as well as the corresponding value of the anisotropy parameter g (yellow, in the right y axis). The dashed line corresponds to the circularly polarised guess pulse, while the solid line corresponds to the optimised control fields. The oscillations of g at short times are a numerical artifact due to the near 0 absorption of the excited states during the first femtoseconds. (b) Optimised pulses in time domain. (c) Optimised pulses in frequency domain. | |
Table 2 Parameters of the circularly polarised guess pulse (anisotropy g = 6.25 × 10−2 after orientational averaging) and the optimised pulse (anisotropy g = 1.0 after orientational averaging)
|
|
Optimised pulse |
Guess pulse |
|
|
E
(0) (GV m−1) |
E
(1) (GV m−1) |
E
(2) (GV m−1) |
ω
(1) (eV) |
ω
(2) (eV) |
φ
|
E
(0) (GV m−1) |
E
(1) (GV m−1) |
E
(2) (GV m−1) |
ω
(1) (eV) |
ω
(2) (eV) |
φ
|
|
E
x
|
4.95 × 10−3 |
27.71 |
3.26 |
3.97 |
1.99 |
π/2 |
0.0 |
25.70 |
0.0 |
4.01 |
— |
π/2 |
|
E
y
|
25.71 |
25.71 |
12.86 |
3.97 |
1.99 |
|
0.0 |
25.70 |
0.0 |
4.01 |
— |
|
Remarkably, the anisotropy obtained with the guess circularly polarised pulse reaches its maximum value in the first few femtoseconds, and remains constant throughout the rest of the dynamics. This stands in sharp contrast to the behaviour under the optimised pulse, which shows a gradual increase of the anisotropy throughout the whole pulse. The parameters in Table 2 also show that the optimisation slightly alters the frequency compared to the resonance frequency ωr from the guess pulse. We attribute this feature to the combined effects of AC and DC Stark shifts induced by the field. Moreover, the optimised pulse not only addresses dipolar transitions at the frequency ωr but also DC field contributions (ω = 0) due to the permanent electric dipole, and two-photon (ω = ω(1)/2) contributions arising from coupling to the electric quadrupole (see also Fig. 2c). Interestingly, only the y field contributes to the DC component. This feature is attributed to the numerical optimisation procedure: in a perfect orientationally averaged system, any simultaneous rotation of the x and y components of the field would yield equivalent results. Therefore the present relative orientations of fields and molecule would only depend on the choice of the initial guess pulse for the optimisation§. The resulting difference in excited-state population between the two enantiomers, and thus the chiral contrast, increases by a factor 2.5 compared to the guess field. Moreover, the overall signal strength in the A-band is also reduced from ≈9% for the circularly polarised pulse to ≈2% for the optimised one. Given that the field strength of both sets of pulses is similar, we can attribute the difference in dynamics to interference effects between the different excitation pathways. All in all, the combination of increase of chiral contrast and decrease of overall absorption results in an improvement of the anisotropy parameter to almost g = 1.0.
Despite the fact that the leading order for circular dichroism is usually given by electric and magnetic dipole transitions, the optimisation results for the (to first order) dipole-forbidden transition in fenchone reveals the significance of multipolar terms beyond the electric and magnetic dipole transition moment. To further illustrate and investigate their significance we optimised a restricted pulse by simulating dynamics using the full Hamiltonian, yet constraining E0 = 0 (respectively E2 = 0) for the control fields. The comparison of the simulations with these different schemes is shown in Fig. 3.
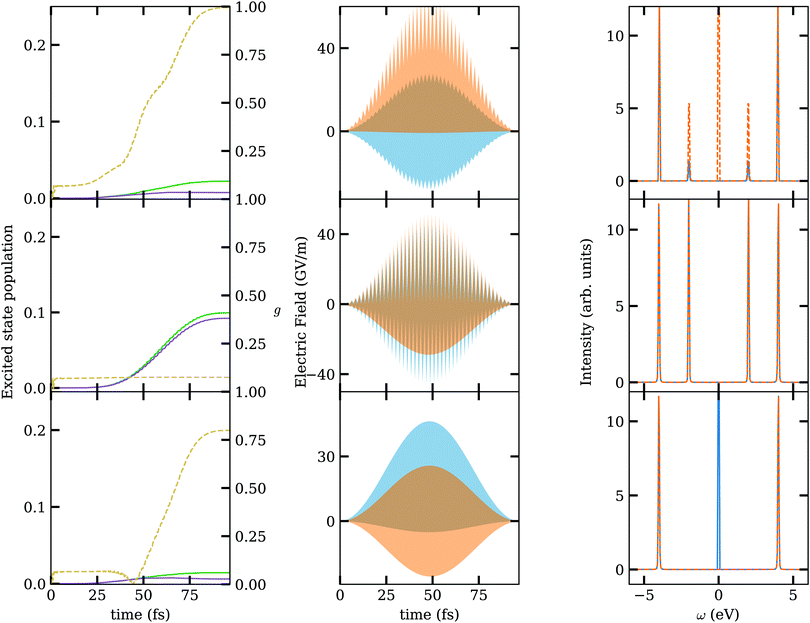 |
| | Fig. 3 Comparison of optimisations with a fully parametrised pulse (top), a restricted pulse without DC contribution (middle) and a restricted pulse without ω(2) contribution (bottom). Left to right: excited state population for the R (solid green) and S (solid purple) enantiomer and anisotropy factor g (dashed yellow, in right y axis); envelope of the optimised pulses in time domain; optimised pulses in frequency domain (Ex blue, Ey orange). | |
From these different setups we can clearly see that the permanent electric dipole, through its interaction with the DC component of the electric field, is the critical ingredient for the success of the ensemble optimisation: An optimisation restricting the pulse to a vanishing zero-frequency component does not significantly increase the anisotropy with respect to the guess. Conversely, an optimisation using a restricted pulse without two-photon contributions still offers a significant increase of the anisotropy factor, but only reaches around 0.75 anistropy in contrast to the almost 1.00 when utilising all possible pathways. Evidently, all multipolar terms in the model provide a significant optimisation resource, since they either open (transition moments) or modify (permanent moments) different photon excitation pathways, which allows to exploit interference effects towards the desired objective.
3.2 Oriented circular dichroism
For typical experiments on circular dichroism in the gas phase the chiral signal is orientationally averaged over all possible orientations of the molecular target. From a theoretical point of view it is nevertheless interesting to also consider how control pulses can induce different absorption between two enantiomers for a single, space-fixed orientation. Specifically, we first investigate optimisations for single orientations of fenchone with respect to the light field. Then, we analysed how the optimal controls obtained from ensemble optimisation act on individiual orientations. The comparison of these two sets of simulations helps to gain insight into the underlying control mechanism.
We analyse the population dynamics for the two enantiomeric forms for a given orientation. For one of the enantiomers the optimised pulse aims to minimise excited state population transfer altogether, or at least to return all intermittent population in the excited state back to the ground state at the end of the pulse. At the same time, for the mirror image, the optimised field tries to maximise population transfer to the excited state. The latter process (maximisation of population in the excited state for one enantiomer) is limited by the available fluence in the pulse. Specifically, taking into account the restrictions on field strength and the limited pulse length (cf. Section 2.3), the optimisation does not have enough resources to get a complete population transfer to the excited state. Remarkably, not all orientations are equally easy to control in terms of distinguishability. Every pulse-molecule geometry yields different values for the components of the permanent dipole and transition multipole moments in the control Hamiltonian, and small values of these moments can prevent the optimisation of CD altogether. Fig. 4 shows the fidelity F of the optimisation for different individual orientations of the system. Using the functional JT defined in eqn (11), this quantity is defined as
and takes the value 1 for perfectly distinguishable systems, and 0 for completely indistinguishable ones,
cf. our discussion in Section 2.3. A closer look at the values of the transition moments for different orientations shows that the possibility for improvement
via optimal control depends strongly on the interplay of the different components of the vectors: For instance, in the orientation
α = 1.35,
β = 2.62,
γ = 5.38, where anisotrpy appears not to be improvable, the value of the electric dipole transition moment
x component is one order of magnitude smaller than in the neighboring optimisable orientation
α = 0.45,
β = 2.62,
γ = 5.38. Similar relations, with one or more relevant transition moments becoming small, can be observed for several other areas that only show negligible improvement though optimisation.
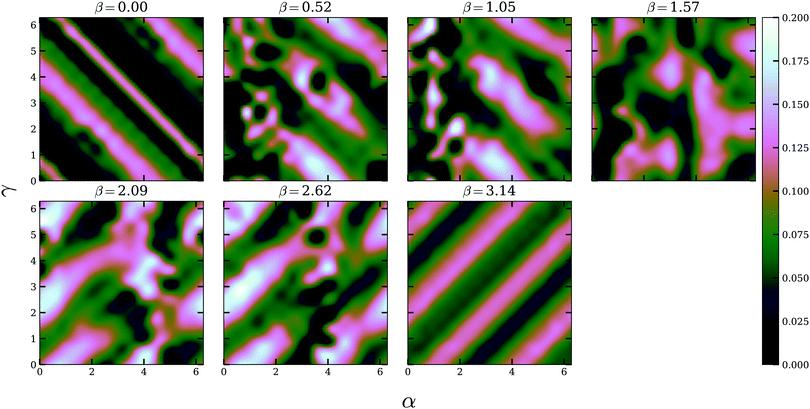 |
| | Fig. 4 Value of the fidelity (eqn (17)) optimised for individual orientations of fenchone as a function of the Euler angles α, β and γ. Lighter areas correspond to higher fidelities, i.e. better chiral distinguishability. | |
The fidelity obtained by considering the action of the pulse optimised for a rotational average (Fig. 2 and eqn (15)) on individual orientations is shown in Fig. 5. We can clearly see that the ensemble optimised pulse increases the distinguishability for a subset of orientations in the region 1.5 < β < 2.7 while having close to no effect on the rest. The reason for this is that due to the weighting factor sinβ appearing from the rotational averaging (cf.eqn (8)), orientations in that region have an above average contribution to the ensemble. This incentivises the optimisation algorithm to focus on this domain. By comparison to Fig. 4 we can see that the optimisation also targets those orientations intrinsically more favourable in terms of distinguishability.
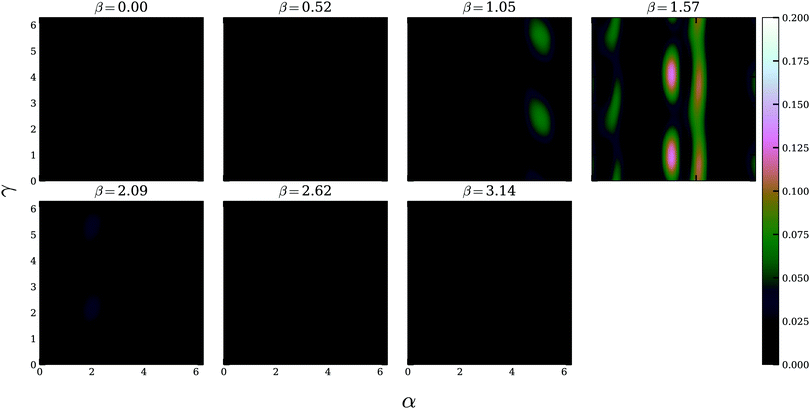 |
| | Fig. 5 Value of the fidelity (eqn (17)) after irradiation with the ensemble optimised pulse (Table 2 and Fig. 2) as a function of the Euler angles α, β and γ. Lighter areas correspond to higher fidelities, i.e. better chiral distinguishability. | |
4 Summary and conclusions
We have shown that optimal control can be used to increase the absorption contrast in the A-band of the two enantiomers of fenchone by independently shaping the x and y components of an external time–dependent electromagnetic field. In order to do so, we have developed a minimal molecular model, including only the electronic ground and first excited state of the molecule. Our model consistently includes all light-matter interaction terms up to one order beyond the dipole approximation, i.e. the electric and magnetic dipole transition moments (which are the leading-order contribution to CD), electric quadrupole moments, and permanent electric dipole moments. All these moments have been obtained from quantum chemical calculations at CCSD/6-31G level. The magnetic and electric dipole moments, including the permanent electric dipole, have a crucial contribution to the excitation dynamics, while the electric quadrupole has a significant, but smaller effect. We have obtained optimised pulses that increase the orientationally averaged contrast in the excited state population between the two enantiomers by almost a factor of twenty compared to a monochromatic circularly polarised pulse, while also decreasing the overall absorption to around a quarter compared to the guess pulse. These effects are a result of the interferences between the different excitation paths generated by the optimised pulses, which feature spectral contributions with frequency ω(1) and ω(1)/2 with ω(1) ≈ ωr, as well as a DC field component for the electric field. The DC component proves to be critical for the optimisation, while the ωr/2 contribution, coupling primarily to the quadrupole, has a smaller yet still clearly noticeable effect. As a result, we have shown that it is possible to achieve control for CD signatures by exploiting different multipolar contributions of the light–matter interaction, even in a basic two-level description. While such a description simplifies the electronic structure to only the ground and a single electronic excited state, the model still captures the excitation step of table-top experiments in the femtosecond regime, which can be afterwards translated to ionisation yields.
To rationalise the results of the ensemble optimisation, we have studied how the optimised pulse affects specific orientations of the fenchone molecule. We have observed that only a subset of geometries shows an increase in the population difference between ground and excited state compared to the guess pulse. In order to explain this behaviour, we have performed full optimisations on individual orientations sampling the whole rotational space. The optimisation results show that the regions where the rotational ensemble optimised pulse performs better correspond to domains in which the optimisation of individual orientations is more favourable. This is related to a stronger coupling, and hence an enhanced addressability, by virtue of larger overlaps between the molecular transition moments and the electromagnetic field.
In a next step, this knowledge is to be transferred to the experiment. Instrumental restrictions will influence the implementation of the optimised pulses: The pulse lengths and peak intensities are, albeit challenging, attainable in state-of-the-art table-top setups, but the optimised solutions also prominently feature a DC component for the electric field which may be problematic for an experimental implementation. Further optimisations show, that attempting to increase the CD signal with a more restricted protocol (i.e. removing the DC component of the field) leads to only marginal increase of the distinguishability, pointing towards the critical role of the DC field. A possible alternative to the DC component would be to include an off-resonant, near-IR pulse in the protocol. By phase-matching both the IR pulse and the high-frequency control, the former could introduce a relevant DC component to the driving. Several further avenues towards obtaining more easily realisable yet efficient pulses can be considered. A first option is to add more electronic levels in the model. This would add more excitation pathways that can be addressed simultaneously by a multicolored laser pulse. The interference between these pathways is expected to lead to better control mechanisms similarly to the case of PECD.14,15 Secondly, we have observed that the excited state population difference can be easily increased for particular orientations of the molecule with respect to the light pulse. This suggests that a pre-pulse which induces a partial orientation of the molecular ensemble might be a promising strategy.60 Moreover, it is conceivable to engineer an optimised pulse which both orients and excites the chiral molecules. Although such a study would require a description of different timescales to account for rotational dynamics, recent advances in controlling the rotational state of chiral molecules show a lot of promise in that direction.61
Conflicts of interest
There are no conflicts to declare.
Appendix
A Light–matter interaction beyond the electric dipole approximation
Circular dichroism is formed by the interplay between different electric and magnetic interaction terms, to first order the electric dipole and the magnetic dipole. Magnetic dipole transitions are usually much weaker than electric dipole transitions and comparable in strength to electric quadrupole transitions. To adequately describe all relevant orders in CD, we move beyond the commonly used electric dipole approximation and take into account the next-highest orders in the form of magnetic dipole effects and electric quadrupole effects. To this end, the electric field of an electromagnetic wave propagating along the z axis is written as a superposition of plane waves,| | 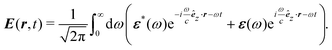 | (18) |
In this expression, the Fourier coefficients ε(ω) are vector quantities which describe the polarisation in the xy plane. By projecting the electric field onto the cartesian unit vectors êx and êy, eqn (18) can be brought into a more familiar form,| | | E(r,t) = Ex(r,t)êx + Ey(r,t)êy, | (19) |
with| | 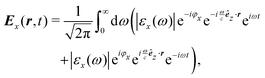 | (20) |
and analogous for the y component.
Eqn (20) describes the electric field of an electromagnetic wave propagating along the z direction. The first order beyond the dipole approximation is obtained by substituting:
| | 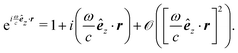 | (21) |
Introducing this into
eqn (20), we obtain:
| | | Ex(r,t) ≈ E(0)x(t) + E(1)x(r,t) | (22) |
| | 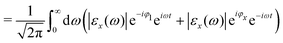 | (22a) |
| | 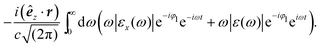 | (22b) |
By performing a Fourier transform to time domain, we finally arrive at the following expression,
| | 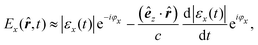 | (23) |
which, together with one of Maxwell's equations in Fourier space,
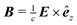
, defines an arbitrary elctromagnetic wave in the time domain beyond the electric dipole approximation to next highest order.
Acknowledgements
We would like to thank Thomas Baumert and Andrés Ordoñez for helpful discussions, and Marec Heger for providing the molecular model from Fig. 1. Financial support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Projektnummer 328961117—SFB ELCH 1319 is gratefully acknowledged.
References
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2018, 98, 063428 CrossRef CAS.
- K. E. Gunde, G. W. Burdicka and F. Richardson, Chem. Phys., 1996, 208, 195–219 CrossRef CAS.
- B. Jansk, A. Rizzo and H. Ågren, Chem. Phys. Lett., 2005, 414, 461–467 CrossRef.
- M. Stener, D. Di Tommaso, G. Fronzoni, P. Decleva and I. Powis, J. Chem. Phys., 2006, 124, 024326 CrossRef CAS PubMed.
- Y. Ma and A. Salam, Chem. Phys., 2006, 324, 367–375 CrossRef CAS.
- A. Rizzo, N. Lin and K. Ruud, J. Chem. Phys., 2008, 128, 164312 CrossRef PubMed.
- P. Horsch, G. Urbasch, K.-M. Weitzel and D. Kröner, Phys. Chem. Chem. Phys., 2011, 13, 2378–2386 RSC.
- D. Kröner, Phys. Chem. Chem. Phys., 2015, 17, 19643–19655 RSC.
- F. Pulm, J. Schramm, J. Hormes, S. Grimme and S. D. Peyerimhoff, Chem. Phys., 1997, 224, 143–155 CrossRef CAS.
- U. Boesl von Grafenstein and A. Bornschlegl, ChemPhysChem, 2006, 7, 2085–2087 CrossRef PubMed.
- R. Li, R. Sullivan, W. Al-Basheer, R. Pagni and R. Compton, J. Chem. Phys., 2006, 125, 144304 CrossRef CAS PubMed.
- A. Bornschlegl, C. Logé and U. Boesl, Chem. Phys. Lett., 2007, 447, 187–191 CrossRef CAS.
- H. G. Breunig, G. Urbasch, P. Horsch, J. Cordes, U. Koert and K.-M. Weitzel, ChemPhysChem, 2009, 10, 1199–1202 CrossRef CAS PubMed.
- R. E. Goetz, C. P. Koch and L. Greenman, Phys. Rev. Lett., 2019, 122, 013204 CrossRef CAS PubMed.
- R. E. Goetz, C. P. Koch and L. Greenman, J. Chem. Phys., 2019, 151, 074106 CrossRef PubMed.
-
M. Leibscher, E. Pozzoli, C. Pérez, M. Schnell, M. Sigalotti, U. Boscain and C. P. Koch, 2020.
- W. J. Meath and E. A. Power, J. Phys. B: At. Mol. Phys., 1987, 20, 1945–1964 CrossRef CAS.
- S. Brennecke and M. Lein, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 094005 CrossRef.
- S. Brennecke and M. Lein, Phys. Rev. A, 2018, 98, 063414 CrossRef CAS.
- A. Hartung, S. Brennecke, K. Lin, D. Trabert, K. Fehre, J. Rist, M. Schöffler, T. Jahnke, L. P. H. Schmidt and M. Kunitski,
et al.
, Phys. Rev. Lett., 2021, 126, 053202 CrossRef CAS PubMed.
- J. Maurer and U. Keller, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 094001 CrossRef CAS.
- A. Gorlach, O. Neufeld, N. Rivera, O. Cohen and I. Kaminer, Nat. Commun., 2020, 11, 1–11 CrossRef PubMed.
-
S. V. B. Jensen and L. B. Madsen, arXiv preprint, 2021, arXiv:2111.04995.
-
N. Berova, K. Nakanishi and R. W. Woody, Circular Dichroism: Principles and Applications, John Wiley & Sons, 2000 Search PubMed.
-
A. Zehnacker, Chiral Recognition in the Gas Phase, CRC Press, 2010 Search PubMed.
- D. Patterson and M. Schnell, Phys. Chem. Chem. Phys., 2014, 16, 11114–11123 RSC.
- U. Boesl, A. Bornschlegl, C. Logé and K. Titze, Anal. Bioanal. Chem., 2013, 405, 6913–6924 CrossRef CAS PubMed.
- A. Hong, C. M. Choi, H. J. Eun, C. Jeong, J. Heo and N. J. Kim, Angew. Chem., 2014, 126, 7939–7942 CrossRef.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, M. Hofmann, J. Rist, M. Weller, A. Hartung and L. P. H. Schmidt,
et al.
, Phys. Rev. Lett., 2021, 126, 083201 CrossRef CAS PubMed.
- T. Ring, C. Witte, S. Vasudevan, S. Das, S. Ranecky, H. Lee, N. Ladda, A. Senftleben, H. Braun and T. Baumert, Rev. Sci. Instrum., 2021, 92, 033001 CrossRef CAS PubMed.
-
R. V. Krems, Molecules in Electromagnetic Fields, Wiley, 2018 Search PubMed.
-
P. W. Milonni, An Introduction to Quantum Optics and Quantum Fluctuations, Oxford University Press, 2019 Search PubMed.
- M. H. Goerz, E. J. Halperin, J. M. Aytac, C. P. Koch and K. B. Whaley, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 032329 CrossRef.
- S. Bernadotte, A. J. Atkins and C. R. Jacob, J. Chem. Phys., 2012, 137, 204106 CrossRef PubMed.
- A. Ludwig, J. Maurer, B. W. Mayer, C. R. Phillips, L. Gallmann and U. Keller, Phys. Rev. Lett., 2014, 113, 243001 CrossRef CAS PubMed.
- A. D. Buckingham, Q. Rev., Chem. Soc., 1959, 13, 183–214 RSC.
- B. Ritchie, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 1411–1415 CrossRef.
- D. Loru, M. A. Bermúdez and M. E. Sanz, J. Chem. Phys., 2016, 145, 074311 CrossRef PubMed.
- G. Longhi, S. Abbate, R. Gangemi, E. Giorgio and C. Rosini, J. Phys. Chem. A, 2006, 110, 4958–4968 CrossRef CAS PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenaes, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjaergaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnaes, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CAS.
-
Dalton, a molecular electronic structure program, Release v2020.0 (2020), see http://daltonprogram.org.
- O. Christiansen, H. Koch, A. Halkier, P. Jørgensen, T. Helgaker and A. Sánchez de Merás, J. Chem. Phys., 1996, 105, 6921–6939 CrossRef CAS.
- O. Christiansen, A. Halkier, H. Koch, P. Jørgensen and T. Helgaker, J. Chem. Phys., 1998, 108, 2801–2816 CrossRef.
- A. Halkier, H. Koch, O. Christiansen, P. Jørgensen and T. Helgaker, J. Chem. Phys., 1997, 107, 849–866 CrossRef CAS.
- R. E. Goetz, T. A. Isaev, B. Nikoobakht, R. Berger and C. P. Koch, J. Chem. Phys., 2017, 146, 024306 CrossRef CAS PubMed.
- Q. Ansel, S. Probst, P. Bertet, S. J. Glaser and D. Sugny, Phys. Rev. A, 2018, 98, 023425 CrossRef CAS.
- L. Van Damme, Q. Ansel, S. Glaser and D. Sugny, Phys. Rev. A, 2018, 98, 043421 CrossRef.
- D. Basilewitsch, H. Yuan and C. P. Koch, Phys. Rev. Res., 2020, 2, 033396 CrossRef CAS.
- I. Barth and C. Lasser, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 235101 CrossRef.
- A. H. G. Rinnooy Kan and G. T. Timmer, Math. Prog., 1987, 39, 57–78 CrossRef.
- A. H. G. Rinnooy Kan and G. T. Timmer, Math. Prog., 1987, 39, 27–56 CrossRef.
- S. Kucherenko and Y. Sytsko, Comput. Optim. Appl., 2005, 30, 297–318 CrossRef.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313 CrossRef.
- M. J. Box, Comput. J., 1965, 8, 42–52 CrossRef.
- J. A. Richardson and J. L. Kuester, Commun. ACM, 1973, 16, 487–489 CrossRef.
-
S. G. Johnson, The NLopt nonlinear-optimization package, http://github.com/stevengj/nlopt.
-
QDYN Library, https://www.qdyn-library.net/.
- M. Goerz, D. Basilewitsch, F. Gago-Encinas, M. G. Krauss, K. P. Horn, D. M. Reich and C. Koch, SciPost Phys., 2019, 7, 080 CrossRef.
- W. Kuhn, Trans. Faraday Soc., 1930, 26, 293–308 RSC.
- C. P. Koch, M. Lemeshko and D. Sugny, Rev. Mod. Phys., 2019, 91, 035005 CrossRef CAS.
- I. Tutunnikov, L. Xu, R. W. Field, K. A. Nelson, Y. Prior and I. S. Averbukh, Phys. Rev. Res., 2021, 3, 013249 CrossRef CAS.
Footnotes |
| † Present address: Institut für Physikalische und Theoretische Chemie, Goethe Universität Frankfurt, Frankfurt am Main, Germany. E-mail: E-mail: manel.mondelo@chemie.uni-frankfurt.de. |
| ‡ Present address: Institut für Theoretische Physik, Universität Innsbruck, Germany. E-mail: E-mail: daniel.basilewitsch@uibk.ac.at. |
| § The discretised nature of the numerical sampling with respect to the orientational average could be an additional potential source of anisotropy. This can lead to some orientations appearing more favourable to the algorithm, which then drives the optimisation towards solutions with a particular spatial orientation. |
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Daniel
Basilewitsch‡
a,
Daniel
Basilewitsch‡
 a,
Hendrike
Braun
b,
Christiane P.
Koch
a,
Hendrike
Braun
b,
Christiane P.
Koch
 a and
Daniel M.
Reich
*a
a and
Daniel M.
Reich
*a
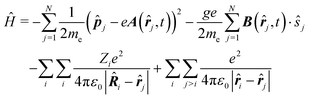
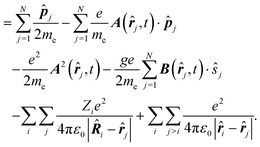
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) j,
j, ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) j and ŝj are the momentum, position and spin operators for the jth electron,
j and ŝj are the momentum, position and spin operators for the jth electron, ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) i and Zi are the position operator and nuclear charge for the ith nuclei, A(
i and Zi are the position operator and nuclear charge for the ith nuclei, A(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) j,t) is the vector potential, and B(
j,t) is the vector potential, and B(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) j,t) the magnetic field. Moreover, the constants e, me, g and ε0 correspond to the charge and mass of the electron, the spin g-factor and the vacuum permittivity. The terms containing squares of the vector potential A can be safely neglected outside the strong-field regime. More specifically, for optical or near UV wavelengths, this approximation is well-motivated for intensities I < 1018 W cm−2.35 Introducing the expansion of the electric field (see eqn (19) and (23) in Appendix A), and performing a suitable gauge transformation, the multipolar form of the light–matter interaction Hamiltonian becomes32,36 for an incident light field propagating in z direction,
j,t) the magnetic field. Moreover, the constants e, me, g and ε0 correspond to the charge and mass of the electron, the spin g-factor and the vacuum permittivity. The terms containing squares of the vector potential A can be safely neglected outside the strong-field regime. More specifically, for optical or near UV wavelengths, this approximation is well-motivated for intensities I < 1018 W cm−2.35 Introducing the expansion of the electric field (see eqn (19) and (23) in Appendix A), and performing a suitable gauge transformation, the multipolar form of the light–matter interaction Hamiltonian becomes32,36 for an incident light field propagating in z direction,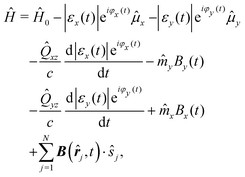
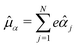
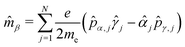
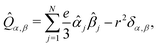
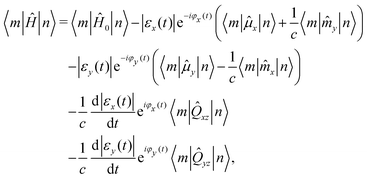
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ,t) in terms of the electric field via the Fourier space Maxwell equation
,t) in terms of the electric field via the Fourier space Maxwell equation 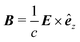 (see Appendix A for details on the expansion of the electric field).
(see Appendix A for details on the expansion of the electric field).
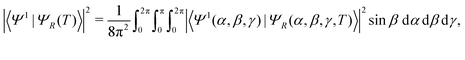
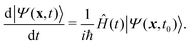
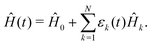
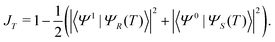
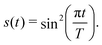
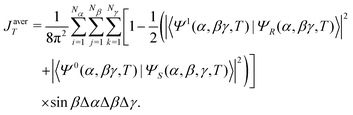
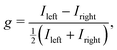


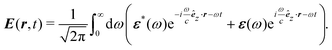
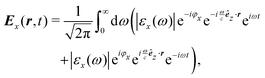
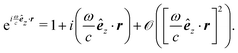
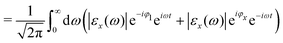
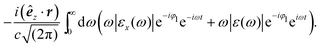
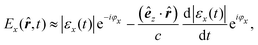
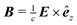 , defines an arbitrary elctromagnetic wave in the time domain beyond the electric dipole approximation to next highest order.
, defines an arbitrary elctromagnetic wave in the time domain beyond the electric dipole approximation to next highest order.