Lower limits for non-radiative recombination loss in organic donor/acceptor complexes†
Yun
Liu
 a,
Zilong
Zheng
a,
Zilong
Zheng
 bc,
Veaceslav
Coropceanu
bc,
Veaceslav
Coropceanu
 bd,
Jean-Luc
Brédas
bd,
Jean-Luc
Brédas
 bd and
David S.
Ginger
*a
bd and
David S.
Ginger
*a
aDepartment of Chemistry, University of Washington, Seattle, WA 98195-2120, USA. E-mail: dginger@uw.edu
bSchool of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA
cCollege of Materials Science and Engineering, Beijing University of Technology, Beijing 100124, China
dDepartment of Chemistry and Biochemistry, The University of Arizona, Tucson, AZ 85721-0088, USA
First published on 22nd May 2021
Abstract
Understanding the factors controlling radiative and non-radiative transition rates for charge transfer states in organic systems is important for applications ranging from organic photovoltaics (OPV) to lasers and LEDs. We explore the role of charge-transfer (CT) energetics, lifetimes, and photovoltaic properties in the limit of very slow non-radiative rates by using a model donor/acceptor system with photoluminescence dominated by thermally activated delayed fluorescence (TADF). This blend exhibits an extremely high photoluminescence quantum efficiency (PLQY = ∼22%) and comparatively long PL lifetime, while simultaneously yielding appreciable amounts of free charge generation (photocurrent external quantum efficiency EQE of 24%). In solar cells, this blend exhibits non-radiative voltage losses of only ∼0.1 V, among the lowest reported for an organic system. Notably, we find that the non-radiative decay rate, knr, is on the order of 105 s−1, approximately 4–5 orders of magnitude slower than typical OPV blends, thereby confirming that high radiative efficiency and low non-radiative voltage losses are achievable by reducing knr. Furthermore, despite the high radiative efficiency and already comparatively slow knr, we find that knr is nevertheless much faster than predicted by Marcus–Levich–Jortner two-state theory and we conclude that CT-local exciton (LE) hybridization is present. Our findings highlight that it is crucial to evaluate how radiative and non-radiative rates of the LE states individually influence the PLQY of charge-transfer states, rather than solely focusing on the PLQY of the LE. This conclusion will guide material selection in achieving low non-radiative voltage loss in organic solar cells and high luminescence efficiency in organic LEDs.
New conceptsThe fate of charge-transfer (CT) states formed at donor/acceptor interfaces is central to the operation of organic optoelectronics. Making CT states more luminescent has advantages in both charge-generating and light-emitting applications. Recently, quantum mechanical mixing of CT states with local excitons (CT-LE mixing) has gained attention as a way to make the CT states brighter by allowing a “dark” CT state to borrow intensity from a “bright” LE state. This effect gains importance when the CT and LE energies are similar. However, we show that it is possible for CT states in wide-gap blends to have photoluminescence quantum yields (PLQYs) higher than those of the individual components. Even when the CT and LE energies are relatively dissimilar, the electronic coupling between the lowest lying LE state and the CT state is nevertheless still important and can dominate the non-radiative transition rate. In such cases, the PLQY of the CT state can be compromised by CT-LE mixing as the CT state acquires a faster non-radiative decay rate from the LE. Material selection for highly efficient CT-based OLEDs and large-gap organic solar cells thus requires scrutiny of not just the PLQY of the LE state, but also the individual radiative and non-radiative lifetimes. |
Introduction
Donor–acceptor (D:A) blends are widely used in efficient organic light-emitting diodes (OLEDs) and organic photovoltaics (OPVs). Detailed balance arguments indicate that these two applications are two sides of the same coin,1,2 which, as OPVs have climbed to higher efficiencies, has led to the realization in the organic solar cell community that OPVs should also be bright (radiatively efficient) if they are to approach theoretical efficiency limits.3 Despite recent efforts to improve the luminescence efficiency of charge-transfer states, OPVs still largely suffer significant energy losses from non-radiative recombination3–5 compared to inorganic systems like perovskites or GaAs.6–9 Typically, polymer/fullerene-based OPVs have non-radiative voltage losses (ΔVnrOC) in the range of ∼0.3–0.4 V,10 with the most efficient polymer/non-fullerene systems reaching ΔVnrOC of 0.2–0.3 V.11–17 While these values approach those for commercial silicon (∼0.18 V),18 they still compare poorly with ΔVnrOC values of 0.027 V for GaAs8 and 0.034 V for emerging perovskite materials.9 The so-called “energy gap law”19 for non-radiative geminate recombination rates has been invoked to set the boundaries for the radiative efficiency of organic D:A blends. Furthermore, Vandewal and co-workers have suggested that organic blends should have intrinsically high non-radiative recombination rates due to the coupling of the electron transfer process with high-frequency intramolecular vibrations.10 Multiple groups have highlighted the importance of controlling reorganization energy and disorder to achieve high radiative efficiency.20–22 Despite these efforts, the radiative and non-radiative rates of organic (macro)molecules in OLEDs and OPVs are still not fully understood at the microscopic level. For example, remarkably emissive CT states have been reported with radiative efficiencies exceeding those predicted by the “energy gap law”.12,13,23,24 Along the same line, after it was demonstrated in 2012 that D:A exciplexes25 can be used to build efficient OLEDs, there have been major advances in exciplex-based OLEDs with external quantum efficiencies (EQEs) of 20.0% for blue and 24.0% for green emitting devices.26 Since many exciplex emitters rely on the thermally activated delayed fluorescence (TADF) mechanism, a significant amount of recent work was mainly focused on understanding intersystem crossing (ISC) and reverse ISC transitions. In contrast, understanding the transition rates of the exciplex or CT state itself has received less attention.To gain insight into the radiative and non-radiative rates of the CT state as well as the impact of these rates on the optoelectronic performance, we use a model TADF-emissive blend composed of 4,4′,4′′-tris[3-methylphenyl(phenyl)amino]triphenylamine (m-MTDATA) as the donor and tris-[3-(3-pyridyl)mesityl]borane (3TPYMB) as the acceptor. TADF blends, compared to typical donor/acceptor OPV blends, are luminescent systems with long PL lifetimes due to thermally activated reverse intersystem crossing from the lowest triplet state to the lowest singlet excited state.27–30 The m-MTDATA/3TPYMB blend is intriguing because it exhibits both a high photoluminescence quantum yield (PLQY ∼ 22%) and an appreciable photovoltaic external quantum efficiency (EQEPV max ∼24%) for converting incident photons into photocurrent.31–34 We find that the non-radiative decay rate is significantly faster than that predicted by the Marcus–Levich–Jortner (MLJ) two-state model within the realm of plausible molecular parameters. Combining our experimental and theoretical results, we conclude that hybridization of the CT states with the local exciton (LE) states speeds up the non-radiative decay and harms the photoluminescence quantum yield, leading to additional non-radiative recombination loss. Our results highlight the importance of controlling CT energetics, namely CT-LE hybridization, to achieve small non-radiative recombination loss in OPVs and high radiative efficiency in OLEDs.
Results
Photoluminescence properties
Fig. 1a shows the molecular structures and reported state energies of both m-MTDATA and 3TPYMB.31 We deposited (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) blend films of m-MTDATA:3TPYMB by thermal co-evaporation of the donor and acceptor materials. Fig. 1b shows the PL of the neat donor and acceptor materials, as well as the blend. Compared to neat donor and acceptor films, the m-MTDATA:3TPYMB blend shows a significantly red-shifted PL spectrum, consistent with charge-transfer state emission, indicating that charge and energy transfer from the local exciton to the CT state are highly efficient, in good agreement with previous reports.31,32
1) blend films of m-MTDATA:3TPYMB by thermal co-evaporation of the donor and acceptor materials. Fig. 1b shows the PL of the neat donor and acceptor materials, as well as the blend. Compared to neat donor and acceptor films, the m-MTDATA:3TPYMB blend shows a significantly red-shifted PL spectrum, consistent with charge-transfer state emission, indicating that charge and energy transfer from the local exciton to the CT state are highly efficient, in good agreement with previous reports.31,32
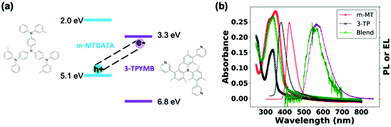 | ||
| Fig. 1 (a) State energies31 and molecular structures of m-MTDATA and 3TPYMB. (b) Absorption (-o-) and PL spectra (-) of neat donor (red), acceptor (black) and blend films/devices (green) overlaid with EL spectrum (purple) of the blend device. The PL spectrum of the blend was measured from the solar cell device stack. | ||
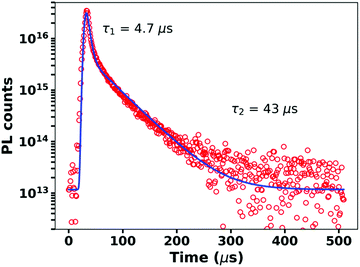
Fig. 2 shows the time-resolved photoluminescence (PL) from the blend measured at room temperature. We observe a clear bi-phasic PL decay with both prompt and delayed emission, characteristic of TADF materials. At 80 K, the delayed component slows down as thermally activated intersystem crossing, the rate-limiting step within this time range, is suppressed (Fig. S1, ESI†). Fig. 2 also shows fits of a bi-exponential decay to the observed PL kinetics, which yields lifetimes of 4.7 μs and 43 μs for the prompt and delayed decays, respectively. These values are consistent with previous reports on this system.31,32,34 On glass substrates, our blends exhibit a PLQY from the CT state of 22%. This PLQY value is 2–3 orders of magnitude higher than typical CT emission in OPVs.12,35 Based on our measured PLQYs and lifetimes, we determine the radiative (kr), intersystem crossing (kISC), and non-radiative (knr) rate constants of the singlet CT state (1CT) to be kr = 2.75 × 104 s−1, kISC = 8.9 × 104 s−1, and knr = 9.8 × 104 s−1, respectively (see ESI,† Section S1 for details on the rate calculation). Compared to previously reported kr and knr values for CT states in D/A OPV blends, the m-MTDATA/3TPYMB blend system exhibits what appears to be a remarkably slow non-radiative rate—roughly 5 orders of magnitude slower than commonly reported knr values for CT states (Table S1, ESI†).
Photovoltaic properties
Next, we explore the photovoltaic properties of the m-MTDATA:3TPYMB blend. We chose the following device structure: glass/ITO/PEDOT-PSS/MeO-TPD/m-MTDATA/m-TDATA:3TPYMB/3TPYMB/Bphen/LiF/Al, in order to avoid formation of any potentially interfering exciplexes at the interfaces of the active layer and transport layers. The device demonstrates a maximum incident photon to charge collection efficiency (EQEPV) of 24% (Fig. 3a). We measured the refractive indices via ellipsometry and modelled the absorption of the m-MTDATA:3TPYMB layer in the device (see Fig. S2, ESI†) using a transfer matrix algorithm to calculate the photovoltaic internal quantum efficiency (IQEPV).36 We find that IQEPV is over 40% over the region corresponding to the majority of the donor and acceptor absorption spectra. Fig. 3c shows the electroluminescence quantum yield (EQEEL) measured as a function of injected current density. In the best performing PV cell, we measure EQEEL to be 1.67% at injection current equivalent to short-circuit current at 1 sun illumination condition (average EQEEL = 1.82 ± 0.02%, number of devices, N = 6). We thus obtain the corresponding ΔVnrOC according to eqn (2) below to be only ∼100 meV, which places this system among the most emissive charge-generating organic photodiode structures, comparable to the best OLED-based OPVs reported so far (Fig. 3d).10,12,13,15,16,24,37–42Fig. 3b shows that under AM1.5G illumination conditions, the best performing PV cell yields a VOC of 2.12 V (2.12 ± 0.03 V, N = 6); however, despite a photocurrent EQEPV of ∼24%, JSC only reaches ∼0.1 mA cm−2 (0.09 ± 0.02 mA cm−2, N = 6) due to the wide bandgap and consequent poor overlap with the solar spectrum. | ||
| Fig. 3 (a) EQEPV and IQEPV spectra. (b) J–V curve measured under simulated AM1.5G illumination. (c) EL (red) and EQEPV (blue) spectra and re-created EQEPV (black) spectrum based on Rau's reciprocity theorem. The EL spectrum is divided by the blackbody radiation spectrum and multiplied by a scaling factor to match the low-energy EQE tail. (inset) Electroluminescence external quantum efficiency (EQEEL) measured at a range of injection current. (d) Survey of ΔVOVnr and ECT of previously reported CT-based donor/acceptor blends (blue and green),10,12,13,15,16,24,37–42 a previously reported OLED exciplex-based blend,37 and our blend. | ||
The experimental VOC of 2.12 V is 0.73 V lower than the Shockley–Queisser VOC limit (VSQOC) of 2.85 V for the bandgap of 3.239 eV. Thus, we next consider the factors governing the overall voltage loss in our CT-based TADF-emissive solar cell. Following the well-established framework based on detailed balance,43,44 we separate the VOC loss into two sources: (1) charge generation loss (ΔVSCOC), which is due to non-ideal EQEPV and (2) charge recombination loss, both radiative and non-radiative, where ΔVnrOC is related to energy loss due to non-radiative recombination (eqn (1)):
| VOC = VSQOC + ΔVSCOC + ΔVrOC + ΔVnrOC | (1) |
qΔVnrOC = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(EQEEL) ln(EQEEL) | (2) |
| E gap | V SQOC | ΔVSCOC | ΔVrOC | ΔVnrOC | V calcOC | V measOC |
|---|---|---|---|---|---|---|
| 3.239 eV | 2.85 V | −0.0484 V | −0.6 V | −0.104 V | 2.098 V | 2.11 V |
Transition rates in the Marcus–Levich–Jortner framework
At this point, we return to analyze the knr values in more detail. It is instructive to compare the emissive properties of the m-MTDATA:3TPYMB blend with those of the m-MTDATA and 3TPYMB components. We measured the radiative rate (kLEr), non-radiative rate (kLEnr) and PLQY, respectively, to be 5.14 × 107 s−1, 4.2 × 108 s−1 and 11% in m-MTDATA, and 6.44 × 107 s−1, 8.97 × 108 s−1 and 6% in 3TPYMB (see ESI,† Section S3 for details). Interestingly, the PLQY of the blend (22%) is over twice as large as the respective values for the D and A components. Another intriguing finding is that the non-radiative rate of the CT state is about four orders of magnitude slower than the non-radiative rates of the related local-exciton (LE) states despite the fact that the CT state is located about 0.7 eV and 1.0 eV below the emissive states of m-MTDATA and 3TPYMB, respectively.Therefore, it is of great interest (1) to examine in detail the radiative and non-radiative transition rates of the CT state and (2) to correlate the luminescence properties with the photovoltaic properties in order to understand whether a small non-radiative recombination loss is expected given the large bandgap in our system.
The radiative and non-radiative transitions involving CT states are commonly investigated within the two-state MLJ formalism (see ESI,† Section S4 for details).4,21,47–49 Briefly, in the MLJ framework, both radiative and non-radiative transitions are described as electron-transfer events between the CT and ground (G) states. We neglect the transitions between charge-carrier states and CT states, as it was previously shown that carrier recombination does not contribute to the PL kinetics of the CT states.32 Thus, this model assumes that the electronic coupling (VCT-G) between the CT and G states is much larger than that between the CT state and donor and/or acceptor LE state (VCT-LE). The non-radiative and radiative transition rates can then be written as a function of the adiabatic CT energy (ECT), electronic coupling (VCT-G), classical (λc) and quantum mechanical (λqm) components of the total reorganization energy (λt = λc + λqm), frequency of an effective quantum vibrational mode (ωqm), and transition dipole moment (dCT). The MLJ model has previously been used extensively to rationalize the experimental non-radiative voltage losses in polymer/NFA,12,13,15,16,24,38–40 polymer/fullerene,10,13,24,37,41,42 and OLED-based OPV materials37 (see ESI,† Section S4 for details and further discussion on the two-state MLJ model).
In order to estimate the non-radiative decay rate constant, the microscopic parameters mentioned above have to be determined first. On the theoretical side, we started by carrying out molecular dynamics (MD) simulations to gain insight into the nano-/meso-scale morphology of the m-MTDATA:3TPYMB (Fig. 4a) blend. We then computed the energy distributions of the lowest excited CT and LE states as well as of the VCT-G and VCT-LE electronic couplings, by performing time-dependent DFT (TDDFT) calculations at the SRSH-ωPBE-D3/6-31G(d) level of theory for 1500 D–A complexes extracted from the MD-derived film morphology. In addition, we performed geometry optimizations of the neutral and charged configurations of the m-MTDATA and 3TPYMB molecules to estimate the intramolecular contributions to the reorganization energy λt. Fig. 4b shows that the singlet (1CT) and triplet (3CT) CT states have similar energy distributions, with the singlet–triplet energy splitting not exceeding 2 meV. The energy distribution of the lowest triplet state in the m-MTDATA molecule overlaps with the 1CT and 3CT distributions.50 Since the spin–orbit coupling between pure CT states is zero,51 the observed proximity between LE and CT states could play a significant effect on the ISC transitions between exciplex states.
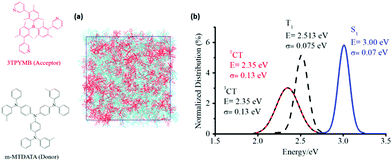 | ||
| Fig. 4 (a) Illustration of the simulated morphologies of the m-MTDATA:3TPYMB blend. (b) Distributions of the calculated energies of the lowest CT and LE singlet and triplet states. | ||
Fig. 5 displays the results derived for the electronic couplings and reorganization energies. Fig. 5a and b shows that the electronic couplings between the singlet CT state and the first LE singlet excited state (VCT-LE) and those between the CT state and the ground state (VCT-G) have exponential-type energy distributions with average values of 3 meV for VCT-LE and 6 meV for VCT-G. We estimate the overall reorganization energy to be 0.41 eV, with 0.18 eV coming from the D component and 0.23 eV from the A component. As seen from Fig. 5c and d, the partition of the reorganization energy over the normal modes indicates that a significant contribution to the reorganization energy comes from low-energy (classical) vibrational modes.
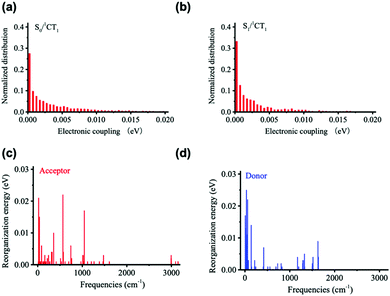 | ||
| Fig. 5 Distributions of (a) VCT-G and (b) VCT-LE electronic couplings, and vibrational normal-mode contributions to the (c) acceptor and (d) donor reorganization energy components of λt. | ||
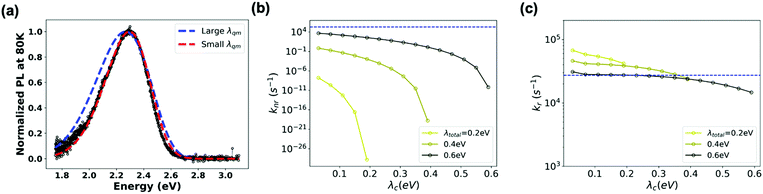
On the experimental side, information on the microscopic parameters can be obtained from the intensity and profile of the absorption or emission CT band.52–54 Here, we estimated ECT, λt, λqm and ωqm by fitting the profile of the blend PL band measured at 80 K to an extended version of the MLJ model that accounts for static disorder (see eqn (S11), ESI†). As seen from Fig. 6a (red trace), an excellent simulation of the CT band can be obtained by using: ECT = 2.65 eV, λt = 0.4 eV, λqm = 0.25 eV, ωqm = 0.1 eV, and σs = 70 meV for the standard deviation of static disorder (70 meV is in the range of reported values for other D:A blends55). For high-energy CT systems, such as the TADF-based system in this study and OLED-material-based systems, the non-radiative transition rates can vary by orders of magnitude as a function of the reorganization energy (and are particularly sensitive to λqm) (see Fig. S5, ESI†). Since the MLJ fitting procedure depends on the multiple parameters listed above and thus is not unique, we checked what could be the upper limit of the reorganization energy. We found that MLJ calculations employing λqm of 0.39 eV or larger yield broader PL bands than that observed experimentally, even for negligible values of λc (Fig. 6a). Thus, we conclude that, in the present system, λqm must be smaller than 0.39 eV. This conclusion is in good agreement with the results of the quantum-mechanical calculations described above, which yield a value of 0.41 eV for the total reorganization energy λt.
We next use the Mulliken–Hush formalism to estimate the VCT-G electronic coupling:53
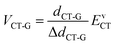 | (3) |
Based on these parameters, we calculated kr and knr within the MLJ framework (see ESI,† Section S4 for details). Fig. 6b and c highlight that a variation of λt (and λqm) in the range of 0.2–0.6 eV results in a variation of the non-radiative transition rates by many orders of magnitude, whereas the radiative transition rates exhibit a less dramatic response. Intriguingly, if we employ the microscopic parameters reported above: VCT-G = 0.01 eV, ECT = 2.65 eV, λt = 0.4 eV, λqm = 0.25 eV, ωqm = 0.1 eV and σs = 70 meV, we find that the MLJ theory estimate for knr is about 8 orders of magnitude smaller than the experimental value. To reproduce the experimental knr value using the MLJ model would require λt values exceeding 0.6 eV and coming nearly exclusively from quantum vibrational modes (Fig. 6b). However, if such high λt were actually the case, the MLJ model predicts that the PL emission spectrum would be significantly broader and shifted from the experimental absorption spectrum. Since the actual situation is inconsistent with this picture, we must conclude that the MLJ framework is unable to provide a self-consistent description of the transition rates and PL spectrum of the m-MTDATA:3TPYMB blend. More importantly, this crosschecking exercise again highlights the importance of using the appropriate microscopic parameters, especially reorganization energy, when predicting CT kinetics and thus non-radiative voltage loss: While it may be possible to fit spectra and rates, doing so with unphysical molecular parameters would not provide the sought-after physical insight.
Three-state model
From this discussion, it is not surprising that high-energy CT systems could exhibit very small non-radiative decay rates. For the m-MTDATA:3TPYMB blend, the question in fact is why the experimental non-radiative rate is dramatically faster than that expected in the framework of the MLJ model, even though it appears much slower than most of the reported values for (lower energy) organic CT states. Finding the explanation requires going beyond the two-state model. Since the local exciton states formed on m-MTDATA and 3TPYMB efficiently dissociate into CT states, it means that that the LE and CT states are also electronically coupled. According to our DFT calculations, the coupling between the CT state and lowest LE state (VCT-LE) is about 3 meV. We have previously shown that a three-state model, which accounts for the couplings of the CT state with both the LE and ground states, is needed in order to rationalize the radiative and non-radiative transitions from inter-molecular and intra-molecular CT states.57 In fact, as we have recently found in the case of D–A neutral radical systems, when the LE state exhibits large non-radiative rates, even a modest hybridization between the LE and CT states can result in a significant increase in the CT knr value.58 The experimental optical-gap (adiabatic) energies (ELE) are 3.09 eV in m-MTDATA and 3.5 eV in 3TPYMB (see ESI,† Section S3). The knr value for the CT state when considering CT-LE hybridization can be roughly estimated as:58,59| knr = (1 − fCT-LE)kMLJnr + fCT-LEkLEnr | (4) |
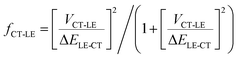 | (5) |
Using the experimental kLEnr rates for m-MTDATA and 3TPYMB, the experimental optical-gap (adiabatic) energy (see ESI,† Section S3), and the DFT electronic coupling between the CT and LE states (assuming that this coupling is the same for both m-MTDATA and 3TPYMB), we estimate that CT-LE mixing leads to an increase in knr by a factor of about 3 × 104 s−1; this value is in very good qualitative agreement with the experimental value of 9.8 × 104 s−1. To rationalize the kr value in the context of the three-state model, a similar procedure can be performed for the transition dipole moments:60,61
| (dCTr)2 = (1 − fCT-LE)(dCT-G)2 + fCT-LE(dLEr)2 | (6) |
These findings for the m-MTDATA:3TPYMB system indicate that in D:A blends with CT energies above 2 eV, the PLQY of the blend can be much larger than the PLQY values of the pristine D and A components as a result of the very small intrinsic non-radiative rates of the CT states. However, the blend's PLQY can be negatively affected by CT-LE mixing since the large knr value of the LE state can significantly speed up the CT-state knr. Overall, what these results tell us is that a strong hybridization between the CT and ground states, and a weak hybridization between the CT and LE states can result in blends with very large PLQYs even for D and A components with moderate individual PLQY values.
This phenomenon is in stark contrast with what is found in donor/acceptor blends commonly used for OPV applications. According to the Shockley–Queisser model, to obtain highly efficient solar cells, the bandgap (and hence CT-state energies) should be in the range of 1.0–1.6 eV.1 In such instances, the CT non-radiative rates are significant. Thus, in order to minimize the non-radiative voltage loss, CT-LE mixing with an LE state having a high PLQY is beneficial, in such a way that the CT-state emission can “borrow intensity” from the LE state.3,24,57 A small LE-CT energy gap is then desirable in this case.24
In order to better illustrate the effect of CT-LE hybridization over a range of CT energies, we calculated the blend's (CT) PLQY as a function of LE-CT energy (Fig. 7, red trace). In this calculation, the electronic couplings between the CT states and the ground and LE states (VCT-G and VCT-LE), the transition dipole moment (dCT-G, estimated according to eqn (3)), the LE adiabatic energy (ELE), and the LE radiative and non-radiative rates (kLEr and kLEnr) are fixed as given in the Fig. 7 caption. In the two-state model (Fig. 7, black trace), the blend's PLQY saturates when ECT approaches 2 eV because knr is significantly smaller than kr. In the three-state model, however, the maximum PLQY of the blend is obtained at CT energies of about 2 eV. When the adiabatic energy of the CT state approaches that of the LE states, the CT-LE hybridization becomes “activated” and the LE-state large knr value carries over to the CT knr (Fig. 7b), which reduces the blend's PLQY.
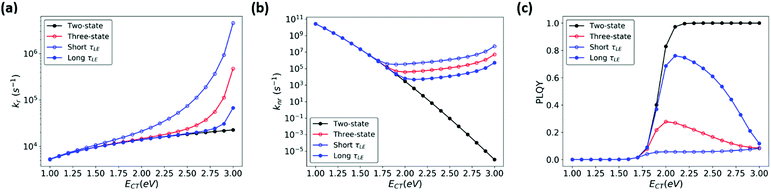 | ||
| Fig. 7 (a) kr (b) knr, and (c) PLQY calculated for a range of ECT values, based on two-state MLJ (black) and three-state models (blue and red). The red line represents results based on a three-state model using the LE lifetime (Table S1, ESI,†τLE = 2.12 ns), while the blue traces represent results from three-state model calculations where τLE was increased (shown in solid circles) or decreased (shown in open circles) by 10-fold, by manipulating kr and knr simultaneously. Parameters used: ECT = 1.0–3.0 eV, VCT-G =10 meV and VCT-LE = 10 meV, dCT-G = 0.049 D, dLEr = 3.58 D, kLEnr = 4.2 × 108 s−1, kLEr = 5.14 × 107 s−1 are based on parameters for pure m-MTDATA and the blend (Table S1, ESI†). | ||
Recent OPV studies concluded that in the context of CT-LE mixing, the LE PLQY sets an upper limit for the CT PLQY. We wondered whether this holds true in the case of high-gap blends, where the LE knr contributes significantly to the CT knr. We calculated the CT transition rates and PLQY, while keeping PLQYLE fixed at 10% but considering a range of values for the LE lifetimes (τLE). Fig. 7 shows that τLE can affect the blend's PLQY. Specifically, when τLE becomes longer, the blend's PLQY increases (Fig. 7c, solid blue circles), whereas a shorter τLE (open blue circles) leads to smaller PLQY of the blend. Furthermore, we evaluated the influence of PLQYLE on the blend (ESI,† Section S7). In this series of calculations, we increased kLEr or decreased kLEnr to obtain a higher PLQYLE (80%) (Fig. S9, ESI†). The blend's (CT) PLQY maximizes when PLQYLE is increased by reducing kLEnr rather than increasing kLEr. Here as well, a longer τLE is beneficial for the blend's PLQY at higher CT energies. Finally, we show in Fig. S10 and S11 (ESI†) that a moderate change of the electronic couplings has little effect on the CT PLQY. Thus, for blends with large LE PLQY values, the CT PLQY increases systematically with an increase in CT energy. This finding is in line with the data obtained for blends where, upon blend dilution, the blend emission energy and PLQY increase concomitantly.62,63
Conclusions
In summary, we have demonstrated that a highly emissive and charge-generating organic photovoltaic blend based on a TADF-emitting CT state can exhibit an extremely small non-radiative recombination loss, ΔVnrOC, of only ∼0.1 V and a photocurrent EQEmax of 24%. Compared to previously reported OPV blends, this model system demonstrates an extremely slow non-radiative recombination rate of 9.8 × 104 s−1, approximately 4 to 5 orders of magnitude slower than in typical efficient polymer/NFA blends.In this context, we re-examined the “Energy Gap Law” for non-radiative voltage loss by using the two-state Marcus–Levich–Jortner approach20 and tuning the molecular parameters such as reorganization energy and change in dipole moment. We find that, for values of reorganization energies that are consistent with the spectral lineshapes in the MLJ picture, the non-radiative recombination rate in our blend is much faster than the MLJ model estimates.
As a result, we conclude that a three-state model that includes the local exciton state in addition to the CT and ground states is required to understand our observations. We show that the hybridization between the CT and LE states, which was previously considered to enhance only the radiative decay rates of the CT states (via intensity borrowing), can in fact also speed up the non-radiative decay, thus compromising the CT PLQY. Furthermore, in the context of the three-state model, for organic blends with CT energies over 2.0 eV, to achieve an optimal PLQY requires not only choosing low-gap components with a high PLQY, but also an evaluation of how the kr and knr rates from the LE states tune the CT PLQY via CT-LE mixing. This consideration must inform the material selection for high-gap CT-based OLEDs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work at the University of Washington (YL and DSG) was supported by the Office of Naval Research through grant numbers N00014-17-1-2201 and N00014-20-1-2191. The theoretical work was supported by the Department of Energy through grant number DEEE0008205 (at the Georgia Institute of Technology), the Office of Naval Research in the framework of Award No. N00014-20-1-2110 (at the University of Arizona), as well as by the University of Arizona. Ellipsometry and time-resolved PL measurements were conducted at the Molecular Analysis Facility, a National Nanotechnology Coordinated Infrastructure site at the University of Washington, which is supported in part by the National Science Foundation (grant ECC-1542101), the University of Washington, the Molecular Engineering & Sciences Institute, the Clean Energy Institute, and the National Institutes of Health. We thank Dr Jian Wang, Dr Mark Ziffer, and Karisse Yamamoto for valuable discussions.Notes and references
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- O. D. Miller, E. Yablonovitch and S. R. Kurtz, IEEE J. Photovoltaics, 2012, 2, 303–311 Search PubMed.
- V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Nat. Rev. Mater., 2019, 4, 689–707 CrossRef.
- X. Liu, Y. Li, K. Ding and S. Forrest, Phys. Rev. Appl., 2019, 11, 024060 CrossRef CAS.
- Y. Xie and H. Wu, Mater. Today Adv., 2020, 5, 100048 CrossRef.
- I. L. Braly, D. W. Dequilettes, L. M. Pazos-Outón, S. Burke, M. E. Ziffer, D. S. Ginger and H. W. Hillhouse, Nat. Photonics, 2018, 12, 355–361 CrossRef CAS.
- D. W. Dequilettes, S. Koch, S. Burke, R. K. Paranji, A. J. Shropshire, M. E. Ziffer and D. S. Ginger, ACS Energy Lett., 2016, 1, 438–444 CrossRef CAS.
- M. A. Green, E. D. Dunlop, J. Hohl-Ebinger, M. Yoshita, N. Kopidakis and A. W. Y. Ho-Baillie, Prog. Photovoltaics Res. Appl., 2020, 28, 3–15 CrossRef.
- J. J. Yoo, S. Wieghold, M. C. Sponseller, M. R. Chua, S. N. Bertram, N. T. P. Hartono, J. S. Tresback, E. C. Hansen, J. P. Correa-Baena, V. Bulović, T. Buonassisi, S. S. Shin and M. G. Bawendi, Energy Environ. Sci., 2019, 12, 2192–2199 RSC.
- J. Benduhn, K. Tvingstedt, F. Piersimoni, S. Ullbrich, Y. Fan, M. Tropiano, K. A. McGarry, O. Zeika, M. K. Riede, C. J. Douglas, S. Barlow, S. R. Marder, D. Neher, D. Spoltore and K. Vandewal, Nat. Energy, 2017, 2, 17053 CrossRef CAS.
- N. An, Y. Cai, H. Wu, A. Tang, K. Zhang, X. Hao, Z. Ma, Q. Guo, H. S. Ryu, H. Y. Woo, Y. Sun and E. Zhou, Adv. Mater., 2020, 2002122, 1–7 Search PubMed.
- M. E. Ziffer, S. B. Jo, H. Zhong, L. Ye, H. Liu, F. Lin, J. Zhang, X. Li, H. W. Ade, A. K.-Y. Jen and D. S. Ginger, J. Am. Chem. Soc., 2018, 140, 9996–10008 CrossRef CAS.
- S. Liu, J. Yuan, W. Deng, M. Luo, Y. Xie, Q. Liang, Y. Zou, Z. He, H. Wu and Y. Cao, Nat. Photonics, 2020, 14, 300–305 CrossRef CAS.
- Y. Cui, H. Yao, J. Zhang, T. Zhang, Y. Wang, L. Hong, K. Xian, B. Xu, S. Zhang, J. Peng, Z. Wei, F. Gao and J. Hou, Nat. Commun., 2019, 10, 2515 CrossRef PubMed.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X.-K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J.-L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed.
- X. Liu, X. Du, J. Wang, C. Duan, X. Tang, T. Heumueller, G. Liu, Y. Li, Z. Wang, J. Wang, F. Liu, N. Li, C. J. Brabec, F. Huang and Y. Cao, Adv. Energy Mater., 2018, 8, 1–9 Search PubMed.
- Y. Cui, H. Yao, J. Zhang, K. Xian, T. Zhang, L. Hong, Y. Wang, Y. Xu, K. Ma, C. An, C. He, Z. Wei, F. Gao and J. Hou, Adv. Mater., 2020, 1908205, 1–7 Search PubMed.
- T. Kirchartz, U. Rau, M. Kurth, J. Mattheis and J. H. Werner, Thin Solid Films, 2007, 515, 6238–6242 CrossRef CAS.
- R. Engleman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef.
- M. Azzouzi, J. Yan, T. Kirchartz, K. Liu, J. Wang, H. Wu and J. Nelson, Phys. Rev. X, 2018, 8, 1–14 Search PubMed.
- F. J. Kahle, A. Rudnick, H. Bässler and A. Köhler, Mater. Horiz., 2018, 5, 837–848 RSC.
- M. Panhans, S. Hutsch, J. Benduhn, K. S. Schellhammer, V. C. Nikolis, T. Vangerven, K. Vandewal and F. Ortmann, Nat. Commun., 2020, 11, 1–10 Search PubMed.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X. K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J. L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed.
- F. D. Eisner, M. Azzouzi, Z. Fei, X. Hou, T. D. Anthopoulos, T. J. S. Dennis, M. Heeney and J. Nelson, J. Am. Chem. Soc., 2019, 141, 6362–6374 CrossRef CAS PubMed.
- G. Giro, M. Cocchi, J. Kalinowski, P. Di Marco and V. Fattori, Chem. Phys. Lett., 2000, 318, 137–141 CrossRef CAS.
- M. Zhang, C. Zheng, H. Lin and S.-L. Tao, Mater. Horiz., 2021, 8, 401–425 RSC.
- S. M. King, S. I. Hintschich, D. Dai, C. Rothe and A. P. Monkman, J. Phys. Chem. C, 2007, 111, 18759–18764 CrossRef CAS.
- X. Chen, D. Kim and J. Bredas, Acc. Chem. Res., 2018, 51, 2215–2224 CrossRef CAS PubMed.
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 2956–2961 CrossRef CAS PubMed.
- P. L. Santos, F. B. Dias and A. P. Monkman, J. Phys. Chem. C, 2016, 120, 18259–18267 CrossRef.
- K. Goushi, K. Yoshida, K. Sato and C. Adachi, Nat. Photonics, 2012, 6, 253–258 CrossRef CAS.
- P. B. Deotare, W. Chang, E. Hontz, D. N. Congreve, L. Shi, P. D. Reusswig, B. Modtland, M. E. Bahlke, C. K. Lee, A. P. Willard, V. Bulovic, T. Van Voorhis and M. A. Baldo, Nat. Mater., 2015, 14, 1130–1134 CrossRef CAS PubMed.
- W. Chang, D. N. Congreve, E. Hontz, M. E. Bahlke, D. P. Mcmahon, T. Van Voorhis, M. A. Baldo, S. Reineke, T. C. Wu and V. Bulovic, Nat. Commun., 2015, 1–6 Search PubMed.
- N. Bunzmann, S. Weissenseel, L. Kudriashova, J. Gruene, B. Krugmann, J. V. Grazulevicius, A. Sperlich and V. Dyakonov, Mater. Horiz., 2020, 7, 1126–1137 RSC.
- D. B. Sulas, E. J. Rabe and C. W. Schlenker, J. Phys. Chem. C, 2017, 121, 26667–26676 CrossRef CAS.
- S. J. Byrnes, 2018, arXiv 1603.02720v3, 1–20.
- S. Ullbrich, J. Benduhn, X. Jia, V. C. Nikolis, K. Tvingstedt, F. Piersimoni, S. Roland, Y. Liu, J. Wu, A. Fischer, D. Neher, S. Reineke, D. Spoltore and K. Vandewal, Nat. Mater., 2019, 18, 459–464 CrossRef CAS PubMed.
- W. Zhao, D. Qian, S. Zhang, S. Li, O. Inganäs, F. Gao and J. Hou, Adv. Mater., 2016, 28, 4734–4739 CrossRef CAS PubMed.
- J. Zhang, B. Kan, A. J. Pearson, A. J. Parnell, J. F. K. Cooper, X. K. Liu, P. J. Conaghan, T. R. Hopper, Y. Wu, X. Wan, F. Gao, N. C. Greenham, A. A. Bakulin, Y. Chen and R. H. Friend, J. Mater. Chem. A, 2018, 6, 18225–18233 RSC.
- J. Liu, S. Chen, D. Qian, B. Gautam, G. Yang, J. Zhao, J. Bergqvist, F. Zhang, W. Ma, H. Ade, O. Inganäs, K. Gundogdu, F. Gao and H. Yan, Nat. Energy, 2016, 1, 16089–16095 CrossRef CAS.
- N. A. Ran, J. A. Love, C. J. Takacs, A. Sadhanala, J. K. Beavers, S. D. Collins, Y. Huang, M. Wang, R. H. Friend and G. C. Bazan, Adv. Mater., 2016, 1482–1488 CrossRef CAS PubMed.
- C. Wang, X. Xu, W. Zhang, J. Bergqvist, Y. Xia, X. Meng, K. Bini, W. Ma, A. Yartsev, K. Vandewal, M. R. Andersson, O. Inganäs, M. Fahlman and E. Wang, Adv. Energy Mater., 2016, 6, 1–10 Search PubMed.
- U. Rau, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 1–8 CrossRef.
- U. Rau, B. Blank, T. C. M. Müller, T. Kirchartz and F. Jülich, Phys. Rev. Appl., 2017, 044016 CrossRef.
- D. Baran, T. Kirchartz, S. Wheeler, S. Dimitrov, M. Abdelsamie, J. Gorman, R. S. Ashraf, S. Holliday, A. Wadsworth, N. Gasparini, P. Kaienburg, H. Yan, A. Amassian, C. J. Brabec, J. R. Durrant and I. Mcculloch, Energy Environ. Sci., 2016, 9, 3783–3793 RSC.
- S. Ullbrich, J. Benduhn, X. Jia, V. C. Nikolis, K. Tvingstedt, F. Piersimoni, S. Roland, Y. Liu, J. Wu, A. Fischer, D. Neher, S. Reineke, D. Spoltore and K. Vandewal, Nat. Mater., 2019, 18, 459–464 CrossRef CAS PubMed.
- J. Jortner, J. Chem. Phys., 1976, 64, 4860–4867 CrossRef CAS.
- M. Azzouzi, J. Yan, T. Kirchartz, K. Liu, J. Wang, H. Wu and J. Nelson, Phys. Rev. X, 2018, 8, 031055 CAS.
- T. Wang, V. Coropceanu and J.-L. Brédas, Chem. Mater., 2019, 31, 6239–6248 CrossRef CAS.
- Z. Zheng, N. R. Tummala, Y. T. Fu, V. Coropceanu and J. L. Brédas, ACS Appl. Mater. Interfaces, 2017, 9, 18095–18102 CrossRef CAS PubMed.
- B. T. Lim, S. Okajima, A. K. Chandra and E. C. Lim, Chem. Phys. Lett., 1981, 79, 22–27 CrossRef CAS.
- N. S. Hush, Electrochim. Acta, 1968, 13, 1005–1023 CrossRef CAS.
- N. S. Hush, Prog. Inorg. Chem., 1967, 8, 391–444 CAS.
- R. S. Mulliken, J. Am. Chem. Soc., 1952, 74, 811–824 CrossRef CAS.
- T. M. Burke, S. Sweetnam, K. Vandewal and M. D. McGehee, Adv. Energy Mater., 2015, 5, 1500123 CrossRef.
- D. H. Oh, M. Sano and S. G. Boxer, J. Am. Chem. Soc., 1991, 113, 6880–6890 CrossRef CAS.
- X.-K. Chen, V. Coropceanu and J.-L. Brédas, Nat. Commun., 2018, 9, 5295 CrossRef CAS PubMed.
- E. Cho, V. Coropceanu and J. L. Brédas, J. Am. Chem. Soc., 2020, 142, 17782–17786 CrossRef CAS PubMed.
- I. R. Gould and S. Farid, J. Phys. Chem. B, 2007, 111, 6782–6787 CrossRef CAS PubMed.
- M. Bixon, J. Jortner, J. Cortes, H. Heitele and M. E. Michel-Beyerle, J. Phys. Chem., 1994, 98, 7289–7299 CrossRef CAS.
- M. Bixon, J. Jortner and J. W. Verhoeven, J. Am. Chem. Soc., 1994, 116, 7349–7355 CrossRef CAS.
- M. Chapran, P. Pander, M. Vasylieva, G. Wiosna-Salyga, J. Ulanski, F. B. Dias and P. Data, ACS Appl. Mater. Interfaces, 2019, 11, 13460–13471 CrossRef CAS PubMed.
- M. Colella, A. Danos and A. P. Monkman, J. Phys. Chem. Lett., 2019, 10, 793–798 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1mh00529d |
| This journal is © The Royal Society of Chemistry 2022 |