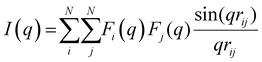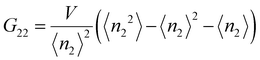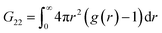Cryogenic electron tomography to determine thermodynamic quantities for nanoparticle dispersions

Abstract

Here we present a method to extract thermodynamic quantities for nanoparticle dispersions in solvents. The method is based on the study of tomograms obtained from cryogenic electron tomography (cryoET). The approach is demonstrated for gold nanoparticles (diameter < 5 nm). Tomograms are reconstructed from tilt-series 2D images. Once the three-dimensional (3D) coordinates for the centres of mass of all of the particles in the sample are determined, we calculate the pair distribution function g(r) and the potential of mean force U(r) without any assumption. Importantly, we show that further quantitative information from 3D tomograms is readily available as the spatial fluctuation in the particles’ position can be efficiently determined. This in turn allows for the prompt derivation of the Kirkwood–Buff integrals with all their associated quantities such as the second virial coefficient. Finally, the structure factor and the agglomeration states of the particles are evaluated directly. These thermodynamic quantities provide key insights into the dispersion properties of the particles. The method works well both for dispersed systems containing isolated particles and for systems with varying degrees of agglomerations.

---

New concepts

Currently, once a dispersion of nanoparticles is formed, very little can be quantitatively known about the thermodynamic state of such dispersion. In this paper we present a whole methodology to derive the radial distribution function, the potential of mean force, the aggregation state, and the structure factor for a generic dispersion of nanoparticles in water. We show that all this information can be readily retrieved from cryogenic electron tomography (cryoET). Furthermore, we prove that image segmentation allows for the determination of the spatial fluctuations in the sample allowing for the calculation of Kirkwood–Buff integrals, that in turn allow to calculate a large number of key statistical thermodynamics quantities.

Introduction

Nanoparticles (NPs) have been the subject of intense research in the last thirty years. They are used in their dispersed form in many putative applications (e.g. nanomedicine) as well as in the most common processing steps.^1–3 To date, there is still significant uncertainty on the colloidal properties of these particles, as determining their state is a significant challenge.^4,5 Colloids with characteristic dimension in the hundreds of nanometres are known to follow DLVO (Boris Derjaguin and Lev Landau, Evert Verwey and Theodoor Overbeek) theory when dispersed in a liquid.^6–8 Their theoretical framework has been validated thanks to a large body of experimental evidence that can reconstruct the three dimensional (3D) position of the micro-particles in their dispersed state.^9–20 Here we present a systematic method to characterize the 3D structure of NPs dispersed in a solvent in a manner common to mixtures of molecular solutions. From the centre-of-mass positions of NPs, the radial distribution function (RDF) g(r) and the potential of mean force (PMF), U(r) between NPs can be determined, leading further to a series of other important thermodynamics quantities. To the best of our knowledge, extracting these quantities without any assumptions has not been achieved before.

Several methods have been used for understanding nanoparticle interactions in solution. Analytical ultracentrifugation (AUC) measures the deviation from ideal solution behaviours of NPs dispersion by means of the osmotic pressure (AUC-sedimentation equilibrium, AUC-SE) or by the changes of the sedimentation coefficients (AUC-sedimentation velocity, AUC-SV) with respect to concentration.^21–24 The second virial coefficients can be extracted and used as an indication of long-range interactions. Direct osmotic pressure measurements using a semipermeable membrane, albeit rarely attempted, have also been demonstrated to give equivalent information.²⁵ Small-angle X-ray scattering (SAXS) and small-angle neutron scattering (SANS) determine essentially the structure factor S(q) and lead to the extrapolation of the scattering intensity at the zero scattering vectors. These measurements, when carried out as a function of concentration, allow for the fit of the second virial coefficient.²⁶ Furthermore, the structure factor, obtained from SAXS or SANS, contains information about how the particles are distributed in the solution via the pair correlation function. However, due to the limited q range of the measurements, a direct Fourier transform of the structure factor cannot be performed to derive the interaction potential, hence indirect Fourier transform techniques are needed. Nevertheless, a unique solution is not always found from such an approach.^17,27

It is well known from statistical mechanics that the positions of the particles in a liquid are captured statistically by g(r) and the potential of mean force.^28,29 This principle has been used in this paper to derive some thermodynamic quantities for NPs imaged in cryoET after the nanoparticle dispersion was rapidly frozen to create a vitrified sample that could be imaged. To date, most of these studies were conducted on samples dilute enough so that two-dimensional (2D) images of their vitreous films could be studied.^30–38 We find this approach truly promising but the 2D nature of the images has the following limitations. First, the assumption that the thermodynamic properties extracted from 2D images apply to a 3D state needs to be validated. Second, the constraint of dilute solution does not allow studying many realistic dispersion conditions. Third, the approach does not offer an easy way to guarantee that the vitrification step does not alter the dispersion state. Nevertheless, it should be pointed out that such an approach has a key advantage that 2D images can be acquired and processed very rapidly.

Here, we have taken inspiration from the 2D work described above and realized that the new instrumental developments in cryoET allow for relatively straightforward tomography of vitrified nanoparticle dispersions. The tomograms can be converted into 3D maps of NPs. These maps lead to the determination of g(r) and U(r). Interaction parameters such as Kirkwood–Buff integrals (KBI), can also be determined straightforwardly. Importantly, it is facile to derive a structure factor for the dispersion imaged. This calculated structure factor can be compared directly to an experimentally measured structure factor for the pre-vitrified dispersion. The comparison enables us to establish the absence of changes in the sample upon vitrification. As a result, we present here a method to extract key colloidal properties for nanoparticle dispersions.

Experimental

Nanoparticle synthesis

HAuCl₄·3H₂O, oleylamine, and t-butylamine-borane complex were purchased from Sigma-Aldrich and used without further purification. In a typical synthesis, 196 mg of HAuCl₄·3H₂O was dissolved in a mixture of 16 ml of oleylamine and 20 ml of n-octane, directly in the 250 ml three-necks round bottom flask. The solution was stirred vigorously until the solid disappeared completely. It was followed by the addition of 86 mg of t-butylamine–borane complex previously prepared in 4 ml of oleylamine in a small vial. The reaction was left in gentle stirring for an hour and then quenched by 120 ml of ethanol. The precipitated NPs were washed by a sequence of dispersion in dichloromethane, precipitation by ethanol, and then gentle centrifugation for several times. The ligand exchange procedure was adopted from ref. 39. All the particles synthesized and studied in this paper are described in Table 1, where their acronyms are introduced. Briefly, for NP1 and NP2, 30 mg of oleylamine coated NPs was dissolved in 4 ml of dichloromethane. To the dissolved sample, we added 106.4 mg of sodium 11-mercaptoundercane sulfonate (MUS) dissolved in 5 ml of water. The mixture was sealed and stirred overnight. NPs obtained from the upper phase were washed thoroughly using ethanol using Amicon® 30 kDa MWCO filters. For NP3, coated with MUS and OT (octanethiol), the thiolated molecules with feed ratio of 55% OT were used in the ligand exchange step. The purity of the AuNP was evaluated by NMR. Pegylated NPs, NP4 and NP5, were purchased from Sigma-Aldrich. They were freeze-dried into powder and used without further chemical modification.

Table 1 List of nanoparticles in this study, their size, and their ligand composition. Conventional TEM analysis is presented in Fig. SI1–S10 (ESI). MUS: 11-mercaptoundercane sulfonate; OT: octanethiol; PEG2000: poly(ethylene glycol) thiol with M_w = 2000 Da; PEG5000: poly(ethylene glycol) thiol with M_w = 5000 Da;

Particle	Core size (nm)	Dispersity (%)	Ligand shell	Ligand ratio (%)
NP1	3.2	9.4	MUS	100
NP2	3.1	16.1	MUS	100
NP3	4.6	10.8	MUS-OT	70–30
NP4	5.4	14.8	PEG2000	100
NP5	4.9	22.4	PEG5000	100

---

Conventional TEM

A drop of dilute dispersion of NPs was dried on a carbon film grid (CF200-Cu, EMS) and inspected by TEM at 200 kV. Particle size analysis was done by using ImageJ v1.53c (NIH).

SAXS

SAXS measurements were performed on a Bruker Nanostar instrument (Bruker AXS GmbH, Karlsruhe, Germany) equipped with a pinhole collimation system and a micro-focused X-ray Cu source (wavelength Cu K_α 1.5406 Å) providing a beam with a diameter of about 300 μm. The instrument was equipped with a semi-transparent beam stop. Measurements were carried out at room temperature in moderate vacuum conditions of about 10⁻² mbar pressure to avoid air scattering. The sample-to-detector distances (SDD) was calibrated with a standard silver behenate powder for SDD = 107 cm. All NPs dispersion samples were prepared in a quartz capillary with a diameter of 1.5 mm (Hilgenberg Company, Germany). The scattering frames of the NPs dispersion and the solvent were recorded in the same conditions. The solvent data was considered as background and subtracted before data analysis. Different NPs concentrations were investigated. The background subtracted I(q) of the sample with the lowest measured concentration in NaCl 30 mM (1.0 mg ml⁻¹) was considered for a form factor, P(q), since there was no increasing in forward scattering for this sample and showed a plateau in small q range indicating the negligible interaction. The structure factors were calculated by diving the I(q) by P(q), and normalized to 1 at high q.⁴⁰

CryoET

Four microliters of dispersion were applied onto a quantifoil grid (200 mesh, EMS). The solution was blotted on one side of the grid using a Whatman filter paper (1440-090) and immediately vitrified in liquid ethane with a homemade plunge freezing apparatus. Observation was made at −170 °C in a Tecnai F20 microscope (Thermo Fisher, Hillboro, USA) operating at 200 kV equipped with a cryo-specimen holder Gatan 626 (Warrendale, PA, USA). Tilt-series were collected automatically from −60° to 60° with 2° angular increments at 29 000× (camera's pixel size = 0.35 nm) and 50 000× (camera's pixel size = 0.20 nm) of magnification using the defocus range from −3 μm to −5 μm for a total dose of 40 e⁻ Å⁻². Digital images were acquired using a camera Falcon III (Thermo Fisher, Hillsboro, USA) 4096 × 4096 pixels. All the data were drift corrected by the software of acquisition Tomo 4.0 (Thermo Fisher, Hillsboro, USA).

Image processing

The tilt series (binned 2×, for magnification of 50 000×) were aligned using cross correlation in Inspect3D (Thermofisher). Tomograms were reconstructed using the Simultaneous Iterative Reconstruction Technique (SIRT) from Inspect3D using 24 iterations. The contrast of the tomogram was inverted and the segmentation was followed using Imaris (Bitplane) and custom-made Matlab codes. The typical size of a tomogram was in the range of 800 nm × 800 nm × 100 nm. Due to the limitation of our computer power, tomograms recorded at 29 000× were divided into four before analysis. Moving box of sub-volumes and particle counting were realized with in-house Matlab codes to calculate KBI values. g(r) was calculated based on the python code provided by ref. 41. Here the bin size of g(r) was set to be comparable with the pixel size of the tomogram. Structure factors based on the positions of the particles in the tomograms were calculated using Matlab codes that implement the histogram-based algorithm presented in ref. 42. Agglomerate states of particles were extracted from the tomograms using Imaris (Bitplane) and in-house Matlab codes that were based on the algorithm reported in ref. 43.

AUC-SV

AUC-SV measurements were carried out in an analytical ultracentrifuge XL-I machine (Beckman-Couter) using absorbance optics. Double-sector cells having 12 mm or 3 mm path lengths were utilized with sapphire windows and titanium centerpieces. A dispersion of nanoparticle (370 microliters) at the absorbance 0.1 < OD < 1 was placed in the sample sector, while water was used in the reference sector. All samples were run at 20 °C, while the set speeds were chosen to record at least 40 data curves. The absorbance was measured at the wavelength of 520 nm, with radial increment set at 0.003 cm and the acquisition was done in a continuous mode without delay. The AUC data C(s) was processed by Sedfit v16.36 (http://www.analyticalultracentrifugation.com/).

Results

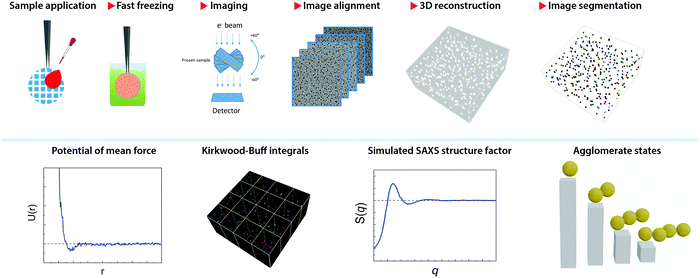
Fig. 1 illustrates the workflow of the present method. After a thin film of NP dispersion was quickly vitrified on a grid, the sample frozen across a grid hole is imaged in a series of discrete tilt angles, mainly from −60° to 60° with angular step of 2°. This acquisition is assisted with on-line drift correction to maintain the same image location. The tilt series is then aligned by cross-correlation and a tomogram is reconstructed by simultaneous iterations reconstruction technique (SIRT) method using 24 iterations. This method has been implemented as a routine and was applied to a series of aqueous dispersions of monolayer-protected gold NPs. The samples used in this paper are presented in Table 1. Examples of their tomograms can be found in the supporting materials, Fig. SI18–S49 (ESI†).

Fig. 1 Cryo-TEM work flow and extraction of thermodynamic information from the tomogram of vitrified dispersion of NPs. Top panel shows a sequence of steps in the workflow. The bottom panel illustrates some thermodynamic parameters that can be obtained from tomograms of NPs.

The tomogram (namely, the 3D image) is used to determine the coordinates of the centres of mass for the particles present in the image. Thanks to the large contrast present between the images of the particles and the background, the identification of the particles can be achieved by intensity thresholding the 3D image. This step is called image segmentation.⁴⁴ Typically, the tomograms were obtained at the image pixel size of 0.41 nm or 0.35 nm, leading to a tomogram size in the range from 2 GB to 7 GB. Large tomograms were divided into four sub-tomograms to facilitate their processing. Due to the limited tilt angles of the microscope used, the tomographic shape of the particle appears slightly elongated in the z-direction (thickness) of the tomogram, commonly known as a missing-wedge effect.⁴⁵ However, given the particles’ centre of mass (CoM) is the key feature for this method, the symmetric elongation did not impose any constraint.

The CoM was used to calculate the radial distribution function (RDF) according to a published method that takes into account the edge effect caused by a finite size of the tomogram.⁴¹ The potential of mean force (PMF, U(r)) equation was calculated by inversion of the g(r) by

U(r) = −K_BT ln[g(r)]

where K_B is Boltzmann constant, and T is temperature.⁴⁶ Here r denotes a centre-to-centre distance.

The structure factor S(q) was determined by means of the Debye formula:

where q is the magnitude of the momentum transfer factor, r_ij is the pairwise inter-particle distance between particle i and j.⁴⁷F(q) is the form factor of the particle, and it was set to one for the calculation of structure factor S(q). The operation could be done readily as the positions of the particles in the tomogram were known. A fast computer algorithm based on the histogram of distance was implemented based on the ref. 42.

The Kirkwood–Buff integrals (KBI) are one of the most common statistical mechanics approaches to determine many key thermodynamic properties such as chemical potential, partial molar volume, compressibility and osmotic pressure.^48–50 They are based on concentration fluctuation. KBIs are commonly used to extract thermodynamics quantities from molecular dynamics simulations where concentration fluctuation is followed along time. In our method, the time is fixed at the moment of vitrification, yet concentration fluctuation can be followed spatially, by dividing the images into sub-volumes and calculating the needed averages for the particles in the 3D image.⁵¹ In this way we calculated the KBI between NPs G₂₂via

where V is the volume of the box, 〈…〉 denotes an ensemble average, and n₂ is the number of CoM in the box. Here, we adopted the index 2 for indicate NPs, and reserved the index 1 for the solvent particles. Sub-volumes, i.e. the box, predefined rectangular parallelepipeds with a square base that was then scanned across the tomogram and, at each relocation step, the number of CoM that lay inside the box was counted. In order for the calculated KBI to be valid, it needs to be independent of the box size. To verify this, we varied the box volume, V, and plot the value of G₂₂ as a function of V (see Fig. SI11, ESI†). The plot shown keeps the z dimension constant and varies the base size. We find that the G₂₂ value plateaus from 150 nm (edge length) onwards. The specific value will vary with particles’ concentration; therefore, to be consistent in all the comparisons performed in this paper we chose the safe value of 200 nm edge lengths. The shape of the box chosen was that of a rectangular parallelepiped with a square base because overall our tomograms are rectangular parallelepipeds with a square base that has an average edge length in the order of 800 nm and a thickness in the order of 100 nm. As a consequence, scanning our box in the z dimension was challenging, hence we decided to adopt the box to be as high as the tomogram and scan only in the x–y plane.

The aggregation states of particles were visualized and quantified using the tomogram. To this end, one needs first to determine a threshold distance below which two particles are deemed to be “touching”. We set such distance as a sum of mean core diameter of NPs and twice the length of the ligand. When CoMs had a distance below such threshold, the corresponding particles were considered to be aggregated. Such aggregated states were classified as dimer, trimer, tetramer, etc. We produced images where particles were attributed an artificial colour (corresponding to the specific aggregate they belonged) for easy visualization.

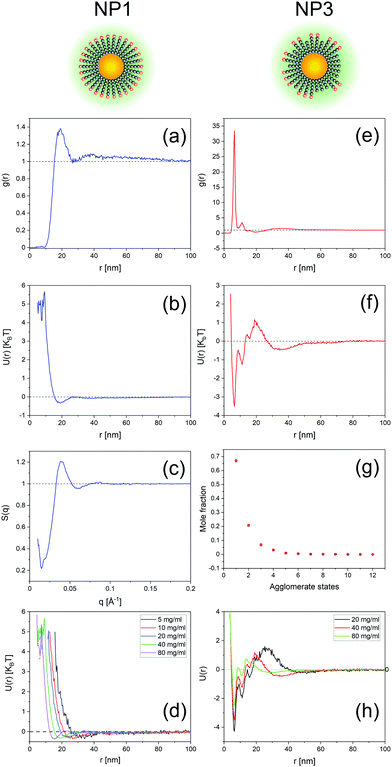
Fig. 2 and 3 show representative results to illustrate what can be achieved with this method. Specifically, it shows the g(r) of NP1 which is a non-aggregate particle in Fig. 2a and its corresponding PMF (U(r)) in Fig. 2b. The calculated structure factor is in Fig. 2c. In Fig. 2e–g we show the g(r), U(r), and agglomerates for NP3 that is an aggregating particle. We then show U(r) for these two particles as varying concentrations in Fig. 2e (for NP1) and Fig. 2h (for NP3). Fig. 3 shows the KBI G₂₂ for NP1 (blue) and NP2 (red) as a function of number concentration. NP2 and NP1 have the same surface chemistry but they are different in particle size distribution.

Fig. 2 Extracted information from tomograms of gold nanoparticle dispersions. Cartoons at top show schematic of nanoparticles presented for NP1 and NP3, respectively. The ligands are represented by grey beads with their negatively charged head by red colour. (a–c) Show the radial distribution function, the potential of mean force, and structure factor for NP1. (e–g) Show the radial distribution function, the potential of mean force, and the agglomerate states for NP3. The agglomerates are plotted as mole fraction concentration against the agglomerate number. (d and h) Present the potential of mean force for NP1 (d) and NP3 (h) at various concentrations.

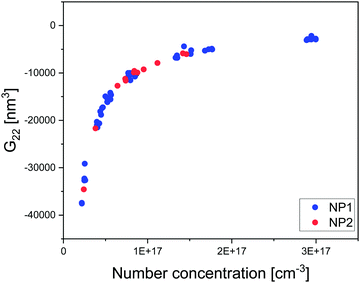Fig. 3 Plot of extracted KBI G₂₂ from tomograms of NP1 and NP2 dispersed in water as a function of number concentration determined directly from the tomograms.

Discussion

We present here a novel method to extract thermodynamic quantities from the tomogram of a generic nanoparticle dispersion in water imaged by cryoET after sample vitrification. The main assumption in this method is that the state of the dispersion is not affected by the vitrification. This assumption needs to be verified. We have carried this out experimentally in two ways. In both cases, we compared the status of the dispersion measured by a known technique, with the knowledge acquired on the status of the dispersion by our method from a vitrified sample. Specifically, in the first case we performed SAXS on a dispersion of NP1 particles and then vitrified such dispersion to apply our method to calculate the dispersion's structure factor. Fig. 4a shows the experimental SAXS and the calculated S(q). It presents a quantitative comparison of the peak position in Fig. SI12 (ESI†). The comparison shows a remarkable agreement in peak position but also finds a small discrepancy in the concentration determined by the two techniques, most probably due to the handling of small volumes in cryoET. Once peak positions were corrected for the small concentration difference, we could overlap the two sets of data in Fig. 4a, which shows a remarkable agreement. This study was also performed on the same NPs dispersed in water having NaCl 30 mM. In this case, we found no difference in concentration between SAXS and our techniques and the structure factors found could be directly overlapped with a truly remarkable agreement as shown in Fig. 4b. The second approach used to validate the central assumption takes advantage of the known ability of AUC-SV to determine precisely the aggregation states for nanoparticle dispersions. In Fig. 2g we present a quantitative calculation of the aggregation state for NP3 particles at a concentration of 40 mg ml⁻¹. The exponential decay of the aggregate populations versus aggregate states is known for nanoparticle dispersions.^52–54 This phenomenon is indeed validated by both AUC-SV (weight-based distribution) and by our method (number-based distribution) for a whole range of concentrations from both at low range (AUC-SV) and to high range (present method). The agreement found confirms that vitrification did not alter the aggregation states. Taken all together, the data presented in Fig. 4 validate the assumption that vitrification does not alter the dispersion state of particles in solution, thus allowing us to study the vitrified sample to extract the relevant thermodynamic properties of the particles’ dispersion.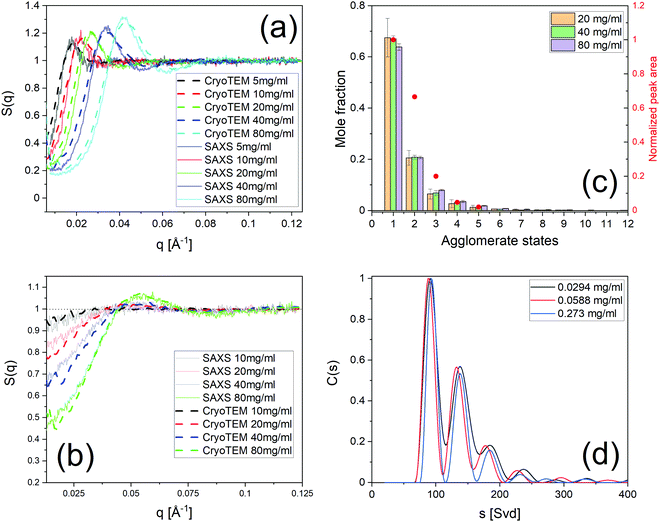

Fig. 4 Validation of cryoET results by known techniques. (a) Structure factor S(q) of NP1 dispersed in water from cryoET and SAXS. (b) S(q) of NP1 dispersed in NaCl 30 mM from cryoET and SAXS. (c) Aggregate states and their populations of NP3 at various concentrations by cryoET. In the same figure are the agglomerate states obtained by AUC-SV with their concentrations normalized by the area under curve of C(s). (d) Histograms C(s) of sedimentation coefficients at three concentrations in the dilute regime for NP3. The attributes of the peaks to presumably aggregate states are presented in Fig. SI17 (ESI†).

Fig. 5 The effect of NaCl on the potentials of mean force of NP2. (a) Tomogram of NP2 at the NaCl 30 mM. (b) Tomogram of NP2 at the NaCl 50 mM. (c) Comparison of the resulted potentials of mean force at various NaCl concentrations.

The number of particles in an ensemble contributes to the standard deviation of g(r) determined through sampling. In our method such a number, N, depends on many factors. First, the size of the tomogram depends on the instrument used. In our case, the tomogram size on average was 800 × 800 × 100 nm (i.e. an average volume of 6.4 × 10⁻¹⁴ cm³). Another factor that determines N is the particle's concentration. This parameter varies from sample to sample. In the measurements performed for this paper we have used as low as ∼850 particles. Indeed, we successfully applied our method for NP5 which was coated by a long PEG molecule (5000 Da) at the concentration 1.2 × 10¹⁶ particles per cm⁻³, resulting in the number of particles counted N of ∼850 particles. The effect of N on the calculation of g(r) is shown in Fig. SI13 (ESI†) where we evaluated the standard deviation (stdev) of the g(r) values at the large interparticle distance (from 80 nm to 100 nm). We chose this approach to gauge the noise in our approach as it is known theoretically that the expected value for g(r) when the interaction is no longer present has to be 1. The plot presented (with stdev calculated with 1 as the expected value) is indeed a plot of noise in the system. We show that for N > 40 000 the noise was less than 0.01. In the case of the measurement with 850 particles (NP5) in one tomogram, we find a noise of 0.12 that should still be acceptable for a coarse evaluation of the sample. For example, we analysed two tomograms of NP5 and NP4 particles with total particles counted of 850 and 1104, respectively. The g(r) calculated for the samples show a first peak at 34 nm (NP5) and 24 nm (NP4) in full agreement with what is expected by the length of their ligands (see Table 1 and Fig. SI14, ESI†).

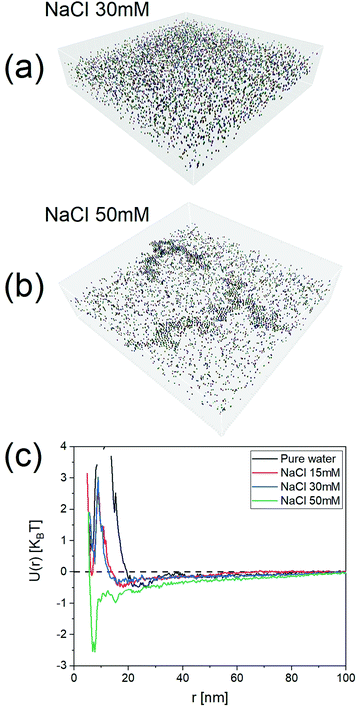
To show the efficacy of our method, we investigated a series of dispersions of particles at varying ionic strengths. The particles selected for this study were NP2 as these particles have their state in water mostly determined by electrostatic repulsion. It is known from the DLVO theory that the long-range part of this repulsion should decrease with increasing ionic strength. We studied 15 mM, 30 mM, and 50 mM salt concentrations. As expected, the potentials of mean force, U(r), obtained with our approach started with a minimum at ∼22 nm for pure water as the dispersant. The minimum shifted to ∼18 nm for 15 mM and then to ∼15 nm for 30 mM. The PMF became quite complex at 50 mM where the higher salt concentration caused extended aggregation, as seen in the tomograms present Fig. 5 and Fig. SI15 (ESI†) (for NaCl 100 mM).

Applying the general Kirkwood–Buff theory for liquid, one can connect the ensemble fluctuations to the macroscopic thermodynamic properties KBI. Here, the KBI G₂₂ is straightforwardly related to the second virial coefficient (B₂) by the equation G₂₂ = −2B₂. G₂₂ is a quantity exhibiting the deviation from the bulk distribution of the particle ensemble around a probe nanoparticle. The calculation of G₂₂ from g(r)

is influenced by the noise and the finite-sized nature of the tomogram, which requires the application of a correct window function.^55,56 In our approach, it is advantageous to have 3D positions of the NPs available so that spatial fluctuation can be obtained. Expected for NP1 in water, the obtained KBI values are negative at all concentrations, a signature of the repulsive PMF between NPs. In Fig. 3 we display the value of G₂₂ as a function of number concentration that is obtained directly from the tomograms (blue dot), and the trend is remarkably clear despite the fact that each point on the plot is derived from a different tomogram. Furthermore, the red dots in the same Fig. 3 are the G₂₂ of NP2, a particle that is nominally the same as NP1 but differs in size distribution. The agreement observed is expected as G₂₂ will depend mostly on the ligands and hence a small difference in size should not have an effect. G₂₂ as a function of a purely repulsive system of hard spheres is calculated based on ref. 57, and it shows a remarkably similar trend to the plot, shown in Fig. SI16 (ESI†).

There is one more aspect, both qualitative and quantitative, of our methods that should be discussed. The use of the CoM of the NPs to calculate the RDF (g(r)) and the PMF (U(r)) provides two key insights. First, a peak in the RDF is the distance at which the probability of finding neighbouring particles is greatest, hence the RDF provides a quick tool to understand if short- or long-range interactions are present. For example, for repulsive non-aggregate particles, we found a peak at ∼4-diameter distance indicating the presence of long-range interactions. As expected, the peak shifted to a shorter distance as the particle concentration was increased. Similar considerations can be made for particles where dimer and larger aggregates are found. Such qualitative information can be coupled with important quantitative evaluation. When aggregates are present, the PMF presents a corresponding energy landscape characterized by a minimum and a barrier. Both quantities are present in the U(r) plot (see for example Fig. 2f). To the best of our knowledge, no other technique can provide energy barriers for dynamic aggregates in such a simple and effective way.

Limitation and future prospect

It is a non-trivial task to characterize the configuration of nanoparticle in 3D. As pointed out previously,^{30,31,58–60} CryoET is an excellent technique to investigate the structural and dispersion properties of NPs. The present method offers a simple but a true 3D approach to obtain a wealth of thermodynamic information relevant to understand nanoparticle dispersion properties. It takes advantage of combining a snap freezing sample preparation and tomographic reconstruction to offer a detailed look into the 3D states of the dispersion, and thereby providing a quantitative approach for obtaining important thermodynamic parameters. One of the key advantages is that the number of concentration and the spatial distribution of NPs are directly accessible. Additionally, the energy barriers for aggregating particles can be quantitatively obtained. The present method was used to study NPs in a wide range of concentrations dispersed in aqueous solutions and can be expected to work well for particles dispersed in different media.^61,62

The present technique, however, suffers from several drawbacks. First of all, what have been presented here are the results for gold NPs that have high contrast against the amorphous ice background. It would be more challenging to study other particles whose core materials are not metallic or particles of nature such as polymer and protein. Nanoparticles with propensity to accumulate at the air liquid interfaces could be problematic to study with this approach. This issue has been recognized in proteins,^63,64 however, some solutions have been provided such as reducing time between blotting and vitrification,⁶⁵ and using surfactants.⁶⁶ Furthermore, the high tilt of the sample holder during imaging, coupled with high concentration of particles used prevents effective imaging of thick samples, which would be valuable in extending the finite z dimension of the tomogram. A major drawback is that the method is composed of multiple sequential steps that are time-consuming, which include sample freezing, grid transferring, holder station cooling, holder stabilization, imaging, image alignment, reconstruction, and image segmentation. For instance, imaging a tilt-series alone in our machine takes about 1.5 h after completing the setup of the sample and microscope. The reconstruction and image segmentation are impeding also by the number of images and the size of the tomogram.

With recent development in both hardware and software associated with cryoET techniques, this method could become a standard for studying NPs. Further improvements of the present work are already available, such as the use TEM with higher acceleration voltage, such as 300 kV, to investigate thicker vitrified samples so that more particles can be counted, and expand the z-scale limit of the already finite-sized tomograms. Electron energy loss filter (GIFT filter) can be also utilized to suppress further background noise. We believe the versatility of this technique applies not only to spherical gold NPs but also to the extension of the method to incorporate the directional interactions of asymmetric particles. With the high contrast bestowed by NPs compared to the medium, this method paves the way to study the distribution of particles in realistic media at the application concentration in a true 3D manner. Furthermore, the presented methodology is well poised to quantify interaction potentials in other soft matter particles such as protein and supramolecular structures.

Conclusion

We have presented a method based on the tomographic reconstruction of vitrified dispersion of NPs to study their thermodynamic properties. We demonstrated the methodology for gold NPs of diameter <5 nm. With the true 3D positions of NPs, g(r) and the potential of mean force U(r) are calculated directly without any assumption. The Kirkwood–Buff integrals, structure factor, and aggregation states are accessible as well to help understand the dispersion. The method can be extended and generalized to a wide variety of soft mater particles in the nanoscale size. We believe this technique will eventually be a powerful tool to understand particle dispersion, as cryoET has already become a popular technique to study protein structures.

Author contributions

Q. O. conceived and performed cryo-ET work. N. IA. carried out SAXS experiments. T. M., L. R., C. M., F. O., A. M. performed NP synthesis and chemical characterization. P. S. performed chemical ligand synthesis. X. X. and Q. O. performed AUC analysis. D. D. provided Q. O. with training and scientific support on cryo EM. A. N. supervised SAXS work. S. S. conceived the statistical thermodynamic approach to data analysis and wrote the theoretical section. F. S. conceived and supervised the research project encompassing present work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

F. S. and T. M. thank the Swiss National Science Foundation for financial support (grant number 200020_185062). Q. O. and F. S. acknowledge the use of BIOP image analysis stations at EPFL. Q. O. thanks Mr Olivier Burri (BIOP) for Imaris training and support. A. N. and N. IA. are grateful for financial support of the Swiss National Science Foundation (grant number 205321_173012).

References

1. M.-C. Daniel and D. Astruc, Chem. Rev., 2003, 104, 293–346.
2. A. Verma and F. Stellacci, Small, 2010, 6, 12–21.
3. Y.-C. Yeh, B. Creran and V. M. Rotello, Nanoscale, 2012, 4, 1871–1880.
4. C. A. S. Batista, R. G. Larson and N. A. Kotov, Science, 2015, 350, 1242477.
5. K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630.
6. D. F. Evans and H. Wennerström, The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet, Wiley, 1999.
7. J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, San Diego, 3rd edn, 2011.
8. L. A. Wijenayaka, M. R. Ivanov, C. M. Cheatum and A. J. Haes, J. Phys. Chem. C, 2015, 119, 10064–10075.
9. M. Brunner, C. Bechinger, U. Herz and H. H. V. Grünberg, Europhys. Lett., 2003, 63, 791–797.
10. M. Brunner, C. Bechinger, W. Strepp, V. Lobaskin and H. H. von Grünberg, Europhys. Lett., 2002, 58, 926–965.
11. J. K. Cho, Z. Meng, L. A. Lyon and V. Breedveld, Soft Matter, 2009, 5, 3599–3602.
12. R. P. A. Dullens, D. Aarts and W. K. Kegel, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 529–531.
13. C. R. Iacovella, R. E. Rogers, S. C. Glotzer and M. J. Solomon, J. Chem. Phys., 2010, 133, 164903.
14. W. K. Kegel and A. van Blaaderen, Science, 2000, 287, 290–293.
15. P. S. Mohanty, D. Paloli, J. J. Crassous, E. Zaccarelli and P. Schurtenberger, J. Chem. Phys., 2014, 140, 094901.
16. C. P. Royall, M. E. Leunissen and A. V. Blaaderen, J. Condens. Matter Phys., 2003, 15, S3581–S3596.
17. C. P. Royall, A. A. Louis and H. Tanaka, J. Chem. Phys., 2007, 127, 044507.
18. A. E. Stones, R. P. A. Dullens and D. G. A. L. Aarts, Phys. Rev. Lett., 2019, 123, 098002.
19. K. Vondermassen, J. Bongers, A. Mueller and H. Versmold, Langmuir, 1994, 10, 1351–1353.
20. H.-J. Wu and M. A. Bevan, Langmuir, 2005, 21, 1244–1254.
21. B. Luigjes, D. M. E. Thies-Weesie, B. H. Erné and A. P. Philipse, J. Condens. Matter Phys., 2012, 24, 245104.
22. B. Luigjes, D. M. E. Thies-Weesie, A. P. Philipse and B. H. Erné, J. Condens. Matter Phys., 2012, 24, 245103.
23. K. L. Planken and H. Cölfen, Nanoscale, 2010, 2, 1849–1869.
24. M. J. Uttinger, S. E. Wawra, T. Guckeisen, J. Walter, A. Bear, T. Thajudeen, P. J. Sherwood, A. Smith, A. M. Wagemans, W. F. Stafford and W. Peukert, Langmuir, 2019, 35, 11491–11502.
25. A. Striolo, J. Ward, J. M. Prausnitz, W. J. Parak, D. Zanchet, D. Gerion, D. Milliron and A. P. Alivisatos, J. Phys. Chem. B, 2002, 106, 5500–5505.
26. A. E. Saunders and B. A. Korgel, J. Phys. Chem. B, 2004, 108, 16732–16738.
27. R. Rajagopalan and K. Srinivasa Rao, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4423–4432.
28. D. A. McQuarrie Statistical Mechanics, Harper & Row, 1975.
29. J.-L. Bretonnet, Statistical Mechanics for the Liquid State, Cambridge Sholars Publishing, 2020.
30. V. Durrieu, J.-L. Putaux, R. Passas and A. Gandini, Cryoelectron Microscopy, 2004, 18, 19–21.
31. H. Friedrich, P. M. Frederik, G. de With and N. A. J. M. Sommerdijk, Angew. Chem., Int. Ed., 2010, 49, 7850–7858.
32. M. Klokkenburg, R. P. A. Dullens, W. K. Kegel, B. H. Erné and A. P. Philipse, Phys. Rev. Lett., 2006, 96, 037203.
33. M. Klokkenburg, C. Vonk, E. M. Claesson, J. D. Meeldijk, B. H. Erné and A. P. Philipse, J. Am. Chem. Soc., 2004, 126, 16706–16707.
34. J. van Rijssel, B. H. Erné, J. D. Meeldijk, M. Casavola, D. Vanmaekelbergh, A. Meijerink and A. P. Philipse, Phys. Chem. Chem. Phys., 2011, 13, 12770–12774.
35. J. van Rijssel, V. F. D. Peters, J. D. Meeldijk, R. J. Kortschot, R. J. A. van Dijk-Moes, A. V. Petukhov, B. H. Erné and A. P. Philipse, J. Phys. Chem. B, 2014, 118, 11000–11005.
36. K. Butter, P. H. H. Bomans, P. M. Frederik, G. J. Vroege and A. P. Philipse, Nat. Mater., 2003, 2, 88–91.
37. A. M. Milosevic, L. Rodriguez-Lorenzo, S. Balog, C. A. Monnier, A. Petri-Fink and B. Rothen-Rutishauser, Angew. Chem., Int. Ed., 2017, 56, 13382–13386.
38. C. A. Monnier, D. C. Thévenaz, S. Balog, G. L. Fiore, D. Vanhecke, B. Rothen-Rutishauser and A. Petri-Fink, AIMS Biophys., 2015, 2, 245–258.
39. Y. Yang, L. A. Serrano and S. Guldin, Langmuir, 2018, 34, 6820–6826.
40. D. I. Svergun, M. H. J. Koch, P. A. Timmins and R. P. May, Small Angle X-Ray and Neutron Scattering from Solutions of Biological Macromolecules, Oxford University Press 2020.
41. B. A. F. Kopera and M. Retsch, Anal. Chem., 2018, 90, 13909–13914.
42. E. Pantos and J. Bordas, Pure Appl. Chem., 1994, 66, 77–82.
43. C. R. Murthy, B. Gao, A. R. Tao and G. Arya, Nanoscale, 2015, 7, 9793–9805.
44. R. C. Gonzalez, Digital Image Processing, Pearson Education, 2009.
45. P. Ercius, O. Alaidi, M. J. Rames and G. Ren, Adv. Mater., 2015, 27, 5638–5663.
46. J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier Science, 2006.
47. O. Glatter, Scattering Methods and their Application in Colloid and Interface Science, Elsevier, 2018.
48. A. Ben-Naim, Molecular Theory of Solutions, OUP, Oxford, 2006.
49. S. Shimizu and N. Matubayasi, J. Colloid Interface Sci., 2020, 575, 472–479.
50. S. Shimizu, Curr. Opin. Colloid Interface Sci., 2020, 48, 53–64.
51. P. Ganguly and N. F. A. van der Vegt, J. Chem. Theory Comput., 2013, 9, 1347–1355.
52. S. V. Sokolov, E. Kätelhön and R. G. Compton, J. Phys. Chem. C, 2015, 119, 25093–25099.
53. D. Vollath, Beilstein J. Nanotechnol., 2020, 11, 854–857.
54. E. Kätelhön, S. V. Sokolov, T. R. Bartlett and R. G. Compton, ChemPhysChem, 2017, 18, 51–54.
55. P. Krüger, S. K. Schnell, D. Bedeaux, S. Kjelstrup, T. J. H. Vlugt and J.-M. Simon, J. Phys. Chem. Lett., 2013, 4, 235–238.
56. N. Dawass, P. Krüger, S. K. Schnell, J.-M. Simon and T. J. H. Vlugt, Fluid Phase Equilib., 2019, 486, 21–36.
57. S. I. Sandler, An Introduction to Applied Statistical Thermodynamics, Wiley, 2010.
58. J. J. De Yoreo and N. A. J. M. Sommerdijk, Nat. Rev. Mater., 2016, 1, 16035.
59. J. P. Patterson, Y. Xu, M.-A. Moradi, N. A. J. M. Sommerdijk and H. Friedrich, Acc. Chem. Res., 2017, 50, 1495–1501.
60. J. Watt, D. L. Huber and P. L. Stewart, MRS Bull., 2019, 44, 942–948.
61. O. Balmes, J.-O. Malm, G. Karlsson and J.-O. Bovin, J. Nanopart. Res., 2004, 6, 569–576.
62. G. T. Oostergetel, F. J. Esselink and G. Hadziioannou, Langmuir, 1995, 11, 3721–3724.
63. A. J. Noble, V. P. Dandey, H. Wei, J. Brasch, J. Chase, P. Acharya, Y. Z. Tan, Z. Zhang, L. Y. Kim, G. Scapin, M. Rapp, E. T. Eng, W. J. Rice, A. Cheng, C. J. Negro, L. Shapiro, P. D. Kwong, D. Jeruzalmi, A. des Georges, C. S. Potter and B. Carragher, eLife, 2018, 7, e34257.
64. I. Drulyte, R. M. Johnson, E. L. Hesketh, D. L. Hurdiss, C. A. Scarff, S. A. Porav, N. A. Ranson, S. P. Muench and R. F. Thompson, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 560–571.
65. A. J. Noble, H. Wei, V. P. Dandey, Z. Zhang, Y. Z. Tan, C. S. Potter and B. Carragher, Nat. Methods, 2018, 15, 793–795.
66. J. Chen, A. J. Noble, J. Y. Kang and S. A. Darst, J. Struct. Biol.: X, 2019, 1, 100005.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1mh01461g

---