Detection of multi-reference character imbalances enables a transfer learning approach for virtual high throughput screening with coupled cluster accuracy at DFT cost

Abstract

Appropriately identifying and treating molecules and materials with significant multi-reference (MR) character is crucial for achieving high data fidelity in virtual high-throughput screening (VHTS). Despite development of numerous MR diagnostics, the extent to which a single value of such a diagnostic indicates the MR effect on a chemical property prediction is not well established. We evaluate MR diagnostics for over 10 000 transition-metal complexes (TMCs) and compare to those for organic molecules. We observe that only some MR diagnostics are transferable from one chemical space to another. By studying the influence of MR character on chemical properties (i.e., MR effect) that involve multiple potential energy surfaces (i.e., adiabatic spin splitting, ΔE_H–L, and ionization potential, IP), we show that differences in MR character are more important than the cumulative degree of MR character in predicting the magnitude of an MR effect. Motivated by this observation, we build transfer learning models to predict CCSD(T)-level adiabatic ΔE_H–L and IP from lower levels of theory. By combining these models with uncertainty quantification and multi-level modeling, we introduce a multi-pronged strategy that accelerates data acquisition by at least a factor of three while achieving coupled cluster accuracy (i.e., to within 1 kcal mol⁻¹ MAE) for robust VHTS.

---

1. Introduction

Approximate density functional theory (DFT) has become an indispensable workhorse in virtual high-throughput screening (VHTS)^1–8 and machine learning (ML)-accelerated chemical discovery^9–18 due to its balanced trade-off in computational cost and accuracy. However, DFT can fail prominently for many of the most promising VHTS targets (e.g., open-shell radicals, transition-metal-containing systems, and strained bonds in transition states).^19–23 These systems may have strong multi-reference (MR) character due to near-degenerate orbitals,²⁴ which cannot be accurately accounted for in DFT due to its single-reference (SR) description of the wavefunction.²⁵ Although benchmarking studies^26–28 can be used to identify the best density functional approximation (DFA) to yield accurate energetic properties for a chosen class of material, the choice of DFA depends strongly on the system of interest and cannot be determined a priori in VHTS where most materials have yet to be characterized.^29,30 Moreover, an imbalanced treatment of systems that have weak or strong MR character can be expected to undermine the data fidelity and bias the candidate materials recommended by chemical discovery efforts.³¹

To quantify the degree of MR character, researchers have devised many MR diagnostics^24,32–42 based on different properties (e.g., occupations or atomization energies) and levels of theory. These MR diagnostics often disagree with each other,^24,43 with the diagnostics derived from DFT being less predictive than those derived from wavefunction theory (WFT).⁴⁴ Data-driven methods have augmented conventional approaches^45–49 for making system-specific decisions associated with carrying out quantum chemical calculations. For example, Jeong et al.⁵⁰ demonstrated an ML protocol that performs automated selection of active spaces for bond dissociation of main group diatomic molecules, alleviating the computational cost. We recently introduced a semi-supervised learning approach to MR classification based on the consensus of 15 MR diagnostics that outperforms the traditional cutoff-based approach (i.e., from a single diagnostic) and is transferable to systems of larger sizes and unseen chemical composition.⁵¹

Potentially strong MR character still poses challenges for VHTS. The applicability of MR diagnostics and associated cutoffs to both organic and transition-metal-containing systems is not clear because most studies focus solely on organic systems. A notable exception is work from Wilson and co-workers^52,53 that demonstrated that coupled cluster (CC)-based diagnostics require larger cutoffs on transition-metal complexes (TMCs). In addition, while most studies focus on the MR character of a single structure, most chemical properties of interest involve multiple structures and/or electronic states. How the MR character of multiple related structures influences a property prediction (i.e., MR effect^24,54) is not well understood. Although MR diagnostics and tools for method selection^55,56 have been developed, they have yet to be adapted to improve data quality in VHTS.

In this work, we demonstrate the lack of transferability of many MR diagnostics from one chemical space to another. Use of the most robust diagnostics shows that imbalances in MR character are more important than cumulative MR character for properties that depend on multiple electronic states (e.g., adiabatic spin splitting or ionization potential). Motivated by these observations, we train transfer learning models to predict CCSD(T)-level properties from inputs including calculations carried out at lower levels of theory (i.e., DFT) and MR diagnostics. We further introduce uncertainty quantification and multi-level modeling into our workflow to apply the transfer learning predictions only when the model has high confidence, accelerating data acquisition while achieving coupled cluster accuracy (i.e., within 1 kcal mol⁻¹ of CCSD(T)) in VHTS.

2. Results and discussion

2.1. Limits of MR diagnostic transferability

To evaluate trends in MR character for more than 10 000 model TMCs (described next), we used the percentage of correlation energy recovered by CCSD relative to CCSD(T) (i.e., %E_corr[(T)]) as a figure of merit for measuring the MR character of a system.⁴⁴ A smaller %E_corr[(T)] suggests stronger MR character because CCSD is insufficient to recover the correlation energy. We previously showed⁴⁴ that %E_corr[(T)] is system size insensitive and correlates well with %E_corr[T] (i.e., from comparison to full CCSDT, see Computational details and ESI Fig. S1†).

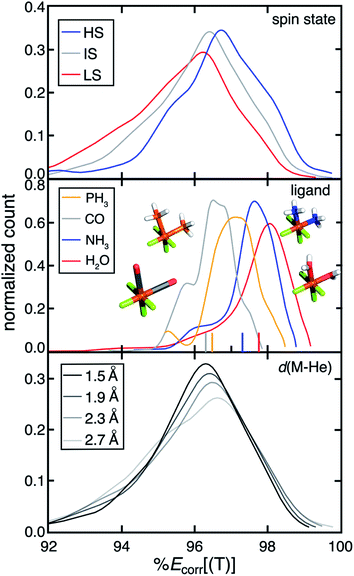
Over our data set consisting of low-spin (LS), intermediate-spin (IS), and high-spin (HS) complexes, we observe a trend of decreasing MR character with increasing number of unpaired electrons (i.e., LS > IS > HS) (Fig. 1). This observation is consistent with both expectations and our prior work⁵⁷ and is due to the increased number of accessible configuration state functions in the LS state. Complexes with stronger-field ligands (i.e. CO) generally exhibit higher MR character (Fig. 1). For example, we observe decreasing %E_corr[(T)] for complexes with increasing ligand field strength from H₂O to NH₃ to CO (Fig. 1). This increased MR character can be attributed to the more covalent metal–organic bonding character for complexes with stronger ligand fields. Consequently, when we substitute a 2p metal-coordinating atom with a 3p element from the same group (e.g., NH₃ to PH₃), both the ligand field strength and the MR character of the complex increases (Fig. 1 and ESI Fig. S2†). In prior work,⁵⁸ Feldt et al. used increased metal–helium bond lengths to weaken effective ligand fields. Here, we indeed find that the effective ligand fields decrease as the metal–helium bond lengths increase (ESI Fig. S3†). Concomitant with decreases in effective ligand field as the M–He bond is elongated, we observe decreases in MR character, although the trend is weak over the full data set and there are some MR compounds for all M–He distances (Fig. 1). This trend is in agreement with the observations from spectrochemical series ligands.

Fig. 1 Distribution of %E_corr[(T)] for more than 10 000 TMCs categorized by their spin states (top, blue for high-spin, gray for intermediate-spin, and red for low-spin), ligands (middle, orange for PH₃, gray for CO, blue for NH₃, and red for H₂O), and metal–helium distances (d(M–He), bottom, with decreasing opacity from 1.0 to 0.4 as d(M–He) increases from 1.5 Å to 2.7 Å). Four representative TMCs with LS Fe(II) and 1.9 Å d(M–He) with different ligands in a cis configuration are shown. Their corresponding %E_corr[(T)] values are shown with a colored tick on the x-axis. All atoms are colored as follows: brown for Fe, gray for C, blue for N, red for O, orange for P, white for H, and green for He.

Next, we investigated the linear correlations between pairs of MR diagnostics (ESI Table S1†). Consistent with our prior observations on equilibrium and distorted organic molecules,⁴⁴ the correlation coefficients are generally low between pairs of diagnostics obtained from different levels of theory (ESI Fig. S4–S5†). As was also observed for organic molecules,⁴⁴ WFT-based MR diagnostics generally have better linear and rank-order correlations with %E_corr[(T)] in comparison to those derived from DFT (ESI Fig. S6–S7†). An exception to this are fractional occupation-based diagnostics (i.e., Matito's degree of nondynamical correlation, I_ND[B3LYP],^40,41 and the ratio of nondynamical to total correlation, r_ND[B3LYP]⁴³) that are readily obtained at DFT cost (ESI Table S1†). Their low cost has motivated use of DFT-based diagnostics in VHTS⁵⁷ where MR detection at low cost is needed to avoid computational bottlenecks and can be used to identify “DFT-safe” islands in VHTS.⁵⁷ Although over the present set, I_ND[B3LYP]^40,41 and r_ND[B3LYP]⁴³ yield the best linear and rank-order correlation with %E_corr[(T)], their performance on organic molecules was significantly poorer⁴⁴ (ESI Fig. S6–S7†). This suggests that WFT-based diagnostics are more predictive of whether a system has strong MR character.

A closely related question is to what extent MR diagnostics and associated cutoffs are transferable from one chemical space to another. We compare the relationship between %E_corr[(T)] and MR diagnostics for TMCs to that for equilibrium or stretched organic molecules. We observe divergent behavior for representative MR diagnostics across these two sets. Organic molecules and TMCs have distinct T₁ diagnostic vs. %E_corr[(T)] distributions (Fig. 2). We therefore conclude that the T₁ diagnostic is not a transferable metric for measuring MR character, because organic molecules and TMCs have different ranges of the T₁ diagnostic for the same value of %E_corr[(T)]. This lack of transferability across compounds supports previous arguments for distinct cutoff values for the T₁ diagnostic when it is used for organic molecules or inorganic complexes.⁵² Distinct distributions for organic molecules and TMCs are generally observed for all DFT- and CC-based diagnostics and %E_corr[(T)] (ESI Fig. S8†).

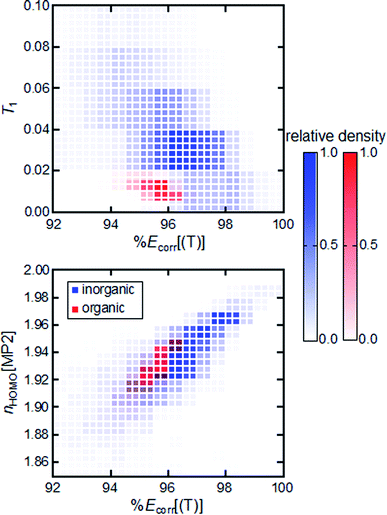Fig. 2 2D histogram for %E_corr[(T)] vs. T₁ (top) and %E_corr[(T)] vs. n_HOMO[MP2] (bottom) for more than 10 000 TMCs in this work (blue) and for the 12 500 equilibrium or distorted organic molecules in our prior work⁴⁴ (red). The relative density of systems within a specific bin is represented by the opacity of the coloring.

Overall, the MP2- and CASSCF-based diagnostics all have a greater degree of overlap with respect to %E_corr[(T)] for organic molecules and TMCs, suggesting their greater transferability (ESI Fig. S9†). The one low-cost diagnostic for which organic molecules and TMCs have overlapping values at the same %E_corr[(T)] is the MP2-based n_HOMO[MP2] diagnostic. Because n_HOMO[MP2] evaluation is not overly computationally demanding, this analysis highlights its potential use as a relatively low-cost, transferable metric for MR character determination (Fig. 2). Surprisingly, the DFT-based I_ND and r_ND diagnostics, although also motivated from the occupation of virtual orbitals upon electron excitation, are not transferable across chemical spaces (ESI Fig. S8†). The lack of transferability of I_ND and r_ND diagnostics may arise from the different degrees of accuracy of DFT for organic molecules and TMCs. We find that the distinct behavior of diagnostics across the two types of molecules is not due to their difference in size; invariant 2D distributions of %E_corr[(T)] vs. MR diagnostics are observed between subsets of organic molecules and TMCs grouped by size (ESI Fig. S10 and S11†).

We previously showed that MR classification is more robust when multiple diagnostics are used rather than a single diagnostic and cutoff,⁵¹ motivating the use of not just a single diagnostic such as the reasonably performing n_HOMO[MP2] but a range of WFT-based diagnostics to more robustly predict different regimes of MR effect. To bridge the gap in performance between low-cost DFT-based diagnostics and computationally demanding WFT-based diagnostics, we trained ANN models to predict the WFT-based diagnostics and %E_corr[(T)] using DFT-based diagnostics and Coulomb-decay revised autocorrelations (CD-RACs),⁴⁴ a set of graph-based descriptors that encode 3D geometric information of TMCs as inputs (see Computational details). With this approach, we predict WFT-based diagnostics for TMCs with similar accuracies to predictions for organic molecules,⁴⁴ despite the poor linear correlations between DFT- and WFT-based diagnostics (Fig. 3, ESI Fig. S4–S5 and Table S2†). In addition, we predict %E_corr[(T)] particularly well from the combination of DFT-based diagnostics and CD-RACs with a Pearson's r of 0.95 and an MAE of 0.21% (i.e., scaled MAE = 0.015). Given the relatively poor linear correlation between individual MR diagnostics and %E_corr[(T)] for the TMCs, the accurate prediction of %E_corr[(T)] highlights the utility of our model in practical VHTS (ESI Fig. S6†).

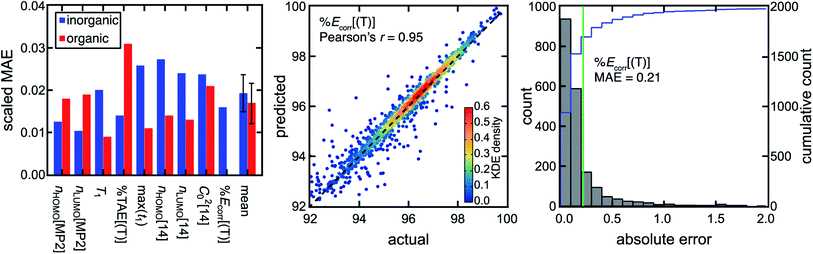Fig. 3 (left) Scaled MAE for WFT-based diagnostics and %E_corr[(T)] for the TMCs (blue) and organic structures (red) on the set-aside test data. The mean scaled MAE for all WFT-based diagnostics and %E_corr[(T)] is also shown, with the error bar representing a standard deviation. The scaled MAE is not shown for %E_corr[(T)] on the organic space, because %E_corr[(T)] is not an ML model target property in ref. 44. (middle) Predicted vs. actual %E_corr[(T)] on the set-aside 20% test data points (i.e., from more than 10 000 TMCs) colored by kernel density estimation (KDE) density values, as indicated by the inset color bar. A black dashed parity line is also shown. (right) Distributions of absolute test errors for %E_corr[(T)] (unitless, bins of 0.1) with the MAE annotated as a green vertical bar and the cumulative count shown in blue according to the axis on the right.

2.2. Cancellation of error in MR effect

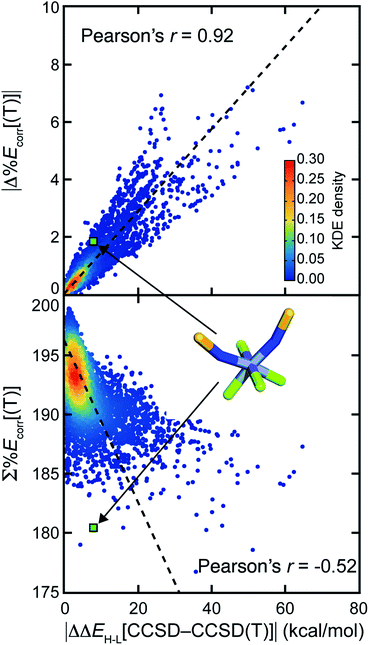
Numerous efforts^{24,38,40,41,43,52} have focused on quantifying the MR character of a single structure and the MR effect on energy evaluation using single-reference methods. However, most property predictions in chemistry are determined from the relative energy of multiple geometric and/or electronic structures, potentially leading to cancellation of error. Here, we investigate whether the MR effect between multiple structures tends to accumulate or cancel for representative properties. We studied the adiabatic HS-to-LS splitting, ΔE_H–L, which we obtain from the relative electronic energies of two spin states of the same compound in their respective optimized geometries. We also compute the adiabatic ionization potential, IP, which we compute as the electronic energy difference between a molecule before and after electron removal, including any reorganization of the oxidized species.

For both properties, we observe that differences in MR character are more important than the total degree of MR character because the MR effect cancels when calculating properties involving multiple structures. The error for ΔE_H–L obtained with CCSD in comparison to CCSD(T), i.e., |ΔΔE_H–L[CCSD–CCSD(T)]|, correlates well (Pearson's r = 0.92) with the absolute difference of %E_corr[(T)] of the two structures (Fig. 4). If we instead attempt to predict CCSD errors from the total MR character summed over both structures, we obtain a much poorer correlation (Pearson's r = −0.52, Fig. 4). To probe why high MR character does not always lead to high MR effect, we considered representative compounds. For the example of cis Cr(II)(NS⁻)₂He₄, the ΔΔE_H–L[CCSD–CCSD(T)] is small at 7.2 kcal mol⁻¹, although both the LS and HS structures have significant and comparable MR character (LS %E_corr[(T)] = 89.2, HS %E_corr[(T)] = 91.1). Another complex, Co(III)(NH₂⁻)He₅, has a relatively small amount of MR character, as judged by the sum of two spin states (LS %E_corr[(T)] = 94.9, HS %E_corr[(T)] = 98.4). However, the imbalance in MR character (i.e., %E_corr[(T)]) for the two spin states leads to a large ΔΔE_H–L[CCSD-CCSD(T)] (18.2 kcal mol⁻¹).

Fig. 4 The absolute difference in adiabatic spin-splitting energy between CCSD and CCSD(T), i.e., |ΔΔE_H–L[CCSD-CCSD(T)]|, vs. the absolute difference (top) and the sum (bottom) of %E_corr[(T)] of the two spin states. Points are colored by kernel density estimation (KDE) density values, as indicated by the inset color bar. A black dashed best-fit line is shown along with the Pearson correlation coefficient. Cr(II)(NS⁻)₂He₄ is shown as a representative example for the cancellation of MR character in property prediction MR effect. Atoms are colored as follows: purple for Cr, blue for N, yellow for S, and green for He.

The relationship between differences in MR character and errors that are indicative of MR effect also applies to DFT errors, albeit more weakly. Choosing B3LYP as a representative functional, its error with respect to the CCSD(T) ΔE_H–L, i.e., |ΔΔE_H–L[B3LYP-CCSD(T)]|, shows a moderate correlation with the absolute difference of %E_corr[(T)] (Pearson's r = 0.45), which is stronger than that observed for the sum of %E_corr[(T)] (Pearson's r = −0.11) (ESI Fig. S12†). Observations of better correlations of property errors to MR character differences than to total MR character also hold when evaluating adiabatic IP (ESI Fig. S13†).

2.3. Transfer learning to improve prediction accuracy

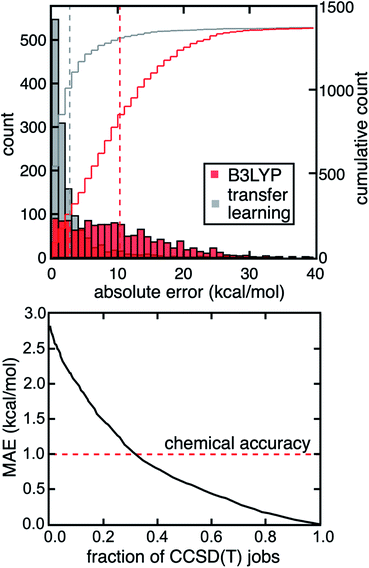
Because high MR character in one structure or electronic state does not necessarily lead to large DFT (or single-reference WFT) errors for property evaluations, strategies are needed to predict and correct errors for a property of interest rather than relying on MR character to serve as a proxy for high property uncertainty. We previously developed an approach⁴⁴ to predict the degree of MR character of a single structure at low cost (i.e., with DFT-level diagnostics and CD-RAC descriptors), which we now extend to property prediction (ESI Table S3†). Here, we demonstrate a transfer learning approach with ANN models to predict the CCSD(T) adiabatic ΔE_H–L and IP from CD-RACs and information obtained from DFT calculations, including the sums and differences of the six DFT-based MR diagnostics and DFT-evaluated ΔE_H–L and IP from four density functionals used in evaluating the MR diagnostics (i.e., BLYP, B3LYP, PBE, and PBE0, see Methods and ESI Table S3†). These trained ANN transfer learning models accurately predict the CCSD(T) result at DFT cost (Fig. 5 and ESI Fig. S14†). With this model, we obtain a mean absolute error (MAE) of 2.8 kcal mol⁻¹ for ΔE_H–L that is three-fold lower than the error obtained from using the B3LYP hybrid functional (Fig. 5). We observe similar behavior for the IP, where the transfer learning MAE of 0.14 eV is one third of the error obtained using the B3LYP hybrid functional (ESI Fig. S14†).

Fig. 5 Distributions of absolute errors for ΔE_H–L predicted with DFT using B3LYP (red) and transfer learning models (gray) on the set-aside test data, with the cumulative count shown according to the axis on the right (top). The MAEs are shown as vertical bars at 10.2 kcal mol⁻¹ for DFT and 2.8 kcal mol⁻¹ for transfer learning. The MAE of the multi-pronged strategy of transfer learning, uncertainty quantification, and multi-theory modeling vs. the fraction of CCSD(T) calculations required (bottom). In all cases, the CCSD(T) result is treated as the reference against which MAEs are evaluated.

In addition, our transfer learning ANN model can be systematically improved by using WFT-based (i.e., MP2, CCSD) diagnostics that are more predictive of strong correlation but still lower cost to compute than CCSD(T) (ESI Table S4†). For example, by including MP2-based diagnostics (i.e., n_HOMO[MP2] and n_LUMO[MP2]) and ΔE_H–L (or IP) computed by MP2, we lower the MAE of ΔE_H–L to 2.2 kcal mol⁻¹ and IP to 0.12 eV. These MAEs are further reduced to 0.4 kcal mol⁻¹ for ΔE_H–L and 0.06 eV for IP if we include CCSD-based diagnostics and CCSD-computed ΔE_H–L and IP. More interestingly, we see these large improvements of the transfer learning model performance even though the MP2- or CCSD-evaluated ΔE_H–L and IP do not show significant improvements over DFT in comparison to the CCSD(T) reference (ESI Table S4†). This observation suggests our transfer learning models do learn from these WFT-based diagnostics to better predict ΔE_H–L and IP computed by CCSD(T). In addition, we achieve comparable performance to other transfer learning approaches^59,60 demonstrated on organic molecules in terms of scaled MAEs on set-aside test data. By focusing on properties involving multiple geometric and/or electronic structures, we are able to take advantage of error cancellation in MR effects, in comparison to previous transfer learning efforts that treat each electronic state and structure separately in predicting properties such as the correlation energy.

Although the transfer learning models demonstrated good overall performance in the prediction of CCSD(T)-level properties, we next investigated whether we could identify specific compounds with large model uncertainty where errors might also be expected to be large. In such cases, a transfer learning correction may lead to large errors that would motivate carrying out the full CCSD(T) calculation instead. To quantify uncertainty, we used the distance in latent space developed in our previous work⁶¹ as an uncertainty quantification (UQ) metric on our transfer learning models to select complexes likely to benefit from explicit CCSD(T) calculations. In this approach, we selectively perform CCSD(T) calculations on the TMCs that have the largest distance to training data in latent space, and thus highest model uncertainty, but use transfer learning predictions for the others at DFT cost. If we carry out CCSD(T) on the 30% of the data with the highest uncertainty, we reduce errors by a factor of three and achieve coupled cluster accuracy (i.e., 1 kcal mol⁻¹ MAE) for the prediction of the CCSD(T) ΔE_H–L value (Fig. 5). Given that the computational cost of the DFT calculations is negligible relative to CCSD(T) calculations for the moderately sized TMCs in our dataset, we achieve a three-fold acceleration in data acquisition compared to an all-CCSD(T) approach while maintaining close-to-CCSD(T) accuracy. If we aim for an MAE of 1.5 kcal mol⁻¹ and accept transfer learning predictions on points with higher uncertainty, we reduce the number of complexes that require WFT calculations to only 19% (i.e., five-fold speedup).

Similar speedups are observed for the prediction of adiabatic IP. We only need to carry out the 40% of the CCSD(T) calculations with the largest ML model uncertainty to achieve a MAE of 0.042 eV (i.e., 1 kcal mol⁻¹). The percentage of CCSD(T) calculations carried out can be further reduced to 30% if we aim for a MAE of 0.065 eV (i.e., 1.5 kcal mol⁻¹, ESI Fig. S14†). This strategy of performing CCSD(T) calculations on high-uncertainty points shows significant improvement over the previous strategy⁶¹ where we would avoid making a prediction on the these points. For example, we must discard 74% of complexes for ΔE_H–L and 90% of the complexes for IP transfer learning to retain the CCSD(T) accuracy of 1 kcal mol⁻¹ on the points for which a prediction is still made (ESI Fig. S15†). Thus, this multi-pronged strategy of transfer learning, ML model UQ, and multi-level modeling accelerates data acquisition while maintaining high overall data fidelity for chemical discovery.

3. Conclusions

In conclusion, we studied trends in MR character for over 10 000 TMCs. Over this set, we observed that complexes with fewer unpaired d electrons (i.e., LS) and stronger ligand fields have more significant MR character. Taking both organic molecules and TMCs into consideration, we showed that DFT- and CC-based diagnostics (e.g., T₁ diagnostic) have distinct relationships with %E_corr[(T)] for the two classes of molecules, thus limiting their transferability. In contrast, MP2- and CASSCF-based diagnostics have more consistent relationships with %E_corr[(T)] for organic molecules and TMCs, demonstrating greater transferability. Therefore, we built ML models to predict these computationally demanding and transferable WFT-based diagnostics and %E_corr[(T)] from less costly DFT-based diagnostics. We obtained excellent accuracy to directly predict %E_corr[(T)] (i.e., MAE = 0.21), demonstrating the potential of these models for use in VHTS.

Motivated by the fact that most chemical properties are determined from the relative energies of multiple geometric and/or electronic structures, we investigated the effect of MR character on two properties that depend on multiple optimized geometries, the adiabatic spin splitting (ΔE_H–L) and ionization potential (IP). We observed that differences in MR character are more important than the cumulative degree of MR character, suggesting that cancellation of MR effects outweighs their accumulation. As a result, strong MR character in a single structure does not necessarily lead to large DFT errors. Motivated by this observation, we built two ML models to predict the CCSD(T) adiabatic ΔE_H–L and IP via a transfer learning approach. This approach demonstrated a three-fold reduction in errors compared to using B3LYP on both properties. Finally, we introduced UQ and multi-level modeling into our workflow in which we carried out CCSD(T) calculations on the most uncertain points and used transfer learning predictions on the others. We demonstrated that this multi-pronged strategy accelerates data acquisition by a factor of three while maintaining high overall data fidelity (i.e., 1 kcal mol⁻¹ CCSD(T) accuracy) for chemical discovery. We emphasize that this great performance is observed on energetic properties of a chemical system and further investigations are required on more complex electronic structure properties such as the wavefunction. However, we would expect our multi-pronged strategy to be general and have similar accuracy if data from higher-level theory (e.g., phaseless auxiliary field quantum Monte-Carlo⁶²) and experiments are provided as the reference. We anticipate our observations on the cancellation of MR effects in property evaluations and our multi-pronged strategy to overcome cost-accuracy trade-off limitations in VHTS to be broadly applicable for challenging transition-metal compound spaces.

4. Computational details

4.1. Data sets

Mononuclear octahedral transition-metal complexes (TMCs) with Cr, Mn, Fe, and Co in +2 and +3 oxidation states were studied in up to three spin states, i.e., high, intermediate, and low, as follows: quintet, triplet, and singlet for d⁶ Co(III)/Fe(II) and d⁴ Mn(III)/Cr(II); sextet, quartet, and doublet for d⁵ Fe(III)/Mn(II), and quartet and doublet for d³ Cr(III) and d⁷ Co(II) (ESI Table S5†). We used monodentate ligands from both the spectrochemical series⁶³ and our prior OHLDB set⁶⁴ (ESI Table S6†). To restrict the system size, we employed He atoms as four to six of the six ligands. For the remaining non-He ligands, we considered both cis and trans symmetry, and we varied the metal–He distance to mimic ligand field strength differences while all other metal–ligand distances were freely optimized (ESI Table S7†).

4.2. DFT geometry optimizations

DFT geometry optimizations with the B3LYP^65–67 global hybrid functional were carried out using a developer version of graphical-processing unit (GPU)-accelerated electronic structure code TeraChem.^68–70 The LANL2DZ effective core potential⁷¹ basis set was used for metals and the 6-31G* basis for all other atoms. Singlet spin states were calculated with the spin-restricted formalism while all other calculations were carried out in a spin-unrestricted formalism. In all DFT geometry optimizations, level shifting⁷² of 0.25 Ha on all virtual orbitals was employed. Initial geometries were assembled by molSimplify^73,74 and optimized using the L-BFGS algorithm in translation rotation internal coordinates (TRIC)⁷⁵ to the default tolerances of 4.5 × 10⁻⁴ hartree per bohr for the maximum gradient and 1 × 10⁻⁶ hartree for the energy change between steps. During the optimization, the positions of the metal and He atoms were fixed to maintain the target metal–He distances and angles. Geometry checks^76,77 were applied to eliminate optimized structures that deviated from the expected octahedral shape following previously established metrics^76,77 without modification (ESI Table S7†).

4.3. MR diagnostic calculations

Following our prior studies,^44,51 we calculated 14 MR diagnostics^24,32–41 using ORCA 4.0.2.1 (ref. 78,79) with the cc-pVTZ basis set on the metals as well as P and S elements and the cc-pVDZ basis set on all other atoms (ESI Table S1†). To evaluate the MR character, the restricted open-shell formalism was used in all DFT and Hartree–Fock (HF) calculations. We chose the restricted open-shell formalism because it was observed^24,52 that unrestricted formalism can recover some MR effects in open-shell systems and thus lead to smaller MR diagnostics. We converged a B3LYP calculation and used it to initialize both DFT calculations with other density functionals (i.e., BLYP, B1LYP, PBE, and PBE0) and the HF calculations. This ensured we converged a consistent electronic state over multiple calculations and also saved computational time. The converged HF wavefunction was then used for MP2 and CCSD(T) calculations. Finally, the MP2 natural orbitals were used to set up a CASSCF calculation with active spaces of 10, 12, and 14 orbitals (ESI Fig. S16†).

All MR diagnostics were computed using the default parameters in ORCA (ESI Table S8†). During the computation of total atomization energy (TAE)-based diagnostics, we assumed heterolytic dissociation for the metal–ligand bond (i.e., the oxidation state of the metal does not change) and homolytic dissociation for the atoms in the ligands, where each individual atom kept its formal charge (ESI Table S6†). We chose the percentage of correlation energy recovered by CCSD compared to CCSD(T) (i.e., %E_corr[(T)]) as the figure of merit, as we observed good correspondence of %E_corr[(T)] and %E_corr[T] in both equilibrium and distorted organic molecules in our previous work.⁴⁴ We also tested it for complexes with six helium atoms as ligands in this work and found excellent agreement between %E_corr[(T)] and %E_corr[T] (ESI Fig. S1†).

If all 14 MR diagnostics could not be successfully computed (e.g., due to lack of SCF convergence or one of the calculations exceeding the allowed wall time), we removed the single TMC structure (i.e., at a single M–He bond length) from the dataset (ESI Table S9†). A few (274, ca. 2%) CCSD(T) calculations resulted in significantly different perturbative triples corrections among TMCs with different metal–He distances but same chemical composition, potentially due to the CCSD wavefunctions converging to different electronic states. We removed those cases by the Grubbs outlier test⁸⁰ and Z-score test by comparing the perturbative triples corrections obtained using TMCs with the same chemical composition and ligand symmetry but different metal–He distances (ESI Fig. S17 and Tables S10–S11†). We also removed TMCs where the standard deviation of the leading weight of the CASSCF wavefunction, C₀², obtained with the three active spaces (i.e., with 10, 12, and 14 active orbitals) was larger than 0.1 (334, ca. 3%), which indicated that a final active space of 14 orbitals was not sufficient (ESI Fig. S18 and Table S12†).

4.4. ML models

As in prior work,^44,51 we use Coulomb-decay revised auto-correlations (CD-RACs)⁴⁴ as descriptors for all of our machine learning models. CD-RACs are sums of products and differences of five atom-wise heuristic properties (i.e., topology, identity, electronegativity, covalent radius, and nuclear charge) on the 2D molecular graph divided by the pairwise atomic distance. This incorporation of the pairwise distance imparts 3D geometric information to graph-based RACs⁸¹ to distinguish TMCs with the same chemical composition but different metal–He distances. We chose CD-RACs as descriptors because RACs have been previously demonstrated to provide good performance in equilibrium properties of TMCs^77,82 and CD-RACs have shown superior performance on predicting MR diagnostics for both equilibrium and non-equilibrium geometries of organic molecules in comparison to several alternatives.⁴⁴ As motivated previously,⁸¹ we apply the maximum bond depth of three and eliminate constant RACs (ESI Text S1†). For properties that involve two structures (i.e., adiabatic spin splitting and ionization potential), the CD-RACs of the two geometries were concatenated (ESI Table S3†). For all artificial neural network (ANN) models, the hyperparameters were selected using HyperOpt⁸³ with 200 evaluations, using a random 80/20 train/test split, with 20% of the training data (i.e., 16% overall) used as the validation set (ESI Table S13†). All ANN models were trained using Keras⁸⁴ with Tensorflow⁸⁵ as a backend. All models used the Adam optimizer up to 2000 epochs, and dropout, batch normalization, and early stopping to avoid over-fitting.

Data availability

The datasets supporting this article have been uploaded as part of the ESI.† The machine learning models are available on Zenodo at the URL https://zenodo.org/record/5851432#.YeHOoS-B1pQ.

Author contributions

C. D., D. B. K. C., and H. J. K.: conceptualization, methodology, C. D. and D. B. K. C.: data curation, writing – original draft preparation. C. D., D. B. K. C., and H. J. K.: visualization, investigation. H. J. K.: supervision. C. D., D. B. K. C, A. N., and H. J. K.: writing – reviewing and editing.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by the Department of Energy under grant number DE-SC0018096 and the Office of Naval Research under grant numbers N00014-18-1-2434 and N00014-20-1-2150. A. N. and D. B. K. C. were partially supported by a National Science Foundation Graduate Research Fellowship under Grants #1122374 and #1745302, respectively. H. J. K. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund and an AAAS Marion Milligan Mason Award, which supported this work. This work was carried out in part using computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. The authors thank Adam H. Steeves for providing a critical reading of the manuscript.

References

1. Y. N. Shu and B. G. Levine, Simulated Evolution of Fluorophores for Light Emitting Diodes, J. Chem. Phys., 2015, 142(10), 104104.
2. R. Gomez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D. G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. L. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Design of efficient molecular organic light-emitting diodes by a high-throughput virtual screening and experimental approach, Nat. Mater., 2016, 15(10), 1120–1127.
3. I. Y. Kanal, S. G. Owens, J. S. Bechtel and G. R. Hutchison, Efficient Computational Screening of Organic Polymer Photovoltaics, J. Phys. Chem. Lett., 2013, 4(10), 1613–1623.
4. K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Computational Approach to Molecular Catalysis by 3d Transition Metals: Challenges and Opportunities, Chem. Rev., 2018, 119, 2453–2523.
5. M. Foscato and V. R. Jensen, Automated in silico design of homogeneous catalysts, ACS Catal., 2020, 10(3), 2354–2377.
6. S. Curtarolo, G. L. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, The high-throughput highway to computational materials design, Nat. Mater., 2013, 12(3), 191–201.
7. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319.
8. J. K. Nørskov and T. Bligaard, The catalyst genome, Angew. Chem., Int. Ed., 2013, 52(3), 776–777.
9. J. P. Janet, C. R. Duan, A. Nandy, F. Liu and H. J. Kulik, Navigating Transition-Metal Chemical Space: Artificial Intelligence for First-Principles Design, Acc. Chem. Res., 2021, 54(3), 532–545.
10. A. S. Rosen, S. M. Iyer, D. Ray, Z. P. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Machine learning the quantum-chemical properties of metal-organic frameworks for accelerated materials discovery, Matter, 2021, 4(5), 1578–1597.
11. M. Ceriotti, C. Clementi and O. A. von Lilienfeld, Introduction: Machine Learning at the Atomic Scale, Chem. Rev., 2021, 121(16), 9719–9721.
12. J. A. Keith, V. Vassilev-Galindo, B. Q. Cheng, S. Chmiela, M. Gastegger, K. R. Mueller and A. Tkatchenko, Combining Machine Learning and Computational Chemistry for Predictive Insights Into Chemical Systems, Chem. Rev., 2021, 121(16), 9816–9872.
13. M. Ceriotti, Unsupervised machine learning in atomistic simulations, between predictions and understanding, J. Chem. Phys., 2019, 150(15), 150901.
14. A. Grisafi, A. Fabrizio, B. Meyer, D. M. Wilkins, C. Corminboeuf and M. Ceriotti, Transferable Machine-Learning Model of the Electron Density, ACS Cent. Sci., 2018, 5(1), 57–64.
15. K. Jorner, A. Tomberg, C. Bauer, C. Skold and P. O. Norrby, Organic reactivity from mechanism to machine learning, Nat. Rev. Chem., 2021, 5(4), 240–255.
16. M. F. Kasim and S. M. Vinko, Learning the Exchange-Correlation Functional from Nature with Fully Differentiable Density Functional Theory, Phys. Rev. Lett., 2021, 127(12), 126403.
17. A. Glielmo, B. E. Husic, A. Rodriguez, C. Clementi, F. Noe and A. Laio, Unsupervised Learning Methods for Molecular Simulation Data, Chem. Rev., 2021, 121(16), 9722–9758.
18. T. Dimitrov, C. Kreisbeck, J. S. Becker, A. Aspuru-Guzik and S. K. Saikin, Autonomous Molecular Design: Then and Now, ACS Appl. Mater. Inter., 2019, 11(28), 24825–24836.
19. A. J. Cohen, P. Mori-Sánchez and W. Yang, Challenges for density functional theory, Chem. Rev., 2012, 112(1), 289–320.
20. A. D. Becke, Perspective: Fifty years of density-functional theory in chemical physics, J. Chem. Phys., 2014, 140(18), 18A301.
21. C. J. Cramer and D. G. Truhlar, Density functional theory for transition metals and transition metal chemistry, Phys. Chem. Chem. Phys., 2009, 11(46), 10757–10816.
22. C. Duan, F. Liu, A. Nandy and H. J. Kulik, Putting Density Functional Theory to the Test in Machine-Learning-Accelerated Materials Discovery, J. Phys. Chem. Lett., 2021, 12(19), 4628–4637.
23. H. Y. S. Yu, S. H. L. Li and D. G. Truhlar, Perspective: Kohn-Sham Density Functional Theory Descending a Staircase, J. Chem. Phys., 2016, 145(13), 130901.
24. U. R. Fogueri, S. Kozuch, A. Karton and J. M. L. Martin, A simple DFT-based diagnostic for nondynamical correlation, Theor. Chem. Acc., 2013, 132(1), 1291.
25. B. G. Janesko, Replacing hybrid density functional theory: motivation and recent advances, Chem. Soc. Rev., 2021, 50(15), 8470–8495.
26. N. Mardirossian and M. Head-Gordon, Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals, Mol. Phys., 2017, 115(19), 2315–2372.
27. J. D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128(8), 084106.
28. L. E. Aebersold and A. K. Wilson, Considering Density Functional Approaches for Actinide Species: The An66 Molecule Set, J. Phys. Chem. A, 2021, 125(32), 7029–7037.
29. C. Duan, S. X. Chen, M. G. Taylor, F. Liu and H. J. Kulik, Machine learning to tame divergent density functional approximations: a new path to consensus materials design principles, Chem. Sci., 2021, 12(39), 13021–13036.
30. M. Reiher, Molecule-Specific Uncertainty Quantification in Quantum Chemical Studies, Isr. J. Chem., 2022, 62(1–2) DOI:10.1002/ijch.202100101.
31. A. Nandy, C. Duan and H. J. Kulik, Audacity of huge: overcoming challenges of data scarcity and data quality for machine learning in computational materials discovery, Curr. Opin. Chem. Eng., 2022, 36, 100778.
32. T. J. Lee and P. R. Taylor, A Diagnostic for Determining the Quality of Single-Reference Electron Correlation Methods, Int. J. Quantum Chem., 1989, 199–207.
33. J. S. Sears and C. D. Sherrill, Assessing the performance of density functional theory for the electronic structure of metal-salens: The d(2)-metals, J. Phys. Chem. A, 2008, 112(29), 6741–6752.
34. J. S. Sears and C. D. Sherrill, Assessing the performance of density functional theory for the electronic structure of metal-salens: The 3d(0)-metals, J. Phys. Chem. A, 2008, 112(15), 3466–3477.
35. S. R. Langhoff and E. R. Davidson, Configuration interaction calculations on the nitrogen molecule, Int. J. Quantum Chem., 1974, 8(1), 61–72.
36. C. L. Janssen and I. M. B. Nielsen, New diagnostics for coupled-cluster and Moller-Plesset perturbation theory, Chem. Phys. Lett., 1998, 290(4–6), 423–430.
37. I. M. B. Nielsen and C. L. Janssen, Double-substitution-based diagnostics for coupled-cluster and Moller-Plesset perturbation theory, Chem. Phys. Lett., 1999, 310(5–6), 568–576.
38. N. E. Schultz, Y. Zhao and D. G. Truhlar, Density functionals for inorganometallic and organometallic chemistry, J. Phys. Chem. A, 2005, 109(49), 11127–11143.
39. O. Tishchenko, J. J. Zheng and D. G. Truhlar, Multireference model chemistries for thermochemical kinetics, J. Chem. Theory Comput., 2008, 4(8), 1208–1219.
40. E. Ramos-Cordoba and E. Matito, Local Descriptors of Dynamic and Nondynamic Correlation, J. Chem. Theory Comput., 2017, 13(6), 2705–2711.
41. E. Ramos-Cordoba, P. Salvador and E. Matito, Separation of dynamic and nondynamic correlation, Phys. Chem. Chem. Phys., 2016, 18(34), 24015–24023.
42. A. Karton, S. Daon and J. M. L. Martin, W4-11: a high-confidence benchmark dataset for computational thermochemistry derived from first-principles W4 data, Chem. Phys. Lett., 2011, 510(4–6), 165–178.
43. M. K. Kesharwani, N. Sylvetsky, A. Kohn, D. P. Tew and J. M. L. Martin, Do CCSD and approximate CCSD-F12 variants converge to the same basis set limits? The case of atomization energies, J. Chem. Phys., 2018, 149(15), 154109.
44. C. Duan, F. Liu, A. Nandy and H. J. Kulik, Data-Driven Approaches Can Overcome the Cost-Accuracy Trade-off in Multireference Diagnostics, J. Chem. Theory Comput., 2020,(16), 4373–4387.
45. C. J. Stein and M. Reiher, Automated selection of active orbital spaces, J. Chem. Theory Comput., 2016, 12(4), 1760–1771.
46. J. B. Schriber and F. A. Evangelista, Communication: an adaptive configuration interaction approach for strongly correlated electrons with tunable accuracy, J. Chem. Phys., 2016, 144(16), 161106.
47. A. Baiardi, A. K. Kelemen and M. Reiher, Excited-State DMRG Made Simple with FEAST, J. Chem. Theory Comput., 2021, 18(1), 415–430.
48. D. S. King and L. Gagliardi, A Ranked-Orbital Approach to Select Active Spaces for High-Throughput Multireference Computation, J. Chem. Theory Comput., 2021, 17(5), 2817–2831.
49. N. He and F. A. Evangelista, A zeroth-order active-space frozen-orbital embedding scheme for multireference calculations, J. Chem. Phys., 2020, 152(9), 192107.
50. W. Jeong, S. J. Stoneburner, D. King, R. Li, A. Walker, R. Lindh and L. Gagliardi, Automation of Active Space Selection for Multireference Methods via Machine Learning on Chemical Bond Dissociation, J. Chem. Theory Comput., 2020, 16, 2389–2399.
51. C. Duan, F. Liu, A. Nandy and H. J. Kulik, Semi-supervised Machine Learning Enables the Robust Detection of Multireference Character at Low Cost, J. Phys. Chem. Lett., 2020, 11(16), 6640–6648.
52. W. Y. Jiang, N. J. DeYonker and A. K. Wilson, Multireference Character for 3d Transition-Metal-Containing Molecules, J. Chem. Theory Comput., 2012, 8(2), 460–468.
53. J. Wang, S. Manivasagam and A. K. Wilson, Multireference character for 4d transition metal-containing molecules, J. Chem. Theory Comput., 2015, 11(12), 5865–5872.
54. M. K. Sprague and K. K. Irikura, Quantitative estimation of uncertainties from wavefunction diagnostics, in T. H. Dunning Jr, Springer, 2015, pp. 307–318.
55. S. McAnanama-Brereton and M. P. Waller, Rational Density Functional Selection Using Game Theory, J. Chem. Inf. Model., 2017, 58(1), 61–67.
56. M. Gastegger, L. Gonzalez and P. Marquetand, Exploring density functional subspaces with genetic algorithms, Monatsh. Chem., 2019, 150(2), 173–182.
57. F. Liu, C. Duan and H. J. Kulik, Rapid Detection of Strong Correlation with Machine Learning for Transition-Metal Complex High-Throughput Screening, J. Phys. Chem. Lett., 2020, 11(19), 8067–8076.
58. M. Feldt, Q. M. Phung, K. Pierloot, R. A. Mata and J. N. Harvey, Limits of Coupled-Cluster Calculations for Non-Heme Iron Complexes, J. Chem. Theory Comput., 2019, 15(2), 922–937.
59. T. Husch, J. C. Sun, L. X. Cheng, S. J. R. Lee and T. F. Miller, Improved accuracy and transferability of molecular-orbital-based machine learning: organics, transition-metal complexes, non-covalent interactions, and transition states, J. Chem. Phys., 2021, 154(6), 064108.
60. J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning, Nat. Commun., 2019, 10, 2903.
61. J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, A quantitative uncertainty metric controls error in neural network-driven chemical discovery, Chem. Sci., 2019, 10, 7913–7922.
62. J. Shee, E. J. Arthur, S. W. Zhang, D. R. Reichman and R. A. Friesner, Phaseless Auxiliary-Field Quantum Monte Carlo on Graphical Processing Units, J. Chem. Theory Comput., 2018, 14(8), 4109–4121.
63. R. Tsuchida, Absorption Spectra of Co-ordination Compounds. I, BCSJ, 1938, 13(5), 388–400.
64. S. Gugler, J. P. Janet and H. J. Kulik, Enumeration of de novo inorganic complexes for chemical discovery and machine learning, Mol. Syst. Des. Eng., 2020, 5(1), 139–152.
65. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789.
66. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5652.
67. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98(45), 11623–11627.
68. S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, C. M. Isborn, S. I. L. Kokkila-Schumacher, X. Li, F. Liu, N. Luehr, J. W. Snyder, C. C. Song, A. V. Titov, I. S. Ufimtsev, L. P. Wang and T. J. Martinez, TeraChem: a graphical processing unit-accelerated electronic structure package for large-scale ab initio molecular dynamics, Wires Comput. Mol. Sci., 2021, 11(2), 1494.
69. L. L. C. Petachem, PetaChem, https://www.petachem.com/, accessed May 23, 2020.
70. I. S. Ufimtsev and T. J. Martinez, Quantum chemistry on graphical processing units. 3. Analytical energy gradients, geometry optimization, and first principles molecular dynamics, J. Chem. Theory Comput., 2009, 5(10), 2619–2628.
71. P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg, J. Chem. Phys., 1985, 82(1), 270–283.
72. V. R. Saunders and I. H. Hillier, Level-Shifting Method for Converging Closed Shell Hartree-Fock Wave-Functions, Int. J. Quantum Chem., 1973, 7(4), 699–705.
73. E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, molSimplify: A toolkit for automating discovery in inorganic chemistry, J. Comput. Chem., 2016, 37, 2106–2117.
74. molSimplify molSimplify github page, https://github.com/hjkgrp/molSimplify, accessed January 11, 2022.
75. L.-P. Wang and C. Song, Geometry optimization made simple with translation and rotation coordinates, J. Chem. Phys., 2016, 144(21), 214108.
76. C. Duan, J. P. Janet, F. Liu, A. Nandy and H. J. Kulik, Learning from Failure: Predicting Electronic Structure Calculation Outcomes with Machine Learning Models, J. Chem. Theory Comput., 2019, 15(4), 2331–2345.
77. A. Nandy, C. Duan, J. P. Janet, S. Gugler and H. J. Kulik, Strategies and Software for Machine Learning Accelerated Discovery in Transition Metal Chemistry, Ind. Eng. Chem. Res., 2018, 57(42), 13973–13986.
78. F. Neese, The ORCA program system, Wires Comput. Mol. Sci., 2012, 2(1), 73–78.
79. F. Neese, Software update: the ORCA program system, version 4.0, Wires Comput. Mol. Sci., 2018, 8(1), e1327.
80. F. E. Grubbs, Sample Criteria for Testing Outlying Observations, Ann. Math. Stat., 1950, 21(1), 27–58.
81. J. P. Janet and H. J. Kulik, Resolving transition metal chemical space: feature selection for machine learning and structure-property relationships, J. Phys. Chem. A, 2017, 121(46), 8939–8954.
82. J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, Accurate multi-objective design in a space of millions of transition metal complexes with neural-network-driven efficient global optimization, ACS Cent. Sci., 2020, 6(4), 513–524.
83. J.C. Bergstra, D. Yamins, D.D. Cox, Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms, Proceedings of the 12th Python in science conference, 2013, pp. 13–20.
84. F. Chollet, Keras, https://keras.io/, accessed June 24 2021.
85. M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, R. Jozefowicz, Y. Jia, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, M. Schuster, R. Monga, S. Moore, D. Murray, C. Olah, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015.

---

Footnote

† Electronic supplementary information (ESI) available: %E_corr[T] vs. %E_corr[(T)] for select complexes; ΔE_H–Lversus metal–helium distance for Fe(II)(CO)He₅; distribution of %E_corr[(T)]; level of theory for each computed MR diagnostic; Pearson's r matrix of MR diagnostics and %E_corr[(T)]; bar plot of unsigned Pearson's r and Spearman's r for MR diagnostics; 2D histogram for %E_corr[(T)] and MR diagnostics; summary of ANN model performance; MR effect cancellation vs. accumulation for adiabatic ΔE_H–L and IP; summary of ML features; MAE of transfer learning models on adiabatic ΔE_H–L and IP; comparison of the combined strategy and UQ only approach; metals, oxidation states, spin states, and ligands for constructing the data set; data attrition counts, reasons, and cutoffs; workflow of computing MR diagnostics and calculation parameters; potential energy curves and T₁ diagnostic for select TMCs; extended description of the CD-RAC featurization; range of hyperparameters during hyperparameter selections; ML model h5 files (https://zenodo.org/record/5851432#.YeHOoS-B1pQ); optimized TMC geometries xyz files; data csv files. See https://doi.org/10.1039/d2sc00393g

---