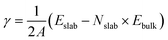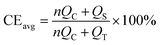Open Access Article
Open Access ArticleTowards understanding the nucleation and growth mechanism of Li dendrites on zinc oxide-coated nickel electrodes†
Abdolkhaled
Mohammadi
 *abc,
Arthur
Hagopian
*abc,
Arthur
Hagopian
 ad,
Syreina
Sayegh
ad,
Syreina
Sayegh
 e,
Mikhael
Bechelany
e,
Mikhael
Bechelany
 e,
Jean-Sébastien
Filhol
e,
Jean-Sébastien
Filhol
 ad,
Reza
Younesi
ad,
Reza
Younesi
 bc,
Lorenzo
Stievano
bc,
Lorenzo
Stievano
 acd and
Laure
Monconduit
acd and
Laure
Monconduit
 *acd
*acd
aICGM, Univ. Montpellier, CNRS, ENSCM, Montpellier, France. E-mail: Laure.monconduit@umontpellier.fr; Abdolkhaled.mohammadi@umontpellier.fr
bDepartment of Chemistry, Ångström Laboratory, Uppsala University, Uppsala, Sweden
cAlistore-ERI, CNRS, Amiens, France
dRS2E, CNRS, Amiens, France
eInstitut Européen des Membranes, IEM, UMR 5635, Univ. Montpellier, CNRS, ENSCM, Montpellier, France
First published on 1st August 2022
Abstract
While lithium metal is considered an ideal anode for the next generation of high-energy-density batteries, some major issues such as huge volume change and continuous dendrite formation during lithium plating have hindered its practical applications. Zinc oxide (ZnO) modification of surfaces has shown great potential for inducing a homogeneous Li plating to attain dendrite-free lithium metal anodes. Although considerable improvements in electrochemical performance have been achieved, the detailed mechanism of the evolution of Li nucleation and growth morphology remains elusive. Here, we combine experimental and theoretical calculations to study the Li deposition behaviour during and after the initial nucleation on a thin and uniform layer of ZnO-coated 3D nickel foam. Upon lithiation of the ZnO layer, Li2O and LiZn are formed through a conversion reaction; this composite layer provides specific properties ensuring a homogeneous Li plating. The results showed that dendrite growth not only leads to the formation of cracks on the surface but also provokes the breakoff of some parts of the converted layers from the bulk surface. In addition, no new nucleation occurs upon continued Li deposition, with Li plating mainly taking place on the initial nuclei underneath the protective layer. As a result, large granular Li particles grow at the site of the initial Li nucleation centre, leading to the improvement of electrochemical performances. A deeper understanding of the mechanism of Li nucleation and growth and the morphology of the formed dendrites can help with the development of lithium metal batteries.
Introduction
Lithium metal batteries promise to be the future of battery technology with widespread use in next-generation electronic devices due to their low electrochemical potential (−3.04 V vs. standard hydrogen electrode) and high theoretical specific capacity (3860 mA h g−1).1–3 A major technical problem associated with Li metal anodes, however, is the growth of dendrites, which leads to the formation of inactive Li during the plating and stripping process, resulting in poor cycle life, low coulombic efficiency (CE) as well as battery safety concerns.4–6 To tackle the dendrite formation issue, researchers have proposed a wide range of solutions and strategies, from the use of various electrode designs and composite anodes to electrolyte engineering and interface modification, often including theoretical simulation methods.7–10 One promising approach that has recently gained attention is the use of three-dimensional (3D) host structures to contain the Li metal anodes.11 The high surface area of 3D structures can help delay the systematic build-up of dendrites observed in host-less Li metal anodes,12,13 by dissipating the local current density and regulating the important volume changes. As suggested in previous works, the lithiophilic nature of the 3D host could be one of the significant factors allowing for a uniform Li deposition.14 Since the conventional 3D host may not possess intrinsic lithiophilic properties, it is usually considered as necessary to coat the 3D host mesh with a lithiophilic layer to ensure a uniform Li deposition.15–17Zinc oxide (ZnO) has been proposed as one of the materials supposed to improve the lithiophilicity of the 3D host since the electrochemical conversion of ZnO with lithium produces an intimate mixture of LiZn and Li2O, which acts as a composite buffer layer on which Li metal is further plated.18–21 For example, Liu et al. developed vertical cactus-like carbon nanotubes containing lithiophilic ZnO quantum dots grown on the surface of a 3D copper foam, resulting in higher CE and improved cycling stability.22 Although remarkable improvements in both CE and cycle life have been achieved in ZnO-modified substrates, an in-depth understanding of the underlying mechanism of Li nucleation and morphology evolution remains elusive on these substrates. Furthermore, it is widely accepted that the morphology of Li deposition is one of the determining factors for the electrochemical properties and performance of Li metal batteries.23–25 Many studies rely on low-magnification scanning electron microscope (SEM) imaging of the 3D host surface, showing the bulk morphology of the deposited Li metal as a sign of improvement in the Li plating process.26–31 However, the final bulk morphology does not provide insight into the actual Li nucleation and developmental process, and especially on the effective lithiophilic nature of the products of ZnO conversion. Therefore, it is important to have a fundamental understanding of the initial stages of nucleation and growth mechanisms, which may lead to the design of solutions for improving the performance of lithium metal batteries.
In this work, we focus on the nucleation and the morphological evolution of dendrite on the ZnO-modified substrate both experimentally and theoretically. To do so, a thin layer of ZnO was deposited on the 3D Ni foam by atomic layer deposition (ALD). ALD was shown to be a powerful technique for fabricating electrodes with uniform coatings with a precisely controlled thickness on the surface.32,33 Among different techniques that already exist, ALD has proved nanoengineering capabilities and versatility for different applications, which makes it a good candidate for industrial applications.34 For lithium-ion batteries, interesting advancements have been already devoted to opening the way for large-scale application of electrodes. For example, Hesieh et al. prepared TiO2-coated NCM cathode using the roll-to-roll ALD technique.35 The authors demonstrated the structural stability and cycling performance of Ni-rich NCM cathodes prepared through this ALD technique. Our prepared thin layer of ZnO-coated on the surface of Ni reacts electrochemically with lithium to form a composite layer containing Li2O and LiZn. The experimental observations (vide infra) show that Li is in reality deposited underneath the Li2O–LiZn composite coating, with Li dendrites growing from its roots at the Ni foam electrode surface. Density functional theory (DFT) calculations made on the different experimentally observed interfaces reveal that the Li plating is favoured below the protective layer, because (1) the Ni foam possess higher lithiophilicity than the Li2O–LiZn coating layer, and (2) the LiZn phase, that is dominant on the coating surface, provides a thermodynamic driving force for Li to migrate through it. Importantly, the high lithiophilicity computed for the Ni foam is in opposition with what is often claimed in the literature, i.e., that the 3D host is not lithiophilic and that a protective coating improves the cell electrochemical performances by increasing the interface lithiophilicity and seems to be a necessary condition allowing for a stable underneath plating mechanism. As introduced in previous works,36 an underneath plating mechanism is necessary for the interface stability on the long-term cycling. Notably, such underneath Li plating mechanism induces stress and causes fractures on the surface of the Li2O–LiZn coating layer, which partially breaks off from the 3D mesh surface. By continued Li deposition, no new nucleation sites are observed, and Li deposition occurs on the initial Li nuclei indicating that the latter ones are essential for subsequent Li growth. In addition, we show that the growth mode and morphology of deposited Li can be related to the surface chemistry. There is a clear morphological difference between the pure Ni (whisker-like) and ZnO-coated Ni foam (large granular shape), which can be correlated with the surface and root growth mechanism proposed by Kushima et al.37 Consequently, the ZnO-coated electrode with a large granular Li deposition on the surface achieves higher CE and a more stable cycle life compared to pure Ni foam. The experimental investigation combined with DFT calculations in this work significantly advanced our understanding of Li nucleation and growth on the ZnO-modified electrodes and their advantages.
Methods
Reagents and materials
Diethyl zinc (DEZ), bis(trifluoromethylsulfonyl)amine lithium salt (LiTFSI), 1,3-dioxolane (DOL), 1,2-dimethoxyethane (DME), lithium nitrate (LiNO3) and Li metal foil (350 μm thick) were all purchased from Sigma. Nickel (Ni) foam with a thickness of 300 μm, >99% purity, and >0.1 g cm−3 volume density was purchased from TMAX company in China. All other chemicals used in this work were of analytical reagent grade and were used without further purification.Material synthesis
ZnO thin films were deposited by ALD on the surface of Ni foam used as substrates. The deposition was held in a homebuilt reactor at 100 °C using DEZ and Milli-Q water as precursors and co-reactant, respectively. The precursors were kept at room temperature and the lines connected to the chamber were heated at 80 °C to avoid any condensation. A typical ALD sequence was applied with a 0.4 s pulse of DEZ and a 2 s pulse of water. Between each pulse, an exposure time of the 30 s and a purge time of 40 s using argon were maintained. The optimal thickness of ZnO was depicted by varying the number of ALD cycles from 50 to 500 cycles.38,39 After about 300 cycles, the ZnO coating reached the desired Li wetting property.Electrochemical measurements
Type 2032 coin cells were used to measure the electrochemical performance of the cells. The coin cells were assembled in an argon-filled glovebox (MBraun), in which both the oxygen and moisture contents were less than 1 ppm. The ZnO-coated or pure Ni foam (1.27 cm Ø) was used as a working electrode, while the reference and counter electrode was a piece of Li metal foil (1.2 cm Ø). The electrolyte was 100 μL of 1 M LiTFSI in DOL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DME (1
DME (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio) with 2 wt% LiNO3 and we have used a piece of Celgard 2325 as a separator. The data was collected using the potentiostat capabilities of the Biologic MPG-2 system at 25 ± 1 °C.
1 volume ratio) with 2 wt% LiNO3 and we have used a piece of Celgard 2325 as a separator. The data was collected using the potentiostat capabilities of the Biologic MPG-2 system at 25 ± 1 °C.
Characterizations
Before characterization by scanning electron microscopy (SEM), energy dispersive spectroscopy (EDS), and optical microscopy analyses, the working electrode surface was rinsed with DME in an Ar-filled glove box to remove residual salt. SEM images were taken by using a Zeiss/LEO 1550 at 1 and 20 kV accelerating voltage instruments equipped with the EDS detector. Optical images were collected inside the Ar-filled glovebox by using a Bresser LCD microscope (40×). X-ray diffraction (XRD) patterns were collected on a PANalytical X'Pert Pro MPD diffractometer with a Cu Kα radiation source (λ = 1.5418 Å) in the 2θ range 20°–80°.DFT calculations
Periodic calculations were performed within the density functional theory (DFT) framework, using the Vienna ab initio simulation package (VASP).40 The electronic wave functions have been expanded in a plane-wave basis set with a kinetic energy cutoff up to 450 eV. Projector augmented wave (PAW) pseudopotentials were used as implemented in VASP. Exchange-correlation effects have been accounted for by the generalized gradient approximation (GGA) using the functional of Perdew, Burke, and Ernzerhof (PBE).41 The convergence criterion has been set to 1.0 × 10−5 eV for the electronic self-consistent iterations. The structural relaxation was performed until the maximum force on any atom was below 2.0 × 10−2 eV Å−1. Surface calculations were performed on LiZn (100), (110), and (111) slabs with 9, 7, and 13 atomic layers, respectively, on Ni (100) slab with 7 atomic layers and on Li2O (100) slab with 9 atomic layers (Fig. S5†). The Brillouin zone integration in k-space was performed on a 6 × 6 × 1, 10 × 6 × 1, 6 × 6 × 1, 6 × 6 × 1, and 6 × 6 × 1 Γ-centred k-point grid,42 for LiZn (100), LiZn (110), LiZn (111), Ni (100) and Li2O (100) surfaces, respectively. To avoid interactions between adsorbed atoms of periodic images, 2 × 2 supercells were considered for all LiZn surfaces and 3 × 3 supercells were considered for Ni and Li2O surfaces. For LiZn (100) surface, 5 different surface terminations were computed: Li, Li0.75Zn0.25, Li0.5Zn0.5, Li0.25Zn0.75, and Zn. For LiZn (110) and (111), only Li and Zn terminated surfaces were computed. For Li2O (100) surface, Li and O terminated surfaces were computed. Cells were built symmetrically in the z-direction which allows a precise calculation of surface tension in particular under applied bias on polyatomic materials. The bottom and upper layers were allowed to relax while the central layer was kept frozen to avoid interaction through strain of the two slab surfaces. To avoid interaction between periodic images of the slab, a vacuum layer of 20 Å has been set in the z-direction. The surrounding surface environment was described with an implicit solvent by using the polarizable continuum model (PCM) as implemented in VASPsol.43 The dielectric constant (εb = 7) of DME was used. To avoid numerical instabilities, the effective surface tension parameter τ has been set to 0 eV Å−2 and the cutoff charge density parameter ρcut has been set to 5.0 × 10−5 Å−3.44 The cavity diffusion parameter σ has been set to the default value, 0.6. Surface calculations were carried out at various applied potentials. To vary the potential, the grand canonical density functional theory (GC-DFT) framework has been used in association with the homogeneous background method.45 As detailed in previous works,46 in this approach the potential is varied by changing the charge of the unit cell, i.e. adding or subtracting electrons from the neutral system. The added/subtracted charge is neutralized by a homogeneous background of the exact opposite charge. The difference between the Fermi energy and the vacuum potential allows obtaining the work function, corresponding to the potential Φ of the system. The potential can be scaled and referenced relatively to the Li potential through ΦLi = Φ − 1.46. To compute the surface tension γ of a given (hkl)-surface, the following relation were used:In this expression, 2A, Eslab, Nslab and Ebulk stand for the area of the two surfaces generated from bulk cleavage, the total energy of the slab, the number of atoms in the slab, and the bulk reference energy (per atom), respectively. The surface tensions were computed at various applied electrode potentials to obtain the electro-capillary curves of each (hkl)-surface (Fig. S6†), which allowed us to determine the surface that is the most stable at a given potential value.47 The binding energies Eb were calculated by using
| Eb = Eslab@Li − Eslab − EatomLi |
| UPE = Eslab + NEbulkLi − Eslab@N×Li |
Results and discussions
Fig. 1 a presents the XRD patterns of the pristine and the ZnO-coated Ni foam. The XRD pattern of bare Ni foam shows, as expected, the characteristic diffraction peaks of metallic Ni (JCPDS no. 96-210-0650) at 44.6° (111) and 52.1° (200). After modification of the Ni foam by ALD, the XRD pattern exhibits additional broad diffraction peaks located at 32.0°, 34.6°, 36.5°, and 56.8° which correspond to the (100), (002), (101), and (110) reflections of hexagonal ZnO (JCPDS File No. 01-079-0205), thus confirming the formation of nanocrystalline ZnO on the surface of the Ni foam.The morphology and the chemical composition of the bare and ZnO-coated Ni foam samples were investigated by SEM and EDS analysis. As can be seen in Fig. 1b, the bare Ni foam forms a three-dimensional macroporous cross-linked skeleton structure. In addition, the SEM top view shows that the surface of the bare nickel foam is made of a tightly knit nickel block body carpeted with small nanoparticles (Fig. S1a and b†). After coating with ZnO, no significant changes in the surface morphology of Ni foam are observed. The high-magnification SEM image (Fig. S1c and d†) reveals that even if the nickel block body assumes a smooth and even surface, the seams remain visible. Furthermore, as shown in the enlarged view of the modified sample in Fig. S1e,† the spongy layer of ZnO with an estimated thickness of ≈90 to 100 nm covers the surface of Ni foam. EDS elemental mapping was employed to characterize the distribution of ZnO on the Ni foam surface (Fig. 1d and e). The EDS spectra demonstrate the presence of Ni, Zn, O, and traces of C, uniformly distributed on the surface of the Ni foam. The EDS elemental mapping also confirms the presence of a thin layer of ZnO uniformly wrapped on the surface of the Ni foam.
To better follow the evolution of the morphology of electrodeposited Li on the surface of the ZnO-coated Ni foam electrode during plating-stripping cycling, the results are presented separately in the two following sections: (I) nucleation and (II) dendrite growth mechanism.
Nucleation mechanism
During the first half-discharge (from the open-circuit voltage (OCV) to 0 V), the ZnO inevitably gets reduced to form a mixture of Li2O and LiZn.48 According to previous studies, the reactions follow two subsequent distinct processes of conversion and alloying, as described below:49| ZnO + 2Li → Zn + Li2O |
| Zn + xLi → LixZn (x ≤ 1) |
SEM images collected after discharge to 0 V (Fig. S2a and b†) show that the surface of modified Ni foam becomes slightly rougher than in pristine ZnO-coated Ni foam. Furthermore, the elemental mapping of the surface shows the presence of F, C, O, and S homogeneously distributed on the surface of the substrate (Fig. S2c†), originating from the reduction of the electrolyte to form a solid electrolyte interphase (SEI) layer. The chemical composition of the SEI formed in these systems, in fact, normally includes Li2O, Li2CO3, Li3N, LiF, as well as organic ROCO2Li and ROLi.50,51 More importantly, elemental mapping also shows a homogeneous distribution of the Zn, which means that the LiZn layer starts to uniformly covers the Ni foam surface before Li metal plating.
During the first discharge cycle, electrodeposition of Li is expected to occur when the voltage goes below 0 V. The initial morphology of electrodeposited Li on the ZnO-coated Ni foam electrode was followed by plating 0.25 mA h cm−2 of Li at 0.5 mA cm−2 (Fig. 2a). Low-magnification SEM (Fig. 2b) shows that Li nucleation uniformly occurs over the entire structure of 3D Ni foam. By sharp contrast, for the pure Ni sample, Li nucleus were accumulated on the surface (Fig. S4†). High-magnification SEM, on the other hand, shows that Li plates as hair-like structures on the ZnO-coated electrode surface (Fig. 2c). The direction of this initially plated structure also changes by forming kinks, which is consistent with previous studies carried out using environmental transmission electron microscopy (ETEM) and ex situ SEM.37,52 Interestingly, the corresponding elemental mapping (Fig. 2c) shows that Zn is not just homogeneously dispersed on the surface, but also accumulates at the bottom of the dendrites. To depict more surface details of these dendrites, a low-energy electron beam (1 kV) was used. As shown by the orange colour in Fig. S3,† part of the layers formed on the Ni foam surface was separated from the surface and grows together with the dendrite. These results are similar to those shown in a recent report by Sun et al., where the authors revealed that during Li deposition on the Li6.4La3Zr1.4Ta0.6O12 (LLZTO) solid-state electrolyte, some dark particles broke off from the LLZTO bulk and were carried away by Li dendrite.53
To further understand the accumulation of zinc at the bottom of the Li nuclei, elemental mapping images were collected at high magnification on the top surface of the sample (Fig. 2d). Indeed, open cracks formed and cylindrical shaped dendrites emerged on the surface of ZnO-coated Ni foam (red arrows in Fig. 2d). In addition, elemental mapping confirms that these open cracks are systematically associated with zinc accumulation. The Li deposition scenario on the modified electrode can be described as diffusion through the Li2O–LiZn coating layer followed by nucleation at the electrode/coating interface. Accordingly, the deposition of Li on the Ni foam surface creates stress and generates a crack in the Li2O–LiZn layer. The broken surface layer is then lifted off by further Li deposition, as shown by the accumulation of zinc on the bottom of dendrites.
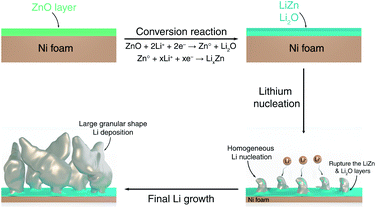
The mechanistic explanation of the early growth of a Li dendrite on the ZnO-coated electrode is schematized in Fig. 2e where the observations shown in Fig. 1 and 2 are summarized. During the migration of Li from the counter electrode, Li+ ions react with the ZnO layer that covers the surface of Ni foam to form a homogeneous composite coating containing Li2O and LiZn. Once Li plating starts, Li is deposited on the bottom of the converted Li2O–LiZn coating layer. Li dendrite nucleation and growth can induce large tensile stress near the surface and generate cracks on these layers. By continued Li deposition, some parts of Li2O and LiZn are chipped off from the surface and carried away by the growing dendrites.
Ancillary DFT calculations were carried out to rationalize this Li deposition under the protective layer. The Li plating process is initially governed by the termination of the surface layer as it corresponds to the first adsorption site of Li ions. The surface tension, which can be computed by DFT calculations for different (hkl)-orientations, surface composition, and also as a function of the applied potential, dictates which compound is thermodynamically the most stable at the surface layer. As discussed above, the electrode surface after the reaction with Li is mainly composed of a homogeneous mixture of nanocrystalline LiZn and Li2O. Thus, we have first computed the surface tension of LiZn (100), LiZn (110), and LiZn (111) with various surface compositions and as a function of the applied potential φ (Fig. S6†). Results show that the surface LiZn (100) terminated by Li atoms is the most stable over the whole potential range (from −2 to +2 V vs. Li+/Li).46 The surface tension of the Li2O (100) surface has also been computed at PZC with Li and O termination, resulting in surface tensions of 0.12 and 0.41 eV Å−2, respectively, always higher than 0.03 eV Å−2 computed for the Li-terminated LiZn (100) surface at PZC. Consequently, the Li-terminated LiZn (100) surface is the most stable surface which should be dominant at the interface with the electrolyte. The following calculations of surface energies are therefore mainly computed relatively to this surface. First, the binding energies of a Li atom are calculated to evaluate the affinity of Li ions, i.e., the lithiophilicity, with the different investigated surfaces present at the interface (Fig. 3a). The computed Li binding energy with Ni (100) surface results higher than with any other surfaces, suggesting that the Li will preferentially plate underneath the coating layer (directly on the Ni surface) and not on top of it. This result, which is coherent with the observed underneath plating mechanism, is in opposition with the often-claimed hypothesis that the protective layer should possess a higher lithiophilicity than the 3D host. Moreover, the binding energy of Li on a Li-terminated LiZn (100) surface is lower than the one on pure metal Li (100) and (110) surfaces. Thus, if Li atoms start to accumulate and form a fresh Li metal layer on the coating surface, all the subsequent Li ions will plate on this new Li metal surface, creating a new nucleation centre. This process, which suggest that a stable underneath plating mechanism can be obtained until a limiting current density is not reached, is undesired as the Li-plating on Li metal necessarily leads to hazardous dendrite growth.47,54
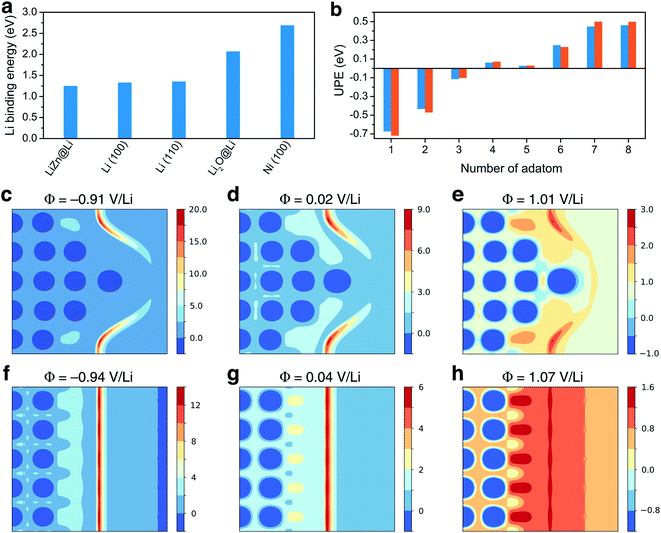 | ||
| Fig. 3 Theoretical study: (a) Li binding energy computed for LiZn@Li (100), Li (100), Li (110), Li2O@Li (100), and Ni (100) surfaces. (b) Underneath plating energy computed on LiZn@Li (100), for different numbers of adatom. (c)–(e) and (f)–(h) Electrostatic potential computed for different potential values and projected on the [200] plane of the calculation cell, with and without the Li tip, respectively, as provided in Fig. S7.† Values are given in volt. | ||
To evaluate such an underneath plating mechanism, we computed the underneath plating energy (UPE, already introduced and detailed in ref. 36 and 55) which corresponds to the energy cost for Li atoms to plate in a new Li bulk phase, i.e., in between the Ni foam and the protective layer.36,55 If the UPE is negative, it is thermodynamically more favorable for the Li atoms plate underneath rather than staying on top of the coating. On the contrary, if the UPE is positive, it means that the Li atoms are more stable on the coating surface. The UPE has therefore been computed on Li-terminated LiZn (100) surface for a different number of adsorbed atoms, which can be qualitatively related to Li accumulation with increasing current density. As a matter of fact, the surface accumulation of Li is the balance between the Li transport inside the protective layer and the current density. If the current density is too large relative to the Li diffusion in the layer, the Li atoms start to accumulate at the interface. Fig. 3b shows that the UPE is negative while the number of adsorbed atoms does not exceed 4. As consequence, a LiZn alloy layer effectively allows a stable underneath plating mechanism, as long as the current density threshold is not exceeded. When the current threshold is exceeded thick Li layers are formed and the growth on these layers becomes thermodynamically favored. This result agrees with binding energies calculations suggesting that Li ions prefer not to plate underneath the protective layer if a fresh Li metal layer is formed on its surface.
To gain insight into the initial growth mechanism, we have investigated the diffusion pathways close to a starting dendritic instability modelled by a Li tip (Fig. 3c to h), assuming that they are governed by the local electric field.56 The Li tip that we modelled (Fig. S7†) represents a possible structural fluctuation in the early-stage plating process. Results show that the electrostatic potential at the tip is localised on the sides of the tip and that a strong electric field is generated in these specific regions. In reductive conditions, the local electric field can be approximately 40% higher on the tip sides than on a bare Li surface. Consequently, the formation of a small tip enhances the surface electric field in some specific regions, inducing a self-propagating instability hindering a homogenous epitaxial plating and the formation of smooth surfaces. Moreover, the fact that the electric field is not localised above the tip suggests that Li dendrites should grow not only in length but also in thickness, which is coherent with the thick dendrites observed experimentally.
Evolution of the Li dendrite morphology
To further investigate the size and morphology evolution of Li deposits on the previously formed Li nuclei during continued electrodeposition, pure Ni and modified Ni electrodes were studied after plating a fixed capacity of 4 mA h cm−2 of Li at a current density of 0.5 mA cm−2. As shown by SEM in Fig. 4a and optical microscopy in Fig. S8c,† Li dendrites tend to deposit locally and agglomerate on the pure Ni electrode surface during the continuous Li deposition. By contrast, for the ZnO-coated Ni foam electrode (Fig. 4d and S7e†), Li dendrites are uniformly deposited on the skeleton of Ni foam and no new Li dendrite grows independently. The digital photographs of the electrodes (Fig. S8b and c†) also confirm that Li metal is uniformly distributed on the surface of the ZnO-coated Ni foam while, for the pure Ni foam electrode, Li is distributed with uneven island-like morphology. This indicates that the modified layer on the Ni foam is responsible not only for regulating nucleation at the onset of the Li deposition process but also for the subsequent Li growth.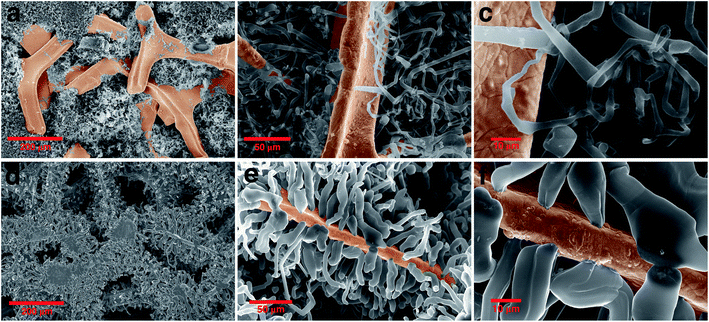 | ||
| Fig. 4 Morphology evolution of the Li dendrite: comparing the SEM image of (a)–(c) pure nickel and (d)–(f) ZnO-coated Ni foam electrodes after growth of dendrite in different magnifications. | ||
Similar results are observed also on the backside surface of the electrodes (Fig. S8f–i†), meaning that Li is unevenly accumulated on bare Ni foam, while it grows evenly and only on the bone of ZnO-coated Ni. It is noteworthy that Li has a lesser tendency to be deposited on the backside than the front side of the electrodes in both samples. For the 300 μm thick Ni foam sample (commercially available), it is not surprising to observe the gradient of Li deposition between the top and bottom of the electrodes. While it may be possible to further achieve maximum Li plating on the backside with a thinner thickness of Ni foam. Furthermore, the use of 3D frameworks implies that the volumetric or gravimetric specific capacity of the Li metal anode is reduced by including the mass or volume of the framework component. Hence, by using the thinner Ni foam the volumetric and gravimetric specific capacity of the cell will be improved along with reducing the mass and utilizing all the volume spaces inside the 3D framework.
The Li growth morphology shows significant differences in the dendrite shape when looked at a higher magnification. As shown in Fig. 4b–f, the Li dendrite morphology on the ZnO-coated electrode is much larger with an ordered granular shape, while on bare Ni foams it takes a thin individual whisker-like morphology. According to the growth mechanism models,37,57,58 in the ZnO-coated sample, the deposited Li morphology acts in accordance with the surface growth model (fast surface diffusion, formation of large agglomerates and thick dendrites), whereas on bare Ni electrodes it follows a tip or root growth model (slow surface diffusion, formation of small nucleates and thin whiskers). On the ZnO-coated Ni foam, the deposited Li morphology follows the surface model which can be attributed to three main reasons: (1) Li surface diffusion is fast on LiZn surface, at least faster than the diffusion of Li on Li surface (energy barrier Li–LiZn = 0.09 eV < Li–Li = 0.169 eV);26 (2) the Li deposition takes place underneath the protective layer, due to the negative UPE as demonstrated below, inducing a mechanical resistance which favours the growth of thick structures;59 (3) the nucleation of Li protrusions lead to an increased electric field on the sides of the tip which favour the formation of thick dendrites. Such surface deposition mechanism causes the local detachment and perforation of the coating layer during the first growth steps of the nucleated Li grains, as shown in Fig. S3.† We have further found that in the growth stage no new Li nuclei emerge (Fig. S9†), and Li tends to preferentially deposit on the initially formed Li nuclei. This indicates that the initial Li nucleation is a determining step governing the subsequent growth of the Li deposits, which is the basis for the electrochemical performance of the batteries.
Electrochemical performance
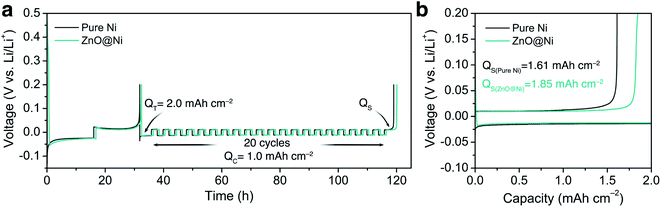
To verify the effect of the ZnO-coated Ni electrodes on the electrochemical performance, a galvanostatic test was performed in coin cells, the derived average CE being calculated based on Adam's reservoir method.60Fig. 5 shows the cycling behaviour of the bare and ZnO-coated Ni foam at a current density of 0.5 mA cm−2 at the current density of 0.5 mA cm−2. Based on this protocol, it is necessary to first stabilize the electrode surfaces to mitigate the effect of the initial side reactions between Li and the electrodes. To do so, 8.0 mA h cm−2 of Li was deposited on the Ni foam and then stripped off completely to the cut-off voltage at 0.2 V. After this initial passivation process, once again, the Ni foam was coated with 2.0 mA h cm−2 (QT) of Li and the cell was allowed to cycle with a fixed capacity of 1.0 mA h cm−2 (QC) then completely stripped to 0.2 cutoff voltage (QS). An average value of CE can be calculated by using the following equation:As shown in Fig. 5b, the ZnO-coated Ni electrode remaining capacity is higher compared to the pure Ni foam. The ZnO-coated Ni electrode exhibits an average CE of 99.3% after 20 cycles, significantly higher than that of bare Ni foam (98.2%). These results are consistent with previous studies by Meng and co-workers,25 who concluded that the loss of CE in Li-metal batteries can be attributed mostly to the unreacted Li metal rather than to the continuous formation of SEI, and that larger amounts of unreacted Li are more likely to remain in whisker-shaped deposits rather than in granular ones. Hence, Li deposits with large granular sizes are expected to show better electrochemical performance.
Combining insights from complementary characterization tools, we propose a complete description of the growth morphology of a protective ZnO coating layer deposited on the surface of a Ni foam electrode, as well as of its role in Li electrodeposition, as shown schematically in Fig. 6. During the first half-discharge, the ZnO coating layer on the surface of Ni foam reacts with Li to form an intimate mixture of LiZn and Li2O. Such composite coating enables fast Li+ diffusion towards the surface of the Ni foam, where it deposits at the interface between Ni and the LiZn species. As a result, homogeneously dispersed Li nuclei form underneath the coating layer, while the growing dendrites perforate the LiZn–Li2O composite coating layer and lead to the fast growth of Li granular deposits, which remain decorated with some LiZn and Li2O at their surface being carried out from the surface by the growth of the dendrites. This uniform nucleation with the debris of LiZn and Li2O on the surface of dendrite leads to the formation of large Li granular morphologies with the progression of Li deposition. Such large Li granular shape dendrites are expected to reduce the amount of Li metal trapped in the SEI, thus leading to an improvement in the reversibility of Li plating and stripping.
Conclusions
In this study, combining experimental studies with DFT calculation, we have demonstrated and provided a mechanistic detail for the nucleation and growth morphology of Li on the ZnO-coated Ni foam electrode. Our experimental study shows that applying a thin film of ZnO on the surface of 3D Ni foam effectively promotes uniform Li nucleation over the entire electrode surface. DFT calculations reveal that the lithium plating process occurs underneath the LiZn protective layer, which is favourable for a stable deposition, therefore improving the electrochemical performance of this system. The electrostatic potential profile of a modelled lithium tip highlights how the electric field is enhanced by a small protrusion and suggests that dendrites should grow not only in length but also in thickness, coherently with experimental observations. With continued Li electrodeposition, Li plating occurs on the previously homogeneous formed Li nuclei leading to the formation of large Li granular morphologies. These merits jointly contribute to improving the electrochemical performance of ZnO-coated Ni electrodes compared to the pristine Ni foam. The proposed Li nucleation behaviour and its relationship with the growth mechanism provide new fundamental insights into Li deposition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors would like to thank Anastasiia Mikheenkova and Wessel van Ekeren for recording the SEM images. The Alistore-European Research Institute (ALISTORE-ERI) network is warmly thanked for funding the Ph.D. grant of A. M. The authors gratefully acknowledge financial support from the French National Research Agency (project Labex STORE-EX, ANR-10-LABX-76-01) and from the Swedish Energy Agency via StandUp for Energy for financial support. Computational work was performed using HPC resources from GENCI-CINES (Grant 2021-A0100910369).Notes and references
- P. Zou, Y. Sui, H. Zhan, C. Wang, H. L. Xin, H. M. Cheng, F. Kang and C. Yang, Chem. Rev., 2021, 121, 5986–6056 CrossRef CAS PubMed.
- R. Younesi, G. M. Veith, P. Johansson, K. Edström and T. Vegge, Energy Environ. Sci., 2015, 8, 1905–1922 RSC.
- A. Mohammadi, L. Monconduit, L. Stievano and R. Younesi, J. Electrochem. Soc., 2022, 169(7), 070509 CrossRef.
- H. Chen, C.-J. Zhou, X.-R. Dong, M. Yan, J.-Y. Liang, S. Xin, X.-W. Wu, Y.-G. Guo and X.-X. Zeng, ACS Appl. Mater. Interfaces, 2021, 13, 22978–22986 CrossRef CAS PubMed.
- S. Li, W. Zhang, Q. Wu, L. Fan, X. Wang, X. Wang, Z. Shen, Y. He and Y. Lu, Angew. Chem., Int. Ed., 2020, anie.202004853 Search PubMed.
- Y. Xu, K. Dong, Y. Jie, P. Adelhelm, Y. Chen, L. Xu, P. Yu, J. Kim, Z. Kochovski, Z. Yu, W. Li, J. LeBeau, Y. Shao-Horn, R. Cao, S. Jiao, T. Cheng, I. Manke and Y. Lu, Adv. Energy Mater., 2022, 2200398 CrossRef.
- G. M. Hobold, J. Lopez, R. Guo, N. Minafra, A. Banerjee, Y. Shirley Meng, Y. Shao-Horn and B. M. Gallant, Nat. Energy, 2021, 6, 951–960 CrossRef CAS.
- J. Touja, N. Louvain, L. Stievano, L. Monconduit and R. Berthelot, Batteries Supercaps, 2021, 4, 1252–1266 CrossRef CAS.
- X. He, D. Bresser, S. Passerini, F. Baakes, U. Krewer, J. Lopez, C. T. Mallia, Y. Shao-Horn, I. Cekic-Laskovic, S. Wiemers-Meyer, F. A. Soto, V. Ponce, J. M. Seminario, P. B. Balbuena, H. Jia, W. Xu, Y. Xu, C. Wang, B. Horstmann, R. Amine, C.-C. Su, J. Shi, K. Amine, M. Winter, A. Latz and R. Kostecki, Nat. Rev. Mater., 2021, 6, 1036–1052 CrossRef CAS.
- X. Sun, X. Zhang, Q. Ma, X. Guan, W. Wang and J. Luo, Angew. Chem., Int. Ed., 2020, 59, 6665–6674 CrossRef CAS PubMed.
- Y. X. Zhan, P. Shi, X. Q. Zhang, F. Ding, J. Q. Huang, Z. Jin, R. Xiang, X. Liu and Q. Zhang, Energy Technol., 2021, 9, 1–13 Search PubMed.
- Y. Liu, Y. Zhai, Y. Xia, W. Li and D. Zhao, Small Struct., 2021, 2, 2000118 CrossRef CAS.
- S. Park, H. J. Jin and Y. S. Yun, Adv. Mater., 2020, 32, 1–22 CAS.
- J. Yun, E. S. Won, H. S. Shin, K. N. Jung and J. W. Lee, J. Mater. Chem. A, 2019, 7, 23208–23215 RSC.
- E. Cha, J. H. Yun, R. Ponraj and D. K. Kim, Mater. Chem. Front., 2021, 5, 6294–6314 RSC.
- C. Jin, O. Sheng, M. Chen, Z. Ju, G. Lu, T. Liu, J. Nai, Y. Liu, Y. Wang and X. Tao, Mater. Today Nano, 2021, 13, 100103 CrossRef CAS.
- C. Zhang, S. Liu, G. Li, C. Zhang, X. Liu and J. Luo, Adv. Mater., 2018, 30, 1–7 Search PubMed.
- M. Genovese, A. J. Louli, R. Weber, R. J. Sanderson, M. B. Johnson and J. R. Dahn, J. Electrochem. Soc., 2018, 165, A3000–A3013 CrossRef CAS.
- Z. Wang, P. Zhang, S. Chen, K. A. S. Usman, D. Hegh, R. Kerr, H. Zhang, S. Qin, C. Zhang, D. Liu, X. Wang, W. Lei and J. M. Razal, Chem. Commun., 2022, 58, 1946–1949 RSC.
- F. Zhao, X. Zhou, W. Deng and Z. Liu, Nano Energy, 2019, 62, 55–63 CrossRef CAS.
- Y. Liu, D. Lin, Z. Liang, J. Zhao, K. Yan and Y. Cui, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- T. Liu, S. Chen, W. Sun, L. P. Lv, F. H. Du, H. Liu and Y. Wang, Adv. Funct. Mater., 2021, 31, 1–12 Search PubMed.
- A. J. Sanchez, E. Kazyak, Y. Chen, K. H. Chen, E. R. Pattison and N. P. Dasgupta, ACS Energy Lett., 2020, 5, 994–1004 CrossRef CAS.
- T. Foroozan, S. Sharifi-Asl and R. Shahbazian-Yassar, J. Power Sources, 2020, 461, 228135 CrossRef CAS.
- C. Fang, J. Li, M. Zhang, Y. Zhang, F. Yang, J. Z. Lee, M. H. Lee, J. Alvarado, M. A. Schroeder, Y. Yang, B. Lu, N. Williams, M. Ceja, L. Yang, M. Cai, J. Gu, K. Xu, X. Wang and Y. S. Meng, Nature, 2019, 572, 511–515 CrossRef CAS PubMed.
- N. Xu, L. Li, Y. He, Y. Lu, L. Li, Y. Lu and Y. Tong, J. Mater. Chem. A, 2020, 8, 6229–6237 RSC.
- Q. Chen, Y. Yang, H. Zheng, Q. Xie, X. Yan, Y. Ma, L. Wang and D. L. Peng, J. Mater. Chem. A, 2019, 7, 11683–11689 RSC.
- Y. Ye, Y. Liu, J. Wu and Y. Yang, J. Power Sources, 2020, 472, 228520 CrossRef CAS.
- R. Zhang, Y. Li, L. Qiao, D. Li, J. Deng, J. Zhou, L. Xie, Y. Hou, T. Wang, W. Tian, J. Cao, F. Cheng, B. Yang, K. Liang, P. Chen and B. Kong, Energy Storage Mater., 2021, 37, 123–134 CrossRef.
- Y. Jiang, Z. Wang, C. Xu, W. Li, Y. Li, S. Huang, Z. Chen, B. Zhao, X. Sun, D. P. Wilkinson and J. Zhang, Energy Storage Mater., 2020, 28, 17–26 CrossRef.
- X.-Y. Yue, J. Bao, S.-Y. Yang, R.-J. Luo, Q.-C. Wang, X.-J. Wu, Z. Shadike, X.-Q. Yang and Y.-N. Zhou, Nano Energy, 2020, 71, 104614 CrossRef CAS.
- R. Viter, A. Abou Chaaya, I. Iatsunskyi, G. Nowaczyk, K. Kovalevskis, D. Erts, P. Miele, V. Smyntyna and M. Bechelany, Nanotechnology, 2015, 26, 105501 CrossRef PubMed.
- J. Elias, M. Bechelany, I. Utke, R. Erni, D. Hosseini, J. Michler and L. Philippe, Nano Energy, 2012, 1, 696–705 CrossRef CAS.
- M. Weber, A. Julbe, A. Ayral, P. Miele and M. Bechelany, Chem. Mater., 2018, 30, 7368–7390 CrossRef CAS.
- C. Te Hsieh, J. K. Chang, R. S. Juang, C. H. Chao, W. J. Ke, Y. F. Lin, H. W. Liu, Y. A. Gandomi, S. Gu, C. Y. Su, J. Li, C. C. Fu and B. C. Mallick, ACS Appl. Energy Mater., 2020, 3, 10619–10631 CrossRef.
- A. Hagopian, J. Touja, N. Louvain, L. Stievano, J. S. Filhol and L. Monconduit, ACS Appl. Mater. Interfaces, 2022, 14, 10319–10326 CrossRef CAS PubMed.
- A. Kushima, K. P. So, C. Su, P. Bai, N. Kuriyama, T. Maebashi, Y. Fujiwara, M. Z. Bazant and J. Li, Nano Energy, 2017, 32, 271–279 CrossRef CAS.
- J. Elias, I. Utke, S. Yoon, M. Bechelany, A. Weidenkaff, J. Michler and L. Philippe, Electrochim. Acta, 2013, 110, 387–392 CrossRef CAS.
- R. Raghavan, M. Bechelany, M. Parlinska, D. Frey, W. M. Mook, A. Beyer, J. Michler and I. Utke, Appl. Phys. Lett., 2012, 100, 191912 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. Hu, M. Wu, S. Hinokuma, T. Ohto, M. Wakisaka, J. I. Fujita and Y. Ito, J. Mater. Chem. A, 2019, 7, 2156–2164 RSC.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140(8), 084106 CrossRef PubMed.
- A. Hagopian, A. Falcone, M. Ben Yahia and J. S. Filhol, J. Phys.: Condens. Matter, 2021, 33, 304001 CrossRef CAS PubMed.
- J. S. Filhol and M. Neurock, Angew. Chem., Int. Ed., 2006, 45, 402–406 CrossRef CAS PubMed.
- A. Kopač Lautar, A. Hagopian and J. S. Filhol, Phys. Chem. Chem. Phys., 2020, 22, 10569–10580 RSC.
- A. Hagopian, M. L. Doublet and J. S. Filhol, Energy Environ. Sci., 2020, 13, 5186–5197 RSC.
- H. Song, T. He, J. Liu, Y. Wang, X. L. Li, J. Liu, D. Zhang, H. Y. Yang, J. Hu and S. Huang, Carbon, 2021, 181, 99–106 CrossRef CAS.
- A. Kushima, X. H. Liu, G. Zhu, Z. L. Wang, J. Y. Huang and J. Li, Nano Lett., 2011, 11, 4535–4541 CrossRef CAS PubMed.
- W. Li, H. Yao, K. Yan, G. Zheng, Z. Liang, Y. M. Chiang and Y. Cui, Nat. Commun., 2015, 6, 7436 CrossRef CAS PubMed.
- D. Luo, L. Zheng, Z. Zhang, M. Li, Z. Chen, R. Cui, Y. Shen, G. Li, R. Feng, S. Zhang, G. Jiang, L. Chen, A. Yu and X. Wang, Nat. Commun., 2021, 12, 1–11 CrossRef PubMed.
- M. Dollé, L. Sannier, B. Beaudoin, M. Trentin and J. M. Tarascon, Electrochem. Solid-State Lett., 2002, 5, A286 CrossRef.
- H. Sun, Q. Liu, J. Chen, Y. Li, H. Ye, J. Zhao, L. Geng, Q. Dai, T. Yang, H. Li, Z. Wang, L. Zhang, Y. Tang and J. Huang, ACS Nano, 2021, 15, 19070–19079 CrossRef CAS PubMed.
- A. Hagopian, D. Kopač, J. S. Filhol and A. Kopač Lautar, Electrochim. Acta, 2020, 353, 136493 CrossRef CAS.
- C. Pechberty, A. Hagopian, J.-B. Ledeuil, D. Foix, J. Allouche, J.-N. Chotard, O. Luzanin, J. Bitenc, R. Dominko, R. Dedryvère, J.-S. Filhol, L. Stievano and R. Berthelot, J. Mater. Chem. A, 2022, 10, 12104–12113 RSC.
- E. Santos and W. Schmickler, Angew. Chem., 2021, 133, 5940–5945 CrossRef.
- P. Bai, J. Li, F. R. Brushett and M. Z. Bazant, Energy Environ. Sci., 2016, 9, 3221–3229 RSC.
- J. Steiger, D. Kramer and R. Mönig, J. Power Sources, 2014, 261, 112–119 CrossRef CAS.
- Y. He, X. Ren, Y. Xu, M. H. Engelhard, X. Li, J. Xiao, J. Liu, J. G. Zhang, W. Xu and C. Wang, Nat. Nanotechnol., 2019, 14, 1042–1047 CrossRef CAS PubMed.
- B. D. Adams, J. Zheng, X. Ren, W. Xu and J. G. Zhang, Adv. Energy Mater., 2018, 8, 1–11 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta04466h |
| This journal is © The Royal Society of Chemistry 2022 |