Benchmarks for transition metal spin-state energetics: why and how to employ experimental reference data?†
Mariusz
Radoń

Faculty of Chemistry, Jagiellonian University, Gronostajowa 2, 30-387 Krakow, Krakow, Poland. E-mail: mradon@chemia.uj.edu.pl; Tel: +48-12-686-2489
First published on 23rd October 2023
Abstract
Accurate prediction of energy differences between alternative spin states of transition metal complexes is essential in computational (bio)inorganic chemistry—for example, in characterization of spin crossover materials and in the theoretical modeling of open-shell reaction mechanisms—but it remains one of the most compelling problems for quantum chemistry methods. A part of this challenge is to obtain reliable reference data for benchmark studies, as even the highest-level applicable methods are known to give divergent results. This Perspective discusses two possible approaches to method benchmarking for spin-state energetics: using either theoretically computed or experiment-derived reference data. With the focus on the latter approach, an extensive general review is provided for the available experimental data of spin-state energetics and their interpretations in the context of benchmark studies, targeting the possibility of back-correcting the vibrational effects and the influence of solvents or crystalline environments. With a growing amount of experience, these effects can be now not only qualitatively understood, but also quantitatively modeled, providing the way to derive nearly chemically accurate estimates of the electronic spin-state gaps to be used as benchmarks and advancing our understanding of the phenomena related to spin states in condensed phases.
1 Introduction
Transition metal (TM) complexes with d4–d8 electronic configurations may exist in alternative spin states with different magnetic and spectroscopic properties, molecular geometries, and chemical reactivities.1–5 If the energy difference separating the low-spin (LS) and high-spin (HS) states is small enough, it may be overcome by entropic effects, resulting in a spin crossover (SCO) behavior.6–8 If the energy difference is larger, it may be still of significant interest for spectroscopy and the description of reactions in which the ordering of spin states flips along the pathway.9,10 Thus, knowledge of the energy differences between alternative spin states—so called spin-state energetics or spin-state splittings—is highly relevant in various areas of (bio)inorganic chemistry. However, accurate computation of these energy differences is a grand challenge for quantum chemistry because different methods usually give divergent results.4,8,9,11 Benchmark studies are thus necessary to quantify the accuracy of computed spin-state energetics and devise the best computational protocols.In widely used approximate density functional theory (DFT) methods, the results obtained for TM complexes are strongly dependent on the choice of the exchange–correlation functional.9,12 The primary influencing factor is the admixture of exact exchange (EE) from Hartree–Fock theory: with more EE admixed, the HS state is stabilized relative to the LS state.13,14 (This effect, although mediated by the exchange functional, has been recently connected to the description of nondynamic correlation in DFT.15,16) The functionals with 10–15% of the EE, such as TPSSh or B3LYP*, were reported to perform well for typical SCO complexes,17 but they do not maintain consistent accuracy for different oxidation states (FeIIvs. FeIII),18 and can lead to significant overstabilization of the intermediate-spin (IS) state in FeIII porphyrins.19,20 There is hope in the community of quantum (bio)inorganic chemistry to find functionals capable of providing a balanced description of the spin-state energetics for diverse bonding situations and different oxidation states,4,8,21,22 but there is also a growing amount of evidence that none of the commonly used functionals is universal enough to fulfill these expectations.23,24
One should be aware that failure to accurately compute spin-state energetics may have profound consequences in the studies of reaction mechanisms. The most obvious issue is when a qualitatively wrong spin state is predicted for some reactants or products. This can be corrected if the spin state is known from the experiment. For example, in the computational studies of oxygen reduction in cytochrome c oxidase, Blomberg and Siegbahn decided to assume the experimental HS state for some intermediates although their DFT calculations (incorrectly) pointed to an LS ground state.25,26 However, a similar approach cannot be used—due to a lack of experimental information—for short-living intermediates or in a computational exploration of hypothetical mechanisms. Moreover, even if the spin states are assigned qualitatively correctly, the energy differences computed between species with different spin states on both ends of the reaction, such as in spin-forbidden reactions,10 may still suffer from imperfect descriptions of the spin-state energetics. This problem manifests even in seemingly simple ligand binding reactions. For example, the present author has shown27 that common DFT methods notoriously fail in reproducing the comparative experimental data of NO binding energies to MnII and CoII porphyrins, which is partly rooted in the difficulty of calculating accurately the spin-state relaxation energy accompanying formation of the MnII–NO bond. Similar effects are relevant for ligand binding to heme.28,29 It is now appreciated that the problems of approximate functionals in accurately describing spin-state energetics, metal–ligand bond energies, and redox potentials of TM systems may hamper our understanding of complicated reaction mechanisms, for example in the case of nitrogenase.30
The accuracy limitations of approximate DFT methods stimulate interest in correlated wave function theory (WFT) methods,9,11,31–34 such as the “gold standard” coupled cluster (CC) method with singles, doubles, and approximate triples [CCSD(T)] or multireference methods (i.e., based on multiconfigurational complete active space reference wave function), including relatively cheap perturbational approaches (CASPT2 and NEVPT2) and more expensive multireference configuration interaction (MRCI). Recently, Phung et al. proposed a hybrid method CASPT2/CC35 intended to address the inaccuracy of CASPT2 in describing the TM's outer-core correlation effects.36 Another hybrid method called CASPT2 + δMRCI was proposed by Reimann and Kaup.37,38 In this approach a high-level correction estimated using MRCI with a small basis set is added to the CASPT2 energy extrapolated to the complete basis set limit (CBS), in order to obtain a method performing as good as MRCI/CBS, while being computationally cheaper. Some of the quantum Monte Carlo (MC) approaches, especially DMC (diffusion MC),39,40 AFQMC (auxiliary field quantum MC)41 and FCIQMC (full configuration interaction quantum MC)42 have also been applied to TM complexes with the aim of providing accurate energetics.
The WFT methods, owing to their high computational cost, are still mainly used for single-point energy calculations on top of DFT-optimized geometries or in low-dimensional energy scans, although their potential for applications is increasing. For example, full geometry optimization at the CASPT2 level was recently demonstrated to be feasible for relatively large TM complexes.43 Wherever WFT calculations for a realistic model are computationally too expensive, it may be possible to extrapolate the results of WFT calculations from a simplified model to the larger one by describing the effect of model extension at the DFT level.19,44,45 We have recently illustrated20 how this approach can be used to correct deficiencies in DFT thermochemical functions and equilibrium constants for FeIII porphyrins. Last but not least, with local correlation approaches, for instance, Neese's domain-based local pair natural orbital (DLPNO) technique46,47 or Werner's implementation of pair natural orbital (PNO) technique,48,49 there is great potential for extending the applicability of CC calculations to study large molecules, including TM complexes.50–53 Here, one should be aware of a possible accuracy loss in local CCSD(T) calculations, as was reported by Feldt et al.,54,55 although a new formulation of the triples correction [(T1)] and tightening of the accuracy thresholds may reduce these problems.56
The WFT methods have an important advantage of being systematically improvable towards the exact solution, but approximations and compromises have to be made in practically affordable calculations for systems as large as typical TM complexes with organic ligands (e.g., a limited number of active orbitals in multireference calculations, and a limited level of excitations covered in single-reference CC calculations). Therefore, with the growing popularity of calculations employing approximate WFT methods, such as CASPT2, CASPT2/CC, CCSD(T), MRCI or DMC, it becomes critical to address the question of their actual reliability for a given problem. The answer, in the context of TM spin-state energetics, is far from being obvious. As will be detailed below, even calculations with “high-level” and “respectable” methods may lead to contradictory results for spin-state energetics, with mutual discrepancies up to ∼20 kcal mol−1, suggesting that one should be very careful in assuming any of them as reliable before making a detailed comparison with the experimental data. Although some of these methods were presented in the literature as producing “accurate”35 or “benchmark”40 data of spin-state energetics, these usually reflect the authors' experience or presumptions, rather than the results of thorough benchmark studies. In this context, one should be aware that TM spin-state energetics are not yet part of any standard benchmark set used in computational chemistry, even these sets that include TM molecules,57–62 making it a pressing problem to establish widely accepted reference datasets of TM spin-state energetics.
In this perspective recent benchmark studies of TM spin-state energetics, including the author's contributions, will be selectively reviewed and some new results will also be presented. The scope is limited to mononuclear TM complexes, where different spin states originate from different numbers of unpaired electrons (thus, for example, exchange couplings in polynuclear complexes or solids will not be covered). Being aware of limitations in virtually all of the presently available benchmarks—for instance, due to a small number of studied TM complexes or the way in which the reference values were obtained—it will not be attempted here to make definite conclusions on the accuracy of particular methods for TM spin-state energetics. Rather, the discussion will be focused on general aspects of establishing reference values for spin-state energetics, using either high-level theoretical calculations or experimental data. The main focus will be on the use of experimental data, concerning both their availability and their relation to computed spin-state splittings. As the experimentally measured quantities are not straight electronic energy differences and they are nearly always determined in condensed phases (solution or crystal), it becomes necessary to quantify the role of vibrational effects and the impact of the molecular environment on the spin-state splittings, so that objective reference values for the benchmark studies can be derived. State-of-the-art approaches to describe the vibrational and environmental effects will be reviewed along with numerous examples in the context of spin-state energetics. Understanding and quantification of these effects are not only essential for developing experiment-based benchmarks, but also relevant in a broader context of molecular modeling: to enhance the interpretative and predictive value of theoretical calculations for TM complexes and models of metalloenzymes.
2 How to establish reference values?
2.1 Reference values from theory
The majority of benchmark studies in quantum chemistry are based on theoretically computed reference data,63i.e., the quality of the results from approximate methods is judged by comparison with those of a more reliable method (eventually full configuration interaction, FCI, as an exact solution of the time-independent Schrödinger equation within a given one-particle basis set). The main advantage of this approach is the possibility of direct comparisons between electronic energies calculated for well-defined molecular models, whose geometries can be precisely controlled. There is no need to bother about possible inaccuracies or limitations of the experimental data, or ambiguities in their interpretations. There is also no need to introduce vibrational zero-point or thermodynamics corrections, solvation effects, or performing conformational sampling, which all might be potentially relevant when benchmarking against experimental data. Moreover, the reference values can be generated for any desired molecular structure, even for hypothetical models or artificial molecules,64 or species that cannot be studied experimentally due to their instability. However, the limitation of theory-based benchmarks is the difficulty of choosing a theory level that is always sufficiently accurate to provide the reference data. In principle, the accuracy of calculations using WFT methods can be systematically improved towards the FCI limit (for example, by increasing the excitation level in CC calculations) and when the results are extrapolated to the CBS limit and relativistic corrections are included, nearly exact results can be obtained. This approach has been shown to be very effective for small molecules (for recent examples, see ref. 65–69). However, for larger molecules, like TM complexes, such a rigorous approach is usually not affordable, resulting in approximations and compromises that have to be made in practice, for example concerning the basis set quality, the size of the active space (in multi-reference calculations), whereas in single-reference CC calculations it is seldom affordable to fully include the triples, let alone higher excitations. How the approximations made affect the accuracy of the calculated energy differences is not always clear to predict, making it challenging to systematically approach FCI accuracy. Consequently, as Zhang and Truhlar most appropriately pointed out, “in large systems, it is often hard to evaluate the accuracy of the most accurate available value used as the benchmark.”70During the last two decades, a number of theory-based benchmark studies have been reported for TM spin-state energetics, where various approximate WFT methods were employed to provide the reference data. The CASPT2 method was extensively used in this context, starting from seminal studies of Pierloot and Vancoillie,71,72 Fouqueau et al.73,74 (who also used SORCI, the spectroscopically oriented configuration interaction method), as well as Robert75 and de Graaf76 with their respective co-workers. Alternatively, the CCSD(T) method was used, for example by Harvey with co-workers,77,78 Pierloot with co-workers,79 Lawson Daku et al.,80 and by the present author.19 Over the years, the number of studied molecular systems tended to increase and some limitations of the original approaches were addressed. For example, when it became clear that CASPT2 does not deal well with the outer-core correlation effects in first-row TM complexes,36 a modified CASPT2/CC method was proposed by Phung et al.,35 in which the outer-core correlation is obtained from separate CCSD(T) calculations. The CASPT2/CC energies were subsequently taken as the reference data by several research groups to benchmark the accuracy of either local-correlation approximations to CCSD(T),53–55 the multiconfigurational pair-density DFT (MC PDFT),81 or DFT+U results.82,83 A benchmark study of DFT methods against the CASPT2/CC reference data was also presented by Mark Iron at the WATOC conference (Vancouver, July 2022). In variance, Zhang and Truhlar proposed their CASPT2.5 results (the average of CASPT2 and CASPT3) as reference data for testing DFT methods.70 Song et al. advocated the usage of DMC results as the reference data,40 and the same choice was made by others.84,85 Finally, in a recent work, Reimann and Kaupp used the energies computed with their CASPT2 + δMCRI hybrid method as reference data of FeII octahedral complexes for testing the accuracy of DFT and other WFT methods.37
The main limitation of such studies is the arbitrariness in choosing the “high-level”' method to provide the reference data. Approximate WFT methods like CCSD(T), CASPT2/CC or DMC are used for this purpose because they are assumed to produce reliable results (usually based on the positive experience with a given method in previous studies), but one should bear in mind that all of these methods have strengths and limitations when dealing with a complicated interplay of dynamic and non-dynamic correlation effects in TM complexes.76,86,87 For example, single-reference CCSD(T) energies are potentially less reliable if some excitations contribute with large amplitudes.‡ On the other hand, the currently available multireference methods are also not perfect. CASPT2 calculations based on typically affordable active spaces may suffer from an imbalanced description of electronic states with different amounts of charge transfer89,92 (and, indeed, spin states of TM complexes differ in the amount of metal–ligand charge transfer; see ref. 15 and 93, and references therein), whereas MRCI suffers from the lack of appropriate size extensivity. Overall, it is a very complicated problem to determine which of the approximate WFT methods applicable to TM complexes can predict their spin-state energetics most accurately.
In cases where the reference value is uncertain, good mutual agreement between predictions from different “high-level” methods can be treated as a support of their reliability (unless these methods are subject to the same systematic error95). However, in the context of TM spin-state energetics, the application of methods assumed by different authors to be “reliable” can lead in some cases to strikingly divergent results (Table 1). The first example is the adiabatic singlet–quintet gap of [Fe(NCH)6]2+ complex, which is a well-studied model in the context of SCO (albeit it is not itself an SCO system and hence there is no experimental reference for the discussed energy difference). In this case, the best available CCSD(T)23,56,80 and DMC39,40 predictions published in the literature differ from each other by as much as 20 kcal mol−1!
| Theory level | ΔEada | Ref. | Geomb | Detailsc |
|---|---|---|---|---|
| a Adiabatic energy difference between indicated spin states, defined as E(higher-spin) − E(lower-spin), values in kcal mol−1. b Different sets of molecular geometries for [Fe(CNH)6]2+: g1 = ref. 80, g2 = ref. 56, g3 = ref. 40, g4 = ref. 39. c rel = scalar relativistic, nrel = nonrelativistic, CBS = estimate of the complete basis set limit, either from extrapolation or F12 approach. d ANO-RCC basis [7s6p5d3f2g1h] for Fe, [4s3p2d1f] for C and N, [3s1p] for H. e DLPNO-CCSD(T1). f Using computational protocol from ref. 23, see Section 1 in the ESI for details. g DMC(B3LYP), cc-pVTZ basis set. h DMC(PBE0), pVQZ basis set with pseudopotential. i ANO-RCC basis [10s9p8d6f4g2h] for Co, [5s4p3d2f1g] for N and O, [3s2p1d] for H. | ||||
| Singlet–quintet splitting for [Fe(NCH)6]2+ | ||||
| CCSD(T) | −2.0 | 80 | g1 | rel CBS |
| −2.7 | 23 | g1 | rel CBS | |
| −6.6 | 23 | g1 | nrel CBS | |
| −5.5 | 36 | g1 | reld | |
| −8.8 | 56 | g2 | rel CBSe | |
| −8.0 | This workf | g2 | rel CBS | |
| −6.8 | This workf | g3 | nrel CBS | |
| −3.1 | This workf | g4 | rel CBS | |
| CASPT2 | −7.3 | 36 | g1 | reld |
| CASPT2/CC | −3.6 | 36 | g1 | reld |
| DMC | −27.0 | 40 | g3 | nrelg |
| −21.2 | 39 | g4 | relh | |
| Singlet–triplet splitting for [Co(NH3)5(NO)]2+ | ||||
| CCSD(T) | 13.4 | 94 | rel CBS | |
| CASPT2 | −9.8 | 94 | reli | |
| −8.4 | This workf | rel CBS | ||
| CASPT2/CC | −0.1 | This workf | rel CBS | |
Only to some extent, these discrepancies may originate from incompleteness effects of one-particle basis sets (or different protocols used in different studies to estimate the CBS limit), different treatments of relativistic effects, and the use of slightly different molecular geometries in single-point energy calculations. With the aim of gauging the importance of these factors, Table 1 contains additional results where only one factor is varied at a time. It is then found, for instance, that the scalar relativistic correction to the singlet–quintet splitting at the CCSD(T) level amounts to 4 kcal mol−1. There is also a considerable dependence on the choice of molecular geometries when comparing those from ref. 56 (“g2” in Table 1) and those from other studies39,40,80 (“g1”', “g3”, “g4” in Table 1). Altogether, if the comparison between the CCSD(T) and DMC results is made for exactly the same set of geometries and consistently either with or without the scalar relativistic effects, the discrepancies of 18–20 kcal mol−1 remain.§
For the discussed case of [Fe(NCH)6]2+, it is also possible to compare the CCSD(T) with the CASPT2 and CASPT2/CC results.36 When using identical basis sets, the differences are within 3 kcal mol−1, therefore tolerably small. However, for the second example shown in Table 1, the singlet–triplet gap in the [Co(NH3)5(NO)]2+ complex, the present author with co-workers94 found that the discrepancy between CCSD(T) and CASPT2 results is again as large as 20 kcal mol−1. (The CASPT2 calculations were based on a decent active space of 14 orbitals, taking into account the character of the NO ligand.) The corresponding CASPT2/CC result lies almost exactly in between the two numbers with a discrepancy to CCSD(T) of 13 kcal mol−1 (Table 1). As with the previous example, it remains unclear which of the three different values is the best approximation of the true energy difference.
These two examples of large discrepancies between various WFT methods are emphasized here not to argue in favor of (or against) one particular method, but rather to show the potential danger of blindly trusting any of them as a provider of reference data for TM spin-state energetics.
Although it is not our main goal here to judge the relative performance of different methods, some insight into the accuracy of single-reference CCSD(T) calculations can be obtained by inspection of the leading cluster amplitudes and the convergence pattern of the relative energies: starting from HF, through CCSD, up to the inclusion of the perturbative triples correction. Such an analysis is provided in the ESI,† showing that [Fe(NCH)6]2+ looks like a well-behaving case for single-reference calculations, in which however dynamic correlation related to metal–ligand bonding contributes substantially to the spin-state splitting. This perfectly aligns with the conclusions of ref. 80 and 56, but note that other authors expressed slightly37 or very40 different opinions on the accuracy of CCSD(T) for this complex. The case of [Co(NH3)5(NO)]2+ is more peculiar because certain single and double excitations (involving orbitals of the Co–NO group) contribute to the CC wave function with very large amplitudes, which is a signature of nondynamic correlation. However, these effects are apparently comparable in the two spin states resulting in rather small differential correlation effects and suggesting that single-reference CCSD(T) calculations may still provide a balanced description of the relative energy, due to favorable error cancellations. Other examples were reported in which CCSD(T) maintains high accuracy of computed energy differences despite the presence of large cluster amplitudes.31,68 As a matter of fact,94 the CCSD(T) energy difference for [Co(NH3)5(NO)]2+ is at least qualitatively consistent with the experimental ground state (singlet), which is not the case of CASPT2. Perhaps, neither CCSD(T) nor CASPT2 (with the typical choice of active space) can describe the energetics of complexes like [Co(NH3)5(NO)]2+ rigorously and accurately.
In addition to the inspection of the leading amplitudes, it is common in the literature to judge the reliability of single-reference CC calculations based on the so-called diagnostics of multireference character (see ref. 96 and 97 for a discussion and review of various diagnostics in the context of TM complexes). The diagnostics, including the historically first and still widely used T1 of Lee and Taylor,98 were proposed with the aim of determining the quality of a single-reference description and filtering out difficult cases where either genuine multireference or higher-order single-reference coupled-cluster calculations are needed to attain a realistic description. However, an extensive statistical analysis by Sprague and Irikura99 (for atomization energies of small molecules composed of main-group elements) shows that these diagnostics are rather ineffective in predicting the error of single-reference CCSD(T) calculations with respect to the experimental values. The similar ineffectiveness of commonly used diagnostics to predict the magnitude of multireference corrections was demonstrated by Aoto et al. in their study of 60 TM diatomic molecules.69 Also for a larger set and more diverse set of 225 small TM molecules studied by Jiang, DeYonker and Wilson, “no linear correlation has been established between the diagnostics and the accuracy of single reference methods.”97 Thus, the criteria of reliable single-reference calculations appearing in the literature (for example T1 < 0.05 from ref. 97) are not to be treated as strict and absolute in terms of the accuracy of the obtained energies. Moreover, the most popular diagnostics T1 and D1 actually measure the effect of orbital relaxation in response to the Coulomb correlation, and hence, it is unjustified to directly interpret them as diagnostics of multireference character.100 Replacing Hartree–Fock (HF) orbitals in the reference function with Kohn–Sham (KS) orbitals reduces the T1 and D1 diagnostics and sometimes also improves the convergence of CC iterations.77,78 In cases where the HF method does not converge to the desired electronic state, switching to the KS method is obviously beneficial,19,32,54 but is unclear whether the use of KS orbitals systematically improves the accuracy of the CCSD(T) energies.101 In particular, the lowering of the T1 and D1 diagnostics does not prove this.
2.2 Reference data from the experiment
In view of the practical difficulties in establishing reliable reference data based on theoretical calculations, it is an attractive alternative to employ the experimental data of spin-state energetics. Various approaches making use of experiment-derived reference data will be therefore discussed in this section.A limitation of this approach is its qualitative character: the success rate of predicting the correct spin state is important, but it cannot be used to quantify the accuracy of calculated energy differences. For a complex with a large spin-state gap, even a relatively inaccurate method will most likely capture the ground state correctly. By contrast, for a complex with a small gap, a method giving a reasonably small error on the energy differences may accidentally fail to reproduce the correct ground state. (The impact of these issues can be partly mitigated by increasing the number and diversity of complexes in the test set.) Moreover, the experimentally observed ground state is the one with the lowest free energy, which is not necessarily the one with the lowest electronic energy,106 and the ordering of spin states in condensed phases may also be influenced by intermolecular interactions, for example with the solvent molecules.107 The entropic and other thermal effects as well as corrections due to solvation or crystal packing can be modeled (see Section 3.3), but are usually ignored in the computational studies focused on a qualitative ground-state prediction, such as in ref. 105.
Although atomic spectroscopy provides highly accurate reference energies, one should be careful in generalizing the conclusions of such benchmark studies to molecular TM complexes. First, due to the high symmetry of atomic systems, their electronic states are more often inherently multiconfigurational than in the case of typical TM complexes, in which the lowest-energy state corresponding to a given electronic configuration can be usually represented qualitatively correct with a single Slater determinant.24,32 For this reason, single-reference methods that have the potential to perform well for molecular systems may show large errors for atomic systems. As an example, the already mentioned study of Zhang and Truhlar shows very poor performance of CCSD(T) for atomic spin-state splittings as compared with CASPT2 or even CASSCF;70 this is of course not transferable to molecular TM complexes.23 Also the DFT methods which perform best in reproducing experimental ground states of FeII complexes are very inaccurate for the spin-state splittings of bare Fe2+ ions.105 Second, some of the correlation effects that make TM complexes so challenging in computational treatment are intimately related to the presence of metal–ligand bonds and thus, by definition, cannot be benchmarked for single-atom models. For instance, the well-known sensitivity of DFT spin-state splitting to the admixture of exact exchange is no longer observed when the ligands are replaced by point charges (i.e., in the absence of covalent bonding with the ligands).15 Moreover, Pierloot and co-workers demonstrated that the CASPT2 method recovers the outer-core (3s3p) correlation effects more accurately for TM ions (bare or surrounded by point charges) than in TM complexes with covalently bound ligands.36 Overall, CASPT2 calculations with the standard choice of active space seem to perform better for spin-state splitting of bare TM ions36,70 than for molecular TM complexes.23,24 When comparing TM complexes with atomic systems, one should be particularly careful with methods that lack size-extensivity, such as truncated multi-reference configuration interaction (MRCI), which is not strictly size extensive even with the approximate Davidson correction (MRCI + Q).110 For methods which are not size-extensive, the accuracy may be drastically different for small systems (atoms or diatomics) than for TM complexes with a large number of electron pairs that undergo post-CASSCF correlation treatment. In particular, the present author's results23 suggest that internally contracted MRCI + Q, at least when using the standard Davidson correction, yields errors of around 8–10 kcal mol−1 for the spin-state energetics of SCO complexes (with respect to experimentally derived reference data with uncertainties probably no larger than 2–3 kcal mol−1) despite being definitely more accurate for bare TM ions70 and small molecules.111 One should also be aware that there exist several different formulations of the size-consistency correction110 (for example, Davidson, Davidson–Silver–Siegbahn, Pople), which do not give equivalent results for TM complexes.23
In principle, it would be desirable to have computational methods which are accurate for both atomic and molecular systems, but the practical problem in (bio)inorganic chemistry is nowadays to establish accurate computational protocols for TM complexes with relatively large organic ligands, for example, SCO complexes and metalloporhyrins. In this regard, the good performance of a given method for atomic systems is neither necessary nor sufficient, and benchmarking on bare TM ions is not necessarily the right approach to identify promising methods.
(1) Thermochemical parameters of SCO complexes,
(2) Energies of spin-forbidden d–d transitions.
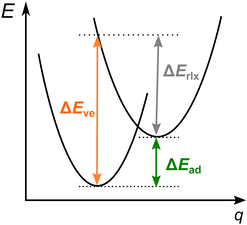
For SCO complexes (1), the electronic energy difference between the LS and HS states is small enough so that the observed spin state changes due to an external stimulus, such as temperature or pressure. In turn, optical spin-forbidden d–d transitions (2) are observed when the energy difference between the ground state and the other spin state is large compared with the thermal energy, but it can be overcome by photon absorption. It is usually only one electron being flipped in an optical transition (for example, singlet to triplet for LS FeII; sextet to the quartet for HS FeIII), by contrast to typical SCO transitions in FeII and FeIII systems, where two electrons are flipped. Moreover, due to the physics of light absorption, the band maximum position for a spin-forbidden band gives information on the vertical energy difference between two involved spin states, whereas the SCO enthalpy or free energy is related to the adiabatic energy (Fig. 1). In the next section, it will be discussed in detail how the experimental data from both sources can be back-corrected for relevant vibrational and environmental effects in order to yield quantitative estimates of electronic energy differences between the involved spin states, either adiabatic (1) or vertical (2) ones, and thus to provide valuable reference data for benchmarking computational methods.
The idea of benchmarking with respect to SCO data is clearly not new, especially in the context of DFT methods. We will not follow in detail numerous studies in which the experimental SCO data are treated only qualitatively, i.e., DFT methods are scored for their ability to predict the gaps (electronic energy or free energy difference) close to zero, which is assumed as a criterion of the SCO behavior. This approach, being somewhat similar to scoring the method's ability to recover the experimental ground state (Section 2.2.1), is certainly useful for large screening studies,112 but it is not appropriate to quantify the accuracy of computed energy differences. To achieve this goal, it is necessary to quantitatively interpret the experimental values of SCO enthalpies or transition temperatures (T1/2). In the seminal paper,113 Jensen and Cirera studied the SCO enthalpies of 9 TM complexes containing FeIII, FeII, and CoII in order to benchmark the performance of DFT methods. More recently, Kepp17 studied the enthalpies and entropies for 30 SCO complexes of FeII and FeIII, to create the benchmark set (30SCOFe) for the assessment of enthalpies computed by DFT methods, with the inclusion of solvation, dispersion and scalar-relativistic effects. Cirera et al.114 analyzed the performance of DFT methods in reproducing the experimental T1/2 temperatures for 20 SCO complexes of CrII, MnIII, MnII, FeIII, FeII, and CoII, albeit not including the environmental effects. Recently, Kulik with co-workers studied the ability of DFT methods to recover experimental T1/2 temperatures for a large number of FeII SCO complexes.112 Vela et al.115 developed the methodology of periodic DFT+U calculations for crystalline SCO complexes and used the experimental enthalpies to optimize the Hubbard-correction parameter. (More on this important work in the context of estimating crystal packing effects is given in Section 3.3.4.) Mariano et al.83 used the experimental SCO enthalpies of five FeII complexes, back-corrected from the crystal to the gas phase, for benchmarking DFT methods and their new formulation of the DFT+U approach. Finally, the experimental data of some SCO complexes have been also occasionally employed for the assessment of WFT methods,19,36,116–119 albeit in a less systematic way than in the case of DFT (considering the number of complexes studied and methods benchmarked).
The importance of spin-forbidden d–d transition energies as a second source of experimental data for spin-state energetics is often overlooked, despite their great historical role in the development of ligand field theory. In a modern context, Hughes and Friesner120 pointed out the necessity of using spin-forbidden d–d transition energies for establishing a representative and reliable benchmark set of spin-state energetics. There are further examples of theoretical studies attempting to assess the quality of calculations by comparison with the experimental positions of spin-forbidden absorption bands e.g. for TM aqua complexes121–124 or metallocenes.111,125–128 Some of these studies were performed for only one or just a few complexes and for a limited number of methods (often in the context of developing new ones) and therefore cannot be regarded as complete benchmark studies.
Since the two above-mentioned sources of experimental spin-state energetics are largely complementary in terms of the ligand field strengths and types of spin transitions that can be probed, it is best to combine them in order to construct a diverse benchmark set. This strategy was illustrated by the present author in his pilot study from 2019,23 where the experimental data for two SCO and two other (non-SCO) Fe complexes were used to study the performance of both DFT and WFT methods, including CASPT2, CASPT2/CC, NEVPT2, MRCI + Q, and CCSD(T). Although the number of complexes studied in this work was very limited, this was the first experiment-based benchmark study of TM spin-state energetics in which both SCO and non-SCO data were included on equal footing and the same set of experimental data (back-corrected for environmental effects) was used to quantify the errors of DFT and WFT methods. In a subsequent work,24 the analogous benchmarking strategy was applied to derive the reference value of spin-state energetics from the experimental data of metallocene complexes containing FeII, RuII, MnII and CoIII. Some highlights of these two studies, along with new important developments, are detailed in the next section while discussing current state-of-the-art in deriving the spin-state energy differences from the experimental data.
3 From experiments to reference values
In this section, we review in more detail the available experimental data of spin-state energetics for TM complexes and discuss the vibrational and environmental contributions, which must be suitably estimated and back-corrected in order to derive reference values of electronic energy differences for benchmarking theory.3.1 Adiabatic energies from SCO data
The standard molar enthalpy (ΔH) and entropy (ΔS) change during a SCO transition are experimentally determined either calorimetrically (by integration of the excess heat capacity) or by analysis of the temperature-dependent equilibrium between the spin states6,129–131| LS ⇌ HS. | (1) |
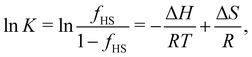 | (2) |
Regardless of how the SCO enthalpy ΔH is determined in the experiment, it contains valuable information on the adiabatic electronic energy difference between the two spin states
| ΔEad = Ee(HS) − Ee(LS). | (3) |
| ΔH = ΔEad + ΔHvib, | (4) |
In order to estimate the vibrational correction, harmonic frequencies from approximate DFT methods are typically used.17,87,141–143 Table S2 (ESI†) contains examples of calculated vibrational corrections for several SCO complexes containing FeII, FeIII and MnII with diverse ligand architectures. For consistency with the experimentally determined ΔH values, the corrections were calculated at the experimental transition temperatures T = T1/2; the vibrational zero-point energy (ZPE) corrections are also provided for comparison. In the zero-T limit, ΔHvib reduces to the ZPE correction, but is less negative at T1/2 due to the thermal population of higher vibrational levels.
The comparison in Table S2 (ESI†) shows that the enthalpy corrections are relatively small (around −1 kcal mol−1) and similar values are found for different SCO systems, as was also observed by other authors.143 Moreover, the enthalpy corrections based on frequencies computed using different DFT methods, here exemplified using PBE and PBE0, agree with each other to within 0.5 kcal mol−1. (To put this in a proper perspective, the electronic energy differences for SCO complexes computed with different functionals, such as PBE and PBE0, can differ by as much as 20 kcal mol−1.23,24) Also the recent study of 95 FeII SCO complexes by Kulik with co-workers confirms that these vibrational corrections are not strongly dependent on the choice of functional.112 Further results in Table S2 (ESI†) show that switching from gas-phase to solution frequencies (here, within the COSMO model) alters the enthalpy corrections by only 0.3 kcal mol−1 or less. This holds true even for the case of [Fe(phen)2(NCS)2] (phen = 1,10-phenantroline), where the arrangement of the ligands is quite different in the gas phase than in the COSMO model and in the crystal structure (see Fig. S3, ESI†). For [Fe(phen)2(NCS)2] in the crystalline state, Bučko et al. estimated that the differential effect of crystal packing on the vibrational enthalpy correction is only 0.2 kcal mol−1.144 (This is an order of magnitude smaller than the crystal packing effect on the electronic energy difference identified in their study;144 see below for the discussion of environmental effects). Thus, based on the data available in the literature and our experience, it seems that the vibrational enthalpy correction can be estimated with an accuracy better than 1 kcal mol−1 based on frequencies calculated for isolated molecules in a vacuum, and the choice of DFT method to compute the frequencies is relatively unimportant.
Eqn (4) is typically used to predict the SCO enthalpy based on the computed ΔEad and ΔHvib terms; the resulting computational estimate can be compared with the experimental value (see for example ref. 17 and 113). However, in the context of method benchmarking, it may be advantageous to employ the experimental enthalpy and calculated vibrational correction in order to estimate the reference value for the electronic energy difference:
| ΔErefad = ΔHexptl − ΔHcalcdvib. | (5) |
An alternative approach to estimate the adiabatic energy difference is based on the standard Gibbs free energy difference between the two spin states
| ΔG = ΔEad + ΔHvib − TΔS | (6) |
| ΔErefad = −ΔHcalcdvib + Texptl1/2ΔScalcd | (7) |
A particular problem with the vibrational entropy calculated within the harmonic approximation is the singularity in the limit of zero frequency, leading to unphysical overestimation of the entropies for low-frequency modes.147 In order to overcome this issue, two quasi-harmonic (QH) models were proposed147,150,151 as simple modifications of the harmonic approximation; they do not require additional calculations (beyond the standard harmonic frequencies) and are very easy to use in conjunction with post-processing software.152 In the QH model of Cramer and Truhlar (QH-CT),150 thermochemical functions are evaluated under the harmonic oscillator approximation, but all frequencies below the cutoff value (typically ∼100 cm−1) are raised to this value. In the alternative QH model of Grimme and Head-Gordon (QH-GHG),147,151 the free energy is continuously interpolated between that for the harmonic oscillator (in the high-frequency limit) and that for rigid-rotor model (in the low-frequency limit) using a frequency-dependent damping function.
The performance of QH models for SCO complexes is illustrated in Fig. 2 on the example of [Fe(1-bpp)2]2+ (where 1-bpp = 2,6-di(pyrazol-1-yl)pyridine). This complex has a few low-frequency bending modes, especially in the HS state, for which the lowest harmonic frequency is as small as 7 cm−1 (compared with 36 cm−1 for the LS state). Concerning first the entropic contribution (shown in the bottom part of Fig. 2), both QH models predict a smaller change of the vibrational entropy during the SCO transition, as compared with the harmonic approximation, reducing the TΔSvib term by ∼1.5 kcal mol−1 at T1/2. This reduction in SCO entropy upon switching to QH models is expected to be the general trend as long as the HS state contains a larger number of low-frequency modes than the LS state (which is typically the case). For the enthalpy correction ΔHvib (top part of Fig. 2), the difference between the harmonic and the QH-CT results is not seen at all (except in the zero-T limit, due to a slight change of ZPE caused by raising the lowest frequencies), whereas the QH-GHG model produces a small deviation with respect to the harmonic approximation, in this example 0.5 kcal mol−1, near the experimental T1/2. The appearance of this is related to the strange behavior of the QH-GHG enthalpy at high temperatures. In this limit, due to different high-T enthalpy limits for the harmonic oscillator (RT) and one-dimensional rigid rotor (RT/2), the QH-GHG model predicts that the ΔHvib term should asymptotically go to −∞ (see the ESI† for details). The harmonic approximation and the QH-CT model predict that it goes to zero in the high-T limit, which is a consequence of the energy equipartition theorem.
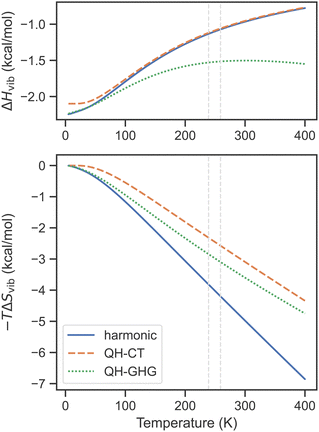 | ||
| Fig. 2 Vibrational enthalpy and entropy contribution to free energy as a function of temperature for the singlet–quintet SCO transition of [Fe(1-bpp)2]2+ calculated within the harmonic and two QH approximations (cutoff 100 cm−1) based on PBE0-D3(BJ)/def2-TZVP frequencies. Dashed lines show the experimental transition temperatures in the solid and in the solution.153,154 | ||
Wu et al. systematically studied the accuracy of the harmonic approximation for SCO systems.155 Their calculations of ZPEs and thermochemical corrections were based on eigenvalues resulting from the numerical solution of the vibrational Schrödinger equation in the Born–Oppenheimer potential which was obtained by scanning the energy surface along each normal mode. This approach allows the anharmonicity to be realistically modeled (in the uncoupled mode approximation145), but is computationally more expensive than harmonic frequency calculations and is not implemented in any standard quantum-chemical package. The results for 11 complexes studied by Wu et al. show that a harmonic approximation can lead to either an overestimation or an underestimation of the vibrational entropy change. Thus, the use of a simple QH model, which always tends to reduce the harmonic ΔS values, does not necessarily lead to a more accurate prediction of these entropy changes. This is consistent with the results of Kepp, who found on a large probe of Fe complexes that the SCO entropies calculated under the harmonic approximation can be either larger or smaller than the experimental ones, with relatively large spread in both directions (Fig. 3).
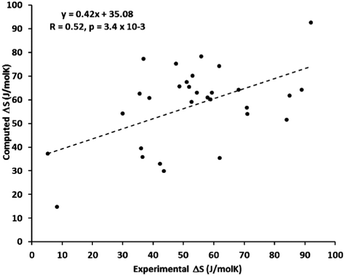 | ||
| Fig. 3 Scatter plot of the experimental and computed entropy changes during spin crossover for 30 complexes studied by Kepp with the trend line showing relatively poor linear correlation. Reprinted with permission from ref. 17, Copyright (2016) American Chemical Society. | ||
With regard to the vibrational enthalpy correction, Wu et al. studied only the ZPE term (which is the limiting value at T = 0 K). They found that the anharmonicity effects on the ZPEs are small, within 0.6 kcal mol−1, with the exception of one complex for which the LS and HS states have qualitatively different coordination geometries.155 It is not clear how these small deviations from the harmonic approximation behave as a function of temperature, and further studies would be desirable. Another potentially interesting direction to include anharmonicity in thermochemical corrections is vibrational perturbation theory (VPT2),156 although it has received so far little attention for SCO complexes.
3.2 Vertical energies from spin-forbidden d–d bands
In addition to the thermodynamics of SCO complexes, valuable data of spin-state energetics can also be obtained from optical transitions between different spin states. Although such transitions are forbidden in the non-relativistic approximation, they gain non-zero intensity through the spin–orbit coupling, and hence, they can be observed in the UV-vis-NIR spectra of some transition metal complexes as weak bands or shoulders on more intense bands (spin-allowed d–d or charge transfer).157 In the case of band overlapping, the technique of Gaussian decomposition can be used to extract the positions of individual bands.158 Too strong overlap with more intense bands may hinder detection of the spin-forbidden ones and usually only a limited number of them, often only the lowest-energy one, can be credibly assigned. The assignment of spin-forbidden bands is often guided by the ligand-field theory (Tanabe-Sugano diagrams) and can also be supported by magnetic circular dichroism spectra.159,160 The typical examples where spin-forbidden bands can be experimentally characterized are:• HS complexes with d5 configuration (FeIII, MnII); in this case, there are no spin-allowed d–d transitions, and hence, it is possible to observe weak bands due to sextet–quartet transitions, often more than one (depending on the energy of the lowest charge-transfer band). Good examples are FeIII and MnII aqua complexes (ref. 123 and 124 and references therein).
• LS complexes with d6 configuration (FeII, CoIII); in this case, it is often possible to observe the lowest singlet–triplet transition because it has lower energy than the corresponding singlet–singlet transition. A good example is ferrocene (see ref. 24 and references therein).
Due to their low intensities and overlap with more intense bands, reliable detection of spin-forbidden bands may be an experimental challenge. For example, the energy of the first singlet–triplet band for ferrocene (FeCp2) was subject to long-standing controversies, which were resolved by the present author with co-workers in ref. 24. Knowing that the ε coefficient of FeCp2 rapidly varies by 3 orders of magnitude between 400 and 800 nm, we carefully determined the absorption spectrum from a series of measurements at varying concentrations, making it possible to accurately describe both the low- and high-ε regions. The failure to do so in earlier experimental studies was presumably a reason for the appearance of artifacts in the old spectra, leading to the reporting of contradictory (and incorrect) positions of the singlet–triplet band. Curiously, these suspicious data have been circulating in the literature until very recently: one or the other of the available values was picked as the reference for the singlet–triplet gap of FeCp2 in different studies (see ref. 24 for longer discussion and references). In fact, most of these problematic experimental data were only given in tabulated form: the original spectra were not provided at all or only as low-resolution graphics, from which it is not possible to reliably determine the spin-forbidden band. Upon this experience, the present author recommends to always critically look at the experimental spectra and consider their re-determination if the provided original data are not convincing.
Assuming that the spin-forbidden band was reliably determined, its position gives valuable information on the vertical electronic energy difference between the two spin states. Under the vertical energy approximation, which is currently state-of-the-art in interpreting the electronic spectra of TM complexes, the band maximum position is identical with the vertical excitation energy, i.e. ΔEmax ≈ ΔEve. However, in order to determine the vertical energy reliably (for the purpose of benchmarking theory), it may be necessary to account for a small difference between the two quantities, the vibronic correction:
| ΔEmax = ΔEve + δvibr. | (8) |
The vibronic correction (δvibr) can be determined from the simulated vibrational progression of the electronic transition (as the difference between the position of the simulated band maximum and the underlying vertical energy). In ref. 24, the present author with co-workers introduced this concept to the benchmark study of singlet–triplet excitations of metallocenes: FeCp2, RuCp2, and [CoCp2]+. The vibronic simulations to yield δvibr were based on the harmonic oscillator eigenstates and the Franck–Condon (FC) approximation, under which the transition dipole moment (TDM) is assumed to be independent of the molecular geometry (so that the intensity of the elementary transition between individual vibrational states is proportional to their overlap, also known as the FC factor). The simulations employed the time-dependent formalism,161,162 which supports efficient calculation of vibronic spectra even for large transition metal complexes and is now available in an open-source program FCclasses of Santoro and Cerezo.163 The methodology introduced in ref. 24 can be applied to obtain vibronic corrections also for the d–d band of other TM complexes and some examples are given in Table 2.
| Complexc | Transition | δ vibr | ΔZPEe | ΔErlxf |
|---|---|---|---|---|
| a Values in kcal mol−1. b Calculated at the PBE0-D3(BJ)/def2-TZVP level. c Ligand abbreviations: en = etylenediamine, Cp = cyclopentadienyl, acac = acetylacetonate. d Vibronic correction from simulations at FC level using TD approach analogously as in ref. 24 using automatically generated internal coordinates; the band maxima were read from spectra convoluted with a Gaussian with HWHM 0.05eV. e The ZPE difference between the excited and ground state. f Purely electronic relaxation energy. | ||||
| [Co(en)3]3+ | Singlet–triplet | −2.0 | −2.5 | 10.5 |
| [FeCp2] | Singlet–triplet | −2.2 | −2.4 | 16.9 |
| [Fe(en)3]3+ | Doublet–quartet | −1.2 | −2.1 | 12.4 |
| [Mn(en)3]2+ | Sextet–quartet | 1.7 | 1.2 | 9.8 |
| Fe(acac)3 | Sextet–quartet | 0.4 | 1.2 | 6.2 |
| [Fe(H2O)6]3+ | Sextet–quartet | −0.6 | −0.4 | 5.8 |
The vibronic corrections determined for the singlet–triplet bands of metallocenes24 were found to be negative (indicating that the band maximum is below the electronic vertical energy) and their numerical values of about −2 kcal mol−1 are close to the ZPE differences between both states. This suggests that the main effect contributing to these corrections is the lowering of the vibrational frequencies in the excited triplet state as compared with the singlet ground state.24 This interpretation agrees with the general analysis of Bai et al. for photoabsorption spectra of organic molecules and model systems.164 Additional data provided in Table 2 show that similar negative vibronic corrections occur for other singlet–triplet and doublet–quartet transitions. However, the vibronic corrections may be positive e.g. for some sextet–quartet transitions. The correspondence between the vibronic correction and the ZPE change is visible, although not perfect.
Instead of focusing on the vertical energy, as was detailed above, it is also possible to use the spectroscopic data to estimate the adiabatic energy difference. The most rigorous method would be to back-correct the band origin (the 0-0 line) for the differential ZPE. This approach is generally preferred in benchmark studies of excitation energies,165 but due to inherent experimental difficulties there exist only very few cases of spin-forbidden d–d bands for which the band origin can be observed. One of them is the singlet–triplet transition for ruthenocene (see discussion and references in ref. 24). Another example is the singlet–triplet transition for [Co(NH3)6]3+, theoretically studied by Rotzinger166 based on the experimental spectra of Wilson and Solomon.167 A very limited number of similar experimental data makes this approach impractical to create a representative benchmark set of TM spin-state energetics.
Hughes and Friesner in their already mentioned work120 proposed to estimate the adiabatic energy by subtracting from the position of the d–d band maximum a simple estimate of the vibrational relaxation energy. The latter was taken to be the “difference between the peak and onset values of the spin-forbidden shoulder from the experimental spectra.”120 In practice, the band was fitted to a Lorentzian function and the onset was determined as the peak position minus three times the HWHM. Moreover, instead of using a unique relaxation energy for each complex, they used an average value obtained by studying a few bands of a given type: t2g → t2g, eg → eg, and t2g ↔ eg. For the presently interesting t2g ↔ eg transitions, the average relaxation energy was determined by analyzing data for a few such transitions and by comparison with the average relaxation energies of the t2g → t2g and eg → eg transitions. The resulting estimate of vibrational relaxation energy was 6.8 kcal mol−1 with the claimed uncertainty of 1.7 kcal mol−1.120 The uncertainty suggests a considerable variation of relaxation energies for individual complexes within a given class of electronic transitions (like t2g ↔ eg), which is confirmed by a few examples of calculated relaxation energies for octahedral complexes and ferrocene given in Table 2. Note, however, that the tabulated values are purely electronic relaxation energies (cf.Fig. 1), whereas the quantity used in ref. 120 implicitly includes a vibrational contribution.
Using their simple estimate of vibrational relaxation energy, Hughes and Friesner were able to create a dataset of adiabatic spin-state energetics for chemically diverse sets of TM complexes.120 Recently, a subset of their data (singlet–triplet splittings for CoIII complexes) was used by Neale et al. as the reference data for assessing the accuracy of DPLNO-CCSD(T), NEVPT2, and DFT calculations.168 When using data from ref. 120 in benchmark studies, one should consider the average character of the applied vibrational relaxation correction and somewhat arbitrary assumptions used for its derivation.
3.3 Environmental effects
Modern quantum chemistry methods—armed with dispersion-corrected DFT,170 solvation models171,172 and periodic calculations for crystals115,144—are able to treat the energy effects of intermolecular interactions at the level of chemical accuracy. However, treating the environment in all calculations is neither convenient nor necessary. For instance, it would be virtually impossible to use correlated WFT methods in periodic calculations for crystals and even implicit solvation models are not always implemented for such methods. Moreover, the environmental corrections are not expected to be particularly sensitive to the applied theory level due to their transferability, i.e., the efficient cancelation of a method's intrinsic error when comparing the energy difference for an isolated molecule and the same molecule in a solution or crystal.23 From our experience, it is practical to determine the environmental correction at a fixed theory level (for instance, an approximate DFT method in combination with a solvation model) and use the resulting estimate to back-correct the experimental data. By back-correcting both the environmental and vibrational effects (see above in Sections 3.1 and 3.2) from the experimental data, one obtains an estimate of the electronic energy difference corresponding to the isolated molecule in a vacuum, which is a very convenient reference data for method benchmarking.9,23 Below in this section, we discuss examples of environmental effects and strategies to model them in the context of benchmark studies.
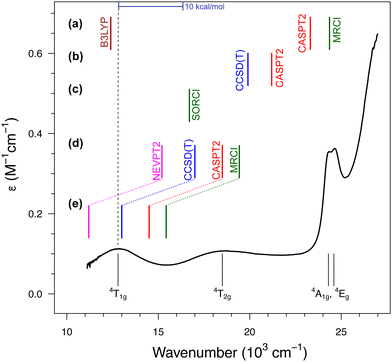 | ||
| Fig. 4 Absorption spectrum of [Fe(H2O)6]3+ with the d–d bands assigned to the lowest-energy excited states according to the ligand-field theory (bottom part). The dashed line represents the experimental position of the band maximum for the lowest sextet–quartet transition, 6A1g → 4T1g, whereas the colored bars represent calculated values of the corresponding vertical energy: (a) results of Schatz et al. from ref. 122 and 175; (b) results of Ghosh and Taylor from ref. 174; (c) results of Neese et al. from ref. 121; (d) results of the present author with co-workers from ref. 123 for the gaseous [Fe(H2O)6]3+; (e) the same results corrected for a solvation effect estimated at the CASPT2 level based on the model with explicit hydrogen-bonded water molecules.123 The experimental spectrum of the FeIII aqua complex (in HClO4 to prevent hydrolysis) was obtained courtesy of Prof. Janusz Szklarzewicz, Jagiellonian University. | ||
In all studies prior to ours, it was found that the sextet–quartet excitation energy computed with the best available WFT methods (CCSD(T), CASPT2, NEVPT2 or MRCI) is significantly above the experimental band position, with the discrepancies up to 10 × 103 cm−1 (i.e., ≈30 kcal mol−1) reported for CASPT2 and MRCI calculations in ref. 122. In view of such large discrepancies between the computation and experiment, it was even speculated that the experimental spectrum was misinterpreted; specifically, that the lowest-energy band (or even the two of them) may arise from the presence of impurities: the hydrolysis product174 or FeII contamination,122 whereas one of the higher energy bands corresponds to the “true” 6A1g → 4T1g transition of [Fe(H2O)6]3+. These conjectures undermine the traditional and well-established interpretation of this spectrum under the ligand–field theory.157 Our studies on aqua complexes123,124 have shown that the discrepancies observed in earlier studies can be somewhat reduced by improving the basis set and/or the active space (see part (d) of Fig. 4). However, it turned out that the main problem was the use of isolated [Fe(H2O)6]3+ model optimized in vacuum. By adopting a better model incorporating explicit solvent (water) molecules in the second coordination sphere, we demonstrated a significant shift (by 11 kcal mol−1 or 4 × 103 cm−1) of the excited state down in energy due to the solvation effect, which is shown in part (e) of Fig. 4. Only after including or back-correcting this solvation effect, it is meaningful to use the vertical energy derived from the experimental spectrum as a benchmark for theory. When this is done properly, a very good match with the experiment is obtained for WFT calculations, particularly at the CCSD(T) level. At the time of performing these calculations, we were not yet aware of the potential significance of the vibronic correction for d–d transitions (Section 3.2). However, in this case, the correction is within 1 kcal mol−1 (estimated as in ref. 24, cf.Table 2) and taking it into account would not change the conclusions.
The case of aqua complexes is not the only one where solvent-induced geometry changes are relevant. Deeth with co-workers176 found that vacuum geometries are generally unreliable for understanding structural features, such as the trans effect or sterically induced bond elongations, in several series of [MAnBm−n]-type complexes. It is now generally accepted by many authors that structures of TM complexes optimized with a solvation model (e.g., COSMO, PCM) are more realistic than gaseous structures to describe not only the situation in solution, but also in the solid state.176–179
The importance of geometry changes motivates to split the total solvation effect into the direct and structural components, whose sum is by definition the total solvation effect. The direct component measures the solvation effect for fixed geometry. The structural component measures how the interesting energy difference is affected by solvent-induced geometry changes. Precise definitions of the two components and details of their computation for adiabatic and vertical energy differences can be found in the ESI.†Table 3 summarizes solvation effects and their splitting into direct and structural parts for some vertical and adiabatic energy differences in TM complexes. The tabulated results were computed using implicit solvation models (COSMO/PCM, as detailed in the ESI†) and therefore the total solvation effect of 4.6 kcal mol−1 predicted for the vertical sextet–quartet energy of [Fe(H2O)6]3+ is underestimated compared with that determined in ref. 123 (based on the model with explicit solvent molecules). In agreement with the above discussion, the solvation effect on the vertical sextet–quartet energy of [Fe(H2O)6]3+ is entirely structural. This also explains why it was overlooked in previous studies attempting to estimate the solvation effect using vacuum geometry.174 Interestingly enough, a very strong solvation effect is also observed for the adiabatic energy of the same system, but in this case, the direct component becomes more important.
| Complexb | Solvent | Theory level | Excitation | Type | Solvation effect | Ref.c | ||
|---|---|---|---|---|---|---|---|---|
| Direct | Structural | Total | ||||||
a Energies in kcal mol−1.
b Ligand abbreviations: bpy = 2,2′-bipyridine, Cp = cyclopentadienyl, H2acac2trien = Schiff base obtained from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 condensation of triethylenetetramine with acetylacetone, 1-bpp = 2,6-di(pyrazol-1-yl)pyridine, 3-bpp = 2,6-di(pyrazol-3-yl)pyridine, tacn = 1,4,7-triazacyclononane.
c For data reported in this work, see ESI; for data quoted from ref. 24, see Tables S60 and S61 therein; for data quoted from ref. 23, see Tables S3 and S4 therein.
d CASPT2 calculations with the optional PCM solvation (non-equilibrium for excited states when calculating vertical energies) performed for either gaseous or COSMO geometry; see the ESI.
e BP86-D3/def2-TZVP, COSMO. 2 condensation of triethylenetetramine with acetylacetone, 1-bpp = 2,6-di(pyrazol-1-yl)pyridine, 3-bpp = 2,6-di(pyrazol-3-yl)pyridine, tacn = 1,4,7-triazacyclononane.
c For data reported in this work, see ESI; for data quoted from ref. 24, see Tables S60 and S61 therein; for data quoted from ref. 23, see Tables S3 and S4 therein.
d CASPT2 calculations with the optional PCM solvation (non-equilibrium for excited states when calculating vertical energies) performed for either gaseous or COSMO geometry; see the ESI.
e BP86-D3/def2-TZVP, COSMO.
|
||||||||
| [Fe(H2O)6]3+ | Water | CASPT2c | 6A1g → 4T1g | Vertical | 0.0 | −4.6 | −4.6 | This work |
| 6A1g → 4T1g | Adiabatic | −10.1 | −1.0 | −11.1 | This work | |||
| 6A1g → 6LMCT | Vertical | 4.9 | 10.2 | 15.1 | This work | |||
| [Ru(bpy)2Cl2(CO)2] | Acetonitrile | CASPT2d | 1GS → 1MLCT(A1) | Vertical | 6.9 | −0.9 | 6.0 | This work |
| 1GS → 1MC(A1) | Vertical | −7.2 | −0.9 | −8.1 | This work | |||
| [Fe(Cp)2] | Ethanol | CASPT2d |
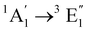
|
Vertical | −0.1 | 0.6 | 0.5 | 24 |
| [Co(Cp)2]+ | Water | CASPT2d |
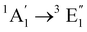
|
Vertical | −0.7 | 1.2 | 0.5 | 24 |
| [Fe(acac2trien)]+ | Acetone | DFTe | 2A → 6A | Adiabatic | 0.8 | 0.4 | 1.2 | 23 |
| [Fe(1-bpp)2]2+ | Acetone | DFTe | 1A1 → 5A | Adiabatic | 2.4 | 0.2 | 2.2 | This work |
| [Fe(3-bpp)2]2+ | Acetone | DFTe | 1A1 → 5A | Adiabatic | 1.9 | 0.2 | 2.1 | This work |
| [Fe(tacn)2]2+ | Water | DFTe | 1A → 5B | Adiabatic | 2.7 | 0.1 | 2.8 | 23 |
| [Fe(tacn)2]3+ | Methanol | DFTe | 2A → 6A | Adiabatic | 5.4 | −0.2 | 5.6 | This work |
To put these results in a broader context, Table 3 also includes solvation effects on the ligand-to-metal charge transfer (LMCT) excitation of [Fe(H2O)6]3+ as well as metal-centered (MC) and metal-to-ligand charge transfer (MLCT) excited states for the [Ru(bpy)2Cl2(CO)2] complex (bpy = 2,2′-bipyridine), which was extensively studied by the groups of de Graaf180 and González.181 The results show that solvation effects can be comparable for MC d–d excited states as they are for LMCT/MLCT states with significant charge reorganization. Moreover, the relative importance of the direct and structural contributions varies from case to case. In a larger and less symmetric [Ru(bpy)2Cl2(CO)2], the direct solvation effect is dominant for both MC and MLCT excitations, but in a smaller and more symmetric [Fe(H2O)6]3+, the structural component is predominant also for the LMCT excitation. For singlet–triplet splittings of metallocenes FeCp2 and [CoCp2]+, both components of the solvation effect are small and additionally tend to cancel out, resulting in the total solvation effect being negligible. This is probably rooted in a high covalency (i.e., low ionicity) of the metal–ligand bonds in metallocenes.
The last five entries in Table 3 are solvation effects on adiabatic spin-state splittings of some typical SCO complexes ([FeIII(acac2trien)]+, [FeII(1-bpp)2]2+, [FeII(3-bpp)2]2+, [Fe(tacn)2]2+) and LS complex [FeIII(tacn)2]3+, which was chosen because it features the largest solvation effect in the study of Swart.103 For these complexes, all with bulky organic ligands, the solvation effects on the spin-state splittings vary from 1 to 6 kcal mol−1, tending to increase with the total charge of the complex. They are strongly dominated by the direct solvation component (with the exception of a singly-charged [Fe(acac2trien)]+, for which both components are comparable, but small). It is expected that these small-to-moderate solvation effects on adiabatic energies of SCO complexes can be modelled within the chemical accuracy by implicit solvation models,17,103,113,182 although with a possible concern for the importance of hydrogen bonding or other specific interactions with strongly associating solvents.106 For the case of a singlet–quintet splitting of [Fe(tacn)2]2+ in water, the present author investigated the effect of going beyond the implicit model (COSMO) by explicitly treating six water molecules that may form a network of hydrogen bonds with the solvent-exposed N–H groups of the ligands. This extension of the model was found to change the singlet–quintet energy difference by only 0.3 kcal mol−1, supporting the adequacy of the implicit solvation approach.23 In fact, even for the sextet–quartet splitting of [Fe(H2O)6]3+ experiencing a much stronger hydrogen bonding effect, the implicit approach performs remarkably good for the adiabatic energy difference, predicting the solvation effect of −11.1 kcal mol−1 (cf.Table 3), compared with −12.3 kcal mol−1 from the model with explicit solvation (see Table S7 in ref. 123).
As the above examples show, the typical solvation effect is an increase in the LS–HS splitting compared with that in vacuum (albeit with certain exceptions known9). This can be intuitively explained based on a smaller molecular volume for the LS state, resulting in its stronger electrostatic stabilization in a polarizable environment, than for the HS state. Although solvation effects on adiabatic energies are dominated by the direct component (see above), they are accompanied by important changes in molecular geometries caused by the presence of solvent. Consistent with the observations for aqua complexes,123,124 the typical solvation effect is a decrease of the metal–ligand bond distance as compared with that in the gas phase.9,106 Interestingly, however, the opposite structural effect is observed for complexes containing solvent-exposed halogen ligands in addition to bulky organic ligands, like FeP(Cl) and [Fe(amp)2Cl2] (P = porphin, amp = 2-pyridylmethylamine): their Fe–Cl bonds become longer in solution than in a vacuum, which is correlated with the solvated Cl ligands accumulating more negative charge (see Table S10 and Fig. S5, ESI†). Deeth with co-workers observed somewhat related structural effects of solvent in a series of square-planar complexes [PtCln(NH3)4−n]2−n.176 However, monoleptic metal–halogen complexes, such as FeF63− or CuCl42−, behave regularly by having their M–X bonds shorter in solution than in the gas phase (see Table S11, ESI†).
One of the earliest attempts to quantitatively model the CPE is the study of Fe(phen)2(NCS)2 (phen = 1,10-phenanthroline) by Bučko et al.144 By performing periodic PBE-D2 calculations, they found that the singlet–quintet adiabatic energy difference in the crystal is larger than that for the isolated molecule by almost 3 kcal mol−1. More recently, Vela et al. have developed a methodology based on the dispersion-corrected PBE+U approach (which gives more realistic spin-state splittings than pure PBE) and applied it to study 9 crystalline SCO complexes of FeII and FeIII.115,183 They found the CPEs on the spin-state energy differences ranging from 0.2 to 3.4 kcal mol−1, with different signs for different complexes (sometimes stabilizing the LS, sometimes the HS state in the crystal as compared with the isolated molecule); moreover, the CPE values were somewhat dependent on the dispersion correction used.115 Another example of using a similar methodology is the study by Phung, Domingo and Pierloot, who used periodic DFT to quantify the CPE for a binuclear FeII SCO complex.119 When comparing CPEs reported in different studies, one should pay attention to the geometry used for isolated TM complexes. For instance, Bučko et al. reoptimized the isolated molecule in the gas phase,144 whereas Vela et al. defined the packing effect with respect to the geometry of isolated molecule identical as in the crystal.115 Which of these choices is made, clearly affects the obtained CPE (this is analogous to the difference between the direct and structural solvation effects, discussed above).
| Environment | Exptl ΔHb | Calcd δenvc |
|---|---|---|
| a All values in kcal mol−1. b Ref. 153 and 154. c Environmental correction was calculated using the COSMO model for solution (see Table 3) or periodic DFT for the two crystalline environments (see Tables S12 and S13, ESI) with respect to gaseous [Fe(1-bpp)2]2+. | ||
| Acetone solution | 5.8 | 2.3 |
| Crystal [Fe(1-bpp)2][BF4]2 | 4.1 | −0.7 |
| Crystal [Fe(1-bpp)2][PF6]2 | <0 | −20.9 |
Most interestingly in the context of benchmarking, the experimental SCO enthalpies for acetone solution and the BF4+ salt can be used to independently derive two estimates of the electronic energy difference (singlet–quintet gap) for isolated [Fe(1-bpp)2]2+: by subtracting from each ΔH value the appropriate environmental correction and a vibrational correction (calculated for T1/2 in each environment). This leads to the singlet–quintet energy difference of 5.9 kcal mol−1, back-corrected from the crystal data (4.1 + 0.7 + 1.1) and 4.7 kcal mol−1, back-corrected from the solution data (5.8 − 2.3 + 1.2). The two values are not identical and the discrepancy of 1.2 kcal mol−1 between them reflects errors made in the solvation model and in the periodic DFT calculations. The discrepancy, which can be treated as a rough measure of the uncertainty, is still relatively small compared with the chemical accuracy and typical variations of calculated spin-state splittings for SCO complexes (see Section 2.1). Taking the average of the two values back-corrected from different environments (here, 5.3 kcal mol−1 with the uncertainty ± 0.6 kcal mol−1) provides the most objective reference value for the interesting energy difference, and such a strategy is recommended if experimental data from multiple environments are available.
Another kind of interesting experimental data is SCO enthalpies measured in multiple solvents. Also here, the best procedure seems to be averaging the energies back-corrected from enthalpies measured in different solvents. In our experience, implicit solvation models (PCM, COSMO) are not capable of quantitatively describing variations of the experimental SCO enthalpies determined in different solvents. This is to be expected because these effects are subtle, usually within 1 kcal mol−1 (excluding cases where the change of solvent affects the ligation of the metal center or leads to decomposition of the complex; such cases should be obviously excluded from the benchmarks).131 Moreover, some of the solvent effects discussed in the literature may actually have entropic, rather than enthalpic origin. For instance, Halcrow and co-workers studied the SCO thermodynamic parameters of [Fe(3-bpp)2]2+ (3-bpp = 2,6-di(pyrazol-3-yl)pyridine) in a number of organic solvents and water.133 Although the authors summarized their results as a “dramatic stabilization of the LS state in water,” the ΔH values obtained in all solvents (including water) were identical to within 1.2 kcal mol−1 and the value in water was actually the lowest one, indicating slight enthalpic stabilization of the HS (not the LS) state in water. The significant solvation effect originates in the entropy change, with the ΔS value being 30% lower in water than in organic solvents.133 Although this effect was originally ascribed to hydrogen bonding with the solvent-exposed protons of the 3-bpp ligand,133 a recent theoretical study by Reimann and Kaupp149 shows that the entropic effect observed in aqueous solution is more likely due to the isobaric expansion coefficient of water being much smaller than for organic solvents. This shows again that accurate modeling of the entropy changes, especially in solution, is notoriously difficult; therefore, for the purpose of benchmarking it is safer to focus on complexes with measured SCO enthalpies.
To illustrate these considerations, Table 5 reports vertical singlet–triplet excitation energy calculated for isolated [Co(en)3]3+ (en = ethylenediamine) and the cluster model of crystalline [Co(en)3]Cl3.185,186 The excitation energies were calculated using the CASPT2 method and only serve to quantify the differential effects caused by the change in the model or geometry. For the considered electronic transition (1A1g → 3T1g under idealized octahedral symmetry) the excited state is almost, but not quite triply-degenerate when computed for the ground-state geometry. The table therefore reports the average excitation energy and the spread (i.e., the difference between the lowest and the highest of the three energy levels being averaged). The spread is very small for all considered models and will not play any role here when interpreting the experimental band position as the d–d bands typically observed in the experiment are much broader (HWHM ∼ 3 kcal mol−1).
| Model | Geometry | ΔEvec | Spreadd |
|---|---|---|---|
| a Values in kcal mol−1. b Calculations at CASPT2 level, see the ESI for details (and Table S14 therein for total energies). c Average excitation energy for the three lowest triplets. d Energy difference between the highest and the lowest of the three lowest triplets. e Calculated at the PBE0-D3(BJ)/def2-TZVP in the gas phase or with the COSMO model (ε = ∞). f Coordinates taken from crystalline [Co(en)3]Cl3 at T = 90 K (IRIRAC01)185 or at T = 193 K (IRIRAC);186 all X–H bond lengths (X = C, N) were increased by 10% compared with the crystallographic ones. g Calculated energies include the Ewald potential of the infinite ionic lattice (ESI). | |||
| [Co(en)3]3+ | Gaseouse | 27.9 | 0.1 |
| COSMOe | 32.8 | 0.1 | |
| Crystal (90 K)f | 33.3 | 0.1 | |
| Crystal (193 K)f | 33.2 | 0.2 | |
{[Co(en)3]Cl9}6−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g g |
Crystal (90 K)f | 32.2 | 0.2 |
| Crystal (193 K)f | 32.1 | 0.2 | |
As can be seen from the data in Table 5, the excitation energy for isolated [Co(en)3]3+ changes by as much as 5 kcal mol−1 when going from the geometry optimized in the gas phase to that excised from the crystal. A further improvement of the model—by including the nearest counterions to give the {[Co(en)3]Cl9}6− cluster (presented in Fig. 5) and also by adding the Ewald potential from the ionic lattice—changes the excitation energy by only 1 kcal mol−1. These observations are consistent with the general prevalence of structural over direct environmental effects in the case of vertical excitation energies (see above). In fact, the considered excitation energy is mainly governed by changes in the Co–N distance: from 1.994 Å in the gas phase (computed) to 1.965–1.968 Å in the crystal structure (experimental). In this case, there is not much difference in the excitation energy between the crystal structures determined at the two different temperatures, suggesting a minor importance of the thermal expansion. Remarkably, the structure of isolated ions optimized within the COSMO model gives good agreement with the crystalline data in terms of both the excitation energy (cf.Table 5) and the equilibrium Co–N distance (1.965 Å). The COSMO geometry of [Co(en)3]3+ thus provides a good starting point for studying the excitation energy in the crystal, with the environmental correction of only −0.6 kcal mol−1 (calculated from the excitation energies in Table 5). The good agreement of the COSMO geometry with the crystal one is not accidental,177 but it is clear that the accuracy of this approach may vary with the nature of the metal–ligand bond and in some cases strong interactions with the lattice may critically influence the coordination geometry.187
4 Conclusions and outlook
In this perspective, two approaches to benchmark studies for the challenging problem of TM spin-state energetics are discussed. The theory-based benchmarks are attractive for their conceptual simplicity, but the choice of the “accurate” method to provide the reference data is arguable in practice. The experiment-based benchmarks avoid this difficulty, but in turn, they require a proper understanding of the quantities being measured and back-correcting the vibrational and environmental contributions.Vibrational correction (either enthalpy correction for SCO systems or vibronic correction for spin-forbidden d–d transitions) originates from the variation of metal–ligand vibrational frequencies with spin state. The environmental correction expresses the change in spin-state splitting energy caused by the solvent or the crystal lattice and may have an important contribution from the environment-induced geometry changes in the first coordination sphere. As both corrections have to be estimated subject to approximations and the experimental data also have uncertainties (for example, the error of determining the maximum position for a weak band, the fitting error when determining the SCO enthalpy in the van't Hoff method), the experiment-based approach cannot be used to provide super-accurate reference data. However, with state-of-the-art models used in computational chemistry to describe the vibrational and environmental effects, it is possible to obtain reference data of electronic energies with estimated uncertainties of 1–3 kcal mol−1, therefore still useful for method benchmarking.
Here, one should note that benchmarking to a sub-kcal mol−1 precision may be relevant for computatational studies of highly accurate gas-phase data,67 but is rarely needed in (bio)inorganic chemistry, where the experimental data are typically less accurate and the results of electronic structure calculations have to be, nearly always, combined with approximate thermochemical corrections and/or solvation models. It is important to keep the balance between the accuracy of these approximations and the electronic structure methods being used. In this context, benchmarking the method's accuracy for data similar to “real life” problems and employing approximations analogous to those made in practical applications (e.g., solvation or cluster models, periodic DFT, thermochemical functions from the harmonic oscillator approximation) to extract environmental and vibrational corrections, puts the benchmarking effort closer to the daily practice of molecular modeling. In fact, the benchmarking and interpretation aspects of computational chemistry are interconnected. Without credible computational protocols, misleading conclusions and even qualitatively wrong interpretations of experimental data may be obtained, as was discussed here in the example of the sextet–quartet splitting of the FeIII aqua complex.123,124 On the other hand, the same challenging problem can serve as a valuable benchmark for theory if the experimental results are interpreted properly.
The best strategy to obtain quantitative, experimentally derived benchmark data for TM spin-state energetics is to combine SCO enthalpies with spin-forbidden d–d excitation energies in order to obtain estimates of the adiabatic and vertical energies for small-gap and large-gap TM complexes, respectively. The present author with co-workers applied the outlined strategy in two benchmark studies of octahedral Fe complexes23 and metallocenes.24 The obtained results showed relatively high accuracy of single-reference CCSD(T) calculations, outperforming multireference approaches such as CASPT2/CC and MRCI + Q. It was confirmed that the main issue with DFT methods is the lack of universality, resulting in functionals performing well for narrow classes of complexes, but producing much larger errors for other complexes. In this context, double-hybrid functionals appeared promising. These conclusions are considered preliminary and must be verified on a more representative probe of TM complexes. We are currently developing a new dataset of TM spin-state energetics based on the experimental data for a larger number of complexes, with different ligand strengths and architectures, representing the diversity of bonding types in (bio)inorganic chemistry, and using strategies highlighted above to treat the vibrational and environmental corrections.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
I am grateful to Professor Janusz Szklarzewicz (Jagiellonian University) for long-lasting experimental collaboration and providing the spectrum shown in Fig. 4. I also thank Dr Paweł Rejmak (Polish Academy of Sciences) and Dr Sergi Vela (University of Barcelona) for discussions and anonymous reviewers of this paper for valuable suggestions. This work was supported in part by the National Science Centre, Poland (grant no. 2017/26/D/ST4/00774). We gratefully acknowledge Poland's high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH, PCSS) for providing computer facilities and support within the computational grant no. PLG/2022/015281.Notes and references
- M. Swart, Int. J. Quantum Chem., 2013, 113, 2–7 CrossRef CAS.
- M. Costas and J. N. Harvey, Nat. Chem., 2013, 5, 7–9 CrossRef CAS PubMed.
- M. Swart and M. Costas, Spin States in Biochemistry and Inorganic Chemistry, Wiley, 2015, pp. 1–5 Search PubMed.
- M. Swart, New Directions in the Modeling of Organometallic Reactions, Springer, Cham, 2020, vol. 67 of Topics in Organometallic Chemistry, pp. 191–226 Search PubMed.
- B. Wang, P. Wu and S. Shaik, J. Phys. Chem. Lett., 2022, 13, 2871–2877 CrossRef CAS PubMed.
- P. Gütlich and H. A. Goodwin, in Spin Crossover in Transition Metal Compounds I, ed. P. Gütlich and H. Goodwin, Springer, Berlin, Heidelberg, 2004, pp. 1–47 Search PubMed.
- R. J. Deeth, C. M. Handley and B. J. Houghton, in Spin-Crossover Materials, ed. M. A. Halcrow, Wiley, 2013, ch. 17, pp. 443–454 Search PubMed.
- K. P. Kepp, in Transition Metals in Coordination Environments: Computational Chemistry and Catalysis Viewpoints, ed. E. Broclawik, T. Borowski and M. Radoń, Springer, Cham, 2019, vol. 29 of Challenges and Advances in Computational Chemistry and Physics, ch. 1, pp. 1–33 Search PubMed.
- M. Radoń, in Advances in Inorganic Chemistry, ed. R. van Eldik and R. Puchta, Academic Press, 2019, vol. 73, ch. 7, pp. 221–264 Search PubMed.
- J. N. Harvey, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 1–14 CAS.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2019, 119, 2453–2523 CrossRef CAS PubMed.
- J. N. Harvey, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2006, 102, 203–226 RSC.
- H. Paulsen, L. Duelund, H. Winkler, H. Toftlund and A. X. Trautwein, Inorg. Chem., 2001, 40, 2201–2203 CrossRef CAS PubMed.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- M. Radoń, Phys. Chem. Chem. Phys., 2014, 16, 14479–14488 RSC.
- B. Pinter, A. Chankisjijev, P. Geerlings, J. N. Harvey and F. D. Proft, Chem. – Eur. J., 2018, 24, 5281–5292 CrossRef CAS PubMed.
- K. P. Kepp, Inorg. Chem., 2016, 55, 2717–2727 CrossRef CAS PubMed.
- O. Siig and K. P. Kepp, J. Phys. Chem. A, 2018, 122, 4208–4217 CrossRef CAS PubMed.
- M. Radoń, J. Chem. Theory Comput., 2014, 10, 2306–2321 CrossRef PubMed.
- M. Oszajca, G. Drabik, M. Radoń, A. Franke, R. van Eldik and G. Stochel, Inorg. Chem., 2021, 60, 15948–15967 CrossRef CAS PubMed.
- J. Cirera and E. Ruiz, Comments Inorg. Chem., 2019, 39, 216–241 CrossRef CAS.
- S. Ye and F. Neese, Inorg. Chem., 2010, 49, 772–774 CrossRef CAS PubMed.
- M. Radoń, Phys. Chem. Chem. Phys., 2019, 21, 4854–4870 RSC.
- G. Drabik, J. Szklarzewicz and M. Radoń, Phys. Chem. Chem. Phys., 2021, 23, 151–172 RSC.
- M. R. A. Blomberg and P. E. M. Siegbahn, Biochim. Biophys. Acta, Bioenerg., 2015, 1847, 364–376 CrossRef CAS PubMed.
- M. R. A. Blomberg and P. E. M. Siegbahn, J. Comput. Chem., 2016, 37, 1810–1818 CrossRef CAS PubMed.
- M. Radoń, Inorg. Chem., 2015, 54, 5634–5645 CrossRef PubMed.
- M. Radoń and K. Pierloot, J. Phys. Chem. A, 2008, 112, 11824–11832 CrossRef PubMed.
- N. Strickland and J. N. Harvey, J. Phys. Chem. B, 2007, 111, 841–852 CrossRef CAS PubMed.
- L. Cao and U. Ryde, Phys. Chem. Chem. Phys., 2019, 21, 2480–2488 RSC.
- J. N. Harvey, J. Biol. Inorg. Chem., 2011, 16, 831–839 CrossRef CAS PubMed.
- F. Neese, D. Liakos and S. Ye, JBIC, J. Biol. Inorg. Chem., 2011, 16, 821–829 CrossRef CAS PubMed.
- M. Feldt and Q. M. Phung, Eur. J. Inorg. Chem., 2022, e202200014 CrossRef CAS.
- M. Roemelt and D. A. Pantazis, Adv. Theory Simul., 2019, 2, 1800201 CrossRef.
- Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, J. Chem. Theory Comput., 2018, 14, 2446–2455 CrossRef CAS PubMed.
- K. Pierloot, Q. M. Phung and A. Domingo, J. Chem. Theory Comput., 2017, 13, 537–553 CrossRef CAS PubMed.
- M. Reimann and M. Kaupp, J. Chem. Theory Comput., 2022, 28, 7442–7456 CrossRef PubMed.
- M. Reimann and M. Kaupp, J. Chem. Theory Comput., 2023, 19, 97–108 CrossRef CAS PubMed.
- M. Fumanal, L. K. Wagner, S. Sanvito and A. Droghetti, J. Chem. Theory Comput., 2016, 12, 4233–4241 CrossRef CAS PubMed.
- S. Song, M.-C. Kim, E. Sim, A. Benali, O. Heinonen and K. Burke, J. Chem. Theory Comput., 2018, 14, 2304–2311 CrossRef CAS PubMed.
- B. Rudshteyn, J. L. Weber, D. Coskun, P. A. Devlaminck, S. Zhang, D. R. Reichman, J. Shee and R. A. Friesner, J. Chem. Theory Comput., 2022, 18, 2845–2862 CrossRef CAS PubMed.
- E. Vitale, G. Li Manni, A. Alavi and D. Kats, J. Chem. Theory Comput., 2022, 18, 3427–3437 CrossRef CAS PubMed.
- B. A. Finney, S. R. Chowdhury, C. Kirkvold and B. Vlaisavljevich, Phys. Chem. Chem. Phys., 2022, 44, 1390–1398 RSC.
- A. Vargas, I. Krivokapic, A. Hauser and L. M. Lawson Daku, Phys. Chem. Chem. Phys., 2013, 15, 3752–3763 RSC.
- A. Missana, A. Hauser and L. M. Lawson Daku, J. Phys. Chem. A, 2022, 126, 6221–6235 CrossRef CAS PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- Y. Guo, C. Riplinger, D. G. Liakos, U. Becker, M. Saitow and F. Neese, J. Chem. Phys., 2020, 152, 024116 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2020, 16, 3135–3151 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2021, 17, 902–926 CrossRef CAS PubMed.
- S. Bhattacharjee, M. Isegawa, M. Garcia-Ratés, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2022, 18, 1619–1632 CrossRef CAS PubMed.
- M. Drosou, C. A. Mitsopoulou and D. A. Pantazis, Polyhedron, 2021, 115399 CrossRef CAS.
- M. Drosou and D. A. Pantazis, Chem. – Eur. J., 2021, 27, 12815–12825 CrossRef CAS PubMed.
- M. Drosou, C. A. Mitsopoulou and D. A. Pantazis, J. Chem. Theory Comput., 2022, 18, 3538–3548 CrossRef CAS PubMed.
- M. Feldt, Q. M. Phung, K. Pierloot, R. A. Mata and J. N. Harvey, J. Chem. Theory Comput., 2019, 15, 922–937 CrossRef CAS PubMed.
- M. Feldt, C. Martín-Fernández and J. N. Harvey, Phys. Chem. Chem. Phys., 2020, 22, 23908–23919 RSC.
- B. M. Flöser, Y. Guo, C. Riplinger, F. Tuczek and F. Neese, J. Chem. Theory Comput., 2020, 16, 2224–2235 CrossRef PubMed.
- T. Weymuth, E. P. A. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092–3103 CrossRef CAS PubMed.
- S. Dohm, A. Hansen, M. Steinmetz, S. Grimme and M. P. Checinski, J. Chem. Theory Comput., 2018, 14, 2596–2608 CrossRef CAS PubMed.
- K. Moltved and K. P. Kepp, J. Chem. Theory Comput., 2018, 14, 3479–3492 CrossRef CAS PubMed.
- B. Chan, P. M. W. Gill and M. Kimura, J. Chem. Theory Comput., 2019, 15, 3610–3622 CrossRef CAS PubMed.
- M. A. Iron and T. Janes, J. Phys. Chem. A, 2019, 123, 3761–3781 CrossRef CAS PubMed.
- L. R. Maurer, M. Bursch, S. Grimme and A. Hansen, J. Chem. Theory Comput., 2021, 17, 6134–6151 CrossRef CAS PubMed.
- R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018 CrossRef CAS PubMed.
- M. Korth and S. Grimme, J. Chem. Theory Comput., 2009, 5, 993–1003 CrossRef CAS PubMed.
- J. H. Thorpe, J. L. Kilburn, D. Feller, P. B. Changala, D. H. Bross, B. Ruscic and J. F. Stanton, J. Chem. Phys., 2021, 155, 184109 CrossRef CAS PubMed.
- J. M. L. Martin, Mol. Phys., 2014, 112, 785–793 CrossRef CAS.
- S. H. Yuwono, I. Magoulas and P. Piecuch, Sci. Adv., 2020, 6, eaay4058 CrossRef CAS PubMed.
- L. Cheng, J. Gauss, B. Ruscic, P. B. Armentrout and J. F. Stanton, J. Chem. Theory Comput., 2017, 13, 1044–1056 CrossRef CAS PubMed.
- Y. A. Aoto, A. P. de Lima Batista, A. Köhn and A. G. S. de Oliveira-Filho, J. Chem. Theory Comput., 2017, 13, 5291–5316 CrossRef CAS PubMed.
- D. Zhang and D. G. Truhlar, J. Chem. Theory Comput., 2020, 16, 4416–4428 CrossRef CAS PubMed.
- K. Pierloot and S. Vancoillie, J. Chem. Phys., 2006, 125, 124303 CrossRef PubMed.
- K. Pierloot and S. Vancoillie, J. Chem. Phys., 2008, 128, 034104 CrossRef PubMed.
- A. Fouqueau, S. Mer, M. E. Casida, L. M. L. Daku, A. Hauser, T. Mineva and F. Neese, J. Chem. Phys., 2004, 120, 9473–9486 CrossRef CAS PubMed.
- A. Fouqueau, M. E. Casida, L. M. L. Daku, A. Hauser and F. Neese, J. Chem. Phys., 2005, 122, 044110 CrossRef PubMed.
- M. Kepenekian, V. Robert, B. Le Guennic and C. De Graaf, J. Comput. Chem., 2009, 30, 2327–2333 CrossRef CAS PubMed.
- A. Domingo, M. À. Carvajal and C. de Graaf, Int. J. Quantum Chem., 2010, 110, 331–337 CrossRef CAS.
- J. N. Harvey and M. Aschi, Faraday Discuss., 2003, 124, 129–143 RSC.
- J. Olah and J. Harvey, J. Phys. Chem. A, 2009, 113, 7338–7345 CrossRef CAS PubMed.
- S. Vancoillie, H. Zhao, M. Radoń and K. Pierloot, J. Chem. Theory Comput., 2010, 6, 576–582 CrossRef CAS PubMed.
- L. M. Lawson Daku, F. Aquilante, T. W. Robinson and A. Hauser, J. Chem. Theory Comput., 2012, 8, 4216–4231 CrossRef CAS PubMed.
- S. J. Stoneburner, D. G. Truhlar and L. Gagliardi, J. Phys. Chem. A, 2020, 124, 1187–1195 CrossRef CAS PubMed.
- L. A. Mariano, B. Vlaisavljevich and R. Poloni, J. Chem. Theory Comput., 2020, 16, 6755–6762 CrossRef CAS PubMed.
- L. A. Mariano, B. Vlaisavljevich and R. Poloni, J. Chem. Theory Comput., 2021, 17, 2807–2816 CrossRef CAS PubMed.
- L. Wilbraham, C. Adamo and I. Ciofini, J. Chem. Phys., 2018, 148, 041103 CrossRef PubMed.
- S. Romero, T. Baruah and R. R. Zope, J. Chem. Phys., 2023, 158, 054305 CrossRef CAS PubMed.
- C. J. Stein, V. von Burg and M. Reiher, J. Chem. Theory Comput., 2016, 12, 3764–3773 CrossRef CAS PubMed.
- H. Paulsen, V. Schünemann and J. A. Wolny, Eur. J. Inorg. Chem., 2013, 628–641 CrossRef CAS.
- M. Włoch, J. R. Gour and P. Piecuch, J. Phys. Chem. A, 2007, 111, 11359–11382 CrossRef PubMed.
- C. J. Cramer, M. Włoch, P. Piecuch, C. Puzzarini and L. Gagliardi, J. Phys. Chem. A, 2006, 110, 1991–2004 CrossRef CAS PubMed.
- P. M. Kozlowski, M. Kumar, P. Piecuch, W. Li, N. P. Bauman, J. A. Hansen, P. Lodowski and M. Jaworska, J. Chem. Theory Comput., 2012, 8, 1870–1894 CrossRef CAS PubMed.
- V. P. Vysotskiy, M. Torbjörnsson, H. Jiang, E. D. Larsson, L. Cao, U. Ryde, H. Zhai, S. Lee and G. K.-L. Chan, J. Chem. Phys., 2023, 159, 044106 CrossRef CAS PubMed.
- M. F. Rode and H.-J. Werner, Theor. Chem. Acc., 2005, 114, 309–317 Search PubMed.
- M. Swart, Inorg. Chim. Acta, 2007, 360, 179–189 CrossRef CAS.
- A. Stepniewski, M. Radoń, K. Góra-Marek and E. Broclawik, Phys. Chem. Chem. Phys., 2016, 18, 3716–3729 RSC.
- P. Pernot and A. Savin, Computation, 2022, 10, 27 CrossRef.
- X. Xu, W. Zhang, M. Tang and D. G. Truhlar, J. Chem. Theory Comput., 2015, 11, 2036–2052 CrossRef CAS PubMed.
- W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460–468 CrossRef CAS PubMed.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207 CrossRef.
- M. K. Sprague and K. K. Irikura, Theor. Chem. Acc., 2014, 133, 1544 Search PubMed.
- T. J. Lee and G. E. Scuseria, in Quantum Mechanical Electronic Structure Calculations with Chemical Accuracy, ed. S. R. Langhoff, Springer, Dordrecht, 1995, pp. 47–108 Search PubMed.
- Z. Benedek, P. Timár, T. Szilvási and G. Barcza, J. Comput. Chem., 2022, 43, 2103–2120 CrossRef CAS PubMed.
- M. Swart, Chem. Phys. Lett., 2013, 580, 166–171 CrossRef CAS.
- M. Swart, J. Chem. Theory Comput., 2008, 4, 2057–2066 CrossRef CAS PubMed.
- C. Daul, M. Zlatar, M. Gruden-Pavlović and M. Swart, in Application of Density Functional and Density Functional Based Ligand Field Theory to Spin States, ed. M. Swart and M. Costas, John Wiley & Sons, Ltd, 2015, ch. 2, pp. 7–34 Search PubMed.
- P. Verma, Z. Varga, J. E. M. N. Klein, C. J. Cramer, L. Que and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 13049–13069 RSC.
- K. P. Kepp, Coord. Chem. Rev., 2013, 257, 196–209 CrossRef CAS.
- D. Sahoo, M. G. Quesne, S. P. de Visser and S. P. Rath, Angew. Chem., Int. Ed., 2015, 54, 4796–4800 CrossRef CAS PubMed.
- A. Kramida, Y. Ralchenko, J. Reader and N. A. Team, NIST Atomic Spectra Database (ver. 5.9), 2021, Available: https://physics.nist.gov/asd (accessed Oct 2022). National Institute of Standards and Technology, Gaithersburg, MD.
- S. Luo, B. Averkiev, K. R. Yang, X. Xu and D. G. Truhlar, J. Chem. Theory Comput., 2014, 10, 102–121 CrossRef CAS PubMed.
- P. G. Szalay, T. Müller, G. Gidofalvi, H. Lischka and R. Shepard, Chem. Rev., 2012, 112, 108–181 CrossRef CAS PubMed.
- K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101 CrossRef CAS PubMed.
- V. Vennelakanti, M. G. Taylor, A. Nandy, C. Duan and H. J. Kulik, J. Chem. Phys., 2023, 159, 024120 CrossRef CAS PubMed.
- K. P. Jensen and J. Cirera, J. Phys. Chem. A, 2009, 113, 10033–10039 CrossRef CAS PubMed.
- J. Cirera, M. Via-Nadal and E. Ruiz, Inorg. Chem., 2018, 57, 14097–14105 CrossRef CAS PubMed.
- S. Vela, M. Fumanal, J. Cirera and J. Ribas-Arino, Phys. Chem. Chem. Phys., 2020, 22, 4938–4945 RSC.
- M. Radoń, E. Broclawik and K. Pierloot, J. Phys. Chem. B, 2010, 114, 1518–1528 CrossRef PubMed.
- Q. M. Phung, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2012, 8, 883–892 CrossRef CAS PubMed.
- N. Bibi, E. G. R. de Arruda, A. Domingo, A. A. Oliveira, C. Galuppo, Q. M. Phung, N. M. Orra, F. Béron, A. Paesano, K. Pierloot and A. L. B. Formiga, Inorg. Chem., 2018, 57, 14603–14616 CrossRef CAS PubMed.
- Q. M. Phung, A. Domingo and K. Pierloot, Chem. – Eur. J., 2018, 24, 5183–5190 CrossRef CAS PubMed.
- T. F. Hughes and R. A. Friesner, J. Chem. Theory Comput., 2011, 7, 19–32 CrossRef CAS PubMed.
- F. Neese, T. Petrenko, D. Ganyushin and G. Olbrich, Coord. Chem. Rev., 2007, 251, 288–327 CrossRef CAS.
- Y. Yang, M. A. Ratner and G. C. Schatz, J. Phys. Chem. C, 2014, 118, 29196–29208 CrossRef CAS.
- M. Radoń, K. Gassowska, J. Szklarzewicz and E. Broclawik, J. Chem. Theory Comput., 2016, 12, 1592–1605 CrossRef PubMed.
- M. Radoń and G. Drabik, J. Chem. Theory Comput., 2018, 14, 4010–4027 CrossRef PubMed.
- L. M. J. Huntington and M. Nooijen, J. Chem. Phys., 2015, 142, 194111 CrossRef PubMed.
- Y. Lei, W. Liu and M. R. Hoffmann, Mol. Phys., 2017, 115, 2696–2707 CrossRef CAS.
- E. R. Sayfutyarova, Q. Sun, G. K.-L. Chan and G. Knizia, J. Chem. Theory Comput., 2017, 13, 4063–4078 CrossRef CAS PubMed.
- A. Heil, M. Kleinschmidt and C. M. Marian, J. Chem. Phys., 2018, 149, 164106 CrossRef PubMed.
- M. Sorai, in Spin Crossover in Transition Metal Compounds III, ed. P. Gütlich and H. A. Goodwin, Springer, Berlin, Heidelberg, 2004, pp. 153–170 Search PubMed.
- M. Sorai, Bull. Chem. Soc. Jpn., 2001, 74, 2223–2253 CrossRef CAS.
- M. P. Shores, C. M. Klug and S. R. Fiedler, in Spin-Crossover Materials, ed. M. A. Halcrow, Wiley, 2013, pp. 281–301 Search PubMed.
- J. W. Turner and F. A. Schultz, Coord. Chem. Rev., 2001, 219, 81–97 CrossRef.
- S. A. Barrett, C. A. Kilner and M. A. Halcrow, Dalton Trans., 2011, 40, 12021–12024 RSC.
- J. F. Berry, F. A. Cotton, T. Lu and C. A. Murillo, Inorg. Chem., 2003, 42, 4425–4430 CrossRef CAS PubMed.
- L. Piñeiro-López, N. Ortega-Villar, M. C. Muñoz, G. Molnár, J. Cirera, R. Moreno-Esparza, V. M. Ugalde-Saldívar, A. Bousseksou, E. Ruiz and J. A. Real, Chem. – Eur. J., 2016, 22, 12741–12751 CrossRef PubMed.
- J. W. Turner and F. A. Schultz, Inorg. Chem., 2001, 40, 5296–5298 CrossRef CAS PubMed.
- J. Li, Q. Peng, A. Barabanschikov, J. W. Pavlik, E. E. Alp, W. Sturhahn, J. Zhao, J. T. Sage and W. R. Scheidt, Inorg. Chem., 2012, 51, 11769–11778 CrossRef CAS PubMed.
- J. A. Real, M. C. Muñoz, J. Faus and X. Solans, Inorg. Chem., 1997, 36, 3008–3013 CrossRef CAS PubMed.
- S. Rat, K. Ridier, L. Vendier, G. Molnár, L. Salmon and A. Bousseksou, CrystEngComm, 2017, 19, 3271–3280 RSC.
- F. Jensen, Introduction to Computational Chemistry, Wiley, 2nd edn, 2007 Search PubMed.
- M. Reiher, Inorg. Chem., 2002, 41, 6928–6935 CrossRef CAS PubMed.
- A. Rudavskyi, C. Sousa, C. de Graaf, R. W. A. Havenith and R. Broer, J. Chem. Phys., 2014, 140, 184318 CrossRef PubMed.
- J. A. Wolny, H. Paulsen, A. X. Trautwein and V. Schünemann, Coord. Chem. Rev., 2009, 253, 2423–2431 CrossRef CAS.
- T. Bučko, J. Hafner, S. Lebègue and J. G. Ángyán, Phys. Chem. Chem. Phys., 2012, 14, 5389 RSC.
- Y.-P. Li, A. T. Bell and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 2861–2870 CrossRef CAS PubMed.
- G. Brehm, M. Reiher and S. Schneider, J. Phys. Chem. A, 2002, 106, 12024–12034 CrossRef CAS.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- H. Paulsen, R. Benda, C. Herta, V. Schünemann, A. I. Chumakov, L. Duelund, H. Winkler, H. Toftlund and A. X. Trautwein, Phys. Rev. Lett., 2001, 86, 1351–1354 CrossRef CAS PubMed.
- M. Reimann and M. Kaupp, J. Phys. Chem. A, 2022, 126, 3708–3716 CrossRef CAS PubMed.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed.
- Y.-P. Li, J. Gomes, S. Mallikarjun Sharada, A. T. Bell and M. Head-Gordon, J. Phys. Chem. C, 2015, 119, 1840–1850 CrossRef CAS.
- G. Luchini, J. Alegre-Requena, I. Funes-Ardoiz and R. Paton, F1000Research, 2020, 9, 291 Search PubMed.
- J. M. Holland, J. A. McAllister, Z. Lu, C. A. Kilner, M. Thornton-Pett and M. A. Halcrow, Chem. Commun., 2001, 577–578 RSC.
- J. M. Holland, J. A. McAllister, C. A. Kilner, M. Thornton-Pett, A. J. Bridgeman and M. A. Halcrow, J. Chem. Soc., Dalton Trans., 2002, 548–554 RSC.
- J. Wu, C. Sousa and C. de Graaf, Magnetochemistry, 2019, 5, 49 CrossRef CAS.
- J. Bloino, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2012, 8, 1015–1036 CrossRef CAS PubMed.
- C. K. Jørgensen, Acta Chem. Scand., 1954, 8, 1502–1512 CrossRef.
- L. Antonov and D. Nedeltcheva, Chem. Soc. Rev., 2000, 29, 217–227 RSC.
- M. Srnec, S. D. Wong, J. England, L. Que and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14326–14331 CrossRef CAS PubMed.
- D. Larcher and M. Gabriel, J. Phys. France, 1975, 36, 447–449 CrossRef CAS.
- R. Borrelli, A. Capobianco and A. Peluso, J. Phys. Chem. A, 2012, 116, 9934–9940 CrossRef CAS PubMed.
- F. J. Avila Ferrer, J. Cerezo, J. Soto, R. Improta and F. Santoro, Comput. Theor. Chem., 2014, 1040–1041, 328–337 CrossRef CAS.
- J. Cerezo and F. Santoro, J. Comput. Chem., 2022, 44, 626–643 CrossRef PubMed.
- S. Bai, R. Mansour, L. Stojanović, J. M. Toldo and M. Barbatti, J. Mol. Model., 2020, 26, 107 CrossRef CAS PubMed.
- P.-F. Loos, A. Scemama and D. Jacquemin, J. Phys. Chem. Lett., 2020, 11, 2374–2383 CrossRef CAS PubMed.
- F. P. Rotzinger, J. Chem. Theory Comput., 2009, 5, 1061–1067 CrossRef CAS PubMed.
- R. B. Wilson and E. I. Solomon, J. Am. Chem. Soc., 1980, 102, 4085–4095 CrossRef CAS.
- S. E. Neale, D. A. Pantazis and S. A. Macgregor, Dalton Trans., 2020, 49, 6478–6487 RSC.
- F. S. T. Khan, A. K. Pandey and S. P. Rath, Chem. – Eur. J., 2016, 22, 16124–16137 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- B. Mennucci, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 386–404 CAS.
- C. K. Jørgensen, Absorption Spectra and Chemical Bonding in Complexes, Pergamon Press, 1962 Search PubMed.
- A. Ghosh and P. R. Taylor, Curr. Opin. Chem. Biol., 2003, 7, 113–124 CrossRef CAS PubMed.
- Y. Yang, M. A. Ratner and G. C. Schatz, J. Phys. Chem. C, 2013, 117, 21706–21717 CrossRef CAS.
- R. K. Hocking, R. J. Deeth and T. W. Hambley, Inorg. Chem., 2007, 46, 8238–8244 CrossRef CAS PubMed.
- F. Neese, T. Schwabe and S. Grimme, J. Chem. Phys., 2007, 126, 124115 CrossRef PubMed.
- G. M. Sandala, K. H. Hopmann, A. Ghosh and L. Noodleman, J. Chem. Theory Comput., 2011, 7, 3232–3247 CrossRef CAS PubMed.
- M. Pápai and G. Vankó, J. Chem. Theory Comput., 2013, 9, 5004–5020 CrossRef PubMed.
- S. Saureu and C. de Graaf, Chem. Phys., 2014, 428, 59–66 CrossRef CAS.
- D. Escudero and L. González, J. Chem. Theory Comput., 2012, 8, 203–213 CrossRef CAS PubMed.
- M. Gruden, S. Stepanović and M. Swart, J. Serbian Chem. Soc., 2015, 80, 1399–1410 CrossRef CAS.
- S. Vela, M. Fumanal, J. Ribas-Arino and V. Robert, Phys. Chem. Chem. Phys., 2015, 17, 16306–16314 RSC.
- M. Bühl and H. Kabrede, J. Chem. Theory Comput., 2006, 2, 1282–1290 CrossRef PubMed.
- S. Takamizawa, T. Akatsuka and T. Ueda, Angew. Chem., Int. Ed., 2008, 47, 1689–1692 CrossRef CAS PubMed.
- T. Ueda, G. M. Bernard, R. McDonald and R. E. Wasylishen, Solid State Nucl. Magn. Reson., 2003, 24, 163–183 CrossRef CAS PubMed.
- M. Hodorowicz, J. Szklarzewicz, M. Radoń and A. Jurowska, Cryst. Growth Des., 2020, 20, 7742–7749 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional derivations and computational details including optimized geometries. See DOI: https://doi.org/10.1039/d3cp03537a |
| ‡ For typical problems of the nondynamic correlation, such as bond dissociation curves, it has been shown that the standard perturbative (T) correction performs worse than alternative, completely-renormalized (CR) corrections.88 While there exist some (but still relatively few) applications of the CR methods to TM systems,89–91 the standard (T) correction is still predominately used both in general-purpose thermochemistry protocols and in specific applications to the TM spin-state energetics problem. The present author once compared the results of standard CCSD(T) and completely renormalized CR-CC(2,3) methods for simplified heme models and found differences up to 2.5 kcal mol−1 in relative spin-state energies.19 |
| § We further note that the (fixed-node) DMC calculations cited here have some dependence on the choice of trial wave function (TWF).39 The presently quoted DMC results were obtained with a single determinant Slater–Jastrow TWF based on DFT orbitals. This choice is supported by extensive comparison with the alternative choices of the TWF provided in ref. 39 and it seems that none of the alternative choices tested therein could substantially reduce the discrepancy between the DMC and CCSD(T) results. |
| ¶ In principle, there is also a rotational contribution to the SCO entropy, but it is very small compared with the other two contributions,146 and it is arguable whether the expressions used to calculate this contribution based on the assumption of freely rotating molecules are physically valid for SCO in solution or in the solid state. |
| This journal is © the Owner Societies 2023 |