Elucidating mechanochemical reactivity of a ternary halogen-bonded cocrystal system by computational and calorimetric studies

Abstract

Discovery of a halogen-bonded ternary cocrystal of 1,3,5-trifluoro-2,4,6-triiodobenzene with pyrazine and triphenylphosphine sulfide has revealed a complex landscape of multicomponent phases, all achievable by mechanochemical interconversion. The observed solid-state reaction pathways were explained by periodic density-functional calculations and comprehensive intermolecular interaction analysis, supported by dissolution calorimetry measurements.

---

Formation of cocrystals, multicomponent crystalline materials containing neutral molecules, is driven by molecular recognition and assembly of the individual components based on noncovalent intermolecular interactions.^1,2 These supramolecular self-assembly processes are mostly driven by the formation of hydrogen bonds,^3–5 and/or σ-hole type interactions like tetrel,^6,7 pnictogen,⁸ chalcogen,^9–11 and halogen bonds.^12,13 The σ-hole type interactions, especially halogen bonds are more tuneable and directional compared to the hydrogen bonds.¹⁴ The strength of the halogen bonds gradually increases as we move from F to I donor atoms in otherwise similar molecules, with the vast majority of halogen-bonded cocrystals involving Br and I acceptor atoms. Although the halogen bond has been reported by O. Hassel in 1954, the field remained largely unexplored until the last two decades.^15–17 The recent increased interest in halogen bonding is attributed to the promising functional properties of halogen bonded cocrystals in pharmaceutical solids,^18–20 polymers,^21,22 luminescent materials,²³ optical materials,²⁴ and others.^14,25–28

Mechanochemical methods offer a clean and efficient way to synthesise halogen-bonded cocrystals and perform their interconversions.^29–32 However, it is always desirable to predict the possible products prior to experimental synthesis. With this in mind, we have recently used periodic density-functional theory (DFT) calculations and dissolution calorimetry measurements to predict the interconversion of halogen-bonded cocrystals via mechanochemical exchange of donor and acceptor components.³³ This was the first example of a combined use of periodic DFT and dissolution calorimetry to explore the thermodynamics of solid-state transformations of binary halogen and hydrogen-bonded cocrystals. The excellent accuracy of periodic DFT calculations in predicting the reaction energies was demonstrated, highlighting the opportunities presented by this approach in predicting the solid-state reactivity of halogen-bonded materials from first principles. In the present study we will apply this methodology to explore a more complex reaction system, involving a ternary halogen-bonded cocrystal composed of 1,3,5-trifluoro-2,4,6-triiodobenzene (tftib) acting as a halogen bond donor, combined with two halogen bond acceptors: pyrazine (pyr) and triphenylphosphine sulphide (tpss) (Fig. 1). In addition to the ternary cocrystal, reported in the current work, the above-mentioned molecules also form two binary cocrystals, namely (tftib)(pyr)_1/2 recently reported by us (CSD LICDEK),³³ as well as (tftib)(tpss) reported by Hasija et al.³⁴ Furthermore, the (tftib)(tpss) cocrystal exists in two polymorphic forms (CSD refcodes RUWVEN and RUWPUX), however all our mechanochemical reactions resulted in the formation of only one polymorph, RUWVEN (see ESI,‡ Fig. S2), therefore throughout this manuscript, we will be referring to this specific polymorph as (tftib)(tpss). We will explore the thermodynamic stability of the ternary cocrystal with respect to the individual coformers and binary cocrystals, by using a combination of periodic DFT calculations and dissolution calorimetry measurements. We will then investigate the role of individual supramolecular interactions found in binary and ternary cocrystal structures in order to provide insights on how these interactions contribute to the overall cocrystal stability.

Fig. 1 Molecular diagram of the components used in the crystallisation experiment.

In general, cocrystals are formed due to the preference of heteromolecular synthons over homomolecular synthons.^35–37 It has been shown that halogen-bonded cocrystals can undergo interconversions via exchange of donor or acceptor components.^31,33 Such transformations may involve switching between different types of halogen bonding, or even between halogen- and hydrogen bonding. The thermodynamic outcomes of such transformations are controlled by the relative lattice stability of the corresponding cocrystals, which, in turn, is related to the strength of the individual supramolecular interactions present in their crystal structures. In terms of their ability to act as halogen bond acceptor atoms, nitrogen and sulfur have been shown to form the strongest interactions, resulting in favourable cocrystal formation.^38,39 Sulfur is well known as a halogen bond acceptor, particularly against iodine.⁴⁰ Also, I⋯S interactions were identified as critical players in thyroid chemistry,⁴¹ some biological processes,^41–43 and in organic catalysis.⁴⁴ A Cambridge structural database (CSD)⁴⁵ search for the potential S-containing coformers for halogen-substituted benzenes was performed and the coformers which exhibited I⋯S interactions were considered (see details in ESI,‡ Table S1). The tpss acceptor was found to form cocrystals with all the substituted iodobenzenes, which makes it a promising coformer molecule to be tested for cocrystal interconversion reactions.

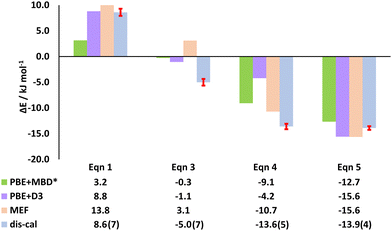
In this work, we selected the tpss acceptor to study the interconversion reaction by replacing the pyr acceptor in (tftib)(pyr)_1/2 (eqn (1)). As an initial step we theoretically predicted the enthalpy of interconversion by periodic DFT in CASTEP22⁴⁶ using PBE⁴⁷ functional with two different corrections: MBD* (many-body dispersion)^48–50 and Grimme D3.⁵¹ Positive energy values from computational results indicated that such a reaction should not proceed experimentally, and (tftib)(pyr)_1/2 should remain unreacted in the resulting mixture. Finally, the dissolution calorimetry (dis-cal) measurements also revealed a positive experimental value for the reaction enthalpy, consistent with the periodic DFT and molecular energy framework (MEF) calculations (Fig. 2). Conversely, the reverse reaction (eqn (2)), where (tftib)(tpss) reacts with the pyr acceptor to form the (tftib)(pyr)_1/2 has negative calculated enthalpy (opposite value to the forward reaction), and is therefore expected to proceed experimentally.

(tftib)(pyr)_1/2 + tpss → (tftib)(tpss) + 1/2pyr – forward (1)

(tftib)(tpss) + 1/2pyr → (tftib)(pyr)_1/2 + tpss – reverseFurther assessment of the validity of the chosen periodic DFT methods was performed by comparing the geometric parameters of the experimentally-determined and DFT-optimised crystal structures (ESI,‡ Fig. S1 and Table S6). These comparisons reveal that both methods offer excellent agreement with the experimental structures, with the optimised unit cell volumes within ±4% of experiment, and XB lengths within 0.13 Å for both methods, although PBE+D3 offers a closer overall agreement with the experimental structure parameters. (2)

In order to verify the validity of the thermodynamic predictions of reaction outcomes by DFT and calorimetry, milling reactions for eqn (1) and (2) were performed by liquid-assisted grinding (LAG)⁵² with ethanol (for further experimental details see ESI‡). Interestingly, the experimental outcome of both forward and reverse reaction gave the reaction products, for which powder X-ray diffraction pattern (PXRD) did not match either (tftib)(pyr)_1/2 or (tftib)(tpss) cocrystals. Most curiously, the PXRD patterns of the products of both forward and reverse reaction matched each other, suggesting that both reactions had led to the formation of the same product, of yet unknown structure. The same material was subsequently obtained by mixing the three individual components (tftib), (pyr), (tpss) and milling under LAG conditions with ethanol, suggesting that the new material might be a ternary cocrystal (see ESI,‡ Fig. S3–S5).

Fig. 2 Cocrystal interconversion energies (in kJ mol⁻¹) obtained from periodic DFT calculations, molecular energy frameworks (MEF) and dissolution calorimetry (dis-cal) measurements. Red error bars are shown for the energies measured by dis-cal.

Recrystallisation of the product obtained by milling, followed by single-crystal X-ray diffraction structure determination and refinement in SHELX package,⁵³ revealed that a three-component cocrystal of the formula (tftib)(pyr)_1/2(tpss)_1/2 (hereafter labelled as 3-comp) had been formed. Such a cocrystal could, indeed, form starting from both (tftib)(pyr)_1/2 and (tftib)(tpss) cocrystals, and also by milling the individual components tftib, tpss, pyr according to the following reaction equations:

(tftib)(pyr)_1/2 + 1/2tpss → (tftib)(pyr)_1/2(tpss)_1/2 (3)

(tftib)(tpss) + 1/2pyr → (tftib)(pyr)_1/2(tpss)_1/2 + 1/2tpss (4)

tftib + 1/2pyr + 1/2tpss → (tftib)(pyr)_1/2(tpss)_1/2 (5)

In order to rationalise the experimental occurrence of all these reactions, the transformation energies were computed using the periodic DFT calculations and measured by dissolution calorimetry (see ESI,‡ Table S5). Both calculated and experimentally determined interconversion energies consistently showed that formation of the 3-comp starting from either of the binary cocrystals (eqn (3) and (4)) presents a thermodynamically more favourable outcome than the interconversions between binary cocrystals (eqn (1) and (2)).

The thermodynamics of the formation of 3-comp from either of the binary cocrystals is well understood from the periodic DFT calculations, also supported by experimental calorimetric measurements. Neither of these methods, however, truly explain the reason for the higher stability of the 3-comp compared to the two-component cocrystals. In order to rationalise the observed mechanochemical reactivity, we have looked into the structures of all three cocrystals and explored the role of different non-covalent interactions in stabilising the corresponding packing arrangements.

The (tftib)(pyr)_1/2 crystallises with one tftib and half pyr molecule in the asymmetric unit. Two of the three iodine atoms of tftib interact with pyrvia I⋯N, while the remaining free iodine of tftib interacts with two neighbouring tftib molecules through bifurcated I⋯I and I⋯F interactions. This cocrystal is also stabilised by the parallel offset π–π stacking of the tftib molecules.

In the case of (tftib)(tpss) cocrystal, the coformers interact through an I⋯S halogen bond. The other two I-atoms are involved in I⋯I interaction to the neighbouring tftib molecules (see ESI,‡ Fig. S10). Finally, this cocrystal is also stabilised by the stacked tftib–tftib interaction. Contribution of all the interactions involved in stabilising the binary cocrystal as obtained from 2D-fingerprint plots are given in the ESI,‡ Fig. S6.

Compared to the binary cocrystals, 3-comp has two potential halogen bond acceptors (N of pyr and S of tpss), capable of interacting with tftib. The energies of individual supramolecular interactions must be the key to explaining the higher stability of 3-comp with respect to the binary counterparts.

Molecular energy framework (MEF) analysis,⁵⁴ performed in Crystal Explorer,⁵⁵ was used to evaluate the role of individual supramolecular interactions in stabilizing the crystal structures of the ternary and binary cocrystals.^54,56 Before embarking on the analysis of the energies of individual supramolecular interaction energies, we have verified whether total lattice energies computed by MEF method can be used to compute the energies of cocrystal interconversion reactions. Indeed, as can be seen in Fig. 2, reaction energies computed by MEF method are highly consistent with periodic DFT calculations. The only exception is reaction (3), which is predicted to have positive energy by MEF, while having negative according to periodic DFT calculations and dis-cal measurements. One possible reason for this discrepancy might be the lack of consideration of intramolecular conformation energy by MEF method, as opposed to periodic DFT. Overall, we consider the agreement between periodic DFT and MEF to be highly satisfactory, giving us confidence that the analysis of individual interaction energies by this method will be reliable.

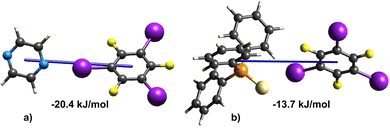
Upon comparing the strengths of the supramolecular dimers, involving the I⋯N and I⋯S interactions (Fig. 3) in (tftib)(pyr)_1/2 and (tftib)(tpss) binary cocrystals, with energies of −20.4 kJ mol⁻¹ and −13.7 kJ mol⁻¹, respectively, it can be inferred that the I⋯N interaction will likely be favoured in the three-component cocrystal containing both N and S acceptors. As anticipated, 3-comp exhibits the I⋯N interaction with an energy value of −19.2 kJ mol⁻¹, which is very similar to that found in (tftib)(pyr)_1/2.

Fig. 3 Intermolecular interaction energy of (a) (tftib)(pyr)_1/2 and (b) (tftib)(tpss) cocrystal.

However, this alone does not explain the preference for the formation of 3-comp over the binary cocrystals, the role of sulphur atom has to be explored further.

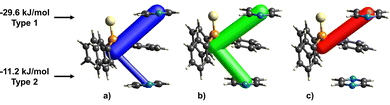
The sulfur atom in tpss does not form a halogen bond to tftib, however, a close C–H⋯S contact with a neighbouring pyr molecule is found, with this pyr moiety simultaneously involved in π–π stacking with one of the phenyl rings of tpss (type 1 in Fig. 4). The total energy of this interaction between tpss and pyr molecules is −29.6 kJ mol⁻¹, which is stronger than the interaction energy between the coformers in the (tftib)(tpss) cocrystal, where they form an I⋯S halogen bond. This explains the lack of I⋯S interactions in the structure of 3-comp. Further on, the phenyl ring in tpss is involved in the second interaction with another pyr moiety (type 2 in Fig. 4) with a total interaction energy of −11.2 kJ mol⁻¹. The phenyl ring of tpss is therefore sandwiched between the two pyr moieties, where type 1 interaction is supported by a combination of electrostatic and dispersion forces, whereas type 2 is primarily driven by the dispersion forces associated with π–π stacking between the phenyl rings (Fig. 4c). The enhanced stability of pyr–tpss–pyr trimers within 3-comp highlights the significance of incorporating pyr as the third component into this cocrystal, resulting in higher thermodynamic stability of 3-comp over (tftib)(tpss) cocrystal.

Fig. 4 Energy framework of trimer of tpss stacked between pyr (a) total energy (b) electrostatic energy (c) dispersion energy.

Next, we performed a systematic comparison of strong interactions (above −20 kJ mol⁻¹) found in all cocrystal structures, in a quest to find the interactions causing the most pronounced effect on the overall lattice stability. In all three cocrystals, the most significant contribution to the total energy is made by the tftib–tftib π–π stacking interactions. Yet specific modes of these interactions differ between the cocrystals: 3-comp features a parallel stacked trimer interaction of tftib–tftib–tftib, whereas (tftib)(pyr)_1/2 exhibits a trimer interaction with displaced and tilted edge-to-face stacking, and (tftib)(tpss) features a dimer configuration (Fig. 5).

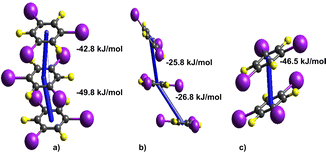Fig. 5 Specific interaction tftib–tftib stacking involved in (a) 3-comp (b) (tftib)(pyr)_1/2 (c) (tftib)(tpss) having average energy of −46.3 kJ mol⁻¹, −26.3 k mol⁻¹ and −46.5 kJ mol⁻¹, respectively.

The trimer arrangement of parallel-stacked tftib molecules found in 3-comp offers the highest energy contribution to the overall structure stability, with individual stacking energies at −42.8 and −49.8 kJ mol⁻¹. Conversely, the offset trimer found in (tftib)(pyr)_1/2 reveals a much weaker arrangement (−25.8 and −26.3 kJ mol⁻¹). Finally, the parallel stacking arrangement found in (tftib)(tpss) is strong at −46.5 kJ mol⁻¹, yet, since it is only a dimer and not a trimer arrangement, it contributes less to the overall stability of the corresponding cocrystal.

The final strong interactions contributing to the stability of 3-comp are the H⋯S interaction between pyr and tpss and the I⋯π interaction involving tftib and tpss, with energies of −29.6 kJ mol⁻¹ and −20.5 kJ mol⁻¹, respectively. However, the I⋯π interaction in 3-comp is weaker than the corresponding interaction in (tftib)(tpss) at −33.6 kJ mol⁻¹ (see ESI,‡ Table S7).

Collectively, these findings suggest that the presence of strong I⋯π interactions along with the unique combination of the trimer tftib–tftib–tftib stacking, and favourable H⋯S interaction involving tpss and pyr, play a vital role in driving the formation of 3-comp.

In summary, this comprehensive study has demonstrated how formation of the ternary halogen-bonded cocrystal in preference to the binary competing structures, can be explained by thermodynamic arguments based on periodic DFT calculations and dissolution calorimetry measurements. Moreover, detailed analysis of individual intermolecular interactions provided us with microscopic insights into the causes of the high stability of the ternary cocrystal.

Author contributions

Conceptualization: NB, DC, MA. Funding acquisition: DC, NB, MA. Investigation: LK, SGD, KL, DT. Supervision: NB, DC, MA. Writing – original draft: LK, SGD. Writing – review and editing: all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Dr Danielle Laurencin for helpful scientific discussions. LK, SGD and MA acknowledge the financial support from National Science Center (NCN) grant 2020/37/B/ST5/02638, as well as the support of PLGrid for access to the Ares supercomputer. KL and NB thank the support of the European Regional Development Fund (infrastructural project CIuK, KK.01.1.1.02.0016) and Croatian Science Foundation grant IP-2019-04-9560. DC thanks the support of Croatian Science Foundation grant IP-2019-04-1868.

Notes and references

1. G. Berger, P. Frangville and F. Meyer, Chem. Commun., 2020, 56, 4970–4981.
2. S. H. Gellman, Chem. Rev., 1997, 97, 1231–1232.
3. C. B. Aakeröy and K. R. Seddon, Chem. Soc. Rev., 1993, 22, 397–407.
4. G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 8342–8356.
5. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
6. A. Karim, N. Schulz, H. Andersson, B. Nekoueishahraki, A.-C. C. Carlsson, D. Sarabi, A. Valkonen, K. Rissanen, J. Gräfenstein, S. Keller and M. Erdélyi, J. Am. Chem. Soc., 2018, 140, 17571–17579.
7. S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 5702–5717.
8. L. de Azevedo Santos, T. A. Hamlin, T. C. Ramalho and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2021, 23, 13842–13852.
9. P. Scilabra, G. Terraneo and G. Resnati, Acc. Chem. Res., 2019, 52, 1313–1324.
10. L. Vogel, P. Wonner and S. M. Huber, Angew. Chem., Int. Ed., 2019, 58, 1880–1891.
11. W. Wang, B. Ji and Y. Zhang, J. Phys. Chem. A, 2009, 113, 8132–8135.
12. L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195.
13. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601.
14. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757.
15. O. Hassel, J. Hvoslef, E. H. Vihovde and N. A. Sörensen, Acta Chem. Scand., 1954, 8, 873.
16. O. Hassel, Science, 1970, 170, 497–502.
17. L. Turunen, J. H. Hansen and M. Erdélyi, Chem. Rec., 2021, 21, 1252–1257.
18. M. Baldrighi, G. Cavallo, M. R. Chierotti, R. Gobetto, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, Mol. Pharmaceutics, 2013, 10, 1760–1772.
19. M. Benito, A. Frontera and E. Molins, Cryst. Growth Des., 2023, 23, 2932–2940.
20. D. Choquesillo-Lazarte, V. Nemec and D. Cinčić, CrystEngComm, 2017, 19, 5293–5299.
21. G. Berger, J. Soubhye and F. Meyer, Polym. Chem., 2015, 6, 3559–3580.
22. H. Guo, R. Puttreddy, T. Salminen, A. Lends, K. Jaudzems, H. Zeng and A. Priimagi, Nat. Commun., 2022, 13, 7436.
23. O. Bolton, K. Lee, H.-J. Kim, K. Y. Lin and J. Kim, Nat. Chem., 2011, 3, 205–210.
24. J.-C. Christopherson, F. Topić, C. J. Barrett and T. Friščić, Cryst. Growth Des., 2018, 18, 1245–1259.
25. M. Đaković, M. Borovina, M. Pisačić, C. B. Aakeröy, Ž. Soldin, B.-M. Kukovec and I. Kodrin, Angew. Chem., Int. Ed., 2018, 57, 14801–14805.
26. M. D. Perera and C. B. Aakeröy, New J. Chem., 2019, 43, 8311–8314.
27. S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918–1931.
28. P. J. Costa, Phys. Sci. Rev., 2017, 2, 1–16.
29. D. Cinčić, T. Friščić and W. Jones, Chem. – Eur. J., 2008, 14, 747–753.
30. D. Cinčić, T. Friščić and W. Jones, J. Am. Chem. Soc., 2008, 130, 7524–7525.
31. M. Arhangelskis, F. Topić, P. Hindle, R. Tran, A. J. Morris, D. Cinčić and T. Friščić, Chem. Commun., 2020, 56, 8293–8296.
32. L. Loots, H. Wahl, L. van der Westhuizen, D. A. Haynes and T. le Roex, Chem. Commun., 2012, 48, 11507–11509.
33. L. Kumar, K. Leko, V. Nemec, D. Trzybiński, N. Bregović, D. Cinčić and M. Arhangelskis, Chem. Sci., 2023, 14, 3140–3146.
34. A. Hasija and D. Chopra, Cryst. Growth Des., 2020, 20, 6272–6282.
35. G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311–2327.
36. M. C. Etter, Z. Urbakzyk-Lipkowska, M. Zia-Ebrahimi and T. W. Panunto, J. Am. Chem. Soc., 1990, 112, 8415–8426.
37. M. C. Etter, Acc. Chem. Res., 1990, 23, 120–126.
38. B. Pinter, N. Nagels, W. A. Herrebout and F. De Proft, Chem. – Eur. J., 2013, 19, 519–530.
39. A. M. Abeysekera, B. B. Averkiev, P. Le Magueres and C. B. Aakeröy, Org. Biomol. Chem., 2021, 19, 6671–6681.
40. H. D. Arman, R. L. Gieseking, T. W. Hanks and W. T. Pennington, Chem. Commun., 2010, 46, 1854–1856.
41. A. Wojtczak, V. Cody, J. R. Luft and W. Pangborn, Acta Crystallogr., 2001, D57, 1061–1070.
42. A. R. Voth, P. Khuu, K. Oishi and P. S. Ho, Nat. Chem., 2009, 1, 74–79.
43. P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794.
44. J. Wolf, F. Huber, N. Erochok, F. Heinen, V. Guérin, C. Y. Legault, S. F. Kirsch and S. M. Huber, Angew. Chem., Int. Ed., 2020, 59, 16496–16500.
45. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., 2016, B72, 171–179.
46. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570.
47. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.
48. A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508.
49. A. M. Reilly and A. Tkatchenko, Chem. Sci., 2015, 6, 3289–3301.
50. A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402.
51. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
52. T. Friščić, D. G. Reid, I. Halasz, R. S. Stein, R. E. Dinnebier and M. J. Duer, Angew. Chem., Int. Ed., 2010, 49, 712–715.
53. G. M. Sheldrick, Acta Crystallogr., 2008, A64, 112–122.
54. M. J. Turner, S. P. Thomas, M. W. Shi, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2015, 51, 3735–3738.
55. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011.
56. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.

---

Footnotes

† Open access dataset, containing periodic DFT input and output files, PXRD patterns, DSC and TGA curves and dissolution calorimetry curves, is available at: https://www.doi.org/10.17605/OSF.IO/FRUVB.

‡ Electronic supplementary information (ESI) available. CCDC 2289502. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3cp04358d

§ These authors contributed equally to the manuscript

---