Transferrable selectivity profiles enable prediction in synergistic catalyst space

Abstract

Organometallic intermediates participate in many multi-catalytic enantioselective transformations directed by a chiral catalyst, but the requirement of optimizing two catalyst components is a significant barrier to widely adopting this approach for chiral molecule synthesis. Algorithms can potentially accelerate the screening process by developing quantitative structure–function relationships from large experimental datasets. However, the chemical data available in this catalyst space is limited. Herein, we report a data-driven strategy that effectively translates selectivity relationships trained on enantioselectivity outcomes derived from one catalyst reaction systems where an abundance of data exists, to synergistic catalyst space. We describe three case studies involving different modes of catalysis (Brønsted acid, chiral anion, and secondary amine) that substantiate the prospect of this approach to predict and elucidate selectivity in reactions where more than one catalyst is involved. Ultimately, the success in applying our approach to diverse areas of asymmetric catalysis implies that this general workflow should find broad use in the study and development of new enantioselective, multi-catalytic processes.

---

1 Introduction

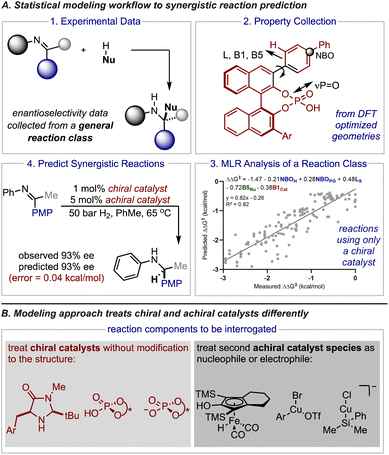
Small organic molecules effectively catalyze a significant number of reactions and, in particular, have been essential to advances in the preparation of stereochemically pure compounds.^1–6 Often, these transformations proceed through low energy pathways that involve a single chiral catalyst. For many examples the catalyst activates either substrate (nucleophile or electrophile) and in some cases both substrates can simultaneously be primed for a reaction.^7–11 However, some transformations are still challenging or completely unobtainable using one catalyst systems. Accordingly, synergistic catalysis (also referred to as co-operative or multi-catalysis) in which more than one catalyst is involved in the activation of substrates is an important technique.^12–14 This approach has been greatly enabling the discovery of new enantioselective, catalytic processes. Indeed, there are many examples of powerful classes of reactions that were developed by combining an organocatalyst with a metal.^15–22 Unfortunately, implementing this valuable tactic in asymmetric synthesis is often met with the formidable challenge of optimizing two catalyst components (as well as other reaction parameters) to achieve high levels of enantioselectivity.^23,24 While ideal reaction conditions have conventionally been discovered through empiricism, recent applications of data-driven reaction optimization have demonstrated that algorithms can streamline this process. Indeed, significant research efforts have been dedicated to developing a statistical toolset that combines numerical descriptors, regression analysis, and chemical data to correlate reaction outcomes.^25–27 The resulting mathematical models can then be leveraged to predict the outcome of new experiments typically through interpolation and provide mechanistic insight in the process. In some cases, researchers combine experimental data sets gathered from separate literature reports to increase the number of existing data points for implementing this approach. However, experimental results gathered from synergistic reactions cannot be meaningfully combined to create such combinatorial datasets since protocols involving multiple catalysts have been developed for individual transformations operating under different mechanisms. This severely constrains the amount of data available for model building, making the application of these statistical techniques to the multi-catalyst domain less straightforward. Accordingly, a different statistical approach must be employed to achieve efficient and robust prediction of enantioselectivity values in complex catalyst space.

On the basis of our recent efforts to deploy comprehensive multidimensional analysis to develop and leverage general mechanistic models,^28,29 we became interested in investigating if our multireaction workflows can be embedded in the optimization and quantitative prediction of reaction systems involving two catalysts (Fig. 1A). In this approach the features of all the reaction components are correlated to the experimentally obtained enantioselectivity outcomes conveyed as ΔΔG^‡ using density functional theory (DFT) calculated descriptors and multivariate linear regression (MLR). Essentially, these techniques permit the development of mechanistically informative correlations providing the basis to transfer enantioselectivity outcomes to predict the impact of reaction components not included in the initial training correlation, like a new catalyst or substrate.

Fig. 1 Application of statistical modeling workflow to multi-catalysis. (A) Workflow for MLR analysis and further application in reaction systems involving more than one catalyst. (B) Overview of the study's goals and approach in vetting the techniques on three catalyst systems involving distinct catalytic modes of activation.

In the context of this study, the success of this approach to predict synergistic catalysis would be contingent on the model's ability to transfer the stereochemical information from one or more reactions facilitated by a single catalyst to another mechanistically similar process that involves two catalyst systems. Although multi-catalyst reaction designs share some common mechanistic features with single catalyst systems (e.g., optimal chiral catalyst structure), comparative studies that would reveal reaction specific contacts and general connections have not been performed. Such investigations would be valuable for formalizing mechanistic principles and considering the limits of model generality. As a result, despite the practical appeal of an approach that would preclude the requirement for explicit chemical data on synergistic reaction systems, the applicability domain of such statistical models would likely be challenging to estimate. To that extent, we envisioned that the general mechanisms of stereoinduction in asymmetric catalysis should extend to multi-catalyst reaction strategies that focus on combining a chiral catalyst with a reactive intermediate that is generated from a second achiral catalyst species. Because these types of transformations are not significantly affected by the presence of a second catalyst, they should be particularly amenable to our modelling approach that uses data from one or more reactions to predict the result of a similar system (Fig. 1B).

To effectively assess how broadly applicable this approach could be we decided to select three case studies that encompass different modes of organocatalysis. Since statistical models describing the nucleophilic additions to iminiums catalysed by chiral phosphoric acids and phosphates are easily accessible through previous reports these were both identified as suitable case studies for an initial evaluation. The second criteria in selecting a predictive platform is determining a chiral catalyst system that has been widely used in synergistic catalyst space such that significant validation data exists. Consequently, we identified reactions involving secondary amines as a third study. To this end, we develop and deploy MLR as a transferability method to achieve quantitative predictions and mechanistic analysis in diverse synergistic catalyst space.

2 Results and discussion

2.1. Assessment of previously reported statistical models

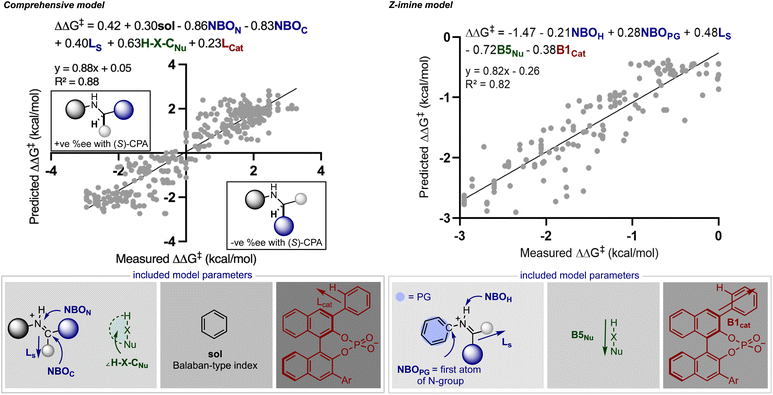
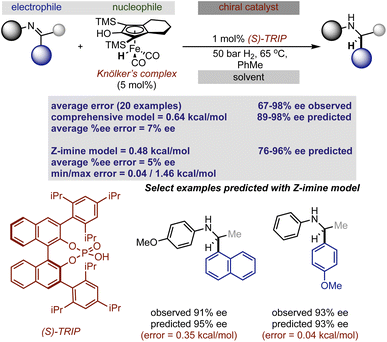
Rather than statistically evaluate reactions involving multiple catalysts directly, we pursued a transfer learning strategy wherein we curated enantioselectivity data from various transformations deploying a single catalyst chemotype responsible for stereoinduction. By focusing reaction selection on those operating under a common catalytic mode of activation, reactions can be connected via general selectivity features revealed by regression analysis and a predictive model assembled. Since existing statistical models in chiral Brønsted acid³⁰ and anion catalyst space²⁹ are available for experimentation we first evaluated their ability to extrapolate to reactions facilitated by two catalysts. It should be noted that these models were applied without alteration to the identified parameters or data sets from their published forms. Because the full details for constructing and applying the models are described elsewhere,^29,30 we will only discuss the model components necessary for analysing the predicted results.

In seeking an ambitious and relevant first test, we selected the hydrogenation of imines using molecular hydrogen.³¹ Since this process cannot be simply facilitated solely by chiral organic molecules,³² approaches have focused on two catalyst systems. Beller and co-workers demonstrated that Knölker's complex, a simple achiral iron hydrogenation catalyst, can be used in combination with a chiral Brønsted acid to provide enantioenriched secondary amines.³¹ Considering the overlap in structural features of the reaction components we anticipated that a previously generated statistical model constructed of chiral phosphoric acid catalysed additions of nucleophiles to imines could be deployed to predict the reaction outcomes (Fig. 2).³⁰ In the previous study, reaction performance was first evaluated using a comprehensive model built from the entire data set constructed of reactions that proceeded through two different pathways, an E (+ee) or Z (−ee) transition state. While prediction errors were typically larger with this all-inclusive model, its use is imperative to determine the stereochemistry of the final product and the pathway under operation. Use of this inclusive model is particularly important for predicting reactions involving ketimines as these can progress through either the E or Z iminium geometries making it difficult to determine the favoured reaction pathway. This is in contrast to imines derived from aldehydes which have been shown to proceed solely through structures possessing the E configuration.¹¹ Following the E or Z mechanistic assignment, the prediction accuracy can be improved by applying the mechanism specific models (E or Z). Because two different data sets are used in the construction of these statistical models the included terms and final predictions are slightly different. For example, the comprehensive model emphasizes solvent (black), imine (blue), nucleophile (green) and catalyst (red) terms distributed over six parameters, as contributors to the enantioselectivity across seventeen reaction types. These parameters capture the general steric and electronic influences of the individual reaction components on the experimental outcome allowing for accurate out-of-sample prediction and further mechanistic interpretation. Focused correlations can then be produced by modeling only a subset of these reactions to reveal more intricate mechanistic details through better feature selection. In other words, truncating the data set will facilitate the identification of the structural features that affect particular mechanistic pathways (E or Z) allowing better predictions to be achieved. Although having this option to model only portions of the data has been proven to be beneficial, it is not common or necessary. The comprehensive model does not naturally allow for the prediction of stereochemistry but the product configuration can be assigned by applying the simple models displayed in Fig. 2. These are based on the amine product generated from an E or Z TS and catalysed by the (S)-CPA. The standard steps for ee prediction and the assignment of product stereochemistry include: (1) locating the ground state of the targeted reaction variable by DFT, (2) obtaining the key molecular features necessary for prediction, and (3) submitting these to both mathematical equations.

Fig. 2 Published statistical models for predicting chiral phosphoric acid catalysed reactions involving imines and protic nucleophiles. The comprehensive model on the left is used to first determine the double bond configuration of the iminium intermediate and the stereochemistry of the final product. This model includes 367 training data points while the mechanism specific model used to refine predictions was trained on 147 data points. ‘Sol’ is a molecular graph representation of the solvent, ‘NBO_N’ and ‘NBO_C’ are imine natural bond orbital parameters, ^‘L_s^’ is the length (Sterimol L) of the smallest imine substituent, ‘H–X–CNu’ is the nucleophile angle measurement and L_cat is the length of the catalyst 2-substituent. Key parameters included in the Z-imine only model include ‘NBO_H’ and ‘NBO_PG’ which are imine natural bond orbital parameters, L_s is a steric descriptor of the smallest imine substituent, ‘B5_Nu’ is the Sterimol B5 term representing the nucleophile's maximum width and ‘B1_cat’ is the Sterimol B1 term describing the minimum width. The NBO values exist for specific atoms as indicated by the superscript. For example, N, C, and H superscripts correspond to nitrogen, carbon and hydrogen atoms. PG stands for protecting group and refers to the atom connecting the PG to the imine N, typically a carbon. A positive free energy value indicates the E-imine transition state, and a negative free energy value indicates the Z-imine transition state.

To put it generally, the application of these models to synergistic reactions requires the second achiral catalyst to be featurized as an electrophile or nucleophile. This can be determined by considering the reaction mechanism and the structures involved in the key transition states. On this basis, to predict the enantioselectivity of this reaction type the achiral iron complex is categorized as the nucleophile and the necessary parameters, the H–X–CNu (the nucleophile angle measurement) and B5Nu (the nucleophile steric descriptor) parameters are to be collected from this structure. For consistent results, the same level of theory that was used to optimize the nucleophiles incorporated in the original model should be applied to optimize the iron complex (organometallic nucleophile); however, the M06-2X density functional that was implemented is not applicable for molecules containing metals.³³ Instead, we employed M06/def2TZVP calculations which are suitable for organometallic systems, and when tested against a subset of nine nucleophiles, geometry minimizations provide the same value for the key bond angle and Sterimol B5 nucleophile terms when compared to M06-2X/def2TZVP (average deviation was calculated to be 0.8° and 0.02 Å, respectively). Confident that this adjustment would not significantly impact the results, we optimized the iron complex with this set of computational conditions and collected the necessary Sterimol B5 and angle nucleophile parameters for prediction from this structure. In other words, this computational method comparison suggested that a predictive model built from M06-2X descriptors could be used to predict the impact of hydrogenation reactions given the key nucleophile parameters calculated at the M06 level. Taking these steps, we evaluated the twenty reported hydrogenations involving aromatic imines catalysed by TRIP. Both the catalyst and most of the imines were part of the published training set making the nucleophile (achiral iron complex) the only component not to be explicitly included. Each result was predicted using the comprehensive model, with an average absolute ΔΔG^‡ error of 0.64 kcal mol⁻¹ (14 examples within 5% ee) and the absolute stereochemistry was correctly assigned as S, demonstrating the ability of the model to extrapolate effectively to an organometallic nucleophilic intermediate (Fig. 3). A slightly improved outcome is observed using the Z-imine mechanistic model with a 0.48 kcal mol⁻¹ average error (15 examples within 5% ee). Considering this, the average error is slightly inflated and inspection of the maximum errors shows that this is due to two reactions that had prediction errors >1 kcal mol⁻¹. In these cases the reaction performed less well than expected considering the conditions employed are associated with very high enantioselectivities. Accordingly, the model cannot capture the few results where the general enantioselectivity trends do not translate. Mechanistically, the ability to extrapolate to complex multi-catalytic reaction space suggests that transition state features like the arrangement of the reactants and hydrogen bonding contacts to the catalyst are similar to those found in one catalyst systems. This observation is consistent with previous computational studies which show an iron-phosphoric acid mediated hydrogenation with a similar substrate.³⁴

Fig. 3 Extrapolation of a previously reported chiral Brønsted acid imine reaction model to iron catalysed hydrogenation.

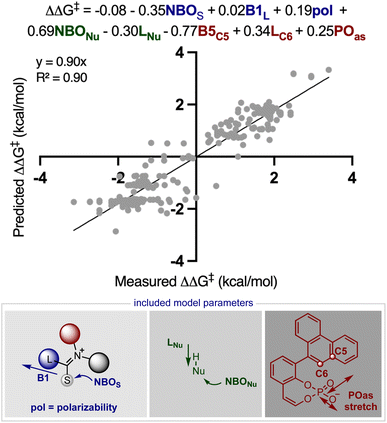
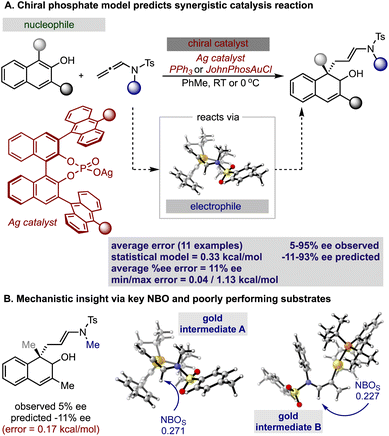
Inspired by these successful results, we selected to further evaluate the generality in our observations by investigating chiral phosphate catalysed reaction systems.²⁹ In considering this we noted that the addition of 2-naphthols to gold(I) activated allenamides exhibited overlapping transition state features with our previously built statistical model, i.e., combines an iminium with a nucleophile in the presence of a chiral phosphate (Fig. 4).³⁵ As with the chiral phosphoric acid study, to deploy the published chiral phosphate model to predict the impact of utilizing an organometallic intermediate as a reaction component, the sensitivity of the previously identified parameters to the computational method must be taken into account. Guided in part by the proposed transition state, the second achiral catalyst species was to be combined with the allenamide to form a cationic intermediate which undergoes nucleophilic addition in the enantiodetermining step. As such, the necessary parameters NBO_S (the NBO charge of the first atom on the smallest iminium group), Sterimol B1 of the large iminium group (B1_L) and polarizability that represent the electrophile components are to be collected from these organometallic structures. Because we expected NBO charges to be sensitive to the computational methods employed, we re-optimized each iminium intermediate at the M06/def2TZVP level to ensure that all electrophilic components (organic and organometallic) were treated uniformly. After replacing the iminium parameters (NBO, Sterimol B1 and polarizability) calculated at M06-2X/def2TZVP with those acquired from M06/def2TZVP optimized structures, the statistical model was re-created in MATLAB using the same enantioselectivity data and identified parameters from the previous publication (Fig. 4).²⁹ This model could then be deployed to predict the organometallic data set (Fig. 5A). However, this is a more challenging scenario, as the structural overlap between the training and the prediction set is slightly reduced. More specifically, the reaction components to be predicted are not explicitly included in the training data but belong to general subclasses of iminiums, naphthols, and chiral phosphates. Following calculations, the key iminium parameters (NBO, Sterimol B1 and polarizability) were collected from the electrophilic gold complex and inputted into the model for prediction. Again, accurate predictions were construed with the statistical model with an average absolute ΔΔG^‡ error of 0.33 kcal mol⁻¹ (4 examples within 2% ee and 6 examples within 5% ee). Like the previous test, one poorly predicted reaction (with an error of around 1 kcal mol⁻¹) inflated the average mean error. Again, this situation arises from a reaction that should be high-performing given the general enantioselectivity trend. The presence of a methyl group had the most detrimental effect on selectivity (4% ee experimental and −11% ee predicted) and excitingly, this could be accurately captured by the model (Fig. 5B). While it is superficially surprising that the model can successfully anticipate significant enantioselectivity changes due to minor substrate modifications (i.e., switching a phenyl for a methyl), close examination of key parameters in the model reveals that the lower enantioselectivity for this substrate can be attributed to the more positive NBO (Fig. 5B, gold intermediate A). This is intriguing as in both cases the atom remains a hydrogen suggesting the model is describing a subtler effect on the enantioselectivity outcome. Perhaps the most powerful analysis of the model is illustrated by comparing the substrate profiles of the one (chiral phosphate only)³⁶ and two (chiral phosphate combined with gold) catalyst systems. Remarkably, the optimal iminium intermediate was reversed between the two methods. In other words, the lead substrate with chiral phosphate catalysis failed to provide high enantioselectivities under the gold conditions and vice versa. Once again, the model clearly explains why certain substrates should be particularly amenable to different protocols. Under chiral phosphate catalysis the NBOS values are comparable for the two substrates (0.246, Ph and 0.247, 4-CF₃Ph) and the difference in polarizability, the second important iminium term, explains the contrast in enantioselectivity. Under gold catalysis, the more negative NBO values associated with gold intermediate B, largely compensate for a slightly lower polarizability term, and the ee is increased (Fig. 5B). This demonstrates that gold binding to the substrate and changes to the N-substituent (i.e. switching a Ph to a Me) alters the electron density of the iminium hydrogen, a key site for establishing non-covalent interactions with the catalyst,²⁹ ultimately suggesting that the iminiums ability to engage in weak hydrogen bonding interactions is attenuated allowing for these substrate effects to emerge. The ability of the model to accurately reflect the outcomes with different substrates suggests that it could be applied to guide successful reaction scope extension. Based on the previous evaluation and the included model parameters we considered that the model could be reliably broadened to include 1-naphthols as the nucleophile component. By deploying the descriptor set and the training model, the resultant extrapolation of the nucleophile space predicted only moderately good enantioselectivities, an observation validated by new experiments (Table 1). This result is compelling in that we could reach an informed decision about pursuing 1-naphthols as a substrate class while also providing a useful starting point for further reaction optimization. Ultimately, this demonstrates that the model’s capabilities are not limited to classifying and predicting literature data sets but can be applied to analyze and predict new reactions even in complex multi-catalytic reaction space. Because the models are only capable of predicting enantioselectivities, one limitation to acknowledge is that the tools can only guide users in substrate scope expansion where the desired reactivity is more certain. This is exemplified by the fact that no reactivity was observed with 2-phenylcyclohexanone under our conditions although these substrates work effectively with chiral phosphate only protocols (see the ESI†).³⁷

Fig. 4 The published statistical model describing the chiral phosphate catalysed nucleophilic addition to iminium intermediates. ‘NBO_S’ and ‘NBO_Nu’ are the natural bond orbital parameters corresponding to the first atom of the iminium small group (usually a hydrogen) and the nucleophilic site (either a carbon, hydrogen, oxygen, or nitrogen), ‘B1_L’ is the minimum width (Sterimol B1) of the largest iminium substituent, ‘pol’ is the calculated polarizability of the iminium, ‘L_Nu’ is the nucleophile length (Sterimol L), B5_C5 is the maximum width (Sterimol B5) of the catalyst 5-substituent, L_C6 is the length of the catalyst 6-substituent, and finally ‘PO_as’ is the asymmetric P–O stretching frequency.

Fig. 5 (A) Application of the previously reported chiral phosphate iminium reaction model to the gold catalyzed dearomatization of naphthols. (B) Interpretation of key NBO charges to describe poorly performing substrates.

Table 1 Testing and predicting the effect of including a 1-naphthol as the nucleophile in this reaction^a

Entry	CPA	L	Yield^b (%)	ee^c (%)	Predicted ee (%)
a Reactions were run with the following conditions: allene substrate (0.15 mmol), naphthol (0.1 mmol), gold phosphine (5 mol%), chiral silver phosphate (5 mol%), toluene (1 mL), rt, 16 h. b Isolated yields are given. c Enantioselectivities (ee) were measured by HPLC.
1	9-Anthryl	PPh3	68	76	62
2	9-Anthryl	JohnPhos	66	74	67

---

2.2. Secondary amine model development

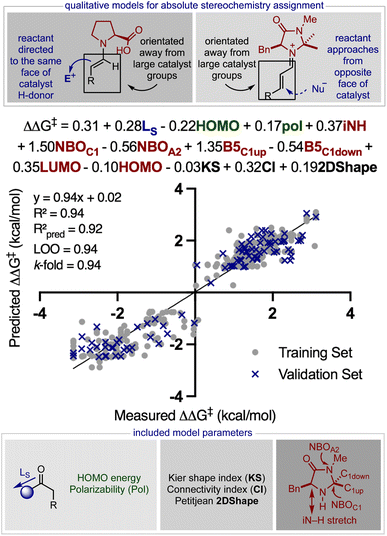
After evaluating the two published statistical models in chiral phosphoric acid and phosphate catalysed reaction space, the second stage of this study was directed at evaluating a wider set of synergistic reactions involving secondary amines. To accomplish this, a comprehensive MLR model that relates the features of all of the reaction components to the experimentally obtained enantioselectivity outcomes conveyed as ΔΔG^‡ for this catalyst class would be required (see the ESI† for full details).

Despite the potential for extensive catalyst structure modulation, only a limited set of secondary amines have witnessed broad application. This is in contrast to the many other catalyst chemotypes employed in asymmetric synthesis where necessary and extensive optimization efforts have generated considerably sized catalyst libraries. Thus, the most significant challenge in the early stages of implementing our workflow was defining a useful data set containing both high and low enantioselectivities for model construction. Consequently, to supplement our data mining efforts on published data from scientific journals, we explored the use of publicly available PhD theses. Because the reported data meet the degree requirements for characterisation PhD theses typically contain experimental data of high quality. But they remain unpublished presumably because the research objective of delivering the product in high enantioselectivity was not met.³⁸ Accordingly, we postulated that these data could be a targetable source of negative results required for robust model building. Throughout this literature evaluation, we strategically avoided two types of reaction examples. First we ignored reactions that showed product racemization to be strongly contributing to the overall enantioselectivity outcome (i.e. time and temperature sensitive).^39,40 In the absence of strongly supporting experimental data, it is only possible to minimize rather than eliminate the influence of such effects in our analysis through the removal of unusual experimental results.⁴¹ Consequently, some proportion of variation between measured and predicted enantioselectivity values will likely be attributable to these factors in addition to experimental and analytical error. Secondly, we did not include examples that combined proline type catalysts with reactants that did not contain strongly electronegative atoms. In these cases, the structure of the reactant would make it difficult to determine if hydrogen bonding was directing its approach and therefore, hard to assign the mode of enantioinduction (in more detail below).

On this basis, to construct a predictive model, an expanded inventory of 452 reactions with varied components was curated from multiple sources (for a list of references see the ESI†). From this survey, we categorized the dataset by general catalyst structure which is a significant factor in determining the mode of enantioinduction (steric blocking or hydrogen bonding) wherein imidazolidinone⁴² and diphenylprolinol ethers⁴³ are grouped by a +ee value and proline type catalysts, a −ee value (Fig. 6). Therefore, the sign of the ee represents one of two transition state (TS) categories, depending on the catalyst involved. This is important in understanding the product enantioselectivities, because reactant addition to the top or bottom face will produce opposite enantiomers. Accordingly, the statistical model will be able to determine whether the reaction proceeds through steric blocking (predicts + ee value) or hydrogen bonding modes of enantioinduction (predicts −ee value) and this information can be used to make predictions about the absolute configurations by using the qualitative pictures shown in Fig. 6. Furthermore, the TS-guided categorization strategy is useful in producing a well-distributed data set which would be hard to achieve by not taking into account the absolute product stereochemistry and demonstrated to be an effective technique in other studies.^29,30 Next, a diverse array of molecular descriptor values were collected from DFT optimized geometries to describe the overlapping structural features of each electrophile, nucleophile, catalyst, solvent, and co-catalyst.^44,45 Because this model is being built with the sole aim of predicting reactions involving an organometallic intermediate, we naturally choose the appropriate computational methods from the beginning. This involved optimizing the reactant at the M06/def2TZVP level and all other components with M06-2X/def2TZVP. The commonality in the substrate and catalyst substructure allowed collection of natural bond orbital (NBO) charges and Sterimol values from the conserved portions. However, the nucleophile had a minimal structure overlap; thus, polarizability, highest occupied molecular orbital (HOMO), and lowest unoccupied molecular orbital (LUMO) energies, which do not rely on common substructures, were collected to describe this component. Unfortunately, the lack of consistency in the reaction conditions renders the identification of readily comprehensible and extensive parameter sets for the remaining components a challenge. For example, several reactions required Brønsted acid co-catalysts and employed solvent mixtures while many others did not. Guided by the proposed mechanism of catalysis, we postulated that in cases where the acid additive was absent, the proton could originate from another source, a reagent or catalyst, and relevant descriptors could be collected from these components. Because solute–solvent interactions with polar substances will likely dominate over those with non-polar molecules, we collected topological, two-dimensional descriptors from the solvent with the largest dielectric constant (see the ESI†).^46,47

Fig. 6 Comprehensive model development and validation. The regression model is trained on 361 data points and validated with the remaining 91. ‘KS’, ‘CI’, and ‘2D shape’ are molecular graph representations of the solvent, ‘L_s’ is the length (Sterimol L) of the smallest carbonyl substituent, ‘HOMO’ is the calculated highest occupied molecular orbital of the reactant (green) or catalyst (red), ‘pol’ is the calculated polarizability of the reactant, ‘iNH’ is the intensity of the N–H stretching frequency, ‘NBO_C1’ and ^‘NBO_A2^’ are catalyst natural bond orbital parameters, ‘B5_C1Up’ and ^‘B5_C1down’, are Sterimol B5 steric descriptors of those particular amine groups and ‘LUMO’ is the calculated lowest unoccupied molecular orbital of the catalyst. A positive free energy value indicates the steric blocking transition state, and a negative free energy value indicates the hydrogen bonding transition state.

Prior to model building, the data set was partitioned into 80 : 20 training:validation sets using MATLAB's deterministic equidistant splitting function. Linear regression algorithms were then applied to the training set (80% of the entire data set that incorporates both + ee and −ee reactions) to identify prospective correlations between the molecular structure of every reaction variable defined by the parameters collected in the previous step of the workflow and the measured enantioselectivity, ΔΔG^‡ (where ΔΔG^‡ = −RT ln(e.r.) and T is the temperature at which the reaction was performed). Since the training set includes significant diversity in the reaction component structure and mechanism, we anticipated that several descriptors would be required to achieve predictive correlations. Using forward stepwise linear regression⁴⁸ we determined a model that includes solvent (black), substrate (blue), reactant (green), and catalyst (red) terms distributed over thirteen parameters to be appropriate. Despite the high R² value and validation scores, a relatively small number of outliers appeared at around 0 kcal mol⁻¹ on the x-axis. Essentially, these correspond to a few reactions that provided almost racemic mixtures in the experiment. Such unique reaction features will not conform to trends revealed by comprehensive MLR models as these operate by linking reactions via general connections i.e., structural effects that apply to the majority of reactions included in the data set.

Previous computational studies show that enantioselectivity arises from the geometry of the enamine/iminium double bond (s-trans or s-cis) and the approach of the reactant (top or bottom).⁴⁹ Therefore, it is possible that the mathematical model also reveals some of these mechanistic features despite the complex equation. Notably, the catalyst descriptors have the largest coefficients in the normalized equation, demonstrating that stereocontrol is dominated by catalyst architecture for this class of reactions. The presence of B5_C1(up) lends to a straightforward analysis by implying that larger substituents at this position makes reactant approach to the double bond from the top less possible. Additionally, large groups at C1 would direct the double bond to occupy the opposite side of the catalyst thereby favoring the formation of the s-trans isomer. We interpreted the inclusion of the NBO_C1 term as a categorical descriptor that essentially highlights that proline type catalysts (typically negative NBO_C1 and −ee) direct the reactant to the top via a hydrogen bonding interaction whereas steric blocking catalysts (usually positive NBO_C1 and +ee) that incorporate large alkyl or aromatic groups at this position promote reaction on the opposite face. Importantly, the presence of B5_C1(down) with a negative coefficient likely indicates that TS_major is also sensitive to the catalyst features. In other words, larger substituents at this position may enhance repulsive interactions between the catalyst and reactant in the TS that forms the major product, ultimately favouring the formation of the opposite enantiomer. Indeed, imidazolidinone catalysts that have two large groups at the C1 position generally provide lower levels of enantioselectivity supporting this assertion. The s-trans/s-cis isomer ratio also depends on the substrate, and having inversely sized groups on either side of the carbonyl will strongly reinforce the preference for the s-trans. This is expressed by the L_S model term and reflected in the lower enantioselectivities obtained for ketones compared to aldehydes. Because ketones are predominantly used in combination with proline (i.e., resulting in −ee reactions) the coefficient associated with L_S is positive. The role of the reactant is described through polarizability which likely acts as a proxy for chemical size (see the ESI†) and the HOMO energy. The relationship also includes three solvent parameters with relatively small coefficients, suggesting that most solvents are compatible and the assortment of optimal solvents is a reflection of reaction component solubility.^50,51 Although relating the correlation to previous findings demonstrates that the model also provides insightful mechanistic information, another important test is to remove correlated parameters and replace these with dummy values. This test is more important in this example as many parameters are being used to fit the data. Model building with these meaningless reaction barcodes shows the statistical scores to be much worse (R2 = 0.69, Q2 = 0.65, LOO = 0.63, and 10-fold CV = 0.62), suggesting that the descriptors are correlating something meaningful (see the ESI† for more details).

Considering that the goal of the prediction analysis is to transfer enantioselectivity trends of one catalyst systems to multi-catalysis, the next step is validating the secondary amine model’s ability of extrapolating to new reaction types involving a single catalyst (Fig. 7). Thus, for each out-of-sample prediction platform, both the catalyst and substrate are contained in our training set (see the ESI† for additional out-of-sample predictions). It should be noted that the model can only make predictions about the reaction enantioselectivity and not the diastereoselectivity if two stereocenters are created. This second aspect of selectivity arises from the orientation of the reactant substituents relative to those on the enamine/iminium, and this may be governed by a different set of molecular features. However, diastereoselectivity is typically not the experimental output that requires significant optimization and high levels are usually observed regardless of the reaction conditions. Thus, the prediction of diastereoselectivity is not crucial for reaction development, providing an incentive to exclude this output from our regression analysis. As a first assessment, we evaluated the ability to predict nine hydroxylation reactions, involving an oxime and diphenylprolinol ether.⁵² This set was predicted accurately, with an average absolute ΔΔG^‡ error of 0.12 kcal mol⁻¹ (eight examples predicted within 5% ee). By using the simple reaction model presented in Fig. 6, the absolute configuration is correctly assigned as R. As a second case study, the model was assessed in the same manner with seven proline catalyzed amination reactions involving an azodicarboxylate.⁵³ Again accurate predictions were obtained with this statistical model (ΔΔG^‡ error of 0.19 kcal mol⁻¹, six examples predicted within 5% ee) with the qualitative diagram shown in Fig. 6 confidently determining the stereochemical outcome to be R. The small maximum observed error in both cases shows that all of the reactions were well predicted by the model.

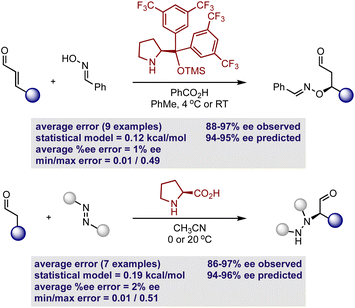Fig. 7 Demonstration of mechanistic transferability by predicting enantioselectivity outcomes involving the hydroxylation and amination of aldehydes.

2.3. Application to synergistic catalysis

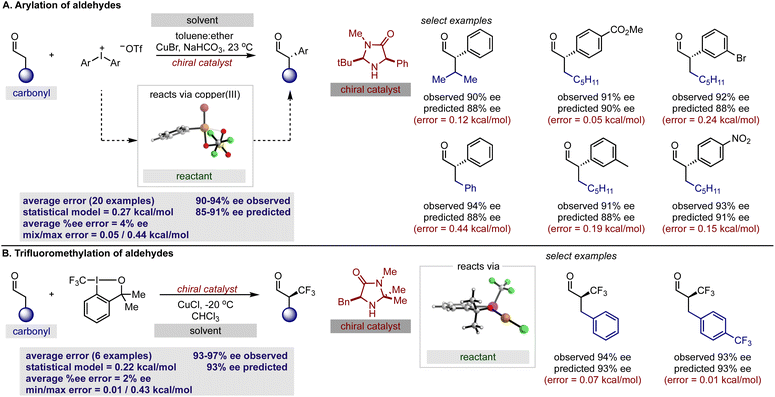
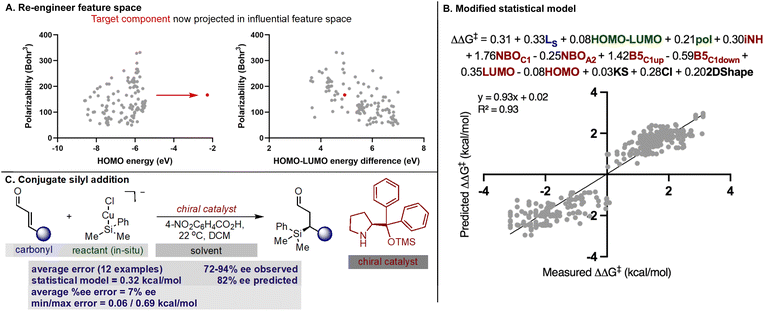
With our secondary amine statistical model thoroughly validated, we next sought to test its performance in the prediction of synergistic reaction systems involving secondary amines (Fig. 8 and 9). Because copper can generate both electrophilic and nucleophilic reactive intermediates complementing the reactivity profile of enamide and iminium catalysis, there are a number of examples in the chemical literature where this type of merger is employed. We focused on the arylation and trifluoromethylation of aldehydes reported by MacMillan as representative systems involving enamide.^54,55 The predictions obtained from the model are shown in Fig. 8 alongside the experimental results, and satisfyingly, the agreement was generally excellent. More specifically, the first case utilizes an aryl copper(III) species and a catalyst not included in the training set. With a novel catalyst/reactant pairing, an average ΔΔG^‡ error of 0.27 kcal mol⁻¹ over twenty examples was determined (Fig. 8A). As exemplified in the second case, copper can also be employed as a Lewis acid to increase the reactivity of the electrophilic trifluoromethylation agent, and in the presence of an imidazolidinone, we predicted six reactions with an average ΔΔG^‡ error of 0.22 kcal mol⁻¹ (Fig. 8B). Because the model only incorporates a single substrate parameter that essentially classifies if an aldehyde or ketone was employed, the model correctly predicts that large changes in aldehyde structure leads to small changes in the observed ΔΔG^‡ for both cases. In other words, this statistical model appropriately envisages that a wide spectrum of aldehydes should, in principle, constitute excellent substrates. As before, the qualitative pictures displayed in Fig. 6 can be applied to correctly assign the stereochemistry as S for both examples. To test this approach on reactions proceeding via iminium intermediates, copper catalysed silyl addition was probed.⁵⁶ On collecting the key reactant HOMO parameters required for prediction, we detected that the values were significantly different from those included in the training set. Based on the premise that we can predict reactions most similar to that of the training set, we hypothesized that proximity in the chemical space representation provided by mapping the HOMO against polarizability (i.e., influential feature space) would correspond to accuracy in out-of-sample prediction. Ultimately, our plot shown in Fig. 9A suggested that extrapolation to this reaction component would lead to large errors in predicting the enantioselectivity. This prompted us to search for an alternative descriptor that would capture the reactant in influential feature space. Since the HOMO–LUMO energy gap is correlative to the original parameter we generated property maps including this descriptor. Intriguingly, these indicated that the organometallic intermediate is now projected in the same feature space as the training set (Fig. 9A). Next, we manually altered the model by replacing the HOMO energy term for the HOMO–LUMO difference and predicted the enantioselectivity outcomes (Fig. 9B). Each result was predicted using the modified model, with an average absolute ΔΔG^‡ error of 0.32 kcal mol⁻¹ (ten examples within 10% ee) and the absolute stereochemistry was correctly assigned as S (Fig. 9C). This result is compelling in that we could rationally re-engineer the influential features to generalize the statistical model across diverse reaction space. Like the previous one catalyst examples, only small maximum errors were calculated on comparing model predicted values to experimental data.

Fig. 8 Applying the secondary amine regression model to predict reaction outcomes involving copper catalyzed intermediates. (A) Assessing prediction capabilities with the arylation of aldehydes. (B) Effective prediction of trifluoromethylation reactions.

Fig. 9 Application to combinations involving copper and iminium catalysis. (A) Location of the target component (red point) relative to the training set (grey points) in influential feature space determined by the MLR model. (B) Modified model that includes the HOMO–LUMO descriptor. (C) Summary of the model's performance in predicting copper catalyzed conjugate silyl addition.

3 Conclusions

Here, we describe three case studies involving different modes of catalysis that demonstrate the benefits of utilizing MLR as a transferability tool to predict and elucidate enantioselectivity outcomes in reactions where more than one catalyst is involved. Specifically, our strategy focused on revealing general mechanistic models produced through extensive data mining and advanced parameter sets. Because the selectivity discriminants were consistent across a reaction range, the resulting correlation could be leveraged for the translation of experimental observations derived from reactions utilizing a single catalyst to another similar process that involves two catalyst systems. In general, we expect this transferability workflow to be valuable in data limiting situations, for example, where practitioners have incomplete data sets either early in an optimization campaign or the complexity of reaction conditions makes it difficult to explore reaction component space completely. Consequently, our findings should be broadly applicable and beneficial for the prediction and investigation of other catalytic systems widely applied in asymmetric synthesis.

Data availability

The Cartesian coordinates of all computed geometries and extracted parameters are provided in the ESI.†

Author contributions

Y. K. and J. P. R performed the statistical modelling. J. L. performed the experiments. All authors contributed to writing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the University of British Columbia and the Natural Sciences and Engineering Research Council of Canada (NSERC). Y. K. thanks the Chinese Scholarship Council (CSC) for a graduate research fellowship. Computational resources were provided from Compute Canada and the Advanced Research Computing (ARC) center at the University of British Columbia. We thank Isaiah O. Betinol for useful discussions regarding statistical model validation.

Notes and references

1. R. R. Knowles and E. N. Jacobsen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20678–20685.
2. T. P. Yoon and E. N. Jacobsen, Science, 2003, 299, 1691–1693.
3. A. Berkessel and H. Gröger, Asymmetric Organocatalysis : From Biomimetic Concepts to Applications in Asymmetric Synthesis, Wiley-VCH, 2005.
4. T. Akiyama, Chem. Rev., 2007, 107, 5744–5758.
5. A. G. Doyle and E. N. Jacobsen, Chem. Rev., 2007, 107, 5713–5743.
6. D. M. Flanigan, F. Romanov-Michailidis, N. A. White and T. Rovis, Chem. Rev., 2015, 115, 9307–9387.
7. P. J. Walsh and M. C. Kozlowski, Fundamentals of Asymmetric Catalysis, University Science Books, 2009.
8. H. Yamamoto, Lewis Acids in Organic Synthesis, Wiley, 2000.
9. R. J. Phipps, G. L. Hamilton and F. D. Toste, Nat. Chem., 2012, 4, 603–614.
10. K. N. Houk and P. H.-Y. Cheong, Nature, 2008, 455, 309–313.
11. J. P. Reid, L. Simón and J. M. Goodman, Acc. Chem. Res., 2016, 49, 1029–1041.
12. A. E. Allen and D. W. C. MacMillan, Chem. Sci., 2012, 3, 633–658.
13. U. bin Kim, D. J. Jung, H. J. Jeon, K. Rathwell and S. G. Lee, Chem. Rev., 2020, 120, 13382–13433.
14. S. Martínez, L. Veth, B. Lainer and P. Dydio, ACS Catal., 2021, 11, 3891–3915.
15. Z. Shao and H. Zhang, Chem. Soc. Rev., 2009, 38, 2745.
16. Z. Du and Z. Shao, Chem. Soc. Rev., 2013, 42, 1337–1378.
17. B. G. Jellerichs, J.-R. Kong and M. J. Krische, J. Am. Chem. Soc., 2003, 125, 7758–7759.
18. K. J. Schwarz, J. L. Amos, J. C. Klein, D. T. Do and T. N. Snaddon, J. Am. Chem. Soc., 2016, 138, 5214–5217.
19. X. Jiang, J. J. Beiger and J. F. Hartwig, J. Am. Chem. Soc., 2017, 139, 87–90.
20. S. Afewerki and A. Córdova, Chem. Rev., 2016, 116, 13512–13570.
21. M. Rueping, R. M. Koenigs and I. Atodiresei, Chem. - Eur. J., 2010, 16, 9350–9365.
22. M. H. Wang and K. A. Scheidt, Angew. Chem., Int. Ed., 2016, 55, 14912–14922.
23. D. W. Robbins and J. F. Hartwig, Science, 2011, 333, 1423–1427.
24. A. McNally, C. K. Prier and D. W. C. MacMillan, Science, 2011, 334, 1114–1117.
25. N. I. Rinehart, A. F. Zahrt, J. J. Henle and S. E. Denmark, Acc. Chem. Res., 2021, 54, 2041–2054.
26. A. M. Żurański, J. I. Martinez Alvarado, B. J. Shields and A. G. Doyle, Acc. Chem. Res., 2021, 54, 1856–1865.
27. J. M. Crawford, C. Kingston, F. D. Toste and M. S. Sigman, Acc. Chem. Res., 2021, 54, 3136–3148.
28. A. Shoja and J. P. Reid, J. Am. Chem. Soc., 2021, 143, 7209–7215.
29. A. Shoja, J. Zhai and J. P. Reid, ACS Catal., 2021, 11, 11897–11905.
30. J. P. Reid and M. S. Sigman, Nature, 2019, 571, 343–348.
31. S. Zhou, S. Fleischer, K. Junge and M. Beller, Angew. Chem., Int. Ed., 2011, 50, 5120–5124.
32. P. A. Chase, G. C. Welch, T. Jurca and D. W. Stephan, Angew. Chem., Int. Ed., 2007, 46, 8050–8053.
33. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
34. K. Hopmann, Chem. – Eur. J., 2015, 21, 10020–10030.
35. R. Pedrazzani, J. An, M. Monari and M. Bandini, Eur. J. Org. Chem., 2021, 2021, 1732–1736.
36. B. Yang, X. Zhai, S. Feng, D. Hu, Y. Deng and Z. Shao, Org. Lett., 2019, 21, 330–334.
37. X. Yang and F. D. Toste, Chem. Sci., 2016, 7, 2653–2656.
38. D. M. Andrews, L. M. Broad, P. J. Edwards, D. N. A. Fox, T. Gallagher, S. L. Garland, R. Kidd and J. B. Sweeney, Chem. Sci., 2016, 7, 3869–3878.
39. N. Halland, A. Braunton, S. Bachmann, M. Marigo and K. A. Jørgensen, J. Am. Chem. Soc., 2004, 126, 4790–4791.
40. M. Marigo, J. Franzén, T. B. Poulsen, W. Zhuang and K. A. Jørgensen, J. Am. Chem. Soc., 2005, 127, 6964–6965.
41. J. Burés, A. Armstrong and D. G. Blackmond, Acc. Chem. Res., 2016, 49, 214–222.
42. G. Lelais and D. W. C. MacMillan, Aldrichimica Acta, 2006, 39, 79–87.
43. C. Palomo and A. Mielgo, Angew. Chem., Int. Ed., 2006, 45, 7876–7880.
44. C. B. Santiago, J. Y. Guo and M. S. Sigman, Chem. Sci., 2018, 9, 2398–2412.
45. L. C. Gallegos, G. Luchini, P. C. st. John, S. Kim and R. S. Paton, Acc. Chem. Res., 2021, 54, 827–836.
46. Y. Amar, A. M. Schweidtmann, P. Deutsch, L. Cao and A. Lapkin, Chem. Sci., 2019, 10, 6697–6706.
47. T. T. Metsänen, K. W. Lexa, C. B. Santiago, C. K. Chung, Y. Xu, Z. Liu, G. R. Humphrey, R. T. Ruck, E. C. Sherer and M. S. Sigman, Chem. Sci., 2018, 9, 6922–6927.
48. F. E. Harrell, Regression Modeling Strategies, Springer New York, New York, NY, 2001.
49. P. H. Y. Cheong, C. Y. Legault, J. M. Um, N. Çelebi-Ölçüm and K. N. Houk, Chem. Rev., 2011, 111, 5042–5137.
50. J. Burés, P. Dingwall, A. Armstrong and D. G. Blackmond, Angew. Chem., Int. Ed., 2014, 53, 8700–8704.
51. G. Hutchinson, C. Alamillo-Ferrer and J. Burés, J. Am. Chem. Soc., 2021, 143, 6805–6809.
52. S. Bertelsen, P. Dinér, R. L. Johansen and K. A. Jørgensen, J. Am. Chem. Soc., 2007, 129, 1536–1537.
53. B. List, J. Am. Chem. Soc., 2002, 124, 5656–5657.
54. A. E. Allen and D. W. C. MacMillan, J. Am. Chem. Soc., 2010, 132, 4986–4987.
55. A. E. Allen and D. W. C. MacMillan, J. Am. Chem. Soc., 2011, 133, 4260–4263.
56. I. Ibrahem, S. Santoro, F. Himo and A. Córdova, Adv. Synth. Catal., 2011, 353, 245–252.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc05974f

---