Open Access Article
Open Access ArticleScrutinizing formally NiIV centers through the lenses of core spectroscopy, molecular orbital theory, and valence bond theory†
Ida M.
DiMucci
a,
Charles J.
Titus
b,
Dennis
Nordlund
c,
James R.
Bour‡
d,
Eugene
Chong
d,
Dylan P.
Grigas
a,
Chi-Herng
Hu
e,
Mikhail D.
Kosobokov
f,
Caleb D.
Martin
 g,
Liviu M.
Mirica
g,
Liviu M.
Mirica
 e,
Noel
Nebra
h,
David A.
Vicic
e,
Noel
Nebra
h,
David A.
Vicic
 f,
Lydia L.
Yorks
f,
Lydia L.
Yorks
 f,
Sam
Yruegas
f,
Sam
Yruegas
 g,
Samantha N.
MacMillan
g,
Samantha N.
MacMillan
 *a,
Jason
Shearer
*a,
Jason
Shearer
 *i and
Kyle M.
Lancaster
*i and
Kyle M.
Lancaster
 *a
*a
aDepartment of Chemistry and Chemical Biology, Cornell University, Baker Laboratory, 162 Sciences Drive, Ithaca, NY 14853, USA. E-mail: kml236@cornell.edu; snm64@cornell.edu
bDepartment of Physics, Stanford University, Stanford, California 94305, USA
cStanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, Menlo Park, California 94025, USA
dDepartment of Chemistry, University of Michigan, Ann Arbor, Michigan 48109, USA
eDepartment of Chemistry, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA
fDepartment of Chemistry, Lehigh University, Bethlehem, Pennsylvania 18015, USA
gDepartment of Chemistry and Biochemistry, Baylor University, Waco, Texas 76798, USA
hLaboratoire Hétérochimie Fondamentale et Appliquée (LHFA), Université Paul Sabatier, CNRS, 118 Route de Narbonne, 31062 Toulouse, France
iDepartment of Chemistry, Trinity University, San Antonio, Texas 78212-7200, USA. E-mail: jshearer@trinity.edu
First published on 9th June 2023
Abstract
Nickel K- and L2,3-edge X-ray absorption spectra (XAS) are discussed for 16 complexes and complex ions with nickel centers spanning a range of formal oxidation states from II to IV. K-edge XAS alone is shown to be an ambiguous metric of physical oxidation state for these Ni complexes. Meanwhile, L2,3-edge XAS reveals that the physical d-counts of the formally NiIV compounds measured lie well above the d6 count implied by the oxidation state formalism. The generality of this phenomenon is explored computationally by scrutinizing 8 additional complexes. The extreme case of NiF62− is considered using high-level molecular orbital approaches as well as advanced valence bond methods. The emergent electronic structure picture reveals that even highly electronegative F-donors are incapable of supporting a physical d6 NiIV center. The reactivity of NiIV complexes is then discussed, highlighting the dominant role of the ligands in this chemistry over that of the metal centers.
Introduction
Motivated in part by the desire to replace effective but costly Pd catalysts with more earth-abundant, first-row transition metal surrogates, chemists have explored the synthesis and reactivity of organometallic Ni complexes for use in C–H activation1 and C–C bond forming reactions.2–5 One area of focus has been accessing formally NiIV species to test the viability of Ni as a replacement metal in reactions that invoke Pd redox couples.6 These efforts have spurred important discoveries, not only in terms of the first syntheses of stable complexes bearing formally NiIV centers, but also of new applications of Ni. For example, Sanford and co-workers7 reported (Tp)NiIV(aryl)(CF3) (Tp = trispyrazolylborate) species that undergo formal reductive elimination to generate aryl–CF3 bonds in high yields. The NiIV species [(Me3tacn)NiIV(CH2CMe2-o-C6H4)(MeCN)](BF4)2 (Me3tacn = 1,4,7-trimethyl-1,4,7-triazacyclononane) was reported by Mirica and co-workers8 to generate cyclic products through C–C bond formation following illumination with blue LEDs. More recently, Nebra and co-workers9 reported C–H scission and C–CF3 bond forming events catalyzed by the formally NiIV species [(py)2NiIVF2(CF3)2] (py = pyridine). Extending beyond the synthetic literature, NiIV has even been recently implicated in the bioinorganic chemistry of NiFe hydrogenase.10The electronic structures of formally NiIV species merit discussion. A key point of contention is the rift between the formal oxidation state arrived at by electron counting formalism and the physical oxidation state that better reflects the occupation of d-orbitals at the metal center. A recent computational examination of reductive elimination at the formally NiIV center in Sanford's (Tp)NiIV(aryl)(CF3) by Klein and coworkers11 suggests that these complexes bear physically d8 NiII centers, and that this electron count persists along the entire reaction coordinate. This claim echoes recent investigations of the electronic structures of formally CuIII complexes that contends that such species do not have d8 electronic configurations, no matter the coordination environment.12–15 Rather, these species have electronic structures in which their frontier molecular orbitals—the conventional “ligand field”—are partially or completely inverted: their parentage features greater contributions from the ligand orbitals than the metal d-orbitals.
Ligand field inversion implies that electron hole character is localized to the ligand as opposed to the metal center.12,16 In the case of Cu, this perspective has been used to rationalize the reactivity of [CuF]2+ complexes in C–H fluorination,17 and it has been offered as an explanation for why dipyrrin complexes bearing formally CuIII–imido centers present electronic structures and reactivities more consistent with complexes bearing CuI–nitrene centers.13 Analogous electronic structure arguments have been leveled to explain the reactivity of formally CuII–amido complexes in H-atom transfer and C–C bond formation.18 Some of us have credited ligand field inversion as enabling C–C bond formation from formally CuIII centers by rendering ligands electron deficient and thus able to proceed through transition states consistent with intramolecular nucleophilic attack and intramolecular radical coupling.19 In the case of NiIV centers, localization of hole character to ligands appears evident in the case of tert-butylbenzene adducts of TpNi—in the case of the formally NiIV complex, the coordinated alkyl is sufficiently electrophilic to be attacked by acetate to form a C–O bond.20 In analogous NiIII species, this reactivity is not observed.
The functional implications of reassigning holes from the metal to its ligand in Ni complexes extend to materials science. In the early 1990s, studies revealed that Li doping of NiO semiconductors produced materials with electron holes localized on the O sites as opposed to the metal centers.21 Recent studies on Ni-containing Li-rich layered oxides further probed the involvement of O redox in NiO moieties using resonant inelastic X-ray scattering (RIXS) to reveal significant oxygen hole character produced during charging of the material.22 Additionally, investigation of Ni deficient NiO films showed that Ni vacancies cause ligand holes (Ni d8![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) state) to be formed near the Fermi level, significantly enhancing the electrical conduction in NiO.23 Other studies have shown that stabilizing Ni in unconventional formal oxidation states can impart previously unattainable superconductivity in lattice nickelates.24 These insights fall in line with the implication of O-localized holes as vital electronic characteristics of cuprate superconductors.25
state) to be formed near the Fermi level, significantly enhancing the electrical conduction in NiO.23 Other studies have shown that stabilizing Ni in unconventional formal oxidation states can impart previously unattainable superconductivity in lattice nickelates.24 These insights fall in line with the implication of O-localized holes as vital electronic characteristics of cuprate superconductors.25
Redox neutrality and ligand field inversion in reductive elimination by formally NiIV species has been proposed on the basis of computational results.11 We now supply experimental support for these electronic structure hypotheses using L2,3-edge XAS in concert with calibrated electronic structure calculations. Our assessment of the physical oxidation states of formally NiIV species leverages sum-rule analysis of electric-dipole allowed Ni 2p → 3d XAS transitions.26–28 In short, we show that the total integrated L2,3-edge intensity scales proportionally with Ni 3d character in acceptor orbitals using [Ni(mnt)2]2− (mnt = maleonitriledithiolate) and [NiCl4]2− as calibrants. We extend our discussion with an experimentally-calibrated, multi-approach computational analysis of the NiF62− ion to evaluate the extent to which Ni can be pushed to a limiting d6 electron count by highly electronegative fluoride ligands. We ultimately show that none of the formally NiIV species approach the d6 limit, but rather are better described as having physical d8 NiII centers.
Results and discussion
Count vs. configuration
In advance of the following discussion, it is worth differentiating a few key concepts concerning physical manifestations of “oxidation state”. Of primary importance is distinguishing d-count from d-configuration. The former concerns the electron density assigned to a transition metal on the basis of partitioning electrons between the metal and its ligands. Variable degrees of covalent admixture between metal d-orbitals and ligand orbitals will lead to variations in d-count, and these d-counts will be fractional. This concept, whose physical relevance was made manifest by Owen and Griffith's observation of Ir–Cl covalency in IrCl62−,29 formed a basis for Jørgensen to make nuanced oxidation state assignments.16,30 He argued that if hole character on the ligands in IrCl62− exceeded that on Ir, an IrIII assignment was more appropriate than IrIV. However, experimental quantification of Cl hyperfine coupling revealed greater hole character on Ir. Thus, Jørgensen concluded a d-count of 5 and therefore an IrIV assignment for this ion. Germane to the current topic of NiIV, a d-count of 6 implies a quadruply oxidized Ni center—physical NiIV. Species presenting a higher d-count would be assigned as bearing more reduced Ni centers. The hole character is attributed to the ligands, and this has consequences for reactivity (vide infra).Computational methods enable a means to extract d-counts via electron partitioning schemes, i.e. population analyses. This partitioning is highly method dependent and, depending on the scheme, yields different values.31,32 A more qualitative perspective is that some population analyses favor more ionic descriptions of bonding, whereas others provide more covalent descriptions. Consequently, it is important to calibrate these methods to physical observables. In the present case, sum-rule L2,3-edge XAS analysis furnishes a of quantification of d-count—this value is directly observable. The absorptivity of L2,3-edge main-lines is a reflection of the dipole-allowed nature of 2p → nd excitations. Dilution of this nd character by ligand admixture diminishes this absorptivity, and thus the integrated area of the L2,3-edge main lines directly reflects the amount of nd character in acceptor MOs, thus affording a measure of d-count.14,26–28,33
The d-configuration, on the other hand, is an integer count of valence electrons that affords a means to interpret experimental data (e.g. optical spectroscopy and magnetism) while remaining ambiguous concerning the nature of the electrons/holes. Although d-configurations are highly useful and frequently align with formal oxidation state assignments, problems arise through overinterpretation. To illustrate this point, we recall the visible spectrum of [NiF6]2−, which was interpreted in 1969 by Allen and Warren34 using a crystal-field multiplet approach. This approach succeeds when considering 4 valence holes bearing some d-parentage. However, a reasonable fit to Tanabe–Sugano matrices is only achieved when employing a substantially diminished electron–electron repulsion integral (Racah's B parameter). Thus, 4 valence holes for [NiF6]2− (or any other formally NiIV-containing species) does not imply that the d-count is 6, only that the resulting ground and excited states exhibit the state symmetry of a frontier molecular orbital (MO) manifold with 4 holes bearing some degree of Ni 3d character. In fact, we will show that the d-count for this species approaches 8, implying nickel possesses an oxidation state significantly lower than +4.
Cutsail and co-workers,35 in a recent rebuttal of our study of formally CuIII complexes, blurs this distinction between count and configuration to arrive at “physical d8 CuIII” assignments for a series of organocopper complexes. They note that these species display “highly covalent [metal–ligand] bonding interactions”. The observation of pre-edge features in the Cu K-edge XAS spectra of formally CuIII species was proffered as key evidence for d-vacancies and thus “d8 CuIII”. However, such formally 1s → 3d transitions arise principally due to the quadrupolar mechanism, and thus cannot readily be used to quantify the parentage of acceptor orbitals. So, while one can argue that indeed there are two frontier vacancies in formally CuIII complexes, their partitioning between metal and ligand cannot be extracted from a K-edge spectrum. These authors claim additional support for their assignments via analysis of both K pre-edge energies as well as Cu Kβ X-ray emission spectroscopy (XES) energies, which are ascribed to changes in Cu 1s binding energies owing to increases in Cu Zeff due to progressive oxidation of the metal center. This analysis will be discussed further below.
Klein and co-workers36 recently conflated the concepts of d-configuration with d-count by coining the term “quasi-dn configuration”. Using [Cu(CF3)4]− as an example, Klein assigned the complex as quasi-d10 by application of an intrinsic bond order and energy decomposition analyses. In Klein's formalism, the quasi-d10 configuration results from the summation of the 8 non-bonding localized Cu 3d electrons (the “intrinsic configuration” i.e. d8 CuIII) and the two electrons partitioned to copper in the four occupied localized Cu–C bonding orbitals (these possess 25% Cu 3d-character accounting for two additional Cu 3d electrons). This formalism was extended to Au complexes, with “quasi” vs. intrinsic d10 differentiated both computationally and by qualitative comparison of L3-edge XAS profiles.37 Experimental quantification of d-count was not provided (an accurate d-count cannot be provided without also obtaining L2-edges). We would argue that this is unnecessarily cumbersome as the difference in spectral profile can be ascribed to differences in d-configuration. A formally AuI compound with an “intrinsic” d10-configuration effectively lacks frontier d-orbital vacancy. However, a formally AuIII compound with a “quasi-d10” configuration will have frontier vacancies with some d parentage, and thus additional XAS features. Thus, analogous to the case of [NiF6]2− described above, the d8 configuration state manifold applies—“quasi-d10” is a d8 configuration with a d-count approaching 10. What is ultimately important is the nature of the vacancies, which lead to a more reduced metal center and more oxidized ligands. As will be highlighted below for Ni, it is the electron-depleted ligands that are rendered reactive, not an oxidized nickel-center.
Both Cutsail et al. and Klein et al.'s arguments invoke covalency concepts. For the purposes of the present discussion, we employ the widely used definition that within a MO-framework, metal–ligand covalency is the degree of metal and ligand character comprising a particular MO; a highly covalent metal–ligand MO possesses approximately equal contributions from both metal- and ligand-based atomic orbitals. Complications arise when the terms “highly covalent” and “approximately equal” are employed. For example, with [Cu(CF3)4]−, Cutsail describes the lowest unoccupied MO (LUMO) as “highly covalent”, yet on the basis of our L2,3-edge XAS data14 (and calculations from several groups38,39) it contains only ca. 30–35% Cu 3d character. Although the LUMO is covalent in nature, it is polarized towards the ligands, resulting in a d-count of 9.3. We therefore suggest that descriptions such as “CuIII with highly covalent metal–ligand bonding” are not informative – in the case of organocopper complexes such a description inherently ignores the electron deficient nature of the ligands that promotes their reactivity. We contend that if one has an accurate d-count, obtained experimentally, theoretically using accurate methods that have been rigorously calibrated to experimental results, or through knowledge of how similar compounds behave, one can estimate the charge build-up on the ligands and hence make knowledgeable predictions regarding reactivity and stability.
What remains missing from a complete treatment is a reconciliation of a physical oxidation state with atomic charge. In the following study, we report d-counts obtained by experiment. However, charges at Ni (which are subject to variation due again to the arbitrary nature of partitioning schemes) will also be governed by partial 4s and 4p occupancy. These values are not readily probed experimentally. Consequently, d-count affords an upper limit to oxidation state, and thus will not capture the charge at metal in its entirety. However, we argue that scrutinizing this quantity is sufficient, because one expects the s and p contributions to the chemically relevant frontier MOs to be small – as will be shown in detail with [NiF6]2−, s and p contributions change the metal atomic charge by less than −1. Therefore, chemical insight is not eroded by a consideration of only the d-count, and one can accept inconsistencies between oxidation state assignments and atomic charge.
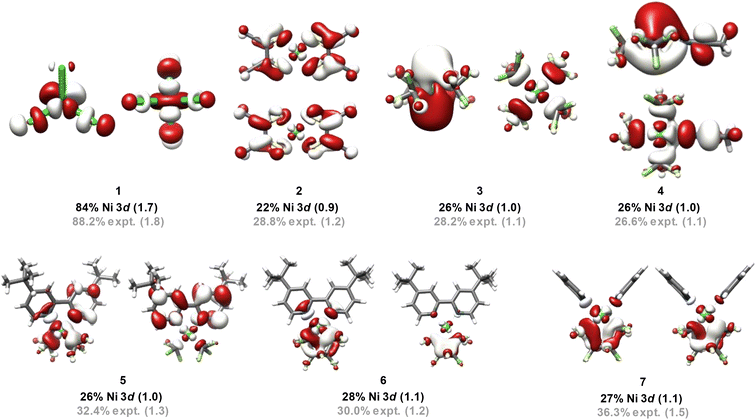
Compounds under investigation
To extend this discussion to formally high-valent Ni, X-ray spectroscopic data were obtained for the 16 Ni complexes shown in Fig. 1. Compounds 1 and 2 are covalency calibrants; compounds 3–7 are highly fluorinated NiII species, compounds 8–11 are formally NiIII species, and 12–16 are formally NiIV species.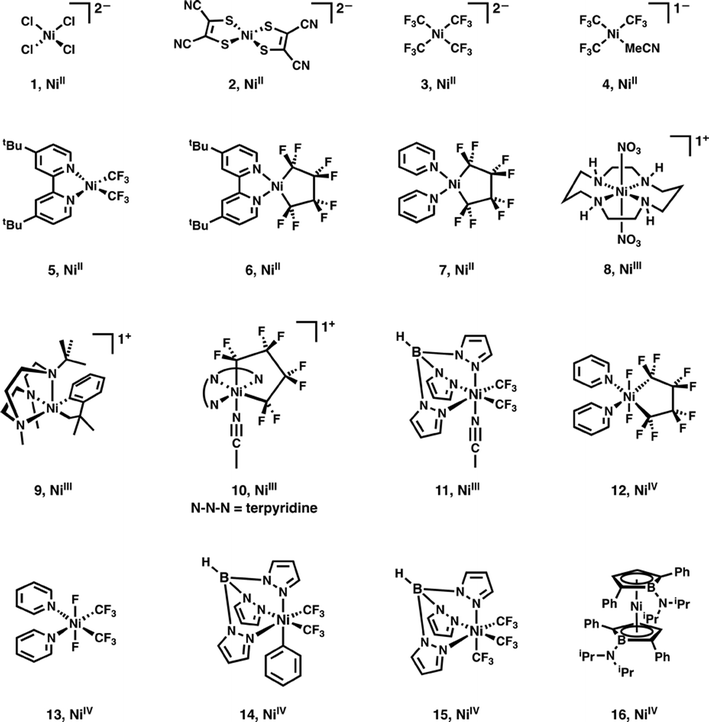 | ||
| Fig. 1 Ni complexes and complex ions investigated using XAS in this study. Formal Ni oxidation states are shown below each complex. | ||
Ni K-edge XAS
Experimental Ni K pre-edge and rising edge XAS features for species 3–7 and 11–15 are compiled in Table 1. Representative K-edge XAS data are shown in Fig. 2a. Ni K pre-edge peak energies are plotted vs. formal oxidation state in Fig. 3. The data in Fig. 3 are complemented with values obtained from literature for additional formally NiIII compounds. All species display well resolved pre-edge features between 8332.6 and 8334.2 eV. The formally NiII species 3–7 also display one or two additional rising edge features between 8334.3 and 8336.8 eV. The pre-edge features are assigned as quadrupole-allowed excitations from Ni 1s to acceptor orbitals bearing variable amounts of Ni 3d character, and the rising edge features in the formally NiII species are into orbitals with significant Ni d and Ni p character (Fig. S2–S9†). These assignments are supported by time-dependent DFT (TDDFT) calculations (vide infra). Overall, the formally NiIV species have pre-edge features that are blue-shifted relative to formally NiII species. As seen in Fig. 3, when only considering formally NiII and NiIV compounds, pre-edge peak energies exhibit a rising trend with increasing formal oxidation state. However, this does not necessarily reflect oxidation of Ni commensurate with a physical 2-electron oxidation from d8 NiII to d6 NiIV. First of all, the correlation between pre-edge peak energy and formal oxidation state is disrupted by the inclusion of formally NiIII compounds including values from the literature.40–42 The pre-edge peak energies of these compounds are not intermediate between those of formally NiII and NiIV compounds, rather, they cluster with either of the two classes of compound. This reflects the fact that pre-edge energies have contributions from both the binding energy of the metal 1s orbital as well as the ligand field strength.33,40 Preferably, comparison within homologous redox series is carried out when attempting to make claims about oxidation states using K-edge XAS pre-edge features.43,44 In the present case, this is not feasible as isoleptic NiII,III,IV series are scarce. Although rising edge energies better directly reflect charge at the metal, unambiguously assigning these energies is made difficult in the presence of large amounts of rising edge structure arising from higher-energy bound transitions (e.g. Ni(1s → 4pz) transitions), as encountered with the compounds under investigation.| Compound | Pre-edge energy (eV) | Edge feature 1 energy (eV) | Edge feature 2 energy (eV) |
|---|---|---|---|
| 3 | 8332.6 | 8335.2 | — |
| 4 | 8332.6 | 8335.3 | — |
| 5 | 8332.7 | 8334.4 | 8336.8 |
| 6 | 8333.0 | 8334.3 | 8335.7 |
| 7 | 8333.0 | 8335.4 | — |
| 11 | 8333.9 | ||
| 12 | 8334.2 | — | — |
| 13 | 8334.0 | — | — |
| 14 | 8334.2 | — | — |
| 15 | 8334.2 | — | — |
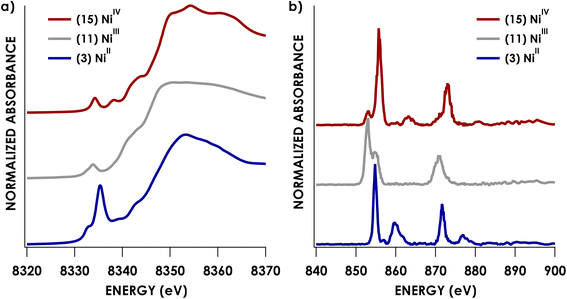 | ||
| Fig. 2 Representative Ni K-edge (a) and L2,3-edge (b) XAS spectra for formally NiII, NiIII, and NiIV species. | ||
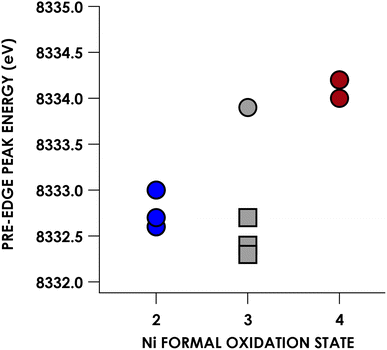 | ||
| Fig. 3 Plot of Ni K-edge XAS pre-edge peak positions vs. formal Ni oxidation state for compounds 3–7 and 11–15. Gray squares correspond to formally NiIII compounds whose K pre-edge energies have been reported previously: 8332.7 eV for [Ni(II)(14-TMC)(O2)]+ (12-TMC = 1,4,7,10-tetramethyl-1,4,7,10-tetraazacyclododecane),40 8332.4 eV for [NiIII(ONO2)(PyCarb2)] (PyCarb2 = N,N′-(2,6-dimethylphenyl)-2,6-pyridinedicarboxamidate),42 and 8332.7 eV for [NiIII(NCO)(P(C6H3-3-SiMe3-2-S)3)]−.41 | ||
Regardless, a more important point concerns 1s binding energies—these manifest with very small changes in d-count. This will be reinforced after discussion of experimentally quantified Ni d-counts—correlation of vacancy in Ni 3d with calculated Ni 1s binding energies indicates that trends in K-edge XAS energies alone should not be considered diagnostic of physical oxidation state in Ni (vide infra).
Ni L2,3-edge XAS: quantification of Ni 3d count
We and others have demonstrated that L2,3-edge XAS affords a direct means to quantify d-count.14,26–28 This process is applied here for the Ni species investigated. Example Ni L2,3-edge data are shown in Fig. 2b. The remaining L2,3-edge XAS data are included in the ESI (Fig. S11–S26).† All L2,3-edge spectra were corrected for intensity saturation as described in the ESI.† The energies of L3- and L2-edge main line intensity maxima can be found in Table 2. The L3- and L2-edge main line maxima of the formally NiIV species span over 3 eV (852.5–855.5 eV and 869.5–872.8 eV for the L3 and L2 respectively). Perhaps more surprisingly, the L3- and L2-edge maxima of the formally NiII species span nearly the same range (852.7–854.8 eV and 870.9–871.7 eV for the L3 and L2 respectively). L2,3-edge areas found in Table 2 were obtained by fitting both the L2- and L3-edge peaks to Gaussian lineshapes and summing to obtain total areas.| Compound | Formal oxidation state | L3 max. (eV) | L2 max. (eV) | L2 + L3 area | Experimental d-vacancy | Calculated d-vacancy |
|---|---|---|---|---|---|---|
| a Calculated d-vacancies were obtained by Löwdin population analysis of RKS orbitals or UKS orbitals subjected to QRO transformation. All calculations employed the B3LYP hybrid density functional with the CP(PPP) basis set on Ni and ZORA-def2-TZVP(-f) basis on all other atoms. b Estimated saturation correction performed as 22% for 1 and 10% for 13 based on estimated tabulated transmission coefficients.45 c Experimental Ni 3d vacancy for 1 (ref. 46) and 2 (ref. 47) taken from previously reported values. | ||||||
| 1 | 2 | 852.7 | 871.7 | 14.7(9)b | 1.8c | 1.7 |
| 2 | 2 | 853.7 | 871.7 | 10.0(7) | 1.2c | 0.9 |
| 3 | 2 | 854.8 | 871.7 | 9.4(7) | 1.1(1) | 1.0 |
| 4 | 2 | 854.7 | 871.5 | 8.9(6) | 1.1(1) | 1.0 |
| 5 | 2 | 854.1 | 870.9 | 10.8(8) | 1.3(1) | 1.0 |
| 6 | 2 | 854.6 | 871.4 | 10.0(7) | 1.2(1) | 1.1 |
| 7 | 2 | 854.6 | 871.4 | 12.1(8) | 1.5(1) | 1.1 |
| 8 | 3 | 853.6 | 871.8 | 18(1) | 2.3(1) | 1.8 |
| 9 | 3 | 852.3 | 869.7 | 12.0(8) | 1.4(1) | 1.5 |
| 10 | 3 | 854.3 | 871.1 | 17(1) | 2.1(2) | 1.6 |
| 11 | 3 | 853.0 | 870.7 | 15(1) | 1.9(1) | 1.7 |
| 12 | 4 | 855.6 | 872.6 | 17(1) | 2.1(1) | 1.8 |
| 13 | 4 | 852.9 | 871.2 | 16.7(9) | 2.0(1) | 1.9 |
| 14 | 4 | 855.9 | 873.2 | 14(1) | 1.8(1) | 1.7 |
| 15 | 4 | 855.7 | 873.2 | 14(1) | 1.8(1) | 1.7 |
| 16 | 4 | 852.8 | 869.9 | 8.6b | 1.0(1) | 1.0 |
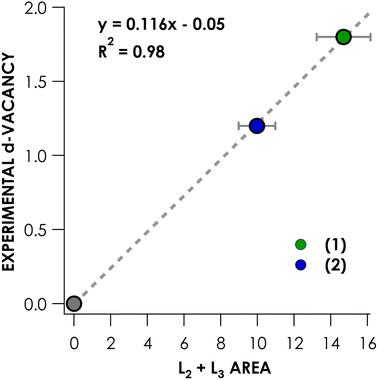
(NEt4)2[NiCl4]46 and {Na(benzo-15-crown-5)}2[Ni(mnt)2],48 whose Ni 3d counts have been established by complementary ligand K-edge XAS measurements, were used as calibrants (Fig. 4). This calibration was then applied to obtain d-counts from experimental peak areas. Because we are probing partially occupied and/or vacant MOs, we report 3d-vacancies. This has the added benefit of obviating the need to establish via calculation or otherwise the number of vacant, 3d-containing MOs. Put simply, the 3d vacancy = 10 − 3d count. To obtain these values, the experimental L2,3-edge main line areas for species 3–16 are entered into the linear expression shown in Fig. 4 and then divided by 100 to obtain d-vacancies. In this manner, one finds that, e.g., compound 14 is missing 1.8 electrons from a 3d10 count (and thus physically lies nearer NiII than NiIV). Via this approach, one is not required to explicitly address d-configuration in order to address the discrepancy between physical and formal oxidation state. These experimental Ni 3d-vacancies are compiled in Table 2.
Two key observations may be made. The first is that formally NiIII and NiIV complexes generally exhibit larger d-vacancies than formally NiII compounds. A notable exception is formally NiIV compound 16, whose d-vacancy of 1.0 places it among the values exhibited by the NiII species. The other is that, of the compounds experimentally surveyed, no d-vacancy significantly exceeds 2—the largest value obtained is 2.3 for formally NiIII-containing compound 8.
Influence of Ni 3d count on Ni 1s binding energy
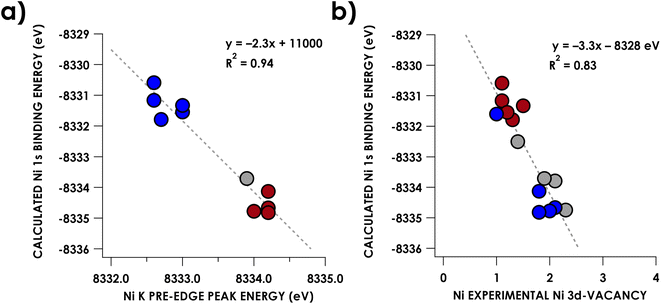
The increase of Ni K pre-edge energies with formal Ni oxidation state, at least as presents upon comparing formally NiII with NiIV compounds, may appear at odds with the contention that the formally high-valent Ni species maintain physically more reduced metal centers. As discussed above, K-edge XAS and Kβ XES have been used to assign a physical d8 CuIII oxidation state to a series of organometallic Cu complexes by Cutsail and co-workers.35 The applicability of these techniques to assign oxidation state is predicated on the metal 1s orbital binding energy being a reporter of physical oxidation state. In short, 3d orbital penetration toward the nucleus exerts some degree of shielding upon Ni 1s electrons. Thus, depopulation of 3d orbitals diminishes this shielding, resulting in shifts of the 1s orbital to a deeper binding energy. Indeed, correlation (R2 = 0.94) is apparent between DFT-calculated Ni 1s binding energies and pre-edge peak energies (Fig. 5a), with formally higher oxidation state complexes trending toward deeper 1s binding energies. Another (weaker) correlation (R2 = 0.83) is encountered when plotting these calculated Ni 1s energies vs. the Ni 3d vacancies obtained via L2,3-edge sum-rule analysis (Fig. 5b). However, we note that while these shifts indeed reflect changes in valence electron population at the metal, these shifts manifest with small changes in d-population. The experimental difference in d-vacancy between the presently scrutinized complexes bearing formally NiII centers from those bearing NiIV centers is on the order of 1 electron. This is sufficient to manifest in ca. 3 eV (0.5 parts-per-thousand) changes to the calculated Ni 1s orbital binding energies – in other words, small changes in d-population result in measurably significant changes in Ni 1s binding energies. To further put this in perspective, the [Ni(mft)2]2−,1−,0 (mft = maleotrifluoromethyldithiolate) series contain redox non-innocent ligands, and thus the three compounds are assigned as having an invariant physical oxidation state on nickel.49 Yet they yield a change of 2.2 eV in Ni 1s binding energy over the series and corresponding measurable shifts in rising edge energy (Fig. S32†).49 Regarding organocopper oxidation state assignments, this behavior is even more exaggerated for Cu where 1-electron d-vacancy changes on Cu manifest in ca. 7 eV (0.8 parts-per-thousand) changes in calculated 1s binding energy (Fig. S33†). This difference in changes in Ni vs. Cu 1s binding energies upon oxidation can plausibly be attributed to the larger ZCuvs. ZNi. Thus, we assert that spectroscopic signatures of 1s binding energy are insufficient to justify physical oxidation state assignments in late transition metal systems because seemingly appreciable changes to this quantity can manifest from small, non-integer changes in 3d count.Calculations
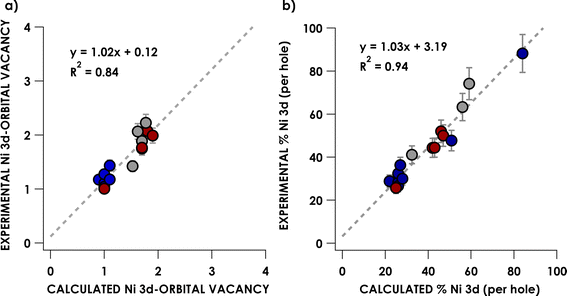
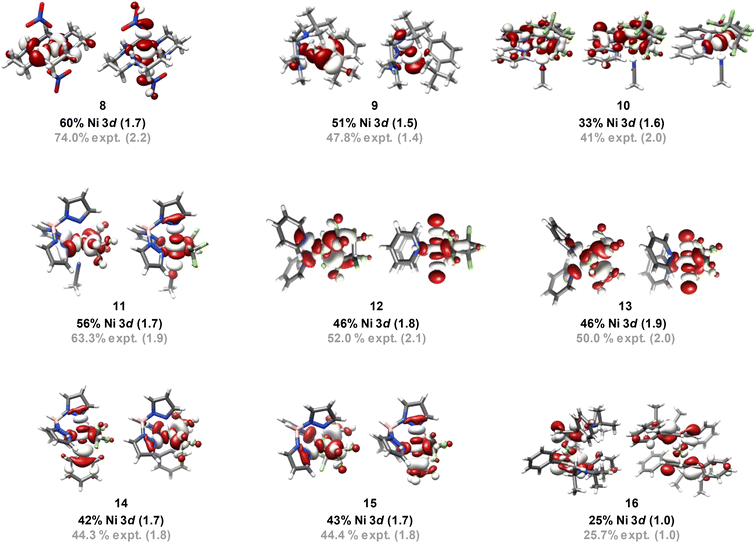
The finding above that, among the experimentally probed compounds, no d-vacancy significantly exceeds 2, prompts consideration of the limits to which the Ni d-manifold may be depopulated upon oxidation of complexes/complex ions. An exhaustive collection of XAS for Ni compounds is prohibitive. To this end, we expanded our study using computational approaches, although first assuring accord with experiment for the data discussed above. We employed the B3LYP hybrid density functional, the CP(PPP) basis on Ni, and the scalar relativistically recontracted all-electron ZORA-def2-TZVP(-f) basis on all other atoms. Orbital coefficients were obtained via Löwdin population analysis. In previous studies we found that this approach yields values that agree with experiment.Now applied to Ni, excellent agreement (R2 = 0.84) is obtained when correlating DFT-calculated percent 3d-vacancies to the experimental values obtained from application of the standard curves (Fig. 6a). In a more fine-grained analysis, consideration of Ni 3d character per hole reveals agreement between experiment and theory (R2 = 0.94) (Fig. 6b). Orbital depictions, parentages, and Ni 3d vacancies for the formally NiIII and NiIV species are shown in Fig. 7. Perhaps unsurprisingly, the NiIII and NiIV species display less than 63% average Ni 3d character among their unoccupied and partially occupied MOs. However, all but one of the NiII species also have frontier MOs with Ni d character falling well below 50% (Fig. 8), with Ni 3d orbital percentages ranging from 22% to 28%. A consensus emerges that accords with experiment: d6-count NiIV is not encountered in any of the systems we have considered. Rather, these species have d-counts between d8 and d9. The formally NiIII complexes generally exhibit d-counts similar to the NiIV species. Additionally, the highly fluorinated NiII (3–7) complexes are likely better described as having d-counts of d9, and thus physical NiI centers.
Calibrated Ni covalency calculations: application to additional reported NiIV complexes
With the exception of 16, the formally NiIV compounds discussed above possess highly fluorinated ligands. The agreement between sum-rule analysis of the L2,3-edge XAS and Ni 3d-vacancy calculated using the aforementioned hybrid DFT protocol prompted us to consider additional complexes with a greater diversity of coordination spheres. Five additional crystallographically characterized formally NiIV compounds are shown in Fig. 9.8,50–53 Unoccupied frontier MOs bearing Ni 3d character are shown for these compounds in Fig. S27–S31.† Summing the Ni 3d hole character over the unoccupied orbitals reveals d-counts substantially greater than d6: they range from a Ni 3d vacancy of 1.1 in 18 to a vacancy of 1.8 in 21. These experimentally-calibrated calculations thus reveal that the complexes are better described physically having d-counts that place them in the range between NiI and NiII. Thus, highly fluorinated coordination spheres are not responsible for the large rift between the formal NiIV oxidation state and the physical d-count. | ||
| Fig. 9 Structurally characterized formally NiIV complexes investigated by experimentally-calibrated DFT calculations. Ni 3d-vacancies from the calculations are given in parentheses. | ||
Electronic structure of NiIV in a highly oxidizing coordination environment: [NiF6]2−
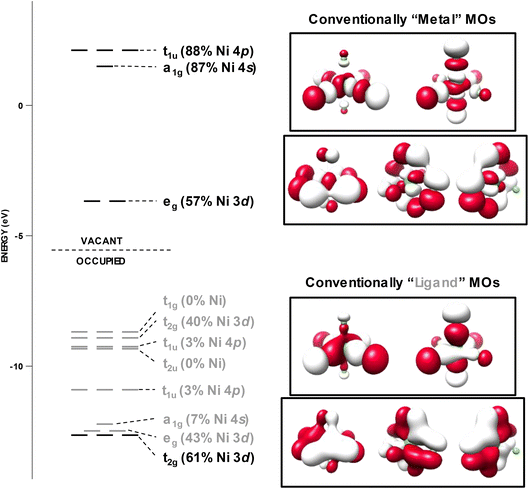
A particularly interesting extension of the previous computational exercise is the extreme case of [NiF6]2− (22), where Ni could be considered to be in its most oxidizing environment. In 1969, the teams of Allen and Warren34 as well as Reisfeld, Asprey, and Penneman54 applied Tanabe–Sugano analysis to scrutinize the electronic structure of this ion. They noted extremely low values of Racah's B-parameter, with the former team obtaining a value of 515 cm−1 and the latter of 485 cm−1 (the gas-phase atomic value is 1238 cm−1). This signifies significant delocalization of the valence electrons resulting in a substantial reduction in electron/electron repulsion. Further analysis by Allen and Warren after the manner of Jørgensen55 provided an estimate of the charge at Ni of +1.6.34 The d-count implied by this analysis can be no greater than 8.4, and thus the physical oxidation state is more appropriately assigned as NiII, rather than NiIV.Early semi-empirical MO calculations by Allen and co-workers56 using the complete neglect of differential orbital overlap (CNDO/s) method yielded a d-count of 7.4 at Ni (NiIII oxidation state) in 22; depending on the semi-empirical method used we arrive at d-counts ranging from 7.1 to 8.2. Considering the variation in the d-count based on the choice of semi-empirical method, we revisited the electronic structure of 22 using a variety of modern quantum mechanical methods, including: hybrid DFT, post-Hartree–Fock (HF), and ab initio valence bond (VB) methods.
The MO diagram resulting from a B3LYP calculation for 22 is presented in Fig. 10. The calculated % Ni 3d character of the vacant eg orbitals is 57%. Employing the correlation established using the experimental spectra and plotted in Fig. 6a, this corresponds to a predicted 62% experimental Ni 3d character. This translates to a d-vacancy of 2.4 (a d-count of d7.6), or a physical oxidation state intermediate between NiII and NiIII. Scrutinizing the MO diagram more thoroughly reveals that the fully occupied t2g manifold (that would correspond to the canonical Oh ligand field t2g orbitals) comprises only 40% calculated Ni 3d character and lies interspersed among the non-bonding F 2p lone-pair MOs. What would conventionally be considered the “ligand” t2g manifold lies to deeper binding energy and contains the residual 60% Ni 3d character. Taken together, this implies that in NiF62−, Ni 3d and F 2p are effectively isoenergetic, indicating that even with highly oxidizing fluorine, the NiIV physical oxidation state is not achieved. This contention is reinforced through ab initio VB calculations that explicitly consider covalent and ionic configurations.57
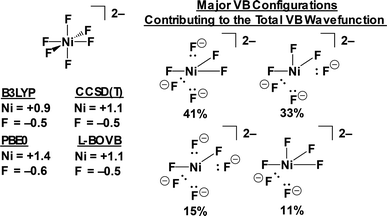
The many-electron VB wavefunction (ΨVB) results from a linear combination of Heitler–London–Slater–Pauling (HLSP) state functions (Φi) weighted by structural coefficients Ci. To limit the number of state functions, the electrons and VB orbitals (φk) were divided into active and inactive electrons/orbitals; only those explicitly involved in bonding were considered active. Based on initial calculations at the VBSCF level,58 where φk are identical in each HLSP state function, we identified four dominant VB configurations (along with their symmetry related configurations) that strongly contribute to the overall VB wavefunction (Fig. 11).59 These configurations all contain Ni–F (covalent) and Nin+⋯F− (ionic) bonding interactions. At the VBSCF level it is already apparent that the totally ionic [Ni4+F6−]2− description of 22 is untenable; when included in the VBSCF calculation we find that the totally ionic HLSP state function lies 7.9 eV above the next lowest energy Φ and does not contribute to the total VB wavefunction.
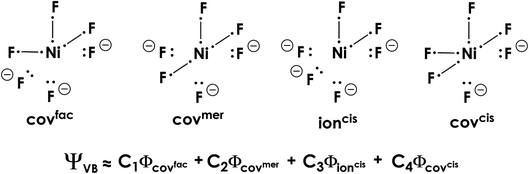 | ||
| Fig. 11 Heitler–London–Slater–Pauling (HLSP) state functions of 22 that dominate the overall valence bond wavefunction. Only the active orbitals/electrons are depicted. | ||
More accurate VB results can be obtained at the localized breathing orbital VB (L-BOVB) level of theory.60,61 Here the φk functions are still localized on their individual atomic centers, but are allowed to optimize (breathe) for each individual HLSP state function. It has been shown that these methods give results comparable to high-level molecular orbital methods (e.g. CCSD(T) and full-CI calculations), and more accurate contributions of ionic configurations,62 which we find are underweighted at the VBSCF level of theory. At the L-BOVB level we obtain a ΨVB that is predominantly [Ni+F3F3−]2− in character (74.3%) with minor contributions by the [Ni2+F2F4−]2− (14.5%) and [Ni0F4F2−]2− (11.2%) configurations (Fig. 12).
These ab initio VB results accord with high level hybrid-DFT and post-HF MO calculations. The L-BOVB wavefunction yields a Ni charge of +1.1e, an average F charge of −0.51e and an average Ni–F Mayer bond order of 0.47. This coincides with B3LYP/CP(PPP)/ZORA-def2-TZVP(-f) (Ni+0.90/F−0.48/Ni–F B.O. = 0.69), PBE0/def2-QZVPP (Ni+1.39/F−0.57/Ni–F B.O. = 0.61) and CCSD(T)/def2-QZVPP (Ni+1.10/F−0.52/Ni–F B.O. = 0.52) calculations. Lastly, these calculations all suggest that, counterintuitively, the physical Ni1+ center of [NiF6]2− is best described as a 3d8 ion! In the VB calculations, the nickel-based valence bond orbitals involved in bonding are not pure Ni 3d orbitals, but instead have significant Ni 4s and Ni 4p character owing to orbital hybridization, thus reducing the total Ni 3d character. The molecular orbital calculations support a Ni d8 configuration – Löwdin population analyses at both the PBE0 and CCSD(T) levels yield a Ni 3d84s0.54p0.5 configuration for the physically Ni1+ ion in 22.
To summarize, both VB and high-level MO calculations converge on an identical physical description of the formally NiIV center of 19; it is a low-valent 3d84s/p1 NiI ion. This reinforces the notion that 3d6 NiIV is physically unrealistic. Such a conclusion can also be reached on the basis of electronegativity arguments. Using Ni ionization energies,63 we determine a Mulliken electronegativity64 (scaled to the Pauling electronegativity scale)65 for Ni4+ (χNi(IV)) of 25.1, demonstrating that Ni4+ will readily oxidize F−. In fact, the electronegativities for Ni3+ through Ni0 (χNi(III) = 17.3; χNi(II) = 10.3; χNi(I) = 5.1; χNi(0) = 1.8) demonstrate that only Ni0 has an electronegativity that is less than fluorine (4.1) and the Ni1+ ion has an electronegativity comparable to fluorine. This is consistent with our above findings that the charge on nickel converges to ∼Ni1+ in (NiF6)2−. Taken together, we interpret this as such: outside of the gas phase, the Ni4+ ion is unstable and thus will be reduced in any ligand environment. If the extraordinarily electronegative hexafluoride ligand set about Ni is partially oxidized, then it should not be surprising that any other, less electronegative ligands will be oxidized as well.
Formally NiIV case studies
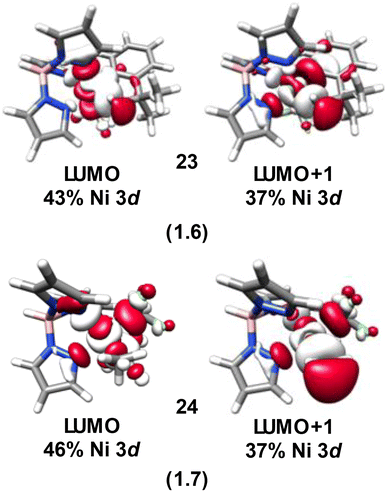
From the analyses above it becomes apparent that the majority of the Ni species investigated present with diminished Ni 3d character in their frontier molecular orbitals. Analogous to the Cu species we previously investigated,4 these inverted or covalent electronic structures have bearing on reactivity. NiIV species are commonly invoked in 2-electron transfer reactions used to replace expensive and environmentally scarce metals such as Pd and Pt. The Sanford lab reported on the reductive elimination and C–C bond formation of a series of species with formally NiIV centers5 including 14. Recently, through intrinsic bond orbital (IBO) analysis Klein and co-workers11 invoked ligand field inversion to rationalize the C–CF3 bond formation that occurs with 14. They further attribute reactivity to an attack of anionic CF3 on an electrophilic aryl cation, while the Ni center remains effectively NiII throughout the reaction. Our own IBO analysis of 14 based on our experimentally-validated calculations reveals a +0.54e charge for the coordinated C of the CF3 groups, while the coordinated C of the phenyl is calculated to have a −0.15e charge. This is in line with our conclusion that the Ni center in 14 is best described as physically NiII, at odds with a physical 2-electron reductive elimination. An electrostatic attraction between the positively and negatively charged carbons of the CF3 and phenyl groups drives reactivity, akin to our contention for the Cu(alkyl)(CF3)3 species we scrutinized previously.14,19The localization of hole character to bound ligands in formally NiIV complexes enables intermolecular reactivity. Camasso and Sanford66 reported that [(Tp)Ni(CH2CMe2-o-C6H4)(CF3)] (23), which has a calculated d-vacancy of 1.6, undergoes nucleophilic attack by a range of nucleophiles resulting in functionalization and detachment of the coordinated t-butyl methyl group (Fig. 13). Similarly, Sanford and co-workers67 have provided strong evidence that TpNi(CF3)2(CH3) (24), which has a similar calculated d-vacancy of 1.7, reacts with radicals (R˙) to furnish R–CH3 (Fig. 13). The calculated electronic structures for 23 and 24 follow the trend discussed above, where the metal d-count is intermediate between d8 and d9. In both cases, there is a large degree of hole character localized to the coordinated methyl groups (Fig. 14). The reaction pathways for attack by nucleophiles (in the case of 23) or R˙ (in the case of 24) are thus evident. This also suggests that 24 may be susceptible to nucleophilic attack. Similar behavior is noted for 21, which is completely consumed upon reaction with nucleophiles, although C–X bond formation is only noted in the presence of Cl−. Outcomes of reactions with e.g. acetate, azide, and other nucleophiles were not discussed in detail.8
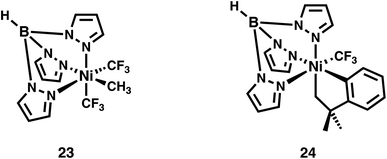 | ||
| Fig. 13 Formally NiIV complexes whose coordinated alkyl ligands undergo C–R bond formation via attack by nucleophiles (23) or radicals (24). | ||
Recently Kulka-Peschke and co-workers10 proposed that oxygen tolerant [NiFe]H2ase forms a coordinatively saturated glutamate bound high-valent S = 0 NiIV state under high O2 levels (Fig. 15, [NiFe]H2asehex). This assignment was based on the lack of an EPR signal, and a good match between calculated single-determinant DFT CO/CN vibrational frequencies and experimental data. Taken at face value, one may interpret the formally high-valent Ni-center in [NiFe]H2asehex as being an extraordinarily potent Lewis acid, which could readily promote dioxygen initiated reactive oxygen species (ROS) formation, and subsequent oxidative damage. This necessitates a coordinatively saturated NiIV site to protect that active-site. However, our further investigation demonstrates the nickel-center of the proposed structure is itself not oxidized. A NEVPT2/CASSCF(14,13) calculation of the purported [NiFe]H2asehex structure demonstrates that the active-site is highly multiconfigurational in nature, and that the triplet state (S = 1) rests above the singlet and quintet states (Fig. S33, Tables S1 and S2†). Furthermore, a population analysis yields a Ni d-count of 9.4, which is inconsistent with physical NiIV. In fact, what becomes oxidized are the thiolate ligands bound to the Ni center, not the Ni or Fe centers themselves. It is the ligand environment that affords redox buffering, emphasizing the importance of coordination by biological ligands with high charge plasticity.
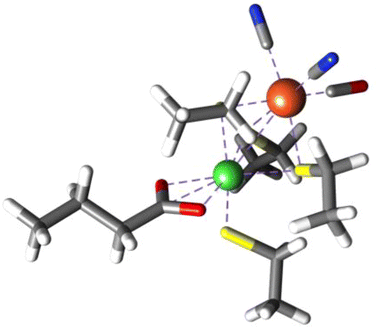 | ||
| Fig. 15 Computationally proposed structure of the active site of O2-oxidized H. thermoluteolus NiFe hydrogenase. Coordinates obtained from ref. 10. | ||
Small Ni 3d vacancies in formally NiII complexes
The disparity between formal and physical oxidation states is not unique to the unusually high valent Ni complexes, but also occurs in the formally NiII systems 2–7. As with the NiIV systems, fluorinated ligands are not necessary for this unconventional electronic structure, as the S-coordinated Ni(mnt)2 complex 2 is also best described with a d9 count and bears no fluorinated ligands. The high covalency of these NiII systems and distribution of hole character into the ligands could have critical implications in materials science as the NiO moieties in those materials do not typically incorporate high valent Ni species, but rather NiII species that are frequently supported by O-donors.Implications for ligand design
Highly oxidized metal centers are a common synthetic target because of the expectation that they will exhibit enhanced reactivity. A coordination chemist may approach this using a highly anionic ligand scaffold—e.g. the tetraanionic tetraamidate macrocyclic ligand (TAML) scaffold or tribasic corrole ligands. Alternatively, organometallic chemists may favor ligands with a propensity for covalent bonding, e.g. phosphines or σ-alkyl donors. Regardless of the approach, the outcome is the same—successful generation of these highly oxidized species are only achieved using ligands that can surrender significant electron density to the highly electronegative metal center, not merely stabilize a high metal oxidation state through electrostatic interactions. In either case, electron deficiency manifests in the ligands, which provide loci for reactivity.Conclusion
The complexes discussed above showcase the generality of low dn counts in formally NiIV centers. Furthermore, it is evident that even species with commonly observed oxidation states, such as NiII, can display similar discrepancies between their dn counts and values implied by their formal oxidation state. The consensus picture emerges that the d-count for Ni centers in coordination and organometallic complexes remains between d8 and d9. This accords with a proposal by Wolczanski68 that the charge at Ni centers remains within 0.5e of +1.3. Additionally, we have reinforced that high metal oxidation states do not necessarily correlate to reactivity, as revealed by our discussions of the influence of electrostatic interactions of substituents, spin state and spin density on the reactivity of these species.The use of Ni species as starting points for catalytic transformations such as C–C bond formation, C–H activation and C–H amination could enable replacement of expensive third-row transition metals in numerous catalytically relevant cycles. Furthermore, harnessing ligand oxidation in Ni containing thin films or semiconductors would allow application of this work to materials and battery chemistry resulting in more efficient substrates and transformations. We argue that analysis of all these transformations and electronic properties can be facilitated through understanding the localization of electrons, charge and radical character in the species of interest. Combined, the present work represents our continued effort to establish connections between more physically grounded oxidation states and observed reactivity that will influence further efforts in catalyst design, and materials science.
Data availability
Data can be requested by emailing the corresponding authors.Author contributions
SNM, JS, and KML conceptualized the study, administered the project, collected and interpreted data, carried out calculations, and co-wrote the original draft of the manuscript. IMD synthesized compounds, collected and interpreted data, carried out calculations, and co-wrote the original draft of the manuscript. CJT and DN contributed methodology, and to both data collection and analysis. JRB, EC, DPG, C-HH, MDK, NN, LLY, and SY synthesized compounds. KML, JS, CDM, DAV, NN, and LMM acquired funding for the project. All listed authors reviewed and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Harry Gray, Roald Hoffmann, and Peter Wolczanski for valuable discussions. We acknowledge the NSF (CHE-1954515 to K. M. L., CHE-1753025 to C. D. M., CHE-2153730 to D. A. V., and CHE-2155160 to L. M. M.), the NIH (R15 GM141650 to J. S.), the Welch Foundation (AA-1846 to C. D. M.), and the Agence Nationale de la Recherche (ANR-JCJC-20-CE07-0023-Ni4Rf to N. N.) for support. XAS data were obtained at SSRL, which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the Department of Energy's Office of Biological and Environmental Research, and by NIH/NIGMS (including P30GM133894). The work at SSRL was also supported by the U.S. Department of Energy Office of Basic Energy Sciences proposal no. 100487.References
- N. A. Harry, S. Saranya, S. M. Ujwaldev and G. Anilkumar, Catal. Sci. Technol., 2019, 9, 1726–1743 RSC.
- J. B. Sweeney, A. K. Ball and L. J. Smith, Chem.–Eur. J., 2018, 24, 7354–7357 CrossRef CAS PubMed.
- V. P. Ananikov, ACS Catal., 2015, 5, 1964–1971 CrossRef CAS.
- S. Ge and J. F. Hartwig, Angew. Chem., Int. Ed., 2012, 51, 12837–12841 CrossRef CAS.
- S. Z. Tasker, E. A. Standley and T. F. Jamison, Nature, 2014, 509, 299–309 CrossRef CAS PubMed.
- L. M. Mirica, S. M. Smith and L. Griego, in Nickel Catalysis in Organic Synthesis, John Wiley & Sons, Ltd, 2020, pp. 223–248 Search PubMed.
- J. R. Bour, N. M. Camasso and M. S. Sanford, J. Am. Chem. Soc., 2015, 137, 8034–8037 CrossRef CAS PubMed.
- M. B. Watson, N. P. Rath and L. M. Mirica, J. Am. Chem. Soc., 2017, 139, 35–38 CrossRef CAS PubMed.
- F. D'Accriscio, P. Borja, N. Saffon-Merceron, M. Fustier-Boutignon, N. Mézailles and N. Nebra, Angew. Chem., Int. Ed., 2017, 56, 12898–12902 CrossRef PubMed.
- C. J. Kulka-Peschke, A.-C. Schulz, C. Lorent, Y. Rippers, S. Wahlefeld, J. Preissler, C. Schulz, C. Wiemann, C. C. M. Bernitzky, C. Karafoulidi-Retsou, S. L. D. Wrathall, B. Procacci, H. Matsuura, G. M. Greetham, C. Teutloff, L. Lauterbach, Y. Higuchi, M. Ishii, N. T. Hunt, O. Lenz, I. Zebger and M. Horch, J. Am. Chem. Soc., 2022, 144, 17022–17032 CrossRef CAS PubMed.
- J. S. Steen, G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2019, 58, 13133–13139 CrossRef CAS PubMed.
- R. Hoffmann, S. Alvarez, C. Mealli, A. Falceto, T. J. Cahill, T. Zeng and G. Manca, Chem. Rev., 2016, 116, 8173–8192 CrossRef CAS PubMed.
- K. M. Carsch, I. M. DiMucci, D. A. Iovan, A. Li, S.-L. Zheng, C. J. Titus, S. J. Lee, K. D. Irwin, D. Nordlund, K. M. Lancaster and T. A. Betley, Science, 2019, 365, 1138–1143 CrossRef CAS PubMed.
- I. M. DiMucci, J. T. Lukens, S. Chatterjee, K. M. Carsch, C. J. Titus, S. J. Lee, D. Nordlund, T. A. Betley, S. N. MacMillan and K. M. Lancaster, J. Am. Chem. Soc., 2019, 141, 18508–18520 CrossRef CAS PubMed.
- R. C. Walroth, J. T. Lukens, S. N. MacMillan, K. D. Finkelstein and K. M. Lancaster, J. Am. Chem. Soc., 2016, 138, 1922–1931 CrossRef CAS PubMed.
- C. K. Jørgensen, Coord. Chem. Rev., 1966, 1, 164–178 CrossRef.
- J. K. Bower, A. D. Cypcar, B. Henriquez, S. C. E. Stieber and S. Zhang, J. Am. Chem. Soc., 2020, 142, 8514–8521 CrossRef CAS PubMed.
- N. P. Mankad, W. E. Antholine, R. K. Szilagyi and J. C. Peters, J. Am. Chem. Soc., 2009, 131, 3878–3880 CrossRef CAS PubMed.
- J. Shearer, D. Vasiliauskas and K. M. Lancaster, Chem. Commun., 2022, 59, 98–101 RSC.
- C. C. Roberts, N. M. Camasso, E. G. Bowes and M. S. Sanford, Angew. Chem., Int. Ed., 2019, 58, 9104–9108 CrossRef CAS PubMed.
- M. A. van Veenendaal and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 11326–11331 CrossRef CAS PubMed.
- J. Xu, M. Sun, R. Qiao, S. E. Renfrew, L. Ma, T. Wu, S. Hwang, D. Nordlund, D. Su, K. Amine, J. Lu, B. D. McCloskey, W. Yang and W. Tong, Nat. Commun., 2018, 9, 947 CrossRef PubMed.
- D.-Y. Cho, S. J. Song, U. K. Kim, K. M. Kim, H.-K. Lee and C. S. Hwang, J. Mater. Chem. C, 2013, 1, 4334–4338 RSC.
- D. Li, K. Lee, B. Y. Wang, M. Osada, S. Crossley, H. R. Lee, Y. Cui, Y. Hikita and H. Y. Hwang, Nature, 2019, 572, 624–627 CrossRef CAS PubMed.
- Y. Guo, J.-M. Langlois and W. A. Goddard, Science, 1988, 239, 896–899 CrossRef CAS PubMed.
- H. Wang, S. Friedrich, L. Li, Z. Mao, P. Ge, M. Balasubramanian and D. S. Patil, Phys. Chem. Chem. Phys., 2018, 20, 8166–8176 RSC.
- H. Wang, P. Ge, C. G. Riordan, S. Brooker, C. G. Woomer, T. Collins, C. A. Melendres, O. Graudejus, N. Bartlett and S. P. Cramer, J. Phys. Chem. B, 1998, 102, 8343–8346 CrossRef CAS.
- S. J. George, M. D. Lowery, E. I. Solomon and S. P. Cramer, J. Am. Chem. Soc., 1993, 115, 2968–2969 CrossRef CAS.
- J. H. E. Griffiths, J. Owen and B. Bleaney, Proc. R. Soc. London, Ser. A, 1997, 226, 96–111 Search PubMed.
- C. K. Jørgensen, Oxidation Numbers and Oxidation States, Springer, Berlin, Heidelberg, 1969 Search PubMed.
- F. Neese, Inorg. Chim. Acta, 2002, 337, 181–192 CrossRef.
- A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Dover, 1996 Search PubMed.
- S. N. MacMillan and K. M. Lancaster, ACS Catal., 2017, 7, 1776–1791 CrossRef CAS.
- G. C. Allen and K. D. Warren, Inorg. Chem., 1969, 8, 753–756 CrossRef CAS.
- B. L. Geoghegan, Y. Liu, S. Peredkov, S. Dechert, F. Meyer, S. DeBeer and G. E. Cutsail, J. Am. Chem. Soc., 2022, 144, 2520–2534 CrossRef CAS.
- I. F. Leach, R. W. A. Havenith and J. E. M. N. Klein, Eur. J. Inorg. Chem., 2022, e202200247 CAS.
- E. A. Trifonova, I. F. Leach, W. B. de Haas, R. W. A. Havenith, M. Tromp and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2023, 62, e202215523 CrossRef CAS PubMed.
- C. Gao, G. Macetti and J. Overgaard, Inorg. Chem., 2019, 58, 2133–2139 CrossRef CAS PubMed.
- J. P. Snyder, Angew. Chem., Int. Ed. Engl., 1995, 34, 80–81 CrossRef CAS.
- J. Cho, R. Sarangi, J. Annaraj, S. Y. Kim, M. Kubo, T. Ogura, E. I. Solomon and W. Nam, Nat. Chem., 2009, 1, 568–572 CrossRef CAS.
- T.-W. Chiou, Y.-M. Tseng, T.-T. Lu, T.-C. Weng, D. Sokaras, W.-C. Ho, T.-S. Kuo, L.-Y. Jang, J.-F. Lee and W.-F. Liaw, Chem. Sci., 2016, 7, 3640–3644 RSC.
- P. Pirovano, E. R. Farquhar, M. Swart and A. R. McDonald, J. Am. Chem. Soc., 2016, 138, 14362–14370 CrossRef CAS PubMed.
- H. Kropp, A. E. King, M. M. Khusniyarov, F. W. Heinemann, K. M. Lancaster, S. DeBeer, E. Bill and K. Meyer, J. Am. Chem. Soc., 2012, 134, 15538–15544 CrossRef CAS PubMed.
- J. F. Berry, E. Bill, E. Bothe, S. D. George, B. Mienert, F. Neese and K. Wieghardt, Science, 2006, 312, 1937–1941 CrossRef CAS PubMed.
- B. L. Henke, E. M. Gullikson and J. C. Davis, At. Data Nucl. Data Tables, 1993, 54, 181–342 CrossRef CAS.
- E. I. Solomon, B. Hedman, K. O. Hodgson, A. Dey and R. K. Szilagyi, Coord. Chem. Rev., 2005, 249, 97–129 CrossRef CAS.
- R. Sarangi, S. DeBeer George, D. J. Rudd, R. K. Szilagyi, X. Ribas, C. Rovira, M. Almeida, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2007, 129, 2316–2326 CrossRef CAS PubMed.
- D.-L. Long, Y. Cui, J.-T. Chen, W.-D. Cheng and J.-S. Huang, Polyhedron, 1998, 17, 3969–3975 CrossRef CAS.
- W. Gu, H. Wang and K. Wang, Dalton Trans., 2014, 43, 6406–6413 RSC.
- G. E. Martinez, C. Ocampo, Y. J. Park and A. R. Fout, J. Am. Chem. Soc., 2016, 138, 4290–4293 CrossRef CAS PubMed.
- V. Dimitrov and A. Linden, Angew. Chem., Int. Ed., 2003, 42, 2631–2633 CrossRef CAS PubMed.
- S. Shimada, M. L. N. Rao and M. Tanaka, Organometallics, 1999, 18, 291–293 CrossRef CAS.
- H.-F. Klein, A. Bickelhaupt, T. Jung and G. Cordier, Organometallics, 1994, 13, 2557–2559 CrossRef CAS.
- M. J. Reisfeld, L. B. Asprey and R. A. Penneman, J. Mol. Spectrosc., 1969, 29, 109–119 CrossRef CAS.
- C. K. Jørgensen, in Progress in Inorganic Chemistry, John Wiley & Sons, Ltd, 1962, pp. 73–124 Search PubMed.
- G. C. Allen, D. W. Clack and M. S. Farrimond, J. Chem. Soc. A, 1971, 2728–2733 RSC.
- S. S. Shaik and P. C. Hiberty, A Chemist's Guide to Valence Bond Theory, John Wiley & Sons, 2007 Search PubMed.
- J. H. Van Lenthe and G. G. Balint-Kurti, Chem. Phys. Lett., 1980, 76, 138–142 CrossRef CAS.
- Consideration of Ni and F centered lone pairs in the active space did not significantly change the overall weights of the HLSP state function to ΨVB. Furthermore, those Φ constructed in terms of two-center 3e− bonds resulted in high-energy configurations that did not contribute to ΨVB.
- P. C. Hiberty, J. P. Flament and E. Noizet, Chem. Phys. Lett., 1992, 189, 259–265 CrossRef CAS.
- P. C. Hiberty, S. Humbel, C. P. Byrman and J. H. van Lenthe, J. Chem. Phys., 1994, 101, 5969–5976 CrossRef CAS.
- W. Wu, P. Su, S. Shaik and P. C. Hiberty, Chem. Rev., 2011, 111, 7557–7593 CrossRef CAS PubMed.
- Atomic Spectra Database, https://www.nist.gov/pml/atomic-spectra-database, accessed March 15, 2022 Search PubMed.
- R. S. Mulliken, J. Chem. Phys., 1934, 2, 782–793 CrossRef CAS.
- Mulliken Electronegativity, https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Physical_Properties_of_Matter/Atomic_and_Molecular_Properties/Electronegativity/Mulliken_Electronegativity, accessed March 15, 2022 Search PubMed.
- N. M. Camasso and M. S. Sanford, Science, 2015, 347, 1218–1220 CrossRef CAS.
- J. R. Bour, D. M. Ferguson, E. J. McClain, J. W. Kampf and M. S. Sanford, J. Am. Chem. Soc., 2019, 141, 8914–8920 CrossRef CAS PubMed.
- P. T. Wolczanski, Organometallics, 2017, 36, 622–631 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: ORCA inputs, input coordinates for calculations, experimental and calculated Ni K-edge XAS, experimental Ni L2,3-edge XAS and desaturation, molecular orbital plots, correlation of Cu d-vacancy to 1s binding energy. See DOI: https://doi.org/10.1039/d3sc02001k |
| ‡ Current address: Department of Chemistry, Wayne State University, 5101 Cass Avenue, Detroit, MI. |
| This journal is © The Royal Society of Chemistry 2023 |