A wealth of structures for the Ge₂H₂⁺ radical cation: comparison of theory and experiment

Abstract

Five structures of Ge₂H₂ and Ge₂H₂⁺ are investigated in this study. Optimized geometries at the CCSD(T)/cc-pwCVQZ-PP level of theory were obtained. Focal point analyses were performed on these optimized geometries to determine relative energies using the CCSD(T) method with polarized basis sets up to quintuple-zeta. Energy corrections include full T and pertubative (Q) coupled-cluster effects plus anharmonic corrections to the zero-point vibrational energy. Relative ordering in energy from lowest to highest of the five Ge₂H₂⁺ structures is butterfly, germylidene, monobridged, trans, then linear. In neutral Ge₂H₂, the monobridged structure lies lower in energy than the germylidene structure. Fundamental vibrational frequencies and IR intensities were computed for the minima at the CCSD(T)/cc-pwCVTZ-PP level of theory to compare with experimental research. Partial atomic charges and natural bonding orbital analyses indicated that the positive charge of Ge₂H₂⁺ is contained in the region of the Ge–Ge bond.

---

Introduction

Germanium, as well as other group 14 elements, continues to be studied for its use in the production of high-purity nanoparticles,^1–5 nanowires,^6–8 and thin films.^9–14 Use of germanium in the electronics industry is advantageous, as it has a greater carrier mobility than commonly-used silicon.^14,15 As a result, thin-film and field-effect germanium transistors have the potential to increase performance speed while maintaining acceptable operating temperatures.^10,11,16 Further benefits include nonhazardous, electrochemically-stable biological imaging and therapeutics using germanium nanocrystals instead of the frequently used Cd, Hg, and Pb.^1,2,14

GeH₄ and Ge₂H₆ are common germanium-hydride precursors used in the production of the aforementioned nanomaterials.^{3–5,7,12,13} In 2002, Wang, Andrews, and Kushto observed the formation of GeH₄, Ge₂H₆, and Ge₂H₂ from reactions of atomic germanium and hydrogen gas.¹⁷ These germanium hydrides were isolated in argon and neon matrices and identified using IR spectroscopy. Ge₂H₂ was identified from bands at 964.3 cm⁻¹ and 972.2 cm⁻¹ in argon and neon, respectively. They proposed these bands to be the absorption of the Ge₂H₂ global minimum, butterfly geometry. Gas-phase formation of another Ge₂H₂ structure, the atypical monobridged geometry, was observed by Kaiser and coworkers in 2022. Time-of-flight mass spectrometry (TOF-MS) was used to determine an experimental reaction enthalpy of −16 ± 4 kcal mol⁻¹ for the formation of the monobridged Ge₂H₂ structure from atomic germanium and GeH₄ (eqn (1)). Computationally, Kaiser and coworkers determined this reaction enthalpy to be −15 kcal mol⁻¹. Harmonic CCSD/cc-pVTZ ZPVE corrected CCSD(T)/CBS//CCSD/cc-pVTZ relative energies for the neutral Ge₂H₂ species were computed by Kaiser and coworkers, which were butterfly, monobridged (8.4 kcal mol⁻¹), germylidene (10.5), and trans (15.8).¹⁸

Ge + GeH₄ → Ge₂H₂ + H₂ (1)

Si₂H₂ was the first molecule of interest in the group 14 M₂H₂ acetylene analogues with theoretical studies dating back to 1972.¹⁹ In 1983, Lischka and Kohler were the first to correctly propose the Si₂H₂ global minimum to be the butterfly geometry, also identifying the disilavinylidene geometry to be a local minimum.²⁰ Surprisingly, another Si₂H₂ stationary point was found to have an unusual, low-lying, monobridged equilibrium geometry in 1990 by Colgrove and Schaefer.²¹ 1990 was also the year of the first theoretical study of Ge₂H₂ by Grev and Schaefer, though it was absent of a monobridged equilibrium geometry. Stationary points of Ge₂H₂ predicted in 1990 included the germylidene, butterfly, planar dibridged, linear, and trans structures. The planar dibridged and linear structures were found to be transition states and the butterfly, germylidene, and trans structures were identified as minima. Using the most accurate yet computationally feasible ab initio methods at the time, they predicted the relative energies of these structures to be butterfly, germylidene (9.5 kcal mol⁻¹), planar dibridged (11.0), trans (17.7), and linear (45.8). Stationary point geometries were optimized by Grev at the Hartree–Fock level of theory using basis set “B1” with the contraction scheme Ge(13s9p6d/7s5p4d), H(4s/2s); relative energies were computed at the CISD+Q level of theory with basis set “B1” augmented with f-type polarization functions on germanium.²²

In 1993, Pálagyi and Schaefer were the first to predict a monobridged local minimum for Ge₂H₂.²³ In that paper, they provided geometries, energies, and vibrational frequencies for the butterfly, monobridged, and germylidene structures. Due to computational limitations of the time, there was disagreement between theory and the subsequent matrix isolation experiments of Wang, Andrews, and Kushto in 2002; the b₂ Ge–H stretching mode of the butterfly structure was computed to have a frequency of 1056 cm⁻¹ compared to the experimental value of 972.2 cm⁻¹. Vibrational frequencies for the three structures were evaluated at the CCSD/DZP level of theory. Although the the energy of the monobridged structure computed by Pálagyi cannot be compared to the enthalpy of formation in the gas phase experiment observed by Kaiser and coworkers, the respective 8.9 and 8.4 kcal mol⁻¹ relative computational energies compare well. Energetics were evaluated by Pálagyi at the CCSD(T) level of theory with a TZP basis set and corrected with harmonic ZPVEs. While the germylidene structure of Ge₂H₂ has yet to be observed experimentally, there are similar relative energy predictions of 11.0 kcal mol⁻¹ by Pálagyi and 10.5 kcal mol⁻¹ by Kaiser and coworkers.^18,23

Methods

Our work involving Ge₂H₂ and Ge₂H₂⁺ examines five of the previously presented structures of Ge₂H₂: butterfly, monobridged, germylidene, trans, and linear.^22–25 Each structure considered here was investigated using high-level ab initio quantum chemical methods. The correlation consistent small core pseudopotential-containing basis set family cc-pwCVXZ-PP (X = D,T,Q,5)^26–30 was used to account for relativistic effects on the core electrons of the germanium atoms.³¹ Ten of the 32 electrons in germanium were contained in the pseudopotential, having the noble gas configuration of neon (1s² 2s² 2p⁶). Hydrogen was assigned the basis set family of cc-pVXZ.³²

A restricted open shell Hartree–Fock (ROHF) reference wavefunction was used for calculations involving the cationic species and restricted Hartree–Fock (RHF) was used for the neutral species. Geometries were optimized at the coupled cluster singles, doubles, and perturbative triple excitations [CCSD(T)]³³ level of theory with the respective quadruple-zeta (QZ) polarized basis sets on hydrogen and germanium. Fundamental vibrational frequencies were computed at the CCSD(T)/TZ level of theory. Single point energies were computed at Hartree–Fock (HF), Møller–Plesset second-order perturbation theory (MP2), coupled cluster singles and doubles (CCSD), and CCSD(T), with double, triple, quadruple, and quintuple-zeta polarized basis sets. Focal point analysis^34–37 was used to extrapolate these energies to the CBS limit using a three-point fitting equation for HF (eqn (2)) and a two-point fitting equation for correlated levels of theory (eqn (3)).

E_HF = A + Be^−cx (2)

E_corr = A + BX⁻³ (3)

Energy corrections incorporated coupled cluster singles, doubles, and triple excitations (CCSDT)³⁸ and coupled cluster singles, doubles, triples, and perturbative quadruple excitations (CCSDT(Q)),³⁹ both with double-zeta polarized basis sets. In addition, CCSD(T)/TZ harmonic ZPVEs with VPT2 anharmonic corrections at the same level of theory were used to obtain the final energies of the minimum structures. All computations done on Ge₂H₂⁺ were replicated for its neutral counterpart, Ge₂H₂.

CFOUR 2.0⁴⁰ was used for the aforementioned computations. Natural bond order (NBO) analyses were performed using NBO 7.0⁴¹ to determine natural bonding orders and partial charges. The NBO results were computed using the HF/def2-TZVP method and the CCSD(T)/QZ optimized structures.⁴²

Results and discussion

Geometries

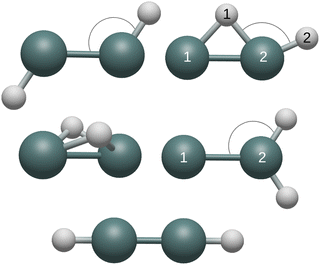
CCSD(T)/QZ optimized geometries of five Ge₂H₂ and Ge₂H₂⁺ structures are presented in Table 1. The butterfly (C_2v), monobridged (C_s), germylidene (C_2v), and trans (C_2h) structures were found to be minima while the linear (D_∞h) structure was determined to be a second-order transition state (Fig. 1). Classification of these five stationary points is in agreement with previous theoretical work on Ge₂H₂.^22,23 Furthermore, the same minima were identified by Schueller and coworkers for the isovalent Si₂H₂⁺. They found the Si–Si bond distances to be larger in Si₂H₂⁺ compared to neutral Si₂H₂.⁴³ Similarly, this trend is also seen here in Ge₂H₂⁺, as all Ge–Ge bond distances are larger than in neutral Ge₂H₂.

Table 1 Optimized geometries at the CCSD(T)/cc-pwCVQZ-PP level of theory for five structures of the neutral and cationic Ge₂H₂ species are presented. Bond lengths are reported in Ångstroms and angles in degrees

Geometry	Internal coordinate	Cation	Neutral
Butterfly	Ge–Ge	2.437	2.346
	Ge–H	1.764	1.750
	τ(H–Ge–Ge–H)	108.5	105.0
Monobridged	Ge–Ge	2.326	2.216
	Ge(1)–H(1)	1.812	1.791
	Ge(2)–H(1)	1.747	1.712
	Ge(2)–H(2)	1.528	1.529
	H–Ge–H	105.3	105.8
Germylidene	Ge–Ge	2.417	2.280
	Ge–H	1.516	1.521
	Ge–Ge–H	123.2	124.7
trans	Ge–Ge	2.302	2.186
	Ge–H	1.535	1.533
	Ge–Ge–H	122.5	124.2
Linear	Ge–Ge	2.092	2.037
	Ge–H	1.490	1.480

---

Fig. 1 From left to right and top to bottom, the five Ge₂H₂ structures of interest are shown: trans, monobridged, butterfly, germylidene, and linear. Structures containing non-equivalent atoms and bonds are henceforth referenced with the numbers in the figure. (ex: the terminal Ge–H bond of the monobridged structure would be Ge₍₂₎–H₍₂₎).

As a triply-bonded structure, linear Ge₂H₂ and Ge₂H₂⁺ have the shortest Ge–Ge and Ge–H bonds. Consequently, the linear Ge₂H₂⁺ had the smallest increase in Ge–Ge bond length from its neutral counterpart at 0.055 Å. Bridged hydrogens appear to hamper the increase of the Ge–Ge bond lengths when comparing the cationic and the neutral species. Therefore, the butterfly and monobridged structures exhibit limited increases in Ge–Ge bond lengths from the neutral to cationic structures at 0.091 and 0.110 Å, respectively. Containing a single bridged hydrogen compared to the doubly-bridged butterfly structure, the monobridged structure has a modestly larger increase than the butterfly structure of 0.110 Å from the neutral to cationic structure. Containing no bridged hydrogen, the trans and germylidene structures have the greatest increase in Ge–Ge bond distance between the neutral and cationic structures. Having the weaker Ge–Ge bond of the two, the germylidene structure also has a larger increase in Ge–Ge bond length than the trans structure at 0.137 Å compared to 0.116 Å.

Changes in Ge–H bond lengths between the cation and the neutral structures were modest. An observed trend was the increase in Ge–H distances from the neutral to cationic species, with exceptions in the Ge₍₂₎–H₍₂₎ bond of the monobridged structure and the Ge–H bonds of the germylidene structure. Likewise, changes in the angles between the germanium and hydrogen atoms were also quite small when comparing the cation and neutral structures. Nonetheless, the most significant change was in the butterfly τ (H–Ge–Ge–H) angle, which increased from 105.0 in the neutral structure to 108.5 in the cation.

Energetics

Focal point analysis with harmonic ZPVE and aZPVE corrections for the neutral Ge₂H₂ species is shown in Table 2 and for the cationic species in Table 3. CCSD(T)/cc-pwCV5Z-PP single point energies were extrapolated to the CBS limit with CCSDT and CCSDT(Q) corrections. Tables 4–7 contain the incremented focal point energies for each structure, relative to its respective cationic or neutral butterfly structure, considered in this study.

Table 2 CCSD(T)/CBS energies with CCSD(T)/cc-pwCVTZ-PP harmonic ZPVE and anharmonic corrections computed for the neutral Ge₂H₂ species in kcal mol⁻¹. See text for higher-level theoretical corrections

Structure	CCSD(T)/CBS	δZPVE	δaZPVE	Total energy
Monobridged	10.44	−0.80	0.03	9.67
Germylidene	13.77	−0.32	0.02	13.47
trans	20.23	−0.93	0.14	19.44
Linear	49.70	—	—	49.70

---

Table 3 CCSD(T)/CBS energies with CCSD(T)/cc-pwCVTZ-PP harmonic ZPVE and anharmonic corrections computed for the cationic Ge₂H₂⁺ species in kcal mol⁻¹. See text for higher-level theoretical corrections

Structure	CCSD(T)/CBS	δZPVE	δaZPVE	Total energy
Germylidene	9.78	0.04	0.01	9.83
Monobridged	10.77	−0.93	0.03	9.87
trans	20.73	−0.98	−0.07	19.68
Linear	56.31	—	—	56.31

---

Table 4 Incremented focal point energies in kcal mol⁻¹ for the cationic and neutral monobridged structures

Monobridged	HF	+δ MP2	+δ CCSD	+δ CCSD(T)	+δ CCSDT	+δ CCSDT(Q)	Net
Cation
cc-pwCVDZ-PP	+8.54	+2.90	+0.26	−0.39	−0.03	−0.05	[+11.23]
cc-pwCVTZ-PP	+8.74	+2.91	−0.32	−0.27	[−0.03]	[−0.05]	[+10.98]
cc-pwCVQZ-PP	+8.73	+2.82	−0.36	−0.26	[−0.03]	[−0.05]	[+10.85]
cc-pwCV5Z-PP	+8.74	+2.74	−0.32	−0.25	[−0.03]	[−0.05]	[+10.82]
CBS limit	[+8.74]	[+2.66]	[−0.29]	[−0.25]	[−0.03]	[−0.05]	[+10.77]
Neutral
cc-pwCVDZ-PP	+14.70	−4.49	+1.84	−1.51	+0.10	−0.14	[+10.50]
cc-pwCVTZ-PP	+14.58	−4.30	+1.67	−1.52	[+0.10]	[−0.14]	[+10.40]
cc-pwCVQZ-PP	+14.57	−4.29	+1.72	−1.55	[+0.10]	[−0.14]	[+10.41]
cc-pwCV5Z-PP	+14.61	−4.33	+1.77	−1.56	[+0.10]	[−0.14]	[+10.44]
CBS limit	[+14.61]	[−4.37]	[+1.81]	[−1.57]	[+0.10]	[−0.14]	[+10.44]

---

Table 5 Incremented focal point energies in kcal mol⁻¹ for the cationic and neutral germylidene structures

Germylidene	HF	+δ MP2	+δ CCSD	+δ CCSD(T)	+δ CCSDT	+δ CCSDT(Q)	Net
Cation
cc-pwCVDZ-PP	+4.45	+14.25	−2.54	+1.55	−0.05	−0.00	[+9.26]
cc-pwCVTZ-PP	−3.81	+15.60	−3.98	+2.02	[−0.05]	[−0.00]	[+9.78]
cc-pwCVQZ-PP	−3.82	+15.62	−4.15	+2.14	[−0.05]	[−0.00]	[+9.74]
cc-pwCV5Z-PP	−3.81	+15.58	−4.14	+2.18	[−0.05]	[−0.00]	[+9.76]
CBS limit	[−3.81]	[+15.54]	[−4.12]	[+2.22]	[−0.05]	[−0.00]	[+9.78]
Neutral
cc-pwCVDZ-PP	+6.70	+9.04	−3.31	+0.27	−0.12	−0.08	[+12.50]
cc-pwCVTZ-PP	+6.92	+10.50	−4.40	+0.67	[−0.12]	[−0.08]	[+13.49]
cc-pwCVQZ-PP	+6.88	+10.66	−4.50	+0.76	[−0.12]	[−0.08]	[+13.61]
cc-pwCV5Z-PP	+6.90	+10.68	−4.47	+0.78	[−0.12]	[−0.08]	[+13.70]
CBS limit	[+6.91]	[+10.69]	[−4.44]	[+0.80]	[−0.12]	[−0.08]	[+13.77]

---

Table 6 Incremented focal point energies in kcal mol⁻¹ for the cationic and neutral trans structures

trans	HF	+δ MP2	+δ CCSD	+δ CCSD(T)	+δ CCSDT	+δ CCSDT(Q)	Net
Cation
cc-pwCVDZ-PP	+18.47	+3.78	−0.35	−1.15	−0.17	−0.13	[+20.46]
cc-pwCVTZ-PP	+19.06	+4.22	−1.29	−0.94	[−0.17]	[−0.13]	[+20.76]
cc-pwCVQZ-PP	+19.02	+4.21	−1.31	−0.92	[−0.17]	[−0.13]	[+20.71]
cc-pwCV5Z-PP	+19.03	+4.16	−1.25	−0.92	[−0.17]	[−0.13]	[+20.72]
CBS limit	[+19.03]	[+4.11]	[−1.20]	[−0.92]	[−0.17]	[−0.13]	[+20.73]
Neutral
cc-pwCVDZ-PP	+26.11	−5.86	+1.96	−2.66	+0.02	−0.30	[+19.28]
cc-pwCVTZ-PP	+26.22	−5.02	+1.51	−2.50	[+0.02]	[−0.30]	[+19.94]
cc-pwCVQZ-PP	+26.24	−4.95	+1.59	−2.53	[+0.02]	[−0.30]	[+20.07]
cc-pwCV5Z-PP	+26.28	−4.95	+1.65	−2.55	[+0.02]	[−0.30]	[+20.16]
CBS limit	[+26.30]	[−4.95]	[+1.72]	[−2.56]	[+0.02]	[−0.30]	[+20.23]

---

Table 7 Incremented focal point energies in kcal mol⁻¹ for the cationic and neutral linear structures

Linear	HF	+δ MP2	+δ CCSD	+δ CCSD(T)	+δ CCSDT	+δ CCSDT(Q)	Net
Cation
cc-pwCVDZ-PP	+55.69	+5.24	+0.77	−1.15	+0.13	−0.24	[+60.45]
cc-pwCVTZ-PP	+55.09	+4.49	−0.75	−1.04	[+0.13]	[−0.24]	[+57.68]
cc-pwCVQZ-PP	+54.94	+3.98	−0.89	−1.02	[+0.13]	[−0.24]	[+56.89]
cc-pwCV5Z-PP	+54.92	+3.60	−0.81	−1.01	[+0.13]	[−0.24]	[+56.60]
CBS limit	[+54.92]	[+3.21]	[−0.72]	[−1.01]	[+0.13]	[−0.24]	[+56.31]
Neutral
cc-pwCVDZ-PP	+55.85	−3.83	+3.07	−2.38	+0.22	−0.31	[+52.62]
cc-pwCVTZ-PP	+54.89	−4.09	+2.22	−2.38	[+0.22]	[−0.31]	[+50.55]
cc-pwCVQZ-PP	+54.90	−4.41	+2.16	−2.42	[+0.22]	[−0.31]	[+50.15]
cc-pwCV5Z-PP	+54.94	−4.72	+2.23	−2.42	[+0.22]	[−0.31]	[+49.94]
CBS limit	[+54.95]	[−5.04]	[+2.31]	[−2.43]	[+0.22]	[−0.31]	[+49.70]

---

As seen in previous theoretical work on Si₂H₂,^20,21 Si₂H₂⁺,⁴³ and Ge₂H₂,^22,23 the butterfly structure is likewise the Ge₂H₂⁺ global minimum geometry. Unlike the neutral Ge₂H₂ species, the Ge₂H₂⁺ germylidene structure lies very slightly lower in energy than the monobridged structure. This is also seen in Si₂H₂⁺ compared to neutral Si₂H₂. In Si₂H₂⁺, the relative energy of the vinylidene-like structure is 6.61 kcal mol⁻¹ and the monobridged structure is 10.31 kcal mol⁻¹.⁴³ The germylidene and monobridged structures have respective relative energies of 9.83 and 9.87 kcal mol⁻¹ for Ge₂H₂⁺, while the neutral Ge₂H₂ germylidene and monobridged structures have respective relative energies of 13.47 and 9.67 kcal mol⁻¹. An enthalpy of formation for the monobridged structure was determined by Kaiser and coworkers using TOF-MS. However, because they did not also measure the butterfly structure, the relative energy of the monobridged structure cannot be obtained. Nonetheless, a relative energy of 8.4 kcal mol⁻¹ was predicted by Kaiser and coworkers at the CCSD(T)/CBS//CCSD/cc-pVTZ level of theory. The geometry obtained by Kaiser and coworkers has little deviation from our work, therefore, the disagreement is ascribed to our higher-order corrections and pseudopotential-containing basis set family. We include quintuple-zeta polarized basis functions in our extrapolation to the CBS limit along with full T, perturbative Q, and anharmonic corrections to the ZPVE whereas Kaiser and coworkers do not. Considering these additional corrections, located in Tables 2 and 4, have little effect on the total energy, the difference in energy between our work and the work of Kaiser and coworkers should be attributed to the difference in basis set family.

As noted in the 1993 Ge₂H₂ study by Pálagyi and Schaefer, the monobridged structure is favored by correlation effects whereas the germylidene structure is disfavored.²³ Our work is in agreement with their previous observations, and it can be seen in Table 4 for the monobridged structure and in Table 5 for the germylidene structure. Both the monobridged and germylidene structures of Ge₂H₂⁺ are disfavored by correlation effects, although the monobridged structure less so. The Ge₂H₂⁺δMP2 energies at the CBS limit for the monobridged and germylidene isomers are +2.66 and +15.54 kcal mol⁻¹, respectively. However, considering the CCSDT(Q) energy correction is 0.00 kcal mol⁻¹ for the germylidene structure and −0.05 kcal mol⁻¹ for the monobridged structure, it is unlikely that higher levels of correlation beyond the scope of this study would continue to affect the energies of the monobridged and germylidene structures of Ge₂H₂⁺.

Highest in relative energy of the minimum stationary points studied, the trans structure has respective relative energies of 20.23 and 20.73 kcal mol⁻¹ for the neutral and cationic species. Similar to the monobridged structure, the neutral trans structure is favored by correlation effects and the cationic structure is disfavored. This can be seen in the δMP2 contribution, which is −4.95 kcal mol⁻¹ for the neutral structure but +4.11 kcal mol⁻¹ in the cationic structure at the CBS limit. In addition, the neutral trans structure has the largest energetic contribution due to including perturbative triple excitations in CCSD(T), which is −2.56 kcal mol⁻¹ at the CBS limit. In the cationic trans structure, the CCSD(T) contribution is a more modest −0.92 kcal mol⁻¹. The incremented focal point energies for the trans structures are contained in Table 6.

Although the acetylene linear structure is the commonly known C₂H₂ minimum geometry, it is a transition state in Si₂H₂, Ge₂H₂, and their cations. Not appearing to be influenced much by correlation effects until higher levels of electronic excitation, the linear Ge₂H₂ structures have the largest CCSDT(Q) correction in this study at −0.24 and −0.31 for the respective cationic and neutral structures. However, when considering the magnitude of the relative energies of these Ge₂H₂ linear structures, the (Q) corrections are not so important. Table 7 contains the incremented focal point energies for the linear structures in kcal mol⁻¹.

Vibrational frequencies

Fundamental vibrational frequencies computed at the CCSD(T)/cc-pwCVTZ-PP level of theory for the neutral Ge₂H₂ minimum species are presented in Table 8 and for the cationic species in Table 9. Harmonic vibrational frequencies and vibration–rotation constants are located in the ESI.† As a second order transition state with a doubly degenerate π_g bend, anharmonic treatment of the linear structure was not performed. Containing the largest IR intensity vibrational mode, the butterfly structure has been previously observed via matrix isolation in neon and argon by Wang, Andrews, and Kushto in 2002.¹⁷ Wang, Andrews, and Kushto identified the b₂ absorption band of the butterfly structure, having a frequency of 972.3 cm⁻¹ in neon and 964.3 cm⁻¹ in argon, by comparing their results to the previous theoretical study by Pálagyi and Schaefer in 1993.²³ Herein, we present the most accurate theoretical prediction to date, calculating the b₂ absorption band to have a frequency of 991 cm⁻¹. Having by far the largest IR intensity in the neutral and cationic species at 352 and 457 km mol⁻¹, respectively, this band corresponds to the conjoined Ge–H stretch of the hydrogen atoms parallel to the Ge–Ge bond. As the nuclei are displaced along this vibrational mode, their positions begin to resemble that of the germylidene structure. Given that the dipole moments of the butterfly and germylidene structures are perpendicular to one another, the b₂ vibrational mode of the butterfly structure constitutes a significant change in the dipole moment, resulting in a large IR intensity. Also identified in the 2002 paper by Wang, Andrews, and Kushto was the b₁ band, at a frequency of 1352.3 cm⁻¹.¹⁷ Our computations predict this band to be at 1362 cm⁻¹ and it corresponds to the non-conjoined Ge–H stretch perpendicular to the Ge–Ge bond.

Table 8 CCSD(T)/cc-pwCVTZ-PP fundamental vibrational frequencies in cm⁻¹ and IR intensities in km mol⁻¹ are reported for the neutral minimum structures

Butterfly	Monobridged	Germylidene	trans
a Member of Fermi dyad: other transition at 383 cm^−1. b Member of Fermi dyad: other transition at 1370 cm^−1.
C 2v	C s	C 2v	C 2h
284 (<1, a1)	185 (34, a′′)	208 (19, b2)	220 (0, bu)
790 (31, a1)	307^a (5, a′)	292 (5, b1)	243 (0, ag)
899 (0, a2)	479 (3, a′)	305 (6, a1)	393 (<1, au)
991 (352, b2)	916 (112, a′)	822 (63, a1)	576 (0, ag)
1362 (32, b1)	1494^b (75, a′)	2036 (74, a1)	1975 (0, ag)
1427 (8, a1)	1986 (120, a′)	2060 (82, b2)	1988 (176, bu)

---

Table 9 CCSD(T)/cc-pwCVTZ-PP fundamental vibrational frequencies in cm⁻¹ and IR intensities in km mol⁻¹ are reported for the cationic minimum structures

Butterfly	Monobridged	Germylidene	trans
a Member of Fermi dyad: other transition at 949 cm^−1.
C 2v	C s	C 2v	C 2h
189 (<1, a1)	166 (5, a′′)	253 (2, a1)	78 (12, au)
759 (18, a1)	256 (8, a′)	260 (7, b2)	125 (39, bu)
922 (0, a2)	474 (4, a′)	376 (<1, b1)	252 (0, ag)
1039 (457, b2)	834^a (126, a′)	835 (38, a1)	588 (0, ag)
1340 (31, b1)	1429 (38, a′)	2074 (2, a1)	1989 (0, ag)
1434 (2, a1)	2011 (3, a′)	2111 (9, b2)	2000 (11, bu)

---

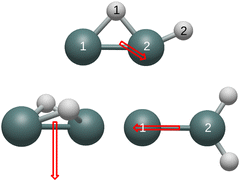
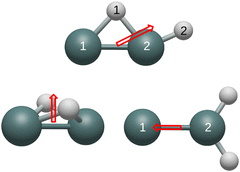
All of the remaining unidentified Ge₂H₂ and Ge₂H₂⁺ structures contain detectable vibrational modes in the IR region. The respective 916 and 840 cm⁻¹ a′ modes of the neutral and cationic monobridged structure have intensities of 112 and 126 km mol⁻¹, which correspond to the Ge–H stretch of the bridged hydrogen between the two germanium atoms. Although the cationic butterfly structure also contains a mode at 916 cm⁻¹, this non-conjoined Ge–H stretching mode has no effect on the dipole and is therefore undetectable in the IR region. The 2036 cm⁻¹ symmetric and 2060 cm⁻¹ asymmetric Ge–H stretches have the greatest IR intensities in the neutral germylidene structure at respective values of 74 and 82 km mol⁻¹, but the intensities of these two modes decrease dramatically in the cationic structure to 2 and 9 km mol⁻¹. Both the neutral and cationic germylidene structures have measureable a₁ Ge–H in-plane wagging modes, respectively at 822 and 835 cm⁻¹ with intensities of 63 and 38 km mol⁻¹. Measuring the neutral trans structure in the IR region is more likely than the cationic trans structure due to the 1988 cm⁻¹ b_u Ge–H stretching mode with an intensity of 176 km mol⁻¹. This mode shifts to 2000 cm⁻¹ and decreases to an intensity of 11 km mol⁻¹ in the cationic trans structure. However, the 125 cm⁻¹ b_u in-plane wagging mode has a substantial intensity of 39 km mol⁻¹ in the cationic trans structure, whereas this vibrational mode has a near-zero IR intensity in the neutral trans structure. Table 10 reports, in Debye, vibrationally averaged zero-point dipole moments originating from the center of mass. Fig. 2 depicts the dipole moments of the neutral structures and Fig. 3 the dipole moments of the cationic structures. The dipole moment of the trans and linear structures are necessarily zero.

Table 10 Vibrationally averaged zero-point dipole moments originating from the center of mass are given in Debye

Geometry	Cation	Neutral
Butterfly	0.20	0.70
Monobridged	0.43	0.29
Germylidene	0.21	0.51

---

Fig. 2 Dipole moments originating from the center of mass of the neutral structures are displayed.

Fig. 3 Dipole moments originating from the center of mass of the cationic structures are displayed.

Similar to carbon dioxide, in which the dipole moment points to carbon, the dipole moment of the neutral and cationic germylidene species point toward the less electronegative germanium atoms. However, the combination of a Ge–Ge double bond and a lone pair on Ge₍₁₎ supplements the direction of the dipole moment in the germylidene structure. Likewise, the dipole moment of the neutral butterfly structure points in the direction of the Ge–Ge bond. Containing a lone pair on both germanium atoms, the neutral butterfly structure also contains sufficient electron density within and around the Ge–Ge bond for the dipole moment to point to the less electronegative germanium atoms. On the other hand, the cationic butterfly structure has a dipole moment pointing to the hydrogen atoms, opposite of the neutral butterfly structure. The singly-occupied molecular orbital (SOMO) of the butterfly structure is the sole Ge–Ge bond; having one less electron in this molecular orbital is enough to flip the direction of the dipole moment from germanium to hydrogen. With both a Ge–Ge double bond and a lone pair on Ge₍₁₎, it is unclear why the dipole moment of the neutral monobridged structure points in the direction of Ge₍₂₎. As also seen in the butterfly structure, the dipole moment of the cationic monobridged structure changes direction from germanium to hydrogen in its neutral counterpart.

Natural bonding orbital analysis

Natural bond orders are reported in Table 11 and partial charges in Table 12. The electron removed from neutral Ge₂H₂ is primarily a Ge–Ge bonding electron as suggested by the decrease in bond order and the distribution of positive charge. Already containing a partial positive charge in the neutral species, the germanium atoms unsurprisingly gain more positive charge in the cationic species. Also considering the size, ionization potential, and electronegativity of the germanium and hydrogen atoms, chemical intuition would also suggest this location.⁴⁴

Table 11 HF/def2-TZVP natural bond orders computed at CCSD(T)/cc-pwCVQZ-PP optimized geometries

Geometry	Bond	Cation	Neutral
Butterfly	Ge–Ge	0.79	1.31
	Ge–H	0.43	0.42
Monobridged	Ge–Ge	1.59	2.23
	Ge(1)–H(1)	0.37	0.36
	Ge(2)–H(1)	0.49	0.48
	Ge(2)–H(2)	0.91	0.90
Germylidene	Ge–Ge	1.48	1.99
	Ge–H	0.95	0.96
trans	Ge–Ge	2.01	2.60
	Ge–H	0.76	0.80
Linear	Ge–Ge	2.40	2.97
	Ge–H	0.95	0.95

---

Table 12 HF/def2-TZVP partial charges computed at CCSD(T)/cc-pwCVQZ-PP optimized geometries

Geometry	Atom	Cation	Neutral
Butterfly	Ge	+0.83	+0.27
	H	−0.33	−0.27
Monobridged	Ge(1)	+0.79	+0.22
	Ge(2)	+0.61	+0.11
	H(1)	−0.11	−0.14
	H(2)	−0.28	−0.19
Germylidene	Ge(1)	+0.70	+0.24
	Ge(2)	+0.57	+0.07
	H	−0.13	−0.15
trans	Ge	+0.67	+0.18
	H	−0.17	−0.18
Linear	Ge	+0.52	+0.07
	H	−0.02	−0.07

---

Ge–H bond orders have small changes between the cationic and neutral structures. If the positive charge of Ge₂H₂⁺ is located completely within Ge–Ge bonding orbitals, a decrease of a half of a bond order could be expected for the Ge–Ge bond. Slightly larger decreases than half of a bond order are seen in these five structures when comparing the cationic to the neutral species.

Structures containing the most Ge–H bonds might be assumed to have the weakest Ge–Ge bond order. However, this is not the case when considering the lower Ge–Ge bond order in the germylidene structure compared to the monobridged structure. Summing the Ge–H bond orders in the germylidene and monobridged structures, respectively 1.92 and 1.74 in the cations and 1.90 and 1.77 in the neutral structures, illustrates why the additional Ge–H bond in the monobridged structure does not necessitate the Ge–Ge bond to be weaker than that of the germylidene structure. Due to the asymmetric distribution of Ge–H bonds in the germylidene and monobridged structures, the positive charge is not equally shared between the two germanium atoms. In both cases, the germanium with fewer bonds to hydrogen has the lower partial positive charge.

Because the hydrogens are symmetrically bound about the germanium atoms of the butterfly, trans, and linear structures, the respective germanium atoms of these structures contain equal partial positive charges. Having the most Ge–H bonds (four) of the five structures considered, the butterfly structure also has the lowest Ge–Ge bond order in both the cationic and neutral species. The bond order of the bridged hydrogen atoms in the butterfly structure lies directly in between the Ge₍₁₎–H₍₁₎ and Ge₍₂₎–H₍₁₎ bond orders of the bridged hydrogen in the monobridged structure for both the cationic and neutral species. Similar to the butterfly structure, the trans and linear structures equally share the partial positive charge between the two germanium atoms and exhibit respective decreases of 0.59 and 0.57 in Ge–Ge NBO from the neutral to cationic structures.

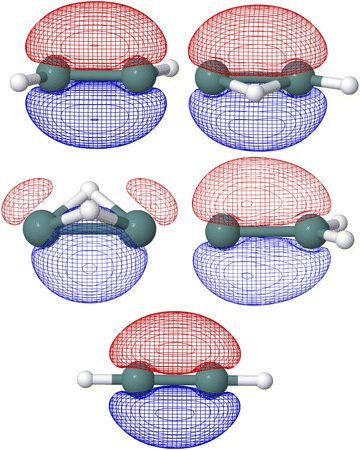
In the five Ge₂H₂ structures considered, the highest occupied molecular orbital (HOMO) in the neutral species is the SOMO of the respective cationic species. As seen in Fig. 4, the SOMOs of the trans (C_2h; ²A_u), monobridged (C_s; ²A′′), germylidene (C_2v; ²B₂), and linear (D_∞h; ²Π_u) structures have almost entirely p-character. The butterfly (C_2v; ²A₁) structure is the only exception, as the SOMO has 90 percent p-character, 8 percent s-character, and 2 percent d-character. Knowing the linear structure has a triple Ge–Ge bond, first and foremost a σ-bonding molecular orbital is expected but also a degenerate π-bonding orbital to the SOMO. NBO analysis confirms this, as the HOMO of the neutral linear structure (SOMO in the cation) has a degenerate, 99 percent p-character π-bonding orbital. NBO analysis also indicates the trans structure to have three Ge–Ge bonds, with an NBO of 2.60. One could visualize the hydrogen of the trans structure sticking into where one of the degenerate Ge–Ge π-bonding orbitals of the linear structure was located, resulting in a π-like b_u orbital with 77 percent p-character and 22 percent s-character. In addition to the a′′ π-character HOMO, the monobridged structure also has a σ-like a′ Ge–Ge bonding orbital. Ge₍₁₎ contributes 29 percent of the a′ Ge–Ge bond while Ge₍₂₎ contributes 71 percent. The contribution of Ge₍₁₎ is 90 percent p-character, 9 percent s-character while the contribution of Ge₍₂₎ is 59 percent s-character, 41 percent p-character. Similarly, the germylidene structure has a σ-like Ge–Ge bonding orbital, which is of a₁ symmetry. Because Ge₍₂₎ is bound to both hydrogen atoms, it may be surprising that Ge₍₂₎ contributes 62 percent of the a₁ Ge–Ge bond. However, the lone pair orbital on Ge₍₁₎ lies only slightly higher in energy than the a₁ Ge–Ge bonding orbital, suggesting a propensity for electronic localization around Ge₍₁₎. The contribution of Ge₍₁₎ to the a₁ Ge–Ge bonding orbital of the germylidene structure is 14 percent s-character, 85 percent p-character and the contribution of Ge₍₂₎ is 42 percent s-character, 58 percent p-character. Fig. 5 shows the trans b_u, monobridged a′, and germylidene a₁ Ge–Ge bonding orbitals.

Fig. 4 HF/def2-TZVP singly-occupied molecular orbitals of the Ge₂H₂⁺ structures computed at CCSD(T)/cc-pwCVQZ-PP optimized geometries are shown. From left to right and top to bottom: trans (C_2h; ²A_u), monobridged (C_s; ²A′′), butterfly (C_2v; ²A₁), germylidene (C_2v; ²B₂), and linear (D_∞h; ²Π_u).

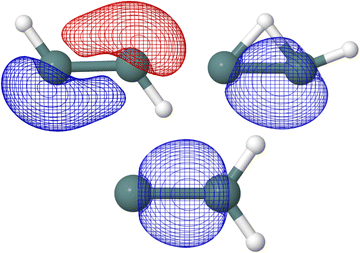Fig. 5 Trans b_u, monobridged a′, and germylidene a₁ Ge–Ge bonding orbitals computed at HF/def2-TZVP are shown.

Conclusions

Using state-of-the-art ab initio methods, it is determined that the relative ordering in energy for these five structures of Ge₂H₂⁺ is butterfly, germylidene, monobridged, trans, then linear. The ordering in the neutral species is different, as the monobridged structure has a significantly lower energy than that of the germylidene structure. Analysis of NBOs and partial charges revealed the positive charge is localized between the germanium atoms. As the first characterization of these five Ge₂H₂⁺ structures, this study should serve to instigate future experimental work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge support from the US Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES) Division of Chemistry, Computational Theoretical Chemistry (CTC), and Gas Phase Chemical Physics Programs under Contract No. DE-SC0018412. Gregory H. Robinson acknowledges National Science Foundation (NSF) Grant CHE-2153987. Yohannes Abate acknowledges the NSF Grant No. 2152159 (NRT-QuaNTRASE).

References

1. D. D. Vaughn II and R. E. Schaak, Chem. Soc. Rev., 2013, 42, 2861–2879.
2. J. Fan and P. K. Chu, Small, 2010, 6, 2080–2098.
3. S. Mezhenny, I. Lyubinetsky, J. Levy and J. T. Yates, J. Vac. Sci. Technol., B, 2001, 19, 567–568.
4. S. Kim, B. Walker, S. Y. Park, H. Choi, S.-J. Ko, J. Jeong, M. H. Yun, J. C. Lee, D. S. Kim and J. Y. Kim, Nanoscale, 2014, 6, 10156–10160.
5. T.-H. Kim, H.-K. Song and S. Kim, Nanotechnology, 2019, 30, 275603.
6. D. Wang, Y.-L. Chang, Q. Wang, J. Cao, D. B. Farmer, R. G. Gordon and H. Dai, J. Am. Chem. Soc., 2004, 126, 11602–11611 , PMID: 15366907.
7. G. D. Martino, F. B. Michaelis, A. R. Salmon, S. Hofmann and J. J. Baumberg, Nano Lett., 2015, 15, 7452–7457 , PMID: 26501872.
8. C. Kim, G. Song, L. Luo, J. Y. Cheong, S.-H. Cho, D. Kwon, S. Choi, J.-W. Jung, C.-M. Wang, I.-D. Kim and S. Park, ACS Nano, 2018, 12, 8169–8176 , PMID: 30056695.
9. K. Toko, I. Nakao, T. Sadoh, T. Noguchi and M. Miyao, Solid-State Electron., 2009, 53, 1159–1164.
10. C.-Y. Liao, S.-H. Chen, W.-H. Huang, C.-H. Shen, J.-M. Shieh and H.-C. Cheng, IEEE Electron Device Lett., 2018, 39, 367–370.
11. P. S. Goley and M. K. Hudait, Materials, 2014, 7, 2301–2339.
12. P. Jahandar, D. Weisshaupt, G. Colston, P. Allred, J. Schulze and M. Myronov, Semicond. Sci. Technol., 2018, 33, 034003.
13. Y.-H. Kil, S.-H. Yuk, J. H. Kim, T. S. Kim, Y. T. Kim, C.-J. Choi and K.-H. Shim, Solid-State Electron., 2016, 124, 35–41.
14. D. Carolan, Prog. Mater. Sci., 2017, 90, 128–158.
15. Y. Kamata, Mater. Today, 2008, 11, 30–38.
16. P. S. Chakraborty, A. S. Cardoso, B. R. Wier, A. P. Omprakash, J. D. Cressler, M. Kaynak and B. Tillack, IEEE Electron Device Lett., 2014, 35, 151–153.
17. X. Wang, L. Andrews and G. P. Kushto, J. Phys. Chem. A, 2002, 106, 5809–5816.
18. Z. Yang, B.-J. Sun, C. He, S. Fatimah, A. H. H. Chang and R. I. Kaiser, Chem. – Eur. J., 2022, 28, e202103999.
19. B. Wirsam, Theor. Chim. Acta, 1972, 25, 169–180.
20. H. Lischka and H. J. Koehler, J. Am. Chem. Soc., 1983, 105, 6646–6649.
21. B. T. Colegrove and H. F. I. Schaefer, J. Phys. Chem., 1990, 94, 5593–5602.
22. R. S. Grev, B. J. Deleeuw and H. F. Schaefer, Chem. Phys. Lett., 1990, 165, 257–264.
23. Z. Palagyi, H. F. I. Schaefer and E. Kapuy, J. Am. Chem. Soc., 1993, 115, 6901–6903.
24. M. Lein, A. Krapp and G. Frenking, J. Am. Chem. Soc., 2005, 127, 6290–6299 , PMID: 15853336.
25. S. Nagase, K. Kobayashi and N. Takagi, J. Organomet. Chem., 2000, 611, 264–271.
26. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibsom and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820.
27. D. Feller, J. Comput. Chem., 1996, 17, 1571–1586.
28. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
29. K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112.
30. K. A. Peterson and K. E. Yousaf, J. Chem. Phys., 2010, 133, 174116.
31. P. Pyykko, Chem. Rev., 1988, 88, 563–594.
32. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
33. J. F. Stanton, Chem. Phys. Lett., 1997, 281, 130–134.
34. A. G. Császár, W. D. Allen, I. Schaefer and F. Henry, J. Chem. Phys., 1998, 108, 9751–9764.
35. M. S. Schuurman, S. R. Muir, W. D. Allen, I. Schaefer and F. Henry, J. Chem. Phys., 2004, 120, 11586–11599.
36. D. Feller, J. Chem. Phys., 1993, 98, 7059–7071.
37. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646.
38. J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041–7050.
39. Y. J. Bomble, J. F. Stanton, M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 054101.
40. D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108.
41. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, F. NBO 7.0, 2018.
42. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
43. K. M. Schueller, H. F. Mull, J. T. Turney and H. F. Schaefer, Isr. J. Chem., 2023, e202300033.
44. D. R. Lide, Handbook of Chemistry and Physics, 1992, 10, 211.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06098e

---