Open Access Article
Open Access ArticleCO2 electroreduction on single atom catalysts: the role of the DFT functional†
Debolina
Misra
a,
Giovanni
Di Liberto
 *b and
Gianfranco
Pacchioni
*b and
Gianfranco
Pacchioni
 b
b
aDepartment of Physics, Indian Institute of Information Technology, Design and Manufacturing, Kancheepuram, Chennai 600127, India
bDipartimento di Scienza dei Materiali, Università di Milano – Bicocca, via R. Cozzi 55, Milano 20125, Italy. E-mail: giovanni.diliberto@unimib.it
First published on 8th March 2024
Abstract
One key process involving single atom catalysts (SACs) is the electroreduction of CO2 to fuels. The chemistry of SACs differs largely from that of extended catalytic surfaces, presenting an opportunity to improve the ability to activate very stable molecules, such as CO2. In this work, we performed a density functional theory (DFT) study of CO2 activation on a series of SACs, focusing on the role played by the adopted functional in activity predictions. The role of the exchange–correlation functional has been widely investigated in heterogenous catalysts, but it is less explored in SACs. We tested the widely used PBE and the PBE+U corrected functionals against the more robust hybrid PBE0 functional. The results show that PBE is reliable if one is interested in qualitative predictions, but it leads to some inaccuracies in other cases. A possible way to attenuate this effect is by adopting the PBE+U framework, as it gives results that are very similar to PBE0 at an acceptable computational cost. The results of this study further underline the importance of the computational framework adopted in predicting the activity of SACs. The work suggests that one needs to go beyond PBE for quantitative estimates, an important consideration when performing screening and high-throughput calculations.
1. Introduction
The capture of CO2 and its conversion into valuable chemicals, including fuels, is involved in key processes in the ongoing energy transition.1–4 The conversion of CO2 to fuels would create, in principle, a carbon neutral cycle that can mitigate the impact of the greenhouse effect. The main issue associated with this objective is the strong stability of CO2, which in turn makes its activation hard.5 The process can be activated by working under harsh conditions with the help of a catalyst.6–8 The process can be conducted either under thermal or electrochemical conditions, depending on the way energy is supplied.9,10Electrocatalysis offers a viable method for electroreducing CO2 under ambient conditions.11–13 A significant amount of research is dedicated to the discovery of novel catalytic materials and gaining a fundamental understanding of the physical chemistry behind this reaction. Typical catalytic materials are metal particles,14–16 based on critical and noble metals.
Single atom catalysis is a relatively new frontier with the potential to reduce the amount of metal loading in catalytic materials.17–20 A single atom catalyst (SAC) is made by depositing transition metal atoms with atomic precision on a given support. In addition, metal atom SACs exhibit a specific local coordination that strongly affects their reactivity.21–24 This characteristic makes SACs analogous to coordination chemistry compounds,25 as they can form molecular adducts that do not form on conventional extended surfaces.26–30 This includes not only unconventional reaction intermediates, but also complexes with the solvent, that can compete with the classical reaction intermediates identified on the surface of metal electrodes. If the solvent can also act as a ligand (such as water), it can play a twofold role in SACs, serving both as a solvent and as a ligand. We have recently observed this effect in CO2 electroreduction on a set of SACs supported on nitrogen-doped graphene by means of DFT calculations.31
Quantum chemical calculations provide a valuable contribution to the fundamental understanding of the chemistry of SACs.32,33 Calculations enable access to a SAC with atomistic precision, which would otherwise be difficult to achieve experimentally. It is however important to underline that quantitative predictions can only be made if the simulated model corresponds to the real one. To access this information, it is often mandatory to combine theory with spectroscopy techniques.34,35
Besides the quality of the model, the way in which the electronic structure of the system is described plays a primary role.36 The most widely used methodology for simulating a SAC is DFT, which relies heavily on the parametrization of the exchange and correlation functional. Although there is an extensive literature dedicated to the assessment of the accuracy and reliability of different functionals on extended catalytic surfaces,37–41 this aspect is less explored in SACs. The number of screening and high-throughput studies aimed at the discovery of new SACs is increasing steadily, but it largely depends on the standard parametrization of the functional known as generalized gradient approximation (GGA).33,42–52 However, it is well known that self-interaction error corrected functionals such as the DFT+U approach or hybrid functionals can provide a more accurate description of the chemistry, in particular when transition metals with open shell structures are involved.
In this work, we assessed the accuracy of different DFT functionals in simulating the CO2 electroreduction on SACs. We tested two popular choices against a reference hybrid functional: the widely adopted PBE functional (GGA),53 and the PBE+U correction54 (DFT+U) vs the PBE0 functional (hybrid).55,56 Previous studies showed that PBE0 can be considered a good benchmark in the framework of DFT.36 We investigated the role of the functional in (i) the CO2 activation process, (ii) the nature and stability of the first electrochemical intermediates, and (iii) the competing action of the solvent. CO2 activation and the first electrochemical step (addition of the first H+/e− couple) are two key processes in CO2 electroreduction. The main purpose of this work is to investigate the effect of the adopted functional on the predictions of the activation of CO2 on SACs. To address this point, we studied a specific model system, comprising a graphene nanosheet doped with nitrogen exhibiting pyridinic coordination, which is a likely active site, although it is not the only one.57 Indeed, N-doped graphene is widely adopted as a support for SACs, due to its capability to stably bind metal atoms.58,59 A distribution of different active sites can be present in real samples. There are basically three most common configurations; a nitrogen atom replacing a carbon one (graphitic defect), four nitrogen atoms having a porphyrin-like arrangement close to a carbon divacancy (pyridinic defect), and a nitrogen atom terminating 5-membered rings instead of the lattice hexagonal ones (pyrrolic defect).60,61 The catalytic activity may be affected by the local coordination. Some insight into the nature of the species can be evinced from XPS measurements.62 Also, given the complexity of catalytic pathways leading to fuel formation, in this study we do not proceed further with the reaction mechanism since we are not focused on a specific product, but rather on assessing the accuracy of the DFT functional for describing CO2 activation. The results show that the use of PBE leads to significant deviations when compared to PBE0, while the use of PBE+U strongly attenuates the discrepancy. This study suggests that despite PBE being reliable for establishing general trends, it may lead to inaccurate results when trying to be quantitative. This problem can be attenuated by adopting the PBE+U approach.
2. Computational details
The calculations have been performed at the level of density functional theory (DFT) as implemented in the Vienna Ab Initio Simulation Package (VASP).63–65 Simulations were performed including spin polarization and employing the projector-augmented wave (PAW) method.66,67 The valence electrons were expanded on a set of plane waves with a kinetic cutoff of 400 eV. The dispersion interactions were included using Grimme's D3 correction.68 The reciprocal space was sampled in order to provide converged results. A 5 × 5 × 1 Monkhorst–Pack grid was adopted.69 The convergence criteria for the electronic and ionic loops were set at 10−6 eV and 10−3 eV Å−1 respectively. In the case of PBE+U, the U values for TM were taken from the literature. These values have been discussed for SACs, tested and benchmarked elsewhere (see Table S1, ESI†).70,71We fully optimized a 4 × 4 supercell of graphene, with a = b = 9.87 Å and γ = 120°.72,73 This was used to build the 4N-Gr support, where a 15 Å-thick vacuum layer was included along the non-periodic direction to avoid interaction between the periodic replicas of the system. A C-divacancy was created in the cell, and four C atoms were replaced with N atoms to build the 4N-Gr (pyridine) support. The TM atom was embedded into the coordination site resulting in the TM@4N-Gr structure.30,74,75Fig. 1 shows the prototype structure of the SACs and the investigated TM atoms.
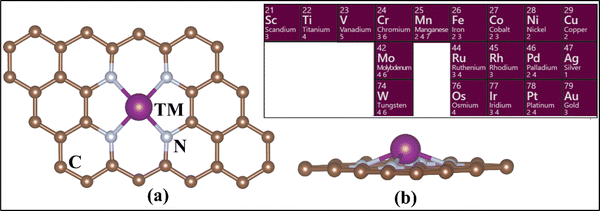 | ||
| Fig. 1 (a) Top view and (b) side view of the TM-embedded N-doped graphene structure. The inset shows the TM considered in this study. | ||
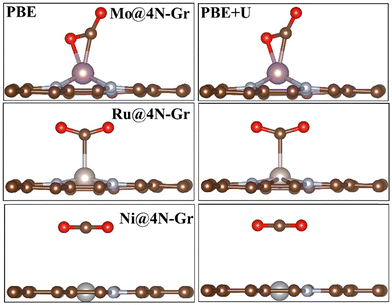
In each case, the atomic coordinates have been fully relaxed. The approximation of keeping the lattice vectors frozen at those of graphene implies a negligible error, less than 0.1 eV,70 and therefore it can be considered acceptable for the purpose of the study. The adhesion energies and magnetization of the TMs are reported in Table S1 (ESI†). When adsorbed in the cavity, the metal atom can either remain in the same plane as the C atoms or it can protrude from the surface layer. Fig. S1 (ESI†) shows the structure of two representative cases, namely, Mo@4N-Gr and Ni@4N-Gr.
The adsorption energy (ΔEads) of an adsorbed species on the TM@4N-Gr SAC is calculated as:
| ΔEads = ESAC+mol − ESAC − Emol | (1) |
| ΔG = ΔEads − TΔS + ΔEzpe | (2) |
3. Results
As mentioned before, we investigated the performance of three popular DFT exchange–correlation functionals. The first is the PBE functional,53 one of the most popular for the study of SACs. It is known that this functional may lead to some inaccuracies when compared to high level benchmark calculations,36,75 mainly because it tends to over delocalize electrons in a system. However, given its efficiency, it is widely used for screening and predictive studies.33,44,45,86–89 One approach to overcome the issues with PBE is to employ hybrid functionals, i.e., including a given fraction of exact Fock exchange into the functional.90–92 A popular choice is the PBE0 parametrization.55,56 A previous work by Patel et al. demonstrated that PBE0 shows negligible differences from high level CCSD(T) calculations of a SAC used as a test case.36 Therefore, PBE0 can be considered a solid benchmark for other functionals. Hybrid functionals are however rather expensive when associated with plane wave approaches. A compromise between accuracy and computational cost is represented by the DFT+U approach.54 In this framework one adds an ad hoc correction term mimicking the effect of the exact Fock exchange in hybrid functionals. The extra computational cost is negligible with respect to PBE, but the choice of the U correction term is delicate.3.1. Benchmarking PBE and PBE+U against PBE0
We start by benchmarking the reliability of PBE and PBE+U against the PBE0 hybrid functional in the activation of CO2, eqn (3a).| CO2 + * → *CO2 | (3a) |
| CO2 + H+ + e− * → *COOH | (3b) |
| CO2 + H+ + e− * → *OCHO | (3c) |
Table 1 presents the reaction energies, reaction free energies and structural geometries related to *CO2, *COOH, and *OCHO adsorbed species on TM@4N-Gr obtained using PBE, PBE+U, and PBE0 approaches (* indicates the site where an adsorbed molecular fragment is bound). In the case of *COOH adsorption on Ni@4N-Gr with PBE0 we encountered unsurmountable convergence issues, and therefore we are not reporting any value in Table 1. Reaction free energies reported in Table 1 are calculated according to eqn (3a)–(3c) and refer to the adsorption of reaction intermediates to the SACs.
| PBE0 | PBE+U | PBE | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *CO2 | *COOH | *OCHO | *CO2 | *COOH | *OCHO | *CO2 | *COOH | *OCHO | ||||||||||
| TM | E ads | ΔG | E ads | ΔG | E ads | ΔG | E ads | ΔG | E ads | ΔG | E ads | ΔG | E ads | ΔG | E ads | ΔG | E ads | ΔG |
| Sc | −1.01 | −0.33 | −1.72 | −0.69 | −3.39 | −2.38 | −0.92 | −0.24 | −1.47 | −0.44 | −3.14 | −2.13 | −0.84 | −0.16 | −1.38 | −0.35 | −3.01 | −2 |
| Ti | −1.39 | −0.71 | −1.66 | −0.63 | −2.84 | −1.83 | −1.31 | −0.63 | −1.41 | −0.38 | −2.78 | −1.77 | −1.58 | −0.9 | −1.57 | −0.54 | −2.61 | −1.61 |
| Ni | 0.02 | 0.70 | — | — | 1.12 | 2.13 | −0.13 | 0.56 | 1.03 | 2.06 | 0.86 | 1.87 | −0.13 | 0.55 | 1.04 | 2.07 | 0.78 | 1.79 |
| Mo | −0.84 | −0.16 | −0.37 | 0.66 | −1.75 | −0.74 | −0.73 | −0.05 | −0.59 | 0.44 | −1.84 | −0.83 | −1.41 | −0.73 | −1.45 | −0.41 | −2.21 | −1.2 |
| Ru | 0.38 | 1.06 | −0.77 | 0.26 | −0.09 | 0.92 | 0.16 | 0.84 | −0.64 | 0.39 | 0.07 | 1.08 | −0.11 | 0.57 | −0.99 | 0.04 | −0.16 | 0.85 |
| W | −1.56 | −0.88 | −1.15 | −0.12 | −2.5 | −1.49 | −1.65 | −0.97 | −1.27 | −0.24 | −2.47 | −1.46 | −1.92 | −1.24 | −1.96 | −0.92 | −2.6 | −1.59 |
| Os | −0.47 | 0.21 | −1.17 | −0.14 | −0.69 | 0.33 | −0.45 | 0.23 | −1.01 | 0.02 | −0.65 | 0.36 | −0.74 | −0.06 | −1.12 | −0.09 | −0.71 | 0.3 |
PBE offers large deviations from PBE0, with a mean absolute error (MAE) of 0.30 eV, 0.43 eV, and 0.23 eV for *CO2, *COOH, and *OCHO, respectively. The maximum deviation is very high, being 0.57 eV, 1.08 eV, and 0.46 eV for *CO2, *COOH, and *OCHO respectively. This result already shows the problems connected with the use of the PBE functional: in the adsorption of CO2 the differences can be up to 0.6 eV and for the formation of the intermediates, they can be even larger, exceeding 1 eV in some cases, Table 1 and Fig. 2. PBE+U provides estimates closer to PBE0, as the MAE is 0.11 eV, 0.19 eV, and 0.13 eV for *CO2, *COOH, and *OCHO, respectively. Similarly, the maximum deviation is nearly the same in all the cases, 0.22 eV (*CO2), 0.25 eV (*COOH), and 0.26 eV (*OCHO), Fig. 2. Thus, the energy computed at the PBE+U level is very similar to that obtained at the PBE0 level, with a MAE always lower than 0.2 eV and a maximum deviation always smaller than 0.3 eV. This shows that PBE+U is sufficiently reliable for providing quantitative estimates of the reaction energetics at an acceptable computational cost. These results are in line with previous findings showing that PBE+U estimates of H atom adsorption on TM@4N-Gr SACs closely match with the PBE0 ones (MAE less than 0.2 eV).75
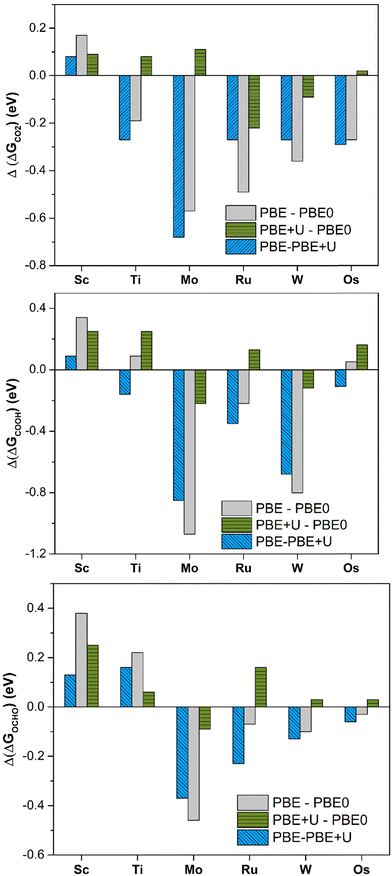 | ||
| Fig. 2 Deviation of Gibbs free energies comparing different levels of theory for *CO2, *COOH, and *OCHO adsorption on TM@4N-Gr. | ||
3.2. CO2 activation
The results show that PBE+U provides results that closely resemble those obtained with the benchmark PBE0 functional. Therefore, in the following, discussion is restricted to the comparison of PBE and PBE+U results.We concentrate first on the activation of CO2 on the full set of 19 SACs, Fig. 1. Fig. 3 shows representative cases of CO2 adsorption. The CO2 molecule can be attached to the SAC by means of TM–O and TM–C interactions (Mo@4N-Gr), or through a TM–C bond (Ru@4N-Gr). In the first case, the complex shows bidentate bonding, while in the latter case the interaction occurs only via the C atom of the CO2 molecule. In the case of physisorption, the CO2 molecule is distant from the SAC (∼3.0 Å). Fig. S2 (ESI†) shows the structure of *CO2 adsorbed on various SACs. Table 2 presents the calculated adsorption energy, Gibbs free energies of *CO2 and structural parameters.
| TM | PBE | PBE+U | ||||||
|---|---|---|---|---|---|---|---|---|
| E ads (eV) | ΔG (eV) | <O–C–O | TM–C (Å) | E ads (eV) | ΔG (eV) | <O–C–O | TM–C (Å) | |
| a MAE of PBE with respect to PBE+U: MAE chemisorption 0.41 eV; MAE physisorption 0.04 eV. | ||||||||
| Sc | −0.84 | −0.16 | 139 | 2.42 | −0.92 | −0.24 | 139.48 | 2.44 |
| Ti | −1.58 | −0.90 | 133 | 2.05 | −1.31 | −0.63 | 133.73 | 2.06 |
| V | −0.08 | 0.60 | 177 | 3.19 | −0.07 | 0.61 | 178.53 | 3.23 |
| Cr | −0.11 | 0.57 | 179 | 3.40 | −0.10 | 0.58 | 179.7 | 3.40 |
| Mn | −0.10 | 0.58 | 180 | 3.44 | −0.09 | 0.59 | 179.7 | 3.45 |
| Fe | −0.10 | 0.58 | 180 | 3.32 | −0.09 | 0.59 | 179.94 | 3.32 |
| Co | 0.93 | 1.61 | 180 | 3.24 | −0.11 | 0.57 | 179.06 | 3.29 |
| Ni | −0.13 | 0.55 | 179 | 3.24 | −0.13 | 0.56 | 179.09 | 3.26 |
| Cu | 0.04 | 0.72 | 180 | 3.31 | −0.10 | 0.58 | 179.86 | 3.32 |
| Mo | −1.41 | −0.73 | 131 | 2.03 | −0.73 | −0.05 | 132.70 | 2.04 |
| Ru | −0.11 | 0.57 | 147 | 2.16 | 0.16 | 0.84 | 148.60 | 2.20 |
| Rh | −0.18 | 0.50 | 176 | 3.22 | −0.15 | 0.53 | 177.85 | 2.30 |
| Pd | −0.13 | 0.55 | 179 | 3.32 | −0.13 | 0.55 | 178.95 | 3.32 |
| Ag | −0.17 | 0.51 | 179 | 4.20 | −0.37 | 0.31 | 178.73 | 4.22 |
| W | −1.92 | −1.24 | 129 | 2.02 | −1.65 | −0.97 | 130.75 | 2.06 |
| Os | −0.74 | −0.06 | 139 | 2.02 | −0.45 | 0.23 | 140.14 | 2.02 |
| Ir | −0.19 | 0.49 | 176 | 3.28 | −0.16 | 0.52 | 177.60 | 3.34 |
| Pt | −0.14 | 0.54 | 178 | 3.35 | −0.14 | 0.54 | 178.45 | 3.35 |
| Au | −0.12 | 0.56 | 180 | 3.44 | −0.12 | 0.56 | 179.83 | 3.44 |
The number of SACs capable of activating CO2 remains unchanged when adopting the PBE+U approach, indicating that PBE is sufficiently reliable for obtaining qualitative predictions. The picture changes when looking at quantitative estimates. In fact, on average, the PBE values deviate by 0.41 eV from the PBE+U ones, with cases where the difference reaches 1 eV (Co@4N-Gr), see Fig. 4. Not surprisingly, PBE+U impacts the results only when CO2 is chemisorbed. If one restricts to the physisorption cases, the MAE is 0.04 eV, Fig. 4.
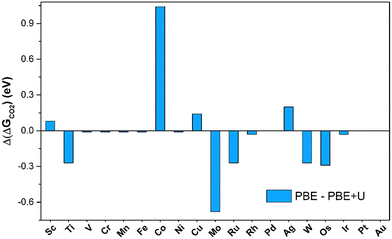 | ||
| Fig. 4 Deviation of Gibbs free energies computed at PBE and PBE+U levels for CO2 adsorption on TM@4N-Gr. | ||
3.3. Reaction intermediates
After discussing the activation of CO2, we now move to the reaction intermediates arising from the addition of the first H+ and e− couple to CO2, the first step in CO2 electroreduction. Fig. S3 (ESI†) shows the structure of *COOH and *OCHO molecular fragments adsorbed on the SACs considered.When comparing the stability of the *COOH intermediate at PBE and PBE+U levels of theory, we see that the MAE is still high, 0.32 eV, comparable to that of CO2 activation (0.41 eV), Table 3. Even the maximum deviation is large, 0.86 eV (Mo@4N-Gr), close to 1 eV, as found before. Besides Mo@4N-Gr, two other systems are critical, namely, Ru@4N-Gr and W@4N-Gr, with a deviation equal to 0.35 eV and 0.69 eV, respectively. This implies that the stability of reaction intermediates is very sensitive to the adopted functional and the usage of PBE can lead to significant errors.
| PBE | PBE+U | |||||||
|---|---|---|---|---|---|---|---|---|
| *COOH | *OCHO | *COOH | *OCHO | |||||
| TM | E ads | ΔG | E ads | ΔG | E ads | ΔG | E ads | ΔG |
| Sc | −1.38 | −0.35 | −3.01 | −2.00 | −1.47 | −0.44 | −3.14 | −2.13 |
| Ti | −1.57 | −0.54 | −2.61 | −1.61 | −1.41 | −0.38 | −2.78 | −1.77 |
| Ni | 1.04 | 2.07 | 0.78 | 1.79 | 1.03 | 2.06 | 0.86 | 1.87 |
| Mo | −1.45 | −0.41 | −2.21 | −1.20 | −0.59 | 0.44 | −1.84 | −0.83 |
| Ru | −0.99 | 0.04 | −0.16 | 0.85 | −0.64 | 0.39 | 0.07 | 1.08 |
| W | −1.96 | −0.92 | −2.60 | −1.59 | −1.27 | −0.24 | −2.47 | −1.46 |
| Os | −1.12 | −0.09 | −0.71 | 0.30 | −1.01 | 0.02 | −0.65 | 0.36 |
The stability of OCHO* seems to be less sensitive to the functional adopted, since the MAE is 0.17 eV and the maximum deviation is 0.37 eV only, Table 3. Regarding CO2 adsorption, PBE is still reliable in providing qualitative predictions, since the relative stability of the two intermediates remains unchanged. In particular, with both PBE and PBE+U, OCHO* is more stable than COOH* on Sc, Ti, Ni, Mo, and W@4N-Gr, while COOH* is more stable on Ru and Os@4N-Gr.
3.4. Competing action of water
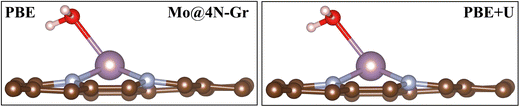
In this section, we analyze the impact of the exchange–correlation functional on another relevant point for the study of the electrochemical reduction of CO2 with SACs: the role of water. In electrochemical reactions, a fundamental role is played by the solvent, water. An appropriate way to account for it requires a dynamic approach that explicitly considers the catalyst/water interface. Interestingly, we have recently reported that on SACs, water does not only act as a solvent in the reaction but can also act as a ligand competing with CO2 and the other reaction intermediates in binding to the TM center.31 In this respect, this finding is another demonstration of the similarity between SACs and organometallic compounds. Here we discuss the effect of the adopted functional on the prediction of the “coordination” effect played by water. A dedicated study is planned to address the complex problem of solvation.We first adsorbed a water molecule on the SACs considered in this work, as shown in Table 4, where the calculated Gibbs free energies at PBE and PBE+U levels are reported along with the relevant structural information. If one considers the structure of the complex, negligible changes are found between the two functionals, as shown in Fig. 5 where the representative case of Mo@4N-Gr is shown.
| TM | PBE | PBE+U | ||||||
|---|---|---|---|---|---|---|---|---|
| E ads (eV) | ΔG (eV) | <H–O–H | d TM–O (Å) | E ads (eV) | ΔG (eV) | <H–O–H | d TM–O (Å) | |
| Sc | −1.00 | −0.42 | 107 | 2.30 | −1.05 | −0.47 | 107 | 2.30 |
| Ti | −0.97 | −0.39 | 106 | 2.20 | −0.91 | −0.33 | 106 | 2.20 |
| Ni | −0.14 | 0.44 | 103 | 3.31 | −0.14 | 0.44 | 103 | 3.26 |
| Mo | −0.63 | −0.05 | 105 | 2.30 | −0.49 | 0.09 | 105 | 2.30 |
| Ru | −0.25 | 0.33 | 105 | 2.70 | −0.29 | 0.29 | 105 | 2.70 |
| W | −0.73 | −0.15 | 106 | 2.30 | −0.74 | −0.16 | 106 | 2.30 |
| Os | −0.06 | 0.52 | 105 | 2.80 | −0.25 | 0.33 | 105 | 2.80 |
The analysis of the energetics suggests that in this case PBE provides acceptable results, since the MAE is less than 0.1 eV (0.07 eV) and the maximum deviation is 0.19 eV only, Fig. 6. Comparing the Gibbs free energy of *CO2 and *H2O to that of SACs, one can evince that the two ligands have comparable interactions with the TM center and in fact compete for bonding to it. A comparison of the Gibbs free energies of adsorption is reported in Tables 2 and 4. On Sc, Ni, and Ru@4N-Gr, water adsorption is more favorable than CO2 adsorption. In the latter case, *H2O is more stable by 0.55 eV than *CO2, Tables 2 and 4. Of course, this is a simplified model since here the nature of liquid water is not considered. Other approaches should be adopted in order to properly describe the catalyst/water interface including bulk water and explicit solvation spheres.82,97–101
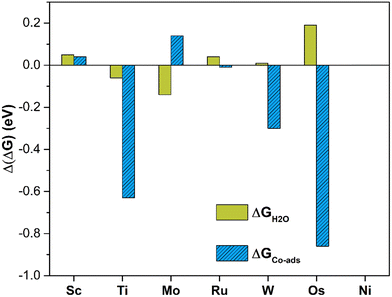 | ||
| Fig. 6 Deviation of Gibbs free energies computed at PBE and PBE+U levels for H2O adsorption (green) and CO2 co-adsorption (blue) in the presence of *H2O on TM@4N-Gr. | ||
Finally, we considered the adsorption of CO2 in the presence of *H2O. Here we assume that the adsorption occurs on the opposite side. Further work in the future will be dedicated to the exploration of the several possible co-adsorption configurations. The adsorption energy is calculated as follows.
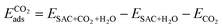 | (4) |
Table 5 presents the calculated Gibbs free energies. Fig. S5 (ESI†) shows the structure of *CO2 in the presence of *H2O on the various SACs. Even in this case PBE and PBE+U provide similar results, with a MAE of 0.19 eV, but with relevant exceptions. In fact, in the case of Ti@4N-Gr, PBE and PBE+U differ by 0.63 eV, Fig. 6. This value largely contributes to the MAE, as MAE decreases to 0.11 eV by excluding Ti@4N-Gr. It this respect, the adoption of PBE+U in place of PBE looks more solid.
| TM | PBE | PBE+U | ||
|---|---|---|---|---|
| E ads | ΔG | E ads | ΔG | |
| Sc | −0.08 | 0.60 | −0.12 | 0.56 |
| Ti | −0.79 | −0.11 | −0.16 | 0.52 |
| Ni | −0.14 | 0.54 | −0.14 | 0.54 |
| Mo | 0.39 | 1.07 | 0.25 | 0.93 |
| Ru | −0.15 | 0.53 | −0.14 | 0.54 |
| W | −1.37 | −0.69 | −1.07 | −0.39 |
| Os | −0.36 | −0.32 | −0.14 | 0.54 |
4. Conclusions
In this work we performed a computational study of the initial phases of CO2 electroreduction on single atom catalysts consisting of TM atoms stabilized in nitrogen-doped graphene. We simulated the bonding and activation of CO2 as well as the first hydrogenation step leading to the formation of *COOH and *OCHO intermediates, as they usually represent the most complex steps to overcome. The focus is on the role of the exchange–correlation functional used to simulate CO2 activation and reduction on SACs. Previous studies have demonstrated that the PBE functional, one of the most commonly used functionals for this kind of calculation, is sufficiently reliable when looking at trends and general rules, while it may fail in providing quantitative estimates. The picture can be improved by invoking the PBE+U approach, or even better hybrid functionals, such as the PBE0 functional that we used as a benchmark. The results of this study show that PBE+U reproduces the PBE0 results with satisfactory accuracy, at a much lower computational cost. Both PBE+U and PBE0 provide more reliable results than the standard PBE functional. In particular, for CO2 adsorption, PBE estimates deviate on average by 0.3 eV from PBE0 ones, while the maximum deviation can reach up to 0.5 eV. The effect can be tamed by invoking PBE+U as the MAE decreases to 0.1 eV. The picture is similar when looking at *COOH and *OHCH intermediates, as the deviation between PBE and PBE0 is 0.43 eV and 0.23 eV, respectively, with a maximum deviation of up to one eV. The difference between PBE0 and PBE+U is much lower, 0.19 eV and 0.13 eV. Therefore, PBE+U is an acceptable compromise between accuracy and computational cost. Despite the important quantitative effect on the reaction energies, PBE looks sufficiently reliable when looking at qualitative trends, such as the energetic ordering of stability of *COOH and *OCHO intermediates, which remains unchanged when the self-interaction correction is introduced.Finally, we investigated the competing effects of water adsorption and CO2 binding to the active site. We first considered simple water adsorption, finding that the discrepancy between PBE and PBE+U is small, as shown by a MAE of 0.07 eV, and a maximum deviation of 0.19 eV. Next, we considered co-adsorption on the same site of water and CO2. Here the MAE between PBE and PBE+U becomes more relevant, 0.19 eV.
In general, the work serves as another example highlighting the importance of moving beyond the PBE functional when trying to provide quantitative predictions of the catalytic activity of SACs. In fact, while PBE looks sufficiently reliable for a preliminary screening of the catalytic activity, significant differences arise when the system is treated with the more rigorous PBE+U or even better PBE0 functionals. This level of theory becomes essential when one is interested in determining the reaction profile and the expected activity of a potential new catalyst.
Further work will be dedicated to searching for correlations between thermodynamic and activation energies, aiming to provide insight to verify if the universal relations discovered for extended catalysts are valid also in the context of SACs.
Author contributions
D. M. performed the calculations and analysis. G. D. L. and G. P. supervised the project. G. D. L. wrote the first draft. All authors contributed to designing the study, analyzing the results, and preparing the final draft.Data availability
The data reported in this article can be found in the cited literature and can be requested from the authors upon reasonable inquiry.Conflicts of interest
■■■■There are no conflicts to declare.Acknowledgements
D. M. is grateful to the Science and Engineering Research Board (SERB), Govt. of India, for the SIRE fellowship (award no. SIR/2022/000690) which supported her three-month visit to University of Milano-Bicocca in 2022, where most of the calculations have been carried out. We acknowledge the financial support from the Italian Ministry for University and Research MUR, through the projects UNDERSAC and SACtoH2. Access to CINECA supercomputing resources was granted via ISCRAB and ISCRAC. We also thank the COST Action 18234 supported by COST (European Cooperation in Science and Technology).References
- G. Centi and J. Čejka, Needs and Gaps for Catalysis in Addressing Transitions in Chemistry and Energy from a Sustainability Perspective, ChemSusChem, 2019, 12, 621–632 CrossRef CAS PubMed.
- C. Gürsan and V. de Gooyert, The systemic impact of a transition fuel: Does natural gas help or hinder the energy transition?, Renewable Sustainable Energy Rev., 2021, 138, 110552 CrossRef.
- W. A. Smith, T. Burdyny, D. A. Vermaas and H. Geerlings, Pathways to Industrial-Scale Fuel Out of Thin Air from CO2 Electrolysis, Joule, 2019, 3, 1822–1834 CrossRef CAS.
- H. C. Lau, S. Ramakrishna, K. Zhang and A. V. Radhamani, The Role of Carbon Capture and Storage in the Energy Transition, Energy Fuels, 2021, 35, 7364–7386 CrossRef CAS.
- X. Chang, T. Wang and J. Gong, CO2 photo-reduction: insights into CO2 activation and reaction on surfaces of photocatalysts, Energy Environ. Sci., 2016, 9, 2177–2196 RSC.
- A. Álvarez, M. Borges, J. J. Corral-Pérez, J. G. Olcina, L. Hu, D. Cornu, R. Huang, D. Stoian and A. Urakawa, CO2 Activation over Catalytic Surfaces, Chem. Phys. Chem., 2017, 18, 3135–3141 CrossRef PubMed.
- H.-J. Son, C. Pac and S. O. Kang, Inorganometallic Photocatalyst for CO2 Reduction, Acc. Chem. Res., 2021, 54, 4530–4544 CrossRef CAS PubMed.
- S. Fang, M. Rahaman, J. Bharti, E. Reisner, M. Robert, G. A. Ozin and Y. H. Hu, Photocatalytic CO2 reduction, Nat. Rev. Methods Primers, 2023, 3, 61 CrossRef CAS.
- S. Xie, W. Zhang, X. Lan and H. Lin, CO2 Reduction to Methanol in the Liquid Phase: A Review, ChemSusChem, 2020, 13, 6141–6159 CrossRef CAS PubMed.
- P. Saha, S. Amanullah and A. Dey, Selectivity in Electrochemical CO2 Reduction, Acc. Chem. Res., 2022, 55, 134–144 CrossRef CAS PubMed.
- A. Senocrate and C. Battaglia, Electrochemical CO2 reduction at room temperature: Status and perspectives, J. Energy Storage, 2021, 36, 102373 CrossRef.
- X. Duan, J. Xu, Z. Wei, J. Ma, S. Guo, S. Wang, H. Liu and S. Dou, Metal-Free Carbon Materials for CO2 Electrochemical Reduction, Adv. Mater., 2017, 29, 1701784 CrossRef PubMed.
- M. Bevilacqua, J. Filippi, H. A. Miller and F. Vizza, Recent Technological Progress in CO2 Electroreduction to Fuels and Energy Carriers in Aqueous Environments, Energy Technol., 2015, 3, 197–210 CrossRef CAS.
- A. A. Peterson and J. K. Nørskov, Activity Descriptors for CO2 Electroreduction to Methane on Transition-Metal Catalysts, J. Phys. Chem. Lett., 2012, 3, 251–258 CrossRef CAS.
- M. C. O. Monteiro, F. Dattila, B. Hagedoorn, R. García-Muelas, N. López and M. T. M. Koper, Absence of CO2 electroreduction on copper, gold and silver electrodes without metal cations in solution, Nat. Catal., 2021, 4, 654–662 CrossRef CAS.
- F. Dattila, R. R. Seemakurthi, Y. Zhou and N. López, Modeling Operando Electrochemical CO2 Reduction, Chem. Rev., 2022, 122, 11085–11130 CrossRef CAS PubMed.
- S. K. Kaiser, Z. Chen, D. Faust Akl, S. Mitchell and J. Pérez-Ramírez, Single-Atom Catalysts across the Periodic Table, Chem. Rev., 2020, 120, 11703–11809 CrossRef CAS PubMed.
- H.-Y. Zhuo, X. Zhang, J.-X. Liang, Q. Yu, H. Xiao and J. Li, Theoretical Understandings of Graphene-based Metal Single-Atom Catalysts: Stability and Catalytic Performance, Chem. Rev., 2020, 120, 12315–12341 CrossRef CAS PubMed.
- A. Wang, J. Li and T. Zhang, Heterogeneous single-atom catalysis, Nat. Rev. Chem., 2018, 2, 65–81 CrossRef CAS.
- M. A. Bajada, J. Sanjosé-Orduna, G. Di Liberto, S. Tosoni, G. Pacchioni, T. Noël and G. Vilé, Interfacing single-atom catalysis with continuous-flow organic electrosynthesis, Chem. Soc. Rev., 2022, 51, 3898–3925 RSC.
- N. Sathishkumar and H.-T. Chen, Regulating the Coordination Environment of Single-Atom Catalysts Anchored on Thiophene Linked Porphyrin for an Efficient Nitrogen Reduction Reaction, ACS Appl. Mater. Interfaces, 2023, 15, 15545–15560 CrossRef CAS PubMed.
- X. Li, Q. Zhou, S. Wang, Y. Li, Y. Liu, Q. Gao and Q. Wu, Tuning the Coordination Environment to Effect the Electrocatalytic Behavior of a Single-Atom Catalyst toward the Nitrogen Reduction Reaction, J. Phys. Chem. C, 2021, 125, 11963–11974 CrossRef CAS.
- H. Xu, Y. Zhao, Q. Wang, G. He and H. Chen, Supports promote single-atom catalysts toward advanced electrocatalysis, Coord. Chem. Rev., 2022, 451, 214261 CrossRef CAS.
- G. Di Liberto, L. A. Cipriano and G. Pacchioni, Single Atom Catalysts: What Matters Most, the Active Site or The Surrounding?, ChemCatChem, 2022, 14, e202200611 CrossRef CAS.
- M. K. Samantaray, V. D’Elia, E. Pump, L. Falivene, M. Harb, S. Ould Chikh, L. Cavallo and J.-M. Basset, The Comparison between Single Atom Catalysis and Surface Organometallic Catalysis, Chem. Rev., 2020, 120, 734–813 CrossRef CAS PubMed.
- G. Di Liberto and G. Pacchioni, Modeling Single-Atom Catalysis, Adv. Mater., 2023, 35, 2307150 CrossRef CAS PubMed.
- G. Di Liberto, L. A. Cipriano and G. Pacchioni, Role of Dihydride and Dihydrogen Complexes in Hydrogen Evolution Reaction on Single-Atom Catalysts, J. Am. Chem. Soc., 2021, 143, 20431–20441 CrossRef CAS PubMed.
- L. Zhong and S. Li, Unconventional Oxygen Reduction Reaction Mechanism and Scaling Relation on Single-Atom Catalysts, ACS Catal., 2020, 10, 4313–4318 CrossRef CAS.
- L. A. Cipriano, G. Di Liberto and G. Pacchioni, Superoxo and Peroxo Complexes on Single-Atom Catalysts: Impact on the Oxygen Evolution Reaction, ACS Catal., 2022, 11682–11691 CrossRef CAS.
- I. Barlocco, L. A. Cipriano, G. Di Liberto and G. Pacchioni, Does the Oxygen Evolution Reaction follow the classical OH*, O*, OOH* path on single atom catalysts?, J. Catal., 2023, 417, 351–359 CrossRef CAS.
- D. Misra, G. Di Liberto and G. Pacchioni, CO2 electroreduction on single atom catalysts: Is water just a solvent?, J. Catal., 2023, 422, 1–11 CrossRef CAS.
- S. Tosoni, G. Di Liberto, I. Matanovic and G. Pacchioni, Modelling single atom catalysts for water splitting and fuel cells: A tutorial review, J. Power Sources, 2023, 556, 232492 CrossRef CAS.
- Z. Chen, J. Zhao, C. R. Cabrera and Z. Chen, Computational Screening of Efficient Single-Atom Catalysts Based on Graphitic Carbon Nitride (g-C3N4) for Nitrogen Electroreduction, Small Methods, 2019, 3, 1800368 CrossRef.
- G. Di Liberto, S. Tosoni, L. A. Cipriano and G. Pacchioni, A Few Questions about Single-Atom Catalysts: When Modeling Helps, Acc. Mater. Res., 2022, 3, 986–995 CrossRef CAS.
- F. Kraushofer and G. S. Parkinson, Single-Atom Catalysis: Insights from Model Systems, Chem. Rev., 2022, 122, 14911–14939 CrossRef CAS PubMed.
- A. M. Patel, S. Ringe, S. Siahrostami, M. Bajdich, J. K. Nørskov and A. R. Kulkarni, Theoretical Approaches to Describing the Oxygen Reduction Reaction Activity of Single-Atom Catalysts, J. Phys. Chem. C, 2018, 122, 29307–29318 CrossRef CAS.
- A. J. Garza and G. E. Scuseria, Predicting Band Gaps with Hybrid Density Functionals, J. Phys. Chem. Lett., 2016, 7, 4165–4170 CrossRef CAS PubMed.
- G. Pacchioni, Modeling doped and defective oxides in catalysis with density functional theory methods: Room for improvements, J. Chem. Phys., 2008, 28, 182505 CrossRef PubMed.
- P. Janthon, S. (Andy) Luo, S. M. Kozlov, F. Viñes, J. Limtrakul, D. G. Truhlar and F. Illas, Bulk Properties of Transition Metals: A Challenge for the Design of Universal Density Functionals, J. Chem. Theory Comput., 2014, 10, 3832–3839 CrossRef CAS PubMed.
- K. C. Ko, O. Lamiel-García, J. Y. Lee and F. Illas, Performance of a modified hybrid functional in the simultaneous description of stoichiometric and reduced TiO2 polymorphs, Phys. Chem. Chem. Phys., 2016, 18, 12357–12367 RSC.
- P. Janthon, S. (Andy) Luo, S. M. Kozlov, F. Viñes, J. Limtrakul, D. G. Truhlar and F. Illas, Bulk Properties of Transition Metals: A Challenge for the Design of Universal Density Functionals, J. Chem. Theory Comput., 2014, 10, 3832–3839 CrossRef CAS PubMed.
- L. Xu, L.-M. Yang and E. Ganz, Mn–graphene single-atom catalyst evaluated for CO oxidation by computational screening, Theor. Chem. Acc., 2018, 137, 1–13 Search PubMed.
- H. Niu, X. Wang, C. Shao, Z. Zhang and Y. Guo, Computational Screening Single-Atom Catalysts Supported on g-CN for N2 Reduction: High Activity and Selectivity, ACS Sustainable Chem. Eng., 2020, 8, 13749–13758 Search PubMed.
- M. Umer, S. Umer, M. Zafari, M. Ha, R. Anand, A. Hajibabaei, A. Abbas, G. Lee and K. S. Kim, Machine learning assisted high-throughput screening of transition metal single atom based superb hydrogen evolution electrocatalysts, J. Mater. Chem. A, 2022, 10, 6679–6689 RSC.
- Y. Zhou, G. Gao, J. Kang, W. Chu and L.-W. Wang, Computational screening of transition-metal single atom doped C 9 N 4 monolayers as efficient electrocatalysts for water splitting, Nanoscale, 2019, 11, 18169–18175 RSC.
- X. Zhai, L. Li, X. Liu, Y. Li, J. Yang, D. Yang, J. Zhang, H. Yan and G. Ge, A DFT screening of single transition atoms supported on MoS2 as highly efficient electrocatalysts for the nitrogen reduction reaction, Nanoscale, 2020, 12, 10035–10043 RSC.
- Z. Wang, J. Zhao, Q. Cai and F. Li, Computational screening for high-activity MoS2 monolayer-based catalysts for the oxygen reduction reaction via substitutional doping with transition metal, J. Mater. Chem. A, 2017, 5, 9842–9851 RSC.
- V. Fung, G. Hu, Z. Wu and D. Jiang, Descriptors for Hydrogen Evolution on Single Atom Catalysts in Nitrogen-Doped Graphene, J. Phys. Chem. C, 2020, 124, 19571–19578 CrossRef CAS.
- H.-C. Huang, Y. Zhao, J. Wang, J. Li, J. Chen, Q. Fu, Y.-X. Bu and S.-B. Cheng, Rational design of an efficient descriptor for single-atom catalysts in the hydrogen evolution reaction, J. Mater. Chem. A, 2020, 8, 9202–9208 RSC.
- S. Agarwal, R. Kumar, R. Arya and A. K. Singh, Rational Design of Single-Atom Catalysts for Enhanced Electrocatalytic Nitrogen Reduction Reaction, J. Phys. Chem. C, 2021, 125, 12585–12593 CrossRef CAS.
- M. D. Hossain, Z. Liu, M. Zhuang, X. Yan, G.-L. Xu, C. A. Gadre, A. Tyagi, I. H. Abidi, C.-J. Sun, H. Wong, A. Guda, Y. Hao, X. Pan, K. Amine and Z. Luo, Rational Design of Graphene-Supported Single Atom Catalysts for Hydrogen Evolution Reaction, Adv. Energy Mater., 2019, 9, 1803689 CrossRef.
- L. Wu, T. Guo and T. Li, Rational design of transition metal single-atom electrocatalysts: a simulation-based, machine learning-accelerated study, J. Mater. Chem. A, 2020, 8, 19290–19299 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- B. Singh, M. B. Gawande, A. D. Kute, R. S. Varma, P. Fornasiero, P. McNeice, R. V. Jagadeesh, M. Beller and R. Zbořil, Single-Atom (Iron-Based) Catalysts: Synthesis and Applications, Chem. Rev., 2021, 121, 13620–13697 CrossRef CAS PubMed.
- H. Fei, J. Dong, D. Chen, T. Hu, X. Duan, I. Shakir, Y. Huang and X. Duan, Single atom electrocatalysts supported on graphene or graphene-like carbons, Chem. Soc. Rev., 2019, 48, 5207–5241 RSC.
- C. Rivera-Cárcamo and P. Serp, Single Atom Catalysts on Carbon-Based Materials, ChemCatChem, 2018, 10, 5058–5091 CrossRef.
- Y. Wang, Y. Shao, D. W. Matson, J. Li and Y. Lin, Nitrogen-Doped Graphene and Its Application in Electrochemical Biosensing, ACS Nano, 2010, 4, 1790–1798 CrossRef CAS PubMed.
- X.-F. Li, K.-Y. Lian, L. Liu, Y. Wu, Q. Qiu, J. Jiang, M. Deng and Y. Luo, Unraveling the formation mechanism of graphitic nitrogen-doping in thermally treated graphene with ammonia, Sci. Rep., 2016, 6, 23495 CrossRef CAS PubMed.
- V. Dao, L. A. Cipriano, S.-W. Ki, S. Yadav, W. Wang, G. Di Liberto, K. Chen, H. Son, J.-K. Yang, G. Pacchioni and I.-H. Lee, 2D/2D Z-scheme-based α-Fe2O3 @NGr heterojunction implanted with Pt single-atoms for remarkable photocatalytic hydrogen evolution, Appl. Catal., B, 2023, 330, 122586 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- G. Di Liberto, L. A. Cipriano and G. Pacchioni, Universal Principles for the Rational Design of Single Atom Electrocatalysts? Handle with Care, ACS Catal., 2022, 5846–5856 CrossRef CAS.
- I. Barlocco, G. Di Liberto and G. Pacchioni, Hydrogen and oxygen evolution reactions on single atom catalysts stabilized by a covalent organic framework, Energy Adv., 2023, 2, 1022–1029 RSC.
- D. Van Dao, L. A. Cipriano, G. Di Liberto, T. T. D. Nguyen, S.-W. Ki, H. Son, G.-C. Kim, K. H. Lee, J.-K. Yang, Y.-T. Yu, G. Pacchioni and I.-H. Lee, Plasmonic Au nanoclusters dispersed in nitrogen-doped graphene as a robust photocatalyst for light-to-hydrogen conversion, J. Mater. Chem. A, 2021, 9, 22810–22819 RSC.
- D. Van Dao, G. Di Liberto, H. Ko, J. Park, W. Wang, D. Shin, H. Son, Q. Van Le, T. Van Nguyen, V. Van Tan, G. Pacchioni and I.-H. Lee, LaFeO3 meets nitrogen-doped graphene functionalized with ultralow Pt loading in an impactful Z-scheme platform for photocatalytic hydrogen evolution, J. Mater. Chem. A, 2022, 10, 3330–3340 RSC.
- I. Barlocco, G. Di Liberto and G. Pacchioni, New scaling relationships for the oxygen evolution reaction on single atom catalysts, Catal. Today, 2024, 427, 114409 CrossRef CAS.
- I. Barlocco, L. A. Cipriano, G. Di Liberto and G. Pacchioni, Modeling Hydrogen and Oxygen Evolution Reactions on Single Atom Catalysts with Density Functional Theory: Role of the Functional, Adv. Theory Simul., 2022, 2200513 Search PubMed.
- J. K. Nørskov, T. Bligaard, A. Logadottir, S. Bahn, L. B. Hansen, M. Bollinger, H. Bengaard, B. Hammer, Z. Sljivancanin, M. Mavrikakis, Y. Xu, S. Dahl and C. J. H. Jacobsen, Universality in Heterogeneous Catalysis, J. Catal., 2002, 209, 275–278 CrossRef.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, Trends in the Exchange Current for Hydrogen Evolution, J. Electrochem. Soc., 2005, 152, J23 CrossRef.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the computational design of solid catalysts, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- Y. Yang, J. Li, C. Zhang, Z. Yang, P. Sun, S. Liu and Q. Cao, Theoretical Insights into Nitrogen-Doped Graphene-Supported Fe, Co, and Ni as Single-Atom Catalysts for CO2 Reduction Reaction, J. Phys. Chem. C, 2022, 126, 4338–4346 CrossRef CAS.
- J. A. Gauthier, C. F. Dickens, L. D. Chen, A. D. Doyle and J. K. Nørskov, Solvation Effects for Oxygen Evolution Reaction Catalysis on IrO2 (110), J. Phys. Chem. C, 2017, 121, 11455–11463 CrossRef CAS.
- G. Di Liberto, G. Pacchioni, Y. Shao-Horn and L. Giordano, Role of Water Solvation on the Key Intermediates Catalyzing Oxygen Evolution on RuO2, J. Phys. Chem. C, 2023, 127, 10127–10133 CrossRef CAS.
- S. Rojas-Carbonell, K. Artyushkova, A. Serov, C. Santoro, I. Matanovic and P. Atanassov, Effect of pH on the Activity of Platinum Group Metal-Free Catalysts in Oxygen Reduction Reaction, ACS Catal., 2018, 8, 3041–3053 CrossRef CAS.
- A. Goyal and M. T. M. Koper, The Interrelated Effect of Cations and Electrolyte pH on the Hydrogen Evolution Reaction on Gold Electrodes in Alkaline Media, Angew. Chem., Int. Ed., 2021, 60, 13452–13462 CrossRef CAS PubMed.
- T. Cheng, L. Wang, B. V. Merinov and W. A. Goddard, Explanation of Dramatic pH-Dependence of Hydrogen Binding on Noble Metal Electrode: Greatly Weakened Water Adsorption at High pH, J. Am. Chem. Soc., 2018, 140, 7787–7790 CrossRef CAS PubMed.
- J. Wang, Z. Zhang, Y. Li, Y. Qu, Y. Li, W. Li and M. Zhao, Screening of Transition-Metal Single-Atom Catalysts Anchored on Covalent–Organic Frameworks for Efficient Nitrogen Fixation, ACS Appl. Mater. Interfaces, 2022, 14, 1024–1033 CrossRef CAS PubMed.
- X. Zhai, L. Li, X. Liu, Y. Li, J. Yang, D. Yang, J. Zhang, H. Yan and G. Ge, A DFT screening of single transition atoms supported on MoS2 as highly efficient electrocatalysts for the nitrogen reduction reaction, Nanoscale, 2020, 12, 10035–10043 RSC.
- C. Ling, Y. Ouyang, Q. Li, X. Bai, X. Mao, A. Du and J. Wang, A General Two-Step Strategy–Based High-Throughput Screening of Single Atom Catalysts for Nitrogen Fixation, Small Methods, 2019, 3, 1800376 CrossRef.
- M. Zafari, D. Kumar, M. Umer and K. S. Kim, Machine learning-based high throughput screening for nitrogen fixation on boron-doped single atom catalysts, J. Mater. Chem. A, 2020, 8, 5209–5216 RSC.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- R. Kortlever, J. Shen, K. J. P. Schouten, F. Calle-Vallejo and M. T. M. Koper, Catalysts and Reaction Pathways for the Electrochemical Reduction of Carbon Dioxide, J. Phys. Chem. Lett., 2015, 6, 4073–4082 CrossRef CAS PubMed.
- P. Huang, M. Cheng, H. Zhang, M. Zuo, C. Xiao and Y. Xie, Single Mo atom realized enhanced CO2 electro-reduction into formate on N-doped graphene, Nano Energy, 2019, 61, 428–434 CrossRef CAS.
- P. Lozano-Reis, H. Prats, P. Gamallo, F. Illas and R. Sayós, Multiscale Study of the Mechanism of Catalytic CO2 Hydrogenation: Role of the Ni(111) Facets, ACS Catal., 2020, 10, 8077–8089 CrossRef CAS.
- A. Jurado, Á. Morales-García, F. Viñes and F. Illas, Molecular Mechanism and Microkinetic Analysis of the Reverse Water Gas Shift Reaction Heterogeneously Catalyzed by the Mo 2 C MXene, ACS Catal., 2022, 12, 15658–15667 CrossRef CAS.
- N. Daelman, M. Capdevila-Cortada and N. López, Dynamic charge and oxidation state of Pt/CeO2 single-atom catalysts, Nat. Mater., 2019, 18, 1215–1221 CrossRef CAS PubMed.
- G. Di Liberto and L. Giordano, Role of solvation model on the stability of oxygenates on Pt(111): A comparison between microsolvation, extended bilayer, and extended metal/water interface, Electrochem. Sci. Adv., 2024, 4, e2100204 CrossRef CAS.
- G. Di Liberto, R. Conte and M. Ceotto, “Divide-and-conquer” semiclassical molecular dynamics: An application to water clusters, J. Chem. Phys., 2018, 148, 104302 CrossRef PubMed.
- P. Gono, F. Ambrosio and A. Pasquarello, Effect of the Solvent on the Oxygen Evolution Reaction at the TiO2 –Water Interface, J. Phys. Chem. C, 2019, 123, 18467–18474 CrossRef CAS.
- A. Bouzid, P. Gono and A. Pasquarello, Reaction pathway of oxygen evolution on Pt(1 1 1) revealed through constant Fermi level molecular dynamics, J. Catal., 2019, 375, 135–139 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: additional DFT data, supporting figures and tables. See DOI: https://doi.org/10.1039/d4cp00175c |
| This journal is © the Owner Societies 2024 |