Enthalpies and entropies of hydration from Monte Carlo simulations

Abstract

The changes in free energy, enthalpy, and entropy for transfer of a solute from the gas phase into solution are the fundamental thermodynamic quantities that characterize the solvation process. Owing to the development of methods based on free-energy perturbation theory, computation of free energies of solvation has become routine in conjunction with Monte Carlo (MC) statistical mechanics and molecular dynamics (MD) simulations. Computation of the enthalpy change and by inference the entropy change is more challenging. Two methods are considered in this work corresponding to direct averaging for the solvent and solution and to computing the temperature derivative of the free energy in the van’t Hoff approach. The application is for neutral organic solutes in TIP4P water using long MC simulations to improve precision. Definitive results are also provided for pure TIP4P water. While the uncertainty in computed free energies of hydration is ca. 0.05 kcal mol⁻¹, it is ca. 0.4 kcal mol⁻¹ for the enthalpy changes from either van’t Hoff plots or the direct method with sampling for 5 billion MC configurations. Partial molar volumes of hydration are also computed by the direct method; they agree well with experimental data with an average deviation of 3 cm³ mol⁻¹. In addition, the results permit breakdown of the errors in the free energy changes from the OPLS-AA force field into their enthalpic and entropic components. The excess hydrophobicity of organic solutes is enthalpic in origin.

---

Introduction

For the equilibration of a solute between the gas phase and solution at constant temperature and pressure, the Gibbs equation (eqn (1)) applies where ΔG_sol, ΔH_sol, ΔS_sol, ΔE_sol and ΔV_sol are the changes in free energy, enthalpy, entropy, internal energy, and volume upon solvation. For

ΔG_sol = ΔH_sol − TΔS_sol = ΔE_sol + PΔV_sol − TΔS_sol (1)

simulations of organic and biomolecular systems in solution, it is important that the accuracy of the modeling procedures and the description of the molecular energetics through force fields be tested in computing these properties for prototypical systems. Fortunately, it was found in the 1980s that precise free energy changes could be computed using Monte Carlo (MC) or molecular dynamics (MD) simulations in conjunction with thermodynamic integration (TI) or free-energy perturbation theory (FEP).^1–7 The solvent of greatest interest is water, and some studies have provided FEP results for free energies of hydration (ΔG_hyd) for large collections of organic molecules.^8–14

In contrast, few precise results have been computed for enthalpies and entropies of hydration, though such information would be very valuable in understanding the sources of errors for ΔG_hyd. The two key computational approaches in this case are a “direct” calculation viaeqn (2) or by using eqn (3) or equivalently the van’t Hoff relationship in eqn (4) where ΔG_sol = −RT ln K.

ΔH_sol = 〈H_N+A〉 − 〈H_N〉 − 〈H_A〉 (2)

ΔG_sol/T = ΔH_sol/T − ΔS_sol (3)

ln K = −ΔH_sol/RT + ΔS_sol/R (4)

To apply eqn (2), MC or MD simulations are run for the solute A in solution with N solvent molecules, the pure solvent with N molecules, and the solute in the gas phase where the 〈x〉 is the configurational average for x in the isothermal isobaric (NPT) ensemble. The problem with this approach is that for an aqueous solution the first two averages in eqn (2) are ca. −10 × N kcal mol⁻¹. Thus, for N > 100, long simulations are required to obtain acceptable precision for their difference. Alternatively, eqn (3) and (4) require precise computation of ΔG_sol at several temperatures in order to obtain ΔH_sol from the slope of plots of ΔG_sol/T or ln K vs. 1/T. In view of the computational demands, calculations of this type remain rare and did not begin to be reported until more than ten years after the introduction of molecular FEP calculations.¹ Pioneering efforts were made by Gallichio and Levy, who applied the van’t Hoff or “finite difference” approach in MD simulations for ten small, neutral molecules in TIP3P water at three temperatures.^15,16 They showed that enthalpy and entropy results could be obtained “with an uncertainty on the order of 1 kcal mol⁻¹”.¹⁵ Subsequently, there was a related MD study by Wan et al. for two solutes, methylamine and N-methylacetaamide, in TIP3P water that supported the viability of the van’t Hoff approach.¹⁷ Carlsson and Åqvist then applied the method to ion hydration,^18,19 while the Åqvist group moved on to seminal applications for enzyme kinetics.^20–25 The temperature dependence of the hydration of alkanes in a united-atom format has also received attention,²⁶ though, as illustrated below, obtaining good linearity for van’t Hoff plots is difficult for small enthalpy changes.

With this background, the present study was carried out to test the current viability of the direct and van’t Hoff methods for computing enthalpies and entropies of hydration using long Monte Carlo simulations for organic solutes. In the pre-FEP days, our group and others had tried direct calculations, but found unacceptable precision, e.g., with uncertainties of ca. ±10 kcal mol⁻¹ or more.²⁷ However, this was with 100–200 solvent molecules and averaging for ca. 2 million (2 M) MC configurations. The present work has used 500 water molecules and averaging for 5 billion (5 B) or more configurations. As it is now possible to obtain ΔG_aq results from MC/FEP simulations with a precision of ca. ±0.05 kcal mol⁻¹,^14,28 the van’t Hoff approach was also applied. In addition, besides providing better understanding of the performance of the utilized OPLS-AA force field, the work complements our prior study of computing volumes of solution by the direct method or from the pressure-dependence of ΔG_sol.²⁹

Computational details

All Monte Carlo simulations and free energy perturbation calculations were carried out with the BOSS program using the isothermal–isobaric ensemble at 1 atm.³⁰ Each system consisted of 1 solute molecule plus 500 water molecules in a cube with periodic boundary conditions. The TIP4P model was used for water and the solutes were represented with the latest version of the OPLS-AA force field.^31,32 The combining rules for the Lennard–Jones parameters are σ_ij = (σ_iiσ_jj)^1/2 and ε_ij = (ε_iiε_jj)^1/2. The TIP4P water molecules are rigid, while the sampling of the solutes includes all internal degrees of freedom. Standard procedures were followed with attempted changes for the solute and volume every 120 and 3125 configurations, respectively, and with ranges for translations, rotations, and internal coordinate variations chosen to give ca. 40% acceptance rates for new configurations. Interactions between water molecules are truncated at an O–O distance of 10.0 Å, and solute–water interactions are truncated if no intermolecular distance between the water oxygen and non-hydrogen atoms of the solute is less than 10.0 Å; quadratic smoothing is applied over the last 0.5 Å, and a standard correction for Lennard–Jones interactions neglected beyond the cutoff is included.³² After an equilibration of 25 M configurations starting from a stored water box, the MC calculations for the direct method were run in batches of 500 M configurations for a total of 5 B configurations at 25 °C. The FEP calculations to obtain the free energies of hydration were carried out exactly as described previously.³² Absolute free energies of hydration are obtained by annihilating the solute in both the gas phase and in TIP4P water through four FEP calculations for the elimination of the partial charges and the Lennard–Jones interactions. For the aqueous calculations, 20 evenly spaced windows are used, and the total number of MC configurations is 4 B and 10 B for the charge and Lennard–Jones annihilations. The time required to execute 1 B configurations is 7 h on a 3.2-GHz Intel i5-4570 processor. To obtain the van’t Hoff plots, the free-energy calculations were mostly run at four temperatures (15, 25, 35 and 45 °C), which was augmented in some cases with calculations at 20, 30, and 40 °C.

Results for TIP4P water

The precision of the calculations can be addressed by first considering the results for taking the solute as a TIP4P water molecule in solution with 500 TIP4P molecules. For the direct method, a key limitation is the precision for the energy of the solvent box. In Table 1, the computed energy and volume are listed along with their conversion to heat of vaporization and density for four independent runs of 5 B configurations each for the system with 501 TIP4P water molecules. It is found that the mean of the energy is −5040.72 kcal mol⁻¹ with a standard deviation (1σ) of 0.26 kcal mol⁻¹. The computed heat of vaporization (10.654 ± 0.001 kcal mol⁻¹) and density (1.0030 ± 0.0001 g cm⁻³) are consistent with many prior results including the original report from 1983 (10.66 ± 0.03 kcal mol⁻¹ and 0.999 ± 0.007 g cm⁻³)³¹ in spite of differences in the number of water molecules (500 vs. 125) and cutoff distance (10.0 vs. 7.5 Å).

Table 1 Results for liquid TIP4P water (N = 501)^a

Run (5 B)	Energy	Volume	ΔHvap	Density
a Energies in kcal mol^−1; volume in Å^3; density in g cm^−3 at 25 °C and 1 atm. b See ref. 31.
1	−5040.821	14 942.589	10.654	1.00286
2	−5040.385	14 941.301	10.653	1.00295
3	−5041.077	14 937.599	10.654	1.00320
4	−5040.593	14 942.867	10.654	1.00284
Mean	−5040.719	14 941.089	10.654	1.00296
Stnd dev	0.258	2.100	0.001	0.00014
Expt^b			10.51	0.997

---

The minimal dependence of the energy and density for such water models with spherical cutoff distances beyond ca. 7 Å is reexamined in Table 2 with averaging for 1 B configurations. The results for cutoffs of 7 to 11.5 Å are not far from the statistical noise level, while a cutoff of 12.0 Å is likely too long given that the box edge length, which averages 24.6 Å, is fluctuating. This pattern been known for 40 years,^33–35 and is related to the fact that the OO, OH, and HH radial distribution functions for water at 25 °C and 1 atm are flat (g = 1.0) beyond 8 Å, as illustrated in Fig. 1 for g_OO.^36,37 The orientations of water molecules separated by more than 8 Å are not correlated. There is no spatial ordering or net electrostatic interaction that is lost by using a cutoff of 8–10 Å. Thus, there is no need for treatments such as Ewald sums for electrostatic interactions beyond such cutoffs in simulations of small, neutral solutes with water models like TIP4P. Similarly, there is no need for treatments of neglected electrostatic interactions beyond 8 Å in simulations for other pure organic liquids such as ethanol.³²

Table 2 Cutoff dependence of results for liquid TIP4P water (N = 501)^a

Cutoff (Å)	Energy	Volume	ΔHvap	Density
a Energies in kcal mol^−1; volume in Å^3; density in g cm^−3. Results at 25 °C and 1 atm. for averaging for 1 B Monte Carlo configurations except 5 B for cutoff = 10.0 Å. b See ref. 31.ΔHvap = −energy/N + RT (ref. 35).
7.0	−5047.60	15 094.41	10.667	0.99293
8.0	−5043.03	15 056.91	10.658	0.99541
9.0	−5027.39	14 978.71	10.627	1.00060
10.0	−5041.09	14 947.37	10.654	1.00252
11.0	−5030.30	15 034.18	10.633	0.99681
11.5	−5023.28	15 055.02	10.619	0.99553
12.0	−5014.14	15 060.41	10.601	0.99518
Expt^b			10.51	0.997

---

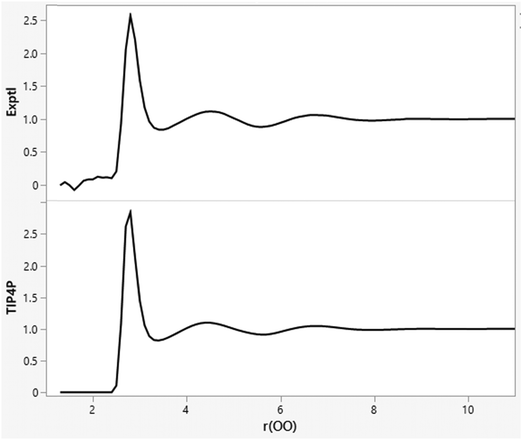Fig. 1 Experimental (top; ref. 36) and TIP4P (bottom) oxygen–oxygen radial distribution functions (g_OO) for liquid water at 25 °C and 1 atm. The computed results are from an MC simulation with 11.5 Å O–O cutoffs. The g_OO curves are flat beyond 8 Å.

Turning to the free energy, the current procedure yielded −6.190 ± 0.035 kcal mol⁻¹ for TIP4P water at 25 °C and 1 atmosphere. The uncertainty was obtained from the batch means procedures with batch sizes of 50 M configurations. The experimental value is −6.324 kcal mol⁻¹ for H₂O.³⁸ As in prior work,^15–19 the standard-state convention of Ben–Naim and Marcus is used such that the gas is ideal and the gas-phase and solution concentrations are the same.³⁸ This removes the need for a pressure-volume term in computing the heats of solution. The computed free-energy result is in agreement with the other highly precise MC result of −6.22 ± 0.02 kcal mol⁻¹ that involved twice as much averaging in each window and 10 replicas.²⁸ It is also notably consistent with the first free-energy result for TIP4P water that was reported in 1989 (−6.06 ± 0.3 kcal mol⁻¹),⁴ which used 216 water molecules and 8.5 Å cutoffs. Subsequently, an MD value of −6.11 ± 0.03 kcal mol⁻¹ was reported in 2005, which used 900 water molecules, 7.5 Å cutoffs, and Ewald corrections.³⁹ Further consistent MD results have been published.^40–42

The results obtained here for the free energy, heat of vaporization and density of TIP4P water at seven temperatures from 15 °C to 45 °C at 1 atm are listed in Table 3. The resulting van’t Hoff plot for the free-energy results is shown in Fig. 2. The fit to a line shows good linearity over this temperature range with a correlation coefficient r² = 0.9900. The slope yields a ΔH of −10.93 kcal mol⁻¹, and in combination with the ΔG of −6.19 kcal mol⁻¹, −TΔS is 4.74 ± 0.3 kcal mol⁻¹. However, focusing around 25 °C, if the five points from 15 to 35 °C are used, ΔH and −TΔS values of −10.64 kcal mol⁻¹ and 4.45 kcal mol⁻¹ are obtained with an r² of 0.9858. From the alternative linear fits and considering the uncertainties in the individual ΔG results, the uncertainty in the computed enthalpies is ca. 0.4 kcal mol⁻¹. For comparison, the experimental ΔH and −TΔS values are −9.97 and 3.65 kcal mol⁻¹,³⁸ as summarized in Table 4.

Table 3 Temperature dependence of results for liquid TIP4P water^a

Temp (C)	ΔGaq	ΔHvap	Density
a Energies in kcal mol^−1; density in g cm^−3. Pressure is 1 atm.
15	−6.402	10.788	1.00822
20	−6.294	10.719	1.00567
25	−6.190	10.654	1.00294
30	−6.206	10.582	0.99960
35	−6.080	10.515	0.99722
40	−5.933	10.451	0.99329
45	−5.945	10.387	0.98915

---

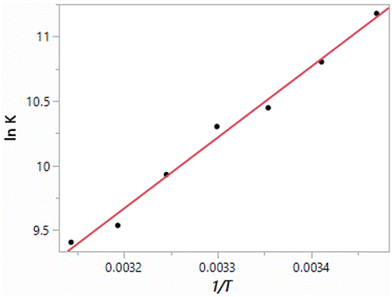Fig. 2 van’t Hoff plot (eqn (4)) computed for TIP4P water.

Table 4 van’t Hoff enthalpies and entropies of hydration (kcal mol⁻¹)^a

Molecule	ΔHhyd TIP4P^b	ΔHhyd exptl^c	−TΔShyd TIP4P^b	−TΔShyd exptl^c	r ^2
a For transfer from the gas phase to aqueous solution at 25 °C and 1 atm. r^2 is the correlation coefficient for the van’t Hoff plot. b Computed by FEP; uncertainties are ca. ±0.4 kcal mol^−1. c Ref. 38.
Ethane	−0.89	−4.172	3.66	6.00	0.7181
Propane	−1.21	−4.826	4.15	6.79	0.9377
Butane	−1.83	−5.655	5.03	7.73	0.9504
Benzene	−5.75	−7.076	6.00	6.22	0.9818
Methanol	−9.39	−10.25	4.78	5.15	0.9965
Ethanol	−11.30	−12.05	6.63	7.05	0.9990
Methylamine	−6.44	−10.269	3.18	5.70	0.9926
Propylamine	−9.62	−12.821	6.64	8.43	0.9996
Water-TIP4P	−10.64	−9.974	4.45	3.65	0.9858
Mean signed error	2.38		−1.35
Mean unsigned error	2.38		1.54

---

Results for organic solutes

Free energies of hydration from FEP calculations and enthalpies of hydration from the direct calculations were carried out for 22 solutes including the 19 molecules in Table 8 of ref. 38 plus phenol, 2-methyl-2-propanol, and water. The results are listed in Table 5 and a plot of the computed enthalpies of hydration vs. the experimental ones is provided in Fig. 3. van’t Hoff plots were generated for eight of the solutes in addition to water. Representative plots are shown in Fig. 4 and the resultant entropy and entropy data are listed in Table 4 along with the correlation coefficients for the linear fits. Based on the results in Table 1 for water and the standard deviations for the total energies using batch sizes of 0.5 B configurations, the uncertainty in the computed enthalpies of hydration from the direct method is ca. ±0.4 kcal mol⁻¹, essentially the same as the uncertainties from the van’t Hoff method. The van’t Hoff plots become more linear as ΔH_hyd becomes more exothermic (Fig. 4), which reflects stronger intermolecular interactions and greater sensitivity of ΔG_hyd to temperature. Thus, the more challenging calculations are for the more hydrophobic solutes, i.e., alkanes, which were not treated in the original studies.^15–19

Table 5 Free energies, enthalpies, and volumes of hydration^a

Molecule	ΔGhyd TIP4P^b	ΔGhyd exptl^c	ΔHhyd TIP4P^d	ΔHhyd exptl^c	ΔVhyd TIP4P^e	ΔVhyd exptl^f
a For transfer from the gas phase to aqueous solution with at 25 °C and 1 atm; energies in kcal mol^−1, volumes in cm^3 mol^−1. b Computed by FEP; uncertainties are ca. ±0.05 kcal mol^−1. c Ref. 38. d Computed by the direct method with MC sampling over 5 B configurations; uncertainties are ca. ±0.4 kcal mol^−1. e The average uncertainty is ±2 cm^3 mol^−1. f Ref. 43. g Ref. 43, estimated. h Ref. 44. i Ref. 45. j Uncertainty is ±0.001 kcal mol^−1.
Methane	2.595	1.99	−0.356	−2.747	38.81	42.5
Ethane	2.767	1.83	−0.722	−4.172	55.71	(52.1)^g
Propane	2.944	1.96	−2.293	−4.826	68.29	57.3
Butane	3.199	2.07	−2.219	−5.655	91.65	(83.9)^g
2-Methylpropane	3.342	2.32	−1.832	−4.825	83.47	(83.9)^g
Benzene	0.251	−0.86	−6.071	−7.076	87.03	82.4^h
Toluene	−0.192	−0.88	−7.346	−8.101	101.63	98.4^h
Ethylbenzene	−0.147	−0.79	−8.730	−9.037	116.34	114.8^h
Methanol	−4.612	−5.10	−9.310	−10.25	41.32	38.2
Ethanol	−4.665	−5.00	−11.411	−12.05	58.22	55.1
Propanol	−4.307	−4.85	−11.398	−13.25	73.74	70.6
Butanol	−4.160	−4.72	−13.256	−13.95	81.66	86.6
2-Methyl-2-propanol	−3.204	−4.47	−10.897	−14.73^i	89.15	87.6
Phenol	−4.557	−6.61	−11.369	−13.06^i	84.40	86.1
Ammonia	−2.928	−4.305	−6.132	−7.874	28.57
Methylamine	−3.259	−4.569	−8.711	−10.269	42.01	41.7
Ethylamine	−3.236	−4.507	−11.166	−12.502	56.23	58.0
Propylamine	−2.978	−4.401	−10.824	−12.821	71.54	74.0
Butylamine	−3.221	−4.302	−12.712	−13.563	86.23	88.8
Diethylamine	−2.723	−4.07	−13.164	−14.762	88.35	90.8
Triethylamine	−1.327	−3.04	−13.756	−16.211	117.77	120.9
Water - TIP4P	−6.190	−6.324	−10.061^j	−9.974	18.07	17.96
Mean signed error	1.00		1.726		0.95
Mean unsigned error	1.00		1.734		3.15

---

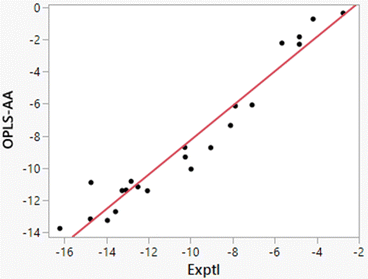Fig. 3 Comparison of experimental and computed enthalpies of hydration from the direct method for 22 solutes (Table 5). The line is the best linear fit and has r² = 0.9433.

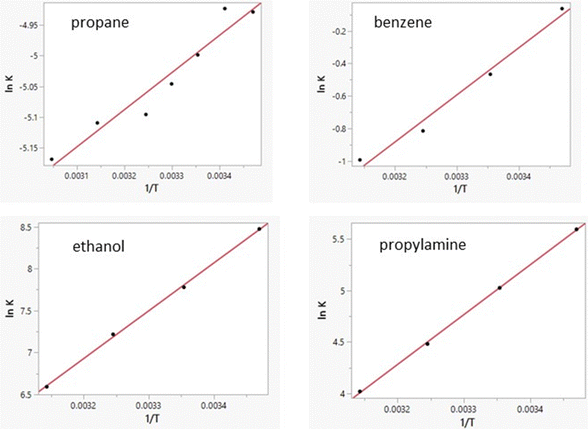Fig. 4 Computed van’t Hoff plots for four solutes in TIP4P water. Linearity improves with increasing slope. i.e., sensitivity of ΔG_aq to temperature.

Additional points should be made. Starting with the FEP results for ΔG_hyd in Table 5, the computed values are generally 1 kcal mol⁻¹ too positive with smaller errors for alcohols and water. As discussed previously,³² OPLS-AA and other non-polarizable force fields, which are optimized for simulations of pure organic liquids, utilize atomic partial charges that are under-polarized for the higher dielectric environment in aqueous solutions.^14,26 The results in Tables 4 and 5 show that the error is enthalpic in origin with the heats of solution for organic molecules being too positive by 2–3 kcal mol⁻¹; the best linear fit illustrated in Fig. 3 is ΔH(OPLS-AA) = 1.072 × ΔH(Exptl) + 2.447. The enthalpy error is partially compensated by the entropy contribution being less unfavorable by 1–2 kcal mol⁻¹. The errors are most serious for alkanes and highly alkylated molecules like triethylamine. Polarization of the solutes by the solvent is needed for proper treatment of solvation in general, and especially in these cases.⁴⁶

As illustrated in Fig. 3, the computed heats of solution parallel well the experimental data. Consequently, differences ΔΔH_hyd benefit from cancellation of errors as for ΔΔG_hyd, which contributes to the success of relative FEP calculations in many contexts including protein–ligand binding.^32,47,48 The computed enthalpies of hydration from the two methods, direct and van’t Hoff, also correlate well, as shown in Fig. 5; their average difference is 0.69 kcal mol⁻¹, which is within the expected uncertainties. The largest deviation is for methylamine for which the two methods differ by 2.27 kcal mol⁻¹ (−8.71 vs. −6.44 kcal mol⁻¹). The similar results for ethane, propane, and butane from the two methods are reassuring for the accuracy of the results in view of the more challenging convergence in these cases.

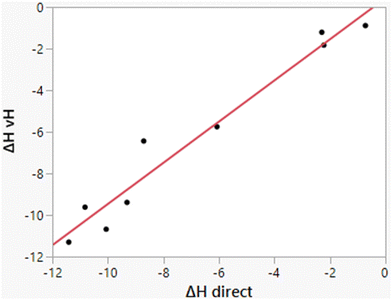Fig. 5 Comparison of results for ΔH_hyd from the direct and van’t Hoff calculations. The line represents the best linear fit and has r² = 0.9559. The mean difference is 0.69 kcal mol⁻¹.

The enthalpy of TIP4P water, −10.061 ± 0.001 kcal mol⁻¹, in Table 5 just comes from dividing the total energy in Table 1 by N = 501. Combination with the free energy of −6.190 ± 0.035 yields −TΔS = 3.872 ± 0.035 kcal mol⁻¹. These results are in close accord with the corresponding experimental values of −9.974, −6.324, and 3.650 kcal mol⁻¹.³⁸ The discrepancy between the precise enthalpy change (−10.061 kcal mol⁻¹) and the van’t Hoff result (−10.64 kcal mol⁻¹) can be attributed to the uncertainty in the van’t Hoff result and to the fact that the ΔH_hyd is not fully temperature independent, as assumed in the van’t Hoff analysis. However, the change in heat capacity for the system upon transfer of the solute from the gas phase into aqueous solution, ΔC_p,hyd, is sufficiently small that the resultant curvature in the van’t Hoff plots is not detectable given the temperature range and precision of the computed free energy changes.⁴⁹

The computed partial molar volumes from the direct calculations are also included in Table 5 and compared with available experimental data.^43,44 In this case, the average uncertainty in the computed values is ±2.2 cm³ mol⁻¹ from the batch means procedure with batch sizes of 0.5 B configurations, while alternative experimental measurements often differ by 1–2 cm³ mol⁻¹.⁴⁴ The mean unsigned error between the computed and experimental values is 3.15 cm³ mol⁻¹, which is within the combined uncertainties. It may be noted that the current result for benzene in TIP4P water, 87.0 ± 2.2 cm³ mol⁻¹, is consistent with the prior report²⁹ of 81.2 ± 5.1 cm³ mol⁻¹ that was obtained from averaging over 1 B MC configurations as opposed to the current 5 B configurations. The good computed results for the volumes of solution undoubtedly benefit from the average errors of only 1% in the densities of TIP4P water and OPLS-AA organic liquids.^31,32

Overall, this study finds that the present MC-based methodologies for computing enthalpies of hydration are competitive in precision with both giving average uncertainties of ±0.4 kcal mol⁻¹. However, the direct method is much faster since it requires 5 B configurations of averaging, while the van’t Hoff approach uses FEP calculations at four temperatures encompassing 14 B configurations of averaging at each temperature. On a 3.5-GHz Intel i5 processor, the run times are about 35 hours for the direct calculation and 392 hours to obtain the 4-point van’t Hoff result or 294 hours for 3 temperatures. It is straightforward to improve the precision of the calculations by extending the MC averaging in both cases. Quadrupling the length of the MC averaging can be expected to halve the statistical uncertainty for the computed enthalpies of hydration to ca. ±0.2 kcal mol⁻¹. Though the calculations are already long by traditional MC standards, the four-fold extension for the direct approach to 6 days of computing per solute would be manageable, while 50–65 days for the van’t Hoff calculations would be taxing for processing many solutes. Nevertheless, observance of strong linearity in the van’t Hoff plots provides reassurance for the absence of significant sampling problems in the calculations (Fig. 4). In the end, both approaches are viable, and applying both provides a valuable check for consensus. For computation of volumes of solution, it was also found that the direct method was more efficient for a given level of precision than the FEP-based derivative one.²⁹

Conclusions

Computation of enthalpies and entropies of hydration for organic solutes has been examined using long Monte Carlo simulations in the direct and van’t Hoff approaches. Both methods are viable with the current implementations yielding similar uncertainties of ca. ±0.4 kcal mol⁻¹. The direct method used 5 B configurations of averaging, while the demands for the van’t Hoff alternative are about 10 times greater owing to the use of 20 FEP windows, separate annihilations of the partial charges and Lennard–Jones interactions, and four temperatures. Nevertheless, the van’t Hoff plots are appealing with their linearity providing a measure of confidence in precision. The direct calculations were also found to yield volumes of solution in good accord with experimental data and with precision of ca. ±2 cm³ mol⁻¹. Furthermore, the present results provided valuable insights on the performance of the OPLS-AA force field. The error in computed free energies of hydration of 1 kcal mol⁻¹ is found to come from enthalpies of hydration that are not exothermic enough by 2–3 kcal mol⁻¹, which is partially compensated by a less unfavorable entropy contribution by 1–2 kcal mol⁻¹. With fixed-charge force fields parameterized to give accurate results for pure organic liquids, interactions between organic solutes and water are not attractive enough. The problem can be remedied with polarizable force fields. Testing on not only free energies of hydration, but also its enthalpic and entropic components should now become routine.

Conflicts of interest

The author declares that there are no competing interests.

Acknowledgements

Gratitude is expressed to the National Institutes of Health (GM032136) for support of this research.

References

1. W. L. Jorgensen and C. Ravimohan, J. Chem. Phys., 1985, 83, 3050–3056.
2. T. P. Straatsma, H. J. C. Berendsen and J. P. M. Postma, J. Chem. Phys., 1986, 85, 6720–6727.
3. J. Hermans, A. Pathiaseril and A. Anderson, J. Am. Chem. Soc., 1988, 110, 5982–5986.
4. W. L. Jorgensen, J. F. Blake and J. K. Buckner, Chem. Phys., 1989, 129, 193–200.
5. W. L. Jorgensen, Acc. Chem. Res., 1989, 22, 184–189.
6. P. A. Kollman, Chem. Rev., 1993, 93, 2395–2417.
7. C. Chipot and A. Pohorille, in Springer Series in Chemical Physics, Free Energy Calculations: Theory and Applications in Chemistry and Biology, ed. C. Chipot and A. Pohorille, Springer-Verlag, Berlin, 2007, vol. 86, pp. 33–75.
8. W. L. Jorgensen and J. Tirado-Rives, Perspect. Drug Discovery Des., 1995, 3, 123–128.
9. D. J. Price and C. L. Brooks, III, J. Comput. Chem., 2005, 26, 1529–1541.
10. W. L. Jorgensen and L. L. Thomas, J. Chem. Theory Comput., 2008, 4, 869–876.
11. D. L. Mobley, C. I. Bayly, M. D. Cooper, M. R. Shirts and K. A. Dill, J. Chem. Theory Comput., 2009, 5, 350–358.
12. D. L. Mobley and J. P. Guthrie, J. Comput.-Aided Mol. Des., 2014, 28, 711–720.
13. E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren and J. L. Knight, et al. , J. Chem. Theory Comput., 2016, 12, 281–296.
14. L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 3864–3870.
15. M. M. Kubo, E. Gallicchio and R. M. Levy, J. Phys. Chem. B, 1997, 101, 10527–10534.
16. R. M. Levy and E. Gallicchio, Annu. Rev. Phys. Chem., 1998, 49, 531–567.
17. S. Wan, R. H. Stote and M. Karplus, J. Chem. Phys., 2004, 121, 9539–9548.
18. J. Carlsson and J. Åqvist, Phys. Chem. Chem. Phys., 2006, 8, 5385–5395.
19. J. Carlsson and J. Åqvist, J. Phys. Chem. B, 2009, 113, 10255–10260.
20. S. Bjelic, B. O. Brandsdal and J. Åqvist, Biochem., 2008, 47, 100049–100057.
21. J. Åqvist and S. C. L. Kammerlin, Sci. Rep., 2015, 5, 15817.
22. J. Åqvist, M. Kazemi, G. V. Isaksen and B. O. Brandsdal, Acc. Chem. Res., 2017, 50, 199–207.
23. J. Socan, M. Purg and J. Åqvist, Nat. Commun., 2020, 11, 2644.
24. J. Åqvist, ACS Catal., 2022, 12, 1452–1460.
25. R. S. Wilkins, B. A. Lund, G. V. Isaksen, J. Åqvist and B. O. Brandsdal, J. Chem. Theory Comput., 2024, 20, 451–458.
26. H. S. Ashbaugh, L. Liu and L. N. Surampudi, J. Chem. Phys., 2011, 135, 054510.
27. W. L. Jorgensen, B. Bigot and J. Chandrasekhar, J. Am. Chem. Soc., 1982, 104, 4584–4591.
28. I. Cabeza de Vaca, R. Zarzuela, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2019, 15, 3941–3948.
29. J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, Phys. Chem. Chem. Phys., 2015, 17, 8407–8415.
30. W. L. Jorgensen and J. Tirado-Rives, J. Comput. Chem., 2005, 26, 1689–1700.
31. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
32. W. L. Jorgensen, M. Ghahremanpour, A. Saar and J. Tirado-Rives, J. Phys. Chem. B, 2024, 128, 250–262.
33. C. Pangali, M. Rao and B. J. Berne, Mol. Phys., 1980, 40, 661–680.
34. W. L. Jorgensen, Chem. Phys. Lett., 1982, 92, 405–410.
35. W. L. Jorgensen and J. D. Madura, Mol. Phys., 1985, 56, 1381–1392.
36. L. B. Skinner, C. Huang, D. Schlesinger, L. G. M. Pettersson, A. Nilsson and C. J. Benmore, J. Chem. Phys., 2013, 138, 074506.
37. T. Head-Gordon and G. Hura, Chem. Rev., 2002, 102, 2651–2670.
38. A. Ben-Naim and Y. Marcus, J. Chem. Phys., 1984, 81, 2016–2027.
39. M. R. Shirts and V. J. Pande, J. Chem. Phys., 2005, 122, 134508.
40. M. J. Vlot, J. Huinink and J. P. van der Eerden, J. Chem. Phys., 1999, 110, 55–61.
41. F. Saija, A. M. Saitta and P. V. Giaquinta, J. Chem. Phys., 2003, 119, 3587–3589.
42. L. Wang, R. Abel, R. A. Friesner and B. J. Berne, J. Chem. Theory Comput., 2009, 5, 1462–1473.
43. L. Lepori and P. Gianni, J. Solution Chem., 2000, 29, 405–447.
44. S. Sawamura, K. Nagaoka and T. Machikawa, J. Phys. Chem. B, 2001, 105, 2429–2436.
45. G. I. Makhatadze and P. L. Privalov, J. Mol. Biol., 1993, 232, 639–659.
46. C. R. Rupakheti, A. D. MacKerell, Jr. and B. Roux, J. Chem. Theory Comput., 2021, 17, 7085–7095.
47. Z. Cournia, B. Allen and W. Sherman, J. Chem. Inf. Model., 2017, 57, 2911–2937.
48. C. Chipot, Annu. Rev. Biophys., 2023, 52, 113–138.
49. Collin D. Wick, J. I. Siepmann and M. R. Schure, J. Phys. Chem. B, 2003, 107, 10623–10627.

---