Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unraveling the enigma of Craig-type Möbius-aromatic osmium compounds†
Antonia
Rabe
 ab,
Qian
Wang
ab,
Qian
Wang
 b and
Dage
Sundholm
b and
Dage
Sundholm
 *b
*b
aDepartment Chemie, Johannes Gutenberg-Universität Mainz, Duesbergweg 10–14, 55128 Mainz, Germany. E-mail: arabe@students.uni-mainz.de
bDepartment of Chemistry, Faculty of Science, University of Helsinki, P. O. Box 55 (A. I. Virtasen aukio 1), FIN-00014, Helsinki, Finland. E-mail: dage.sundholm@helsinki.fi
First published on 13th June 2024
Abstract
Nuclear magnetic resonance (NMR) chemical shifts and the magnetically induced current density (MICD) susceptibility of four osmium containing molecules have been calculated at the density functional theory (DFT) level using three relativistic levels of theory. The calculations were performed at the quasi-relativistic level using an effective core potential (ECP) for Os, at the all-electron scalar exact two-component (X2C) relativistic level, and at the relativistic X2C level including spin–orbit coupling (SO-X2C). In earlier studies, the osmapentalene (1) and the osmapentalynes (2 and 3) were considered Craig-type Möbius aromatic and it was suggested that the analogous osmium compound (4) is Craig-type Möbius antiaromatic. Here, the ring-current strengths were obtained with the gauge including magnetically induced currents (GIMIC) method by integrating the MICD susceptibility passing through planes that intersect chemical bonds and by line integration of the induced magnetic field using Ampère-Maxwell's law. The ring-current calculations suggest that 1, 2 and 3 are weakly aromatic and that 4 is nonaromatic. The accuracy of the MICD susceptibility was assessed by comparing calculated NMR chemical shifts to available experimental data. Visualization of the MICD susceptibility shows that the ring current does not pass from one side of the molecular plane to the other, which means that the MICD susceptibility of the studied molecules does not exhibit any Möbius topology as one would expect for Craig-type Möbius aromatic and for Craig-type Möbius antiaromatic molecules. Thus, molecules 1–3 are not Craig-type Möbius aromatic and molecule 4 is not Craig-type Möbius antiaromatic as previously suggested. Calculations of the 1H NMR and 13C NMR chemical shifts of atoms near the Os atom show the importance of including spin–orbit effects. Overall, our study revisits the understanding of the aromaticity of organometallic molecules containing transition metals.
1 Introduction
International Union of Pure and Applied Chemistry (IUPAC) states in the Gold Book that cyclic molecular systems are aromatic when they are energetically stabilized due to electron delocalization and they are structurally more stable than nonaromatic molecules when undergoing chemical transformations.1–3 The structural aromaticity criterion is a small bond-length alternation and the magnetic criterion is that aromatic molecular rings sustain a net diatropic ring current when they are exposed to an external magnetic field. The magnetically induced diatropic ring current is experimentally observed in 1H NMR spectra as a shift of the NMR signal of the protons on the outside of the ring to larger chemical shifts (smaller magnetic shielding constants) than in the absence of the ring current. The structural and magnetic criteria of antiaromaticity are larger bond-length alternation and their ability to sustain a net paratropic ring current when exposed to an external magnetic field, respectively. The paratropic ring current shields the outer protons of antiaromatic molecules leading to a shift of the 1H NMR chemical shift signals to smaller values (larger magnetic shielding constants). Antiaromatic molecules must be energetically more stable than nonaromatic molecules because nothing else prevents antiaromatic molecules from becoming nonaromatic. Thus, the delocalized electrons of antiaromatic molecules sustaining a paratropic ring current stabilize the ring. Since the energetic stabilization of antiaromatic molecules is much smaller than the aromatic stabilization energy, antiaromatic molecules are difficult to synthesize and are therefore rather rare.Based on Hückel's molecular orbital (HMO) theory,4–6 the aromatic nature of molecular rings can be estimated by counting the number of electrons in the conjugated bonds of the ring. A ring with 4n + 2 electrons in the conjugated orbitals is expected to be aromatic, whereas 4n electrons in them lead to antiaromaticity, if that is energetically more favourable than nonaromaticity. Hückel's aromaticity rules hold for closed-shell molecules. The rules can be applied to open-shell molecules by separately considering spin-up and spin-down electrons.7 They can also be generalized to open-shell systems by counting the number of occupied conjugated orbitals. The generalized aromaticity rule then reads: a molecular ring with odd number of occupied conjugated orbitals is aromatic and when it has even number of occupied conjugated orbitals, it is antiaromatic.8 Hückel's aromaticity rules can easily be applied to organic molecules, whereas it is challenging to count the number of occupied conjugated orbitals and their electrons when the molecular ring contains a transition metal with a partially filled d shell. The electron density of the conjugated bonds might also provide information about the aromatic stabilization involving the d orbitals.9
Hückel's aromaticity rules that were originally aimed for planar molecules have been extended to Möbius-twisted molecular structures.10–15 The aromaticity of molecules whose linking number (Lk) is even follows largely the aromaticity rules of planar molecules, whereas the aromaticity rules for molecules whose linking number is odd are the opposite, namely molecular ring with even number of conjugated orbitals are aromatic and they are antiaromatic when they have odd number of conjugated orbitals in the twisted ring.
The linking number (Lk) consists of the twist (Tw) and the writhe (Wr) contributions, the sum of which is always equal to Lk.16–18 Twist is a local property of the molecular frame, whereas writhe is a global property representing the deformation of the molecular ring. The Lk value can be positive or negative. The energy depends only on the absolute Lk value, whereas rings with different sign of Lk have different chirality. For example, a doubly Möbius-twisted molecular ring can continuously change from a circular twisted structure with a Tw value of close to two to a lemniscular structure with a Wr value of nearly two. Calculations of the magnetically induced ring current for a series of doubly Möbius-twisted C40H40 annulenes showed that strongly twisted rings sustain a stronger magnetically induced ring current than lemniscular structures.15
In planar rings with conjugated bonds, the p orbitals of the individual atoms can be considered to have the same phase around the ring. A Möbius-twisted molecular structure leads to a phase shift of the p orbitals implying that when following the phase of the p orbitals, one has to make two laps around the ring to return to the starting point. Craig and Paddock suggested that Möbius topology of the molecular orbitals can also be introduced by d orbitals of a transition metal in the ring, which also may lead to reverse aromaticity rules even for planar molecules.19,20 The d orbitals of the transition metal forming d-p π bonding cause a phase shift of the p orbitals around the molecular ring as shown in Fig. 1. They proposed that the periodicity in the Craig-type Möbius case also involves two laps around the ring. The formal change in the orbital phase is considered to occur between the p orbital of the carbon atom on one side of the d orbital of the osmium atom.19 However, when following the orbital phase around the ring, another phase change must occur along the ring to obtain the initial orbital phase when reaching the osmium atom again. Since there must be two or at least an even number of phase changes around the molecular ring, the aromatic nature of the ring follows the aromaticity rule of evenly Möbius twisted molecular rings, which is the same as the Hückel aromaticity rule of planar conjugated hydrocarbon rings.13–15
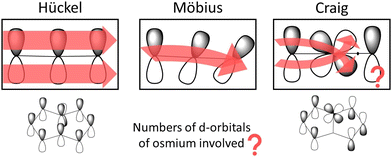 | ||
| Fig. 1 The phase of the orbitals of molecular rings with Hückel, Möbius and Craig-type Möbius topology. The picture has been made with PerkinElmer ChemDraw and Microsoft PowerPoint. | ||
However, there is also another significant difference between Möbius and Craig-type Möbius topologies, i.e., molecular structures can be observed, whereas orbitals and their phase are not observables. The electron probability density of time-independent electronic states is positively definite implying that it cannot be used for detecting an eventual Craig-type Möbius topology. The magnetically induced current density susceptibility, which is a vector function for a given direction of the external magnetic field, may reveal whether a molecular ring has Craig-type Möbius topology in the presence of an external magnetic field.
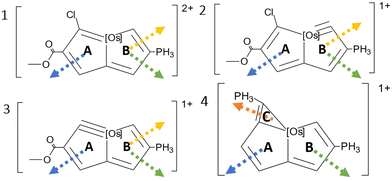
Here, we calculate the magnetically induced current density (MICD) susceptibility and nuclear magnetic resonance (NMR) shielding constants for the aromatic osmapentalene (1) and aromatic osmapentalynes (2 and 3) as well as for an analogous osmium compound (4), which is considered to be antiaromatic. The studied osmium compounds have been suggested to exhibit Craig-type Möbius topology.21–26 Ring-current pathways and their strengths are calculated to determine the aromatic character and the topology of the current density of the studied molecules. The calculations are performed at different relativistic levels of theory. The reliability of the calculated MICD susceptibilities are assessed by comparing calculated NMR shielding constants to experimental data. The main result of the study is that Craig-type Möbius aromaticity and Craig-type Möbius antiaromaticity may not exist because the MICD susceptibility lacks Möbius topology.
2. Computational methods
The molecular structures were optimized with Turbomole27–29 at the density functional theory (DFT) level employing the ωB97X-D functional,30,31 triple-ζ polarization (def2-TZVP) basis sets,32 and an effective core potential (ECP)33,34 that replaces the core electrons of osmium. The structures were optimized for the lowest singlet state without using any symmetry constraints. Solvent effects in CDCl2 were estimated by using COSMO as implemented in Turbomole.35,36 The Cartesian coordinates of the molecular structures are given in the ESI.† Calculated bond lengths are also compared to experimental data in the ESI.†The nuclear magnetic resonance (NMR) shielding tensors were calculated with the mpshift program of Turbomole.37–39 The NMR shielding tensors were calculated at the quasi-relativistic level using a relativistic ECP for osmium using the def2-TZVP and quadruple-ζ polarization (def2-QZVP) basis sets.32,37,40 They were also calculated at the scalar relativistic exact two-component (X2C) level38 and at the SO-X2C level including spin–orbit coupling39 using triple-ζ polarization basis sets developed for one- and two-component all-electron relativistic electronic structure calculations.41
The magnetically induced current-density (MICD) susceptibility tensor was calculated in the limit of zero magnetic field using the gauge-including magnetically induced current (GIMIC) method,42–46 which uses the one-particle density matrix, the three magnetically perturbed density matrices, the Cartesian coordinates of the molecular structure, and basis set information as input. The magnetically induced current (MIC) density for a given direction of the external was obtained with GIMIC by contracting the MICD susceptibility tensor with a magnetic field that is perpendicular to the molecular plane in Fig. 2. Ring-current profiles and ring-current strengths were obtained by integrating the MIC passing through planes that intersect chemical bonds as shown with the arrows in Fig. 2. The integration plane begins in the geometrical center of the ring and ends very far away from the molecule where the MIC vanishes. The MIC was also separated into diatropic and paratropic contributions by using a Runge-Kutta approach.47 The diatropic contributions to the MIC pathways are visualised using Para-View.48
The ring-current strengths were also calculated by using Ampère-Maxwell's law.49 When the external magnetic field (B) is applied along the z axis, the induced magnetic field along the z axis (Binduced,z) can be obtained from the zz-component of the NMR shielding tensor (σzz).
| Binduced,z = −σzz·Bexternal | (1) |
The ring-current strength can then be calculated by integrating Binduced,z along the center line of the ring-current vortex, which is assumed to be vertical and perpendicular to the ring in the xy-plane. The integration line passes through the center of the ring and continues to infinity in the positive and negative z-direction, where σzz vanishes. The geometrical center and the vortex center are assumed to coincide.
Equal ring-current strengths are obtained by integrating the MIC (J) passing through the cross section S or by the line integration along the edges of S.
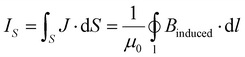 | (2) |
Line integration along the three other edges of the integration plane does not contribute to the ring-current strength because Binduced vanishes far away from the molecule. Since the shielding cone of the ring current declines very slowly with the distance from the molecule, the line integration range must extend very far outside the electron density of the molecule.
The line-integration approach is robust and easy to implement, since the ring-current strength depends only on the values of the magnetic shielding tensor elements. However, when choosing the starting coordinates of the line integration, it is necessary to find the center of the current vortex, which can be done by using the ring-current profile analysis implemented in GIMIC or by visually inspecting the calculated current-density contributions using ParaView. Once an appropriate vortex center has been determined, the line-integration approach can be easily used for comparing ring-current strengths that are for example obtained at different levels of theory. Ring-current strengths are obtained by integrating the ring-current profile.43 In the complete basis-set limit, the two approaches yield the same ring-current strength.
The line integration was performed using a general Gauss-Lobatto-Legendre (GLL) quadrature that was implemented as in Ref. 50. To ensure that the whole ring current is considered, an integration range of z = [0,106] bohr was used. Since the studied molecules have a mirror xy-plane, the strength of the ring current is the same above and below the plane. The integration range was divided into five elements with 20 integration points in each interval. The first four intervals cover z = [0,20] bohr, whereas the fifth interval has logarithmic scaling in the range z = [log(20), log(106)] bohr. The line integration has higher numerical accuracy than the numerical precision of the σzz values calculated with the mpshift program.
The ring-current strength is used as aromaticity index. Aromatic molecules sustain a net diatropic ring current in the classical direction, whereas antiaromatic molecules sustain a paratropic ring current, i.e., in the nonclassical direction. Nonaromatic molecules sustain a very weak net ring current.
We calculated ring-current profiles (dIS(x)/dx) passing through the integration planes (S) shown in Fig. 2, where x is the in-plane direction of S. The ring-current strength (IS) passing through the plane is obtained by numerically integrating dIS(x)/dx. The ring current on the outside of the molecular frame far away from the molecule is always diatropic and set to be positive. The sign of IS must be carefully assessed because it depends on the relative direction of the magnetic field and on the integration direction. The ring-current profile shows positive and negative regions due the direction the ring current. When the net ring-current strength is positive, the ring current is diatropic, whereas it is negative for paratropic ring currents. Benzene, which is a typical aromatic molecule, has a net diatropic ring current of 11.8 nA T−1.51 Benzene sustains a diatropic ring current on the outside and a paratropic ring current on the inside of the aromatic ring.51 The ring-current profile of antiaromatic molecules is dominated by the paratropic contribution. In this work, the line integration using Ampère-Maxwell's law yields the total ring-current strength, even though ring-current profiles can also be calculated with that approach.49
3 Results and discussion
3.1 Ring-current strengths
The ring-current strengths in Table 1 were calculated with the ωB97X-D functional using line integration and Ampère-Maxwell's law. Relativistic effects were considered by using an effective core potential (ECP) for Os, at the all-electron scalar-relativistic one-component X2C level and at the all-electron fully relativistic two-component X2C level (SO-X2C) that also considers spin–orbit coupling effects. Basis sets developed for all-electron relativistic electronic structure calculations were used.41 In the ECP calculations we used def2-TZVP basis sets.32 Almost the same ring-current strengths are obtained at the three levels of theory. The profile of the ring current passing the planes in Fig. 2 are shown in the ESI.†| Molecule | Ring | ECP | X2C | SO-X2C |
|---|---|---|---|---|
| 1 | A | 5.29 | 5.38 | 5.31 |
| B | 6.85 | 6.89 | 6.65 | |
| 2 | A | 5.63 | 5.69 | 5.58 |
| B | 5.53 | 5.51 | 5.54 | |
| 3 | A | 4.71 | 4.72 | 4.78 |
| B | 7.96 | 8.03 | 7.81 | |
| 4 | A | −1.15 | −1.11 | −1.18 |
| B | 0.34 | 0.31 | 0.28 | |
| C | 8.40 | 8.44 | 8.31 |
At the SO-X2C level, 1 sustains a net diatropic ring current of 5.31 nA T−1 and 6.65 nA T−1 in ring A and B, respectively. Since the ring-current strengths are about half the one for benzene and of about the same strength around the two rings, 1 can be considered to be weakly global aromatic.
Molecule 2 sustains a net ring current of 5.58 nA T−1 around ring A, which is similar to the ring current of 5.54 nA T−1 in ring B suggesting that 2 is also weakly global aromatic.
The A ring of 3 sustains a ring current of 4.78 nA T−1 and the ring current of the B ring is 7.81 nA T−1 suggesting that 3 is weakly global aromatic with a dominating ring current around B.
The A and B rings of 4 do not sustain any strong ring currents. The net ring current at A is weakly paratropic and the one around B is close to zero. As the ring-current strengths are very small, 4 is considered nonaromatic. The three-membered ring C sustains a diatropic ring current of 8.31 nA T−1, which is 70% of the ring-current strength of benzene.
Calculations of the ring-current strengths at different levels of theory show that roughly the same ring-current strengths are obtained at all relativistic levels of theory. Thus, spin–orbit coupling has a small effect on ring-current strengths, which has also been previously reported for osmabenzene and similar molecules.52 We performed current-density and NICS calculations on osmabenzene and obtained results that agree with those reported in Ref. 52
3.2 Ring current pathways
The current-density pathway of 1 is shown in Fig. 3. The molecule sustains a global ring current around rings A and B. The ring current avoids Os making a bent detour on the inside of it due to the strong paratropic atomic current on Os. The conflicting directions of the diatropic and paratropic current-density pathways at Os forces the diatropic one to pass on the inside of Os, notably without crossing from one side of the molecular plane to the other side. Thus, the current-density pathway has no Möbius topology.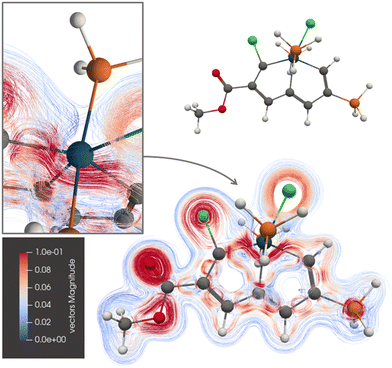 | ||
| Fig. 3 The diatropic current-density pathways in 1. The detailed picture shows that the ring current avoids Os. A 3D molecular structure of 1 is also shown. The figure is made with ParaView. | ||
The current-density pathway around ring A of 2 is similar to the one for 1 as seen in Fig. 4. Again, the ring current passes on the inside of the osmium atom to avoid its paratropic atomic current. The ring current does not exhibit any Möbius topology.
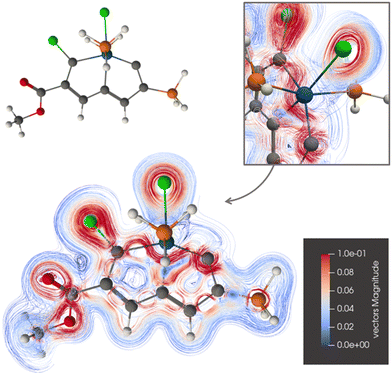 | ||
| Fig. 4 The diatropic current-density pathways in 2. The detailed picture shows that the ring current avoids Os. A 3D molecular structure of 2 is also shown. The figure is made with ParaView. | ||
Ring B of 3 sustains a ring current of 7.81 nA T−1, whereas the ring-current strength of the A ring is only 4.78 nA T−1. The picture of the current-density pathways of 3 in Fig. 5 shows that the ring current passing on the inside of the Os atom splits at its neighbouring carbon atom of ring A into a ring-current branch around ring A and a shortcut route to ring B on the inside of A leading to the weaker ring-current strength at plane A. One branch of the current-density pathway flows along the C–Os bond in the middle and bends towards the carbon atom next to Os of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C moiety, it returns towards Os and passes on the inside of it.
C moiety, it returns towards Os and passes on the inside of it.
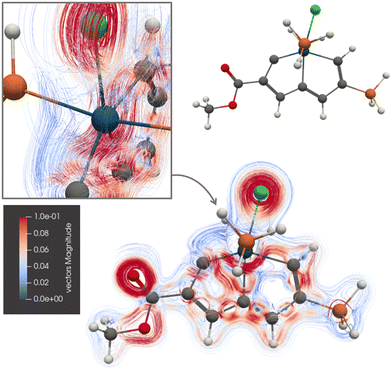 | ||
| Fig. 5 The diatropic current-density pathways in 3. The detailed picture shows that the ring current avoids Os. A 3D molecular structure of 3 is also shown. The figure is made with ParaView. | ||
The current-density pathways of 4 differ from the ones for 1, 2, and 3, which Zhu et al.22,23 and Cai et al.25 suggested that are aromatic. Chen et al. suggested that 4 is antiaromatic.26 The picture of the current-density pathway of 4 in Fig. 6 and the ring-current strengths in Table 1 shows that 4 is globally nonaromatic. Molecule 4 sustains local paratropic ring currents inside ring A and B as naphthalene.44 The paratropic current density of 4 is shown in the ESI.† There is a strong diatropic ring current around ring C that passes on the inside of the Os atom, where it avoids the paratropic atomic current of Os. The ring current of ring C makes a shortcut through ring A and follows the common bond of ring A and B towards Os. The global ring current around rings A and B is very weak and of different sign corresponding to nonaromaticity.
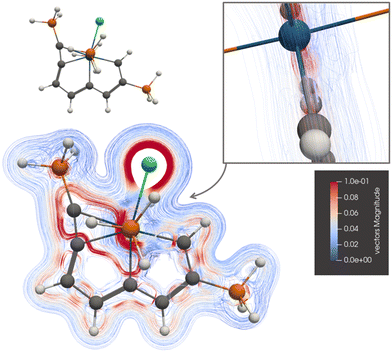 | ||
| Fig. 6 The diatropic current-density pathways in 4. The detailed picture shows that the ring current avoids Os. A 3D molecular structure of 4 is also shown. The figure is made with ParaView. | ||
The deviations between calculated and measured 13C NMR and 1H NMR chemical shifts of 3 and 4 are shown in Fig. 7 and 8, respectively. Similar comparisons for 1 and 2 are reported in the ESI.† Almost the same 1H NMR chemical shifts are obtained in calculations at quasi-relativistic and scalar relativistic levels, whereas significant spin–orbit contributions are obtained for the 1H NMR chemical shifts of the H1 proton at the C1 carbon atom next to Os. Solvent effects calculated using COSMO shift the signal only slightly. The spin–orbit contribution increases the deviation from the measured 1H NMR chemical shifts because the expected accuracy of the DFT calculations is of the same size as the discrepancy between the calculated and measured values. Vibrational effects are not considered here. The 13C NMR chemical shifts have also large spin–orbit contributions leading to significantly smaller deviations between calculated and measured 13C NMR chemical shifts for C1, C4 and C7, which are bound to Os. The calculated NMR chemical shifts are compared to experimental values in the ESI.† Calculations with the def2-QZVP basis sets yielded practically the same chemical shifts regarding 1H NMR, whereas the 13C NMR chemical shifts are a few ppm larger with the def2-QZVP basis sets than with the def2-TZVP basis sets.
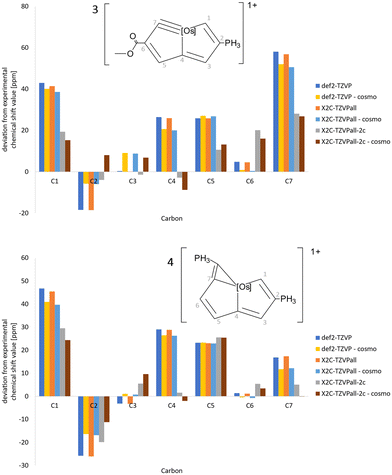 | ||
| Fig. 7 The deviations of the 13C NMR chemical shift values of 3 and 4 calculated at different levels of theory from experimental values. | ||
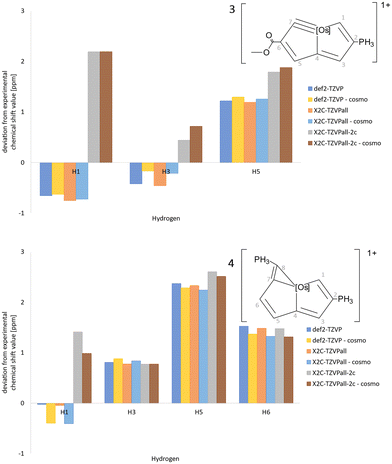 | ||
| Fig. 8 The deviations of the 1H NMR chemical shift values of 3 and 4 calculated at different levels of theory from experimental data. | ||
The 13C NMR chemical shift of C8 in ring C of 4 is most likely incorrectly assigned in the experimental study by Chen et al.26 because the corresponding signal of the compound with the triphenyl phosphine substituent at C8 replaced by para-methylated triphenyl phosphine appears at 21.42 ppm, which is in excellent agreement with the calculated 13C NMR chemical shift of 24.70 ppm.
4. Conclusions
The aromatic nature of the osmium-containing molecules 1–4 has been determined by calculating the magnetically induced current density (MICD) susceptibility and the magnetically induced current density (MIC) when the external magnetic field is perpendicular to the molecular ring. The integrated ring-current strengths show that molecule 1, 2 and 3 are weakly aromatic, whereas 4 is globally non-aromatic. Visualising the current-density pathways shows that molecule 1, 2 and 3 are completely dominated by diatropic ring currents. Some local paratropic contributions appear in the center of the five-membered rings as well as around the Os atom and at the carbon atom with the triple bond next to osmium. The main diatropic ring current bends inwards and avoids the Os atom, while showing Hückel topology. Thus, the number of electrons in the conjugated bonds must be 4n + 2, if the aromaticity follows the same rules as for conjugated hydrocarbon rings. Planar Craig-type Möbius twisted molecules must involve an even number of changes of the phase of the orbitals around the ring implying that they should follow Hückel's aromaticity rules for planar conjugated hydrocarbon rings. Since the ring current does not cross nor touch the molecular plane, molecules 1–3 are Hückel aromatic.Calculations on molecule 4 show that the eight-membered ring does not sustain any global diatropic ring current, whereas its third ring sustains a diatropic ring current, whose strength is 70% of the ring-current strength of benzene. Spin–orbit coupling does not significantly affect the ring-current strengths as previously reported for osmabenzene and similar molecules,52 whereas the spin–orbit coupling contributions to the 13C NMR chemical shift can be a few tens of ppm. Chen et al. reported nucleus independent chemical shift (NICS(0)πzz) values of 28.4 and 28.6 ppm for ring A and B of molecule 4 even though the molecule does not sustain any significant ring current. We obtained similar NICS(0)zz values of 31.7 and 27.0 ppm. NICS values are not a reliable aromaticity index for organometallic rings containing osmium and other transition metals with a partially filled d shell because they sustain a strong paratropic atomic current density in the d orbitals. The atomic current density contributes significantly to NICS values in the vicinity of the metal, which has also been previously reported in a study on osmabenzene and similar molecules.52
Our study shows that the molecules are neither Craig-type Möbius aromatic nor Craig-type Möbius antiaromatic as previously proposed.23,25,26 Despite our efforts to identify an eventual Craig-type Möbius topology and associated aromaticity, the obtained ring-current pathways instead confirm Hückel aromaticity, which suggests that Craig-type Möbius aromaticity is not completely understood or that it may even be a theoretical construct lacking experimental evidence. Overall, our study changes the understanding of the aromatic nature of organometallic molecules containing transition metals.
Data availability
The data supporting this article have been included as part of the ESI.† The DFT calculations were performed with Turbomole version 7.8-beta. The Turbomole webpage is https://www.turbomole.org/. GIMIC, version 2.0 can be freely downloaded from https://github.com/qmcurrents/gimic and https://zenodo.org/record/8180435. ParaView can be downloaded from https://www.paraview.org/.Author contributions
A. R. performed the calculations and prepared the pictures. D. S. and Q. W. supervised A. R. All authors contributed to writing the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. R. thanks the ERASMUS + SMP program for financial support. Q. W. thanks China Scholarship Council for a predoctoral fellowship. This work has also been supported by the Academy of Finland through project 340583. The CSC – the Finnish IT Center for Science is acknowledged for computer time.References
- Aromaticity, in IUPAC Compendium of Chemical Terminology, International Union of Pure and Applied Chemistry, 2006. Online version 3.0.1, 2019, DOI:10.1351/goldbook/terms/view/A00442, https://goldbook.iupac.org.
- V. I. Minkin, Pure Appl. Chem., 1999, 71, 1919–1981 CrossRef CAS.
- G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Chem. Sci., 2023, 14, 5569–5576 RSC.
- E. Hückel, Z. Phys., 1931, 70, 204–286 CrossRef.
- E. Hückel, Z. Phys., 1931, 72, 310–337 CrossRef.
- E. Hückel, Grundzüge der Theorie ungesättigter und aromatischer Verbindungen, Verlag Chemie, Berlin, 1938 Search PubMed.
- M. Mandado, A. M. Graña and I. Pérez-Juste, J. Chem. Phys., 2008, 129, 164114 CrossRef PubMed.
- R. R. Valiev, T. Kurtén, L. I. Valiulina, S. Y. Ketkov, V. N. Cherepanov, M. Dimitrova and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 1666–1674 RSC.
- D. W. Szczepanik and M. Solà, ChemistryOpen, 2019, 8, 219–227 CrossRef CAS PubMed.
- E. Heilbronner, Tetrahedron Lett., 1964, 5, 1923–1928 CrossRef.
- H. E. Zimmerman, J. Am. Chem. Soc., 1966, 88, 1564–1565 CrossRef CAS.
- R. Herges, Chem. Rev., 2006, 106, 4820–4842 CrossRef CAS PubMed.
- P. W. Fowler and H. S. Rzepa, Phys. Chem. Chem. Phys., 2006, 8, 1775–1777 RSC.
- S. M. Rappaport and H. S. Rzepa, J. Am. Chem. Soc., 2008, 130, 7613–7619 CrossRef CAS PubMed.
- L. N. Wirz, M. Dimitrova, H. Fliegl and D. Sundholm, J. Phys. Chem. Lett., 2018, 9, 1627–1632 CrossRef CAS PubMed.
- G. Călugăreanu, Czech. Math. J., 1961, 11, 588–625 Search PubMed.
- F. B. Fuller, Proc. Natl. Acad. Sci., 1971, 68, 815–819 CrossRef CAS PubMed.
- J. H. White, Am. J. Math., 1969, 91, 693–728 CrossRef.
- D. P. Craig and N. L. Paddock, Nature, 1958, 181, 1052–1053 CrossRef CAS.
- D. P. Craig, J. Chem. Soc., 1959, 997–1001 RSC.
- M. Mauksch and S. Tsogoeva, Chem. – Eur. J., 2010, 16, 7843–7851 CrossRef CAS PubMed.
- C. Zhu, S. Li, M. Luo, X. Zhou, Y. Niu, M. Lin, J. Zhu, Z. Cao, X. Lu, T. Wen, Z. Xie, P. v. R. Schleyer and H. Xia, Nat. Chem., 2013, 5, 698–703 CrossRef CAS PubMed.
- C. Zhu, M. Luo, Q. Zhu, J. Zhu, P. v. R. Schleyer, J. I.-C. Wu, X. Lu and H. Xia, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- K. An, T. Shen and J. Zhu, Organometallics, 2017, 36, 3199–3204 CrossRef CAS.
- Y. Cai, Y. Hua, Z. Lu, Q. Lan, Z. Lin, J. Fei, Z. Chen, H. Zhang and H. Xia, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2102310118 CrossRef CAS PubMed.
- L. Chen, L. Lin, A. R. Nath, Q. Zhu, Z. Chen, J. Wu, H. Wang, Q. Li, W.-F. Lin, J. Zhu and H. Xia, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2215900120 CrossRef CAS PubMed.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. Della Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodyński, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, J. Chem. Theory Comput., 2023, 19, 6859–6890 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. Lehtola, C. Steigemann, M. J. T. Oliveira and M. A. L. Marques, SoftwareX, 2018, 7, 1–5 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Andrae, U. Häussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- M. Dolg and X. Cao, Chem. Rev., 2012, 112, 403–480 CrossRef CAS PubMed.
- A. Klamt and G. J. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. Schäfer, A. Klamt, D. Sattel, J. C. W. Lohrenz and F. Eckert, Phys. Chem. Chem. Phys., 2000, 2, 2187–2193 RSC.
- K. Reiter, F. Mack and F. Weigend, J. Chem. Theory Comput., 2018, 14, 191–197 CrossRef CAS PubMed.
- Y. J. Franzke, J. Chem. Theory Comput., 2023, 19, 2010–2028 CrossRef CAS PubMed.
- Y. J. Franzke and C. Holzer, J. Chem. Phys., 2023, 159, 184102 CrossRef CAS PubMed.
- Y. J. Franzke and F. Weigend, J. Chem. Theory Comput., 2019, 15, 1028–1043 CrossRef CAS PubMed.
- Y. J. Franzke, R. Treß, T. M. Pazdera and F. Weigend, Phys. Chem. Chem. Phys., 2019, 21, 16658–16664 RSC.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678 CAS.
- D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362–12378 RSC.
- GIMIC, version 2.0, a current density program, Can be freely downloaded from https://github.com/qmcurrents/gimic and https://zenodo.org/record/8180435 Search PubMed.
- Q. Wang, J. Pyykkö, M. Dimitrova, S. Taubert and D. Sundholm, Phys. Chem. Chem. Phys., 2023, 25, 12469–12478 RSC.
- J. Ahrens, B. Geveci and C. Law, in Visualization Handbook, ed. C. D. Hansen and C. R. Johnson, 2005, pp. 717–731 Search PubMed.
- R. J. F. Berger, M. Dimitrova, R. T. Nasibullin, R. R. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 624–628 RSC.
- C. Ciardelli, E. Bozdağ, D. Peter and S. van der Lee, Comput. Geosci., 2022, 159, 105007 CrossRef.
- H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676 CrossRef CAS PubMed.
- C. Foroutan-Nejad, J. Vícha and A. Ghosh, Phys. Chem. Chem. Phys., 2020, 22, 10863–10869 RSC.
- R. M. Stevens, R. M. Pitzer and W. N. Lipscomb, J. Chem. Phys., 1963, 38, 550–560 CrossRef CAS.
- C. J. Jameson and A. D. Buckingham, J. Phys. Chem., 1979, 83, 3366–3371 CrossRef CAS.
- W. Bieger, G. Seifert, H. Eschrig and G. Grossmann, Chem. Phys. Lett., 1985, 115, 275–280 CrossRef CAS.
- G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2019, 21, 3145–3153 RSC.
- R. K. Jinger, H. Fliegl, R. Bast, M. Dimitrova, S. Lehtola and D. Sundholm, J. Phys. Chem. A, 2021, 125, 1778–1786 CrossRef CAS PubMed.
- H. Fliegl, M. Dimitrova, R. J. F. Berger and D. Sundholm, Chemistry, 2021, 3, 1005–1021 CrossRef CAS.
- M. Kaupp, O. L. Malkina, V. G. Malkin and P. Pyykkö, Chem. – Eur. J., 1998, 4, 118–126 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Calculated bond lengths and NMR chemical shifts are compared to experimental data. Calculated ring-current profiles are shown. Population analysis and Cartesian coordinates of the studied molecular structures are reported. See DOI: https://doi.org/10.1039/d4dt01110d |
| This journal is © The Royal Society of Chemistry 2024 |