Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Convergence of dissolving and melting at the nanoscale†
C.
Chen‡
ad,
X.
Wang‡
ae,
K.
Binder
b,
U.
Pöschl
 c,
H.
Su
c,
H.
Su
 c and
Y.
Cheng
c and
Y.
Cheng
 *a
*a
aMinerva Research Group, Max Planck Institute for Chemistry, 55122 Mainz, Germany. E-mail: yafang.cheng@mpic.de
bInstitute of Physics, Johannes Gutenberg University of Mainz, Staudinger Weg 7, 55128 Mainz, Germany
cMultiphase Chemistry Department, Max Planck Institute for Chemistry, Hahn-Meitner-Weg 1, 55128 Mainz, Germany
dTsinghua University, 100084 Beijing, China
eInstitute for Carbon-Neutral Technology, Shenzhen Polytechnic, Shenzhen 518055, China
First published on 8th August 2023
Abstract
Phase transitions of water and its mixtures are of fundamental importance in physical chemistry, the pharmaceutical industry, materials sciences, and atmospheric sciences. However, current understanding remains elusive to explain relevant observations, especially at the nanoscale. Here, by using molecular dynamics simulations, we investigate the dissolution of sodium chloride (NaCl) nanocrystals with volume-equivalent diameters from 0.51 to 1.75 nm. Our results show that the dissolution of NaCl in aqueous nanodroplets show a strong size dependence, and its solubility can be predicted by the Ostwald–Freundlich equation and Gibbs–Duhem equation after considering a size-dependent solid–liquid surface tension. We find that the structure of dissolved ions in the saturated aqueous nanodropplet resembles the structure of a molten NaCl nanoparticle. With decreasing nanodroplet size, this similarity grows and the average potential energy of NaCl in solution, the molten phase and the crystal phase converges.
Introduction
Water solubility is an important physicochemical property of a substance influencing many processes, such as the absorption of drugs, nucleation in solution and hygroscopic growth of atmospheric nanoparticles.1–3 Besides chemical composition and temperature, particle size has been recognized as another factor controlling the solubility of nanoparticles.4–7 For example, size-dependent solubilities have been found for sodium chloride (NaCl) and ammonium sulfate (AS) nanoparticles, which can be well explained by the Ostwald–Freundlich effect.3 As the particle size of NaCl decreases, increased solubility and dissolution rate have also been reported based on MD simulations.8,9Then comes the question of what will happen if the particle size keeps decreasing, e.g., down to 1 nm or smaller? Will the solubility become infinitely large? What’s the state of these nanoparticles? So far, there are very few quantitative studies on size-dependent solubility of nanoparticles with a diameter of 2 nm or smaller. The reason for the few studies is the experimental challenge involved when investigating solubilities of particles of a few nanometers or less.10–12
Here, the size-dependent solubility of NaCl nanoparticles in water droplets is investigated for a diameter range from 0.507 to 1.745 nm by classical MD simulations. The size-dependent solid–liquid surface tension and structures under the corresponding critical conditions were also analyzed. In the MD simulations, an improved detection approach is developed to directly distinguish solid-like and liquid-like structures of NaCl nanoparticles in water droplets. With this approach, the solubility of a certain size of NaCl nanoparticles is determined. Then, solid–liquid surface tension and solubility of NaCl nanoparticles at other sizes are calculated by the Gibbs–Duhem equation, the Ostwald–Freundlich equation and the Tolman equation. We also analyzed the structure of saturated aqueous nanodroplets of different sizes. In the end, the connection of dissolution and melting processes and its implications in the phase transition of aerosol particles is also discussed.
Results and discussion
Size-dependent solubility of NaCl nanoparticles
Fig. 1 shows the solubility of NaCl nanoparticles with 7 to 108 pairs of NaCl ions calculated by the MD simulations. Here, we used the q8 detection method, a local order parameter approach29 to determine the solubility of NaCl (see Methods section). A strong size dependence of solubility is found for NaCl particles with diameters larger than 0.665 nm (13 pairs of NaCl ions) (red and orange bars in Fig. 1) according to the improved q8 detection approach. At a particle diameter equal to 0.665 nm with 13 pairs of NaCl ions, the saturation mass fraction is ∼3.2 times higher than the simulated saturation mass fraction of bulk NaCl particle (gray circle in Fig. 1).9,13–16 The trend is qualitatively consistent with the experimental results (green triangles in Fig. 1).3 The simulated solubility data are a bit lower compared to the experimental data, where the experimental saturation mass fraction of bulk NaCl (brown triangle in Fig. 1) is ∼1.5 times higher than the simulated saturation mass fraction of bulk NaCl.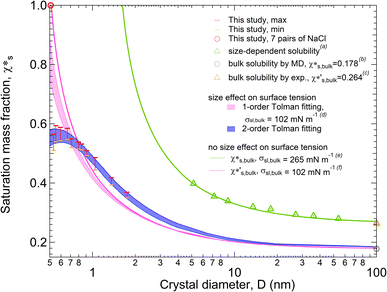 | ||
| Fig. 1 Size-dependent solubility (saturation mass fraction) of NaCl nanoparticles at 300 K. The solubility range of NaCl nanoparticles is obtained from the MD simulations for particles with 8 to 108 pairs of NaCl ions (red and orange bars) and 7 pairs of NaCl ions (red circle). aThe size-dependent solubility of NaCl nanoparticles is taken from experiments for particles with dry diameters of 5.18 to 54.2 nm (green triangles). b,cThe NaCl bulk solubility from MD simulations (grey circle) and from experiment (brown triangle) is taken from ref. 9. The size-dependent solubility curves are obtained based on the combination of the Ostwald–Freundlich and the Gibbs–Duhem equation with and without considering size effects on surface tension. The size effect on solid–liquid surface tension is considered based on the 2nd order Tolman equations for the light blue shaded curves. dThe size effect on solid–liquid surface tension is considered based on the 1st order Tolman equation with the bulk solid–liquid surface tension from ref. 17 for the light pink shaded curves. eThe green curve without considering the size effect of surface tension is based on the NaCl bulk solubility obtained experimentally and the bulk solid–liquid surface tension from ref. 3. fThe pink curve without considering the size effect of surface tension is based on the NaCl bulk solubility from MD simulations and the bulk solid–liquid surface tension from ref. 17. | ||
Size-dependent solubility based on the simulations cannot be explained by the combination of the Ostwald–Freundlich and Gibbs–Duhem equations with a single bulk solid–liquid surface tension (σsl,bulk) (eqn (3)). The prediction curve obtained based on the single σsl,bulk = 102 mN m−1 and the bulk saturation mass fraction 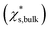 calculated by MD simulations17 (pink line in Fig. 1) does not fit the data well. This indicates that the simulated solubility data become sensitive to σsl as the crystal gets smaller. Therefore, the size-dependent solid–liquid surface tension of NaCl nanoparticles should be considered to reproduce the size-dependent solubility of NaCl nanoparticles.
calculated by MD simulations17 (pink line in Fig. 1) does not fit the data well. This indicates that the simulated solubility data become sensitive to σsl as the crystal gets smaller. Therefore, the size-dependent solid–liquid surface tension of NaCl nanoparticles should be considered to reproduce the size-dependent solubility of NaCl nanoparticles.
The saturation mass fraction 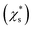 of NaCl particles with diameters less than 0.665 nm does not vary monotonically. The saturation ratio
of NaCl particles with diameters less than 0.665 nm does not vary monotonically. The saturation ratio 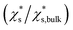 remains similar when the diameter of the crystal decreases from 0.665 to 0.530 nm, with 13 to 8 pairs of NaCl ions. The saturation mass fraction suddenly jumps to ∼1 when the diameter of the crystal drops to 0.507 nm (7 pairs of NaCl ions), suggesting an infinite solubility. This result is consistent with that in the melting process simulations (Fig. S9†), where the NaCl particle with 7 pairs of NaCl ions is considered as molten at 300 K.
remains similar when the diameter of the crystal decreases from 0.665 to 0.530 nm, with 13 to 8 pairs of NaCl ions. The saturation mass fraction suddenly jumps to ∼1 when the diameter of the crystal drops to 0.507 nm (7 pairs of NaCl ions), suggesting an infinite solubility. This result is consistent with that in the melting process simulations (Fig. S9†), where the NaCl particle with 7 pairs of NaCl ions is considered as molten at 300 K.
With a size-dependent solid–liquid surface tension (σsl) based on the second-order Tolman equation (ESI Note 3†),40–42 the size-dependent solubility from MD simulations can be well explained by the combination of the Ostwald–Freundlich and Gibbs–Duhem equations (blue shaded curves in Fig. 1). Compared to the fitting curves from the first-order Tolman equation (light pink shaded curves in Fig. 1), the blue fitting curves from the second-order Tolman equation better capture the variation of NaCl solubilities. In addition, the size-dependent surface tension competes with the effect of crystal size on the solubility of nanoparticles. The reduction in particle size contributes to an increase in solubility, but this gain is inhibited by the reduced surface tension, particularly when the particles are smaller than 0.665 nm with 13 pairs of NaCl ions.
Structures of NaCl nanoparticles at different dissolution states
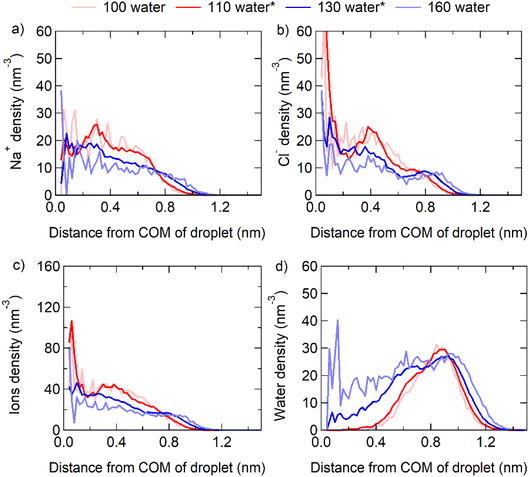
Here, we examined the structures of NaCl nanoparticles at three states of dissolution: the incomplete, critical, and complete dissolutions. By incrementally adding water molecules and the q8 criteria, we determined the range of water molecule quantities and corresponding solubility range for crystal dissolution. When the number of water molecules surrounding the crystal falls within the solubility range (between the upper and lower limits in Table S1†), we consider it to be in a critical dissolution state. When the crystal is surrounded by fewer water molecules than the solubility range, we consider it to be in an incomplete dissolution state. Conversely, when the crystal is surrounded by more water molecules than the solubility range, we consider it to be in a complete dissolution state. At this stage, we can compare the distribution of NaCl ions and water molecules within the nanoscale particle under the three different states. We find that the distribution of ions and water molecules is inhomogeneous in the incomplete and critical dissolution states, but close to homogeneous in the complete dissolution state. The droplet composed of 32 NaCl pairs (corresponding to 1 nm diameter) with 100 to 160 water molecules is taken as an example, where the particle containing 110–130 water molecules is in the critical dissolution state.As shown by the light red lines in Fig. 2, in the incomplete dissolution state, both Na+ and Cl− ions are primarily distributed within ∼1 nm distance from the center of mass (COM) of the particle, and more concentrated within distances of ∼0.4 nm. Na+ ions have the highest density distribution at ∼0.3 nm distance from the COM, while Cl− ions are concentrated at the COM and ∼0.4 nm distance from the COM. Meanwhile, water molecules are distributed at distances >0.4 nm and mostly concentrated at distances of ∼1 nm from the COM.
As shown by the red and blue lines in Fig. 2, in the critical dissolution state, the concentration distribution of Na+ and Cl− ions becomes similar but not homogeneous, and the concentration of ions decreases gradually from the COM to the particle surface. Water molecules are concentrated at a position closer to the COM compared to that in the incomplete dissolution state, and individual water molecules enter the interior of the particle (<0.4 nm distance from the COM). This shows that only a few water molecules are required to destroy the crystal structure inside the NaCl nanoparticle, where saturation can be much higher than that on the surface of the particle.
As shown by the light blue lines in Fig. 2, in the complete dissolution state, the distribution of Na+ and Cl− ions is even more similar. This indicates that the distribution of ions and water molecules would be homogeneous when the mass saturation of NaCl particle is close to the bulk mass saturation. Note that the fixed COM position of the total system in the MD algorithm might cause small fluctuations of the nanocrystal position relative to the total COM, which may give rise to some smearing of the profiles of the ion and water molecule densities near the COM of the total system.
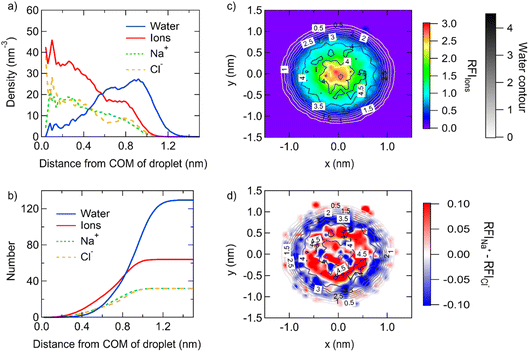
The structure of different-size droplets in the critical dissolution state is further analyzed to quantify the characteristics of the inhomogeneous distribution of ions and water. The saturated droplet composed of 32 pairs of NaCl ions (corresponding to 1 nm diameter) with 130 water molecules is taken as an example. As shown in Fig. 3a, the profile of number density of ions and water molecules at different distances from the center of mass (COM) indicates ions are highly concentrated in the area around the COM of the droplet and are more diluted in the area near the surface. For example, the profile of the number of ions and water molecules at different distances from the COM in this droplet suggests only ∼4 water molecules exist in the area around the COM of the droplet with a radius of 0.5 nm, while there are 16 ions in the same area (Fig. 3b).
The two-dimensional density map of the relative fraction of ions shows more visually the gradient distribution of the ions (Fig. 3c). Except for a thin interface where no ion exists, the bulk solution with a concentration of 14.4 mol kg−1 is homogeneous. This is similar to the result from the previous simulation, where the smooth density profile of ions in the bulk solution with a concentration of 11.48 mol kg−1 indicates the homogeneous structure of the system.18 In contrast, the droplet composed of 32 NaCl and 130 water molecules shows inhomogeneity of the ion/water distribution with a gradient. The concentration becomes larger when the position is closer to the center. Furthermore, the distribution of Na+ and Cl− ions is rather stratified. The bidimensional density map of the difference of the relative fraction of Na+ and Cl− ions (Fig. 3d) shows that Na+ ions are more concentrated in the center of the droplet, while Cl− ions are more concentrated at the surface of the droplet.
Dissolution and melting of NaCl nanoparticles
Following the approach of Qi et al.,19 we determined the melting temperature for the nanocrystals above the size of 15 pairs and the melting points of the NaCl nanocrystals show a clear size dependence (ESI Note 1). As shown in Fig. S8,† the heat capacity (blue circles) is obtained from the derivative of the average potential energy (red circles) with respect to the temperature (see eqn (S1)†), and the melting temperature of each crystal is at the temperature with the maximum apparent heat capacity.Above the size of 15 pairs of NaCl nanocrystals, the depression of the melting point of the nanocrystals in comparison to the bulk is quite proportional to N(−1/3), showing a significant size dependence (red dashed line in Fig. S9† and N is the number of ions). This phenomenon also occurs in other substances, i.e., pure metal and alloy nanoparticles.19–21 The dependence can be derived from the decrease in phase stability of the nanoparticles due to surface effects.22 By using the q8 calculation, the melting point of the NaCl nanocrystals is also determined (blue diamonds in Fig. S9†). The results show that above the size of 8 pairs of NaCl nanocrystals, the melting point depression of the nanocrystals is proportional to N(−1/3) (blue dashed line in Fig. S9†). The approach of Qi et al.19 (2001) cannot be applied to determine the melting temperature for NaCl nanocrystals below the size of 15 pairs. Note that the melting temperature for the NaCl nanocrystals below the size of 15 pairs is already less than the Debye temperature, and the heat capacity no longer follows the Dulong–Petit law. The vibrations of the atoms must be considered for accurate heat capacity data.
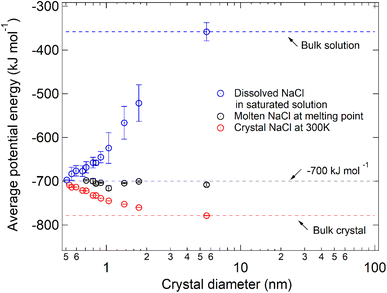
By comparing the average potential energy of dissolved and molten NaCl nanoparticles with diameters below 6 nm, we find that the structure of dissolved NaCl in saturated solution becomes similar to the structure of molten NaCl when the NaCl particle size decreases. The average potential energy of NaCl (μNaCl) only depends on the relative position of the ions,14 so that it can reflect the spatial distribution of the ions. The average potential energies in different simulated systems are compared to analyze the similarity of NaCl in the dissolved state and molten state quantitatively (Fig. 4). Dark circles represent μNaCl in the molten NaCl particles at the respective melting points, and the values are all close to −700 kJ mol−1 (grey line). This means that the spatial distribution of ions in a molten NaCl particle at the respective melting point is almost the same and independent of size. This phenomenon was also found for other substances, such as copper.23 However, μNaCl in the dissolved droplets at the critical dissolution state (blue circles) decreases with the decrease of size. The blue circles approach −700 kJ mol−1 and deviate from the blue dashed line (≈−358.35 ± 20.95 kJ mol−1), which represents μNaCl in bulk saturated solution. It suggests the structural similarity of dissolved NaCl in saturated nanodroplets to molten NaCl at the melting point increases when the size of the NaCl particle decreases.
In Fig. 4, the red circles represent μNaCl of the NaCl nanoparticles at 300 K, which deviate from the red line that represents μNaCl of the bulk NaCl crystal (≈−780 kJ mol−1). The increase of μNaCl with the decrease of particle size is because the bigger particle is more stable and thus has a higher melting point temperature. As the particle size decreases to ∼7 pairs of NaCl ions, the red circles and blue circles almost converge at around −700 kJ mol−1. The convergence of μNaCl suggests that 7 pairs of NaCl ions at 300 K is in a molten state and can be considered as a saturated droplet of NaCl with infinite solubility. Due to the size-dependent solubility, smaller molten NaCl particles at 300 K (≤7 pairs of NaCl ions) can also be considered as a saturated droplet of NaCl with infinite solubility.
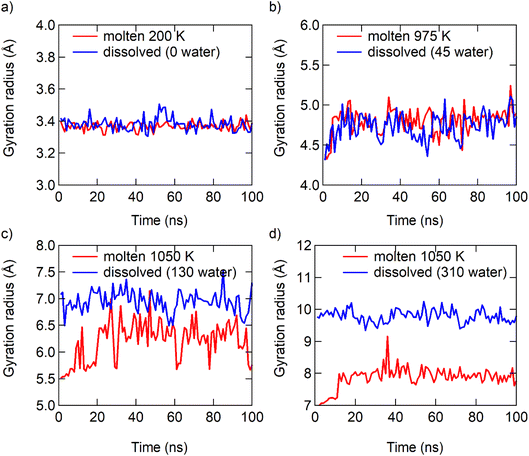
The radius of gyration of the particles and the radial distribution function of ions to ions (RDFion–ion) also supports the analysis of μNaCl. The similarity of the radius of gyration of the NaCl particles in the dissolution and melting processes becomes more pronounced when the particle size decreases (Fig. 5). The similarity of the relative positions of ions in the dissolution and melting processes increases when the particle size decreases (Fig. S12†). Harbury4 gave a similar assumption that there is a significant comparability between a supersaturated solution and undercooled melts. In summary, the dissolution of bulk NaCl solids is a traditional dissolution, while the dissolution of NaCl particles at the nanoscale is analogous to the melting process of NaCl particles at the nanoscale. These two different types of phase transition, dissolving and melting, “meet” at ≤7 pairs of NaCl ions at 300 K.
The radial distribution functions of Na+ to Na+ (RDFNa–Na), Cl− to Cl− (RDFCl–Cl), Na+ to Cl− (RDFNa–Cl), and Cl− to Na+ (RDFCl–Na) give valuable additional information that the q8-determined solubility and melting point of NaCl nanocrystals are on firm ground. The RDFNa–Na and RDFCl–Cl of the q8-determined unmelted NaCl nanocrystals and undissolved NaCl in saturated nanodroplets show rather sharp peaks at the first to fourth nearest neighbor distances of ∼0.40 nm, ∼0.56 nm, ∼0.69 nm, and ∼0.79 nm (Fig. S13 and S15†). The RDFNa–Cl and RDFCl–Na of the q8-determined unmelted NaCl nanocrystals and undissolved NaCl in saturated nanodroplets show the same sharp peaks at the first to fourth nearest neighbor distances of ∼0.28 nm, ∼0.49 nm, ∼0.63 nm, and ∼0.84 nm (Fig. S17 and S19†). This is well compatible with the simple predictions from the snapshot of 9 pairs in a NaCl crystal shown in Fig. S20,† indicating that the nanocrystals are still crystalline despite their smallness, and the crystal structure is not disturbed by the condensation of a few water molecules. Meanwhile, the RDFNa–Na and RDFCl–Cl as well as the RDFNa–Cl and RDFCl–Na of the q8-determined molten NaCl nanocrystals at the melting points and dissolved NaCl in saturated nanodroplets show flatter peaks compared to the ones of the unmelted and undissolved NaCl nanoparticles (Fig. S12, S14, S16 and S18†). This captures well the different structural features between the solid and liquid states of NaCl, thus supporting the results of the solubility and melting point of NaCl nanoparticles determined by the q8 method. Snapshots of NaCl nanoparticles during the melting and dissolution processes in Fig. S20† support the solubility and melting point of NaCl nanoparticles determined by the q8 method as well. The snapshots of NaCl nanoparticles at a temperature lower than the q8-determined melting points show that the typical shape of nano-sized NaCl nanocrystals is not spherical. Both in the case of melting and the dissolution process, a spherical shape occurs only when the transition to the fluid phase takes place.
Implications
Our MD simulations demonstrate that the solubility of NaCl at the nanoscale is size-dependent and can be much higher than that of a bulk solution. The melting point of NaCl is also found to be size-dependent. To transform a NaCl particle with a temperature of 300 K into the liquid state, the temperature of the environment should be increased or water should be added to the NaCl. In these processes, heat from a higher-temperature environment or the interaction with water molecules changes the NaCl crystal to the liquid state. In other words, the heat, and the interaction with water for NaCl nanocrystals are equivalent. As the size decreases, a lower temperature or less surrounding water molecules are needed to change the phase of NaCl. The nanoparticle with only 7 pairs of NaCl ions cannot exist in the solid state at 300 K, thus no heat or interaction with a few water molecules is needed to transform it into liquid.Overall, this study provides a new perspective to connect the dissolution and melting processes of NaCl nanoparticles, and this connection may also be suitable for other solids. For a substance whose melting point is higher than 300 K at the macroscopic level, there exists a critical diameter (Dc) at which the melting point is 300 K. Naturally, when the diameter of the nanoparticle composed by this substance is below Dc, the particle is expected to be liquid at room temperature. The nanoparticle whose diameter is larger than Dc is solid at room temperature, while a small amount of adsorbed water molecules can turn it into a molten-like liquid with a thin solution coating. These general principles may be useful for studies about nanoparticles in various fields, including the environmental, pharmaceutical and materials sciences.24–26 This study mainly focuses on the thermodynamics of dissolution. A deep understanding of the NaCl dissolution mechanism also requires knowledge of the kinetics, and we would like to direct the readers to other related research.27,28
Methods
MD simulations
The Joung–Cheatham (JC) force field for NaCl with the SPC/E water model has been proved to nicely predict the experimental value of solubility (∼6.15 mol kg−1).9,13–16 Therefore, this force field combination is applied in the study to simulate the NaCl–water mixture. The MD simulations are carried out with the GROMACS 2016.6 package.29,30 NaCl nanocrystals with different diameters are surrounded by certain water molecules initially. The systems are then energetically minimized by the steepest-descent method and equilibrated for 100 ps at 300 K. The MD simulations are further performed in the NVT ensemble with periodic boundary conditions and velocity-rescaling thermostat. Electrostatic interactions are calculated using the particle mesh Ewald (PME) algorithm, and van der Waals interactions are accounted for up to a cutoff distance of 10 Å. All simulations are carried out for at least 600 ns using a 1 fs time step, and conformations for analysis are saved every 2 ps. To determine the solubility, we kept increasing the number of water molecules in the system until we found a critical number that allows NaCl to dissolve completely based on the q8 algorithm. Ideally, we would add water molecules one by one, but in practice, due to the limitations of the computational resources, we increased the step size by 5 to 20 molecules. Thus, instead of an exact number, we determine a narrow range of water molecules required for crystal dissolution and Table S1† summarizes the upper and lower limits of this range. We chose a simulation duration of at least 600 ns, ensuring that even the largest simulated NaCl nanoparticle (108 pairs of NaCl ions with 650 water molecules, ∼1.745 nm diameter) would completely dissolve (Fig. S10†). Each simulation box has a uniform size of 10 × 10 × 10 nm3, ensuring it can accommodate the largest simulated NaCl nanoparticle (108 pairs of NaCl ions with 650 water molecules, ∼1.745 nm diameter). More detailed information about the number of ions/water molecules, the initial structure setup, and simulation times are summarized in Table S1 and Fig. S11.†In this study, the melting processes of NaCl nanocrystals is also simulated. The JC force field is adopted to keep synchronous with the simulations of the NaCl dissolution process. The particles with different diameters are simulated at different temperatures to determine the melting point. More details about the setup are shown in ESI Note 1.†
Solubility determination: q8 detection approach
To detect the dissolution and melting progress of NaCl nanocrystals, it is important to distinguish ions that are in the solid-like and liquid-like structures. To do this, the local order parameter approach of Steinhardt et al.31 is adopted. For each ion (i), the local bond-orientational order parameter ql(i) is calculated as: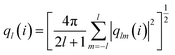 | (1) |
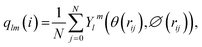 | (2) |
The NaCl nanocrystal is considered as dissolved or molten when the time average of the q8 value of each ion in the crystal is less than 0.35. q8 is the local bond-orientational order parameter to provide the best separation between solid-like (>0.35) and liquid-like (≤0.35) states of each NaCl ion in the nanoparticles (Fig. S5†). We added 5 water molecules each time for the certain NaCl nanocrystal in the simulation. The crystal with N + 5 water molecules is considered as dissolved when the time average of the q8 value of each ion in the crystal is less than 0.35. At this point, we consider the solubility range of the crystal to be within the range of water molecule quantities of N to N + 5. Furthermore, based on the known molar masses of NaCl ions and water molecules, we can calculate the corresponding range of saturated mass fraction values, which represents the solubility range.
Since at 300 K the crystal structure of NaCl is already close to perfectly rigid, a simple study of the radial pair distribution functions between the different pairs of ions can clearly identify which NaCl clusters are still in a nanocrystal state and which are already in a liquid state (Fig. S6†).
Size-dependent solubility estimation
Size-dependent solubility can be determined by the combination of the Ostwald–Freundlich6,7 and Gibbs–Duhem equations34–36 as: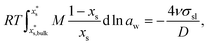 | (3) |
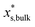 is the mass fraction of solute in a saturated bulk solution, and
is the mass fraction of solute in a saturated bulk solution, and 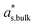 is the solute activity at
is the solute activity at 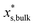 .
. 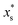 is the mass fraction of solute in a saturated droplet of diameter D. aw is the water activity retrieved from the modified Tang–Munkelwitz (TM) model (ESI Note 2†).3,38σsl is the size-dependent solid–liquid surface tension estimated by the Tolman equation (ESI Note 3†).39 In this study, D is the volume equivalent diameter of a NaCl crystal at the saturation dissolution point, which is equal to the diameter of the NaCl droplet of equivalent volume,
is the mass fraction of solute in a saturated droplet of diameter D. aw is the water activity retrieved from the modified Tang–Munkelwitz (TM) model (ESI Note 2†).3,38σsl is the size-dependent solid–liquid surface tension estimated by the Tolman equation (ESI Note 3†).39 In this study, D is the volume equivalent diameter of a NaCl crystal at the saturation dissolution point, which is equal to the diameter of the NaCl droplet of equivalent volume,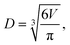 | (4) |
Structure analysis
The profiles of number density and number of ions and water molecules at different distances from the center of mass (COM) are used to analyze the structure of saturated droplets. The relative fraction of ions is calculated by the following equation: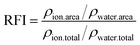 | (5) |
The radial distribution functions (RDFs) of ions with respect to other ions can reflect the spatial distribution of ions.29,37 They are calculated as:
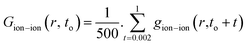 | (6) |
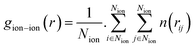 | (7) |
Average potential energy calculation
To calculate the average potential energy of dissolved or molten NaCl, the trajectories only containing the Na+ and Cl− ions after the MD simulations of a given NaCl–water system are extracted and then rerun for the new trajectories. In the rerun simulation, energy is calculated every 2 ps, and the average value over the time after the equilibrium of a system is taken to describe the system.Radius of gyration
The radius of gyration is defined as: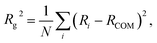 | (8) |
Conflicts of interest
Authors declare that they have no competing interests.Acknowledgements
This study was supported by the Max Planck Society (MPG). Open Access funding provided by the Max Planck Society.Notes and references
- R. H. Müller, C. Jacobs and O. Kayser, Adv. Drug Delivery Rev., 2001, 47, 3–19 CrossRef
.
- N. T. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630 CrossRef CAS
.
- Y. Cheng, H. Su, T. Koop, E. Mikhailov and U. Poschl, Nat. Commun., 2015, 6, 5923 CrossRef CAS
.
- L. Harbury, J. Phys. Chem., 1946, 50, 190–199 CrossRef CAS
.
- R. H. Müller and K. Peters, Int. J. Pharm., 1998, 160, 229–237 CrossRef
.
- W. Ostwald, Z. Phys. Chem., 1900, 34U, 495–503 CrossRef
.
-
H. Freundlich, Kapillarchemie, eine Darstellung der Chemie der Kolloide und verwandter Gebiete, akademische Verlagsgesellschaft, 1922 Search PubMed
.
- G. Lanaro and G. N. Patey, J. Phys. Chem. B, 2015, 119, 4275–4283 CrossRef CAS PubMed
.
- J. R. Espinosa, J. M. Young, H. Jiang, D. Gupta, C. Vega, E. Sanz, P. G. Debenedetti and A. Z. Panagiotopoulos, J. Chem. Phys., 2016, 145, 154111 CrossRef CAS PubMed
.
- I. Tang, H. Munkelwitz and N. Wang, J. Colloid Interface Sci., 1986, 114, 409–415 CrossRef CAS
.
- C. K. Chan, Z. Liang, J. Zheng, S. L. Clegg and P. Brimblecombe, Aerosol Sci. Technol., 1997, 27, 324–344 CrossRef CAS
.
- C. Vicente, W. Yao, H. Maris and G. Seidel, Phys. Rev. B, 2002, 66, 214504 CrossRef
.
- H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS
.
- I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed
.
- J. L. Aragones, E. Sanz and C. Vega, J. Chem. Phys., 2012, 136, 244508 CrossRef CAS PubMed
.
- F. Moučka, I. Nezbeda and W. R. Smith, J. Chem. Phys., 2013, 138, 154102 CrossRef
.
- R. Bahadur and L. M. Russell, Aerosol Sci. Technol., 2008, 42, 369–376 CrossRef CAS
.
- X. Wang, C. Chen, K. Binder, U. Kuhn, U. Pöschl, H. Su and Y. Cheng, Atmos. Chem. Phys., 2018, 18, 17077–17086 CrossRef CAS
.
- Y. Qi, T. Çağin, W. L. Johnson and W. A. Goddard III, J. Chem. Phys., 2001, 115, 385–394 CrossRef CAS
.
- P. Couchman and W. Jesser, Nature, 1977, 269, 481–483 CrossRef CAS
.
- C. Chen, J.-G. Lee, K. Arakawa and H. Mori, Appl. Phys. Lett., 2011, 99, 013108 CrossRef
.
- Q. Jiang and C. Yang, Curr. Nanosci., 2008, 4, 179–200 CrossRef CAS
.
- F. Delogu, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(20), 205418 CrossRef
.
- B. E. Rabinow, Nat. Rev. Drug Discovery, 2004, 3, 785–796 CrossRef CAS
.
- T. Koop, J. Bookhold, M. Shiraiwa and U. Pöschl, Phys. Chem. Chem. Phys., 2011, 13, 19238–19255 RSC
.
- L. Suo, Y.-S. Hu, H. Li, M. Armand and L. Chen, Nat. Commun., 2013, 4, 1481 CrossRef PubMed
.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Chem. Phys., 2013, 139, 234702 CrossRef
.
- L. M. Liu, A. Laio and A. Michaelides, Phys. Chem. Chem. Phys., 2011, 13, 13162–13166 RSC
.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef
.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B, 1983, 28, 784–805 CrossRef CAS
.
- G. Lanaro and G. N. Patey, J. Phys. Chem. B, 2016, 120, 9076–9087 CrossRef CAS PubMed
.
- H. Jiang, P. G. Debenedetti and A. Z. Panagiotopoulos, J. Chem. Phys., 2019, 150, 124502 CrossRef PubMed
.
- M. D. Cohen, R. C. Flagan and J. H. Seinfeld, J. Phys. Chem., 1987, 91, 4583–4590 CrossRef CAS
.
- C. Richardson and T. D. Snyder, Langmuir, 1994, 10, 2462–2465 CrossRef CAS
.
- J. H. Seinfeld, S. N. Pandis and K. Noone, Phys. Today, 1998, 51, 88 CrossRef
.
-
B. Hess, L. E. van der Spoel and E. Lindahl, User Manual, Version 4, 2010 Search PubMed
.
- I. N. Tang, J. Geophys. Res.: Atmos., 1996, 101, 19245–19250 CrossRef CAS
.
- R. C. Tolman, J. Chem. Phys., 1949, 17, 333–337 CrossRef CAS
.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42, 621–629 CrossRef CAS
.
- N. E. Zimmermann, B. Vorselaars, D. Quigley and B. Peters, J. Am. Chem. Soc., 2015, 137, 13352–13361 CrossRef CAS
.
- B. Patrov, Zh. Prikl. Khim., 1997, 70, 1900–1902 CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00095h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |