Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Diffractive mirrors for neutral-atom matter-wave optics†
Lee Yeong
Kim‡
 a,
Do Won
Kang‡
a,
Do Won
Kang‡
 b,
Sanghwan
Park
b,
Sanghwan
Park
 c,
Seongyeop
Lim
c,
Seongyeop
Lim
 c,
Jangwoo
Kim
c,
Jangwoo
Kim
 d,
Wieland
Schöllkopf
d,
Wieland
Schöllkopf
 e and
Bum Suk
Zhao
e and
Bum Suk
Zhao
 *ab
*ab
aDepartment of Physics, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea. E-mail: zhao@unist.ac.kr
bDepartment of Chemistry, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea
cSchool of Energy and Chemical Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea
dPohang Accelerator Laboratory, POSTECH, Pohang, Gyeongbuk 37673, Korea
eFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: wschoell@fhi-berlin.mpg.de
First published on 30th January 2024
Abstract
Mirrors for atoms and molecules are essential tools for matter-wave optics with neutral particles. Their realization has required either a clean and atomically smooth crystal surface, sophisticated tailored electromagnetic fields, nanofabrication, or particle cooling because of the inherently short de Broglie wavelengths and strong interactions of atoms with surfaces. Here, we demonstrate reflection of He atoms from inexpensive, readily available, and robust gratings designed for light waves. Using different types of blazed gratings with different periods, we study how microscopic and macroscopic grating properties affect the mirror performance. A holographic grating with 417 nm period shows reflectivity up to 47% for He atoms, demonstrating that commercial gratings can serve as mirrors for thermal energy atoms and molecules. We also observe reflection of He2 and He3 which implies that the grating might also function as a mirror for other breakable particles that, under typical conditions, do not scatter nondestructively from a solid surface such as, e.g., metastable atoms or antihydrogen atoms.
1 Introduction
In 1923, Louis de Broglie postulated the wave nature of particles in his thesis, introducing the concept of matter-wave wavelength, which is inversely proportional to the product of the particle's mass and velocity. In the same decade, his idea was experimentally confirmed for electrons (1927)1 and atoms of thermal energy (1930)2 sequentially. Shortly after that, the short wavelength due to the small mass of the electron and the expected analogy of matter-wave optics to photon optics led to the development of the electron-optical imaging system, the first electron microscope (1932).3 This rapid development was possible because the strong interaction of electrons with static electromagnetic fields allows easy focusing of electrons. Since then, the electron microscope has become an indispensable tool in various fields of modern science and engineering, including physics, material science, chemistry, life sciences, and chemical engineering.As for neutral atoms, however, their interaction with fields is not strong enough to manipulate them easily. This difficulty has delayed the establishment of the atom microscope. Only in the twenty-first century were two types of scanning helium microscopes (SHeM) in operation. In these apparatuses, probe atoms, typically thermal energy (5–100 meV) neutral helium atoms, are either collimated by a pinhole4–9 or focused by a Fresnel zone plate.10–13 Spatial resolutions of 0.35 μm (ref. 5) and 1 μm (ref. 13) have been reported, respectively. The new scanning microscopes can image delicate surfaces such as biological samples, nonconducting material, and organic films, even under the influence of electric or magnetic fields.7 Such surfaces are challenging to image with the electron microscope. On the other hand, the weak interaction, which was a hurdle for controlling atoms, is beneficial for interferometry applications. Therefore, atom interferometry has found numerous applications in modern sciences, of which examples are inertial sensors, the detection of the He2 molecule, and polarizability measurements.14 These microscopes and interferometers employing atoms and molecules are based mostly on their transmission through nanostructures such as Fresnel zone plates and transmission gratings, pinholes, or non-material diffraction gratings formed by a laser field. However, these instruments surprisingly rarely use mirrors, which are ubiquitous components in traditional optical instruments.
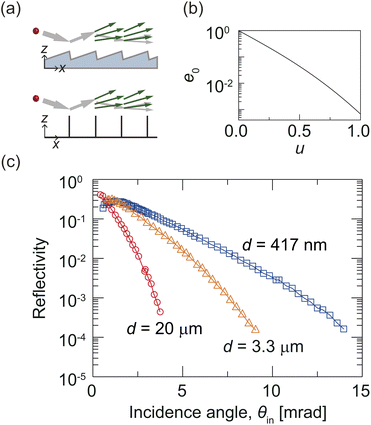
On the other hand, various mirrors for atoms and molecules have been suggested, which can be categorized into three types according to the underlying reflection mechanisms: classical-reflection mirrors, quantum-reflection mirrors, and mirrors based on multiple edge-diffraction reflection. In the classical description of scattering from a solid surface, the particle is reflected when it reaches the classical turning point of the particle–surface interaction potential. That is the well-defined point along the particle trajectory where the particle's kinetic energy has been fully converted into potential energy. In the quantum mechanical picture, on the other hand, partial reflection of the particle's wave can occur at both positive and negative potential slopes without reaching a classical turning point. A familiar example of this counterintuitive quantum phenomenon is the partial reflection of a wave from a downward potential step, an illustrative problem found in most quantum mechanics textbooks. This effect can occur at the attractive long-range branch of the particle–surface potential and is referred to as quantum reflection (or quantum threshold reflection). The probability of quantum reflection depends strongly on the incident particle's kinetic energy. It approaches unity in the limit of vanishing incident energy. Another intriguing non-classical reflection mechanism is multiple edge-diffraction reflection. This occurs when particles scatter from a periodic array of half planes, as shown schematically in the lower part of Fig. 2(a). Here reflection is mediated solely by diffraction of the matter waves at the half plane edges. The edges of a blazed optical diffraction grating can effectively serve as an array of half planes, as indicated in the upper part of Fig. 2(a). The three reflection mechanisms can be differentiated experimentally through different dependencies of their reflectivity on parameters such as incidence angle, initial kinetic energy of the particle, type of particle, surface structure, and surface temperature.
Atomically smooth solid surfaces, namely crystal surfaces, were the first atomic/molecular mirrors dating back to the earliest atom optics experiments. Using a LiF crystal surface, Estermann and Stern proved the wave-type properties of atoms and molecules.2 Since then, atom scattering via classical reflection from a crystal surface has flourished as a tool for studying surface physics and chemistry.15,16 In these experiments, an atomically smooth surface is generally necessary to reflect thermal energy atoms and molecules with a speed of hundreds of m s−1 since their de Broglie wavelengths are on the order of 100 pm. Alternatively, magnetic fields,17–19 electrostatic fields,20 and electromagnetic waves21 have been used as mirrors for slow atoms and molecules of relatively long wavelengths. The underlying physics of these mirrors is also classical reflection of atoms and molecules slower than 30 m s−1 from the interaction potential between the particle and field.
Liquid helium films coated on a solid surface22–24 and, subsequently, flat25–29 and structured solid surfaces30,31 have served as quantum-reflection mirrors. Since quantum reflection allows an atom or molecule to be reflected from a surface before reaching the classical turning point,32,33 the quantum-reflection mirror does not need to be as atomically smooth as the crystal-surface mirror. However, its reflectivity is negligible for typical conditions of thermal kinetic energies and near-normal incidence. Observable quantum-reflection probabilities can only be expected if the incident velocity component normal to the surface is exceedingly small. Accordingly, the first quantum-reflection mirrors were demonstrated for slow atoms incident at grazing incidence angles of 1–10 mrad.22,25 Under normal incidence these mirrors only work for ultracold atoms of minimal velocities, such as a Bose–Einstein condensate.27,31 Grazing incidence, on the contrary, allows thermal atoms to be quantum reflected from various surfaces.26,29 Furthermore, a curved quantum-reflection mirror made a thermal-energy beam of 4He atoms one-dimensionally focused to a spot width below 2 μm,28 which could become a focusing element of a scanning He microscope.
Multiple edge-diffraction reflection (MEDR), which is a coherent reflection process of the particle's wave,34 was first demonstrated with nanoscale ridged structures for ultra-cold atoms under grazing incidence conditions.35,36 An experimental analysis of the diffraction efficiencies for He and D2 beams reflected from a square-wave grating composed of 10 μm wide strips separated by 400 μm confirmed the MEDR model description.37 Yet, in order to achieve high reflection efficiency, as needed for a useful mirror, finer ridged surfaces prepared by nanofabrication techniques will be needed.
Each type of mirror comes with specific challenges. For instance, the crystal surface mirror typically requires substantial surface preparation and maintenance processes such as annealing, ultrahigh vacuum, and possibly low surface temperature of 100 K. Although these mirrors can work for atoms and molecules, their lifetime is less than ten hours even in ultrahigh vacuum of 10−10 mbar.38,39 To overcome this limitation efforts have been made to stabilize crystal surfaces by coating them with a graphene monolayer. The maximum reflectivity of monolayer graphene-coated Ru [MLG/Ru(0001)] at 100 K is approximately 20% for He atoms, which can be recovered by annealing to 450 K even after being exposed to air.40 Electromagnetic-field mirrors can reflect thermal energy atoms under grazing incidence conditions with reflectivity close to 100%.41,42 But they lack the robustness and compactness of solid mirrors. As for quantum-reflection mirrors their reflectivity approaches unity for extreme grazing incidence, but it readily decreases with increasing incidence angle. MEDR mirrors require nanofabrication (nanoscale ridged surface) or have low reflectivity for a mirror (400 μm-period grating). Bulky and low-reflectivity mirrors get less suitable as the number of mirrors in an instrument increases. Delicate prerequisites in manufacturing, preparing, and maintaining processes make a mirror expensive. Therefore, these mirrors are not well established in matter-wave optical instruments.
A robust, compact, and, ideally, inexpensive mirror with near 100% reflectivity for atoms and molecules would expedite the development of neutral-particle matter-wave instruments, such as microscopes and interferometers, paralleling applications of conventional mirrors in the wide variety of optical systems used in science and technology.
Here, we show that a commercial blazed grating with sub-micrometer period can function as a mirror for He atoms with a reflection probability of up to about 50%. While the reflectivity of this grating decreases slowly as the incidence angle increases, it still remains above 10% even when the incidence angle is 4 mrad. To determine the underlying reflection mechanism of this mirror, we measure the specular reflection efficiencies of three blazed gratings with different periods for He atomic beams under grazing incidence. The trends of the observed reflection probabilities for the gratings with different periods are qualitatively explained by the MEDR model.34,37 Comparison of the experimental results obtained with plane-ruled and holographic gratings of identical period but different microscopic and macroscopic shapes allows us to study how these properties affect their performance as mirrors. In addition, by using the mirrors to reflect fragile helium clusters, He2 and He3, with high reflectivity, we demonstrate that the new mirror can work for more complex and delicate particles as well.
2 Method
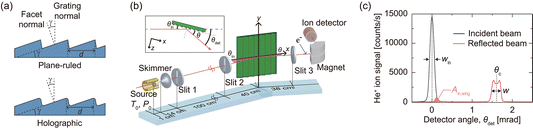
Fig. 1(a) and (b) show schematics of the blazed gratings and the experimental setup, respectively (see ESI†43 for details). In brief, the molecular beam of mean de Broglie wavelength λdB (327, 164, and 109 pm for He, He2, and He3) is produced by supersonic expansion of pure He gas from a source reservoir with stagnation pressure P0 and temperature T0. At T0 = 9.0 K, we set P0 to 0.5 and 2 bar for the atom and cluster experiments, respectively. The beam is collimated by two 20 μm wide slits (Slit 1 and Slit 2) before it scatters off the commercial optical grating. We investigate four blazed gratings: three plane-ruled gratings and one holographic grating. Grating periods (d) range from 417 nm to 20 μm and nominal blaze angles (γ) range from 0.8° to 16.8° [see Fig. 1(a)]. An angular spectrum of the incident or reflected beam is measured by precisely rotating the homemade mass spectrometer equipped with an entrance slit (Slit 3). As shown in the inset of Fig. 1(b), in the plane of incidence formed by the incident wavevector and grating normal, we define the incidence angle θin and detection angle θdet with respect to the grating plane and the incident beam axis, respectively. Examples of measured incident and reflected spectra are shown in Fig. 1(c). From these angular profiles we determine the widths (win and w) and areas (Ain and A) of the incident and reflected beam together with θin. For specular reflection θin = θc/2, where θc is the central angle of the reflected peak indicated in Fig. 1(c). See ESI†43 for details of data analysis.3 Results and discussion
In our first experiment, we study the underlying reflection mechanism of the gratings by comparing the measured reflectivity for the three plane-ruled gratings of period d = 20 μm, 3.3 μm, and 417 nm as a function of θin with the behavior predicted by the MEDR mechanism as shown in Fig. 2. For each grating, the reflectivity increases with decreasing θin (except for the smallest θin values). At any θin the reflectivity increases as the period decreases (except for the smallest θin values). We apply the MEDR model by approximating the blazed grating by an array of parallel half-planes, as depicted in Fig. 2(a), and introduce the universal parameter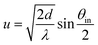 of the MEDR mechanism. In this model, the efficiency of specular reflection from the structure approaches unity as u approaches zero, as shown in Fig. 2(b). Therefore, a decrease in θin or d reduces u, leading to stronger reflection. This trend qualitatively agrees with the experimental results for the three gratings. Note that, for the given geometry of the gratings, the largest θin is much smaller than the blaze angle γ. Thus, specular reflection cannot result from reflection at the grating facets, but can only result from scattering at the edges.
of the MEDR mechanism. In this model, the efficiency of specular reflection from the structure approaches unity as u approaches zero, as shown in Fig. 2(b). Therefore, a decrease in θin or d reduces u, leading to stronger reflection. This trend qualitatively agrees with the experimental results for the three gratings. Note that, for the given geometry of the gratings, the largest θin is much smaller than the blaze angle γ. Thus, specular reflection cannot result from reflection at the grating facets, but can only result from scattering at the edges.
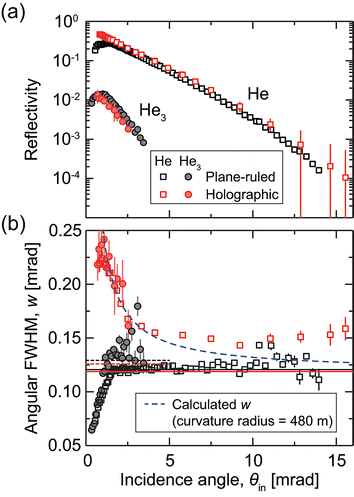
To study how the microscopic and macroscopic properties of a grating affect its reflectivity and the width of the reflected beam, we compare two series of experimental results for plane-ruled and holographic blazed gratings with d = 417 nm (Fig. 3). We choose the gratings of the shortest period since their largest reflectivity is desirable for future usage. According to the manufacturer, holographic gratings, inherently, show fewer periodic errors, spacing errors, and surface irregularities than plane-ruled gratings. AFM images of the two gratings (see Fig. S1 in ESI†43) confirm that the edges of the holographic grating are smoother than those of the plane-ruled grating. The standard deviations of edge heights for the holographic and plane-ruled gratings are observed to be 10 and 19 nm, respectively. Furthermore, their macroscale flatness (over the entire grating area) is different. The plane-ruled grating appears to be effectively flat, with an average radius of curvature greater than 2000 m. In contrast, the holographic grating exhibits a convex overall shape corresponding to a radius of curvature of ∼500 m. See ESI†43 for details of the grating characterization results.
The holographic grating exhibits higher reflectivity for He atoms than the plane-ruled grating over the entire range of θin from 0.5 to 15 mrad, as demonstrated in Fig. 3(a). We attribute this to the fact that the edges of the holographic grating are more homogeneous than those of its ruled counterpart. In particular, the reflectivity decrease observed for the smallest incidence angles (θin < 1 mrad) might result from microscopic imperfections in the plane-ruled grating that are absent for the holographic grating, which has a more regular shape. The maximum reflection probability reaches 47% at θin = 0.82 mrad, which is 2.5 times greater than the MLG/Ru(0001) mirror based on the classical reflection mechanism.40
Note that under maximum reflection conditions, the reflected beam differs in shape compared to the incident beam, with an increased peak width (namely, w > win), as shown in Fig. 1(c). The wider peak width implies that the grating surface is not macroscopically flat. The macroscopic curvature of the holographic grating accounts for the increased peak width. Fig. 3(b) shows the variation in w with θin for the two gratings. The change in w for the holographic grating confirms the convex shape of the nominally flat grating in agreement with the AFM results. The measured width agrees reasonably well with the calculated width at θin < 5 mrad.44 However, since the radius of curvature of the grating is ill-defined (see Fig. S2(f) in ESI†43) and the alignment among the three slits and the grating plane [see Fig. 1(a)] is not perfect, we do not expect agreement over the entire θin range. If the grating were concave, w would have shown a minimum at a certain incidence angle.28
In contrast, the width of the beam reflected from the plane-ruled grating is close to win [black horizontal line in Fig. 3(b)] at θin > 1.6 mrad (open squares), which is expected for reflection from a flat surface. For θin < 1.6 mrad, the projected width of the grating is smaller than the width of the collimated incident beam, so only a part of the incident beam hits the grating. This fraction of the beam increases with θin. This partial reflection explains the decrease in w at θin < 1.6 mrad.
These observations confirm that the gratings function as efficient mirrors for He atoms under grazing incidence conditions. In particular, the 417 nm-period gratings can work as mirrors whose performance depends on their macroscopic and microscopic properties, such as macroscopic curvature and surface irregularities.
Knowing that optical gratings can work as a good mirror for He atoms, we investigate their performance for small helium clusters, He2 and He3. As a result of the extremely small binding energies of He2 and He3 (0.15 μeV (ref. 45) and 11.4 μeV (ref. 46), respectively), they represent ideal model systems for studying non-destructive scattering of weakly-bound or metastable particles. For instance, classical reflection would lead to break-up of fragile He clusters, de-excite metastable atoms, or annihilate antihydrogen atoms. We utilized the plane-ruled and holographic blazed gratings with d = 417 nm to reflect a mixture of He clusters, mainly He3 with a small amount of He2. In Fig. 3(a) and (b), the black and red filled circles represent the reflectivity and peak widths observed for the clusters reflected from the plane-ruled and holographic gratings, respectively. The mirror reflectivity for clusters is found to be lower than that for He atoms. We attribute this to the fact that the de Broglie wavelength of He3 in the helium beam is three times shorter than that of He, thereby increasing u which is inversely proportional to 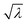 . Although the reflectivity for He3 is not as high as that for He atoms, the substantial reflectivity is expected to facilitate further studies with these fragile particles.
. Although the reflectivity for He3 is not as high as that for He atoms, the substantial reflectivity is expected to facilitate further studies with these fragile particles.
Regarding the peak widths, the variations in w for the helium clusters closely follow those observed for He atoms. This confirms that the width variation is independent of the particle type, and depends solely on the grating's macroscopic shape.
The macroscopic curvature of a grating-type mirror for matter waves is significant in two ways. First, the low peak height of a broadened beam results in a reduction in the signal-to-noise (S/N) ratio. Therefore, a simple reflection experiment with a low reflectivity for the particle would suffer from a small S/N value when the mirror is curved. A planar grating over a range of a few centimeters is thus favorable for such an experiment. Second, we can exploit the grating curvature to focus an incident beam. A concave grating with a properly tailored radius of curvature resulting in a focal length of tens of centimeters works as a concave mirror in matter-wave optics. The high reflectivity of a grating-type mirror facilitates an advanced Kirkpatrick–Baez (AKB) geometry for matter waves that allows tight beam focusing under grazing incidence conditions and requires four reflections.47,48 For example, if each mirror's reflectivity is 80, 50, or 20%, the intensity of the beam focused by the AKB system is 41, 6.3, or 0.16% of the incident beam intensity. The performance of an AKB system consisting of four grating MEDR mirrors of 50% reflectivity would, hence, be forty times better than one with four MLG/Ru mirrors. Therefore, an AKB microscope using the reflection of neutral helium atoms from concave gratings could complement the other types of scanning helium microscopes that have been demonstrated thus far based on a Fresnel zone plate10–13,49 and a pinhole.5,8,50,51
4 Conclusions
In conclusion, we demonstrated that commercially available plane-ruled or holographic blazed gratings can serve as mirrors for matter waves under grazing incidence conditions. The maximum reflection probability is as high as approximately 50% for a 417 nm-period holographic grating. Moreover, we applied this grating to reflect fragile He2 and He3 molecules, which readily dissociate upon colliding with a flat surface. Our results imply that reflection from grating mirrors via the MEDR mechanism offers a general approach that could be used with other fragile or metastable particles, such as antihydrogen atoms, for example. However, inherent imperfections of the grating edges on the microscale and the deviation from flatness of our gratings on the macroscale reduce the performance of the gratings as a mirror and cause the reflection probability to deviate from the MEDR model predictions. In the future, we can improve the quality of the gratings as mirrors by reducing the period, minimizing periodic errors and edge roughness, and maintaining an appropriate macroscopic surface flatness. Furthermore, a fine grating with a well-defined macroscopic curvature could function as an excellent focusing element. These findings can, therefore, pave the way for developing improved microscopes and interferometers that use atomic or molecular matter waves.Author contributions
B. S. Z. and W. S. conceived and supervised the experiment. B. S. Z., D. W. K., S. P., S. L., and J. W. K. performed the measurements. L. Y. K., D. W. K., and B. S. Z. analyzed the data. B. S. Z. and W. S. wrote the manuscript with input from L. Y. K. and D. W. K.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by NRF (National Research Foundation of Korea) grants funded by the Korean government (NRF-2019R1A2C1086215, NRF-2020R1A2C3003701, NRF-2022R1A4A1033247, and NRF-2017H1A2A1042369).Notes and references
- C. Davisson and L. H. Germer, Nature, 1927, 119, 558–560 CrossRef CAS.
- I. Estermann and O. Stern, Z. Phys., 1930, 61, 95–125 CrossRef.
- M. Knoll and E. Ruska, Z. Phys., 1932, 78, 318–339 CrossRef CAS.
- A. S. Palau, S. D. Eder, G. Bracco and B. Holst, Ultramicroscopy, 2023, 251, 113753 CrossRef CAS PubMed.
- P. Witham and E. Sánchez, Rev. Sci. Instrum., 2011, 82, 103705 CrossRef PubMed.
- P. J. Witham and E. J. Sanchez, J. Microsc., 2012, 248, 223–227 CrossRef CAS PubMed.
- P. Witham and E. Sanchez, Cryst. Res. Technol., 2014, 49, 690–698 CrossRef CAS.
- M. Barr, A. Fahy, J. Martens, A. P. Jardine, D. J. Ward, J. Ellis, W. Allison and P. C. Dastoor, Nat. Commun., 2016, 7, 10189 CrossRef CAS PubMed.
- A. Fahy, S. Eder, M. Barr, J. Martens, T. Myles and P. Dastoor, Ultramicroscopy, 2018, 192, 7–13 CrossRef CAS PubMed.
- O. Carnal, M. Sigel, T. Sleator, H. Takuma and J. Mlynek, Phys. Rev. Lett., 1991, 67, 3231–3234 CrossRef CAS PubMed.
- R. B. Doak, R. E. Grisenti, S. Rehbein, G. Schmahl, J. P. Toennies and C. Wöll, Phys. Rev. Lett., 1999, 83, 4229–4232 CrossRef CAS.
- T. Reisinger, S. Eder, M. M. Greve, H. I. Smith and B. Holst, Microelectron. Eng., 2010, 87, 1011–1014 CrossRef CAS.
- S. D. Eder, T. Reisinger, M. M. Greve, G. Bracco and B. Holst, New J. Phys., 2012, 14, 073014 CrossRef.
- A. D. Cronin, J. Schmiedmayer and D. E. Pritchard, Rev. Mod. Phys., 2009, 81, 1051–1129 CrossRef CAS.
- Helium Atom Scattering from Surfaces, ed. E. Hulpke, Springer, Berlin, 1992 Search PubMed.
- D. Farías and K. H. Rieder, Rep. Prog. Phys., 1998, 61, 1575 CrossRef.
- T. M. Roach, H. Abele, M. G. Boshier, H. L. Grossman, K. P. Zetie and E. A. Hinds, Phys. Rev. Lett., 1995, 75, 629–632 CrossRef CAS PubMed.
- H. Merimeche, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 3723–3731 CrossRef CAS.
- M. Metsälä, J. J. Gilijamse, S. Hoekstra, S. Y. T. van de Meerakker and G. Meijer, New J. Phys., 2008, 10, 053018 CrossRef.
- S. A. Schulz, H. L. Bethlem, J. van Veldhoven, J. Küpper, H. Conrad and G. Meijer, Phys. Rev. Lett., 2004, 93, 020406 CrossRef PubMed.
- M. A. Kasevich, D. S. Weiss and S. Chu, Opt. Lett., 1990, 15, 607–609 CrossRef CAS PubMed.
- V. U. Nayak, D. O. Edwards and N. Masuhara, Phys. Rev. Lett., 1983, 50, 990–992 CrossRef CAS.
- I. A. Yu, J. M. Doyle, J. C. Sandberg, C. L. Cesar, D. Kleppner and T. J. Greytak, Phys. Rev. Lett., 1993, 71, 1589–1592 CrossRef CAS PubMed.
- J. J. Berkhout, O. J. Luiten, I. D. Setija, T. W. Hijmans, T. Mizusaki and J. T. M. Walraven, Phys. Rev. Lett., 1989, 63, 1689–1692 CrossRef CAS PubMed.
- F. Shimizu, Phys. Rev. Lett., 2001, 86, 987–990 CrossRef CAS PubMed.
- V. Druzhinina and M. DeKieviet, Phys. Rev. Lett., 2003, 91, 193202 CrossRef CAS PubMed.
- T. A. Pasquini, Y. Shin, C. Sanner, M. Saba, A. Schirotzek, D. E. Pritchard and W. Ketterle, Phys. Rev. Lett., 2004, 93, 223201 CrossRef CAS PubMed.
- H. C. Schewe, B. S. Zhao, G. Meijer and W. Schöllkopf, New J. Phys., 2009, 11, 113030 CrossRef.
- B. S. Zhao, H. C. Schewe, G. Meijer and W. Schöllkopf, Phys. Rev. Lett., 2010, 105, 133203 CrossRef PubMed.
- F. Shimizu and J. Fujita, J. Phys. Soc. Jpn., 2002, 71, 5–8 CrossRef CAS.
- T. Pasquini, M. Saba, G. Jo, Y. Shin, W. Ketterle, D. Pritchard, T. Savas and N. Mulders, Phys. Rev. Lett., 2006, 97, 093201 CrossRef CAS PubMed.
- H. Friedrich, G. Jacoby and C. G. Meister, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 032902 CrossRef.
- J. Petersen, E. Pollak and S. Miret-Artés, Phys. Rev. A, 2018, 97, 042102 CrossRef CAS.
- E. Bogomolny and C. Schmit, Nonlinearity, 2003, 16, 2035–2059 CrossRef.
- H. Oberst, D. Kouznetsov, K. Shimizu, J. Fujita and F. Shimizu, Phys. Rev. Lett., 2005, 94, 013203 CrossRef PubMed.
- D. Kouznetsov and H. Oberst, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 013617 CrossRef.
- J. H. Lee, L. Y. Kim, Y.-T. Kim, C. Y. Lee, W. Schöllkopf and B. S. Zhao, Phys. Rev. Lett., 2019, 122, 040401 CrossRef CAS PubMed.
- D. Barredo, F. Calleja, A. Weeks, P. Nieto, J. Hinarejos, G. Laurent, A. V. de Parga, D. MacLaren, D. Farías, W. Allison and R. Miranda, Surf. Sci., 2007, 601, 24–29 CrossRef CAS.
- G. Anemone, A. A. Taleb, S. D. Eder, B. Holst and D. Farías, Phys. Rev. B, 2017, 95, 205428 CrossRef.
- A. Politano, B. Borca, M. Minniti, J. J. Hinarejos, A. L. Vázquez de Parga, D. Farías and R. Miranda, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035450 CrossRef.
- V. I. Balykin, V. S. Letokhov, Y. B. Ovchinnikov and A. I. Sidorov, J. Exp. Theor. Phys., 1987, 45, 353–356 Search PubMed.
- V. I. Balykin, V. S. Letokhov, Y. B. Ovchinnikov and A. I. Sidorov, Phys. Rev. Lett., 1988, 60, 2137–2140 CrossRef CAS PubMed.
- See ESI† for the details of the gratings, the experimental setup, and the data analysis.
- L. Y. Kim, D. W. Kang, J. C. Lee, E. Chae, W. Schöllkopf and B. S. Zhao, arXiv, 2023, preprint, arXiv:2311.12416, DOI:10.48550/arXiv.2311.12416.
- S. Zeller, M. Kunitski, J. Voigtsberger, A. Kalinin, A. Schottelius, C. Schober, M. Waitz, H. Sann, A. Hartung, T. Bauer, M. Pitzer, F. Trinter, C. Goihl, C. Janke, M. Richter, G. Kastirke, M. Weller, A. Czasch, M. Kitzler, M. Braune, R. E. Grisenti, W. Schöllkopf, L. P. H. Schmidt, M. S. Schöffler, J. B. Williams, T. Jahnke and R. Dörner, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14651–14655 CrossRef CAS PubMed.
- E. Hiyama and M. Kamimura, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 062505 CrossRef.
- R. Kodama, N. Ikeda, Y. Kato, Y. Katori, T. Iwai and K. Takeshi, Opt. Lett., 1996, 21, 1321–1323 CrossRef CAS PubMed.
- R. Sauneuf, J.-M. Dalmasso, T. Jalinaud, J.-P. Le Breton, D. Schirmann, J.-P. Marioge, F. Bridou, G. Tissot and J.-Y. Clotaire, Rev. Sci. Instrum., 1997, 68, 3412–3420 CrossRef CAS.
- R. Flatabø, M. M. Greve, S. D. Eder, M. Kalläne, A. S. Palau, K. K. Berggren and B. Holst, J. Vac. Sci. Technol., B, 2017, 35, 06G502 CrossRef.
- M. Bergin, S. M. Lambrick, H. Sleath, D. J. Ward, J. Ellis and A. P. Jardine, Sci. Rep., 2020, 10, 2053 CrossRef CAS PubMed.
- G. Bhardwaj, K. R. Sahoo, R. Sharma, P. Nath and P. R. Shirhatti, Phys. Rev. A, 2022, 105, 022828 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00155e |
| ‡ L. Y. K. and D. W. K. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |