Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Identification of reaction intermediates in the decomposition of formic acid on Pd†
Jan
Fingerhut
 *a,
Loïc
Lecroart
b,
Michael
Schwarzer
a,
Stefan
Hörandl
a,
Dmitriy
Borodin‡
*a,
Loïc
Lecroart
b,
Michael
Schwarzer
a,
Stefan
Hörandl
a,
Dmitriy
Borodin‡
 ab,
Alexander
Kandratsenka
b,
Theofanis N.
Kitsopoulos
ab,
Alexander
Kandratsenka
b,
Theofanis N.
Kitsopoulos
 bc,
Daniel J.
Auerbach
bc,
Daniel J.
Auerbach
 b and
Alec M.
Wodtke
b and
Alec M.
Wodtke
 abd
abd
aInstitute for Physical Chemistry, Georg-August University of Goettingen, 37077 Goettingen, Germany. E-mail: jan.fingerhut@mpinat.mpg.de
bDepartment of Dynamics at Surfaces, Max Planck Institute for Multidisciplinary Sciences, 37077 Goettingen, Germany
cSchool of Mathematics and Natural Sciences, University of Southern Mississippi, Hattiesburg, MS 39406, USA
dInternational Center for Advanced Studies of Energy Conversion, Georg-August University of Goettingen, 37077 Goettingen, Germany
First published on 13th March 2024
Abstract
Uncovering the role of reaction intermediates is crucial to developing an understanding of heterogeneous catalysis because catalytic reactions often involve complex networks of elementary steps. Identifying the reaction intermediates is often difficult because their short lifetimes and low concentrations make it difficult to observe them with surface sensitive spectroscopic techniques. In this paper we report a different approach to identify intermediates for the formic acid decomposition reaction on Pd(111) and Pd(332) based on accurate measurements of isotopologue specific thermal reaction rates. At low surface temperatures (∼400 K) CO2 formation is the major reaction pathway. The CO2 kinetic data show this occurs via two temporally resolved reaction processes. Thus, there must be two parallel pathways which we attribute to the participation of two intermediate species in the reaction. Isotopic substitution reveals large and isotopologue specific kinetic isotope effects that allow us to identify the two key intermediates as bidentate formate and carboxyl. The decomposition of the bidentate formate is substantially slower than that of carboxyl. On Pd(332), at high surface temperatures (643 K to 693 K) we observe both CO and CO2 production. The observation of CO formation reinforces the conclusion of calculations that suggest the carboxyl intermediate plays a major role in the water–gas shift reaction, where carboxyl exhibits temperature dependent branching between CO2 and CO.
1. Introduction
Catalysis plays a pivotal role in a wide range of chemical processes including the production of commodity chemicals, fertilizers, pharmaceuticals, efficient energy conversion and storage, and environmental remediation. It does so by making chemical reactions possible under conditions where they would otherwise be impractically slow. Often, these processes involve a complex network of elementary reactions that proceed through transient, hard to probe intermediates that effectively control the rate of product formation. Consequently, a key challenge in research aimed at understanding and improving heterogeneous catalysis is the identification of these intermediates and the determination of their binding energies and the energetic barriers to their formation and decay.A common approach to identifying intermediates is based on the use of chemically specific surface spectroscopic methods to directly observe species that are formed and decay during the reaction process. Examples of such spectroscopies include IR adsorption spectroscopy,1,2 electron energy loss spectroscopy,3 X-ray photoelectron spectroscopy, surface enhanced Raman and IR absorption spectroscopy,4,5 and low-energy electron diffraction.6 However, in some cases the limited sensitivity and time resolution of these techniques make it difficult or impossible to observe all the relevant intermediates. For example, theory indicates carboxyl is an intermediate in the decomposition of formic acid on Pd and in the water–gas shift reaction7–10 (WGSR) but direct evidence from surface spectroscopies for the carboxyl intermediate is lacking.11
In this paper, we take a different approach to the problem of intermediates in formic acid decomposition on Pd based on the time profile of the formation of products after the initiation of the decomposition reaction with a short molecular beam pulse. If multiple intermediates are involved, the measured product formation rate is the sum of multiple components with differing rates. Thus, the observation of multiple components can establish the existence of multiple pathways and, therefore, that multiple intermediates or active sites are involved. Accurate measurements of the rates of these components as a function of temperature provide information on the energy barriers and entropic parameters of the species involved. Comparison of these results with theoretical calculations of reaction pathways for hypothesized intermediates may enable identification of the intermediates.
Formic acid is a simple and abundant organic compound that has attracted considerable interest as a promising hydrogen carrier and renewable energy storage medium.12 Pd-based catalysts are highly active for decomposition of formic acid into CO2 and H2 (HCOOH → CO2 + H2, ΔH° = −14.9 kJ mol−1).13–17 Formic acid decomposition is also interesting because it can proceed through a dehydration pathway (HCOOH → CO + H2O, ΔH° = 26.2 kJ mol−1). Since formic acid can decompose into both the products and reactants of the WGSR (CO + H2O ⇌ CO2 + H2), understanding formic acid decomposition provides insights into the potential energy landscape of this important reaction. Furthermore, intermediates in the pathways for formic acid decomposition are also likely to be important in the WGSR. For example, Mavrikakis and coworkers9 found that density functional theory (DFT) calculations on the WGSR on Cu(111) indicate that carboxyl (C*OOH) is a key intermediate of the reaction while bidentate formate (HCO*O*) is only a spectator species.
There has been an extensive effort to clarify which intermediate species are formed in the decomposition of formic acid, but results remain controversial. The most prominent intermediate in this surface reaction is formate, which denotes a molecule with the composition HCOO but depending on its adsorption configuration is labelled monodentate (HCOO*) or bidentate formate (HCO*O*). (The latter is sometimes referred to as bridge-bonded formate). This intermediate has been more thoroughly studied as it can easily be formed on oxygen covered Pt or Pd; oxygen adatoms promote the deprotonation of the acidic OH in the parent formic acid molecule. Avery3 reported some of the first evidence for the existence of a HCOO* structure on O/Pt(111) at 130 K using high resolution electron energy loss spectroscopy and found it undergoes a fast irreversible conversion to HCO*O* when the surface is annealed to 190 K. Since then there have been observations of a formate intermediate in formic acid decomposition on many surfaces using a variety of surface analytical techniques.1,2,4,6,18,19 In addition, Campbell and coworkers20 measured the heat of adsorption of formic acid on O/Pt(111) using single crystal adsorption calorimetry (SCAC). They assigned a fast feature in the calorimeter response to the formation of HCOO* and a slow feature to the formation of HCO*O*. The difference between the formation enthalpies of these two species is about 0.45 eV. DFT studies find this energy difference is larger than 0.45 eV and that there is a small (or no) barrier to decomposition into CO2 and H.8,21,22 As these calculations were for an oxygen-free surface whereas the SCAC experiments were on O/Pt(111), there is a clear need for further calculations to characterize the effect of co-adsorbed oxygen. In other DFT calculations, Mavrikakis and coworkers determined that C*OOH plays a major role in the overall reactivity of formic acid;7 they also suggested that the carboxyl-intermediate is the major intermediate in the WGSR.9
In this article, we report high temporal resolution kinetics experiments using the recently developed velocity-resolved kinetics (VRK) technique23,24 and DFT calculations of the decomposition of formic acid on Pd. We do this for both the close packed Pd(111) facet and the stepped Pd(332) facet, which has a step density of 1/6. We observe both CO2 and CO products. The rate of CO2 formation shows two clearly resolved components, one decaying much more rapidly than the other. To identify the intermediates involved in these pathways, we measured the decomposition rate for three different isotopologues of formic acid (HCOOH, DCOOH and HCOOD). Large and isotopologue specific kinetic isotope effects (KIEs) demonstrate that the key intermediates in this reaction are a bidentate formate species, which decomposes slowly, and a carboxyl intermediate, which decomposes much more rapidly. By comparing CO2 and CO formation data on Pd(111) and Pd(332), we see that the B-type steps present on Pd(332) increase the importance of the carboxyl intermediate to the reaction and consequently also enhance the formation of CO. Finally, we briefly discuss the implications for these results for the WGSR and suggest directions for future work on formic acid decomposition.
2. Methods
2.1. Experimental
We study the decomposition of formic acid by initiating the reaction with a short molecular beam pulse (approximately 30 µs full width at half maximum) of formic acid seeded in helium incident on the surfaces of Pd(111) and Pd(332) single crystals and measure the time evolution of the reaction products using multiphoton laser ionization and ion imaging in the recently developed VRK technique.The molecular beam of formic acid is produced by bubbling helium (7 bar) through liquid formic acid at room temperature (296 K) and expanding this gas mixture (∼1% formic acid in He) through a custom pulsed nozzle (nozzle diameter = 1 mm) operating at 25 Hz. The absence of impurities is verified using mass analysis of the incident molecular beam. The supersonic molecular beam pulse passes through two differential pumping chambers and enters the surface-scattering chamber where it impinges upon the Pd surface (MaTeck GmbH) at an incidence angle of 30° to the surface normal. The formic acid flux incident on the surface is estimated to be 1.5 ± 0.5 × 1011 molecules per cm2 per pulse.25 The surface is prepared by sputtering with Ar+ (3 keV) for 15 min and then annealing at 1050 K for 15 min. Surface cleanliness is verified using Auger electron spectroscopy. Further information about the apparatus and experimental procedures have been described elsewhere.23
In this work, we use a Pd single crystal surface that is polished to expose two different facets – (111) and (332). We estimate the step density of the Pd(111) facet is <0.1% based on the specified accuracy (<0.1°) of the polished face of the crystal relative to the 111 facet. The step density of the Pd(332) crystal is 1/6 (16.7%).The facets are spatially well separated and are large enough to prevent molecular beam exposure of both facets at the same time. The use of this two-facet crystal allows us to rapidly switch between the two facets and observe the influence of increased step density on the mechanism and reactivity, while other experimental conditions are held constant. Using the reflection of a HeNe-laser from the surface, we align the (111) and (332) facets so that their surface normal is parallel to the scattering plane, i.e. the plane defined by the molecular beam and the ionization laser propagation directions.
Desorbing reactant and product molecules are ionized ∼20 mm from the surface, using non-resonant multiphoton ionization with a focused Ti:Sapphire laser beam (<100 fs, ≈16 mJ mm−2 at 1 kHz). A pulsed homogeneous electric field projects the ions onto a time-gated microchannel plate (MCP)-Phosphor anode imaging detector. The mass-to-charge ratio of the detected ions is selected by setting the time-gate on the MCP with respect to the pulsed-field extraction. The ion image appearing on the phosphor screen is recorded with a CCD camera.
The flux of desorption products as a function of time is obtained by recording the product density, which is proportional to the number ions produced by the laser pulse, as a function of the time delay between the ionizing laser and the pulsed molecular beam. Velocities of both reactants and the scattered/desorbing products are obtained from ion images and are used to convert the observed product density to flux. We determine the flight time of the desorption products to the ionization laser using our knowledge of the laser–surface distance and the measured ion velocities. This is then subtracted from the time delay between the ionizing laser and the pulsed molecular beam to get the residence/reaction time at the surface associated with a given detected ion. To account for the arrival time of the incident molecular beam at the surface, we measure its time-profile and incident velocity in a separate experiment where the laser focus is moved to the position of the incident beam in the center of the ion optics and the molecular density as a function of the delay between the ionization laser and pulsed molecular beam is recorded. We model this observed time-profile as a Gaussian. With this information and the known distance between laser and surface, the mean arrival time of the formic acid at the surface is determined. This information and the density to flux conversion described above are used to determine the fluxes of desorbing species as a function of residence time, referred to hereafter as the “kinetic trace” of the reaction.
2.2. Computational
DFT calculations for formic acid on Pd(111) and Pd(332) were performed using VASP 5.3.5.26–29 The GGA XC functional PBE30 is employed with the help of the Tkatchenko–Scheffler31 method to reckon with the van der Waals energy-corrections as it was previously found to work well for formic acid adsorption on Pd(111).32 The optimized lattice constant for the Pd crystal is a0 = 3.945 Å, which agrees within 1% with the experimental lattice constant.33 The plane wave energy cut-off is set to 450 eV and partial electronic occupations were modeled with the Methfessel–Paxton (N = 1) smearing scheme34 with a width of σ = 0.1 eV. The interaction between valence and core electrons is described by the projector augmented-wave method.35 The electronic self-consistent loop breaks if the total energy is below 10−5 eV. Optimized structures are found using the conjugate gradient algorithm when the energy change between two ionic steps is below 10−4 eV. The nudged elastic band (NEB) method36 enables us to determine reaction saddle points. Only atoms of the adsorbed species were allowed to move while slab atoms are fixed during optimization and NEB calculations.The Pd(111) surface is modeled as a slab of three (3 × 3) Pd layers arranged in ABC stacking with a vacuum layer of 20 Å. For the Pd(332) surface, three (6 × 3) Pd layers arranged in steps along the first axis with a vacuum layer of 20 Å were utilized (see ESI S4 Fig. S6†). The Brillouin zone is sampled by an 8 × 8 × 1 Γ-point centered and 2 × 8 × 1 Γ-point centered k-point mesh, for Pd(111) and Pd(332) surfaces, respectively.
Vibrational frequencies for adsorbates are calculated using VASP 5.3.5. To calculate the Hessian matrix, we perform 4 displacements for each direction and 0.015 Å width for each nucleus. The frequencies of the deuterated isotopologues are calculated through diagonalization of the Hessian matrix, obtained for hydrogenated species, and replacing H-atoms with D-atoms as necessary for each isotopologue.
3. Results and discussion
To study the kinetics of formic acid decomposition, we record ion images corresponding to the CO2 product of the decomposition reaction of formic acid on the surfaces of Pd(111) and Pd(332) single crystals over the temperature range of 373 to 473 K. In almost all cases, the ion images show broad angular distributions symmetric about the surface normal and broad speed distributions consistent with desorption of thermally equilibrated products. Examples of speed distributions can be found in the ESI Section S1.† On Pd(111), we also see a small contribution of hyperthermal CO2. Similar to our previous work on formic acid oxidation on Pt but unlike the case of CO oxidation on Pt, the temporal profile of kinetic traces for both speed components are identical.24,37 Using the VRK analysis described in Section 2.1, we integrate the images over speed and angular distributions to obtain the product flux vs. reaction time – the kinetic trace. It is important to note that at the surface temperatures considered in this study, desorption of any unreacted formic acid as well as CO2 product occurs rapidly. Thus, the CO2 kinetic traces are controlled by the formation rate.On Pd(111) the reactive signal (yield) of CO2 from sequential 90 seconds scans is constant while on Pd(332) it decreases slightly. We attribute this decrease to the build-up of a steady-state coverage of hydrogen atoms (H*) which reduces the initial sticking probability of formic acid. We estimate the upper limit of the steady-state hydrogen coverage in our experiments to be ∼0.02 ML at 383 K38 and lower at higher surface temperatures. Importantly, as verified by experiments on the CO2 formation rates in the presence of background hydrogen gas, the kinetic information extracted from the CO2 formation rates are not affected by the presence of co-adsorbed hydrogen. The decrease in the reactive signal is reversed by flashing the sample to 873 K. For further details, see ESI Section S2.†
In contrast, the effect of CO co-adsorption on the CO2 formation rates on Pd(332) show that co-adsorbed CO at high coverages ([COad] ≈ 0.28 ML at 413 K) does change the shape of the CO2 kinetic traces. However, the CO build up due to formic acid decomposition is not enough to induce this effect even after running the molecular beam of formic acid for up to 84 minutes. Based on this experiment and the fact that we restricted the data acquisition time to be less than 6 minutes before flashing the surface to remove CO build up, we can be certain that the effect of co-adsorbed CO on our kinetic traces is negligible. For further details, see ESI Section S2.†
3.1. Observation of two channels in CO2 formation
Fig. 1 shows typical kinetic traces for CO2 formation at 403 K on Pd(111) and Pd(332). On both facets we observe an initial feature with a rapid rise and rapid decay followed by a second feature that decays much more slowly. This observation indicates that the kinetic traces are composed of two components originating from two reaction pathways.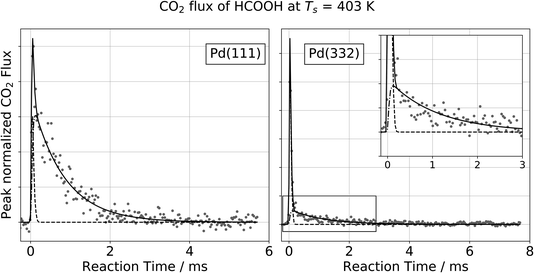 | ||
Fig. 1 Observation of two temporally resolved CO2 formation channels in formic acid decomposition on Pd. Typical peak normalized kinetic traces of CO2 on Pd(111) (left) and Pd(332) (right) at 403 K using HCOOH. The VRK data are fit according to eqn (2) (Pd(111): k1 > 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1 and k2 = 1200 s−1; Pd(332): k1 > 80 000 s−1 and k2 = 1200 s−1; Pd(332): k1 > 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1 and k2 = 900 s−1). The inset in the right panel shows an enlarged view of the slow component which decays over several milliseconds at this temperature whereas the fast component is on the timescale of the incident molecular beam (dashed line). 000 s−1 and k2 = 900 s−1). The inset in the right panel shows an enlarged view of the slow component which decays over several milliseconds at this temperature whereas the fast component is on the timescale of the incident molecular beam (dashed line). | ||
To describe each of these components, we use a function f(t,k,σ), which is the convolution of a Gaussian distribution of width σ (to represent the arrival time distribution of the molecular beam pulse) with an exponential function with a decay rate k to represent the decrease in product flux from a first order reaction.
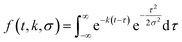 | (1) |
| flux(t) = a1f(t,k1,σ) + a2f(t,k2,σ). | (2) |
For all of our data, the reaction rate of the slow channel for CO2 formation on the higher-step density Pd(332) facet is lower than it is on Pd(111). For example, kPd(111)2 = 1200 s−1 at 403 K, and kPd(332)2 = 900 s−1. The contribution of the fast component is systematically larger on Pd(332) than on Pd(111) (43% for Pd(332) vs. 8% for Pd(111) at 403 K).
The observation of two features in the kinetic traces strongly suggests a mechanism for formic acid decomposition with two pathways for CO2 formation. These two pathways could arise from either the existence of two active sites or two reaction intermediates. Below, we will use isotope substitution experiments to reveal that two intermediates are involved.
3.2. Observation of CO formation in the decomposition reaction
At higher surface temperatures, we find there is a reactive process producing CO on Pd(332). Working at higher surface temperatures is necessary to observe CO because the desorption-lifetime of CO is too long at low surface temperatures to be observed in our VRK experiments (∼240 min at 403 K).39 The lifetime ranges from 100 to 600 µs for temperatures between 643 and 693 K, making it easily observable.Fig. 2a shows typical VRK data for CO formation from formic acid decomposition on Pd(332). The kinetic trace has both a fast and a slow component. Based on analysis of ion images, we identify the fast component in the trace is not related to formic acid decomposition on Pd, but results from laser induced multiphoton dissociation of gaseous formic acid followed by non-resonant multi-photon ionization of CO, see insets of Fig. 2 and ESI Section S3† for further discussion.40,41
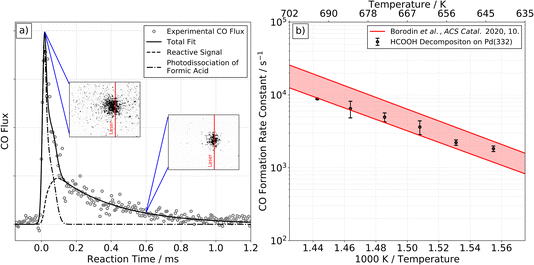 | ||
| Fig. 2 CO formation from formic acid decomposition on Pd. Experimental kinetic trace of CO on Pd(332) at 663 K from HCOOH (left panel, (a)) and corresponding Arrhenius plot of the rate constant of CO formation (right panel, (b)). (a) The kinetic traces of CO exhibit two components. The fast component is the result of photodissociation of formic acid, see ESI Section S3† for further discussion. The slow component is reactive signal arising from formic acid decomposition. The two insets show representative ion images at the corresponding reaction time. The image seen at short times reflects large CO recoil velocities produced in the photodissociation of gas-phase formic acid. Note that photodissociation of formic acid leading to CO+ and OH+/H or CO+ and H2O+ with fs-pulses of a Ti:Sapphire laser has been reported previously.40,41 (b) Comparison of the extracted rate constants for the slow component with previous Arrhenius parameters for CO desorption from Pd(332).39 This comparison indicates that the rate of CO formation observed is desorption limited under these conditions. | ||
We fit the experimental data for the slower component in Fig. 2a and find the derived rate constant agrees with the experimental desorption rate constant of CO from Pd(332)39 as shown in Fig. 2b. We conclude that the rate of CO formation from formic acid decomposition is limited by the CO desorption rate. On Pd(111) we are not able to detect any reactive signal of CO formation.
3.3. Isotope labeling experiments
To gain information on which intermediates are involved in the slow and fast decomposition channels, we performed isotopic labeling experiments and observed KIEs. In this section, we describe an intuitive picture of what can be inferred from such KIEs, and how we can use them to make an assignment of reaction intermediates. A quantitative comparison of the magnitude of the KIE and temperature dependence will be given in Section 4 to support these assignments.Formic acid has two structurally nonequivalent H atoms, one involved in the O–H bond and the other involved in the C–H bond. Substituting D for H at these two positions (i.e. HCOOD or DCOOH) provides diagnostic capability, as these substitutions will have different effects on the rate of formation and decomposition of hypothetical intermediates. For example, the C–H bond must break to form carboxyl; hence, substitution of D for H in the hydroxyl position (HCOOD), will have little effect on the carboxyl formation rate (it is a secondary KIE). On the other hand, substitution of H for D at the carbon position (a primary KIE) will lower the carboxyl formation rate. This is because the C–D bond possesses lower zero-point energy (ZPE) than the C–H bond, whereas isotopic substitution does not appreciably change the ZPE of the transition state. Hence, the barrier to C–H bond cleavage is increased and the rate of carboxyl formation is reduced. Thus, the rate of formation of carboxyl will be lower for DCOOH than for HCOOH.
To facilitate the discussion, we introduce a concise notation for the trends in the KIE δHCOOD and δDCOOH, which denote the direction of change in the rate for HCOOD and DCOOH, respectively, relative to the rate for HCOOH. We focus here on whether there is an increase, no change or a decrease in rate with isotopic substitutions and indicate the trends as +, =, or − respectively.
Applying similar arguments to those presented above for the carboxyl formation rate, we construct a table of predicted KIEs for the branching into the fast channel and the KIEs for the rate of the slow channel. As discussed in Section 1, previous work suggested three species might be involved: monodentate formate (HCOO*), bidentate formate (HCO*O*), and carboxyl (C*OOH). Table 1 shows predicted KIEs for all plausible choices of intermediates. In making these predictions we assume that the intermediates decay exclusively to CO2. We will show later how CO formation affects the fast channel branching fraction and that it does not change the assignments made here.
| Possible intermediate assignment to fast & slow channels | Intermediate formation rate δHCOOD/δDCOOH | Branching fraction between fast and slow channels δHCOOD/δDCOOH | Intermediate decomposition rate to CO2δHCOOD/δDCOOH | ||
|---|---|---|---|---|---|
| Fast | Slow | Fast channel | Slow channel | F/(F + S) | Slow channel |
| HCOO* | HCO*O* | −/= | −/= | =/= | =/− |
| HCOO* | C*OOH | −/= | =/− | −/+ | −/= |
| HCO*O* | C*OOH | −/= | =/− | −/+ | −/= |
| C*OOH | HCO*O* | =/− | −/= | +/− | =/− |
| Observed | +/− | =/− | |||
Table 1 displays expected KIEs for the four plausible choices of how to assign intermediates to the fast and slow channels. For the fast component, monodentate formate, bidentate formate and carboxyl are all possible intermediates. For the slow component we exclude monodentate formate as a candidate intermediate, since our own and previous7 DFT calculations show that it is not stable and would not survive the millisecond time scale of the slow component’s decay. The final row in Table 1 shows the experimentally observed isotope effects on the fast channel branching fraction and the slow channel decay rate over the range 373 K to 473 K. The observed pattern of isotope effects supports an assignment where the fast channel reflects the formation and decomposition of carboxyl while the slow channel arises from a bidentate formate intermediate. In Section 4, we will critically examine and confirm these assignments by comparison of the results of detailed theoretical calculations and measurements of decomposition rates as a function of temperature.
3.4. Theoretical calculations of formic acid decomposition
Motivated by our interpretation of the kinetic isotope effect data and previous DFT work on the decomposition reaction,7 we performed DFT calculations of the minimum energy paths, transition state configurations and barriers for the elementary steps shown in Fig. 3 for reactions on both Pd(111) and Pd(332). To the best of our knowledge, no calculations have been previously published for formic acid decomposition on the Pd(332); there are calculations for the stepped Pd(211) surface,42 but this surface has a different step type. For these calculations, we use the PBE exchange correlation energy functional with the TS-dispersion correction because we have shown that it provides a better description of the binding energy of formic acid adsorption on Pd(111) than the PW91 or RPBE-D3 functionals.32 Further support for this choice is given by the work of Hu and coworkers43 who compared the performance of different DFT functionals and van der Waals correction schemes for formic acid adsorption on Pt(111) and found that PBE-TS is one of the best performing functionals. Binding energies and geometrical parameters are summarized in the ESI Section S4.†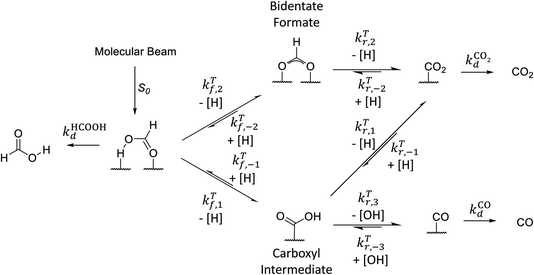 | ||
| Fig. 3 Simplified reaction scheme proposed by Mavrikakis and coworkers7 for formic acid decomposition on Pd(111). | ||
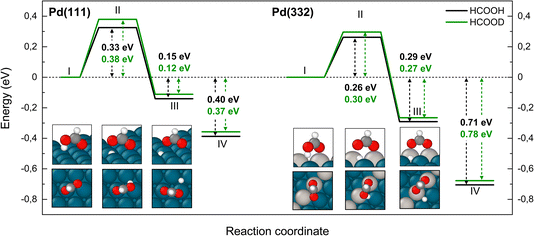
Fig. 3 shows that adsorbed formic acid may undergo O–H bond or C–H bond dissociation. O–H bond dissociation leads to the formation of bidentate formate, the minimum energy path for which is shown for Pd(332) and Pd(111) in Fig. 4. In the initial formic acid adsorption structure the carbonyl O-atom is at a top-site while the hydroxyl group is above a bridge site. On Pd(332), the most favorable adsorption site is similar but the carbonyl O-atom is located at the step while the hydroxyl group is orientated towards the terrace. To form bidentate formate, the molecule rotates the O-atom of the hydroxyl group towards a top site while the hydrogen atom moves to an fcc-hollow site. This reaction pathway is the same for Pd(111) and Pd(332). The energy barrier for this reaction is slightly lower on the step-site than on the terrace. Deuteration of the OH-bond increases the ZPE corrected barrier for bidentate formation by ∼0.04 eV.
Fig. 5 shows corresponding reaction paths for C–H bond dissociation leading to carboxyl. Here, the calculations suggest that the molecule first rotates to bring the C–H bond close to a Pd atom and subsequently the C–H bond breaks. The initial rotation shows no isotope dependence; however, the bond dissociation step proceeds over an additional barrier, which is higher for DCOOH compared to HCOOH by 0.02 eV on Pd(111) and 0.04 eV on Pd(332).
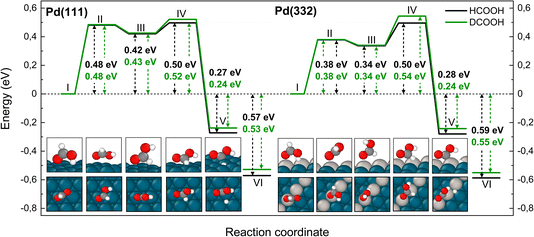 | ||
| Fig. 5 Reaction pathway for carboxyl formation from HCOOH (black) and from DCOOH (green) on Pd(111) and Pd(332) obtained from NEB calculations using PBE-TS functional. On the scheme the initial state (I), the first transition state (II), the intermediate state (III), the second transition state (IV) and the final state (V) are shown. Energy level VI corresponds to final state V without interaction between products. Atom representation is the same as in Fig. 4. The energy values include ZPE correction. | ||
We turn next to the decomposition of the intermediates; both bidentate formate and carboxyl intermediates can form CO2. Consistent with our assignment of bidentate formate to the slow channel, we find that the barrier for CO2 formation from bidentate formate is significantly larger than from carboxyl (see Fig. 6 and 7).
We have identified two reaction paths for decomposition of bidentate formate to CO2 (see Fig. 6). The first (Fig. 6a) describes a two-step dissociation where the bidentate formate first breaks one O–Pd bond to bring the C–H bond closer to the surface, before the C–H bond breaks forming CO2 and an H atom bound to Pd. The first step is associated with a ZPE corrected energy barrier of 0.78 eV (0.79 eV) on Pd(111) and 0.85 eV (0.86 eV) on Pd(332), almost independent of deuteration (i.e. HCO*O* vs. DCO*O*). The subsequent C–H bond dissociation is barrier less. The second reaction path (Fig. 6b) involves rotation of the bidentate formate molecule from an upright to a flat adsorption geometry, bringing the C–H bond closer to the surface, where it can dissociate. The barrier along this path is 0.90 eV (0.93 eV) for HCO*O* (DCO*O*) on Pd(111) and 0.86 eV (0.90 eV) for HCO*O* (DCO*O*) on Pd(332). As we will show in Section 4 below, only this reaction path can explain the observed KIE.
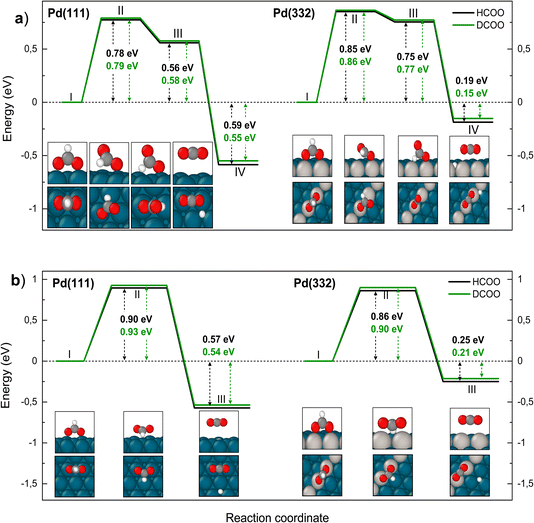 | ||
| Fig. 6 Reaction pathway for carbon dioxide formation from two isotopologues of bidentate formate (HCO*O*) (black) and from DCO*O* (green) on Pd(111) and Pd(332). Panel (a) shows the sequential reaction pathway proposed by Mavrikakis and coworkers7 and panel (b) shows a concerted reaction pathway with a larger KIE found in this work. In (a) (I) denotes the initial, (II) the transition, (III) the intermediate and (IV) the final state. In (b) (I) denotes the initial, (II) the transition and (III) the final state. Atom representation is the same as in Fig. 4. The energy values include ZPE correction. | ||
The reaction paths for carboxyl decomposition to form CO2 are shown in Fig. 7. Here, the reaction coordinate involved elongation of the O–H bond; hence the change in barrier height upon isotopic substitution is significant. The barrier to decomposition of C*OOH is 0.05 eV lower than that of C*OOD on Pd(111). The difference between isotopes is 0.02 eV on Pd(332), where the barrier is ∼0.15 eV lower compared to Pd(111).
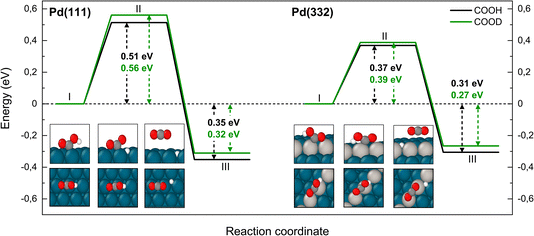 | ||
| Fig. 7 Reaction pathway for CO2 formation from two isotopologues of carboxyl C*OOH (black) and from C*OOD (green) on Pd(111) and Pd(332) obtained from NEB calculations using PBE-TS functional. On the scheme the initial (I), transition (II) and final state (III) are shown. Atom representation is the same as in Fig. 4. The energy values include ZPE correction. | ||
The reaction path for the carboxyl intermediate to form CO by C–OH bond dissociation is shown in Fig. 8. Here, the rotation about the CO bond facilitates formation of a Pd–O bond in the adsorbed OH product. The transition state is located on a bridge site while the final CO is bound at an fcc hollow and the OH on a bridge site. The ZPE corrected energy barrier is 0.18 eV higher on Pd(332) compared to Pd(111) and there is a negligible effect of isotope substitution on the barrier height. This suggests there should be little or no KIE in this reaction on either Pd(111) or Pd(332).
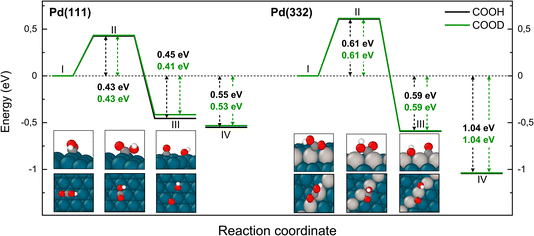 | ||
| Fig. 8 Reaction pathway for CO formation from two isotopologues of carboxyl C*OOH (black) and from C*OOD (green) on Pd(111) and Pd(332) obtained from NEB calculations using PBE-TS functional. In the scheme the initial (I), transition (II) and final state (III) are shown. Energy level IV corresponds to final state III without interaction between products. Atom representation is the same as in Fig. 4. | ||
In Table 2 we summarize the classical barrier heights (neglecting ZPE corrections) for the forward reactions and reaction energies and compare with previous calculations. While not all previous publications have considered all reactions reported here, we note that calculated barriers previously reported based on use of the PW91 and RPBE exchange correlation functionals are systematically higher than the results reported here. We attribute this effect to the choice of the TS-dispersion correction scheme.
| Elementary step | This work | Comparison to previous work | ||||||
|---|---|---|---|---|---|---|---|---|
| Pd(111) | Pd(332) | Pd(111) | Pd(111) | Pd(111) | Pd(111) | |||
| E f/eV | ΔE/eV | E f/eV | ΔE/eV | E f/eV7 | E f/eV44 | E f/eV22 | E f/eV45 | |
| HCO*OH* → HCO*O* + H* | 0.50 | −0.28 | 0.41 | −0.60 | 0.60 | 0.58 | — | 1.00 |
| HCO*OH* → H*CO*OH | 0.48 | 0.40 | 0.36 | 0.32 | 0.72 | — | — | 0.73 |
| H*CO*OH* → C*OOH + H* | 0.18 | −0.84 | 0.32 | −0.81 | 0.34 | — | — | 0.84 |
| (a) HCO*O* → CO2 + H* | 0.87 | −0.48 | 0.93 | −0.11 | 0.93 | 0.76 | 0.92 | 0.88 |
| (b) HCO*O* → CO2 + H* | 1.05 | −0.48 | 1.05 | −0.11 | — | — | — | 1.48 |
| C*OOH → CO2 + H* | 0.68 | −0.22 | 0.45 | −0.18 | 0.70 | — | 0.72 | 1.09 |
| C*OOH → C*O + O*H | 0.49 | −0.42 | 0.65 | −0.97 | 0.80 | — | 0.86 | 0.15 + 1.67 |
Finally, Fig. 9 shows an energy diagram of formic acid decomposition on Pd(111) and Pd(332) summarizing the DFT calculations of this work (harmonic frequencies of initial and transition states are summarized in the ESI Section S4†). This energy landscape forms the basis for quantitative comparison to VRK rate data and KIEs discussed in the following section.
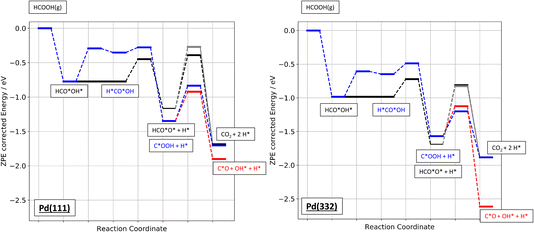 | ||
| Fig. 9 Zero-point energy corrected energy diagram of formic acid decomposition on Pd(111) and Pd(332). The black lines show the bidentate formate pathway, blue the carboxyl to CO2 pathway and red the carboxyl to CO pathway. The grey line shows the alternative pathway for bidentate formate dissociation as shown in Fig. 6b). | ||
4. Quantitative comparison of experimentally observed and theoretically predicted CO2 formation rates
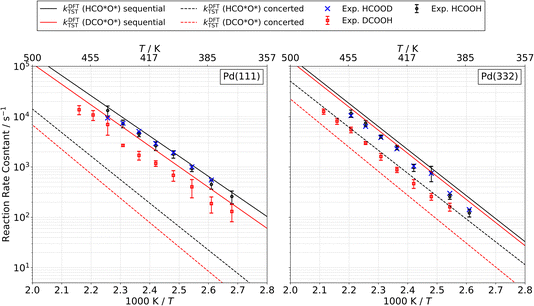
We measured kinetic trace data like that shown in Fig. 1 for CO2 production as a function of temperature for formic acid decomposition on both Pd(111) and Pd(332). In most cases, the data show well-resolved fast and slow components. Depending on the isotopologue, in some case the two components are not clearly distinguishable at higher surface temperature; however, we can still fit a first order rate constant to the slow component. Using eqn (2) to fit the kinetic traces, we derive the temperature dependent rate constant k2 for the slow channel as a function of temperature for the three isotopologues HCOOH, HCOOD and DCOOH. The results are shown in Fig. 10. The rate constants exhibit Arrhenius behavior over this temperature range. The Arrhenius parameters derived from the data are presented in Table 3.| Species | Pd(111) | Pd(332) | ||
|---|---|---|---|---|
| A/s−1 | E a/eV | A/s−1 | E a/eV | |
| HCO*O* | 1013.1±0.3 | 0.79 ± 0.02 | 1014.7±0.6 | 0.95 ± 0.05 |
| DCO*O* | 1013.2±0.5 | 0.83 ± 0.04 | 1013.7±0.3 | 0.90 ± 0.02 |
A distinctive KIE is seen, which as discussed above is consistent with our assignment of the slow channel to the decomposition of the bidentate formate intermediate. Specifically, bidentate decomposition rate constants are indistinguishable from one another for experiments carried out with HCOOH or HCOOD, whereas experiments employing DCOOH lead to rate constants that are smaller by a factor of 2 to 3 over the temperature range studied.
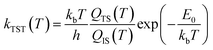 | (3) |
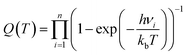 | (4) |
The predictions of TST for the bidentate decomposition rate constants are shown as solid and dashed lines in Fig. 10. Solid lines are the results of using TST assuming the reaction path of Fig. 6a, which describes a sequential mechanism where Pd–O bond dissociation is followed by Pd–H bond formation. The dashed lines are the TST predictions using the reaction path from Fig. 6b, which describes concerted rearrangement of Pd–O and Pd–H bonding. Red and black line show TST predictions of the KIE.
For the sequential mechanism, the magnitudes of the rate constants found from TST are in remarkable agreement (within a factor of 2) with experimentally derived rate constants. However, the predicted KIE is much smaller than that observed. The concerted mechanism correctly predicts the large KIE, but fails to predict the rate constants accurately, likely due to DFT’s inability to predict highly accurate reaction barrier heights. By adjusting the classical barrier height for the concerted reaction by only −0.1 eV on Pd(111) and −0.03 eV on Pd(332), we achieve quantitative agreement with the measured rate constants. The difference in the predicted KIEs reflects differences between the two transition states. In the sequential mechanism, elongation of the C–H bond is not required to reach the transition state; instead the Pd–O bond must be stretched. Consequently, the ZPE corrected energy of the TS with respect to the initial state E0 is not strongly affected by isotopic substitution. On the other hand, for concerted decomposition, dramatic C–H bond elongation is required to reach the transition state, such that the ZPE along the C–H bond nearly disappears at the transition state. Under such conditions, E0 becomes strongly isotope dependent, reflecting the lower ZPE of the deuterated initial state with respect to the protiated initial state. This results in a large KIE as seen in experiment.
These comparisons strongly suggest that the mechanism of bidentate formate decomposition on Pd involves a concerted rearrangement of Pd–O and H–Pd bonding. We favor the concerted mechanism despite the fact that our DFT calculations give a barrier for the concerted reaction that is 0.18 eV higher on Pd(111) and 0.12 eV higher on Pd(332) than that of the sequential reaction. This energy ordering is the basis of the conclusion from prior theoretical studies favoring the sequential reaction mechanism. However, it is doubtful that a DFT computed transition-state energy difference of this magnitude is trustworthy.
It is worth noting that vibrational anharmonicity is another important factor relevant to this discussion. We speculate that a more accurate description of the partition functions including vibrational anharmonicity might show that the concerted reaction is entropically favored, even if it is not energetically favored. Such an analysis goes beyond the scope of this work, as it requires a challenging characterization of the potential energy surface beyond the harmonic approximation.
Although the arguments above favoring a concerted mechanism are strong, we cannot exclude the possibility that a different sequential mechanism might exhibit a large KIE. Using a PW91 functional, Zhang et al.45 calculated a sequential bidentate formate decomposition pathway, which exhibits a small barrier to C–H bond dissociation, i.e. a barrier between structures like III and IV in Fig. 6a. While this barrier is small, it could lead to a large KIE. Our calculations show no such barrier, likely due to a different choice of exchange–correlation functional. Regardless of the exact mechanism, the observed KIE can only be described by a transition state that requires extensive C–H bond elongation.
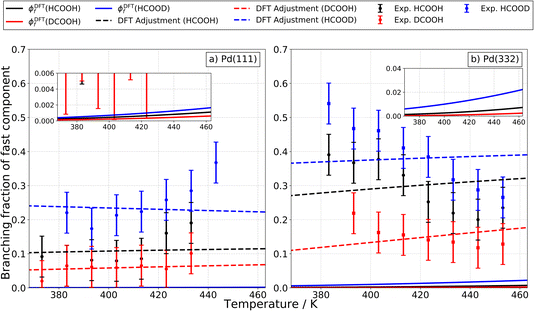
It is also useful to compare the branching fraction of the fast channel, ϕf(T), with the theoretically predicted contribution of the carboxyl intermediate to the total CO2 formation rate. To derive the branching fraction from experiment ϕexpf(T), we use data like that shown in Fig. 1 to determine the area under the kinetic traces corresponding to the fast channel and divide this by the total area under the trace.
Theoretical branching fractions ϕDFTf(T) are a product of two terms:
 | (5) |
More specifically, kDFTf,1(T) and kDFTf,2(T) denote the rate constants for formation of the carboxyl and bidentate formate, respectively. kDFTr,1(T) and kDFTr,3(T) are the rate constants for carboxyl decomposition to CO2 and CO, respectively. As described above, we have used our DFT computed reaction pathways along with the help of TST to compute the temperature and isotope dependent branching fractions.
Fig. 11a shows how these predictions compare to experiments done on Pd(111). Here, theoretical values are shown as solid lines and experimentally derived values are shown as points with error bars. Theory drastically underestimates the branching fraction; however, by reducing the barrier to carboxyl formation by only 0.14 eV and increasing the barrier to CO formation by 0.10 eV, agreement is within experimental uncertainty. See the dashed lines in Fig. 11a. We do not consider these adjusted barrier heights to be established values; our point is simply to show that relatively small errors in the DFT barrier heights are likely responsible for the underestimation of the branching fraction. We note that the isotopic substitution trends agree with experiment with or without these adjustments.
For Pd(332), the measured branching fraction is larger than in the case of Pd(111), a result that is reproduced by theory. Though the DFT prediction of the branching fraction is 10 times smaller than the experiment, it does substantially better than the Pd(111) prediction where the disagreement is a factor of 100 off. For Pd(332), we get reasonable agreement for the theoretical and experimental magnitude of the branching fraction by decreasing the energy barrier for carboxyl formation by 0.20 eV and for CO formation by 0.25 eV, see Fig. 11b. However, the dependence of the branching fraction on temperature is not given correctly by theory: the experimental branching fraction decreases with temperature whereas theory predicts an increase. We leave this as a challenge to theory.
Despite the difficulties in obtaining quantitative agreement between theory and experiment, it is important to note that there is agreement on the ordering of rate constants for the different isotopologues; this agreement supports our assignment of the carboxyl intermediate as the origin of the fast CO2 formation channel.
5. Conclusions
In this work, we used velocity resolved kinetics to temporally resolve two parallel CO2 formation channels in the decomposition of formic acid on both Pd(111) and Pd(332). We observe large KIEs, indicating that formic acid is first rapidly converted to one of two intermediates, bidentate formate (HCO*O*) or carboxyl (C*OOH). The bidentate formate intermediate decomposes slowly to CO2, while the carboxyl intermediate decomposes rapidly to both CO2 and CO. We investigated possible reaction pathways with DFT and were able to make quantitative comparisons of rates and KIEs that are consistent with these mechanistic insights. We also identified a new concerted dissociation reaction mechanism for the bidentate formate decomposition reaction that is consistent with the observed KIEs.This work presents clear evidence for the presence of the carboxyl intermediate in formic acid decomposition and shows that this intermediate can decompose to both CO and CO2 under mild reaction conditions. These observations are therefore consistent with previous theoretical studies that identified the carboxyl intermediate in the WGSR (CO + H2O ⇌ CO2 + H2).9 The formic acid decomposition reaction involves the relevant elementary steps currently discussed for the WGSR except for the H2O activation. In the future we plan to focus on developing a micro-kinetic model that captures quantitatively the experimental CO2 formation rates as well as the temperature dependent yields for formic acid, CO2, H2, CO and H2O. We hope that such a model will be able to capture the kinetically controlled branching between the reactant and products of the WGSR and can be quantitatively verified against experimental rates.
Author contributions
Conceptualization: J. F., M. S., D. B., T. N. K., D. J. A. and A. M. W. Data curation: J. F., L. L., M. S. and A. K. Formal analysis: J. F., L. L., S. H. and D. B. Supervision: A. K., T. N. K., D. J. A. and A. M. W. Funding acquisition: T. N. K. and A. M. W. Validation: J. F., A. K., T. N. K., D. J. A and A. M. W. Investigation: J. F., L. L. and S. H. Visualization: J. F., L. L., A. K., D. J. A. and A. M. W. Methodology: J. F., D. B. and T. N. K. Writing – original draft: J. F., L. L. and D. J. A. Writing – review & editing: all authors.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
JF, LL, MS, SH, AK and TNK acknowledge support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. [833404]). MS thanks the BENCh graduate school, funded by the DFG (389479699/GRK2455). DJA thanks the International Center for Advanced Studies of Energy Conversion (ICASEC) for support.References
- Y. X. Chen, M. Heinen, Z. Jusys and R. J. Behm, Angew. Chem., Int. Ed., 2006, 45, 981–985 CrossRef CAS PubMed.
- K. Nishimura, K. Kunimatsu, K. Machida and M. Enyo, J. Electroanal. Chem., 1989, 260, 181–192 CrossRef CAS.
- N. R. Avery, Appl. Surf. Sci., 1983, 14, 149–156 CrossRef CAS.
- S. Pronkin, M. Hara and T. Wandlowski, Russ. J. Electrochem., 2006, 42, 1177–1192 CrossRef CAS.
- G. Samjeské, A. Miki, S. Ye and M. Osawa, J. Phys. Chem. B, 2006, 110, 16559–16566 CrossRef PubMed.
- T. Zheng, D. Stacchiola, D. K. Saldin, J. James, D. S. Sholl and W. T. Tysoe, Surf. Sci., 2005, 574, 166–174 CrossRef CAS.
- J. Scaranto and M. Mavrikakis, Surf. Sci., 2016, 650, 111–120 CrossRef CAS.
- J. Scaranto and M. Mavrikakis, Surf. Sci., 2016, 648, 201–211 CrossRef CAS.
- A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, J. Am. Chem. Soc., 2008, 130, 1402–1414 CrossRef CAS PubMed.
- S. Bhandari, S. Rangarajan, C. T. Maravelias, J. A. Dumesic and M. Mavrikakis, ACS Catal., 2020, 10, 4112–4126 CrossRef CAS.
- N. C. Nelson, M. T. Nguyen, V. A. Glezakou, R. Rousseau and J. Szanyi, Nat. Catal., 2019, 2, 916–924 CrossRef CAS.
- J. Eppinger and K. W. Huang, ACS Energy Lett., 2017, 2, 188–195 CrossRef CAS.
- X. C. Zhou, Y. J. Huang, W. Xing, C. P. Liu, J. H. Liao and T. H. Lu, Chem. Commun., 2008, 3540–3542, 10.1039/b803661f.
- Y. J. Huang, X. C. Zhou, M. Yin, C. P. Liu and W. Xing, Chem. Mater., 2010, 22, 5122–5128 CrossRef CAS.
- K. Tedsree, T. Li, S. Jones, C. W. A. Chan, K. M. K. Yu, P. A. J. Bagot, E. A. Marquis, G. D. W. Smith and S. C. E. Tsang, Nat. Nanotechnol., 2011, 6, 302–307 CrossRef CAS PubMed.
- S. Zhang, O. Metin, D. Su and S. H. Sun, Angew. Chem., Int. Ed., 2013, 52, 3681–3684 CrossRef CAS PubMed.
- B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- A. Miki, S. Ye and M. Osawa, Chem. Commun., 2002, 1500–1501, 10.1039/b203392e.
- M. E. Vela, R. O. Lezna, N. R. Detacconi, A. J. Arvia, B. Beden, F. Hahn and C. Lamy, J. Electroanal. Chem., 1992, 323, 289–302 CrossRef CAS.
- T. L. Silbaugh, E. M. Karp and C. T. Campbell, J. Am. Chem. Soc., 2014, 136, 3964–3971 CrossRef CAS PubMed.
- R. R. Yin, B. Jiang and H. Guo, ACS Catal., 2022, 12, 6486–6494 CrossRef CAS.
- J. S. Yoo, F. Abild-Pedersen, J. K. Norskov and F. Studt, ACS Catal., 2014, 4, 1226–1233 CrossRef CAS.
- D. J. Harding, J. Neugebohren, H. Hahn, D. J. Auerbach, T. N. Kitsopoulos and A. M. Wodtke, J. Chem. Phys., 2017, 147, 013939 CrossRef PubMed.
- J. Neugebohren, D. Borodin, H. W. Hahn, J. Altschaffel, A. Kandratsenka, D. J. Auerbach, C. T. Campbell, D. Schwarzer, D. J. Harding, A. M. Wodtke and T. N. Kitsopoulos, Nature, 2018, 558, 280 CrossRef CAS PubMed.
- H. Chadwick, H. Guo, A. Gutiérrez-González, J. P. Menzel, B. Jackson and R. D. Beck, J. Chem. Phys., 2018, 148, 014701 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- J. Fingerhut, D. Borodin, L. Lecroart, M. Schwarzer, S. Hoerandl, A. Kandratsenka, D. J. Auerbach, A. M. Wodtke and T. N. Kitsopoulos, J. Phys. Chem. A, 2023, 127, 142–152 CrossRef CAS PubMed.
- J. W. Arblaster, Platinum Met. Rev., 2012, 56, 181–189 CrossRef CAS.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Mills, H. Jonsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- J. Fingerhut, D. Borodin, M. Schwarzer, G. Skoulatakis, D. J. Auerbach, A. M. Wodtke and T. N. Kitsopoulos, J. Phys. Chem. A, 2021, 125, 7396–7405 CrossRef CAS PubMed.
- M. Schwarzer, N. Hertl, F. Nitz, D. Borodin, J. Fingerhut, T. N. Kitsopoulos and A. M. Wodtke, J. Phys. Chem. C, 2022, 126, 14500–14508 CrossRef CAS PubMed.
- D. Borodin, K. Golibrzuch, M. Schwarzer, J. Fingerhut, G. Skoulatakis, D. Schwarzer, T. Seelemann, T. Kitsopoulos and A. M. Wodtke, ACS Catal., 2020, 10, 14056–14066 CrossRef CAS PubMed.
- C. Wang, D. Ding, M. Okunishi, Z. G. Wang, X. J. Liu, G. Prumper and K. Ueda, Chem. Phys. Lett., 2010, 496, 32–35 CrossRef CAS.
- C. Wang, B. Wang, M. Okunishi, W. G. Roeterdink, D. Ding, R. Zhu, G. Prumper, K. Shimada and K. Ueda, Chem. Phys., 2014, 430, 40–46 CrossRef CAS.
- Q. Q. Luo, T. Wang, M. Beller and H. J. Jiao, J. Mol. Catal. A: Chem., 2013, 379, 169–177 CrossRef CAS.
- D. W. Yuan, H. T. Liao and W. Y. Hu, Phys. Chem. Chem. Phys., 2019, 21, 21049–21056 RSC.
- Q. Q. Luo, G. Feng, M. Beller and H. J. Jiao, J. Phys. Chem. C, 2012, 116, 4149–4156 CrossRef CAS.
- R. G. Zhang, H. Y. Liu, B. J. Wang and L. X. Ling, J. Phys. Chem. C, 2012, 116, 22266–22280 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00174a |
| ‡ Present address: Center for Quantum Nanoscience, Ewhayeodae-gil 52, Daehyeon-dong, Seodaemun-gu, 03760 Seoul, South Korea. |
| This journal is © The Royal Society of Chemistry 2024 |