Open Access Article
Open Access ArticleShedding light on thermally-activated delayed fluorescence
Francesco
Di Maiolo†
 ,
D. K. Andrea
Phan Huu†
,
D. K. Andrea
Phan Huu†
 ,
Davide
Giavazzi
,
Davide
Giavazzi
 ,
Andrea
Landi
,
Andrea
Landi
 ,
Ottavia
Racchi
,
Ottavia
Racchi
 and
Anna
Painelli
and
Anna
Painelli
 *
*
Dept. Chemistry, Life Science and Environmental Sustainability, University of Parma, Parco Area delle Scienze 17/A, 43124 Parma, Italy. E-mail: anna.painelli@unipr.it
First published on 27th February 2024
Abstract
Thermally activated delayed fluorescence (TADF) is a hot research topic in view of its impressive applications in a wide variety of fields from organic LEDs to photodynamic therapy and metal-free photocatalysis. TADF is a rare and fragile phenomenon that requires a delicate equilibrium between tiny singlet–triplet gaps, sizable spin–orbit couplings, conformational flexibility and a balanced contribution of charge transfer and local excited states. To make the picture more complex, this precarious equilibrium is non-trivially affected by the interaction of the TADF dye with its local environment. The concurrent optimization of the dye and of the embedding medium is therefore of paramount importance to boost practical applications of TADF. Towards this aim, refined theoretical and computational approaches must be cleverly exploited, paying attention to the reliability of adopted approximations. In this perspective, we will address some of the most important issues in the field. Specifically, we will critically review theoretical and computational approaches to TADF rates, highlighting the limits of widespread approaches. Environmental effects on the TADF photophysics are discussed in detail, focusing on the major role played by dielectric and conformational disorder in liquid solutions and amorphous matrices.
1 Introduction
In purely organic materials, spin–orbit coupling (SOC), roughly scaling as the fourth power of the atomic number, is a very tiny quantity, typically less than 1 cm−1 (∼3 cal mol−1). Being much weaker than intramolecular and (most of) intermolecular interactions, SOC can be treated as a negligible perturbation. Accordingly, the eigenstates of an organic dye (or polymer) are safely assigned to a specific spin subspace, so that, dealing with closed shell systems, molecular states are classified as singlets, triplets etc. In optical spectroscopy, the selection rule that defines as forbidden the transitions occurring between states with different spin multiplicity also results from neglecting SOC. Although tiny, SOC is responsible for the (typically slow) intersystem crossing (ISC) processes where singlet states depopulate towards lower-lying triplets. Phosphorescence in organic molecules is also due to the tiny SOC and in the early days it was difficult for Kasha to convince other scientists (including Teller and Frank) about this concept that is nowadays well established.1 Once populated, the elusive triplet states are typically long-lived and are responsible for a wealth of intriguing phenomena including e.g. long-lasting luminescence and photosensitization. Triplets are exploited in photodynamic therapy and favour charge separation in OPV, but are detrimental energy sinks in first generation OLED where spin statistics reduces the internal quantum efficiency to a disappointing 25%. Here we address thermally-activated delayed fluorescence (TADF), a phenomenon that, reported by Perrin almost one century back,2 remained a spectroscopic curiosity up to 2011, when Adachi proposed its exploitation to harvest triplets in OLED, bringing their theoretical internal quantum efficiency to 100%.3,4TADF occurs in dyes whose lowest triplet state T1 is very close to the lowest excited singlet S1, so that thermal energy is enough to transfer population from T1 to S1 in a reverse intersystem crossing (RISC) process. As schematically shown in Fig. 1, when a TADF dye is photoexcited and reaches S1, the Kasha's state, several processes can occur including prompt fluorescence (with typical timescales 1–20 ns), internal conversion to the ground state (a phenomenon that is not very competitive in good fluorescent dyes) and ISC to T1. Once T1 is populated either via ISC or directly upon charge injection in OLED devices, RISC occurs, generating population in S1. RISC is a spin-forbidden and hence very slow process, so that fluorescence from S1 populated via RISC is observed as a delayed fluorescence with typical timescale in the microsecond window.
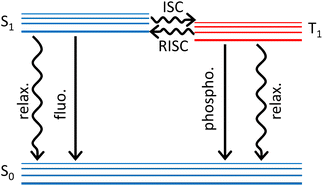 | ||
| Fig. 1 A simplified Jablonski diagram highlighting the main photophysical processes relevant to TADF. Straight and wavy lines refer to radiative and non-radiative processes, respectively. | ||
Spin statistic enforces a 3 to 1 ratio between electro-generated triplet and singlet excitons and since fluorescence is only extracted from singlet states, the efficiency of the first generation OLED was very poor. To overcome this problem, Forrest proposed to use phosphorescent dyes, where the presence of heavy metals favors ISC and phosphorescence.5 The so-called phOLED are efficient and are currently exploited in commercial devices for red and green emission. However, blue phOLED have not reached the market. Moreover, the color purity in phOLED is a concern, as well as the need to use heavy metals, that are costly and poorly recyclable. The possibility to exploit TADF in OLED, as pioneered by Adachi, boosted the research activity on TADF dyes with coordinated efforts of synthetic chemists, theoreticians and computational chemists, spectroscopists and device physicists, as described in recent reviews.6–15
Once rediscovered, TADF found interesting applications also in other fields, besides OLED. Metal-free, bio-friendly TADF emitters are of interest in microscopy and biomedicine.16–19 The very long lifetime of delayed fluorescence is useful for fluorescence lifetime applications and allows for gated experiments to get rid of interfering autofluorescence signals.19 TADF is effectively quenched by molecular oxygen that depletes the triplet state population. On one side, this deserves special care when designing TADF microscopy probes, on the other side, it offers an effective way to monitor the oxygen concentration in biological samples. Apart from bioimaging, TADF dyes find applications as photosensitizers in photodynamic therapy,20,21 opening a perspective for theranostic applications.
TADF dyes are also exploited as purely organic photocalysts with efficiency similar to classical (and more expensive) iridium complexes.22–25 While the mechanism of TADF-driven photocatalysis needs still to be clarified, the persistence of the excited state singlet over a long time (of the same order as observed in iridium complexes) is expected to play a role.26 In materials science, TADF main scope is definitely related to OLED, yet TADF-systems are also actively investigated as good transport media for both singlet and triplet excitons,27 and for highly efficient solar cell concentrators.28
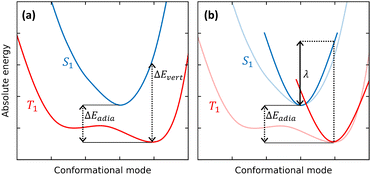
TADF dyes are scarce, as stringent conditions must be met to observe this intriguing phenomenon. RISC, the process where S1 is populated from the lower-lying T1 state (Fig. 1), can only occur if the needed energy is extracted from the ambient, so that the first and foremost requirement for RISC is a singlet–triplet gap comparable to thermal energy (∼26 meV at room temperature). In other terms, the singlet state must be accessible within a few kT from the bottom of the T1 state. This means that the adiabatic singlet–triplet (ST) gap ΔEadia must be of the order of kT, while the vertical transition gap ΔEvert from the T1 equilibrium geometry to S1 can be much larger, as illustrated in Fig. 2a.
Computational estimates of the tiny ST gaps are challenging, due to the large uncertainties introduced by the choice of the basis sets, of the functional in TD-DFT calculations, or of the specific flavor of the wavefunction-based approach.29,30 Even more dramatic in this respect is the choice of the solvation approach to deal with environmental effects (section 3.1). On the other hand, experimental estimates of the ST gap are also affected by large uncertainties. A popular approach relies on the difference between the onsets of fluorescence and phosphorescence bands.31,32 Of course the estimate of the onset itself is affected by large uncertainties. Moreover, it should be stressed that the approach is only acceptable if the two spectra are collected in the same experimental conditions, and, since phosphorescence is typically only observed in solid matrices at low temperature, very little is known about the ST gap in liquid solvents and/or ambient conditions. Another approach relies on the temperature dependence of the RISC rate.33 However, extracting RISC rates from experimental data concerning a phenomenon where several competing processes occur (Fig. 1) is very delicate and leads again to large uncertainties.34
While the estimate of the ST gap is a delicate issue, the strategies to minimize it are pretty clear since the early days. Specifically, the ST gap is related to the HOMO–LUMO exchange integral so that a winning strategy towards a small ST gap relies on the design of dyes with disconnected HOMO and LUMO. Along this line, charge transfer (CT) dyes proved suitable. CT dyes have electron donor (D) and acceptor (A) groups connected by poorly conjugated bridges, so that the HOMO and LUMO reside on the D and A moieties, respectively, and both S1 and T1 have a major CT character. More recently, multi-resonant CT dyes came to attention.35–39 In these systems, the HOMO and LUMO do not reside on spatially separated molecular fragments, but are localized on complementary subsets of atoms. In this case, the resulting small HOMO–LUMO exchange integral allows dynamic spin polarization to come into play, thus leading to a tiny (and possibly negative) ST gap.39
The second requirement for TADF is the presence of non-vanishing interaction between states in the singlet and triplet manifolds as to make the ISC and RISC processes possible.40 This of course relies on SOC, again a tiny quantity difficult to estimate computationally and rather tough (or even impossible in the case of organic systems) to address experimentally. Unfortunately, the two basic requirements for TADF, namely a small ST gap and sizable SOC, are mutually incompatible. Indeed small ST gaps are achieved in systems with disconnected HOMO and LUMO as to minimize the relevant exchange integral. In these conditions, the El Sayed rule41 predicts vanishing SOC between S1 and T1, as both states are dominated by HOMO → LUMO excitations. A trade-off between the two constraints is the key towards the successful design of novel TADF dyes, a demanding endeavor that must account for several intertwined factors. Molecular vibrations and conformational motions can be instrumental in boosting both ISC and RISC rates in molecular systems with small SOC,40,42–45 but they may alter the ST gap as well. Admixture of charge-transfer triplets (3CT) with local excited triplets (3LE) is another effective strategy towards improved SOC,46–48 but at the expense of a wider ST gap.
To make this scenario even more complex, the influence of the environment must be carefully considered. In particular, the medium polarizability and polarity affect in a highly non-trivial way the energy of CT states, thus affecting their mixing with LE states and therefore the SOC interaction. The frequency of the transitions, and hence the color of the emitted light is also affected, possibly leading to color purity issues. Devices rely on dye dispersed in solid amorphous matrices: solid state solvation is tricky to understand49–53 and the medium rigidity may alter the conformational flexibility of dispersed dyes,54–57 or even their orientation.58 When going from dilute samples to highly concentrated or possibly to single component amorphous matrices a plethora of additional phenomena occur, ranging from trivial self-absorption,53,59,60 to more subtle phenomena including energy delocalization as due to aggregation,61 concentration quenching,62 Förster energy transfer,59,60 triplet–triplet annihilation,63etc. While interesting, the physics of TADF in highly concentrated media is well beyond the scope of this perspective and will not be addressed here.
Guiding the design of efficient TADF dyes for different applications, ranging from efficient OLED to solar concentrators, innovative fluorescent tags for bioimaging and/or theranostic applications, requires a deep understanding of the different intertwined competitive and/or cooperative interactions that govern the TADF physics.
In this perspective, we offer our personal view of some of the most important issues in the field. Next section will critically review theoretical and computational methods to calculate RISC and ISC rates, taking into account approaches strictly relying on ab initio calculations as well as approaches relying on the definition of specific models. Section 3 addresses environmental effects on the TADF photophysics focusing on the role played by dielectric and conformational disorder in dilute liquid solutions and amorphous matrices. In the conclusion section, we summarize the main messages, giving a perspective for future work.
2 RISC and ISC rates
Adachi's suggestion to exploit TADF to increase the efficiency of purely organic LEDs spurred an enormous interest in understanding and hence modeling RISC. We cannot attempt to exhaustively cite all relevant papers, rather we will do our best to provide a systematic view of the several approaches proposed to calculate RISC rates, underlining their pros and cons. While all classifications are somewhat arbitrary, they may help to systematize a variegated and busy field. To start with, we will distinguish between two very large families of approaches: (a) those relying on a first-principle description of the electronic structure, and (b) those relying on semiempirical models (possibly parametrized against first-principle calculations). Clinging on first-principle calculations, without the mediation of semiempirical models, has the main advantage of wide applicability. Once the molecular structure is known, calculations can be run to extract relevant numbers. The price to be paid is a fairly intense computational effort, as needed to deal with many atoms and many degrees of freedom, and, more critically, the need to rely on some approximations (e.g., the adiabatic approximation and the harmonic approximation, to cite the two most frequently adopted approximation schemes). Working with models is trickier, as each model must be fine-tuned and parametrized for each system at hand, then limiting their applicability. However, models are crucial to recognize trends and to single out the interactions responsible of the physical behavior of interest. Moreover, typically accounting for just few degrees of freedom, they allow for exploratory studies in a wide range of model parameters, and for stringent tests of different approximation schemes.2.1 First-principle approaches to RISC
As recently discussed in detail,15ab initio approaches to RISC rates rely on the Fermi golden rule (FGR). Linear-order time-dependent perturbation theory leads to the following FGR expression for the rate of the transition from an initial state |i〉 to a final state |f〉: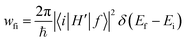 | (1) |
In the adiabatic approximation, the matrix element driving RISC reads:
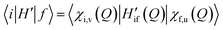 | (2) |
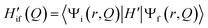 | (3) |
The earliest and easiest approaches to RISC rates rely on a Marcus-like approximation to eqn (2).64,65 Specifically, the Q-dependence of Hif′ is neglected in the so-called Condon approximation and the expression for the integral in eqn (2) simplifies into the product of a constant Hif′ term times the overlap of vibrational wavefunctions belonging to the two electronic states 〈χi,v(Q)‖χf,u(Q)〉. For low-frequency modes (either molecular vibrations or environmental degrees of freedom) Marcus adopted a classical description of the harmonic oscillators to derive a simple expression for the transition probability in eqn (1). Estimating the Marcus rate for RISC requires few parameters easily retrieved from quantum chemical calculations: the SOC matrix element, the adiabatic ST gap and the relaxation energy, λ, as illustrated in Fig. 2b.66,67 Recently, a modified Marcus approach was proposed by Aizawa et al., where the RISC rate is computed accounting for the activation energy required to reach the crossing between S1 and an higher energy triplet state, T2.68
An improved Marcus model, due to Levich and Jortner, accounts for the non-classical nature of high-frequency vibrational modes. In the Marcus–Levich–Jortner (MLJ) model the relaxation energy is split in a component due to low frequency (classical) modes plus a component associated to a single high frequency vibration.66,69 Both the Marcus and MLJ models are widely adopted to estimate RISC rates.67,70–74
Dealing with more than a single vibrational mode becomes rapidly demanding due to the boring and time consuming need to calculate a large number of Frank–Condon integrals. This issue is addressed in very efficient time-dependent approaches that, via a Laplace transform, avoid the intractable summation in the calculations of Frank–Condon integrals, so that all vibrational modes of the dye can be explicitly accounted for ref. 75–77. Along similar lines, once the FGR is recast in the time-domain, adopting the Fourier Transform (FT) representation of the δ-function,78,79 the RISC rate is expressed as the FT of a correlation function that is analytically calculated at each time step as the path integral of a multidimensional harmonic oscillator.80,81 Quite interestingly, time-dependent approaches lend themselves quite naturally to account for the mixing of modes in different states (Duschinsky rotation).75–77
An issue arises however in all these approaches, related to the Condon approximation, as first recognized by Mewes.82 The Marcus model, relying on the Condon approximation, was developed to describe electron transfer65 and was successfully extended to account for the electronic mobility in organic media in the hopping regime.66 But the applicability of the Condon approximation in RISC models is questionable. Indeed the SOC interaction is strongly dependent on conformational modes so that the main approximation of Marcus and related approaches is problematic.55 Time-dependent approaches to vibrational overlaps can be extended to account for the linear term in the expansion of the SOC matrix element on the vibrational coordinates (Herzberg–Teller coupling or spin-vibronic coupling83) and/or for the non-adiabatic coupling between electronic states in the same spin manifold (leading again to a linear dependence of the SOC matrix element on the coordinates).42,84–89 As extensively discussed by Penfold et al.,90 discriminating between contributions from non-adiabatic and spin-vibronic terms is tricky, yet these terms play a major role in RISC.7,40,43,86,89
In this respect, we underline that all approaches to RISC/ISC rates rely on the FGR and hence on time-dependent perturbation theory truncated to the first order. Some authors40,77 dub as “time-dependent second-order perturbation theory” expressions where the mixing matrix element entering the FGR in eqn (1) is expanded according to static perturbation theory:
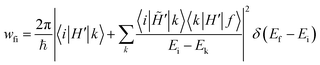 | (4) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) ′≠H′.
′≠H′.
The Herzberg–Teller expansion for sure improves over the Condon approximation, but it is not fully clear if truncating the expansion to the linear term is enough. Moreover, all time-dependent approaches describe vibrations in the harmonic approximation, a reasonable approach to high frequency modes, typically characterized by small displacements, but hardly adequate for low-frequency conformational modes that often are the most important modes for RISC.
Molecular dynamics (MD) simulations offer an interesting approach to address the role of conformational flexibility in the TADF photophysics. Classical MD simulations have been exploited to investigate TADF dyes in matrices (either single component matrices or dye-doped matrices),10,52,93,94 QM/MM studies have shed light on the TADF photophysics in single molecule amorphous matrices and crystalline samples,21,95 and and first-principle MD simulations were run for a TADF dye in solution and in the crystalline phase.96 These calculations give useful information on conformational disorder and on its effects on the ST gap, on optical spectra, etc. As an additional bonus, environmental effects may also be addressed. Olivier et al.93 exploited the Marcus equation to evaluate RISC rates from ST gaps and SOC matrix elements averaged over the MD trajectories, extracting at the same time reliable information about the relaxation energy via a dynamical model for the fluctuations of the ST gap. In a slightly different approach, rates are calculated for different snapshots and hence mediated.94 Finally in ref. 96 a distribution of rates is obtained from ab initio MD snapshot, using, for each snapshot, the time-dependent approach (in the Condon approximation). MD simulations are very useful to describe conformational disorder, possibly addressing some of the pitfalls of the Marcus estimate of RISC rates, however the proposed strategies to the rate calculations are not fully justified. Indeed relying on a MD simulation, the matrix element entering eqn (2) can be calculated for a large number of significant configurations, representative of the equilibrium ensemble. However, as recently discussed,55 there is no way to properly factorize the integral on vibrational wavefunctions as to recover the Condon approximation at the heart of the Marcus and related rate equations. A similar issue applies to a recently proposed approach, where the conformational sampling is done by a very efficient kinetic Monte Carlo approach.97
2.2 Modeling RISC
The first-principle approaches described above quite unavoidably rely on several approximations including the adiabatic separation of electronic and nuclear degrees of freedom, the Condon or the Herzberg–Teller approximation, the harmonic approximation to molecular vibrations and conformational modes or possibly a classical description of these modes. Assessing the reliability of the different approximations is difficult. Some approximations, including the adiabatic approximation, the Condon approximation and the harmonic approximation to conformational modes, are hardly justified when dealing with TADF dyes.55 In semiempirical models, these approximations can be relaxed, the price to be paid being a less detailed description of the molecular system. Typically, semiempirical models rely on the selection of a reduced number of degrees of freedom, thus defining comparatively simple model Hamiltonians to be parametrized either ab initio or via the comparison with experimental data. Accounting for a reduced number of interactions, semiempirical models have the added advantage of focusing attention on the main physics underlying the phenomenon at hand. In most semiempirical models, the TADF dye is described by a subset of electronic excited states, often including, in addition to the 1CT and 3CT states, one or more 3LE states. Along this line, a purely-electronic four-state model was introduced by De Silva et al. to extract design principles for efficient TADF in the donor–acceptor exciplex based on triphenylamine donor and 2,4,6-triphenyl-1,3,5-triazine acceptor.99The most successful models for RISC include coupling to molecular vibrations to drive the dynamics of the system. This is the case of one of the first models for RISC proposed by Penfold and coworkers.40 The model, parametrized against ab initio calculations for a specific donor–acceptor dye with phenothiazine donor and dibenzothiophene-S,S-dioxide acceptor, accounts for three excited electronic states 1CT, 3CT and 3LE and for their vibronic coupling (linear approximation) as driven by a torsional coordinate. Quantum dynamical simulations are then performed adopting the density operator version of the multi-configuration time-dependent Hartree (MCTDH) approach to extract ISC and RISC rates. These calculations demonstrate that the hyperfine interaction is actually irrelevant to TADF, while the vibronically induced mixing between 3CT and 3LE is pivotal to RISC, leading to a very similar picture as proposed by Siebrand83 and discussed and implemented by Marian and coworkers.90 The main limitation of this approach is the tiny accessible time-window (∼1 ns), making the analysis of slow, spin-forbidden processes difficult. Along similar lines, Lyskov and Marian proposed a detailed model for the TADF spiro compound ACRSA.100 The model, parametrized ab initio, accounts for 6 electronic states, linearly coupled to 7 vibrations including a high frequency molecular vibration (a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode) and a low-frequency conformational mode. Once again, it is not obvious how a calculation spanning a time interval of 50 ps can give reliable information on processes occurring on much longer timescales. The same model (with 3 electronic states and 4 low-frequency vibrational modes) and dynamics approach were also adopted by Garain et al. to model RISC in a boron-based spiro compound, reaching similar conclusions.72
O stretching mode) and a low-frequency conformational mode. Once again, it is not obvious how a calculation spanning a time interval of 50 ps can give reliable information on processes occurring on much longer timescales. The same model (with 3 electronic states and 4 low-frequency vibrational modes) and dynamics approach were also adopted by Garain et al. to model RISC in a boron-based spiro compound, reaching similar conclusions.72
A very interesting toy-model was proposed by Carreras and Casanova.45 Relying on a minimal number of electronic diabatic states, 1CT, 3CT, 3LE (and possibly 1LE), these authors have integrated the relevant Lindblad master equation, accounting for the coupling to a quantum thermostat, described by an ad hoc ohmic spectral density with a Lorentz–Drude cutoff. The model is simple, but gives important information on the role of the different interactions, namely 1CT–3LE SOC interaction, the 3CT–3LE vibronic coupling, and the 1CT–3CT coupling that may originate either from residual SOC, due to the non-perfect equivalence (or CT nature) of the two relevant states, or from the hyperfine interaction. Quite interestingly, the tiny 1CT–3CT coupling introduced in the model justifies RISC rates of the same order of magnitude as experimentally observed, even if, in line with previous results,40,100 RISC is largely amplified by the 3CT-3LE vibronic coupling. A comparison with Marcus and related expressions for RISC clearly points to the inadequacy of these approaches. The results in ref. 45 contrast sharply with a recent paper suggesting that RISC is actually driven by spin-vibronic coupling, with local excited states playing a marginal (if any) role.67 However, these conclusions are obtained exploiting the Marcus rate equation for dyes in different configurations and, most probably, a contribution from 3LE states enters (unnoticed) into the effective 3CT state, then reconciling these apparently contradictory results.
Addressing RISC and ISC rates is a single facet of the problem, as TADF is a complex phenomenon whose detailed modeling must account for several concurring or competing relaxation pathways involving several excited states.34 Relaxation dynamics can only be described in open quantum systems approaches: to dissipate energy in ISC and in other non-radiative decay processes or to exploit thermal energy for RISC, the system must exchange energy with the environment, or, in technical terms, with a thermal bath. This very fundamental issue is often overlooked or, possibly, not explicitly addressed in the TADF community. Indeed, the δ -function appearing in the FGR in eqn (1) ensures finite rates only among degenerate states, as to guarantee for energy conservation: strictly speaking, the FGR cannot describe either ISC or RISC processes. In Marcus and related model, the classical treatment of low-frequency modes leads to a continuum of states, then ensuring for energy matching. When the quantum nature of vibrations is considered, rates can be estimated from the FGR only substituting the δ -function with some distribution having a finite width.55,100–104 This of course implies assigning the relevant states finite lifetimes, leading to an open quantum system in the crudest representation. When time-dependent approaches are applied to evaluate the vibrational overlaps that enter the rate equations, dissipation is implicitly introduced in the FT step, when the signal at long times is damped by apodization functions, then effectively imposing a finite lifetime to relevant states.75–77 Without apodization, the calculated signals for a non-dissipating system would be periodic, showing recurrences in time intervals that, in models accounting for a single vibrational mode, would coincide with the vibrational period. In these conditions, the choice of the apodization function is crucial. In more detailed models, where all molecular vibrations are considered, the recurrences are much less frequent (upon increasing the number of vibrational modes, going back to the original geometry becomes more and more unlikely) and the choice of the apodization function is much less critical. However, it is important to recognize that all approaches to RISC (and more generally to excited state dynamics) must rely on some dissipation mechanism.
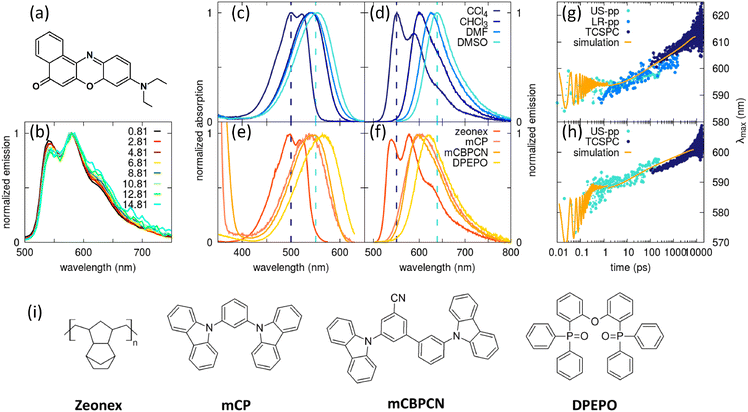
In an effort to relax the main approximations of current approaches to RISC rate calculations, an essential state model (ESM) was recently proposed98 for a prototypical TADF dye, DMAC-TRZ in Fig. 3a. As sketched in Fig. 3b, the model is just an extension of the two-state model for donor–acceptor dyes that was developed and extensively validated in our laboratory.105,106 Specifically, we account for two diabatic states in the singlet subspace, corresponding to the neutral DA, |N〉, and zwitterionic D+A−, |Z〉 structures. In the triplet subspace at least two diabatic states, a CT triplet |T〉 and a local excited triplet |L〉 are introduced. As discussed in detail in ref. 98 the local excited triplet is an effective state mimicking the several local excited triplet found by TD-DFT. Its role is pivotal to rationalize the geometry of the lowest adiabatic triplet state (Fig. 3d). A conformational coordinate, simulating the torsional angle between the D and A fragments (Fig. 3a), modulates the mixing matrix element between N and Z states and between T and L states (Fig. 3e). All other quantities of interest, including SOC matrix elements are constant in the diabatic states (Fig. 3g). Finally, an effective molecular vibration is introduced, as needed to simulate optical spectra and hence to validate the model against experiment. In spite of its comparative simplicity, many parameters enter the model that can be fixed as to best reproduce TD-DFT results for the low-lying adiabatic states, S0, S1 and T1.
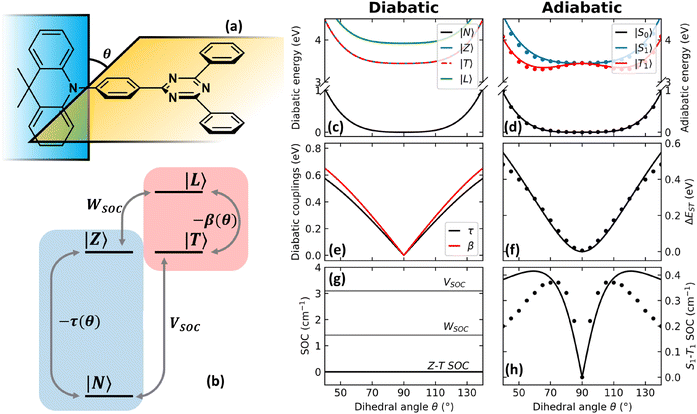 | ||
| Fig. 3 The DMAC-TRZ essential state model. (a) The molecular structure of DMAC-TRZ, showing the dihedral angle, θ; (b) schematic view of the four diabatic states entering the model: blue (red) area highlights the singlet (triplet) subspace. Arrows indicate mixing matrix elements −τ(θ) and −β(θ) as well as the SOC matrix elements. (c) The energy of the diabatic states vs. θ; (d) Energies of the three relevant adiabatic states as a function of the dihedral angle: symbols and lines refer to TD-DFT and ESM results, respectively; (e) mixing matrix elements between diabatic states as a function of the dihedral angle; (f) S1–T1 energy gap as a function of the dihedral angle: dots and lines refer to TD-DFT and ESM results, respectively; (g) SOC matrix elements among diabatic states; (h) S1–T1 SOC matrix element as a function of the dihedral angle: symbols and lines refer to TD-DFT and ESM results, respectively. Adapted from ref. 98. | ||
The T1 energy plotted against the conformational coordinate in Fig. 3d has two well pronounced minima and definitely cannot be approximated by a harmonic potential. Moreover, the SOC matrix element between S1 and T1 shows a strong dependence on the conformational coordinate (Fig. 3h): the Marcus model, relying on the Condon approximation, is inadequate and the applicability of the Herzberg–Teller approach is not obvious. Finally, the very small ST gap (Fig. 3f) calls for the breakdown of the adiabatic approximation. All these approximations can indeed be relaxed. Specifically, neglecting SOC, a brute force non-adiabatic diagonalization of the vibronic Hamiltonian in the singlet and triplet subspaces is performed. As discussed in ref. 55, the non-adiabatic Hamiltonian is diagonalized on the (very large) basis obtained as the direct product of electronic, conformational and vibrational states. The energies of the resulting vibronic eigenstates are shown in Fig. 4 as blue and red lines for the singlet and triplet subspaces, respectively. The lines are very crowded because of the tiny spacing between conformational states, and, more interestingly, they are not equally spaced, an effect that, resulting from the anharmonicity of the system, is more conspicuous in the triplet subspace.
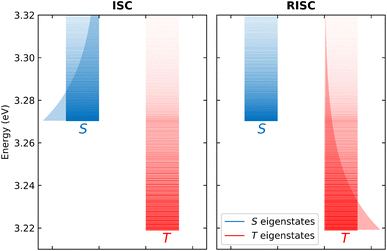 | ||
| Fig. 4 A schematic representation of the non-adiabatic calculation of ISC (left panel) and RISC (right panel). In both panels, red and blue lines show the energy of the vibronic triplet and singlet eigenstates, respectively, the opacity of the lines gives information on the Boltzmann population of the equilibrated singlet and triplet states. The global ISC rate is calculated summing all the rates of the singlet to triplet processes, averaging on the thermal population of singlet states (graphically represented by the blue shaded area). RISC rates (right panel) are calculated in a similar way, summing all the rates of the triplet to singlet processes, averaging on the thermal population of triplet states (graphically represented by the red shaded area). Adapted from ref. 55. | ||
Once the vibronic eigenstates are known in the two spin subspaces, the transition probability between singlet and triplet vibronic eigenstates is calculated according to the FGR in eqn (1), setting H′ as the SOC Hamiltonian. More specifically, for RISC rate calculations, |i〉 and |f〉 are vibronic eigenstates in the triplet and singlet manifolds, respectively, the opposite being true for ISC rate calculations. Each vibronic eigenstate is assigned a finite width as to allow for the energy matching, or, in other terms, each vibronic eigenstate is assigned a finite lifetime whose specific value (in the reasonable window 50–200 fs) marginally affects calculated rates.55 Finally, as illustrated in Fig. 4 left panel, the RISC rate is evaluated summing up the state-to-state rates from the triplet to the singlet subspace, accounting for the thermal population of the triplet states. Similarly, the ISC rate is calculated summing up the rates from the singlet to the triplet states and averaging on the thermal population of singlet states (Fig. 4 right panel). The large anharmonicity of the system, responsible for the increased density of triplet states in the energy region corresponding to the bottom of the S1 manifold, clearly favors both RISC and ISC processes. The calculated rates are numerically exact results for the adopted Hamiltonian, fully accounting for anharmonic and non-adiabatic interactions as well as for geometry-dependent SOC interactions.
3 Environmental effects
3.1 From liquid to solid state solvation
The important role played by solid-state solvation (SSS) on the performance of OLED and more generally of devices based on molecular materials is well established since the pioneering work of Forrest.49,50 Understanding SSS is particularly important when designing optimized TADF-OLED. CT and local excited states are in fact affected in different ways by the dielectric properties of the local environment, with highly non-trivial impacts on the delicate TADF photophysics. Moreover, as discussed above, conformational degrees of freedom affect both the ST gap and the SOC and drive RISC via non-adiabatic couplings. Dispersing a dye in a solid amorphous matrix will significantly alter the TADF photophysics, as a result of the constrained conformational mobility of the dye. Several experiments have demonstrated the crucial role of environmental interactions in TADF materials,54,56,74,107–109 with somewhat contrasting interpretations about the relative role of polar solvation and conformational disorder. To properly address this delicate issue reliable approaches to SSS are needed.The easiest and by far most widely adopted approaches to describe how the dielectric properties of the medium affect the spectral properties of a dye rely on continuum solvation models, like PCM110 and COSMO.111 Compiling a full list of papers relying on continuum solvation models to account for environmental effects on TADF dyes is a hopeless endeavor, therefore we just mention here early and most representative examples.9,52,70,85,90,97,112–116 As discussed by Mewes,82,117 continuum solvation models are implemented in different flavors. The easiest and most widely adopted implementation is the so-called linear response (LR) approach that, poorly applying to CT states, is not suitable for TADF systems. State specific (SS) approaches typically rely on perturbative corrections and apparently solve some of the issues related to the treatment of CT states. A combination of LR and SS approaches seems to provide most reasonable results.82,118 However, while perturbative approaches may possibly provide reasonable approximation to the energies, they cannot account for environmental effects on the wavefunctions, so that, just as a relevant example, SOC matrix elements and/or radiative rates obtained in this approximation are hardly reliable.
MD simulations are computationally more demanding than continuum solvation models, but give important information on dielectric and conformational disorder93 and dynamics.52,74 However, both continuum and atomistic solvation models fail to properly address the contribution to the dielectric screening due to the electronic degrees of freedom of the environment.119 A good solvent/matrix is transparent in the spectral region of interest for organic dyes (typically ranging from the near-IR to the visible or near UV). Therefore, the dielectric response of the medium can be safely ascribed to: (a) electronic degrees of freedom, who contribute to the dielectric response at optical frequencies (as usually described by the squared refractive index), and (b) the vibrational/conformational/orientational (VCO) degrees of freedom that also contribute to the static dielectric constant. With respect to the solute degrees of freedom of interest, the electronic degrees of freedom of the solvent are faster, while VCO degrees of freedom are slower. As recently discussed,119 in either continuum or atomistic solvation models the Hamiltonian for the solvated molecule is constructed accounting for the potential generated by a specific distribution of charges in the surrounding medium. This amounts to an adiabatic separation of solute–solvent degrees of freedom, that, while well suited for slow VCO degrees of freedom, is clearly untenable for the fast electronic degrees of freedom. Rather, an antiadiabatic approximation should be adopted that, instead of freezing the electronic degrees of freedom of the medium, assumes that they instantaneously readjust in response to charge fluctuations in the solute. The proper treatment of electronic solvation has a profound impact on TADF, and more specifically on the ST gap.120 The more impressive result in this context is the demonstration that the negative ST gaps sometimes predicted in polar solvents,93 are most probably an artifact that can be cured if electronic solvation is properly accounted for.
Polar solvation is easier to address, as the familiar adiabatic approximation works well for the slow VCO degrees of freedom. A sample where a TADF dye is dispersed in a polar medium (either a solution or an amorphous film) can be simulated as a collection of dyes, each one surrounded by the medium in a slightly different configuration as to produce, at the solute location, a slightly different potential. The problem then reduces to the diagonalization of the molecular Hamiltonian accounting for the potential due to the environment. Whatever property (including spectra) of the sample is then computed as an average of the same property weighted over the relevant Boltzmann distribution.105 This is definitely what is done in MD simulations where averaging over a trajectory corresponds to an average over the distribution (ergodic principle).
Solvatochromism of polar (or multipolar) dyes has been successfully addressed exploiting the Onsager model.105,106,121–123 Much as in the popular continuum solvation models (PCM, COSMO, etc…) implemented in computational packages, the Onsager model describes the solvent as a continuum elastic dielectric medium. At variance with more refined models, Onsager adopts the dipolar approximation for the solute–solvent interaction. Accordingly, a polar medium generates at the solute location an electric field, called the reaction field, For, that enters the molecular Hamiltonian as follows:
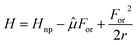 | (5) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) is the dipole moment operator of the solute. The last term is the elastic energy associated with the solvent, where r is the proportionality constant between the equilibrium reaction field and the solute dipole moment of the relevant state:
is the dipole moment operator of the solute. The last term is the elastic energy associated with the solvent, where r is the proportionality constant between the equilibrium reaction field and the solute dipole moment of the relevant state:(For)eq = r〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 〉 〉 | (6) |
The r value depends on the medium dielectric constant and refractive index, as well as on the size and shape of the cavity occupied by the solute. Of course r increases with the solvent polarity.105
Top panels of Fig. 5 illustrate the basic features of solvatochromism: the reaction field stabilizes the ground and the excited states of a polar dye by an amount For〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 〉, where 〈
〉, where 〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) 〉 is the expectation value of the solute dipole moment in the state of interest. If, as in the figure, the excited state is more polar than the ground state, a progressive red-shift of the absorption and emission frequencies is expected when increasing the solvent polarity. More specifically, the reaction field relevant to absorption spectra is proportional to the ground state dipole moment: for most TADF dyes this dipole moment is negligible, and absorption spectra are typically marginally solvatochromic.53 Emission spectra instead respond to the reaction field associated with the excited state dipole moment that is very large for the emissive CT state of TADF dyes: large emission solvatochromism is indeed observed, as illustrated in Fig. 5d for DMAC-TRZ.
〉 is the expectation value of the solute dipole moment in the state of interest. If, as in the figure, the excited state is more polar than the ground state, a progressive red-shift of the absorption and emission frequencies is expected when increasing the solvent polarity. More specifically, the reaction field relevant to absorption spectra is proportional to the ground state dipole moment: for most TADF dyes this dipole moment is negligible, and absorption spectra are typically marginally solvatochromic.53 Emission spectra instead respond to the reaction field associated with the excited state dipole moment that is very large for the emissive CT state of TADF dyes: large emission solvatochromism is indeed observed, as illustrated in Fig. 5d for DMAC-TRZ.
 | ||
| Fig. 5 Panels (a)–(c) show qualitative sketches of the ground and excited state energies of a polar dye as a function of the orientational reaction field (For). Panel (a) refers to the dye in a non-polar solvent, so that For = 0 and absorption and emission frequencies virtually coincide (we are not considering here the vibrational relaxation of the dye). Panel (b) and (c) refer to a mildly and a strongly polar solvent, respectively. The shadowed areas show the thermal distributions associated to the different states. (d) Experimental absorption (dashed lines) and emission (continuous lines) of DMAC-TRZ in cyclohexane, toluene and chloroform. (e) Absorption (dashed lines) and emission (continuous lines) calculated using the ESM. Adapted from ref. 98. | ||
A more detailed analysis of the spectra must also account for inhomogeneous broadening induced by polar solvation. As illustrated in panels b and c, upon increasing the solvent polarity the energy required to generate large fields decreases and the curvatures of the PES decrease (cf the last term in eqn (5)). Consequently, larger For regions around the equilibrium get thermally populated, explaining the progressive broadening of optical spectra in polar solvents. In order to account for inhomogeneous broadening, absorption and emission spectra are calculated on a grid of For values and are averaged over the relevant Boltzmann distribution. This approach to optical spectra was applied with success to the large family of polar CT dyes,106,124 also addressing time-resolved spectra125,126 and subtle phenomena including symmetry breaking in multipolar dyes.121,123,127 When applied to DMAC-TRZ98 the approach nicely validates the relevant model, as shown in Fig. 5e.
Having validated the model, RISC and ISC rates can be addressed. Once again, the Hamiltonian in eqn (5) is diagonalized for different For, and, following the procedure discussed in section 2.2, For-dependent RISC and ISC rates are calculated, relevant data being shown as dashed and continuous lines, respectively, in Fig. 6a–c for the three solvents of interest. RISC and ISC rates are finally averaged over the thermal distributions, shown as colored areas in the same panels (in the specific case of DMAC-TRZ the For distributions relevant to either the S1 or T1 states practically coincide). Fig. 6d and e compares calculated RISC and ISC rates with experimental data.128 The agreement is really impressive for RISC rates, but most notably the model captures the increasing trend of the RISC rates with the solvent polarity. The agreement is less good for ISC rates. While a perfect agreement is not expected in view of the comparative simplicity of the adopted model, this discrepancy is most likely due to the neglect in the ESM model of triplet states lying close to T1.98 These states are not thermally accessible from T1 and hence do not contribute to RISC, however they offer effective decay channels from S1, contributing to ISC.
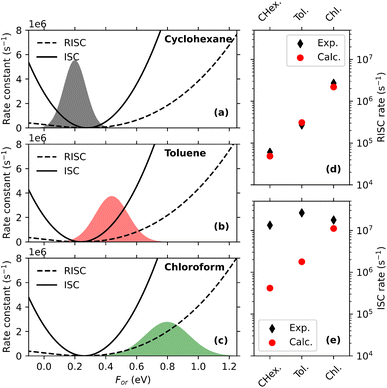 | ||
| Fig. 6 Panels (a)–(c) show RISC and ISC rates (dashed and continuous lines, respectively) calculated as a function of the reaction field, for three different solvents. For convenience, the reaction field is multiplied by μ0, the dipole moment associated to the zwitterionic state, so that it has energy dimensions. The colored areas in the three panels show the solvent thermal distributions as relevant to S1. Panels (d) and (e) compare calculated and experimental values of RISC and ISC rates, respectively. Adapted from ref. 128. | ||
It is important to recognize that there are two sources of broadening in TADF dyes, one due to dielectric disorder, i.e. to the thermal distribution of For, as discussed above, the second one due to conformational disorder. If conformational degrees of freedom are introduced as quantum modes and are dealt with explicitly (section 2.2), their effect on optical spectra is quite naturally calculated.128 As long as optical spectra are of interest, however, an adiabatic treatment of conformational degrees of freedom is much more convenient. In this approach the kinetic energy associated to the conformational modes is neglected, the Hamiltonian is diagonalized for different geometries to calculate geometry-dependent optical spectra that are finally thermally averaged. Within the ESM model for DMAC-TRZ the adiabatic and non-adiabatic treatment of the conformational modes led exactly to the same optical spectra, confirming that an adiabatic treatment of conformational degrees of freedom is fully reliable in this respect.128 When addressing RISC and ISC rates, however, the adiabatic approximation to conformational degrees of freedom dramatically fails: the tiny ST gap characteristic of TADF dyes is in fact of the same order of magnitude as the (tiny) conformational frequencies. A full non-adiabatic approach, also accounting for anharmonicity, is needed to properly address RISC and ISC rates, as discussed in section 2.2.
Going from liquid solutions to amorphous solid matrices, as relevant to devices, is far from trivial. In polar solvents, the major contribution to the static dielectric constant comes from orientational degrees of freedom that, in non-viscous liquid solvents, are characterized by relaxation times of the order of few picoseconds.129,130 Fluorescence has typical lifetimes of the order of nanoseconds (or longer in TADF dyes) so that steady state fluorescence occurs after the solvent relaxation is completed. In solid matrices, however, the orientational and possibly the conformational motions are hindered and it is not clear if the matrix does relax after the photoexcitation of the dye and, if so, in which timescale. The issue is interesting and delicate. MD simulations52,93 suggest that after an initial fast (few picoseconds) relaxation of the matrix, nothing occurs on a longer timescale (∼10 ns). On the other hand, the initial red-shift of emission spectra of TADF dyes in polar matrices suggests a slower relaxation,128 even if conformational disorder in the flexible TADF dyes may also contribute to the same phenomenon.54
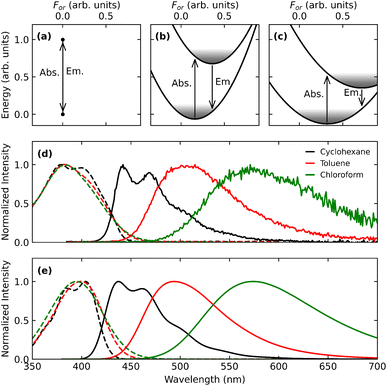
To sort out this issue we undertook a detailed study of several matrices of interest for TADF-OLED (Fig. 7i).53 Nile-red (NR, Fig. 7a), a well known solvatochromic dye106 with a fairly rigid molecular structure was selected as a microscopic polarity probe. Fluorescence spectra of NR dispersed in the non-polar Zeonex matrix in Fig. 7b show a negligible time-evolution, confirming the rigidity of the molecular structure, making the dye a reliable probe for our aims. Comparing absorption spectra of NR dissolved in solvents of increasing polarity (from CCl4 to DMSO, Fig. 7c) with the spectra collected in Zeonex, mCP, mCBPCN and DPEPO (Fig. 7e), a polarity scale emerges (also confirmed by Raman data53) that sets DPEPO as polar as (or possibly a little more polar than) DMSO. However, emission spectra in Fig. 7d and f tell a different story, suggesting that DPEPO is less polar than DMSO. This puzzling result can be easily rationalized. Absorption (and Raman) spectra probe the polarity of the environment equilibrated around the ground state solute, so that the dynamical behavior of the (liquid or solid) environment is irrelevant. Fluorescence instead comes from the excited solute: in liquid non-viscous solvents, as discussed above, the solvent dynamics is fast enough to ensure that steady state emission occurs when the solvent is fully relaxed around the excited solute. Accordingly, a large Stokes shift is observed in polar solvents. In a polar solid matrix instead VOC motions are hindered, and the medium is not able to fully relax before fluorescence takes place, leading to reduced Stokes shifts in amorphous matrices than in liquid solvents of similar polarity.
 | ||
| Fig. 7 Excited state dynamics in amorphous matrices. (a) The molecular structure of NR, used here as a microscopic polarity probe; (b) time resolved emission spectra of NR in Zeonex. The legend shows the delay time in ns; (c) and (d) show absorption and steady state emission spectra, respectively, of NR in liquid solvents; (e) and (f) show fluorescence excitation and steady state emission spectra, respectively, of NR in amorphous matrices. Vertical lines across panels (c) and (e) and (d) and (f) are drawn as guide for the eye; (g) and (h) show the time evolution of the maximum of NR emission spectrum in DPEPO and mCBPCN matrices, respectively: bluish dots refer to experimental data collected with different techniques (see ref. 53, the orange line shows simulated results. For better comparison, simulated spectra are red shifted by 2.5 nm for DPEPO (g panel) and by 6 nm for mCBPCN (h panel). (i) Molecular structures of Zeonex, mCP, mCBPCN and DPEPO. Adapted from ref. 53. | ||
To validate this view, time-resolved emission spectra of NR in mCBPCN and DPEPO were collected in a wide time window, 15 fs-15 ns. Fig. 7g and h show the time-evolution of the maximum of the emission band in the two matrices. In both matrices, the emission band progressively red-shifts, clearly demonstrating that the dielectric relaxation is not completed in 15 ns. Quite interestingly, the time evolution of emission spectra was modeled exploiting the ESM proposed and validated 20 years back for NR.106 To address time-resolved spectra the model is extended to account for relaxation: the solute relaxation is introduced coupling the system to a quantum bath in the Redfield approximation,131 while the solvent relaxation is described classically by the Smoluchowsky equation.132 Along these lines, the relaxation dynamics of the two matrices is quantified, and DPEPO turns out to be a more sluggish medium than mCBPCN.53
3.2 TADF in amorphous matrices
Optical spectra collected in matrices must be considered with care. Self-absorption of the emitted light can result in an apparent red-shift of the fluorescence spectrum already in fairly dilute samples,53,59,60 spectral diffusion due e.g. to fluorescence energy transfer, can further red-shift the emission band,59,60 and dye aggregation can alter the picture even more dramatically. Here, we only address the photophysics of dilute enough samples as to exclude these spurious phenomena.In section 3.1, we discussed the importance of inhomogeneous broadening induced by dielectric and conformational disorder. The two phenomena can be addressed quite neatly in liquid solutions, where the conformational degrees of freedom of the dye are marginally hindered by the environment and the dielectric relaxation, occurring in the picosecond timescale, does not interfere with subsequent slower processes. In solid amorphous matrices the situation is much more complex. As summarized in the previous section, the relaxation dynamics in polar matrices occurs on a long timescale (>10 ns), interfering with the intrinsic photophysics of the dye.53 Moreover, the matrix may effectively hinder, if not suppress, the conformational motion of the dye. When TADF is investigated in amorphous matrices,56,60,133–139 a long non-exponential tail is observed in the time-dependence of the intensity of the emitted light. Moreover the emission band, moving to the red at early time, moves back to the blue at longer times. This anomalous behavior is commonly ascribed to inhomogeneous broadening but the relative importance of the dielectric and conformational disorder stays controversial.
Getting reliable experimental information about the conformational degrees of freedom of a dye is difficult as sophisticated NMR57 or single-molecule spectroscopy studies109 are needed. From a computational perspective, MD simulations may help, but simulations on matrices are costly and the robustness of the results depends on the quality of the force fields and of the preparation steps. Moreover, the timescale and the sample dimensions accessible to MD are too short to simulate realistic films. Available MD results are mostly relevant to neat or highly concentrated samples,93,94,140 and are therefore marginally relevant to our discussion. In any case, a distribution of conformational angles is clearly predicted,93 and the autocorrelation function of the dihedral angles suggests a very fast (sub-nanoseconds) rearrangement of conformational degrees of freedom. Proper treatment of dielectric disorder in these systems requires a careful coupling of MD and TD-DFT analysis mediated by microelectrostatic approaches.93
Very relevant to our discussion is the work by Penfold and coworkers52 where a TADF dye is embedded in a DPEPO matrix and the evolution of the emission frequency is calculated as a function of the delay time after photoexcitation. An initial large (>1 eV) red-shift is ascribed to the matrix relaxation that, however, is fully accomplished within the first few picoseconds. After this initial relaxation the matrix evolution is done, leading to the conclusion that the anomalous inhomogeneous broadening phenomena observed in TADF photophysics in amorphous matrices are governed by conformational rather than by dielectric disorder. However, this result contrasts sharply with experimental results discussed in the previous section, showing that DPEPO dynamics is not completed after 15 ns. This discrepancy can be ascribed to the different packing of the matrix grown in silico vs. the spin-coated or drop-cast matrices. In this respect, experimental data collected from matrices grown exploiting different techniques would be very useful.
The comparatively simple and reliable model built for DMAC-TRZ invites to address the intriguing issue of TADF dynamics in amorphous matrices. Following the approach discussed in section 3.1, the molecular properties, including RISC, ISC and radiative rates as well as fluorescence spectra can be calculated as a function of the two sources of disorder: the local reaction field and the dihedral angle, as illustrated in Fig. 8.
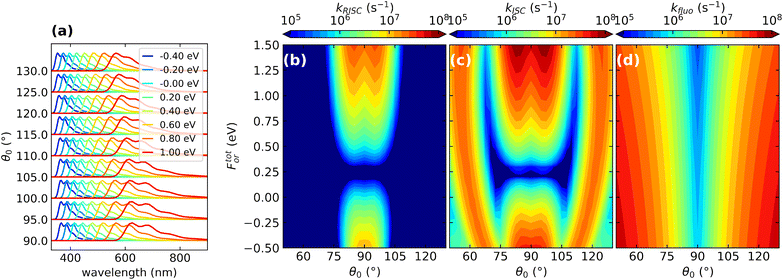 | ||
| Fig. 8 The effect of conformational and dielectric disorders on TADF photophysics. (a) Normalized fluorescence spectra calculated for DMAC-TRZ. Different colors refer to spectra calculated for For values shown in the legend. Spectra obtained for different values of the dihedral angle θ0 are shifted along the vertical axis. (b)–(d) Color maps show the dependence of the different rates (RISC, ISC and fluorescence rates, respectively) as a function of the reaction field and of the dihedral angle. For convenience, the reaction field is multiplied by μ0 the dipole moment associated to the zwitterionic state, so that it has energy dimensions. Adapted from ref. 128. | ||
Without entering in any specific detail, the results in Fig. 8 demonstrate the correlated nature of the disorder in TADF systems, leading to more important and subtle effects besides band broadening. The fluorescence rates are marginally affected by the dielectric disorder that however affects heavily the emission frequency (Fig. 8a). The torsional angle has little influence on the emission frequency but heavily affects the fluorescence rate that vanishes in orthogonal geometry and very quickly increases when moving away from orthogonality (Fig. 8d). RISC and ISC rates show a more complex behavior being affected by both sources of disorder (Fig. 8b and c). In particular RISC is sizable in the orthogonal geometry (and indeed it does not vanish there, as incorrectly predicted by the Marcus model or, more generally, in the Condon approximation) and quickly decreases when moving away from orthogonality. But, even more interestingly, dielectric disorder may fully suppress RISC (cf. also Fig. 6).
With the detailed information in Fig. 8, the complex TADF photophysics of DMAC-TRZ in different matrices was simulated introducing few reasonable assumptions about the two sources of disorder.128 As for conformational disorder, a Gaussian distribution of torsional angles is considered, whose width is estimated from MD simulations.52 It should be stressed that the distribution refers to the equilibrium torsional angle (θ0 in Fig. 8), oscillations around the equilibrium are properly accounted for, as needed to address RISC and ISC rates in the non-adiabatic approach, discussed in section 2.2. Dielectric disorder is more delicate because of its dynamical nature. To make the simulation feasible, the environmental degrees of freedom responsible for the dielectric disorder are partitioned in two components, a dynamical component that relaxes before prompt fluorescence and a static component. Along these lines, experimental data were satisfactorily simulated.128
The detailed analysis reported for DMAC-TRZ in ref. 128 highlights the importance of conformational and dielectric disorder to properly understand and simulate the complex TADF photophysics. In liquid solvents, the low viscosity of the medium marginally affects the conformational motion of the dye and, at the same time, guarantees for the full relaxation of the medium before any relevant photophysical process occurs. In contrast, in amorphous solid matrices, the conformational motion of the dye is hindered, giving rise to distributions of conformational angles that can possibly largely deviate from equilibrium.59,60 The dielectric relaxation of the matrix is slow and occurs across several timescales.53 Both phenomena not only make a detailed analysis complex, but can also be affected by the way the sample is prepared. It is reasonable to believe that matrices grown by vapor phase deposition are more compact than matrices obtained from solution,141 and matrices grown from different solvents could behave in a different way.
4 Conclusions
TADF is an intriguing phenomenon that finds most popular applications in OLED, and specifically in the quest for efficient blue OLED, but is also promising in bioimaging and biosensing as well as in photocatalysis, where TADF dyes are used as efficient metal-free photocatalysts. TADF photophysics is extremely delicate relying on a fragile equilibrium between tiny ST energy gap, sizable SOC, a balanced contribution of CT and local excited states and some well-designed conformational flexibility. Reliable guidelines for the design of optimized TADF dyes require a deep comprehension of this complex photophysics and reliable computational tools. The task is challenging: the small ST gaps characteristic of TADF are of the same order of magnitude as the typical uncertainties in energies calculated in popular computational codes, and the calculation of the tiny SOC matrix elements is similarly challenging.Even more delicate is the estimate of the rates governing the TADF photophysics. In the first place, one needs to abandon the familiar field of closed quantum-mechanical systems, to enter the much less comfortable field of open quantum systems, as to allow for energy exchange between the system and a thermal bath. Modeling the thermal bath and its coupling with the quantum system unavoidably introduces some degree of arbitrariness, that is often overlooked in current approaches to TADF photophysics.
Conformational degrees of freedom are pivotal in defining RISC rates and in this respect several messages emerge from our analysis: (a) the tiny singlet-triplet gap, comparable to conformational frequencies, makes the adiabatic approximation untenable; (b) the harmonic approximation is similarly dangerous since anharmonicity affects the density of states in the singlet and triplet manifolds, with important effects on rates; (c) the Condon approximation is definitely unsuitable (making Marcus-like approaches to RISC rates poorly reliable) and the validity of the Herzberg–Teller approach is not demonstrated. Effective, semiempirical models needs to be developed, parametrized and validated (either ab initio or experimentally) to fully appreciate the subtle photophysics of TADF dyes.
This requirement is even more urgent because environmental effects cannot be disregarded: in OLED, in bioimaging applications, in photocatalytic processes the TADF dye is embedded in a medium whose polarity, polarizability, viscosity and rigidity can profoundly alter the fragile TADF photophysics. Once again, models can help to disentangle different contributions to the system photophysics. The main take-home message here is that disorder should not be disregarded. Disorder is not just a source of spectral broadening, since it affects not only the energies of the transitions but also the rates of the different processes. The profound impact of disorder on the TADF photophysics becomes more obvious in solid environments. Indeed, the matrix rigidity amplifies conformational disorder and the slow and possibly partially frozen dielectric dynamics intertwines with the TADF dynamics leading to a very complex scenario.
The concurrent optimization of the TADF emitter and the hosting medium is crucial to fully exploit the promise of TADF for different applications, ranging from efficient blue-emitting OLEDs to photodynamic therapy or photocatalysis. More work is needed to simulate in detail several families of dyes, as to validate or disprove relevant approximation schemes. But just focusing on the dye is far from enough: the subtle environmental effects on the TADF photophysics require a deep understanding of the dielectric properties of the medium and of its dynamical behavior. This is a particularly stringent requirement for the promising biomedical applications of TADF dyes (e.g. in bioimaging and photodynamic therapy) where, on one side, the presence of oxygen cannot be avoided and, on the other side, the need to work in aqueous media requires attention to specific interactions driven by hydrogen bonding. Strategies to protect the delicate TADF photophysics from the harsh biological environment can be considered by, e.g., encapsulating the dye in a proper nanocarrier that however must be selected with extreme care. Once again a careful theoretical analysis of the interactions at the nanoscale can help to devise the best strategy.
Theoreticians need to face the problem of environmental effects on TADF photophysics exploiting several tools including state of the art ab initio approaches, semiempirical models and atomistic MD simulations. The information extracted from this extensive analysis is however not enough as it must be exploited to build open quantum system models able to describe the energy exchange between the system and the environment. Such a complex theoretical endeavor must rely on an extensive experimental validation. Comprehensive steady-state and time-resolved spectroscopic studies are definitely in demand for dyes in liquid solvents and amorphous matrices. But more information is needed on the matrices themselves, and in this respect single molecule spectroscopy studies will prove to be crucial.
Author contributions
DG, AL and OR performed literature search and organized relevant material. FDM, DKAPH and AP wrote the original draft and prepared figures. All authors reviewed and edited the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Work funded by PNRR MUR project ECS-00000033-ECOSISTER and PNRR MUR project PE0000023-NQSTI. We acknowledge the support from the local HPC (High Performance Computing) facility and from the equipment and framework of the COMP-HUB and COMP-R Initiatives, funded by the “Departments of Excellence program of the Italian Ministry for University and Research” (MIUR, 2018–2022 and MUR, 2023–2027). F.D.M. position was co-funded by the European Union - PON Research and Innovation 2014–2020.Notes and references
- M. Kasha, Pure Appl. Chem., 1990, 62, 1615–1630 CrossRef CAS
.
- F. Perrin, Ann. Phys., 1929, 10, 169–275 Search PubMed
.
- A. Endo, K. Sato, K. Yoshimura, T. Kai, A. Kawada, H. Miyazaki and C. Adachi, Appl. Phys. Lett., 2011, 98, 083302 CrossRef
.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed
.
- M. A. Baldo, D. F. O'Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1998, 395, 151–154 CrossRef CAS
.
- Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915–1016 RSC
.
- T. J. Penfold, F. B. Dias and A. P. Monkman, Chem. Commun., 2018, 54, 3926–3935 RSC
.
- Y. Liu, C. Li, Z. Ren, S. Yan and M. R. Bryce, Nat. Rev. Mater., 2018, 3, 18020 CrossRef CAS
.
- X.-K. Chen, D. Kim and J.-L. Brédas, Acc. Chem. Res., 2018, 51, 2215–2224 CrossRef CAS
.
- Y. Olivier, J.-C. Sancho-Garcia, L. Muccioli, G. D'Avino and D. Beljonne, J. Phys. Chem. Lett., 2018, 9, 6149–6163 CrossRef CAS
.
- J. Eng and T. J. Penfold, Commun. Chem., 2021, 4, 91 CrossRef PubMed
.
- Y. Xiao, H. Wang, Z. Xie, M. Shen, R. Huang, Y. Miao, G. Liu, T. Yu and W. Huang, Chem. Sci., 2022, 13, 8906–8923 RSC
.
- Y.-Z. Shi, H. Wu, K. Wang, J. Yu, X.-M. Ou and X.-H. Zhang, Chem. Sci., 2022, 13, 3625–3651 RSC
.
- B. Li, M. Liu, L. Sang, Z. Li, X. Wan and Y. Zhang, Adv. Opt. Mater., 2023, 11, 2202610 CrossRef CAS
.
- M. T. do Casal, K. Veys, M. H. E. Bousquet, D. Escudero and D. Jacquemin, J. Phys. Chem. A, 2023, 10033–10053 CrossRef CAS PubMed
.
- X. Xiong, F. Song, J. Wang, Y. Zhang, Y. Xue, L. Sun, N. Jiang, P. Gao, L. Tian and X. Peng, J. Am. Chem. Soc., 2014, 136, 9590–9597 CrossRef CAS PubMed
.
- C. I. C. Crucho, J. Avó, A. M. Diniz, S. N. Pinto, J. Barbosa, P. O. Smith, M. N. Berberan-Santos, L.-O. Pålsson and F. B. Dias, Front. Chem., 2020, 8, 404 CrossRef CAS PubMed
.
- S. Qi, S. Kim, V.-N. Nguyen, Y. Kim, G. Niu, G. Kim, S.-J. Kim, S. Park and J. Yoon, ACS Appl. Mater. Interfaces, 2020, 12, 51293–51301 CrossRef CAS PubMed
.
- F. Fang, L. Zhu, M. Li, Y. Song, M. Sun, D. Zhao and J. Zhang, Advanced Science, 2021, 8, 2102970 CrossRef CAS PubMed
.
- F. Fang, Y. Yuan, Y. Wan, J. Li, Y. Song, W.-C. Chen, D. Zhao, Y. Chi, M. Li, C.-S. Lee and J. Zhang, Small, 2022, 18, 2106215 CrossRef CAS
.
- J. Zhang, J. Ma, S. Zhang, X. Lou, Y. Ding, Y. Li, M. Xu, X. Xie, X. Jiao, X. Dou, X. Wang and B. Tang, ACS Nano, 2023, 23430–23441 CrossRef CAS PubMed
.
- J. Lu, B. Pattengale, Q. Liu, S. Yang, W. Shi, S. Li, J. Huang and J. Zhang, J. Am. Chem. Soc., 2018, 140, 13719–13725 CrossRef CAS PubMed
.
- T.-Y. Shang, L.-H. Lu, Z. Cao, Y. Liu, W.-M. He and B. Yu, Chem. Commun., 2019, 55, 5408–5419 RSC
.
- S. Paul, D. Filippini, F. Ficarra, H. Melnychenko, C. Janot and M. Silvi, J. Am. Chem. Soc., 2023, 145, 15688–15694 CrossRef CAS PubMed
.
- S. Paul, D. Filippini and M. Silvi, J. Am. Chem. Soc., 2023, 145, 2773–2778 CrossRef CAS PubMed
.
- M. A. Bryden and E. Zysman-Colman, Chem. Soc. Rev., 2021, 50, 7587–7680 RSC
.
- S. M. Menke and R. J. Holmes, J. Phys. Chem. C, 2016, 120, 8502–8508 CrossRef CAS
.
- F. Mateen, S. Y. Lee and S.-K. Hong, J. Mater. Chem. A, 2020, 8, 3708–3716 RSC
.
- P.-F. Loos, F. Lipparini, M. Boggio-Pasqua, A. Scemama and D. Jacquemin, J. Chem. Theory Comput., 2020, 16, 1711–1741 CrossRef CAS PubMed
.
- M. Véril, A. Scemama, M. Caffarel, F. Lipparini, M. Boggio-Pasqua, D. Jacquemin and P. Loos, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1517 Search PubMed
.
- F. B. Dias, K. N. Bourdakos, V. Jankus, K. C. Moss, K. T. Kamtekar, V. Bhalla, J. Santos, M. R. Bryce and A. P. Monkman, Adv. Mater., 2013, 25, 3707–3714 CrossRef CAS PubMed
.
- F. B. Dias, T. J. Penfold and A. P. Monkman, Methods Appl. Fluoresc., 2017, 5, 012001 CrossRef PubMed
.
- M. Zheng, Y. Li, Y. Wei, L. Chen, X. Zhou and S. Liu, J. Phys. Chem. Lett., 2022, 13, 2507–2515 CrossRef CAS PubMed
.
- Y. Tsuchiya, K. Mizukoshi, M. Saigo, T. Ryu, K. Miyata, K. Onda and C. Adachi, Faraday Discuss., 2024 10.1039/D3FD00151B
.
- N. Aizawa, Y.-J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka, H. Inuzuka, B. Dhara, Y. Koyama, K.-i. Nakayama, S. Maeda, F. Araoka and D. Miyajima, Nature, 2022, 609, 502–506 CrossRef CAS PubMed
.
- J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2019, 123, 8099–8108 CrossRef CAS PubMed
.
- R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Matter, 2021, 4, 1654–1682 CrossRef CAS
.
- D. Hall, J. C. Sancho-García, A. Pershin, G. Ricci, D. Beljonne, E. Zysman-Colman and Y. Olivier, J. Chem. Theory Comput., 2022, 18, 4903–4918 CrossRef CAS PubMed
.
- M. Bedogni, D. Giavazzi, F. Di Maiolo and A. Painelli, J. Chem. Theory Comput., 2024, 20, 902–913 CrossRef CAS PubMed
.
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956–2961 CrossRef CAS
.
- M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS
.
- X.-K. Chen, S.-F. Zhang, J.-X. Fan and A.-M. Ren, J. Phys. Chem. C, 2015, 119, 9728–9733 CrossRef CAS
.
- M. K. Etherington, J. Gibson, H. F. Higginbotham, T. J. Penfold and A. P. Monkman, Nat. Commun., 2016, 7, 13680 CrossRef CAS PubMed
.
- S. Lin, Z. Pei, B. Zhang, H. Ma and W. Liang, J. Phys. Chem. A, 2022, 126, 239–248 CrossRef CAS PubMed
.
- A. Carreras and D. Casanova, ChemPhotoChem, 2022, 6, e202200066 CrossRef CAS
.
- F. B. Dias, J. Santos, D. R. Graves, P. Data, R. S. Nobuyasu, M. A. Fox, A. S. Batsanov, T. Palmeira, M. N. Berberan-Santos, M. R. Bryce and A. P. Monkman, Advanced Science, 2016, 3, 1600080 CrossRef PubMed
.
- Y. Olivier, M. Moral, L. Muccioli and J.-C. Sancho-García, J. Mater. Chem. C, 2017, 5, 5718–5729 RSC
.
- J. Chen, X. Xiao, S. Li, Y. Duan, G. Wang, Y. Liao, Q. Peng, H. Fu, H. Geng and Z. Shuai, J. Phys. Chem. Lett., 2022, 13, 2653–2660 CrossRef CAS PubMed
.
- V. Bulović, A. Shoustikov, M. Baldo, E. Bose, V. Kozlov, M. Thompson and S. Forrest, Chem. Phys. Lett., 1998, 287, 455–460 CrossRef
.
- V. Bulović, R. Deshpande, M. Thompson and S. Forrest, Chem. Phys. Lett., 1999, 308, 317–322 CrossRef
.
- C. F. Madigan and V. Bulović, Phys. Rev. Lett., 2003, 91, 247403 CrossRef
.
- T. Northey, J. Stacey and T. J. Penfold, J. Mater. Chem. C, 2017, 5, 11001–11009 RSC
.
- B. Bardi, D. Giavazzi, E. Ferrari, A. Iagatti, M. Di Donato, D. K. A. Phan Huu, F. Di Maiolo, C. Sissa, M. Masino, A. Lapini and A. Painelli, Mater. Horiz., 2023, 10, 4172–4182 RSC
.
- T. Serevičius, R. Skaisgiris, J. Dodonova, I. Fiodorova, K. Genevičius, S. Tumkevičius, K. Kazlauskas and S. Juršėnas, J. Phys. Chem. Lett., 2022, 13, 1839–1844 CrossRef PubMed
.
- D. K. A. Phan Huu, S. Saseendran and A. Painelli, J. Mater. Chem. C, 2022, 4620–4628 RSC
.
- G. Chen, J. R. Swartzfager and J. B. Asbury, J. Am. Chem. Soc., 2023, 25495–25504 CrossRef CAS PubMed
.
- K. Suzuki and H. Kaji, J. Am. Chem. Soc., 2023, 145, 16324–16329 CrossRef CAS PubMed
.
- A. Cakaj, M. Schmid, A. Hofmann and W. Brütting, ACS Appl. Mater. Interfaces, 2023, 15, 54721–54731 CrossRef CAS PubMed
.
- E. Crovini, R. Dhali, D. Sun, T. Matulaitis, T. Comerford, A. Slawin, C. Sissa, F. Azzolin, F. D. Maiolo, A. Painelli and E. Zysman-Colman, J. Mater. Chem. C, 2023, 8284–8292 RSC
.
- K. Stavrou, L. G. Franca, T. Böhmer, L. M. Duben, C. M. Marian and A. P. Monkman, Adv. Funct. Mater., 2023, 33, 2300910 CrossRef CAS
.
- H. Zhang, P.-Z. Chen, L.-Y. Niu and Q.-Z. Yang, Mater. Chem. Front., 2020, 4, 285–291 RSC
.
- H. S. Kim, S.-R. Park and M. C. Suh, J. Phys. Chem. C, 2017, 121, 13986–13997 CrossRef CAS
.
- F. Rodella, R. Saxena, S. Bagnich, D. Banevičius, G. Kreiza, S. Athanasopoulos, S. Juršėnas, K. Kazlauskas, A. Köhler and P. Strohriegl, J. Mater. Chem. C, 2021, 9, 17471–17482 RSC
.
- R. A. Marcus, Angew Chem. Int. Ed. Engl., 1993, 32, 1111–1121 CrossRef
.
-
A. Nitzan, Chemical dynamics in condensed phases : relaxation, transfer, and reactions in condensed molecular systems, Oxford University Press, Oxford, 2013 Search PubMed
.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef PubMed
.
- I. E. Serdiuk, M. Mońka, K. Kozakiewicz, B. Liberek, P. Bojarski and S. Y. Park, J. Phys. Chem. B, 2021, 125, 2696–2706 CrossRef CAS PubMed
.
- N. Aizawa, Y. Harabuchi, S. Maeda and Y.-J. Pu, Nat. Commun., 2020, 11, 3909 CrossRef CAS PubMed
.
- N. R. Kestner, J. Logan and J. Jortner, J. Phys. Chem., 1974, 78, 2148–2166 CrossRef CAS
.
- P. K. Samanta, D. Kim, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2017, 139, 4042–4051 CrossRef CAS
.
- Q. Zhu, S. Feng, X. Guo, X. Chen and J. Zhang, Spectrochim. Acta, Part A, 2019, 221, 117214 CrossRef CAS PubMed
.
- B. C. Garain, P. K. Samanta and S. K. Pati, J. Phys. Chem. A, 2021, 125, 6674–6680 CrossRef CAS PubMed
.
- H. Abroshan, V. Coropceanu and J.-L. Brédas, ACS Mater. Lett., 2020, 2, 1412–1418 CrossRef CAS
.
- A. J. Gillett, A. Pershin, R. Pandya, S. Feldmann, A. J. Sneyd, A. M. Alvertis, E. W. Evans, T. H. Thomas, L.-S. Cui, B. H. Drummond, G. D. Scholes, Y. Olivier, A. Rao, R. H. Friend and D. Beljonne, Nat. Mater., 2022, 21, 1150–1157 CrossRef CAS PubMed
.
- R. Borrelli and A. Peluso, J. Chem. Phys., 2003, 119, 8437–8448 CrossRef CAS
.
- F. Santoro, A. Lami, R. Improta and V. Barone, J. Chem. Phys., 2007, 126, 184102 CrossRef PubMed
.
- Q. Peng, Y. Niu, Q. Shi, X. Gao and Z. Shuai, J. Chem. Theory Comput., 2013, 9, 1132–1143 CrossRef CAS PubMed
.
- S. H. Lin, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1973, 335, 51–66 Search PubMed
.
- S. H. Lin, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1976, 352, 57–71 CAS
.
- B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2018, 148, 034104 CrossRef
.
- B. de Souza, G. Farias, F. Neese and R. Izsák, J. Chem. Theory Comput., 2019, 15, 1896–1904 CrossRef CAS
.
- J.-M. Mewes, Phys. Chem. Chem. Phys., 2018, 20, 12454–12469 RSC
.
- B. R. Henry and W. Siebrand, J. Chem. Phys., 1971, 54, 1072–1085 CrossRef CAS
.
- Z. Shuai, D. Wang, Q. Peng and H. Geng, Acc. Chem. Res., 2014, 47, 3301–3309 CrossRef CAS
.
- Q. Peng, D. Fan, R. Duan, Y. Yi, Y. Niu, D. Wang and Z. Shuai, J. Phys. Chem. C, 2017, 121, 13448–13456 CrossRef CAS
.
- Z. Shuai, Chin. J. Chem., 2020, 38, 1223–1232 CrossRef CAS
.
- L. Lv, K. Yuan, T. Zhao and Y. Wang, J. Mater. Chem. C, 2020, 8, 10369–10381 RSC
.
- L. Lv, K. Yuan, T. Zhao and G. Dai, J. Phys. Chem. A, 2022, 126, 6695–6709 CrossRef CAS PubMed
.
- S. Lin, Q. Ou and Z. Shuai, ACS Mater. Lett., 2022, 4, 487–496 CrossRef CAS
.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed
.
-
G. C. Schatz and M. A. Ratner, Quantum mechanics in chemistry, Prentice Hall, 1993 Search PubMed
.
- B. Orr and J. Ward, Mol. Phys., 1971, 20, 513–526 CrossRef CAS
.
- Y. Olivier, B. Yurash, L. Muccioli, G. D'Avino, O. Mikhnenko, J. C. Sancho-García, C. Adachi, T.-Q. Nguyen and D. Beljonne, Phys. Rev. Mater., 2017, 1, 075602 CrossRef
.
- E. Cho, M. Hong, V. Coropceanu and J.-L. Brédas, Adv. Opt. Mater., 2021, 9, 2002135 CrossRef CAS
.
- K. Zhang, Y. Zhang, Y. Ma, J. Fan, C.-K. Wang and L. Lin, J. Phys. Chem. A, 2020, 124, 8540–8550 CrossRef CAS
.
- T. Francese, A. Kundu, F. Gygi and G. Galli, Phys. Chem. Chem. Phys., 2022, 24, 10101–10113 RSC
.
- L. E. de Sousa and P. de Silva, J. Chem. Theory Comput., 2021, 17, 5816–5824 CrossRef CAS
.
- R. Dhali, D. K. A. Phan Huu, F. Bertocchi, C. Sissa, F. Terenziani and A. Painelli, Phys. Chem. Chem. Phys., 2021, 23, 378–387 RSC
.
- P. De Silva, C. A. Kim, T. Zhu and T. Van Voorhis, Chem. Mater., 2019, 31, 6995–7006 CrossRef CAS
.
- I. Lyskov and C. M. Marian, J. Phys. Chem. C, 2017, 121, 21145–21153 CrossRef CAS
.
- A. Toniolo and M. Persico, J. Comput. Chem., 2001, 22, 968–975 CrossRef CAS
.
- K. Shizu and H. Kaji, J. Phys. Chem. A, 2021, 125, 9000–9010 CrossRef CAS PubMed
.
- Y. Wada, Y. Wakisaka and H. Kaji, ChemPhysChem, 2021, 22, 625–632 CrossRef CAS PubMed
.
- K. Shizu and H. Kaji, Commun. Chem., 2022, 5, 53 CrossRef CAS PubMed
.
- A. Painelli, Chem. Phys., 1999, 245, 185–197 CrossRef CAS
.
- B. Boldrini, E. Cavalli, A. Painelli and F. Terenziani, J. Phys. Chem. A, 2002, 106, 6286–6294 CrossRef CAS
.
- P. L. dos Santos, J. S. Ward, M. R. Bryce and A. P. Monkman, J. Phys. Chem. Lett., 2016, 7, 3341–3346 CrossRef CAS PubMed
.
- B. L. Cotts, D. G. McCarthy, R. Noriega, S. B. Penwell, M. Delor, D. D. Devore, S. Mukhopadhyay, T. S. D. Vries and N. S. Ginsberg, ACS Energy Lett., 2017, 2, 1526–1533 CrossRef CAS
.
- R. Noriega, E. S. Barnard, B. Ursprung, B. L. Cotts, S. B. Penwell, P. J. Schuck and N. S. Ginsberg, J. Am. Chem. Soc., 2016, 138, 13551–13560 CrossRef CAS
.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed
.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC
.
- R. Ishimatsu, S. Matsunami, K. Shizu, C. Adachi, K. Nakano and T. Imato, J. Phys. Chem. A, 2013, 117, 5607–5612 CrossRef CAS
.
- H. Sun, C. Zhong and J.-L. Brédas, J. Chem. Theory Comput., 2015, 11, 3851–3858 CrossRef CAS PubMed
.
- C. M. Marian, J. Phys. Chem. C, 2016, 120, 3715–3721 CrossRef CAS
.
- J. Föller and C. M. Marian, J. Phys. Chem. Lett., 2017, 8, 5643–5647 CrossRef PubMed
.
- H. Sun, Z. Hu, C. Zhong, X. Chen, Z. Sun and J.-L. Brédas, J. Phys. Chem. Lett., 2017, 8, 2393–2398 CrossRef CAS PubMed
.
- L. Kunze, A. Hansen, S. Grimme and J.-M. Mewes, J. Phys. Chem. Lett., 2021, 12, 8470–8480 CrossRef CAS PubMed
.
- J.-M. Mewes, Z.-Q. You, M. Wormit, T. Kriesche, J. M. Herbert and A. Dreuw, J. Phys. Chem. A, 2015, 119, 5446–5464 CrossRef CAS
.
- D. K. A. Phan Huu, R. Dhali, C. Pieroni, F. Di Maiolo, C. Sissa, F. Terenziani and A. Painelli, Phys. Rev. Lett., 2020, 124, 107401 CrossRef CAS
.
- R. Dhali, D. K. A. Phan Huu, F. Terenziani, C. Sissa and A. Painelli, J. Chem. Phys., 2021, 154, 134112 CrossRef CAS PubMed
.
- F. Terenziani, A. Painelli, C. Katan, M. Charlot and M. Blanchard-Desce, J. Am. Chem. Soc., 2006, 128, 15742–15755 CrossRef CAS PubMed
.
- F. Terenziani, C. Sissa and A. Painelli, J. Phys. Chem. B, 2008, 112, 5079–5087 CrossRef CAS PubMed
.
- J. Campo, A. Painelli, F. Terenziani, T. Van Regemorter, D. Beljonne, E. Goovaerts and W. Wenseleers, J. Am. Chem. Soc., 2010, 132, 16467–16478 CrossRef CAS PubMed
.
- F. Terenziani, A. Painelli, A. Girlando and R. M. Metzger, J. Phys. Chem. B, 2004, 108, 10743–10750 CrossRef CAS
.
- F. Terenziani and A. Painelli, Chem. Phys., 2003, 295, 35–46 CrossRef CAS
.
- F. Terenziani and A. Painelli, Phys. Chem. Chem. Phys., 2015, 17, 13074–13081 RSC
.
- F. Terenziani, O. V. Przhonska, S. Webster, L. A. Padilha, Y. L. Slominsky, I. G. Davydenko, A. O. Gerasov, Y. P. Kovtun, M. P. Shandura, A. D. Kachkovski, D. J. Hagan, E. W. Van Stryland and A. Painelli, J. Phys. Chem. Lett., 2010, 1, 1800–1804 CrossRef CAS
.
- D. K. A. Phan Huu, S. Saseendran, R. Dhali, L. G. Franca, K. Stavrou, A. Monkman and A. Painelli, J. Am. Chem. Soc., 2022, 144, 15211–15222 CrossRef CAS PubMed
.
- E. W. Castner, M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1987, 86, 1090–1097 CrossRef CAS
.
- M. L. Horng, J. A. Gardecki, A. Papazyan and M. Maroncelli, J. Phys. Chem., 1995, 99, 17311–17337 CrossRef CAS
.
- F. Di Maiolo and A. Painelli, J. Chem. Theory Comput., 2018, 14, 5339–5349 CrossRef CAS PubMed
.
- F. D. Maiolo and A. Painelli, Phys. Chem. Chem. Phys., 2020, 22, 1061–1068 RSC
.
- V. Jankus, P. Data, D. Graves, C. McGuinness, J. Santos, M. R. Bryce, F. B. Dias and A. P. Monkman, Adv. Funct. Mater., 2014, 24, 6178–6186 CrossRef CAS
.
- G. Méhes, K. Goushi, W. J. Potscavage and C. Adachi, Org. Electron., 2014, 15, 2027–2037 CrossRef
.
- J. S. Ward, R. S. Nobuyasu, A. S. Batsanov, P. Data, A. P. Monkman, F. B. Dias and M. R. Bryce, Chem. Commun., 2016, 52, 2612–2615 RSC
.
- C. S. Oh, D. de Sa Pereira, S. H. Han, H.-J. Park, H. F. Higginbotham, A. P. Monkman and J. Y. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 35420–35429 CrossRef CAS PubMed
.
- C. M. Legaspi, R. E. Stubbs, M. Wahadoszaman, D. J. Yaron, L. A. Peteanu, A. Kemboi, E. Fossum, Y. Lu, Q. Zheng and L. J. Rothberg, J. Phys. Chem. C, 2018, 122, 11961–11972 CrossRef CAS
.
- T. Serevičius, R. Skaisgiris, J. Dodonova, K. Kazlauskas, S. Juršėnas and S. Tumkevičius, Phys. Chem. Chem. Phys., 2020, 22, 265–272 RSC
.
- D. Kelly, L. G. Franca, K. Stavrou, A. Danos and A. P. Monkman, J. Phys. Chem. Lett., 2022, 13, 6981–6986 CrossRef CAS PubMed
.
- H. Abroshan, Y. Zhang, X. Zhang, C. Fuentes-Hernandez, S. Barlow, V. Coropceanu, S. R. Marder, B. Kippelen and J. Brédas, Adv. Funct. Mater., 2020, 30, 2005898 CrossRef CAS
.
- F. Balzer, T. Breuer, G. Witte and M. Schiek, Langmuir, 2022, 38, 9266–9277 CrossRef CAS PubMed
.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |