Imaging the orientation of hydroxyapatite crystallites across full mouse femora

Abstract

Imaging the orientations of crystallites in bone requires the usage of synchrotron X-ray radiation, which is a limited resource for researchers. Thus scans have historically been limited to either small regions or few samples. In the present study, we scan 16 full frontal cross sections of mouse femora. This makes it possible to study structure, orientation, and composition, statistically across many different bones and animals, while preserving the structural context. From the following analysis, we can deduce that while the trabecular bone in the shaft has a larger fraction of oriented crystallites than other regions in the bone, the oriented fraction is more well aligned in the cortical bone in the shaft compared to other regions in the bone. We also see that the crystallites in the cortical and trabecular bone are longer than those in the femoral head and the condyle. The study also shows a larger Sr content in the cortical bone compared to other regions, and a larger Zn content in the femoral head compared to other regions of the bones. This study shows the need for and possibility of scanning larger regions to understand bioinorganic materials.

---

Introduction

Bone is a highly hierarchical material with different structures across different length scales.^1–4 These different structures require the use of a wide array of techniques to understand the material. Among these techniques options such as μXRF,^5–8 μXRD,^9–12 and μSAXS^13–16 have been proven to provide useful information. All these techniques require synchrotron radiation. Hence the experimental time is inherently limited, which in turn has historically limited the scope of studies conducted with these techniques, in regard to sample size. Studies have traditionally either focused on a few or singular samples,^9,15,17 or instead elected to scan multiple smaller regions of interest across many samples.^10,18,19 These approaches do without a doubt produce highly valuable results and provide a great insight into the materials of study. Yet there is an inherent statistical limit to approaches focusing on small regions or lone standing samples. Scanning only small regions means that the biological variations within a full sample are easily lost or overlooked, and scanning only single samples makes it impossible to perform statistical analysis.

These limits have been inherent to the collection of the data, but with the increase in flux at synchrotron facilities made possible by the advent of 4th generation synchrotrons such as MAX IV²⁰ and the ESRF EBS,²¹ and the continued development of detector technology, scan speed can be greatly increased at modern facilities. With these developments, it is now possible to scan larger areas with a higher resolution than previously achievable. In the present study, the DanMAX beamline at MAX IV is utilized to scan 16 full frontal cross sections of mouse femora from different animals, with a 15 × 15 μm² pixel size, providing a high degree of details, across full samples. The aim of the study is to examine how bone parameters vary on the larger scale, across different regions of bone. We expect to see that different regions of bone will have different structural parameters e.g. not all regions will have the same orientation, crystallite size, or composition.

Material and methods

Sample preparation

Femoral bones from C57BL/6 mice, raised for other studies,^22,23 were prepared. Here only bones from wild type mice were used. 3 groups of mice were used. Two groups of female mice, sacrificed at ages 24 weeks (N = 6) and 36 weeks (N = 4) respectively, and 1 group of male mice, sacrificed at age 36 weeks (N = 6) were scanned. Collection of mouse bone was approved by the Animal Care and Use Committee of Nagasaki University Graduate School of Biomedical Sciences No. 1903131520-2. The mice had free access to tap water, were fed standard feed (CLEA Japan, Tokyo), and were kept in cages of three mice, with a 12-h day–night cycle. The mice were kept in a pathogen-free environment.

After their sacrifice, the femoral bones of the mice were extracted before being embedded in Technovit 7200 VLC (KULZER, Germany) later being sliced using a bandsaw K-100 (HOZAN, Japan) to a thickness of 2 mm. The bones were then polished using abrasive SiC paper of increasing grit (#2400–#4000) (Presi, France) until they reached a final thickness of 150–200 μm.

Synchrotron X-ray experiments

XRD and XRF mapping experiments were done at the DanMAX beamline at the MAX IV synchrotron. The samples were mounted on Kapton tape (DuPont, USA) on aluminium frames, before being scanned with a pencil beam of either size 21.6 × 36.0 μm² (V × H) with a flux of 9 × 10¹¹ ph per s or size 33.6 × 30.0 μm² (V × H) with a flux of 8 × 10¹¹ ph per s. The samples were scanned across two visits requiring a refocusing in between. A sample to detector distance of 350 mm was used. The samples were scanned using an energy of 25 keV allowing XRF from both Ca, Sr, and Zn. A 3 mm W beamstop was used. The beamstop was filled with Al to block the W L XRF as this signal would overlap with the Zn K lines in the spectra. A Pilatus X3 2M CdTe detector (Dectris, Switzerland) was used to measure XRD. For the XRF signal a RaySpec silicon drift detector (RaySpec, United Kingdom) was used.

The samples were scanned using flyscans with a step size of 15 × 15 μm² and an acquisition rate of 40 Hz. This rate was chosen to get high quality data for the orientation analysis. For unit cell parameters and XRF data alone a faster acquisition time could have been used. For every sample the full femur was scanned, with a total scan time of 2–4 h per sample. A sample XRF spectrum is shown in Fig. 1(a), the iron signal stems from organic material, and is localized inside the marrow cavity. The corresponding diffraction pattern is shown in Fig. 1(b). In total more than 5 million data points were measured.

Fig. 1 Examples of raw data. X-ray fluorescence spectra of a single point (red) and average of a region (black). Elements marked with dashed lines from left to right: Ca, Fe, Zn Sr. Fe is only present outside the bone (a). XRD from the same point as in (a). Red line shows a fit to the 002 peak (b).

Dose calculations

The dose delivered to a sample can induce damage in the sample when studying biological structures.²⁴ To avoid damage, we aim to stay below a dose of 5 kGy.^24,25 To calculate the deposited dose, the following formula can be used:^26,27
where ϕ is the photon flux, A is the absorbed fraction of light A = 1 − e^μd (μ is the attenuation coefficient, d the sample depth), ε is the energy of the beam, t the time the beam is on the sample, m is the mass in the beam. For bone we assume 50% v/v HAp, as an overestimate,^1,28–31 and a density of ρ = 1.8 g cm⁻³, resulting in an absorption coefficient³² of μ = 5.79 cm⁻¹. This results in a dose of 1.67 kGy, including that the beam is larger than the step size such that every point sees approximately two exposures. This dose is below the limit of 5 kGy for bone.^24,25,33,34 While collagen is not a part of the present study, it should not be affected adversely by such a low dose, leaving the bone unaffected. HAp is capable of withstanding a much larger dose before being affected in the MGy range.²⁴

Data analysis

The XRD experiments were calibrated using measurements of LaB₆ in conjunction with pyFAI-calib.^35,36 The data was integrated using the MatFRAIA pipeline used at MAX IV.³⁷ The XRF energy was calibrated using the elastic peak and the Ca K peak present in bone. The XRF spectra were fitted using pyMCA³⁸ with a custom batch fitter. The major components were Ca, Zn, and Sr, and these elements were extracted. Maps of all samples scanned are shown in Fig. S1.†

Crystallite parameter calculation

The HAp peak (002) was fitted using a Gaussian distribution and a local background subtraction as shown in Fig. 1(b). Using the scattering angle and the full width half maximum (FWHM) of the peak, the unit cell c-axis and the apparent crystallite size parallel to the crystallographic c-axis (ACS_c) can be calculated through Bragg’s law³⁹ and the Scherrer equation,^40,41 respectively. As systematic peak broadening was not taken into account, the ACS_c presented is a lower bound for the crystallite size. Maps of the unit cell c-axis and the ACS_c are shown for all samples in Fig. S2 and S3† respectively.

Crystallite orientation analysis

The raw data was integrated into both 1 (Fig. 1(b)) and 180 azimuthal bins for analysis of crystallite parameters and orientation respectively. The process of finding the orientation is shown in Fig. 2. A raw detector frame and the azimuthally resolved integration are shown in Fig. 2(a) and (b) respectively. The azimuthally resolved (002) peak was extracted from the dataset with 180 azimuthal bins. The (002) peak was then analysed using angular Gaussian fits,^18,37 as seen in Fig. 2(c), to extract the degree of orientation (DoO) and the FWHM of the oriented fraction of the crystallites, or the orientation distribution function FWHM (ODF FWHM). In the 002 orientation maps, the hue represents the crystallite 002 orientation, in the lab frame, the saturation shows the DoO, and the value shows the total intensity in the point, as seen in Fig. 3(a). Orientation maps for all samples are shown in Fig. S4.†

Fig. 2 Orientation analysis. Raw detector frame (a). Azimuthally resolved detector frame after integration. The red box indicates the (002) peak, which shows the c-axis orientation of the apatite crystallites (b). Local background subtracted (002) orientation signal. The dots show the data, line shows fit. The position of the peak gives the orientation, the ratio I_oriented/(I_oriented + I_random) gives the DoO and the total signal is the sum of the red and blue areas (c).

Fig. 3 Scan of the frontal section of full femoral bone. (002) Orientation map, showing hue: orientation, saturation: degree of orientation, and value: total signal, based on the hydroxyapatite (002) peak (a). XRF data showing red: Ca, green: Sr, blue: Zn (b). Unit cell c-axis shown from 6.875 Å to 6.890 Å on the colour scale shown on the bottom of the figure (c). Segmentation of the bone with yellow: trabecular bone in the shaft (Tb), blue: cortical bone in the shaft (Ct), green: femoral head (Fh), and red: condyle (Cn) (d).

Statistical analysis

Each bone was segmented into the regions including trabecular bone in the shaft (Tb), cortical bone in the shaft (Ct), femoral head (Fh), condyle (Cn). In very few cases, the frontal sections included cortical bone instead of the marrow cavity visible in Fig. 3. This cortical bone is viewed from a different orientation compared to the Ct visible in Fig. 3, and hence different crystallites can be probed in this section, due to the scattering criterion (q = k_f − k_i). Thus, the parameters measured in this cortical bone might differ from the parameters measured in the Ct marked in Fig. 3. This cortical bone is only visible in a few samples, and thus this region has been segmented out, and is not used in the statistical analysis. Suitable regions of all four bone regions are still found in such samples, and hence these regions are still used. After the segmentation the mean of a parameter of interest was taken for all points in that region of the bone. The tested parameters were DoO, ODF FWHM, c-axis, ACS_c, Ca K, Sr K, and Zn K. These parameters are neither normally nor log-normally distributed, Kruskal–Wallis⁴² was hence used pairwise to test the H₀ hypothesis that the parameters from different regions of bone have the same value (rejection of the H₀ hypothesis with *p ≤ 0.05 and **p ≤ 0.01). As each bone is scanned in full, all sections are present for all bones, which results in N = 16 for all four bone regions. To check which regions of bone had the smaller or larger value for a parameter, Vargha–Delaney A effect size⁴³ (VDa) was used. Note that due to the nonparametric nature of both the VDa and the Kruskal–Wallis, they can produce identical results for different datasets. This is an inherent feature of using ranking to compute the statistic values.

Results

Analysis of the measured data resulted in maps of various parameters, as shown in Fig. 3. All maps of all samples are shown in the ESI.† An example map of the 002 orientation is shown in Fig. 3(a), it is seen that the major 002 orientation of the HAp is along the long axis of the bone. This is as expected based on other studies of bone structure.⁴⁴ It is also clear that the DoO and total intensity seem smaller in the Cn and Fh compared to the Ct, the Tb are not visible. This is due to them having a small intensity, as they are thinner than the full sample, the trabeculae naturally have a smaller scattering volume.

The XRF data show that all three elements are present throughout the samples, although the Sr is concentrated in the Ct in the present sample, as seen in Fig. 3(b). The computed unit cell c-axis varies throughout the sample, but stays within a narrow band, across all samples, the standard deviation of the unit cell c-axis is 0.04 Å. This variation is expected,^45,46 as the c-axis of HAp in bone is known to be ∼6.88 Å. The fluctuations in the unit cell value arise mainly from the variations in composition of the bone.^9,47,48 However, near the edge of the samples the uncertainty increases, making exact determination of the unit cell c-axis difficult.

This can be seen clearly in Fig. 3(c), as the edges are too bright to fit within the colour scale. For this reason, the edge is not included in further statistical analysis of the unit cell c-axis and the ACS_c parameters. An example of the segmentation is shown in Fig. 3(d). Segmentation maps for all samples are shown in Fig. S5.†

Discussion

Fluorescence data

Statistical comparisons of the XRF signals are done using Kruskal–Wallis tests, these comparisons of the different XRF signals are shown in Fig. 4. XRF data for all regions of the bones have been compared based on the segmentations shown in Fig. 3(d). However, it is worthwhile to note that the Tb is much thinner than the other regions, as Tb are typically thinner than the sample thickness of 150–200 μm. This leads to the Tb having a smaller effective cross section compared to other bone regions. This effect is smallest for the Ca signal, due to the escape depth of Ca in bone of ∼23 μm.⁴⁹ While the effect is smaller for the Ca signal compared to other signals, it is still present, leading to a lowered absorption cross section. This variance in thickness between the Tb and other bone regions, mean that Tb have a significantly smaller XRF signal when compared to the other regions of bone for all elements measured, as the thicker bone regions effectively have a larger absorption cross section. This difference in absorption cross section leads to Tb being statistically significantly lower for all elements, however, it does not affect the relationship of the other regions. While the difference between Tb and the other bone regions are thus expected, the p values are provided for completeness.

Fig. 4 Statistics analysis of XRF data. Ca (a). Sr (B). And Zn (c) a solid line shows a significance level *(p < 0.05) whereas a dashed line shows a difference of significance level **(p < 0.01). Black dots show outliers.

For Ca: Tb vs. Ct **(p = 1.4 × 10⁻⁶), VDa = 0; Tb vs. Fh **(p = 1.7 × 10⁻⁶), VDa = 3.9 × 10⁻³; Tb vs. Cn **(p = 3.0 × 10⁻⁶), VDa = 0.016; Ct vs. Cn *(p = 0.016), VDa = 0.75, shown in Fig. 4(a). No other significant differences. Beside the expected difference for the Tb, we also see a difference between Ct and Cn with Ct generally having a higher Ca content than Cn. This could indicate that the Ct is more mature in comparison to the Cn, and thus has a higher degree of mineralization, but the exact mechanism is outside the scope of the present work.

For Sr: Tb vs. Ct **(p = 1.4 × 10⁻⁶), VDa = 0; Tb vs. Fh **(p = 1.7 × 10⁻⁶), VDa = 3.9 × 10⁻³; Tb vs. Cn **(p = 1.7 × 10⁻⁶), VDa = 3.9 × 10⁻³; Ct vs. Fh **(p = 4.7 × 10⁻³), VDa = 0.79; Ct vs. Cn **(p = 1.0 × 10⁻⁴), VDa = 0.90; Fh vs. Cn *(p = 0.045), VDa = 0.71, shown in Fig. 4(b). With no other significant differences. Ct generally has more Sr than both the Fh and the Cn, this aligns with the intuitive impression one might have from Fig. 3(b). An explanation for this could likewise be that the Ct is more mature, but finding the exact mechanism of the variations is outside the scope of the present work.

For the Zn signal: Tb vs. Ct **(p = 6.1 × 10⁻⁶), VDa = 0.031; Tb vs. Fh **(p = 1.0 × 10⁻⁵), VDa = 0.043; Tb vs. Cn **(p = 2.0 × 10⁻⁶), VDa = 7.8 × 10⁻³; Ct vs. Cn **(p = 5.3 × 10⁻³), VDa = 0.21; Fh vs. Cn *(p = 0.019), VDa = 0.26; shown in Fig. 4(c). Note here, as mentioned in the methods section, that due to the nonparametric nature of both the Kruskal–Wallis test,⁴² and the VDa parameter⁴³ along with their use of ranks for computing their statistical values, these parameters can be the same for different datasets, so long as the datasets have the same sorting order. Hence why the p-value and VDa are identical for Tb vs. Ct and Tb vs. Fh for the Zn comparison. This analysis shows that the Zn level is statistically higher in the Cn compared to the other regions. Zn is known as a growth indicator in bone.⁵ This indicates an increased bone growth activity in the Cn compared to other regions of the bone. This combines with the observed differences in the Sr and Ca levels to show that the Cn is less mature than the other regions of bone, while the Ct is possibly the most mature bone.

As expected, we see that the Tb have a significantly lower amount of all the elements studied here, most likely due to the smaller effective absorption cross section. Between the other regions of the bone, we see a clear difference between Ct and Cn for Ca, Ct and both Fh and Cn for Sr, and Cn and both Ct and Fh for Zn. Possibly indicating a difference in bone maturity between the different regions. This could be important for the effect of e.g. implants, and thus it shows the importance of studying either all regions or ensuring that the region of study is similar to the region of relevance, when studying the effect of e.g. coated implants^49–51 or structural effects of different animal models.^23,52 The composition is dependent on the location that is studied and hence could influence the response.

Diffraction data

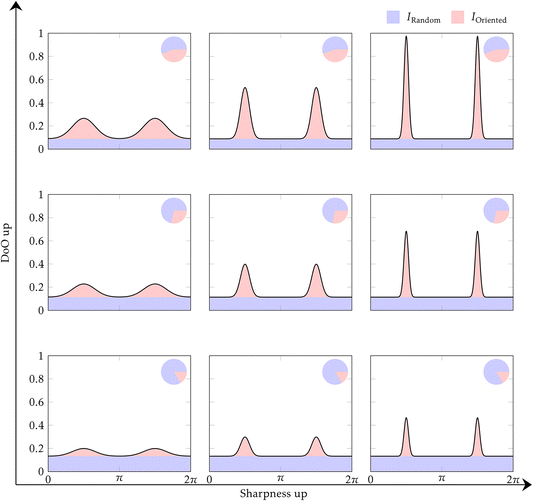
Statistical analysis was carried out in the same fashion for the parameters obtained from the XRD measurements. For the orientation of the 002 HAp peak there are two parameters of interest: the DoO is the fraction of crystallites that are oriented compared to the total amount of crystallites in the sample.^14,37,53 The DoO shows which part of the crystallites are oriented, as shown in Fig. 2(c). Thus, the DoO is a useful measure to understand the amount of texture throughout the sample. However, it does not show the alignment of the crystallites in the oriented fraction of crystallites. The effect of the DoO on the orientation distribution is shown by going up and down in Fig. 5. The alignment of the crystals stays constant, but the DoO increases from bottom to top in the figure. For that we must utilize the sharpness of the orientation distribution. This is done by the ODF FWHM parameter. This parameter shows how uniformly the oriented fractions of the crystallites are distributed across the circle. The effect of the ODF FWHM on the orientation distribution is shown by going left–right in Fig. 5. The DoO does not change, but the FWHM decreases going left to right. Using a combination of these two measures it is thus possible to study both the size of the oriented fraction of crystallites, and how well aligned the crystallites in these oriented fractions are. A smaller ODF FWHM leads to a larger alignment.

Fig. 5 Effect of Degree of Orientation (DoO) and ODF FWHM (shown as sharpness) on the orientation distribution. Going up and down on the figure changes the DoO but not the sharpness. Going left and right on the figure shows the changes in sharpness at a constant DoO. DoO is shown in every figure in the small circle. Red area is oriented. Blue area is randomly oriented.

Unlike the XRF data, where the relative thickness of the Tb compared to the other bone regions meant that the comparison does not hold much information, the thickness does not impact the crystallographic parameters to the same degree, as the measurements utilized here are geometrical in nature, and the difference in resolution from the different thicknesses are not problematic for the present experiment.⁵⁴

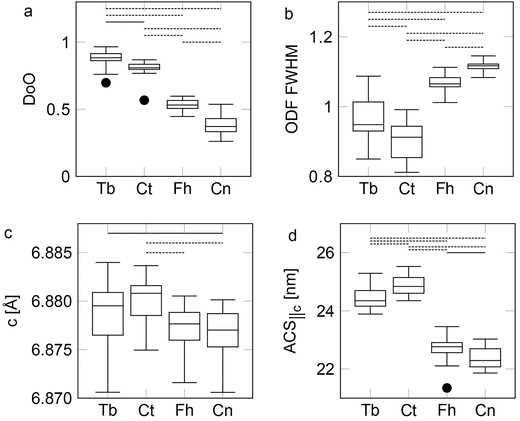
For the DoO: Tb vs. Ct *(p = 2.3 × 10⁻³), VDa = 0.82; Tb vs. Fh **(p = 1.4 × 10⁻⁶), VDa = 1; Tb vs. Cn **(p = 1.4 × 10⁻⁶), VDa = 1; Ct vs. Fh **(p = 3.0 × 10⁻⁶), VDa = 0.98; Ct vs. Cn **(p = 1.4 × 10⁻⁶), VDa = 1; Fh vs. Cn **(p = 1.2 × 10⁻⁵), VDa = 0.95; shown in Fig. 6(a). Here we see that all groups differ significantly. Indicating that the degree of orientation is highly dependent on the region of the bone measured. From the VDa parameters, it is clear that the data can be bunched into two groups: the Tb and Ct are consistently more oriented than Fh and Cn.

Fig. 6 Statistics analysis of diffraction data. With the Degree of Orientation (DoO) mean (a). Orientation distribution function FWHM (b). Unit cell c-axis (c). Apparent crystallite size parallel to the c-axis (d). A solid line shows a significance level of *(p < 0.05) whereas a dashed line shows a significance level of **(p < 0.01). Black dots indicate outliers.

While the Fh is mostly more oriented than the Cn, there is some overlap between the distributions, in the same manner there is an overlap between the distributions of Tb and Ct. As the long bone needs to carry the full load, and the other regions need to transfer it in different directions, there could be a difference in mechanical load direction, and hence a different need for DoO in the different sections. Sectioning the bone from other directions might show a larger DoO in the Fh and Cn, as we are only probing the crystallites not parallel to the beam. Finding the underlying mechanism for the variation in DoO across the different regions is outside the scope of the present work.

For the ODF FWHM: Tb vs. Ct *(p = 0.010), VDa = 0.77; Tb vs. Fh **(p = 4.0 × 10⁻⁵), VDa = 0.13; Tb vs. Cn **(p = 1.7 × 10⁻⁶), VDa = 3.9 × 10⁻³; Ct vs. Fh **(p = 1.4 × 10⁻⁶), VDa = 0; Ct vs. Cn **(p = 1.4 × 10⁻⁶), VDa = 0; Fh vs. Cn **(p = 1.5 × 10⁻⁵), VDa = 0.051; shown in Fig. 6(b). The ODF FWHM shows that the highly oriented regions in the bone are also the regions with a more aligned crystallite population, that is to say: the oriented fractions of crystallites in Ct and Tb are more co-aligned than the oriented fractions of crystallites in the Fh and Cn. However, the VDa between Tb and Ct shows that the Ct has a smaller ODF FWHM, this is in contrast to the DoO where the Tb was larger. Showing that the Ct, while having more randomly oriented crystallites, has a more uniform orientation for the oriented fraction of the crystallites. If the Tb is in the top middle in Fig. 5, Ct would be in the right middle.

For the unit cell c-axis: Tb vs. Cn *(p = 0.046), VDa = 0.71; Ct vs. Fh **(p = 2.3 × 10⁻³), VDa = 0.82; Ct vs. Cn **(p = 8.0 × 10⁻⁴), VDa = 0.85; shown in Fig. 6(c). The unit cell c-axis is mostly similar for all bone regions. The Tb has a larger unit cell than Cn. The Ct does have a larger unit cell compared to the Fh and Cn. One explanation for the observed difference could be when the bone was grown, as slight variations in the animal diet could change the unit cell, due to inclusions of different trace elements.^47,48 From the XRF data, we know that the Ct has the highest level of Sr. Inclusions of Sr in the HAp lattice should increase the unit cell c-axis.^55–57 Hence the elevated unit cell c-axis, and the elevated Sr level, indicate that the unit cell is substituting for Ca in HAp rather than being present outside the mineral.

For the ACS_c: Tb vs. Ct **(p = 5.9 × 10⁻³), VDa = 0.21; Tb vs. Fh **(p = 1.4 × 10⁻⁶), VDa = 1; Tb vs. Cn **(p = 1.4 × 10⁻⁶), VDa = 1; Ct vs. Fh **(p = 1.4 × 10⁻⁶), VDa = 1; Ct vs. Cn **(p = 1.4 × 10⁻⁶), VDa = 1; Fh vs. Cn *(p = 0.022), VDa = 0.74; shown in Fig. 6(d). Again, there is a clear difference between the Tb and Ct in comparison to the Fh and Cn. While both groups are internally significantly different, with Tb having generally shorter crystallites compared to the Ct, and the Cn generally having smaller crystallites than the Fh, there is no overlap between the ACS_c for Tb and Ct together and Fh and Cn. By comparing the ODF FWHM and ACS_c (Fig. 6(b and d)), it seems that the more well aligned crystallites correlate with longer crystallites. However, this could also in part be due to the difference in elemental composition across the different regions of bone, as it has previously been shown that an increased Sr content can increase the crystallite size.¹⁹

Both the XRF and XRD data show a large variance in structural and compositional parameters across the different regions in the bone. Bone mineral properties are of high importance for the mechanical properties of the bone; hence it is important to understand the effect of animal models, treatments, and diseases of bone structure. If a disease has a large effect on the orientation of the crystallites, it could change the mechanical strength of the bone, understanding the underlying cause could lead to potential treatments. It has been shown that knocking out osteocalcin influences the orientation of the HAp crystallites.^22,23 If a model or treatment shows such an effect, it can decrease the stability of the bone. Typically bone mineral density is used as a measure for the strength of bone. However, if a treatment loses the bone strength while the mineral density is kept constant, this can be difficult to discover. As the parameters vary across the bone, it is important to scan across the full bones to capture the full variation. Hence this study shows the importance of being aware of the regions when designing studies utilizing either μXRF or μXRD. Taking the regions into account can be achieved in different ways: ensure that the regions of interest scanned are spread across different regions or represent fully the question of interest. Or ensure that all regions in the bone are tested when doing experiments. With modern 4th generation light sources, such as MAX IV²⁰ or the ESRF EBS,²¹ it is now possible to carry out these experiments over a much larger area, and thus to do statistical analysis on scans on full bones e.g. at the DanMAX beamline at MAX IV, as shown here. Beamtime at synchrotrons is still a limited resource for researchers, as proposals need to go through an acceptance committee and as the resolution is increased the time needed to scan the same area increases rapidly. Thus, being aware of the regions of interest in the bone for higher resolution scans will continue to be important. While faster scanning could be done if the orientation is not of interest there is still a limit to how fast large regions can be scanned. Hence this increase in scan speed cannot fully overcome much higher resolutions. As new detector technologies continue to be developed, scan speeds will continue to increase, allowing for a further increase in the scope of studies utilizing μXRD and μXRF, pushing both the field of view and the resolution to resolve smaller features within larger samples.

Conclusions

Traditional μXRF and μXRD experiments are often limited in scope to either a single sample, or small regions of interest across many samples, due to the long scan times inherent to these methods and to the inherently limited experimental time at facilities for these experiments. Utilizing the brilliance of the DanMAX beamline at the MAX IV synchrotron, we have shown that it is possible to scan more than 10 cm² of samples with a 15 μm resolution, within the time allocated through the normal proposal process. By scanning such large areas with such a high resolution, it is possible to draw spatially resolved statistical conclusions by scanning multiple samples fully rather than only individual regions.

By segmenting the resulting scans into different regions in the bone, we show structural parameters and composition vary in the different regions. We show that there is a higher Sr and Ca content in the cortical bone compared to the femoral head and condyle. We further show that the unit cell c-axis is larger in the cortical bone, indicating that Sr is substituting into the unit cell. We also see a larger Zn content in the condyle compared to other regions. These variations in composition could indicate that there is a different level of maturity in the different regions. We show that there is a higher DoO in the trabecular and cortical bone in the shaft compared to other regions, and that the crystallite size is generally larger in the more heavily oriented regions. This difference between regions of otherwise the same material underlines the importance of measuring the full scope to understand the full structure. In particular when studying the effects on bone structure from external factors, such as implants or when utilizing different animal models.

Data availability

The data is available at: https://doi.org/10.48391/d7dcf27a-5f2f-4dad-b8f2-d7a54c105815. This is a dataset with XRF and XRD scanning of 16 healthy mouse bones.

Author contributions

TM and TK raised and sacrificed the mice. TM prepared the samples. TEKC scanned the samples. TEKC analysed the data. TEKC wrote the first draft. TEKC, TM, and TK reviewed and edited the article. Conceptualization: TEKC. Methodology: TEKC, TM, and TK. Software: TEKC. Investigation: TEKC, TM, and TK. Writing – original draft: TEKC. Writing – review & editing: TEKC, TM, and TK. Visualization: TEKC. Funding acquisition: TEKC and TK.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the MAX IV Laboratory for beamtime on the DanMAX beamline under proposal 20231616. Research conducted at MAX IV, a Swedish national facility is supported by Vetenskabsrådet (Swedish Research Council, VR) under contract 2018-07152, Vinnova (Swedish Governmental Agency for Innovation Systems) under contract 2018-04969 and Formas under contract 2019-02496. DanMAX is funded by the NUFI grant no. 4059-00009B. The XRF detector was made available by Aarhus University through grant CF18-0802 from the Carlsberg Foundation. We acknowledge support from the ESS lighthouse on hard materials in 3D, SOLID, funded by the Danish Agency for Science and Higher Education, grant number 8144-00002B. This research was funded by grants from the Japanese Ministry of Education, Culture, Sports, Science and Technology to TM (grant number: 23K09120) and TK (23H00440).

Notes and references

1. N. Reznikov, M. Bilton, L. Lari, M. M. Stevens and R. Kröger, Science, 2018, 360, eaao2189.
2. D. J. Buss, N. Reznikov and M. D. McKee, J. Struct. Biol., 2020, 212, 107603.
3. D. J. Buss, R. Kröger, M. D. McKee and N. Reznikov, J. Struct. Biol.:X, 2022, 6, 100057.
4. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69.
5. H. Dejea, D. B. Raina, I. Silva Barreto, K. Sharma, Y. Liu, D. Ferreira Sanchez, U. Johansson and H. Isaksson, Acta Biomater., 2023, 167, 135–146.
6. B. Pemmer, A. Roschger, A. Wastl, J. G. Hofstaetter, P. Wobrauschek, R. Simon, H. W. Thaler, P. Roschger, K. Klaushofer and C. Streli, Bone, 2013, 57, 184–193.
7. T. Swanston, T. L. Varney, M. Kozachuk, S. Choudhury, B. Bewer, I. Coulthard, A. Keenleyside, A. Nelson, R. R. Martin, D. R. Stenton and D. M. L. Cooper, PLoS One, 2018, 13, e0202983.
8. N. Peruzzi, S. Galli, H. Helmholz, N. Kardjilov, D. Krüger, H. Markötter, J. Moosmann, D. Orlov, Z. Prgomet, R. Willumeit-Römer, A. Wennerberg and M. Bech, Acta Biomater., 2021, 136, 582–591.
9. N. K. Wittig, J. Palle, M. Østergaard, S. Frølich, M. E. Birkbak, K. M. Spiers, J. Garrevoet and H. Birkedal, ACS Nano, 2019, 12, 34.
10. B. Zeller-Plumhoff, C. Malich, D. Krüger, G. Campbell, B. Wiese, S. Galli, A. Wennerberg, R. Willumeit-Römer and D. C. F. Wieland, Acta Biomater., 2020, 101, 637–645.
11. S. R. Stock, F. De Carlo and J. D. Almer, J. Struct. Biol., 2008, 161, 144–150.
12. E. S. Statnik, A. I. Salimon, C. Besnard, J. Chen, Z. Wang, T. Moxham, I. P. Dolbnya and A. M. Korsunsky, Quantum Beam Sci., 2020, 4, 29.
13. P. Fratzl, M. Groschner, G. Vogl, H. Plenk, J. Eschberger, N. Fratzl-Zelman, K. Koller and K. Klaushofer, J. Bone Miner. Res., 1992, 7, 329–334.
14. S. Rinnerthaler, P. Roschger, H. F. Jakob, A. Nader, K. Klaushofer and P. Fratzl, Calcif. Tissue Int., 1999, 64, 422–429.
15. M. Liebi, M. Georgiadis, J. Kohlbrecher, M. Holler, J. Raabe, I. Usov, A. Menzel, P. Schneider, O. Bunk and M. Guizar-Sicairos, Acta Crystallogr., Sect. A:Found. Adv., 2018, 74, 12–24.
16. T. A. Grünewald, M. Liebi, N. K. Wittig, A. Johannes, T. Sikjaer, L. Rejnmark, Z. Gao, M. Rosenthal, M. Guizar-Sicairos, H. Birkedal and M. Burghammer, Sci. Adv., 2020, 6, eaba4171.
17. J. Palle, N. K. Wittig, A. Kubec, S. Niese, M. Rosenthal, M. Burghammer, T. A. Grünewald and H. Birkedal, J. Struct. Biol., 2020, 212, 107631.
18. J. Q. I. Chua, T. E. K. Christensen, J. Palle, N. K. Wittig, T. A. Grünewald, J. Garrevoet, K. M. Spiers, H. Castillo-Michel, A. Schramm, W. L. Chien, R. M. Sobota, H. Birkedal and A. Miserez, Acta Biomater., 2023, 170, 479–495.
19. N. Schenz-Spisic, T. E. K. Christensen, J. Palle, M. Østergaard, M. Berglund, J. Hubner, H. Huber, I. Artioli, V. Offermanns, C. Chen, M. Foss, A. G. Crismani and H. Birkedal, Materialia, 2025, 102385.
20. N. Martensson and M. Eriksson, Nucl. Instrum. Methods Phys. Res., Sect. A, 2018, 907, 97–104.
21. P. Raimondi, Synchrotron Radiat. News, 2016, 29, 8–15.
22. T. Komori, J. Oral Biosci., 2020, 62, 223–227.
23. T. Moriishi, R. Ozasa, T. Ishimoto, T. Nakano, T. Hasegawa, T. Miyazaki, W. Liu, R. Fukuyama, Y. Wang, H. Komori, X. Qin, N. Amizuka and T. Komori, PLoS Genet., 2020, 16, e1008586.
24. K. Sauer, I. Zizak, J.-B. Forien, A. Rack, E. Scoppola and P. Zaslansky, Nat. Commun., 2022, 13, 7829.
25. M. M. Pendleton, S. R. Emerzian, J. Liu, S. Y. Tang, G. D. O'Connell, J. S. Alwood and T. M. Keaveny, Bone, 2019, 128, 115043.
26. A. C. Deymier-Black, J. D. Almer, S. R. Stock and D. C. Dunand, J. Mech. Behav. Biomed. Mater., 2012, 5, 71–81.
27. T. A. Grünewald, A. Johannes, N. K. Wittig, J. Palle, A. Rack, M. Burghammer and H. Birkedal, IUCrJ, 2023, 10, 189–198.
28. J. D. Currey, J. Biomech., 1979, 12, 313–319.
29. M. N. Aslam, K. J. Jepsen, B. Khoury, K. H. Graf and J. Varani, Bone Rep., 2016, 5, 141–149.
30. H. H. Mitchell, T. S. Hamilton, F. R. Steggerda and H. W. Bean, J. Biol. Chem., 1945, 158, 625–637.
31. J. D. Currey, J. Biomech., 1990, 23, 837–844.
32. D. T. Cromer and D. A. Liberman, Acta Crystallogr., Sect. A, 1981, 37, 267–268.
33. A. J. Bailey, D. N. Rhodes and C. W. Cater, Radiat. Res., 1964, 22, 606.
34. M. M. Pendleton, S. R. Emerzian, J. Liu, S. Y. Tang, G. D. O'Connell, J. S. Alwood and T. M. Keaveny, Bone, 2019, 128, 115043.
35. G. Ashiotis, A. Deschildre, Z. Nawaz, J. P. Wright, D. Karkoulis, F. E. Picca and J. Kieffer, J. Appl. Crystallogr., 2015, 48, 510–519.
36. A. P. Hammersley, J. Appl. Crystallogr., 2016, 49, 646–652.
37. A. B. Jensen, T. E. K. Christensen, C. Weninger and H. Birkedal, J. Synchrotron Radiat., 2022, 29, 1420–1428.
38. V. A. A. Solé, E. Papillon, M. Cotte, Ph. Walter and J. Susini, Spectrochim. Acta, Part B, 2007, 62, 63–68.
39. W. H. Bragg and W. L. Bragg, Proc. R. Soc. London, Ser. A, 1913, 88, 428–438.
40. P. Scherrer, in Kolloidchemie Ein Lehrbuch, Springer, Berlin Heidelberg, 1912, pp. 387–409.
41. A. L. Patterson, Phys. Rev., 1939, 56, 978–982.
42. W. H. Kruskal and W. A. Wallis, J. Am. Stat. Assoc., 1952, 47, 583–621.
43. A. Vargha and H. D. Delaney, J. Educ. Behav. Stat., 2000, 25, 101–136.
44. S. Weiner and H. D. Wagner, Annu. Rev. Mater. Sci., 1998, 28, 271–298.
45. A. S. Posner, A. Perloff and A. F. Diorio, Acta Crystallogr., 1958, 11, 308–309.
46. M. I. Kay, R. A. Young and A. S. Posner, Nature, 1964, 204, 1050–1052.
47. J. M. Hughes, M. Cameron and K. D. Crowley, Am. Mineral., 1989, 74, 870–876.
48. C. A. Beevers and D. B. McIntyre, Mineral. Mag. J. Mineral Soc., 1946, 27, 254–257.
49. T. E. K. Christensen, M. Berglund Davidsen, S. Van Malderen, J. Garrevoet, V. Offermanns, O. Z. Andersen, M. Foss and H. Birkedal, ACS Biomater. Sci. Eng., 2022, 8, 620–625.
50. V. Offermanns, O. Z. Andersen, M. Sillassen, K. P. Almtoft, I. H. Andersen, F. Kloss and M. Foss, Int. J. Nanomed., 2018, 13, 2189–2197.
51. V. Tsakiris, C. Tardei and F. M. Clicinschi, J. Magnesium Alloys, 2021, 9, 1884–1905.
52. B. Hoac, M. Østergaard, N. K. Wittig, T. Boukpessi, D. J. Buss, C. Chaussain, H. Birkedal, M. Murshed and M. D. McKee, J. Bone Miner. Res., 2020, 35, 2032–2048.
53. P. Fratzl, H. F. Jakob, S. Rinnerthaler, P. Roschger and K. Klaushofer, J. Appl. Crystallogr., 1997, 30, 765–769.
54. D. Chernyshov, V. Dyadkin, H. Emerich, G. Valkovskiy, C. J. McMonagle and W. van Beek, Acta Crystallogr., Sect. A:Found. Adv., 2021, 77, 497–505.
55. T. Nagyné-Kovács, L. Studnicka, A. Kincses, G. Spengler, M. Molnár, M. Tolner, I. E. Lukács, I. M. Szilágyi and G. Pokol, Ceram. Int., 2018, 44, 22976–22982.
56. F. Baldassarre, A. Altomare, E. Mesto, M. Lacalamita, B. Dida, A. Mele, E. M. Bauer, M. Puzone, E. Tempesta, D. Capelli, D. Siliqi and F. Capitelli, Crystals, 2023, 13, 117.
57. A. Rodriguez-Palomo, P. A. S. Vibe, M. R. V. Jørgensen and H. Birkedal, Faraday Discuss., 2025 10.1039/D5FD00030K.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5fd00009b

---