Solution-phase synthesis of graphene nanoribbons: a review on polymerization strategies

Abstract

A promising approach to opening the band gap of intrinsic graphene is through the synthesis of graphene nanoribbons (GNRs)—quasi-one-dimensional (1D) cutouts of the graphene sheet whose electronic and physical properties are governed by edge structure, chemical modifications, and backbone doping or pore integration. GNRs can be synthesized using both top-down and bottom-up approaches, with solution-phase synthesis emerging as a particularly attractive bottom-up method due to its advantages in diverse edge functionalization, possibilities in gram-scale production and characterization using various spectroscopy techniques, as well as exploration in practical applications. Solution-phase synthesis of GNRs typically involves a polymerization step followed by cyclodehydrogenation to form the final structure. This review provides an overview of the different polymerization strategies employed in GNRs solution-phase synthesis, highlighting their recent advancements and unique advantages. The Diels–Alder reaction enables the synthesis of GNRs with considerable lengths (up to 600 nm) and tunable edge functionalization. Suzuki polymerization facilitates the creation of porous GNRs while preserving heterostructures for post-synthetic modifications, whereas Yamamoto polymerization allows for the efficient production of laterally extended GNRs with varying bandgaps. Additionally, we discuss alternative cyclodehydrogenation methods, including photochemical approaches, for transforming polymer precursors into GNRs. By consolidating recent progress in solution-phase polymerization techniques, this review aims to provide valuable insights for the development of next-generation GNRs with tailored properties for electronic and optoelectronic applications.

---

Kaysa Sekhavati

Mr Kaysa Sekhavati is currently a doctoral researcher in the Keerthi research group, Department of Chemistry at the University of Manchester, UK. He received his BSc from the University of Nottingham, UK, where he graduated top of his cohort. His third-year research concerned variations in oxidative addition/transmetalation in the Suzuki coupling reactions. His current research focuses on the synthesis of spin functionalized and chiral nanographenes/graphene nanoribbons.

Vikas Sharma

Dr Vikas Sharma is a postdoctoral research associate in the Keerthi research group, Department of Chemistry at The University of Manchester, UK, since 2021. He received his PhD from the Indian Institute of Science Education and Research Bhopal, India. His PhD thesis research is focused on rylene imide derivatives and their applications in organic electronics as white-light emitters and sensors. After a brief postdoctoral position at the University of Calgary, Dr. Sharma joined the Keerthi group at the University of Manchester. His current research focuses on the synthesis of graphene nanoribbons and helical polymers for advanced nanoelectronics applications.

Ashok Keerthi

Dr Ashok Keerthi is a Presidential Academic Fellow in the Department of Chemistry at the University of Manchester, UK. He received his PhD from the National University of Singapore in 2014. Subsequently, he took postdoctoral positions at the Max-Planck Institute for Polymer Research in Mainz, Germany, and at The University of Manchester in the United Kingdom. In addition, he was awarded the esteemed Ramsay Memorial Fellowship in 2019, which facilitated him to start his independent research group in the Department of Chemistry at Manchester and explore properties of Angstrom-scale architectures of 2D materials and graphene. The Keerthi group is currently working on the synthetic engineering of molecular architectures, including chiral nanographenes, one-dimensional graphene nanoribbons, and two-dimensional framework materials via bottom-up synthesis.

---

1. Introduction

Carbon, the sixth most abundant element in the universe, which comprises approximately 18% of human body weight, is remarkably versatile, existing in various allotropes such as diamond, graphite, graphene, carbon nanotubes, and fullerenes (Fig. 1).¹ In graphene, each carbon atom forms three Sigma (σ) bonds, with the fourth electron contributing to a delocalized network of pi (π) bonds. These π bonds arise from the overlap of perpendicular p-orbitals, creating a continuous electron cloud across the graphene sheet. This delocalized π system is responsible for graphene's exceptional electrical conductivity, high charge carrier mobility, and optical transparency.^2,3

Fig. 1 Schematic representation of some carbon-based allotropes.

Graphene had been theoretically studied for over sixty years before its first isolation by Geim and Novoselov in 2004, via micromechanical cleavage⁴ which has since opened possibilities in fundamental and applied research, notably spintronic and electronic applications.⁵ However, owing to the intrinsic zero bandgap behaviour of graphene originating from the convergence of the Dirac cones at one point, graphene for semiconducting purposes poses a challenge. The solutions to open a bandgap in graphene span from dopant adsorption⁶ to applying external electric fields⁷ however to form reproducible structures with tuned bandgaps the structures and geometries of these graphene materials must be precisely engineered.⁸

Carbon-based nanostructures come in many forms yet share a similar quality which opens bandgaps compared to that of 2D graphene, structural confinement. These come in the form of graphene quantum dots (GQDs) and graphene nanoribbons (GNRs). The properties of both are mainly governed by their size and edge configurations.⁹ GNRs show promising applications in the fields of spintronics, field-effect transistors (FETs), nanoelectronics and optoelectronics. They can be regarded as a quasi-one-dimensional cut-out of a graphene lattice.¹⁰ Depending on how the graphene lattice is cut, various edge structures and widths of these ribbons can be created (Fig. 2), each with distinctive properties depending on these qualities.⁹

Fig. 2 Different ways a graphene lattice can be cut producing (a) variety of edge features and (b) conventional numbering methods of different sized GNRs.

GNRs synthesis can be split into two types: top-down and bottom-up methods.¹⁰ Top-down methods include breaking down a graphene lattice to form the ribbon structure. These methods include nanofabrication,^11,12 sonochemical,¹³ nanowire lithography,^14,15 unzipping carbon nanotubes (CNTs)^16,17 and various controlled nanocutting/etching methods.^18–20 Bottom-up synthesis uses precise molecular precursors and builds them up into the desired GNRs. These methods consist of on-surface synthesis (OSS), where metallic substrates are used as a platform to aid the synthesis of GNRs usually under ultra-high vacuum (UHV) conditions and in-solution synthesis which uses organic molecular precursors and various cross-coupling/polymerization synthetic techniques to afford polymer precursors, followed by a cyclodehydrogenation step to ‘graphitize’ the polymer precursors.^10,21,22

While top-down methods of GNR synthesis have provided a variety of lengths and promising properties, such as high on–off ratios (up to 10⁶), applicable for FET devices.²³ Most GNRs prepared by top-down methods possess undefined edge structures and little control over changing the edge structures on an atomic scale.¹⁰ Bottom-up OSS of GNRs allows for conformation of theoretical predictions of GNRs by use of scanning probe techniques. However, a significant challenge in OSS of GNRs is the strong coupling between the GNRs and the metal substrate. Additionally, following synthesis, the GNRs remain adhered to the metal surface along with by products, making their removal and utilisation in devices challenging, thereby reducing practical application.^24–29 On the other hand, solution-phase synthesis of GNRs allows for gram-scalability and edge-functionalisation of GNRs opening doorways for unique electronic and magnetic properties.^10,30,31 In general, the route to solution-phase synthesis of GNRs follows two basic steps: (1) polymerization of rationally designed monomers and (2) planarization of the polymer precursors to afford the GNR (Fig. 3). The first step generally utilizes reactions such as Diels–Alder, Suzuki and Yamamoto polymerizations and the second step is an oxidative cyclodehydrogenation using oxidants such as FeCl₃, AlCl₃, DDQ/TfOH, Cu(OTf)₂ which ‘graphitizes’ the polymer.³²

Fig. 3 A generalized schematic of bottom-up solution-phase synthetic steps towards GNRs.

This review focuses on the bottom-up, solution-phase synthesis of GNRs, categorized by the polymerization techniques employed, discussed chronologically while highlighting recent advancements. By examining the various polymerization methods, this review aims to provide a comprehensive overview of how these reactions produce a diverse range of GNRs. It begins by discussing the structure and properties of GNRs, followed by an overview of synthesis approaches. The core of the review concerns the key polymerization reactions used in GNRs synthesis, concluding with a brief discussion of the Scholl reaction and its alternatives such as topochemical polymerizations and photochemical methods including cyclodehydrochlorination (CDHC).

2. Structure and properties of GNRs

As mentioned in the previous section, depending on how a graphene lattice is ‘cut’, GNRs with various edge geometries and widths can be created, each with distinct properties.⁹ Many edge geometries are possible for GNRs (Fig. 2). Zigzag and armchair GNRs (ZGNRs and AGNRs, respectively) were amongst the first theoretically studied edge geometries.

Fujita et al. first studied ZGNRs and AGNRs using the tight-binding approach and found that AGNRs show semi-conducting behavior and found a ‘peculiar’ flat band for ZGNRs. Upon applying the Hubbard-model within the mean field approximation, it was found that a band gap opening occurs in ZGNRs due to spin polarized electron–electron interactions.³³ Further theoretical investigations using more complex first-principle calculations have further confirmed these initial results^34,35 and built on them. For example, AGNRs can be split into three distinct families based on their width: semiconducting N = 3p, N = 3p + 1 and metallic N = 3p + 2 (where N refers to the width of the AGNR as defined in Fig. 2). ZGNRs spin polarization is predicted to be ferromagnetic along a given edge and antiferromagnetic across the width of the ribbon.³⁶

Both theoretical predictions have been either directly or indirectly confirmed via experimental investigations. G. Z. Magda et al. used OSS synthesis of a variety of AGNRs and ZGNRs and found an inverse proportionality between bandgap and width for AGNRs with good theoretical agreement on separation of AGNRs into their respective classes (Fig. 4a). The researchers indirectly confirmed the presence of edge magnetism in ZGNRs by assessing the electronic structure. It was concluded that only the presence of magnetic edges explains both the bandgap and observed semiconductor-to-metal transition (Fig. 4b), supporting the presence of room temperature stable magnetic order in precisely engineered zigzag edges.²⁴

Fig. 4 Bandgap measurements from tunnelling spectra: (a) AGNRs exhibit an inverse relationship between bandgap and ribbon width, consistent with theoretical classifications. (b) ZGNRs display band structures influenced by edge magnetism, showing a sharp semiconductor (antiferromagnetic) to metal (ferromagnetic) transition. Theoretical results use the Hubbard model within a mean-field approximation. Error bars reflect thermal broadening and substrate interactions.²⁴ Reproduced from ref. 24 with permission from [Springer], copyright [2014].

Aside from zigzag and armchair edges, other edge geometries also exist with their own distinct properties. Notably, cove and fjord edge GNRs are of particular interest due to their curved conformations leading to helically twisted ribbons.^37,38 These properties prove ideal as reduced π–π stacking interactions of these curved GNRs lead to increased dispersibility in organic solvents thereby leading to highly liquid processable GNRs allowing more facile characterization by solid state nuclear magnetic resonance (ss-NMR), Fourier-transform Infrared spectroscopy (FT-IR), Raman spectroscopy, UV/vis spectroscopy and matrix assisted laser desorption/ionization time of flight mass spectrometry (MALDI-TOF MS).³⁹ The non-planarity arises from the steric repulsion between hydrogen atoms in the [4]-helicene and [5]-helicene precursor shapes.⁴⁰

Other factors affecting GNR properties include chemical modification. These range from backbone nitrogen doped or boronated GNRs^41–43 to edge functionalization such as chlorination.⁴⁴ The introduction of non-hexagonal rings⁴⁵ and nanopores⁴⁶ also proves an effective way to engineer properties. Above all, presence of multi-edge systems giving rise to chiral GNRs^{37,38,47–51} are amongst the most effective way to produce GNRs with unique properties, as will be discussed vastly in this review.

3. Bottom-up solution-phase synthesis of GNRs

3.1. Polymerization methods

3.1.1. A₂B₂ Diels–Alder polymerization. Amongst the first reactions utilized to afford the polymer precursors for planarization of GNRs was the A₂B₂ Diels–Alder reaction. In 2000, Shifrina et al. investigated the Diels–Alder reaction between 1,4-bis(2,4,5-triphenylcyclopentadienone-3-yl) benzene (1.0) and 1,4-diethynylbenzene (1.1) (Scheme 1) using different concentrations of the monomeric building block and different reaction times.

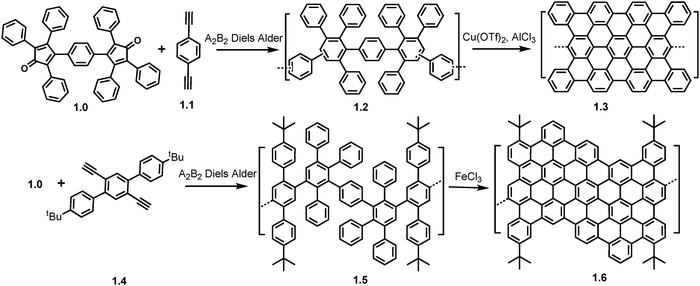Scheme 1 Synthetic routes towards GNRs 1.3 and 1.6 using A₂B₂ Diels–Alder polymerization. Reproduced from ref. 52 with permission from [ACS], copyright [2000] Reproduced from ref. 53 with permission from [ACS], copyright [2003].

Regioisomeric branched polyphenylenes (1.2) with M_W in the range of 12–120 kg mol⁻¹ were obtained and subjected to cyclodehydrogenation reactions using copper(II) trifluoromethanesulfonate and AlCl₃ producing a dark brown product (1.3) which was studied by FT-IR and Raman spectroscopy as NMR analysis was not possible due to the products insolubility in standard solvents.⁵² Later in 2003, the same group replaced the bisdienophile from 1,4-diethynylbenzene (1.1) to 1,4-diethynyl-2,5-di(4′-tert-butylphenyl) benzene (1.4) (Scheme 1). The polymer precursor (1.5) (M_W ∼ 62.5 kg mol⁻¹, polydispersity index (PDI) ∼ 2.5) from this A₂B₂ Diels–Alder reaction was subjected to cyclodehydrogenation by FeCl₃ affording an AGNR (1.6) with kinked structure which as well as the previous spectroscopic techniques, also underwent UV/Vis spectroscopy to confirm its increased conjugation compared to the polymer precursor.⁵³

Despite the use of the AB Diels–Alder reaction being the more popular choice in GNR synthesis due to its ability to afford long (>200 nm) gulf edged GNRs,⁵⁴ as will be mentioned later in this review. The A₂B₂ Diels–Alder reaction was recently used to synthesize and characterize multi-edged GNRs. In this 2022 paper,³⁸ Yang et al. successfully synthesized curved GNRs (cGNRs) with hybrid cove–armchair–gulf edge structures. To test the efficiency of the Scholl reaction, the synthesis of model compounds 11,11′′-diethynyl-5,5′′-bichrysene (1.8) and 7-di-tert-butyl-9,11-bis(4-(tert-butyl) phenyl)-10H-cyclopenta[e]pyren-10-one (1.7) via Diels–Alder reactions yielded 1.9 in 80%. This was subsequently planarized using a Scholl reaction with FeCl₃. MALDI-TOF MS revealed a 50/50 mixture of products, a fully and partially cyclized 1.9. To improve cGNR yield and efficiency, a pre-fused approach was used (Scheme 2a). 2.1 was synthesized from 2.0 which had an integrated bichrysene unit and additional t-Bu groups for solubility. This underwent a complete cyclization under Scholl conditions at room temperature in 2 hours.

Scheme 2 (a) Synthesis of model compounds 1.9 and 2.1; (b) synthetic route toward cGNR (2.4) via A₂B₂ Diels–Alder polymerization. Reproduced from ref. 38 with permission from [Wiley], copyright [2022].

Finally, an A₂B₂ Diels–Alder reaction between 2.0 and 2.2 yielded precursor polymer 2.3 (M_W ∼ 108.3 kg mol⁻¹, PDI ∼ 1.9), which was planarized into cGNRs 2.4 averaging 71 nm in length (Scheme 2b). FTIR, Raman, and solid-state NMR characterized the product. UV/Vis spectroscopy showed an optical band gap of 1.61 eV, matching theoretical values, and terahertz spectroscopy revealed a charge carrier mobility above 2 cm² V⁻¹ s⁻¹, highlighting a potential for single-GNR nanoelectronics.

Using a similar model compound approach as well as assistance in rational design using density functional theory (DFT) calculations, Feng et al. in 2024⁴⁵ optimised the A₂B₂-type Diels–Alder polymerization between dibenzocyclooctadiyne (2.6) and dicyclopenta[e,l]pyrene-5,11-dione derivative (2.5). A subsequent selective Scholl reaction of the obtained ladder-type polymer (LTP) precursor 2.7 (M_W ∼ 30.4 kg mol⁻¹, PDI ∼ 1.15) produced wavy GNRs (wGNRs) 2.8 of lengths up to 30 nm which incorporate periodic eight-membered rings into its backbone (Scheme 3). Similarly to the cGNRs, the non-planar geometry of wGNR (2.8) efficiently prevents the inter-ribbon π–π aggregation, leading to photoluminescence in solution. Using these properties, the researchers fabricated the first GNR-based organic light-emitting electrochemical cells (GOLECs). The cells showed fast response and short turn on times of under 10 s. The current density–voltage–luminance characteristics a peak luminance of 120 cd m⁻² with high stability (Fig. 5).

Scheme 3 Synthesis of wGNRs (2.8) via A₂B₂ Diels–Alder reaction between 2.5 and 2.6. Reproduced from ref. 45 with permission from [Wiley], copyright [2024].

Fig. 5 GOLEC fabrication with 2.8 as emissive layer. (a) Schematic representation of the GOLECs; (b) current density and luminance against voltage for GOLECs with various weight fractions of 2.8; (c) EL spectra for GOLECs with 5 wt% and 10 wt% 2.8 and PL spectra of 2.8 in solution with THF as solvent; (d) luminance and voltage against time for GOLECs with 5 wt% 2.8 with a current density at 100 A m⁻².⁴⁵ Reproduced from ref. 45 with permission from [Wiley], copyright [2024].

3.1.2. A₂B₂ Suzuki polymerization. The A₂B₂ type Diels–Alder polymerization reaction provides a simple way to produce GNRs with unique multi-edge structures and innovative designs without the use of a metal catalyst.^38,45,52,53 However, the high temperature requirements for this method leave room for improvement.¹⁰ In 2008, Yang et al. developed an A₂B₂ Suzuki coupling reaction between the bis-boronic ester (2.9) with diiodobenzene derivative (3.0) at 120 °C which successfully produced the polyphenylenes (3.1) in 75% yield.⁵⁵ This reaction was amongst the most sterically hindered Suzuki couplings at the time. The polyphenylene 3.1 (M_W ∼ 13.9 kg mol⁻¹, PDI ∼ 1.2) was subjected to Scholl reaction conditions with FeCl₃ providing linear AGNRs (3.2) of lengths up to 12 nm (Scheme 4). The bulky 3,7-dimethyloctyl groups as sidechains increased the processability of AGNRs causing excellent dispersibility in common organic solvents. Both UV/vis absorption spectroscopy and MALDI-TOF MS studies revealed the formation of the AGNRs with an optical band gap of 2.2 eV revealed. Various microscopic studies of these novel structures showed a high tendency to self-assemble opening a gateway into the use of GNRs in FETs and optoelectronic devices.

Scheme 4 Synthesis of linear AGNRs (3.2) from Suzuki reaction between 2.9 and 3.0. Reproduced from ref. 55 with permission from [ACS], copyright [2008].

The high functional group tolerance of the Suzuki reaction,⁵⁶ allows for band gap engineering in GNRs synthesis by addition of heterostructures in the Suzuki precursors. In 2018, using a model study synthesis, Li et al. synthesized two unsymmetrical edged GNRs containing benzothiadiazole and benzotriazole groups.⁴⁹ The bispinacol borates (BPin) (3.3) were reacted with triaryl dibromide 3.4 under Suzuki coupling conditions using Pd(PtBu₃)₂/K₃PO₄ as the catalyst-base combination to form the desired polymer precursors 3.5 (Scheme 5a). Subsequently, precursor 3.5 of similar molecular weights (M_W ∼ 37.4 kg mol⁻¹, PDI ∼ 1.73) were cyclodehydrogenated using a 2,3-dichloro-5,6-dicyano-1,4-benzoquinone/triflic acid (DDQ/TfOH) protocol forming 3.6 (Scheme 5a). Once the AGNRs (3.6) were isolated as black powders, they were found to have good dispersibility in THF, chlorobenzene, and o-dichlorobenzene. Thus, allowing for characterization by FTIR, Raman, UV-Vis spectroscopy, X-ray photoelectron spectroscopy (XPS), MALDI-TOF MS, atomic force microscopy (AFM), and scanning tunnelling microscopy (STM). Narrow optical band gaps of 1.03 eV and 1.09 eV for 3.6 were extracted for the S and N-butyl functionalised AGNRs, respectively. Due to the survival of such heterostructures via the Suzuki reaction, post-functionalisation of 3.7 was possible via a directed C–H borylation using BCl₃ followed by ZnPh₂ producing 3.8 (Scheme 5b) with a further reduced optical band gap of 0.95 eV. These narrow band gaps achieved fall in a similar range of the band gap of intrinsic silicon (1.12 eV)⁵⁷ possibly opening up the use of GNRs as a future replacement. Further engineering of band gaps through post-functionalisation paves a way for precision band gap engineering in future synthesis.

Scheme 5 (a) Suzuki reaction to form polymers 3.5 then GNR 3.6 (b) directed C–H borylation of 3.7 to form engineered GNR 3.8. Reproduced from ref. 49 with permission from [Springer], copyright [2018].

In 2023, Niu et al. reported the first solution-phase synthesis of porous GNRs (pGNRs).⁴⁶ The chemical identity of pGNR was unambiguously verified by FT-IR, Raman and ss-NMR spectroscopies as well as supported by the successful synthesis of two model compounds. Using Pd(PPh₃)₄ as catalyst and K₂CO₃ as base the A₂B₂ Suzuki polymerization reaction between the dihalogen 4,4′′ -didodecyl-4′,5′-bis(4-dodecylphenyl)-3′,6′-diiodo-1,1′:2′,1′′ -terphenyl (3.9) and 4.0 furnished the poly-phenylene precursor (4.1) in 90% yield (M_W ∼ 33 kg mol⁻¹, PDI ∼ 1.32). Upon conformation of synthesis of 4.1 via MALDI-TOF MS, a subsequent Scholl reaction with FeCl₃ afforded pGNRs (4.2) (Scheme 6) with average lengths of 20 nm with periodic hexagonal pores in the backbone and a (carbon-to-carbon) diameter of 0.6 nm and adjacent-pores-distance of 1.7 nm. UV/Vis spectroscopy revealed an enlarged optical band gap of ∼2.0 eV, compared with the reported solution-synthesized GNRs with similar widths. Thus, this work provides another example of band-gap engineering via the tolerant Suzuki coupling reactions,⁵⁶ however unlike the reduced bandgap caused by heterostructures,⁴⁹ enlarged bandgaps are also possible.

Scheme 6 Synthesis of pGNR 4.2 from A₂B₂ Suzuki polymerisation of 3.9 and 4.0. Reproduced from ref. 46 with permission from [Wiley], copyright [2023].

The versatility of the Suzuki reaction allowed for Obermann et al. to introduce curvature into GNRs via the introduction of pyrene units leading to the first successful formation of pyrene GNRs (PyGNRs).⁴⁸ These PyGNRs were fully characterized by Raman, FT-IR, UV/Vis spectroscopy and STM. Following the successful synthesis of model compounds, the diborylated pyrene derivative (4.3) underwent an A₂B₂ type Suzuki reaction with the dihalogenated monomer (4.4) (with 3,7-dimethyloctyl chains to increase the processibility of the PyGNR) using Pd(PPh₃)₄/K₂CO₃ as the catalyst-base combination forming polymer precursor 4.5 (M_W ∼ 28.8 kg mol⁻¹, PDI ∼ 1.2). Subsequent Scholl treatment using FeCl₃ formed the PyGNR (4.6) (Scheme 7) with an average length of 35 nm. The accessible pyrene K-regions are open to post-functionalisation allowing further property engineering in the PyGNRs. The survival of these sp³ pyrene carbons in 4.5 aims to solve intrinsic solubility issues during GNR synthesis.

Scheme 7 Synthesis of PyGNRs (4.6) from pyrene integrated bis-boronic ester 4.3. Reproduced from ref. 48 with permission from [RSC], copyright [2023].

3.1.3. AB Suzuki polymerization. While the synthesis of cGNRs was made possible with the A₂B₂ Diels–Alder polymerization,³⁸ highly distorted edge structures such as fjord edge GNRs (fGNRs) can be synthesized by utilizing AB-type Suzuki polymerization reactions. Yao et al. conducted an efficient solution synthesis of fGNRs via an AB type Suzuki reaction.³⁷ Following reaction optimisations using model compounds, polymerization of 4.7 gave tert-butylphenyl-substituted poly(p-phenylene) precursor 4.8 (M_W ∼ 36 kg mol⁻¹, PDI ∼ 2.4). MALDI-TOF MS confirmed the formation of 4.8 therefore a subsequent Scholl reaction with FeCl₃ afforded the fGNR 4.9 (Scheme 8) as a dark red solid with an estimated length of 17 nm. The fGNR was characterized by FT-IR, Raman and UV/Vis spectroscopy. Twisted conformations of the model compounds were unambiguously confirmed via crystallographic studies suggesting a similar conformation for the fGNR supported also by DFT calculations. Photoconductivity analysis revealed an intrinsic charge carrier mobility of 100 cm² V⁻¹ s⁻¹, higher than values for other cGNRs³⁸ placing these highly distorted GNRs as a potential candidates for nanoelectronic devices.

Scheme 8 Synthesis of fjord edge GNRs (4.9) from the AB Suzuki polymerization and subsequent Scholl reaction of 4.7. Reproduced from ref. 37 with permission from [ACS], copyright [2021].

GNR heterojunctions combine the distinct topological features of the individual ribbons allowing for further electronic bandgap engineering. Zhang et al. reported a novel chain-growth polymerization strategy that allowed for formation of a GNR heterojunction with N = 9 (where N refers to the number of pairs of atoms per GNR unit cell) armchair and chevron GNRs segments (9-AGNR/cGNR).⁴⁷ The controlled Suzuki catalyst-transfer polymerization (SCTP) between 2-(6′-bromo-4,4′′-ditetradecyl-[1,1′:2′,1′′-terphenyl]-3′-yl) boronic ester (5.1) and 2-(7-bromo-9,12-diphenyl-10,11-bis(4-tetradecylphenyl)-triphenylene-2-yl) boronic ester (5.3), followed by the Scholl reaction of the obtained block copolymer (5.4) with controlled M_W of 26.1 kg mol⁻¹ (PDI ∼ 1.45), led to the formation of the 9-AGNR/cGNR (5.5) (Scheme 9) which was unambiguously validated by FT-IR, Raman, and UV/Vis spectroscopies and estimated to be 14 nm in length.

Scheme 9 Synthetic route toward 9-AGNR/cGNR (5.5) using subsequent SCTP of 5.1 and 5.3. Reproduced from ref. 47 with permission from [Wiley], copyright [2023].

Lee et al. also reported SCTP type reactions to synthesise AGNRs of a controlled length. 5.6 was subjected to optimised SCTP conditions using a RuPhos-Pd catalyst system giving polymer (5.7) in an excellent 85% yield (M_n ∼ 29.8 kg mol⁻¹, PDI ∼ 1.14–1.39). This alkyne containing precursor underwent mild alkyne benzannulation forming 5-AGNRs (5.8). Subsequently, Scholl conditions were applied to 5.8 using a DDQ/TfOH protocol to laterally extend the conjugated framework and form the 11-AGNR 5.9 (Scheme 10).⁵⁸ These innovative SCTP type reactions prove to be a useful method in controlling the length of GNRs and allow for milder conditions to be used such as alkyne benzannulation.

Scheme 10 Alkyne benzannulation of polymer precursor 5.7 to form 5-AGNR 5.8 and subsequently 11-AGNR 5.9. Reproduced from ref. 58 with permission from [ACS], copyright [2023].

3.1.4. AA Yamamoto polymerization. The A₂B₂ type Diels–Alder and Suzuki polymerization require two monomers for reactions to form GNRs making them stoichiometrically sensitive. This limits its ability to form consistent high weight polyphenylene precursors due to possible inefficient reactions.^59,60 On the other hand, the AA type Yamamoto coupling requires only one dihalogenated monomer thereby reducing this effect. The monomer can be of high molecular weight allowing for facile lateral extensions of GNRs as well of the incorporation of multiple edge structures within one monomer.

In 2012, Schwabz et al. produced monomer 6.0 through a multistep synthesis, enabling its AA Yamamoto polymerization using bis(cycloocta-(1,5)-diene) nickel (0) cycloocta-(1,5)-diene (Ni(COD)₂) to form polyphenylene precursor 6.1 (Scheme 11).⁶¹ Precursor 6.1 had a weight (M_W) of up to 52 kg mol⁻¹ (PDI ∼ 1.2) corresponding to 21–24 repeating units of 6.0 leading to GNRs of lengths up to 30 nm, which at the time was superior to the widely used A₂B₂ Suzuki polymerization. The subsequent Scholl reaction using FeCl₃ as an oxidant yielded the GNR (6.2). These GNRs were found to be soluble/dispersible in N-methyl-2-pyrrolidone (NMP) allowing for characterization by MALDI TOF, FT-IR and Raman spectroscopy. UV/Vis spectroscopy extracted a narrow optical band gap of 1.12 eV matching well with theoretical calculations of 1.09 eV. Due to the lateral extension of GNRs via the AA Yamamoto reaction, this led to high dispersibility allowing for facile liquid phase processing which offers benefits in characterization but also in device fabrication. M. El Gemayel et al. fabricated thin-film FET devices using a co-deposited GNR/poly(3-hexylthiophene) (P3HT) blend.⁶² The device showed a 24% increase in charge-carrier mobility compared to a pristine P3HT device. The on/off ratio remained robust upon addition of the GNR, and the photo response of the transistor was doubled compared to the pristine FET.

Scheme 11 Synthetic route toward GNR (6.2) via AA type Yamamoto polymerization of monomer 6.0. Spectroscopic studies on single GNRs were conducted by Huang et al. in 2018.²¹ Reproduced from ref. 61 with permission from [ACS], copyright [2012].

Monomer 6.3 substituted with N-n-hexadecyl maleimide units was subjected to AA Yamamoto conditions using Ni(COD)₂/COD yielding polymer precursors (6.4) (M_W ∼ 15.6–186 kg mol⁻¹, PDI ∼ 1.2–1.5). Intramolecular oxidative cyclodehydrogenation using FeCl₃ as the Lewis acid and oxidant, converted the polymer precursors into armchair edged GNR-AHMs (6.5) with uniform width (1.7 nm) and lengths of 6, 11, and 58 nm, respectively (Scheme 12). The bulky AHM side groups caused excellent dispersibility (concentrations of up to 5 mg mL⁻¹) in many organic solvents such as tetrahydrofuran (THF). Loss of extended tail in Near Infrared (NIR) region (compared to previously synthesised GNRs) during UV/Vis experiments confirm that dilute dispersions in THF (<0.1 mg mL⁻¹) consist mainly of nonaggregate ribbons (Fig. 6), exhibiting high fluorescence quantum yield (9.1%) and long fluorescence lifetime (8.7 ns). This dispersibility allows resolving the real-time ultrafast excited-state dynamics of the GNRs, which displays features of small, isolated molecules in solution. This successful synthesis and edge functionalisation using the AA Yamamoto coupling reduces the limitations of solution-based synthesis, allowing for improved characterization of individual GNRs, which is typically difficult compared to OSS methods.

Scheme 12 Synthetic route to GNR (6.5) via AA type Yamamoto polymerization of monomer 6.3. Reproduced from ref. 21 with permission from [ACS], copyright [2018].

Fig. 6 (a) Absorption and (b) PL spectra of GNR-AHMs (6.5) in THF (0.03 and 0.003 mg mL⁻¹ for absorption and PL measurements, respectively).²¹ Reproduced from ref. 21 with permission from [ACS], copyright [2018].

The AA type Yamamoto polymerization can be used to form multi-edge cGNRs much like the A₂B₂ Diels–Alder.³⁸ Niu et al. reported the first synthesis of a cGNR with cove, armchair and usually unstable, zigzag edges.⁵¹ This feature is of particular interest due to the survival of intrinsic zigzag properties in chiral GNRs.²⁸ Following the multi-step synthesis of monomer 6.6, AA type Yamamoto polymerization afforded 6.7 (M_W ∼ 20.8 kg mol⁻¹, PDI ∼ 1.15) which was subjected to Scholl reaction conditions using FeCl₃ producing the cGNR (6.8) (Scheme 13) with a narrow width of 0.7 nm and average length of 23 nm. Along with FT-IR, Raman MALDI-TOF MS, UV/Vis spectroscopy revealed a bandgap of 1.22 eV and incredibly, by THz photoconductivity analysis, a record high intrinsic charge carrier mobility of 600 cm² V⁻¹ s⁻¹ was calculated.

Scheme 13 Synthetic route toward multi-edged GNR 6.8 via AA type Yamamoto of monomer 6.6. Reproduced from ref. 38 with permission from [Wiley], copyright [2022].

Incorporation of periodic zig-zag segments was later executed by Wang et al. in 2021.⁵⁰ Following the synthesis of the structurally flexible S-shaped monomer 6.9, AA Yamamoto polymerization was carried out using Ni(COD)₂ as a catalyst, producing the ‘snakelike’ polymer precursor 7.0 (M_W ∼ 29.8 kg mol⁻¹, PDI ∼ 1.2). Upon ‘graphitization’ using FeCl₃ as Lewis acid and oxidant the multi-edged cGNR (7.1) was formed (Scheme 14) with an average length of 20 nm. The successful synthesis of the cGNR (7.1) was confirmed by FT-IR, Raman and ss-NMR investigations. UV/Vis spectroscopy revealed a narrow bandgap of 0.99 eV and THz photoconductivity analysis calculated a charge carrier mobility of 20 cm² V⁻¹ s⁻¹. Interestingly DFT simulations show an ‘up-down’ curved topology for the ribbon.

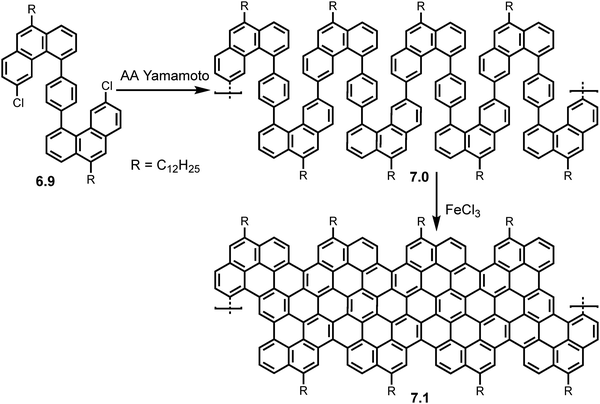Scheme 14 Synthetic route toward GNR 7.1 with periodic zigzag segments via AA type Yamamoto polymerization of monomer 6.9. Reproduced from ref. 50 with permission from [ACS], copyright [2022].

Recent theoretical studies into the use of porphyrin units in GNR backbones have been of interest due to their enhanced delocalization and spin ground states making them useful for molecular wires⁶³ or spintronic applications.⁶⁴ Efforts in OSS to functionalize GNRs with porphyrins has been successful with the intrinsic properties of the porphyrin remaining intact.⁶⁵ However, Chen et al. managed to successfully synthesize the first solution-made porphyrin-fused GNR (PGNR)⁶⁶ by utilizing the AA Yamamoto polymerization of 7.2 yielding 7.3 (M_W ∼ 132.7 kg mol⁻¹, PDI ∼ 2.46) in 93%, followed by an oxidative cyclodehydrogenation using a DDQ/TfOH protocol forming 7.4 (Scheme 15). The PGNRs (7.4) were characterized by ss-NMR, FT-IR, Raman and XPS. 7.4 functionalised with the dodecyl aryl group was found to exhibit a charge carrier mobility of >400 cm² V⁻¹ s⁻¹ via THz photoconductivity analysis, an optical bandgap of 1.0 eV was extracted from absorption spectra. The charge transport behaviour of 7.4 was investigated by fabricating single nanoribbon devices (Fig. 7) which showed FET behaviour at room temperature and clean single-electron-transistor behaviour at millikelvin temperatures. The non-differential conductance (NDC) regions showed a minimum voltage below 10 mV indicating low power operation possibilities.

Scheme 15 Synthesis of PGNR (7.4) from monomer 7.2 using AA type Yamamoto polymerization. Reproduced from ref. 66 with permission from [Springer], copyright [2024].

Fig. 7 Scheme of the electronic devices, where a single strand of PGNR (7.4) bridges two graphene electrodes (separated by a nanogap) connected to gold pads. A palladium gate is deposited on the SiO₂/Si surface and covered with a 10-nm-thick HfO₂ dielectric.⁶⁶ Reproduced from ref. 66 with permission from [Springer], copyright [2024].

3.1.5. AB type Diels–Alder polymerization. The synthesis of long GNRs (>100 nm) is inherently difficult using transition-metal (TM) catalysed reactions due to termination by loss of functional groups.⁶⁷ Therefore, the Diels–Alder polymerization is a desired route to this target. Use of the A₂B₂ Diels–Alder polymerization affords GNRs with lengths up to 71 nm.³⁸ However, stoichiometric inefficiency limits this reaction.^59,60

In 2014, Narita et al. subjected the monomer building block (7.5), which consists of a cyclopentadienone as the conjugated diene and an ethynyl group as the dienophile, to AB type Diels–Alder conditions affording polymer (7.6) which had an M_W between 24–620 kg mol⁻¹ (PDI ∼ 3–14), higher than any reported weights using Yamamoto or Suzuki reactions at the time. The polymer precursor (7.6) was finally ‘graphitized’ using Scholl reaction conditions with FeCl₃ affording the GNR (7.7) with lengths >200 nm (Scheme 16a).⁵⁴ Model dimer and trimer compounds were subjected to ‘graphitization’ and analysed by MALDI-TOF MS to confirm the successful formation of the GNR (7.7). 7.7 was fully characterised by FT-IR, Raman and ss-NMR spectroscopy. THz probing found the intrinsic charge carrier mobilities as large as 15 000 cm² V⁻¹ s⁻¹ along with a large optical bandgap of 1.88 eV from absorption spectra. The strong aggregation of the GNRs made characterization difficult however the presence of dodecyl chains in monomer 7.5 improved their dispersibility allowing for characterization, nonetheless.

Scheme 16 Synthesis of (a) GNR (7.7) and (b) laterally extended GNR (8.0) via AB type Diels–Alder reaction. Reproduced from ref. 54 with permission from [Springer], copyright [2014]; Reproduced from ref. 68 with permission from [ACS], copyright [2014].

Installation of different functional groups on the periphery of such GNRs is feasible by modification to the starting monomer. To diminish the bandgap, the same researchers shortly after performed a simple lateral phenyl extension to produce monomer 7.8 which was heated to 260–270 °C to induce AB type Diels–Alder polymerization forming wider (∼2 nm) polymer precursors 7.9 with a largely improved M_W ∼ 230–550 kg mol⁻¹ and PDI of 2.8–3.8. Post oxidative cyclodehydrogenation afforded 8.0 with lengths up to 390 nm (Scheme 16b).⁶⁸ Similarly, the GNRs were fully characterized and UV-vis spectroscopy eluded a smaller bandgap of 1.24 eV.

Götz et al. used methoxy-functionalized monomer 8.1 to yield polymer 8.2 (M_W ∼ 31–54 kg mol⁻¹, PDI ∼ 1.5–1.7) which was planarized to methoxy-functionalised GNR (8.3) by oxidative cyclodehydrogenation using FeCl₃ (Scheme 17). Theoretical simulations predicted a reduced bandgap of 8.3 compared to a hydrogen passivated parent (Fig. 8) due to geometric distortion caused by the methoxy groups along with the electron donating nature of the functionality. This was verified by the fingerprint of band shrinkage seen in the red shift of the UV/Vis spectra. THz analysis revealed a 25% increase in photoconductivity due to reduced effective mass of charge carriers in 8.3.⁶⁹

Scheme 17 Synthesis of methoxy-functionalised GNRs (8.3) via AB type Diels–Alder polymerization of monomer 8.1. Reproduced from ref. 69 with permission from [RSC], copyright [2022].

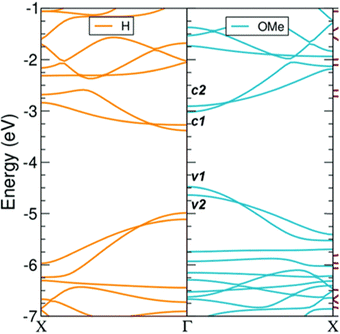Fig. 8 DFT band structures of GNR-OMe (8.3) (R = OMe; blue, right) and GNR-H (R = H; orange, left) The two band structures are aligned to the vacuum level, which is set to zero.⁶⁹ Reproduced from ref. 69 with permission from [RSC], copyright [2022].

The modifications on the periphery of these monomers are not limited to simple lateral extensions. Keerthi et al. successfully synthesized GNRs with anthraquinone (AQ) and naphthalene/perylene monoamide (NMI/PMI) units achieved through Suzuki coupling of polyphenylene precursors with bromo groups, validated by MALDI-TOF MS, FTIR, Raman and XPS.³⁰ AB Diels–Alder polymerization of monomer 8.4 produced polymer precursor 8.5 which was subjected to Suzuki coupling conditions (Pd(PPh₃)₄/K₂CO₃) with three boronic esters, 2-(4,4,5,5-tetramethyl-1,3,2-dioxaborolan-2-yl)anthracene-9,10-dione (AQ-BPin), N-(2-ethylhexyl)-4-(4,4,5,5-tetramethyl-1,3,2-dioxaborolan-2-yl)naphthalene-1,8-dicarboximide (NMI-BPin), and N-(1-heptyloctyl)-9-(4,4,5,5-tetramethyl-1,3,2-dioxaborolan-2-yl)perylene-3,4-dicarboximide (PMI-BPin), producing functionalised polymer precursors 8.6 (A = AQ, NMI, PMI) with M_W as high as 161 kg mol⁻¹ and PDI < 3. Subsequent intramolecular oxidative cyclodehydrogenation using FeCl₃ as oxidant afforded the GNRs (8.7) (Scheme 18), with possible lengths of up to 1000 nm.

Scheme 18 Synthetic route to peripherally modified GNRs (8.7) with AQ, NMI and PMI electron withdrawing groups. Reproduced from ref. 30 with permission from [ACS], copyright [2017].

However, these vast lengths could have also been due to end-to-end tangling of individual ribbons. Interestingly, drop casting the three GNRs (8.7) (A = AQ, NMI, PMI), revealed a self-assembling behaviour. The PMI functionalised GNR (8.7) formed a fascinating rectangular network providing evidence that edge functionalisation of GNRs can be used to tune their supramolecular assemblies.

More sophisticated edge functionalization was later developed by Slota et al. where GNRs functionalized with spin-bearing nitronyl nitroxide (NIT) radicals (8.9) were synthesized from the AB Diels–Alder polymerization. A non-cyclized polyphenylene precursor (8.8) with NIT radicals was also synthesized as means of a control (Fig. 9). Using electron paramagnetic resonance (EPR) spectroscopy, the researchers manipulated the spin states to measure the spin-dynamics and spin-environment interactions. Spin coherence times were measured and found to be in a promising range of microseconds at room temperature, ideal for spintronic applications and decoherence channels were identified.³¹ The survival of the brominated monomer through the AB Diels–Alder polymerization in this case, opened the possibility of edge functionalization and direct manipulation and observance of magnetism in GNRs for the first time.

Fig. 9 Structures of NIT-polyphenylene 8.8 and NIT-GNRs 8.9 synthesized via AB Diels–Alder polymerization. Reproduced from ref. 31 with permission from [Springer], copyright [2018].

The functionalization opportunities provided by the AB Diels–Alder polymerization has expanded GNR applications. Rogers et al. demonstrated that GNRs 9.0 effectively supported gold nanoparticles (AuNPs) for electrocatalytic CO₂ reduction (Fig. 10). The GNR-AuNP interaction reduced the onset potential by several hundred millivolts, increased catalytic activity, and improved nanoparticle dispersion, enhancing the electrochemically active surface area. The GNR-AuNPs also exhibited over 100-fold greater stability and performance compared to amorphous carbon supports. Edge functionalization of the GNRs with ester groups tuned the catalytic environment, shifting the rate-determining step and altering the reaction mechanism.⁷⁰

Fig. 10 (a) GNRs (9.0) synthesized (b) as support for AuNPs for electrocatalytic CO₂ reduction.⁷⁰ Reproduced from ref. 70 with permission from [ACS], copyright [2017].

Other innovative uses include the inclusion of additional ‘capping’ monomers to form GNR heterostructures for applications in next generation molecular diodes (Fig. 11)⁷¹ and bulky edge functionalization has led to pure carbon based GNRs to be used as single electron transistors.⁷² Also, advancements in ‘clickable’ GNRs have been made for functionalisation with fluorescent dyes for facile imaging,⁷³ or for successful application in biosensor interfaces (Fig. 12).⁷⁴

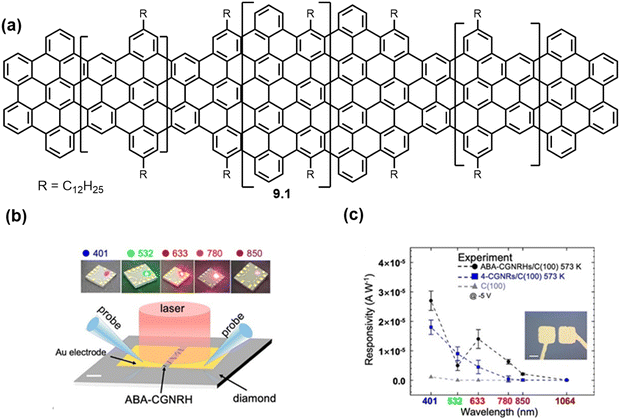Fig. 11 (a) GNR heterostructures (9.1) synthesized for use in molecular diodes (b) Schematic I–V measurement of GNR-based device (100) (c) Average photoresponsivity of six GNR-based devices on diamond at 573 K and −5 V under vacuum conditions.⁷¹ Reproduced from ref. 71 with permission from [ACS], copyright [2023].

Fig. 12 Structures of ‘clickable’ GNRs used for (a) facile imaging via inclusion of fluorescent dyes (9.2) and (b) applications in biosensor interfaces (9.3). Reproduced from ref. 73 with permission from [ACS], copyright [2018] Reproduced from ref. 74 with permission from [RSC], copyright [2024].

Manipulation of the cyclopentadienone monomer is also possible (Scheme 19) as demonstrated by Veber et al. in 2020 where modifications to a boranted AB Diels–Alder monomer (9.4) via Suzuki coupling with 9.5 formed an acetal protected cyclopentadienone monomer 9.6 and thus an acetal functionalised polyphenylene precursor (9.7). Acid catalysed deprotection yielded the aldehyde functionalised precursor which was subjected to Scholl reaction conditions to yield the aldehyde functionalised GNRs (9.8). Subsequent Lewis acid catalysed interfacial polymerization caused the growth of Covalent Organic Framework GNRs (COF-GNRs) using imine cross links (Fig. 13). These COF-GNRs showed 2D self-assembly and crystals gave access to a large surface area (>10⁵ nm²).⁷⁵

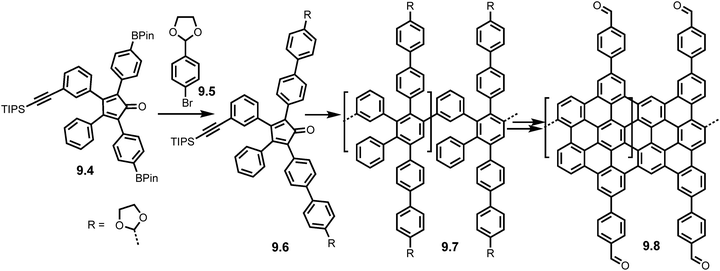Scheme 19 Synthesis of COF-GNRs 9.8 using acetal protected cyclopentadienone monomer 9.4. Reproduced from ref. 75 with permission from [Cell Press], copyright [2020].

Fig. 13 Structural model of COF-GNRs with unit cell (black box), orientation displaying lattice plane (01–1) corresponding to distance between linkers (0.7 nm) (top), orientation displaying interlayer packing and lattice planes (001) (orange), (002) (gray), and (105) (blue) corresponding to 2.5, 1.25, and 0.35 nm (bottom).⁷⁵ Reproduced from ref. 75 with permission from [Cell Press], copyright [2020].

Outside the realm of AB/A₂B₂ Diels–Alder polymerisations, the Diels–Alder reaction can be used post-polymerization using Ring Opening Alkyne Metathesis (ROAMP) techniques.⁷⁶ Kugelgen et al. initiated ROAMP of the rationally designed alkyne 9.9 using catalyst 10.0 and alkyne 10.1 to terminate. This repeating alkyne polymer 10.3 underwent a Diels–Alder benzannulation to form the GNR precursor polymer 10.4. A FeCl₃ Scholl condition was applied forming the desired cGNR 10.5 with lengths up to 68 nm. The ROAMP method proves useful due to the structural control in functionalized end groups and controlled lateral extension by taking advantage of precise Diels–Alder reactions (Scheme 20).

Scheme 20 ROAMP synthesis of cGNR 10.5 using catalyst 10.0. Reproduced from ref. 76 with permission from [ACS], copyright [2019].

3.2. Alternative planarization techniques

So far, the planarization techniques discussed have been using Scholl reactions. The Scholl Reaction is traditionally an oxidative cyclodehydrogenation reaction using FeCl₃ as a Lewis acid and oxidant. The mechanism of this reaction is not definitively known due to the dual behaviour of FeCl₃ however it is generally accepted to follow either a radical cation mechanism or via the formation of an arenium ion.⁷⁷ The Scholl reaction is an easy procedure which produces good yields for GNRs.¹⁰ However, in some cases it can lead to a mixture of fully cyclized and partially cyclized products³⁸ or undesirable ring formation/chlorination.⁷⁸ The uncertainty in the reaction mechanism of the Scholl reaction, contributes to variability in efficiency across novel substrates.⁷⁹ While FeCl₃ is commonly used, alternative systems like DDQ/TfOH are also effective.^49,66 Oxidant choice is influenced on the substrates electronics: theoretically, electron-rich arenes would react via an arenium ion pathway promoted by strong Lewis acids (e.g., FeCl₃, AlCl₃), whereas electron-poor substrates would favour a radical cation mechanism, which can be facilitated by single-electron oxidants (e.g., DDQ) in the presence of strong Brønsted acids like TfOH.^32,80 In this section, alternative pathways to planarization, using alkyne precursors and photochemical methods, are briefly discussed. Whilst some of these methods are not strictly solution-mediated synthesis, they are important to mention to give depth into the variety of methods used in the field. Other reviews have discussed these methods in more detail^80,81 however such depth is beyond the scope of this review.

3.2.1. GNRs from alkyne precursors. Alkyne rich precursors are favourable for the formation of carbon nanostructures owing to their intrinsic thermal instability.⁸⁰ Topochemical polymerization is the solid-state photo/heat induced 1,4-addition polymerization of conjugated triple bonds giving rise to a polymer with three cumulated double bonds per repeating unit.⁸² In 2016, Jordan et al. used monomers containing butadiyne units (10.6) and using topochemical polymerization converted these units into polydiacetylenes (10.7) set up for further aromatization to afford GNRs (10.9) (Scheme 21a) (∼1.36 nm in width).

Scheme 21 Synthesis of GNRs from alkyne precursors (a) topochemical polymerization from butadiyne precursors 10.6 and (b) low bandgap AGNR (11.2). Reproduced from ref. 83 with permission from [Cell Press], copyright [2016]; Reproduced from ref. 84 with permission from [ACS], copyright [2017].

The GNRs (10.9) had a bandgap of 1.4 eV. The solid-state reaction only required UV light or heat to proceed with the addition of no other reagents.⁸³ The same group later synthesized an AGNR (11.2) of the 3p + 2 class (Scheme 21b) using this method which would be predicted to have a very low bandgap. Use of Raman, FT-IR, ss-NMR show the target structure was synthesized however the harsh conditions used to perform the cyclization resulted in loss of the bulky side chains, causing analysis and processing to be difficult.⁸⁴ Other methods using alkyne precursors include alkyne benzannulation⁵⁸ (Scheme 10) however these methods typically still make use of a Scholl reaction as a last step.⁸⁰

3.2.2. Photochemical methods. Whilst the use of alkyne precursors removes the need for additional reagents relying solely on heat and/or light, photochemical methods only rely on light removing the requirement of very high temperature reactions and can also be done in solution phase.⁸⁰

The Mallory reaction is amongst the oldest photochemical carbon–carbon bonding reaction.⁸⁵ This reaction has been used widely in the synthesis of nanographene's from polyaromatic hydrocarbons (PAHs) however is rarely used in GNR synthesis.⁸⁰ Zhong et al. used monobromo, dibromo and monostannane derivatives and subjected them to Stille coupling conditions to form perylene diimides (PDIs) which afforded GNRs 11.4 after a Mallory reaction.⁸⁶ Scheme 22 shows the synthesis using a dibromo monomer 11.3.

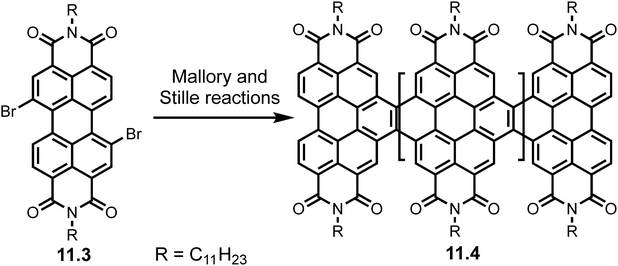Scheme 22 Synthesis of GNRs (11.4) using combination of Stille and Mallory reactions of dibromo monomer 11.3. Reproduced from ref. 86 with permission from [ACS], copyright [2014].

A more popular photochemical method for GNR synthesis is reactions most notably the CDHC. The mechanism is believed to be a photochemical conrotatory electrocyclization followed by elimination of HCl. This reaction affords very high conversion attributed to the entropic benefit of HCl release.⁸¹ Scheme 23 shows the synthesis of thiophene annulated GNRs (11.8 And 12.1) synthesized by Suzuki polymerization methods but with the replacement of the Scholl reaction with CDHC reaction due to the inclusion of chlorinated precursor 11.5.⁸⁷

Scheme 23 Synthetic route toward thiophene annulated GNRs (11.8 and 12.1) via Suzuki polymerization and using CDHC mechanism for aromatization. Reproduced from ref. 87 with permission from [Wiley], copyright [2018].

4. Conclusion and future perspectives

Each polymerization technique discussed in this review offers distinct advantages and remains relevant in current literature for tailoring GNR structures for specific applications (Table 1). The A₂B₂ Diels–Alder reaction, despite being one of the earliest methods, continues to be utilized in recent studies for synthesizing multi-edged GNRs with unique electronic properties nm.³⁸ It has also enabled the incorporation of eight-membered rings, opening pathways for photoluminescent properties with successful device applications.⁴⁵ However, its broader use has declined due to advancements in other polymerization techniques.

Table 1 Summary of the referenced GNRs discussed throughout this review providing information on lengths, molecular weights (M_W unless stated otherwise), polymerization and graphitization methods. ‘—’ in place where information was not available in original article

GNR	Average length (nm)	Molecular weight of polymer precursor (kg mol^−1)	Polymerization method	Graphitization method	Ref.
1.3	—	12–120	A2B2 Diels–Alder	AlCl3	52
1.6	—	62.5	A2B2 Diels–Alder	FeCl3	53
2.4	71	108.3	A2B2 Diels–Alder	FeCl3	38
2.8	30	30.4	A2B2 Diels–Alder	FeCl3	45
3.2	12	13.9	A2B2 Suzuki	FeCl3	55
3.6–3.8	86	37.4	A2B2 Suzuki	DDQ/TfOH	49
4.2	20	33	A2B2 Suzuki	FeCl3	46
4.6	35	28.8	A2B2 Suzuki	FeCl3	48
4.9	17	36	AB Suzuki	FeCl3	37
5.5	14	26.1	AB Suzuki	FeCl3	47
5.8	—	29.8 (Mn)	AB Suzuki	Benzannulation	58
5.9	—	—	AB Suzuki	DDQ/TfOH	58
6.2	30	52	AA Yamamoto	FeCl3	61
6.5	6, 11, 58	15.6–186	AA Yamamoto	FeCl3	21
6.8	23	20.8	AA Yamamoto	FeCl3	51
7.1	20	29.8	AA Yamamoto	FeCl3	50
7.4	—	132.7	AA Yamamoto	DDQ/TfOH	66
7.7	200	24–620	AB Diels–Alder	FeCl3	54
8.0	390	230–550	AB Diels–Alder	FeCl3	68
8.3	—	31–54	AB Diels–Alder	FeCl3	69
8.7	—	161	AB Diels–Alder	FeCl3	30
8.9	100		AB Diels–Alder		31
9.0	—	—	AB Diels–Alder	FeCl3	70
9.1	—	—	AB Diels–Alder	FeCl3	71
9.2	—	125–278	AB Diels–Alder	FeCl3	73
9.3	10–371	—	AB Diels–Alder	FeCl3	74
9.8	—	26 (Mn)	AB Diels–Alder	FeCl3	75
10.5	68	14 (Mn)	ROAMP	FeCl3	76
10.9	—	—	Topochemical polymerization	Topochemical polymerization	83
11.2	—	—	Topochemical polymerization	Topochemical polymerization	84
11.4	—	—	Stille/Mallory	—	86
11.8	—	9.7 (Mn)	A2B2 Suzuki	CDHC	87
12.1	—	9.5 (Mn)	A2B2 Suzuki	CDHC	87

---

Suzuki coupling remains widely adopted due to its broad functional group tolerance, which facilitates bandgap engineering. It enables both bandgap narrowing through the preservation of heterostructures in monomeric units with post-borylation options⁴⁹ and bandgap widening, owing to the stability of defined pores in GNR structures.⁴⁶ Unique AB variations of SCTP have also led to the synthesis of weight controlled GNR heterostructures, enabling precise topological engineering for potential quantum applications.^47,58

The AA Yamamoto polymerization overcomes the stoichiometric inefficiencies of A₂B₂ polymerization^59,60 while retaining the ability to synthesize multi-edged GNRs, including those with typically unstable magnetic zigzag edges.^50,51 This method has also enabled the solution-phase synthesis of highly sought porphyrin GNRs.⁶⁶ However, the reliance on TM catalysts in Suzuki and Yamamoto reactions limits the achievable GNR lengths due to functional group degradation.^59,60

The AB Diels–Alder reaction addresses these limitations, enabling the synthesis of GNRs up to 600 nm in length⁵⁴ and offering versatile functionalization options.^38,60 Functional groups can be incorporated into monomeric building blocks^68–70 or retained through halogenated monomers, allowing post-functionalization with electron-withdrawing units for supramolecular assembly tuning,³⁰ spin-containing radicals for magnetic probing,³¹ and fluorescent compounds for facile characterization.⁷³ These advances have broadened GNR applications, including catalytic enhancements with tunable reaction mechanisms,⁷⁰ molecular diode integration,⁷¹ and biosensor development.⁷⁴

Emerging directions include further rational design of monomers incorporating pores and non-hexagonal rings—areas that are still underexplored in the literature. The OSS method has demonstrated multiple examples of boron-containing GNRs via boronated monomers.⁴³ In contrast, solution-phase synthesis has so far only achieved post-functionalization with boron,⁴⁹ highlighting a key challenge: developing monomers with pre-installed boron units to enable precise incorporation into the GNR backbone. Such strategies would offer fine control over bandgaps and optoelectronic properties, enhancing the potential for device integration. For practical implementation, techniques like SCTP and ROAMP show strong promise,^47,58,76 as they enable control over GNR length and highly ordered heterojunction formation—critical parameters for high-performance devices.⁸⁸

One of the main challenges in GNR synthesis remains the ‘graphitization’ step. The Scholl reaction, while widely used and generally high yielding, suffers from significant drawbacks. These include ring rearrangements and unwanted chlorination when using Lewis acid oxidants like FeCl₃,⁸⁹ as well as degradation of solubilizing groups with AlCl₃,³² resulting in poor solubility and limited post-synthetic characterization. Alternative oxidative conditions, such as DDQ/TfOH, can lead to oxidized/triflated by-products,^32,79 introducing structural defects that negatively impact the intrinsic properties⁸⁹ and device performance of the resulting GNRs. Furthermore, for GNRs to be viable at an industrial scale, synthesis methods must deliver gram-scale, defect-free material—something that remains a significant hurdle.⁸⁰ Beyond traditional polymerization methods, alternative strategies such as topochemical polymerization using alkyne precursors leverage thermodynamic driving forces from heat or light, offering milder conditions and sustainability benefits.⁸⁰ Notably, photochemical approaches, particularly CDHC, provide a faster and regioselective route for synthesizing GNRs, enabling fine-tuning of structural properties.^80,87

Furthermore, while GNR mobilities have reached up to 600 cm² V⁻¹ s⁻¹,⁵¹ they remain far below CNTs, which exceed 50 000 cm² V⁻¹ s⁻¹.⁹⁰ This gap stems from various reasons, such as device fabrication, device optimization, contact resistance, defects in GNRs backbone or terminals, GNR aggregation via π–π stacking, which complicates isolation and hinders reproducible measurements,⁹¹ even with advanced deposition.⁹² In contrast, CNTs benefit from defect-free structures and well-established fabrication methods.⁹³

Overall, AB Diels–Alder polymerization remains the most promising strategy for GNR synthesis due to its ability to produce long, highly functionalized ribbons which have already led to various device implementation including, molecular diodes, bioimaging, and transistors.^70–74 Whilst other methods remain useful for their respective purposes, SCTP and ROAMP polymerizations also show high potential for device implemented GNRs due to their superior structural control and pathway for milder ‘graphitization’ methods.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. K. acknowledges Royal Society grants ICA\R1\231014, IES\R3\243222 and Presidential Fellowship from the University of Manchester. A. K. and K. S. thanks EPSRC DTP studentship (EP/W524347/1) and Centre for Quantum Science and Engineering (CQSE) at the University of Manchester for the studentship support. A. K. acknowledge EPSRC strategic equipment grant EP/W006502/1. This work was partly supported by the UK-India Education Research Innovation (UKIERI) award supported by British Council (IND/CONT/G/23-24/37).

References

1. S. Nasir, M. Z. Hussein, Z. Zainal and N. A. Yusof, Materials, 2018, 11, 295.
2. A. R. Urade, I. Lahiri and K. S. Suresh, JOM, 2023, 75, 614–630.
3. V. B. Mbayachi, E. Ndayiragije, T. Sammani, S. Taj, E. R. Mbuta and A. U. Khan, Results Chem., 2021, 3, 100163.
4. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
5. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
6. T. Ohta, A. Bostwick, T. Seyller, K. Horn and E. Rotenberg, Science, 2006, 313, 951–954.
7. C. Bao, W. Yao, E. Wang, C. Chen, J. Avila, M. C. Asensio and S. Zhou, Nano Lett., 2017, 17, 1564–1568.
8. Y. Zhang, Z. Li, P. Kim, L. Zhang and C. Zhou, ACS Nano, 2012, 6, 126–132.
9. A. Narita, X.-Y. Wang, X. Feng and K. Müllen, Chem. Soc. Rev., 2015, 44, 6616–6643.
10. A. Narita, Z. Chen, Q. Chen and K. Müllen, Chem. Sci., 2019, 10, 964–975.
11. Z. Chen, Y.-M. Lin, M. J. Rooks and P. Avouris, Phys. E, 2007, 40, 228–232.
12. M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805.
13. X. Li, X. Wang, L. Zhang, S. Lee and H. Dai, Science, 2008, 319, 1229–1232.
14. J. Bai, X. Duan and Y. Huang, Nano Lett., 2009, 9, 2083–2087.
15. A. Sinitskii and J. M. Tour, Appl. Phys. Lett., 2012, 100, 103106.
16. D. V. Kosynkin, A. L. Higginbotham, A. Sinitskii, J. R. Lomeda, A. Dimiev, B. K. Price and J. M. Tour, Nature, 2009, 458, 872–876.
17. L. Jiao, L. Zhang, X. Wang, G. Diankov and H. Dai, Nature, 2009, 458, 877–880.
18. L. Ci, Z. Xu, L. Wang, W. Gao, F. Ding, K. F. Kelly, B. I. Yakobson and P. M. Ajayan, Nano Res., 2008, 1, 116–122.
19. L. C. Campos, V. R. Manfrinato, J. D. Sanchez-Yamagishi, J. Kong and P. Jarillo-Herrero, Nano Lett., 2009, 9, 2600–2604.
20. N. Mohanty, D. Moore, Z. Xu, T. S. Sreeprasad, A. Nagaraja, A. A. Rodriguez and V. Berry, Nat. Commun., 2012, 3, 844.
21. Y. Huang, F. Xu, L. Ganzer, F. V. A. Camargo, T. Nagahara, J. Teyssandier, H. Van Gorp, K. Basse, L. A. Straasø, V. Nagyte, C. Casiraghi, M. R. Hansen, S. De Feyter, D. Yan, K. Müllen, X. Feng, G. Cerullo and Y. Mai, J. Am. Chem. Soc., 2018, 140, 10416–10420.
22. C. Tian, W. Miao, L. Zhao and J. Wang, Rev. Phys., 2023, 10, 100082.
23. X. Wang, Y. Ouyang, X. Li, H. Wang, J. Guo and H. Dai, Phys. Rev. Lett., 2008, 100, 206803.
24. G. Z. Magda, X. Jin, I. Hagymási, P. Vancsó, Z. Osváth, P. Nemes-Incze, C. Hwang, L. P. Biró and L. Tapasztó, Nature, 2014, 514, 608–611.
25. P. Ruffieux, S. Wang, B. Yang, C. Sánchez-Sánchez, J. Liu, T. Dienel, L. Talirz, P. Shinde, C. A. Pignedoli, D. Passerone, T. Dumslaff, X. Feng, K. Müllen and R. Fasel, Nature, 2016, 531, 489–492.
26. G. D. Nguyen, H. Z. Tsai, A. A. Omrani, T. Marangoni, M. Wu, D. J. Rizzo, G. F. Rodgers, R. R. Cloke, R. A. Durr, Y. Sakai, F. Liou, A. S. Aikawa, J. R. Chelikowsky, S. G. Louie, F. R. Fischer and M. F. Crommie, Nat. Nanotechnol., 2017, 12, 1077–1082.
27. J. Lawrence, P. Brandimarte, A. Berdonces-Layunta, M. S. G. Mohammed, A. Grewal, C. C. Leon, D. Sánchez-Portal and D. G. de Oteyza, ACS Nano, 2020, 14, 4499–4508.
28. J. Li, S. Sanz, N. Merino-Díez, M. Vilas-Varela, A. Garcia-Lekue, M. Corso, D. G. de Oteyza, T. Frederiksen, D. Peña and J. I. Pascual, Nat. Commun., 2021, 12, 5538.
29. R. E. Blackwell, F. Zhao, E. Brooks, J. Zhu, I. Piskun, S. Wang, A. Delgado, Y. L. Lee, S. G. Louie and F. R. Fischer, Nature, 2021, 600, 647–652.
30. A. Keerthi, B. Radha, D. Rizzo, H. Lu, V. Diez Cabanes, I. C. Hou, D. Beljonne, J. Cornil, C. Casiraghi, M. Baumgarten, K. Müllen and A. Narita, J. Am. Chem. Soc., 2017, 139, 16454–16457.
31. M. Slota, A. Keerthi, W. K. Myers, E. Tretyakov, M. Baumgarten, A. Ardavan, H. Sadeghi, C. J. Lambert, A. Narita, K. Müllen and L. Bogani, Nature, 2018, 557, 691–695.
32. R. S. Jassas, E. U. Mughal, A. Sadiq, R. I. Alsantali, M. M. Al-Rooqi, N. Naeem, Z. Moussa and S. A. Ahmed, RSC Adv., 2021, 11, 32158–32202.
33. M. Fujita, K. Wakabayashi, K. Nakada and K. Kusakabe, J. Phys. Soc. Jpn., 1996, 65, 1920–1923.
34. L. Yang, C.-H. Park, Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2007, 99, 186801.
35. O. V. Yazyev and M. I. Katsnelson, Phys. Rev. Lett., 2008, 100, 047209.
36. O. V. Yazyev, Acc. Chem. Res., 2013, 46, 2319–2328.
37. X. Yao, W. Zheng, S. Osella, Z. Qiu, S. Fu, D. Schollmeyer, B. Müller, D. Beljonne, M. Bonn, H. I. Wang, K. Müllen and A. Narita, J. Am. Chem. Soc., 2021, 143, 5654–5658.
38. L. Yang, J. Ma, W. Zheng, S. Osella, J. Droste, H. Komber, K. Liu, S. Böckmann, D. Beljonne, M. R. Hansen, M. Bonn, H. I. Wang, J. Liu and X. Feng, Adv. Sci., 2022, 9, 2200708.
39. Y. Gu, Z. Qiu and K. Müllen, J. Am. Chem. Soc., 2022, 144, 11499–11524.
40. A. Keerthi, C. Sánchez-Sánchez, O. Deniz, P. Ruffieux, D. Schollmeyer, X. Feng, A. Narita, R. Fasel and K. Müllen, Chem. – Asian J., 2020, 15, 3807–3811.
41. K. T. Kim, J. W. Lee and W. H. Jo, Macromol. Chem. Phys., 2013, 214, 2768–2773.
42. T. H. Vo, M. Shekhirev, D. A. Kunkel, F. Orange, M. J. F. Guinel, A. Enders and A. Sinitskii, Chem. Commun., 2014, 50, 4172–4174.
43. J.-J. Zhang, J. Ma and X. Feng, Macromol. Chem. Phys., 2023, 224, 2200232.
44. Y.-Z. Tan, B. Yang, K. Parvez, A. Narita, S. Osella, D. Beljonne, X. Feng and K. Müllen, Nat. Commun., 2013, 4, 2646.
45. S. Obermann, X. Zhou, L. A. Guerrero-León, G. Serra, S. Böckmann, Y. Fu, E. Dmitrieva, J.-J. Zhang, F. Liu, A. A. Popov, A. Lucotti, M. R. Hansen, M. Tommasini, Y. Li, P. W. M. Blom, J. Ma and X. Feng, Angew. Chem., Int. Ed., 2024, 63, e202415670.
46. W. Niu, Y. Fu, G. Serra, K. Liu, J. Droste, Y. Lee, Z. Ling, F. Xu, J. D. Cojal González, A. Lucotti, J. P. Rabe, M. Ryan Hansen, W. Pisula, P. W. M. Blom, C.-A. Palma, M. Tommasini, Y. Mai, J. Ma and X. Feng, Angew. Chem., Int. Ed., 2023, 62, e202305737.
47. J.-J. Zhang, K. Liu, Y. Xiao, X. Yu, L. Huang, H.-J. Gao, J. Ma and X. Feng, Angew. Chem., Int. Ed., 2023, 62, e202310880.
48. S. Obermann, W. Zheng, J. Melidonie, S. Böckmann, S. Osella, N. Arisnabarreta, L. A. Guerrero-León, F. Hennersdorf, D. Beljonne, J. J. Weigand, M. Bonn, S. De Feyter, M. R. Hansen, H. I. Wang, J. Ma and X. Feng, Chem. Sci., 2023, 14, 8607–8614.
49. G. Li, K.-Y. Yoon, X. Zhong, J. Wang, R. Zhang, J. R. Guest, J. Wen, X. Y. Zhu and G. Dong, Nat. Commun., 2018, 9, 1687.
50. X. Wang, J. Ma, W. Zheng, S. Osella, N. Arisnabarreta, J. Droste, G. Serra, O. Ivasenko, A. Lucotti, D. Beljonne, M. Bonn, X. Liu, M. R. Hansen, M. Tommasini, S. De Feyter, J. Liu, H. I. Wang and X. Feng, J. Am. Chem. Soc., 2022, 144, 228–235.
51. W. Niu, J. Ma, P. Soltani, W. Zheng, F. Liu, A. A. Popov, J. J. Weigand, H. Komber, E. Poliani, C. Casiraghi, J. Droste, M. R. Hansen, S. Osella, D. Beljonne, M. Bonn, H. I. Wang, X. Feng, J. Liu and Y. Mai, J. Am. Chem. Soc., 2020, 142, 18293–18298.
52. Z. B. Shifrina, M. S. Averina, A. L. Rusanov, M. Wagner and K. Müllen, Macromolecules, 2000, 33, 3525–3529.
53. J. Wu, L. Gherghel, M. D. Watson, J. Li, Z. Wang, C. D. Simpson, U. Kolb and K. Müllen, Macromolecules, 2003, 36, 7082–7089.
54. A. Narita, X. Feng, Y. Hernandez, S. A. Jensen, M. Bonn, H. Yang, I. A. Verzhbitskiy, C. Casiraghi, M. R. Hansen, A. H. Koch, G. Fytas, O. Ivasenko, B. Li, K. S. Mali, T. Balandina, S. Mahesh, S. De Feyter and K. Müllen, Nat. Chem., 2014, 6, 126–132.
55. X. Yang, X. Dou, A. Rouhanipour, L. Zhi, H. J. Räder and K. Müllen, J. Am. Chem. Soc., 2008, 130, 4216–4217.
56. J. Dai, D. Lu, T. Ye, S. Yu and X. Cheng, J. Chem. Educ., 2019, 96, 2672–2675.
57. W. Zhang, C. Chai, Q. Fan, Y. Song and Y. Yang, Results Phys., 2020, 18, 103271.
58. J. Lee, H. Ryu, S. Park, M. Cho and T.-L. Choi, J. Am. Chem. Soc., 2023, 145, 15488–15495.
59. W. H. Carothers, Trans. Faraday Soc., 1936, 32, 39–49.
60. G. Odian, Principles of Polymerization, 2004, pp. 464–543 DOI:10.1002/047147875X.ch6.
61. M. G. Schwab, A. Narita, Y. Hernandez, T. Balandina, K. S. Mali, S. De Feyter, X. Feng and K. Müllen, J. Am. Chem. Soc., 2012, 134, 18169–18172.
62. M. El Gemayel, A. Narita, L. F. Dössel, R. S. Sundaram, A. Kiersnowski, W. Pisula, M. R. Hansen, A. C. Ferrari, E. Orgiu, X. Feng, K. Müllen and P. Samorì, Nanoscale, 2014, 6, 6301–6314.
63. G. Sedghi, V. M. García-Suárez, L. J. Esdaile, H. L. Anderson, C. J. Lambert, S. Martín, D. Bethell, S. J. Higgins, M. Elliott, N. Bennett, J. E. Macdonald and R. J. Nichols, Nat. Nanotechnol., 2011, 6, 517–523.
64. F. Gao, R. E. Menchón, A. Garcia-Lekue and M. Brandbyge, Commun. Phys., 2023, 6, 115.
65. J. Li, N. Merino-Díez, E. Carbonell-Sanromà, M. Vilas-Varela, D. G. de Oteyza, D. Peña, M. Corso and J. I. Pascual, Sci. Adv., 2018, 4, eaaq0582.
66. Q. Chen, A. Lodi, H. Zhang, A. Gee, H. I. Wang, F. Kong, M. Clarke, M. Edmondson, J. Hart, J. N. O’Shea, W. Stawski, J. Baugh, A. Narita, A. Saywell, M. Bonn, K. Müllen, L. Bogani and H. L. Anderson, Nat. Chem., 2024, 16, 1133–1140.
67. K. C. Nicolaou, S. A. Snyder, T. Montagnon and G. Vassilikogiannakis, Angew. Chem., Int. Ed., 2002, 41, 1668–1698.
68. A. Narita, I. A. Verzhbitskiy, W. Frederickx, K. S. Mali, S. A. Jensen, M. R. Hansen, M. Bonn, S. De Feyter, C. Casiraghi, X. Feng and K. Müllen, ACS Nano, 2014, 8, 11622–11630.
69. A. Götz, X.-Y. Wang, A. Ruini, W. Zheng, P. Soltani, R. Graf, A. Tries, J. Li, C.-A. Palma, E. Molinari, M. R. Hansen, H. I. Wang, D. Prezzi, K. Müllen and A. Narita, J. Mater. Chem. C, 2022, 10, 4173–4181.
70. C. Rogers, W. S. Perkins, G. Veber, T. E. Williams, R. R. Cloke and F. R. Fischer, J. Am. Chem. Soc., 2017, 139, 4052–4061.
71. X. Zhang, Y. Hu, C. R. Lien-Medrano, J. Li, J. Shi, X. Qin, Z. Liao, Y. Wang, Z. Wang, J. Li, J. Chen, G. Zhang, J. V. Barth, T. Frauenheim, W. Auwärter, A. Narita, K. Müllen and C.-A. Palma, J. Am. Chem. Soc., 2023, 145, 8757–8763.
72. W. Niu, S. Sopp, A. Lodi, A. Gee, F. Kong, T. Pei, P. Gehring, J. Nägele, C. S. Lau, J. Ma, J. Liu, A. Narita, J. Mol, M. Burghard, K. Müllen, Y. Mai, X. Feng and L. Bogani, Nat. Mater., 2023, 22, 180–185.
73. D. Joshi, M. Hauser, G. Veber, A. Berl, K. Xu and F. R. Fischer, J. Am. Chem. Soc., 2018, 140, 9574–9580.
74. R. Hasler, G. E. Fenoy, A. Götz, V. Montes-García, C. Valentini, Z. Qiu, C. Kleber, P. Samorì, K. Müllen and W. Knoll, Nanoscale Horiz., 2024, 9, 598–608.
75. G. Veber, C. S. Diercks, C. Rogers, W. S. Perkins, J. Ciston, K. Lee, J. P. Llinas, A. Liebman-Peláez, C. Zhu, J. Bokor and F. R. Fischer, Chem, 2020, 6, 1125–1133.
76. S. von Kugelgen, I. Piskun, J. H. Griffin, C. T. Eckdahl, N. N. Jarenwattananon and F. R. Fischer, J. Am. Chem. Soc., 2019, 141, 11050–11058.
77. M. Grzybowski, K. Skonieczny, H. Butenschön and D. T. Gryko, Angew. Chem., Int. Ed., 2013, 52, 9900–9930.
78. M. Shekhirev and A. Sinitskii, Phys. Sci. Rev., 2017, 2(5), 20160108.
79. M. Grzybowski, B. Sadowski, H. Butenschön and D. T. Gryko, Angew. Chem., Int. Ed., 2020, 59, 2998–3027.
80. A. Jolly, D. Miao, M. Daigle and J.-F. Morin, Angew. Chem., Int. Ed., 2020, 59, 4624–4633.
81. J. S.-J. Yang and L. Fang, Chem, 2024, 10, 1668–1724.
82. G. Wegner, Die Makromol. Chem., 1972, 154, 35–48.
83. R. S. Jordan, Y. Wang, R. D. McCurdy, M. T. Yeung, K. L. Marsh, S. I. Khan, R. B. Kaner and Y. Rubin, Chem, 2016, 1, 78–90.
84. R. S. Jordan, Y. L. Li, C.-W. Lin, R. D. McCurdy, J. B. Lin, J. L. Brosmer, K. L. Marsh, S. I. Khan, K. N. Houk, R. B. Kaner and Y. Rubin, J. Am. Chem. Soc., 2017, 139, 15878–15890.
85. F. B. Mallory and C. W. Mallory, Organic Reactions, 2005, 1–456,  DOI:10.1002/0471264180.or030.01.
86. Y. Zhong, B. Kumar, S. Oh, M. T. Trinh, Y. Wu, K. Elbert, P. Li, X. Zhu, S. Xiao, F. Ng, M. L. Steigerwald and C. Nuckolls, J. Am. Chem. Soc., 2014, 136, 8122–8130.
87. D. Miao, M. Daigle, A. Lucotti, J. Boismenu-Lavoie, M. Tommasini and J.-F. Morin, Angew. Chem., Int. Ed., 2018, 57, 3588–3592.
88. P. S. Costa, J. D. Teeter, A. Enders and A. Sinitskii, Carbon, 2018, 134, 310–315.
89. N. Ponugoti and V. Parthasarathy, Chem. – Eur. J., 2022, 28, e202103530.
90. A. Javey, J. Guo, Q. Wang, M. Lundstrom and H. Dai, Nature, 2003, 424, 654–657.
91. M. Shekhirev, T. H. Vo, D. A. Kunkel, A. Lipatov, A. Enders and A. Sinitskii, RSC Adv., 2017, 7, 54491–54499.
92. X. Yao, H. Zhang, F. Kong, A. Hinaut, R. Pawlak, M. Okuno, R. Graf, P. N. Horton, S. J. Coles, E. Meyer, L. Bogani, M. Bonn, H. I. Wang, K. Müllen and A. Narita, Angew. Chem., Int. Ed., 2023, 62, e202312610.
93. J. Wang, X. Jin, Z. Liu, G. Yu, Q. Ji, H. Wei, J. Zhang, K. Zhang, D. Li, Z. Yuan, J. Li, P. Liu, Y. Wu, Y. Wei, J. Wang, Q. Li, L. Zhang, J. Kong, S. Fan and K. Jiang, Nat. Catal., 2018, 1, 326–331.

---