Layer-polarization-engineered ferroelectricity and anomalous valley hall effects in a van der Waals bilayer†
Nini Guoa,
Jie Lib,
Huijie Liana,
Shu Wangb,
Yi Sun*c,
Xiaojing Yao *a and
Xiuyun Zhang
*a and
Xiuyun Zhang
 *b
*b
aCollege of Physics and Hebei Advanced Thin Films Laboratory, Hebei Normal University, Shijiazhuang 050024, China. E-mail: xjyao@hebtu.edu.cn
bCollege of Physics Science and Technology & Microelectronics Industry Research Institute, Yangzhou University, Yangzhou 225002, China. E-mail: xyzhang@yzu.edu.cn
cSchool of Electronic Engineering, Jiangsu Vocational College of Electronics and Information, Huaian 223003, China. E-mail: sunyi@jsei.edu.cn
First published on 9th May 2025
Abstract
Layertronics, engineering the electronic properties through the layer degree of freedom, has attracted considerable attention due to its promising applications in next-generation spintronic technologies. Here, by coupling sliding ferroelectricity with A-type antiferromagnetism, we demonstrate a mechanism for layer-polarization-engineered electronic property through symmetry analysis based on the tight-binding (TB) model. It is found that breaking the inversion symmetry and time-inversion symmetry in the model gives rise to ferroelectricity and a layer-polarized anomalous valley Hall effect. Crucially, this valley polarization is ferroelectrically switchable, enabling non-volatile electrical control of the layer-resolved Berry curvature. Using first-principles calculations, this mechanism and phenomenon are verified in the multiferroic bilayer Janus RuClF. Our findings provide a promising platform for 2D bilayer materials, which hold great potential for applications in nanoelectronic and spintronic devices.
New conceptsTwo-dimensional van der Waals (vdW) structures provide new flexibility for manipulating physical properties. Combining the tight binding model and first-principles calculations, we propose a mechanism for manipulating layer-polarized ferroelectricity and ferrovalleys in the A-type antiferromagnetic bilayer system through the interlayer sliding and interlayer exchange interactions. It is revealed that the ferroelectrically controllable layer-polarized anomalous valley Hall effect (AVHE) can be achieved by F–F interlayer termination in bilayer RuClF. Moreover, the electronic properties of the RuClF bilayer can be changed by different stacking configurations. |
1. Introduction
In recent years, the discovery of various ferroic materials, whose properties are driven by different degrees of freedom of electron orbitals, has allowed advanced applications in information processing, spintronics, valleytronics, and electronics.1 For example, the (anti)ferromagnetic candidates utilizing the spin degree of freedom are crucial in spintronic devices, where spin-aligned ferromagnetic (FM) materials can be used for spin-directed data storage in magnetic random access memory devices (MRAMs), and spin-antiparallel antiferromagnetic (AFM) materials offer high stability, ultra-high speeds, and low-power-consumption spin transport properties. Ferrovalley (FV) materials are complementary to modern semiconductor technology, utilizing the valley degree of freedom to encode and process information.2 Ferroelectric (FE) materials are also important in nonvolatile memory devices,3 field-effect transistors,4 etc., by spontaneously generating an electric polarization. Additionally, multiferroic materials, which couple two or more types of ferroic order parameters, are of significant interest due to their multiple physical properties.5 However, most intrinsic candidates are found to favor a single ferroic order due to the difficulty in balancing their origin mechanisms, maintaining structural stability as well as experimental feasibility, and so on.6,7 Even for single ferroic materials, many suffer from the deficiencies that limit their practical applications, such as the non-spontaneous character of in-plane magnetization,8 spin degeneration,9 and lower magnetic transition temperature (TC).10Alternatively, two-dimensional (2D) van der Waals (vdW) homo-/hetero-bilayer or few-layer structures provide new flexibility for manipulating the physical properties by adjusting the vdW stacking, interlayer distance, and through atom or molecule intercalation, etc.11–17 Firstly, varying the interlayer distance of vdW bilayers can assist in tuning the interlayer magnetic orders and electronic properties. For example, bilayer transition metal dichalcogenides, TMX2 (TM = V, Cr, Mn; X = S, Se, Te), prefer interlayer AFM ordering at shorter interlayer distances and FM ordering at longer interlayer distances. The AFM–FM transition is governed by the competition between Pauli repulsion in the interlayer region and kinetic-energy gain across the bilayer.18,19 The MnPS3/MnCl3 heterostructure undergoes transitions from semiconductor to metal to half-metal as the interlayer distance decreases.20 Secondly, stacking or twisting is another effective method to modulate the electron correlation properties.21–28 For example, MnBr3 bilayers exhibit a high-Chern-number quantum anomalous Hall (QAH) state when stacked in the AB style, whereas the application of external electrostatic fields or circularly polarized light induces the layer Hall effect in the AC-stacked layer.13 Switchable room-temperature out-of-plane electric polarization can be induced by changing the stacking order in the hexagonal BN bilayer.22 Additionally, valley polarizations associated with twist angle and stacking configurations have been found for the WSe2/WS2 heterostructure28 and the YI2 bilayer.29 Although these layered 2D materials exhibit a wealth of physical properties and modulation characteristics, there are still many unknowns to be explored in terms of the interlayer interactions and their impact on new physical phenomena. In particular, the interaction between sliding ferroelectricity and A-type antiferromagnetism in bilayer systems may lead to a series of unique physical effects.
In this study, we propose a mechanism to manipulate layer-polarized ferroelectricity and ferrovalley in the A-type AFM bilayer system through the interlayer sliding and interlayer exchange interactions. We first demonstrate this mechanism through the tight-binding (TB) model and then realize it in the bilayer Janus RuClF. By sliding the F–F oriented bilayers, ClRuF–FRuCl, the ferroelectrically controllable layer-polarized anomalous valley Hall effect (AVHE) can be achieved. The Cl–F facing bilayer, FRuCl–FRuCl, is a bipolar magnetic half-metal (BMHM), in which the spin-up and spin-down electrons in the upper and lower layers are conductive. The Cl–Cl-oriented FRuCl–ClRuF exhibits antiferrovalley behavior with a valley polarization of 300 meV in the RuClF sublayer.
2. Computational methods
All density functional theory (DFT) calculations were carried out within the Vienna Ab initio Simulation Package (VASP).30,31 The exchange correlation interaction was characterized by the general gradient approximation (GGA) with the Perdew–Burke–Ernzerholf (PBE) functional.32,33 The interaction between ion nuclei and valence electrons was described by the projector-augmented wave potential (PAW) method;34 the energy cut-off for the plane-wave basis set was set as 500 eV. The vacuum spaces were set larger than 15 Å to avoid the physical interactions caused by periodic boundary conditions, and the vdW interaction in bilayer RuClF was considered using the DFT-D2 method.35 To consider the Coulomb interaction and exchange interactions of the Ru-d electrons, the GGA+U method with Ueff = 3.0 eV was used. For structural relaxation and electronic structure calculation, k meshes were set as 11 × 11 × 1 and 33 × 33 × 1, respectively. The criteria for energy and atom force convergence were set to 10−5 eV and 0.01 eV Å−1, respectively. The Berry curvatures of the bilayer RuClF were calculated by using the maximally localized Wannier functions (MLWFs)36,37 implemented in the WANNIER90 package.38 The energy barrier of sliding FE switching was calculated by the climbing image nudged elastic band (CI-NEB) method.393. Results and discussion
The proposed mechanism originates from monolayer hexagonal lattices that exhibit spontaneous valley polarization. These systems typically exhibit FM exchange interaction with either the time-reversal (T) or inversion symmetry (P) broken. Subsequently, we constructed bilayer systems by stacking two hexagonal lattices. In the bilayer lattice, antiferromagnetism typically prevails in the interlayer exchange interaction due to competition among various interlayer orbital hybridizations. When a small out-of-plane electric polarization is applied, a pronounced Berry curvature of opposite sign is observed in the vicinity of the K-valley and K′-valley. As illustrated in Fig. 1(a), the K-valley and K′-valley come from the spin-up channel in the upper layer and the spin-down channel in the lower layer, respectively. This structure enables layer-locked spin and Berry curvature within the bilayer lattice. As shown in Fig. 1(b)–(d), the P-symmetry of the system is further broken as the applied out-of-plane electric polarization is enhanced, thus lifting the energetic degeneracy between the K and K′ valleys; consequently, it becomes feasible to manipulate the Berry curvature exclusively within a specific layer, paving the way for the realization of AVHE.Notably, energetically degenerate states with opposite polarization directions can be generated by interlayer sliding or other strategies, as shown in Fig. 1(b) and (c). With FE switching, both the electric polarization and the sign of valley polarization are reversed simultaneously, thus providing the possibility for FE control over the layer-locked physical properties. Moreover, the conduction band minimum (CBM) and valence band maximum (VBM) at the K and K′ valleys intersect or cross to form valley polarization when the out-of-plane electric polarization is further increased, as illustrated in Fig. 1(d).
To validate this hypothesis, we adopted a single-orbit TB model to describe the low-energy band dispersions near the Fermi level in the bilayer hexagonal system. The Hamiltonian for the TB model is formulated as:
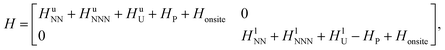 | (1) |
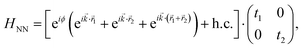 | (2) |
 | (3) |
HU is the Hubbard interaction term, describing on-site Coulomb repulsion:
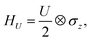 | (4) |
HP is the out-of-plane electric polarization term, modeling interfacial charge redistribution:
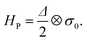 | (5) |
| Honsite = t0⊗σ0. | (6) |
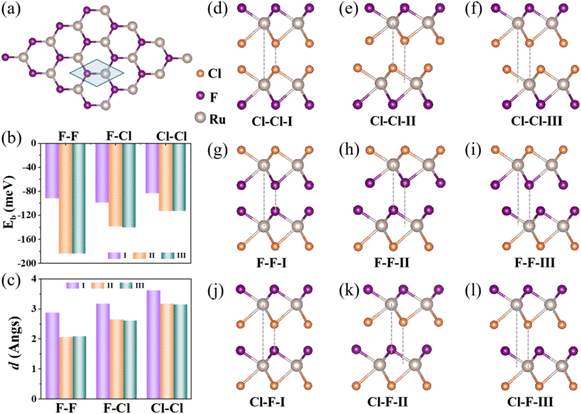
By using density functional theory, we found a realistic Janus multiferroic system that verifies this mechanism, namely, bilayer RuClF. Fig. 3(a) and Fig. S1(b) (ESI†) show the crystal structure of the monolayer of Janus RuClF, which consists of three atomic layers, with the upper and lower atomic layers occupied by Cl and F atoms, respectively, and the transition metal Ru atoms sandwiched in the middle layer. As the analogue Janus MoSSe (WSSe) monolayer has been obtained in experiments,40,41 it is expected that the RuClF monolayer can also be fabricated with similar methods. The monolayer RuClF has a hexagonal lattice with the space group P3m1, and the optimized lattice constant is 3.30 Å, which is in agreement with a previous study (3.34 Å).42 The ground state of monolayer RuClF is the FM order, which is energetically more favorable than the AFM state by 0.61 eV, as shown in Fig. S1(b) in ESI,† with the magnetic moment of 4.0μB per unit cell. The band structure of the RuClF monolayer is shown in Fig. S1(a) (ESI†), which is a direct bandgap FM semiconductor with the bandgap of 0.36 eV. After considering the spin–orbit coupling (SOC) effect, the VBM is located at the high-symmetry K point, which is higher than that of point K′, resulting in an obvious valley polarization of 0.29 eV, as illustrated in Fig. S1(c) and (d) (ESI†), which show the band structures of the RuClF monolayer considering SOC with the magnetization along z and −z direction, respectively.
Then, the physical behaviors dependent on the stacking orders of bilayer RuClF were studied. Three types of interlayer contact faces (FRuCl–ClRuF, ClRuF–FRuCl, and FRuCl–FRuCl with Cl–Cl, F–F, and Cl–F interfacing), and three kinds of stacking patterns, stack-I, stack-II, stack-III, were considered, as shown in Fig. 3(d)–(l). The binding energy of bilayer RuClF is defined as follows:
| Eb = EBL − 2 × ERuClF, | (7) |
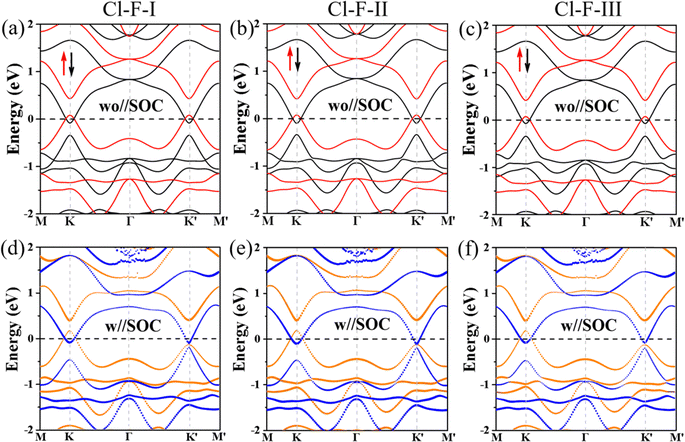
Next, the electronic properties of interlayer AFM RuClF bilayers with different configurations were explored. First of all, the band structures of three stacked FRuCl–ClRuF configurations without and with SOC effect are shown in Fig. 4(a)–(f). For the bilayer FRuCl–ClRuF with Cl–Cl interface, the interlayer interactions are weak due to the relatively small electronegativity of Cl atoms. As a result, the spin-up and spin-down bands of the Cl–Cl-I, Cl–Cl-II and Cl–Cl-III configurations completely overlap without considering the SOC effect, as shown in Fig. 4(a)–(c). After considering SOC, spontaneous valley polarization of the RuClF monolayer is induced due to breaking of the T-symmetry. Due to the direct overlap of two RuClF sublayers, no global energy polarization appears at the K and K′ valleys (see Fig. 4(d)–(f)). By doping the holes, spin-up and spin-down holes at K and K′ valleys will be aggregated on the left side of the upper layer and on the right side of the lower layer by applying in-plane electric field, resulting in the layer-locked spin and Berry curvature in the bilayer lattice.
Fig. 5(a)–(c) show the energy band structures of the ClRuF–FRuCl configurations in three stacks without and with considering SOC effects. For the F–F-I stacking with P-symmetry, the bands of spin-up and spin-down channels are completely degenerate (see Fig. 5(a)). As for F–F-II and F–F-III stacked bilayers, they are bipolar magnetic semiconductors (BMS) with a direct bandgap of 21.55 meV. By considering the SOC effect, the two RuClF sublayers in F–F-I stacks are valley polarized, but the energies at the K-valley and K′-valley are degenerate, originating from the upper and lower RuClF layers, respectively. Differently, global valley polarization occurs in the case of F–F-II and F–F-III stacks under the SOC effect. For the former, the VBM comes from the spin-up channel of the upper layer with a valley polarization value of Δv = 68.7 meV 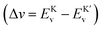 . For the latter, the VBM comes from the spin-down channel of the lower layer, and the valley polarization value is around Δv = −68.7 meV. All the results indicate that the electronic properties of the valley are significantly influenced by the layer-locked Berry curvature.
. For the latter, the VBM comes from the spin-down channel of the lower layer, and the valley polarization value is around Δv = −68.7 meV. All the results indicate that the electronic properties of the valley are significantly influenced by the layer-locked Berry curvature.
Moreover, when sliding from F–F-II stack to F–F-III stack, the ClRuF–FRuCl bilayer displays electric polarization featuring two switchable FE states. The out-of-plane electric polarizations under F–F-II and F–F-III stack configurations are 5 × 10−12 C m−1 and −5 × 10−12 C m−1, respectively, as calculated by the Berry phase approach. The feasibility of such sliding ferroelectricity is evaluated by the NEB method, and the calculated energy barrier is about 30 meV (see Fig. 5(d)), which is comparable with that in bilayer VSi2P4,46 suggesting the sliding between RuClF bilayers is energetically possible. The Berry curvatures for the two configurations are shown in Fig. 5(e) and Fig. S2 (ESI†), which is defined as:47
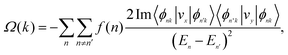 | (8) |
 under an in-plane electric field and accumulate at the left side of the upper layer. By reversing the FE polarization direction to the stack-III direction through sliding, the spin-down holes in the K′ valley will acquire opposite anomalous velocity and accumulate on the right side of the lower layer because of the opposite Berry curvature, generating the ferroelectrically reversible layer-polarized AVHE (see Fig. 5(f)).
under an in-plane electric field and accumulate at the left side of the upper layer. By reversing the FE polarization direction to the stack-III direction through sliding, the spin-down holes in the K′ valley will acquire opposite anomalous velocity and accumulate on the right side of the lower layer because of the opposite Berry curvature, generating the ferroelectrically reversible layer-polarized AVHE (see Fig. 5(f)).
The band structures of the Cl–F oriented FRuCl-FRuCl bilayer without/with considering SOC effect are shown in Fig. 6(a)–(f). It is observed that the three stack configurations (stack-I, stack-II, stack-III) show the same electronic structures, in which both spin-up conduction bands and spin-down valence bands cross the Fermi level and form a metallic state. Particularly, the conducting channels are layer dependent, i.e., the upper RuClF layer conducts in the spin-up channel, while the lower RuClF layer conducts in the spin-down channel. Such spin filter character is referred to as BMHM. Unlike the traditional FM half-metal, which has only one spin-conducting channel, BMHM can attain spin flows with different directions in different layers.
4. Conclusions
By combining the tight-binding (TB) model and first-principles calculations, we propose a mechanism for engineering layer-polarized electronic properties through the coupling of out-of-plane ferroelectricity and A-type AFM ordering in vdW Janus bilayers. Our analysis reveals that the F–F interlayer termination in bilayer RuClF hosts a layer-locked Berry curvature and enables layer-polarized AVHE. Furthermore, the layer-polarized AVHE exhibits ferroelectrically reversible switching upon sliding the two RuClF sublayers. Additionally, the electronic properties of the RuClF bilayer are highly sensitive to stacking configurations. These findings establish a feasible approach for manipulating layer-polarized electronic states in realistic bilayer materials.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Science and Technology Project of Hebei Education Department (BJK2024158). We thank the computational resources at Hebei Normal University and Yangzhou University.References
- J. W. Chu, Y. Wang, X. P. Wang, K. Hu, G. F. Rao, C. H. Gong, C. C. Wu, H. Hong, X. F. Wang, K. H. Liu, C. L. Gao and J. Xiong, Adv. Mater., 2021, 33, 2004469 CrossRef CAS PubMed.
- C. B. Luo, Z. Y. Huang, H. Qiao, X. Qi and X. P. Peng, J. Phys. Mater., 2024, 7, 022006 CrossRef CAS.
- R. C. G. Naber, K. Asadi, P. W. M. Blom, D. M. de Leeuw and B. de Boer, Adv. Mater., 2010, 22, 933 CrossRef CAS PubMed.
- R. C. G. Naber, C. Tanase, P. W. M. Blom, G. H. Gelinck, A. W. Marsman, F. J. Touwslager, S. Setayesh and D. M. de Leeuw, Nat. Mater., 2005, 4, 243 CrossRef CAS.
- Y. Y. Gao, M. Y. Gao and Y. R. Lu, Nanoscale, 2021, 13, 19324 RSC.
- N. A. Hill, J. Phys. Chem. B, 2000, 104, 6694 CrossRef CAS.
- N. A. Hill and A. Filippetti, J. Magn. Magn. Mater., 2002, 242, 976 CrossRef.
- R. J. K. Barik, S. Mishra, M. Khazaei, S. Y. Wang, Y. Y. Liang, Y. Sun, A. Ranjbar, T. L. Tan, J. J. Wang, S. J. Yunoki, K. Ohno, Y. Kawazoe and A. K. Singh, Nano Lett., 2024, 24, 13213 CrossRef CAS PubMed.
- D. I. Khomskii, J. Magn. Magn. Mater., 2006, 1, 1 CrossRef.
- J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig and R. Ramesh, Science, 2003, 299, 1719 CrossRef CAS PubMed.
- W. Chen, Z. Sun, Z. Wang, L. Gu, X. Xu, S. Wu and C. Gao, Science, 2019, 366, 983 CrossRef CAS PubMed.
- Y. Xu, A. Ray, Y. T. Shao, S. Jiang, K. Lee, D. Weber, J. E. Goldberger, K. Watanabe, T. Taniguchi, D. A. Muller, K. F. Mak and J. Shan, Nat. Nanotechnol., 2022, 17, 143 CrossRef CAS PubMed.
- X. Li, X. Xu, H. Zhou, H. Jia, E. Wang, H. Fu, J. T. Sun and S. Meng, Nano Lett., 2023, 23, 2839 CrossRef CAS PubMed.
- W. Xun, C. Wu, H. Sun, W. Zhang, Y.-Z. Wu and P. Li, Nano Lett., 2024, 24, 3541 CrossRef CAS PubMed.
- Z. M. Yu, S. Guan, X. L. Sheng, W. Gao and S. S. A. Yang, Phys. Rev. Lett., 2020, 124, 037701 CrossRef CAS PubMed.
- D. Chen, Z. Lian, X. Huang, Y. Su, M. Rashetnia, L. Yan, M. Blei, T. Taniguchi, K. Watanabe and S. Tongay, Nat. Commun., 2022, 13, 4810 CrossRef CAS PubMed.
- L. Liu, J. H. Hua, X. Zhang, M. H. Lu and Y. F. Chen, Phys. Rev. Appl., 2023, 19, 044055 CrossRef CAS.
- C. Wang, X. Zhou, Y. Pan, J. Qiao, X. Kong, C. C. Kaun and W. Ji, Phys. Rev. B, 2018, 97, 245409 CrossRef.
- C. Wang, X. Zhou, L. Zhou, Y. Pan, Z. Y. Lu, X. Wan, X. Wang and W. Ji, Phys. Rev. B, 2020, 102, 020402(R) CrossRef.
- T. Guo, Y. Liu, Y. Sun, S. Zhang, X. Xu, L. Wang, W. Zhou, Y. Liu, X. Yao and X. Zhang, Appl. Phys. Lett., 2023, 122, 192403 CrossRef CAS.
- W. Xun, X. Liu, Y. Zhang, Y.-Z. Wu and P. Li, Appl. Phys. Lett., 2025, 126, 161903 CrossRef CAS.
- K. Yasuda, X. Wang, K. Watanabe, T. Taniguchi and P. JarilloHerrero, Science, 2021, 372, 1458 CrossRef CAS PubMed.
- S. Deb, W. Cao, N. Raab, K. Watanabe, T. Taniguchi, M. Goldstein, L. Kronik, M. Urbakh, O. Hod and M. Ben Shalom, Nature, 2022, 612, 465 CrossRef CAS PubMed.
- L. Rogee, L. Wang, Y. Zhang, S. Cai, P. Wang, M. Chhowalla, W. Ji and S. P. Lau, Science, 2022, 376, 973 CrossRef CAS PubMed.
- X. Wang, K. Yasuda, Y. Zhang, S. Liu, K. Watanabe, T. Taniguchi, J. Hone, L. Fu and P. Jarillo-Herrero, Nat. Nanotechnol., 2022, 17, 367 CrossRef CAS PubMed.
- C. Wu, H. Sun, P. Dong, Y.-Z. Wu and P. Li, Adv. Funct. Mater., 2025, 35, 2501506 CrossRef.
- X. Han, J. Y. You, S. Wu, R. Li, Y. P. Feng, K. P. Loh and X. Zhao, J. Am. Chem. Soc., 2023, 145, 3624 CrossRef CAS PubMed.
- D. Dai, B. Fu, J. Yang, L. Yang, S. Yan, X. Chen, H. Li, Z. Zuo, C. Wang, K. Jin and Q. Gong, Sci. Adv., 2024, 10, 1281 CrossRef PubMed.
- Y. Wu, J. Tong, L. Deng, F. Luo, F. Tian, G. Qin and X. Zhang, Nano Lett., 2023, 23, 6226 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Mater. Sci., 1996, 6, 15 CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309 CrossRef CAS.
- X. Kong, L. Li, O. Leenaerts, X. J. Liu and F. M. Peeters, Phys. Rev. B, 2017, 96, 035123 CrossRef.
- A. A. Mostofi, J. R. Yates, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685 CrossRef CAS.
- G. Mills, H. Jónsson and G. Schenter, Surf. Sci., 1995, 324, 305 CrossRef CAS.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192 CrossRef CAS PubMed.
- D. B. Trivedi, G. Turgut, Y. Qin, M. Y. Sayyad, D. Hajra, M. Howell, L. Liu, S. Yang, N. H. Patoary, H. Li, M. M. Petrić, M. Meyer, M. Kremser, M. Barbone, G. Soavi, A. V. Stier, K. Müller, S. Yang, I. S. Esqueda, H. Zhuang, J. J. Finley and S. Tongay, Adv. Mater., 2020, 32, 2006320 CrossRef CAS PubMed.
- Y. B. Ma, Y. Z. Wu, J. W. Tong, L. Deng, X. Yin, L. Q. Zhou, X. L. Han, F. B. Tian and X. M. Zhang, Nanoscale, 2023, 15, 8278 RSC.
- E. Mostaani, N. D. Drummond and V. I. Falko, Phys. Rev. Lett., 2015, 115, 115501 CrossRef CAS PubMed.
- Z. Wang, Q. Chen and J. Wang, J. Phys. Chem. C, 2015, 119(9), 4752 CrossRef CAS.
- Y. Zhu, M. Su, H. Ye, D. Bai and J. Wang, Phys. Rev. B, 2023, 108, 125413 CrossRef CAS.
- T. Zhang, X. L. Xu, B. B. Huang, Y. Dai, L. Z. Kou and Y. D. Ma, Mater. Horiz., 2023, 10, 483 RSC.
- D. J. Thouless, M. Kohmoto, M. P. Nightingale and M. den Nijs, Phys. Rev. Lett., 1982, 49, 405 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nh00215j |
| This journal is © The Royal Society of Chemistry 2025 |