TMB (TM = Cr, Fe) monolayers: a new type of room temperature antiferromagnetic topological nodal line semimetal†
Chenqian
Yan
,
Yuqing
Mao
,
Jie
Li
,
Zijin
Wang
,
Ailei
He
*,
Yuanyuan
Duan
and
Xiuyun
Zhang
 *
*
College of Physics Science and Technology, Yangzhou University, Yangzhou 225002, China. E-mail: heailei@yzu.edu.cn; xyzhang@yzu.edu.cn
First published on 16th May 2025
Abstract
Two-dimensional materials that combine magnetism and topology offer unique advantages in the fields of spintronics and quantum computing. However, the design of two-dimensional (2D) materials simultaneously integrating both properties remains a significant challenge. Through systematic first-principles calculations, we predict two highly stable two-dimensional transition metal borides (TMBs). Our results reveal that both structures are antiferromagnetic (AFM) Dirac nodal line semimetals (NLSMs) with multiple band crossings near the Fermi level. Under biaxial strain, FeB can be transformed into a ferromagnetic state under 2% tensile strain, which is further verified to possess Weyl nodal loops (Weyl NLs). This discovery provides novel insights for the regulation of magnetic topological materials and holds promising potential for applications in low-power-consumption spintronic devices.
New conceptsTwo-dimensional antiferromagnetic nodal-line semimetals represent an emerging frontier in condensed matter physics and materials science. When two electronic bands intersect in a solid, they form one-dimensional nodal lines within the Brillouin zone. In single-particle systems, these topological features invariably form closed loops, commonly termed nodal loops in the literature. Current research on nodal lines has expanded along two novel dimensions: (i) nodal lines in 2D materials. (ii) nodal lines in magnetic systems. However, 2D materials exhibit exceptional mechanical properties and broad tunability, while antiferromagnetism offers distinct advantages including zero net magnetic moment, negligible stray fields, and ultrafast magnetic response. Through first-principles calculations, we have successfully predicted a new class of boron-based 2D antiferromagnetic materials. These structures ingeniously integrate antiferromagnetic ordering with nodal-line semimetallic characteristics in two-dimensional systems, demonstrating remarkable potential for applications in spintronics and quantum computing technologies. |
Introduction
In condensed matter physics and materials science, the interaction between magnetic and topological properties1–4 has stimulated strong research interest in spintronics. In particular, the emergence of two-dimensional (2D) materials provides an ideal platform for the design and control of nanoscale spintronic devices.5–7 Among these materials, magnetic topological semimetals (MTSs)8–10 have the feature of a gapless bulk-band structure where the conduction and valence bands cross each other in the Brillouin zone (BZ), and have attracted tremendous research interest. The band crossings of the MTSs are protected by the combination of exact crystal symmetry and topology.According to the dimensionality and nature of their band crossings, 2D MTSs can be classified into two categories: (i) nodal point semimetals, whose energies are dispersed linearly along all momentum directions around the point nodes. They can be classified into Dirac semimetals (DSMs) with quadruple nodal degeneracy,11 and Weyl semimetals (WSMs) with double nodal degeneracy,12,13 the latter of which requires either the inversion symmetry or the time reversal symmetry to be broken. (ii) Nodal-line semimetals (NLSMs), characterized with the nontrivial nodal line state in the Brillouin zone (BZ), formed by the one-dimensional band crossings in the low-energy band structures. They can be classified into Dirac NLSMs and Weyl NLSMs.14–17
The rapid development of 2D ferromagnetic (FM) materials can be traced back to the successful fabrication of 2D van der Waals (vdW) crystals of Cr2Ge2Te618 and CrI3.19 Accordingly, some topological NLSM candidates in FM 2D materials were found, such as MnN,20 GdCl,21 Cu2Si22 and h-InC,23 GdAg2,24 and Fe3GeTe2,25 metal organic frameworks,14etc. Compared with FM candidates, the zero net magnetization of antiferromagnetic (AFM) materials makes them less susceptible to external magnetic fields.26 Moreover, the interplay between AFM and band topology has emerged as a rich frontier in condensed matter physics, giving rise to novel phenomena such as spin-split bands and magnetic Weyl fermions.27 However, most discovered AFM-NLSMs are 3D materials,28–30 and few are found for 2D candidates, including TM2B3, germanene/Mn2S2,31 MoB3 monolayer,32 CrAs2,15 and MnC4.33 Considering the great success in the field of graphene, it is expected that searching for 2D AFM-NLSMs will most likely lead to the discovery of numerous noteworthy physical phenomena and novel topological states.
In our study, we predicted two highly stable 2D transition metal borides, TMB (TM = Cr, Fe), through first-principles calculations. Both TMBs are found to favor AFM ground states with Néel temperatures (TNs) of 240 K and 712 K, respectively. Moreover, both CrB and FeB monolayers exhibit AFM NLSM features accompanied by multiple Dirac points around the Fermi level. By applying biaxial strains, we found that the FeB monolayer can be transitioned into a FM Weyl NLSM.
Computational methods
All first-principles calculations were carried out based on density functional theory (DFT) implemented in the Vienna ab initio simulation package (VASP).34,35 The exchange–correlation functional was treated using the Perdew–Burke–Ernzerhof (PBE)36 method, which is based on the generalized gradient approximation (GGA);37 meanwhile the interaction between electrons and ions was described by the projector-augmented wave (PAW) method.38 The energy cutoff was set at 400 eV. The convergences for force and energy were −0.001 eV Å−1 and 10−6 eV, respectively. Given the strongly correlated interactions of 3d TM elements, the GGA+U method (Ueff) was employed. To verify the impact of Ueff on the magnetic ground states of both TMB monolayers, we examined the magnetic ground state by varying Ueff within the range of 2–5 eV. As a result, no appreciable variations were detected, as shown in Fig. S1 (ESI†). Based on the analysis, the Hubbard corrections of Ueff = 4 eV were chosen in this study to analyse the electronic structure, which has been adopted in previous literature.39,40 In geometry optimization and electronic property analysis, the Brillouin zone was sampled using a 15 × 15 × 1 and 25 × 25 × 1 centered Monkhorst–Pack grid. The vacuum layer with a thickness of 15 Å is applied to avoid the interaction between periodic images.The PHONOPY program, based on density functional perturbation theory (DFPT)41 was utilized to calculate the phonon dispersion spectra of the 4 × 4 × 1 supercells of FeB and CrB monolayers. Ab initio molecular dynamics (AIMD) simulations were employed using 3 × 3 × 1 supercells at the temperature of 300 K for 6 ps to evaluate the thermal stability. Second-order perturbation theory was performed to calculate the magnetic anisotropy energy (MAE).42 In addition, the TNs of both monolayers were calculated, with a lattice of 100 × 50 × 1 adopted in the Monte Carlo (MC) simulations by using the EspinS package.43
Results and discussion
Top and side views of the TMB (TM = Cr, Fe) monolayer are shown in Fig. 1(a), in which the TM ions and B ions form a tetragonal sublattice, and the space group of both monolayers is P4/mmm. The lattice constants of the CrB and FeB monolayers are a = b = 2.73 Å and 2.85 Å, respectively, with the Fe–B and Cr–B bond lengths of around 1.93 Å and 2.02 Å, respectively (see Table 1). To verify the experimental feasibility of these materials, we calculated the formation energy (Ef) by using eqn (1),| Ef = [E(TMB) − μ(TM) − μ(B)]/2, | (1) |
 | (2) |
 | (3) |
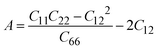 and
and  . As shown in Fig. 1(e) and Fig. S2 in the ESI,† both monolayers exhibit anisotropic Young's modulus and Poisson's ratios.
. As shown in Fig. 1(e) and Fig. S2 in the ESI,† both monolayers exhibit anisotropic Young's modulus and Poisson's ratios.
| System | a (Å) | b (Å) | d TM–B(Å) | α 1 (°) | α 2 (°) | E f (eV) | ΔE (eV) | GS |
|---|---|---|---|---|---|---|---|---|
| FeB | 2.73 | 2.73 | 1.93 | 90.00 | 90.0 | −6.87 | 0.22 | AFM metal |
| CrB | 2.85 | 2.85 | 2.02 | 90.00 | 90.0 | −7.08 | 1.03 | AFM metal |
In order to determine the magnetic ground states of the FeB and CrB monolayers, three different magnetic configurations are considered in a 2 × 2 supercell, including the FM state and two types of AFM (AFM1, AFM2) states, as shown in Fig. 2(a). Our calculations show that both monolayers favor the AFM1 states with the local magnetic moments per Cr/Fe atom of 2.16/3.02μB. In both monolayers, the energy differences between the AFM ground states and FM states are about 0.22 eV and 1.03 eV per unit cell for the FeB and CrB monolayer, respectively. To determine the magnetic stability, we calculated the angular dependence of the magnetic anisotropic energy (MAE) of the FeB (Fig. 2(b)) and CrB (Fig. 2(c)) monolayers, respectively. For both systems, the total energy of the out-of-plane (z) direction is the lowest with considerable MAE values of 1.15 meV and 9.0 meV for the TM atom, respectively, indicating that their easy magnetization axes are in the z direction. Next, the TNs of both systems were extended by performing classical MC simulations in the Heisenberg spin Hamiltonian in eqn (4):
 | (4) |
![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) i represents the magnetic moment of the atom at site i, and J1, J2, and J3 denote the nearest-neighbor (NN), second-nearest-neighbor (NNN), and third-nearest-neighbor (3NN) exchange coupling parameters, respectively. As shown in the specific heat plots of Fig. 2(b) and (c), the TNs for FeB and CrB are around 240 K and 712 K, respectively, close to or over room temperature, which proves their potential for applications in spintronic devices.
i represents the magnetic moment of the atom at site i, and J1, J2, and J3 denote the nearest-neighbor (NN), second-nearest-neighbor (NNN), and third-nearest-neighbor (3NN) exchange coupling parameters, respectively. As shown in the specific heat plots of Fig. 2(b) and (c), the TNs for FeB and CrB are around 240 K and 712 K, respectively, close to or over room temperature, which proves their potential for applications in spintronic devices.
The element-resolved band structures of FeB and CrB monolayers are shown in Fig. 3(a)–(d), respectively, in which the Fe and Cr elements contribute more significantly to the band structures near the Fermi level. In particular, it is found that the valence and conduction bands meet in the vicinity of the Fermi level, resulting in three intersection points, P1, P2, and P3, which are marked by green circles in Fig. 3(b) and (e). Moreover, these band crossing points exhibit fourfold degeneracy because of their overlapping spin-up and spin-down channels induced by the presence of PT symmetry [the combined symmetry of spatial-inversion (P) and time – reversal (T)]. Further analysis shows that the NLs along the kx direction for FeB and CrB monolayers are formed in the entire BZ by three Dirac points (P1, P2, P3), which belong to the open NL as shown in Fig. 3(c) and (f). By considering spin-orbital coupling (SOC)44 with the magnetization direction along the z axis, all the nodal points are gapped with small band gaps, as shown in Fig. S3(a) and (b) in the ESI,† due to the breaking of a specular mirror-reflection symmetry (σh). Moreover, due to the presence of σh symmetry in the FeB and CrB monolayers, all momentum points are hosted in the small group of Cs in the 2D BZ. The opposite two linear cross bands belong to different irreducible representations (IRs) of Γ1 and Γ2 with mirror eigenvalues of 1 and −1. An inspection of IR in the two bands reveals that the ordering of the CB and VB is inverted, forming a continuous nodal-ring around the Γ point. This is responsible for the existence of this topological nontrivial state. Seen from Fig. 3, we can observe that the bands near the Fermi level are primarily composed of the d orbitals of metal atoms and the p orbitals of non-metal atoms. Therefore, we constructed a tight-binding (TB) model based on the p orbitals of non-metal atoms and the d orbitals of metal atoms by using the maximally localized Wannier functions, and it can be observed that its band structure nearly coincides with the DFT-calculated bands at the Fermi level, as shown in Fig. S4 in the ESI.†
In order to experimentally validate viable synthetic routes for FeB and CrB monolayers, we used the most commonly used method, i.e. selective etching of aluminium metal layers from the MAB bulk phase.45,46 By setting the Fe–Al bond lengths from 3 to 7 Å and comparing their energies with those at a bond length of 2.5 Å, as shown in Fig. 4(a), our findings demonstrate that the energy difference increases with Fe–Al bond length in the FeAlB material, where longer Fe–Al distances correspond to higher system energies. This energetically favors Al layer exfoliation, thereby facilitating the synthesis of FeB monolayer materials. Moreover, the ELF counter plot of bulk FeAlB is shown in Fig. 4(b), and it is evident that the ELF value for the Fe - Al bond is close to 0, while the ELF value for the Fe–B bond is close to 0.5, indicating that the covalent bonding strength of the Fe–B bond is significantly stronger than that of the Fe–Al bond.
 | ||
| Fig. 4 (a) Comparison of the strength of Fe–Al bonds under different band lengths. (b) The ELF contour plots of the FeB monolayer. | ||
Finally, we explored the effect of biaxial strains (ε) on the electronic and magnetic properties of these 2D materials, where ε = (a − a0)/a0, and a and a0 are the lattice constants with and without strain. The red line in Fig. 5(a) and (c) represents the energy differences between the FM and the lowest-energy AFM states of the FeB and CrB monolayer. It is clear that the energy differences are in the range of 0–1 eV and 0.8–1.8 eV for FeB and CrB, respectively. In the range of ε = −4% to 1%, the FeB monolayer retains its AFM metallic properties; when subjected to a tensile strain of 2%, it is changed to be a FM metal. Differently, the CrB monolayer consistently maintains its AFM metallic characteristics in the range of ε = −4% to 4%. As shown by the blue line in Fig. 5(a) and (c), the TNs of the AFM FeB and CrB monolayers exhibit a monotonic decreasing trend within the strain ranges of ε = 4% to 1% and ε = −4% to 4%, respectively. In contrast, for the strains ranging from 2% to 4%, the Curie temperature (TC) of the FM FeB monolayer shows an increasing trend. Importantly, in most cases, the TNs remain above room temperature, enhancing their spintronic device applicability. Moreover, the strain-dependent MAEs for both monolayers are analyzed and presented in Fig. 5(b) and (d). The MAEs of both monolayers exhibit a decreasing trend under tensile strain. Notably, their responses to compressive strain differ significantly, in which the FeB material shows a continuous MAE enhancement, while for CrB, it displays an initial increase followed by a decrease. Also, the easy axis for all systems remained to be along the z-direction throughout the strain variations.
 | ||
| Fig. 5 Energy differences (ΔE, red line) and the TN (blue line) as a function of strain for FeB (a) and CrB (c) monolayers. The MAE as a function of strain for FeB (b) and CrB (d) monolayers. | ||
The band structures of FeB and CrB monolayers under different biaxial strains (ε) are shown in Fig. 6(a), (b), (d) and (e) and Fig. S5 and S6 in the ESI.† For the FeB monolayer, it retains AFM NLSM properties under 1% tensile strain as well as compressive strain, whereas under 2% or larger tensile strain, the spin up and spin down channels of the FeB monolayer are split and the system is changed to the FM state (see Fig. 6(b) and Fig. S5(b)–(d) in the ESI†). As shown in Fig. 6(b) and S7(a) in the ESI,† there are three band crossing points with double degeneracy that appear near the Γ point (marked by green circles above the Fermi level) of FeB, with additional experimental evidence confirming the formation of a closed nodal loop within the BZ, indicating that it is transitioned to be FM Weyl NLSM. As for the CrB monolayer, it retains AFM NLSM properties under tensile and compressive strains, as shown in Fig. S6 and S7(b) in the ESI.†
In conclusion, through first-principles calculations, we have successfully predicted two stable 2D TMB monolayers, FeB and CrB monolayer. Our results show that both monolayers exhibit thermal, dynamic, and mechanical stabilities. Both TMB monolayers have AFM states with high TNs and large MAEs. Moreover, FeB and CrB monolayers are robust AFM NLSMs with several Dirac cones near the Fermi level. Besides, the CrB monolayer maintains the AFM NLSM property in the range of ε = −4% to 4%, while the AFM NLSM property of the FeB monolayer is subjected to a biaxial tensile strain of 1%, and then it transitions to a FM NLSM under larger tensile strains. Our results propose a potential way to design 2D TM borides with promising magnetic and topological properties.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 12004098, 12104130) and the Yangzhou University Student Science and Innovation Project (XCX20240283). We acknowledge the computational resources at Yangzhou University.References
- C. Fang, H. M. Weng, X. Dai and Z. Fang, Chin. Phys. B, 2016, 25, 117106 CrossRef.
- F. D. M. Haldane, Phys. Rev. Lett., 1998, 61, 2015 CrossRef PubMed.
- Y. Deng, Y. Yu, M. Z. Shi, Z. Guo, Z. Xu, J. Wang, X. H. Chen and Y. Zhang, Science, 2020, 367, 895–900 CrossRef CAS PubMed.
- T. Li, S. Jiang, B. Shen, Y. Zhang, L. Li, Z. Tao, T. Devakul, K. Watanabe, T. Taniguchi, L. Fu, J. Shan and K. F. Mak, Nature, 2021, 600, 64–646 CrossRef PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- J.-C. Lei, X. Zhang and Z. Zhou, Front. Phys., 2015, 10, 276–286 CrossRef.
- S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutiérrez, T. F. Heinz, S. S. Hong, J. Huang, A. F. Ismach, E. Johnston-Halperin, M. Kuno, V. V. Plashnitsa, R. D. Robinson, R. S. Ruoff, S. Salahuddin, J. Shan, L. Shi, M. G. Spencer, M. Terrones, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 2898–2926 CrossRef CAS PubMed.
- W. Meng, X. Zhang, T. He, L. Jin, X. Dai, Y. Liu and G. Liu, J. Adv. Res., 2020, 24, 523–528 CrossRef CAS PubMed.
- L. Jin, X. Zhang, T. He, W. Meng, X. Dai and G. Liu, Appl. Surf. Sci., 2020, 520, 146376 CrossRef CAS.
- C. Zhang, Z. Yuan, Q. Jiang, B. Tong, C. Zhang, X. C. Xie and S. Jia, Phys. Rev. B, 2017, 95, 085202 CrossRef.
- Z. Wang, Y. Sun, X. Chen, C. Franchini, G. Xu, H. Weng, X. Dai and Z. Fang, Phys. Rev. B, 2012, 85, 195320 CrossRef.
- S. Murakami, New J. Phys., 2007, 9, 356 CrossRef.
- X. Wan, A. M. Turner, A. Vishwanath and S. Y. Savrasov, Phys. Rev. B, 2011, 83, 205101 Search PubMed.
- Y. Wang, J. Jiang and W. Mi, J. Phys. Chem. C, 2022, 126, 9998–10006 Search PubMed.
- B. Wang, H. Gao, Q. Lu, W. Xie, Y. Ge, Y.-H. Zhao, K. Zhang and Y. Liu, Phys. Rev. B, 2018, 98, 115164 CrossRef CAS.
- C. W. Niu, J.-P. Hanke, P. M. Buhl, H. B. Zhang, L. Plucinski, D. Wortmann, S. Blügel, G. Bihlmayer and Y. Mokrousov, Nat. Commun., 2019, 10, 3179 CrossRef PubMed.
- W. L. Sun, B. Y. Li, X. R. Zou, R. H. Li, B. B. Huang, Y. Dai and C. W. Niu, Adv. Sci., 2023, 10, 2301474 CrossRef CAS PubMed.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269 CrossRef CAS PubMed.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- S. S. Wang, Z. M. Yu, Y. Liu, Y. Jiao, S. Guan, X. L. Sheng and S. A. Yang, Phys. Rev. Mater., 2019, 3, 084201 CrossRef CAS.
- Y. Wang, X. Zhang, Z. Gao, T. Cao, J. Shi and X. Fan, J. Phys. Chem. C, 2023, 127, 4375–4832 Search PubMed.
- J. Xu, C. Liu, X. Y. Guo, J. K. Zhang, K. Liu, H. J. Qian, K. Q. Nie, Z. Y. Wang and J. Wang, Surf. Sci., 2025, 752, 122632 CrossRef CAS.
- S. Jeon, Y.-T. Oh and Y. Kim, Phys. Rev. B, 2019, 100, 035406 CrossRef CAS.
- M. Ormaza, L. Fernández, M. Ilyn, A. Magaña, B. Xu, M. J. Verstraete, M. Gastaldo, M. A. Valbuena, P. Gargiani, A. Mugarza, A. Ayuela, L. Vitali, M. Blanco-Rey, F. Schiller and J. E. Ortega, Nano Lett., 2016, 16, 4230–4235 CrossRef CAS PubMed.
- K. Kim, J. Seo, E. Lee, K.-T. Ko, B. S. Kim, B. G. Jang, J. M. Ok, J. Lee, Y. J. Jo, W. Kang, J. H. Shim, C. Kim, H. W. Yeom, B. I. Min, B.-J. Yang and J. S. Kim, Nat. Mater., 2018, 17, 794–799 CrossRef CAS PubMed.
- C. Gong and X. Zhang, Science, 2019, 363, 706 CrossRef PubMed.
- L. Smejkal, R. González-Hernández, T. Jungwirth and J. Sinova, Sci. Adv., 2020, 6, eaaz8809 CrossRef CAS PubMed.
- P. Tang, Q. Zhou, G. Xu and S.-C. Zhang, Nat. Phys., 2016, 12, 1100–1104 Search PubMed.
- G. Hua, S. Nie, Z. Song, R. Yu, G. Xu and K. Yao, Phys. Rev. B, 2018, 98, 201116 CrossRef.
- F. Máca, J. Mašek, O. Stelmakhovych, X. Martí, H. Reichlová, K. Uhlířová, P. Beran, P. Wadley, V. Novák and T. Jungwirth, J. Magn. Magn. Mater., 2012, 324, 1606–1612 CrossRef.
- Q. Lv, P.-H. Fu, Q. Zhuang, X.-L. Yu and J. Wu, J. Phys.: Condens. Matter, 2022, 34, 505702 CrossRef CAS PubMed.
- Z. Gao, F. Ma, Z. Zhu, Q. Zhang, Y. Liu, Y. Jiao and A. Du, Nano Lett., 2024, 24, 10964–10971 CrossRef CAS PubMed.
- H. Fernandez, R. Gonzalez-Hernandez, J. Paez, D. M. Hoat, N. Tan Tan, J. Guerrero-Sanchez and E. G. Perez-Tijerina, J. Phys.: Condens. Matter, 2024, 36, 155801 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 2019, 6, 15–50 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- C. Liu, B. T. Fu, H. B. Yin, G. B. Zhang and C. Dong, Appl. Phys. Lett., 2000, 117, 103101 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505–1509 CrossRef CAS.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- S. Subkow and M. Fähnle, Phys. Rev. B, 2009, 80, 212404 CrossRef.
- N. Rezaei, M. Alaei and H. Akbarzadeh, Comput. Mater. Sci., 2022, 202, 110947 CrossRef CAS.
- D. Hobbs, G. Kresse and J. Hafner, Phys. Rev. B, 2000, 62, 11556 CrossRef CAS.
- Z. Guo, J. Zhou and Z. Sun, J. Mater. Chem. A, 2017, 5, 23530–23535 RSC.
- B. Zhang, J. Zhou and Z. Sun, J. Mater. Chem. A, 2022, 10, 15865–15880 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Band structures of FeB and CrB monolayers with different U values added; Poisson's ratios of the FeB (a) and CrB (b) monolayers; the band structure of (a) FeB and (b) CrB monolayers with SOC applied along the z-direction; band structure of FeB (a) and CrB (b) under DFT calculations and the tight-binding model; the band structure of FeB and CrB monolayers in the range of ε = −4% to 4%. See DOI: https://doi.org/10.1039/d5nh00224a |
| This journal is © The Royal Society of Chemistry 2025 |





