Intrinsic microkinetic effects of spray-drying and SiC co-support on Mn–Na2WO4/SiO2 catalysts used in oxidative coupling of methane†
Received
20th August 2024
, Accepted 9th February 2025
First published on 10th February 2025
Abstract
This paper presents a microkinetic model to evaluate the effects of a silicon carbide (SiC) co-support and the shaping method on Mn–Na2WO4/SiO2 catalysts used for the oxidative coupling of methane. The model considers mass transfer, catalytic, and gas-phase kinetics, and it is trained with experimental values (product composition) of three Mn–Na2WO4 catalysts for calculating the kinetic parameters using catalytic descriptors while maintaining thermodynamic consistency. The catalysts were an SiO2-supported catalyst prepared through impregnation and two SiO2–SiC-supported catalysts (with βSiC and α + βSiC) prepared via spray-drying. Our analysis shows how the type of SiC and preparation method affect the textural properties and result in distinct CH3˙ radical oxidation, HO2˙ quenching, C2H4 oxidation, and COX transformation pathways, eventually leading to CH4 conversion and C2 selectivity. Our approach facilitates the assessment of the effects of the promoter and support on individual and global reaction networks.
1. Introduction
Oxidative coupling of methane (OCM) is a promising route for natural gas valorization as C2 chemicals are produced by the reaction of CH4 and O2 in a single pass in the presence of a catalyst. It has some inherent advantages over other ethylene production routes, including (i) lower greenhouse gas emissions than steam cracking of naphtha;1 (ii) lower energy requirement and capital cost than routes involving feedstock gasification; and (iii) use of noble-metal-free catalysts, unlike ethane dehydrogenation.2,3 However, unlike the methanol-to-olefins technology, which provides high ethylene yields and allows the adjustment of the ethylene/propylene ratio, OCM gives low ethylene and propylene yields.4 Thus, for OCM to be economically viable for industrial use, it is necessary to develop active and highly selective catalysts to improve the ethylene yield, preferably above 30%.5
Among OCM catalyst families, trimetallic combinations of Mn–Na–W/SiO2 show remarkable CH4 conversion (15–40%) and C2 selectivity (55–80%). These three metals show a noteworthy synergy, which is evident from the inferior catalytic performance that results when one of them is absent.6,7 The thermal stability of these catalysts is widely recognized. However, recent studies8–13 have reported a concerning trend of performance drop over time on stream. Various research lines have emerged to enhance the activity/stability of Mn–Na2WO4/SiO2 catalysts, including (i) the use of mixtures of Mn–Na2WO4/SiO2 catalysts with alkali chlorides,14 (ii) the addition of new dopants;15 and (iii) support material.16 Our previous studies17,18 proposed the introduction of silicon carbide (SiC) as a co-support material for Mn–Na2WO4/SiO2 catalysts through spray drying. The uniform distribution of SiC and its high thermal resistance prolong the catalyst lifespan. We also found that the crystal structure of SiC plays a pivotal role in the catalyst's performance. Compared with catalysts with βSiC, α + βSiC offers enhanced metal exposure stemming from its enhanced resistance to being oxidized to SiO2.
In this work, we investigated catalytic differences observed when SiC was introduced on Mn–Na2WO4/SiO2 catalysts and the shaping method, from a microkinetic viewpoint. The developed microkinetic models of OCM represent a unique tool to analyze the interplay between radical chemistry in the gas phase and catalytic surface reactions.19 This study builds upon previous experimental findings by examining the role of SiC in the support and shaping method, now from a microkinetic standpoint that accounts for irreducible mass transport limitations, gas-phase reactions, and surface chemistry. Additionally, this work accentuates the interrelation between catalyst surface properties, crystal phases, and their consequential effects on reaction pathways and product distributions. To achieve this, we modeled two Mn–Na2WO4 catalysts prepared by spray-drying with different SiC phases in their co-support, using a Mn–Na2WO4/SiO2 catalyst (where Mn–Na-W is impregnated onto SiO2) as a reference.
2. Methodology
2.1 Catalyst preparation
A SiO2-supported Mn–Na2WO4 catalyst, hereafter referred to as IMP SiO2, was prepared via wetness impregnation and used as the benchmark. Precursor salts were incorporated into the support at 80 °C to obtain a target composition of 2 wt% Mn, 5 wt% Na, and 3.1 wt% W. Following impregnation, water was removed through drying at 100 °C for 6 h. With the same nominal metal loading, two different Mn–Na2WO4 catalysts with SiO2/SiC supports (70/30 wt/wt) were prepared by spray-drying. Different types of SiC (i.e., SiC with different crystal phases) were introduced: one with a nanosized α + βSiC and the other with commercial porous βSiC. These two types are hereafter referred to as SD SiO2–α + βSiC and SD SiO2–βSiC, respectively. All catalysts were ultimately calcined in air at 800 °C for 6 h with a heating rate of 10 °C min−1. Additional information regarding materials used and catalyst synthesis procedures can be found elsewhere.20
2.2 Catalyst characterization
Textural properties were studied using liquid Ar (−186 °C) adsorption–desorption (Micromeritics ASAP 2040). Before the measurements, samples were degassed for 10 h at 250 °C. The Brunauer–Emmett–Teller (BET) method was employed to calculate the specific surface areas, and the Barrett–Joyner–Halenda model was used to measure the cumulative pore volume. Temperature-programmed experiments were conducted using an Altamira AMI-200ip instrument equipped with a mass spectrometer. A typical experiment began with sample pretreatment under 50 NmL min−1 Ar flow at 200 °C for 2 h to remove impurities, which was followed by cooling to the initial temperature. Subsequently, the sample was exposed to O2 with a flow rate of 50 NmL min−1 for 4 h (10 vol% O2 in N2) at room temperature. The catalyst bed temperature ranged from room temperature to 850 °C, and then held for 30 min using a carrier gas. Following the previous procedure, when the carrier gas was pure Ar, the experiment was considered O2 temperature-programmed desorption (O2-TPD). In contrast, when the carrier contained different CH4 partial pressures (0.05 bar balanced with Ar or pure CH4), the experiment was considered a temperature-programmed surface reaction (TPSR).
2.3 Steady state kinetic data acquisition
To examine the kinetic behavior of the three OCM catalysts, we used a set of 16 tubular fixed-bed quartz microreactors arranged in parallel. Information regarding the reactor specifications, analytical methods, and definitions of performance metrics can be found in this reference,20 where a data curation strategy is proposed for high-throughput kinetic data collected for the three catalysts. The range of operating conditions was as follows: temperature, 740–800 °C; pressure, 101 kPa; feed CH4/O2 ratio, 2.2−3.8; feed dilution, 10.8–71.2 kPa; space time, 0.68–6.15 gc h molC−1; CH4 conversion, 1.1–14.1%; and O2 conversion, 1.4−36.1%.
2.4 Reactor model
Under OCM conditions, there are constraints on the transport of radicals, which are highly reactive, that cannot be reduced. To address these irreducible mass transfer limitations, Couwenberg et al.21 proposed an isothermal model that considers two radial phases: the solid or intraparticle phase (characterized by the dimensionless particle coordinate ξ) and the fluid phase or interstitial phase (characterized by the dimensionless radial coordinate r). The continuity equations of each gas-phase species can be formulated for both the interstitial phase and catalyst particle or intraparticle phase (eqn (1) and (2)). In the interstitial phase, the model considers that molecular diffusion and gas-phase reactions occur. In the intraparticle phase, diffusion through pores occurs along with gas-phase and catalytic reactions.| |  | (1) |
| | 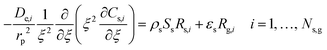 | (2) |
where Fv is the total gas volumetric flow rate and calculated from the total mass flow rate using ideal gas law as equation of state, εb is the average bed packing porosity, Ar is the reactor cross-section, Cg,i is the concentration of gas-phase species i in the interstitial phase, z is reactor bed length, Dm,i is the molecular diffusivity of gas-phase species i in the interstitial phase, rv is the radius of the interstitial phase or average half distance between catalyst pellets, r is the dimensionless radial interstitial coordinate, Rg,i is the homogeneous net production rate of gas-phase species i, De,i is the effective diffusivity of gas-phase species i in the intraparticle phase, rp is the radius of the intraparticle phase or the average pellet radius, ξ is the dimensionless radial intraparticle coordinate, Cs,i is the concentration of the gas-phase species i in the intraparticle phase, ρs is the catalyst density, Ss is the catalyst specific surface area, Rs,i is the heterogeneous net production rate of gas-phase species i and εs is the catalyst porosity. Note that Rg,i and Rs,i are defined per unit volume of gas and Ns,g represents the number of gas species in the reaction mechanism.
Both phases are coupled by the conservation of mass at the interphase, through boundary conditions that enforce equality of mass fluxes (eqn (3)) and concentrations (eqn (4)) at r = ξ = 1. The remaining boundary conditions pertain to the symmetry of the phases (eqn (5) and (6)), and the initial condition defines the feed concentration in the interstitial phase (eqn (7)). At z = 0, the concentration in the intraparticle phase is determined by eqn (2). Since no inert solid is introduced to dilute the particle, the areas of mass flux in the phases (i.e., interphase area and solid external area) are identical. The reactor is hence modeled by integrating the axial coordinate of a cylindrical gas volume with a contiguous catalyst sphere, with mass transport occurring across the phases, as schematized in Fig. 1. Assuming fully spherical particles is consistent with the previously reported SEM images of the spray-dried catalysts used in this work.17,18 The subscript 0 indicates feed conditions.
| |  | (3) |
| | | ∀z∧ξ = 1 Cg,i = Cs,i i = 1, …, Ns,g | (4) |
| |  | (5) |
| |  | (6) |
| | | z = 0 ∧ 0 < r < 1 Cg,i = C0,i i = 1, …, Ns,g | (7) |
As the catalytic net production rate of each gas species depends on the rate of individual elementary catalytic reactions and, therefore, on the coverages of surface intermediates, the conservation of surface species (
eqn (8)) should be coupled with the continuity equations
via the pseudo-steady-state approximation (PSSA), together with the site balance (
eqn (9)).
| | 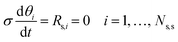 | (8) |
| |  | (9) |
where
σ is the active site density,
θi is the fractional coverage of surface intermediate
i,
t is time,
θ* is the fractional coverage of the vacant sites or vacancies and
Ns,s represents the number of surface intermediates in the reaction mechanism, excluding the vacancies. Species molecular diffusivities in the mixture (
Dm,i) are determined from the Chapman–Enskog theory by using a mixture-averaged approach in which the molar diffusion velocity is expressed with respect to the molar average velocity and the velocities of all species
j, with
j ≠
i, are approximated to be equal.
22| |  | (10) |
where
Di,j is the binary molecular diffusivity of gas-phase species
i in gas-phase species
j and
Xi is the molar fraction of gas-phase species
i in the mixture. The effective diffusivity in the catalyst particle (
De,i) is determined by modifying the Dupuit law to incorporate pore constriction effects. This modification disregards the Bosanquet formula since an order-of-magnitude estimation of the average catalyst pore radius showed the effect of the Knudsen diffusion to be negligible.
| |  | (11) |
where
τs is the term combining constriction and tortuosity of the catalyst.
 |
| | Fig. 1 Schematic of Couwenberg et al.'s model,21 which was used in the present work for modeling OCM kinetics responsible for irreducible mass transfer limitations. | |
2.5 Homogeneous kinetic model
A reliable gas-phase mechanism is important as the coupling of CH3˙ radicals is the primary pathway for the formation of C2 products, which occur exclusively in the gas phase. Wang et al.23 highlighted the importance of using detailed combustion models over ad-hoc gas-phase models developed for OCM. However, increasing the complexity of the model increases the number of equations to be solved for both phases, and therefore, this work used the most refined ad-hoc homogeneous model, which was proposed by Chen et al.24 (with 39 reactions and 23 species) and validated under catalytic OCM conditions. Details of this model are available in ESI† (section S1). The net production rate of gas-phase species i (Rg,i) is computed from the forward and backward rates of each homogeneous elementary reaction step (rj) and the stoichiometric number of i in each j (νj,i), where f and b denote forward and backward:| |  | (12) |
where Nr,g denotes the total number of homogeneous elementary steps in the mechanism. Every gas-phase reaction is modeled as an elementary reaction that follows the law of mass action, such that, the reaction rate of step j (rj) in the homogeneous mechanism is calculated from the product of its rate constant (kj) and the concentration of the reactants (Ci) to the power of their stoichiometric number, applicable for both forward and backward steps. Note that νj,i is the stoichiometric number of reacting species i in gas-phase elementary step j (i.e., νj,i wherein all non-negative values are set to 0).| |  | (13) |
The subscript j denotes the step number in the homogeneous reaction mechanism (Table S1†). In three-body elementary reactions, CM denotes the concentration of an unspecified collision partner that carries away excess energy to stabilize the product molecule (forward direction) or that supplies energy to break the product molecule bond (reverse direction).| |  | (14) |
Forward reaction rate constants follow the two-parameter Arrhenius equation, and their values are presented in Table S1.† The backward rate constant is computed from the forward and equilibrium constants (section 2.7).| |  | (15) |
where Afj and Efa,j denote prefactor and activation energy of forward homogeneous reaction step j, respectively, R is the universal gas constant and T is temperature.
2.6 Heterogeneous kinetic model
The first step of the heterogeneous reaction network involves H˙ abstraction from CH4 to form CH3˙ Whether CH4 is adsorbed on the catalyst surface or whether H˙ abstraction occurs through an Eley–Rideal step as well as the nature of O* have been discussed extensively, even via large-scale density functional theory calculations.25 In this work, an Eley–Rideal CH4 initiation with dissociative O2 chemisorption was considered, following the model of Alexiadis et al.,26 who applied this model to diverse catalysts, including Mn–Na2WO4/SiO2, and considered a second-order chemisorption kinetics observed in pulsing experiments.27 Nonetheless, for other catalyst families, CH4 surface dissociation has also been reported.28
A catalyst capable of abstracting H˙ from CH4 can also abstracting H˙ from C2H6 owing to the lower C–H bond strength in C2H6, and even from C2H4 despite this compound's bond strength being greater than that of CH4 by 5 kJ mol−1.29 Heterogeneous H˙ abstraction from C2H6 produces a C2H5˙ radical, which undergoes successive Eley–Rideal reactions with O* to form catalytic C2H4.30 Homogeneous C2H4 formation from C2H5˙ is also possible through branched chain reactions. However, catalytic H˙ abstraction from C2H4 yields C2H3˙, a secondary source of CO in gas-phase reactions.31,32 Thus, for a selective catalyst, effectively generating CH3˙ radicals and facilitating their recombination to form C2H6 is crucial, for it is a termination step that prevents the consumption/oxidation of the radicals through COX-forming chain branching reactions with HO2˙ radicals. The sequence that starts with CH3˙ adsorption as CH3O* and ends with  formation primarily involves Langmuir–Hinshelwood reactions, with one H atom being removed from the reactant as OH* via the formation of CH2O*.30,31 Other relevant COX sources include gas-phase oxidation of C2H5˙ and C2H3˙ radicals produced through H˙ abstraction and surface C2H4 oxidation through adsorption, H˙ abstraction, and C–C bond cleavage.32 Therefore, effective catalysts not only activate CH4 but also prevent deep oxidation paths, represented by HO2˙ quenching in the surface mechanism. Finally, the regeneration of active sites involves water desorption, resulting from adsorbed OH˙ radicals yielding O*. The catalytic reaction network with 10 surface species (excluding vacancies) and 26 reversible elementary steps used in this work is presented in Table 1.
formation primarily involves Langmuir–Hinshelwood reactions, with one H atom being removed from the reactant as OH* via the formation of CH2O*.30,31 Other relevant COX sources include gas-phase oxidation of C2H5˙ and C2H3˙ radicals produced through H˙ abstraction and surface C2H4 oxidation through adsorption, H˙ abstraction, and C–C bond cleavage.32 Therefore, effective catalysts not only activate CH4 but also prevent deep oxidation paths, represented by HO2˙ quenching in the surface mechanism. Finally, the regeneration of active sites involves water desorption, resulting from adsorbed OH˙ radicals yielding O*. The catalytic reaction network with 10 surface species (excluding vacancies) and 26 reversible elementary steps used in this work is presented in Table 1.
Table 1 Set of heterogeneous reversible elementary reactions used in this work
| Step |
Equation |
Step |
Equation |
| 1 |
O2 (g) + 2* (s) ⇄ 2O* (s) |
15 |
CH2O* (s) + O* (s) ⇄ CHO* (s) + OH* (s) |
| 2 |
H2O (g) + * (s) ⇄ H2O* (s) |
16 |
CH2O (g) + O* (s) ⇄ CHO˙ (g) + OH* (s) |
| 3 |

|
17 |
CHO* (s) + O* (s) ⇄ CO* (s) + OH* (s) |
| 4 |
CO (g) + * (s) ⇄ CO* (s) |
18 |
CHO˙ (g) + O* (s) ⇄ CO (g) + OH* (s) |
| 5 |
CH4 (g) + O* (s) ⇄ CH3˙ (g) + OH* (s) |
19 |
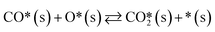
|
| 6 |
C2H6 (g) + O* (s) ⇄ C2H5˙ (g) + OH* (s) |
20 |
H2 (g) + O* (s) ⇄ H˙ (g) + OH* (s) |
| 7 |
C2H5˙ (g) + O* (s) ⇄ C2H4 (g) + OH* (s) |
21 |
H2O (g) + O* (s) ⇄ OH˙ (g) + OH* (s) |
| 8 |
C2H4 (g) + O* (s) ⇄ C2H3˙ (g) + OH* (s) |
22 |
OH˙ (g) + O* (s) ⇄ O˙ (g) + OH* (s) |
| 9 |
CH3˙ (g) + O* (s) ⇄ CH3O* (s) |
23 |
H2O2 (g) + O* (s) ⇄ HO2˙ (g) + OH* (s) |
| 10 |
CH3O* (s) + O* (s) ⇄ CH2O* (s) + OH* (s) |
24 |
HO2˙ (g) + O* (s) ⇄ O2 (g) + OH* (s) |
| 11 |
CH3O˙ (g) + O* (s) ⇄ CH2O (g) + OH* (s) |
25 |
HO2˙ (g) + * (s) ⇄ OH˙ (g) + O* (s) |
| 12 |
C2H4 (g) + O* (s) ⇄ CH3CHO* (s) |
26 |
OH* (s) + OH* (s) ⇄ H2O* (s) + O* (s) |
| 13 |
CH3CHO* (s) + O* (s) ⇄ CH2CHO* (s) + OH* (s) |
|
|
| 14 |
CH2CHO* (s) + O* (s) ⇄ CH2O* (s) + CHO* (s) |
|
|
Heterogeneous net production rates are computed from the forward (rfj) and backward (rbj) rates of each heterogeneous reaction step.
| | 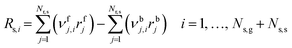 | (16) |
Nr,s is the total number of heterogeneous elementary steps in the mechanism and the subscript
j denotes the step number in the heterogeneous reaction mechanism (
Table 1). For the surface intermediates, fractional coverages are calculated from
eqn (8) and
(9). Rate values of each individual surface step in both forward and backward directions are calculated using the mean field approximation, law of mass action, and the two-parameter Arrhenius law.
| |  | (17) |
| | | kj = Aje−Ea,j/RT j = 1, …, Nr,s | (18) |
where
nj is the number of sites involved in the heterogeneous elementary reaction step
j. Adsorption steps are treated as sticking reactions (
i.e.,
Efa,j = 0,
j = 1–4, 9, 12), and their prefactors (
Afj) are calculated from collision theory.
| |  | (19) |
where
sj,i is the sticking coefficient of adsorbing gas-phase species
i in heterogeneous reaction step
j and
Mw,i is the molecular weight of gas-phase species
i. Brønsted–Evans–Polanyi (BEP) relationships are used to relate the activation energy of a forward surface step to its reaction enthalpy, and reaction family-specific constants are used in the relationships.
33 BEP relationships are applicable only to the forward rate activation energy (
eqn (20)), as the microscopic reversibility relates both forward and backward rate activation energies to the reaction enthalpy. The BEP parameters of the reaction families considered in this study are presented in
Table 2.
| |  | (20) |
where
E0,f is the intrinsic energy barrier for any reaction in reaction family
f,
αf is the transfer coefficient for any reaction in reaction family
f and

is the standard reaction enthalpy of heterogeneous reaction step
j.
Table 2 Reaction families and their corresponding Polanyi parameters
| Reaction family |
Step (Table 1) |
α
f
|
Ref. |
E
0,f
|
Ref. |
| (−) adsorptions |
1–4, 9, 12, 25 |
0 |
— |
0 |
— |
| (f1) H abstraction via Eley–Rideal |
5–8, 11, 16, 18, 20−24 |
0.75 |
34
|
96.8 |
26
|
| (f2) H abstraction via Langmuir–Hinshelwood |
10, 13, 15, 17 |
0.50 |
35
|
141.3 |
26
|
| (f3) OH˙ radical recombination via Langmuir–Hinshelwood |
26 |
0.65 |
36
|
73.9 |
30
|
| (f4) CO oxidation via Langmuir–Hinshelwood |
19 |
0.26 |
37
|
67.6 |
26
|
| (f5) C–C bond cleavage via Langmuir–Hinshelwood |
14 |
0.97 |
37
|
186.7 |
26
|
In Table 2, for H abstraction via Eley–Rideal reactions (f1), the intrinsic barrier is low and the transfer coefficient is high. In the BEP relationship, for reaction enthalpy values below −129 kJ mol−1, highly exothermic reactions yield negative activation energy values. This applies to many exothermic reactions in that family. Here, a new scaling relationship is proposed for these reactions:
| | 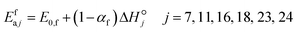 | (21) |
In this relationship, most of the exothermicity is attributed to the backward rather than the forward reaction.
2.7 Thermodynamic consistency
For any reversible reaction, the concentration-based thermodynamic equilibrium constant can be written as a function of the reaction entropy and enthalpy, and by combining it with the Arrhenius expressions, the enthalpic and entropic contributions to the forward (denoted with superscript f) and backward (denoted with superscript b) kinetic parameters can be isolated.| | 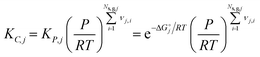 | (22) |
| |  | (23) |
| |  | (24) |
| | 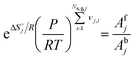 | (25) |
where Ns,g,j is the total number of gaseous species in reaction step j, KC,j is the concentration-based thermodynamic equilibrium constant of reaction step j, KP,j is the pressure-based thermodynamic equilibrium constant of reaction step j, P is pressure,  is the standard reaction Gibbs free energy of reaction step j and
is the standard reaction Gibbs free energy of reaction step j and  is the standard reaction entropy of reaction step j. Both enthalpy and entropy are temperature-dependent state functions. Hence, the activation energies and forward and backward prefactor values should also vary with temperature. For the homogeneous mechanism, thermodynamic consistency is ensured by directly computing the backward reaction rate constant from the forward reaction rate constant and the equilibrium constant:
is the standard reaction entropy of reaction step j. Both enthalpy and entropy are temperature-dependent state functions. Hence, the activation energies and forward and backward prefactor values should also vary with temperature. For the homogeneous mechanism, thermodynamic consistency is ensured by directly computing the backward reaction rate constant from the forward reaction rate constant and the equilibrium constant:| |  | (26) |
The equilibrium constant can be computed from the reaction Gibbs free energy, i.e., from the Gibbs energy of the formation of reactants and products. Temperature-dependent entropies and enthalpies of formation for each gaseous species are calculated via the NASA seven-coefficient polynomial parametrization of sensible heat at constant pressure within the temperature range of 200–1000 K and 1000–3500 K.| |  | (27) |
where Ns,j is the total number of species in reaction step j and  ,
,  and
and  are the standard Gibbs energy, enthalpy and entropy of species i, respectively. Ensuring thermodynamic consistency in surface reaction mechanisms is more challenging because of the unavailability of Gibbs free energy values for surface species. One way to overcome this challenge is to construct the state functions for surface reactions as combinations of adsorption and analogous gas-phase reactions.38 By identifying the minimum number of linearly independent surface reactions, we can categorize all reactions within the mechanism (Nr,s) into Nr,i linearly independent and Nr,d linearly dependent reactions. Once reactions are reordered such that the first Nr,i reactions are the linearly independent ones (i.e.,
are the standard Gibbs energy, enthalpy and entropy of species i, respectively. Ensuring thermodynamic consistency in surface reaction mechanisms is more challenging because of the unavailability of Gibbs free energy values for surface species. One way to overcome this challenge is to construct the state functions for surface reactions as combinations of adsorption and analogous gas-phase reactions.38 By identifying the minimum number of linearly independent surface reactions, we can categorize all reactions within the mechanism (Nr,s) into Nr,i linearly independent and Nr,d linearly dependent reactions. Once reactions are reordered such that the first Nr,i reactions are the linearly independent ones (i.e.,  ), any linearly dependent surface reaction can be expressed as a combination of linearly independent surface reactions.
), any linearly dependent surface reaction can be expressed as a combination of linearly independent surface reactions.| | 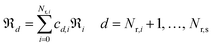 | (28) |
where ℜd is the dth dependent reaction outside the basis set, ℜi is the ith independent reaction inside the basis set and is cd,i the coefficient of linearly decomposed reaction d onto reaction i belonging to the basis set. The set of independent reactions, known as basis set, remains fixed in size but does not limit the kinetic relevance of linearly dependent steps. The basis set size in a reaction network can be determined by finding the rank of the stoichiometric coefficient matrix; the rank often corresponds to the number of surface species. Typically, reversible adsorption–desorption steps are selected as the basis set, even if all of them are not directly included in the mechanism. In the present work, the basis set comprised the chemisorption steps of the 10 surface species, namely, O˙, OH˙, H2O, CO2, CO, CH3O˙, CH2O, CHO˙, CH3CHO, and CH2CHO˙. With the basis set, for the general reaction A* (s) + B* (s) ⇄ C* (s) + D* (s), the enthalpy and entropy of every catalytic surface reaction (denoted with subscript sur) in Table 1 are computed from the analogous gas-phase reaction (denoted with subscript gas) and the chemisorption functions (denoted with subscript ads) as shown in eqn (29) and (30).| |  | (29) |
| |  | (30) |
where Ns,s,j is the total number of surface intermediates in heterogeneous reaction step j and cj,i is the coefficient for the adsorption of surface species i in reaction step j.
2.8 Temperature dependency of the basis set
Because the temperature dependency of the analogous gas-phase reactions is known from available thermochemistry, only temperature dependencies for chemisorption enthalpies and entropies (i.e., the basis set) are to be provided. For enthalpies, the statistical mechanics treatment of the chemisorption sensible heat considers the effect of changes in the degree of freedom (DOF). Every translational, rotational, and vibrational DOF contributes an amount of 0.5R, 0.5R, and R to the sensible heat, respectively, whereas a free, rigid, internal rotor contributes 0.5R.39 The change in DOFs assumes that (i) all translational DOFs are converted to vibrational DOFs, (ii) weakly adsorbed molecules  lose only one translational DOF, (iii) rotational DOFs are converted to vibrational DOFs, and (iv) for adsorbed species with a vertical axis through the adsorbed atom, one vibrational DOF gained is a free, rigid, internal rotor. With these assumptions, the temperature dependence of chemisorption enthalpy is deduced for the four cases in Table 3, and the chemisorption enthalpy at any given temperature is
lose only one translational DOF, (iii) rotational DOFs are converted to vibrational DOFs, and (iv) for adsorbed species with a vertical axis through the adsorbed atom, one vibrational DOF gained is a free, rigid, internal rotor. With these assumptions, the temperature dependence of chemisorption enthalpy is deduced for the four cases in Table 3, and the chemisorption enthalpy at any given temperature is| | 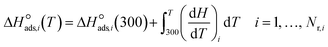 | (31) |
The chemisorption enthalpies in the basis set at 300 K serve as model descriptors. To reduce model parameters, Su et al.40 linked CH3O˙ and OH˙ chemisorption enthalpies by determining of the bond energy difference between R–OH and R–OCH3, and they set the average at 41 kJ mol−1, in agreement with values in ref. 41 up to R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3H7. Thus, the chemisorption enthalpy of CH3O˙ is no longer a descriptor, but is related to the chemisorption enthalpy of OH˙ (eqn (32)). This study proposes a similar relationship for CH2CHO˙ and CHO˙ (eqn (33)) on the basis of the average bond energy difference between R–CHO and R–CH2CHO from aldehydes (i.e., difference in bond energy between carbonyl groups of different lengths), which is estimated to be 10 kJ mol−1.42
C3H7. Thus, the chemisorption enthalpy of CH3O˙ is no longer a descriptor, but is related to the chemisorption enthalpy of OH˙ (eqn (32)). This study proposes a similar relationship for CH2CHO˙ and CHO˙ (eqn (33)) on the basis of the average bond energy difference between R–CHO and R–CH2CHO from aldehydes (i.e., difference in bond energy between carbonyl groups of different lengths), which is estimated to be 10 kJ mol−1.42| |  | (32) |
| |  | (33) |
where ΔQavg denotes the average bond energy difference between two types of hydrocarbons. The chemisorption entropy's temperature dependence is described by eqn (34), where βi is a constant that is independent of adsorbate characteristics and binding strength. By propagating the entropic dependency over temperature evenly for the adsorption and desorption prefactors, we find that the adsorption prefactor is proportional to Tβi, while the desorption prefactor is proportional to T−βi; βi = 0.25 is chosen consistently.38| |  | (34) |
Table 3 Temperature dependencies of chemisorption enthalpies for the steps in the basis set
| Molecule |
Species |
Contribution of the degree of freedom |
(dH/dT)i |
| Translational |
Rotational |
Vibrational |
Internal rigid rotor |
| Monoatomic |
O˙ |
−3 × 0.5R |
|
3 × R |
|
1.5R |
| Diatomic |
OH˙, CO |
–3 × 0.5R |
–2 × 0.5R |
4 × R |
1 × 0.5R |
2R |
| Nonlinear polyatomic |
CO2, CHO˙, CH2O, CH3O˙, CH2CHO˙ |
–3 × 0.5R |
–3 × 0.5R |
5 × R |
1 × 0.5R |
2.5R |
| Weakly bound nonlinear polyatomic |
H2O, CH3CHO |
−1 × 0.5R |
−3 × 0.5R |
4 × R |
|
2R |
2.9 Model descriptors
Model descriptors are primarily the enthalpies and entropies of the 10 chemisorption steps at 300 K. Empirical analogies can help reduce the enthalpic descriptors from 10 to 8, and the enthalpic descriptors are calculated at the reaction temperature. Forward and backward rate activation energies are calculated from BEP relationships and thermodynamic consistency, respectively. Adsorptions are assumed to be nonactivated, and hence, heats of chemisorption represent desorption activation energies. Temperature effects also apply to chemisorption entropies, which are linked to forward and backward rate prefactors by the even propagation of the entropic contribution to initial prefactor estimates (eqn (35) and (36)). The initial prefactor estimates (denoted with subscript init) are obtained from transition-state theory and the literature (ESI,† section S2). For adsorptions, the forward adsorption prefactor from eqn (35) is used to obtain the sticking coefficient from collision theory to ensure that the sticking coefficient does not exceed unity. If it exceeds unity, it is adjusted to unity while maintaining the prefactor ratio determined by the reaction entropy.| |  | (35) |
| | 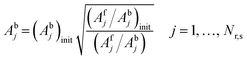 | (36) |
In theory, thermodynamic properties of reactions in the basis set should suffice as descriptors. However, in practice, the density of active sites should also be considered. Under the assumption of a uniform distribution of surface intermediates and active sites, the model includes 19 descriptors: 8 chemisorption enthalpies at 300 K, 10 chemisorption entropies at 300 K, and the active site density. Fig. 2 shows the relationship between catalytic descriptors and kinetic parameters.
 |
| | Fig. 2 Relationship between model descriptors and kinetic parameters of the microkinetic model. | |
2.10 Solution procedure and parameter estimation
The system of equations defined by the continuity equations are a set of partial differential-algebraic equations (PDEs), and they are converted into a set of differential-algebraic equations (DAEs) by using the orthogonal collocation method (ESI,† section S3), with seven and four collocation points for the intraparticle and interstitial phases, respectively. The resulting system of DAEs is solved using the SUNDIALS IDA package43via the scikits.odes wrapper for Python.44 Conversion of reactants and carbon molar selectivity of products are determined from the average mass fraction in the interstitial phase at the reactor outlet. All kinetic, thermodynamic, and transport calculations are performed in the Cantera framework45 by using the GRI thermodynamic and transport database.46
The vector of the 19 catalytic descriptor estimates (β) are determined through regression by minimizing the objective function in a two-step process: (i) genetic-algorithm-based optimization to conduct an order-of-magnitude search of parameters using a PFR model with the DEAP library47 and (ii) gradientless optimization using a 1D heterogeneous reactor model with the SciPy library48 for the refinement of the parameters. Furthermore, the associated confidence interval is calculated for each estimated descriptor value, at the 5% significance level.49
| |  | (37) |
where
Nobs is the number of observations,
Nres is the number of experimental responses per observation,
f is the model multiresponse function,
xi is the variable representing the
ith observation and
ψi,j is the experimental (denoted with superscript “exp”) or calculated (denoted with superscript “calc”) performance metric of species
j for the
ith observation. To identify key descriptors in the model, after the Jacobian has been calculated, we calculate the first-order normalized sensitivity (
ϕij) of each descriptor (
βj) estimate for every response at each experimental condition (
ψi), as shown in
eqn (38). The Jacobian is evaluated with the numdifftools library,
50 with the spacing scaled to the order of magnitude of each descriptor to avoid round-off errors in the approximation. From the Jacobian matrix, the correlation matrix is calculated.
| |  | (38) |
Lastly, the global significance test of the model is performed to test the null hypothesis that all parameters would simultaneously be equal to zero. This null hypothesis is verified by comparing the regression sum of squares to the residual sum of squares divided by the number of DOFs with respect to the corresponding statistic.
51| |  | (39) |
where
FE is Fisher's E,
n is the number of experiments and responses,
p is the total number of catalytic descriptors of the model,
Finv is the inverse
F distribution and
α is the significance of the statistical test.
3. Results
3.1 Textural property estimation
To measure the surface area of nonporous surfaces via adsorption–desorption experiments, Ar physisorption experiments were performed. The multipoint BET surface areas are considered for the model, along with pore volume estimates that fall between the single point and Barrett–Joyner–Halenda methods. Estimated surface areas and pore volumes of the three catalysts are listed in Table 4, along with other textural properties. In the literature, only surface area values for SiO2-supported catalysts are available, and they are consistent with those of IMP SiO2 obtained in the present study.26,52 Nevertheless, the values reported herein are small (<10 mc2 kgc−1) for the chosen analytical method, bearing a high uncertainty and thus demanding careful consideration, especially knowing that Mn–Na2WO4/SiO2 undergo severe phase transformations under reaction condition. Differences in the surface area between IMP SiO2 and the SiC-containing catalysts are attributed to the presence of SiC, which, unlike SiO2, does not collapse under calcination; consequently, the SiC-containing catalysts have larger surface areas. The importance of a large surface area was shown by Wang et al.,53 who linearly correlated the surface area and OCM productivity for Mn–Na2WO4/SiC catalysts calcined under different conditions. We set the tortuosity to 2.5 mg2 mc−2 based on previous results.54 The bulk material density was estimated by weighing various catalyst volumes, and the average bed packing density was determined by loading various catalyst weights and measuring the height of the bed in the reactor. The low average bed packing density of IMP SiO2 agrees with those reported for Mn–Na2WO4/SiO2 (333 kgc mc−3 in ref. 52 and 400 kgc mc−3 in ref. 54). A key feature of SiC at the macroscopic level is that it endows the catalyst with higher density, resulting in the catalyst having an average packing density closer to the expected average packing density of a solid catalyst. From the estimates of both densities, the average bed packing porosity was obtained, and the bulk catalyst porosity was determined from the pore volume and bulk catalyst density. The intraparticle phase radius was set at 125 μm since the catalyst was sieved in the 150–300 μm range, and the interstitial phase radius was determined from the average bed packing porosity and the average particle radius.55
Table 4 Textural properties of the catalysts studied
| Property |
IMP SiO2 |
SD SiO2–α + βSiC |
SD SiO2–βSiC |
| Surface area (mc2 kgc−1) |
2720 |
3580 |
4340 |
| Pore volume (mg3 kgc−1) |
3.4 × 10−5 |
2.8 × 10−5 |
2.2 × 10−5 |
| Bulk catalyst porosity (mg3 mc−3) |
0.255 |
0.336 |
0.286 |
| Catalyst tortuosity (mg2 mc−2) |
2.5 |
2.5 |
2.5 |
| Bulk catalyst density (kgc mc−3) |
750 |
1200 |
1300 |
| Average bed packing density (kgc mb−3) |
450 |
700 |
800 |
| Average bed packing porosity (mg3 mb−3) |
0.40 |
0.42 |
0.38 |
| Intraparticle phase radius (m) |
125 × 10−6 |
125 × 10−6 |
125 × 10−6 |
| Interstitial phase radius (m) |
56 × 10−6 |
60 × 10−6 |
51 × 10−6 |
3.2 Temperature-programmed experiments and simulations
Temperature-programmed O2 desorption (O2-TPD) experiments shown in Fig. 3 revealed significant differences between the catalysts. SiC-containing catalysts exhibited single desorption peaks at lower temperatures compared with IMP SiO2, which showed a main peak (at 792 °C) and a secondary low-temperature peak. The two types of reactive lattice oxygen are exclusive to trimetallic Mn–Na2WO4/SiO2 catalysts; the strongly bonded oxygen and weakly bonded oxygen can be reversibly removed through reduction at temperatures above 700 °C and above 650 °C, respectively.27 Other authors56 have proposed that peaks at high temperatures may be linked to bulk lattice oxygen, adversely affecting OCM performance. Fig. 3 suggests that incorporating SiC into the support via spray-drying reduced the lattice oxygen strength in Mn or W species compared with that in Mn–Na2WO4/SiO2. Furthermore, the breadth of peaks for the SiC-containing catalysts indicates the presence of multiple oxygen species that can be released, similar to the case of IMP SiO2, where phases containing W and Mn interact differently with oxygen. Additionally, SD SiO2–α + βSiC exhibited the highest value for the total amount of O2 desorbed (64 μmol gc−1), and it was followed by IMP SiO2 (47 μmol gc−1). These differences observed are associated with the metal to which oxygen is bonded. In other words, the preparation method, the presence of SiC, and the crystal phase of SiC influence the interaction between active sites and O2 by modifying the electronic environment of Mn and W species, thereby altering their interaction with oxygen. This is evidenced by the observed changes in oxygen uptake, which reflect variations in oxygen mobility and dispersion. This interaction is denoted by σ in the model. This is in accord with the fact that O2 uptake has been reported to be proportional to the Mn content.57
 |
| | Fig. 3 Evolution of temperature and measured (solid) and predicted (dashed) O2 desorption normalized concerning the total amount of O2 desorbed (area under the curve) over time for each of the fresh catalysts. Conditions: P = 1 bar, TI = 25 °C, TF = 850 °C, β = 7.5 min−1, t∞ = 30 min, FT = 50 NmL min−1, pCH4,0 = 0 bar, W = 50 mgc. O2 chemisorption occurred for 6 h at 25 °C and 50 NmL min−1 (10% O2). Simulations were performed assuming plug-flow conditions and model descriptors in Table 5. | |
Table 5 Estimates of descriptors for each catalyst along with their 95% confidence intervals. Units: chemisorption enthalpies at 300 K, kJ mol−1; chemisorption entropies at 300 K, J mol−1 K−1; active site density, kmol mc−2
| Catalyst descriptor |
IMP SiO2 |
SD SiO2–α + βSiC |
SD SiO2–βSiC |
|
H
1
|
Chemisorption enthalpy, O˙ |
−319 ± 17 |
−327 ± 23 |
−327 ± 29 |
|
H
2
|
Chemisorption enthalpy, OH˙ |
−279 ± 14 |
−300 ± 20 |
−297 ± 25 |
|
H
3
|
Chemisorption enthalpy, H2O |
−27 ± 3 |
−22 ± 3 |
−16 ± 6 |
|
H
4
|
Chemisorption enthalpy, CH2O |
−138 ± 31 |
−154 ± 39 |
−146 ± 50 |
|
H
5
|
Chemisorption enthalpy, CHO˙ |
−205 ± 33 |
−140 ± 50 |
−256 ± 51 |
|
H
6
|
Chemisorption enthalpy, CO |
−100 ± 12 |
−99 ± 4 |
−109 ± 21 |
|
H
7
|
Chemisorption enthalpy, CO2 |
−241 ± 23 |
−261 ± 19 |
−255 ± 42 |
|
H
8
|
Chemisorption enthalpy, CH3CHO |
−27 ± 4 |
−37 ± 7 |
−70 ± 7 |
|
S
1
|
Chemisorption entropy, O˙ |
−101 ± 15 |
−110 ± 29 |
−103 ± 31 |
|
S
2
|
Chemisorption entropy, OH˙ |
−170 ± 15 |
−201 ± 30 |
−184 ± 34 |
|
S
3
|
Chemisorption entropy, H2O |
−286 ± 15 |
−277 ± 24 |
−250 ± 29 |
|
S
4
|
Chemisorption entropy, CH3O˙ |
−130 ± 14 |
−148 ± 21 |
−138 ± 29 |
|
S
5
|
Chemisorption entropy, CH2O |
−146 ± 34 |
−206 ± 48 |
−175 ± 57 |
|
S
6
|
Chemisorption entropy, CHO˙ |
−157 ± 25 |
−112 ± 50 |
−201 ± 48 |
|
S
7
|
Chemisorption entropy of CO |
−216 ± 26 |
−228 ± 36 |
−231 ± 44 |
|
S
8
|
Chemisorption entropy, CO2 |
−153 ± 21 |
−164 ± 23 |
−154 ± 37 |
|
S
9
|
Chemisorption entropy, CH3CHO |
−309 ± 37 |
−299 ± 66 |
−230 ± 41 |
|
S
10
|
Chemisorption entropy, CH2CHO˙ |
−286 ± 35 |
−246 ± 43 |
−289 ± 49 |
|
σ
|
Active site density |
(5.02 ± 0.03) × 10−9 |
(3.76 ± 0.04) × 10−9 |
(2.59 ± 0.07) × 10−9 |
The simulated desorption profiles represented by dashed lines in Fig. 3 were obtained from descriptors estimated through regression and initial coverages on the basis of the observed O2 uptake. Since the variation of the O2 chemisorption enthalpy across catalysts was minimal (Table 5), differences in chemisorption entropy and initial coverage could explain the experimentally observed disparities. For all three catalysts, the model predicted a low-temperature main peak around 600 °C, which was close to the experimental observation for SD SiO2–α + βSiC and in contrast to the dual peaks of IMP SiO2 at higher temperatures. The model predictions supported the concept that weakly bonded oxygen influences the catalytic activity in the steady-state regime.58 However, the simulations highlighted a key model assumption, namely the mean field approximation, which may not accord with the observed O2-active site interplay, at least for IMP SiO2. Extending the model with two types of active sites—strong and weaker oxygen bonding sites—could provide a more realistic description, but the number of model parameters would then increase. Fleischer et al.59 accounted for two types of oxygen species via two-step dissociative chemisorption.
Fig. 4 depicts the CH4 temperature-programmed surface reaction (CH4-TPSR), for which ion currents corresponding to m/z values of 2 (H2+), 17 (OH+, CH5+), 18 (H2O+), 28 (CO+, C2H4+), 29 (C2H5+), 30 (C2H6+), 32 (O2+), and 44 (CO2+) were monitored. Fig. 4 shows marginal desorption of O2 at temperatures below 600 °C, and as the temperature rises, products are formed. IMP SiO2 exhibits two C2H6 peaks, at approximately 740 and 850 °C, representing a primary product, whereas SiC-containing catalysts show a single high-temperature peak, in agreement with observations in previous O2-TPD experiments. This supports the notion that CH4 activation occurs through strongly bound oxygen, while weakly bound oxygen leads to product formation at lower temperatures, albeit at significantly reduced rates.60 The primary peaks of other products such as C2H4/CO and CO2 is at 850 °C. Thus, low temperature C2H6 formation is also indicative of the prevalence of CH3˙ radical onto the catalyst surface.59 Furthermore, the H2 signal reveals different kinetic behavior as SD SiO2–α + βSiC shows activity even at low temperatures, consistent with signals such as C2H4/CO and H2O whose presence is required for H2 formation.
 |
| | Fig. 4 Evolution of temperature and MS signals over time for each catalyst at different CH4 partial pressures in the carrier gas. Conditions: P = 1 bar, TI = 25 °C, TF = 850 °C, β = 7.5 min−1, t∞ = 30 min, FT = 100 NmL min−1, W = 50 mgc. O2 chemisorption occurred for 6 h at 25 °C and 50 NmL min−1 (10% O2). | |
Simulations performed with the kinetic model corresponding to Fig. 4 (pCH4,0 = 1 bar) are described in ESI† (section S4). Primary carbon-containing products, namely C2H6 and CO, dominated at lower temperatures (around ∼600 °C), which indicated their primary nature compared with C2H4 and CO2, which appeared at higher temperatures. In particular, the absence of predicted C2H4 suggests that m/z = 28 in Fig. 4 could be attributed to CO. An analysis of the coverage distribution showed initial enrichments of O* and the absence of exposure to H-containing species, unlike steady-state simulations. This implies that the CH4-TPSR experiments conducted in this work did not involve the operating regime found in steady-state conditions, which is consistent with the absence of predicted C2H4 controlled by the existing O* at the initial condition. O* coverage reduced over the simulation, declining noticeably upon CO2 production. Notably, the maximum of OH* corresponded to the peak production of C2H6, underscoring the relationship between OH* and O* and their impact on catalyst activity. In fact, under these conditions, a positive correlation was observed between the desorbed O2 amount and the catalyst activity (i.e., the reason for SD SiO2–α + βSiC showing larger peaks).
3.3 Parameter estimation
Model descriptors and their significance are estimated through regression with steady-state kinetic data presented in ref. 20 are shown in Table 5.
The O˙ chemisorption enthalpy is related to the O2 chemisorption enthalpy through the bond dissociation energy of O2, for activating CH4via the heterogeneous primary initiation of H abstraction. The estimated O˙ chemisorption enthalpies of all three catalysts, do not show statistically significant differences, thus implicitly suggesting a lack of tendency of SiC-containing catalysts to show stronger bonding with or affinity for O˙. O˙ chemisorption enthalpy values expressed as heats of O2 chemisorption at 800 °C were 113, 130, and 130 kJ mol−1 for IMP SiO2, SD SiO2–α + βSiC, and SD SiO2–βSiC, respectively. As a result, it is clear that the O2 chemisorption enthalpy alone does not describe the temperature-programmed experiment in Fig. 3 (i.e., the desorption is not entirely driven by the O2 desorption barrier), wherein O* plays a pivotal role in the overall catalyst activity.
The estimated OH˙ chemisorption values were not statistically different for the three catalysts, despite the values for SD SiO2–α + βSiC and SD SiO2–βSiC being higher than that for IMP SiO2. The absolute chemisorption value or heat of chemisorption of the hydroxyls indicates their degree of stability, which increases proportionally with the heat value.26,32 These surface intermediates determine the activation barriers to many key heterogeneous steps, such as the Eley–Rideal steps, including heterogeneous CH4 initiation, whose reaction enthalpy is proportional to  (40, 27, and 30 kJ mol−1 for IMP SiO2, SD SiO2–α + βSiC, and SD SiO2–βSiC, respectively). Note that the OH˙ chemisorption enthalpy influences other critical routes related to deep catalytic oxidation of CH3˙ radicals and C2H4, as well as the hydroxyl species regeneration step. The expected larger H2O chemisorption entropies in Table 5, render the regeneration step more kinetically favorable for SD SiO2–α + βSiC, especially compared with IMP SiO2. Furthermore, weaker H2O adsorption has been reported to result in higher CH4 activity.30
(40, 27, and 30 kJ mol−1 for IMP SiO2, SD SiO2–α + βSiC, and SD SiO2–βSiC, respectively). Note that the OH˙ chemisorption enthalpy influences other critical routes related to deep catalytic oxidation of CH3˙ radicals and C2H4, as well as the hydroxyl species regeneration step. The expected larger H2O chemisorption entropies in Table 5, render the regeneration step more kinetically favorable for SD SiO2–α + βSiC, especially compared with IMP SiO2. Furthermore, weaker H2O adsorption has been reported to result in higher CH4 activity.30
Differences in O˙ and OH˙ chemisorptions also influence the HO2˙ quenching kinetics. In that regard, IMP SiO2 is expected to have lower activation barriers for backward quenching reactions and overall enhanced rates. These differences are especially significant for the O*-mediated quenching reaction compared with the vacancy-mediated quenching reaction. HO2˙ are active chain carriers in the gas phase. This interpretation cannot be decoupled from the active site density value, which influences reaction rates in linear proportion to the rate constant and quadratically for second-order reactions. The estimated active site density was significantly different across the catalysts, for IMP SiO2 being twice that for SD SiO2–βSiC, confirming that SiC reduced the HO2˙ quenching capability of the Mn–Na2WO4 catalyst.
Another notable difference in Table 5 concerns deep oxidation routes. CH3CHO chemisorption enthalpy showed stronger interaction with C2H4 for SD SiO2–βSiC compared with SD SiO2–α + βSiC and particularly with IMP SiO2. Together with the sticking coefficient of CH3˙,26,32,61 CH3CHO chemisorption enthalpy is crucial for C2 selectivity.30 A statistically corroborated less negative entropy indicates more kinetically prone C2H4 oxidation by SD SiO2–βSiC, which is indicated by the catalyst's C2H4 sticking coefficient of 1.3 × 10−7 at 800 °C; the C2H4 sticking coefficient of SD SiO2–α + βSiC and IMP SiO2 were smaller, namely 6.1 × 10−9 for the latter. This trend was reversed for the C–C bond scission step, which was much more favorable for SD SiO2–α + βSiC owing to its less negative CH2CHO˙ chemisorption enthalpy and entropy. IMP SiO2 behaved similar to SD SiO2–α + βSiC with regard to C2H4 oxidation. The difference between the CH3O˙ and CH2O chemisorption entropies for SD SiO2–α + βSiC suggests low oxidation tendency for single-carbon intermediates, in line with a significantly lower CHO˙ chemisorption enthalpy. No significant differences were observed between CO and CO2 chemisorption descriptors for the catalysts.
The effect of model descriptors on the Arrhenius parameters of each elementary and reversible step is shown in Fig. 5. Note that the use of the 3-parameter Arrhenius expression (eqn (18)) can lead to a pronounced correlation between the activation energy and the prefactor, thereby influencing results in Fig. 5.62,63 Based on the figure, the forward rate activation energy and prefactor values for H-abstraction steps (r5–r8) follow the sequence IMP SiO2 > SiO2–βSiC > SD SiO2–α + βSiC, regardless of whether the hydrocarbon acts as an H source. The difference in activation energies of H abstraction from CH4 leads to higher endothermicity, slowing CH4 conversion and reducing the overall catalytic contribution.26,32 This also applies to C2H4 yielding C2H3˙ and to the eventual COX product formation, as the latter oxidizes in the contiguous gas-phase. This trend is reversed in the case of the adsorption of C2H4 (r12), which is more prominent in the case of SD SiO2–βSiC. Despite higher C2H4 sticking coefficients, this catalyst showed smaller kinetic parameters related to C2H4 dehydrogenation and scission (r13–r14). Thus, differences in the catalytic contribution to C2H4 oxidation are expected between the catalysts. While the sticking rate of CH3˙ (r9) is similar for all catalysts, its reverse counterpart is slightly faster at lower temperatures for SD SiO2–α + βSiC, which is indicated by the catalyst's marginally larger desorption activation energy. The sticking coefficients of r9 are relatively high, on the order of 10−5–10−4, suggesting that the high activity resulting from the O2 heat of chemisorption is not directed by strong inhibition of the oxidation rate of CH3˙ radicals. Moreover, Fig. 5 shows that SD SiO2–α + βSiC hinders the CH2O* route more.
 |
| | Fig. 5 Activation energy values of all three catalysts obtained with the microkinetic model descriptors in Table 5 for all heterogeneous (a) forward and (b) backward reactions, and prefactor values for all three catalysts obtained with the microkinetic model descriptors in Table 5 for all heterogeneous (c) forward and (d) backward reactions. The line width shows temperature-dependent variations in the 25–800 °C range. Reaction nomenclature is as presented in Table 1. | |
The regeneration step (r26) parameters significantly differ for SD SiO2–α + βSiC. Notably, forward and backward rate prefactors differ by two orders of magnitude unlike the other catalysts, indicating the large weight of the entropic descriptor contribution, as the OH˙ and H2O chemisorption entropy differences are not greater than 30 J mol−1 K−1. This observation results from the ratio of prefactors being proportional to the exponent of the surface reaction entropy, and it is also evident from the prefactor values of H2O chemisorption (r2) on SD SiO2–βSiC.
3.4 Regression assessment
Parity plots in Fig. 6 compare measured and predicted performance metrics with descriptors from Table 5. The calculated FE values of 1329.6, 706.4, and 650.3 for IMP SiO2, SiO2–βSiC, and SD SiO2–α + βSiC, respectively, reject the null hypothesis with a tabulated value of 1.6 and substantiate the global significance of the model validation. High FE values, in order of hundreds or thousands, especially for IMP SiO2, confirm the model's adaptability to the experimental data.51 Overall, the parity plots depict a satisfactory match for selectivities and CH4 conversion, though the accurate capture of the experimental trends of O2 conversion poses a challenge. This generalized disparity is because of unmeasured H2 and H2O yields impacting predictions. Specifically, heterogeneous steps 20–26, devoid of carbon products, are solely bound by O2 conversion. The difficulty in capturing O2 conversion trends is again observed when comparing the residuals to a standard normal distribution (ESI,† Fig. S3). Despite the overall linear trends, O2 conversion deviates from linearity for all three catalysts, and variance differences across predicted values (i.e., heteroscedasticity) also exist, as indicated by slope changes in quantiles. Despite this, the relative error for O2 conversion generally remains below the 25% relative deviation mark. Furthermore, some discrepancies in the predictions of C2 product selectivities across the three catalysts are highly noticeable at lower CH4 conversion rates, approximately below 5%. It is worth noting that some of these deviations may also be ascribed to heat effects causing temperature gradients64–66 despite the flow ideality, intrinsic kinetic regime, and isothermicity of the reactor (2 mm i.d., 1 cm long) having been previously checked.20
 |
| | Fig. 6 Parity plots obtained by fitting experimental performance metrics to the microkinetic model with the descriptors in Table 5 for (a and b) IMP SiO2, (c and d) SD SiO2–α + βSiC, and (e and f) SD SiO2–βSiC. | |
The binary correlation matrix of model descriptors (ESI,† Fig. S4) shows associations between certain parameters. However, the absence of strong correlations exceeding 0.95 suggests model descriptor redundancy.51 The largest binary correlation is between the chemisorption enthalpies of O˙ (H1) and OH˙ (H2), in the range of 0.68–0.77 across catalysts. Smaller binary correlations across the three catalysts include the CH3O˙ chemisorption entropy (S4), the chemisorption enthalpy of O˙ (H1), and the chemisorption enthalpy and entropy of CO2 (H7 and S8). Catalyst-specific correlations also exist, such as the chemisorption enthalpy and entropy of OH˙ (H2 and S2) for SiO2–α + βSiC and SD SiO2–βSiC, and the chemisorption enthalpy of CO and entropy of CO2 (H6 and S8) for IMP SiO2 and SD SiO2–βSiC. Still, most descriptors exhibit absolute correlation values closer to 0 than 0.95.
3.5 Model descriptor benchmarking
Normalized sensitivity coefficients quantify the effect of model inputs on outputs at specific conditions. To identify the most influential model descriptors, we used box plots of the sensitivity coefficients of all descriptors over all the experimental conditions, and they are presented in ESI† (Fig. S5). O˙ and OH˙ chemisorption enthalpies (H1 and H2) had the most significant effect, consistent with being part of all Eley–Rideal steps. On the one hand, O2 heat of chemisorption played a key role in O2 activity and COX selectivity, in line with the results of Thybaut et al.30 On the other hand, OH˙ chemisorption enthalpy positively influenced CH4 conversion and C2 product selectivity. Other remarkable effects include CO2 chemisorption enthalpy (H7) inhibiting both reactant conversions and aligning with global rate type-based kinetic models reported in the literature,67 and active site density (σ) exhibiting different effects on model responses, depending on experimental conditions.
Fig. 7 compares descriptors from this study with descriptors in the literature,26,30–32,61 namely, H abstraction from CH4 reaction enthalpy, O2 chemisorption enthalpy, CH3˙ sticking coefficient, and active site density. The significance of these four descriptors is shown in Fig. S5,† for the H abstraction from CH4 reaction enthalpy is a function of the O2 chemisorption enthalpy and the OH˙ chemisorption enthalpy. For instance, La–Sr/CaO and Sr/La2O3 in Fig. 7 exhibit OH˙ chemisorption heats of 257 kJ mol−1 and 278 kJ mol−1, which correlate with the respective enthalpies of H abstraction from CH4 of 65 kJ mol−1 and 44 kJ mol−1.26,32 Similar trends were observed with OH˙ chemisorption heats for IMP SiO2, SiO2–βSiC, and SD SiO2–α + βSiC, resulting in H-abstraction from CH4 reaction enthalpies of 57 kJ mol−1, 44 kJ mol−1 and 47 kJ mol−1 at 800 °C. It is important to highlight that while these descriptor values are directly linked to the intrinsic properties of the catalyst, they are also influenced by operating conditions. For example, exposure of La–Sr/CaO to CO2 cofeeding may alter these descriptors due to the formation of carbonates.68
 |
| | Fig. 7 Comparison of four main descriptors obtained in this work with values reported in the literature by using descriptor-based microkinetic models: (a) reaction enthalpy of H-abstraction from CH4, (b) heat of chemisorption of O2, (c) CH3˙ sticking coefficient, and (d) active site density. Descriptor sources: A, Sun et al.;31 B, Thybaut et al.;30 C, Alexiadis et al.;32 D, Kechagiopoulos et al.;55 E, Alexiadis et al.;26 F, Ahari et al.;52 G, Karakaya et al.;54 H, this work. Descriptors include virtual optimal values (striped bars) and physical boundaries from Pirro et al.69 (dashed lines). CH3˙ sticking coefficients have been estimated from collision theory at 800 °C. | |
Careful examination of the descriptor values in Fig. 7 is important since they were derived under different conditions and with different considerations. For example, Ahari et al.52 used an isothermal plug-flow reactor, while Karakaya et al.54 focused on nonisothermal effects in the microkinetics. Additionally, Alexiadis et al.61 demonstrated how the heat of O2 chemisorption could vary by up to 30 kJ mol−1 with changes in catalyst dilution in the bed. Hence, Fig. 7 does not depict clear trends for descriptors and catalyst families, not even between promoted and unpromoted catalysts (e.g., Li/MgO vs. Sn–Li/MgO) or within the same catalyst type (e.g., Mn–Na2WO4/SiO2). In the latter case, factors such as metal loading, calcination conditions, SiO2 type, and catalyst synthesis method significantly influence performance. Still, it appears from Fig. 7 that Mn–Na2WO4/SiO2 catalysts have low CH3˙ and C2H4 sticking coefficients while also exhibiting lower enthalpies of H-abstraction from the CH4 reaction. Furthermore, Mn–Na2WO4/SiO2 catalysts have low O2 heat of chemisorption and low CH3˙ sticking coefficients, which are crucial for improved OCM yields by SiC.
In Fig. 7, dashed lines delineate the lower and upper bounds defining feasible values,69 and all descriptors fall within those limits. Nonetheless, chemisorption functions as descriptors have the advantage of facilitating the assessment of their physical viability. For enthalpies, the necessity for the heat of adsorption of species i to be positive as shown in Table 5. Furthermore, thermodynamics dictate that for any endothermic reaction, the forward activation energy should be larger than the heat of reaction; this is satisfied through the selection of the Polanyi parameters E0,f and αf to ensure that the relationship
to be positive as shown in Table 5. Furthermore, thermodynamics dictate that for any endothermic reaction, the forward activation energy should be larger than the heat of reaction; this is satisfied through the selection of the Polanyi parameters E0,f and αf to ensure that the relationship  holds. For chemisorption entropies, upholding the “Langmuirian integrity” requires
holds. For chemisorption entropies, upholding the “Langmuirian integrity” requires  , which accounts for the loss of translational contribution upon adsorption. A less strict constraint, proposed by Vannice et al.,70 is
, which accounts for the loss of translational contribution upon adsorption. A less strict constraint, proposed by Vannice et al.,70 is  (in J mol−1 K−1) from the decrease of free volume upon adsorption at the standard state coverage of 0.5, with the upper limit dictated by the relationship described before. Values associated with both entropic constraints are presented in Table 6.
(in J mol−1 K−1) from the decrease of free volume upon adsorption at the standard state coverage of 0.5, with the upper limit dictated by the relationship described before. Values associated with both entropic constraints are presented in Table 6.
Table 6 Chemisorption entropies of the species in the basis set at 800 °C and their corresponding constraints. Values in bold denote violation of thermodynamic constraints. Units: chemisorption entropies, J mol−1 K−1
| Species |
IMP SiO2 |
SD SiO2–α + βSiC |
SD SiO2–βSiC |
| O˙ |
0 < |−96.0| < 188.3 |
0 < |−104.7| < 188.3 |
0 < |−97.9| < 188.3 |
| 41.8 < |−96.0| < 484.3 |
41.8 < |−104.7| < 495.3 |
41.8 < |−97.9| < 495.7 |
| OH˙ |
0 < |−164.8| < 221.9 |
0 < |−195.9| < 221.9 |
0 < |−179.1| < 221.9 |
| 41.8 < |−164.8| < 423.6 |
41.8 < |−195.9| < 452.3 |
41.8 < |−179.1| < 448.9 |
| H2O |
0 < |−280.7| < 235.7
|
0 < |−272.2| < 235.7
|
0 < |−244.3| < 235.7
|
|
41.8 < |−280.7| < 65.8
|
41.8 < |−272.2| < 59.1
|
41.8 < |−244.3| < 51.1
|
| CH3O˙ |
0 < |−124.9| <301.8 |
0 < |−143.0| < 301.8 |
0 < |−132.8| < 301.8 |
| 41.8 < |−124.9| < 363.1 |
41.8 < |−143.0| < 391.8 |
41.8 < |−132.8| < 388.4 |
| CH2O |
0 < |−140.8| < 279.8 |
0 < |−200.3| < 279.8 |
0 < |−170.2| < 279.8 |
| 41.8 < |−140.8| < 221.8 |
41.8 < |−200.3| < 243.9 |
41.8 < |−170.2| < 233.4 |
| CHO˙ |
0 < |−151.8| < 276.5 |
0 < |−106.5| < 276.5 |
0 < |−195.5| < 276.5 |
| 41.8 < |−151.8| < 314.9 |
41.8 < |−106.5| < 225.0 |
41.8 < |−195.5| < 386.9 |
| CO |
0 < |−210.9| < 236.9 |
0 < |−222.8| < 236.9 |
0 < |−225.4| < 236.9 |
|
41.8 < |−210.9| < 173.0
|
41.8 < |−222.8| < 171.0
|
41.8 < |−225.4| < 185.4
|
| CO2 |
0 < |−147.5| < 273.2 |
0 < |−158.9| < 273.2 |
0 < |−148.9| < 273.2 |
| 41.8 < |−147.5| < 366.4 |
41.8 < |−158.9| < 394.3 |
41.8 < |−148.9| < 384.8 |
| CH3CHO |
0 < |−303.8| < 371.2 |
0 < |−293.4| < 371.2 |
0 < |−224.7| < 371.2 |
|
41.8 < |−303.8| < 66.2
|
41.8 < |−293.4| < 80.5
|
41.8 < |−224.7| < 125.9
|
| CH2CHO˙ |
0 < |−280.9| < 365.5 |
0 < |−240.7| < 365.5 |
0 < |−283.8| < 365.5 |
| 41.8 < |−280.9| < 301.5 |
41.8 < |−240.7| < 211.0
|
41.8 < |−283.8| < 372.9 |
In Table 6, only the H2O chemisorption entropy violates the strict constraint, which weakens model interpretability. This anomaly could result from the absence of H2O as a model response, impacting O2 conversion predictions. Addressing this issue may involve measuring the H2O yields experimentally or recalibrating transition state initial estimates, such as adjusting prefactors for specific reactions. For instance, the initial estimate for the H2O sticking coefficient was set at approximately 0.05, based on the reported value for Sn–Li/MgO.55 However, this coefficient has been reported to be 0.5 for Li/MgO.31 These corrections could also resolve violations of the constraints of Vannice,70 which serve as a heuristic guide rather than a thermodynamic constraint.
3.6 Steady-state simulations
To assess diffusional limitations for radicals and molecules, we can compare gas-phase species consumption and diffusion rates by using the diffusion length, which is determined from the square root of the effective diffusivity and the species lifetime.71 The latter is determined from the local consumption rate per unit volume of catalyst and the gas concentration in the intraparticle phase (eqn (40)). Note that only negative production rates are used as local consumption rates; otherwise, the denominator of eqn (40) is replaced by the net production rate.| | 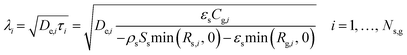 | (40) |
Fig. 8 shows the effective diffusivity and lifetime of each gas-phase species at the catalyst center (ξ = 0) and end of the catalyst bed (z = Lb). For the three catalysts, stable molecules, including reactants and products, result in the absence of concentration gradients along the radial axis of the particle since their diffusion lengths are approximately one order of magnitude larger than the average particle radius (125 μm).55 However, H2O2 and CH2O have smaller diffusion lengths, around 220 μm and 160 μm, respectively, larger than the average particle radius but smaller than the diameter. Hence, they are likely to develop concentration gradients. Previous studies71 have reported even smaller diffusion lengths for CH2O. The radical intermediates have diffusion lengths below 10 μm, significantly smaller than the average particle size, thus validating the chosen heterogeneous reactor model. Fig. 8 indicates that the most notable expected intraparticle concentration gradients are linked to the HO2˙ radical, which has a diffusion length of less than 1 μm. This is attributed to the rapid HO2˙ catalytic quenching reactions despite the radical produced in both phases via homogeneous reactions.
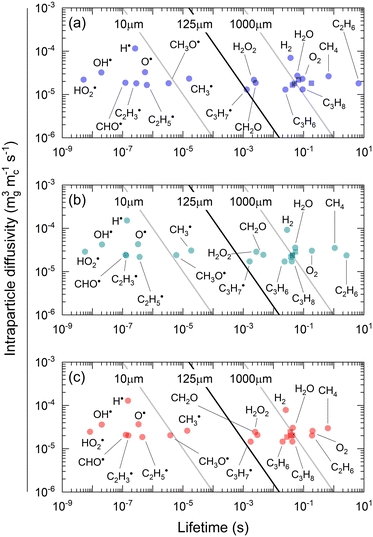 |
| | Fig. 8 Effective intraparticle diffusivities and lifetimes of all species at the center of the particle (ξ = 0) and at the end of the catalytic reactor (z = Lb) for (a) IMP SiO2, (b) SD SiO2–α + βSiC, and (c) SD SiO2–βSiC. Square symbols represent CO, CO2, C2H2, and C2H4. Simulation conditions: T = 800 °C, P = 1 atm, feed molar ratio of CH4/O2/He = 3/1/0.6, W/FCH4,0 = 4.4 gc h molC−1. | |
Fig. 9 shows the simulated concentration profiles along the catalyst bed for IMP SiO2. Stable molecules such as CH4 and C2H6 (Fig. 9a and c) do not develop discernible radial gradients, while CH2O (Fig. 9e) exhibits a subtle radial deviation consistent with its estimated diffusion length. These species exhibit linear trends along with z, ascending (e.g., C2H6) or descending (e.g., CH4). However, radicals such as CH3˙ (Fig. 9b), produced and consumed at similar rates in the intraparticle phase, show a plateau in their concentration profiles, sharply decaying in concentration through the radial interphase because of diffusion into the interstitial phase. This underscores the catalytic role in activating the C–H bond of CH4. Along the axial coordinate, there is an increase in interstitial phase concentrations that can be attributed to the CH3˙ radical not being part of the initial conditions. Nevertheless, the concentration profile along the length of the bed in the interstitial phase shows a slight decrease, owing to lower CH4 and O2 concentrations and an increase in the CO2 concentration, with the latter being known to hinder OCM yields.
 |
| | Fig. 9 Axial and radial (interstitial and intraparticle phases) concentration profile predictions for IMP SiO2 for (a) CH4, (b) CH3˙, (c) C2H6, (d) C2H5˙, (e) CH2O, (f) CHO˙, (g) H˙, and (h) HO2˙. Simulation conditions: T = 800 °C, P = 1 atm, feed molar ratio of CH4/O2/He = 3/1/0.6, W/FCH4,0 = 4.4 gc h molC−1 obtained from the equivalent Lb value of 0.03 m. Simulation results: 9.7% CH4 conversion, 19.5% O2 conversion, 35.4% C2H4 selectivity, 37.6% C2H6 selectivity, 13.2% CO selectivity, 13.8% CO2 selectivity. | |
As secondary product intermediates, the C2H5˙ and CHO˙ radicals (Fig. 9d and f) originate from the heterogeneous H-abstraction of C2H6 and diffuse at a low rate into the interstitial phase. The contribution of the interstitial phase to the gas-phase formation of C2H5˙ radicals via H-abstraction from C2H6 by OH˙ or CH3˙ is significantly lower than that of the intraparticle phase via Eley–Rideal H-abstraction from C2H6. A similar analysis can be performed to produce C2H4. The concentration disparity for the H˙ radical between the intraparticle and interstitial phases (Fig. 9g) arises from the substantially higher total intraparticle radical concentration from heterogeneous initiations. The H˙ radical concentration also increases along the axial coordinate due to increased C2H6 concentration, which accelerates chain propagation and branching rates. Thus, higher rates of primary initiations by H˙ can be expected in the catalyst pores through homogeneous mechanisms, in contrast to the interstitial phase.61,71
The radial distribution of the HO2˙ radical (Fig. 9h) exhibits a sharp decline in the intraparticle phase, mainly because of significant heterogeneous termination or quenching reactions compared with the production rate in the interstitial phase. Interestingly, HO2˙ concentrations develop gradients in the interstitial phase, which become more pronounced. Increased HO2˙ concentrations positively influence CH4 conversions, attributed to higher C2H6 concentrations accelerating propagation and branching rates in a branched-chain mechanism.71 However, the higher interstitial HO2˙ concentration leads to lower C2 selectivities. This emphasizes the importance of an effective OCM catalyst for efficiently activating CH4 and effectively quenching HO2˙ radicals and underscores the importance of the HO2˙ concentration in the interstitial phase.
The simulated concentration profiles for SD SiO2–α + βSiC are presented in ESI† (Fig. S6). Under similar conditions, SD SiO2–α + βSiC exhibited reduced CH4 conversion and C2H4 selectivity but increased C2H6 selectivity, resulting in similar overall C2 selectivities. Notably, selectivity toward CO was significantly higher than that for CO2 for SD SiO2–α + βSiC, unlike IMP SiO2, as evidenced by lower overall radical concentrations (crucial for OCM), such as CH3˙, C2H5˙, H˙, and HO2˙ concentrations. This can be attributed to significantly more negative OH˙ chemisorption entropy and the reduced active site density of SD SiO2–α + βSiC compared with IMP SiO2, which led to decreased formation of C2H6 and eventually lower production of C2H5˙, explaining the lower CH4 conversion and C2H4 selectivity. More pronounced concentration profiles of CHO˙, H˙, and HO2˙ between radial phases are also an outcome of this effect, with lower concentration peaks in their respective prevalent radial phase.
For SD SiO2–βSiC (ESI,† Fig. S7), the predicted CH4 conversion did not exceed that of IMP SiO2 while similar C2 selectivity was maintained, placing it between the latter catalyst and SD SiO2–α + βSiC in terms of predicted activity. The CO/CO2 ratio between the catalysts varied at the end of the catalyst bed, with SiC-containing catalysts showing molar ratios closer to 2 and IMP SiO2 showing a ratio closer to 1. This can be key if the generated C2H4 undergoes further hydroformylation into propanal, where both CO and C2H4 are reactants and the suitability of a CO/H2/C2H4 ratio of 1/1/1 for hydroformylation has been previously reported.72 For instance, the simulated CO/H2/C2H4 ratios are 1/1.1/1.3 and 1/0.9/0.9 for IMP SiO2 and SD SiO2–βSiC, respectively.
The enhanced performance of SD SiO2–βSiC, which had a lower active site density than IMP SiO2, also highlights the influence of textural properties. The effect of catalyst porosity and surface area was observed in SD SiO2–βSiC, which exhibited an approximately 60% larger surface area and higher catalyst porosity than IMP SiO2. This is in accord with higher CH4 conversions and loss of C2 selectivity reported for larger surface areas under the same kinetics.55 This is because higher surface areas promote initiation, generating radicals, yet homogeneous reactions in the interstitial phase do not match the consumption rate. Consequently, despite the amount of radicals in the catalyst pores, most produced radicals eventually undergo heterogeneous oxidation. Moreover, the increase in particle porosity balances the positive impact of gas-phase reactions in a CH3˙-rich environment (where the CH3˙ coupling rate is second order to the CH3˙ concentration), owing to the absence of intraparticle mass transport limitations. This modulation significantly increases CH3˙ coupling compared with deep oxidation routes.71
Fractional coverage profiles of surface intermediates for IMP SiO2 are shown in Fig. 10; OH* is the dominant intermediate. The OH* concentration increased radially from the particle surface to the center (Fig. 10a), consistent with the production of numerous radicals such as CH3˙ through heterogeneous initiation as a byproduct of heterogeneous Eley–Rideal steps. Despite the reactants in the primary heterogeneous initiation, namely CH4 and O*, not showing mass transport limitations, the consumption of the CH3˙ radical was noticeably influenced not only by its decreasing concentration but also by the intraparticle profile of OH*. This reasoning extends to other radicals primarily originating from the surface, such as C2H5˙. Another significant surface intermediate at z = 0 was O*, produced directly through O2 chemisorption. This step, along with all other chemisorption steps in the reaction mechanism, is quasi-equilibrated based on the partial equilibrium indices (in the 0.46–0.5 range). Vacancies constitute a minor fraction at z = 0.
 |
| | Fig. 10 Axial and radial (intraparticle phase) fractional coverage profile predictions for IMP SiO2 for (a) OH*, (b)  , (c) O*, (d) * (vacancies), (e) CH3O*, (f) CH3CHO*, (g) CO*, and (h) H2O*. Simulation conditions and results are identical to those of Fig. 9. , (c) O*, (d) * (vacancies), (e) CH3O*, (f) CH3CHO*, (g) CO*, and (h) H2O*. Simulation conditions and results are identical to those of Fig. 9. | |
A decrease in the OH* radical concentration was observed along the axial direction. Although expecting an increased OH* concentration due to heterogeneous initiation steps is reasonable, heightened recombination rates reduce these surface species. Subsequently, as reactions progressed, the catalyst surface became increasingly rich in  (Fig. 10b).
(Fig. 10b).  does not form any intraparticle concentration gradient, leading to an anticipated plateau in CH4 conversion as the
does not form any intraparticle concentration gradient, leading to an anticipated plateau in CH4 conversion as the  concentration becomes predominant; this is in accord with studies on CO2 inhibition in various catalyst families, including Li/MgO,73 La2O3,74 and Mn–Na2WO4/SiO2.75 Unlike surface CO2, CO* shows intraparticle profiles (Fig. 10g), possibly because of the low concentration of CO*. Notably, in the case of IMP SiO2, no significant concentrations of oxygenates result from direct sticking reactions. The catalyst hence has high C2 selectivity.
concentration becomes predominant; this is in accord with studies on CO2 inhibition in various catalyst families, including Li/MgO,73 La2O3,74 and Mn–Na2WO4/SiO2.75 Unlike surface CO2, CO* shows intraparticle profiles (Fig. 10g), possibly because of the low concentration of CO*. Notably, in the case of IMP SiO2, no significant concentrations of oxygenates result from direct sticking reactions. The catalyst hence has high C2 selectivity.
The primary difference between SD SiO2–α + βSiC (ESI,† Fig. S8) and IMP SiO2 lies in the faster heterogeneous oxidation pathway of CH3˙ radicals, increasing CH3O* and  concentrations. Despite the lower CH4 conversion and C2 selectivity predicted for SD SiO2–α + βSiC compared with IMP SiO2, which are reflected in reduced OH* concentrations, an increase in
concentrations. Despite the lower CH4 conversion and C2 selectivity predicted for SD SiO2–α + βSiC compared with IMP SiO2, which are reflected in reduced OH* concentrations, an increase in  coverages significantly affects CH4 conversion. This is driven by increased CH3O* concentrations, generating pronounced radial intraparticle gradients. In SD SiO2–α + βSiC, concentrations of CH3O*, CH2O*, and CHO* are comparable, around 10−5, while concentrations of CO* and CH3CHO* are around 10−10, indicating the susceptibility of CH3˙ radicals rather than C2H4 to depletion.
coverages significantly affects CH4 conversion. This is driven by increased CH3O* concentrations, generating pronounced radial intraparticle gradients. In SD SiO2–α + βSiC, concentrations of CH3O*, CH2O*, and CHO* are comparable, around 10−5, while concentrations of CO* and CH3CHO* are around 10−10, indicating the susceptibility of CH3˙ radicals rather than C2H4 to depletion.
The intraparticle species distribution of SD SiO2–βSiC (ESI,† Fig. S9) exhibited behavior intermediate between the behavior of IMP SiO2 and that of SD SiO2–α + βSiC, with CH3O* presence but a lower amount than that in SD SiO2–α + βSiC, and the  concentration was similar to that in IMP SiO2. This could explain the CH4 conversion of SD SiO2–βSiC being intermediate between IMP SiO2 and SD SiO2–α + βSiC. Despite its high predicted C2 selectivity, SD SiO2–βSiC showed greater propensity to chemisorb C2H4.
concentration was similar to that in IMP SiO2. This could explain the CH4 conversion of SD SiO2–βSiC being intermediate between IMP SiO2 and SD SiO2–α + βSiC. Despite its high predicted C2 selectivity, SD SiO2–βSiC showed greater propensity to chemisorb C2H4.
3.7 Consumption analysis of steady-state simulations
The interpretation of concentration profiles can be further improved by using a quantitative approach involving reaction path analysis, such as the consumption analysis of Gupta and Vlachos,76 which was used in this work for the interstitial and intraparticle phases separately; averaged concentrations along radial coordinates at the end of the catalyst bed were used in the analysis. Specifically, C-containing species were targeted, with a default equilibrium tolerance and a reaction rate cutoff value of 10−12. Fig. 11 shows the interstitial phase species consumption analysis for the three catalysts.
 |
| | Fig. 11 Species consumption analysis in the interstitial phase at the end of the catalyst bed (z = Lb) based on consumption rates of each carbon-containing species for (a) IMP SiO2, (b) SD SiO2–α + βSiC, and (c) SD SiO2–βSiC. Simulation conditions: T = 800 °C, P = 1 atm, feed molar ratio of CH4/O2/He = 3/1/0.6, W/FCH4,0 = 4.4 gc h molC−1. Numbers denote the molar consumption rate (in percentage) of the reactant for each specific product. The arrow width is proportional to the reaction rates at the simulation conditions. | |
In this phase, CH4 is primarily consumed through reactions with H˙ and OH˙, which exclusively generate CH3˙ radicals. The former reaction accounts for approximately 51%, 41%, and 50% of interstitial CH3˙ production for IMP SiO2, SD SiO2–α + βSiC, and SD SiO2–βSiC, respectively, while the latter contributes around 30%, 32%, and 31% for these catalysts, respectively. This is because, under OCM conditions without a catalyst, the reaction between CH4 and O2 is not the most important initiation step. CH3˙ production in the interstitial phase is much lower than in the intraparticle phase, which is confirmed by the CH3˙ profile in Fig. 9. The produced CH3˙ undergoes various reactions in the interstitial phase, mainly CH3˙ coupling to yield C2H6 (around 92% of CH3˙ consumption rate), apart from reactions involving CH3˙-mediated H abstraction from hydrocarbons such as CH2O, C2H6, and C2H4.
Less relevant pathways depleting CH3˙ radicals yield undesired products, including reactions with O2 resulting in CH2O and OH˙ production. CH2O mainly originates from C2H3˙ radicals formed from C2H4 in IMP SiO2 (52% of CH2O compared with 29% and 40% for SD SiO2–α + βSiC and SD SiO2–βSiC, respectively). For SD SiO2–α + βSiC, CH2O in the interstitial phase mainly results from CH3˙ reacting with O2, which accounts for 59% of CH2O. However, this observation is not evident from Fig. 11 as contributions are expressed in terms of species consumption. The differences observed arise from higher C2H3˙ concentrations in IMP SiO2 and SD SiO2–βSiC compared with SD SiO2-α + βSiC owing to higher C2H4 concentrations, which lead to higher intrinsic hydrocarbon H-abstraction rates, including both CH4 and C2H4. Additionally, concentration effects explain the lower CH3˙ recombination rates in SD SiO2–α + βSiC compared with the other two catalysts, as evidenced by scale differences in the legends across catalysts in Fig. 11. C2H4 primarily originates from pyrolytic dehydrogenation of C2H5˙ radical (accounting for >95%) in all three catalysts. Similarly, the primary pathway generating interstitial CO involves the pyrolytic route, accounting for more than 98% of CO-producing reactions. Notably, in the interstitial phase, CO can be consumed only via reaction with HO2˙ to yield CO2. Variations observed in homogeneous rates in the interstitial phase are primarily associated with the catalyst's capability to generate and consume radicals in the intraparticle phase.
In the intraparticle phase (Fig. 12), CH4 conversion mainly occurs via heterogeneous Eley–Rideal H-abstraction, and this conversion accounts for 74%, 77%, and 77% of the CH3˙ radical produced in IMP SiO2, SiO2–α + βSiC, and SD SiO2–βSiC, respectively. Gas-phase contribution within catalyst pores involves CH4 consumption via H˙ and OH˙ reactions that yield CH3˙ radicals, and these reactions account for 25%, 22%, and 22% of the total intraparticle CH4 consumption for IMP SiO2, SiO2–α + βSiC, and SD SiO2–βSiC, respectively. The intraparticle phase accounts for 91.9%, 92.7%, and 93.5% of the total CH4 net consumption rates at the end of the catalyst bed of 1.6 × 10−3 kmol mb−3 s−1, 1.3 × 10−3 kmol mb−3 s−1 and 2.1 × 10−3 kmol mb−3 s−1 for IMP SiO2, SiO2–α + βSiC, and SD SiO2–βSiC, respectively, highlighting the crucial role of the catalyst and differences in radical generation between the catalysts. CH3˙ radicals in the intraparticle phase mainly recombine to form C2H6 within catalyst pores (Fig. 12), with 65%, 64%, and 67% conversion rates for IMP SiO2, SiO2–α + βSiC, and SD SiO2–βSiC, respectively. Although CH3˙ radicals favor recombination in the interstitial phase, competition with oxidation routes intensifies in the intraparticle phase.
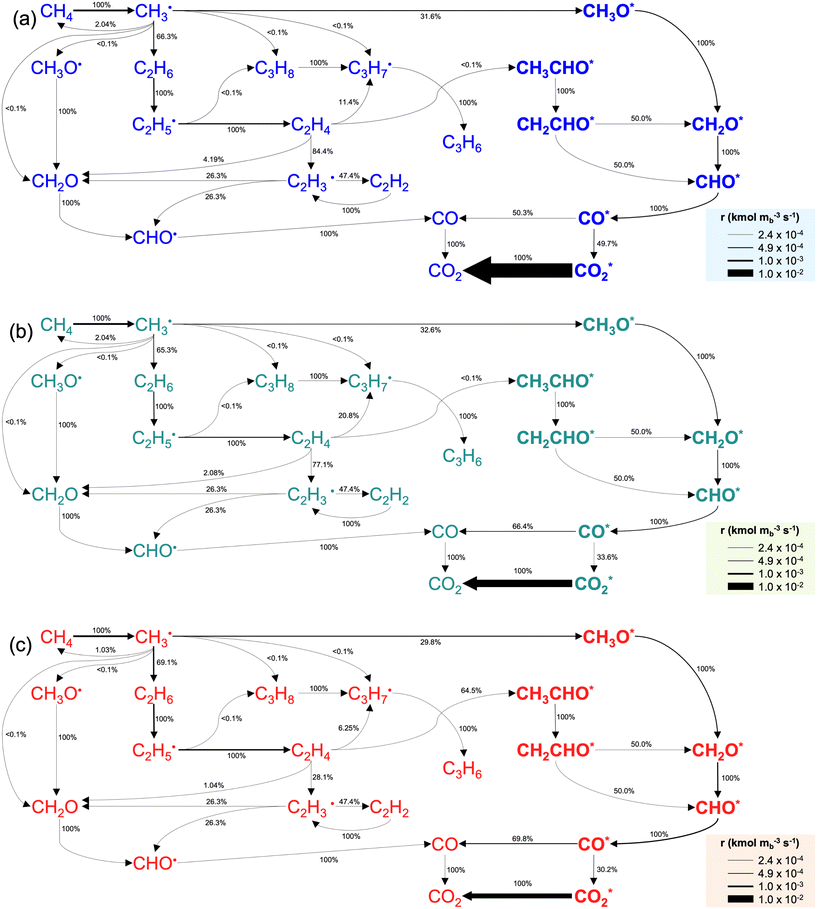 |
| | Fig. 12 Species consumption analysis for the intraparticle phase at the end of the catalyst bed (z = Lb) based on consumption rates of each carbon-containing species for (a) IMP SiO2, (b) SD SiO2–α + βSiC, and (c) SD SiO2–βSiC. Simulation conditions: T = 800 °C, P = 1 atm, feed molar ratio of CH4/O2/He = 3/1/0.6, W/FCH4,0 = 4.4 gc h molC−1. Numbers denote the molar consumption rate (in percentage) of the reactant for each specific product. The arrow width is proportional to the reaction rates at the simulation conditions. | |
In the intraparticle phase, catalytic oxidation pathways surpass homogeneous ones. Uncoupled CH3˙ predominantly chemisorb CH3O* on the catalyst surface, representing 31%, 32%, and 29% of the consumption, respectively. Gas-phase oxidation of CH3˙ through CH3O˙–CH2O–CHO˙ or direct CH2O/CHO˙ formation is limited, as most CH3˙ is converted homogeneously to C2H6via H abstraction, yielding C2H5˙ and CH4. Conversely, C2H5˙ is mainly converted to C2H4 (>97% for all catalysts) in the gas phase, indicating that catalyst properties should balance homogeneous-heterogeneous interactions effectively.
As noted, the origins of CO and CO2 vary with the catalyst. IMP SiO2 (Fig. 12a) mainly originates from CH3˙ direct sticking, following the CH3O*–CH2O*–CHO*–CO*– sequence, with minimal involvement of C2H4 oxidation. The favored pathway from C2H4 to C2H3˙ involves gas-phase oxidation, primarily through O2 (28%), catalytic H-abstraction by O* (24%), or reaction with H˙ (21%). Furthermore, gas-phase chain growth to C3H7˙ consumes 11% of C2H4. CH3O* follows the expected catalytic path to CO, with 70% formed catalytically via CO desorption from CHO* through the Langmuir–Hinshelwood route.28 Eley–Rideal H abstraction of CHO˙ is a minor contributor, and the remaining CO comes from gas-phase CHO˙ collision. Around half (50.3%) of CO* is desorbed, while 49.7% is oxidized to CO2, almost entirely catalytically. Catalysts play a key role in radical quenching. HO2˙ consumption occurs solely through heterogeneous collision with vacancies, and H-abstraction of HO2˙ by O* partly explains the decreasing OH* concentration. Recombination consumes surface hydroxyl radicals at a rate of 1.4 × 10−3 kmol mb−3 s−1.
sequence, with minimal involvement of C2H4 oxidation. The favored pathway from C2H4 to C2H3˙ involves gas-phase oxidation, primarily through O2 (28%), catalytic H-abstraction by O* (24%), or reaction with H˙ (21%). Furthermore, gas-phase chain growth to C3H7˙ consumes 11% of C2H4. CH3O* follows the expected catalytic path to CO, with 70% formed catalytically via CO desorption from CHO* through the Langmuir–Hinshelwood route.28 Eley–Rideal H abstraction of CHO˙ is a minor contributor, and the remaining CO comes from gas-phase CHO˙ collision. Around half (50.3%) of CO* is desorbed, while 49.7% is oxidized to CO2, almost entirely catalytically. Catalysts play a key role in radical quenching. HO2˙ consumption occurs solely through heterogeneous collision with vacancies, and H-abstraction of HO2˙ by O* partly explains the decreasing OH* concentration. Recombination consumes surface hydroxyl radicals at a rate of 1.4 × 10−3 kmol mb−3 s−1.
Regarding the origin of CO and CO2, SD SiO2–α + βSiC (Fig. 12b) resembles IMP SiO2, where CH3˙ sticking predominantly drives heterogeneous deep oxidation to surpass gas-phase CH2O generation. Notably, in SD SiO2–α + βSiC, up to 87% of CO is produced heterogeneously. Gas-phase CH2O mostly reconverts CH4 (51%) through CH3˙ reaction, while the remaining CH2O is converted via heterogeneous Eley–Rideal H abstraction by O* into CHO˙. In fact, from a mechanistic viewpoint, SD SiO2–α + βSiC is comparable to SD SiO2–βSiC (Fig. 12c). SD SiO2–βSiC significantly influences catalytic oxidation, which accounts for 88% of CO and nearly 100% of CO2. Furthermore, surface oxidation intermediates such as CH2O* and CHO* originate from C2H4 catalytic oxidation, which accounts for 13% and 12% of the two intermediates, respectively. In particular, for all three catalysts, the HO2˙ quenching rates were high (2.9 × 10−5 kmol mb−3 s−1, 4.73 × 10−5 kmol mb−3 s−1, and 1.6 × 10−4 kmol mb−3 s−1), which substantially reduced the HO2˙ concentration (compared with ref. 55, 61 and 71) in the interstitial phase as well as the gas-phase oxidation contribution.
4. Conclusions
The present work delved into the microkinetics of OCM by using three Mn–Na2WO4 catalysts (IMP SiO2, SD SiO2–α + βSiC, and SD SiO2–βSiC) to elucidate the effect of SiC in the catalyst support. The microkinetic analysis involved a reactor model that combined irreducible mass transfer limitations and the homogeneous–heterogeneous kinetics of OCM, while maintaining thermodynamic consistency across the kinetic parameters. In the model, textural properties, especially surface area and catalyst porosity, were pivotal factors influencing reaction outcomes. The surface area directly influenced CH4 conversion rates and undesirable side reactions. In contrast, catalyst porosity facilitated enhanced diffusion of reactants and products, alleviating internal transport constraints while providing a confined environment for critical gas-phase reactions, such as CH3˙ radicals coupling. Thus, incorporating SiC as a support component endows the Mn–Na2WO4 catalysts with increased surface area and porosity, facilitating a more balanced interplay between textural properties and kinetics.
On the kinetic side, the influence of SiC, particularly its crystal phase (βSiC vs. α + βSiC), hinges on the origin of COX products. While all three catalysts exhibited noteworthy selectivity toward C2 products, SD SiO2–βSiC showed a higher propensity for C2H4 chemisorption and its subsequent oxidation, unlike the other catalysts, which showed a greater inclination toward CH3˙ oxidation, leading to the formation of CH2O* and CHO* intermediates. SD SiO2–α + βSiC promoted the oxidation of CH3˙ radicals, resulting in an increased concentration of CH3O* and an abundance of  on the catalyst surface. Furthermore, the excessive accumulation of
on the catalyst surface. Furthermore, the excessive accumulation of  on the catalyst surface, particularly from CH3O*, adversely affected the global reaction rate. Consequently, the catalytic contribution of CO was higher for the SiC-containing catalysts (87–88%) compared to the IMP SiO2 catalyst (70%). This underscores the notion that in the OCM process, radicals should not only be generated at high rates but also consumed judiciously, with HO2˙ rates contributing to high C2 selectivities.
on the catalyst surface, particularly from CH3O*, adversely affected the global reaction rate. Consequently, the catalytic contribution of CO was higher for the SiC-containing catalysts (87–88%) compared to the IMP SiO2 catalyst (70%). This underscores the notion that in the OCM process, radicals should not only be generated at high rates but also consumed judiciously, with HO2˙ rates contributing to high C2 selectivities.
Overall, while SiC enhances leads to more favorable textural properties for OCM, these improvements come at the cost of a smaller active site density, leading to milder catalytic contributions. This study serves as a foundational step in the microkinetic modeling of SiC-containing catalysts for Mn–Na2WO4-based OCM, providing valuable insights into the catalytic role of SiC and highlighting potential areas for further model refinement, such as incorporating a more rigorous temperature-dependent characterization of chemisorption entropies, implementation of more comprehensive homogeneous models, conducting tailored experiments to propose a model that accounts for a more realistic interaction between surface and reactive oxygen and incorporating heat effects into the reactor model.
Nomenclature
Abbreviations
| BEP | Brønsted–Evans–Polanyi |
| BET | Brunauer–Emmett–Teller |
| CH4-TPSR | Temperature-programmed surface reaction |
| CSTR | Continuously-stirred tank reactor |
| DAEs | Differential-algebraic equations |
| DOFs | Degrees of freedom |
| O2-TPD | Temperature-programmed O2 desorption |
| OCM | Oxidative coupling of methane |
| ODEs | Ordinary differential equations |
| PDEs | Partial differential-algebraic equations |
| PFR | Plug-flow reactor |
| PSSA | Pseudo-steady-state approximation |
Symbols
|
A
j
| Prefactor of homogeneous or heterogeneous reaction step j, c.u. |
|
A
r
| Reactor cross-section, mb2 |
|
c
d,i
| Coefficient of linearly decomposed reaction d onto reaction i belonging to the basis set |
|
c
j,i
| Coefficient for the adsorption of surface species i in heterogeneous reaction step j |
|
C
g,i
| Concentration of the gas-phase species i in the interstitial phase, kmol mg−3 |
|
C
i
| Concentration of gas-phase species i, kmol mg−3 |
|
C
M
| Concentration of an unspecified collision partner in three-body reaction step j, kmol mg−3 |
|
C
s,i
| Concentration of the gas-phase species i in the intraparticle phase, kmol mg−3 |
|
D
e,i
| Effective diffusivity of gas-phase species i in the mixture, mg3 mc−1 s−1 |
|
D
i,j
| Binary molecular diffusivity of gas-phase species i in gas-phase species j, mg2 s−1 |
|
D
m,i
| Molecular diffusivity of gas-phase species i in the mixture, mg2 s−1 |
|
E
0,f
| Intrinsic energy barrier for any reaction in reaction family f, kJ mol−1 |
|
E
a,j
| Activation energy of homogeneous or heterogeneous reaction step j, kJ mol−1 |
|
f
| Model multiresponse function |
|
F
E
| Fisher's E, unitless |
|
F
i
| Carbon molar flow rate of species i, molC s−1 |
|
F
inv
| Inverse F distribution, unitless |
|
F
v
| Total gas volumetric flow rate, mg3 s−1 |
|
F
T
| Total molar flow rate of species i, NmL min−1 |

| Standard Gibbs energy of species i, J mol−1 |

| Standard enthalpy of species i, J mol−1 |
|
K
C,j
| Concentration-based thermodynamic equilibrium constant of homogeneous or heterogeneous reaction step j, c.u. |
|
k
j
| Rate constant of homogeneous or heterogeneous reaction step j, c.u. |
|
K
P,j
| Pressure-based thermodynamic equilibrium constant of homogeneous or heterogeneous reaction step j, unitless |
|
L
| Bed length, m or cm |
|
M
w,i
| Molecular weight of gas-phase species i, kg kmol−1 |
|
n
| Number of experiments and responses |
|
n
j
| Number of sites involved in the heterogeneous elementary reaction step j |
|
N
obs
| Number of observations |
|
N
r,d
| Total number of linearly dependent reaction steps in the surface mechanism |
|
N
r,g
| Total number of homogeneous elementary steps in the mechanism |
|
N
r,i
| Total number of linearly independent reaction steps in the surface mechanism |
|
N
r,s
| Total number of heterogeneous elementary steps in the mechanism |
|
N
res
| Number of experimental responses per observation |
|
N
s,g
| Total number of gas-phase species |
|
N
s,j
| Total number of species in homogeneous or heterogeneous reaction step j |
|
N
s,g,j
| Total number of gaseous species in homogeneous or heterogeneous reaction step j |
|
N
s,s
| Total number of surface intermediates |
|
N
s,s,j
| Total number of surface intermediates in heterogeneous reaction step j |
| OF | Objective function, unitless |
|
P
| Pressure, bar |
|
p
| Total number of catalytic descriptors of the model |
|
p
i
| Partial pressure of species i, atm |
|
R
| Universal gas constant, 8314 Pa mg3 kmol−1 K−1 or 8.314 × 10−3 kJ mol−1 K−1 |
|
r
| Radial interstitial coordinate, dimensionless |
|
R
g,i
| Homogeneous net production rate of gas-phase species i, kmol mg−3 s−1 |
|
r
j
| Rate of homogeneous or heterogeneous elementary reaction step j, kmol mg−3 s−1 or kmol mc−2 s−1 |
|
r
p
| Radius of the intraparticle phase or the average particle radius, mc |
|
R
s,i
| Heterogeneous net production rate of gas-phase or surface species i, |
|
ℜ
d
|
dth dependent reaction outside the basis set |
|
ℜ
i
|
ith independent reaction inside the basis set |
|
r
v
| Radius of the interstitial phase or average half distance between catalyst particles, mg |

| Standard entropy of species i, J mol−1 K−1 |
|
s
j,i
| Sticking coefficient of adsorbing gas-phase species i in heterogeneous reaction step j, unitless |
|
S
s
| Catalyst specific surface area, mc2 kgc−1 |
|
t
| Time, s |
|
t
∞
| Holdup time, s |
|
T
| Temperature, K |
|
W
| Catalyst mass, mgc or gc |
|
x
i
| Variable representing the ith observation, unitless |
|
X
i
| Molar fraction of gas-phase species i in the mixture |
|
z
| Axial reactor bed coordinate, mb |
Greek symbols
|
α
| Significance of the statistical test, unitless |
|
α
f
| Transfer coefficient for any reaction in reaction family f, unitless |
|
β
|
β∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) p vector of catalytic descriptor estimates of the model, c.u., or heating rate of the catalyst bed under temperature-programmed experiments, °C min−1 p vector of catalytic descriptor estimates of the model, c.u., or heating rate of the catalyst bed under temperature-programmed experiments, °C min−1 |
|
β
i
| Constant accounting for the temperature dependence of the chemisorption entropy, unitless |

| Standard reaction Gibbs free energy of homogeneous or heterogeneous reaction step j, kJ mol−1 |

| Standard reaction enthalpy of homogeneous or heterogeneous reaction step j, kJ mol−1 |
| ΔQavg | Average bond energy difference between two types of hydrocarbons, kJ mol−1 |

| Standard reaction entropy of homogeneous or heterogeneous reaction step j, J mol−1 K−1 |
|
ε
b
| Average bed packing porosity, mg3 mb−3 |
|
ε
s
| Catalyst porosity, mg3 mc−3 |
|
θ
*
| Fractional coverage of the vacant sites or vacancies |
|
θ
i
| Fractional coverage of surface intermediate i |
|
λ
i
| Diffusion length of gas-phase species i, m, or ith eigenvalue, dimensionless |
|
ν
j,i
| Stoichiometric number of gas-phase species i in homogeneous or heterogeneous reaction step j |
|
ξ
| Radial intraparticle coordinate, dimensionless |
|
ρ
b
| Average bed packing density, kgc mb−3 |
|
ρ
s
| Catalyst density, kgc mc−3 |
|
σ
| Active site density, kmol mc−2 |
|
τ
i
| Lifetime of gas-phase species i, s |
|
τ
s
| Term combining constriction and tortuosity of the catalyst, mg2 mc−2 |
|
ν
j,i
| Stoichiometric number of gas-phase species i reacting in homogeneous or heterogeneous reaction step j (i.e., νj,i wherein all non-negative values 0) |
|
ϕ
ij
|
ϕ
ij
∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nres first-order normalized sensitivity of the descriptor j at the ith experimental conditions, unitless Nres first-order normalized sensitivity of the descriptor j at the ith experimental conditions, unitless |
|
ψ
i
|
ψ
i
∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nres vector of all performance metrics for the ith observation, % Nres vector of all performance metrics for the ith observation, % |
|
ψ
i,j
| Performance metric of species j for the ith observation, % |
Subscripts and superscripts
| 0 | Feed |
| ads | Chemisorption step |
| b | Backward (superscript) or reactor bed (subscript) |
| C | Carbon |
| c | Catalyst |
| calc | Model-based prediction |
| exp | Experimental |
| F | Final |
| f | Forward |
| g | Gas |
| gas | Gas-phase analogous reaction |
| I | Initial |
| init | Initial estimate |
| min | Minimum |
| s | Species |
| sur | Surface reaction step |
Data availability
The data supporting this article have been included as part of the ESI.†
Author contributions
Gontzal Lezcano: investigation; data curation; software; formal analysis; visualization; writing – original draft. Shekhar R. Kulkarni: validation; formal analysis; writing – original draft. Vijay K. Velisoju: investigation; validation; formal analysis; writing – review & editing. Natalia Realpe: formal analysis; writing – review & editing. Pedro Castaño: conceptualization; methodology; funding acquisition; supervision; project administration; writing – review and editing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors acknowledge the financial support, resources, and facilities provided by the King Abdullah University of Science and Technology (KAUST), BAS/1/1403.
References
- Y. Gao, L. Neal, D. Ding, W. Wu, C. Baroi, A. M. Gaffney and F. Li, ACS Catal., 2019, 9, 8592–8621 CrossRef CAS.
- H. Saito and Y. Sekine, RSC Adv., 2020, 10, 21427–21453 RSC.
- D. Fairuzov, I. Gerzeliev, A. Maximov and E. Naranov, Catalysts, 2021, 11, 833 CrossRef CAS.
- J. Q. Chen, A. Bozzano, B. Glover, T. Fuglerud and S. Kvisle, Catal. Today, 2005, 106, 103–107 CrossRef CAS.
- Y. Gambo, A. A. Jalil, S. Triwahyono and A. A. Abdulrasheed, J. Ind. Eng. Chem., 2018, 59, 218–229 CrossRef CAS.
- D. Kiani, S. Sourav, J. Baltrusaitis and I. E. Wachs, ACS Catal., 2019, 9, 5912–5928 CrossRef CAS.
- C. A. Ortiz-Bravo, C. A. Chagas and F. S. Toniolo, J. Nat. Gas Sci. Eng., 2021, 96, 104254 CrossRef CAS.
- N. S. Hayek, N. S. Lucas, C. Warwar Damouny and O. M. Gazit, ACS Appl. Mater. Interfaces, 2017, 9, 40404–40411 CrossRef CAS PubMed.
- N. S. Hayek, G. J. Khlief, F. Horani and O. M. Gazit, J. Catal., 2019, 376, 25–31 CrossRef CAS.
- A. Aseem, G. G. Jeba, M. T. Conato, J. D. Rimer and M. P. Harold, Chem. Eng. J., 2018, 331, 132–143 CrossRef CAS.
- T. Chukeaw, S. Sringam, M. Chareonpanich and A. Seubsai, Mol. Catal., 2019, 470, 40–47 CrossRef.
- D. Matras, A. Vamvakeros, S. D. M. Jacques, N. Grosjean, B. Rollins, S. Poulston, G. B. G. Stenning, H. R. Godini, J. Drnec, R. J. Cernik and A. M. Beale, Faraday Discuss., 2021, 229, 176–196 RSC.
- J. Ramos-Yataco and J. Notestein, Catal. Today, 2023, 416, 113770 CrossRef CAS.
- N. Hiyoshi and T. Ikeda, Fuel Process. Technol., 2015, 133, 29–34 CrossRef CAS.
- P. Wang, G. Zhao, Y. Wang and Y. Lu, Sci. Adv., 2017, 3, e1603180 CrossRef PubMed.
- M. Yildiz, U. Simon, T. Otremba, Y. Aksu, K. Kailasam, A. Thomas, R. Schomäcker and S. Arndt, Catal. Today, 2014, 228, 5–14 CrossRef CAS.
- G. Lezcano, S. R. Kulkarni, V. K. Velisoju, V. E. Musteata, I. Hita, A. Ramirez, A. Dikhtiarenko, J. Gascon and P. Castaño, Mol. Catal., 2022, 527, 112399 CrossRef CAS.
- G. Lezcano, V. K. Velisoju, S. R. Kulkarni, A. Ramirez and P. Castaño, Ind. Eng. Chem. Res., 2021, 60, 18770–18780 CrossRef CAS.
- S. R. Kulkarni, G. Lezcano, V. K. Velisoju, N. Realpe and P. Castaño, ChemCatChem DOI:10.1002/cctc.202301720.
- G. Lezcano, A. Gobouri, N. Realpe, S. R. Kulkarni, V. K. Velisoju and P. Castaño, Chem. Eng. Sci., 2024, 283, 119412 CrossRef CAS.
- P. M. Couwenberg, Q. Chen and G. B. Marin, Ind. Eng. Chem. Res., 1996, 35, 3999–4011 CrossRef CAS.
-
R. J. Kee, M. E. Coltrin, P. Glarborg and H. Zhu, in Chemically Reacting Flow, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2005, pp. 487–539 Search PubMed.
- H. Wang, C. Shao, J. Gascon, K. Takanabe and S. M. Sarathy, ACS Omega, 2021, 6, 33757–33768 CrossRef CAS PubMed.
- Q. Chen, P. M. Couwenberg and G. B. Marin, Catal. Today, 1994, 21, 309–319 CrossRef CAS.
- A. Ishikawa and Y. Tateyama, ACS Catal., 2021, 11, 2691–2700 CrossRef CAS.
- V. I. Alexiadis, M. Chaar, A. van Veen, M. Muhler, J. W. Thybaut and G. B. Marin, Appl. Catal., B, 2016, 199, 252–259 CrossRef CAS.
- Y. Gordienko, T. Usmanov, V. Bychkov, V. Lomonosov, Z. Fattakhova, Y. Tulenin, D. Shashkin and M. Sinev, Catal. Today, 2016, 278, 127–134 CrossRef CAS.
- Z. Xiong, J. Guo, Y. Deng, M. Zeng, Z. Wang, Z. Zhou, W. Yuan and F. Qi, Catal. Sci. Technol., 2024, 6882–6892 RSC.
- M. Y. Sinev, Z. T. Fattakhova, V. I. Lomonosov and Y. A. Gordienko, J. Nat. Gas Chem., 2009, 18, 273–287 CrossRef CAS.
- J. W. Thybaut, J. Sun, L. Olivier, A. C. Van Veen, C. Mirodatos and G. B. Marin, Catal. Today, 2011, 159, 29–36 CrossRef CAS.
- J. Sun, J. W. Thybaut and G. B. Marin, Catal. Today, 2008, 137, 90–102 CrossRef CAS.
- V. I. Alexiadis, J. W. Thybaut, P. N. Kechagiopoulos, M. Chaar, A. C. Van Veen, M. Muhler and G. B. Marin, Appl. Catal., B, 2014, 150–151, 496–505 CrossRef CAS.
- A. H. Motagamwala and J. A. Dumesic, Chem. Rev., 2021, 121, 1049–1076 CrossRef CAS PubMed.
- O. V. Krylov, Catal. Today, 1993, 18, 209–302 CrossRef CAS.
-
J. A. Dumesic, D. F. Rudd, L. M. Aparicio, J. E. Rekoske and A. A. Treviño, in The Microkinetics of Heterogeneous Catalysis, American Chemical Society (ACS), 1st edn, 1993 Search PubMed.
- N. Schumacher, A. Boisen, S. Dahl, A. Gokhale, S. Kandoi, L. Grabow, J. Dumesic, M. Mavrikakis and I. Chorkendorff, J. Catal., 2005, 229, 265–275 CrossRef CAS.
- A. Michaelides, Z.-P. Liu, C. J. Zhang, A. Alavi, D. A. King and P. Hu, J. Am. Chem. Soc., 2003, 125, 3704–3705 CrossRef CAS PubMed.
- A. B. Mhadeshwar, H. Wang and D. G. Vlachos, J. Phys. Chem. B, 2003, 107, 12721–12733 CrossRef CAS.
- A. B. Mhadeshwar and D. G. Vlachos, Combust. Flame, 2005, 142, 289–298 CrossRef CAS.
- Y. S. Su, J. Y. Ying and W. H. Green, J. Catal., 2003, 218, 321–333 CrossRef CAS.
-
Y.-R. Luo, Handbook of Bond Dissociation Energies in Organic Compounds, CRC Press, 2002 Search PubMed.
- P. C. St. John, Y. Guan, Y. Kim, S. Kim and R. S. Paton, Nat. Commun., 2020, 11, 2328 CrossRef CAS PubMed.
- A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker and C. S. Woodward, ACM Trans. Math. Softw., 2005, 31, 363–396 CrossRef.
- B. Malengier, P. Kišon, J. Tocknell, C. Abert, F. Bruckner and M.-A. Bisotti, J. Open Source Softw., 2018, 3, 165 CrossRef.
-
D. G. Goodwin, H. K. Moffat, I. Schoegl, R. L. Speth and B. W. Weber, Cantera: An object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes, Version 3.0.0., 2023, https://www.cantera.org, DOI:10.5281/zenodo.8137090.
-
G. P. Smith, D. M. Golden, M. Frenklach, N. W. Moriarty, B. Eiteneer, M. Goldenberg, C. T. Bowman, R. K. Hanson, S. Song, Jr., W. C. Gardiner, V. V. Lissianski and Z. Qin, GRI-Mech 3.0, http://combustion.berkeley.edu/gri-mech/version30/text30.html, (accessed 16 December 2021).
- F.-A. Fortin, F.-M. De Rainville, M.-A. Gardner, M. Parizeau and C. Gagné, Journal of Machine Learning Research, 2012, 13, 2171–2175 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt, A. Vijaykumar, A. Pietro Bardelli, A. Rothberg, A. Hilboll, A. Kloeckner, A. Scopatz, A. Lee, A. Rokem, C. N. Woods, C. Fulton, C. Masson, C. Häggström, C. Fitzgerald, D. A. Nicholson, D. R. Hagen, D. V. Pasechnik, E. Olivetti, E. Martin, E. Wieser, F. Silva, F. Lenders, F. Wilhelm, G. Young, G. A. Price, G.-L. Ingold, G. E. Allen, G. R. Lee, H. Audren, I. Probst, J. P. Dietrich, J. Silterra, J. T. Webber, J. Slavič, J. Nothman, J. Buchner, J. Kulick, J. L. Schönberger, J. V. de Miranda Cardoso, J. Reimer, J. Harrington, J. L. C. Rodríguez, J. Nunez-Iglesias, J. Kuczynski, K. Tritz, M. Thoma, M. Newville, M. Kümmerer, M. Bolingbroke, M. Tartre, M. Pak, N. J. Smith, N. Nowaczyk, N. Shebanov, O. Pavlyk, P. A. Brodtkorb, P. Lee, R. T. McGibbon, R. Feldbauer, S. Lewis, S. Tygier, S. Sievert, S. Vigna, S. Peterson, S. More, T. Pudlik, T. Oshima, T. J. Pingel, T. P. Robitaille, T. Spura, T. R. Jones, T. Cera, T. Leslie, T. Zito, T. Krauss, U. Upadhyay, Y. O. Halchenko and Y. Vázquez-Baeza, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
-
R. Tesser and V. Russo, Advanced Reactor Modeling with MATLAB, De Gruyter, 2020 Search PubMed.
-
P. A. Brodtkorb and J. D'Errico, numdifftools 0.9.11, https://github.com/pbrod/numdifftools.
- K. Toch, J. W. Thybaut and G. B. Marin, AIChE J., 2015, 61, 880–892 CrossRef CAS.
- J. Sadeghzadeh Ahari, S. Zarrinpashne and M. T. Sadeghi, Fuel Process. Technol., 2013, 115, 79–87 CrossRef CAS.
- H. Wang, R. Schmack, B. Paul, M. Albrecht, S. Sokolov, S. Rümmler, E. V. Kondratenko and R. Kraehnert, Appl. Catal., A, 2017, 537, 33–39 CrossRef CAS.
- C. Karakaya, H. Zhu, C. Loebick, J. G. Weissman and R. J. Kee, Catal. Today, 2018, 312, 10–22 CrossRef CAS.
- P. N. Kechagiopoulos, J. W. Thybaut and G. B. Marin, Ind. Eng. Chem. Res., 2014, 53, 1825–1840 CrossRef CAS.
- J. Liu, M. Huo and Y. Zhu, J. Nanosci. Nanotechnol., 2017, 17, 8818–8826 CrossRef CAS.
- J. Li, J. Chen, A. Zanina, Y. Li, C. Yu, M. Liu, G. Cui, Y. Wang, M. Zhou, E. V. Kondratenko and G. Jiang, J. Catal., 2023, 428, 115176 CrossRef CAS.
- V. I. Lomonosov, Y. A. Gordienko, M. Y. Sinev, V. A. Rogov and V. A. Sadykov, Russ. J. Phys. Chem. A, 2018, 92, 430–437 CrossRef CAS.
- V. Fleischer, R. Steuer, S. Parishan and R. Schomäcker, J. Catal., 2016, 341, 91–103 CrossRef CAS.
- W. Sun, Y. Gao, G. Zhao, J. Si, Y. Liu and Y. Lu, J. Catal., 2021, 400, 372–386 CrossRef CAS.
- V. I. Alexiadis, T. Serres, G. B. Marin, C. Mirodatos, J. W. Thybaut and Y. Schuurman, AIChE J., 2018, 64, 2603–2611 CrossRef CAS.
- M. Schwaab, L. P. Lemos and J. C. Pinto, Chem. Eng. Sci., 2008, 63, 2895–2906 CrossRef CAS.
- M. Schwaab and J. C. Pinto, Chem. Eng. Sci., 2007, 62, 2750–2764 CrossRef CAS.
- L. Pirro, P. S. F. Mendes, B. D. Vandegehuchte, G. B. Marin and J. W. Thybaut, React. Chem. Eng., 2020, 5, 584–596 RSC.
- J. Chawla, S. Schardt, P. Lott, S. Angeli, S. Tischer, L. Maier and O. Deutschmann, Chem. Eng. J., 2024, 482, 148719 CrossRef CAS.
- L. Pirro, A. Obradović, B. D. Vandegehuchte, G. B. Marin and J. W. Thybaut, Ind. Eng. Chem. Res., 2018, 57, 16295–16307 CrossRef CAS.
- R. Petrov, S. Reshetnikov and Y. Ivanova, Fuel Process. Technol., 2021, 213, 106667 CrossRef CAS.
- Y. Cheng, P. S. F. Mendes, P. Yazdani and J. W. Thybaut, Int. J. Chem. Kinet., 2024, 703–717 CrossRef.
- L. Pirro, P. S. F. Mendes, S. Paret, B. D. Vandegehuchte, G. B. Marin and J. W. Thybaut, Catal. Sci. Technol., 2019, 9, 3109–3125 Search PubMed.
- M. A. Vannice, S. H. Hyun, B. Kalpakci and W. C. Liauh, J. Catal., 1979, 56, 358–362 Search PubMed.
- P. M. Couwenberg, Q. Chen and G. B. Marin, Ind. Eng. Chem. Res., 1996, 35, 415–421 CrossRef CAS.
- H. Zhang, J. Wu, B. Xu and C. Hu, Catal. Lett., 2006, 106, 161–165 CrossRef CAS.
- S. Al-Zahrani, Q. Song and L. L. Lobban, Ind. Eng. Chem. Res., 1994, 33, 251–258 CrossRef CAS.
- S. Lacombe, Z. Durjanova, L. Mleczko and C. Mirodatos, Chem. Eng. Technol., 1995, 18, 216–223 CrossRef CAS.
- M. Ghiasi, A. Malekzadeh, S. Hoseini, Y. Mortazavi, A. Khodadadi and A. Talebizadeh, J. Nat. Gas Chem., 2011, 20, 428–434 CrossRef CAS.
- U. Gupta and D. G. Vlachos, SoftwareX, 2020, 11, 100442 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Shekhar R.
Kulkarni
a,
Shekhar R.
Kulkarni
 a,
Vijay K.
Velisoju
a,
Vijay K.
Velisoju
 a,
Natalia
Realpe
a,
Natalia
Realpe
 a and
Pedro
Castaño
a and
Pedro
Castaño
 *ab
*ab

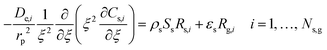



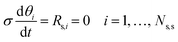








 formation primarily involves Langmuir–Hinshelwood reactions, with one H atom being removed from the reactant as OH* via the formation of CH2O*.30,31 Other relevant COX sources include gas-phase oxidation of C2H5˙ and C2H3˙ radicals produced through H˙ abstraction and surface C2H4 oxidation through adsorption, H˙ abstraction, and C–C bond cleavage.32 Therefore, effective catalysts not only activate CH4 but also prevent deep oxidation paths, represented by HO2˙ quenching in the surface mechanism. Finally, the regeneration of active sites involves water desorption, resulting from adsorbed OH˙ radicals yielding O*. The catalytic reaction network with 10 surface species (excluding vacancies) and 26 reversible elementary steps used in this work is presented in Table 1.
formation primarily involves Langmuir–Hinshelwood reactions, with one H atom being removed from the reactant as OH* via the formation of CH2O*.30,31 Other relevant COX sources include gas-phase oxidation of C2H5˙ and C2H3˙ radicals produced through H˙ abstraction and surface C2H4 oxidation through adsorption, H˙ abstraction, and C–C bond cleavage.32 Therefore, effective catalysts not only activate CH4 but also prevent deep oxidation paths, represented by HO2˙ quenching in the surface mechanism. Finally, the regeneration of active sites involves water desorption, resulting from adsorbed OH˙ radicals yielding O*. The catalytic reaction network with 10 surface species (excluding vacancies) and 26 reversible elementary steps used in this work is presented in Table 1.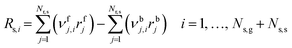



 is the standard reaction enthalpy of heterogeneous reaction step j.
is the standard reaction enthalpy of heterogeneous reaction step j.
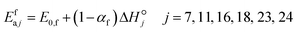
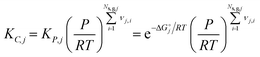


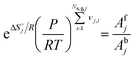
 is the standard reaction Gibbs free energy of reaction step j and
is the standard reaction Gibbs free energy of reaction step j and  is the standard reaction entropy of reaction step j. Both enthalpy and entropy are temperature-dependent state functions. Hence, the activation energies and forward and backward prefactor values should also vary with temperature. For the homogeneous mechanism, thermodynamic consistency is ensured by directly computing the backward reaction rate constant from the forward reaction rate constant and the equilibrium constant:
is the standard reaction entropy of reaction step j. Both enthalpy and entropy are temperature-dependent state functions. Hence, the activation energies and forward and backward prefactor values should also vary with temperature. For the homogeneous mechanism, thermodynamic consistency is ensured by directly computing the backward reaction rate constant from the forward reaction rate constant and the equilibrium constant:

 ,
,  and
and  are the standard Gibbs energy, enthalpy and entropy of species i, respectively. Ensuring thermodynamic consistency in surface reaction mechanisms is more challenging because of the unavailability of Gibbs free energy values for surface species. One way to overcome this challenge is to construct the state functions for surface reactions as combinations of adsorption and analogous gas-phase reactions.38 By identifying the minimum number of linearly independent surface reactions, we can categorize all reactions within the mechanism (Nr,s) into Nr,i linearly independent and Nr,d linearly dependent reactions. Once reactions are reordered such that the first Nr,i reactions are the linearly independent ones (i.e.,
are the standard Gibbs energy, enthalpy and entropy of species i, respectively. Ensuring thermodynamic consistency in surface reaction mechanisms is more challenging because of the unavailability of Gibbs free energy values for surface species. One way to overcome this challenge is to construct the state functions for surface reactions as combinations of adsorption and analogous gas-phase reactions.38 By identifying the minimum number of linearly independent surface reactions, we can categorize all reactions within the mechanism (Nr,s) into Nr,i linearly independent and Nr,d linearly dependent reactions. Once reactions are reordered such that the first Nr,i reactions are the linearly independent ones (i.e.,  ), any linearly dependent surface reaction can be expressed as a combination of linearly independent surface reactions.
), any linearly dependent surface reaction can be expressed as a combination of linearly independent surface reactions.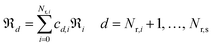


 lose only one translational DOF, (iii) rotational DOFs are converted to vibrational DOFs, and (iv) for adsorbed species with a vertical axis through the adsorbed atom, one vibrational DOF gained is a free, rigid, internal rotor. With these assumptions, the temperature dependence of chemisorption enthalpy is deduced for the four cases in Table 3, and the chemisorption enthalpy at any given temperature is
lose only one translational DOF, (iii) rotational DOFs are converted to vibrational DOFs, and (iv) for adsorbed species with a vertical axis through the adsorbed atom, one vibrational DOF gained is a free, rigid, internal rotor. With these assumptions, the temperature dependence of chemisorption enthalpy is deduced for the four cases in Table 3, and the chemisorption enthalpy at any given temperature is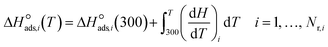
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C3H7. Thus, the chemisorption enthalpy of CH3O˙ is no longer a descriptor, but is related to the chemisorption enthalpy of OH˙ (eqn (32)). This study proposes a similar relationship for CH2CHO˙ and CHO˙ (eqn (33)) on the basis of the average bond energy difference between R–CHO and R–CH2CHO from aldehydes (i.e., difference in bond energy between carbonyl groups of different lengths), which is estimated to be 10 kJ mol−1.42
C3H7. Thus, the chemisorption enthalpy of CH3O˙ is no longer a descriptor, but is related to the chemisorption enthalpy of OH˙ (eqn (32)). This study proposes a similar relationship for CH2CHO˙ and CHO˙ (eqn (33)) on the basis of the average bond energy difference between R–CHO and R–CH2CHO from aldehydes (i.e., difference in bond energy between carbonyl groups of different lengths), which is estimated to be 10 kJ mol−1.42



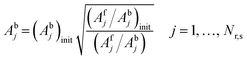




 (40, 27, and 30 kJ mol−1 for IMP SiO2, SD SiO2–α + βSiC, and SD SiO2–βSiC, respectively). Note that the OH˙ chemisorption enthalpy influences other critical routes related to deep catalytic oxidation of CH3˙ radicals and C2H4, as well as the hydroxyl species regeneration step. The expected larger H2O chemisorption entropies in Table 5, render the regeneration step more kinetically favorable for SD SiO2–α + βSiC, especially compared with IMP SiO2. Furthermore, weaker H2O adsorption has been reported to result in higher CH4 activity.30
(40, 27, and 30 kJ mol−1 for IMP SiO2, SD SiO2–α + βSiC, and SD SiO2–βSiC, respectively). Note that the OH˙ chemisorption enthalpy influences other critical routes related to deep catalytic oxidation of CH3˙ radicals and C2H4, as well as the hydroxyl species regeneration step. The expected larger H2O chemisorption entropies in Table 5, render the regeneration step more kinetically favorable for SD SiO2–α + βSiC, especially compared with IMP SiO2. Furthermore, weaker H2O adsorption has been reported to result in higher CH4 activity.30


 to be positive as shown in Table 5. Furthermore, thermodynamics dictate that for any endothermic reaction, the forward activation energy should be larger than the heat of reaction; this is satisfied through the selection of the Polanyi parameters E0,f and αf to ensure that the relationship
to be positive as shown in Table 5. Furthermore, thermodynamics dictate that for any endothermic reaction, the forward activation energy should be larger than the heat of reaction; this is satisfied through the selection of the Polanyi parameters E0,f and αf to ensure that the relationship  holds. For chemisorption entropies, upholding the “Langmuirian integrity” requires
holds. For chemisorption entropies, upholding the “Langmuirian integrity” requires  , which accounts for the loss of translational contribution upon adsorption. A less strict constraint, proposed by Vannice et al.,70 is
, which accounts for the loss of translational contribution upon adsorption. A less strict constraint, proposed by Vannice et al.,70 is  (in J mol−1 K−1) from the decrease of free volume upon adsorption at the standard state coverage of 0.5, with the upper limit dictated by the relationship described before. Values associated with both entropic constraints are presented in Table 6.
(in J mol−1 K−1) from the decrease of free volume upon adsorption at the standard state coverage of 0.5, with the upper limit dictated by the relationship described before. Values associated with both entropic constraints are presented in Table 6.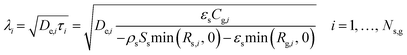

 , (c) O*, (d) * (vacancies), (e) CH3O*, (f) CH3CHO*, (g) CO*, and (h) H2O*. Simulation conditions and results are identical to those of Fig. 9.
, (c) O*, (d) * (vacancies), (e) CH3O*, (f) CH3CHO*, (g) CO*, and (h) H2O*. Simulation conditions and results are identical to those of Fig. 9. (Fig. 10b).
(Fig. 10b).  does not form any intraparticle concentration gradient, leading to an anticipated plateau in CH4 conversion as the
does not form any intraparticle concentration gradient, leading to an anticipated plateau in CH4 conversion as the  concentration becomes predominant; this is in accord with studies on CO2 inhibition in various catalyst families, including Li/MgO,73 La2O3,74 and Mn–Na2WO4/SiO2.75 Unlike surface CO2, CO* shows intraparticle profiles (Fig. 10g), possibly because of the low concentration of CO*. Notably, in the case of IMP SiO2, no significant concentrations of oxygenates result from direct sticking reactions. The catalyst hence has high C2 selectivity.
concentration becomes predominant; this is in accord with studies on CO2 inhibition in various catalyst families, including Li/MgO,73 La2O3,74 and Mn–Na2WO4/SiO2.75 Unlike surface CO2, CO* shows intraparticle profiles (Fig. 10g), possibly because of the low concentration of CO*. Notably, in the case of IMP SiO2, no significant concentrations of oxygenates result from direct sticking reactions. The catalyst hence has high C2 selectivity. concentrations. Despite the lower CH4 conversion and C2 selectivity predicted for SD SiO2–α + βSiC compared with IMP SiO2, which are reflected in reduced OH* concentrations, an increase in
concentrations. Despite the lower CH4 conversion and C2 selectivity predicted for SD SiO2–α + βSiC compared with IMP SiO2, which are reflected in reduced OH* concentrations, an increase in 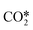 coverages significantly affects CH4 conversion. This is driven by increased CH3O* concentrations, generating pronounced radial intraparticle gradients. In SD SiO2–α + βSiC, concentrations of CH3O*, CH2O*, and CHO* are comparable, around 10−5, while concentrations of CO* and CH3CHO* are around 10−10, indicating the susceptibility of CH3˙ radicals rather than C2H4 to depletion.
coverages significantly affects CH4 conversion. This is driven by increased CH3O* concentrations, generating pronounced radial intraparticle gradients. In SD SiO2–α + βSiC, concentrations of CH3O*, CH2O*, and CHO* are comparable, around 10−5, while concentrations of CO* and CH3CHO* are around 10−10, indicating the susceptibility of CH3˙ radicals rather than C2H4 to depletion. concentration was similar to that in IMP SiO2. This could explain the CH4 conversion of SD SiO2–βSiC being intermediate between IMP SiO2 and SD SiO2–α + βSiC. Despite its high predicted C2 selectivity, SD SiO2–βSiC showed greater propensity to chemisorb C2H4.
concentration was similar to that in IMP SiO2. This could explain the CH4 conversion of SD SiO2–βSiC being intermediate between IMP SiO2 and SD SiO2–α + βSiC. Despite its high predicted C2 selectivity, SD SiO2–βSiC showed greater propensity to chemisorb C2H4. sequence, with minimal involvement of C2H4 oxidation. The favored pathway from C2H4 to C2H3˙ involves gas-phase oxidation, primarily through O2 (28%), catalytic H-abstraction by O* (24%), or reaction with H˙ (21%). Furthermore, gas-phase chain growth to C3H7˙ consumes 11% of C2H4. CH3O* follows the expected catalytic path to CO, with 70% formed catalytically via CO desorption from CHO* through the Langmuir–Hinshelwood route.28 Eley–Rideal H abstraction of CHO˙ is a minor contributor, and the remaining CO comes from gas-phase CHO˙ collision. Around half (50.3%) of CO* is desorbed, while 49.7% is oxidized to CO2, almost entirely catalytically. Catalysts play a key role in radical quenching. HO2˙ consumption occurs solely through heterogeneous collision with vacancies, and H-abstraction of HO2˙ by O* partly explains the decreasing OH* concentration. Recombination consumes surface hydroxyl radicals at a rate of 1.4 × 10−3 kmol mb−3 s−1.
sequence, with minimal involvement of C2H4 oxidation. The favored pathway from C2H4 to C2H3˙ involves gas-phase oxidation, primarily through O2 (28%), catalytic H-abstraction by O* (24%), or reaction with H˙ (21%). Furthermore, gas-phase chain growth to C3H7˙ consumes 11% of C2H4. CH3O* follows the expected catalytic path to CO, with 70% formed catalytically via CO desorption from CHO* through the Langmuir–Hinshelwood route.28 Eley–Rideal H abstraction of CHO˙ is a minor contributor, and the remaining CO comes from gas-phase CHO˙ collision. Around half (50.3%) of CO* is desorbed, while 49.7% is oxidized to CO2, almost entirely catalytically. Catalysts play a key role in radical quenching. HO2˙ consumption occurs solely through heterogeneous collision with vacancies, and H-abstraction of HO2˙ by O* partly explains the decreasing OH* concentration. Recombination consumes surface hydroxyl radicals at a rate of 1.4 × 10−3 kmol mb−3 s−1. on the catalyst surface. Furthermore, the excessive accumulation of
on the catalyst surface. Furthermore, the excessive accumulation of  on the catalyst surface, particularly from CH3O*, adversely affected the global reaction rate. Consequently, the catalytic contribution of CO was higher for the SiC-containing catalysts (87–88%) compared to the IMP SiO2 catalyst (70%). This underscores the notion that in the OCM process, radicals should not only be generated at high rates but also consumed judiciously, with HO2˙ rates contributing to high C2 selectivities.
on the catalyst surface, particularly from CH3O*, adversely affected the global reaction rate. Consequently, the catalytic contribution of CO was higher for the SiC-containing catalysts (87–88%) compared to the IMP SiO2 catalyst (70%). This underscores the notion that in the OCM process, radicals should not only be generated at high rates but also consumed judiciously, with HO2˙ rates contributing to high C2 selectivities.

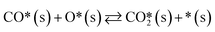









![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) p vector of catalytic descriptor estimates of the model, c.u., or heating rate of the catalyst bed under temperature-programmed experiments, °C min−1
p vector of catalytic descriptor estimates of the model, c.u., or heating rate of the catalyst bed under temperature-programmed experiments, °C min−1

