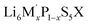Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhancing ionic conductivity in Li6+xGexP1−xS5Br: impact of Li+ substructure on ionic transport and solid-state battery performance†
Vasiliki
Faka
a,
Bibek
Samanta
bc,
Martin A.
Lange
ad,
Bianca
Helm
e,
Xabier
Martinez de Irujo-Labalde
a,
Niklas
Kierdorf
a,
Lukas
Ketter
ac,
Emmanuelle
Suard
 f,
Marvin A.
Kraft
f,
Marvin A.
Kraft
 ad,
Brian E.
Francisco
g,
Michael Ryan
Hansen
ad,
Brian E.
Francisco
g,
Michael Ryan
Hansen
 *bc and
Wolfgang G.
Zeier
*bc and
Wolfgang G.
Zeier
 *ad
*ad
aInstitute of Inorganic and Analytical Chemistry, University of Münster, Corrensstraße 28/30, 48149 Münster, Germany. E-mail: wzeier@uni-muenster.de; mhansen@uni-muenster.de
bInstitute of Physical Chemistry, University of Münster, Corrensstraße 28/30, 48149 Münster, Germany
cInternational Graduate School BACCARA, Wilhelm-Schickard-Straße 8, 48149 Münster, Germany
dInstitute of Energy Materials and Devices (IMD), IMD 4: Helmholtz-Institut Münster Ionics in Energy Storage, Forschungszentrum Jülich GmbH, 48149 Münster, Germany
eBavarian Center for Battery Technology (BayBatt), University of Bayreuth, Universitätsstrasse 30, 95447 Bayreuth, Germany
fInstitut Laue-Langevin, BP 156, 38042 Grenoble Cedex 9, France
gSolid Power Inc, 486 S Pierce Ave Ste E, Louisville, Colorado 80027, USA
First published on 8th May 2025
Abstract
Solid-state batteries have been investigated as efficient energy storage systems due to the increased power and energy densities that they can offer compared to liquid-based batteries. The search for solid electrolytes with high ionic conductivities, sufficient electrochemical and mechanical stability is indispensable. In this work, the Li6+xGexP1−xS5Br substitution series is investigated via X-ray and neutron powder diffraction, as well as impedance and solid-state nuclear magnetic resonance spectroscopy. Structural analyses reveal the expansion of the cage-like Li+ substructure with increasing degree of substitution of Ge(IV) for P(V) in Li6+xGexP1−xS5Br. Solid-state nuclear magnetic resonance spectroscopy measurements reveal the gradual changes in cation environments (6Li and 31P) and the effect of Ge(IV) substitution on local Li+ transport. Impedance spectroscopy shows an improvement of ionic conductivity at room temperature up to fivefold for Li6.31Ge0.31P0.69S5Br and decreasing activation energies. Employing Li6.31Ge0.31P0.69S5Br as a catholyte in LiNixMnyCozO2 based solid-state batteries results in reproducibly higher active material utilization and rate stability in comparison to Li6PS5Br. This work emphasizes the importance of understanding the Li+ substructure of argyrodites in correlation with the Li+ transport properties to systematically develop highly conductive Li+ solid electrolytes for improved solid-state batteries.
Introduction
Solid electrolytes and their application in solid-state batteries have gained considerable scientific interest, due to the growing demand for more efficient electrochemical energy storage systems.1,2 Several classes of solid electrolytes, e.g., oxides,3 thiophosphates4 and (oxy)halides5,6 have been investigated, exhibiting advantages such as fast Li+ conduction and high chemo-mechanical stability.7 Among them, lithium-ion conducting argyrodites (Li6PS5X, X = Br, Cl, I)8 have attracted considerable attention, due to their compositional variety, which allows to tune their electrochemical properties, achieving high ionic conductivities.9,10 Additionally, their mechanically soft nature allows them to be easily processed and densified, which is especially beneficial for use in solid-state batteries.11,12The crystal structure of  (M′ = Ge, Si and Sn, while X = Br, Cl, I) (Fig. 1a) consists of the halide anions X−, forming a face-centered cubic lattice (Wyckoff 4a) with the octahedral sites to be occupied by the on average MS4 tetrahedra (where M = P, Ge, Si, Sn on Wyckoff 4b and S on Wyckoff 16e, respectively). The sulfide anions S2− are located on half of the tetrahedral sites (Wyckoff 4d).13 This framework leads to five types of tetrahedral sites in the high-temperature argyrodite structure, which can be potentially occupied by Li+, classified as type 1 (T1) to type 5 (T5).
(M′ = Ge, Si and Sn, while X = Br, Cl, I) (Fig. 1a) consists of the halide anions X−, forming a face-centered cubic lattice (Wyckoff 4a) with the octahedral sites to be occupied by the on average MS4 tetrahedra (where M = P, Ge, Si, Sn on Wyckoff 4b and S on Wyckoff 16e, respectively). The sulfide anions S2− are located on half of the tetrahedral sites (Wyckoff 4d).13 This framework leads to five types of tetrahedral sites in the high-temperature argyrodite structure, which can be potentially occupied by Li+, classified as type 1 (T1) to type 5 (T5).
Occupancy on these positions results in cage-like Li+ structures around the Wyckoff 4d site and the spatial Li+ distribution is described by the rmean distance, which corresponds to the mean distances of Li+ to the center of the “cage”.14 Increasing rmean distance describes expanding cage-like Li+ substructure (Fig. 1c).13,15
In the three-jump model,16 Li+ diffusion is described by motion in terms of “jumps” between the type 5 (T5) and type 5a (T5a) sites. These jumps are classified into three types: (a) doublet jumps represent localized motion between face-sharing T5 tetrahedra, via the T5a site. (b) Intra-cage jumps consist of lithium-ion motion between pairs of non-face-sharing T5 tetrahedra within the same 4d centered cage. (c) Inter-cage jumps consist of lithium-ion motion between T5 positions associated with different 4d-centered Li+ cages.17
The Li+ occupancy of type 2 (T2) sites is related to enhanced ionic conductivities, since it offers the shortest inter-cage distance, facilitating Li+ transport via T5–T2–T2–T5 (Fig. 1b).18 Similar to fast Cu+/Ag+ conducting argyrodites,19 type 3 (T3) and type 4 (T4) tetrahedral sites have been reported for x(Li) > 6 systems, suggesting alternative pathways for interconnecting Li+ cages.20
Another descriptor reported for argyrodites is the degree of the X−/S2− site disorder between the halide anions X− (on Wyckoff 4a) and the sulfide ions S2− (on Wyckoff 4d) has been proven to significantly influence their ionic conductivity.21,22 The X−/S2− site disorder can also be described in the terms of ionic potential to predict argyrodite conductivity by assessing the interaction strength between cations and anions.23
Notably, extensive efforts have been devoted towards modifying lithium argyrodites chemically by cation substitutions, resulting in some of the fastest Li+ conductors, achieving ionic conductivities greater than 10 mS cm−1.24,25 Kraft et al. reported the Ge-substituted Li6PS5I, which has a high ionic conductivity of approximately 18 mS cm−1 in sintered pellets, compared to the very low ionic conductivity (1 μS cm−1) of the non-substituted Li6PS5I.26 Substitution of Si(IV) for P(V) in Li6PS5Br leads to three-fold increase in ionic conductivity.27 Aliovalent doping of Li+ with Ca2+ improves Li+ diffusion and conductivity, due to creation of vacancies; doping with the trivalent Ga3+ and Al3+ however was not successful.28
To date, substitution of Ge(IV) for P(V) in Li6PS5Br using a high temperature synthesis route has been reported as unsuccessful.27 Strauss et al.29 reported Li7GeS5Br as a metastable low-temperature phase, synthesized via ball milling. In their study, the reflection broadening in the X-ray diffraction patterns was attributed to the nanometer range crystallite size of the material and the presence of amorphous side phases. Further annealing at 250 °C under vacuum resulted in decomposition of the material and the formation of LiBr and Li4GeS4.
Motivated by the open question of whether Ge(IV) can be incorporated in the Li6PS5Br structure via ball mill assisted solid-state synthesis, we investigate the substitution series of Li6+xGexP1−xS5Br with increasing Ge(IV) content. X-ray diffraction analyses show the successful incorporation of Ge(IV) up to nominal content of xN(Ge) = 0.35. Rietveld refinements against neutron powder diffraction data reveal the occupation of additional Li+ sites with increasing Ge(IV) content, concurrently resulting in an increasing rmean distance. These findings suggest a better interconnection of Li+ sites, with increasing Ge(IV) content. Solid-state nuclear magnetic measurements indicate that the trends in local activation energies are primarily affected by the Li+ substructure and anion-site disorder. Impedance spectroscopy reveals that Li6.31Ge0.31P0.69S5Br exhibits a five-fold higher ionic conductivity compared to Li6PS5Br, making it a promising candidate for solid-state batteries. The application of Li6.31Ge0.31P0.69S5Br as catholyte suggest enhanced transport properties in solid-state battery cathodes, further supporting that, faster solid electrolytes are needed for well-performing solid-state batteries.
Methods
Synthesis
The ball mill assisted solid-state synthesis of Li6+xGexP1−xS5Br was carried out in Ar atmosphere (H2O < 0.5 ppm, O2 < 0.1 ppm). Lithium sulfide (Li2S, Alfa-Aesar, 99.9%), phosphorous pentasulfide (P4S10, Merck, 99%), germanium(II) sulfide (GeS, Sigma-Aldrich, 99.99%), lithium bromide (LiBr, ultradry, Alfa-Aesar, 99.99%) and sulfur (S, Acros Organics, 99.999%) were mixed in appropriate stoichiometric ratio and hand-ground in an agate mortar to obtain a homogeneous mix. The obtained mixture was transferred into an 80 mL zirconia ball milling cup with 120 g of 5 mm diameter zirconia milling media (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio of milling media to precursor) and milled for a total of 90 cycles with intermediate resting time after each cycle (10 min milling and 10 min resting). During the 90 milling cycles, the ball mill cup was opened twice to remove and grind caked powders from the cups. The obtained powders were pressed into pellets of 1 cm diameter and transferred into carbon-coated quartz ampoules. The ampoules were dried at 1073 K for 2 hours under dynamic vacuum prior to use, to remove any traces of H2O and surface –OH. Subsequently, the ampoules were sealed under vacuum and transferred into a tube furnace preheated to 823 K. The materials were annealed for 2 hours and left to naturally cool to room temperature.
1 mass ratio of milling media to precursor) and milled for a total of 90 cycles with intermediate resting time after each cycle (10 min milling and 10 min resting). During the 90 milling cycles, the ball mill cup was opened twice to remove and grind caked powders from the cups. The obtained powders were pressed into pellets of 1 cm diameter and transferred into carbon-coated quartz ampoules. The ampoules were dried at 1073 K for 2 hours under dynamic vacuum prior to use, to remove any traces of H2O and surface –OH. Subsequently, the ampoules were sealed under vacuum and transferred into a tube furnace preheated to 823 K. The materials were annealed for 2 hours and left to naturally cool to room temperature.
X-ray powder diffraction
A Stoe StadiP powder diffractometer in Debye–Scherrer geometry with Mo Kα1 radiation (λ = 0.70930 Å) was utilized for X-ray diffraction measurements. The 2θ collection ranged from 4° to 60°, with a step size of 0.015° and a counting time of 60 s per step. To avoid material degradation in air, all samples were prepared and sealed in borosilicate glass capillaries in Ar atmosphere (H2O < 0.5 ppm, O2 < 0.1 ppm).Neutron powder diffraction
High-resolution neutron powder diffraction data were collected on the D2B high-resolution two-axis powder diffractometer at the Institute Laue-Langevin (ILL, Grenoble, France), with incident monochromatic constant wavelength of λ = 1.594 Å. A total data collection time of 3 hours, divided in 10 scans, was used to ensure improved statistics for data evaluation. All neutron powder diffraction measurements were carried out at room temperature. Approximately 2.5 g of material of each sample was filled into an 8 mm diameter cylindrical vanadium container (wall thickness 150 μm) in Ar atmosphere (H2O < 0.5 ppm, O2 < 0.1 ppm) and sealed using an indium wire to prevent air exposure during the measurement. The used angular range of diffraction data for refinements was 11° ≤ 2θ ≤ 140°.Rietveld analysis
Rietveld refinements were performed using the TOPAS-Academic V7.25 software package.30 The structural information of Li6PS5Br taken from Gautam et al.31 was used as a starting model for this study. The peak shape was described by a pseudo-Voigt function using the modified Thomson–Cox–Hasting modification.32 Fit indicators Rwp, Rexp, and goodness-of-fit were used to assess the quality of the refined structural model.Solid-state nuclear magnetic resonance (NMR)
Solid-state magic-angle spinning (MAS) NMR experiments for 6Li (υL = 73.6 MHz) and 31P (υL = 202.4 MHz) were carried out at a Bruker DSX 500 spectrometer equipped with a 11.74 T wide-bore magnet. For both 6Li and 31P, single-pulse MAS NMR measurements were performed at a spinning frequency of 25.0 kHz using 2.5 mm zirconia rotors and a 2.5 mm Bruker MAS probe (6Li: p1 = 3.5 μs at 100 W, d1 = 30 s; 31P: p1 = 3.0 μs at 100 W, d1 = 30 s). The magic angle was calibrated using the 23Na spinning sideband signals of solid NaNO3. The 6Li and 31P chemical shift scale was referenced against 6Li-enriched solid Li2CO3 and 85% H3PO4 solution to 0 ppm, respectively. All the samples were in powder form and packed into the NMR rotors in Ar atmosphere (H2O < 0.5 ppm, O2 < 0.1 ppm).Variable temperature static saturation recovery experiments for 7Li (υL = 116.64 MHz) were performed on a Bruker Avance III 300 spectrometer connected to a wide-bore magnet of 7.05 T nominal magnetic field. Samples were packed into 4 mm zirconia rotors. A radio-frequency pulse length of 2.5 μs at 120 W power was used as 90° pulse. Recovery delay lengths were varied from t1 = 10 μs to t27 = 31.623 s with four steps increment per decade. All the FIDs were Fourier-transformed to obtain frequency-domain signals which were integrated in TopSpin software. Corresponding signal intensity curves were fitted with monoexponential-type saturation function with a stretching exponent. Variable temperature data were recorded in the temperature range of 200 K to 420 K with 20 K interval between successive measurements and 20 minutes of temperature stabilization period at each temperature. A combination of N2 gas flow and electrical heating was used to regulate the temperature. For T < 300 K, cooled N2 gas flow from an Air Jet XR compressor from SP Scientific (FTS Systems) controlled the temperature, whereas an uncooled stream of N2 gas was utilized for temperature stabilization in T > 300 K range. Temperature calibration was performed using temperature-dependent 1H NMR signal-shifting of methanol (200 K to 290 K) and ethylene glycol (320 K to 420 K).
Potentiostatic electrochemical impedance spectroscopy (PEIS)
Temperature-dependent PEIS was conducted for powder samples of all various compositions. For each measurement, 250 mg of powder was hand-pressed into a pellet and then isostatically densified at 410 MPa for 45 minutes, resulting in relative densities greater than 88%. Afterwards, gold electrodes (thickness 100 nm) were sputtered onto the pellets, which were then contacted with aluminum current collectors and fixed into pouch cells. Impedance spectra were recorded using an Alpha-A impedance analyzer (Novocontrol Technologies) in a temperature range from 298 K to 173 K (one hour of equilibration time per temperature step), utilizing an amplitude of 10 mV in a frequency range of 5 MHz to 100 mHz. The RelaxIS 3 software (rhd instruments) was utilized for data evaluation and the data quality was tested using the Kramers–Kronig analysis to limit the fitted frequency range. Uncertainties of the ionic conductivity were determined from the standard deviation of triplicate measurements.33Solid-state battery assembly and evaluation of Li6+xGexP1−xS5Br as catholyte
Solid-state battery half-cells were assembled using Li6PS5Br and Li6.31Ge0.31P0.69S5Br as catholytes. The cell building was carried out in Ar atmosphere (H2O < 0.5 ppm, O2 < 0.1 ppm). Commercial LiNi0.83Co0.11Mn0.06O2 (NCM-83, MSE supplies) was dried overnight at 523 K, under vacuum, in a Büchi B-585 glass oven prior to use. NCM-83 was used as the cathode active material in a mass ratio of 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 (NCM-83
35 (NCM-83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li6+xGexP1−xS5Br) with the configuration of In/LiIn|Li5.5PS5.5Cl1.5|NCM-83
Li6+xGexP1−xS5Br) with the configuration of In/LiIn|Li5.5PS5.5Cl1.5|NCM-83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li6+xGexP1−xS5Br, for x = 0 and x = 0.31, respectively.
Li6+xGexP1−xS5Br, for x = 0 and x = 0.31, respectively.
The materials were transferred into a 5 mL ball mill cup with five 5 mm diameter ZrO2 balls and soft milled at 15 Hz for 15 minutes to prepare cathode composites. For the first step of cell assembly, 80 mg of Li5.5PS4.5Cl1.5 were used as the separator and hand-pressed. Afterwards, 12 mg of the composite cathode was distributed homogeneously onto the separator. Subsequently, 3 tons of force (380 MPa) were applied uniaxially for 3 minutes. Then, lithium was cut from a lithium rod (abcr, 99.8%) with a mass between 1.5 mg and 1.8 mg and layered below indium foil (chemPUR, 100 μm thickness, 9 mm diameter, 99.999%) to avoid direct contact with the separator and to ensure a stable In/LiIn counter electrode during cycling. The press cell was fixed in an Al frame and tightened by applying torque of 10 N m, resulting in 50 MPa of stack pressure during cell cycling. Triplicates were built for each composite, to ensure the reproducibility of the results.34 All electrochemical measurements were performed using a BioLogic VMP-300 potentiostat in a climate chamber at constant T = 298 K. For solid-state battery cycling, the cells were charged to 3.7 V vs. In/LiIn and discharged to 2.0 V vs. In/LiIn, applying a current density of j = 0.199 mA cm−2 corresponding to a theoretical C-rate of 0.1, assuming a specific NCM-83 capacity of 200 mA h g−1. To test the rate performance varying applied charge and discharge currents of C/20 (j = 0.099 mA cm−2), C/5 (j = 0.397 mA cm−2), C/2 (j = 0.993 mA cm−2) and 1C (j = 1.986 mA cm−2) were applied in a voltage window from 2.0 V to 3.7 V vs. In/LiIn.
Particle size distribution (PSD)
The volume-weighted particle size distribution was determined using a HELOS particle size analyzer (Sympatec). Therefore, 4.5 mg of powder was placed in a small vial and dispersed into 4 mL of p-xylene mixture containing 1 wt% polyisobutene, which was added to enhance the viscosity. The dispersion was then ultrasonicated with an ultrasonic finger for approximately 15 min in Ar atmosphere (H2O < 0.5 ppm, O2 < 0.1 ppm). Subsequently, the dispersion was injected into a cuvette containing a ratio of 40 mL of p-xylene to 1 wt% polyisobutene mixture outside the glovebox until a sufficient optical saturation for a reliable measurement was achieved. The dispersion was stirred during measurement to prevent sedimentation of particles.Scanning electrode microscopy (SEM)
SEM measurements were carried out using a Phenom ProX Desktop SEM from ThermoFisher, applying an acceleration voltage of 10 keV and using a BSE detector. For each sample, 2 mg of material were dispersed in p-xylene using an ultrasonic finger and drop cast onto a silicon wafer piece glued to a standard SEM-specimen stub. Subsequently, the stubs were sputter coated with a 150 nm layer of gold. All sample preparation was carried out in Ar atmosphere (H2O < 0.5 ppm, O2 < 0.1 ppm).Resistor network modeling
Transport simulations have been performed, using the code published by Ketter et al.35 In the first step, a virtual microstructure was generated, representing a composite of size 180 μm × 180 μm × 180 μm. For this, a SE![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NCM-83 volume ratio of 54
NCM-83 volume ratio of 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 and a resolution of (0.5 μm)3/voxel (Lvox = 360) were specified. NCM-83 was chosen as the continuous phase, while clusters of 3000 voxels (sclust = 3000) were inserted as a dispersed phase to represent SE with d50 ≈ 9 μm. The virtual microstructure was then divided into three equal parts, each representing a positive electrode of size 60 μm × 180 μm × 180 μm. Using these as structural input, in a second step, the effective ionic and electronic conductivities were separately calculated assuming purely ion conducting solid electrolytes (σe,SE ≈ 0 mS cm−1) and purely electron conducting NCM-83 (σion,NCM-83 ≈ 0 mS cm−1). The experimentally assessed ionic conductivities of Li6PS5Br (0.8 mS cm−1) and Li6.31Ge0.31P0.69S5Br (3.8 mS cm−1) from this work, as well as the electronic conductivity of NCM-83 (5.22 mS cm−1) reported by Ketter et al.35 were used as input parameters. The effective conductivities were calculated for each of the three virtual electrodes, taking the mean value as the true conductivity and the standard deviation as the corresponding uncertainty. The software Paraview has been used to visualize the virtual composites.36
46 and a resolution of (0.5 μm)3/voxel (Lvox = 360) were specified. NCM-83 was chosen as the continuous phase, while clusters of 3000 voxels (sclust = 3000) were inserted as a dispersed phase to represent SE with d50 ≈ 9 μm. The virtual microstructure was then divided into three equal parts, each representing a positive electrode of size 60 μm × 180 μm × 180 μm. Using these as structural input, in a second step, the effective ionic and electronic conductivities were separately calculated assuming purely ion conducting solid electrolytes (σe,SE ≈ 0 mS cm−1) and purely electron conducting NCM-83 (σion,NCM-83 ≈ 0 mS cm−1). The experimentally assessed ionic conductivities of Li6PS5Br (0.8 mS cm−1) and Li6.31Ge0.31P0.69S5Br (3.8 mS cm−1) from this work, as well as the electronic conductivity of NCM-83 (5.22 mS cm−1) reported by Ketter et al.35 were used as input parameters. The effective conductivities were calculated for each of the three virtual electrodes, taking the mean value as the true conductivity and the standard deviation as the corresponding uncertainty. The software Paraview has been used to visualize the virtual composites.36
Partial charge transport measurements
To determine ionic partial conductivity values of the cathode composites, electron blocking cells were assembled. 80 mg of Li6+xGexP1−xS5Br was layered between 80 mg of Li5.5PS4.5Cl1.5 with In/InLi-alloy on both sides with the following cell configuration: In/InLi|Li5.5PS4.5Cl1.5|NCM-83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li6+xGexP1−xS5Br|Li5.5PS4.5Cl1.5|In/InLi. The argyrodite Li5.5PS4.5Cl1.5 was employed on both sides due to its good interfacial stability towards the In/InLi.37 Each layer was hand-pressed before adding the next layer. Before the indium and lithium foils were added, a densification step using uniaxial pressure of 3 tons for 3 minutes was carried out to ensure good contact between the layers and the electrodes. The cells were assembled in Ar atmosphere (H2O < 0.5 ppm and O2 < 0.1 ppm) by hand-pressing each layer before adding the next one. The cells were then put into an aluminum frame with an applied torque of 10 kN (50 MPa) and were left for 6 hours at 25 °C for equilibration. Impedance measurements of symmetric cells were performed using an AC excitation voltage amplitude of 10 mV (Vrms = 7.07 mV) and recorded in a frequency range of 7 MHz to 10 mHz. Afterwards, constant DC potentials of 1 mV, 2 mV, 5 mV, 10 mV, 15 mV, 20 mV, 25 mV, 30 mV and 50 mV were applied for one hour each. Equilibrium current values for extracted for all potentials and, assuming it can be solely attributed to ionic transport, fitted from I–V plots based on Ohm's law. Subtracting the resistance contributed to the Li5.5PS4.5Cl1.5, and taking into account the sample geometry, the respective ionic conductivities are obtained. For the evaluation of the data, including the fitting of the Nyquist plots and T-type transmission line modeling (TLM) analysis, the RelaxIS 3 software was used.
Li6+xGexP1−xS5Br|Li5.5PS4.5Cl1.5|In/InLi. The argyrodite Li5.5PS4.5Cl1.5 was employed on both sides due to its good interfacial stability towards the In/InLi.37 Each layer was hand-pressed before adding the next layer. Before the indium and lithium foils were added, a densification step using uniaxial pressure of 3 tons for 3 minutes was carried out to ensure good contact between the layers and the electrodes. The cells were assembled in Ar atmosphere (H2O < 0.5 ppm and O2 < 0.1 ppm) by hand-pressing each layer before adding the next one. The cells were then put into an aluminum frame with an applied torque of 10 kN (50 MPa) and were left for 6 hours at 25 °C for equilibration. Impedance measurements of symmetric cells were performed using an AC excitation voltage amplitude of 10 mV (Vrms = 7.07 mV) and recorded in a frequency range of 7 MHz to 10 mHz. Afterwards, constant DC potentials of 1 mV, 2 mV, 5 mV, 10 mV, 15 mV, 20 mV, 25 mV, 30 mV and 50 mV were applied for one hour each. Equilibrium current values for extracted for all potentials and, assuming it can be solely attributed to ionic transport, fitted from I–V plots based on Ohm's law. Subtracting the resistance contributed to the Li5.5PS4.5Cl1.5, and taking into account the sample geometry, the respective ionic conductivities are obtained. For the evaluation of the data, including the fitting of the Nyquist plots and T-type transmission line modeling (TLM) analysis, the RelaxIS 3 software was used.
Results and discussion
Structural characterization of Li6+xGexP1−xS5Br
The aliovalent substitution of Ge(IV) for P(V) in Li6PS5Br is explored by subsequent Rietveld refinements against X-ray and neutron powder diffraction data, as well as analysis of solid-state nuclear magnetic resonance measurements. The structure of all substitution series can be described by the high temperature argyrodite polymorph crystallizing in the F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group.
3m space group.
The effect of the increasing Ge(IV) content in this substitution series is also investigated using solid-state 31P MAS NMR (Fig. 2c and S6a†). For lower Ge(IV) content, i.e., xR(Ge) ≤ 0.04, a multicomponent 31P MAS NMR spectrum with fairly distinct contributions is observed (Fig. 2c). Higher Ge(IV) contents lead to a gradual upfield shift (shift towards lower ppm values) and a decrease in individual contribution of the local environments to the resulting 31P MAS NMR spectra, finally showing a broad asymmetric signal in Li6.31P0.69Ge0.31S5Br (Fig. S6a†). For xR(Ge) ≤ 0.04, deconvolution of the 31P MAS NMR spectra with five resonance signals is in line with the five possible configurations (from 4S0Br to 0S4Br) in the second coordination sphere around the PS43− units, as already reported.39,40
Five possible arrangements of S2−/Br− in the second coordination sphere can be deconvoluted for Li6.04Ge0.04P0.96S5Br (Fig. 2c and d). For higher Ge(IV) content (xR(Ge) = 0.10 and 0.16), more than five 31P resonance signals are needed to obtain a reasonable deconvolution, whereas the contributions from the signals at lower ppm values become more dominant (Fig. S6b†). While the upfield shift results from the stronger shielding effect of Ge(IV), the strongly overlapping 31P signals originating from similar chemical environments around 31P due to distribution of (GeS4)4− units, leads to the gradual loss in spectral resolution with increasing Ge(IV) substitution. A similar trend has been reported by Hogrefe et al. for Ge(IV) substitution into Li6PS5I, albeit with less drastic loss in spectral resolution due to lower anion-site (S2−/Br−) disorder in Li6PS5I compared to Li6PS5Br.41
The presence of multiple Li+-environments is also observed in the 6Li MAS NMR spectra (Fig. 3b), but assigning them to crystallographic Li+-sites is challenging due to their strong spectral overlap. Computational calculations of 7Li chemical shifts for different crystallographic sites (i.e. 24g/T5a, 48h/T5, 48h/T2, 16e/T4) in Li6PS5Br argyrodite have shown that the 7Li chemical shifts are dependent on (i) the distribution of Li+ in different crystallographic sites, and (ii) Br− occupancy of the 4d site.23 On this basis, the authors have reported a 7Li chemical shift trend in the order T5a (∼2 ppm) > T5, T2 (∼2–1 ppm) > T4 (∼0 ppm). Also, occupancy in the T4 sites was found to cause an upfield shift for Li+ in the T5 sites. Due to the similar electronic environment (both 6Li and 7Li have 3 electrons, only their neutron number is different), these computed trend in chemical shifts can be applied to the chemical shielding of 6Li nuclei also, as shown by Wang et al. for two different theoretical Li6PS5Br structure with Li-occupation at only T5 and T5a sites.39 Their calculation also reveal a broader distribution of 6Li chemical shifts for T5 sites (than T5a), depending on the number of neighbouring Li ions and corresponding Li+–Li+ distances. Thus, for xR(Ge) = 0.00, the sharp signal at lower ppm value and the broader signal at higher ppm value have been tentatively assigned to Li+ in T5 (48h) and T5a (24g) sites, respectively. While the strong overlap stemming from close chemical shift values significantly hinders a meaningful deconvolution of the 6Li MAS NMR spectra, tentative deconvolution of the spectra for xR(Ge) = 0.10 and xR(Ge) = 0.31 are presented in Fig. S6c,† based on the Li+ distribution information (Fig. 3a) and probable trend in chemical shifts calculated for different Li+-sites in Br-based Li-argyrodites.23 As discussed above, the 6Li chemical shifts in Li6+xGexP1−xS5Br seem to be affected by both the Li+ distribution (influencing the Li+–Li+ distances) and the Br−/S2− ratio. The distribution in 6Li chemical shifts of the sharp T5 (48h) signal is prominent for xR (Ge) ≤ 0.4, which shows a gradual downfield shift, possibly resulting from decreasing Br−/S2− ratio that leads to higher effective anionic charge at 4d sites. Finally, for xR(Ge) = 0.31, highest amount of Li+ in the T4 sites along with shielding effects from the larger Ge(IV) seems to dominate the 6Li chemical shift, leading to an upfield shift, as presented in Fig. S6d.†
The overall increased Li+ distribution, from additional added Li+, on the additional sites suggests facilitated transport. The occupation of the T2 and T4 site creates a more interconnected Li+ substructure offering a wider variety of potential jump processes, as it has also been observed in other argyrodite systems.41,42 The higher Li+ content within the cages generates stronger Coulomb repulsion among the Li+, allowing for a faster expansion of the cage, which reflects in the expansion of rmean (Fig. 4a).
The Ge(IV) substitution in the Li6PS5Br structure results in decreasing Br−/S2− site disorder (Fig. 4b). This finding is unexpected, since there is typically a reported strong positive correlation between X−/S2− site disorder and enhanced Li+ transport in Li6PS5X (X = Br, Cl, I) argyrodites.20
Ionic transport
Temperature-dependent electrochemical impedance spectroscopy was performed to assess changes in ionic transport for Li6+xGexP1−xS5Br. All impedance data at room temperature for 0 ≤ xR(Ge) ≤ 0.10 were fit to an equivalent circuit model consisting of two elements in series, containing a resistor in parallel to a CPE (constant phase element), representing the bulk resistance (capacitances 10−11 F) and a CPE element in series, representing the blocking electrodes (schematic representation on top of Fig. 5a). All obtained alpha-values are in the range of approximately 0.9, representing the ideality of the process.43 It should be noted that bulk and grain boundary contributions cannot be deconvoluted, but the obtained ideality of the process corresponds well with bulk transport.44 The room-temperature impedance data for 0.16 ≤ xR(Ge) ≤ 0.31 were fitted to an equivalent circuit consisting of a resistor in series with a CPE, representing the blocking electrodes. Due to the low resistance of the investigated materials, the data points at high frequencies are excluded from the analysis, since the impedances were too low to be captured reliably (depicted as gray data points in Fig. 5a). The increasing Ge(IV) content leads to increasing Li+ conductivities at room temperature (Fig. 5b). The ionic conductivity of Li6.31Ge0.31P0.69S5Br at room temperature reaches a maximum value of 3.8 ± 0.3 mS cm−1; a five-fold improvement compared to Li6PS5Br, which exhibits an ionic conductivity of 0.8 ± 0.1 mS cm−1.Temperature-dependent impedance spectra were fitted similar as described above to lower temperatures in the range of −100 °C to 25 °C to resolve the bulk process. Analysis of the Arrhenius behavior of the extracted impedances (Fig. S10†) results in decreasing activation energies (Fig. 5c). Overall, the expansion of rmean indicates a more interconnected network of diffusion pathways allowing for rapid exchange of Li+ between the cages, resulting in higher ionic conductivity at room temperature and decreasing activation energies, with increasing Ge(IV) content (Fig. 5d).
Ge(IV) substitution and change in local ion transport from 7Li spin–lattice (T1) relaxometry
While impedance spectroscopy can probe the long-range transport of Li+ in solid electrolytes, 7Li spin–lattice (T1) relaxometry can be utilized to observe Li+ jumps at much shorter time scales, i.e., in the order of nanoseconds. For ionic conductors with ionic conductivity in the range of mS cm−1 that includes a Li+ diffusion induced T1-relaxation process. This is reflected by the natural logarithm of the relaxation rate T1−1 passing through a maximum when plotting against the inverse temperature T−1, as observed for Li6.10Ge0.10P0.90S5Br (Fig. 6a). The maximum occurs at the temperature (Tmax) where the condition ω0 ≈ 1/τc is fulfilled. Where ω0 is the angular Larmor frequency of 7Li at the given magnetic field and 1/τc is the motional correlation rate at Tmax. For a fully resolved maximum (also referred to as ‘rate peak’), i.e., a maximum connected by a high- and low-temperature flank, fitting of the data with the modified BPP formula45 (see ESI† for the mathematical framework) can provide several important factors. This includes the asymmetry parameter (β), high- and low-temperature activation energies (Ea,HT and Ea,LT = βEa,HT) as obtained from the high- and low-temperature flank of the rate peak respectively,40,41 coupling pre-factor C, Tmax, and relaxation rate Rmax at the temperature of the maximum (Rmax = T1(Tmax)−1).A symmetric rate curve (β = 1) is expected for isotropic, non-correlated motion (often in liquids) where the activation energies for both high- and low-temperature flanks are equal. For solids, deviation from this ideality is commonly observed, leading to β-values less than one (actual values depend on the difference in activation barriers of jump processes dominating the low- and high-temperature jump processes), resulting in Ea,HT > Ea,LT. For Li-argyrodites, the low-temperature (ω0τc ≫ 1) flank of the T1-relaxation rate curve has been associated with high-frequency localized jumps i.e. doublet and intracage, whereas the high-temperature (ω0τc ≪ 1) flank can probe less frequent long-range intercage jumps.39,40 Since the localized jumps have lower activation energy barriers than the long-range intracage jumps, the value of Ea,HT is higher than Ea,LT in such materials. The results of fitting the 7Li T1-relaxation data of Li6+xGexP1−xS5Br series to the BPP formula are presented in Table S13.†
For the compounds in Li6+xGexP1−xS5Br, observation of a rate peak for all samples within the experimental temperature range (Fig. 6b and S7†) indicates fast local Li+ transport. The asymmetric appearance of the peaks around Tmax, as indicated by β-values less than unity (Table S13†), indicates the difference in activation energies of the Li+ jumps that dominate the relaxation process in corresponding high- and low-temperature ranges. In Li6PS5Br, the activation energies (0.19 eV and 0.07 eV, respectively) extracted from the high- and low-temperature flanks are slightly lower than previous reports (Fig. S7†).40,46,47 Computational investigations using MD simulations at 300 K have predicted activation energies between 0.10 eV and 0.11 eV for short-range doublet/intra-cage jumps and 0.18 eV for long-range inter-cage jumps in Li6PS5Br.16 Thus, the activation energies corresponding to high- and low-temperature flanks are generally considered to be dominated by long-range (inter-cage) and short-range (intra-cage/doublet Li+-jumps), respectively (Fig. 6c).40,41,48
While the high-temperature activation energies remain fairly similar (Ea,HT = 0.17–0.20 eV), showing no clear trend with Ge(IV) content, a small increase in the low-temperature activation energies (Ea,LT = 0.05–0.08 eV) is observed. This increment is reported to be a result of increasing cage radius, that made the intracage jumps more energy-intensive due to the increased jump distances. A gradual increase in the Tmax values (from 280 K to 308 K, see Table S13†) with increasing Ge(IV) substitution is observed, indicating the temperature at which the jump rates approximate the 7Li Larmor frequency (≈116 MHz) shifts towards higher values. In terms of Li+ dynamics, this indicates decreasing overall jump rates at any given temperature (see Table S13† for the values calculated for 300 K). Although this is in opposite trend to increasing ionic conductivity with Ge(IV) substitution, such opposite trends have been observed previously for Br-type Li-argyrodites (Li6−xPS5−xB1+x22 and Li6−xAsS5−xBr1+x49). In these cases, shift of the maxima towards higher temperature has been attributed to increasing intercage movements, which may facilitate the long-range ion transport, but have higher activation barriers leading to high-temperature shift of the Tmax. The modified BPP-fits also provides Rmax, i.e., the relaxation rate at Tmax. A gradual increase in the Rmax values (Table S13†) indicates faster relaxation with increasing Ge(IV) content. This reflects the increased homonuclear coupling between Li+ ions due to higher Li+-content as well as the occupation of additional Li+ positions like T2 and T4, leading to faster relaxation and corresponding higher Rmax values. A similar increasing trend in the coupling pre-factor (C) values can be interpreted as a result of overall decreasing Li+ interatomic distance (r0) as C is inversely proportional to the 6th power of r0 (Table S13†).39 The C-values in the range of 10−9 s−2 are also typical for 7Li quadrupole interaction.41 However, the motional correlation rates (1/τc) for the samples calculated at different measurement temperatures using the Ea,HT and pre-exponential factor τc,0 obtained from the modified BPP-fits (Fig. S8†) seems to correlate with the trend in Br−/S2− site disorder and Li+ jump distance (Fig. S9†).
Cell cycling and C-rate tests
The improved ionic conductivity of Li6.31Ge0.31P0.69S5Br makes this material a promising candidate as catholyte for solid-state batteries. The oxidative stability window of the Ge(IV) substituted Li6PS5Br does not change, according to the study of Banik et al.,50 which proves that cation substitutions like Si(IV) and Ge(IV) on Li6PS5I do not influence the oxidative stability window of argyrodite-type solid electrolytes. In addition to this, we propose the application of Ge(IV) substituted Li6PS5Br only on the positive electrode side, since it is known that Ge(IV) substituted materials (like Li10GeP2S12) show significant degradation against lithium metal.51 Therefore, Li6.31Ge0.31P0.69S5Br and Li6PS5Br are explored as catholytes for NCM−83 based cathodes in half-cell cycling (Fig. 7) to investigate the impact of the higher ionic conductivity on cell performance. The obtained charge capacities of 50 cycles at a charge rate of 0.1C (j = 0.199 mA cm−2) reveal the overall higher capacity in cells with Li6.31Ge0.31P0.69S5Br as catholyte (Fig. 7a), hinting at slightly better capacity retention especially over the initial 30 cycles. However, this difference in the obtained charge capacities is not diverging much from the uncertainty of triplicate measurements. The initial decrease in charge capacities for both catholytes is similar and common in NCM-83 based solid-state battery cycling; explained by the irreversible structural rearrangement, chemo-mechanical effects and the generally known degradative losses during cycling.52–54 The charge–discharge profiles (Fig. S11a and S11b†) emphasize the similar cycling behavior with no additional processes occurring during cycling of any of the two solid electrolytes. The Coulomb efficiency development during the first 50 cycles (Fig. S11c†) confirms this by showing identical trends within experimental error. The only observable difference is the higher first efficiency value of Li6.31Ge0.31P0.69S5Br based half cells, which is in accordance with the similar discharge capacity curves of NCM-83 based half cells for both electrolytes.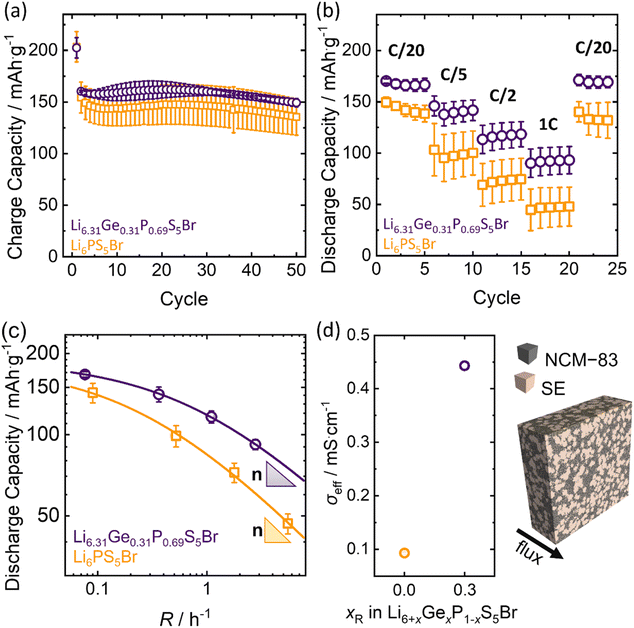 | ||
Fig. 7 Cell performance of In/LiIn|Li5.5PS5.5Cl1.5|NCM-83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li6+xGexP1−xS5Br, for x = 0 and x = 0.31 in half-cell setups. (a) Charge capacities for 50 cycles at 0.1C. (b) Discharge capacities of rate-performance test show that Li6.31Ge0.31P0.69S5Br exhibits enhanced rate-stability. (c) Capacity retention of both systems as a function of the practical rate R. Fits corresponding to the model proposed by Tian et al.55 are given as lines. All errors are calculated from triplicate measurements. (d) Exemplary virtual composite, representing an NCM-83|SE electrode of size 60 μm × 180 μm × 180 μm and effective ionic conductivities as obtained from the resistor network model. Li6+xGexP1−xS5Br, for x = 0 and x = 0.31 in half-cell setups. (a) Charge capacities for 50 cycles at 0.1C. (b) Discharge capacities of rate-performance test show that Li6.31Ge0.31P0.69S5Br exhibits enhanced rate-stability. (c) Capacity retention of both systems as a function of the practical rate R. Fits corresponding to the model proposed by Tian et al.55 are given as lines. All errors are calculated from triplicate measurements. (d) Exemplary virtual composite, representing an NCM-83|SE electrode of size 60 μm × 180 μm × 180 μm and effective ionic conductivities as obtained from the resistor network model. | ||
The discharge capacity of the catholytes is examined by rate-performance tests (Fig. 7b) at constant C-rates (corresponding current densities, j) of C/20 (j = 0.099 mA cm−2), C/5 (j = 0.397 mA cm−2), C/2 (j = 0.993 mA cm−2) and 1C (j = 1.986 mA cm−2). Here, the rate capability of Li6.31Ge0.31P0.69S5Br based cathodes is improved compared to Li6PS5Br, especially at higher current densities. This indicates that substituting Ge(IV) for P(V) in Li6PS5Br leads to higher capacities and enhanced rate performance. Comparing the specific capacities achieved at C/20 before and after the higher C-rate cycling, the similar discharge capacities indicate no significant degradation or decomposition of the two catholytes upon fast dis-/charging. Overall, while the accessible capacity for both materials does not diverge much at low rates, the rate-dependent behavior diverges significantly with the Li6.31Ge0.31P0.69S5Br catholyte showing enhanced rate retention (Fig. 7b). The charge–discharge profiles for the first charge and discharge at each C-rate during the rate-tests (Fig. S11d and e†) emphasize that no additional processes at higher cycling currents, e.g. linked to decomposition of solid electrolyte can be observed.
In order to gain a deeper understanding of the rate behavior, a semi-empirical model describing rate behavior by Tian et al.55 is investigated here. Recently applied in solid-state batteries,56–58 the model quantifies the rate capability of the cathode performance (eqn (1)):55,59
| Q/m = Qm[1 − (R × τ)n × (1 − e−(R × τ)−n)] | (1) |
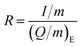 | (2) |
According to Tian et al.,55 the inverse of τ defines the practical rate at which the capacity begins to drop, while n describes the slope of capacity decay. In general, low values of τ and n indicate good rate capabilities and superior cycling kinetics. Application of this model to the given rate behavior results in the fits shown in Fig. 7c.
The similar extrapolated maximum capacity at indefinite low currents (194 ± 3 mA h g−1 and 187 ± 5 mA h g−1, respectively) is in agreement with the fact that the same active material is used and, in principle, accessible. In contrast, the obtained τ and n for Li6PS5Br are τ = 0.52 ± 0.02 and n = 0.46 ± 0.02, while the values for Li6.31Ge0.31P0.69S5Br are τ = 0.153 ± 0.005 and n = 0.45 ± 0.02, respectively. The difference in n is negligible and within uncertainty. However, the respective τ values differ significantly with the Li6.31Ge0.31P0.69S5Br material to present a significantly lower value, indicating a better rate performance than Li6PS5Br. Overall, the cell cycling and C-rate tests suggest that the rate performance of Li6.31Ge0.31P0.69S5Br as a catholyte is significantly better than Li6PS5Br.
However, it may be hypothesized that the enhanced performance of Li6.31Ge0.31P0.69S5Br as a catholyte may be attributed to its microstructure rather than its intrinsic materials properties. Therefore, the microstructure of Li6PS5Br and Li6.31Ge0.31P0.69S5Br is examined using laser diffraction for particle size analysis and scanning electron microscopy (Fig. S12 and S13†). The respective particle sizes and observed microstructures are similar, showing no significant difference. In addition, the determined experimental porosities of the electrodes correspond to φ1 = 20 ± 3% for Li6PS5Br and φ2 = 19 ± 3% for Li6.31Ge0.31P0.69S5Br, indicating that they are similar within experimental uncertainty.
To better understand the superior performance of the solid-state batteries incorporating Li6.31Ge0.31P0.69S5Br catholytes, effective transport is evaluated as a possible origin. Virtual composites approximating the true electrode microstructures are generated (Fig. 7d and S14†) and serve as structural input for the transport simulation on both composite systems. Together with the experimentally assessed ionic conductivities of the pure electrolytes and the electronic conductivity of NCM-83 effective transport can be computed. The simulated effective ionic conductivities of the Li6.31Ge0.31P0.69S5Br containing electrodes clearly exceed those incorporating Li6PS5Br as catholyte (Fig. 7d). The results highlight that the ionic conductivity of the pure phases directly impact the effective conductivity in composites, when no microstructural changes occur. To experimentally corroborate the true effective ion conductivities of both composite systems, DC polarization and impedance measurements were performed. The impedance data (Fig. S15a†) were fitted using the T-type transmission line model (Fig. S15b†).60,61 The values of the effective ionic conductivities obtained by DC polarization and impedance measurements are in good agreement with each other (Fig. S15c†). The experimental data are of the same order of magnitude as the simulated data, with the ionic conductivity in the composite material decreasing by more than an order of magnitude in both cases compared to the pure solid electrolytes, and a higher partial ionic transport in the Li6.31Ge0.31P0.69S5Br containing electrode composites. Therefore, the enhanced battery performance of Li6.31Ge0.31P0.69S5Br can mainly be attributed to differences in transport properties, assuming minimal effects of the material on processing and ruling out any significant influence of microstructural changes.
Conclusion
In this work, the substitution of Ge(IV) for P(V) in Li6+xGexP1−xS5Br is explored and a limit for phase stability is reached near xR(Ge) = 0.31. Changes in the Li+ substructure are monitored by neutron powder diffraction, revealing additional occupied Li+ sites, T2 and T4 sites, with higher Ge(IV) content, also confirmed by solid-state NMR spectroscopy. An expansion of the Li+ cage-like structures, represented by the rmean distance, is found. These findings reveal an overall more interconnected network for increased Li+ diffusion and conduction as reflected in reduced activation energies for ionic transport in the compounds. Solid-state battery cycling reveals that Li6.31Ge0.31P0.69S5Br shows enhanced electrode transport performance in the cathode electrode composite compared to Li6PS5Br.Data availability
After publication, the underlying data of this work will be available on the research data repository of the University of Münster at https://doi.org/10.17879/74928459815.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The research was supported by Solid Power Inc. This work used resources at the Institute Laue-Langevin (ILL, Grenoble, France), instrument D2B high-resolution two-axis diffractometer and the authors thank ILL for the allocation of the beamtime (doi: http://dx.doi.org/10.5291/ILL-DATA.5-22-826).62 The authors further acknowledge funding from the Deutsche Forschungsgemeinschaft under project 459785385. B. S. is a member of the International Graduate School for Battery Chemistry, Characterization, Analysis, Recycling and Application (BACCARA), which is funded by the Ministry for Culture and Science of North Rhine-Westphalia, Germany. The simulations were performed on the high-performance computing cluster PALMA II of the University of Münster. The data from this study is available at: http://dx.doi.org/10.17879/74928459815.References
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Fundamentals of Inorganic Solid-State Electrolytes for Batteries, Nat. Mater., 2019, 18(12), 1278–1291, DOI:10.1038/s41563-019-0431-3.
- J. Janek and W. G. Zeier, A Solid Future for Battery Development, Nat. Energy, 2016, 1(9), 16141, DOI:10.1038/nenergy.2016.141.
- Y. Ren, T. Danner, A. Moy, M. Finsterbusch, T. Hamann, J. Dippell, T. Fuchs, M. Müller, R. Hoft, A. Weber, L. A. Curtiss, P. Zapol, M. Klenk, A. T. Ngo, P. Barai, B. C. Wood, R. Shi, L. F. Wan, T. W. Heo, M. Engels, J. Nanda, F. H. Richter, A. Latz, V. Srinivasan, J. Janek, J. Sakamoto, E. D. Wachsman and D. Fattakhova-Rohlfing, Oxide-Based Solid-State Batteries: A Perspective on Composite Cathode Architecture, Adv. Energy Mater., 2023, 13(1), 2201939, DOI:10.1002/aenm.202201939.
- M. Murayama, R. Kanno, M. Irie, S. Ito, T. Hata, N. Sonoyama and Y. Kawamoto, Synthesis of New Lithium Ionic Conductor Thio-LISICON—Lithium Silicon Sulfides System, J. Solid State Chem., 2002, 168(1), 140–148, DOI:10.1006/jssc.2002.9701.
- B. Singh, Y. Wang, J. Liu, J. D. Bazak, A. Shyamsunder and L. F. Nazar, Critical Role of Framework Flexibility and Disorder in Driving High Ionic Conductivity in LiNbOCl4, J. Am. Chem. Soc., 2024, 146(25), 17158–17169, DOI:10.1021/jacs.4c03142.
- X. Li, J. Liang, X. Yang, K. R. Adair, C. Wang, F. Zhao and X. Sun, Progress and Perspectives on Halide Lithium Conductors for All-Solid-State Lithium Batteries, Energy Environ. Sci., 2020, 13(5), 1429–1461, 10.1039/C9EE03828K.
- F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, Review on Solid Electrolytes for All-Solid-State Lithium-Ion Batteries, J. Power Sources, 2018, 389, 198–213, DOI:10.1016/j.jpowsour.2018.04.022.
- H. Deiseroth, S. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Li6PS5X: A Class of Crystalline Li-Rich Solids With an Unusually High Li + Mobility, Angew. Chem., Int. Ed., 2008, 47(4), 755–758, DOI:10.1002/anie.200703900.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Materials Design of Ionic Conductors for Solid State Batteries, Prog. Energy, 2020, 2(2), 022001, DOI:10.1088/2516-1083/ab73dd.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, High-Power All-Solid-State Batteries Using Sulfide Superionic Conductors, Nat. Energy, 2016, 1(4), 16030, DOI:10.1038/nenergy.2016.30.
- P. Minnmann, F. Strauss, A. Bielefeld, R. Ruess, P. Adelhelm, S. Burkhardt, S. L. Dreyer, E. Trevisanello, H. Ehrenberg, T. Brezesinski, F. H. Richter and J. Janek, Designing Cathodes and Cathode Active Materials for Solid-State Batteries, Adv. Energy Mater., 2022, 12(35), 2201425, DOI:10.1002/aenm.202201425.
- J. Janek and W. G. Zeier, Challenges in Speeding up Solid-State Battery Development, Nat. Energy, 2023, 8, 230–240, DOI:10.1038/s41560-023-01208-9.
- N. Minafra, M. A. Kraft, T. Bernges, C. Li, R. Schlem, B. J. Morgan and W. G. Zeier, Local Charge Inhomogeneity and Lithium Distribution in the Superionic Argyrodites Li6PS5X (X = Cl, Br, I), Inorg. Chem., 2020, 59(15), 11009–11019, DOI:10.1021/acs.inorgchem.0c01504.
- J. Hartel, A. Banik, J. M. Gerdes, B. Wankmiller, B. Helm, C. Li, M. A. Kraft, M. R. Hansen and W. G. Zeier, Understanding Lithium-Ion Transport in Selenophosphate-Based Lithium Argyrodites and Their Limitations in Solid-State Batteries, Chem. Mater., 2023, 35(12), 4798–4809, DOI:10.1021/acs.chemmater.3c00658.
- A. Gautam, H. Al-Kutubi, T. Famprikis, S. Ganapathy and M. Wagemaker, Exploring the Relationship Between Halide Substitution, Structural Disorder, and Lithium Distribution in Lithium Argyrodites (Li6-xPS5-xBr1+x), Chem. Mater., 2023, 35(19), 8081–8091, DOI:10.1021/acs.chemmater.3c01525.
- N. J. J. de Klerk, I. Rosłoń and M. Wagemaker, Diffusion Mechanism of Li Argyrodite Solid Electrolytes for Li-Ion Batteries and Prediction of Optimized Halogen Doping: The Effect of Li Vacancies, Halogens, and Halogen Disorder, Chem. Mater., 2016, 28(21), 7955–7963, DOI:10.1021/acs.chemmater.6b03630.
- S. T. Kong, H. J. Deiseroth, C. Reiner, Ö. Gün, E. Neumann, C. Ritter and D. Zahn, Lithium Argyrodites with Phosphorus and Arsenic: Order and Disorder of Lithium Atoms, Crystal Chemistry, and Phase Transitions, Chem.–Eur. J., 2010, 16(7), 2198–2206, DOI:10.1002/chem.200902470.
- A. Gautam, M. Sadowski, M. Ghidiu, N. Minafra, A. Senyshyn, K. Albe and W. G. Zeier, Engineering the Site-Disorder and Lithium Distribution in the Lithium Superionic Argyrodite Li6PS5Br, Adv. Energy Mater., 2021, 11(5), 2003369, DOI:10.1002/aenm.202003369.
- M. Evain, E. Gaudin, F. Boucher, V. Petricek and F. Taulelle, Structures and Phase Transitions of the A7PSe6 (A = Ag, Cu) Argyrodite-Type Ionic Conductors. I. Ag7PSe6, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54(4), 376–383, DOI:10.1107/S0108768197019654.
- B. J. Morgan, Mechanistic Origin of Superionic Lithium Diffusion in Anion-Disordered Li6PS5X Argyrodites, Chem. Mater., 2021, 33(6), 2004–2018, DOI:10.1021/acs.chemmater.0c03738.
- A. R. Stamminger, B. Ziebarth, M. Mrovec, T. Hammerschmidt and R. Drautz, Ionic Conductivity and Its Dependence on Structural Disorder in Halogenated Argyrodites Li6PS5X (X = Br, Cl, I), Chem. Mater., 2019, 31(21), 8673–8678, DOI:10.1021/acs.chemmater.9b02047.
- H. Al-Kutubi, A. Gautam, A. K. Lavrinenko, A. Vasileiadis, J. R. Heringa, S. Ganapathy and M. Wagemaker, Decoding Structural Disorder, Synthesis Methods, and Short- and Long-Range Lithium-Ion Transport in Lithium Argyrodites (Li6-xPS5-xBr1+x), Chem. Mater., 2025, 37(3), 869–883, DOI:10.1021/acs.chemmater.4c02010.
- A. K. Lavrinenko, T. Famprikis, J. A. Quirk, V. Landgraf, P. Groszewicz, J. R. Heringa, S. Smeets, V. Azizi, S. Ciarella, J. A. Dawson, M. Wagemaker and A. Vasileiadis, Optimizing Ionic Transport in Argyrodites: A Unified View on the Role of Sulfur/Halide Distribution and Local Environments, J. Mater. Chem. A, 2024, 26596–26611, 10.1039/d4ta04628e.
- H. Schneider, H. Du, T. Kelley, K. Leitner, J. ter Maat, C. Scordilis-Kelley, R. Sanchez-Carrera, I. Kovalev, A. Mudalige, J. Kulisch, M. M. Safont-Sempere, P. Hartmann, T. Weiβ, L. Schneider and B. Hinrichsen, A Novel Class of Halogen-Free, Super-Conductive Lithium Argyrodites: Synthesis and Characterization, J. Power Sources, 2017, 366, 151–160, DOI:10.1016/j.jpowsour.2017.09.012.
- S. Li, J. Lin, M. Schaller, S. Indris, X. Zhang, T. Brezesinski, C. W. Nan, S. Wang and F. Strauss, High-Entropy Lithium Argyrodite Solid Electrolytes Enabling Stable All-Solid-State Batteries, Angew. Chem., Int. Ed., 2023, 62(50), e202314155, DOI:10.1002/anie.202314155.
- M. A. Kraft, S. Ohno, T. Zinkevich, R. Koerver, S. P. Culver, T. Fuchs, A. Senyshyn, S. Indris, B. J. Morgan and W. G. Zeier, Inducing High Ionic Conductivity in the Lithium Superionic Argyrodites Li6+xP1-xGexS5I for All-Solid-State Batteries, J. Am. Chem. Soc., 2018, 140(47), 16330–16339, DOI:10.1021/jacs.8b10282.
- N. Minafra, S. P. Culver, T. Krauskopf, A. Senyshyn and W. G. Zeier, Effect of Si Substitution on the Structural and Transport Properties of Superionic Li-Argyrodites, J. Mater. Chem. A, 2018, 6(2), 645–651, 10.1039/C7TA08581H.
- P. Adeli, J. D. Bazak, A. Huq, G. R. Goward and L. F. Nazar, Influence of Aliovalent Cation Substitution and Mechanical Compression on Li-Ion Conductivity and Diffusivity in Argyrodite Solid Electrolytes, Chem. Mater., 2021, 33(1), 146–157, DOI:10.1021/acs.chemmater.0c03090.
- F. Strauss, T. Zinkevich, S. Indris and T. Brezesinski, Li7GeS5Br-An Argyrodite Li-Ion Conductor Prepared by Mechanochemical Synthesis, Inorg. Chem., 2020, 59(17), 12954–12959, DOI:10.1021/acs.inorgchem.0c02094.
- A. A. Coelho, TOPAS and TOPAS-Academic : An Optimization Program Integrating Computer Algebra and Crystallographic Objects Written in C++, J. Appl. Crystallogr., 2018, 51(1), 210–218, DOI:10.1107/S1600576718000183.
- A. Gautam, M. Sadowski, N. Prinz, H. Eickhoff, N. Minafra, M. Ghidiu, S. P. Culver, K. Albe, T. F. Fässler, M. Zobel and W. G. Zeier, Rapid Crystallization and Kinetic Freezing of Site-Disorder in the Lithium Superionic Argyrodite Li6PS5Br, Chem. Mater., 2019, 31(24), 10178–10185, DOI:10.1021/acs.chemmater.9b03852.
- P. Thompson, D. E. Cox and J. B. Hastings, Rietveld Refinement of Debye-Scherrer Synchrotron X-Ray Data from Al203, J. Appl. Crystallogr., 1987, 20, 79–83 CrossRef CAS.
- S. Ohno, T. Bernges, J. Buchheim, M. Duchardt, A. K. Hatz, M. A. Kraft, H. Kwak, A. L. Santhosha, Z. Liu, N. Minafra, F. Tsuji, A. Sakuda, R. Schlem, S. Xiong, Z. Zhang, P. Adelhelm, H. Chen, A. Hayashi, Y. S. Jung, B. V. Lotsch, B. Roling, N. M. Vargas-Barbosa and W. G. Zeier, How Certain Are the Reported Ionic Conductivities of Thiophosphate-Based Solid Electrolytes? An Interlaboratory Study, ACS Energy Lett., 2020, 5(3), 910–915, DOI:10.1021/acsenergylett.9b02764.
- S. Puls, E. Nazmutdinova, F. Kalyk, H. M. Woolley, J. F. Thomsen, Z. Cheng, A. Fauchier-Magnan, A. Gautam, M. Gockeln, S.-Y. Ham, M. T. Hasan, M.-G. Jeong, D. Hiraoka, J. S. Kim, T. Kutsch, B. Lelotte, P. Minnmann, V. Miß, K. Motohashi, D. L. Nelson, F. Ooms, F. Piccolo, C. Plank, M. Rosner, S. E. Sandoval, E. Schlautmann, R. Schuster, D. Spencer-Jolly, Y. Sun, B. S. Vishnugopi, R. Zhang, H. Zheng, P. Adelhelm, T. Brezesinski, P. G. Bruce, M. Danzer, M. El Kazzi, H. Gasteiger, K. B. Hatzell, A. Hayashi, F. Hippauf, J. Janek, Y. S. Jung, M. T. McDowell, Y. S. Meng, P. P. Mukherjee, S. Ohno, B. Roling, A. Sakuda, J. Schwenzel, X. Sun, C. Villevieille, M. Wagemaker, W. G. Zeier and N. M. Vargas-Barbosa, Benchmarking the Reproducibility of All-Solid-State Battery Cell Performance, Nat. Energy, 2024, 9(10), 1310–1320, DOI:10.1038/s41560-024-01634-3.
- L. Ketter, N. Greb, T. Bernges and W. Zeier, Using Resistor Network Models to Predict the Transport Properties of Solid-State Battery Composites, Nat. Commun., 2024, 1–9, DOI:10.1038/s41467-025-56514-5.
- U. Ayachit, The ParaView Guide. A Parallel Visualization Application, Kitware, 2015, DOI:10.5555/2789330.
- S. Boulineau, J. M. Tarascon, J. B. Leriche and V. Viallet, Electrochemical Properties of All-Solid-State Lithium Secondary Batteries Using Li-Argyrodite Li6PS5Cl as Solid Electrolyte, Solid State Ionics, 2013, 242, 45–48, DOI:10.1016/j.ssi.2013.04.012.
- R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A, 1976, 32(5), 751–767, DOI:10.1107/S0567739476001551.
- P. Wang, H. Liu, S. Patel, X. Feng, P. H. Chien, Y. Wang and Y. Y. Hu, Fast Ion Conduction and Its Origin in Li6-xPS5-xBr1+x, Chem. Mater., 2020, 32(9), 3833–3840, DOI:10.1021/acs.chemmater.9b05331.
- I. Hanghofer, M. Brinek, S. L. Eisbacher, B. Bitschnau, M. Volck, V. Hennige, I. Hanzu, D. Rettenwander and H. M. R. Wilkening, Substitutional Disorder: Structure and Ion Dynamics of the Argyrodites Li6PS5Cl, Li6PS5Br and Li6PS5I, Phys. Chem. Chem. Phys., 2019, 21(16), 8489–8507, 10.1039/c9cp00664h.
- K. Hogrefe, N. Minafra, I. Hanghofer, A. Banik, W. G. Zeier and H. M. R. Wilkening, Opening Diffusion Pathways through Site Disorder: The Interplay of Local Structure and Ion Dynamics in the Solid Electrolyte Li6+xP1-xGexS5I as Probed by Neutron Diffraction and NMR, J. Am. Chem. Soc., 2022, 144(4), 1795–1812, DOI:10.1021/jacs.1c11571.
- K. Hogrefe, I. Hanghofer and H. M. R. Wilkening, With a Little Help from 31P NMR: The Complete Picture on Localized and Long-Range Li+ Diffusion in Li6PS5I, J. Phys. Chem. C, 2021, 125(41), 22457–22463, DOI:10.1021/acs.jpcc.1c06242.
- G. J. Brug, A. L. G. van den Eeden, M. Sluyters-Rehbach and J. H. Sluyters, The Analysis of Electrode Impedances Complicated by the Presence of a Constant Phase Element, J. Electroanal. Chem., 1984, 176(1–2), 275–295, DOI:10.1016/S0022-0728(84)80324-1.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: Characterization by Impedance Spectroscopy, Adv. Mater., 1990, 2(3), 132–138, DOI:10.1002/adma.19900020304.
- B. Wankmiller and M. R. Hansen, Observation of Li+ Jumps in Solid Inorganic Electrolytes over a Broad Dynamical Range: A Case Study of the Lithium Phosphidosilicates Li8SiP4 and Li14SiP6, J. Magn. Reson. Open, 2023, 14–15, 100098, DOI:10.1016/j.jmro.2023.100098.
- V. Epp, Ö. Gün, H. J. Deiseroth and M. Wilkening, Highly Mobile Ions: Low-Temperature NMR Directly Probes Extremely Fast Li+ Hopping in Argyrodite-Type Li6PS5Br, J. Phys. Chem. Lett., 2013, 4(13), 2118–2123, DOI:10.1021/jz401003a.
- I. Hanghofer, B. Gadermaier and H. M. R. Wilkening, Fast Rotational Dynamics in Argyrodite-Type Li6PS5X (X: Cl, Br, I) as Seen by 31P Nuclear Magnetic Relaxation - On Cation-Anion Coupled Transport in Thiophosphates, Chem. Mater., 2019, 31(12), 4591–4597, DOI:10.1021/acs.chemmater.9b01435.
- C. Yu, S. Ganapathy, E. R. H. Van Eck, L. Van Eijck, S. Basak, Y. Liu, L. Zhang, H. W. Zandbergen and M. Wagemaker, Revealing the Relation between the Structure, Li-Ion Conductivity and Solid-State Battery Performance of the Argyrodite Li6PS5Br Solid Electrolyte, J. Mater. Chem. A, 2017, 5(40), 21178–21188, 10.1039/c7ta05031c.
- R. Zhou, A. Gautam, E. Suard, S. Li, S. Ganapathy, K. Chen, X. Zhang, C. Nan, S. Wang and M. Wagemaker, Boosting Ionic Conductivity and Air Stability in Bromide-Rich Thioarsenate Argyrodite Solid Electrolytes, Adv. Funct. Mater., 2025, 2420971, DOI:10.1002/adfm.202420971.
- A. Banik, Y. Liu, S. Ohno, Y. Rudel, A. Jiménez-Solano, A. Gloskovskii, N. M. Vargas-Barbosa, Y. Mo and W. G. Zeier, Can Substitutions Affect the Oxidative Stability of Lithium Argyrodite Solid Electrolytes?, ACS Appl. Energy Mater., 2022, 5(2), 2045–2053, DOI:10.1021/acsaem.1c03599.
- S. Wenzel, S. Randau, T. Leichtweiß, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, Direct Observation of the Interfacial Instability of the Fast Ionic Conductor Li10GeP2S12 at the Lithium Metal Anode, Chem. Mater., 2016, 28(7), 2400–2407, DOI:10.1021/acs.chemmater.6b00610.
- H. H. Sun and A. Manthiram, Impact of Microcrack Generation and Surface Degradation on a Nickel-Rich Layered Li[Ni0.9Co0.05Mn0.05]O2 Cathode for Lithium-Ion Batteries, Chem. Mater., 2017, 29(19), 8486–8493, DOI:10.1021/acs.chemmater.7b03268.
- R. Koerver, F. Walther, I. Aygün, J. Sann, C. Dietrich, W. G. Zeier and J. Janek, Redox-Active Cathode Interphases in Solid-State Batteries, J. Mater. Chem. A, 2017, 5(43), 22750–22760, 10.1039/c7ta07641j.
- T. T. Zuo, R. Rueß, R. Pan, F. Walther, M. Rohnke, S. Hori, R. Kanno, D. Schröder and J. Janek, A Mechanistic Investigation of the Li10GeP2S12|LiNi1-x-yCoxMnyO2 Interface Stability in All-Solid-State Lithium Batteries, Nat. Commun., 2021, 12(1), 6669, DOI:10.1038/s41467-021-26895-4.
- R. Tian, S.-H. Park, P. J. King, G. Cunningham, J. Coelho, V. Nicolosi and J. N. Coleman, Quantifying the Factors Limiting Rate Performance in Battery Electrodes, Nat. Commun., 2019, 10(1), 1933, DOI:10.1038/s41467-019-09792-9.
- S. Yanev, H. Auer, C. Heubner, S. Höhn, K. Nikolowski, M. Partsch and A. Michaelis, Rapid Determination of All-Solid-State Battery Performance via Chronoamperometry, J. Electrochem. Soc., 2022, 169(9), 090519, DOI:10.1149/1945-7111/ac8fbb.
- S. Yanev, H. Auer, R. Pertsch, C. Heubner, K. Nikolowski, M. Partsch and A. Michaelis, Quantifying Resistive and Diffusive Kinetic Limitations of Thiophosphate Composite Cathodes in All-Solid-State Batteries, J. Electrochem. Soc., 2024, 171(5), 050530, DOI:10.1149/1945-7111/ad47d7.
- T. Bernges, L. Ketter, B. Helm, M. A. Kraft, K. A. See and W. G. Zeier, Transport Characterization of Solid-State Li2FeS2 Cathodes from a Porous Electrode Theory Perspective, EES Batteries, 2025, 1(1), 172–184, 10.1039/D4EB00005F.
- R. Tian, P. J. King, J. Coelho, S. H. Park, D. V. Horvath, V. Nicolosi, C. O’Dwyer and J. N. Coleman, Using Chronoamperometry to Rapidly Measure and Quantitatively Analyse Rate-Performance in Battery Electrodes, J. Power Sources, 2020, 468, 228220, DOI:10.1016/j.jpowsour.2020.228220.
- Z. Siroma, T. Sato, T. Takeuchi, R. Nagai, A. Ota and T. Ioroi, AC Impedance Analysis of Ionic and Electronic Conductivities in Electrode Mixture Layers for an All-Solid-State Lithium-Ion Battery, J. Power Sources, 2016, 316, 215–223, DOI:10.1016/j.jpowsour.2016.03.059.
- P. Minnmann, L. Quillman, S. Burkhardt, F. H. Richter and J. Janek, Editors' Choice—Quantifying the Impact of Charge Transport Bottlenecks in Composite Cathodes of All-Solid-State Batteries, J. Electrochem. Soc., 2021, 168(4), 040537, DOI:10.1149/1945-7111/abf8d7.
- W. Zeier, V. Faka, M. Kraft, M. A. Lange and E. Suard, Investigating the influence of Ge4+ substitution on the structural and transport properties in Li6+xP1−xGexS5Br, Institut Laue-Langevin (ILL), 2023, DOI:10.5291/ILL-DATA.5-22-826.
Footnote |
| † Electronic supplementary information (ESI) available: X-ray and neutron diffraction data and analyses, tables with crystallographic data, impedance spectroscopy data and analysis, solid-state NMR data and analysis, particle size distribution data and scanning electron microscopy images. See DOI: https://doi.org/10.1039/d5ta01651g |
| This journal is © The Royal Society of Chemistry 2025 |