 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhancing energy predictions in multi-atom systems with multiscale topological learning†
Dong Chen ab,
Rui Wangc,
Guo-Wei Wei
ab,
Rui Wangc,
Guo-Wei Wei *bde and
Feng Pan
*bde and
Feng Pan *a
*a
aSchool of Advanced Materials, Peking University, Shenzhen Graduate School, Shenzhen 518055, China. E-mail: panfeng@pkusz.edu.cn
bDepartment of Mathematics, Michigan State University, MI 48824, USA. E-mail: weig@msu.edu
cSimons Center for Computational Physical Chemistry, New York University, New York, NY 10003, USA
dDepartment of Electrical and Computer Engineering, Michigan State University, MI 48824, USA
eDepartment of Biochemistry and Molecular Biology, Michigan State University, MI 48824, USA
First published on 5th June 2025
Abstract
Lithium, a key element in high-energy-density batteries such as lithium-ion batteries, plays a crucial role in determining battery performance, safety, and longevity. Understanding how lithium atoms interact in clusters is essential for optimizing these properties. However, the complexity of these interactions grows exponentially as the number of Li atoms increases. While the rise of large models offers promising avenues for predictive accuracy in such multi-atom systems, the limited data available in material science hinders such breakthroughs. To answer the challenge, we present an interpretable topological learning framework designed to enhance the accuracy of energy predictions in multi-atom systems. This study explores the application of Persistent Topological Laplacians (PTLs), a multiscale topological method that effectively captures the intrinsic properties of many-body interactions. By applying PTLs, we offer a comprehensive analysis to uncover persistent topological features and geometric nuances in complex material systems. A dataset of 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 lithium clusters was analyzed using the proposed framework, and the results show that the PTL method aligns with traditional many-body theories, demonstrating its efficacy in capturing complex many-body interactions and improving prediction accuracy.
287 lithium clusters was analyzed using the proposed framework, and the results show that the PTL method aligns with traditional many-body theories, demonstrating its efficacy in capturing complex many-body interactions and improving prediction accuracy.
1 Introduction
In the realm of material science, understanding the behavior of multi-atom systems remains a fundamental yet challenging task, with the complexity of interactions increasing exponentially as the number of interacting particles grows.1 One of the most prominent examples is lithium, a key element in high-energy-density batteries like lithium-ion batteries, which plays a critical role in determining performance, safety, and longevity.2 Accurately predicting the energy and interactions within lithium clusters is crucial for advancing next-generation energy storage technologies.However, for multi-atom systems, classical approaches, ranging from quantum chromodynamics in nuclear physics to quantum mechanics in atomic and molecular scales, often resort to reduced one- or two-body approximations.3 Higher-order perturbations, like those in Feynman diagrams and Ursell functions,4,5 are immensely valuable, but sometimes fall short in capturing non-perturbative effects. Similarly, statistical tools such as the BBGKY hierarchy6 provide critical insights into particle correlations but are often beset with formidable computational challenges. These traditional methods for studying such systems are often hindered by the sheer scale of the problem.
The rise of deep learning models, such as ChatGPT,7,8 has demonstrated the immense potential of machine learning in making accurate predictions based on vast amounts of data. These models excel at handling complex tasks in natural language processing by identifying intricate patterns and correlations across large datasets. Inspired by this success, machine learning has been applied to multi-atom systems to improve predictive performance in areas like energy calculations and structure prediction.9,10 However, two critical limitations hinder the applicability of large deep learning models in material science: the scarcity of data and the ‘black box’ nature of these models.11,12 First, the limited availability of high-quality experimental data in material science presents a major bottleneck. Gathering large-scale datasets can be prohibitively expensive and time consuming, limiting the effectiveness of deep models that rely on data richness to generalize across different systems.13,14 Without sufficient data, these models may fail to capture the intricate physical interactions at play in complex material systems like lithium clusters.15 Second, deep learning models, though effective at predictions, often lack interpretability, making it hard to understand the physical mechanisms behind their outcomes. In materials science, this is crucial for material discovery and design, where understanding behavior and properties is as important as accurate predictions.16,17
In the vast landscape of mathematical tools available, topological methods have emerged as powerful lenses through which various scientific disciplines perceive and understand intricate structures and interactions. The simplicial complex,18 for example, provides a topological framework for capturing interactions in multi-atom systems, while persistent homology has advanced our understanding in molecular19 and material science.20–25 And the Quotien Complex was recently introduced to study the inorangic system.26 In computational biology, differential geometry27 and algebraic graph28 theory shed light on the networks underlying life. Building on this, the persistent topological Laplacian (PTL) combines algebraic topology with topological spaces like simplicial complexes and manifolds, producing persistent spectral graph (PSG)29 and Hodge Laplacians,30 respectively. These methods link quantum mechanics, through zero-dimensional Hodge Laplacians, to topological spaces, promising new analytical tools for studying the many-body interactions with multi-atom systems. The reader is referred to a review.31
In this work, we propose a multiscale topological learning (MTL) framework, utilizing topological representations to reveal the intricate relationships of multi-atom systems, focusing on the Li clusters particularly. Drawing inspiration from algebraic topology, we introduce the PTL method, a novel approach designed to capture interactions inherent to multi-atom systems from a topological standpoint. This method allows the PTL to create a unified multiscale framework, adept at revealing topological persistence and distilling geometric shapes from intricate many-body interactions. As we navigate the bridge between the mathematical structures and the multi-atom systems, we harness the power of machine learning to validate our approach. Through rigorous qualitative and quantitative analyses of a diverse set of 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 Li cluster structures, spanning from 4-body to complex 40-body systems, we demonstrate the proficiency of the PTL in capturing and elucidating many-body interactions. Our findings underscore the topological method's capability to not only represent these interactions but also accurately predict properties intrinsic to multi-atom systems. This exploration, blending topological insights with physics, holds promise as a trailblazing framework, shedding light on the elaborate interactions that shape multi-atom systems and offering a fresh perspective on their study.
287 Li cluster structures, spanning from 4-body to complex 40-body systems, we demonstrate the proficiency of the PTL in capturing and elucidating many-body interactions. Our findings underscore the topological method's capability to not only represent these interactions but also accurately predict properties intrinsic to multi-atom systems. This exploration, blending topological insights with physics, holds promise as a trailblazing framework, shedding light on the elaborate interactions that shape multi-atom systems and offering a fresh perspective on their study.
2 Results
In the realm of multi-atom systems, the intricacy of interactions poses a formidable challenge for traditional analytical techniques. To address this, we first introduce the simplicial complexes to represent structures, which provide a structured topological framework to encode many-body interactions. Also, drawing inspiration from the parallels between the Hodge Laplacian in algebraic topology and the kinetic operator in physics, we employ the PTL to facilitate a multiscale spectral analysis of physical systems. We show that the spectra of the PTL built from physical systems capture many-body interactions and reveal multifaceted physics.The workflow of analyzing a multi-atom system using the PTL is illustrated in Fig. 1a. Specifically, the multi-atom system used in this work is a Li cluster system. There are 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 energy-paired Li cluster structures involved in the experiments, including 4-body, 5-body, 6-body, 7-body, 8-body, 9-body, 10-body, 20-body, and 40-body systems.15 The details and statistic information of all Li clusters are given in ESI Fig. S1†. With the PTL approach, multidimensional system information is transformed into features for the given structure. More precisely, the 0-, 1-, and 2-dimensional PTL features are generated for all the filtration parameters from 0.1 Å to 10 Å with an interval of 0.1 Å. Here, the upper bound of 10 Å was selected to prevent isolated atoms, ensuring all relevant interactions are captured. The lower bound of 0.1 Å allows for a fine-grained description of local interactions for Li-cluster system. These multi-dimensional features, acting as representative fingerprints of the many-body interactions, are then channeled into machine learning models to demonstrate their predictive power. When the many-body interactions are present in a multi-atom system, they subtly influence the PTL, creating nuanced deviations in the resulting features. As these features feed into the machine learning model, the prediction accuracy becomes an indirect gauge of these higher-order interactions' presence and impact. As shown in the final chart in Fig. 1a, the Laplacian matrices like L0, L1, and L2 embed the multi-order interactions of the system, representing interactions within vertices (0-simplices), edges (1-simplices), and triangles (2-simplices), respectively. Fig. 1b illustrates these 0, 1, and 2-simplices, which serve as fundamental building blocks in their respective dimensions. The quantitative results indicate that the contribution of features from each dimension of the PTL to energy prediction diminishes as the dimensionality increases, suggesting that while these higher-order interactions are complex and multifaceted, they introduce significant perturbations to the machine learning model's predictions. Fig. 1c illustrates an example of the schema for employing topological Laplacians to capture multi-order interactions within a Li5 cluster. The cluster is first expanded into 0-, 1-, and 2-dimensional spaces, corresponding to 0-, 1-, and 2-simplex topological spaces, and the associated topological Laplacian matrices (L0, L1, and L2) are applied to record interactions of various orders.
287 energy-paired Li cluster structures involved in the experiments, including 4-body, 5-body, 6-body, 7-body, 8-body, 9-body, 10-body, 20-body, and 40-body systems.15 The details and statistic information of all Li clusters are given in ESI Fig. S1†. With the PTL approach, multidimensional system information is transformed into features for the given structure. More precisely, the 0-, 1-, and 2-dimensional PTL features are generated for all the filtration parameters from 0.1 Å to 10 Å with an interval of 0.1 Å. Here, the upper bound of 10 Å was selected to prevent isolated atoms, ensuring all relevant interactions are captured. The lower bound of 0.1 Å allows for a fine-grained description of local interactions for Li-cluster system. These multi-dimensional features, acting as representative fingerprints of the many-body interactions, are then channeled into machine learning models to demonstrate their predictive power. When the many-body interactions are present in a multi-atom system, they subtly influence the PTL, creating nuanced deviations in the resulting features. As these features feed into the machine learning model, the prediction accuracy becomes an indirect gauge of these higher-order interactions' presence and impact. As shown in the final chart in Fig. 1a, the Laplacian matrices like L0, L1, and L2 embed the multi-order interactions of the system, representing interactions within vertices (0-simplices), edges (1-simplices), and triangles (2-simplices), respectively. Fig. 1b illustrates these 0, 1, and 2-simplices, which serve as fundamental building blocks in their respective dimensions. The quantitative results indicate that the contribution of features from each dimension of the PTL to energy prediction diminishes as the dimensionality increases, suggesting that while these higher-order interactions are complex and multifaceted, they introduce significant perturbations to the machine learning model's predictions. Fig. 1c illustrates an example of the schema for employing topological Laplacians to capture multi-order interactions within a Li5 cluster. The cluster is first expanded into 0-, 1-, and 2-dimensional spaces, corresponding to 0-, 1-, and 2-simplex topological spaces, and the associated topological Laplacian matrices (L0, L1, and L2) are applied to record interactions of various orders.
We perform unsupervised cluster analysis on the dataset. The 0-, 1-, and 2-dimensional PTL features are denoted as  ,
,  , and
, and 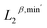 , respectively. Here, the superscript represents the harmonic part of the spectrum (β) and the minimum of the non-harmonic part of the spectrum, such as the smallest nonzero eigenvalues (min′). To investigate the impact of higher-dimensional PTL features on the system, we define three feature sets: (i) only 0-dimensional features
, respectively. Here, the superscript represents the harmonic part of the spectrum (β) and the minimum of the non-harmonic part of the spectrum, such as the smallest nonzero eigenvalues (min′). To investigate the impact of higher-dimensional PTL features on the system, we define three feature sets: (i) only 0-dimensional features  , (ii) both 0- and 1-dimensional features
, (ii) both 0- and 1-dimensional features  , and (iii) 0-, 1-, and 2-dimensional features
, and (iii) 0-, 1-, and 2-dimensional features  . Fig. 2b presents the two-dimensional t-SNE embedding of the representations for
. Fig. 2b presents the two-dimensional t-SNE embedding of the representations for 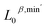 ,
,  , and
, and  . The colored points in the figure represent structures with different atomic numbers. As shown in the figure, the clustering quality of the multi-atom system, reflected in the tendency of data points of the same color to group together, improves with the inclusion of high-dimensional information. However, the rate of improvement noticeably decreases, indicating that high-dimensional information contributes less to structure identification compared to low-dimensional information. A similar trend is observed when using Principal Component Analysis (PCA), a linear dimensionality reduction method, for visualization with the two largest principal components, as shown in Fig. S2.† Similarly, higher-order interactions are often treated as perturbations in many-body physics.32 In the clustering analysis, we only look at the clustering effect of each group feature to perform a qualitative analysis. The final results obtained are consistent with existing findings in many-body physics, which indicate that the PTL method can accurately capture the many-body interactions of the system.
. The colored points in the figure represent structures with different atomic numbers. As shown in the figure, the clustering quality of the multi-atom system, reflected in the tendency of data points of the same color to group together, improves with the inclusion of high-dimensional information. However, the rate of improvement noticeably decreases, indicating that high-dimensional information contributes less to structure identification compared to low-dimensional information. A similar trend is observed when using Principal Component Analysis (PCA), a linear dimensionality reduction method, for visualization with the two largest principal components, as shown in Fig. S2.† Similarly, higher-order interactions are often treated as perturbations in many-body physics.32 In the clustering analysis, we only look at the clustering effect of each group feature to perform a qualitative analysis. The final results obtained are consistent with existing findings in many-body physics, which indicate that the PTL method can accurately capture the many-body interactions of the system.
Fig. 2c–e show the three structures analyzed by the PTL method, including two 10-particle systems (top, middle) and one 40-particle multi-atom system (bottom). For the systems of 10 particles, the structure's topological invariants β1, β2 in Fig. 2d contain a larger shaded area compared to Fig. 2c. It means that as the filtration parameter increases, the Li cluster in Fig. 2d has more 1- and 2-dimensional cavities. Note the topological cavities here are analogous to the many-body interactions within the system. The binding energies of structure in Fig. 2c and d are −0.756 eV per atom and −0.910 eV per atom, which implies that more many-body interactions favor the stability of the system. As for the non-harmonic information 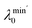 ,
,  , and
, and  , the lines in Fig. 2d also enclose more area, which means that the particles in Fig. 2d have more complex connectivity relationships. Fig. 2e shows a 40-atom lithium cluster, which contains more high-dimensional topological and geometric complexity (β1 and β2,
, the lines in Fig. 2d also enclose more area, which means that the particles in Fig. 2d have more complex connectivity relationships. Fig. 2e shows a 40-atom lithium cluster, which contains more high-dimensional topological and geometric complexity (β1 and β2,  and
and  ) than aforementioned two 10-atom lithium clusters do and has a lower binding energy of −1.183 eV per atom. In addition, we generated topological fingerprints of the structures using the persistent homology method, which is equivalent to the features from the harmonic spectra part in the PTL method, for the three structures mentioned above, as shown in ESI Fig. S3.†
) than aforementioned two 10-atom lithium clusters do and has a lower binding energy of −1.183 eV per atom. In addition, we generated topological fingerprints of the structures using the persistent homology method, which is equivalent to the features from the harmonic spectra part in the PTL method, for the three structures mentioned above, as shown in ESI Fig. S3.†
Fig. 3a demonstrates the binding energy distribution of all 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 Li cluster structures, from bottom to top, which are Li4 to Li10 systems, Li20 system, and Li40 system, respectively. It can be seen that the average binding energy per atom of each type of system gradually decreases with the increase of the number of particles in the system, which indicates that the complex interactions in the multi-particle system enhance the stability of the system. The mean and median energies of all structures can be found in ESI Fig. S1.† To better understand how different dimensional PTL features contribute to the multi-atom system, we first perform a feature analysis of the PTL features. Specifically, to explore the Laplacian spectral information, we extract six key properties from each dimension's Laplacian matrix: the multiplicity of zero eigenvalues (β), the minimum nonzero eigenvalue (min′), the maximum, the mean, the standard deviation of the eigenvalues, and the generalized mean graph energy.33–35 Consequently, six values are used per Laplacian at each dimension and filtration scale. Given a multiscale range from 0.1 Å to 10 Å with a step size of 0.1 Å each dimension contributes 600 features, resulting in a total of 1800 features across the three considered dimensions. The distribution of feature importance for predicting Li20 and Li40 is shown in Fig. 3b and c. It is observed that 0-dimensional features contribute the most to the system, followed by 1-dimensional features, while 2-dimensional features have a certain but relatively minor contribution. This trend aligns with the qualitative analysis in Fig. 2b. Additionally, the feature importance were extracted from gradient-boosted decision trees (GBDT) models trained exclusively on 4- to 10-atom Li clusters, meaning that Li20 and Li40 clusters were unseen during training. Detailed results can be found in ESI Table S2.† Interestingly, using only the L0 features yields the best predictive performance for Li20 and Li40, whereas models incorporating L01 and L012 perform relatively worse. This may be due to the inclusion of additional feature dimensions leading to overfitting in the same model setting, particularly when predicting structurally distinct systems such as the unseen Li20 and Li40 multi-atom clusters.
287 Li cluster structures, from bottom to top, which are Li4 to Li10 systems, Li20 system, and Li40 system, respectively. It can be seen that the average binding energy per atom of each type of system gradually decreases with the increase of the number of particles in the system, which indicates that the complex interactions in the multi-particle system enhance the stability of the system. The mean and median energies of all structures can be found in ESI Fig. S1.† To better understand how different dimensional PTL features contribute to the multi-atom system, we first perform a feature analysis of the PTL features. Specifically, to explore the Laplacian spectral information, we extract six key properties from each dimension's Laplacian matrix: the multiplicity of zero eigenvalues (β), the minimum nonzero eigenvalue (min′), the maximum, the mean, the standard deviation of the eigenvalues, and the generalized mean graph energy.33–35 Consequently, six values are used per Laplacian at each dimension and filtration scale. Given a multiscale range from 0.1 Å to 10 Å with a step size of 0.1 Å each dimension contributes 600 features, resulting in a total of 1800 features across the three considered dimensions. The distribution of feature importance for predicting Li20 and Li40 is shown in Fig. 3b and c. It is observed that 0-dimensional features contribute the most to the system, followed by 1-dimensional features, while 2-dimensional features have a certain but relatively minor contribution. This trend aligns with the qualitative analysis in Fig. 2b. Additionally, the feature importance were extracted from gradient-boosted decision trees (GBDT) models trained exclusively on 4- to 10-atom Li clusters, meaning that Li20 and Li40 clusters were unseen during training. Detailed results can be found in ESI Table S2.† Interestingly, using only the L0 features yields the best predictive performance for Li20 and Li40, whereas models incorporating L01 and L012 perform relatively worse. This may be due to the inclusion of additional feature dimensions leading to overfitting in the same model setting, particularly when predicting structurally distinct systems such as the unseen Li20 and Li40 multi-atom clusters.
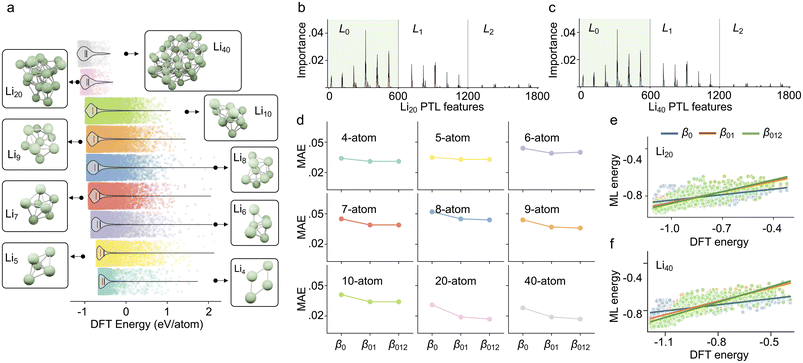 | ||
| Fig. 3 Results analysis. (a) Energy distribution of multi-atom systems containing different numbers of atoms. As the number of atoms increases, the energy (eV per atom) of the system gradually decreases. The red line is the median energy, and the black line is the mean energy (see Fig. S1†). (b) The MAE of cross-validation for multi-atom systems with different numbers of atoms using different topological information. β0 means only 0-dimensional topological information is used. β01 means both β0 and β1 are used. β012 means all β0, β1 and β2 are used in the prediction. (c and d) Comparison between MTL-based prediction results and DFT results of the formation energy of Li20 and Li40. (e) The RMSE of the machine learning prediction results for Li20, and Li40 structures using different topological features. | ||
To avoid the overfitting issues, we further perform supervised learning only using the harmonic spectral features of the PTL to explore the contribution of high-dimensional information to energy prediction. We set up three sets of features, i.e., β0 containing only 0-dimensional topological information, β01 containing 0- and 1-dimensional topological information, and β012 containing 0-, 1-, and 2-dimensional topological information. The RMSE, MAE, and Pearson correlation coefficient (PCC) are used as evaluation metrics, and their definitions are given in ESI Note S1.† Subsequently, for each system, cross-validation is performed for each of these three sets of features. The GBDT algorithm was employed as the regressor for cross-validation, utilizing 1D PTL features as input. Additionally, PTLs can generate image-like features,36 which are suitable for models like CNNs or Transformers that process image-like inputs. Only one parameter set is used in all machine learning processes, as detailed in ESI Note S1.† The results are shown in Fig. 3d. For all types of systems, the MAE of prediction decreases while adding higher dimensional topological information. However, the improvement of prediction accuracy diminishes gradually, indicating that the higher dimensional information contributes less to the prediction accuracy. In addition, we found that the MAE is lower for systems with more atoms, i.e., 20-atom and 40-atom compared to other systems. It indicates that as the number of particles in the system increases, the system will have more higher-order interactions within the system, and the PTL method can capture these higher-order interactions, thus increasing the accuracy of the model prediction. It is also consistent with the previous analysis of the special cases in Fig. 2c–e, indicating that as the number of particles in the system increases, the multi-atom system will contain richer high-order interactions. Furthermore, we trained models separately using β1, β2, and β12. The results were worse compared to those incorporating β0, highlighting the primary contribution of low-dimensional information and low-order interactions. The cross-validation results for all types of cluster systems are listed in Table S4.† All cross-validation experiments were carried out ten times using different random seeds. The final results were reported using the average of the ten experiments.
Furthermore, we explored the contribution of high-dimensional structural features to the ranking power of the multi-atom systems. The ranking power of the model can be used to find the lowest energy structural configurations. Specifically, we trained a machine learning model using all Li4–Li10 data, and subsequently, used such a model to predict the structural energy of Li20 and Li40. To compare the ranking power, the PCC is used to evaluate the model. Fig. 3e shows the comparison between machine learning prediction results and DFT calculation results of the binding energy of Li20. The best-ranking power (PCC = 0.771) is obtained by using β012, while the ranking power for β0 and β01 are 0.508 and 0.742, respectively. We also tested the performance by using β1, β2, and β12, as listed in Table S3,† which were shown worse performances. For β0, adding features of β1 information can improve the prediction accuracy by 46.1%. Although β012 contains information of 0-, 1-, and 2-dimension spaces, the prediction accuracy is only 4.0% better compared to β01. As shown in Fig. 3f, similar results can also be found for Li40. The ranking power for β0, β01, and β012 are 0.592, 0.801, and 0.817. The improvement of β01 for β0 is 35.3%, while the improvement of β012 for β01 is only 2.0%. By adding high-dimensional information, the prediction accuracy of the model continues to improve, but the added higher-dimensional information has only a smaller contribution. Our results indicate that while high-dimensional information enhances prediction accuracy, its contribution gradually diminishes as dimensionality increases. Similarly, the influence of many-body interactions on approximation decreases with higher-order interactions. Models trained using only β1, β2, or β12 performed worse compared to those incorporating β0, further emphasizing the significance of lower-dimensional features. The prediction results using the harmonic part of the Laplacian, evaluated with RMSE, MAE, and PCC, are summarized in Table S3.† The machine learning processes in this work were repeated 10 times and the average results are used in the final demonstration.
3 Discussion
In this work, we explore the intricate relationship between many-body interactions in lithium clusters and the corresponding simplicial complex structures across various dimensions. This mapping allows us to introduce the combinatorial Laplacian operator, akin to the discretized energy operator in physics, offering a new perspective for analyzing material structures. Through the PTL method, we generate a series of combinatorial Laplacians, revealing harmonic and non-harmonic spectra that encapsulate essential topological and geometric features of the multi-atom system, such as Li cluster.By leveraging these spectra through the PTL method, multi-dimensional features emerge, capturing complex many-body interactions at various scales. When integrated with machine learning models, these PTL-based features reveal the subtleties of higher-order interactions, reflected as perturbations in the model's predictive power. In this study, 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 Li cluster structures, ranging from 5-atom to 40-atom systems, were analyzed to validate the proposed PTL-based topological learning scheme. The results of clustering experiments demonstrated that PTL-based features provide strong clustering performance, with high-dimensional information contributing positively to clustering, though its effect diminishes with increasing dimensionality.
287 Li cluster structures, ranging from 5-atom to 40-atom systems, were analyzed to validate the proposed PTL-based topological learning scheme. The results of clustering experiments demonstrated that PTL-based features provide strong clustering performance, with high-dimensional information contributing positively to clustering, though its effect diminishes with increasing dimensionality.
Further validation was conducted by categorizing the data into nine groups based on the number of atoms in the system and performing cross-validation. The cross-validation results reaffirmed that while high-dimensional features enhance prediction accuracy, their contribution diminishes with increasing dimensionality. For larger systems with complex many-body interactions, such as Li20 and Li40, the PTL model effectively ranked these systems by energy, demonstrating that lower-dimensional features are more influential in improving prediction accuracy. Additionally, a comparison was made between the Li40 prediction results and those obtained from a previous persistent homology-based method, which was used to identify stable configurations of Li40.15 The latter method reported a PCC of 0.95, while the proposed method in this study achieved a PCC of 0.968 (without any parameter tuning, as shown in Table S2†).
The proposed multiscale topological learning scheme excels at capturing interactions across multiple orders in Li clusters, approximating the system's intrinsic properties with remarkable accuracy. Experimental results using Li clusters underscore the alignment of this approach with traditional many-body theory, reinforcing its robustness and precision in predicting system energy. Beyond lithium clustering studies, this framework demonstrates significant potential across various fields. In materials science, PTLs can be used to encode materials into a topological space, enabling material discovery within a more manageable, smaller topological space. This not only streamlines the design process but also accelerates the discovery of new materials, enhancing the efficiency of material development. In catalysis, the PTL method effectively models and predicts the unique configurations formed between catalytic surfaces and catalysts. By accurately capturing these configurations, it accelerates the design and optimization of catalytic materials, which is essential for advancing catalytic processes and developing novel catalytic systems. As for the molecular and biological sciences, PTLs can be applied to model molecular systems and interactions within complex environments, such as drug–drug complexes, protein–ligand interactions, and protein–protein systems. Traditional molecular dynamics simulations often face challenges when dealing with large systems, but PTL serves as a promising computational tool for extracting higher-order information. This approach provides more accurate predictions of molecular interactions, offering deeper insights into the complex dynamics of biological systems. As such, PTL holds considerable promise for applications in drug discovery, protein engineering, and bioinformatics.
4 Methods
In this section, we introduce some key principles from classical many-body theories and algebraic topology. We will briefly discuss foundational concepts including simplices, simplicial complexes, and the boundary operator, and then delve deeper into homology, persistent homology, and the persistent topological Laplacian.4.1 Reduced density operator and higher-order interactions
In many-body systems, the reduced density operator (RDO) helps capture interactions between a subset of particles without needing to consider the entire system. For an N-particle system, the n-particle RDO, ρ(n), provides a view of the interactions among n particles while marginalizing out the remaining N − n particles.37 A key insight from RDOs is the ability to break down complex, higher-order interactions into contributions from lower-order ones. As an example in Fig. 4a, consider a three-particle system described by ρ123(3), which can be decomposed as: ρ123(3) = ρ1(1)ρ2(1)ρ3(1) + ρ1(1)c23(2) + ρ2(1)c13(2) + ρ3(1)c12(2) + c123(3), where the correlation function c(n), n = 1, 2, 3, measures the degree of correlation among n particles. This hierarchical representation mirrors the way simplicial complexes in topology use simplices of different dimensions to represent interactions within a structure. Lower-order interactions, like pairwise correlations, are often dominant and easier to compute, while higher-order terms (three or more particles) capture more nuanced relationships and can be treated as perturbative corrections.4,32 This hierarchical decomposition allows us to focus on the essential structure of interactions while systematically including higher-order effects.4.2 Simplex and simplicial complex
Topologically, a simplex is a fundamental building block that generalizes points, line segments, triangles, tetrahedron, and higher-dimensional analogs (Fig. 1b and S4a†). A k-simplex is the convex hull of k + 1 affinely positioned vertices, denoted as σk = 〈v0, v1, …, vk〉. A simplicial complex, denoted as K, is formed by assembling simplices such that every face of a simplex is also in the complex, encapsulating their spatial relationships. The Vietoris–Rips complex connects points within a specified distance, evolving to reveal topological features at different scales (Fig. S4d†). Within such complexes, cycles (e.g., 0-cycle, 1-cycle, 2-cycle) highlight topological attributes like gaps or cavities (Fig. S4c†). Simplicial complexes are versatile tools for depicting and analyzing complex systems. In multi-atom systems, each simplex represents interacting particles, with its dimensionality indicating the number of bodies involved. For instance, Fig. 4b shows a simplicial complex of a 3-body system, K3, containing three 0-simplices (〈v1〉, 〈v2〉, 〈v3〉), three 1-simplices (〈v1, v2〉, 〈v2, v3〉, 〈v3, v1〉), and one 2-simplex (〈v1, v2, v3〉). This representation shows a one-to-one correspondence between the reduced density operator ρ and simplex σ, providing a geometrically and topologically insightful framework to understand multi-atom systems.4.3 Boundary operator and chain complex
With the foundations of simplices and simplicial complexes established, we turn to the hierarchical and topological aspects. k-chains are formal combinations of k-simplices, which can be algebraically combined to form chain groups denoted as Ck(K). Here, these chains are considered under modulo two operations, . The boundary operator ∂k: Ck(K) → Ck−1(K) maps a k-simplex to its (k − 1)-dimensional faces. For example, applying ∂k to a 2-simplex (triangle) yields its three 1-simplices (edges). Fig. S4b† illustrates how ∂k operates from dimension 0 to 3. The matrix representation of ∂k is denoted
. The boundary operator ∂k: Ck(K) → Ck−1(K) maps a k-simplex to its (k − 1)-dimensional faces. For example, applying ∂k to a 2-simplex (triangle) yields its three 1-simplices (edges). Fig. S4b† illustrates how ∂k operates from dimension 0 to 3. The matrix representation of ∂k is denoted  , as shown in ESI Fig. S1.†
, as shown in ESI Fig. S1.†
A chain complex is a sequence of chain groups connected by boundary operators:
 | (1) |
This structure ensures continuity, with a key property: applying a boundary operator twice yields zero, i.e., ∂k∂k+1 = 0. The adjoint boundary operator  acts in the reverse direction, increasing the dimension of simplices. Its matrix representation,
acts in the reverse direction, increasing the dimension of simplices. Its matrix representation,  , is the transpose of
, is the transpose of  .
.
4.4 Laplacian and spectrum analysis
The combinatorial Laplacian is a key tool in discrete geometry and algebraic topology, extending the concept of the graph Laplacian to higher dimensions. It provides insights into the structure of simplicial complexes, similar to how the graph Laplacian reveals connectivity in graphs. For a graph viewed as a 1-dimensional complex, the Laplacian matrix is , where B1 is the boundary matrix. This generalizes to higher dimensions with the Laplacian defined as:
, where B1 is the boundary matrix. This generalizes to higher dimensions with the Laplacian defined as:
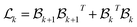 | (2) |
 represents the boundary operator for k-simplices. The term
represents the boundary operator for k-simplices. The term  accounts for connectivity among k-simplices, while
accounts for connectivity among k-simplices, while  captures interactions involving (k + 1)-simplices.
captures interactions involving (k + 1)-simplices.
In chain complexes, the combinatorial Laplacian δk is defined as:
 | (3) |
 are boundary operators and their adjoints.
are boundary operators and their adjoints.
The topological Laplacian extends the graph Laplacian to higher-dimensional simplicial complexes, with eigenvalues revealing topological and geometric properties. It is positive semidefinite, meaning all eigenvalues are non-negative. Zero eigenvalues correspond to topological invariants such as Betti numbers (βk), which count independent components,38 cycles, and cavities. The smallest non-zero eigenvalue, or spectral gap (λmink), reflects the geometric connectivity of the complex. This analysis uses zero multiplicities and the smallest positive eigenvalues to elucidate topological and geometric features.
4.5 Persistent topological Laplacians
Persistent topological Laplacians, or multiscale topological Laplacians, arise from research in both differential manifolds30 and discrete point clouds.29 Central to persistent topological Laplacians29,34,39,40 and persistent homology41,42 is the concept of filtration, which allows for multiscale analysis. Filtration is parametrized by a scale d, adapting to the data structure under study. For instance, in a distance set, edges are added between vertices if their distance is below a cutoff value. Increasing this cutoff generates a sequence of nested graphs, where each graph at a lower cutoff is a subset of those at higher cutoffs (Fig. 2a). Similar nested simplicial complexes can be created using the Vietoris–Rips, Čech, and alpha complexes. This study focuses on the Vietoris–Rips complex.Mathematically, these nested simplicial complexes are represented as follows:
| ∅ ⊆ Kd0 ⊆ Kd1 ⊆ ⋯ ⊆ Kdn = K | (4) |
 | (5) |
The persistent boundary operator, denoted as ∂k+1a,b, maps from Ck+1a,b to Cka and is defined by the action ∂k+1a,bx = ∂k+1bx for any x in Ck+1a,b. The framework can be expressed by:
 | (6) |
The k-th persistent topological Laplacian is defined as
| δka,b = ∂k+1a,b ∘ (∂k+1a,b)* + (∂ka)* ∘ ∂ka | (7) |
Code availability
The source code for the persistent topological Laplacian analysis, implemented in Python, is publicly available in the GitHub repository at https://github.com/ChenDdon/LiCluster.Data availability
The cluster structures and the energy data are publicly available at https://github.com/ChenDdon/LiCluster.Author contributions
Dong Chen designed the project, performed computational studies, analyzed data, wrote the first draft, and revised the manuscript. Rui Wang drafted part of the method. Guo-Wei Wei conceptualized and supervised the project, revised the manuscript, and acquired funding. Feng Pan supervised the project and acquired funding.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The research was partially supported by the National Natural Science Foundation of China (Grant No. 92472206), the Major Science and Technology Infrastructure Project of Material Genome Big-science Facilities Platform supported by Municipal Development and Reform Commission of Shenzhen, International joint Research Center for Electric Vehicle Power Battery and Materials (No. 2015B01015), Guangdong Key Laboratory of Design and calculation of New Energy Materials (No. 2017B030301013), Shenzhen Key Laboratory of New Energy Resources Genome Preparation and Testing (No. ZDSYS201707281026184). The work of Chen and Wei was supported in partial by NIH grants R01AI164266 and R35GM148196, NSF grants DMS-2052983 and IIS-1900473, MSU Research Foundation, and Bristol-Myers Squibb 65109. R. W. is grateful for the support from the Simons Foundation and the Simons Center for Computational Physical Chemistry (SCCPC) at New York University.References
- F. H. Stillinger, Exponential multiplicity of inherent structures, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59(1), 48 CrossRef CAS.
- B. Scrosati and J. Garche, Lithium batteries: Status, prospects and future, J. Power Sources, 2010, 195(9), 2419–2430 CrossRef CAS.
- R. G. Parr, S. R. Gadre and L. J. Bartolotti, Local density functional theory of atoms and molecules, Proc. Natl. Acad. Sci. U. S. A., 1979, 76(6), 2522–2526 CrossRef CAS PubMed.
- G. W. Wei and R. F. Snider, Discrete basis representation of ursell operators, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54(3), 2414 CrossRef CAS PubMed.
- H. D. Ursell, The evaluation of gibbs' phase-integral for imperfect gases, Math. Proc. Cambridge Philos. Soc., 1927, 23, 685–697 CrossRef CAS.
- N. N. Bogoliubov, Problems of dynamical theory in statistical physics (gostekhisdat, moscow, 1946)[in russian]; nn bogoliubov, J. Phys., 1946, 10, 256 Search PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Attention is all you need, Advances in Neural Information Processing Systems, 2017, vol. 30 Search PubMed.
- L. Ouyang, J. Wu, X. Jiang, D. Almeida, C. Wainwright, P. Mishkin, C. Zhang, S. Agarwal, K. Slama and A. Ray, et al., Training language models to follow instructions with human feedback, Adv. Neural Inf. Process. Syst., 2022, 35, 27730–27744 Search PubMed.
- P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. van Hoesel, H. Schopmans and T. Sommer, et al., Graph neural networks for materials science and chemistry, Commun. Mater., 2022, 3(1), 93 CrossRef CAS PubMed.
- J. Wei, X. Chu, X.-Y. Sun, K. Xu, H.-X. Deng, J. Chen, Z. Wei and M. Lei, Machine learning in materials science, InfoMat, 2019, 1(3), 338–358 CrossRef CAS.
- J. F. Rodrigues, L. Florea, M. C. F. de Oliveira, D. Diamond and O. N. Oliveira, Big data and machine learning for materials science, Discover Mater., 2021, 1, 1–27 CrossRef.
- C. Sutton, M. Boley, L. M. Ghiringhelli, M. Rupp, J. Vreeken and M. Scheffler, Identifying domains of applicability of machine learning models for materials science, Nat. Commun., 2020, 11(1), 4428 CrossRef CAS PubMed.
- Y. Zhang and L. Chen, A strategy to apply machine learning to small datasets in materials science, npj Comput. Mater., 2018, 4(1), 25 CrossRef.
- J. Cai, X. Chu, K. Xu, H. Li and J. Wei, Machine learning-driven new material discovery, Nanoscale Adv., 2020, 2(8), 3115–3130 RSC.
- X. Chen, D. Chen, M. Weng, Y. Jiang, G.-W. Wei and F. Pan, Topology-based machine learning strategy for cluster structure prediction, J. Phys. Chem. Lett., 2020, 11(11), 4392–4401 CrossRef CAS PubMed.
- X. Zhong, B. Gallagher, S. Liu, B. Kailkhura, A. Hiszpanski and T. Y.-J. Han, Explainable machine learning in materials science, npj Comput. Mater., 2022, 8(1), 204 CrossRef.
- M. Faraji Niri, C. Reynolds, L. A. A. Román Ramírez, E. Kendrick and J. Marco, Systematic analysis of the impact of slurry coating on manufacture of li-ion battery electrodes via explainable machine learning, Energy Storage Mater., 2022, 51, 223–238 CrossRef.
- H. S. Edwin and E. Henry Spanier, Algebraic Topology, Springer Science & Business Media, 1989 Search PubMed.
- D. Chen, M.-Z. Zhang, H.-B. Chen, Z.-W. Xie, W. Guo-Wei and F. Pan, Persistent homology for the quantitative analysis of the structure and stability of carboranes, Chin. J. Struct. Chem., 2020, 39(6), 999–1008 CAS.
- G. Carlsson, Topology and data, Bull. Am. Math. Soc., 2009, 46(2), 255–308 CrossRef.
- T. Jacob, C. P. Micucci, J. H. Hymel, V. Maroulas and K. D. Vogiatzis, Representation of molecular structures with persistent homology for machine learning applications in chemistry, Nat. Commun., 2020, 11(1), 3230 CrossRef PubMed.
- Y. Lee, S. D. Barthel, P. Dłotko, S. Mohamad Moosavi, K. Hess and B. Smit, Quantifying similarity of pore-geometry in nanoporous materials, Nat. Commun., 2017, 8(1), 1–8 CrossRef CAS PubMed.
- Y. Hiraoka, T. Nakamura, A. Hirata, E. G. Escolar, K. Matsue and Y. Nishiura, Hierarchical structures of amorphous solids characterized by persistent homology, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(26), 7035–7040 CrossRef CAS PubMed.
- Y. Lee, S. D. Barthel, P. Dłotko, S. M. Moosavi, K. Hess and B. Smit, High-throughput screening approach for nanoporous materials genome using topological data analysis: application to zeolites, J. Chem. Theor. Comput., 2018, 14(8), 4427–4437 CrossRef CAS PubMed.
- D. V. Anand, Q. Xu, J. J. Wee, K. Xia and T. C. Sum, Topological feature engineering for machine learning based halide perovskite materials design, npj Comput. Mater., 2022, 8(1), 203 CrossRef.
- C.-S. Hu, R. Mayengbam, K. Xia and T. Chien Sum, Quotient complex (qc)-based machine learning for 2d hybrid perovskite design, J. Chem. Inf. Model., 2025, 65(2), 660–671 CrossRef CAS PubMed.
- D. D. Nguyen and G.-W. Wei, DG-GL: Differential geometry-based geometric learning of molecular datasets, Int. J. Numer. Methods Biomed. Eng., 2019, 35(3), e3179 CrossRef PubMed.
- D. D. Nguyen and G.-W. Wei, AGL-score: algebraic graph learning score for protein–ligand binding scoring, ranking, docking, and screening, J. Chem. Inf. Model., 2019, 59(7), 3291–3304 CrossRef CAS PubMed.
- R. Wang, D. D. Nguyen and G.-W. Wei, Persistent spectral graph, Int. J. Numer. Methods Biomed. Eng., 2020, 36(9), e3376 CrossRef PubMed.
- J. Chen, R. Zhao, Y. Tong and G.-W. Wei, Evolutionary de rham-hodge method, Dyn. Contin. Discret. Impuls. Syst. Ser. B, 2021, 26(7), 3785 Search PubMed.
- W. Xiaoqi and G.-W. Wei, Persistent topological Laplacians–a Survey, Found. Data Sci., 2025, 13(2), 208 Search PubMed.
- R. L. Liboff and G. E. Perona, Compatibility requirements in bbgky expansion, J. Math. Phys., 1967, 8(10), 2001–2012 CrossRef.
- J. J. Wee and K. Xia, Persistent spectral based ensemble learning (PerSpect-EL) for protein–protein binding affinity prediction, Briefings Bioinf., 2022, 23(2), bbac024 CrossRef PubMed.
- Z. Meng and K. Xia, Persistent spectral–based machine learning (PerSpect ML) for protein-ligand binding affinity prediction, Sci. Adv., 2021, 7(19), eabc5329 CrossRef CAS PubMed.
- X. Liu, H. Feng, J. Wu and K. Xia, Persistent spectral hypergraph based machine learning (PSH-ML) for protein-ligand binding affinity prediction, Briefings Bioinf., 2021, 22(5), bbab127 CrossRef PubMed.
- P. Jiang, Y. Chi, X.-S. Li, Z. Meng, X. Liu, X.-S. Hua and K. Xia, Molecular persistent spectral image (mol-psi) representation for machine learning models in drug design, Briefings Bioinf., 2022, 23(1), bbab527 CrossRef PubMed.
- S. Alavi, G. W. Wei and R. F. Snider, Chain relations of reduced distribution functions and their associated correlation functions, J. Chem. Phys., 1998, 108(2), 706–714 CrossRef CAS.
- B. Eckmann, Harmonische funktionen und randwertaufgaben in einem komplex, Comment. Math. Helvetici, 1944, 17(1), 240–255 CrossRef.
- D. Chen, J. Liu, J. Wu and G.-W. Wei, Persistent hyperdigraph homology and persistent hyperdigraph Laplacians, Foundations of Data Science, 2023, 5(4), 558–588 Search PubMed.
- F. Mémoli, Z. Wan and Y. Wang, Persistent laplacians: Properties, algorithms and implications, SIAM J. Math. Data Sci., 2022, 4(2), 858–884 CrossRef.
- H. Edelsbrunner, D. Letscher, and A. Zomorodian, Topological persistence and simplification, in Proceedings 41st Annual Symposium on Foundations of Computer Science, IEEE, 2000, pp. 454–463 Search PubMed.
- A. Zomorodian and G. Carlsson, Computing persistent homology, Discrete Comput. Geom., 2005, 33(2), 249–274 CrossRef.
- J. Liu, J. Li and J. Wu, The algebraic stability for persistent laplacians, Homol. Homotopy Appl., 2024, 26(2), 297–323 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta02687c |
| This journal is © The Royal Society of Chemistry 2025 |






