Ion transport in dry and hydrated Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ and implications for oxygen electrode kinetics of protonic ceramic cells

Abstract

The ion transport of triple-conducting Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ perovskites (x = 0 and 0.2) containing mobile protons, oxygen vacancies and electron holes is investigated. Proton diffusion coefficients are determined from hydration with D₂O and time-of-flight secondary ion mass spectroscopy line scans, the oxygen vacancy conductivity is measured in an oxygen pumping cell. Oversized Y³⁺ dopants on the Fe site are found to decrease the effective proton as well as oxygen vacancy mobility. At 300–500 °C in 20 mbar H₂O, the proton conductivity amounts to 3 × 10⁻⁶ to 10⁻⁴ S cm⁻¹ with an activation energy 0.3 eV for x = 0, and 0.5 eV for x = 0.2. The vacancy conductivity covers a larger range of 3 × 10⁻⁶ to 10⁻² S cm⁻¹ with activation energies of 0.9–1 eV. The consequences of these conductivities for the kinetics of porous triple-conducting oxygen electrodes on protonic electrolytes are discussed. Importantly, both the proton and vacancy conductivity contribute to extending the active zone for the O₂ ↔ H₂O reaction.

---

1. Introduction

Electrochemical cells based on ceramic proton conducting electrolytes (protonic ceramic fuel cells PCFC, electrolysis cells PCEC) represent an interesting alternative to cells based on ceramic oxide ion conductors. Protonic ceramic electrolytes such as Ba(Zr,Ce,Y,Yb)O_3−δ perovskites^1–5 exhibit lower activation energies, reach the required ionic conductivity at lower temperatures and thus offer the possibility to decrease the operating temperature compared to conventional solid oxide fuel and electrolysis cells (SOFC, SOEC). A further advantage is that steam formation or steam consumption occurs at the air side, which facilitates high fuel utilization in fuel cell mode and enables direct production of dry and compressed hydrogen in electrolysis mode (Fig. 1a).

Fig. 1 (a) Electrode processes in SOFC/SOEC versus PCFC/PCEC. Sketch of (b) a dense, and (c) a porous oxygen electrode (positrode) on a protonic ceramic electrolyte.

However, challenges of electrolyte processing and the need of developing adapted oxygen electrode (positrode) materials had impeded the manufacturing of PCFC and PCEC with competitive performances relative to SOFC and SOEC that benefit from a much longer history of technological optimization.⁶ First significant improvements were achieved for fuel cell mode.^7–9 Motivated by the need of long-term energy storage from intermittent renewable energies the interest in the electrolysis mode increased. In recent years strongly improved PCFC and PCEC performances were reported (see e.g.^5,10–15 and reviews^16–19).

Key to high performances of both PCFC and PCEC is a fast oxygen reduction or steam oxidation reaction at the positrode. In cells based on oxide ion conducting electrolytes, positrodes with mixed electronic and oxide ion conductivity represent the state of the art because they allow extension of the oxygen exchange reaction from the triple phase boundary to larger regions of a porous positrode.^20,21 For pore-free model positrodes on protonic electrolytes (Fig. 1b) it is obvious that the positrode material needs a certain proton conductivity, because in actual dense film electrodes the lateral width is orders of magnitudes larger than the film thickness, and the contribution of the triple phase boundary to the overall positrode kinetics becomes marginal. The corresponding scaling of the electrode resistance with reciprocal electrode area has exemplarily been demonstrated for PrBa_0.5Sr_0.5Co_1.5Fe_0.5O_5+δ on an BaZr_0.4Ce_0.4Y_0.1Yb_0.1O₃ electrolyte.⁵ In actual cells, porous electrodes are used, which may further complicate the situation. It is still obvious that a substantial bulk proton conductivity of the positrode material is beneficial, as it increases the region where protons are supplied to the positrode surface to drive direct oxygen reduction to water (or the inverse reaction) there (Fig. 1c). However, as discussed later in the present publication, for porous positrodes also the oxygen ion conductivity may play a role. Indications for such a more complex situation have also been presented by Amezawa in ref. 22 and 23. In this context, one should keep in mind that also for mixed-conducting SOFC/SOEC positrodes the overall electrode resistance is governed by a combination of surface exchange and bulk transport parameters, in that case specifically and for oxygen (Adler–Lane–Steele (ALS) model²¹).

While in actual PCFC/PCEC often multi-phase positrode materials are employed to achieve the required properties, we focus here on the transport properties of single-phase triple-conducting perovskites; these single-phase properties are indispensable for a detailed understanding of any composite. Typical materials are (Ba,Sr)(Fe,Co,Ni)O_3−δ perovskites (see e.g. overviews in ref. 24 and 25); also layered perovskite-related materials such as PrBa_0.5Sr_0.5Co_1.5Fe_0.5O_5+δ (PBSCF), BaGd_0.8La_0.2Co₂O_6−δ (BGLC), Sr₃Fe₂O_7−δ have been used.^5,26,27 They all combine p-type electronic conductivity with proton and oxide ion conductivity. In several studies B-site dopants have been included, e.g. to prevent the materials from transforming into a hexagonal perovskite⁹ or to increase proton uptake.^24,28 Protonic defects (hydroxide ions on oxide ion sites ) and oxygen vacancies may come into close contact with B-site dopants and thus experience perceptible defect interactions. Calculations for BaFe_0.875(Sc,Ga,In,Y)_0.125O₃ perovskites using density functional theory indeed indicate the presence of perceptible and complex defect interactions.²⁹ Therefore, in the present investigation we compare the ion transport properties of Ba_0.95La_0.05FeO_3−δ (BLF) without and Ba_0.95La_0.05Fe_0.8Y_0.2O_3−δ (BLFY) with B-site doping (the 5% La doping on the A-site is necessary to keep BLF in the cubic perovskite structure³⁰ but not expected to significantly affect the defect chemistry, cf. Fig. S3 in the ESI†). Owing to the substantial experimental effort, we concentrate on these two compositions: Y-free Ba_0.95La_0.05FeO_3−δ, and Ba_0.95La_0.05Fe_0.8Y_0.2O_3−δ which represents the maximum Y solubility in BaFeO_3−δ. Measurements on lower Y contents and other dopants with different size and/or chemical character such as Sc³⁺, In³⁺ remain for future studies.

The proton incorporation of BaFeO_3−δ-based perovskites is dominated by the hydration reaction (dissociative water incorporation into oxygen vacancies 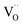forming protonic defects = hyroxide ions on oxide ion sites)

when the concentration exceeds the concentration of electron holes h˙ (e.g. after annealing in inert atmosphere).³¹ It has been investigated by thermogravimetry, e.g. in ref. 28 for BaFeO₃-related perovskites. Generally such positrode materials show lower degrees of hydration compared to Ba(Zr,Ce,Y,Yb)O_3−δ electrolytes. This is attributed to the high covalency of the Fe–O bonds and correspondingly decreased basicity of the oxide ions, which is further affected by dopants.²⁴

The measurement of proton mobility or conductivity in such triple-conductors is much more challenging.^18,32 As electrode materials, they exhibit predominant electronic conductivity approximately in the range of 1–100 S cm⁻¹. Furthermore, the ionic conductivity – expected to be below 10⁻³ S cm⁻¹ in the relevant temperature range of 300–600 °C – comprises proton as well as oxide ion conductivity which need to be properly separated. Attempts to determine the proton conductivity from DC measurements utilizing proton-selective contacts (Hebb–Wagner type experiments^33,34) are hampered by the fact that for example the Ba(Zr,Ce,Y,Yb)O_3−δ “protonic electrolytes” actually have a non-negligible hole conductivity when completely exposed to oxidizing atmosphere³⁵ (in FC/EC application this hole conductivity is suppressed in the region close to the hydrogen electrode). Thus in ref. 36 and 37 a La_1−xCa_xNbO₄ ceramic was used which has much lower electronic transport (but also lower proton conductivity) than Ba(Zr,Ce,Y,Yb)O_3−δ electrolytes. Alternatively, the measurement temperature had to be restricted to ≤ 300 °C when using a SrZr_0.9Y_0.1O_3−δ electrolyte.³⁸ Proton mobilities in triple-conducting perovskites have also been extracted from hydrogen permeation measurements (applying a dense Pd layer intended to protect the samples from decomposition by reduction, e.g. in ref. 14, 39 and 40), but this approach has received also some scepticism (can the hydrogen-permeable Pd layer sufficiently protect the sample).¹⁸ In ref. 41 electromotive force measurements in pH₂O and pO₂ gradients were performed for triple-conducting BaCeO₃–BaFeO₃ composites, but owing to the low proton transference number (<1% in oxidizing conditions) the authors also indicate that the accuracy of this approach to measure is limited.

Measurements of chemical diffusion coefficients by relaxation experiments (e.g. conductivity relaxation such as ref. 42 for oxygen exchange, ref. 43 for hydration kinetics of triple conductors) in principle allow one to determine diffusivities of ionic defects in predominantly electronically conducting materials. However, such integral measurements face two challenges: (i) they crucially rely on the absence of cracks during the whole experiment series. This is not easy to ensure and to verify in materials such as Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ which exhibit substantial chemical expansion upon hydration as well as upon changes of oxygen stoichiometry by redox reaction. (ii) The separation of surface exchange (k) and bulk diffusion coefficient (D) may be ambiguous, in particular when the measured data contain some noise.

In ref. 44 and 45 triple-conducting PrBa_0.5Sr_0.5Co_1.5Fe_0.5O_5+δ and Sr_0.9Ce_0.1Fe_0.8Ni_0.2O_3−δ samples were hydrated with D₂O and the D and DO profiles recorded by secondary ion mass spectroscopy (ToF-SIMS) in depth profiling mode. However, given the high proton and deuterium diffusivities even at low temperatures, depth profiling might not be the optimum measurement technique. In the present investigation we decided to perform a chemical diffusion experiment (hydration with D₂O) combined with ToF-SIMS line scans to measure space-resolved deuterium profiles over a penetration depth of several hundred micrometers. In such profiles cracks – if present – can easily be recognized from locally enhanced deuterium concentrations, and respective regions (or complete samples) are excluded from the analysis. Owing to their comparably large lattice parameters and the absence of cobalt, Ba(Fe,Acc)O_3−δ perovskites (Acc^3+,2+ = redox-inactive dopant, being an acceptor relative to Fe⁴⁺) have only moderate electronic conductivities (e.g. 8 and 0.8 S cm⁻¹ for Ba_0.95La_0.05FeO_3−δ and BaFe_0.8Y_0.2O_3−δ at 600 °C in air²⁸). In an oxygen pumping cell, the range of intermediate oxygen partial pressures 10⁻²⁵ ≤ pO₂ ≤ 10⁻⁵ bar can be accessed, and the present Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ perovskites reach an ionic plateau of pO₂-independent oxygen vacancy conductivity. Finally, we use the obtained proton and oxygen vacancy conductivities to discuss their impact on the overall oxygen exchange kinetics in porous oxygen electrodes of PCFC/PCECs.

We concentrate in the present publication on the effect of ion transport within the positrode material on the overall surface kinetics. Direct measurements of the surface kinetics of oxygen reduction to water (the relevant surface reaction for PCFC cathodes) and related mechanistic investigations are beyond the scope of the present investigation. Such measurements come with their own specific challenges, as briefly discussed at the end of the present publication.

2. Results and discussion

2.1 Relation between D₂O chemical diffusion coefficient and deuteron diffusivity

In order to determine the mobility of protons or deuterons in oxides by SIMS measurements, two experimental designs can be used. (i) Analogous to ¹⁶O/¹⁸O oxygen tracer exchange (see e.g.⁴⁶) one can equilibrate the sample with given pH₂O and T, and then carry out a H/D isotope exchange in identical pD₂O to obtain a space-resolved deuterium isotope profile. (ii) Alternatively, one can hydrate a pre-dried sample with D₂O which also yields a deuterium profile. In case (i) the experiment is purely driven by configurational entropy, and the obtained diffusion coefficient is the deuterium defect diffusivity (strictly speaking, it is the H/D interdiffusion coefficient, cf. ESI Section 5†). In case (ii) the driving force is a D₂O chemical potential gradient ∇μ_D2O, and from fitting the profile one obtains the D₂O chemical diffusion coefficient .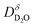

Chemical diffusion of water refers to the coupled incorporation of oxide ions and protons/deuterons in response to a step in μ_H2O or μ_D2O at the surface of the oxide. Such a combined transport of positive and negative ions (or correspondingly oxygen vacancies in the opposite direction) is also denoted ambipolar diffusion. The two charged defects and 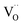are coupled by the bulk electroneutrality condition, and thus the chemical diffusion of the incorporated overall neutral compound-D₂O-can be described by a single single chemical diffusion coefficient 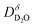which depends on the and diffusivities. For oxides in which only the concentrations of and (or ) are variable (i.e. no pronounced redox activity) and no pronounced association effects are present, it can be shown that the water chemical diffusion coefficient is bounded by the defect diffusivities , and can be expressed as

where X is the degree of hydration (fraction of filled by reaction (1)).^47,48 This equation implies that for low degrees of hydration with high but low , the second term in the bracket dominates. Then the D₂O chemical diffusion coefficient approaches the deuteron diffusivity:

Some more detailed aspects of water chemical diffusion and isotope effect in H/D exchange in a mixed conducting oxide (but with largely fixed oxidation states) are further discussed in the ESI Sections 4–6.†

For the majority of experiments we chose approach (ii) for operational reasons: It allows us to obtain deuteron concentration profiles without extensive equilibration times that otherwise would be required to ensure full equilibration of ≈6 mm thick dense samples with pH₂O at comparably low temperatures. In the present investigation, the Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ samples are first annealed in dry N₂, which brings iron predominantly into 3+ oxidation state.²⁸ Then the proton incorporation is carried out at 300–500 °C by reaction (1), i.e. without any redox process. Thus the Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ samples under the present experimental conditions approach the behavior of a perovskite containing solely fixed-valence B-cations. In first approximation we can therefore use relation (3) which equates values from approach (ii) to the deuteron diffusivity . As a crosscheck, some experiments were performed as actual H/D exchange (approach (i)) directly yielding . As shown below in Fig. 3 the respective values agree well with the data from approach (ii) and relation (3).

In ESI Section 6† the influence of a trapping on protons/deuterons (for example at Fe-site dopants) is discussed. With proton trapping, approaches an effective diffusion coefficient including a differential trapping factor χ_H instead of directly using the diffusivity of an untrapped deuteron.

2.2 Proton transport in Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ

As described in detail in the Experimental section, dense BLF and BLFY pellets with polished surfaces were hydrated with 20 mbar D₂O for certain times, quenched, and finally the deuterium cross-section profiles recorded by SIMS. Fig. 2a shows an exemplary data set for BLFY. The profiles from D⁻ and OD⁻ signals agree well; the images of the metal ions are shown in Fig. S4b.†

Fig. 2 (a) Example of D and OD ToF-SIMS images of BLFY (hydrated in 20 mbar D₂O for 30 min at 400 °C); the dark part at the left side is the embedding resin. (b) Extracted deuterium line profile (normalized to [1 : 0] range) and corresponding fitted curve.

As detailed in the Experimental section, the profiles are normalized to the range of [1 : 0] and the water chemical diffusion coefficient is fitted for the case of semi-infinite diffusion according to eqn (7). As illustrated in Fig. 2b, the measured profiles of the D signal as well as of the OD signal could be well fitted with a single, constant diffusion coefficient. As detailed in ESI Section 3 and Fig. S5,† the applied normalization procedure might lead to an underestimation of the diffusion coefficient by up to 30%. This may appear as a large uncertainty, but compared to the large scatter of proton conductivities for closely related materials – but measured with different techniques – we consider this not to be critical. ESI Section 4† gives some further details why under the present measurement conditions the D₂O chemical diffusion can be described by a single diffusion coefficient.

The extracted D₂O chemical diffusion coefficients are summarized in Fig. 3. As derived form eqn (2), this is expected to approach the deuteron diffusion coefficient for low degrees of hydration. To confirm that the samples actually fall into this regime, several D₂O experiments were conducted with a decreased pD₂O of 2 mbar. The obtained diffusivities agree well with the data from pD₂O = 20 mbar. As a further crosscheck, two experiments for BLFY were performed as H/D exchange experiments with samples prehydrated in H₂O for extended time. As discussed in more detail in ESI Section 5,† proton and deuteron diffusivity differ (not exactly by a factor of √2, but typically not by more than a factor of 1.5,⁴⁹) and the H/D exchange averages over that. The proton/deuteron diffusivities from these H/D exchange experiments agree well with the data, supporting that under the present conditions the D₂O hydration procedure yields diffusion coefficients that closely match the respective deuteron diffusivity . In presence of pronounced proton trapping, instead of the untrapped carrier diffusivity this analysis yields an effective diffusivity 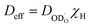(ESI Section 6†).

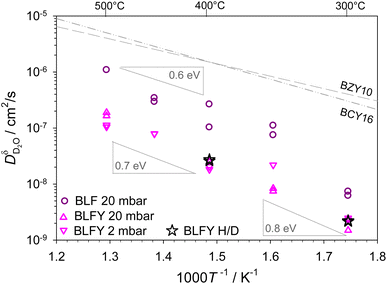Fig. 3 D₂O chemical diffusion coefficients of BLF and BLFY for pD₂O = 2 mbar and pD₂O = 20 mbar, stars correspond to H/D exchange of H₂O-prehydrated samples (extracted from D profiles; results from OD shown in Fig. S6†). The grey dashed lines show the proton diffusivities of BaCe_0.84Y_0.16O_3−δ and BaZr_0.9Y_0.1O_3−δ electrolytes.^50,51

For BLFY for which overall the largest number of measurements was carried out, the uncertainty range for the extracted values is estimated to amount to approximately a factor of 2.

The main observations from Fig. 3 are the following. (i) The deuteron/proton diffusivity of BLF is lower than, but still within an order of magnitude close to BaCe_0.84Y_0.16O_3−δ and BaZr_0.9Y_0.1O_3−δ electrolytes. (ii) The presence of oversized Y dopants on the Fe site in BLFY decreases by a factor of about 6–9 compared to BLF. (iii) The activation energy of BLFY amounts to ca. 0.7 eV at 400–500 °C, and it increases for lower temperatures. Taken together, the latter two features point towards the presence of strong defect interactions in BaFeO_3−δ, in particular in its highly Y-doped variant. These interactions may comprise several contributions, for example trapping effects at B-site dopants.^52,53 Proton trapping at acceptor dopants has been observed in BaZrO₃ electrolytes, and leads to an increased effective activation energy in the low-temperature region (however, a proper description has to extend beyond simple two-state models^3,63). Indications for proton trapping in B-site doped BaFeO₃ have been obtained from DFT calculations; the most pronounced trapping was found for Y.²⁹ Furthermore, that investigation revealed a repulsion zone for protons in the first coordination shell around Y³⁺, with a site energy substantially higher than in the second shell trapping zone, and also higher than for large distances. Such repulsion impedes the formation of percolating low-energy paths for long-range transport. Also in BLF without B-site dopants, some trapping might be caused by the presence of a high concentration under the present experimental conditions. DFT calculations for BaFeO_3−δ indicate an energy landscape with varying site energies for protons depending on their position relative to and the lattice distortions and modifications of Fe–O bonding character caused by oxygen vacancies.⁵⁴

The magnitude of deuteron mobility decrease for BLFY by almost an order of magnitude compared to BLF is reasonably consistent with the proton trapping energy of 0.2 eV in the second shell around Y³⁺ from DFT.²⁹ Assuming that the standard entropy of the trapping reaction is negligible, the mass action constant K of the de-trapping reaction eqn (S3)† amounts to 0.03. Together with the total concentration of Y³⁺ trapping centers of 0.2 this yields a differential trapping factor of 0.15 (eqn (S7)†). So the trapping accounts for the major part of proton mobility decrease. An additional contribution stems from the repulsion of protons from the first shell around Y³⁺, which hinders the formation of long-range low-energy percolating paths. Nevertheless, these numbers are only a first estimate.

From the deuteron/proton diffusivities in Fig. 3 and the proton concentrations measured by thermogravimetry (Fig. S3 in the ESI†) the proton conductivity of BLF and BLFY can be calculated according to the Nernst–Einstein relation (eqn (8) in “Experimental details”). In case of proton trapping, the trapping factor contained in D_eff serves to converting the total proton concentration from thermogravimetry to the untrapped proton concentration. The resulting is shown in Fig. 4a. The proton conductivities of BLF and BLFY are significantly lower than that of Ba(Ce,Zr,Y,Yb)O_3−δ electrolytes which are largely hydrated at temperatures below approx. 500 °C, i.e. have much higher proton concentrations. Owing to the higher proton concentrations of BLFY, the conductivities of BLF and BLFY differ less than their (effective) proton diffusivities. Since the proton concentrations of both BLF and BLFY decrease with increasing temperature in the measured range, the activation energy of of approx. 0.3–0.5 eV (extracted from log(σT) versus T) is lower than that of the proton diffusivity.

Fig. 4 (a) Proton conductivity of BLF and BLFY for pH₂O = 17 mbar calculated from proton diffusivity (Fig. 3) and concentration at 17 mbar (Fig. S3†). The grey dashed line shows the bulk proton conductivity of BaZr_0.9Y_0.1O_3−δ.⁵¹ (b) Comparison to literature data. Open symbols = DC measurements with proton-selective layer: BGLC: BaGd_0.3La_0.7Co₂O_6−δ,³⁶ LaSrNi: La_1.2Sr_0.8NiO₄,³⁸ La2Ni: La₂NiO₄.^37,38 Filled symbols = hydrogen permeation: BCFZr: BaCo_0.4Fe_0.4Zr_0.2O_3−δ, BCFY: BaCo_0.4Fe_0.4Y_0.2O_3−δ,⁴⁰ BCFZrY: BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ,³⁹ BCFZnY: BaCo_0.4Fe_0.4Zn_0.1Y_0.1O_3−δ,⁵⁵ D-BFZr: Ba_0.875Fe_0.875Zr_0.125O_3−δ.¹⁴

Fig. 4b compares the present of BLF and BLFY to literature data of triple-conducting perovskites and perovskite-related materials. The spread by 6 orders of magnitude reflects not only the pronounced variation of proton transport with materials composition, but also the fact that such measurements of a minority carrier in a triple conducting materials are challenging.

2.3 Oxygen vacancy transport in Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ

To complete the ionic transport characterization of the investigated Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ perovskites, and to supply data required for a discussion of porous air electrode kinetics in Section 3, we investigated also the conductivities. The large lattice parameter of Ba-based perovskites substantially decreases the mobility of electronic defects compared to Sr-based perovskites. On the other hand, the expanded lattice may be beneficial for the mobilities. Thus, for the present BLF and BLFY samples it is possible to determine their conductivities in a range of moderately reducing conditions that can be accessed in an oxygen pumping cell. Unfortunately this approach fails for materials with higher electronic and/or lower conducvtities, e.g. already for Ba_0.5Sr_0.5FeO_3−δ (Fig. S8b†), and then alternatives such as DC conductivity measurements with an ion-selective layer, oxygen permeation, chemical or tracer diffusion experiments are required (see e.g.^46,56–59).

Fig. 5a shows the total bulk conductivity of BLFY measured over the extended pO₂ range that can be covered in the oxygen pumping cell. At high pO₂ the total conductivity is mainly dominated by electron holes (h˙) and almost temperature-independent. The plateau in the intermediate pO₂ range corresponds to the conductivity of oxygen vacancies; iron is completely in 3+ oxidation state and electronic transport involving Fe⁴⁺ (holes h˙) or Fe²⁺ (electrons e′) falls below the conductivity. With decreasing pO₂, n-type electronic conductivity dominates. The respective data for BLF in Fig. S8a† also exhibit an extended pO₂-independent plateau from which can be extracted. The Arrhenius plot of in Fig. 5b shows that BLFY has a significantly lower conductivity compared to the Y-free material, and also a slightly increased activation energy. The BLF and BLFY activation energies for of 0.9–1 eV (under conditions of fixed concentration) are within the typical range encountered for perovskites,⁶⁰ albeit at the upper end. When comparing with data for BaCo_0.4Fe_0.4Zr_0.2O_3−δ and BaCo_0.4Fe_0.4Y_0.2O_3−δ,⁶¹ also there the Y-containing material exhibits the lower conductivity.

Fig. 5 (a) Total conductivity of BLFY as a function of pO₂ measured in the oxygen pumping cell. (b) Arrhenius plot of oxygen vacancy conductivity of BLF and BLFY extracted from the plateau region. Grey symbols: of BLF (from D^δ_O, conductivity relaxation under conditions ),⁶² and of BaCo_0.4Fe_0.4Zr_0.2O_3−δ and BaCo_0.4Fe_0.4Y_0.2O_3−δ (oxygen permeation).⁶¹ (c) for BLF and BLFY calculated from using the Nernst–Einstein equation. Grey symbols: of BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ from ¹⁸O exchange/SIMS line scan⁵⁹ ( converted to assuming ).

The oxygen vacancy diffusivity is shown in Fig. 5c. Since the molar fraction of in the conditions of extraction is identical for BLF and BLFY, the lower for BLFY directly translates into lower for the Y-doped material. This trend is similar to that observed for in BaZr_1−xY_xO_3−δ (DFT and KMC calculations⁶³), where an increased Y concentration decreases the effective long-range mobility owing to a combination of trapping effects and increased migration barriers. While Y³⁺ (ion radius 0.9 Å) is only moderately oversized relative to Zr⁴⁺ (0.72 Å) in BaZrO₃, the size difference to Fe (Fe³⁺ 0.645 Å, Fe⁴⁺ 0.585 Å) in BaFeO_3−δ is much larger, which may further aggravate the defect interactions and decrease the mobility.⁶⁴ DFT calculations indicate repulsion of in the first sphere around Y³⁺, followed by attraction in the second sphere. For comparison, also values for BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3−δ are shown.⁵⁹ They come close to the present BLF data, which might be related to the lower Y content compared to the present BLFY, and that the material contains cobalt which in perovskites often increases the mobility.

3 Implications for the kinetics of porous air electrodes

Fig. 6 compiles proton and conductivities for the present BLF and BLFY samples. The values refer to dry conditions, but are not expected to change much in humid atmosphere because most will remain unhydrated. The decreased mobility in the Y-doped material leads to a proportional decrease of because the concentration is the same. In contrast, the hydration thermodynamics differs between BLF and BLFY (Fig. S3a†). The significantly higher degrees of hydration in BLFY partially compensates its decreased proton mobility. Correspondingly, the proton conductivities are within about half an order of magnitude. For BLFY, and are comparable at low temperature but exceeds by one order of magnitude at high T; for BLF the difference is larger in the whole temperature range.

Fig. 6 Proton (symbols and solid lines) and oxygen vacancy conductivity (dashed lines) of BLF and BLFY in conditions where iron is predominantly in Fe³⁺ oxidation state.

For a pore-free thin film air electrode, the positrode-air two phase boundary dominates the oxygen exchange kinetics (the contribution of the triple phase boundary is negligible). The proton transport through the electrode film and oxygen surface reaction are serial processes (Fig. 1b). Unless the film is extremely thick or its bulk proton conductivity very low, the typically large surface reaction resistance dominates clearly over the proton transport resistance within the film.

For porous triple-conducting electrodes on protonic electrolytes the situation becomes more complex as illustrated in Fig. 7. For simplicity we concentrate here on the case that the protonic electrolyte has a negligible transference number. This holds for typical Ba(Zr,Ce)(Y,Yb)O_3−δ protonic electrolytes up to about 600 °C, cf. grey lines in Fig. 6 (the conductivity in humidified operating conditions is much lower than the depicted in dry conditions, see also).⁶⁵ (If the transference number becomes significant, this opens a parallel path in which the cell operates as a conventional -conducting solid oxide device).

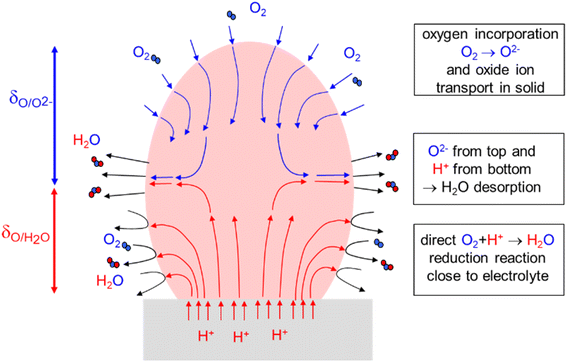Fig. 7 Sketch of a porous air electrode under slight cathodic bias, i.e. operating in oxygen reduction mode (for simplicity only one particle is shown; in an actual electrode these processes will typically extend over several particles (Fig. 1c), but this does not fundamentally change the picture). The electrolyte (grey) is assumed to be a pure proton conductor.

The porous electrode has a region close to the electrolyte δ_O/H2O in which owing to of the triple-conductor protons can be transported through the grain interior of the particles to reach the gas/electrode two-phase boundary, and are directly involved in the reduction of O₂ to H₂O. This region can be treated analogously to a hole/ mixed conducting electrode on an oxide ion conducting electrolyte as done in the ALS model.²¹ We concentrate on the case that ion transfer at the electrolyte/electrode interface and gas diffusion are not limiting. For a mixed conductor with mobile oxygen defects (here ) and electronic defects on an oxide ion conducting electrolyte, the thickness δ_O of the active zone is co-determined by surface reaction kinetics and bulk oxygen transport according to²¹

Factors in the order of unity such as symmetry factors and tortuosity are dropped; α is the specific surface area of the porous electrode, c_O the concentration of regular oxide ions. If the surface kinetics is slow, then bulk oxygen transport occurs in the electrode material up to larger distances from the electrolyte to increase the active surface area, until the point is reached where resistive contributions from surface reaction and bulk transport become comparable. A mixed conductor of and electronic defects under DC bias develops a gradient in oxygen nonstoichiometry starting at the electrolyte/electrode interface, and δ_O represents the characteristic length of the nonstoichiometry decay.²¹ The overall reaction rate is proportional to .

In order to apply this model to a hole/proton mixed conducting electrode on a protonic electrolyte, eqn (4) needs to be adapted (ESI Section 8†):

This δ_O/H2O (red arrows in Fig. 6) would be the overall characteristic length of the active zone if no oxygen transport was possible within the electrode particles or along the particle surface (adsorbed and partially ionized atomic oxygen species on a largely ionic oxide surface do not necessarily have a high mobility).⁶⁶ In materials with low proton conductivity (but unchanged surface rate constant ) this zone may become rather thin.

However, if the electrode material has also a perceptible conductivity, i.e. is a real triple conductor, the zone above δ_O/H2O will still feel the applied cathodic bias (ESI Section 9†). Then O incorporation occurs also in a certain region beyond δ_O/H2O such that protons are not involved directly in the surface reaction. But since the overall reaction is the reduction of O₂ to H₂O, the incorporated O needs to be transported towards the electrolyte (blue arrows in Fig. 7) to finally meet protons and desorb as H₂O. This process expands the overall active area for the sluggish oxygen reduction reaction, and thus decreases the overall electrode resistance. As a first approximation we use the same expression for δ_O as in the ALS model in absence of humidity:

Since both the reduction of O₂ to water and to oxide ions require the kinetically difficult splitting of the strong O=O double bond, is used as a first approximation. The higher of BLF and BLFY compared to their yields a wider active zone δ_O/O²⁻ for oxygen incorporation to oxide ions than δ_O/H2O for direct reduction to water immediately involving protons. It needs to be kept in mind that each oxide ion incorporated into the triple conductors in the upper zone of the electrode still needs to combine with protons, i.e. the resistance of this reaction path still has a serial contribution from proton transport.

For a numerical example, we take α = 30 000 cm⁻¹ for the specific surface area of a representative porous electrode, and (k* of a pore-free Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ film⁶⁷). This yields δ_O/H2O = 2 μm, δ_O/O²⁻ = 11 μm for BLF, and δ_O/H2O = 1 μm, δ_O/O²⁻ = 2 μm for BLFY with moderately lower but strongly decreased . Thus, the total width of the active zone is significantly extended by the conductivity of the triple-conducting air electrode material. This extension is larger for higher ratios, i.e. for comparable and values, the materials with higher is expected to show better performance. However, an increase of 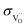at expense of is not recommended as it would decrease δ_O/H2O.

The value of k* = 10⁻⁶ cm s⁻¹ at 500 °C is at the upper end of typical k* values (but found also for uncontaminated La_0.8Sr_0.2(Co,Fe)O_3−δ films⁶⁸). For dense BaCo_0.4Fe_0.4Zr_0.2−xY_xO_3−δ ceramics, k* values around 10⁻⁸ cm s⁻¹ were obtained at 500 °C.⁵⁹ Using this lower k* increases δ_O/H2O, δ_O/O²⁻ from eqn (5) and (6) by one order of magnitude, but does not change the ratio between them. Such extended δ_O/H2O, δ_O/O²⁻ values imply that the active zone comprises several triple-conducting electrode particles (only for graphical simplicity, the scheme in Fig. 7 uses a single particle). The ALS model in ref. 21 and 69 already implicitly considers an extension over several electrode particles. As long as the active zone width does not exceed the thickness of the porous electrode, the overall model remains unchanged. The grain boundaries of triple-conducting electrode particles typically do not show pronounced blocking effects for protons or .⁷⁰

While for simplicity we considered here the direction of oxygen reduction, similar considerations hold also for the water oxidation to O₂ because of microscopic reversibility (for not too large driving forces). Overall, apart from electrode morphology (specific surface area etc.) the resistance of a triple-conducting porous electrode on a proton-conducting electrolyte will be co-determined by , , 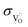and , .

Finally, we want to mention further aspects relevant for positrode kinetics in protonic ceramic cells. (i) Under anodic bias, the enhanced oxygen chemical potential in the active region⁷¹ may decrease the degree of hydration and correspondingly also , because many triple conductors exhibit a detrimental defect interaction between electron holes and protons.^24,28 Typically, in electrolysis mode increased steam concentrations are applied which may compensate this effect.

(ii) For more detailed insight into the kinetics of porous positrodes on protonic electrolytes including proton and 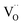current distribution, numerical modelling accounting for transport of all three carriers and surface reaction coefficients 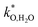, is expected to be helpful (including also the nonideal dependence of on local μ_O).

(iii) The determination of surface reaction coefficients for positrodes on protonic electrolytes comes with its own challenges. For porous electrodes, the fact that both δ_O/H2O and δ_O/O²⁻ regions contribute to the active area (and might vary with local μ_O) causes perceptible uncertainty when attempting to extract , values from measured overall reaction resistances. On the other hand, measurements on pore-free model electrodes with well-defined geometry which proved very useful for positrodes on oxygen ion conductors (e.g.^71,72) encounter a specific issue in the case of protonic ceramic electrolytes. In contrast to Y-stabilized ZrO₂, Ba(Ce,Zr,Y,Yb)O_3−δ electrolytes develop a perceptible electronic transference number when exposed to oxidizing conditions on both sides (half-cells in symmetrical oxidizing atmosphere) at elevated temperature.³⁵ When the true electrode resistance becomes comparable to the electronic resistance of the electrolyte-which may easily happen for pore-free electrodes because of their lower active area-the measured apparent electrode resistance approaches the latter instead of the true electrode surface reaction resistance.^26,73

4 Summary and conclusions

The deuteron diffusivities of triple-conducting Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ perovskites were determined from D₂O hydration experiments of samples pre-annealed in dry N₂ followed by ToF SIMS line scan analysis. For BLF, the proton diffusion coefficient is within the same order of magnitude as in BaZr_0.9Y_0.1O_3−δ, while for BLFY (20% strongly oversized Y³⁺ on the Fe site), 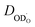is significantly lower, which indicates a decreased mobility caused by pronounced defect interactions. Also the mobility is substantially lower in BLFY compared to BLF. The proton conductivity of BLF amounts to 7 × 10⁻⁶–2 × 10⁻⁴ S cm⁻¹ at 300–500 °C, and is 1–2 orders of magnitude below of BLF. For BLFY, is in the range of 3 × 10⁻⁶–4 × 10⁻⁵ S cm⁻¹ and up to one order lower than .

The width of the electrochemically active zone of a porous triple-conducting positrode on a purely protonic electrolyte is estimated based on adapting the Adler–Lane–Steele model. For BLF and BLFY, the zone width for direct reduction of O₂ to water is in the range of 1–2 μm. However, owing to there is a more extended upper part of the positrode in which under cathodic bias oxygen is incorporated as oxide ions, which are subsequently transported towards the protonic electrolyte and finally also combine with protons to desorb as H₂O. This process enhances the overall oxygen reduction rate, but relies also on proton transport within the triple-conductor (for a more detailed picture, numerical modelling is required).

These findings indicate that to improve materials for porous positrodes, proton and conductivity as well as the effective surface rate constant for oxygen reduction need to be optimized together, not at expense of each other. This differs from the situation of a pore-free electrode film, for which oxygen reduction at the surface can proceed only with immediate proton participation to directly form H₂O, i.e. oxide ion conductivity is not decisive for steady state operation. For the surface kinetics, operation in atmospheres with high humidity represents a particular challenge because adsorbed OH species may largely poison reactive sites such as oxygen vacancies. Multi-phase electrode materials (e.g. from exsolution or surface decoration) exposing also less hydrophilic surfaces might be one approach to overcome this obstacle.

5. Experimental details

5.1. Preparation

Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ powders were synthesised via a sol–gel nitrate combustion method followed by thermal treatment in air as described previously.²⁸ Dense Ba_0.95La_0.05FeO_3−δ (BLF) pellets of ≈6 mm thickness were fabricated by spark plasma sintering (SPS; HP D5, FCT Systeme, Germany) in a 10 mm graphite die at 910 °C for 10 min with 6 kN force. The Ba_0.95La_0.05(Fe_1−xY_x)O_3−δ (BLFY) powder was isostatically pressed in a 15 mm mold and sintered in a tube furnace at 1400 °C for 8 h (heating and cooling rate 5 K min⁻¹) in Ar atmosphere, yielding ρ_rel = 97%. Both sintering procedures result in samples in which iron is completely in 3+ oxidation state (Fe perovskites exhibit a plateau of 3+ oxidation state which extends over a large pO₂ range of inert gas to moderately reducing conditions;^74,75 cf. also the behavior of conductivity in Fig. 5a and S8†). The pellets were polished on top and bottom sides, and cut into 4 sectors for the D₂O chemical diffusion experiments (i.e. 4 samples obtained from one pellet). Samples for oxygen ion conductivity were cut into 5 × 5 mm² slabs with 0.7–1 mm thickness.

5.2. D₂O hydration, H/D exchange

To ensure reproducible starting conditions for the D₂O hydration step, the samples are be dried at 700 °C, and to prevent sample oxidation this is done in dry N₂. For the D₂O hydration the samples were placed on a gold foil in a quartz tube and heated with 2 K min⁻¹ in dry N₂ for 12 h at 700 °C. After quenching (10 K min⁻¹) to the desired hydration temperature, the N₂ gas stream was redirected through a D₂O filled bubbler at room temperature. This D₂O hydration step (typical duration 60 min for 300 °C, 10 min for 500 °C) was followed by moving the sample within the quartz tube to a cold zone with a N₂ stream. Most experiments are carried out in this mode, as this avoids the need for long pre-equilibration with H₂O, which might also induce sample surface degradation after long time in humid conditions.

For H/D isotope exchange, the sample was pre-hydrated in pH₂O = 20 mbar for extended time at the planned exchange temperature (7 days for the 400 °C experiment; for the 300 °C experiment the hydration was performed in three steps with decreasing temperature: 3 days 400 °C, then 3 days 350 °C, then 10 days 300 °C), quenched, and then exposed to pD₂O = 20 mbar for the desired exchange time. After D₂O hydration or H/D exchange the samples were embedded in a Cu: PMMA resin (Technovit 5000), cut and polished such that SIMS line scans can be recorded in the direction perpendicular to the D₂O-exposed surface (more details in Fig. S4a†). Between processing steps, the resin-embedded sample was stored in a −18 °C freezer.

5.3. ToF-SIMS

Time of flight-secondary ion mass spectrometry measurements were carried out using a ToF-SIMS V instrument (ION-TOF) version NCS. Images were acquired on the cross-section. Before imaging the analyzed area is sputtered for 7 min by Cs⁺ at 2 keV ion energy and 105 nA ion current on a region of 800 μm × 800 μm to clean the polished surface. For probing, pulsed Bi⁺ primary ions in spectrometry mode with 30 keV and approx. 2 pA were used to image the 500 μm × 500 μm analysis area. Ions were acquired in negative polarity. Non-interlaced Cs⁺ sputtering (2 keV, 800 μm × 800 μm) was used to ensure a continuous high ion yield for the complete measurement time. During the complete ToF-SIMS measurement time the sample was kept at −140 °C. Data extraction was carried out using the software Surfacelab 7.1. From the images of the analysis area such as Fig. 2 the intensity data were integrated to obtain line scan concentration profiles. For this the intensities of the pixels parallel to the crystal edge were integrated over the entire image width. This yields concentration profiles as a function of the distance from the exposed surface into the depth (cf. Fig. S4a†). In cases where the ion image contained strongly distorted areas, these parts were excluded from the further data analysis. Typically, two line scans from opposite sides of the sample were recorded and analyzed.

5.4. Normalization

For the D₂O hydration experiments which represent a chemical diffusion experiment, normalization to an isotope ratio (as typically done in ¹⁸O isotope exchange) is not possible. Instead, the D and DO ion intensities were normalized to reach unity at the surface and zero at infinite diffusion length. Also in the H/D exchange experiments of H₂O-prehydrated samples (true isotope exchange experiment) a normalization according to [D]/([D]+[H]) or [OD]/([OD]+[OH]) was not possible because the H, OH background signals exceeded D, OD by far (even the H, OH signals in samples which had not been H₂O-prehydrated but dried) indicating that the majority of these signals is related to background gaseous hydrogen in the vacuum chamber rather than H in the sample. According to numerical tests with simulated profiles (ESI Section 3†), it is estimated that the applied normalization procedure might lead to a moderate underestimation of the diffusivity values up to ≈30%. Using this normalization, surface exchange coefficients for the hydration reaction can not be obtained. However, the hydration reaction (1) is kinetically much easier (requiring only proton and hydroxide ion transfer) than the oxygen exchange reaction (requiring O=O double bond splitting, for reduction to water as well as for incorporation as oxide ions) and thus less decisive for electrode operation on protonic ceramic cells. For BaCe_0.9Y_0.1O_3−δ, H/D exchange of the hydration reaction yielded values (activation energy 0.3–0.5 eV)⁷⁶ which are significantly higher and characterized by a lower activation energy than oxygen exchange surface coefficients e.g. on BaCo_1−xFe_xZr_0.1Y_0.1O_3−δ (activation energy 0.9–1.1 eV), and Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ (activation energy 1.7 eV).^59,67 The normalized D and OD concentration profiles were then fitted by the solution for semi-infinite diffusion:⁷⁷

Proton conductivity was calculated from the proton/deuteron diffusivities in Fig. 3 using the Nernst–Einstein equation

Inserting the respective proton concentrations from thermogravimetry (Fig. S3†). Proton and deuteron diffusivities differ by a factor which is typically not larger than ≈1.5 (ESI Section 5†). In lack of precise information of the exact H/D isotope effect in BaFeO₃-based triple-conducting perovskites, we use the deuteron diffusivities from and the H/D interdiffusion coefficients (stars in Fig. 3) without further correction factor as proxy for . Within the unavoidable scatter within the present experiments, and the even larger variation of proton conductivities for closely related materials but measured with different methods (Fig. 4b) this approximation is considered acceptable.

If a material such as BLFY shows trapping of protons, then the diffusivity extracted from the SIMS line profiles corresponds to an effective diffusivity including the proton trapping factor χ which for this specific situation is a constant factor (cf. Section 4 in the ESI†). Using this D_eff in the Nernst–Einstein equation together with the total proton concentration from thermogravimetry (free and trapped protons) gives the correct proton conductivity because yields the concentration of untrapped protons (ESI Section 6†).

5.5. X-ray diffraction

XRD analysis of calcined and sintered samples was performed with a PANalytical Empyrean X-ray diffractometer using a Cu Kα radiation source (λ = 1.5406 Å) operated at 40 kV and 40 mA. The diffractogram was recorded at room temperature with a scanning rate of 0.03° s⁻¹. The instrument-dependent peak broadening was corrected by a preceding measurement with a LaB₆ standard. Topas V5 (ref. 78) was used for Rietveld refinement (cf. ESI Section 1†), reflection broadening was described by convolution of a Voigt function with a modified pseudo Voigt function according to Thompson–Cox–Hastings.⁷⁹

5.6. Oxygen vacancy conductivity

Oxygen was measured in a setup with integrated oxygen pump (Huber Scientific, Austria). It consists of a quartz tube with a pump side (YSZ based oxygen pump) and a sample side (EIS measurement), both equipped with lambda probes and type S thermocouples. A tubular oven with two heating zones (T_pump = 700 °C and T_sample = 700–350 °C) was used. To produce stable, low pO₂ values by the pumping cell, a gas flow of 50 ml min⁻¹ of 0.5% CO₂ in N₂ was applied. The pO₂ on the pump site is determined by the pumping current and resulting CO/CO₂ ratio. The sample side experiences the same CO/CO₂ ratio but the pO₂ measured there changes according to the T-dependence of the K_CO/CO2 mass action constant. The sample was always exposed over night at 700 °C to the new voltage applied to the pumping side which ensures full equilibration with the new pO₂ even if significant changes of the oxygen nonstoichiometry are involved. For measurements at lower T for the given pumping voltage, several impedance spectra are recorded over approx. 1 h at 600–500 °C, and approx. 2 h at 450–350 °C. In any case, the sample started at higher pumping power (i.e. lower pO₂) at 700 °C will be in a more reduced state also at lower measuring temperature compared to the samples started from a higher initial pO₂. The observation of a conductivity plateau for several pumping powers thus indicates the presence of a pO₂-independent plateau even if at the lowest measurement temperatures the sample interior might not fully reach the effective pO₂ corresponding to the T-dependence of K_CO/CO2 at the given CO/CO₂ ratio. For high pO₂, N₂/O₂ mixtures are used.

Two-point impedance measurements were performed with an Alpha-A frequency response analyzer (Novocontrol, Germany) using voltage sinusoids of 20 mV (rms) amplitude between 10 MHz and 1 or 0.1 Hz. Ca. 100 nm Pt was sputtered on both sides of the samples as electrodes. As it is typical for this type of mixed conducting perovskites, the samples exhibited only a bulk semicircle at high frequencies, and-also depending on gas atmosphere-a low frequency arc that is attributed to the electrode response (i.e. no sign of blocking grain boundaries).

5.7. Proton uptake

Thermogravimetry of BLFY (Fig. S3†) was measured on crushed sintered pellets in humidified N₂ as described in ref. 28. BLF data are taken from this reference.

Data availability

The underlying experimental data will be made available upon reasonable request.

Author contributions

C. Berger: conceptualization, investigation, writing – original draft, reviewing and editing. T. Acartürk: investigation, writing – reviewing and editing. U. Starke: discussion, writing – reviewing and editing. J. Maier: discussion, writing – reviewing and editing. R. Merkle: conceptualization, methodology, supervision, writing – original draft, reviewing and editing.

Conflicts of interest

The author declare there is no conflict of interest.

Acknowledgements

The authors thank Barbara Baum for cutting and polishing the SIMS samples and Giulia Raimondi for TG hydration measurements of BLFY (both MPI for Solid State Research, Stuttgart), and Christina Nader (Montanuniversität Leoben, Austria) for SPS. The authors acknowledge fruitful discussions with Koji Amezawa (Tohoku University, Japan), Andrew Chesnokov and Denis Gryaznov (University of Latvia, Riga), Max Hödl (MPI Stuttgart), Truls Norby (University of Oslo, Norway), and Ryan O'Hayre (Colorado School of Mines, Golden, USA). Open Access funding provided by the Max Planck Society.

References

1. H. Iwahara, T. Esaka, H. Uchida and N. Maeda, Proton conduction in sintered oxides and its application to steam electrolysis for hydrogen production, Solid State Ionics, 1981, 3, 359–363.
2. R. H. Ryu and S. M. Haile, Chemical stability and proton conductivity of doped BaCeO₃-BaZrO₃ solid solutions, Solid State Ionics, 1999, 125, 355–367.
3. K. D. Kreuer, Proton-conducting oxides, Annu. Rev. Mater. Res., 2003, 33, 333–359.
4. L. Yang, S. Wang, K. Blinn, M. Liu, Z. Liu and M. L. Liu, Enhanced Sulfur and Coking Tolerance of a Mixed Ion Conductor for SOFCs: BaZr_0.1Ce_0.7Y_0.2-xYb_xO_3-δ, Science, 2009, 326, 126–129.
5. S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H. I. Ji and S. M. Haile, Exceptional power density and stability at intermediate temperatures in protonic ceramic fuel cells, Nat. Energy, 2018, 3, 202–210.
6. D. Udomsilp, C. Lenser, O. Guillon and N. H. Menzler, Performance Benchmark of Planar Solid Oxide Cells Based on Material Development and Designs, Energy Technol., 2021, 9, 2001062.
7. L. Yang, C. Zuo, S. Wang, Z. Cheng and M. L. Liu, A Novel Composite Cathode for Low-Temperature SOFCs Based on Oxide Proton Conductors, Adv. Mater., 2008, 20, 3280–3283.
8. J. Kim, S. Sengodan, G. Kwon, D. Ding, J. Shin, M. L. Liu and G. Kim, Triple-Conducting Layered Perovskites as Cathode Materials for Proton-Conducting Solid Oxide Fuel Cells, ChemSusChem, 2014, 7, 2811–2815.
9. C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Readily processed protonic ceramic fuel cells with high performance at low temperatures, Science, 2015, 349, 1321–1326.
10. H. An, H.-W. Lee, B.-K. Kim, J.-W. Son, K. J. Yoon, H. Kim, D. Shin, H.-I. Ji and J.-H. Lee, A 5 × 5 cm² protonic ceramic fuel cell with a power density of 1.3 W cm^–2 at 600 °C, Nat. Energy, 2018, 3, 870–875.
11. S. Choi, T. C. Davenport and S. M. Haile, Protonic ceramic electrochemical cells for hydrogen production and electricity generation: exceptional reversibility, stability, and demonstrated faradaic efficiency, Energy Environ. Sci., 2019, 12, 206–215.
12. H. Ding, W. Wu, C. Jiang, Y. Ding, W. Bian, B. Hu, P. Singh, C. J. Orme, L. Wang, Y. Zhang and D. Ding, Self-sustainable protonic ceramic electrochemical cells using a triple conducting electrode for hydrogen and power production, Nat. Comm., 2020, 11, 1907.
13. K. Pei, Y. Zhou, K. Xu, H. Zhang, Y. Ding, B. Zhao, W. Yuan, K. Sasaki, Y. M. Choi, Y. Chen and M. L. Liu, Surface restructuring of a perovskite-type air electrode for reversible protonic ceramic electrochemical cells, Nat. Comm., 2022, 13, 2207.
14. Z. Wang, Y. Wang, J. Wang, Y. Song, M. J. Robson, A. Seong, M. Yang, Z. Zhang, A. Belotti, J. Liu, G. Kim 4, J. Lim, Z. P. Shao and F. Ciucci, Rational design of perovskite ferrites as high-performance proton-conducting fuel cell cathodes, Nat. Catal., 2022, 5, 777–787.
15. D. Kim, I. Jeong, S. Ahn, S. Oh, H.-N. Im, H. Bae, S.-J. Song, C.-W. Lee, W. C. Jung and K. T. Lee, On the Role of Bimetal-Doped BaCoO_3−δ Perovskites as Highly Active Oxygen Electrodes of Protonic Ceramic Electrochemical Cells, Adv. Energy Mater., 2024, 14, 2304059.
16. C. Duan, J. Huang and N. Sullivan, Ryan O'Hayre, Proton-conducting oxides for energy conversion and storage, Appl. Phys. Rev., 2020, 7, 011314.
17. N. Tsvetkov, D. Kim, I. Jeong, J. H. Kim, S. Ahn, K. T. Lee and W. C. Jung, Advances in Materials and Interface Understanding in Protonic Ceramic Fuel Cells, Adv. Mater. Technol., 2022, 8, 2201075.
18. S. Guo, L. Jiang, Y. Li, P. Zhong, S. A. Ismail, T. Norby and D. Han, From Electrolyte and Electrode Materials to Large-Area Protonic Ceramic Fuel Cells: A Review, Adv. Funct. Mater., 2024, 34, 2304729.
19. Y. Wang, Y. Ling, B. Wang, G. Zhai, G. Yang, Z. P. Shao, R. Xiao and T. Li, A review of progress in proton ceramic electrochemical cells: material and structural design, coupled with value-added chemical production, Energy Environ. Sci., 2023, 16, 5721–5770.
20. J. A. Kilner and M. Burriel, Materials for Intermediate-Temperature Solid-Oxide Fuel Cells, Annu. Rev. Mater. Res., 2014, 44, 365–393.
21. S. B. Adler, J. A. Lane and B. C. H. Steele, Electrode Kinetics of Porous Mixed-Conducting Oxygen Electrodes, J. Electrochem. Soc., 1996, 143, 3554–3564.
22. K. Amezawa, X-ray absorption spectroscopic studies on solid oxide fuel cells and proton-conducting ceramic fuel cells, Curr. Opin. Electrochem., 2020, 21, 250–256.
23. K. Amezawa, keynote talk KN46 at SSPC-20, September 2021 (online) How Do We Investigate Reaction Mechanism in Oxide Electrode on Proton-Conducting Electrolyte?.
24. R. Merkle, M. F. Hoedl, G. Raimondi, R. Zohourian and J. Maier, Oxides with Mixed Protonic and Electronic Conductivity, Annu. Rev. Mater. Res., 2021, 51, 461–493.
25. Q. Wang, S. Ricote and M. Chen, Oxygen electrodes for protonic ceramic cells, Electrochim. Acta, 2023, 446, 142101.
26. R. Strandbakke, V. A. Cherepanov, A. Y. Zuev, D. S. Tsvetkov, C. Argirusis, G. Sourkouni, S. Prünte and T. Norby, Gd- and Pr-based double perovskite cobaltites as oxygen electrodes for proton ceramic fuel cells and electrolyser cells, Solid State Ionics, 2015, 278, 120–132.
27. Z. Wang, W. Yang, S. P. Shafi, L. Bi, Z. Wang, R. Peng, C. Xia, W. Liu and Y. Lu, A high performance cathode for proton conducting solid oxide fuel cells, J. Mater. Chem. A, 2015, 3, 8405.
28. R. Zohourian, R. Merkle, G. Raimondi and J. Maier, Mixed-Conducting Perovskites as Cathode Materials for Protonic Ceramic Fuel Cells: Understanding the Trends in Proton Uptake, Adv. Funct. Mater., 2018, 28, 1801241.
29. A. Chesnokov, D. Gryaznov, E. A. Kotomin, J. Maier and R. Merkle, Protons in (Ga,Sc,In,Y)³⁺-doped BaFeO₃ triple conductors - site energies and migration barriers investigated by density functional theory calculations, Solid State Ionics, 2025, 421, 116788.
30. C. Chen, D. Chen, Y. Gao, Z. Shao and F. Ciucci, Computational and experimental analysis of Ba_0.95La_0.05FeO_3-δ as a cathode material for solid oxide fuel cells, J. Mater. Chem. A, 2014, 2, 14154–14163.
31. D. Poetzsch, R. Merkle and J. Maier, Stoichiometry relaxation in materials with three mobile carriers - thermodynamics and transport kinetics exemplified for protons, oxygen vacancies and holes, Adv. Funct. Mater., 2015, 25, 1542–1557.
32. L. R. Tarutina, M. A. Gordeeva, D. E. Matkin, M. T. Akopian, G. N. Starostin, A. V. Kasyanova, A. P. Tarutin, N. A. Danilov, I. A. Starostina, D. A. Medvedev and Z. Shao, Why do BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3–δ-derived complex oxides become one of the most promising electrodes for protonic ceramic electrochemical cells? An explanatory review, Chem. Eng. J., 2024, 490, 151615.
33. M. H. Hebb, Electrical Conductivity of Silver Sulfide, J. Chem. Phys., 1952, 10, 185–190.
34. C. Wagner, Galvanische Zellen mit festen Elektrolyten mit gemischter Stromleitung, Z. Elektrochem., 1956, 60, 4–7.
35. K. Nomura and H. Kageyama, Transport properties of Ba(Zr_0.8Y_0.2)O_3−δ perovskite, Solid State Ionics, 2007, 178, 661–665.
36. T. Miruszewski, R. Strandbakke, K. Dzierzgowski, I. Szpunar, A. Mielewczyk-Gryn, S. Wachowski and M. Gazda, A modified DC Hebb-Wagner polarization method for determining the partial protonic electrical conductivity in mixed-conducting BaGd_0.3La_0.7Co₂O_6-δ, J. Mater. Chem. A, 2024, 12, 13488–13497.
37. L. Chen, G. Wang, K. Toyoura and D. Han, High-temperature protonic conduction in La₂NiO_4+δ-based Ruddlesden-Popper type oxides: Correlation with concentration of interstitial oxide ions, Small, 2024, 20, 2311473.
38. P. Zhong, K. Toyoura, L. Jiang, L. Chen, S. A. Ismail, N. Hatada, T. Norby and D. Han, Protonic Conduction in La₂NiO_4+δ and La_2-xA_xNiO_4+δ (A = Ca, Sr, Ba) Ruddlesden–Popper Type Oxides, Adv. Energy Mater., 2022, 12, 2200392.
39. M. Liang, F. He, C. Zhou, Y. Chen, R. Ran, G. Yang, W. Zhou and Z. Shao, Nickel-doped BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3-δ as a new high-performance cathode for both oxygen-ion and proton conducting fuel cells, Chem. Eng. J., 2021, 420, 127717.
40. J. H. Duffy, H. W. Abernathy and K. S. Brinkman, Tuning proton kinetics in BaCo_0.4Fe_0.4Zr_0.2–XY_XO_3–δ triple ionic-electronic conductors via aliovalent substitution, J. Mater. Chem. A, 2023, 11, 8929–8938.
41. Z. Zhao, M. Zou, H. Huang, X. Zhai, H. Wofford and J. Tong, Insight of BaCe_0.5Fe0_.5O_3-δ twin perovskite oxide composite for solid oxide electrochemical cells, J. Am. Ceram. Soc., 2023, 106, 186–200.
42. S. Wang, P. A. W. van der Heide, C. Chavez, A. J. Jacobson and S. B. Adler, An electrical conductivity relaxation study of La_0.6Sr_0.4Fe_0.8Co_0.2O_3-δ, Solid State Ionics, 2003, 156, 201–208.
43. Y. Chen, T. Hong, P. Wang, K. Brinkman, J. Tong and J. Cheng, Investigate the proton uptake process of proton/oxygen ion/hole triple conductor BaCo_0.4Fe_0.4Zr_0.1Y_0.1O_3-δ by electrical conductivity relaxation, J. Power Sources, 2019, 440, 227122.
44. A. Seong, J. Kim, D. Jeong, S. Sengodan, M. Liu, S. Choi and G. Kim, Electrokinetic Proton Transport in Triple (H⁺/O²⁻/e⁻) Conducting Oxides as a Key Descriptor for Highly Efficient Protonic Ceramic Fuel Cells, Adv. Sci., 2021, 8, 2004099.
45. Y. Song, J. Liu, Y. Wang, D. Guan, A. Seong, M. Liang, M. J. Robson, X. Xiong, Z. Zhang, G. Kim, Z. Shao and F. Ciucci, Nanocomposites: A New Opportunity for Developing Highly Active and Durable Bifunctional Air Electrodes for Reversible Protonic Ceramic Cells, Adv. Energy Mater., 2021, 11, 2101899.
46. R. A. De Souza and J. A. Kilner, Oxygen transport in La_1-xSr_xMn_1-yCo_yO_3±δ perovskites: Part I. Oxygen tracer diffusion, Solid State Ionics, 1998, 106, 175–187.
47. J. Maier, Mass Transport in the Presence of Internal Defect Reactions - Concept of Conservative Ensembles: I, Chemical Diffusion in Pure Compounds, J. Am. Ceram. Soc., 1993, 76, 1212–1217.
48. K. D. Kreuer, E. Schönherr and J. Maier, Proton and oxygen diffusion in BaCeO, based compounds: A combined thermal gravimetric analysis and conductivity study, Solid State Ionics, 1994, 701, 278–284.
49. K.-D. Kreuer, A. Fuchs and J. Maier, H/D isotope effect of proton conductivity and proton conduction mechanism in oxides, Solid State Ionics, 1995, 77, 157–162.
50. K. D. Kreuer, T. Dippel, Y. M. Baikov and J. Maier, Water solubility, proton and oxygen diffusion in acceptor doped BaCeO₃: A single crystal analysis, Solid State Ionics, 1996, 86, 613–620.
51. K. D. Kreuer, S. Adams, W. Münch, A. Fuchs, U. Klock and J. Maier, Proton conducting alkaline earth zirconates and titanates for high drain electrochemical applications, Solid State Ionics, 2001, 145, 295–306.
52. M. E. Bjorketun, P. G. Sundell and G. Wahnstrom, Effect of acceptor dopants on the proton mobility in BaZrO₃: A density functional investigation, Phys. Rev. B, 2007, 76, 054307.
53. Y. Yamazaki, F. Blanc, Y. Okuyama, L. Buannic, J. C. Lucio-Vega, C. P. Grey and S. M. Haile, Proton trapping in yttrium-doped barium zirconate, Nat. Mater., 2013, 12, 647–651.
54. M. F. Hoedl, A. Chesnokov, D. Gryaznov, R. Merkle, E. A. Kotomin and J. Maier, Proton migration barriers in BaFeO_3-δ - insights from DFT calculations, J. Mater. Chem. A, 2023, 11, 6336–6348.
55. X. Wang, W. Li, C. Zhou, M. Xu, Z. Hu, C. W. Pao, W. Zhou and Z. Shao, Enhanced proton concentration and favorable hydration for protonic ceramic fuel cells cathode, ACS Appl. Mater. Interfaces, 2023, 15, 1339–1347.
56. W. Zipprich and H.-D. Wiemhöfer, Measurement of ionic conductivity in mixed conducting compounds using solid electrolyte microcontacts, Solid State Ionics, 2000, 135, 699–707.
57. S. Kim, Y. L. Yang, A. J. Jacobson and B. Abeles, Diffusion and surface exchange coefficients in mixed ionic electronic conducting oxides from the pressure dependence of oxygen permeation, Solid State Ionics, 1998, 106, 189–195.
58. E. Bucher, A. Egger, P. Ried, W. Sitte and P. Holtappels, Oxygen nonstoichiometry and exchange kinetics of Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ, Solid State Ionics, 2008, 179, 1032–1035.
59. Y. Shin, Y.-D. Kim, M. Sanders, S. P. Harvey, M. Walker and R. O'Hayre, Tuning the Co/Fe ratio in BaCo_xFe_0.8−xZr_0.1Y_0.1O_3−δ, a promising triple ionic and electronic conducting oxide, to boost electrolysis and fuel cell performance, J. Mater. Chem. A, 2022, 10, 24839–24853.
60. R. A. De Souza, Oxygen Diffusion in SrTiO₃ and Related Perovskite Oxides, Adv. Funct. Mater., 2015, 25, 6326–6342.
61. J. H. Duffy, Y. Meng, H. W. Abernathy and K. S. Brinkman, Surface and Bulk Oxygen Kinetics of BaCo_0.4Fe_0.4Zr_0.2-xY_xO_3-δ Triple Conducting Electrode Materials, Membranes, 2021, 11, 766.
62. H. Bae, B. Singh, L. Mathur, J. H. Joo and S.-J. Song, Defect Structure, Transport Properties, and Chemical Expansion in Ba_0.95La_0.05FeO_3–δ, J. Electrochem. Soc., 2021, 168, 034511.
63. F. M. Draber, J. R. Denninger, P. C. Müller, I. K. Sommerfeld and M. Martin, The Impact of Nanoscale Percolation in Yttrium-Doped BaZrO₃ on the Oxygen Ion and Proton Conductivities: A Density Functional Theory and Kinetic Monte Carlo Study, Adv. Energy Sustainability Res., 2022, 3, 2200007.
64. J. H. Duffy, N. Birkner, C. Kim, R. Jacobs, D. Morgan, S. Sharma, S. T. Misture, E. M. Kelder, H. W. Abernathye and K. S. Brinkman, Structural and thermodynamic analysis of triple conducting ceramic materials BaCo_0.4Fe_0.4Zr_0.2−xY_xO_3−δ, J. Mater. Chem. A, 2025, 13, 10147–10159.
65. D. Han, X. Liu, T. S. Bjørheim and T. Uda, Yttrium-Doped Barium Zirconate-Cerate Solid Solution as Proton Conducting Electrolyte: Why Higher Cerium Concentration Leads to Better Performance for Fuel Cells and Electrolysis Cells, Adv. Energy Mater., 2021, 11, 2003149.
66. Y. A. Mastrikov, R. Merkle, E. Heifets, E. A. Kotomin and J. Maier, Pathways for the oxygen incorporation reaction into mixed conducting perovskites: a DFT-based kinetic analysis for (La,Sr)MnO₃, J. Phys. Chem. C, 2010, 114, 3017–3027.
67. L. Wang, R. Merkle, J. Maier, T. Acartürk and U. Starke, Oxygen tracer diffusion in dense Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ films, Appl. Phys. Lett., 2009, 94, 071908.
68. M. Siebenhofer, C. Riedl, A. Schmid, A. Limbeck, A. K. Opitz, J. Fleig and M. Kubicek, Investigating oxygen reduction pathways on pristine SOFC cathode surfaces by in situ PLD impedance spectroscopy, J. Mater. Chem. A, 2022, 10, 2305–2319.
69. S. B. Adler, Mechanism and kinetics of oxygen reduction on porous La_1-xSr_xCoO_3-δ electrodes, Solid State Ionics, 1998, 111, 125–134.
70. D. Poetzsch, R. Merkle and J. Maier, Proton conductivity in mixed-conducting BSFZ Perovskite from thermogravimetric relaxation, Phys. Chem. Chem. Phys., 2014, 16, 16446–16453.
71. F. S. Baumann, J. Fleig, H.-U. Habermeier and J. Maier, Impedance spectroscopic study on well- defined (La,Sr)(Co,Fe)O_3−δ model electrodes, Solid State Ionics, 2006, 177, 1071–1081.
72. M. Siebenhofer, C. Riedl, A. Schmid, A. Limbeck, A. K. Opitz, J. Fleig and M. Kubicek, Investigating oxygen reduction pathways on pristine SOFC cathode surfaces by in situ PLD impedance spectroscopy, J. Mater. Chem. A, 2021, 10, 2305–2319.
73. D. Poetzsch, R. Merkle and J. Maier, Oxygen exchange kinetics in proton conducting ceramic fuel cells: Effect of electronic leakage current using symmetric cells, J. Power Sources, 2023, 242, 784–789.
74. J. Mizusaki, M. Yoshihiro, S. Yamauchi and K. Fueki, Nonstoichiomentry and defect structure of the perovskite-type oxides La_1-xSr_xFeO_3-δ, J. Solid State Chem., 1985, 58, 257–266.
75. G. Raimondi, F. Giannici, A. Longo, R. Merkle, A. Chiara, M. F. Hoedl, A. Martorana and J. Maier, X-ray Spectroscopy of (Ba,Sr,La)(Fe,Zn,Y)O_3−δ Identifies Structural and Electronic Features Favoring Proton Uptake, Chem. Mater., 2020, 32, 8502–8511.
76. R. Hancke, Z. Li and R. Haugsrud, The Kinetics of Hydration and H/D Isotope Exchange of Y-Doped Barium Cerate and Lanthanum Tungstate Studied by Transient Thermogravimetry, J. Electrochem. Soc., 2013, 160, F757–F763.
77. H. Mehrer, Diffusion in Solids, Springer ( 2007).
78. Bruker AXS Topas V5, General Profile and Structure Analysis Software for Powder Diffraction Data, User's manual, Karlsruhe, Germany ( 2014).
79. R. A. Young, The Rietveld Method, Oxford university press ( 1993).

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta03014e

---