Open Access Article
Open Access ArticleSupervised machine learning for predicting drug release from acetalated dextran nanofibers†
Ryan N.
Woodring
 a,
Elizabeth G.
Gurysh
a,
Elizabeth G.
Gurysh
 a,
Tanvi
Pulipaka
a,
Kevin E.
Shilling
a,
Rebeca T.
Stiepel
a,
Tanvi
Pulipaka
a,
Kevin E.
Shilling
a,
Rebeca T.
Stiepel
 a,
Erik S.
Pena
a,
Erik S.
Pena
 b,
Eric M.
Bachelder
b,
Eric M.
Bachelder
 a and
Kristy M.
Ainslie
a and
Kristy M.
Ainslie
 *abc
*abc
aDivision of Pharmacoengineering and Molecular Pharmaceutics, Eshelman School of Pharmacy, University of North Carolina at, Chapel Hill, USA. E-mail: ainsliek@email.unc.edu
bJoint Department of Biomedical Engineering, University of North Carolina at Chapel Hill and North Carolina State University, USA
cDepartment of Microbiology and Immunology, UNC School of Medicine, University of North Carolina, Chapel Hill, NC, USA
First published on 28th March 2025
Abstract
Electrospun drug-loaded polymeric nanofibers can improve the efficacy of therapeutics for a variety of implications. By design, these biomaterial platforms can enhance drug bioavailability and site-specific delivery while reducing off-target toxicities when compared to other conventional formulations. By incorporating biocompatible and biodegradable polymers with tunable degradation rates, such as acetalated dextran (Ace-DEX), drug-loaded nanofibers can enhance the safety and efficacy of treatment regimens while improving patient compliance through controlled release. Despite these benefits, clinical translation of electrospun formulations is challenged by labor-intensive in vitro studies for ensuring that release kinetics are accurately characterized and reproducible. In this study, we report a novel workflow for assessing in vitro drug release from Ace-DEX nanofibers using machine learning (ML) and develop a predictive model to streamline this rate-limiting step. The developed Gaussian process regression (GPR) model was trained, validated, and optimized using in vitro release profiles from thirty electrospun Ace-DEX scaffolds. The results of GPR model simulations reveal consistent performance across all Ace-DEX formulations considered in this study while also demonstrating a drug-agnostic approach to predict fractional drug release over time.
Introduction
Drug-loaded electrospun nanofibers have shown great promise as a therapeutic platform for various biomedical applications, ranging from cancer therapy to tissue regeneration.1–4 With tunable fabrication methods and nanofiber features, electrospinning can efficiently encapsulate a wide range of therapies and generate flexible, fibrous materials to optimize drug delivery. By design, these electrospun scaffolds exhibit a high surface area to volume ratio which promotes continuous and sustained delivery of loaded cargo through a variety of mechanisms.5 Furthermore, biocompatible and biodegradable polymers such as polyanhydrides can be used to fabricate these drug-loaded biomaterials which can afford safe and efficacious drug release as the nanofibers degrade under physiological conditions.6 For such reasons, electrospinning has been widely explored and proven to be successful in the preclinical setting; however, many of these nanofiber formulations have yet to see the FDA-approval status which highlights the critical need for tools aimed towards bridging the gap between preclinical investigation and clinical application.7With a vast range of applicable electrospinning methods, compatible materials with associated physicochemical properties, and physiological mechanisms governing drug release, drug-loaded electrospun nanofibers require a thorough and laborious preclinical assessment to ensure clinical translation. Optimizing design parameters is critical to early-stage development and can significantly influence the kinetics of drug release. The choice of polymer, for example, must exhibit drug and solvent compatibility when undergoing monoaxial electrospinning, which can directly influence the dynamics of drug release from the formed fibers.8 Furthermore, many FDA-approved polymers degrade via hydrolysis of ester bonds or enzymatic cleavage with unique rates, offering tunability for drug release when formulated as carriers.9,10 These mechanisms can influence not only the persistence of drug-loaded fibers in vivo, but also the release rate of the loaded therapeutic cargo. Understanding the features and mechanisms most influential to drug release from such biomaterials is critical to ensure that the optimum drug release rates are well characterized.
A biocompatible and biodegradable polymer widely investigated for drug delivery applications is acetalated dextran (Ace-DEX).11–14 Deriving from dextran, Ace-DEX degradation rates can be tightly controlled during synthesis where longer reaction times yield a higher relative cyclic to acyclic acetal coverage (%CAC) and, thus, a more hydrophobic polymer. Based on %CAC, degradation via hydrolysis can persist on the order of days to months, offering unique tunable release profiles of encapsulated drugs.15 Our group has previously reported the therapeutic potential of drug-loaded electrospun Ace-DEX nanofibers for localized, interstitial treatment of glioblastoma. When paclitaxel was co-delivered with two different %CAC formulations (low %CAC = fast and high %CAC = slow) of Ace-DEX scaffolds (Ace-PTX), the tumor burden and overall survival of mice with orthotopic U87 tumors were significantly improved.16 The unique rates of degradation and PTX release of the Ace-PTX scaffolds afforded optimum localized delivery of therapeutic cargo, which outperformed PTX-loaded scaffolds electrospun with either FDA-approved polylactic acid or Ace-DEX %CAC scaffold alone.
Another advantage of Ace-DEX over other polymer systems, such as chitosan or polyglycolic acid, is that it can be used to electrospin drug-loaded nanofibers using a wide variety of organic solvent systems.17,18 This offers feasibility for encapsulating drugs with different physicochemical properties in monoaxial electrospinning. By tuning the volatility of the solvent system, for example, drug distribution within the fibers as well as the initial rate of release can be controlled.19 Furthermore, we previously have shown how different drugs loaded into Ace-DEX nanofibers can afford drug-specific release rates, even when electrospun with the same %CAC of the polymer, weight drug loading (%wt/wt), and solvent system.20 Although these differences in release demonstrate how electrospun Ace-DEX nanofibers offer therapeutic versatility, these formulation-specific trends are poorly understood and require laborious in vitro assessment to afford a desired rate of drug release.
Our group has recently reported drug-specific properties that influence rates of drug release from Ace-DEX spherical particles through the development of a mathematical and mechanistic model.21 Termed the ‘diffusion-erosion model’, constitutive equations governing both drug diffusion and polymer surface erosion of drug-loaded Ace-DEX nanoparticles (NPs) were applied to derive an empirical interpretation for predicting drug release. Observed drug release data were fit to this mechanistic model and used to quantify the effective diffusion coefficient (D) of encapsulated drugs – a critical parameter describing the rate of drug movement through a polymer matrix. Additionally, a neural network, or a machine learning (ML) model useful for identifying inter-parametric trends and computing predictions, was optimized to predict D of drugs through varying %CAC Ace-DEX NPs based on various physicochemical properties. The model revealed that the drug's polar surface area was the most influential parameter for determining formulation-specific D and can be used in tandem with the diffusion-erosion model for predicting drug release. The results from this study demonstrate how drug diffusion and Ace-DEX degradation via NP surface erosion influence the kinetics of release and change with respect to the encapsulated drug. Furthermore, incorporating ML with the diffusion-erosion model enhanced the model's predictive power for informing future formulations while also strengthening the preclinical assessment of the relevant polymeric biomaterial.
Our previous work with Ace-DEX NPs takes a model-based approach for predicting drug release with well-defined assumptions for the finite spherical platform. When applying this framework to bulk biomaterials like electrospun nanofibers, this approach becomes less intuitive. This difference can be due to several factors including complex geometry, nanofiber organization, and in vitro conditions for assessing drug release from drug-loaded fibers. For example, electrospun nanofibers often take a cylindrical or ribbon-like shape with lengths significantly longer than observed diameters and are organized into a nonwoven matrix.22 This morphology results in a bulk material with varying thickness and porosity, influencing the dynamic behaviors under physiological conditions. Additionally, these materials do not suspend freely in solution like the NP formulations which can result in spatiotemporal differences in the dynamics of drug release characterized in vitro (e.g. polymer degradation and drug diffusion). To this end, an alternative data-driven approach for model development can be adapted to discern inter-parametric dependencies and predict drug release from systems that lack pre-defined mathematical assumptions and equations.23 Various ML frameworks (e.g., linear regressions, decision trees, support vector machines, and Gaussian processes) offer distinct mechanisms for making regression-based predictions by capturing complex relationships between input parameters and the target response.24 Bannigan et al., for example, used a gradient-boosted ML algorithm and drug release data to build a model for predicting time-dependent drug release from polymeric long-acting injectables.25 Their work identified a ML model that adequately predicts drug release based on formulation parameters with the most influential features being the drug and polymer molecular weight. Buozo et al. used a similar data-driven approach for characterizing vitamin E sphingomyelin nanosystems (VSNs).26 Their work not only demonstrated reliability for predicting VSN kinetics for drug release but also revealed formulation parameters that influence the drug-loading capacity, colloidal stability, and biocompatibility – all of which are critical to support the clinical translation of drug delivery vehicles.
Although limited, there recently has been an increase in research involving ML and the fabrication of electrospun polymeric nanofibers.27 Many of these studies have identified fabrication parameters that can be used to predict the fiber morphology and diameter via ML simulations.28,29 However, there is a void in drug delivery research that exploits ML for predicting drug release from polymeric nanofibers. In this work, we aimed to pioneer this space and develop a ML model that can reliably predict drug release from electrospun Ace-DEX nanofiber scaffolds. Through the ML framework described herein, we explore critical features that influence the release rates for small-molecule drugs encapsulated in electrospun Ace-DEX nanofibers. The resulting model was trained, validated, and refined using in vitro release data obtained in-house and demonstrates reliable predictability for a variety of formulations. Furthermore, the model was used to predict protein release from coaxial electrospun Ace-DEX scaffolds demonstrating flexibility and specificity for Ace-DEX formulations. This study highlights future considerations for fabricating drug-loaded scaffolds with Ace-DEX and supports initiatives that aim to improve the clinical translation of electrospun platforms via ML.
Experimental
Synthesis and characterization of acetalated dextran (Ace-DEX)
Various formulations of Ace-DEX were prepared similarly to previous descriptions.12,16,19,20 In brief, 450–650 kDa dextran from Leuconostoc spp. (Sigma) was first lyophilized and dissolved in anhydrous dimethyl sulfoxide (DMSO, Sigma). Pyridinium p-toluenesulfonate (Sigma) was added as an acid catalyst before starting the reaction with 2-ethoxypropene (Matrix Scientific) under anhydrous conditions. To obtain Ace-DEX with various degradation rates, the reaction time was varied for each batch of polymer and quenched with triethylamine (TEA, Sigma) upon completion. A liquid–liquid extraction vessel and a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) ratio of ethyl acetate and Milli-Q® water were used to isolate and purify the synthesized Ace-DEX into a separate organic phase. The solvent was then removed via rotary evaporation before re-constituting the dried polymer in ethanol (Fisher). Solubilized Ace-DEX was precipitated in basic water (0.04% TEA in Milli-Q® water) dropwise, vacuum filtered, lyophilized, and stored at −20 °C until use. Spectral analysis of the proton nuclear magnetic resonance (1H-NMR, Varian Inova 400 MHz) validated the polymer identity and determined the relative cyclic acetal coverage (%CAC) which governs the Ace-DEX degradation rate. See Fig. S1† for an example 1H-NMR spectrum of Ace-DEX.
1 (v/v) ratio of ethyl acetate and Milli-Q® water were used to isolate and purify the synthesized Ace-DEX into a separate organic phase. The solvent was then removed via rotary evaporation before re-constituting the dried polymer in ethanol (Fisher). Solubilized Ace-DEX was precipitated in basic water (0.04% TEA in Milli-Q® water) dropwise, vacuum filtered, lyophilized, and stored at −20 °C until use. Spectral analysis of the proton nuclear magnetic resonance (1H-NMR, Varian Inova 400 MHz) validated the polymer identity and determined the relative cyclic acetal coverage (%CAC) which governs the Ace-DEX degradation rate. See Fig. S1† for an example 1H-NMR spectrum of Ace-DEX.
Monoaxial electrospinning drug-loaded Ace-DEX scaffolds: fabrication and characterization
All electrospun Ace-DEX scaffolds were prepared in an organic solvent (solvent A or solvent B). For scaffolds made in solvent A, hexafluoro-2-propanol (HFIP)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-butanol [60
1-butanol [60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, v/v] with 1% TEA, an Ace-DEX concentration of 200 mg mL−1 was used. For scaffolds made in solvent B, dichloromethane
40, v/v] with 1% TEA, an Ace-DEX concentration of 200 mg mL−1 was used. For scaffolds made in solvent B, dichloromethane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HFIP
HFIP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-butanol [30
1-butanol [30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, v/v/v], an Ace-DEX concentration of 300 mg mL−1 was used. For drug-loaded scaffolds, single agent drugs were added in solution with theoretical weight loadings of 5%, 10%, 20%, or 30% (wt/wt). The drugs encapsulated in Ace-DEX scaffolds and used for model development included paclitaxel, everolimus, doxorubicin hydrochloride, erlotinib, and trametinib (PTX, EVR, DXR, ERL, and TRM – LC Laboratories), resiquimod (RESI, Accel Pharmtech), ribociclib (RBC, Tocris Bioscience), and sorafenib (SFN, Biosynth Carbosynth). The solvent used for drug-loaded scaffolds was determined by whichever provided optimum solubility and stability of the combined Ace-DEX and drug solution.
40, v/v/v], an Ace-DEX concentration of 300 mg mL−1 was used. For drug-loaded scaffolds, single agent drugs were added in solution with theoretical weight loadings of 5%, 10%, 20%, or 30% (wt/wt). The drugs encapsulated in Ace-DEX scaffolds and used for model development included paclitaxel, everolimus, doxorubicin hydrochloride, erlotinib, and trametinib (PTX, EVR, DXR, ERL, and TRM – LC Laboratories), resiquimod (RESI, Accel Pharmtech), ribociclib (RBC, Tocris Bioscience), and sorafenib (SFN, Biosynth Carbosynth). The solvent used for drug-loaded scaffolds was determined by whichever provided optimum solubility and stability of the combined Ace-DEX and drug solution.
With a blunt 21 G needle, the prepared Ace-DEX solution was loaded into a glass Hamilton syringe and positioned opposite from a collection plate. A voltage differential of −7.5 kV (at the collection plate) and +7.5 kV (at the syringe needle) was applied over a 13 cm working distance. The solution was ejected from the syringe at a constant flow rate of 1 mL h−1 and formed solid, randomly aligned Ace-DEX fibers at the collection plate. The fiber morphology was assessed via scanning electron microscopy (SEM, Hitachi S-4700 Cold Cathode Field Emission) at 2 kV on a palladium sputter-coated stub. The fiber diameter (Fd) was measured using ImageJ software. All measurements were reported as an average ± standard deviation of (n ≥ 30) recorded measurements. Scaffolds were stored at −20 °C until use.
For drug-loaded scaffolds, the experimental drug loading (%Load, wt/wt) was determined in vitro using drug-specific analytical methods and quantified with a drug-matched standard curve using eqn (1).
 | (1) |
PTX and EVR loaded scaffolds were dissolved in acetonitrile at 1 mg mL−1 and assessed for drug content via high performance liquid chromatography (HPLC). A flow rate of 1 mL min−1 of the eluent (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v, acetonitrile
1 v/v, acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water) through an Aquasil C18 column (4.5 × 150 mm) was used to detect the content of PTX (227 nm, 1.9 min retention) and EVR (278 nm, 3.9 min retention). For scaffolds loaded with RESI, DXR, RBC, ERL, SFN, and TRM, the samples were dissolved at 1 mg mL−1 in DMSO and assessed for the drug content via absorbance at 260 nm, 480 nm, 350 nm, 330 nm, 304 nm, and 340 nm, respectively.
water) through an Aquasil C18 column (4.5 × 150 mm) was used to detect the content of PTX (227 nm, 1.9 min retention) and EVR (278 nm, 3.9 min retention). For scaffolds loaded with RESI, DXR, RBC, ERL, SFN, and TRM, the samples were dissolved at 1 mg mL−1 in DMSO and assessed for the drug content via absorbance at 260 nm, 480 nm, 350 nm, 330 nm, 304 nm, and 340 nm, respectively.
Coaxial electrospinning bovine serum albumin-loaded Ace-DEX scaffolds
Bovine serum albumin (BSA, Sigma) was suspended at 30 mg mL−1 in water with 5% glycerol (v/v, Sigma) for the core solution. 51.6% CAC Ace-DEX was prepared in a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 ethyl acetate
30 ethyl acetate![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) butanol solution at 200 mg mL−1 for the polymeric shell solution. Both the core and shell solutions were loaded into separate glass Hamilton syringes with a custom coaxial needle (Rame-Hart), which merges the core and shell solutions at the needle tip. The core and shell solutions were ejected at flow rates of 0.3 mL h−1 and 1 mL h−1, respectively, with a working distance of 13 cm and a voltage differential of ±7.5 kV. Coaxial electrospun fibers were characterized for surface morphology and fiber diameter via SEM and ImageJ measurements (n = 30). The %Load of BSA was determined via fluorescamine (Sigma) with replicate scaffold samples dissolved at 1 mg mL−1 in DMSO, diluted in PBS, and quantified with a BSA standard curve.
butanol solution at 200 mg mL−1 for the polymeric shell solution. Both the core and shell solutions were loaded into separate glass Hamilton syringes with a custom coaxial needle (Rame-Hart), which merges the core and shell solutions at the needle tip. The core and shell solutions were ejected at flow rates of 0.3 mL h−1 and 1 mL h−1, respectively, with a working distance of 13 cm and a voltage differential of ±7.5 kV. Coaxial electrospun fibers were characterized for surface morphology and fiber diameter via SEM and ImageJ measurements (n = 30). The %Load of BSA was determined via fluorescamine (Sigma) with replicate scaffold samples dissolved at 1 mg mL−1 in DMSO, diluted in PBS, and quantified with a BSA standard curve.
In vitro degradation and drug release
The degradation and drug release rates of Ace-DEX scaffolds were assessed in vitro. Briefly, 0.6–1.2 mg scaffold samples were first suspended in phosphate buffered saline (PBS pH 7.4, Corning) at 1 mg mL−1 and added to a shaker plate (37 °C). Incubated scaffolds were agitated for specified time intervals before assessing mass loss and drug release. Upon completion, the samples were removed from PBS, washed with basic water, lyophilized, and reweighed. The scaffold mass loss was obtained using ESI eqn (1).† The drug content remaining in the scaffold at each time point was determined as previously described above. To determine the observed fractional drug release at each time, F(t), eqn (2) was used where Ct is the concentration of the drug retained in the scaffold at time t, and C0 is the empirically measured drug-loading concentration at time 0.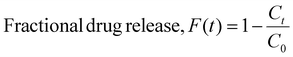 | (2) |
Machine-learning: model development
All observed drug release data and input parameters for model development are included in ESI 1.† Drug release profiles, F(t), for thirty unique drug-loaded Ace-DEX scaffolds were included in this study. For each scaffold, four drug-specific parameters including molecular weight (MW), partition coefficient (LogP), polar surface area (PSA), and pKa reported in the literature correspond to the drug encapsulated in each scaffold (Table S1†). Scaffold-specific parameters, including %CAC of Ace-DEX, % drug loading (%Load, drug wt/Ace-DEX wt), fiber diameter (Fd), and time (in days) were also included for a total of 8 input parameters for predicting F(t). A random 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 partition was applied to the 929 observations within the full data set; 80% for training and 20% for testing within the model developed (ESI 2 and 3†). The Regression Learner application within MATLAB R2024a software was used to simultaneously train 28 models available within the machine learning library using the training data set and a k-fold cross-validation of 10. Feature importance was assigned via −log(p) of a regression F-test. Each model was evaluated for performance following model simulations with the 20% testing data. This process was repeated following the incremental removal of lower-ranked parameters for optimizing the model.
20 partition was applied to the 929 observations within the full data set; 80% for training and 20% for testing within the model developed (ESI 2 and 3†). The Regression Learner application within MATLAB R2024a software was used to simultaneously train 28 models available within the machine learning library using the training data set and a k-fold cross-validation of 10. Feature importance was assigned via −log(p) of a regression F-test. Each model was evaluated for performance following model simulations with the 20% testing data. This process was repeated following the incremental removal of lower-ranked parameters for optimizing the model.
Metrics for model comparison and optimization
To evaluate and compare the performance of all simulated models, metrics associated with error and goodness of fit were used as criteria. Models that minimized mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE) as well as maximized R2 values were considered better performing. The following equations were used to quantify the performance metrics, where n is the total number of observations for the given data, Fi is the observed fractional release for the ith observation, FPi is the associated prediction, and![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) is the average observed fractional release (eqn (3)–(6)). Testing and training performance metrics were pooled for each model type to discern the best performing ML algorithm.
is the average observed fractional release (eqn (3)–(6)). Testing and training performance metrics were pooled for each model type to discern the best performing ML algorithm.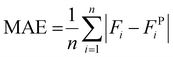 | (3) |
 | (4) |
 | (5) |
 | (6) |
Model hyperparameter optimization and simulations
The Gaussian process regression (GPR) model kernel function was set as an isotropic zero Matérn 5/2 to balance noise variation and time-dependency (ESI eqn (2)†).30 Other hyperparameters, including the noise standard deviation (σ), signal standard deviation (σf), and length scale (σl), were automatically determined by maximizing the log marginal likelihood of the gradient-based optimizer embedded in the Regression Learner application. The optimized GPR model was extracted from the application as a function used for making future predictions (ESI 7†).GPR model predictions were conducted for a total of 929 in vitro observations. To ensure that model performance was consistent for each drug, the error associated with GPR predictions and the corresponding in vitro observations were pooled for scaffolds encapsulating the same drug. GPR simulations were also conducted for each scaffold with n = 100 time points between zero and the maximum time observed in vitro. The performance metrics between GPR simulations and average fractional release observed in vitro (from technical replicates) were determined using eqn (3)–(6). Since the GPR model is a probabilistic regression algorithm, predictions are reported with an associated standard deviation (ϕi). The 90% confidence interval (90% CI) was determined for each prediction using eqn (7):
| 90%CI = FiP ± 1.67·ϕi | (7) |
For comparison of GPR model simulations to classically used empirical models for describing drug release kinetics, five different models were used to capture time-dependent release for the thirty scaffolds included in this study (ESI Table S2†). Constants for each model were determined by linear transformation of the equations describing fractional release (if not already linear) and linear least-squares regression. Simulations using each model with derived constants were conducted for n = 100 time points between zero and the maximum time observed in vitro. Performance metrics for each model simulation were measured between the average of technical replicates in vitro and the predicted drug released. For comparing model predictability across Ace-DEX formulations, performance metrics for all 30 scaffolds were pooled.
Feature SHapley Additive exPlanations (SHAP) and Spearman correlation assessment
The SHAP assessment was conducted on the 929 GPR model predictions using the ‘shapley’ function in MATLAB R2024a. The predictors, or the four parameters associated with the optimized GPR model, were ranked according to the absolute mean Shapley value (SV). Linear interpolation of GPR simulations was used to determine the time associated with the specified release including F(t) = 0.1 (time0.1), 0.25 (time0.25), and 0.5 (time0.5). Spearman's Pearson correlations between %CAC, %Load, Fd, and three interpolated time points (time0.1, time0.25, and time0.5) were performed in MATLAB using the ‘corr’ function.Coding, statistical analysis, and figure rendering
Model development and performance assessment were performed using MATLAB R2024a. All statistical analyses were performed using GraphPad Prism with paired or unpaired t-tests. Figures were made using BioRender, GraphPad Prism, and MATLAB R2024a. Supplemental files include all data assessed in this study with MATLAB code availability in ESI S7.†Results and discussion
Drug-loaded Ace-DEX nanofibers exhibit unique molecular and physicochemical properties considered for model development and predicting the fraction of drug released over time
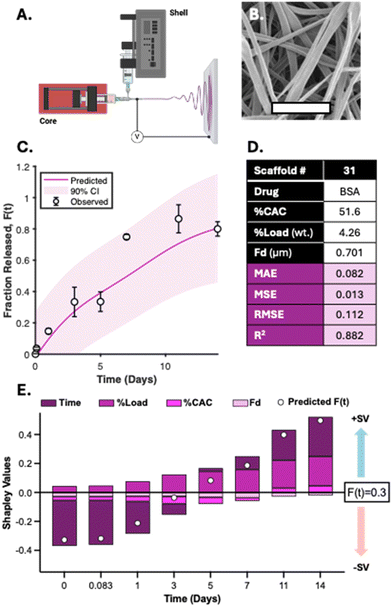
To develop a machine-learning (ML) model for drug release from Ace-DEX nanofibers, the in vitro drug release data from 30 electrospun scaffolds encapsulating one of eight small molecule drugs was included in this workflow (Fig. 1A). All scaffolds were electrospun monoaxially and are identified using an associated ID# (Fig. 1B). For developing a data-driven model to predict the fraction of drug released over time, all in vitro drug release studies were performed for each of the 30 scaffolds, with replicate samples at each time point, and resulting in a combined total of 929 fractional drug release observations (eqn (1) and Table S1†). | ||
| Fig. 1 Drug-loaded electrospun acetalated dextran scaffolds included for machine learning. (A) Table of eight small molecule drugs characterized for release for the prospective study. Scaffolds encapsulating each drug are indicated by the respective range of scaffold ID#s. (B) Schematic of monoaxial electrospinning used for fabricating each of the 30 scaffolds. (C) Heatmap of zeta (Z)-scores for the parameters associated with the 30 scaffolds including four drug-specific parameters and three scaffold-specific parameters separated by a dashed line (see Table S1† for a comprehensive summary). | ||
Apart from time, both drug-specific and Ace-DEX formulation-specific properties can influence drug release kinetics from biodegradable polymeric formulations, and thus we sought to identify and define these critical features as additional parameters for model interpretation.21 Four drug-specific parameters including molecular weight (MW), partition coefficient (LogP), polar surface area (PSA), and pKa were defined for each observation and were assigned according to the encapsulated drug characterized in the scaffold release study (Fig. 1C). Scaffold-specific properties including the cyclic acetal coverage (%CAC) of Ace-DEX and the characterized weight loading of the drug within each scaffold (%Load) were also defined since these properties can alter the degradation kinetics of the electrospun fibers.20 As is evident from SEM images, these scaffolds also encompass a range of measured fiber diameters (Fd) which is another unique feature for each scaffold and included as a scaffold-specific parameter (Fig. S2†). Lastly, Time (in days) was considered a scaffold-specific parameter since this property is critical to both in vitro assessment and determining a time-dependent model for fractional drug release within the observed data. While all other parameters are held constant for each scaffold, Time is the only dynamic property and dependent feature for predicting the kinetics of drug release. Additionally, the time points chosen for assessing drug release are influenced by the %CAC used since higher %CAC is associated with slower degradation rates (Fig. S3†). In total, eight parameters including four drug-specific and four scaffold-specific parameters were considered in this ML framework. All scaffold data used in developing this model including time-matched fractional drug release can be found in ESI 1.†
Drug-specific parameters are the least important features to model performance
Using the Regression Learner application in MATLAB R2024a, 28 ML models belonging to eight unique classes (Fig. 2A) were simulated simultaneously with a randomly partitioned training subset (80%) and validated with a testing subset (20%) of the 929 in vitro observations (ESI 2 and 3†). In MATLAB, the ‘cvpartition’ function was used to generate the training/testing data and ensured that observations from each scaffold are represented in each subset of data (ESI Fig. S4†). The Regression Learner platform was useful for automating data pre-assessment for ML, including standardization and evaluating parameter importance, while applying these considerations to the models available within the library.31 First, all eight parameters were considered for each of the trained models, and statistical F-tests were performed to determine the feature importance score (IS) for the training data (Fig. 2B). Coinciding with the assumed time-dependency, Time had the highest IS for the training data with an IS of 177.63. Other scaffold-specific features, including %CAC, Fd, and %Load followed in IS ranking. The drug-specific properties, PSA, MW, Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, and pKa, had the lowest ISs for the training data. A similar trend was observed for the entire data set where scaffold-specific properties ranked higher in importance than drug-specific properties via the F-test and IS ranking. This result validates that the training data used for model development reflects similar feature variance and relative importance seen within the entire data set.
P, and pKa, had the lowest ISs for the training data. A similar trend was observed for the entire data set where scaffold-specific properties ranked higher in importance than drug-specific properties via the F-test and IS ranking. This result validates that the training data used for model development reflects similar feature variance and relative importance seen within the entire data set.
 | ||
Fig. 2 Machine learning model development. (A) Workflow for using machine learning (ML) to develop a predictive model of drug release from Ace-DEX scaffolds. Parameters are first defined for each of the 929 observations followed by an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 randomized split of the data used for training and testing ML models. The 28 ML models assessed are grouped by model type # (see Table S2† for a comprehensive summary). Once training and testing results reveal the best performing model type, model-associated hyperparameters are tuned for optimizing the model structure. The final model is then evaluated via Shapley additive explanations (SHAP) and predictive performance using unseen data. (B) Results from statistical F-tests and feature importance ranking within the cumulative 929 data set (All Data), the 80% training data, and 20% testing data. The Y-axis shows the eight parameters included in the initial training and testing of ML models and ranked from top to bottom according to ‘All Data’ importance scores. (C and D) Error metrics including mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE) for the training and testing results for each model (indicated by individual points) pooled with respect to model type # (as indicated in A). (C) Metrics for eight parameter simulations and (D) metrics following parameter optimization and removal of the four lowest ranking features (as indicated in B). (E) Goodness of fit as an R2 metric for the four parameter model simulations. **p < 0.01 using a two-tailed, unpaired t-test between the top two performing model types by means of pooled training and testing metrics (shown as colored bars with ±standard deviation). Black/pink bars indicate the best performing model type (#8-Gaussian process regression). 20 randomized split of the data used for training and testing ML models. The 28 ML models assessed are grouped by model type # (see Table S2† for a comprehensive summary). Once training and testing results reveal the best performing model type, model-associated hyperparameters are tuned for optimizing the model structure. The final model is then evaluated via Shapley additive explanations (SHAP) and predictive performance using unseen data. (B) Results from statistical F-tests and feature importance ranking within the cumulative 929 data set (All Data), the 80% training data, and 20% testing data. The Y-axis shows the eight parameters included in the initial training and testing of ML models and ranked from top to bottom according to ‘All Data’ importance scores. (C and D) Error metrics including mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE) for the training and testing results for each model (indicated by individual points) pooled with respect to model type # (as indicated in A). (C) Metrics for eight parameter simulations and (D) metrics following parameter optimization and removal of the four lowest ranking features (as indicated in B). (E) Goodness of fit as an R2 metric for the four parameter model simulations. **p < 0.01 using a two-tailed, unpaired t-test between the top two performing model types by means of pooled training and testing metrics (shown as colored bars with ±standard deviation). Black/pink bars indicate the best performing model type (#8-Gaussian process regression). | ||
The model type selected for further evaluation was determined by comparing the error metrics and goodness-of-fit measures obtained during training with 10-fold cross-validation, as well as the performance results from testing each model on the 20% subset of data that was initially excluded. Out of the eight types of models, all four of the models belonging to the Gaussian process regression (GPR, #8) type had the lowest combined (training + testing) average error including root mean squared error (RMSE), mean squared error (MSE), mean absolute error (MAE), and the highest average R2 when considering all eight parameters for model development (Fig. 2C, Table S2†).
To avoid developing a model that overfits the data with excessive or redundant parameters as criteria, an important ML step of parameter optimization ensures that the final model is simplified and flexible for making future predictions.32 The lowest ranked parameters, according to the importance score, were incrementally removed from model training and testing to evaluate the influence of these parameters on model performance.
Consistent with 8-parameter simulations, each subsequent simulation identified the GPR model (#8) as best performing by RMSE, MSE, MAE, and R2 (ESI Fig. S5†). Surprisingly, the performance of GPR models remained largely unaffected by the removal of the four lower-ranked and drug-specific parameters. However, this removal resulted in a statistically significant performance difference between the GPR model and the next best-performing model, the neural network (#7), reinforcing the suitability of GPR as a robust framework for future development (Fig. 2D and E, p < 0.05). Furthermore, neural networks are commonly associated with overfitting issues when applied to smaller data sets and are more applicable to models with a large number of parameters.33 These challenges oftentimes afford more computationally complex algorithms and limit the predictive performance when applied to excluded, or unseen, data.34 Since all four GPR models performed consistently and are more applicable to smaller data sets, the GPR model type was the chosen ML framework for a predictive drug release model.35,36
The optimal number of parameters included in the GPR model was determined by identifying the simulation at which performance was compromised (i.e., increase in error and decrease in R2). Once the fifth lowest ranked parameter, Fd, was removed from training and testing the GPR models, there was a statistically significant increase in RMSE and, consequently, a reduction in model performance (Fig. 3A and B) (p < 0.05). To balance parameter reduction for avoiding redundancy while prioritizing adequate performance, the 4-parameter GPR model, which excludes all four drug-specific parameters, was selected for further development.
 | ||
| Fig. 3 Parameter optimization. (A) Table of simulations indicated by the number of parameters included. Parameters removed incrementally according to importance score ranking (as in Fig. 2B). Respective colors correspond to (B) average root mean squared error of pooled training and testing results of the Gaussian process regression (GPR) models. Error bars are ±standard deviation. ***p < 0.001 by two-tailed, paired t-test between means. (C) Spearman rank correlation matrix for the parameters included for all 30 scaffolds. Time0.25 is the time for F(t) = 0.25. Cells labeled and colored by correlation value as indicated in the legend. | ||
Additionally, inter-parametric assessment via Spearman correlation validated the exclusion of lower-ranked parameters by observing strong, monotonic correlations among drug-specific properties (Fig. 3C). For example, LogP and PSA both strongly correlate with MW, indicating that removing two of these parameters can offer reduced noise and the computational burden they may add to the model. Furthermore, MW and PSA both have an inverse correlation with Fd, a scaffold-specific parameter retained in the chosen framework. This suggests that drug-specific parameters may influence model behavior indirectly, without the need for explicit interpretation.
Although physicochemical drug properties can influence diffusion and other kinetic behaviors, they may play a less significant role in ML models when compared to formulation-specific parameters. Bannigan et al. demonstrated this by showing that during the optimization of a ML model for drug release from polymeric formulations, most drug-specific parameters had limited influence.25 In their refined 15-parameter model, three of the five drug-related features contributed minimally to performance, and another—number of heteroatoms—was excluded entirely. Similarly, in our model, removing all drug-specific properties resulted in robust performance across the datasets, reduced overfitting and redundancy, and ultimately improved generalizability for future applications.
The optimized GPR model predicts drug release data with minimal error and holds true for drug-specific release profiles from Ace-DEX scaffolds
Supervised GPR models consider the probabilistic distribution of outputs (or targets) conditioned on predictors and use kernel-based covariance functions to inform continuous predictions with quantified uncertainty. Optimizing GPR function hyperparameters provides another opportunity to avoid overfitting and refine the performance of the ML model. This step includes selecting the basis function, which describes the mean, or center, for the Gaussian distribution of outputs. Bayesian optimization of the model revealed a basis function of zero as the best fit and is a common assumption used for model simplification.37 Additionally, the kernel function, or relationship between adjacent inputs within the Gaussian space, can be tuned to control model flexibility and influence predictions. Defined by a mathematical equation, the kernel function captures the covariance between predictors and outputs which can be optimized by defining the function structure and associated hyperparameters.35,38 To ensure that the model balances smooth, continuous drug release with flexibility, an isotropic Matérn 5/2 kernel was selected as the kernel function (ESI eqn (2)†).39 The length-scale (σL), or distance over which inputs are correlated, and the signal standard deviation (σF), or amplitude of variance, were automatically determined from the training data set by maximizing the log-marginal likelihood (Table 1). Furthermore, the isotropic kernel ensures consistent length scales for mitigating feature-specific bias. This optimized model provides not only a smooth and continuous interpretation of drug release kinetics but also ensures flexibility for interpreting scaffold-specific parameters and making future predictions.| Hyperparameter/performance metric | Specification/value |
|---|---|
| Basis function | Zero |
| Kernel function | Isotropic Matérn 5/2 |
| Sigma (σ) | 0.091 |
| Length scale (σL) | 0.734 |
| Signal standard deviation (σF) | 0.545 |
| k-Fold Validation | 10 |
| MAE (train) [test] | (0.071) [0.069] |
| MSE (train) [test] | (0.010) [0.009] |
| RMSE (train) [test] | (0.102) [0.096] |
| R squared (train) [test] | (0.901) [0.904] |
The optimized GPR model was applied to the entire data and assessed for goodness-of-fit and error between the predicted and observed fractional release (F(t)) from in vitro studies (eqn (3)–(6)). Across all 929 observations, the GPR model achieved an R2 value of 0.931, indicating that 93.1% of the fractional drug release variance is captured by the model with only 6.90% of variance left unexplained (Fig. 4A). Assessment of error metrics between GPR predictions and in vitro observations also demonstrates good performance of the optimized model. The residual error was symmetrically distributed across time and the associated predictions indicate that the model avoids systematic bias (Fig. 4B and C). This result was consistent for both training and testing results along with the residual error accrued for each of the other three parameters (ESI Fig. S6†). On average, the predictions for all observations deviated by 5.80% of the total scale (MAE = 0.058), and the low MSE = 0.007 indicates that the model handled outliers effectively. Furthermore, an RMSE of 0.0843 demonstrates that the prediction errors are minimal, occupying only 8.43% of the total fractional drug release range (F(t)Max = 1.0). These results validate an appropriate kernel function and hyperparameters were used to achieve a balance between predictive precision and smoothness.40
To discern if model performance varied with respect to the encapsulated drug, the error associated with the GPR model predictions for each drug-specific subset of release data was determined (Fig. S7A and B†). Interestingly, there were some notable differences in MAE and MSE when predictions were grouped by drug type (Fig. S7C and D†). Predictions for doxorubicin hydrochloride (DXR), paclitaxel (PTX), ribociclib (RBC), and sorafenib (SFN) all had MAEs and MSEs significantly different from the combined (“ALL”) data. Moreover, DXR, RBC, and SFN scaffolds had high associated standard deviations for averaged errors which can be attributed to the high degree of noise discerned from in vitro quantification methods (ESI 1†). Additionally, the number of predictions varied significantly across drug-specific formulations as the data included at the time of this study was constrained to the availability of in vitro data.
To reduce the effect of noise introduced from in vitro replicates, a new data set was generated for assessing GPR model performance by averaging the in vitro fractional drug release replicates corresponding to the same time point (ESI 5†). These “Avg” data were applied to the GPR model function and assessed for performance as previously described. Unsurprisingly, the model demonstrated good performance across all 276 unique observations and achieved an improved R2 value of 0.968 (Fig. 4D). The MAE, MSE, and RMSE were also improved to 0.034, 0.003, and 0.056, respectively (Fig. 4E and F). When assessing the error associated with drug-specific predictions, the MAE, MSE, and RMSE were similarly reduced for each drug. Although the mean errors and RMSEs of DXR, everolimus (EVR), RBC, and SFN predictions were greater than that of the combined predictions (“Avg ALL”), the observed deviation from Avg ALL was reduced. The worst performing drug according to error metrics, DXR, achieved an MAE, MSE, and RMSE of 0.071, 0.010, and 0.101 respectively. These metrics, however, are comparable to those observed from training the GPR model and indicate that all drug-specific predictions perform within the projected error determined in model development (Table 1).
To ensure that these trends hold true for drugs encapsulated in similar Ace-DEX scaffold formulations, the GPR model performances for scaffolds 2 and 7 were compared (Fig. 5A and B). These scaffolds were electrospun with 50% CAC Ace-DEX and a theoretical weight loading of 5% (wt/wt) doxorubicin hydrochloride (DXR) and everolimus (EVR), respectively. Of note, the theoretical loading for each scaffold differs from the experimental loading (%Load parameter) as the encapsulation efficiency via electrospinning is not determined until after fabrication. Similarly, the average fiber diameters are comparable but were not predetermined as this would necessitate alteration to electrospinning parameters (i.e. polymer molecular weight, viscosity, and voltage differential) and tuned for each scaffold.41 Although differences between input parameters were marginal, the GPR model was able to perform consistently across two different drug-loaded scaffolds (Fig. 5C). This not only demonstrates high sensitivity for scaffold-specific parameters but also supports the rationale for removing the less important features, or drug-specific properties, and developing a simplified predictive model.
To further assess model performance with respect to scaffold formulation (e.g., Ace-DEX %CAC, drug loading, and fiber diameter), we performed GPR model simulations for paclitaxel (PTX)-loaded scaffolds across a range of scaffold-specific parameters. Scaffolds 10, 11, and 18 were all formulated with a theoretical loading of 10% wt/wt PTX and 45%, 50%, or 61% CAC Ace-DEX, respectively (Fig. 6A–C). Despite having comparable PTX %Load, in vitro drug release studies show unique drug release profiles for these scaffolds corresponding to %CAC (Fig. 6D and E). When applying the GPR model, the simulations fit the observed in vitro data for each scaffold with an RMSE ≤ 0.051. Additionally, model performance between PTX-loaded scaffolds with comparable %CACs and fiber diameters but different drug %Loads were compared via GPR simulations of scaffolds 11 and 14 (Fig. 6D–F). Scaffold 14 is a 52% CAC Ace-DEX scaffold with a theoretical loading of 20% (wt/wt) PTX (Fig. 6G). As expected, the model fits the data with minimal error (RMSE = 0.035) across all time points revealing that increasing the weight loading of the drug does not negatively affect the model performance (Fig. 6H).
The GPR model captures complex drug release kinetics and outperforms conventional models across Ace-DEX formulations
The developed GPR model can adequately predict drug release over time for Ace-DEX scaffolds based only on scaffold-specific parameters. However, a common limitation of ML model-based solutions is the lack of an intuitive interpretation of inter-parametric interactions for deducing kinetic behavior.42 Many conventional models, including our group's previously developed diffusion-erosion model, use mathematical logic to characterize time-dependent release mechanisms including drug diffusion and polymer degradation resulting in an empirical system of equations.21,43 Of note, the diffusion-erosion model could not be adapted to the electrospun scaffolds because it was derived specifically for Ace-DEX nanoparticles. For comparing the performance of the GPR model predictions to that of conventional models for predicting drug release, the fractional drug release data were fit to five additional models classically used for capturing these kinetics from polymeric systems including zero-order, first-order, Higuchi, Korsmeyer–Peppas, and Kopcha models (Table S3†).Across all time points assessed in vitro, the performance metrics for GPR predictions and the conventional model simulations were compared for two different formulations, scaffolds 22 and 26, to demonstrate model applicability (Fig. 7A and J). Scaffold 22 was formulated with 49% CAC Ace-DEX and a 8.40% wt loading of resiquimod (RESI, Fig. 7B). Scaffold 26 was formulated with 51.6% CAC Ace-DEX and a wt loading of 7.82% ribociclib (RBC) (Fig. 7K). These parameters, as well as the average fiber diameter (1.805 ± 0.408 μm and 2.186 ± 0.063 μm for scaffolds 22 and 26, respectively), were used to simulate the time-associated GPR predictions. Empirical equations, solved via in vitro drug release data, were used to simulate the conventional models.
For scaffolds 22 and 26, the GPR model had the lowest MSE and MAE and the highest R squared when compared to all other models. The RMSEs for scaffolds 22 and 26 (0.044 and 0.040, respectively) were also lower than the RMSEs for each of the five conventional models (Table S4†). For scaffold 22, the first-order model was the only conventional type with significantly higher absolute and squared error for all time points assessed in vitro (Fig. 7C, D and F). Additionally, the zero-order model was identified as the next-best performing model when comparing all model performance metrics (Fig. 7C, D and E). These results for scaffold 22, however, were not shared for scaffold 26. Following the GPR in performance metrics was the first-order model, the only model without significantly higher squared error when compared to the GPR predictions for scaffold 26 (Fig. 7M and O). Furthermore, the zero-order model had the greatest MAE, MSE and RMSE when comparing metrics across all model simulations (Fig. 7L, M and Table S4†). These conflicting results show how conventional models for drug release have limited flexibility and poor reliability in predicting drug release when applying release from different Ace-DEX formulations. The developed GPR model, in contrast, provides improved accuracy for predicting drug release across different drug-loaded formulations and considers only the most relevant parameters of the Ace-DEX nanofibers.
To compare the performance of the GPR model across all thirty scaffolds relative to that of the conventional models, the summary metrics including MAE, RMSE, and R2 of each simulation were pooled with respect to the applied model (Fig. 8A–C). As shown, the GPR model had the smallest combined average MAE and RMSE and the greatest R squared. The differences between all performance means for the GPR model versus each conventional model were statistically significant, proving that a more reliable fit was captured by the developed ML model than the classical derivations. Additionally, the GPR model interprets input parameters pertaining to scaffold formulation rather than fitting a trend to the observed data. This allows for enhanced model flexibility and overall specificity for the kinetics of electrospun Ace-DEX scaffolds, which exhibit unique release rates based on the developed formulation.
SHAP analysis of selected parameters reveals temporal changes in feature importance to drug release kinetics
We next sought to investigate how the GPR model performs to arrive at these accurate predictions. SHAP (Shapley additive explanation) analysis is common in ML to assess how model predictions are interpreted from the defined input parameters, or predictors, of the developed algorithm.44,45 In this assessment, each feature associated with a prediction is assigned a Shapley value (SV), which quantifies the directional shift that the feature has on the model's prediction relative to the average of all predictions, or the baseline. For the developed GPR model, a swarm chart of predictor SVs for all 929 observations can be used to visualize how the model interprets each of the four parameters across the relative feature scale (Fig. 9A). On the y-axis, the features are organized vertically by global feature importance where a larger absolute mean Shapley value indicates a higher overall influence that the feature has on the prediction. In line with the feature importance scores determined via the F-test (Fig. 2B), Time was the most influential predictor followed by %CAC, %Load, and Fd (Fig. 9B).SHAP assessment is also useful for discerning how a parameter influence changes with respect to the feature value.46 The shading of Shapley value points for each feature in the swarm chart shows the input value interpreted for each observation in the data. The value of time has an overall positive correlation with SVs where lower times (shown in blue) tend to have more negative, or lower, SVs whereas longer times (shown in pink) have more positive SVs. The sign of these SVs (±) indicates how the feature contributes to the model's prediction relative to the average prediction, or the baseline (F(t) = 0.303). If lower time values exhibit a negative SV, there will be a negative shift from the mean contributing to the prediction. This result is relatively intuitive for time-dependent models for drug release since one would expect that the release would be lower than the average predicted release at early time points when compared to the release at later time points. Similarly, %CAC has an overall expected influence on model performance but demonstrates a negative correlation with SHAP. A higher %CAC of Ace-DEX results in slower degrading fibers (Fig. S3†), which corresponds to lower SVs. This result shows that observations that have a higher %CAC will tend to have lower predictions than the average prediction for all formulations.
The two predictors that had the lowest spread in Shapley values and the lowest ranking in feature importance by SHAP were %Load and Fd, respectively. These features have a more concentrated distribution of Shapley values around zero with a less defined trend for the low and high predictor values. This is a common limitation of SHAP analysis because it does not clearly illustrate inter-parametric relationships and, instead, assumes that features contribute to the model independently.47 For interpreting how parameters may influence one another and may change with time, Spearman's rank correlation assessment was performed for scaffold-specific parameters along with the GPR model simulation time at which fractional release times of 0.1, 0.25, and 0.5 were predicted (Fig. 9C). For the three interpolated times of fractional release (time0.1, time0.25, and time0.5), there is a consistent monotonic relationship with respect to %CAC, %Load, and Fd. However, Fd was the only parameter to have a negative correlation with time whereas %CAC and %Load had positive correlations. This was interesting to find since %CAC had the opposite relationship discerned from the SHAP assessment. Moreover, there is a negative monotonic correlation between %CAC and Fd (r = −0.444) and a positive correlation between Fd and %Load (r = 0.291), which suggests that an inter-parametric correlation may influence the model predictions.48
Predictive performance of the GPR model for protein release from BSA-loaded Ace-DEX nanofibers
The GPR model considers four scaffold-specific parameters for determining release kinetics and demonstrates a drug-agnostic algorithm for characterizing time-dependent release. Furthermore, we found that the solvent system used to electrospin did not impact the top four most influential features (Time, %CAC, %Load, and Fd) (Fig. S8A†). To validate model sensitivity and drug physicochemical independence, bovine serum albumin (BSA) was encapsulated at 4.8% (wt) loading into a 51.6% CAC Ace-DEX scaffold via coaxial electrospinning (Fig. 10A). This is a common method for encapsulating hydrophilic proteins or peptides in an aqueous core solution and the polymer in an outer, organic phase shell solution.49,50 As many proteins or biological molecules are susceptible to degradation via monoaxial electrospinning (e.g., electrostatic gradients and organic solvent systems), coaxial electrospinning offers improved drug stability and encapsulation for generating protein-loaded nanofibers.51 The resulting fibers had an average fiber diameter of 0.701 ± 0.152 μm and a similar morphology to monoaxial fibers used for model development (Fig. 10B and Fig. S2A†). These input parameters were interpreted to simulate BSA release kinetics using the developed GPR model and assessed for performance. As shown, the resulting performance metrics reveal that adequate predictions were generated by the model simulations (Fig. 10C and D). All observed fractional releases were within the predicted 90% confidence intervals and fit the observed data with an R2 value of 0.875, demonstrating that the model has reliable predictability when applied to Ace-DEX nanofibers encapsulating proteins (ESI S6†).To visualize how each parameter influences the time-dependent GPR predictions for BSA release, SHAP analysis was performed for the eight observations from in vitro studies. Time was found to be the most influential parameter for GPR performance with the highest absolute mean SV. Interestingly, %Load was the second most influential parameter for model performance instead of %CAC found from the F-test and SHAP analysis performed in prior studies. However, the %Load for this scaffold was 4.26% (wt) which was less, but within error, than the average %Load of all thirty scaffolds used for model development (10.0% ± 6.1%). This change in feature importance is common with SHAP assessment since the results capture the feature influence for the local predictions rather than the influence seen across all formulations. Furthermore, %Load is more influential than %CAC when assessing SVs for all scaffolds with a drug weight loading of less than 5%, demonstrating that predictions for BSA release were achieved similarly to drug release from Ace-DEX nanofibers with comparable parameters (Fig. S8B†). In summary, the GPR model demonstrates high specificity for Ace-DEX scaffold formulations, applicability to monoaxial and coaxial formulations, and reliability for predicting the in vitro release of therapeutics ranging from small molecule drugs to therapeutic proteins.
Conclusion
With the growing accessibility of artificial intelligence (AI) and machine learning (ML) technology, there are many opportunities for preclinical researchers to leverage these novel applications and streamline the clinical translation of next-generation therapies.52 In particular, in vitro drug release characterization from electrospun polymeric nanofibers – a major hurdle for the FDA-approval of electrospun formulations – can benefit from AI/ML tools and mitigate the laborious nature of preclinical assessment. Furthermore, AI/ML applications can help unveil critical mechanisms driving release kinetics while informing future electrospinning methods to ensure that drug release from polymeric nanofibers is reliable and reproducible for therapeutic indications.53 In this study, we demonstrate how these powerful tools can innovate the future of drug-loaded nanofibers through the development of a supervised ML model for predicting time-dependent drug release from electrospun scaffolds.Specifically, our group has previously shown that the use of acetalated dextran (Ace-DEX) in electrospun nanofibers can improve glioblastoma treatment by offering controlled drug release rates.16,19 However, achieving the desired release kinetics requires extensive trial and error with lengthy in vitro characterization methods. To streamline this process and leverage this platform for future formulations, a machine learning (ML) model using a Gaussian Process Regression (GPR) algorithm was developed to predict time-dependent drug release from Ace-DEX nanofibers. The model identified scaffold-specific parameters as the most influential, demonstrating high predictive performance with minimal errors.
The refined and developed GPR model does not rely solely on in vitro studies but uses a Gaussian distribution of functions with provided confidence intervals to predictions, aligning with FDA recommendations for drug release from semi-solid formulations.54 This model outperformed conventional models in assessing drug release profiles for various formulations, proving sound reliability. Furthermore, SHAP analysis provided insights into the model's operation, highlighting Time and %CAC as key parameters. The model's predictive power was further validated by simulating protein release from Ace-DEX scaffolds, showing reliable and versatile performance specific to electrospun Ace-DEX nanofibers.
In conclusion, this work provides insight into how AI/ML strategies can innovate the future of drug development research. Although the number of observations interpreted in this framework is relatively small for the field of ML, the developed GPR algorithm demonstrates adequate performance for predicting drug release from electrospun Ace-DEX nanofibers. Applications of this ML framework could also be adapted to include other polymer systems that have a defined, tunable feature—like Ace-DEX %CAC—which influences degradation behavior and, thus, drug release. In the future, further investigation into inter-parametric dependencies and the GPR predictive performance will expand our understanding of the mechanisms contributing to drug release from Ace-DEX scaffolds with the ultimate goal of streamlining the clinical translation of this promising therapeutic platform.
Abbreviations
| Ace-DEX | Acetalated dextran |
| CAC | Cyclic acetal coverage |
| BSA | Bovine serum albumin |
| DXR | Doxorubicin hydrochloride |
| ERL | Erlotinib |
| EVR | Everolimus |
| PTX | Paclitaxel |
| RESI | Resiquimod |
| RBC | Ribociclib |
| SFN | Sorafenib |
| TRM | Trametinib |
| F d | Fiber diameter |
| Load | Drug weight load |
| SEM | Scanning electron microscopy |
| F(t) | Fractional drug released at time (t) |
| ML | Machine learning |
| MAE | Mean absolute error |
| MSE | Mean squared error |
| RMSE | Root mean squared error |
| GPR | Gaussian process regression |
| CI | Confidence interval |
| IS | Importance score |
| SV | Shapley value |
Author contributions
EGG, EMB, and KMA acquired funding for project support. RNW, EGG, TP, RTS, EMB, and KMA were involved in project conceptualization, methodology, and interpretation. RNW, EGG, KES, and ESP were involved in scaffold fabrication, characterization, and in vitro evaluation as part of curating data. RNW, TP, and RTS contributed to ML model development and validation. RNW, EGG, and TP contributed to writing the first draft of the manuscript with EGG, RTS, EMB, and KMA providing revisions. EMB and KMA provided administrative support and oversight throughout. All authors reviewed the manuscript prior to submission.Data availability
All data are available in the ESI.Conflicts of interest
There are no conflicts of interest to disclose.Acknowledgements
This work was funded internally by the National Institutes of Health (NIH R01CA257009). We are thankful for the resources made available at the Eshelman School of Pharmacy at UNC, Chapel Hill, NC including the NMR core and Chapel Hill Analytical and Nanofabrication Laboratory (CHANL).References
- A. Luraghi, F. Peri and L. Moroni, Electrospinning for drug delivery applications: A review, J. Controlled Release, 2021, 334, 463–484 CrossRef CAS PubMed.
- X. Feng, J. Li, X. Zhang, T. Liu, J. Ding and X. Chen, Electrospun polymer micro/nanofibers as pharmaceutical repositories for healthcare, J. Controlled Release, 2019, 302, 19–41 CrossRef CAS PubMed.
- M. Rahmati, D. K. Mills, A. M. Urbanska, M. R. Saeb, J. R. Venugopal, S. Ramakrishna and M. Mozafari, Electrospinning for tissue engineering applications, Prog. Mater. Sci., 2021, 117, 100721 CrossRef CAS.
- A. Partovi, M. Khedrinia, S. Arjmand and S. O. Ranaei Siadat, Electrospun nanofibrous wound dressings with enhanced efficiency through carbon quantum dots and citrate incorporation, Sci. Rep., 2024, 14(1), 19256 CrossRef CAS PubMed.
- J. Xing, M. Zhang, X. Liu, C. Wang, N. Xu and D. Xing, Multi-material electrospinning: from methods to biomedical applications, Mater. Today Bio, 2023, 21, 100710 CrossRef CAS PubMed.
- Q. Su, A. Zhao, H. Peng and S. Zhou, Preparation and characterization of biodegradable electrospun polyanhydride nano/microfibers, J. Nanosci. Nanotechnol., 2010, 10(10), 6369–6375 CrossRef CAS PubMed.
- M. K. Gaydhane, C. S. Sharma and S. Majumdar, Electrospun nanofibres in drug delivery: advances in controlled release strategies, RSC Adv., 2023, 13(11), 7312–7328 RSC.
- S. Farhaj, B. R. Conway and M. U. Ghori, Nanofibres in Drug Delivery Applications, Fibers, 2023, 11(2), 21 CrossRef CAS.
- N. Gupta, C. Sarkar and S. Saha, Biodegradable Polymers—Carriers for Drug Delivery, in Biodegradable Polymers and Their Emerging Applications, ed. S. Saha and C. Sarkar, Springer Nature Singapore, Singapore, 2023, pp. 149–168 Search PubMed.
- M. V. Sushma, A. Kadam, D. Kumar and I. Mutreja, Biodegradable Polymers, in Biomaterials and Biopolymers, ed. A. Domb, B. Mizrahi and S. Farah, Springer International Publishing, Cham, 2023, pp. 33–54 Search PubMed.
- G. L. Williamson, D. D. Middleton, K. M. Ainslie and E. M. Bachelder, Acetalated dextran: a novel delivery platform for particle-based vaccines, Expert Opin. Drug Delivery, 2025, 22(1), 1–5 CrossRef CAS PubMed.
- K. J. Kauffman, C. Do, S. Sharma, M. D. Gallovic, E. M. Bachelder and K. M. Ainslie, Synthesis and characterization of acetalated dextran polymer and microparticles with ethanol as a degradation product, ACS Appl. Mater. Interfaces, 2012, 4(8), 4149–4155 CrossRef CAS PubMed.
- N. Chen, M. M. Johnson, M. A. Collier, M. D. Gallovic, E. M. Bachelder and K. M. Ainslie, Tunable degradation of acetalated dextran microparticles enables controlled vaccine adjuvant and antigen delivery to modulate adaptive immune responses, J. Controlled Release, 2018, 273, 147–159 CrossRef CAS PubMed.
- D. A. Hendy, B. T. Johnson-Weaver, C. J. Batty, E. M. Bachelder, S. N. Abraham, H. F. Staats and K. M. Ainslie, Delivery of small molecule mast cell activators for West Nile Virus vaccination using acetalated dextran microparticles, Int. J. Pharm., 2023, 634, 122658 CrossRef CAS PubMed.
- N. Chen, M. A. Collier, M. D. Gallovic, G. C. Collins, C. C. Sanchez, E. Q. Fernandes, E. M. Bachelder and K. M. Ainslie, Degradation of acetalated dextran can be broadly tuned based on cyclic acetal coverage and molecular weight, Int. J. Pharm., 2016, 512(1), 147–157 CrossRef CAS PubMed.
- E. G. Graham-Gurysh, K. M. Moore, A. N. Schorzman, T. Lee, W. C. Zamboni, S. D. Hingtgen, E. M. Bachelder and K. M. Ainslie, Tumor Responsive and Tunable Polymeric Platform for Optimized Delivery of Paclitaxel to Treat Glioblastoma, ACS Appl. Mater. Interfaces, 2020, 12(17), 19345–19356 CrossRef CAS PubMed.
- M. T. Alam, N. Parvez and P. K. Sharma, FDA-Approved Natural Polymers for Fast Dissolving Tablets, J. Pharm., 2014, 2014, 952970 Search PubMed.
- S. Wang, F. Fontana, M.-A. Shahbazi and H. A. Santos, Acetalated dextran based nano- and microparticles: synthesis, fabrication, and therapeutic applications, Chem. Commun., 2021, 57(35), 4212–4229 RSC.
- E. Graham-Gurysh, K. M. Moore, A. B. Satterlee, K. T. Sheets, F. C. Lin, E. M. Bachelder, C. R. Miller, S. D. Hingtgen and K. M. Ainslie, Sustained Delivery of Doxorubicin via Acetalated Dextran Scaffold Prevents Glioblastoma Recurrence after Surgical Resection, Mol. Pharm., 2018, 15(3), 1309–1318 CrossRef CAS PubMed.
- E. G. Graham-Gurysh, A. B. Murthy, K. M. Moore, S. D. Hingtgen, E. M. Bachelder and K. M. Ainslie, Synergistic drug combinations for a precision medicine approach to interstitial glioblastoma therapy, J. Controlled Release, 2020, 323, 282–292 CrossRef CAS PubMed.
- R. T. Stiepel, E. S. Pena, S. A. Ehrenzeller, M. D. Gallovic, L. M. Lifshits, C. J. Genito, E. M. Bachelder and K. M. Ainslie, A predictive mechanistic model of drug release from surface eroding polymeric nanoparticles, J. Controlled Release, 2022, 351, 883–895 CrossRef CAS PubMed.
- A. Al-Abduljabbar and I. Farooq, Electrospun Polymer Nanofibers: Processing, Properties, and Applications, Polymers, 2022, 15(1), 65 CrossRef PubMed.
- S. Kolluri, J. Lin, R. Liu, Y. Zhang and W. Zhang, Machine Learning and Artificial Intelligence in Pharmaceutical Research and Development: a Review, AAPS J., 2022, 24(1), 19 CrossRef PubMed.
- J. Fitzsimons, A. Al Ali, M. Osborne and S. Roberts, A General Framework for Fair Regression, Entropy, 2019, 21(8), 741 CrossRef PubMed.
- P. Bannigan, Z. Bao, R. J. Hickman, M. Aldeghi, F. Häse, A. Aspuru-Guzik and C. Allen, Machine learning models to accelerate the design of polymeric long-acting injectables, Nat. Commun., 2023, 14(1), 35 CrossRef CAS PubMed.
- B. L. Bouzo, M. Calvelo, M. Martín-Pastor, R. García-Fandiño and M. de la Fuente, In vitro–in silico modeling approach to rationally designed simple and versatile drug delivery systems, J. Phys. Chem. B, 2020, 124(28), 5788–5800 CrossRef CAS PubMed.
- B. Subeshan, A. Atayo and E. Asmatulu, Machine learning applications for electrospun nanofibers: a review, J. Mater. Sci., 2024, 59(31), 14095–14140 CrossRef CAS.
- S. Sukpancharoen, T. Wijakmatee, T. Katongtung, K. Ponhan, N. Rattanachoung and S. Khojitmate, Data-driven prediction of electrospun nanofiber diameter using machine learning: A comprehensive study and web-based tool development, Results Eng., 2024, 24, 102826 CrossRef CAS.
- S. Sarma, A. K. Verma, S. S. Phadkule and M. Saharia, Towards an interpretable machine learning model for electrospun polyvinylidene fluoride (PVDF) fiber properties, Comput. Mater. Sci., 2022, 213, 111661 CrossRef CAS.
- S. Manzhos and M. Ihara, Degeneration of kernel regression with Matern kernels into low-order polynomial regression in high dimension, J. Chem. Phys., 2024, 160(2), 021101 CrossRef CAS PubMed.
- I. The MathWorks, MATLAB Regression Learner Application, R2024a, The MathWorks, Inc., Natick, Massachusetts, 2024 Search PubMed.
- I. Guyon and A. Elisseeff, An Introduction of Variable and Feature Selection, J. Mach. Learn. Res., 2003, 3, 1157–1182 Search PubMed.
- M. Kuhn and K. Johnson, Nonlinear Regression Models, in Applied Predictive Modeling, ed. M. Kuhn and K. Johnson, Springer New York, New York, NY, 2013, pp. 141–171 Search PubMed.
- L. K. Vora, A. D. Gholap, K. Jetha, R. R. S. Thakur, H. K. Solanki and V. P. Chavda, Artificial Intelligence in Pharmaceutical Technology and Drug Delivery Design, Pharmaceutics, 2023, 15(7), 1916 CrossRef CAS PubMed.
- P. D. W. Kirk and M. P. H. Stumpf, Gaussian process regression bootstrapping: exploring the effects of uncertainty in time course data, Bioinformatics, 2009, 25(10), 1300–1306 CrossRef CAS PubMed.
- C. E. Rasmussen, Gaussian Processes in Machine Learning, in Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, February 2–14, 2003, Tübingen, Germany, August 4–16, 2003, Revised Lectures, ed. O. Bousquet, U. von Luxburg and G. Rätsch, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 63–71 Search PubMed.
- C. E. Rasmussen and C. K. I. Williams, Model Selection and Adaptation of Hyperparameters, in Gaussian Processes for Machine Learning, The MIT Press, 2005 Search PubMed.
- J. Park, D. Lechevalier, R. Ak, M. Ferguson, K. H. Law, Y. T. Lee and S. Rachuri, Gaussian Process Regression (GPR) Representation in Predictive Model Markup Language (PMML), Smart Sustain. Manuf. Syst., 2017, 1(1), 121–141 CrossRef CAS PubMed.
- P. S. Palar and K. Shimoyama, Efficient global optimization with ensemble and selection of kernel functions for engineering design, Struct. Multidisc. Optim., 2019, 59(1), 93–116 CrossRef.
- M. Kuhn and K. Johnson, Measuring Performance in Regression Models, in Applied Predictive Modeling, ed. M. Kuhn and K. Johnson, Springer New York, New York, NY, 2013, pp. 95–100 Search PubMed.
- K. P. Matabola and R. M. Moutloali, The influence of electrospinning parameters on the morphology and diameter of poly(vinyledene fluoride) nanofibers- effect of sodium chloride, J. Mater. Sci., 2013, 48(16), 5475–5482 CrossRef CAS.
- A. Tursunalieva, D. L. J. Alexander, R. Dunne, J. Li, L. Riera and Y. Zhao, Making Sense of Machine Learning: A Review of Interpretation Techniques and Their Applications, Appl. Sci., 2024, 14(2), 496 CrossRef CAS.
- P. Costa and J. M. Sousa Lobo, Modeling and comparison of dissolution profiles, Eur. J. Pharm. Sci., 2001, 13(2), 123–133 CrossRef CAS PubMed.
- S. M. Lundberg and S.-I. Lee, A Unified Approach to Interpreting Model Predictions, in Neural Information Processing Systems, 2017 Search PubMed.
- F. Prendin, J. Pavan, G. Cappon, S. Del Favero, G. Sparacino and A. Facchinetti, The importance of interpreting machine learning models for blood glucose prediction in diabetes: an analysis using SHAP, Sci. Rep., 2023, 13(1), 16865 CrossRef CAS PubMed.
- S. M. Lundberg, SHAP Dependence Plots: Understanding Feature Influence, https://shap.github.io/shap/notebooks/plots/dependence_plot.html.
- I. E. Kumar, S. Venkatasubramanian, C. Scheidegger and S. Friedler, In Problems with Shapley-value-based explanations as feature importance measures, International conference on machine learning, PMLR, 2020, pp. 5491–5500.
- S. D. Bolboacă and L. Jäntschi, Pearson versus Spearman in Structure-Activity Relationships of Biologically Active Compounds, Leonardo J. Sci., 2006, 5(9), 179–200 Search PubMed.
- D. Han and A. J. Steckl, Coaxial Electrospinning Formation of Complex Polymer Fibers and their Applications, ChemPlusChem, 2019, 84(10), 1453–1497 CrossRef CAS PubMed.
- R. N. Woodring, E. G. Gurysh, E. M. Bachelder and K. M. Ainslie, Drug Delivery Systems for Localized Cancer Combination Therapy, ACS Appl. Bio Mater., 2023, 6(3), 934–950 CrossRef CAS PubMed.
- W. Ji, F. Yang, J. J. J. P. van den Beucken, Z. Bian, M. Fan, Z. Chen and J. A. Jansen, Fibrous scaffolds loaded with protein prepared by blend or coaxial electrospinning, Acta Biomater., 2010, 6(11), 4199–4207 CrossRef CAS PubMed.
- T. A. Meyer, C. Ramirez, M. J. Tamasi and A. J. Gormley, A User's Guide to Machine Learning for Polymeric Biomaterials, ACS Polym. Au, 2023, 3(2), 141–157 CrossRef CAS PubMed.
- A. J. Gormley, Machine learning in drug delivery, J. Controlled Release, 2024, 373, 23–30 CrossRef CAS PubMed.
- Food, U. S.; Drug, A, FDA Guidance for Industry: Nonsterile Semisolid Dosage Forms: Scale-Up and Postapproval Changes: Chemistry, Manufacturing, and Controls, in In Vitro Release Testing and In Vivo Bioequivalence Documentation, FDA, Rockville, MD, 1997 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5bm00259a |
| This journal is © The Royal Society of Chemistry 2025 |