Exploring the trans effect of the NH3 ligand in platinum halide complexes Pt(NH3)ClX2− (X = Cl, Br, I) using cryogenic photoelectron spectroscopy and quantum chemical calculations†
Qixu
Zhao‡
 a,
Jian
Zhang‡
b,
Xueying
Li
a,
Peng
Tang
a,
Fan
Yang
a,
Junyang
Ma
a,
Zhubin
Hu
a,
Haitao
Sun
a,
Jian
Zhang‡
b,
Xueying
Li
a,
Peng
Tang
a,
Fan
Yang
a,
Junyang
Ma
a,
Zhubin
Hu
a,
Haitao
Sun
 a,
Xue-Bin
Wang
a,
Xue-Bin
Wang
 *c,
Zhenrong
Sun
*ad and
Yan
Yang
*c,
Zhenrong
Sun
*ad and
Yan
Yang
 *a
*a
aState Key Laboratory of Precision Spectroscopy, and School of Physics and Electron Sciences, East China Normal University, Shanghai 200241, China. E-mail: yyang@lps.ecnu.edu.cn
bCollege of Chemistry&Chemical Engineering, Donghua University, Shanghai 201620, China
cPhysical Sciences Division, Pacific Northwest National Laboratory, Richland, WA 99352, USA. E-mail: xuebin.wang@pnnl.gov
dCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, Shanxi 030006, China. E-mail: zrsun@phy.ecnu.edu.cn
First published on 8th May 2025
Abstract
Cryogenic anion photoelectron spectroscopy, combined with quantum chemical calculations, was employed to investigate PtClX2−, Pt(NH3)ClX2− (X = Cl, Br, I), and their isomers. Photoelectron spectra recorded at 193 nm, supported by B3LYP-D3(BJ)/aug-cc-pVTZ(-pp) calculations, provided adiabatic (ADEs) and vertical detachment energies (VDEs) with excellent agreement between experimental and theoretical results. Coordination of the NH3 ligand to PtClX2− reduced the electron binding energy, and substantially elongated trans Pt–halogen bonds. Further computational analyses, including natural population analysis (NPA), frontier molecular orbital (FMO) studies, and dissociation energy calculations, all revealed significant changes in charge distributions and stability of trans halogen ligands. The results demonstrated that NH3 coordination notably elevated FMO orbital energies, with the extent of this elevation correlating strongly with the trans halogen's orbital contributions. These findings provide new insights into ligand-induced electronic and structural transformation in platinum halide systems and establish a theoretical foundation for understanding the underlying molecular mechanisms that dictate the activities of platinum-based anticancer drugs.
Introduction
The concept of the ‘trans effect’ was first introduced by Chernyaev in 1926 during his study of Pt(II) square planar complexes, where he observed that coordinated groups in the trans position influence each other within a complex. Today, the trans effect is a well-established phenomenon in ligand substitution reactions of square planar and octahedral transition metal complexes.1–3 It is defined as the influence of a coordinated group on the substitution rate of the ligand trans to itself, affecting the bond length and stability of the trans ligand.3 This phenomenon has found wide applications in fields such as medicinal chemistry and catalysis. For instance, the trans effect plays a pivotal role in the mechanisms of platinum-based anticancer drugs (e.g., cisplatin and oxaliplatin)4–6 and catalytic processes, such as electrocatalytic CO2 reduction using Ru-based catalysts.7,8 In the case of platinum-based anticancer drugs, where the trans effect governs ligand substitution during interaction with DNA bases, the cis-configuration ensures that the opposite ligands of leaving groups are nitrogen-containing groups, such as NH3. The NH3 ligand exerts the trans effect, facilitates ligand dissociation and enhances the drug's activity.A substantial body of research has been conducted on platinum halide complexes with various types of ligands, such as the Zeise's salt9 anions [PtX3(C2H4)]− (X = Cl, Br, I), among others. Utilizing high-resolution anion photoelectron spectroscopy combined with quantum chemical calculations, Hou et al.10,11 found that both the electron binding energy and the interaction energy between the C2H4 ligand and the platinum halide decrease as the halide size increases. They also demonstrated how variations in ligand type influence the evolution of the electronic structure and molecular configuration in Zeise's family complexes. A wealth of research reporting on the physical and chemical properties of platinum halide complexes containing NH3 ligands has also been well documented. For example, Zhang et al.12,13 focused on the vibrational properties of the NH3 ligand in cisplantin. Warneke and Rohdenburg et al.14,15 reported the electron-induced decomposition of cisplatin, demonstrating the NH3 ligand's role as a reducing agent to promote Cl dissociation. Pinter et al.16 studied the trans effect in ammine substitution reactions of trans-TPtCl2NH3 (T = NH3, PH3, CO, and C2H4) using energy decomposition and chemical valence analyses. Despite these efforts, the comprehensive impact of the NH3 ligand's trans effect on the molecular configuration, electronic structure, and stability of halogenated platinum complexes has remained insufficiently explored to date. In addition, gas-phase photoelectron spectroscopy (PES) studies on halogenated platinum anions containing NH3 ligands are notably lacking.
In this work, we employ cryogenic anion cluster photoelectron spectroscopy (CRACPES) and quantum chemical calculations to systematically investigate PtClX2− (X = Cl, Br, I), Pt(NH3)ClX2− (X = Cl, Br, I), and their isomers. These anions provide an ideal model to explore the microscopic effects of the NH3 ligand's trans effect in platinum halide anion complexes. The use of CRACPES enables precise measurements of electronic structures, stabilities, and energetics in the gas phase. The target anions, which cannot be prepared by electrospray ionization (ESI†) source directly, are produced through collision-induced dissociation (CID) in a two-stage ion funnel system.
Our results demonstrate that NH3, as an electron-donating ligand, upon binding to PtClX2−, significantly decreases the electron binding energy (eBE) and elongates the bond lengths between the halogen ligands and the platinum atom, particularly for the trans halogens. Furthermore, natural population analysis (NPA) and frontier molecular orbital (FMO) calculations reveal that the NH3 ligand transports a substantial amount of its electron density along the NH3–Pt-trans-halogen axis and weakens the stability of the trans halogen ligands while elevating FMO energy levels. These findings provide critical insights into the fundamental role of the NH3 ligand in platinum-based anticancer drugs and offer molecular-level guidance for the design of new metal–ligand anticancer therapeutics.
Methods
CRACPES experiments
The experiments were conducted using the CRACPES system, which has been described in detail elsewhere.17,18 KPt(NH3)Cl3 (Shanghai Boer Chemical Reagents) was dissolved in a water/acetonitrile (CH3CN) mixed solvent (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) to prepare a 2 mM sample solution. To generate Pt(NH3)ClX2− (X = Br, I), potassium halides (KBr and KI) were added to aliquots of this solution, facilitating ligand substitution reactions. PtClX2− (X = Cl, Br, I) anions were subsequently prepared via collision-induced dissociation (CID) of parent Pt(NH3)ClX2− (X = Cl, Br, I) anions. The target anions were cooled to 13 K in a two-stage linear ion trap before extraction into a TOF mass spectrometer for mass analysis. Each target anion was mass-selected, collimated, and momentum decelerated before being irradiated with 193 nm laser pulses (ExciStar™ XS 500, Coherent) in the interaction zone. Photodetached electrons were collected using a magnetic-bottle photoelectron spectrometer. The acquired original photoelectron TOF spectra were converted to electron kinetic energy (eKE) spectra and calibrated by the known spectra of I−,19 and MnO4−.20 The final electron binding energy (eBE) spectra were obtained by subtracting the eKE spectra from the detachment photon energy, with an electron energy resolution (ΔE/E) of ∼1.9% (i.e., ∼30 meV for 1.6 eV KE electrons).
4) to prepare a 2 mM sample solution. To generate Pt(NH3)ClX2− (X = Br, I), potassium halides (KBr and KI) were added to aliquots of this solution, facilitating ligand substitution reactions. PtClX2− (X = Cl, Br, I) anions were subsequently prepared via collision-induced dissociation (CID) of parent Pt(NH3)ClX2− (X = Cl, Br, I) anions. The target anions were cooled to 13 K in a two-stage linear ion trap before extraction into a TOF mass spectrometer for mass analysis. Each target anion was mass-selected, collimated, and momentum decelerated before being irradiated with 193 nm laser pulses (ExciStar™ XS 500, Coherent) in the interaction zone. Photodetached electrons were collected using a magnetic-bottle photoelectron spectrometer. The acquired original photoelectron TOF spectra were converted to electron kinetic energy (eKE) spectra and calibrated by the known spectra of I−,19 and MnO4−.20 The final electron binding energy (eBE) spectra were obtained by subtracting the eKE spectra from the detachment photon energy, with an electron energy resolution (ΔE/E) of ∼1.9% (i.e., ∼30 meV for 1.6 eV KE electrons).
Computational methods
The structures of target anions and their corresponding neutral species were optimized using density functional theory (DFT) with the hybrid B3LYP-D3(BJ) exchange–correlation functional,21 which has been widely used in studying Pt-containing complexes with sufficient accuracy.22–24 The aug-cc-pVTZ-pp basis set with an effective core potential (ECP) was used for both Pt and I atoms to account for scalar relativistic effects,25,26 while the aug-cc-pVTZ basis set was used for H, N, Cl, and Br atoms.27,28 Various initial structures with different spin multiplicities for both anionic and neutral species were explored to identify global minima. Vibrational frequency calculations confirmed the absence of imaginary frequencies, ensuring that the optimized structures correspond to true minima. The adiabatic detachment energy (ADE) values were determined as the energy difference between the neutral and anionic species at their respective optimized geometries, including zero-point energy (ZPE) corrections. The vertical detachment energy (VDE) values were calculated as the energy difference between the neutral and anionic species, with the neutral geometry constrained to that of the optimized anion. Excited states of the neutral species were computed using time-dependent DFT (TDDFT)29 at the CAM-B3LYP30/aug-cc-pVTZ(-pp) level of theory. Spin–orbit coupling effects were not considered in these calculations, as these do not qualitatively impact experimental data interpretation.31–33 Since the three-coordinated platinum halide anions exhibit a pronounced trans effect upon NH3 ligand coordination, we employed extended transition state-natural orbitals for chemical valence (ETS-NOCV),34 natural population analysis (NPA), and ionic bonding contributions to investigate how trans effects influence charge redistribution and electronic interactions/transfer. Additionally, dissociation energy and binding energy calculations were performed to assess how the trans effect affects ligand stability at different coordination sites. For Pt(NH3)ClX2− and their isomers, ETS-NOCV analyses were performed using the Multiwfn 3.8 (dev) program.35 In this approach, anions were divided into two fragments: the halogenated platinum anion and the NH3 ligand, enabling a direct examination of how NH3 impacts the electronic distribution of the halogenated platinum moiety. Additionally, NPA charge distributions and dissociation energies were calculated at the B3LYP-D3(BJ)/aug-cc-pVTZ(-pp) level of theory. The binding energies were calculated with corrections for basis set superposition error (BSSE) using the counterpoise method, and zero-point energy (ZPE) corrections derived from vibrational frequency calculations at the B3LYP-D3(BJ)/aug-cc-pVTZ(-pp) level of theory. The ionic contributions of chemical bonds were evaluated using localized molecular orbital methods implemented in the Multiwfn 3.8 (dev) program, and the highest occupied molecular orbitals (HOMOs) and the ETS-NOCV results were visualized using the VMD36 program. All quantum chemical calculations were performed using the Gaussian 16 Rev. C.02,37 and GaussView 6 was used for structure visualization.Results and discussion
Photoelectron spectra of target anions
Fig. 1 presents the cryogenic anion photoelectron spectra of PtClX2− (X = Cl, Br, I) and Pt(NH3)ClX2− (X = Cl, Br, I) recorded under 193 nm laser excitation. The observed spectral features, labelled as X and A–G, correspond to the transitions from the anionic ground state to the neutral ground and excited states upon electron detachment. The VDE is defined as the maximum of the X state in each spectrum, while the ADE is determined by the intersection of the tangent to the rising edge of the X state with the eBE axis, corrected for the instrumental resolution. Based on the experimental data, the ADEs values for PtClX2− and Pt(NH3)ClX2− (X = Cl, Br, I) were determined to be 4.26, 4.23, 4.08, 3.85, 3.79, and 3.96 eV, respectively, while the corresponding VDE values were found to be 4.46, 4.37, 4.23, 4.06, 4.01, and 4.09 eV. Fig. 1 reveals that the coordination of an NH3 ligand to the three-coordinate platinum halide anions results in a notable decrease in the electron binding energy, shifting the overall spectra toward lower eBE values. Additionally, while the spectral features of PtCl3− and Pt(NH3)Cl3− remain largely unchanged, the spectra of Pt(NH3)ClX2− (X = Br, I) exhibit noticeable changes compared to those of PtClX2− (X = Br, I) in the context of spectral broadening and splitting. Notably, in the spectrum of PtClBr2−, the D and E peaks appear to originate from the splitting of a single spectral feature, arising presumably from the copresence of two isomers with distinct halogen coordination geometries in the experiments. This hypothesis will be further examined through theoretical calculations in subsequent sections.Optimized structures, calculated ADEs and VDEs
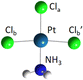
The DFT optimized, lowest-energy structures of PtClX2− and Pt(NH3)ClX2− (X = Cl, Br, I), are summarized in Table 1 (see Fig. S1–S3, ESI† for the details about how to construct the initial structures with different spin multiplicities, and the corresponding optimized neutral molecules). The most stable structures in Table 1 all feature a singlet electronic state with an overall similar platinum trihalide framework, in which one halide at the apex (Xa) is distinct from the other two at the base (Xb, Xb′) that forms a large obtuse Xb–Pt–Xb′ angle (>160°). PtCl3− has two identical Pt–Clb bonds of 2.310 Å, and a slightly shorter Pt–Cla bond at 2.247 Å. Upon coordination of NH3 to PtCl3− from the base, trans- to the apical Cl, all Pt–Cl bonds elongate, with the elongation of the apical Cl nearly twice bigger than the base Cl (0.071 vs. 0.042 Å), while the Clb–Pt–Clb′ angle increases from 166° to 172°. For PtClBr2−, two low-lying isomers are identified with the one featuring Cl at the apex (iso a) being slightly less stable by 0.07 eV compared to the other with the Br on the apical position (iso b). Attaching one NH3 molecule from the base, trans-positioned to the apical halide in PtClBr2− results in two corresponding isomers of Pt(NH3)ClBr2−, in which the coordination of NH3 induces similar geometric changes for the PtClBr2− moiety as described in the PtCl3− case above, i.e., substantially more elongation for the Pt–Xa bond than Pt–Xb with increased Xb–Pt–Xb′ bond angles. Notably, binding NH3 to PtClBr2− reverses the relative stability of the two isomers of PtClBr2− with the iso a of Pt(NH3)ClBr2− featuring a trans-Cl becoming more stable. Similarly, two isomers of PtClI2− are located with iso a featuring an apical Cl lying 0.2 eV higher in energy than iso b. Attaching one NH3 molecule from the base of PtClI2− largely eliminates this relative energy difference and again reverses the energy order with iso a of the ammonium complex become the most stable one, but only by 0.05 eV (Table 1). The same geometric changes brought by NH3 are observed in Pt(NH3)ClI2− as well.| Anions | PtClX2− (singlet) | Pt(NH3)ClX2− (singlet) | ||
|---|---|---|---|---|
| a ΔE represents the energy difference between the isomer structure and the lowest-energy structure. | ||||

|
|
|||
| Pt–Cla | 2.247 | 2.318 | ||
| Pt–Clb | 2.310 | 2.352 | ||
| Pt–Clb′ | 2.310 | 2.352 | ||
| ∠Cla–Pt–Clb | 97 | 94 | ||
| ∠Clb–Pt–Clb′ | 166 | 172 | ||
| Iso a (ΔE = 0.07) | Iso b (ΔE = 0) | Iso a (ΔE = 0) | Iso b (ΔE = 0.03) | |

|

|

|

|
|
| Pt–Cla/b | 2.248 | 2.310 | 2.317 | 2.357 |
| Pt–Bra/b | 2.439 | 2.377 | 2.487 | 2.451 |
| Pt–Brb′ | 2.439 | 2.434 | 2.487 | 2.480 |
| ∠Bra/b–Pt–Cla/b | 98 | 97 | 94 | 94 |
| ∠Bra/b–Pt–Brb′ | 165 | 97 | 172 | 95 |
| Iso a (ΔE = 0.2) | Iso b (ΔE =0) | Iso a (ΔE = 0) | Iso b (ΔE = 0.05) | |
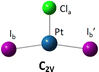
|

|
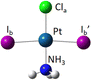
|

|
|
| Pt–Cla/b | 2.251 | 2.315 | 2.317 | 2.367 |
| Pt–Ia/b | 2.610 | 2.548 | 2.666 | 2.625 |
| Pt–Ib’ | 2.610 | 2.595 | 2.668 | 2.647 |
| ∠Ia/b–Pt–Cla/b | 98 | 97 | 94 | 94 |
| ∠Ia/b–Pt–Ib′ | 164 | 97 | 172 | 95 |
Examining the aforementioned optimized structures evidences that the coordination of the NH3 ligand to platinum trihalides leads to an overall elongation of the Pt–halogen bonds. Notably, the bond length of the Pt–Xa, positioned trans to NH3, increases more significantly, showing a clear trans effect, whereas the Pt–Xb bonds adjacent to the NH3 ligand exhibit only minor changes, much less influenced by this interaction. For the mixed ligand platinum trihalides PtClX2− (X = Br, I), iso a in which the sole Cl is at the apex is less favourable than iso b that features the apical Br or I. Binding NH3trans to the apex of PtClX2− preferentially stabilizes more on iso a, rendering iso a the most stable structure for Pt(NH3)ClX2−. Additionally, Fig. S2 (ESI†) presents the optimized structure of the PtCl3− under different spin multiplicities, showing that its D3h-symmetric triplet-state structure is higher in energy by 0.29 eV, compared to its lower-symmetry singlet ground-state configuration. In addition to B3LYP-D3(BJ), we employed CAM-B3LYP and MP2 with the aug-cc-pVTZ(-pp) basis set to optimize the structures of PtClX2− and Pt(NH3)ClX2− (X = Cl, Br, I) and compute their corresponding energies. The optimized geometries from all three methods were in close agreement. However, B3LYP-D3(BJ) provided the best match to the experimental ADE and VDE values, and its results were therefore adopted. Detailed comparisons are provided in Fig. S4 and Table S1 (ESI†).
Table 2 compares the experimental and theoretical ADE and VDE values for PtClX2− and Pt(NH3)ClX2− (X = Cl, Br, I). Excluding the results of iso a of PtClI2− which is 0.2 eV less stable and unlikely contributed to the experiments, an excellent agreement between the experimental and theoretical results is found with the mean absolute errors (MAEs) of 0.096 eV for ADE and 0.106 eV for VDE. Additionally, the excited states of the neutral molecules were calculated using the anionic structures (Table 3) and compared with the corresponding spectra (see the vertical lines in Fig. 1). The simulated TDDFT stick spectra reasonably cover the observed spectral bands, but obvious deviations exist, presumably due to the lack of consideration of multi-reference nature and spin–orbit splitting effects in the calculations.
| Anions | ADE (eV) | VDE (eV) | ||
|---|---|---|---|---|
| Exp.a | Calc. | Exp.a | Calc. | |
| a The experimental uncertainty of ADEs and VDEs is 0.02 eV. | ||||
| PtCl3− | 4.26 | 4.18 | 4.46 | 4.35 |
| Pt(NH3)Cl3− | 3.85 | 3.83 | 4.06 | 4.00 |
| PtClBr2− (iso a) | 4.23 | 4.13 | 4.37 | 4.28 |
| PtClBr2− (iso b) | 4.12 | 4.26 | ||
| Pt(NH3)ClBr2− (iso a) | 3.79 | 3.86 | 4.01 | 4.00 |
| Pt(NH3)ClBr2− (iso b) | 3.84 | 3.98 | ||
| PtClI2− (iso a) | 4.08 | 3.79 | 4.23 | 4.12 |
| PtClI2− (iso b) | 3.99 | 4.10 | ||
| Pt(NH3)ClI2− (iso a) | 3.96 | 3.80 | 4.09 | 3.90 |
| Pt(NH3)ClI2− (iso b) | 3.77 | 3.86 | ||
| Anions | States | VDEs (eV) | |
|---|---|---|---|
| Expt.c | Calc. | ||
| a The isomer a of PtClX2−, or Pt(NH3)ClX2− (X = Br, I). b The isomer b of PtClX2−, or Pt(NH3)ClX2− (X = Br, I). c The experimental uncertainty of VDEs is 0.02 eV. | |||
| PtCl3− | X | 4.46 | 4.35 |
| A | 4.55 | 4.59 | |
| B | 4.87 | 5.06 | |
| C | 5.23 | 5.17 | |
| D | 5.98 | 6.23/6.27 | |
| Pt(NH3)Cl3− | X | 4.06 | 4.00 |
| A | 4.16 | 4.19 | |
| B | 4.35 | 4.26 | |
| C | 4.67 | 4.64 | |
| D | 5.30 | 5.35 | |
| PtClBr2− (iso a, b) | X | 4.37 | 4.28a, 4.26b |
| A | 4.46 | 4.48a, 4.51b | |
| B | 4.77 | 4.97a, 4.93b | |
| C | 5.05 | 5.11a, 5.09b | |
| D | 5.63 | 5.80b | |
| E | 5.75 | 5.77a | |
| Pt(NH3)ClBr2− (Iso a, b) | X | 4.01 | 4.00a, 3.98b |
| A | 4.10 | 4.16a, 4.12b/4.14b | |
| B | 4.34 | 4.23a | |
| C | 4.63 | 4.61a, 4.60b | |
| D | 5.23 | 5.07,1 4.94b | |
| E | 5.72 | 5.64a/5.66a, 5.72b | |
| F | 5.98 | 5.84b | |
| PtClI2− (iso a, b) | X | 4.23 | 4.12a, 4.10b |
| A | 4.29 | 4.30a, 4.27b | |
| B | 4.58 | 4.76a, 4.62b | |
| C | 4.84 | 4.87b | |
| D | 5.17 | 5.10a, 5.09b | |
| E | 5.46 | 5.41a, 5.57b | |
| Pt(NH3)ClI2− (Iso a, b) | X | 4.09 | 3.90a, 3.86b |
| A | 4.14 | 4.30a, 4.19b | |
| B | 4.55 | 4.39a, 4.55b | |
| C | 4.71 | 4.77a/4.79a | |
| D | 4.96 | 4.84b | |
| E | 5.18 | 5.18a | |
| F | 5.36 | 5.27a, 5.48b/5.55b | |
| G | 5.71 | 5.74a, 5.86b | |
Trans effect displayed in charge distribution, MO interaction, and bonding characteristics
To further investigate the trans effect in platinum halide complexes upon NH3 coordination, the NPA charge distributions of the corresponding anions were examined (Fig. 2). In PtCl3−, the central Pt atom carries a positive charge of 0.23, while the apical Cl is at −0.29 and two other Cl ligands at the base possess more negative charges of −0.47. This trend of NPA charges among three Cl atoms can be attributed to that the apical Cl ligand is adjacent to two negatively charged Cl atoms, affording a maximum reduction in electrostatic repulsion. Substituting two base Cl ligands in PtCl3− by two Br or two I generate iso a of PtClBr2− or PtClI2−, respectively, with a structure similar to that of PtCl3−. The amount of negative charges of the base halogens follow their electron negativity, in the order of Cl > Br > I, accompanied by a gradual reduction of the Pt positive charge. Notably, the charge at the apical Cl atom remains largely unchanged and is significantly lower than those at the base ligands. In iso b of PtClBr2−/PtClI2−, the apical Bra/Ia ligand also consistently possesses notable fewer negative charges than the other two halogens at the base. On going from PtCl3− to PtClBr2− and PtClI2−, the positive charge on Pt reduces progressively, and becomes even negative in PtClI2−, following the electron affinities of halogens in the order Cl > Br > I. | ||
| Fig. 2 The natural population analysis (NPA) charge distribution of PtClX2− and Pt(NH3)ClX2− (X = Cl, Br, I) anions, calculated at the B3LYP-D3(BJ)/aug-cc-pVTZ-(pp) level of theory. | ||
Upon NH3 coordination in Pt(NH3)Cl3−, the charges on the two base Cl atoms remain largely unchanged, while the positive charge on the central Pt atom decreases significantly. Concomitantly, the amount of negative charge on the apical Cl atom increases noticeably, and the NH3 ligand itself carries a partial positive charge. The above NPA charge analyses suggest that NH3, as an electron-donating group, transfers its electron density primarily to the central Pt and apical Cl atom. The induced NPA charge distribution change upon coordination of NH3 in Pt(NH3)ClX2− (X = Br, I) closely resembles those observed in the Pt(NH3)Cl3− case. Specifically, the halogen ligand positioned trans to NH3 exhibits a significantly increased negative charge, whereas those at the base remain nearly intact.
To visualize the impact of the trans effect on electron transfer upon NH3 coordination, ETS-NOCV calculations were performed. The results indicate that the NH3 coordination induces electron transfer predominately from NH3 (blue, negative orbital density) to its opposite halogen ligand (green, positive orbital density), while the adjacent ligands remain largely unaffected (Fig. 3). This observation is consistent with the NPA charge distribution analysis, in which the negative charge on the trans halogen ligand substantially increases after NH3 coordination, independent of the halogen type, highlighting the dominate role of the trans effect in this process. Furthermore, the trans effect induced by NH3 coordination significantly impacts the polarity of the trans Pt–halogen bonds. As shown in Fig. 4, the ionic character of the trans Pt–halogen bond increases by more than 16% after NH3 coordination, whereas the ionic character of Pt to the adjacent halogen ligands changes less than 1.5%. Detailed data on the ionic character are provided in Table S1 (ESI†). These results demonstrate the pronounced trans effect brought by coordinating NH3 in platinum trihalides.
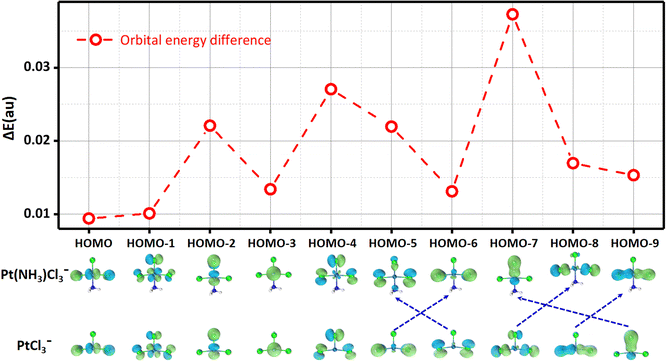
Additionally, the trans effect also influences the frontier molecular orbitals (FMOs) of the system. Taking PtCl3− and Pt(NH3)Cl3− as an example, NH3 coordination does not significantly alter the orbital shapes but upshifts their energies, making them easier to ionize. Molecular orbitals with a higher contribution from the apical Cl atom in PtCl3− (HOMO−2, HOMO−4) exhibit greater energy upshifts upon the trans NH3 binding in Pt(NH3)Cl3−, which can even cause orbital reordering, i.e., HOMO−6 and HOMO−9 of PtCl3− become HOMO−5 and HOMO−7 of Pt(NH3)Cl3−, respectively (Fig. 5). Consistent trends are observed from PtClX2− (X = Br, I) to Pt(NH3)ClX2− (X = Br, I) (Fig. S5–S8, ESI†).
Previous studies have established that cisplatin (cis-Pt(NH3)2Cl2) exhibits potent anticancer activity, whereas its trans analogue transplatin (trans-Pt(NH3)2Cl2) is inactive.38–40 The structural difference between the two lies in the spatial arrangement of the two NH3 ligands: in cisplatin, each NH3 ligand is positioned trans to a Cl atom, while in transplatin, two NH3 ligands (also two Cl) face each other from the opposite side. During the drug activation process inside the cell, the Cl ligand opposite to the NH3 ligand in cisplatin undergoes dissociation. Table 4 presents the theoretical bond dissociation energies (BDE) of Pt–Cla and Pt–Clb. In PtCl3−, the Pt–Cla bond has the shortest bond length of 2.247 Å and highest BDE of 3.61 eV compared to that of Pt–Clb (2.310 Å, 3.29 eV). Upon NH3 combination, the trans effect elongates Pt–Cla in Pt(NH3)Cl3− to 2.318 Å and substantially weakens this bond with BDE = 2.90 eV, rendering it the weakest bond prone to dissociate. More BDE calculations in PtClX2− and Pt(NH3)ClX2− (X = Br, I) (Table S2, ESI†) reveal the same trend, further corroborating the significant role of the trans effect in facilitating the trans halide dissociation by binding a NH3 ligand.
| Channel no. | Dissociation channels | E (eV) | Dissociation channels | E (eV) |
|---|---|---|---|---|
| 1 | PtCl3− → PtCl2 + Cla− | 3.61 | Pt(NH3)Cl3− → Pt(NH3)Cl2 + Cla− | 2.90 |
| 2 | PtCl3− → PtCl2 + Clb− | 3.29 | Pt(NH3)Cl3− → Pt(NH3)Cl2 + Clb− | 2.93 |
| 3 | PtCl3− → PtCl2 + Clb′− | 3.29 | Pt(NH3)Cl3− → Pt(NH3)Cl2 + Clb′− | 2.93 |
Based on these findings, we speculate that in cisplatin and other cis-structured metal-based anticancer drugs, the leaving group ligands are those positioned opposite to the NH3 ligand. In contrast, transplatin has halide ligands all at the adjacent, not trans position to NH3, rendering them less susceptible to this effect. Although the drug activation mechanism occurs in vivo and under liquid-phase environments, our gas-phase study provides valuable insights into the underlying molecular mechanisms that govern such metal-based anticancer drug activities and offers benchmark references for future research aimed at designing therapeutic agents with greater efficacy.
To further investigate the trans effect in tetracoordinated platinum halide complexes with different ligands, we optimized the structures of Zeise's salt analogs, Pt(C2H4)ClX2− (X = Cl, Br, I), using the same level of theory (B3LYP-D3(BJ)/aug-cc-pVTZ(-pp)) (Table S4, ESI†). Structural comparisons between PtClX2− and Pt(C2H4)ClX2− reveal a pronounced trans effect induced by ethylene coordination, characterized by a significant elongation of the Pt–X bond trans to the C2H4 ligand. Taking Pt(NH3)Cl3− and Pt(C2H4)Cl3− as representative examples, we compared their structural parameters and ligand dissociation energies. Upon coordination, the Pt–Cla bond trans to NH3 elongates to 2.318 Å with a corresponding dissociation energy of 2.90 eV. In contrast, in Pt(C2H4)Cl3−, the trans Pt–Cla bond elongates further to 2.338 Å, with a slightly lower dissociation energy of 2.82 eV (Table S5, ESI†). These observations demonstrate that the trans effect exerted by C2H4 is more pronounced than that of NH3, as reflected in both greater bond elongation and reduced bond strength for the trans-positioned halide. To further assess the coordination strength of the two ligands, we calculated the binding energies (BEs) of NH3 and C2H4 with PtClX2− (X = Cl, Br, I), incorporating both basis set superposition error (BSSE) and zero-point energy (ZPE) corrections. The results show that the Pt–C2H4 interaction is consistently stronger than that of Pt–NH3, suggesting that the C2H4-coordinated complexes are thermodynamically more stable. Detailed structural parameters, dissociation energies, and binding energies are provided in Tables S4–S6 (ESI†). Previous work by Hou et al.41 reported significant back-donation from the Pt center to the ethylene ligand in Zeise's salt complexes, which inspired us to investigate whether a similar interaction occurs in Pt(NH3)Cl3−. However, as shown in Fig. S9 (ESI†), an examination of the LUMO to LUMO+10 orbitals in Pt(NH3)Cl3− reveals no evidence of back-donation from Pt to the NH3 ligand, further supporting its role as a classical σ-donor.
Conclusions
In this contribution, we report a combined photoelectron spectroscopic and theoretical study on PtClX2− in comparison to their corresponding NH3 complexes Pt(NH3)ClX2− (X = Cl, Br, I), aimed to provide a molecular level understanding on the widely accepted ‘trans effect’ proposed nearly 100 years ago. Our results show that introducing an electron-donating NH3 ligand leads to a decrease in the eBE of the platinum trihalide anions, and facilitates electron transfer primarily along the H3N–Pt–Xa axis to the trans positioned halogen ligand. Furthermore, our study demonstrates that the most stable apex halide ligand undergoes a substantial reduction in BDE upon NH3 coordination, manifesting an auspicious trans effect. At the electronic state level, this research elucidates how the trans effect influences the physical and chemical properties of platinum trihalide anions when coordinated with NH3. Finally, we also conducted a comparison with the widely utilized Zeise's salt system. The results reveal that PtClX2− (X = Cl, Br, I) coordinated with C2H4 similarly exhibits a pronounced trans effect, and the influence of this effect on the stability of the trans ligand is slightly greater than that observed with the NH3 ligand. These findings provide valuable insights into transition–metal systems and establish a theoretical foundation for understanding platinum-based anticancer drugs, aiding in their design and synthesis.Author contributions
Qixu Zhao: investigation (equal); writing – original draft (equal); formal analysis (equal). Jian Zhang: investigation (equal); writing – original draft (equal); formal analysis (equal). Xueying Li: resources (equal); data curation (supporting). Peng Tang: resources (equal); investigation (supporting). Fan Yang: data curation (lead). Junyang Ma: visualization (equal). Zhubin Hu: software (supportingl); visualization (equal). Haitao Sun: software (lead). Xue-Bin Wang: writing – review and editing (lead); conceptualization (equal). Zhenrong Sun: writing – review and editing (equal); funding acquisition (lead); conceptualization (equal). Yan Yang: writing – review and editing (equal); conceptualization (lead); validation (lead).Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
The work was partly supported by the National Natural Science Foundation of China (No. 92461301, 12034008, and 12250003) and the Program of Introducing Talents of Discipline to Universities 111 Project (B12024). X.-B. W. was supported by the US. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Chemical Science, Geosciences, and Biosciences, Condensed Phase and Interfacial Molecular Science program, FWP 16248.Notes and references
- F. R. Hartley, Chem. Soc. Rev., 1973, 2, 163–179 Search PubMed.
- R. G. Pearson, Inorg. Chem., 1973, 12, 712–713 Search PubMed.
- B. J. Coe and S. J. Glenwright, Coord. Chem. Rev., 2000, 203, 5–80 Search PubMed.
- M. H. Baik, R. A. Friesner and S. J. Lippard, J. Am. Chem. Soc., 2003, 125, 14082–14092 Search PubMed.
- D. V. Deubel, J. Am. Chem. Soc., 2006, 128, 1654–1663 Search PubMed.
- Y. Mantri, S. J. Lippard and M. H. Baik, J. Am. Chem. Soc., 2007, 129, 5023–5030 Search PubMed.
- S. Gonell, M. D. Massey, I. P. Moseley, C. K. Schauer, J. T. Muckerman and A. J. M. Miller, J. Am. Chem. Soc., 2019, 141, 6658–6671 Search PubMed.
- S. Gonell, E. A. Assaf, K. D. Duffee, C. K. Schauer and A. J. M. Miller, J. Am. Chem. Soc., 2020, 142, 8980–8999 Search PubMed.
- W. C. Zeise and O. K. Dan, Vidensk. Selsk. Forh., 1825–1826, 6, 13–14 Search PubMed.
- G. L. Hou, H. Wen, K. Lopata, W. J. Zheng, K. Kowalski, N. Govind, X. B. Wang and S. S. Xantheas, Angew. Chem., Int. Ed., 2012, 51, 6356–6360 Search PubMed.
- G.-L. Hou, N. Govind, S. S. Xantheas and X.-B. Wang, J. Phys. Chem. A, 2018, 122, 1209–1214 Search PubMed.
- A. M. Amado, S. M. Fiuza, M. P. M. Marques and L. A. E. Batista de Carvalho, J. Chem. Phys., 2007, 127, 185104 Search PubMed.
- C. Zhang, E. B. Naziga and L. Guidoni, J. Phys. Chem. B, 2014, 118, 11487–11495 Search PubMed.
- J. Warneke, M. Rohdenburg, Y. Zhang, J. Orszagh, A. Vaz, I. Utke, J. T. M. De Hosson, W. F. van Dorp and P. Swiderek, J. Phys. Chem. C, 2016, 120, 4112–4120 Search PubMed.
- M. Rohdenburg, P. Martinović, K. Ahlenhoff, S. Koch, D. Emmrich, A. Gölzhäuser and P. Swiderek, J. Phys. Chem. C, 2019, 123, 21774–21787 Search PubMed.
- B. Pinter, V. Van Speybroeck, M. Waroquier, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2013, 15, 17354–17365 Search PubMed.
- P. Tang, J. Zhang, X. Li, F. Yang, Q. Zhao, J. Ma, Z. Hu, H. Sun, X.-B. Wang, Z. Sun and Y. Yang, J. Phys. Chem. A, 2024, 128, 5500–5507 Search PubMed.
- Q. Zhao, J. Zhang, X. Li, P. Tang, F. Yang, J. Ma, Z. Hu, H. Sun, X.-B. Wang, Z. Sun and Y. Yang, J. Chem. Phys., 2024, 161, 214305 Search PubMed.
- D. Hanstorp and M. Gustafsson, J. Phys. B:At., Mol. Opt. Phys., 1992, 25, 1773 Search PubMed.
- J. Zhang, Z.-R. Sun and X.-B. Wang, J. Phys. Chem. A, 2015, 119, 6244–6251 Search PubMed.
- N. Mehta, M. Casanova-Páez and L. Goerigk, Phys. Chem. Chem. Phys., 2018, 20, 23175–23194 Search PubMed.
- J. Joseph, K. Pradhan, P. Jena, H. Wang, X. Zhang, Y. Jae Ko and K. H. Bowen, J. Chem. Phys., 2012, 136, 194305 Search PubMed.
- Y. Shi, S. Bian, Y. Ma, Y. Wang, J. Ren and X. Kong, J. Phys. Chem. A, 2018, 123, 187–193 Search PubMed.
- R. Wesendrup and P. Schwerdtfeger, Inorg. Chem., 2001, 40, 3351–3354 Search PubMed.
- K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883 Search PubMed.
- D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, J. Chem. Phys., 2009, 130, 164108 Search PubMed.
- R. A. Kendall, T. H. Dunning, Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 Search PubMed.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358–1371 Search PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 Search PubMed.
- Y. Wei, B.-W. Wang, S.-W. Hu, T.-W. Chu, L.-T. Tang, X.-Q. Liu, Y. Wang and X.-Y. Wang, J. Phys. Org. Chem., 2005, 18, 625–631 Search PubMed.
- M. Otsuka, H. Mori, H. Kikuchi and K. Takano, Comput. Theor. Chem., 2011, 973, 69–75 Search PubMed.
- J. C. Gómez Martín, O. Gálvez, M. T. Baeza-Romero, T. Ingham, J. M. C. Plane and M. A. Blitz, Phys. Chem. Chem. Phys., 2013, 15, 15612–15622 Search PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- L. Bica, P. J. Crouch, R. Cappai and A. R. White, Mol. BioSyst., 2009, 5, 134–142 Search PubMed.
- P. Faller, ChemBioChem, 2009, 10, 2837–2845 Search PubMed.
- P. Faller and C. Hureau, Dalton Trans., 2009, 1080–1094 Search PubMed.
- T. Yang, Z. Li, X. B. Wang and G. L. Hou, Chem. Phys. Chem., 2023, 24, e202200835 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Initial geometries and optimized geometries of PtClX2−, Pt(NH3)ClX2− (X = Cl, Br, I) anions and the corresponding neutrals; lowest energy structures of PtClX2, Pt(NH3)ClX2 (X = Cl, Br, I), and their isomers; the HOMO energy difference upon NH3 coordination and orbital rearrangement between PtClX2− and Pt(NH3)ClX2− (X = Br, I) anions; the LUMO plot of Pt(NH3)Cl3−; the ionic proportion of the chemical bonds Pt–Cl, Pt–Br, and Pt–I of PtClX2−, Pt(NH3)ClX2− (X = Cl, Br, I); the dissociation energies of different dissociation channels of PtClX2−, Pt(NH3)ClX2− and Pt(C2H4)ClX2− (X = Cl, Br, I); and the structures and bonding energies of Pt(C2H4)ClX2− (X = Cl, Br, I). See DOI: https://doi.org/10.1039/d5cp00807g |
| ‡ These two authors contributed equally to this work. |
| This journal is © the Owner Societies 2025 |