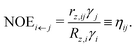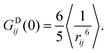Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multiscale modelling of nuclear magnetisation dynamics: spin relaxation, polarisation transfer and chemical exchange in 129Xe@cryptophane(aq) structures†
Perttu
Hilla
 * and
Juha
Vaara
* and
Juha
Vaara

NMR Research Unit, University of Oulu, P.O. Box 3000, FI-90014, Finland. E-mail: perttu.hilla@oulu.fi
First published on 12th May 2025
Abstract
Computational nuclear magnetic resonance (NMR) spectroscopy of supramolecular Xe@cryptophane(aq) complexes requires a multiscale approach due to the interplay of molecular dynamics, spin relaxation, chemical exchange, and solvent effects. The flexible cryptophane cage consists of approximately 150 atoms, including 50 protons, and the encapsulated xenon atom undergoes significant dynamics. Furthermore, the biosensing applications of this structure occur in aqueous, non-deuterated solvents. Consequently, fluctuations in internuclear dipole–dipole (DD) couplings lead to spin relaxation and polarisation transfer between nuclei, with Xe exchange between the solvent and the cage playing a pivotal role. Here, we introduce a novel molecular dynamics (MD)-based approach to simulate DD-driven magnetisation dynamics, incorporating intermolecular relaxation and cross-relaxation effects that are often overlooked in traditional MD–DD modelling. We compute the 129Xe and 1H relaxation times for Xe(aq) and two water-soluble Xe@cryptophane(aq) systems and examine the spin polarisation-induced nuclear Overhauser effect (SPINOE) between hyperpolarised xenon and the surrounding protons, obtaining results in good agreement with the available experimental data. Using a two-site exchange model and first-principles computed Xe chemical shifts, we assess the impact of xenon exchange on observable relaxation and polarisation transfer and simulate the 129Xe NMR spectrum, accounting for both chemical exchange and DD relaxation. This work bridges the gap between fully quantum-mechanical spin dynamics simulations and traditional MD–DD approaches and presents the first comprehensive SPINOE modelling and relaxation analysis in xenon biosensor systems.
1 Introduction
1.1 Background
In addition to single-molecule dynamics, particularly rotation with respect to the direction of the external magnetic field, the time evolution of M(t) is affected by chemical exchange, which typically occurs on a much slower time scale than the molecular tumbling. Chemical exchange can lead to signal decay, coalescence of spectral peaks and magnetisation transfer between the exchanging sites.1 In many cases, a satisfactory model for the dynamics of M(t) requires a combination of coherent evolution, spin relaxation and chemical exchange.
A particularly challenging task is the modelling of relaxation. For approximately rigid molecules in isotropic solvents, it is reasonable to assume that isotropic rotational diffusion of a rigid rotor provides a relevant motional model. This approximation can be applied in the framework of NMR relaxation theory to estimate the auto- and cross-relaxation rates of the spins, which can then be used in spin dynamics simulations. However, this model can be too simple for describing conformationally flexible molecules. In addition, it cannot explicitly describe intermolecular relaxation. These features can become important in relatively large and flexible molecules with tens of spins, in solvents of high proton spin density (such as water) and/or when the system includes non-covalently bonded chemical units or atoms. Due to the complexity of such systems, a fully quantum-mechanical treatment of spin dynamics is usually not feasible.
When the DD mechanism dominates relaxation, a usual situation for liquid-phase spin-1/2 systems in the absence of unpaired electrons, relaxation rates can be computed from molecular dynamics (MD) simulation trajectories.7–15 MD simulations account for all types of motion in the system, and allow straightforward computation of the intermolecular contributions to relaxation.8,9,14,16,17 As opposed to analytical motional models, no distinction between different motional modes, such as rotation and translation, needs to be made. MD simulations are typically more accurate in describing the internuclear dynamics and, therefore, the DD relaxation rates, than the rigid-rotor model. However, it is a common practice in DD-relaxation modelling with MD simulations (termed MD–DD modelling from now on) to neglect cross-relaxation and, thereby, the resulting polarisation transfer between chemically non-equivalent spins. Hence, although the traditional MD–DD modelling provides a better dynamical description than the rigid-rotor model, the inherently coupled time evolution of spins is not routinely taken into account.
From the modelling point of view, the presence of chemical exchange introduces further difficulties. If it plays an important role in the studied system, the coherent and incoherent mechanisms have to be computed for each exchanging site n. The exchange rates between the sites, within a suitable exchange model, can then be used to simulate the combined time evolution of all the {M(n)(t)}. The total size of the combined system is a sum over the sizes of the individual systems, which increases the computational demands.
In addition to the favourable chemical and NMR properties of 129Xe, the spin-exchange optical pumping (SEOP) method25,26 can be used to easily hyperpolarise a sample of xenon gas. This process involves transferring the electron spin polarisation of alkali–metal atoms (typically rubidium) to the polarisation of xenon nuclei. SEOP can enhance the Xe NMR signal by a factor of ε = 104 as compared to thermal polarisation at room temperature. Consequently, hp 129Xe NMR has found use in the study of porous materials and in medical imaging.20,27,28
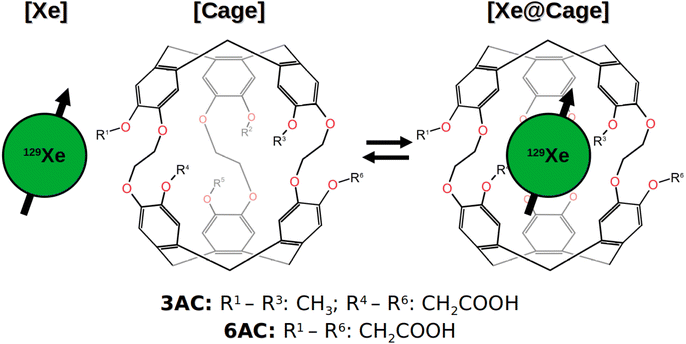
A direct NMR measurement of Xe is not typically feasible due to the low population of the host-bound site prevailing in typical biosensing situations. Because the binding to the host cage is weak, chemical exchange occurs between the bound and free xenon sites, with ‘free’ here referring to the hp Xe in the bulk solvent. The exchange process is illustrated in Fig. 1 and described by the rate equation
 | (1) |
| ν+ = k+[Xe][Cage] |
| ν− = k−[Xe@Cage]. |
| νex ≡ νeq+ + νeq−. | (2) |
 . Here, Δω is the difference in the resonance frequencies of the exchanging sites. The binding equilibrium is also characterised by the association constant
. Here, Δω is the difference in the resonance frequencies of the exchanging sites. The binding equilibrium is also characterised by the association constant | (3) |
The use of XBSs in low-concentration chemical sensing is founded in the combination of the SEOP and CEST methods in the so-called hyper-CEST experiment.54–57 There, hp Xe gas is allowed to undergo chemical exchange [eqn (1)] between the solvent and the host cages, with frequency-swept, continuous irradiation applied over the CS range of Xe. Irradiation coinciding with the resonance frequency of the host-bound Xe renders equal the populations of the nuclear spin states, and destroys the longitudinal magnetisation of the bound site at that frequency. As a result of the exchange back to the majority (solution) site, the intensity of the solution-state Xe signal decreases by an amount that depends on the irradiation frequency. When the bulk signal intensity is plotted as a function of the irradiation frequency, in the so-called z-spectrum, the resonance frequencies of the less populated sites are revealed. Hyper-CEST can increase the signal intensity altogether by a factor of 107, which significantly reduces the minimum concentration of the Xe@Cage complexes that can be detected. This was demonstrated in ref. 58 where picomolar detection of cryptophane-based complexes was possible.
1.2 Relaxation
One of the difficulties in interpreting Xe-proton SPINOE measurements has been the presence of cross-relaxation between protons (spin diffusion), which mixes their SPINOE enhancement intensities and renders the extraction of, e.g., interatomic Xe-proton distances less straightforward.66,80 Experimental techniques that quench the proton–proton cross-relaxation during the SPINOE transfer were demonstrated.81 Computational modelling of SPINOE, which could provide the necessary microscopic information for the interpretation of the experimental results was, however, never conducted.
1.3 Modelling
(1) coherent time evolution due to Xe CS,
(2) spin relaxation and polarisation transfer between the guest and the host, caused by the DD mechanism, as well as
(3) chemical exchange of hp Xe between the bulk solution and the cage confinement.
The Xe@Cr complex consists of the roughly spherical cage containing tens of proton spins, and the encapsulated, non-covalently bonded hp 129Xe, as shown on the right-hand-side of Fig. 1. Hence, a specific Xe-few proton subsystem of relevance cannot be identified. Cryptophanes are structurally flexible and the chemical moieties at the perimeter of the CTB bowls are mobile. In the XBS context the natural solvent environment is water, so intermolecular relaxation due to the H2O protons needs also be considered. All these features suggest that the MD–DD approach is more reasonable than the rigid-rotor model. On the other hand, accounting for cross-relaxation and, hence, spin diffusion is desirable to model the SPINOE polarisation transfer.
The present work advances the theoretical and computational modus operandi for liquid-state NMR modelling of magnetisation dynamics in large and motionally flexible systems, affected by chemical exchange. We aim at bridging the gap between the traditional MD–DD modelling, which neglects cross-relaxation, and fully quantum-mechanical spin-dynamics simulations, which conventionally employ the rigid-rotor model. This is done by (i) organising chemically equivalent spins to a few groups, which allows simulation of large spin systems, (ii) simulating the magnetisation dynamics via direct time propagation of the NMR observables and (iii) replacing the analytical motional models by detailed microscopic MD trajectories. The present approach represents multiscale modelling because it involves computing nuclear spin interactions at the microscopic scale using electronic structure theory and MD simulations. These interactions then drive the time evolution of the macroscopic-scale nuclear magnetisation dynamics, computed by propagating the magnetisation observables. This allows, for the first time, a comprehensive computational modelling of SPINOE experiments. The developed methods are applied to simulate the magnetisation dynamics in three model systems relevant to the XBS field: free Xe and two different water-soluble Xe@cryptophane-A derivatives, named 3AC and 6AC [see Fig. 1], with each system in explicit water solvation. A two-site model is used to combine the time evolution of the free and host-bound Xe sites undergoing chemical exchange. We simulate the longitudinal magnetisation dynamics of the systems, including NOE/SPINOE polarisation transfer, as well as the 129Xe NMR spectrum under different chemical-exchange conditions.
2 Theoretical background
The following assumptions, which are practically always made in MD–DD modelling, are also used throughout the present work:(1) Only the DD-mechanism contributes to relaxation and
(2) cross-correlation between the DD couplings is neglected.
When only DD-relaxation is significant, no quantum-chemical calculations, which are computationally very demanding for large systems, are needed – the atomic MD trajectories contain the necessary information. We restrict ourselves to spin-1/2 nuclei, which means that there is no quadrupolar relaxation. Note that cross-relaxation and cross-correlation are distinct. The former describes the interconnection of the time evolution of different spins, such as those of nuclei 1 and 2, due to incoherent spin interactions. In contrast, cross-correlation refers to the contributions to relaxation rates that arise from correlation between two different spin interactions, such as DD and chemical shift anisotropy, for a single spin. The contribution from cross-correlated DD couplings can be assumed relatively weak as compared to the autocorrelated part, because DD cross-correlation only couples the time evolution of single-spin operators to product operators of spin order (the total number of single-spin operators in the product) three or more, as shown in the ESI.† The latter have nearly zero population at room-temperature thermal equilibrium. Furthermore, they do not gain significant population during the dynamics, either. Hence, their overall effect on the time evolution of the spin system can be deemed small.85 We also assume that, due to the fact that there are no covalent bonds, the Xe-proton J-couplings are negligible, when simulating the 129Xe NMR spectrum.
2.1 Magnetisation dynamics
 | (4) |
 | (5) |
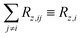 . The summation in each case is carried out over all spins other than i. The longitudinal auto- and cross-relaxation rates between spins i and j,
. The summation in each case is carried out over all spins other than i. The longitudinal auto- and cross-relaxation rates between spins i and j, | (6) |
 | (7) |
 | (8) |
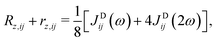 | (9) |
In the case of transverse magnetisation, we have
 | (10) |
 . The transverse auto- and cross-relaxation rates are
. The transverse auto- and cross-relaxation rates are | (11) |
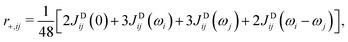 | (12) |
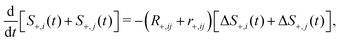 | (13) |
 | (14) |
As the main interest in this work is longitudinal magnetisation dynamics and the NMR spectrum of Xe, we assume that the secular approximation holds between all CnE protons and, therefore, neglect transverse cross-relaxation between them.
 | (15) |
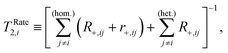 | (16) |
(1) The homonuclear contribution to eqn (15) is strictly speaking only valid for a system of CE spins (such as water protons), and cannot be easily justified using eqn (5) for a general system including CnE spins. In reality, the time evolution between CnE spins is coupled by cross-relaxation and, hence, deviates from the single-exponential decay.
(2) The network of nuclei coupled by cross-relaxation results in polarisation transfer and spin diffusion across the entire spin system, which can become important in large systems and/or in the presence of spin-dense solvents, such as H2O. The traditional approach cannot describe these phenomena.
(3) Even though the experimentally measured magnetisation decay often is approximately single-exponential, due to the presence of cross-relaxation, it does, in fact, arise from coupled time evolution that inherently is not single-exponential. Therefore, the parameter that is obtained from experiments using (typically) a single-exponential fit to the decay, denoted as TFit1 is, in reality, influenced by cross-relaxation. Hence, the parameters obtained from experimental data are results of fitting, whereas those extracted from traditional MD–DD modelling [eqn (15)] are inverses of self-relaxation rates. In general, the two are not the same quantity, TRate1 ≠ TFit1.
If the longitudinal cross-relaxation between the CnE spin groups were negligibly small, e.g., due to very weak DD couplings, the above issues (1–3) regarding T1 would also disappear, but this is not in general the case. In the traditional MD–DD approach, it is also fairly common to neglect intermolecular relaxation, i.e., the terms where the spins i and j belong to different molecules.
Instead of neglecting longitudinal cross-relaxation, in the present work we compute all intra- and intermolecular auto- and cross-relaxation rates from MD trajectories, and simulate in full detail a physically motivated and computationally manageable version of eqn (5). This is done by formally dividing the spin system into groups of CE nuclei, with the details elaborated below. Once cross-relaxation is included, no simple analytical relationship between T1 and the relaxation rates exists.
Let us formally divide the spin system into groups of chemically equivalent nuclei {I}, for which
| Rz,ij ≡ Rz,IJ, ∀i ∈ I and j ∈ J |
| rz,ij ≡ rz,IJ, ∀i ∈ I and j∈J. |
 | (17) |
 | (18) |
| RCEz,I = (NI − 1)(Rz,II + rz,II) |
and the summation in the latter formula is carried out over all groups J other than I.
Eqn (18) generalises the traditional MD–DD approach. Each term therein has a clear interpretation: RCEz,I is the contribution to the observable auto-relaxation rate of MI(t) from the DD interactions (NI − 1 being their number) of a single nucleus within the group I of CE nuclei, and is computed according to eqn (9). RCnEz,I is the contribution to the auto-relaxation rate from the CnE nuclei of the other groups J ≠ I in the spin assembly, and is computed using eqn (6). The last term, which in the traditional MD–DD approach is implicitly neglected, represents the longitudinal cross-relaxation between the CnE groups, computed according to eqn (7). For a system of just two CE spins, there is only one group I, NI = 2, and eqn (8) would be recovered. For two CnE nuclei, there are two groups I and J with NI = 1 in both, which leads to eqn (4).
An exactly analogous derivation for the transverse magnetisation leads to
 | (19) |
| RCE+,I = (NI − 1)(R+,II + r+,II) |
are calculated using eqn (14) and (11), respectively.Eqn (18) reduces to a differential equation for the single-exponential decay of ΔMz,I(t), provided that one approximates that all ΔMz,J(t) ≈ ΔMz,I(t). In this case, the decay of ΔMz,I(t) is described by the traditional MD–DD formulas (15) and (16). This is only true if the spin groups I and J do indeed have very similar time evolution and/or the cross-relaxation rz,IJ between them is negligible. Later we show that the deviation between the relaxation times predicted by the simulations using eqn (18), and those using the traditional formulae, can be significant. This situation prevails for spin groups that have strong cross-relaxation to other CnE groups and do not evolve identically. In the transverse case, due to the absence of cross-relaxation between the CnE spins, the present and the traditional methods remain identical.
The system of eqn (18) can be cast into matrix form as
 | (20) |
 | (21) |
Eqn (21) is still inhomogenous and cannot be solved directly. It can, however, be effectively homogenised by adding one extra dimension to the matrix equation:
 | (22) |
 | (23) |
 | (24) |
Simulated direct time propagation of Mz(t) allows the magnetisation decay to be fitted, which corresponds to extracting TFit1 rather than TRate1. This establishes a more justified comparison between experimental and computational results, as now both parties are referring to the same quantity, and include cross-relaxation effects in both cases. The present method implied by eqn (18) also enables simulations of polarisation transfer including spin diffusion. Furthermore, hyperpolarisation can be easily taken into account in the initial condition.
 . The NOE enhancement of spin i at such a time, t0, is defined as
. The NOE enhancement of spin i at such a time, t0, is defined as | (25) |
 | (26) |
(1) In the usual NOE context, the spin j is irradiated by an external radio-frequency field that depletes its spin polarisation. Then, Sz,j(t) = 0 and ΔSz,j(t) = −Seqz,j. In this situation, the system reaches a steady state, where
Here, ηij is called the NOE enhancement factor of spin i coupled to spin j, and γi is the gyromagnetic ratio of i. We see that a strong cross-relaxation rate does not necessarily lead to a strong NOE enhancement, because ηij can be suppressed by a high self-relaxation rate of spin i. The sign of ηij depends on the ratio
 .
.
The above expression holds for a two-spin system. To take into account the presence of other spins that also contribute to the relaxation of spin i, it is common to replace Rz,i by the inverse of the experimentally obtained relaxation time T1,i, which in the traditional computational MD–DD framework corresponds to TRate1,i:
(2) The second interesting case is when spin j is hyperpolarised and relaxes relatively slowly, such that, for t ≤ t0, we have Rz,jΔSz,j(t) ≫ rz,ijΔSz,i(t), in eqn (5). We then obtain
| ΔSz,j(t0) ≈ ΔSz,j(0)e−Rz,jt0 = (ε − 1)Seqz,je−Rz,j. |
 | (27) |
Interpretation of Xe-proton SPINOE experiments has most often used eqn (27) or formulas derived from it ref. 6, because Xe relaxation is typically much slower than that of protons by more than an order of magnitude (vide infra). However, this neglects the effects of spin diffusion, which cannot be described by a two-spin model, even when using the empirical replacement for the relaxation rate. We will later in the paper compare simulated proton SPINOE enhancements that include spin diffusion with the results predicted by eqn (27).
2.2 Relaxation-rate constants
 | (28) |
| GDij(τ) = 〈VDij(t)VDij(t − τ)〉, |
θij(t) is the angle between the vector connecting the two spins and the external magnetic field direction (the z axis). Note that, in the present work, the approximation rij3(t) ≈ rij3 appropriate to the rigid rotor model is not used. Instead, the dynamically varying distance between the nuclei is taken into account. This is particularly important for the non-covalently bound 129Xe spin, which samples a range of distances to other spins.
In the present MD–DD framework we work with spin groups, and the natural way to compute the relaxation rates is to take the double average over each spin in the groups i ∈ I and j ∈ J, such that 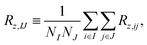 and similarly for the other rates. Due to the finite length and system size (number of atoms) in a MD simulation, however, VDij(τ) for a single nuclear pair ij can be quite noisy. Consequently, their cosine transforms, which would yield the spectral density functions and, eventually, the resulting relaxation rates, are often rendered unfeasible. Instead, the averaging can be carried out in the “grouped” basis, i.e.,
and similarly for the other rates. Due to the finite length and system size (number of atoms) in a MD simulation, however, VDij(τ) for a single nuclear pair ij can be quite noisy. Consequently, their cosine transforms, which would yield the spectral density functions and, eventually, the resulting relaxation rates, are often rendered unfeasible. Instead, the averaging can be carried out in the “grouped” basis, i.e.,
 | (29) |
 | (30) |
Exponentially decaying functions can be fitted to the numerical TCFs, followed by the cosine transform performed analytically. Here, we choose to use the commonly employed Lipari–Szabo double-exponential model,91 which can describe a relatively broad range of different motions. The model is a simple three-parameter fit
 | (31) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]IJ means that each pair IJ obtains its own fitted parameters S2, τg and τe. In the present context this is primarily a convenient analytical form for the fitting function, but we will later interpret the average global correlation time τg between Xe and the cage protons as the rotational correlation time of the cage. Using eqn (29), we then get
]IJ means that each pair IJ obtains its own fitted parameters S2, τg and τe. In the present context this is primarily a convenient analytical form for the fitting function, but we will later interpret the average global correlation time τg between Xe and the cage protons as the rotational correlation time of the cage. Using eqn (29), we then getThe final thing we need is the GDIJ(0) factor, which corresponds to the mean-square amplitude of the DD coupling between spins in groups I and J. For that one has to evaluate the ensemble averages
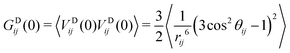 | (32) |
In the above-mentioned rigid-rotor model one would approximate
 . However, this assumption needs not be made, whenever detailed MD simulations are available. The ensemble average is related to the radial distribution function (RDF),92gij(r), between the spins i and j:
. However, this assumption needs not be made, whenever detailed MD simulations are available. The ensemble average is related to the radial distribution function (RDF),92gij(r), between the spins i and j: | (33) |
 | (34) |
Combining all of the above, the final expression for the spectral density functions JDIJ(ω), which is used to compute the relaxation rate constants Rz,IJ, rz,IJ, R+,IJ, and r+,IJ in the present work, is
 | (35) |
2.3 Chemical exchange
 | (36) |
 | (37) |
| pfνeq+ = pbνeq−. | (38) |
 | (39) |
We then define the population-weighted magnetisation vector as
| O(t) = P(t)⊙M(t). |
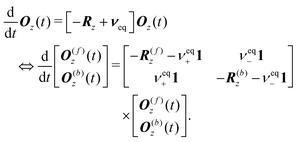 | (40) |
Longitudinal magnetisation does not evolve under the coherent interactions, but in the transverse case we need to account for the coherent time evolution of Xe caused by the nuclear shielding interaction:
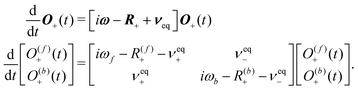 | (41) |
(1) The motionally averaged chemical shifts in ω are obtained by combining MD simulations and quantum-chemical electronic-structure calculations (see Computational details).
(2) The MD simulations allow detailed computation of the (DD) relaxation-rate constants in R, as well as (in some cases) reaction rates in ν.
(3) Magnetisation dynamics simulations combine the previous parameters into the time propagation of the appropriate observables, allowing computational spectroscopy.
3 Computational details
3.1.1 MD simulations and chemical shift calculations
Molecular dynamics simulations were performed on the xTB programme.93 The three different systems, Xe(aq), Xe@3AC(aq) and Xe@6AC(aq), were simulated at the partially polarisable GFN-FF94 force-field level of theory because of its good performance in earlier work.47,95,96 The simulations were performed at constant temperature of 293.15 K, using the Berendsen thermostat,97 a time step Δt = 1.0 fs and a finite droplet model with 1000 or 500 solvent H2O molecules for the Xe(aq) or Xe@3AC/6AC(aq) systems, respectively. A weak confinement potential was used to keep the volume of the droplet approximately constant. For the Xe(aq) system a single production period of 1.8 ns was simulated, whereas for the Xe@3AC/6AC(aq) systems three independent simulations, each of 8…9 ns production period, were carried out. Snapshots were recorded every 0.1 ps.In our previous work,95 using similarly obtained MD trajectories, the dynamically averaged NMR chemical shifts of 129Xe(aq) and 129Xe@6AC(aq) were computed on the Turbomole programme98,99 at the X2C100,101 scalar-relativistic density-functional theory level using the BHandHLYP102–104 exchange–correlation functional. Extensive details of the CS calculations are described in ref. 95.
3.1.2 MD trajectory analysis and DD time-correlation functions
The MD trajectory analysis, including the RDF and TCF computations, were performed using in-house written Python programmes that build upon the NumPy,105 SciPy106 and Numba107 Python libraries. Starting from the MD trajectories, computing the full set of RDFs using a single AMD Ryzen 7 PRO processor on a standard laptop computer took roughly half an hour for each presently modelled system, and 2–3 hours for the TCFs. After the TCFs were obtained, they were fitted to the functional form of eqn (31). The computed TCFs and the fits are shown in the ESI† (Fig. S1–S3). The obtained parameters and the RDFs were used to compute the spectral density functions using eqn (35). The auto- and cross-relaxation rates between each group were then obtained according to eqn (6), (7), (9), (11), (12) and (14). Standard magnetic field of B0 = 9.4 T was used.The resulting longitudinal relaxation matrices, −Rz, for the Xe@Cr(aq) systems, with and without the intermolecular contributions from the solvent H2O molecules, are shown in Fig. 2.
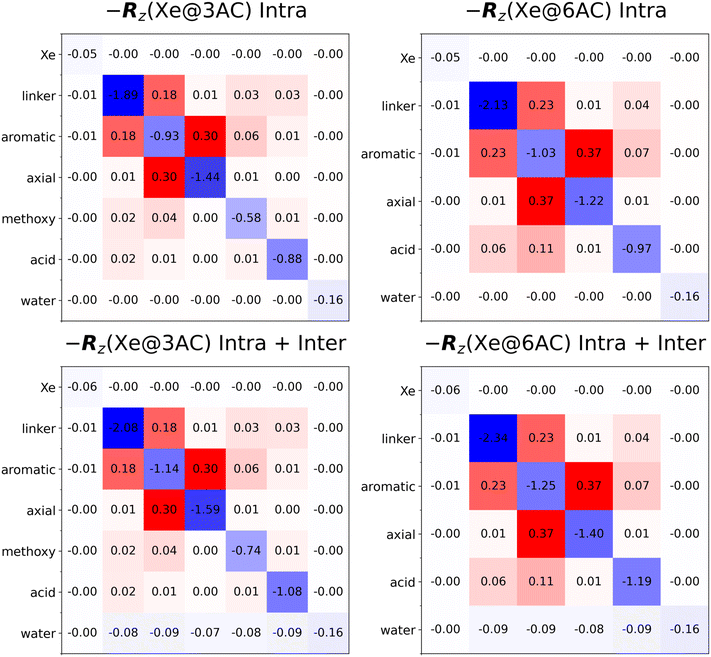 | ||
| Fig. 2 Longitudinal relaxation matrices, −Rz, for the Xe@Cr(aq) systems (in s−1). Intra- and intermolecular (the water solvent) contributions are compared. The values “0.00” correspond to matrix elements with magnitude less than 0.005. The used spin grouping is defined in Fig. 3. | ||
3.1.3 Spin groups and magnetisation dynamics
The presently used division of the Cr cage protons into CE groups is shown in Fig. 3. Due to computational limitations (MD trajectory length), all protons of the CH2 COOH arms were grouped together although they are not exactly equivalent. This rendered the number of spins in each group large enough for gaining sufficient statistics for GDIJ(τ). Protons in the solvent water pool were taken as one spin group in each case. | ||
| Fig. 3 Division of the Cr cage protons into spin groups. The number of spins in each group is shown. Note that the 3AC cage is divided into five groups, and the 6AC cage into four. | ||
Time propagation of eqn (24) and the analysis of the results were carried out on in-house written programmes using the Python and Jupyter Notebook90 environments. To extract TFit1 from the simulated magnetisation decay we used the following single-parameter fit
 | (42) |
 | (43) |
3.1.4 Chemical exchange
The equilibrium exchange-rate constants νeq± are presently the only parameters that had to be obtained using experimental data. Their computation is very difficult because the Xe exchange events are extremely rare in the MD simulation time scale. Hence, gaining statistically trustworthy computational values for νeq± was considered to lie outside the scope of the current computational methodology. The actual parameter that was taken from experiments is Ka = 6800 M−1 for Xe@6AC in D2O, as reported in ref. 48. The input parameters for the simulations are the initial concentrations [Xe]init and [Cage]init, which were here chosen to be equal to obtain comparable peak intensities in the 129Xe NMR spectrum. We then solve for [Xe@Cage]eq using eqn (3) with| [Xe]eq = [Xe]init − [Xe@Cage]eq |
| [Cage]eq = [Cage]init − [Xe@Cage]eq, |
| [f] = [Xe]eq and [b] = [Xe@Cage]eq. |
4 Results and discussion
4.1 Relaxation times of the free and bound sites
First we survey the results obtained in the absence of chemical exchange. Table 1 shows the longitudinal relaxation times and the NOE/SPINOE enhancements of each spin resulting from different initial states Mz(0), which correspond to different inversion recovery experiments. The traditional MD–DD approach (TRate1), the presently introduced method (TFit1), as well as the simulated SPINOE enhancement and the enhancement predicted by the pseudo two-spin model of eqn (27), are compared. The transverse relaxation times TRate2 are also shown.| System | M z (0)a | Property | 129Xe | 1H linker | 1H aromatic | 1H axial | 1H acid | 1H methoxy | 1H water |
|---|---|---|---|---|---|---|---|---|---|
| a Specifies the inverted (ε = −1) or hyperpolarised (by a factor of 1000, ε = 1000) nuclei. εH denotes an initial nonequilibrium state for all protons, whereas εH(xAC) means that only the cage protons were in a nonequilibrium initial state. | |||||||||
| Xe(aq) | T Rate1 (s) | 138.53 | – | – | – | – | – | 6.53 | |
| T Rate2 (s) | 138.63 | – | – | – | – | – | 6.53 | ||
| ε Xe = 1000 | T Fit1 (s) | 138.53 | – | – | – | – | – | 6.53 | |
| t 0 (s) | – | – | – | – | – | – | 20.93 | ||
| SPINOE(t0) [%] | – | – | – | – | – | – | 0.28 | ||
| SPINOE(t0), eqn (27) [%] | – | – | – | – | – | – | 0.28 | ||
| ε H = −1 | T Fit1 (s) | – | – | – | – | – | – | 6.53 | |
| t 0 (s) | 20.93 | – | – | – | – | – | – | ||
| NOE(t0) [%] | −14.59 | – | – | – | – | – | – | ||
| Xe@3AC(aq) | T Rate1 (s) | 16.89 | 0.52 | 1.14 | 0.61 | 0.85 | 1.24 | 6.3 | |
| T Rate2 (s) | 12.86 | 0.09 | 0.26 | 0.04 | 0.51 | 0.52 | 6.3 | ||
| ε Xe = 1000 | T Fit1 (s) | 16.89 | – | – | – | – | – | – | |
| t 0 (s) | – | 2.22 | 3.15 | 3.34 | 2.99 | 4.13 | 8.96 | ||
| SPINOE(t0) [%] | – | 7.62 | 12.76 | 4.75 | 5.84 | 5.79 | 0.22 | ||
| SPINOE(t0), eqn (27) [%] | – | 6.91 | 13.12 | 2.24 | 4.96 | 4.04 | 0.38 | ||
| ε H(3AC) = −1 | T Fit1 (s) | – | 0.59 | 1.28 | 0.85 | 0.98 | 1.51 | – | |
| t 0 (s) | 3.14 | – | – | – | – | – | 2.3 | ||
| NOE(t0) [%] | −10.39 | – | – | – | – | – | 0.61 | ||
| ε H = −1 | T Fit1 (s) | – | 0.52 | 1.03 | 0.74 | 0.8 | 1.21 | 6.29 | |
| t 0 (s) | 4.51 | – | – | – | – | – | – | ||
| NOE(t0) [%] | −14.96 | – | – | – | – | – | – | ||
| Xe@6AC(aq) | T Rate1 (s) | 17.08 | 0.47 | 1.16 | 0.68 | 0.78 | – | 6.07 | |
| T Rate2 (s) | 12.24 | 0.09 | 0.22 | 0.04 | 0.3 | – | 6.07 | ||
| ε Xe = 1000 | T Fit1 (s) | 17.08 | – | – | – | – | – | – | |
| t 0 (s) | – | 2.27 | 3.15 | 3.62 | 3.12 | – | 8.97 | ||
| SPINOE(t0) [%] | – | 5.85 | 12.06 | 5.48 | 4.55 | – | 0.24 | ||
| SPINOE(t0), eqn (27) [%] | – | 5.03 | 13.16 | 2.16 | 3.31 | – | 0.38 | ||
| ε H(6AC) = −1 | T Fit1 (s) | – | 0.55 | 1.32 | 1.06 | 0.95 | – | – | |
| t 0 (s) | 3.12 | – | – | – | – | – | 2.18 | ||
| NOE(t0) [%] | −9.31 | – | – | – | – | – | 0.63 | ||
| ε H = − 1 | T Fit1 (s) | – | 0.48 | 1.06 | 0.89 | 0.78 | – | 6.06 | |
| t 0 (s) | 4.83 | – | – | – | – | – | – | ||
| NOE(t0) [%] | −14.32 | – | – | – | – | – | – | ||
 | ||
| Fig. 4 Longitudinal magnetisation decay of the free and host-bound 129Xe sites starting from a state with εXe = 1000. | ||
Relaxation of Xe in each environment is characterised by the relaxation times shown in Table 1. The computed free-Xe T1 is 138.53 s, whereas for Xe@3AC and Xe@6AC, it is much shorter, 16.89 and 17.08 s, respectively. Notably, the relaxation of Xe in water is very slow with a T1 of more than two minutes. The difference between the T1 values of the two kinds of bound sites is very small, roughly 0.2 s. For both of them, a substantial contribution, roughly 20%, of the encapsulated Xe relaxation-rate values comes from the intermolecular relaxation caused by the water solvent (see the longitudinal relaxation matrices in Fig. 2). In all cases the traditional (TRate1) and the presently used method (TFit1) produce identical results for 129Xe. This is because of the relatively weak cross-relaxation between Xe and the surrounding protons, resulting from the weak Xe-proton DD couplings.
Transverse relaxation times TRate2 of 138.63, 12.86 and 12.24 s were obtained for the free, Xe@3AC and Xe@6AC sites, respectively. T1 and T2 are nearly equivalent for the free site. This is a feature of a slow relaxation caused by rapid rotational tumbling, which is precisely the situation due to the water molecules around the free xenon. The difference between T1 and T2 becomes more pronounced for the bound Xe sites, where the computed T2 values are smaller than T1 by roughly 4… 5 s. The average τg values [see eqn (31)] obtained from the DD-TCF fits between Xe and the cage protons are 1.38 and 1.48 ns for the Xe@3AC and Xe@6AC systems, respectively. These values can be interpreted as due to the relatively slow rotation of the Cr cages. This, in turn, renders the relative contribution of the zero-frequency spectral density function J(0) in the expression for the transverse relaxation rate [eqn (11)] much larger than in the case of the rapidly tumbling H2O molecules, which rationalises the difference from Xe(aq). For comparison, a much faster rotational correlation time of 0.6 ns was experimentally found for a prototypic (0AC) cryptophane-A cage dissolved in deuterated tetrachloroethane (C2D2Cl4).80 The water-soluble 3AC and 6AC cages carry the CH2COOH acetic acid groups [see Fig. 1], which are longer than the six methoxy (CH3) groups of the 0AC cage, extend further into the bulk solvent, and hydrogen-bond with the water molecules. Hence, the CH2COOH groups can be expected to slow down the rotation of the 3AC and 6AC cages, as seen in the MD simulations.
The presently computed longitudinal relaxation time for Xe(aq), T1 = 138.53 s, is in an excellent agreement with the previous experimental result of 137 ± 4 s at 293 K,17 albeit in that work also other relaxation mechanisms were reported to affect the experimental value. For the Xe@3AC and Xe@6AC systems, no directly comparable experimental data are available, but the T1 values of 16 s for Xe@0AC in C2D2Cl4 at 295 K80 and 12 s for Xe@6AC in D2O at 293 K, at a magnetic field of B0 = 11.7 T,48 have been reported. The present simulations predict somewhat slower relaxation of Xe than in these experiments. We suspect that the confinement potential used in the present droplet-model GFN-FF MD simulations might restrict the rotational motion of the Cr cages, leading to longer rotational correlation times and, in fact, slower Xe relaxation (see Fig. S4 and discussion in the ESI†). This issue is not present in the Xe(aq) MD simulations, however. More reliable MD trajectories could be obtained by using a larger droplet model with a thicker layer of solvent around the Xe@3AC and Xe@6AC systems, or, preferably, periodic boundary conditions. Longer MD trajectories would also be desirable for gaining improved DD TCF statistics at large values of the time offset τ.
 | ||
| Fig. 5 Results after the inversion of the cage protons for (a) 3AC and (b) 6AC cages. Results after the inversion of all protons in the system for (c) 3AC and (d) 6AC cages. | ||
All three methods predict that the 3AC and 6AC protons have a T1 around 1 s, which is roughly an order of magnitude smaller than what was found the encapsulated 129Xe. This is because the hydrogen atoms in the Cr cages have other hydrogens (both in the cage and the H2O solvent) relatively near, which renders the average DD couplings stronger than in the Xe-proton case. In addition, the gyromagnetic ratio of 1H is about a factor of four times larger than that of 129Xe. This increases the proton relaxation rates and, hence, decreases T1. The intermolecular relaxation of the cage protons caused by the water solvent amounts to roughly 20… 30% of the total longitudinal relaxation rate values, as shown in Fig. 2.
In the first simulated experiment in which only the cage protons are inverted, εH(3AC) = −1 shown in panels (a) and (b) of Fig. 5, the intramolecular relaxation of the Cr protons dominates because the water group remains close to thermal equilibrium. Apart from contributing to the self-relaxation rates, the water protons in this experiment only have a minor impact on the time evolution of the cage protons. We see that the simulated decay curves are roughly single-exponential, albeit some deviation is caused by cross-relaxation between the CnE groups.
In the second, εH = −1 experiment [Fig. 5(c) and (d)], also the intermolecular cross-relaxation with the water solvent becomes important. The H2O group relaxes relatively slowly as compared to the Cr protons. All presently computed cross-relaxation rates between the cage and the water protons are negative (see Fig. 2). Consequently, after inversion, the negative total magnetisation of the water group drives, in its part, the Cr groups towards the positive equilibrium magnetisation. Hence, cross-relaxation manifests itself in the effectively faster decay towards the equilibrium and leads to a smaller value of TFit1, as compared to the εH(xAC) = −1 simulation without water group inversion [see Table 1]. For t > 3…4 s, the inverted magnetisation of water acts as an additional source of polarisation that results in a long, positive “NOE magnetisation tail” of the cage protons.
In Fig. 6(a) and (b), we see that the TRate1 values are on average closer to TFit1 obtained from the εH = −1 simulations than to those obtained from the εH(xAC) = −1 simulations. This is because TRate1 is calculated by summing up the contributions from all homonuclear spins [eqn (15)], which effectively assumes that all protons are inverted in the NMR experiment (vide supra), corresponding exactly to the εH = −1 situation. The εH(3AC) = −1 simulations, where the water protons are not inverted, lead to TFit1 values that are systematically larger than TRate1. This results from the near-absence of cross-relaxation between the cage and water protons, which would drive the cage protons towards thermal equilibrium, as discussed above.
For the linker, acid and methoxy proton groups, which have no other nearby CnE spins [Fig. 3], the TRate1 values are very close to TFit1 obtained from the εH = −1 simulations. The situation is, however, very different for the aromatic and axial protons that belong to the CTB bowls of the Cr cages. In these cases, the differing self-relaxation rates and the presence of strong mutual cross-relaxation (see Fig. 2) render the difference between the TRate1 and TFit1 approaches to amount to roughly 15…30%, depending on which of the two cages and which proton group is investigated. This reflects the fact that approximating ΔMz,J(t) ≈ ΔMz,I(t) in eqn (18), which leads to the traditional MD–DD approach, is not necessarily justified between such CnE spin groups that do not have nearly identical self-relaxation rates, and which are connected by strong cross-relaxation. Magnetisation transfer between the aromatic and axial protons is seen to effectively intermix their observable relaxation times, which tend to, in the TFit1 simulations, converge towards an average of the two distinct TRate1 values of these spin groups.
The simulated T2 values, roughly 0.05…0.5 s in Fig. 6(c) and (d), are smaller than T1 by a factor of 2…15, depending on the proton group. Similarly as in the case of 129Xe, the J(0) term in the proton T2 [eqn (11) and (14)], which does not appear in the corresponding T1 expressions [eqn (6) and (9)], increases in importance due to the slow rotational tumbling of the Cr cage. The relative differences between the core and arm protons [see Fig. 3], particularly in the 3AC cage, becomes visible. This is because of their different dynamics; the slow rotation of the cage leads to a smaller value of T2 for the core protons than for the arm protons, which undergo less restricted, more dynamic motion. In the 6AC cage, the CH2COOH groups block each other sterically, which somewhat hinders their overall motions. This is different from the situation in the 3AC cage, where the acid protons are less restricted: the smaller methoxy groups on the opposite CTB bowl do not similarly block the mobility of the CH2COOH arms.96 Hence, the acid protons in 6AC are more dynamically similar to the core protons than in the 3AC cage, which leads to the predicted differences in T2.
Experimental relaxation times of the Cr protons are only available for the longitudinal magnetisation in the Xe@0AC(C2D2Cl4) system, at 295 K.80 Therein, T1 values of 0.39, 0.80, 0.31 and 0.83 s were measured for the linker, aromatic, axial and methoxy protons, respectively. The corresponding, presently simulated values of 0.59/0.55, 1.28/1.32, 0.85/1.06 and 1.51 s for the 3AC/6AC cages, are in an order-of-magnitude agreement with these experimental data. As discussed above, we believe that the quality of the MD simulations may contribute to this discrepancy. In addition, the different cage structures and solvents can induce significant differences in the proton relaxation dynamics. In our simulations, the rotational correlation times of the 3AC/6AC cages in H2O (1.38 and 1.48 ns) are much larger than that measured for the 0AC cage in C2D2Cl4 (0.60 ns). According to Fig. S4 (ESI†), in this correlation-time regime, the presently simulated, slower rotational dynamics corresponds to a longer T1—precisely as we see from the simulations results for the latter quantity.
4.2 Polarisation transfer
 , as in eqn (33) and (34), between Xe and each proton group, is shown in panels (c) and (d) of the Figure.
, as in eqn (33) and (34), between Xe and each proton group, is shown in panels (c) and (d) of the Figure.
 | ||
Fig. 7 (a) and (b) Transient SPINOE curves of the proton groups resulting from the presence of hyperpolarised Xe with εXe = 1000. (c) and (d)  [in units of Å−6] as in eqn (33) and (34). All water molecules of the simulation droplet were included in the water proton group. [in units of Å−6] as in eqn (33) and (34). All water molecules of the simulation droplet were included in the water proton group. | ||
Fig. 7(a) and (b) show the typical shape of a transient NOE peak, now resulting from the presence of hp Xe with εXe = 1000. The maximum SPINOE enhancement of the protons is in the range of 4…13%. The maxima are reached at roughly t0 = 2…4 s, after which the protons decay following the relaxation of 129Xe, as is seen by comparing with Fig. 4. Inside the Cr cages, the hp Xe acts as a source of polarisation for the surrounding protons, prolonging their relaxation times as compared to the situation without Xe hyperpolarisation.
Because the Xe-proton DD couplings and the resulting cross-relaxation rates depend on the interatomic distances as 1/r6, the distance distribution of the protons around the encapsulated Xe is an important factor in the SPINOE transfer. Fig. 7(c) and (d) show that the values of the ensemble average  (at the asymptotic limit, RXe–H > 7 Å) for the different proton groups are reflected in the SPINOE enhancements [panels (ab)], but do not alone determine the relative size of the latter. SPINOE is also affected by the self-relaxation rates of the protons, as was discussed in connection with eqn (27). For both Xe@3AC and Xe@6AC, the linker and aromatic protons reside on average in close proximity to the encapsulated Xe (see Fig. 1 and 3). This renders the DD couplings of the Xe-linker and Xe-aromatic pairs strong, as implied by the
(at the asymptotic limit, RXe–H > 7 Å) for the different proton groups are reflected in the SPINOE enhancements [panels (ab)], but do not alone determine the relative size of the latter. SPINOE is also affected by the self-relaxation rates of the protons, as was discussed in connection with eqn (27). For both Xe@3AC and Xe@6AC, the linker and aromatic protons reside on average in close proximity to the encapsulated Xe (see Fig. 1 and 3). This renders the DD couplings of the Xe-linker and Xe-aromatic pairs strong, as implied by the 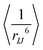 values. The fact that the linker protons relax much faster as compared to the aromatic protons (Fig. 6), is clearly reflected in the SPINOE peaks. Polarisation transfer to the aromatic protons is the strongest among all the proton groups, whereas that to the linker protons is clearly weaker. According to the
values. The fact that the linker protons relax much faster as compared to the aromatic protons (Fig. 6), is clearly reflected in the SPINOE peaks. Polarisation transfer to the aromatic protons is the strongest among all the proton groups, whereas that to the linker protons is clearly weaker. According to the  values, in the Xe@3AC system the linker protons have on average a slightly larger DD coupling to Xe than in the Xe@6AC case. This leads to a higher SPINOE enhancement in the 3AC cage. In both systems, protons in the axial group reside far away from the xenon atom, which weakens their DD couplings and SPINOE transfer. As was discussed earlier, the acid groups of the 6AC cage extend further out into the solvent and block each other from getting close to Xe. In contrast, in the 3AC cage, the methoxy and acid protons are able to reach positions in close vicinity of xenon. These features are reflected in the
values, in the Xe@3AC system the linker protons have on average a slightly larger DD coupling to Xe than in the Xe@6AC case. This leads to a higher SPINOE enhancement in the 3AC cage. In both systems, protons in the axial group reside far away from the xenon atom, which weakens their DD couplings and SPINOE transfer. As was discussed earlier, the acid groups of the 6AC cage extend further out into the solvent and block each other from getting close to Xe. In contrast, in the 3AC cage, the methoxy and acid protons are able to reach positions in close vicinity of xenon. These features are reflected in the  and SPINOE values.
and SPINOE values.
However, even considering both the average Xe-proton DD couplings and the self-relaxation rates of the proton spins, is not sufficient to understand the relative order of the individual simulated SPINOE enhancements. Yet another important mechanism, which affects the efficiency of the SPINOE transfer, is provided by the proton–proton cross-relaxation, i.e., spin diffusion. In Fig. 8, the simulated results are compared with those predicted by the pseudo two-spin model of eqn (27), where the latter neglects the proton–proton cross-relaxation. We see that for the aromatic protons, the two-spin model predicts results that are slightly higher than, but still in good agreement with the full simulations. This is because these protons on average reside relatively close to the Xe guest, such that most of their SPINOE enhancement is a result of direct DD coupling to the xenon nucleus [Fig. 7(c) and (d)]. In contrast, the linker, axial, methoxy and acid protons receive a higher SPINOE enhancement in the simulations than what eqn (27) predicts. Due to the proton–proton cross-relaxation network in the systems (see the off-diagonal elements in Fig. 2), polarisation transfer from the hp Xe is mediated by the aromatic protons, which are in strong contact with Xe and relax relatively slowly, to the faster-relaxing linker and axial protons. Then, the proton–proton cross-relaxation network conveys the polarisation to the methoxy and acid protons, as well. This is reflected in the higher SPINOE maxima predicted for these spin groups by the full simulations, which include spin diffusion effects. It can be concluded that the SPINOE polarisation transfer in the Xe@cryptophane systems is a fairly complicated process influenced by three effects: direct Xe-proton cross-relaxation, proton self-relaxation and proton–proton cross-relaxation.
 | ||
| Fig. 8 Maximum SPINOE transfer to the 3AC and 6AC cage protons from hyperpolarised Xe with enhancement factor εXe = 1000. Simulations that account for proton–proton cross-relaxation are compared to the pseudo two-spin model of eqn (27). | ||
The present simulations were performed at B0 = 9.4 T. We note that, at lower magnetic fields, the proton SPINOE enhancement relative to the thermal polarisation would be much greater in magnitude. Xe hyperpolarisation factors εXe exceeding the value of 1000 used in this paper can nowadays be obtained with modern SEOP setups.
4.3 Effect of chemical exchange
Xenon exchange between the solution and cryptophane cage confinement is treated using the two-site model described above, in the Section Theoretical Background. The longitudinal relaxation times of 129Xe and the SPINOE transfer to the Cr protons are studied as a function of νex ranging from the situation of no exchange (νex = 0) to a rapid exchange with νex = 103 s−1, corresponding to a typical Xe exchange rate in Xe@Cage(aq) systems. We also simulate the 129Xe NMR spectrum as obtained by the present multiscale modelling paradigm (see theoretical background), with the equilibrium constant Ka = 6800 M−1 [experimental result for Xe@6AC(aq)48] constituting the only empirical input. The presently computed transverse relaxation times TRate2 are used, and the CS values of the free and host-bound Xe are adopted from our earlier work.95 We restrict ourselves to the Xe@6AC system, since both the experimental Ka value and the earlier CS calculations involved the 6AC cage. As such, the present methodology can be readily applied for the Xe@3AC, or any other Xe@host system. which is appropriate for exchange that is fast with respect to the relaxation times of the individual exchanging sites. Due to the relatively slow relaxation of 129Xe, the above formula continues, in fact, to be applicable down to νex ≈ 1 s−1, as can be seen from Fig. 9. Note that this situation does not yet, however, correspond to fast exchange in the sense of the difference in the resonance frequencies of the two sites. We will return to this issue below, in the discussion of the 129Xe NMR spectrum.
which is appropriate for exchange that is fast with respect to the relaxation times of the individual exchanging sites. Due to the relatively slow relaxation of 129Xe, the above formula continues, in fact, to be applicable down to νex ≈ 1 s−1, as can be seen from Fig. 9. Note that this situation does not yet, however, correspond to fast exchange in the sense of the difference in the resonance frequencies of the two sites. We will return to this issue below, in the discussion of the 129Xe NMR spectrum.
 | ||
| Fig. 10 (a) SPINOE transfer from hp 129Xe to the 6AC protons as a function of νex for the free and host-bound sites. (b) Total SPINOE transfer. | ||
Fig. 10(b) shows the total SPINOE transfer, equalling the sum of the free and bound sites. The total SPINOE increases with the Xe exchange rate, until the plateau at νex = 100 s−1 is reached. This can be understood based on the very slow relaxation of 129Xe in the free site (T1 = 138.53 s, see Table 1). In water solution, the hp 129Xe retains its high magnetisation level for a long time. Through the chemical exchange, the pool of host-bound Xe spins is replenished from the free Xe pool, which, during the timescale of the SPINOE transfer (2…5 s, see t0 values in Table 1), has not had time to relax by a substantial amount. Thus, the free site in this case acts as a long-lived “storage” of hyperpolarisation, which eventually is conveyed to the cage protons via chemical exchange. The resulting overall increase in the SPINOE transfer with νex = 100 s−1 amounts up to 40%, as compared to the situation with no exchange.
 . In this case the system is in the slow-exchange regime. The peak on the left with CS of 182 ppm corresponds to Xe(aq), and the one on the right to Xe@6AC(aq) at 67 ppm. These are the first-principles calculated shift values from ref. 95. The intensities of the peaks are proportional to the populations pf = 0.32 and pb = 0.68. When the exchange rate increases towards the bottom of the figure, a characteristic, asymmetric exchange broadening of the peaks takes place and a crossover occurs at νex ≈ |Δω|. At this point, the exchange broadening affects the spectrum the most and the combined peak is barely visible. When νex increases further, towards the fast-exchange regime
. In this case the system is in the slow-exchange regime. The peak on the left with CS of 182 ppm corresponds to Xe(aq), and the one on the right to Xe@6AC(aq) at 67 ppm. These are the first-principles calculated shift values from ref. 95. The intensities of the peaks are proportional to the populations pf = 0.32 and pb = 0.68. When the exchange rate increases towards the bottom of the figure, a characteristic, asymmetric exchange broadening of the peaks takes place and a crossover occurs at νex ≈ |Δω|. At this point, the exchange broadening affects the spectrum the most and the combined peak is barely visible. When νex increases further, towards the fast-exchange regime  a single peak at the population-weighted average CS, δ = pfδf + pbδb ≈ 104 ppm, is seen.
a single peak at the population-weighted average CS, δ = pfδf + pbδb ≈ 104 ppm, is seen.
5 Conclusions
Dynamic modelling of large, conformationally flexible molecules and their magnetisation dynamics remains a challenge in computational NMR. On the one hand, fully quantum-mechanical spin dynamics simulations, which incorporate relaxation effects, offer accurate insights into the behaviour of small and relatively rigid molecules. These methods face, however, scalability issues when applied to large molecular systems and/or cases requiring intermolecular relaxation, such as in aqueous solvation environments of relevance to biological applications. On the other hand, molecular dynamics simulations have been used to model particularly the dipole–dipole relaxation in scenarios where full spin dynamics simulations have been unfeasible. Unfortunately the traditional MD–DD approaches have typically neglected cross-relaxation effects, which are responsible for the NOE polarisation transfer, between chemically non-equivalent spin groups. This limitation has complicated direct comparison between experimentally determined relaxation rates and those derived from MD–DD simulations.This work bridges the methodological gap between fully quantum-mechanical spin dynamics simulations and conventional MD–DD methods. We have developed new multiscale modelling techniques for simulating the longitudinal relaxation dynamics in large, flexible molecular systems. Specifically, we improved upon traditional MD–DD modelling by incorporating cross-relaxation effects and directly propagating the equations of motion for the magnetisation observables. This also facilitates the inclusion of chemical exchange processes in relaxation modelling across arbitrary exchange rate regimes. The newly developed methods enable simulation of not only relaxation but also that of polarisation transfer among spins and between the chemically exchanging sites.
Computational feasibility was achieved by partitioning a large spin system into groups of chemically equivalent nuclei, allowing fast simulations on a standard laptop computer. Starting from the Solomon equations, we derived a set of differential equations that generalise the conventional MD–DD approach for spin systems including chemically non-equivalent nuclei, maintaining rigour in the expressions of the spectral densities involving two different spin groups, and presented the computational approach for determining DD relaxation rates between the spin groups and simulating their time evolution.
The developed methods were applied to examine longitudinal magnetisation dynamics in three model systems pertinent to the field of 129Xe NMR biosensors: Xe(aq), Xe@3AC(aq) and Xe@6AC(aq), where 3AC and 6AC are water-soluble derivatives of cryptophane-A. In these Xe@host systems, Xe hyperpolarisation, DD relaxation, and Xe exchange are interdependent, and the present methods enable their simultaneous modelling. Additionally, the 129Xe NMR spectrum was simulated under various exchange conditions. Xe and proton relaxation times, NOE and SPINOE polarisation transfer, and the impact of chemical exchange on these features, were reported. This work establishes a foundation for studying DD relaxation and cross relaxation-mediated polarisation transfer across diverse molecular systems, including those in non-deuterated solvents. Our principal message is that the analysis methodology introduced here is highly general and allows for systematic and theoretically consistent generation of computational data for direct comparison with experiments, provided that carefully calibrated MD force fields are employed and sufficient statistics is reached. The rigorous analysis of the magnetisation dynamics data may, in turn, also aid in the development of the force fields. The present capability for relaxation modelling opens up new avenues for studying Xe@host systems, complementing existing work focused on Xe chemical shifts as means of achieving chemical resolution in sensor applications. We hope that these advances in modelling relaxation and Xe-proton SPINOE experiments will foster new experimental studies in the field, including those involving selective inversion-recovery pulses and/or combined 1H and 129Xe pulse sequences.
Author contributions
P. Hilla was responsible for data curation, general investigation, software coding, visualisation of methods and results, and writing of the original draft; J. Vaara supervised the entire work. Both authors contributed together to conceptualisation of the project and reviewing/editing of the manuscript.Data availbility
The Rela2x Jupyter Notebook file supporting this article has been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Joni Eronen, Pau Mayorga Delgado, Anu Kantola and Ville-Veikko Telkki (Oulu) are thanked for many useful discussions. Funding from Jenny and Antti Wihuri foundation and the University of Oulu Graduate School is appreciated (P. H.). We acknowledge funding from the Academy of Finland (grants 331008 and 361326) and U. Oulu (Kvantum Institute).Notes and references
- J. Kowalewski and L. Mäler, Nuclear Spin Relaxation in Liquids, CRC Press, 2nd edn, 2018 Search PubMed.
- A. W. Overhauser, Phys. Rev., 1953, 92, 411–415 CrossRef CAS.
- G. Navon, Y. Song, T. Rom, S. Appelt, R. E. Taylor and A. Pines, Science, 1996, 271, 1848–1850 CrossRef CAS.
- Y. Song, B. M. Goodson, R. E. Taylor, D. D. Laws, G. Navon and A. Pines, Angew. Chem., Int. Ed. Engl., 1997, 36, 2368–2370 CrossRef CAS.
- T. Pietraß, Colloids Surf., 1999, 158, 51–57 CrossRef.
- Y.-Q. Song, Concepts Magn. Reson., 2000, 12, 6–20 CrossRef CAS.
- G. Lippens, D. van Belle, S. J. Wodak and J. Jeener, Mol. Phys., 1993, 80, 1469–1484 CrossRef CAS.
- M. Odelius, A. Laaksonen, M. H. Levitt and J. Kowalewski, J. Magn. Reson., Ser. A, 1993, 105, 289–294 CrossRef CAS.
- M. Luhmer, A. Moschos and J. Reisse, J. Magn. Reson., Ser. A, 1995, 113, 164–168 CrossRef CAS.
- C. Peter, X. Daura and W. F. van Gunsteren, J. Biomol. NMR, 2001, 20, 297–310 CrossRef CAS PubMed.
- J.-P. Grivet, J. Chem. Phys., 2005, 123, 034503 CrossRef PubMed.
- J. T. Gerig, Mol. Simul., 2012, 38, 1085–1093 CrossRef CAS.
- P. M. Singer, D. Asthagiri, W. G. Chapman and G. J. Hirasaki, J. Magn. Reson., 2017, 277, 15–24 CrossRef CAS PubMed.
- A. Philips and J. Autschbach, Phys. Chem. Chem. Phys., 2019, 21, 26621–26629 RSC.
- D. Asthagiri, W. G. Chapman, G. J. Hirasaki and P. M. Singer, J. Phys. Chem. B, 2020, 142, 10802–10810 CrossRef PubMed.
- P. S. Hubbard, Phys. Rev., 1963, 131, 275–282 CrossRef CAS.
- I. E. Dimitrov, R. Reddy and J. S. Leigh, J. Magn. Reson., 2000, 145, 302–306 CrossRef CAS PubMed.
- M. Gerken and G. J. Schrobilgen, Coord. Chem. Rev., 2000, 197, 335–395 CrossRef CAS.
- B. Goodson, J. Magn. Reson., 2002, 155, 157–216 CrossRef CAS PubMed.
- A.-M. Oros and N. J. Shah, Phys. Med. Biol., 2004, 49, 105–153 CrossRef PubMed.
- D. Raftery, Annu. Rep. NMR Spectrosc., 2006, 57, 206–261 CrossRef.
- K. Bartik, M. Luhmer, J.-P. Dutasta, A. Collet and J. Reisse, J. Am. Chem. Soc., 1998, 120, 784–791 CrossRef CAS.
- T. Brotin and J.-P. Dutasta, Chem. Rev., 2009, 109, 88–130 CrossRef CAS PubMed.
- G. El-Ayle and K. Travis, Comprehensive Supramolecular Chemistry II, Elsevier, 2017, pp. 199–249 Search PubMed.
- T. Walker and W. Happer, Rev. Mod. Phys., 1997, 69, 629–642 CrossRef CAS.
- J. Eills, D. Budker, S. Cavagnero, E. Y. Chekmenev, S. J. Elliott, S. Jannin, A. Lesage, J. Matysik, T. Meersmann and T. Prisner, et al. , Chem. Rev., 2023, 123, 1417–1551 CrossRef CAS PubMed.
- A. Cherubini and A. Bifone, Prog. Nucl. Magn. Reson. Spectrosc., 2003, 42, 1–30 CrossRef CAS.
- B. Driehuys, Science, 2006, 314, 432–433 CrossRef PubMed.
- M. M. Spence, S. M. Rubin, I. E. Dimitrov, E. J. Ruiz, D. E. Wemmer, A. Pines, S. Qin Yao, F. Tian and P. G. Schultz, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10654–10657 CrossRef CAS PubMed.
- M. Spence, J. Ruiz, S. Rubin, T. Lowery, N. Winssinger, P. Schultz, D. Wemmer and A. Pines, J. Am. Chem. Soc., 2004, 126, 15287–15294 CrossRef CAS PubMed.
- P. Berthault, G. Huber and H. Desvaux, Prog. NMR Spectrosc., 2009, 55, 35–60 CrossRef CAS.
- O. Taratula and I. J. Dmochowski, Curr. Opin. Chem. Biol., 2010, 14, 97–104 CrossRef CAS PubMed.
- K. Palaniappan, M. Francis, A. Pines and D. Wemmer, Isr. J. Chem., 2014, 54, 104–112 CrossRef CAS.
- L. Schröder, Phys. Med., 2013, 29, 3–16 CrossRef PubMed.
- Y. Wang and I. J. Dmochowski, Acc. Chem. Res., 2016, 49, 2179–2187 CrossRef CAS PubMed.
- J. Jayapaul and L. Schröder, Molecules, 2020, 25, 4627 CrossRef CAS PubMed.
- T. Brotin, A. Lesage, L. Emsley and A. Collet, J. Am. Chem. Soc., 2000, 122, 1171–1174 CrossRef CAS.
- T. Brotin, T. Devic, A. Lesage, L. Emsley and A. Collet, Chem. – Eur. J., 2001, 7, 1561–1573 CrossRef CAS PubMed.
- T. Brotin and J.-P. Dutasta, Eur. J. Org. Chem., 2003, 973–984 CrossRef CAS.
- H. Fogarty, P. Berthault, T. Brotin, G. Huber, H. Desvaux and J.-P. Dutasta, J. Am. Chem. Soc., 2007, 129, 10332–10333 CrossRef CAS PubMed.
- A. Hill, Q. Wei, R. Eckenhoff and I. Dmochowski, J. Am. Chem. Soc., 2007, 129, 9262–9263 CrossRef PubMed.
- G. Huber, L. Beguin, H. Desvaux, T. Brotin, H. Fogarty, J.-P. Dutasta and P. Berthault, J. Phys. Chem. A, 2008, 112, 11363–11372 CrossRef CAS PubMed.
- S. Korchak, W. Kilian and L. Mitschang, Chem. Commun., 2015, 51, 1721–1724 RSC.
- S. Korchak, W. Kilian, L. Schröder and L. Mitschang, J. Magn. Reson., 2016, 265, 139–145 CrossRef CAS PubMed.
- S. Korchak, T. Riemer, W. Kilian and L. Mitschang, Phys. Chem. Chem. Phys., 2018, 20, 1800–1808 RSC.
- M. Kunth and L. Schröder, Chem. Sci., 2021, 12, 158–169 RSC.
- P. Hilla and J. Vaara, Phys. Chem. Chem. Phys., 2022, 24, 17946–17950 RSC.
- G. Huber, T. Brotin, L. Dubois, H. Desvaux, J.-P. Dutasta and P. Berthault, J. Am. Chem. Soc., 2006, 128, 6239–6246 CrossRef CAS PubMed.
- A. Hill, Q. Wei, T. Troxler and I. Dmochowski, J. Am. Chem. Soc., 2009, 131, 3069–3077 CrossRef PubMed.
- P. Berthault, H. Desvaux, T. Wendlinger, M. Gyejacquot, A. Stopin, T. Brotin, J.-P. Dutasta and Y. Boulard, Chem. – Eur. J., 2010, 16, 12941–12946 CrossRef CAS PubMed.
- R. Fairchild, A. Joseph, T. Holman, H. Fogarty, T. Brotin, J.-P. Dutasta, C. Boutin, G. Huber and P. Berthault, J. Am. Chem. Soc., 2010, 132, 15505–15507 CrossRef CAS PubMed.
- D. R. Jacobson, N. S. Khan, R. Collé, R. Fitzgerald, L. Laureano-Pérez, Y. Baa and I. J. Dmochowski, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10969–10973 CrossRef CAS PubMed.
- K. Ward, A. Aletras and R. Balaban, J. Magn. Reson., 2000, 143, 79–87 CrossRef CAS PubMed.
- L. Schröder, T. Lowery, C. Hilty, D. Wemmer and A. Pines, Science, 2006, 314, 446–449 CrossRef PubMed.
- M. Zaiss, M. Schnurr and P. Bachert, J. Chem. Phys., 2012, 131, 144106 CrossRef PubMed.
- M. Kunth, C. Witte and L. Schröder, J. Chem. Phys., 2014, 141, 1–9 CrossRef PubMed.
- V. Batarchuk, Y. Shepelytskyi, V. Grynko, A. H. Kovacs, A. Hodgson, K. Rodriguez, R. Aldossary, T. Talwar, C. Hasselbrink and I. C. Ruset, et al. , Int. J. Mol. Sci., 2024, 25, 1939 CrossRef CAS PubMed.
- Y. Bai, A. Hill and I. Dmochowski, Anal. Chem., 2012, 84, 9935–9941 CrossRef CAS PubMed.
- M. D. Gomes, P. Dao, K. Jeong, C. C. Slack, C. C. Vassiliou, J. A. Finbloom, M. B. Francis, D. E. Wemmer and A. Pines, J. Am. Chem. Soc., 2016, 138, 9747–9750 CrossRef CAS PubMed.
- H. W. Long, H. C. Gaede, J. Shore, L. Reven, C. R. Bowers, J. Kritzenberger, T. Pietrass and A. Pines, J. Am. Chem. Soc., 1993, 115, 8491–8492 CrossRef CAS.
- H. C. Gaede, Y. Song, R. E. Taylor, E. J. Munson, J. A. Reimer and A. Pines, Appl. Magn. Reson., 1995, 8, 373–384 CrossRef CAS.
- K. Bartik, M. Luhmer, S. J. Heyes, R. Ottinger and A. J. Reisse, J. Magn. Reson., 1995, 109, 164–168 CrossRef CAS.
- Y. Xu and P. Tang, Biochim. Biophys. Acta, 1997, 1323, 154–162 CrossRef CAS PubMed.
- S. M. Rubin, M. M. Spence, B. M. Goodson, D. E. Wemmer and A. Pines, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 9472–9475 CrossRef CAS PubMed.
- A. Stith, T. K. Hitchens, D. P. Hinton, S. S. Berr, B. Driehuys, J. R. Brookeman and R. G. Bryant, J. Magn. Reson., 1999, 139, 225–231 CrossRef CAS PubMed.
- H. Desvaux, T. Gautier, G. L. Goff, M. Pétro and P. Berthault, Eur. Phys. J. D, 2000, 12, 289–296 CrossRef CAS.
- S. Appelt, F. W. Haesing, S. Baer-Lang, N. J. Shah and B. Blümich, Chem. Phys. Lett., 2001, 346, 263–269 CrossRef.
- H. Desvaux, L. Dubois, G. Huber, M. L. Quillin, P. Berthault and B. W. Matthews, J. Am. Chem. Soc., 2005, 127, 11676–11683 CrossRef CAS PubMed.
- M. Kelley, N. Bryden, S. W. Atalla and R. T. Branca, ChemPhysChem, 2023, 24, e202300284 CrossRef CAS PubMed.
- T. Rõõm, S. Appelt, R. Seydoux, E. L. Hahn and A. Pines, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11604–11610 CrossRef.
- M. Haake, A. Pines, J. A. Reimer and R. Seydoux, J. Am. Chem. Soc., 1997, 119, 11711–11712 CrossRef CAS.
- J. Smith, K. Knagge, L. J. Smith, E. MacNamara and D. Raftery, J. Magn. Reson., 2002, 159, 111–125 CrossRef CAS.
- X. Zhou, J. Luo, X. Sun, X. Zeng, S. Ding, M. Liu and M. Zhan, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 80, 052405 CrossRef.
- D. Raftery, E. MacNamara, G. Fisher, C. V. Rice and J. Smith, J. Am. Chem. Soc., 1997, 119, 8746–8747 CrossRef CAS.
- T. Pietraß, R. Seydoux and A. Pines, J. Magn. Reson., 1998, 133, 299–303 CrossRef PubMed.
- E. Brunner, M. Haake, A. Pines, J. Reimer and R. Seydoux, Chem. Phys. Lett., 1998, 290, 112–116 CrossRef CAS.
- E. Brunner, R. Seydoux, M. Haake, A. Pines and J. A. Reimer, J. Magn. Reson., 1998, 130, 145–148 CrossRef CAS PubMed.
- J. C. Leawoods, B. T. Saam and M. S. Conradi, Chem. Phys. Lett., 2000, 327, 359–364 CrossRef CAS.
- A. Cherubini, G. Payne, M. Leach and A. Bifone, Chem. Phys. Lett., 2003, 371, 640–644 CrossRef CAS.
- M. Luhmer, B. M. Goodson, Y.-Q. Song, D. D. Laws, L. Kaiser, M. C. Cyrier and A. Pines, J. Am. Chem. Soc., 1999, 121, 3502–3512 CrossRef CAS.
- H. Desvaux, J. G. Huber, T. Brotin, J.-P. Dutasta and P. Berthault, ChemPhysChem, 2003, 4, 384–387 CrossRef CAS PubMed.
- L. Dubois, P. Berthault, J. G. Huber and H. Desvaux, C. R. Phys., 2004, 5, 305–313 CrossRef CAS.
- L. Dubois, S. Parrès, J. G. Huber, P. Berthault and H. Desvaux, J. Phys. Chem. B, 2004, 108, 767–773 CrossRef CAS.
- P. Berthault, C. Boutin, E. Léonce, E. Jeanneau and T. Brotin, ChemPhysChem, 2017, 18, 1561–1568 CrossRef CAS PubMed.
- A. Karabanov, I. Kuprov, G. T. P. Charnock, A. van der Drift, L. J. Edwards and W. Köckenberger, J. Chem. Phys., 2011, 135, 084106 CrossRef PubMed.
- I. Solomon, Phys. Rev., 1955, 99, 559–565 CrossRef CAS.
- P. Hilla and J. Vaara, J. Magn. Reson., 2025, 372, 107828 CrossRef CAS PubMed.
- I. Kuprov, Spin: From Basic Symmetries to Quantum Optimal Control, Springer, 2023 Search PubMed.
- P. Hilla, Rela2x, 2024, https://github.com/hillaper/Rela2x Search PubMed.
- T. Kluyver, B. Ragan-Kelley, F. Pérez, B. Granger, M. Bussonnier, J. Frederic, K. Kelley, J. Hamrick, J. Grout, S. Corlay, P. Ivanov, D. Avila, S. Abdalla, C. Willing and J. D. Team, Positioning and Power in Academic Publishing: Players, Agents and Agendas, IOS Press, 2016, pp. 87–90 Search PubMed.
- G. Lipari and A. Szabo, J. Am. Chem. Soc., 1982, 104, 4546–4559 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 2nd edn, 2017 Search PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 11, e01493 Search PubMed.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673 CrossRef CAS PubMed.
- P. Hilla and J. Vaara, Phys. Chem. Chem. Phys., 2023, 25, 22719–22733 RSC.
- P. Hilla and J. Vaara, J. Phys. Chem. B, 2024, 25, 3027–3036 CrossRef PubMed.
- H. Berendsen, J. Postma, W. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- TURBOMOLE V7.5.1, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, https://www.turbomole.org.
- Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. D. Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodyński, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, J. Chem. Theory Comput., 2023, 19, 6859–6890 CrossRef CAS PubMed.
- D. Peng, N. Middendorf, F. Weigend and M. Reiher, J. Chem. Phys., 2013, 138, 184105 CrossRef PubMed.
- Y. J. Franzke and F. Weigend, J. Chem. Theory Comput., 2019, 15, 1028–1043 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. V. Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, I. Polat, Y. Feng, E. W. Moore and J. VanderPlas, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- S. K. Lam, A. Pitrou and S. Seibert, ACM Proc., 2015, 1–6 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Discussion of cross-correlated dipole–dipole (DD) couplings, derivation of the equation of motion (EOM) of chemically equivalent spin groups, derivation of the EOM of population-weighted magnetisation in chemical exchange conditions, presently computed DD time-correlation functions, extraction of chemical exchange rates from the experimental association constant and 129Xe relaxation rate as a function of rotational correlation time. See DOI: https://doi.org/10.1039/d5cp00984g |
| This journal is © the Owner Societies 2025 |