The rhodium riddle: computational insights into competitive β-hydride vs. β-fluoride elimination

Abstract

Metal-catalyzed β-eliminations are elementary reaction mechanisms commonly leveraged in organometallic processes, including the renowned Mizoroki–Heck reaction. Although β-hydride elimination has traditionally been the focus of study, β-heteroatom elimination, in particular β-fluoride elimination, has seen a significant rise in contemporary organic methodologies. Intriguingly, rhodium(I) and palladium(II), which are isoelectronic, display opposite chemoselectivity for β-hydride vs. β-fluoride elimination. We investigated the origin of preferential β-fluoride over β-hydride elimination under rhodium(I) catalysis using density functional theory (DFT) calculations. Our modelling indicates that the kinetic preference is to undergo β-hydride elimination, but the observed chemoselectivity arises due to the reversible nature of the reaction. Additional modelling reveals that a Curtin–Hammett scenario enabled by reversibility of β-hydride elimination under the employed reaction conditions accounts for the enantioselectivity observed experimentally.

---

Introduction

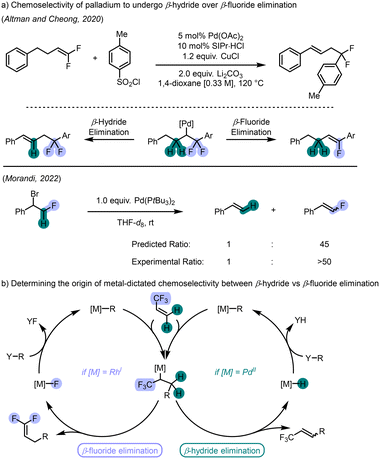
Fluorine-containing organic molecules have captured the attention of chemists for many years, owing to the unique properties imparted by the C–F bond.¹ Fluorine is the lowest molecular weight halogen and is the most electronegative atom in the periodic table. With a van Der Waals radius of 1.47 Å,² its steric effect tends to be minimal and its impact as a functional group is dominated by the highly polarized nature of its bonds. Unlike other halogens that tend to form reactive C–X bonds, the C–F bond is stronger and is challenging to activate, with a bond dissociation energy of 115 kcal mol⁻¹. By comparison, the C–Cl bond dissociation energy is only 83.7 kcal mol⁻¹ and the C–F bond is stronger than a C–H bond by approximately 10 kcal mol⁻¹.³ This enhanced bond strength, coupled with generally desirable lipophilic properties conferred by its incorporation,⁴ has propelled fluorine as a highly desirable component in medicinal chemistry,⁵ materials,⁶ and agrochemicals.⁷

In medicinal chemistry, the incorporation of fluorine atoms provide benefits aside from improved metabolic stability and lipophilicity, influencing conformation⁸ and attenuating basicity.^5c Fluorine atoms have been proposed to act as hydrogen bond acceptors in biological settings and to enable π-stacking interactions, playing a key role in increasing the potency of drug molecules compared to their non-fluorinated counterparts (Scheme 1a).⁹ Many fluorine-containing functional groups are bioisosteres of commonly utilized motifs in drug discovery (Scheme 1b).¹⁰ The earliest, and perhaps simplest, example of bioisosterism involving fluorine is the substitution of hydrogen atoms for fluorine atoms, again, typically to improve metabolic stability. Contemporary bioisosteres are more complex, containing varying topographies and interesting physicochemical properties, and have been used to replace more intricate functional groups. As an example, the gem-difluoroolefin has been leveraged as a carbonyl bioisostere and is present in various pesticides and bioactive compounds, such as phenstatin or artemisinin derivatives.¹¹gem-Difluoroolefins also serve as reliable platforms for functionalization to other value-added molecules, often with high levels of selectivity.¹² As such, methods enabling the synthesis of gem-difluoroolefins have seen remarkable advances and have been of increasing focus in the synthetic organic community.¹³

Scheme 1 Importance of fluorine in organic molecules.

One method for the synthesis of this functionality is from the corresponding trifluoromethyl compounds. Classical conditions relied on S_N2′-like reactions of strongly nucleophilic reagents with trifluoromethylolefins,¹⁴ Wittig-like,¹⁵ or Julia–Kocienski-like¹⁶ reactions. A milder method to access this valuable structural motif is via a transition metal-catalyzed β-fluoride elimination. Numerous transition metals have displayed the ability to perform this elementary step, wherein a metal alkyl species can undergo elimination to generate an alkene and the corresponding metal–fluoride.¹⁷

A meaningful understanding of this process can be obtained by comparison with the related β-hydride elimination reaction. The mechanistic underpinnings of the two elementary processes are similar. The β-fluoride elimination reaction is thought to occur via a syn co-planar conformation of the M–C–C–F dihedral angle, highly reminiscent of the orientation required in β-hydride elimination.^17c,d,18 The presence of a vacant coordination site at the metal center enables the formation of a 3-center, 2-electron agostic interaction consisting of σ_C–F → d donation.¹⁹ Mechanistically, these features exactly mirror those for syn stereospecific β-hydride elimination. However, the key differences lie in the nature of the C–H bond compared to the C–F bond and the formation of the resulting products. First, the C–F σ-orbital is significantly polarized toward the fluorine atom due to its greater electronegativity and is a poor donor.²⁰ Thus, the agostic interaction arising from a C–F bond is not as favourable as the agostic interaction from a C–H bond. It would follow that the C–F bond cleavage is less favoured from a thermodynamic perspective since it is stronger than a C–H bond. However, a general claim of this type cannot be made since the thermodynamics of a β-fluoride, in comparison to the corresponding β-hydride, elimination must also account for the other bonds forming in the reaction. If we assume that the strength of the metal–alkyl and metal–olefin bonds in both cases is approximately equal, then the thermodynamics will depend on the strength of the C–H and C–F bonds, as well as that of the metal–hydride and metal–fluoride bonds in the products. Although the strength of the C–F bond is greater than that of the C–H bond, the strength of the metal–fluoride bond²¹ is typically also greater than that of the corresponding metal–hydride bond,²² which could bias the thermodynamics in favour of β-fluoride elimination.²³

Our interest in this realm lies specifically in the observed chemoselectivity in β-hydride versus β-fluoride elimination in isoelectronic palladium(II) and rhodium(I) catalyst systems. In particular, palladium(II)–hydrides have been invoked as intermediates in countless mechanisms involving β-hydride elimination, most commonly in Mizoroki–Heck reactions.²⁴ Concurrently, β-fluoride elimination as an elementary process in catalysis involving palladium(II) has been established in the 90s²⁵ and has since been proven to be a facile process enabling syntheses of fluorinated alkenes.²⁶ Early computational work by Lin on model systems determined that there is a kinetic preference for palladium(II) to undergo β-hydride elimination over β-fluoride elimination.²⁷ Experimental and further computational evidence supporting these findings was later obtained by the Altman and Cheong groups in a copper- and palladium-catalyzed arylation reaction of gem-difluoroolefins using arylsulfonyl chlorides (Scheme 2a, top).²⁸ Following arylation of the gem-difluoroolefin, the resulting alkylpalladium complex could either undergo β-hydride or β-fluoride elimination, yet perfect selectivity was observed for the hydride elimination. The Morandi group similarly observed exclusive formation of olefin products arising from β-hydride elimination when competitive β-fluoride elimination was viable (Scheme 2a, bottom).²⁹

Scheme 2 (a) Previous reports by Altman and Cheong, and Morandi showcasing the chemoselectivity of palladium(II) for β-hydride elimination over β-fluoride elimination. (b) Investigation on the preference of rhodium(I) to undergo β-fluoride elimination (this work).

In 2008, Murakami reported the first example of a rhodium-catalyzed arylative defluorination reaction between aryl boron reagents and α-trifluoromethylstyrenes.³⁰ Interestingly, the reaction led to the near exclusive formation of the gem-difluoroolefin arising from β-fluoride elimination, despite competing β-hydride elimination available as an alternative pathway. Although the authors highlight that the reaction proceeds with high chemoselectivity for the β-fluoride elimination product, no rationale or explanation was provided. The exploitation of β-fluoride elimination reactions following a rhodium(I)-catalyzed C–C bond forming migratory insertion reaction of electron-poor alkenes was not explored further until 2016, when Hayashi reported the asymmetric variant.³¹ As in the case of Murakami, the reaction displayed remarkable chemoselectivity for the β-fluoride elimination pathway. The Lautens group later reported a rhodium-catalyzed defluorinative arylation reaction of secondary amides.³² Utilizing aryl potassium trifluoroborate salts and β-trifluoromethylacrylamides as electronically-biased Michael acceptors, the rhodium-catalyzed enantioselective arylation reaction occurs with inverted regiochemistry via polarity inversion of the α-position.³³ Interestingly, the alkylrhodium(I) intermediate could undergo a β-hydride elimination to afford the trisubstituted acrylamide, however products arising from this mechanistic pathway were never observed.

Palladium and rhodium are arguably two of the most privileged metal catalysts in organic synthesis, and β-eliminations are commonly observed for both metals. While the experimental trends observed in the literature show a clear preference for palladium to undergo β-hydride elimination and for rhodium to undergo β-fluoride elimination, there exists a fundamental gap accounting for this reactivity difference. We were interested in determining the origin of chemoselectivity for β-fluoride elimination over β-hydride elimination in rhodium(I) catalysis (Scheme 2b). To the best of our knowledge, the methods disclosed by Murakami, Hayashi, and our group are the only known examples of β-fluoride elimination occurring at rhodium(I) where, in theory, competing β-hydride elimination can also take place. Furthermore, all three reported systems are significantly different with respect to catalyst structure, although all three utilize diene ligands, and substrate choice. As described earlier, computational work by Lin and experimental work by Altman and Cheong, and Morandi both support that palladium catalysts prefer β-hydride elimination. Considering this preference of palladium to perform β-hydride elimination when β-fluoride elimination is also possible, we were curious why the same inclination was not also observed with rhodium(I) catalysts. We were particularly intrigued in the orthogonal behaviour between rhodium(I) and palladium(II) since these complexes are found on the same row of the periodic table, precluding differences due to relativistic effects³⁴ or atomic radii, and are isoelectronic d⁸-metal complexes and should display similar behaviour.

The significant preference for β-fluoride elimination in these systems renders experimental investigation difficult. In the studies by Hayashi and Murakami, products arising from β-hydride elimination pathways are formed as minor products in yields of less than 6%. The report by Lautens occurred with even greater chemoselectivity and no products arising from this mechanistic manifold were observed. Experiments deducing why one of these products is not formed are not simple to design and significant perturbation to the system would not provide adequate evidence for the observed reactivity. Thus, we reasoned that a computational approach would be more appropriate and would enable investigation into the apparent selectivity of rhodium(I) to undergo β-fluoride elimination.

Computational methods

All calculations were performed using density functional theory (DFT)³⁵ as implemented in the Jaguar 9.1 suite. Geometry optimizations were performed with the B3LYP³⁶ functional using Grimme's D3 dispersion correction.³⁷ The 6-31G(d,p) Pople basis set³⁸ was used for main group atoms. Rhodium was represented using the Los Alamos LACVP basis set which includes relativistic core potentials.³⁹ The energies of the optimized geometries were re-evaluated by single-point calculations using Dunning's correlation consistent triple-ζ basis set cc-pVTZ(-f)⁴⁰ which includes a double set of polarization functions and the M06 functional.⁴¹ Solvation energies were evaluated by a self-consistent reaction field (SCRF) approach⁴² based on accurate numerical solutions of the Poisson–Boltzmann equation. The solvation calculations were performed at the same level of theory as the geometry optimizations employing a dielectric constant of ε = 2.209 for 1,4-dioxane, ε = 10.3 for DCE, and ε = 9.135 for a 10 : 1 mixture of 1,4-dioxane : H₂O. As with all continuum models, the solvation energies are subject to empirical parameterization of the atomic radii that are used to generate the solute surface.⁴³ Analytical vibration frequencies within the Harmonic approximation were computed at the same level of theory as the geometry optimizations to confirm proper convergence to well-defined minima (no imaginary frequencies) or first-order saddle points (exactly one imaginary frequency) on the potential energy surface. Transitions states were further confirmed by IRC calculations.⁴⁴

The energy components were computed with the following protocol. The free energy in solution, G_sol, has been calculated as follows with T = 298.15 K, T = 373.15 K, T = 333.15 K, or T = 303.15 K to match the experimental conditions for each system under study.

G_sol = G_gas + G_solv (1)

G_gas = H_gas + TS_gas (2)

H_gas = E_SCF + ZPE (3)

ΔE_SCF = ∑ E_{SCF, products} – ∑ E_{SCF, reactants} (4)

ΔG_sol = ∑ G_{sol, products} – ∑ G_{sol, reactants} (5)

Investigation of a model system

We began our investigation by examination of a model system. We selected rhodium(I) complex 1 as our starting point (Scheme 3, top). The use of cyclooctadiene (COD) as the diene ligand reflects the consistent choice of dienes in the experimental conditions and it was used as the ligand by Murakami and by Lautens in generating the racemic products. Furthermore, 1 has a vacant coordination site that can accommodate interaction with either a β-C–H bond 2 or a β-C–F bond 3. Unlike the substrates used experimentally, this model system has an equivalent number of hydrogen and fluorine atoms. Unfortunately, the model complex 1 cannot be accessed via a C–C bond forming migratory insertion reaction and would not be amenable for catalysis. We chose the conformer in which the α-hydrogen was pointed toward the vacant coordination site of 1 as our starting point, since both β-agostic interactions would require bond rotation to form. To mimic the conditions used by Murakami, a solvent model using 1,4-dioxane was employed and entropy calculations were performed at 100 °C. The potential energy landscape for both β-hydride and β-fluoride eliminations from model complex 1 was computed (Scheme 3, bottom). The formation of the C–H agostic interaction forming 2 was found to be more exergonic (ΔG = −6.8 kcal mol⁻¹) than the formation of the C–F agostic interaction forming 3 (ΔG = −2.0 kcal mol⁻¹). Thus, 2 would be the likely resting state of the catalyst. The computational results can be rationalized since the C–F σ-orbital is highly polarized toward the fluorine atom and, based on electronegativity, is less likely to donate electron density to the rhodium atom.

Scheme 3 Reaction profile for β-hydride and -fluoride elimination for the model system.

Our calculations indicate that the β-hydride elimination path traversing 2-TS (ΔG^‡ = 6.5 kcal mol⁻¹) is more favoured than the β-fluoride elimination occurring via3-TS (ΔG^‡ = 9.4 kcal mol⁻¹, ΔΔG^‡ = 2.9 kcal mol⁻¹). This somewhat surprising result, considering the experimental observations, suggests that the rhodium(I) complex 1 has a kinetic preference for β-hydride elimination for the model system. Further examination of the reaction coordinate reveals that the formation of 4via β-hydride elimination is endergonic by 5.5 kcal mol⁻¹, relative to 2. However, the formation of 5 from 2 is endergonic by only 2.8 kcal mol⁻¹. This suggests that the formation of the rhodium(I)–fluoride species 5via β-fluoride elimination could be irreversible, while the formation of the rhodium(I)–hydride 4 can be reversible. Although not evaluated computationally, the resulting rhodium(I)–fluoride complex can react with an equivalent of base or an organoboron species via transmetalation in an irreversible fashion, driving the reaction. On the other hand, rhodium(I)–hydride complexes do not engage in this type of behaviour and, in the absence of an additional driving force, would terminate catalysis if re-insertion to the bound olefin was not viable. Taken together, the initial computational results suggest that the observed chemoselectivity for β-fluoride elimination under rhodium(I) catalysis may not be a kinetic preference, but an artifact of a thermodynamically-driven capture of a kinetically unfavorable intermediate. If this is the case, the observed product ratio between 4 and 5 would be approximately 1 : 35 at 100 °C based on the computed ΔΔG = −2.6 kcal mol⁻¹, which is more consistent with the experimental observation of real systems.

Rh-catalyzed arylative defluorination of α-CF₃ styrenes

We turned our attention to the rhodium-catalyzed arylative defluorination of trifluoromethyl styrenes developed by Murakami,³⁰ since this reaction was most similar to the model system we had developed (Scheme 4a). First, we investigated the potential energy surface for the observed β-fluoride elimination pathway. Starting from the olefin-bound phenyl–rhodium(I) complex 6, the migratory insertion step traversing through 6-TS was found to have an activation barrier of 8.3 kcal mol⁻¹ and afforded the alkyl–rhodium(I) species 7, featuring η²-coordination with the installed arene; this step is exergonic by 15.8 kcal mol⁻¹. For β-fluoride elimination to occur, the C–F agostic interaction must displace the η²-bound arene. Decoordination of the arene affording the alkylrhodium(I) complex with a vacant coordination site 8 was endergonic by 11.3 kcal mol⁻¹. Subsequent coordination of the C–F bond in an agostic fashion 9 was endergonic by a further 4.8 kcal mol⁻¹. The β-fluoride elimination occurs via9-TS at an energy of 3.8 kcal mol⁻¹. The activation energy for this process is approximately 19.5 kcal mol⁻¹ and affords the difluoroolefin-bound rhodium(I)–fluoride complex 10, the formation of which is exergonic by 5.4 kcal mol⁻¹ relative to the agostic complex 9.

Scheme 4 (a) Murakami's arylative defluorination of trifluoromethyl styrenes and the potential energy surface of the reaction mechanism. (b) Comparison of the two β-hydride elimination pathways in Murakami's defluorinative arylation.

Intermediates 7 and 8 serve as common intermediates for both β-elimination pathways and were used as starting points for examination of the β-hydride elimination (Scheme 4b). In this case, two possible pathways for β-hydride elimination exist, one forming the (E)-olefin and one forming the (Z)-olefin. Experimentally, only the (E)-olefin was observed but both pathways were calculated. Intermediate 11 features a C–H agostic interaction that enforces a trans relationship between the two phenyl rings and is exergonic by 3.6 kcal mol⁻¹ relative to 8. β-Hydride elimination via11-TS has an activation barrier of 17.6 kcal mol⁻¹ affording the (Z)-olefin–rhodium(I) complex 12, a process that is endergonic by 6.8 kcal mol⁻¹. In contrast, the formation of the C–H agostic interaction that places the two phenyl rings cis relative to each other 13 is slightly less exergonic (−2.8 kcal mol⁻¹ relative to 8). In this case, the β-hydride elimination transition state 13-TS has an activation barrier of only 3.2 kcal mol⁻¹, affording the (E)-olefin–rhodium(I) product 14 in a process that is endergonic by 2.7 kcal mol⁻¹. These results correlate well with experiments and suggest that the preferred product arising from β-hydride elimination should indeed be the (E)-olefin.

Analysis of 9-TS for β-fluoride elimination (Scheme 4a) and 13-TS for β-hydride elimination (Scheme 4b) again reveals that the rhodium(I) catalyst has a kinetic preference for the unobserved β-hydride elimination pathway. Under the reaction conditions, which employ an organoboron reagent that is activated by an equivalent of MeMgCl, the rhodium(I)–fluoride complex 10 can undergo a transmetalation reaction in an irreversible fashion, which serves to drive the reaction toward the observed difluoroolefin. On the other hand, both of the rhodium(I)–hydride complexes 12 and 14 are formed in an apparent reversible fashion and cannot be funneled in a manner that would liberate the olefin and enable catalysis.

At the onset of our investigation, we were hoping to find a unified explanation that could be applied for all three of the known experimental systems. Our analysis thus far has revealed that the observed selectivity for β-fluoride elimination over β-hydride elimination is likely due to the reactions occurring under thermodynamic control. While this explanation is understandable for the model system and Murakami's achiral reaction,³⁰ the observed product selectivity being a result of thermodynamics is not tractable for the method reported by Hayashi³¹ or Lautens.³² More specifically, these reactions are highly enantioselective. Thus, if the reaction is driven by thermodynamics under equilibrating conditions, then observation of a racemic mixture must necessarily occur. Therefore, we surmised that an alternative explanation must exist for the enantioselective rhodium-catalyzed defluorinative reactions.

Hayashi's enantioselective defluorinative arylation

Hayashi's asymmetric rhodium-catalyzed defluorinative arylation reported in 2016 utilized a protocol which featured a C₂-symmetric tetrafluorobenzobarrelene (tfb) ligand in aqueous dioxane, forming the desired gem-difluoroolefin product A in high yields and enantioselectivity (Scheme 5a).³¹ Notably, the alkene side product B was observed in low yields. The formation of this species was rationalized by competitive β-hydride elimination from alkyl rhodium(I) I, forming the rhodium–hydride complex II. Subsequent hydrorhodation affords isomeric alkyl rhodium(I) III, which undergoes β-oxygen elimination⁴⁵ to afford the olefin-bound species IV (Scheme 5b).

Scheme 5 (a) Enantioselective rhodium-catalyzed arylation–defluorination reaction of trifluoromethyl olefins and (b) β-hydride elimination pathway accounting for side product formation. (c) Reaction coordinate for the enantioselective defluorinative arylation developed by Hayashi in 2016.³¹

We began our investigation of the reaction by examining the rhodium–trifluoromethylolefin complex 15 (Scheme 5c). The enantioselectivity of the reaction is determined during the C–C bond forming migratory insertion of the olefin into the rhodium(I)–aryl bond. The transition state leading to the product with (S)-absolute configuration, 15-TS-(S), was found to have an activation barrier of 9.6 kcal mol⁻¹. By comparison, 15-TS-(R) leading to the enantiomeric product had a much larger activation energy of 22.4 kcal mol⁻¹. The alkyl rhodium(I) complex 16 features η²-coordination of the aryl group. Displacement of the aryl ring by the C–H σ-bond leading to agostic complex 17 was endergonic by 11 kcal mol⁻¹, which undergoes a β-hydride elimination traversing 17-TS, leading to olefin-bound rhodium species 18. Notably, this process has an activation barrier of 12.5 kcal mol⁻¹ from 16. By comparison, formation of the β-fluoride agostic complex 19 is endergonic by 15 kcal mol–1 from 16. The β-fluoride elimination occurs via19-TS leading to the difluoroolefin-bound rhodium–fluoride 20, with an activation barrier of 30.0 kcal mol⁻¹.

Although these results qualitatively support the experimental conditions, which require heat to promote the reaction, there are two troubling observations. Firstly, the quantum chemical calculations once again support that the β-hydride elimination pathway should be favourable over the observed β-fluoride elimination pathway. Secondly, the calculations predict that the enantiomer that should form during the course of the reaction is opposite to that experimentally observed. We will first examine the defluorinative reaction disclosed by Lautens before returning to this alarming finding.

Enantioselective defluorinative α-arylation

The Lautens group later reported a rhodium-catalyzed defluorinative arylation reaction of secondary amides using β-trifluoromethylacrylamides as electronically-biased Michael acceptors (Scheme 6a).³² In this fashion, the secondary amide 21 was formed in 84% yield and 96% ee. Whereas most rhodium-catalyzed arylation reactions functionalize the β-position, this report led to the exclusive formation of the α-arylated product, an alternative to traditional approaches.⁴⁶ The resulting alkyl–rhodium(I) complex 22 undergoes β-fluoride elimination to afford the olefin-bound rhodium(I) 23, which affords α-arylated, β,γ-unsaturated gem-difluoroolefin product 21 following ligand substitution (Scheme 6b, left). Interestingly, intermediate 22 could undergo a β-hydride elimination to afford the rhodium(I) complex 24, which would lead to the trisubstituted acrylamide, however products arising from this mechanistic pathway were never observed (Scheme 6b, right).

Scheme 6 (a) Enantioselective defluorinative arylation reaction and (b) possible reaction outcomes. (c) Energetic landscape for the β-fluoride elimination pathway in Lautens' enantioselective defluorinative α-arylation reaction.

The reaction developed by Lautens utilizes a C₁-symmetric catalyst and β-trifluoromethyl acrylamides. The conjugated olefin could react with the C₁-symmetric catalyst in either the s–cis or s–trans conformation at either enantiotopic face, leading to 8 possible encounter complexes for the initial migratory insertion. Only the lowest energy transition state leading to each enantiomer will be considered for this discussion (see the ESI† for more details). The lowest energy encounter complex 25 was chosen as the reference point (Scheme 6c).

The rhodium–olefin complex 26 at an energy of 6.1 kcal mol⁻¹ was found to lead to the lowest energy migratory insertion transition state 26-TS at 10.4 kcal mol⁻¹. 26-TS leads to the observed enantiomer and is 3.9 kcal mol⁻¹ lower in energy than the lowest energy enantiomeric transition state (see the ESI† for more details), in excellent agreement with the experimental observations. The direct product arising from 26-TS is the alkyl–rhodium(I) complex coordinated by the arene in an η²-fashion 27, found at −14.5 kcal mol⁻¹. Formation of the β-C–F agostic interaction 28 is endergonic by 17.5 kcal mol⁻¹, and subsequent β-fluoride elimination 28-TS was higher in energy by another 4.7 kcal mol⁻¹. This process forming the rhodium(I) complex bound to the product difluoroolefin 29 was exergonic by 4.6 kcal mol⁻¹ relative to 28. The β-fluoride elimination occurs with an activation barrier of 22.2 kcal mol⁻¹ relative to the η²-coordinated species 27.

Instead of forming the C–F agostic interaction, intermediate 27 could also undergo ligand substitution of the bound arene and form the C–H agostic interaction. Since we are using 27 as the common intermediate for these two competitive pathways, the activation energy of the β-hydride elimination transition state 27-TS was calculated relative to 27 with an activation energy of 17.7 kcal mol⁻¹, which is lower in energy than the β-fluoride elimination transition state 28-TS (Scheme 7a). This result is unsurprising based on our findings thus far, but indicates that the preferred pathway involves a stereoablative β-elimination leading to the achiral intermediate 30 in an endergonic fashion. An olefin facial swap occurring via decoordination and recoordination leads to 31 and is slightly exergonic. A hydrorhodation traversing 31-TS with an activation energy of 15.5 kcal mol⁻¹ leads to the C–H agostic intermediate 32. An endergonic ligand exchange to the C–F agostic complex 33 sets the stage for another β-fluoride elimination occurring via33-TS (ΔG^‡ = 7.4 kcal mol⁻¹ relative to 33) affording the rhodium–fluoride complex 34.

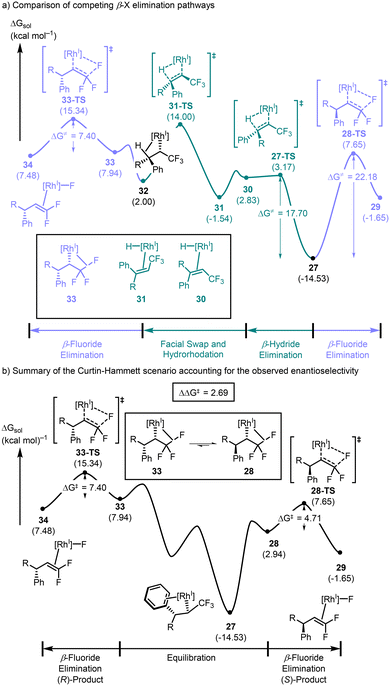Scheme 7 (a) Potential energy surface for competing β-hydride elimination and β-fluoride elimination, and (b) the Curtin–Hammett scenario explaining selectivity.

At first glance, this profile appears to suggest that the absolute configuration of the final product should be opposite to that which is observed since the β-hydride elimination pathway offers a low energy pathway that removes the chiral information imparted in the initial phase of the reaction. However, careful examination of the β-hydride elimination and reverse hydrorhodation steps suggests, again, that these processes should be reversible under the conditions of the reaction. Thus, if the two diastereomeric β-C–F agostic complexes 33 and 28 exist in equilibrium via these intermediary rhodium–olefin and rhodium–hydride complexes, then the observed product distribution should be governed by Curtin–Hammett kinetics (Scheme 7b).⁴⁷ In other words, the difference in activation energy between 28-TS and 33-TS, measured from the respective equilibrating β-C–F agostic complexes, will determine the observed selectivity. The computed ΔΔG^‡ of the reaction is 2.7 kcal mol⁻¹ in favour of the enantiomer with (S)-absolute configuration, in alignment with experimental observations. Interestingly, the ablation of the stereocenter installed in the migratory insertion step during the β-hydride elimination process suggests that the enantio-determining step is actually the β-fluoride elimination and not the C–C bond forming reaction.

Based on these results, we re-examined the Hayashi reaction discussed earlier. We discovered that our quantum chemical calculations were unable to account for the observed enantioselectivity based on the fact that the preferred C–C bond forming migratory insertion was favoured to give the experimentally unobserved isomer. In all of the cases examined in this work, β-hydride elimination has consistently been the kinetically favoured pathway, providing the catalyst an alternative pathway to enantioselectivity. We re-examined the potential energy surface of the defluorinative arylation of trifluoromethyl alkenes (Scheme 8).

Scheme 8 Curtin–Hammett scenario accounting for enantioselectivity in the defluorinative arylation reaction reported by Hayashi in 2016.³¹

As discussed earlier, the β-hydride elimination pathway occurring via17-TS is significantly favoured over β-fluoride elimination 19-TS. Facial swapping of the bound olefin converts rhodium–hydride 18 to its isomer 35. Hydrorhodation via35-TS leads to the β-hydride agostic complex 36. Ligand substitution to the β-fluoride agostic complex 37 is endergonic by 1.9 kcal mol⁻¹. Subsequent β-fluoride elimination traversing 37-TS leads to the difluoroolefin-bound rhodium–fluoride complex 38. Notably, dissociation of the product from 38 would lead to the observed enantiomer of the product. If we again consider that the β-hydride elimination/re-insertion pathway acts as a means of equilibration between diastereomeric rhodium complexes 19 and 37 containing β-fluoride agostic interactions, then the enantioselectivity would be determined by the difference in activation energy between 19-TS and 37-TS, and not the C–C bond forming migratory insertion (15-TS-(R) and 15-TS-(S)). Based on this, the favoured product is the one that forms through 37-TS (ΔΔG^‡ = 6.8 kcal mol⁻¹), which is indeed the enantiomer observed by Hayashi.

Comparison with palladium(II)

The DFT analysis presented thus far has consistently concluded that β-hydride elimination is the preferred elementary step for rhodium(I), and not β-fluoride elimination, as suggested by examples in the literature. This result caused us to question why the isoelectronic d⁸-complexes, namely, those of palladium(II), did not exhibit similar behaviour. The answer is remarkably simple: while rhodium(I) and palladium(II) are isoelectronic, the formal charge at each metal center is different. This controls the class of ligands bound to these complexes. More specifically, the rhodium(I) complexes typically accommodate one anionic X-type ligand, whereas the palladium(II) complexes can accommodate two. This subtle difference renders the β-hydride elimination reversible at rhodium(I), but irreversible at palladium(II) under typical reaction conditions. Under rhodium(I) catalysis, the formation of the rhodium(I)–hydride species represents an endergonic dead-end for catalysis, with no other mechanistic possibility except the reverse hydrorhodation reaction (Scheme 9a). In comparison, the formed palladium(II)–hydride species has an exit vector in the form of reductive elimination due to the presence of the second anionic X-type ligand (Scheme 9b). Under typical Mizoroki–Heck conditions, the presence of base sequesters the formed HX species and makes this process irreversible. Thus, the kinetically preferred β-hydride elimination is observed with great selectivity. These results suggest that future work could alter the chemoselectivity of rhodium(I) complexes toward β-hydride elimination by creating accessible pathways to divert the rhodium(I)–hydride species at a rate that outcompetes β-fluoride elimination.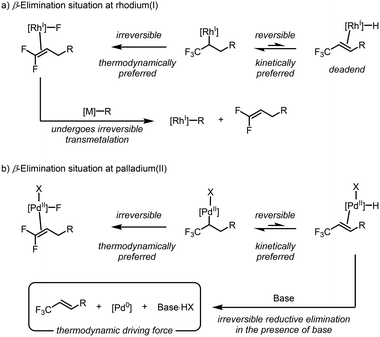

Scheme 9 Explanation for the different reactivity between (a) rhodium(I) and (b) palladium(II) when comparing β-hydride and β-fluoride elimination.

Conclusions

In conclusion, we have unveiled the origin of selectivity for the preferential β-fluoride elimination under rhodium(I) catalysis when competitive β-hydride elimination is possible. Our analysis of a designed model system reveals that the observed selectivity is not a kinetic preference, but a consequence of the thermodynamic conditions employed, enabling the reversibility of the β-hydride elimination. These conclusions were found to correlate well with the results observed by Murakami. In the case of the enantioselective defluorinative α-arylation developed by Hayashi and Lautens, the selectivity of the reaction was explained by invocation of a Curtin–Hammett scenario facilitated by a rapidly occurring and reversible, stereoablative β-hydride elimination. These results suggest that the enantioselectivity of the reaction is determined by β-fluoride elimination, and not in the C–C bond forming migratory insertion, as previously thought. In all studied cases, the computational work supported the experimental findings. The results provide further validation and support for the work disclosed by Lin,²⁷ Altman and Cheong,²⁸ and Morandi²⁹ in explaining the high levels of chemoselectivity for palladium(II) to undergo chemoselective β-hydride elimination.

This work discloses a comparison on rhodium(I) and palladium(II) species, which suggests that chemoselectivity can be obtained in β-hydride vs. β-fluoride elimination by the choice of metal catalyst – palladium(II) would lead to preferential β-hydride elimination, whereas rhodium(I) would lead to preferential β-fluoride elimination. Importantly, this work revealed that the chemoselectivity in this reaction class can be due to mechanistic pathways available to the metal catalyst and may not necessarily be affected by ligand choice. Thus, future methodologies studying chemoselective β-hydride and β-X elimination should consider which mechanistic pathways are available to the metal and not overly rely on ligand discovery, if the metal's intrinsic reactivity cannot be overridden or diverted. Broadly speaking, we anticipate that future work can utilize the disclosed results in designing new synthetic methodologies involving β-elimination with rhodium, palladium, and other organometallic species. We believe that this work provides fundamental understanding for elementary organometallic reaction mechanisms and will serve as a framework for methodology development leveraging chemoselective β-elimination as a crucial step in catalysis.

Data availability

All data are available in the ESI.†

Author contributions

BM: conceptualization, formal analysis, data curation, writing – original draft preparation, writing – review and editing; ML: funding acquisition, writing – review and editing; MHB: funding acquisition, writing – review and editing, supervision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Institute for Basic Science in Korea for financial support (IBS-R010-A1). BM thanks the Natural Science and Engineering Research Council (NSERC) for a CGS-D scholarship and a Michael Smith Foreign Study Supplement.

Notes and references

1. (a) K. Müller, C. Faeh and F. Diederich, Science, 2007, 317, 1881–1886; (b) C. Zhang, K. Yan, C. Fu, H. Peng, C. J. Hawker and A. K. Whittaker, Chem. Rev., 2022, 122, 167–208.
2. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
3. S. J. Blanksby and G. B. Ellison, Acc. Chem. Res., 2003, 36, 255–263.
4. S. Purser, P. R. Moore, S. Swallow and V. Gouverneur, Chem. Soc. Rev., 2008, 37, 320–330.
5. (a) J. Wang, M. Sánchez-Roselló, J. L. Aceña, C. del Pozo, A. E. Sorochinsky, S. Fustero, V. A. Soloshonok and H. Liu, Chem. Rev., 2014, 114, 2432–2506; (b) E. P. Gillis, K. J. Eastman, M. D. Hill, D. J. Donnelly and N. A. Meanwell, J. Med. Chem., 2015, 58, 8315–8359; (c) P. Shah and A. D. Westwell, J. Enzyme Inhib. Med. Chem., 2007, 22, 527–540; (d) I. Ojima, Fluorine in Medicinal Chemistry and Chemical Biology, Wiley & Sons, Limited, 2009; (e) Y. Zhou, J. Wang, Z. Gu, S. Wang, W. Zhu, J. L. Aceña, V. A. Soloshonok, K. Izawa and H. Liu, Chem. Rev., 2016, 116, 422–518.
6. (a) S.-K. Lee, Y. J. Lee, K. Cho, U.-H. Lee and J.-S. Chang, Bull. Korean Chem. Soc., 2021, 42, 286–289; (b) K. Lemoine, A. Hémon-Ribaud, M. Leblanc, J. Lhoste, J.-M. Tarascon and V. Maisonneuve, Chem. Rev., 2022, 122, 14405–14439; (c) S. Dolui, D. Kumar, S. Banerjee and B. Ameduri, Acc. Mater. Res., 2021, 2, 242–251; (d) R. Berger, G. Resnati, P. Metrangolo, E. Weber and J. Hulliger, Chem. Soc. Rev., 2011, 40, 3496–3508; (e) F. Babudri, G. M. Farinola, F. Naso and R. Ragni, Chem. Commun., 2007, 1003–1022; (f) Y. Wang, X. Yang, Y. Meng, Z. Wen, R. Han, X. Hu, B. Sun, F. Kang, B. Li, D. Zhou, C. Wang and G. Wang, Chem. Rev., 2024, 124, 3494–3589; (g) Z. Fang, Y. Peng, X. Zhou, L. Zhu, Y. Wang, X. Dong and Y. Xia, ACS Appl. Energy Mater., 2022, 5, 3966–3978; (h) N. S. Keddie, A. M. Z. Slawin, T. Lebl, D. Philp and D. O'Hagan, Nat. Chem., 2015, 7, 483–488; (i) S. Song, H. I. Choi, I. S. Shin, H. Suh and Y. Jin, Bull. Korean Chem. Soc., 2014, 35, 2245–2250.
7. (a) J. Han, L. Kiss, H. Mei, A. M. Remete, M. Ponikvar-Svet, D. M. Sedgwick, R. Roman, S. Fustero, H. Moriwaki and V. A. Soloshonok, Chem. Rev., 2021, 121, 4678–4742; (b) Y. Ogawa, E. Tokunaga, O. Kobayashi, K. Hirai and N. Shibata, iScience, 2020, 23, 101467; (c) P. Jeschke, Pest Manage. Sci., 2024, 80, 3065–3087.
8. (a) L. Hunter, Beilstein J. Org. Chem., 2010, 6, 38; (b) L. E. Zimmer, C. Sparr and R. Gilmour, Angew. Chem., Int. Ed., 2011, 50, 11860–11871.
9. (a) F. Ibba, G. Pupo, A. L. Thompson, J. M. Brown, T. D. W. Claridge and V. Gouverneur, J. Am. Chem. Soc., 2020, 142, 19731–19744; (b) H. Y. K. Kaan, V. Ulaganathan, O. Rath, H. Prokopcová, D. Dallinger, C. O. Kappe and F. Kozielski, J. Med. Chem., 2010, 53, 5676–5683; (c) J. A. Olsen, D. W. Banner, P. Seiler, U. Obst Sander, A. D'Arcy, M. Stihle, K. Müller and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 2507–2511.
10. (a) N. A. Meanwell, J. Med. Chem., 2018, 61, 5822–5880; (b) S. Meyer, J. Häfliger and R. Gilmour, Chem. Sci., 2021, 12, 10686–10695.
11. (a) W. R. Moore, G. L. Schatzman, E. T. Jarvi, R. S. Gross and J. R. McCarthy, J. Am. Chem. Soc., 1992, 114, 360–361; (b) C. Leriche, X. He, C.-W. T. Chang and H.-W. Liu, J. Am. Chem. Soc., 2003, 125, 6348–6349.
12. (a) H. Zhang, E. Wang, S. Geng, Z. Liu, Y. He, Q. Peng and Z. Feng, Angew. Chem., Int. Ed., 2021, 60, 10211–10218; (b) H.-J. Tang, L.-Z. Lin, C. Feng and T.-P. Loh, Angew. Chem., Int. Ed., 2017, 56, 9872–9876; (c) Z. Zhu, L. Lin, J. Xiao and Z. Shi, Angew. Chem., Int. Ed., 2022, 61, e202113209; (d) Y. Zong and G. C. Tsui, Org. Lett., 2024, 26, 1261–1264; (e) Q. Ma, Y. Wang and G. C. Tsui, Angew. Chem., Int. Ed., 2020, 59, 11293–11297; (f) Y. Wang, X. Qi, Q. Ma, P. Liu and G. C. Tsui, ACS Catal., 2021, 11, 4799–4809; (g) H. Amii and K. Uneyama, Chem. Rev., 2009, 109, 2119–2183; (h) Y. Wang and G. C. Tsui, Org. Lett., 2023, 25, 6217–6221; (i) Z. Luo, Y. Zong and G. C. Tsui, Org. Lett., 2023, 25, 4406–4410; (j) H. Tan, Y. Zong, Y. Tang and G. C. Tsui, Org. Lett., 2023, 25, 877–882; (k) L. V. Hooker and J. S. Bandar, Angew. Chem., Int. Ed., 2023, 62, e202308880; (l) X. Lu, Y. Wang, B. Zhang, J.-J. Pi, X.-X. Wang, T.-J. Gong, B. Xiao and Y. Fu, J. Am. Chem. Soc., 2017, 139, 12632–12637; (m) Y.-Y. Zhang, Y. Zhang, X.-S. Xue and F.-L. Qing, Angew. Chem., Int. Ed., 2024, e202406324; (n) X. Huang, M. Ou, L. Hong, W. Qin and Y. Ma, ACS Catal., 2024, 14, 6432–6439; (o) H. Sakaguchi, Y. Uetake, M. Ohashi, T. Niwa, S. Ogoshi and T. Hosoya, J. Am. Chem. Soc., 2017, 139, 12855–12862.
13. (a) Z. Yang, M. Möller and R. M. Koenigs, Angew. Chem., Int. Ed., 2020, 59, 5572–5576; (b) F. Chen, X. Xu, Y. He, G. Huang and S. Zhu, Angew. Chem., Int. Ed., 2020, 59, 5398–5402; (c) K. Wang, J. Chen, W. Liu and W. Kong, Angew. Chem., Int. Ed., 2022, 61, e202212664; (d) B. Xiong, T. Wang, H. Sun, Y. Li, S. Kramer, G.-J. Cheng and Z. Lian, ACS Catal., 2020, 10, 13616–13623; (e) J. Xiao and J. Montgomery, ACS Catal., 2022, 12, 2463–2471; (f) H. Kim, Y. Jung and S. H. Cho, Org. Lett., 2022, 24, 2705–2710; (g) P. Gao, C. Yuan, Y. Zhao and Z. Shi, Chem, 2018, 4, 2201–2211; (h) W. Xu, H. Jiang, J. Leng, H.-W. Ong and J. Wu, Angew. Chem., Int. Ed., 2020, 59, 4009–4016; (i) T. Fujita, K. Fuchibe and J. Ichikawa, Angew. Chem., Int. Ed., 2019, 58, 390–402; (j) P. Xu, C. G. Daniliuc, K. Bergander, C. Stein and A. Studer, ACS Catal., 2022, 12, 11934–11941; (k) Y. Kojima, T. Takata, K. Hirano and M. Miura, Chem. Lett., 2020, 49, 637–640; (l) Y. Pan, X. Lu, H. Qiu, Tamio Hayashi and Y. Huang, Org. Lett., 2020, 22, 8413–8418.
14. T. Fuchikami, Y. Shibata and Y. Suzuki, Tetrahedron Lett., 1986, 27, 3173–3176.
15. S. A. Faqua, W. G. Duncan and R. M. Silverstein, Tetrahedron Lett., 1964, 5, 1461–1463.
16. Y. Zhao, W. Huang, L. Zhu and J. Hu, Org. Lett., 2010, 12, 1444–1447.
17. (a) S. Koley and R. A. Altman, Isr. J. Chem., 2020, 60, 313–339; (b) M. Karimzadeh-Younjali and O. F. Wendt, Helv. Chim. Acta, 2021, 104, e2100114; (c) T. J. O'Connor, B. K. Mai, J. Nafie, P. Liu and F. D. Toste, J. Am. Chem. Soc., 2021, 143, 13759–13768; (d) A. J. Sicard, B. Ghaffari, B. M. Gabidullin, J. S. Ovens, R. P. Hughes and R. T. Baker, J. Am. Chem. Soc., 2022, 144, 22713–22721; (e) W.-Y. Xu, Z.-Y. Xu, Z.-K. Zhang, T.-J. Gong and Y. Fu, Angew. Chem., Int. Ed., 2023, 62, e202310125.
18. (a) E. J. Alexanian and J. F. Hartwig, J. Am. Chem. Soc., 2008, 130, 15627–15635; (b) T. M. Miller and G. M. Whitesides, Organometallics, 1986, 5, 1473–1480; (c) B. J. Burger, M. Thompson, W. D. Cotter and J. E. Bercaw, J. Am. Chem. Soc., 1990, 112, 1566–1577; (d) R. J. Kazlauskas and M. S. Wrighton, J. Am. Chem. Soc., 1980, 102, 1727–1730.
19. (a) M. Brookhart, M. L. H. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914; (b) S. Trofimenko, Inorg. Chem., 1970, 9, 2493–2499; (c) M. Brookhart, T. H. Whitesides and J. M. Crockett, Inorg. Chem., 1976, 15, 1550–1554; (d) J. T. Gavin, R. G. Belli and C. C. Roberts, J. Am. Chem. Soc., 2022, 144, 21431–21436; (e) R. G. Belli, V. C. Tafuri, M. V. Joannou and C. C. Roberts, ACS Catal., 2022, 12, 3094–3099.
20. D. O'Hagan, Chem. Soc. Rev., 2008, 37, 308–319.
21. (a) T. L. Allen, J. Chem. Phys., 1957, 26, 1644–1647; (b) R. G. Pearson and R. J. Mawby, in Halogen Chemistry, ed. V. Gutmann, Academic Press, 1967, pp. 55–84.
22. (a) J. L. Elkind and P. B. Armentrout, Inorg. Chem., 1986, 25, 1078–1080; (b) J. A. Labinger and J. E. Bercaw, Organometallics, 1988, 7, 926–928.
23. We note that these measurements can be sensitive to ligand choice, especially for metal–hydrides, and that each case may be different. (a) M. Tilset and V. D. Parker, J. Am. Chem. Soc., 1989, 111, 6711–6717; (b) R. H. Morris, J. Am. Chem. Soc., 2014, 136, 1948–1959; (c) R. H. Morris, Chem. Rev., 2016, 116, 8588–8654.
24. (a) I. P. Beletskaya and A. V. Cheprakov, Chem. Rev., 2000, 100, 3009–3066; (b) A. B. Dounay and L. E. Overman, Chem. Rev., 2003, 103, 2945–2964.
25. W. Heitz and A. Knebelkamp, Makromol. Chem., 1991, 12, 69–75.
26. (a) K. Sakoda, J. Mihara and J. Ichikawa, Chem. Commun., 2005, 4684–4686; (b) J. Xu, E.-A. Ahmed, B. Xiao, Q.-Q. Lu, Y.-L. Wang, C.-G. Yu and Y. Fu, Angew. Chem., Int. Ed., 2015, 54, 8231–8235; (c) R. T. Thornbury and F. D. Toste, Angew. Chem., Int. Ed., 2016, 55, 11629–11632.
27. H. Zhao, A. Ariafard and Z. Lin, Organometallics, 2006, 25, 812–819.
28. K. Yuan, T. Feoktistova, P. H.-Y. Cheong and R. A. Altman, Chem. Sci., 2020, 12, 1363–1367.
29. M. K. Bogdos, O. Stepanović, A. Bismuto, M. G. Luraschi and B. Morandi, Nat. Synth., 2022, 1, 787–793.
30. T. Miura, Y. Ito and M. Murakami, Chem. Lett., 2008, 37, 1006–1007.
31. Y. Huang and T. Hayashi, J. Am. Chem. Soc., 2016, 138, 12340–12343.
32. Y. J. Jang, D. Rose, B. Mirabi and M. Lautens, Angew. Chem., Int. Ed., 2018, 57, 16147–16151.
33. (a) Y. Takaya, M. Ogasawara, T. Hayashi, M. Sakai and N. Miyaura, J. Am. Chem. Soc., 1998, 120, 5579–5580; (b) T. Hayashi, M. Takahashi, Y. Takaya and M. Ogasawara, J. Am. Chem. Soc., 2002, 124, 5052–5058; (c) Y. Huang and T. Hayashi, Chem. Rev., 2022, 122, 14346–14404; (d) K. Yoshida, M. Ogasawara and T. Hayashi, J. Am. Chem. Soc., 2002, 124, 10984–10985.
34. (a) P. Pyykkö, Annu. Rev. Phys. Chem., 2012, 63, 45–64; (b) P. Pyykko, Chem. Rev., 1988, 88, 563–594; (c) D. J. Gorin and F. D. Toste, Nature, 2007, 446, 395–403.
35. R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University of Press, New York, 1989.
36. (a) A. D. Becke, Phys. Rev. A Gen. Phys., 1988, 38, 3098–3100; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789; (d) B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
37. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
38. (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305; (b) E. Paulechka and A. Kazakov, J. Phys. Chem. A, 2017, 121, 4379–4387.
39. (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283; (b) W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298; (c) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
40. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
41. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
42. (a) B. Marten, K. Kim, C. Cortis, R. A. Friesner, R. B. Murphy, M. N. Ringnalda, D. Sitkoff and B. Honig, J. Phys. Chem., 1996, 100, 11775–11788; (b) S. R. Edinger, C. Cortis, P. S. Shenkin and R. A. Friesner, J. Phys. Chem. B, 1997, 101, 1190–1197; (c) M. Friedrichs, R. Zhou, S. R. Edinger and R. A. Friesner, J. Phys. Chem. B, 1999, 103, 3057–3061.
43. A. A. Rashin and B. Honig, J. Phys. Chem., 1985, 89, 5588–5593.
44. (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368; (b) H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918–9924; (c) H. P. Hratchian and H. B. Schlegel, J. Chem. Theory Comput., 2005, 1, 61–69.
45. (a) M. Murakami and H. Igawa, Helv. Chim. Acta, 2002, 85, 4182–4188; (b) J. Wang, W.-F. Zheng, X. Zhang, H. Qian and S. Ma, Nat. Commun., 2023, 14, 7399; (c) D. Egea-Arrebola, F. W. Goetzke and S. P. Fletcher, Angew. Chem., Int. Ed., 2023, 62, e202217381; (d) N. Liu, J. Yao, L. Yin, T. Lu, Z. Tian and X. Dou, ACS Catal., 2019, 9, 6857–6863; (e) V. T. Tran, J. A. Gurak Jr, K. S. Yang and K. M. Engle, Nat. Chem., 2018, 10, 1126–1133; (f) G. Zhu and X. Lu, Organometallics, 1995, 14, 4899–4904; (g) M. Lautens, C. Dockendorff, K. Fagnou and A. Malicki, Org. Lett., 2002, 4, 1311–1314; (h) M. Murakami and H. Igawa, Chem. Commun., 2002, 390–391; (i) T. Miura, M. Shimada and M. Murakami, J. Am. Chem. Soc., 2005, 127, 1094–1095.
46. (a) X. Liao, Z. Weng and J. F. Hartwig, J. Am. Chem. Soc., 2008, 130, 195–200; (b) A. M. Taylor, R. A. Altman and S. L. Buchwald, J. Am. Chem. Soc., 2009, 131, 9900–9901; (c) P. M. Lundin and G. C. Fu, J. Am. Chem. Soc., 2010, 132, 11027–11029.
47. (a) J. I. Seeman, Chem. Rev., 1983, 83, 83–134; (b) J. Burés, A. Armstrong and D. G. Blackmond, J. Am. Chem. Soc., 2012, 134, 6741–6750; (c) J. Halpern, Science, 1982, 217, 401–407; (d) P. K. Dornan, K. G. M. Kou, K. N. Houk and V. M. Dong, J. Am. Chem. Soc., 2014, 136, 291–298; (e) J. I. Seeman, J. Chem. Educ., 1986, 63, 42.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy01495b

---