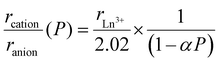Structural stability and polymorphic transitions in LnSI (Ln = lanthanides)

Abstract

Mixed-anion compounds exhibit diverse crystal structures distinct from those of single-anion compounds due to heteroleptic coordination. In this study, we experimentally and theoretically investigate the structural relationships among three polymorphs of lanthanide sulfide iodides, LnSI (Ln = lanthanides). For Ln = Gd–Lu, the system adopts a two-dimensional (2D) FeOCl-type structure with six-fold coordinated Ln (LnS₄I₂). As the ionic radius of Ln³⁺ increases (Ln = Pr–Sm), the structure transitions to the 2D SmSI-type with seven-fold coordinated Ln (LnS₄I₃). Accommodation of a larger Ln (Ln = La and Ce) leads to the formation of a three-dimensional (3D) SrI₂-type structure. These structural transitions are discussed in terms of martensitic-like transformations involving the Ln–I bond creation and rearrangement. Furthermore, we discover that the cation-to-anion radius ratio, r_cation/r_anion, provides a unified descriptor of the Ln size-dependent and pressure-induced polymorphisms. This study offers fundamental insights into the structural control and phase transitions of mixed-anion compounds, paving the way for the design of new materials with tailored structures and properties.

---

Introduction

Isovalent substitution effectively tunes the physical properties of materials by modifying the lattice constant without altering the valence of other metal elements, introducing defects, or incorporating elements into interstitial sites. Lanthanide cations (Ln) are particularly useful in this regard due to their systematic variation in ionic size (i.e., lanthanide contraction), making isovalent substitution a powerful tool for controlling structural and physical properties. For example, in the A-site ordered perovskite LnBaMn₂O₆, various electronic phases can emerge as a function of the lanthanide ionic radius (r_Ln), enabling a colossal magnetoresistance for Ln = Sm.¹ In LnHO, an increase in r_Ln induces a transition from an anion disordered fluorite structure (Ln = Sm–Er) to an ordered one (Ln = La–Nd), influencing their hydride conductivity.²

Mixed-anion compounds exhibit diverse crystal structures distinct from those of single-anion compounds due to heteroleptic coordination.^3–11 Here, we focus on an extensive family of compounds with the LnChX stoichiometry (Ch = chalcogenide, X = halide).^12–18 LnOX oxyhalides exhibit minimal structural diversity, adopting the PbFCl-type structure (or its PrOI-type), except for YbOCl with the SmSI-type structure,^19–21 while reports on Se and Te systems are more limited, making it difficult to establish clear trends.^22–24 In contrast, the LnSI system exhibits three different structural types depending on the lanthanide species (Table 1). As shown in Fig. 1, CeSI adopts the SrI₂-type (space group: Pcab), Sm adopts the SmSI-type (space group: R3̄m), and Gd, Dy, and Ho adopt the FeOCl-type structure (space group: Pmmn). Although early studies assigned Gd–Lu to a hexagonal structure,^25,26 subsequent research demonsrated that these, in fact, crystallize isotypic with FeOCl.¹³ The SrI₂- and SmSI-type structures have lanthanide ions in seven-fold coordination (LnI₃S₄), while the FeOCl-type structure has lanthanide ions in six-fold coordination (LnI₂S₄) (Fig. 1, right). This variation in coordination number appears to correlate with r_Ln. Following the work of Dagron and Thevet,²⁵ Beck and Strobel²⁶ have specifically mapped out the structures adopted by LnSI phases for Ce onwards at ambient and high pressures and rationalize these variations.

Fig. 1 Atomic arrangement of LnSI adopting (a) the SrI₂-type, (b) the SmSI-type, and (c) the FeOCl-type structures, along with their coordination environments around the Ln cations for selected Ln. See Table 1 for the LnSI phase corresponding to each structure type.

Table 1 Crystal structures and the unit-cell volume per formula unit of LnSI identified experimentally and theoretically

	Experiments	Calculation (this work)	Experimental volume (Å^3)	Calculated volume (Å^3)
LaSI	SrI2,^26 this work	SmSI	95.43	104.22
CeSI	SrI2^12,26	SmSI	93.53	104.43
PrSI	SmSI^26	SmSI	101.33	102.22
NdSI	SmSI^26	SmSI	99.87	100.35
PmSI	SmSI^26	SmSI	98.45	98.62
SmSI	SmSI^26	SmSI	97.25	97.29
EuSI		SmSI		95.97
GdSI	FeOCl^13,26	SmSI	105.62	94.63
TbSI	FeOCl^13,26	SmSI	103.9	93.53
DySI	FeOCl^13,26	FeOCl	102.65	102.47
HoSI	FeOCl^13	FeOCl	101.66	101.23
ErSI	FeOCl^13,26	FeOCl	100.50	100.15
TmSI	FeOCl^13,26	FeOCl	99.41	99.11
YbSI	FeOCl^13,26	FeOCl	98.48	93.14
LuSI	FeOCl^13,26	FeOCl	97.82	92.11

---

In this study, LaSI, for which only lattice parameters had been previously reported,²⁵ is synthesized and confirmed to adopt the same SrI₂-type structure as CeSI. We also theoretically examine the relative stability of each structural type for all LnSI compounds to identify the most stable polymorph for each lanthanide and to analyze structural phase transitions from the atomistic point of view. Moreover, we theoretically investigate the structural stability of LnSI under applied pressure. Using the ionic radius ratio of cations to anions as a descriptor, we unify the pressure- and Ln size-dependent polymorphic sequences.

Experimental

Lanthanum sulfide iodide (LaSI) was synthesized via a conventional solid state reaction. The starting reagents, La₂S₃ (Kojundo Chemical, 99.9%) and LaI₃ (Kojundo Chemical, 99.9%), were weighed in a stoichiometric ratio, thoroughly mixed using an agate pestle and mortar, and pelletized in an N₂-filled glovebox to prevent exposure to air, since the precursor iodide is air-sensitve. The pellet was then sealed in an evacuated silica tube and heated at 800 °C for 48 h.

Laboratory powder X-ray diffraction (XRD) measurements were carried out using a Rigaku SmartLab equipped with a Cu Kα radiation source. Synchrotron powder XRD experiments for detailed structural characterization were performed at 293 K using the large Debye–Scherrer camera at the Japan Synchrotron Radiation Research Institute (SPring-8 BL02B2), with a MYTHEN solid-state detector. The incident X-ray beam from a bending magnet was monochromatized to λ = 0.420201 Å. The powder sample was loaded into a glass capillary tube with an inner diameter of 0.2 mm and rotated during measurement to minimize preferential orientation effects. Synchrotron XRD data were collected over a 2θ range of 5–80° with a step interval of 0.02°. Rietveld analysis of the synchrotron XRD data was performed using FullProf, and crystal structures were visualized using VESTA.²⁷

First-principles density functional theory (DFT) calculations for LnSI were carried out using the projector augmented-wave method implemented in the Vienna Ab initio Simulation Package (VASP).²⁸ Three polymorphs, the SrI₂, SmSI, and FeOCl types, were considered, adopting the space groups of Pcab, R3̄m, and Pmmn, respectively. The Perdew–Burke–Ernzerhof functional revised for solids (PBEsol) was employed to describe the exchange–correlation interactions.²⁹ The plane-wave cutoff energy was set to 550 eV, and Brillouin zone integration was performed using Γ-centered meshes of 4 × 2 × 5, 8 × 8 × 1, and 6 × 8 × 3 for the conventional unit cells of SrI₂-, SmSI-, and FeOCl-type structures, respectively. Total energies were minimized until the energy convergence fell below 10⁻⁷ eV during self-consistent cycles, while atomic positions and lattice constants were relaxed until the residual stress and forces were reduced to less than 1 meV Å⁻¹ and 0.01 GPa, respectively. The 4f states were treated as core electrons. To investigate structural stability under high pressure, structural optimizations were carried out under isotropic external pressure ranging from 1 to 10 GPa.

Results and discussion

Preliminary crystallographic characterization of the LaSI sample was conducted using laboratory XRD. As shown in Fig. S1,† the majority of the XRD peaks are indexed to an orthorhombic phase with lattice constants of a = 7.37 Å, b = 14.58 Å, and c = 7.08 Å, which are slightly larger than those of the SrI₂-type CeSI (a = 7.35 Å, b = 14.42 Å, and c = 7.06 Å),¹² reflecting the difference in ionic radii between La (1.1 Å) and Ce (1.07 Å). These values are also consistent with the previously reported ones (a = 7.38 Å, b = 14.57 Å, and c = 7.10 Å).²⁵ Furthermore, the lattice constants of the LaSI sample synthesized under different conditions (750 °C for 48 h) are a = 7.3717(2) Å, b = 14.5861(5) Å, and c = 7.0822(2) Å. They are in perfect agreement with the lattice constants when synthesized at 800 °C as described in the caption of Table 2. Minor impurity peaks corresponding to La₁₀OS₁₄ were also detected,³⁰ likely due to reactions with trace amounts of oxygen present in the glovebox and silica tubes.

Table 2 Structural parameters of LaSI at 293 K obtained from Rietveld refinement against SXRD data

Atom	Site	x	y	z	U iso or Ueq (Å)
Space group Pcab (No. 61), Z = 8. The occupancy parameters are fixed to 1 for all atoms. Lattice parameters: a = 7.37097(3) Å, b = 14.58707(7) Å, and c = 7.08286(3) Å.a Refined anisotropically.
La	8c	0.02786(18)	0.0850(10)	0.2454(3)	0.0152(3)
S	8c	0.02538(13)	0.4768(4)	0.4996(12)	0.0087(16)
I^a	8c	0.4125(2)	0.19781(13)	0.3099(3)	0.0269(12)

---

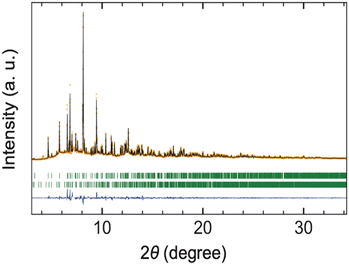
Rietveld refinement of the synchrotron XRD (SXRD) data was carried out, assuming the SrI₂-type structure (space group Pcab, No. 61) as reported for CeSI.¹² In this model, La, S, and I atoms were all positioned at the general Wyckoff position 8c. The atomic coordinates for CeSI were used as initial parameters in our structural analysis. The refinement readily converged to GOF = 5.03, R_p = 17.2%, and R_wp = 16.5% (Fig. 2). Refining the occupancy parameters of each atom does not improve the fit, and the occupation remained at 100% within the standard deviation, indicating the absence of off-stoichiometry or S/I anti-site disorder. In the final refinement, the occupancy parameters were fixed to unity, and the crystallographic parameters obtained are listed in Table 2. The La–S and La–I bond lengths are about 1.1% and 1.4% longer than those in the isostructural CeSI, respectively, which is within a reasonable range. Although CeSI was the only example of LnSI crystallizing in the SrI₂-type structure, our structural analysis confirms that LaSI adopts the same structure, suggesting that polymorphism in these sulfide iodides is governed by cation size. It should be noted that Ce⁴⁺ would not be stable to reduction by the anions and will be present as Ce³⁺.

Fig. 2 Rietveld refinement of SXRD data collected for LaSI (λ = 0.420201 Å), adopting the SrI₂-type structure with space group Pcab. Orange circles, black lines, and blue lines represent the observed, calculated, and residual intensity, respectively. The green ticks indicate the Bragg reflection positions for LaSI (upper) and La₁₀OS₁₄ (lower). The weight fraction of La₁₀OS₁₄ is 13.6(2)%.

To investigate the crystallochemical origin of the polymorphism in the LnSI series discussed by Beck and Strobel,²⁶ we first calculated the total energies of the three polymorphs for each Ln cation by fully relaxing the structures. Fig. 3 shows the DFT total energies of LnSI with the SmSI-type (red) and FeOCl-type (blue) structures with respect to the SrI₂-type structure (black), plotted as a function of the Shannon ionic radii of the Ln³⁺ cation.³¹ For both the SmSI- and FeOCl-type structures, the energy difference increases approximately linearly from Lu to Ce with increasing r_Ln. The slope for the FeOCl-type structure is steeper than that for the SmSI-type, indicating that the FeOCl-type structure is destabilized more rapidly with increasing lanthanide size. The FeOCl-type structure is the most stable from Lu to Dy, but the energy difference between it and the SmSI-type structure gradually decreases as r_Ln increases, with the SmSI type becoming the most stable for ions larger than Tb³⁺.

Fig. 3 Relative energy of the SmSI- and FeOCl-type structures with respect to the SrI₂-type structure as a function of the Shannon radius of the Ln³⁺ cation. Note that both the SrI₂- and SmSI-type structures exhibit seven-fold coordination around the Ln cation; however, we use the ionic radii of six-fold coordination to facilitate comparison.

In contrast to our experimental structural characterization of LaSI and the previous report on CeSI,¹³ where these compounds with the largest lanthanide ions crystallize in the SrI₂-type structure, our DFT calculations suggest that LaSI and CeSI are stable in the SmSI-type structure. This discrepancy indicates that the calculation method employed may not fully capture the behavior of this system. The difference may arise because, in the calculations, the 4f electrons are treated as part of the frozen core,³² whereas for these lighter lanthanides, the 4f states are chemically accessible. Moreover, it is generally difficult within DFT to obtain accurate results for van der Waals (vdW) materials with anisotropic bonding interactions, such as the SmSI- and FeOCl-type phases³³ (see Fig. 1 for contrast with the SrI₂ structure type). When the relative energy of LaSI with SmSI- and FeOCl-type structures is estimated via linear extrapolation (dotted lines in Fig. 3), the total energies of the vdW compounds (SmSI- and FeOCl-type LaSI) are larger than the DFT-calculated values, suggesting over-estimated stability in the calculations. Using the extrapolated line, the SrI₂-type structure of LaSI becomes relatively stable, in agreement with the experimental results. For CeSI, the calculated total energies for the SmSI- and SrI₂-type structures are very close, which is consistent with a previous experimental report showing that previously synthesized bulk samples of CeSI contain mostly the SrI₂-type phase with some of the SmSI-type phase present.²⁷

Note that the DFT-calculated volume of SmSI-type LaSI is smaller than that of CeSI, which contradicts the trend expected from the lanthanide ionic radii (Table 1). This anomaly suggests an overestimation of the structural stability for vdW-type LaSI in the calculations. Such discrepancies point to inherent limitations in the current DFT setup, especially in describing layered structures involving weak interlayer interactions. Although a comprehensive is difficult, the discrepancy between the experimental and predicted structures for TbSI likely stems from the fact that standard DFT calculations are performed at 0 K and neglect finite-temperature effects. In systems like TbSI, where polymorphs are energetically close (see Fig. 3), thermal contributions can alter the phase stability. Nevertheless, our DFT results reproduce the broader polymorphic trends across the LnSI series reasonably well. For cases with marginal energy differences, such as TbSI, improving the computational treatment, e.g., by incorporating vdW corrections or employing alternative exchange, may improve the agreement with experiment.

Since larger cations tend to prefer coordination with more anions, the structural transformation from the FeOCl-type structure with six-fold coordinated LnI₂S₄ to the SmSI-type structure with seven-fold LnI₃S₄ with increasing r_Ln is most likely driven by the coordination preference of the Ln cations. Building on a previous report on the polymorphism between PbFCl- and γ-YSF-type structures in LnSF,³⁴ we illustrate the new Ln–I bond through a martensitic-like transformation. The left panel of Fig. 4 shows the Ln and adjacent I layers in the FeOCl-type structure. Shear deformation brings the Ln cations and the next-nearest I anions closer together in a hypothetical transient state (Fig. 4, middle). Slight displacements of the Ln cations eventually lead to the formation of a new Ln–I bond (Fig. 4, right) in the SmSI-type structure. A similar transformation within the Ln and S layers is depicted in Fig. S2,† where the four Ln–S bonds are preserved. As a result of these displacive distortions, the trigonal SmSI-type structure with edge-sharing LnS₄I₃ polyhedra emerges.

Fig. 4 Schematic representation of the phase transformation from (left) FeOCl-type to (right) SmSI-type structure, via (middle) a hypothetical sheared state, where only Ln and I layers are shown. The blue diamonds correspond to the unit cell of the SmSI-type structure (R3̄m), while the unit cell of the SmSI-type structure (Pmmn) is depicted by black lines.

As for the SmSI- to SrI₂-type transformation, the seven-fold coordination around the Ln cation is preserved while the dimensionality increases from 2D to 3D. Although the 2D SmSI- and 3D SrI₂-type structures appear different, they can also be interpreted as undergoing a displacive transformation involving the rearrangement of Ln–I bonds. Building on the topological similarity between the two phases, we sketch a possible atomistic interpretation of bond rearrangement in Fig. 5. The left panel of Fig. 5 depicts the Ln and adjacent I layers of the SmSI-type structure, along the perpendicular direction to the 2D slab, alongside another I layer separated by the vdW gap, with the three Ln–I bonds highlighted. When iodide anions shift within the layers (Fig. 5, middle), representing a hypothetical transient state, one of the three Ln–I bonds is cleaved.

Fig. 5 Schematic illustration of LnSI with (left) SmSI-type and (right) SrI₂-type structures, along with (middle) a hypothetical transition state for clarity. Ln, upper I, and lower I layers are depicted from front to back. The upper and lower I atoms are positioned at the corners of blue and red diamonds, respectively, emphasing the hexagonal arrangement. While the blue diamond represents the unit cell of the SmSI-type structure (R3̄m), the unit cell of the SrI₂-type structure (Pcab) is given by the black lines.

Subsequently, the SrI₂-type structure is obtained by sliding the lower I layer (Fig. 5, right), which allows the formation of an alternate Ln–I bond with an iodide anion from another layer. As a result, the SrI₂-type structure is no longer a 2D vdW material. Unlike in the SmSI-type structure with the edge-sharing polyhedral network, the LnS₄I₃ polyhedra in the SrI₂-type structure are heavily distorted but exhibit edge-sharing and vertex-sharing connectivity. Vertex-sharing stabilizes the crystal according to Pauling's third rule, which states that the cation–cation electrostatic repulsion is enhanced by edge- and face-sharing connectivity due to the cations being too close. Pressure-dependent polymorphism has also been investigated for the LnSI system before.²⁶ Examples include FeOCl-type GdSI, which shows successive phase transitions to the SmSI-type structure at 0.5 GPa, and to the SrI₂-type phase at 3 GPa. These pressure-induced transitions may have a martensitic nature, as described above.

To assess the similarity between the pressure-induced and r_Ln-dependent phase transformation, we computationally examine the relative stability of LnSI under pressure. The DFT total energies are calculated as a function of pressure (see Fig. S3† for example), and the lowest-energy polymorph is identified for each Ln and as a function of pressure, as summarised in Fig. 6. It is clear that the FeOCl-type structure undergoes a phase transition to the SmSI-type structure, which then transforms to the SrI₂-type polymorph either by applying pressure or by incorporating a larger Ln cation.

Fig. 6 DFT-calculated phase diagram showing the most stable structure of LnSI among the three polymorphs: FeOCl-type (circles), SmSI-type (triangles), and SrI₂-type (squares) structures, as a function of r_Ln and pressure. The overlaid contour map represents the estimated r_cation/r_anion values (see the main text for details).

Since anions are generally larger and more compressible than cations, external pressure serves as an effective tuning knob to adjust the ionic radius ratio of cations to anions, r_cation/r_anion. For instance, the polymorphism of the lithium ionic conductor Li₃MCl₆ varies with r_M/r_Cl, and its increase with pressure explains the formation of the hexagonal phase.³⁵ In mixed-anion compounds, the distinct compressibility of the anions often influences their structures and properties.³⁶ Here, we propose that the polytypic behavior of LnSI is governed by r_cation/r_anion. To roughly model the compression behavior under pressure, we used the average anion radius of 2.02 Å (r_I = 2.20 Å, r_S = 1.84 Å) at ambient pressure and assumed that only anions are compressed under pressure. The ionic radius ratio under pressure, P, r_cation/r_anion(P), is then expressed as

where α represents the compressibility of the anions. The estimated ionic radius ratio under pressure is included in Fig. 6 as a contour plot, where the α value of 7.3 × 10⁻³ GPa⁻¹ is used to best reproduce the polymorphic phase boundary among the FeOCl-, SmSI-, and SrI₂-type structures. The fitting method used to obtain the α value is detailed in ESI.† Despite the rough approximation, a reasonably good overlap is obtained between the r_cation/r_anion distribution and the DFT-calculated phase diagram. This clearly demonstrates that the chemical and physical pressure dependence of the polymorphism is well described by r_cation/r_anion.

Conclusions

We systematically investigate the structural relationships among the three polymorphs reported for the LnSI series. Experimentally, we confirmed that LaSI crystallizes in the SrI₂-type structure, emphasizing the role of cation size in the polymorphism at ambient conditions. The structural transitions from FeOCl-type to SmSI-type, and from the SmSI-type to the SrI₂-type can be discussed from the viewpoint of martensitic-like phase transformations. Our DFT calculations strongly support the experimental observations, including previous ones, on the r_Ln-dependent and pressure-induced polymorphism, revealing a relationship between the cation–anion radius ratio and the structural selectivity. Our findings highlight the importance of the larger compressibility of anion species in tuning the structures, and in general this concept could be a powerful guideline to control structures toward developing new properties of materials.

Author contributions

H. K. conceived and supervised the project. S. K. synthesized the samples with the help of H. U., Y. Y., and R. M. S. K. and S. Y. did the structural analysis with the help of H. U. and C. Y. S. K. and S. Y. performed the DFT calculations. S. K., S. Y., S. J. C., and H. K. discussed the phase transformation. S. K., S. Y., and H. K. wrote the manuscript with the comments from all authors.

Conflicts of interest

There are no conflicts to declare.

Data availability

Crystallographic data for LaSI has been deposited at the CCDC under accession number 2435068 and is provided as a part of the ESI.† All SXRD and DFT calculation results needed to evaluate the conclusions in the paper are present in the paper and/or the ESI.† Additional data related to this paper are available from the authors upon request.

Acknowledgements

This work was supported by JST ASPIRE Program “Next Generation Mixed-Anion Science: Reaction/Structure Control and New Functions” (JPMJAP2408), JSPS Grant-in-Aid for Specially Promoted Research “Hydrogen Ion Ceramics” (JP22H04914) and JSPS Grant-in-Aid for Transformative Research Areas (A) “Supra-ceramics” (JP22H05143). S. J. C. thanks the UK EPSRC (EP/T027991/1) for financial support.

References

1. Y. Ueda and T. Nakajima, Prog. Solid State Chem., 2007, 35, 397–406.
2. H. Yamashita, T. Broux, Y. Kobayashi, F. Takeiri, H. Ubukata, T. Zhu, M. A. Hayward, K. Fujii, M. Yashima, K. Shitara, A. Kuwabara, T. Murakami and H. Kageyama, J. Am. Chem. Soc., 2018, 140, 11170–11173.
3. H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Nat. Commun., 2018, 9, 772.
4. M. Yang, J. O. Sole, J. A. Rodgers, A. B. Jorge, A. Fuertes and J. P. Attfield, Nat. Chem., 2011, 3, 47–52.
5. N. Imanaka, K. Okamoto and G. Y. Adachi, Angew. Chem., Int. Ed., 2002, 41, 3890–3892.
6. T. Yamamoto, D. Zeng, T. Kawakami, V. Arcisauskaite, K. Yata, M. A. Patino, N. Izumo, J. E. McGrady, H. Kageyama and M. A. Hayward, Nat. Commun., 2017, 8, 1217.
7. M. A. Hayward, E. J. Cussen, J. B. Claridge, M. Bieringer, M. J. Rosseinsky, C. J. Kiely, S. J. Blundell, I. M. Marshall and F. L. Pratt, Science, 2002, 295, 1882–1884.
8. H. Ubukata, F. Takeiri, K. Shitara, C. Tassel, T. Saito, T. Kamiyama, T. Broux, A. Kuwabara, G. Kobayashi and H. Kageyama, Sci. Adv., 2021, 7, eabf7883.
9. Y. Sasahara, R. Terada, H. Ubukata, M. Asahi, D. Kato, T. Tsumori, M. Namba, Z. Wei, C. Tassel and H. Kageyama, J. Am. Chem. Soc., 2024, 146, 11694–11701.
10. D. Kato, H. Suzuki, R. Abe and H. Kageyama, Chem. Sci., 2024, 15, 11719–11736.
11. R. D. Smyth, J. N. Blandy, Z. Yu, S. Liu, C. V. Topping, S. J. Cassidy, C. F. Smura, D. N. Woodruff, P. Manuel, C. L. Bull, N. P. Funnell, C. J. Ridley, J. E. McGrady and S. J. Clarke, Chem. Mater., 2022, 34, 9503–9516.
12. J. J. Étienne, Bull. Soc. Fr. Mineral. Cristallogr., 1969, 92, 134–140.
13. B. Blaschkowski, H. Rosner, W. Schnelle and T. Schleid, Z. Anorg. Allg. Chem., 2013, 639, 237–240.
14. S. Zimmermann and G. Meyer, Acta Crystallogr., Sect. E:Struct. Rep. Online, 2007, E63, i193.
15. B. I. Mayer, S. Zolotov and P. Kassierer, Inorg. Chem., 1965, 4, 1637–1639.
16. P. T. Gros, C. M. Schurz and T. Schleid, Acta Crystallogr., Sect. E:Struct. Rep. Online, 2011, 67, i74.
17. F. H. Kruse, L. B. Asprey and B. Morosin, Acta Crystallogr., 1961, 14, 541–542.
18. G. Meyer and T. Schleid, Z. Anorg. Allg. Chem., 1986, 533, 181–185.
19. G. Brandt and R. Diehl, Mater. Res. Bull., 1974, 9, 411–419.
20. T. Aitasalo, J. Hölsä, M. Lastusaari, J. Legendziewicz, L. Lehto, J. Lindén and M. Maryško, J. Alloys Compd., 2004, 380, 296–302.
21. L. H. Brixner and E. P. Moore, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 1983, 39, 1316.
22. C. M. Schurz, S. Frunder and T. Schleid, Eur. J. Inorg. Chem., 2013, 2923–2929.
23. K. Stöwe, Z. Anorg. Allg. Chem., 1997, 623, 1639–1643.
24. M. Larres, I. Pantenburg and G. Meyer, Z. Anorg. Allg. Chem., 2013, 639, 2744–2747.
25. M. C. Dagron, M. F. Thevet and M. G. Chaudron, Acad. Sci., Paris, C. R., 1969, 268, 1867–1869.
26. H. P. Beck and C. Strobel, Z. Anorg. Allg. Chem., 1986, 535, 229–239.
27. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
28. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
29. J. P. Perdow, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
30. T. Schleid and F. Lissner, J. Less-Common Met., 1991, 175, 309–319.
31. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, A32, 751–767.
32. N. Zapp, D. Sheptyakov, A. Franz and H. Kohlmann, Inorg. Chem., 2021, 60, 3972–3979.
33. A. J. Cohen, P. M. Sänchez and W. Yang, Chem. Rev., 2012, 112, 289–320.
34. H. P. Beck and C. Strobel, Z. Naturforsch., B, 1985, 40, 1644–1650.
35. F. Ding, A. Doi, T. Ogawa, H. Ubukata, T. Zhu, D. Kato, C. Tassel, I. Oikawa, N. Inui, S. Kuze, T. Yamabayashi, K. Fujii, M. Yashima, X. Ou, Z. Wang, X. Min, K. Fujita, H. Takamura, A. Kuwabara, T. Zhang, K. J. Griffith, Z. Lin, L. Chai and H. Kageyama, Angew. Chem., Int. Ed., 2024, 63, e202401779.
36. Y. Matsumoto, T. Yamamoto, K. Nakano, H. Takatsu, T. Murakami, K. Hongo, R. Maezono, H. Ogino, D. Song, C. M. Brown, C. Tassel and H. Kageyama, Angew. Chem., Int. Ed., 2019, 58, 756–759.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dt00753d

---