Assessment methods for identifying suitable charge carriers for non-aqueous redox flow batteries

Abstract

Redox flow batteries (RFBs) are emerging as a promising battery technology for grid-scale energy storage. The utilization of non-aqueous solvents expands the repertoire of existing electrolytes toward wider electrochemical windows, which is critical for achieving high energy densities. Successful implementation of non-aqueous RFBs on a large scale necessitates identification of suitable charge carriers through the thorough evaluation of key physicochemical properties, such as redox potential, solubility, solution resistance, transport, and electrokinetic properties. These characteristics further inform the performance metrics of the resulting batteries. To date, there is a lack of systematic guidelines and protocols that direct synthetic chemists with consistent procedures to screen electrolytes for practical applications. This is especially true for researchers interested in studying redox-active inorganic molecules as charge carriers for these applications. In this tutorial-review, we discuss the design criteria, testing methods, and H-cell experimental design for inorganic candidates for emergent non-aqueous redox flow battery technologies. We also present a general framework and recommendations on testing procedures that are suitable in different scenarios based on the relevant chemical information that is desired on a given electrolyte. Finally, we conclude the discussion on our envisioned strategies to enable predictive design strategies for next-generation non-aqueous redox flow batteries.

---

Mamta Dagar and Ellen M. Matson

Dr. Mamta Dagar (right) and Prof. Ellen Matson (left) are researchers from the University of Rochester, working on projects related to the design and analysis of multimetallic charge carriers for non-aqueous redox-flow battery (RFB) technologies. Their research interests are focused on the elucidation of structure–function properties that influence the stability and redox-properties of polyoxometalate complexes that possess rapid electron transfer kinetics. During her time as a PhD student at the University of Rochester, Dr. Mamta Dagar investigated heterometal-substituted polyoxovandate and polyoxotungstate clusters. Her projects encompassed fundamental studies on the mutual dynamics of different components of the electrolyte media to improve the performance of polyoxovanadate-based electrolytes for applications in non-aqueous RFBs. She also worked towards studying the thermodynamic changes occurring in polyoxotungstate clusters during charge transfer via variable temperature electrochemistry. Dr. Dagar is currently a postdoctoral researcher at the University of Texas at Austin in the laboratory of Prof. Hang Ren, investigating Li extraction from brine using bipolar electrochemistry. Prof. Ellen Matson's research group focuses on the development of novel strategies for renewable energy storage and fuel production.

Key learning points

The readers of this review will learn about: (1) Prevalent methodologies for assessing the physicochemical properties of inorganic electrolytes in non-aqueous redox flow batteries (RFBs). (2) Key design considerations for improving the efficiency of the battery electrolyte. (3) A systematic framework encompassing initial screening criteria and advanced characterization techniques for selecting suitable electrolyte candidates for RFBs. (4) A step-by-step guide for data collection, interpretation, and benchmarking of transport, electrokinetic, and electrochemical properties of electrolyte systems.

Introduction

The development of grid-scale energy storage technologies is crucial for a reliable and sustainable energy future.^1,2 An emergent technology uniquely suited for the flexible operation and requirements of grid-scale energy storage are redox flow batteries (RFBs).^3,4 RFBs are attractive alternatives for grid-scale energy storage due to their scalability, lifetimes, durability, low cost, and efficiency.⁵ These secondary batteries are stationary electrochemical energy storage devices that store energy in the form of charged redox-active molecules in either all-liquid or hybrid-phase systems. The active species are stored in tanks outside the cell stack in two separate chambers. One tank stores the charge carrier that undergoes an oxidation reaction and is known as the positive electrolyte or posolyte. The second chamber stores the species that undergoes a reduction reaction, which is referred to as the negative electrolyte or negolyte. Often, terminologies such as catholyte (electrolyte associated with the cathode) and anolyte (electrolyte associated with the anode) are also used to refer to the electrolyte solutions. In the cell stack, each of these half-cell reactions are separated by a membrane or other style of separator.

The operational distinction between conventional batteries and RFBs lie in the fact that the electrodes in the latter do not directly undergo any faradaic reactions themselves. This leads to decoupling of energy storage capacity from power capacity, as the electroactive redox couples are stored in external reservoirs and brought together in the reactor during operation.⁶ Decoupling of energy and power is difficult to implement in rechargeable metal-ion batteries because of their enclosed nature, where energy is stored in solid-state electrode materials.⁷ RFBs are also considered more versatile than their solid-state counterparts owing to wider operable temperature range and require low maintenance due to stable chemistries of the electrolyte.^8–10 As such, RFBs hold promise in meeting the ever-growing energy demands of society by providing stable strategies for the integration of renewable resources into the electrical grid.

In considering the construction of a flowable electrochemical energy storage device, one can dissolve redox mediators in either aqueous or non-aqueous solution. The identity of the solvent differentiates between two major classifications of RFBs, aqueous and non-aqueous. Non-aqueous RFBs, the focus of this tutorial, offer a wider operational potential window and temperatures, which are important factors in considering the variable design needs for energy storage (for example, 1.4 V versus 2.2 V for aqueous and non-aqueous RFBs, respectively).^11,12 The use of organic solvents also expands the library of organic and inorganic complexes as candidates for charge carriers, including molecular entities that might have reduced stability or compatibility with water. Despite these advantages, key challenges remain in the development of energy carriers for non-aqueous flowable energy storage, including persistent limitations in both cost and performance that stem in large part from solubility and cell voltage (note that these obstacles remain prevalent in even the most mature RFB technologies based on aqueous transition metal compounds, like vanadium). However, in our opinion, continued investment in non-aqueous RFB technologies is necessary to avoid premature technology “lock-in”.

The advancement of non-aqueous RFB technologies hinges on the identification and optimization of charge carriers that balance high energy density, robust stability, and favorable electron transfer kinetics. Several studies have summarized the fundamental concepts,^13,14 performance trends,^10,15 or focused on specific key physicochemical properties relevant to RFB operation.^16–18 There is also a comprehensive review that provides a detailed account of device engineering, flow visualization, and diagnostic techniques for the electrolyte.¹⁹ However, there is a lack of reports that delve into the intricacies of evaluating transport, stability, and electrochemical properties of electrolyte systems. One notable exception is the work by Odom and Minteer,¹³ which has been instrumental in establishing methodology-driven investigations of non-aqueous RFBs, particularly for organic charge carriers. However, comprehensive evaluation strategies tailored to inorganic redox-active compounds are less developed.

Inorganic charge carriers refer to electroactive species based on metal centers or non-carbon redox-active elements that undergo reversible redox reactions to store and transfer charge within the electrolyte system (Fig. 1). These include simple ions (typically metal ions in aqueous solutions; for e.g., V²⁺/V³⁺), inorganic complexes (e.g., M(acac)₃ and M(bpy)₃; M = metal; acac = acetylacetonate; bpy = 2,2′-bipyridine), and organometallic compounds (e.g., ferrocene). Some of these metal-based charge carriers exhibit multiple, stable oxidation states that enable reversible redox reactions, and often exhibit improved thermal and chemical stability across a range of charge states in comparison to their organic counterparts. Moreover, multimetallic systems (such as polyoxometalates) can prevent crossover through common ion-exchange membranes due to their tunable size and charge.

Fig. 1 Examples of inorganic charge-carriers for non-aqueous redox flow batteries.

The goal of this tutorial review is to complement the work on organic active materials by providing a detailed framework specifically for inorganic charge carriers, encompassing both initial screening criteria and advanced characterization techniques. We subsequently present a detailed analysis of uncompensated resistance, kinetic assessment, and lay out the distinctions between different cycling strategies. Finally, the discussion addresses the critical link between H-cell testing and flow cell performance. This work aims to bridge the methodological deficiencies and guide synthetic inorganic chemists with recommended best practices in advancing non-aqueous RFB technology.

Identifying suitable inorganic charge carriers

The identification of suitable inorganic charge carriers for non-aqueous RFB technologies requires a systematic approach that integrates well-defined selection criteria with robust screening techniques. These general initial screening criteria for the redox mediator include redox potential, compatibility with the electrolyte system's stability window, solubility, and prolonged durability under operational conditions (Fig. 2). The motivation behind assessing these specific characteristics stems from the need to maximize the energy density of the battery electrolyte. The energy density (E) of a redox flow battery can be estimated by integrating the cell voltage versus capacity and dividing by volume or weight.²⁰ Capacity is a measure of the total amount of electricity generated due to the electrochemical reactions that the battery can store (typically expressed in Ah) or deliver (typically expressed in Wh). Since the theoretical capacity is related to the number of electrons transferred by each charge carrier and the total number of charge carriers, a simple relationship emerges if the cell voltage (V_cell) is treated as a constant, typically the value at a 50% state-of-charge (SoC). In the latter case, the theoretical energy density can be expressed as shown in eqn (1).

E = V_cell × capacity (1)

Fig. 2 Design characteristics of effective electrolytes for non-aqueous redox flow batteries.

When the charge carriers are dissolved or suspended in a solution, the capacity in coulombs is related to the number of electrons stored or released per mole of the charge carrier (n), the concentration (C_active), and volume (Vol_active) of either the negative or positive electrolyte, and Faraday's constant (F) as shown in eqn (2).

Capacity = n × F × C_active × Vol_active (2)

The theoretical energy corresponding to the charge carrier can be evaluated using eqn (3), which is derived by combining eqn (1) and (2).

E = n × F × V_cell × C_active × Vol_active (3)

Dividing the above expression by the total device volume (Vol_total) gives the means to calculate the volumetric energy density (E_vol) of a given battery electrolyte (eqn (4)).

E_vol = (n × F × V_cell × C_active × Vol_active)/Vol_total (4)

The derivation of eqn (4) demonstrates how key molecular parameters correlate to the theoretical energy density of an RFB – for example, redox potential of the charge carrier is equivalent to V_cell, solubility of the compound is correlated to C_active, and the charge accessed by the active species during the redox reaction affects n. However, there remain molecular traits that are absent from eqn (4), but are important when evaluating a charge carrier's suitability for implementation. The redox mediator (and electrolyte system) must exhibit extended stability over the entire voltage window accessed during battery (dis)charging schematics, as this translates directly to the lifetime and associated costs of the system. Additionally, the molecular charge carriers should be able to facilitate rapid electron transfer at the electrode–electrolyte interface, as this is a limiting factor in the overall energy efficiency in flow-based technologies.

Redox potential. Often, the initial physicochemical property considered when identifying suitable charge carriers is the redox potential(s) of the molecule of interest (measured in volts, V). This information can be readily obtained by using electrochemical techniques such as cyclic voltammetry, linear sweep voltammetry, or square wave voltammetry (SWV). The resulting voltammograms allow for the determination of oxidation and reduction potentials under specific electrochemical conditions, providing information about the reversibility of the redox couples. In asymmetric RFBs where the positive and negative half-reactions are carried out by different active species, identifying the complementary redox pair is a main challenge. A good rule of thumb is to pair redox couples in such a way that the overall battery cell potential is above 1 V (i.e., the redox couples of the two charge carriers are separated by more than 1 V). In scenarios where symmetric RFBs are desirable, assessing whether the positive and negative half-cell reactions are sufficiently separated (ΔE_1/2 > 1 V) in the same species is key.²¹ Symmetric RFBs refer to systems where the positive and negative electrolytes bear the same compound as the charge carrier. A key feature of symmetric charge carriers is their ability to exhibit both an oxidation and reduction reaction, which are separated by a large voltage gap; this trait is easily deduced using cyclic voltammetry. Symmetric RFB systems offer an added advantage of mitigating the relevance of active species crossover that would be detrimental in asymmetric systems.²² For instance, the traditional VRFB is a symmetric system where both electrolytes are vanadium-based albeit in different oxidation states. However, it has been observed that vanadium ions can permeate through the membrane leading to an imbalance in the electrolyte concentrations in the posolyte and negolyte. One way to combat this problem is via electrolyte rebalancing i.e., restoring capacity by transferring and remixing electrolytes between the positive and negative compartments, which would have been difficult to achieve if the system was asymmetric.

Solubility. High solubility of the charge carrier is critical in achieving high energy densities in RFBs. The solubility of charge carriers (measured as molarity, M) in non-aqueous electrolytes poses a greater challenge than in aqueous systems due to the intrinsic differences in solvent polarity and solvation properties.²³ The typical solubilities of charge carriers for non-aqueous RFBs lie in the range of 0.2–0.4 M, inhibiting the use of these electrolytes in the deployment of large-scale batteries. To achieve solubilities >1 M, molecular modifications (e.g., ligand modifications) can aid in improving solubility without compromising the electrochemical properties of charge carriers (see Fig. 1 for examples).^24–26 As such, solubility should be quantified under relevant conditions before deploying materials under charge–discharge conditions.

There are multiple approaches to measure the solubilities of redox mediators, including electronic absorption spectroscopy and gravimetric analysis. These measurements should be performed in the corresponding electrolyte system (i.e., in the presence of supporting electrolyte and desired solvent) to mirror the battery's operating conditions. Such considerations become pertinent as the presence of ten-fold concentration of supporting electrolyte will impact the solubility of the charge carrier in a given amount of solvent. Electronic absorption spectroscopy can determine saturation limits by monitoring changes in absorbance as a function of solute concentrations, revealing the point at which no further solute dissolves. On the other hand, gravimetric analysis involves dissolving a known excess of the charge carrier in the solvent, filtering out undissolved material, and weighing the solution residue after solvent evaporation to quantify the maximum solubility. Our recommendation is to use electronic absorption spectroscopy for solubility measurements, as it not only yields quantitative information about the maximum concentration of the analyte but also provides insight into the electronic structure and properties of a charge carrier across various redox states, which is unavailable through gravimetric analysis. This technique is especially useful for inorganic charge carriers as compared to their organic counterparts as transition metal-based complexes tend to yield simpler, sharper spectra with well-defined, diagnostic peaks. We recommend that researchers should at a minimum assess the solubilities of the least soluble charge state, but it is preferable to synthesize all disparate charge states involved in the battery cycling and measure their corresponding solubility for accuracy. A step-by-step guide on determining solubility values for a molecular complex using electronic absorption spectroscopy is included in the ESI.†

A caveat to high solubilities of the charge carriers is the trade-off between ionic conductivity and solution viscosity, which typically results in a hyperbolic trend for conductivity as a function of redox species concentration. While higher concentration improves charge storage capacity and ionic strength, it often leads to elevated viscosity of the solution, which translates to reduced mass transport and impaired cell performance.²⁷ Several strategies have emerged to manage this balance, including solvent optimization using low-viscosity, high-permittivity media, molecular tuning of redox-active species to include solubilizing side chains or ionic groups, and co-solvent systems that maintain solubility while reducing viscosity. In parallel, symmetric or mixed-electrolyte designs (e.g., 1 : 1 posolyte/negolyte) can be adopted to address crossover through membranes with limited selectivity, mitigating net concentration gradients and preserving cell efficiency. As such, electrolyte formulations must be assessed to evaluate transport properties (diffusion coefficients, conductivity, viscosity) to elicit design trade-offs and better understand structure–function relationships.

Stability. Establishing the durability of the electrolyte involves assessment of both chemical and electrochemical stabilities. Charge carriers should resist degradation during repeated redox cycling for better performance. Moreover, they should exhibit prolonged stability in their charged forms accessed during cycling of the battery. Several spectroscopic and electrochemical techniques can be used to assess the stability of the electrolyte prior to battery operation. We recommend generating these charged states electrochemically by employing bulk electrolysis techniques (such as, chronoamperometry or chronopotentiometry) and testing the stability of each of these charged species. The electrochemical stability can be evaluated through electroanalytical techniques; charged samples should be stored under the relevant conditions (i.e., temperature regulation and under N₂ or ambient atmosphere), with cyclic voltammograms recorded over an extended period of time relevant to the duration of the charge–discharge experiment. To illustrate, if a charge–discharge experiment takes 7 days to reach the desired number of cycles under the employed conditions, then daily cyclic voltammetric monitoring for a week can be useful in tracking decomposition (decrease in current response) and electroactive side product formation in metal-based systems. Furthermore, open circuit voltage (OCV) measurements can be valuable in assessing the thermodynamic stability of the electrolyte. OCV is a measure of the equilibrium potential of an electrochemical cell, which should exhibit a stable value if the electrolyte species are not undergoing any chemical decomposition. Periodic monitoring of the OCV of the bulk electrolyzed samples can provide insights into whether the electrolyte solution in a particular charge state is amenable to voltage changes as a function of homogeneous reactions (as indicated by significant fluctuation of OCV values). In some cases, the product of decomposition is not electroactive; degradation of the redox mediator may be indicated by a decrease in current response in cyclic voltammtery data collected over time. We suggest the use of complementary analytical techniques to identify the nature of the product of decomposition, as this information can be used to further iterate the molecular structure of the redox mediator. For example, electronic absorption and nuclear magnetic resonance (NMR) spectroscopies can be valuable to determine the identity of the decomposition product. Specifically, ligand dissociation is a common problem in metal-based systems, which is easily detected by ¹H NMR spectroscopy. Alternatively, electronic absorption spectroscopy can be a useful handle (especially for inorganic charge carriers) to monitor the changes in absorbance at specific wavelengths and indicate the presence of new species or degradation products.

Electron paramagnetic resonance (EPR) is another spectroscopic handle that can be valuable in determining the durability of the electrolyte if the redox-active complex is EPR active (i.e., it contains unpaired electrons in the relevant oxidation states). EPR parameters such as g-value, hyperfine splitting, linewidth, and signal intensities are fingerprints of specific oxidation states, coordination environments, and unpaired electron densities. As such, periodic monitoring of the EPR signal intensities (with appropriate spin quantification techniques) can reveal information about decomposition of the paramagnetic species through either change in oxidation state or ligand loss. The appearance of any new signatures can aid in further deducing the identity of the degradation products. Additionally, kinetic degradation profiles of the electrolyte system can be mapped by plotting EPR signal intensity versus time to define a threshold value (for example, 50% EPR signal loss) on calendar life.

Computational methods, such as Density Functional Theory (DFT), can complement experimental efforts by predicting redox potentials, solubility trends, and possible degradation pathways of molecular charge carriers (Fig. 3). For instance, DFT calculations can simulate solvent interactions to estimate solubility limits or assess the stability of coordination complexes under varying electrochemical conditions.²⁸ Indeed, computational insights serve as a useful tool to narrow down the pool of candidate materials before experimental validation and streamlining the discovery process.

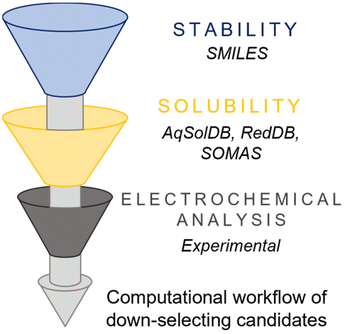Fig. 3 Available computational databases to perform initial screening of solubility (for e.g., AqSolDB, RedDB, and SOMAS) and stability (such as SMILES) for prospective charge carriers.

It should be noted that the discovery of high-performing materials for applications in RFBs relies on an understanding that these criteria serve as an initial screening step for the identification of good candidates for redox mediators. The following section details experimental methodologies that can be adopted to garner deeper insights into the physicochemical properties of the electrolyte system.

Evaluating physicochemical properties

A polarization curve illustrates the relationship between the voltage output as a function of current flowing through an electrode. It is a standard method for characterizing the performance of electrochemical devices, such as batteries. In the context of RFBs, the voltage efficiency (i.e., ratio of discharge voltage to the charge voltage) is dictated by the kinetic losses, resistive losses, and concentration polarization in the system. As shown in Fig. 4, the losses in the cell are primarily attributed to high kinetic overpotential at low current densities. These overpotentials arise due to the sluggish charge transfer kinetics at the electrode–electrolyte interface. At intermediate current density values, the polarization curve exhibits a linear relationship between current and voltage. The slope of this straight line is proportional to the internal resistance within the cell, which is often governed by the ionic resistance of the membrane. Lastly, concentration losses or mass transport limitations occur at the highest current densities. In such cases, the charge carrier's diffusion to and from the electrode surface limits cell operation. This prevents the current from increasing despite increasing overpotential in the cell. As such, the estimation of physicochemical properties such as diffusivity and electrochemical kinetics is crucial prior to RFB testing as these parameters directly influence charge transport, reaction rates, and overall battery performance.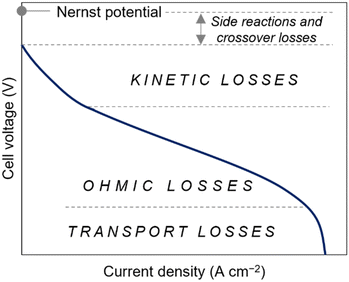

Fig. 4 General depiction of a polarization curve for an electrochemical system and the corresponding dominant losses affecting the cell voltage at lower and higher current density regimes.

Diffusion coefficients. The first step in establishing physicochemical parameters of charge carriers in RFBs involves measuring the diffusivity as it directly influences mass transport limitations. Without adequate diffusion, even electrochemically reversible redox couples with fast electron transfer kinetics may suffer from concentration polarization, leading to diminished (dis)charge efficiency. Thus, it is imperative to establish D₀ (measured in cm² s⁻¹) of charge carriers using either electrochemical or spectroscopic tools.
Pulsed field gradient NMR spectroscopy. Pulsed Field Gradient (PFG) NMR spectroscopy directly measures the diffusion coefficients of charge carriers in a given solvent, providing insights into their transport properties. A PFG-NMR spectrum tracks the displacement of molecules by acquiring a set of data after varying either the field gradient strength (g) or the length of the gradient pulse (δ). During the application of these pulsed magnetic field gradients, the other parameters are held constant and the plot of the intensity of the echo versus g or δ allows for the determination of diffusivity with high precision.²⁹ Diffusion ordered spectroscopy (DOSY) combines principles from conventional NMR spectroscopy with PFG-NMR spectroscopy to separate similarly diffusing species in a mixture based on their resonance frequency.³⁰ A detailed description of using DOSY for estimating diffusion coefficients is included in the ESI.† This method is particularly valuable for assessing how electrolyte composition and solvent viscosity influence charge transport, revealing the impact of solvation structure and ionic interactions on charge carrier mobility. For a detailed reading on the fundamentals of PFG techniques specifically for battery research, the readers are referred to the review published by Han and Mueller.³¹
Rotating disk voltammetry. The D₀ values can also be calculated electrochemically by utilizing rotating disk electrodes (RDEs). RDE voltammetry is a technique used to determine the diffusion coefficients of charge carriers by measuring steady state limiting currents (i_L) as a function of rotation speed (ω). The slope of the i_Lversus ω^1/2 plot, known as the Levich plot can be used to extract the associated D₀ values.

i_L = 0.620 × n × F × A × D^2/3₀ × ω^1/2×ϑ^−1/6×C (5)

In eqn (5), ϑ is the kinematic viscosity and A is the electrode area.

RDE studies have been employed to compare the diffusivity of different metal-based coordination complexes, revealing how ligand modifications influence solubility and charge transport.³² While this approach has been invoked to establish the diffusivity of inorganic charge carriers, the major limitation of Levich method arises when applied to systems with lower Schmidt numbers (S_c < 1000).³³ The S_c value is a dimensionless quantity that relates the viscosity of a fluid to its diffusion coefficient. Viscous solutions, such as polymeric electrolytes, metal-based eutectic systems, and non-aqueous solutions (solvents such as propylene carbonate and dimethylformamide), possess low S_c values. Consequently, the Levich equation cannot be used to predict the diffusion coefficients accurately in such media due to edge effects.^33,34 Other electrochemical protocols, such as the Randles–Ševčík method, can be a better method for electroanalysis in such scenarios.

Randles–Ševčík cyclic voltammetry method. Randles–Ševčík analysis is one of the most straightforward and popular methods for estimating diffusion coefficients.^35,36 It involves recording peak currents (i_p) at variable scan rates (ν) using cyclic voltammetry. The linear relationship between i_p and ν^1/2 yields a slope proportional to the D₀ of the charge carrier. At room temperature, the Randles–Ševčík equation for an electrochemical reversible redox process can be expressed as eqn (6).

i_p = 2.69 × 10⁵ × n^3/2 × A × C × D^1/2₀ × ν^1/2 (6)

This method is particularly useful when conducting initial screening experiments, as it requires minimal sample preparation and provides estimates of diffusivity of relevance to battery cycling (i.e., under electrochemical conditions). In cyclic voltammetry measurements obtained to estimate D₀, glassy carbon is often employed as the working electrode owing to its non-catalytic nature and a Pt plate or wire can serve as the counter electrode. For accurate recording of potential-current curves, it is important to employ appropriate reference electrodes; Ag/AgNO₃ should be employed in non-aqueous conditions.³⁷ The variations in mathematical relations for Randles–Ševčík analysis of electrochemically irreversible and quasi-reversible redox processes are provided in the ESI.†

Uncompensated resistance. Along with the choice of the reference electrode, its physical placement within the electrochemical cell also becomes pertinent during electroanalysis. In a three-electrode electrochemical cell, the reference electrode measures the potential at the working electrode. However, due to operational constraints, the placement of a reference electrode cannot be perfectly adjacent to the working electrode surface, introducing a small but significant resistance that can distort voltage measurements (Fig. 5a). This unaccounted electrical resistance between the working electrode and the tip of the reference electrode is known as uncompensated resistance (R_u).³⁸ Many studies rely on kinetic parameters extracted from cyclic voltammograms without systematically accounting for R_u, which can lead to overestimation or misinterpretation of rates of charge transfer. This oversight is particularly problematic in non-aqueous RFBs, where solvent viscosity, ion pairing, and supporting electrolyte composition contribute to significant resistive losses further impacting the reduction potentials of the charge carrier. Furthermore, reports comparing charge carriers often fail to normalize kinetic parameters to correct for R_u, making direct comparisons between materials unreliable.

Fig. 5 (a) Cyclic voltammetry curves for an illustrative example with (blue) and without (yellow) appropriate iR compensation. The peak separation yields erroneous values if proper uncompensated resistance correction is not employed, which impacts the evaluated physicochemical properties. Plot (b) shows the changes in potential versus normalized capacity (or state-of-charge) traces in uncompensated systems as compared to compensated measurements. If not properly compensated, the increased internal resistance in a battery manifest as a steeper drop in voltage under load (i.e., during discharge) and a shallower slope in voltage during the charging process.

R _u should be thoroughly accounted for prior to performing kinetic analysis to ensure reliable extraction of rate constants and reproducibility across experiments. To begin with, the experimental conditions should be kept such that the solution resistance can be minimized. This includes ensuring sufficient conductivity of the electrolyte by employing an excess of the supporting electrolyte. Additionally, the working electrode must be kept as close to the reference electrode as possible without touching to avoid short-circuiting during the measurement. It has been demonstrated that R_u declines exponentially as this distance is decreased. Caution must also be placed towards the geometry and placement of the counter electrode. The counter electrode must be much larger in area than the working electrode and a large interelectrode distance should be adopted. R_u can still persist after these practical considerations have been addressed in the cell setup. Some recommended techniques for measuring R_u include positive feedback compensation, iR-free extrapolation, electrochemical impedance spectroscopy (EIS), and four-electrode configuration.

Four-electrode configuration. Modern electrochemical potentiostats are four-probe instruments that can be used to carry out a variety of measurements with either two electrode, three electrode, or four electrode setups. The four-electrode configuration uses two separate electrode pairs – the working sense is decoupled from the working electrode and current is passed through one pair (working and counter) while the potential drop is measured across a separate pair (sense and reference). The latter allows for accurate estimation of R_u. While it is a useful technique for measuring the impedance of an electrochemical system, or studying potential drops across a specific region (for instance, between the working and reference electrodes), a four-electrode setup must be extremely robust when applied for highly resistive non-aqueous media. Particularly, high impedance of the reference and sensing electrodes in organic solvents can introduce artifacts in the measurements. Thus, careful analysis of different contributions, such as sample resistance, positioning, and geometry of the electrodes, becomes necessary in organic media.³⁹
Electrochemical impedance spectroscopy. EIS is a suitable method for quantifying the ohmic drop of an electrolyte regardless of the kinetics of the system. R_u is estimated by analyzing the response of an electrochemical cell to a small amplitude of alternating current signal across a wide range of frequencies. This method gives information about the resistance of the electrolyte solution between the working electrode and the reference electrode, which is not automatically compensated by the instrument itself. To primarily isolate R_u, the high-frequency region of the EIS spectrum is analyzed, as this part is primarily dominated by the solution resistance with minimal contributions from other electrochemical processes. EIS is widely used in battery research to evaluate the internal resistance of the cell. However, analyzing impedance data is not straightforward; it is subject to correct fitting of the data to appropriate equivalent electrical circuit models and subsequently using specialized software to extract the uncompensated resistance value based on the circuit model chosen for a given system. Incorrect choice of equivalent circuit models to fit the data can lead to inaccurate estimations of solution resistance and thus leaves more room for error via misinterpretation, making it sometimes challenging to get reliable data.
Positive feedback compensation. The positive feedback iR compensation is a technique that corrects for the voltage drop caused by solution resistance between the working and reference electrodes by feeding back a portion of the measured current to the potentiostat. This feedback process involves multiplying the observed current value with the estimated R_u and adding the resulting voltage value back to the applied potential, effectively compensating for the voltage loss in the solution. The accuracy of the compensation relies on knowing the precise value of the solution resistance and feeding it into the software. However, if the solution resistance changes during the experiment due to external factors such as transient changes in temperature, electrodeposition, or material decomposition, the compensation may become inaccurate. Moreover, over-compensation can lead to oscillations in the system due to the positive feedback loop. To avoid these unfavorable scenarios, iR-free extrapolation is a better choice.
iR-free extrapolation. The electronics in a potentiostat is inclined to oscillate when fully compensated for the ohmic drop. This can have a deleterious impact on the internal circuitry as well as the attached electrodes. Thus, rather than fully accounting for the R_u value as sometimes done using positive feedback, we recommend using the iR-free extrapolation method. Moreover, full R_u compensation might lead to artificial overcompensation, resulting in peak separation values which are less than the theoretical peak potential separation of 59 mV. The suggested technique involves correcting a percentage of the recorded solution resistance using the potentiostat and then accounting for the remaining R_u manually to correct for the observed potential.⁴⁰ This extrapolates the results in a way that results in 100% compensation without introducing the complications associated with instrumental oscillations to the system. To illustrate, the default correction value in most potentiostats is 85% for solution resistance. However, partial instrumental iR correction can be performed between 85% and 95%. The first step involves monitoring the cyclic voltammograms at a given correction value for all employed scan rates. In cases where the voltammograms look distorted, we recommend decreasing this value. For multimetallic inorganic compounds, such as polyoxovanadate-alkoxide clusters and octadecavanadate assemblies, 95% compensation via the instrument works well in the scan range of 10–10 000 mV s⁻¹. Moving towards higher values, say 98%, warps the cyclic voltammogram profile. The remaining amount can be accounted for manually to achieve full compensation as shown in eqn (7).

E_true = E_app − UI (7)

In eqn (7), E_app is the potential after the software's internal correction, U is the percent uncompensated resistance left after the instrumental iR correction, and I is the current response. While it might seem feasible to stick with the default value and do the remaining 15% manually using eqn (7) to achieve 100% compensation, this can lead to erroneous calculations of properties based on the data as well as lead to larger errors on the obtained values (see ESI† for a detailed example). We recommend choosing a suitable value in between 85% to 95% range and account for the remaining percentage manually. The readers are also advised to ensure that the employed iR correction value does not result in peak separations less than the theoretical value of 59 mV.

While the foregoing estimation of uncompensated resistance is focused on determining the charge transfer resistance and electrode kinetics in a three-electrode setup, the resistance of a two-electrode cell (as observed in a battery setup) includes additional components such as those introduced by the membrane. Thus, the experimentally determined impedance values can significantly differ in a cyclic voltammetry analysis versus a battery experiment. In a two-electrode system, it is difficult to deconvolute the behavior of individual components (charge transfer resistance, double-layer capacitance, and diffusion resistance) as the electrochemical measurements generally yield the total cell resistance. In such scenarios, pre-screening using cyclic voltammetry or EIS analysis can come in handy to assign the source of resistance more precisely. For example, if the charge transfer resistance of a given redox process is high at low potentials in a three-electrode measurement, one can expect to observe sluggish kinetics at low voltage end of (dis)charge in a full cell. It is quite likely that the corresponding reaction will become a bottleneck in the overall performance of a battery, which can be prevented by either modifying the underlying electrode surface or employing a different electrolyte system. The increased internal resistance in the battery leads to premature cutoffs if not properly compensated, thus affecting overall performance (Fig. 5b). Thus, prior screening of electrodes and redox-active materials in half-cell conditions can help identify low-resistance, high-rate candidates before integrating them into a full battery.

Heterogeneous rates of charge transfer. The accurate determination of electrochemical kinetics (usually measured in cm s⁻¹) of the charge carrier in a given electrolyte is crucial as it influences charge transfer efficiency, activation losses, and overall battery performance. Activation losses, which arise from sluggish charge transfer at the electrode–electrolyte interface, can significantly reduce voltage efficiency and power output of the resulting RFBs. These losses are particularly significant in non-aqueous conditions where lower electrolyte conductivity exacerbates kinetic limitations. As such, rigorous kinetic analysis is a critical step in charge carrier evaluation that can allow for kinetic enhancements through tailoring the electrode materials, modifying electrolyte formulations, and optimizing operating conditions. Several methods exist for determining the heterogeneous rates of electron transfer, which provide valuable insights into electrochemical reaction mechanisms and kinetic parameters.
Koutecký–Levich method. The Koutecký–Levich method employs RDE voltammetry to deduce the standard rate constant (k₀) and the symmetry factor (α). This method distinguishes between the diffusion-controlled and kinetically controlled processes and allows for the accurate determination of k₀ (eqn (8)).⁴¹ However, it should be noted that the Koutecký–Levich analysis is only valid for sluggish reactions (k₀ ≤ 10⁻² cm s⁻¹). We recommend employing other strategies for deducing k₀ values for cluster-based charge carriers where the electron transfer can be inherently fast as a virtue of charge delocalization.

log i_k = log(nFCAk₀) + (nFαη/2.303RT) (8)

In eqn (8), R is the gas constant, T is temperature, and η is the overpotential.

Gileadi method. The Gileadi method for evaluation of heterogeneous rate constants relies on the identification of a critical scan rate (ν_c) at which the nature of the electrode reaction changes from reversible to irreversible. The latter is determined by plotting the E_1/2 values against the logarithm of ν ranging from low to high scan rates.⁴² The working principle lies in separately fitting the two linear curves obtained from the lower and higher ranges of scan rates, extrapolating them, and finding the precise scan rate at which the two curves intersect. This scan rate is the ν_c of the system. Subsequent fitting of the data to eqn (9) yields the corresponding k₀.

log k₀ = −0.48α + 0.52 + log[nFαν_cD₀/2.303RT] (9)

The Gileadi method is attractive as it allows for direct rate constant determination and does not rely on peak separation between the anodic and cathodic waves of the corresponding cyclic voltammograms. However, this approach often necessitates employment of extremely high scan rates to determine ν_c (scan rate >10 V s⁻¹). This can be problematic in cases where the cyclic voltammograms become distorted (i.e., lose the classical “duck” shape) at higher scan rates. Moreover, the method also requires precise information about α for accurate k₀ determination, which can vary with slight changes in ligand composition in inorganic active materials.

Kochi–Klinger method. The method proposed by Kochi and Klinger correlates the separation of peak potentials to the rate constant for heterogeneous electron transfer (eqn (10)). This method is applicable to electrochemically irreversible systems (nΔE_p > 150 mV) and thus is particularly useful for inorganic redox mediators, as they can often exhibit borderline electrochemical irreversible behavior if accurate values of the transfer coefficient are not accounted.⁴³ The Kochi–Klinger strategy incorporates correction for electrode reaction mechanisms, which can arise because of electronic and structural differences in the charge carrier. Thus, this method for k₀ evaluation is useful for non-aqueous redox systems where modulation of the inorganic complex may impact the sterics and electronics of the resulting charge carrier. However, its applicability is limited as the Kochi-Klinger method is specifically suited for entirely electrochemically reversible systems, and a majority of the inorganic redox couples are quasi-reversible in nature.

k₀ = 2.18 × (αnFD₀ν/RT)^−1/2 × exp[−α²nF(ΔE_p)/RT] (10)

Nicholson method. The Nicholson method for estimating rate constants at the electrode–electrolyte interface is the most popular voltammetry technique to evaluate electrochemical kinetics. It is a peak separation method that is applicable to electrochemically quasi-reversible systems (60 < nΔE_p < 220 mV).⁴⁴ The mathematical relation associates k₀ with a dimensionless parameter Ψ, which is usually evaluated graphically. While this method is ideal for the assessment of rate constants owing to the relatively simple electroanalytical procedure, skepticism toward the adoption of this method germinates from the poor understanding of calculating Ψ. Seminal texts like Bard and Faulkner state the values of Ψ for certain specific values of ΔE_p.⁴⁵ As such, interpreting Ψ for other peak potential separation values is not always straightforward. We recommend using Nicholson's working curve (Fig. S5†) to discern the specific Ψ values for the corresponding ΔE_p obtained after appropriate iR compensation from the variable scan rate voltammetry data. Moreover, the employed scan rates should be as high as possible to get an upper bound of the rates being measured.

k₀ = Ψ(πnFD₀ν/RT)^1/2 (11)

The slope of the Ψ versus the square root of scan rate yields the value of k₀ (eqn (11)). A detailed example of using this strategy to evaluate the heterogeneous rates of charge transfer for a polyoxovanadate-based charge carrier is included in the ESI.†

Battery testing in static H-cells

While flow testing serves as a pivotal performance indicator in realizing the potential of an electrolyte system for large-scale implementation, the resulting metrics are an outcome of not only the redox chemistries of the electrolyte components but also several engineering constraints (such as cell and stack design, flow dispersion, fluid flow rate, etc.).⁴⁶ To understand the behavior of the underlying chemistries, H-cell testing serves as an important first step in evaluating electrolyte systems for RFB applications. Such cells provide a controlled environment to assess the intrinsic electrochemical properties of candidate materials without the complexities introduced by full flow systems. For instance, by isolating variables such as mass transport and flow dynamics, H-cells allow to decouple fundamental kinetic and stability parameters from engineering considerations. These insights form a foundation for transitioning promising materials to flow configurations with greater confidence, ensuring efficient resource utilization and accelerating efforts towards deployment.

Pre-cycling requirements. The use of non-aqueous solvents necessitates rigorous drying and degassing of solvents to prevent water contamination prior to electrolyte preparation.⁴⁷ While it can be difficult to completely remove moisture from specific solvents, we encourage quantifying the amount of water using trusted methods such as the Karl–Fischer (KF) titration. It is a powerful technique to determine trace amounts of water in a sample; such information can yield useful information about the effect of water on the underlying chemistries, if any.

The H-cell is usually a glass container with two compartments separated by either a semi-permeable membrane or a glass frit of appropriate porosity (Fig. 6). The separator material must be resistant to the organic solvents used during testing, lower ionic resistance to enable operation at higher current densities, and stabilize net electrolyte transport to circumvent capacity imbalance. The compatibility of the separator can be assessed by soaking the H-cell with the desired electrolyte for at least 24 h and assessing for any precipitation or disintegration of the membrane. The employed electrodes must exhibit high surface area to minimize resistance in the electrochemical cell.

Fig. 6 Schematic representation of an H-cell used in a symmetric cell setup.

Lastly, voltammograms must be recorded of both the positive and negative electrolytes prior to their introduction to the H-cell. Cyclic voltammetry analyses establish baseline redox behavior of the electrolyte immediately before testing and can serve as a reference (especially for the associated current) for post-cycling analytical protocols.

Charge–discharge cycling. The charge–discharge cycling refers to the repeated oxidation and reduction of the battery electrolyte. The redox cycling method and choice of input parameters can be tuned to gain specific information about the performance of the battery ensemble. Cycling can be performed at either constant current or charge (i.e., galvanostatic), constant voltage (i.e., potentiostatic), or a combination of both. Each of these cycling strategies are used under specific conditions to garner particular information about the underlying chemistries. A detailed description of the different cycling protocols is mentioned in the following sections.

An important consideration in choosing cycling parameters, irrespective of the charge–discharge strategy, is choosing the current densities and voltage limits. For example, the ohmic resistance of an operating cell can be different than the ones used in the initial screening stages. This resistance can be measured using EIS by calculating the area specific resistance (ASR). Generally, non-aqueous RFBs exhibit high ASRs owing to meager ionic conductivities, which limits the cell operation to lower current densities to achieve decent efficiency. To illustrate, a thin porous separator (∼175 μm) with 2.5 mm thick graphite-felt electrodes exhibit ASR values in the range of 3 to 18 Ω cm², which can allow to operate at higher current densities (up to 600 mA m⁻²).⁴⁸ Thus, the operating current densities and the voltage limits should be carefully selected during electrolyte screening by accounting for all overpotentials (ohmic, transport, kinetic).

Galvanostatic cycling. Galvanostatic charge–discharge is the commonly used methodology to gain insights into the long-term battery performance and capacity retention. It involves charging the electrolyte at a specific current (or charge) value until an upper cut-off voltage is reached. Subsequently, either the same or different constant current (or charge) value is used to discharge the battery until the lower cut-off voltage is achieved. This process is repeated for the desired number of cycles/time duration. The observed capacity reflects the overall effect of the cell resistance, geometry, temperature fluctuations, and decomposition of the electrolyte. As such, it becomes difficult to deconvolute the different sources of capacity fade. Moreover, galvanostatic cycling is not a true representation of the overall capacity as it is greatly affected by the polarization resistance that changes the state of charge at which the voltage limits are reached.
Potentiostatic cycling. Potentiostatic charge–discharge is the appropriate method if the purpose of the cycling experiment is to characterize the true capacity of the electrolyte. It involves using a constant voltage for the charge and discharge processes until a steady state background current is achieved. While this approach limits the occurrence of side reactions due to strict monitoring of the applied potential, it is however a time-consuming approach as the process becomes slower with cycling time due to the lower concentration of the active species. This limitation makes it a non-ideal approach for scenarios where the purpose of the experiment is to quickly screen robust electrolytes and identify molecular decomposition using H-cell cycling.
Galvanostatic-potentiostatic cycling. To overcome the individual limitations associated with galvanostatic only and potentiostatic only (dis)charge modes, galvanostatic cycling with potential holds is a neat approach which combines the advantages of both methods. It involves charging the battery first at a constant current until the set cut-off voltage limit is reached and subsequently holding this voltage until the desired state-of-charge is achieved. The battery is then allowed to discharge in a similar manner. Essentially, the major difference between this protocol and a purely potentiostatic mode of charge–discharge is the time distribution of the applied potential. Moreover, the total capacity accessed during a galvanostatic cycling with potential hold remains unaffected by any temperature fluctuations arising within the battery electrolyte during the redox reactions.⁴⁹ This method of battery cycling is particularly useful for organic and organometallic charge carriers where capacity fade is independent of the number of charge–discharge cycles imposed and the molecular decomposition is a function of time, which may be state-of-charge dependent.

Fig. 7 depicts the differences in charge–discharge curves obtained from a purely galvanostatic and galvanostatic-potentiostatic charge–discharge experiment. In Fig. 7a, a polyoxovanadate-alkoxide charge carrier was subjected to galvanostatic cycling at a constant current of 0.2 mA between the potential limits of 1.9 V and 1.4 V. The corresponding potential versus time trace shows an increase in the potential during the charging mode until the upper cutoff of 1.9 V is reached followed by the subsequent drop in potential in the discharge mode until the lower cutoff of 1.4 V is achieved. One cycle (i.e., cycle number 2) under this mode takes approximately 3 h 45 minutes. However, the cycling duration increases to approximately 5 h (for cycle number 2) when the same electrolyte formulation is subjected to galvanostatic cycling followed by a potentiostatic hold, resulting in enhanced capacity of the system (Fig. 7b). The differences in these capacities are a reflection of polarization resistance occurring in the cell that changes the state of charge at which the voltage limits are reached. As such, galvanostatic-potentiostatic cycling represents the true capacity of the system.

Fig. 7 An illustrative example depicting the different charge–discharge curves obtained from different cycling modes on the same charge carrier – (a) galvanostatic only, and (b) galvanostatic-potentiostatic cycling.

Polarity-reversal cycling. Polarity-reversal refers to the process during symmetric charge–discharge where the positive and negative sides are completely switched so that the respective oxidation and redox reactions occur at the opposite electrode. It can be used in scenarios where the electroactive species needs to be regenerated, the state-of-charge has to be rebalanced in the electrochemical cell, or testing the performance of symmetrical cells using different cycling protocols. This technique is not ideal for solid-state and aqueous batteries, as the heat generated by the battery's reverse polarity may produce flammable hydrogen gas and destroy the ensemble. However, polarity reversal cycling experiments can be particularly useful for symmetric non-aqueous systems to limit capacity fade arising due to decomposition. For example, if only one half-cell reaction is prone to instability, polarity-reversal cycling can distribute the degradation over both electrolyte sides so that the capacity improves without significant decomposition of one electrolyte. Several studies have alluded to the formation of solid electrolyte interphase (SEI) in semi-solid RFBs, analogous to their solid-state counterparts.^50,51 Polarity reversal cycling can be a powerful strategy in such scenarios where a more uniform electrode surface can be maintained by alternating the current direction. Fig. 8 depicts an illustration of a galvanostatic polarity cycling methodology and the corresponding charge–discharge curve.

Fig. 8 An illustrative example of sequential inputs to achieve a galvanostatic polarity-reversal charge–discharge in a redox flow battery (top) and the corresponding cycling curves (bottom) retrieved after the experiment (reproduced with permission from ref. 52).

Our team has demonstrated that the practical capacity of polyoxovanadate-based charge carrier remains higher (20% average capacity fade as compared to 62% with other techniques for the same number of cycles) when degradation is distributed over both of the symmetric battery electrolytes.⁵² We also observed the least amount of formation of the decomposition product using polarity reversal (as compared to galvanostatic-potentiostatic and compositionally imbalanced cycling) and the results obtained from this cycling strategy were further instrumental in assigning a purely chemical decomposition mechanism as the source of capacity fade. As such, our recommendation is that all symmetric RFB systems should be assessed with polarity reversals and conventional cycling to compare capacity fades to get a deeper understanding of the role of intrinsic chemistries of the active species on battery performance.

Compositionally imbalanced cycling. Compositionally imbalanced cycling, either volumetric or concentration, is a useful charge–discharge protocol to gain a thorough understanding of the prevalent molecular decay mechanisms in RFBs, such as electrolyte side reactions and self-decomposition of the charge carrier. Both volumetric or concentration imbalanced cycling operate on the principle that creating a capacity limiting side by the virtue of different compositions can limit decomposition, improve state-of-charge and ultimately improve the observed capacity. Our team and others have tested the efficacy of this unbalanced compositionally-symmetric cell methodology in revealing and quantifying different mechanisms for capacity fade and minimizing them as compared to other charge–discharge techniques.^49,52

Post-cycling analysis. Post-cycling analysis is a necessary step to garner critical insights into degradation mechanisms affecting the battery performance and longevity. A combination of spectroscopic, microscopic, and electrochemical techniques can be employed to assess changes both at the electrode and electrolyte. Comparison of pre- and post-characterization of the electrolyte using cyclic voltammetry and electronic absorption spectroscopy can provide information about structural changes occurring in the charge carrier dynamics during repeated charge–discharge.

The primary features to look for in post-cycling analysis include crossover and decomposition of the active material. These two phenomena account for the major capacity fade during battery operation. Crossover can be detected by monitoring the resulting electrolyte solutions (posolyte and negolyte) using electronic absorption spectroscopy and/or cyclic voltammtery. During electronic absorption analysis, any changes in absorption features of each electrolyte should be evaluated before and after charge–discharge and then compared to the corresponding change in the other electrolyte. For example, if the positive electrolyte shows a single absorption feature after chemical oxidation but other features emerge after cycling that match with the absorption profile of the negative electrolyte, then it is quite likely that the species have crossed over during the experiment. However, if the additional features do not match with any charge state of the negative electrolyte, then it is probable that the positive electrolyte has undergone decomposition during the course of the experiment. Similar pre- and post-analysis can also be done using cyclic voltammetry.

In addition to electrolyte characterization, thorough investigations of the electrodes pre- and post-cycling can yield information about the interfacial chemistries specifically in cases where capacity losses are attributable to degradation. Surface characterization techniques, such as scanning electron microscopy (SEM) and atomic force microscopy (AFM), are valuable to visualize changes in surface morphology as a result of structural degradation such as roughening, cracking, or material deposition. X-ray photoelectron spectroscopy (XPS), Raman spectroscopy, and energy-dispersive X-ray spectroscopy (EDS) can detect compositional changes, revealing electrode corrosion, passivation layers, or unwanted side reactions that contribute to performance fade. Additionally, techniques such as electrochemical quartz crystal microbalance (EQCM) offers a dynamic method to track real-time mass fluctuations at the electrode surface, shedding light on material dissolution, film formation, or ion adsorption during redox cycling. Collectively, these analyses give a comprehensive understanding of how capacity loss, increased resistance, and efficiency decline occur over time, guiding the development of more stable and durable RFB materials.

Conclusions

The evaluation of inorganic charge carriers for non-aqueous redox flow batteries requires a systematic approach that integrates fundamental electrochemical analysis, kinetic and transport properties assessment, and rigorous battery testing. We discussed the utility of a myriad of experimental, spectroscopic, and electroanalytical tools to understand the physicochemical properties and robustness of charge carriers to identify the most promising candidates for efficient and stable energy storage. Notably, synthetic chemists can use the foregoing discussion to adopt the most viable methods for their desired charge carrier to guide material optimization and electrolyte formulation. Future work should focus on establishing clear correlations between H-cell experiments and full flow battery performance to ensure lab-scale findings translate effectively into practical systems. We envision that in situ characterization techniques and refining existing kinetic models will help to bridge this gap and enable predictive design strategies for next-generation redox flow batteries.

Data availability

All data for this project has been deposited in the main text or ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are thankful to Dr. Tessa Baker for helpful advice on collecting and interpreting DOSY NMR spectra. M. D. and E. M. M. acknowledge support from the National Science Foundation Division of Chemical, Bioengineering, Environmental & Transport Systems through award 2350223. The authors also acknowledge the use of JEOL NMR spectrometers acquired with support from the NSF (MRI-2215973).

References

1. M. Amir, R. G. Deshmukh, H. M. Khalid, Z. Said, A. Raza, S. M. Muyeen, A.-S. Nizami, R. M. Elavarasan, R. Saidur and K. Sopian, J. Energy Storage, 2023, 72, 108694.
2. B. Obama, Science, 2017, 355, 126–129.
3. A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. H. Liu, J. Appl. Electrochem., 2011, 41, 1137–1164.
4. L. Y. Zhang, R. Z. Feng, W. Wang and G. H. Yip, Nat. Rev. Chem., 2022, 6, 524–543.
5. J. Winsberg, T. Hagemann, T. Janoschka, M. D. Hager and U. S. Schubert, Angew. Chem., Int. Ed., 2017, 56, 686–711.
6. G. L. Soloveichik, Chem. Rev., 2015, 115, 11533–11558.
7. L. Trahey, F. R. Brushett, N. P. Balsara, G. Ceder, L. Cheng, Y. M. Chiang, N. T. Hahn, B. J. Ingram, S. D. Minteer, J. S. Moore, K. T. Mueller, L. F. Nazar, K. A. Persson, D. J. Siegel, K. Xu, K. R. Zavadil, V. Srinivasan and G. W. Crabtree, Proc. Natl. Sci. Acad., 2020, 117, 12550–12557.
8. Z. Liang, R. K. Jha, T. M. Suduwella, N. H. Attanayake, Y. Wang, W. Zhang, C. Cao, A. P. Kaur, J. Landon and S. A. Odom, J. Mater. Chem. A, 2022, 10, 24685–24693.
9. J. Luo, B. Hu, M. Hu, Y. Zhao and T. L. Liu, ACS Energy Lett., 2019, 4, 2220–2240.
10. K. Gong, Q. R. Fang, S. Gu, S. F. Y. Li and Y. S. Yan, Energy Environ. Sci., 2015, 8, 3515–3530.
11. M. Skyllas-Kazacos and F. Grossmith, J. Electrochem. Soc., 1987, 134, 2950–2953.
12. Q. H. Liu, A. E. S. Sleightholme, A. A. Shinkle, Y. D. Li and L. T. Thompson, Electrochem. Commun., 2009, 11, 2312–2315.
13. M. Li, S. A. Odom, A. R. Pancoast, L. A. Robertson, T. P. Vaid, G. Agarwal, H. A. Doan, Y. L. Wang, T. M. Suduwella, S. R. Bheemireddy, R. H. Ewoldt, R. S. Assary, L. Zhang, M. S. Sigman and S. D. Minteer, ACS Energy Lett., 2021, 6, 3932–3943.
14. A. C. Lazanas and M. I. Prodromidis, ACS Meas. Sci. Au, 2023, 3, 162–193.
15. T. C. Palmer, A. Beamer, T. Pitt, I. A. Popov, C. X. Cammack, H. D. Pratt, T. M. Anderson, E. R. Batista, P. Yang and B. L. Davis, ChemSusChem, 2021, 14, 1214–1228.
16. H. Wang, S. Y. Sayed, E. J. Luber, B. C. Olsen, S. M. Shirurkar, S. Venkatakrishnan, U. M. Tefashe, A. K. Farquhar, E. S. Smotkin, R. L. McCreery and J. M. Buriak, ACS Nano, 2020, 14, 2575–2584.
17. D. O. Wipf, E. W. Kristensen, M. R. Deakin and R. M. Wightman, Anal. Chem., 1988, 60, 306–310.
18. O. Nolte, I. A. Volodin, C. Stolze, M. D. Hager and U. S. Schubert, Mater. Horiz., 2021, 8, 1866–1925.
19. Y. A. Gandomi, D. S. Aaron, J. R. Houser, M. C. Daugherty, J. T. Clement, A. M. Pezeshki, T. Y. Ertugrul, D. P. Moseley and M. M. Mench, J. Electrochem. Soc., 2018, 165, A970–A1010.
20. Q. Huang and Q. Wang, ChemPlusChem, 2015, 80, 312–322.
21. M. A. Raihan and C. A. Dyker, J. Energy Chem., 2025, 100, 125–143.
22. R. A. Potash, J. R. McKone, S. Conte and H. D. Abruna, J. Electrochem. Soc., 2016, 163, A338–A344.
23. A. F. Barton, Chem. Rev., 1975, 75, 731–753.
24. M. Li, Z. Rhodes, J. R. Cabrera-Pardo and S. D. Minteer, Sustainable Energy Fuels, 2020, 4, 4370–4389.
25. J. D. Milshtein, A. P. Kaur, M. D. Casselman, J. A. Kowalski, S. Modekrutti, P. L. Zhang, N. Harsha Attanayake, C. F. Elliott, S. R. Parkin, C. Risko, F. R. Brushett and S. A. Odom, Energy Environ. Sci., 2016, 9, 3531–3543.
26. L. Su, M. Ferrandon, J. A. Kowalski, J. T. Vaughey and F. R. Brushett, J. Electrochem. Soc., 2014, 161, A1905–A1914.
27. A. M. Fenton, R. K. Jha, B. J. Neyhouse, A. P. Kaur, D. A. Dailey, S. A. Odom and F. R. Brushett, J. Mater. Chem. A, 2022, 10, 17988–17999.
28. L. Cheng, R. S. Assary, X. Qu, A. Jain, S. P. Ong, N. N. Rajput, K. Persson and L. A. Curtiss, J. Phys. Chem. Lett., 2015, 6, 283–291.
29. G. Pagès, V. Gilard, R. Martino and M. Malet-Martino, Analyst, 2017, 142, 3771–3796.
30. K. F. Morris and C. S. Johnson Jr, J. Am. Chem. Soc., 1992, 114, 3139–3141.
31. K. S. Han, J. D. Bazak, Y. Chen, T. R. Graham, N. M. Washton, J. Z. Hu, V. Murugesan and K. T. Mueller, Chem. Mater., 2021, 33, 8562–8590.
32. A. M. Kosswattaarachchi, L. E. VanGelder, O. Nachtigall, J. P. Hazelnis, W. W. Brennessel, E. M. Matson and T. R. Cook, J. Electrochem. Soc., 2019, 166, A464–A472.
33. H. Chen, E. Kätelhön and R. G. Compton, Anal. Chem., 2023, 95, 12826–12834.
34. J. Legrand, E. Dumont, J. Comiti and F. Fayolle, Electrochim. Acta, 2000, 45, 1791–1803.
35. J. E. B. Randles, Trans. Faraday Soc., 1948, 44, 327–338.
36. A. Ševčík, Collect. Czech. Chem. Commun., 1948, 13, 349–377.
37. N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, J. Chem. Educ., 2018, 95, 197–206.
38. W. Zheng, ACS Energy Lett., 2023, 8, 1952–1958.
39. V. F. Lvovich and M. F. Smiechowski, ECS Trans., 2010, 25, 1–25.
40. J. C. Myland and K. B. Oldham, Anal. Chem., 2000, 72, 3972–3980.
41. S. Treimer, A. Tang and D. C. Johnson, Electroanalysis, 2002, 14, 165–171.
42. H. Muhammad, I. A. Tahiri, M. Muhammad, Z. Masood, M. A. Versiani, O. Khaliq, M. Latif and M. Hanif, J. Electroanal. Chem., 2016, 775, 157–162.
43. R. J. Klingler and J. K. Kochi, J. Phys. Chem., 1981, 85, 1731–1741.
44. R. S. Nicholson, Anal. Chem., 1965, 37, 1351–1355.
45. A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2^nd edn, 2000.
46. L. F. Arenas, C. Ponce de León and F. C. Walsh, J. Energy Storage, 2017, 11, 119–153.
47. D. R. Burfield and R. H. Smithers, J. Org. Chem., 1978, 43, 3966–3968.
48. X. L. Wei, W. T. Duan, J. H. Huang, L. Zhang, B. Li, D. Reed, W. Xu, V. Sprenkle and W. Wang, ACS Energy Lett., 2016, 1, 705–711.
49. M. A. Goulet and M. J. Aziz, J. Electrochem. Soc., 2018, 165, A1466–A1477.
50. E. Ventosa, G. Zampardi, C. Flox, F. La Mantia, W. Schuhmann and J. R. Morante, Chem. Commun., 2015, 51, 14973–14976.
51. A. Narayanan, D. Wijnperlé, F. Mugele, D. Buchholz, C. Vaalma, X. Dou, S. Passerini and M. H. G. Duits, Electrochim. Acta, 2017, 251, 388–395.
52. M. Dagar, D. Dissanyake, D. N. Kesler, M. Corr, J. D. McPherson, W. W. Brennessel, J. R. McKone and E. M. Matson, Dalton Trans., 2023, 53, 93–104.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dt00830a

---