Unusually short Au(III)⋯Au(III) aurophilic contacts between anions. Necessity of counterions

Abstract

Certain crystals contain unusually short contacts between Au(III) species, sometimes interpreted as unsupported aurophilic interactions. Calculations at various levels of theory, including CCSD(T)/CBS, demonstrate the potentials between anions containing these Au(III) centers are purely repulsive, despite the presence of noncovalent bonding between the Au centers. The occurrence of these anion⋯anion dimers in the crystal structure are dependent on the presence of counterions. On the other hand, rearranging the orientations of the anions relative to one another can yield metastable minima, albeit with energies much higher than a pair of fully dissociated species.

---

Introduction

The literature offers many examples of anions forming stable complexes with one another, bound together by noncovalent interactions, within the constraints of a polarizable medium such as a crystal or solvent.^1–9 In the context of the gas phase, such anion pairs are metastable at best, meaning that they are higher in energy than the fully separated monomers, and their immediate dissociation is obstructed by an energy barrier.^5,9–11 Thus, situations when the anion pair forms a stable complex in the gas phase can be considered highly exceptional. Such counterintuitive systems were reported in a theoretical study where exothermic association reactions were obtained for anions comprising long-chain organic molecules, terminated by a deprotonated carboxyl group or oxygen anion on one end, and an iodine atom on the other.¹² This unit complexed with a simple Cl anion, or NH₂ group incorporated in an alkyl chain terminating in a COO⁻ group. Recently, it has been shown that there is the possibility of an attractive interaction between neutral sub-systems containing Au(III) in the vicinity of anionic and neutral ligands.^13–15 These observations raise the question as to the possible existence of stable dimers between pairs of anions containing Au(III) without the aid of counterions or other stabilizing crystal packing forces.

It is therefore of interest to note two recent reports^13,16 of crystal structures containing the similar structural motif of two anions containing an Au(III)⋯Au(III) distance significantly shorter than the sum of van der Waals radii (4.58 Å (ref. 17)). The first work¹⁶ observed parallel pairs of Au(CN)₄⁻ anions which was claimed to be a stable equilibrium geometry, even in the absence of counterions or a surrounding polarizable medium, 0.5 kcal mol⁻¹ more stable than a fully separated pair of isolated anions. Such a stable anion between a pair of anions of this type in the gas phase would seem quite unlikely, particularly in the face of a substantial body of literature that has fruitlessly attempted to identify any system where two ions of like charge engage in a stable dyad in the gas phase.^{2,3,6–10,18–28} In the second work,¹³ MP2 calculations of the [Au(N₃)₄]₂²⁻ dimer, studied earlier by Klapotke,²⁹ proposed a minimum with an Au(III)⋯Au(III) distance of 3.21 Å. This issue was a bit muddied as the authors found a distance of 3.09 Å at the RI-MP2/def2-TZVP level while the complex spontaneously dissociates via RI-DFT/B3LYP-D3 (BJ)/def2-TZVP level.

These uncertainties motivated us to examine both of these systems more closely, and at a consistently high level of theory. It was of particular interest to determine whether these anions could indeed engage in a stable, or even metastable, complex in the absence of the stabilizing forces emanating from surrounding counterions within the crystal environment. And if such a stable complex was identified, to dissect the bonding so as to better understand the underlying forces.

Computational methods

Calculations were performed at the M06-2X/def2tzvpp,^30–33 PBE0-D3/def2tzvpp,³⁴ MP2/def2TZVP,³⁵ (with the Douglas–Kroll–Hess 2nd order scalar relativistic correction³⁶ for the Au atoms) levels of theory using the Gaussian 16 (Rev. C.01) package.³⁷ The counterpoise protocol proposed by Boys and Bernardi corrected the basis set superposition error (BSSE).³⁸ Additionally, the interaction energies of dimers I and II were determined at the CCSD(T)/complete basis set (CBS) level. The CCSD(T)/CBS interaction energy was calculated as the sum of the MP2/CBS interaction energy and the CCSD(T) correction term.³⁹ The MP2/CBS energy was extrapolated from the MP2 energies evaluated at the MP2/aug-cc-pVDZ and MP2/aug-ccpVTZ levels, using the extrapolation method of Helgaker et al.⁴⁰ The CCSD(T) correction term (the difference between the CCSD(T) and MP2 interaction energies) was determined with the aug-cc-pVDZ basis set.^41,42 Solvent effects were calculated by using the polarization continuum model (PCM) method within the self-consistent reaction field (SCRF) approach.^43,44 The AIMAll program⁴⁵ was applied for the purpose of QTAIM topological analysis.^46,47 Decomposition of the interaction energy into its various components was accomplished in the framework of the ALMO-EDA scheme via Q-Chem 6^48,49 software.

Results

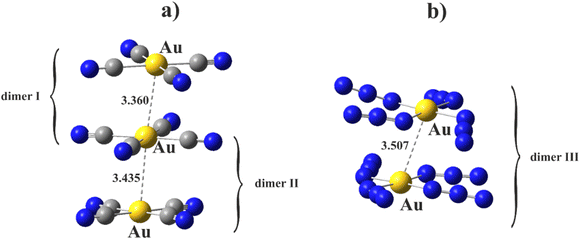
The first step comprised a reexamination of the prior calculations of the anions and their dyads, in the absence of counterions. Starting geometries were taken directly from the pertinent crystals, and the initial calculations carried out at the MP2/def2TZVP+DKH2 level of theory. The relevant portions of the structure provided by the [Lu(bipyO₂)₄][Au(CN)₄]₃·H₂O crystal study as well as methylammonium tetraazidoaurates(III) are summarized in Fig. 1.

Fig. 1 Dimers studied in this work: (a) [Au(CN)₄]₂²⁻, (b) [Au(N₃)₄]₂²⁻. Distances in Å.

As regards the former system, the stacking between these planar anions contains Au⋯Au distances that alternate between 3.360 and 3.435 Å. The pair containing the shorter contact is designated here as dimer I, while dimer II refers to the longer distance. While both I and II are staggered, there is some difference in their C–Au⋯Au–C dihedral angles which are 39.6° and 31.5°, respectively. The [Au(N₃)₄]₂²⁻ dimer from the latter complex has a Au⋯Au contact distance of 3.507 Å. This complex is labelled as dimer III.

First the total energies were calculated as the two anions in these stacked orientations were translated in a direction parallel to the Au⋯Au axis. The energetics arising from this translation are shown in Fig. 2 for dimer I and Fig. S1† for dimer II.

Fig. 2 Trend of the energy versus the Au⋯Au distance calculated at MP2 level for the [Au(CN)₄]₂²⁻ dimer I. Reference (zero) value of energy was set at infinite separation.

The trends for both dyads are comparable. As can be seen from Fig. 2 this curve is purely repulsive in the sense that the energy drops smoothly and monotonically as the two units drift further apart. There is clearly no minimum in this potential or even an inflection. Rather than the minimum mentioned by the original authors at 3.60 Å, with an energy 0.5 kcal mol⁻¹ below that with R = 4.4 Å, it was found that the former is higher in energy than the latter by 2 kcal mol⁻¹. Indeed, the energy of the 3.60 Å structure is fully 52.2 kcal mol⁻¹ higher than that of a fully separated pair of anions, so can hardly be considered a stable configuration in any sense.

The scenario for dimer III in Fig. 3 is different in that it contains a metastable minimum. There is an energy minimum for this dyad at around 3.31 Å with an accompanying barrier to dissociation of about 7.5 kcal mol⁻¹. Nonetheless, it must be stressed that this local minimum lies a full 31 kcal mol⁻¹ higher in energy than the fully separated anions.

Fig. 3 Trend of the energy versus the Au⋯Au distance calculated at MP2 level for the [Au(N₃)₄]₂²⁻ dimer III. Reference (zero) value of energy was set at infinite separation.

Rather than a rigid displacement of the two anions from one another, one can also allow relaxation of the geometries of the two subunits as they move away from each other. However, just as in the rigid motion, such an optimization results in a steady separation to a pair of fully separated anions for both dimers I and II as depicted in Tables S1 and S2.† Full optimization of dimer III leads to a nearly similar scenario. One obtains a metastable complex, but with a highly positive interaction energy, +41.60 kcal mol⁻¹ at the MP2/LANL2DZ/aug-cc-pVDZ level of theory (LANL2DZ basis set was used for the Au atom and aug-cc-pVDZ for the others), much less stable than the fully separated species. Fig. 4 illustrates the MP2 optimized structure of the [Au(N₃)₄]₂²⁻ metastable complex.

Fig. 4 MP2 optimized structure of the [Au(N₃)₄]₂²⁻ metastable complex. Distances in Å.

One can analyze the various bonding interactions via the QTAIM formalism which identifies bond paths between atoms. The QTAIM molecular diagram of this dimer is shown in Fig. S2.† It should be underscored that this diagram contains no Au⋯Au bonding, and the distance between these Au centers is 0.296 Å longer than in dimer III (Fig. 3). It is only the relatively strong interactions between nitrogen and gold atoms that are responsible for the existence of this metastable complex, as illustrated clearly by the dashed lines in Fig. S2.† Identical electron density values of 0.024 au at the bond critical points indicate that these interactions are of comparable strength. These results are summarized in Table 1 which displays the interaction energies of these three dimers, taken directly from the crystal structures, at various levels of theory. Although the precise values differ slightly from one level to the next, the data consistently show the dimers to be substantially higher in energy than the separated monomers. These data include the very high level CCSD(T)/CBS protocol which was also used to calculate the interaction energies. In this same vein, the change from D3 dispersion correction to D3(BJ) has very little influence, changing results by less than 3%.

Table 1 Interaction energies (kcal mol⁻¹, BSSE corrected) for dimers within the crystal structure

Method	Dimer I	Dimer II	Dimer III
	Gas phase
CCSD(T)/CBS	+46.91	+46.64	+36.83
MP2/def2tzvp+DKH2	+52.21	+51.59	+41.73
M06-2X/def2tzvpp	+54.50	+54.00	+47.89
PBE0-D3/def2tzvpp	+52.56	+51.73	+44.84
	Aqueous solution
M06-2X/def2tzvpp	−3.22	−8.83	−7.97
PBE0-D3/def2tzvpp	−9.11	−6.23	−10.51

---

As these anion pairs would spontaneously decay to separate species in the gas phase, it would appear that it is the crystalline environment that stabilizes their close approach. A first rough approximation to this milieu is represented by a polarizable continuum surrounding the anion pair. Such a PCM modeling of this environment, with a dielectric constant of water (ε = 78), greatly stabilizes these ion pairs. As delineated in the last two rows of Table 1, this medium produces negative, i.e. attractive, interaction energies, wherein the dyads are more stable than the separated anions. This stabilization is quite dramatic, reversing endothermic values in the neighborhood of +50 kcal mol⁻¹ to negative quantities between −3 and −11 kcal mol⁻¹.

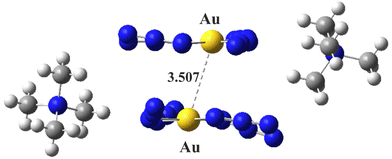
Rather than a generic polarizable continuum, the effects of the crystal environment can be mimicked instead by adding a pair of neighboring counterions. Fig. 5 displays the system wherein the anionic dimer III is bracketed by a pair of NMe₄⁺ counterions, again in their crystal structure positions. These cations also have a strong stabilizing effect on the anion pair. The interaction energy of the dyad, consisting of a pair of (anion + cation) species was calculated to be −33.52 kcal mol⁻¹, quite a stable system.

Fig. 5 The [Me₄N]₂[Au(N₃)₄]₂ fragment of the crystal structure. Distance in Å.

The influence of counterions was likewise examined for dimers I and II that involve the Au(CN)₄ dimers. The large [Ln(bipyO₂)₄]³⁺ ligand which is present in the crystal was replaced by two potassium cations so as to obtain an overall electrically neutral system. The K⁺ positions were then optimized, as displayed in Fig. S3.† The MP2 interaction energies within these neutral K₂[Au(CN)₄]₂ complexes were evaluated to be −34.85 and −32.94 kcal mol⁻¹ for complexes derived from dimer I and II, respectively. This result closely parallels the findings for the Au(N₃)₄ dimers of large stabilization offered by counterions.

The molecular diagram of the [Me₄N]₂[Au(N₃)₄]₂ complex is contained in Fig. S4.† There is a bond path between the two Au nuclei with a bond critical point density of 0.010 au, characteristic of a moderately strong noncovalent bond. But there are also a number of other bonds. Some N⋯H bonds have densities which together sum to 0.067 au. Also present are a pair of N⋯N contacts whose densities sum to 0.022 au. These findings suggest the counterions stabilize the system in two ways. They first help to disperse the negative charges of the anions, thereby reducing their coulombic repulsion. The counterions also add a sort of glue to the dyad through the intermediacy of secondary H-bonds. This multifold activity is consistent with previous studies in the literature.^1–3,11,50

The total interaction energy of each complex containing counterions was separated into its components by ALMO-EDA decomposition, which provides electrostatic (ES), dispersion (DISP), polarization (POL), and charge transfer (CT) as separate attractive elements, all countered by Pauli repulsion. The percentage contributions to the total attractive energies of these components are listed in Table S3.† As can be seen from this table, ES is the leading component of stabilization forces followed by DISP, POL and CT in that order. In the case of the [Me₄N]₂[Au(N₃)₄]₂ complex the DISP term is nearly as large as ES. One may note that CT contributes only 5–6% for all complexes. There is in fact substantial transfer of charge from the Au anions to the counterions, as indicated by the last column of Table S3.†

The AIM diagrams of the three naked anion dyads are presented in Fig. 6. It might be noted there is a bond path between the two Au centers in all cases, with a density between 0.010 and 0.013 au. These bond paths are present even though the potentials of these structures are quite repulsive. It is therefore important to stress that the presence of a bond path may be indicative of a bonding interaction, but is not in and of itself evidence of an attractive potential, echoing earlier findings to this effect in the literature.^1,51

Fig. 6 QTAIM molecular diagrams of dimers I, II and III. Electron densities at BCPs in au.

While the calculations clearly demonstrate that the stacked dimers are unstable with respect to dissociation, it was thought that perhaps another arrangement, even one quite different than in the crystal, might be more stable, even in the absence of crystal packing forces. As an example of such a scenario, one of the two anions was rotated by 90° to form a T-shaped dimer, as depicted for dimer I in Fig. 7. An optimization of this structure, again within the gas phase at the MP2/def2tzvp+DKH2 level, does in fact lead to a true minimum, with all real vibrational frequencies. However, this configuration with an Au⋯N distance of some 2.916 Å, represents a metastable state.

Fig. 7 Trend of the energy versus the Au⋯Au distance calculated at MP2 level for metastable dimer. Reference (zero) value of energy was set at 100 Å.

This T-shaped dimer is less stable than the fully separated pair of dimers by 36.2 kcal mol⁻¹. On the other hand, its dissociation is impeded by an energy barrier, albeit a small one, as seen in Fig. 7. This barrier height is equal to 0.91 kcal mol⁻¹, low enough to be overcome fairly easily. The bonding within this metastable dyad is attributed to an Au⋯N bond, as exemplified by the AIM diagram in Fig. S5.† The density at this Au⋯N bond critical point is somewhat larger than that in the parallel structure (0.018 vs. 0.013 au), which helps account for its metastability.

This same idea of a T-shaped arrangement was also tested for dimer III. However, it was found to be even less stable than the metastable dimer discussed earlier (see Fig. 4) by 7.61 kcal mol⁻¹. The MP2 optimized structure of this complex along with the AIM diagram are shown in Fig. S6.†

Discussion

The literature contains some data that provide a broader perspective on interanionic interactions. Within our own research group, several works have addressed such interactions between anions containing transition metals. The Pd⋯Cl interaction between two tetrachloridopalladate(II) centers was characterized by computational protocols to contain a metastable minimum in the gas phase,² with an interaction energy of +211.8 kcal mol⁻¹. This quantity is roughly five times larger than that between Au centers calculated here. But a major reason for this higher energy is the examination of pairs of dianions, rather than the monoanionic Au units. Like the Au systems, the barrier to dissociation was rather small at 1.3 kcal mol⁻¹, similar to 0.9 kcal mol⁻¹ obtained here for the T-shape Au dimer. Encircling the [PdCl₄]²⁻ dimer by organic counterions in a crystal environment strongly stabilized the complex, yielding an interaction energy of −54.8 kcal mol⁻¹. It was thus concluded that these counterions aided the interaction in the amount of 140 kcal mol⁻¹. This result is quite comparable to the effects of the counterions in the [Me₄N]₂[Au(N₃)₄]₂ system, where the interaction energy was lowered from +45 to −34 kcal mol⁻¹. Just as in the current work, QTAIM analysis suggested metal-to-metal bonding, despite the overall repulsive nature of the potentials.

In contrast to the face-to-face Au(I)⋯Au(I) interaction, that between Au(III) species might be somewhat surprising, due to the largely empty d_z² orbitals in the latter. The literature suggests that the different occupation of the orbitals of Au(I) and Au(III), as well as the coordination environment does not necessarily inhibit the presence of dispersion forces as a large contributor to aurophilicity.¹³ Our own results on the variation of interaction energies in Au(III)⋯Au(III) complexes containing counterions confirm the significant role of dispersion as the second most attractive term.

Another study shifted to Pd, and reinforced the strong role of counterions in stabilizing the anion⋯anion interactions, in that case via NH⋯N hydrogen bonds.¹¹ Fig. S2† of the present work echoes this idea, with numerous CH⋯N hydrogen bonds which serve as “gluing” agents of a sort. Pd was also the focus of another work¹ where this atom interacted directly with Cl and Br within the context of X-ray structures. The progression of the interaction energy from around +200 kcal mol⁻¹ to nearly +100 kcal mol⁻¹ was monitored as cationic counterions were added to as many as four [NH₃(CH₂)₆NH₂]⁺ ligands. Again, AIM bond paths suggested Pd⋯X bonds despite the overall repulsive nature of the interactions.

The literature extends to other metals as well. CN⁻⋯MCl₃⁻ dimers (M = Zn, Cd, Hg)⁶ contain metastable minima, with interaction energies in the range between +4 to +15 kcal mol⁻¹, but immersion of these dyads in water reversed the interaction energies to negative sign, between −26 and −13 kcal mol⁻¹. One difference with the Au and Pd systems described above is the higher energy barrier here, roughly 25 kcal mol⁻¹, impeding the dissociation of these dyads. On a similar line, stacked (MX₃⁻)₂ anion dimers (M = Zn, Cd, Hg, X = Cl, Br, I) are stable in water or methanol.³

Shifting to other types of atoms, Grabarz et al.⁵ demonstrated that even aerogen bonded anion⋯anion complexes can yield stable minima when submerged in an aqueous medium. The AeX₅⁻ (Ae = Kr, Xe, X = F, Cl) species linked to the bare F⁻, Cl⁻ and CN⁻ anions achieved negative interaction energies, albeit only small ones. Aqueous solvent yielded more negative values than less polar dimethylformamide, while for even less polarizable tetrahydrofuran only metastable minima were produced. In 2021, Daolio and co-workers⁸ considered the stability of MaO₄⁻ matere bonded dimers (Ma = Mn, Tc, Re). Without counterions, the dimers were unstable in the gas phase, causing the monomers to break apart. Within water and DMSO solvent, a stable minimum was found for Re within the former solvent, whereas only metastable minima were identified for the latter DMSO. The energetic barrier to dissociation of this metastable structure was quite small, only 0.8 kcal mol⁻¹. Anion⋯anion interaction patterns have also been examined for complexes containing halogen bond,²² chalcogen bond²⁴ or between aspartate dimers⁹ are also available in the literature.

With respect to systems that explicitly contain Au, Andreo et al. synthesized and characterized the [AuI₄]⁻⋯[AuI₂]⁻ complex enclosed by tetramethylammonium cations.²⁸ Rather than a direct interaction between the Au centers, these anionic dimers had T-shape forms (like that discussed above) which were stable in water solvent, but which spontaneously dissociated in the gas phase. Both QTAIM and NCI plots indicated the presence of Au(III)⋯I attractive interactions. Tetrachloridoaurate(III) anionic centers were scrutinized by Daolio et al.⁷ The interaction between [AuCl₄]⁻ units in the crystal structures of salts of the methyl ester of (S,S)-dimethyl-β-propiothetin and acetylocholine was indicated by QTAIM and NCI analyses. The ρ values at Au⋯Cl BCPs were around 0.001 au, equivalent to those obtained in other works including the current one. Finally, two years ago Li et al.¹⁰ checked the nature and binding energy profiles for the [Au(CN)₄]⁻, [AuCl₄]⁻, [AuBr₄]⁻, [AuI₄]⁻ and [AuO]⁻ anions in dimers with F⁻, Cl⁻, Br⁻, I⁻ and CN⁻ or OCl⁻. Metastable dimers were found in the gas phase for six complexes with energy barriers below 10 kcal mol⁻¹.

Conclusions

The results presented here affirm the previous literature that in most instances gas-phase contacts between anions can at best yield a metastable minimum, considerably higher in energy than the separated ions. A metastable minimum of this sort is separated from the dissociated pair by an energy barrier between 1 and 10 kcal mol⁻¹. Conversion of the potential to one where the associated dyad is more stable than the separated ion pair requires external mediation. The latter may arise in the form of neighboring counterions or immersion in a polarizable continuum meant to simulate solvent. Whether it is the metastable minimum that is examined, or the geometry extracted from the crystal, QTAIM or NCI analysis may well reveal a bond path between metal centers, indicative of a bonding interaction, but this bonding will in general be insufficient to override the coulombic repulsion between the two anions. The difficulty of overcoming such anion–anion repulsions is exemplified by a survey of the CSD. A query considering Au⋯Au contacts between neutral gold centers returns 568 examples, but this number is dramatically reduced to only 16 hits when the Au atoms are negatively charged.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge Wrocław Center for Networking and Supercomputing (WCSS). This work was financed by a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology. This material is based upon work supported by the U.S. National Science Foundation under Grant No. 1954310.

References

1. N. Trzęsowska, R. Wysokiński, F. Hajlaoui, N. Zouari, M. Michalczyk, S. Scheiner and W. Zierkiewicz, ChemPhysChem, 2024, e202400712.
2. W. Zierkiewicz, M. Michalczyk, T. Maris, R. Wysokinski and S. Scheiner, Chem. Commun., 2021, 57, 13305–13308.
3. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 13853–13861.
4. R. Wysokinski, M. Michalczyk, W. Zierkiewicz and S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 4818–4828.
5. A. Grabarz, M. Michalczyk, W. Zierkiewicz and S. Scheiner, Molecules, 2021, 26, 2116.
6. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 1119–1125.
7. A. Daolio, A. Pizzi, G. Terraneo, M. Ursini, A. Frontera and G. Resnati, Angew. Chem., Int. Ed., 2021, 60, 14385–14389.
8. A. Daolio, A. Pizzi, G. Terraneo, A. Frontera and G. Resnati, ChemPhysChem, 2021, 22, 2281–2285.
9. M. O. Miranda, D. J. R. Duarte and I. Alkorta, ChemPhysChem, 2020, 21, 1052–1059.
10. J. Y. Li, Q. Y. Feng, C. W. Wang and Y. R. Mo, Phys. Chem. Chem. Phys., 2023, 25, 15371–15381.
11. R. Wysokinski, W. Zierkiewicz, M. Michalczyk, T. Maris and S. Scheiner, Molecules, 2022, 27, 7.
12. S. Scheiner, Phys. Chem. Chem. Phys., 2022, 24, 6964–6972.
13. D. Blasco, F. Reboiro, D. Sundholm, M. E. Olmos, M. Monge and J. M. Lopez-de-Luzuriaga, Dalton Trans., 2023, 52, 2219–2222.
14. F. Mendizabal and P. Pyykkö, Phys. Chem. Chem. Phys., 2004, 6, 900–905.
15. R. Hayoun, D. K. Zhong, A. L. Rheingold and L. H. Doerrer, Inorg. Chem., 2006, 45, 6120–6122.
16. T. E. Karpiuk, S. Mahato, T. Storr and D. B. Leznoff, Chem. Commun., 2024, 60, 3914–3917.
17. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
18. M. Michalczyk, W. Zierkiewicz, R. Wysokinski and S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 25097–25106.
19. W. Zierkiewicz, R. Wysokinski, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 870–877.
20. R. Wysokinski, Phys. Chem. Chem. Phys., 2022, 24, 12860–12869.
21. A. Pizzi, A. Dhaka, R. Beccaria and G. Resnati, Chem. Soc. Rev., 2024, 53, 6654–6674.
22. T. Maxson, A. S. Jalilov, M. Zeller and S. V. Rosokha, Angew. Chem., Int. Ed., 2020, 59, 17197–17201.
23. N. Liu, Z. Han, Y. Lu, Z. Xu, W. Zhu and H. Liu, Chem. Phys., 2024, 576, 112113.
24. D. Fan, L. Chen, C. W. Wang, S. W. Yin and Y. R. Mo, J. Chem. Phys., 2021, 155, 234302.
25. L. Chen, Q. Y. Feng, C. W. Wang, S. W. Yin and Y. R. Mo, J. Phys. Chem. A, 2021, 125, 10428–10438.
26. R. Beccaria, A. Dhaka, M. Calabrese, A. Pizzi, A. Frontera and G. Resnati, Chem. – Eur. J., 2024, 30, e202303641.
27. L. M. Azofra, J. Elguero and I. Alkorta, J. Phys. Chem. A, 2020, 124, 2207–2214.
28. L. Andreo, R. M. Gomila, E. Priola, A. Giordana, S. Pantaleone, E. Diana, G. Mahmoudi and A. Frontera, Cryst. Growth Des., 2022, 22, 6539–6544.
29. T. M. Klapötke, B. Krumm, J. C. Galvez-Ruiz and H. Nöth, Inorg. Chem., 2005, 44, 9625–9627.
30. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
31. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
32. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
33. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
34. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
35. C. Moller and M. S. Plesset, Phys. Rev., 1934, 46, 0618–0622.
36. M. Reiher, Theor. Chem. Acc., 2006, 116, 241–252.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. C.01, Gaussian Inc.: Wallingford, CT, 2016.
38. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
39. J. A. Pople, R. Seeger and R. Krishnan, Int. J. Quantum Chem., 1977, 149–163.
40. A. Halkier, T. Helgaker, P. Jorgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252.
41. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
42. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
43. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
44. R. Cammi, B. Mennucci and J. Tomasi, J. Phys. Chem. A, 2000, 104, 4690–4698.
45. T. A. Keith, AIMAll; TK Gristmill Software: Overland Park KS 2014.
46. R. Bader, Atoms In Molecules. A Quantum Theory, Clarendon Press, Oxford, 1990.
47. R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.
48. P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079.
49. P. R. Horn, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2016, 144, 114107.
50. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2021, 22, 818–821.
51. S. Scheiner, CrystEngComm, 2023, 25, 5060–5071.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dt00879d

---