Design of shape morphing of liquid crystal elastomers through pre-shaping methods
Xinyu Wang†
 ,
Qin Xu
,
Qin Xu and
Rui Zhang
and
Rui Zhang *
*
Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China. E-mail: ruizhang@ust.hk
First published on 10th July 2025
Abstract
Responsive shape-changing materials with driven and spontaneous transitions have wide applications in biological systems, soft robots, artificial muscles, and consumer products. Among different shape-morphing materials, liquid crystal elastomers (LCEs) have recently emerged as a promising type of material for their ability to undergo large, reversible strains and to generate programmable deformation modes in response to external stimuli, such as temperature change, light stimulation, or humidity change. Existing research on LCE deformations usually assume a flat or an undeformed shape as the initial configuration, which morphs into a targeted nontrivial shape when external stimuli are applied. Here, we use continuum simulation to explore the deformation of pre-shaped LCE strips to analyze how the initial shape geometry can be used to tune the shape-morphing behaviors of LCEs. We first validate our simulation method by successfully reproducing the deformations of a thin strip of LCE with two well-studied director fields, i.e., a splay–bend director and a twist director along the thickness direction, respectively. We next consider nontrivial combinations of different pre-shapes and different director fields to study the thermo-mechanical response of an LCE strip. Specifically, we pre-bend an otherwise flat LCE strip along its short axis, long axis, and an off-axis direction, and study its deformations assuming a twist director field. We find that pre-bending along the short axis can facilitate the LCE strip to transition from a helicoid into a spiral ribbon, and an off-axis pre-bent LCE strip can form a tubule more easily than its flat counterpart. For a pre-twist LCE strip, we find that its deformed shape preserves the handedness of the initial twist. For a constrained pre-bent LCE strip, it can spontaneously break the symmetry of the initial shape by bending toward one side. Taken together, we have systematically studied the interplay between the initial shape and the director field of an LCE strip, and our work implies that pre-deformation can be an effective parameter to control the shape-morphing behaviors of LCEs.
Design, System, ApplicationLiquid crystal elastomers (LCEs) are a highly programmable functional material, whose material response can be designed via the control of their microstructure, namely the director field. Therefore, in silico design of the shape-morphing behavior of an LCE is important for its applications in, for example, sensors, actuators, and soft robots. In this work, therefore, we use continuum simulation to combine different pre-shapes of an LCE strip and various director fields to investigate the possible shape-morphing modes. This LCE system, as a function of its microstructure and initial shapes, exhibits rich, highly tunable deformation modes. |
1 Introduction
Responsive, deformable structures are widely used in soft functional materials for diverse applications, including propulsive motors in granular media,1 soft grippers,2,3 microswimmers,4 artificial muscles,5 camouflage materials,6 and autonomous robots.7–9 These structures can respond to environmental stimuli or use ambient energy to morph their shapes, thereby realizing desirable functionalities without the need of tethered or heavy on-board devices. Both experimental and theoretical efforts have been recently devoted to responsive materials, such as hydrogels,10,11 liquid crystal polymers,12 shape memory alloys,13 and shape memory polymers.14 Here, we focus on responsive liquid crystal elastomers (LCEs). LCEs are slightly crosslinked liquid crystalline polymer networks.15–17 This type of material combines anisotropic liquid crystalline order with the hyperelasticity of the polymer network.15 They can respond to light, heat, solvent, or magnetic/electric field18–22 by generating large, programmable deformations. This is because the degree of the orientational order of the mesogenic groups in LCEs can change in response to stimuli, such as temperature and photothermal reactions, and yield large and anisotropic deformations. The orientational ordering of an LCE, namely the director field, can be designed in the experiment via various methods. These remarkable features of LCEs, or more general, LCPs (liquid crystal polymers), have led to a range of promising applications, such as sensors,23 energy harvesting,24 actuators,25–27 and soft robots.28–30The basic deformation modes for a shape-morphing material are bending and torsion (twisting). Bending mode is of great use in terms of soft actuators,31,32 wave guides,33 and motors.34,35 Torsion mode, on the other hand, is one of the most common structural motifs in biomaterials and supramolecular systems, such as tendrils on climbing plants,36,37 elastic bi-layer strips,38,39 and minimal surface films.40
The basic deformation mode for an LCE is that it can contract along its optical axis and elongate in the other two orthogonal directions upon heating or via photothermal effect, and vice versa on cooling or on recovery in the dark state.41 To realize bending and torsion in an LCE, a spatially varying director field42–47 or a non-uniform external stimulus (e.g., light),35,48 is required.
The strategy of director variation to obtain bending for a thin trip of LCE can be achieved by applying a step-wise or continuous splay–bend configuration along the thickness direction41,49 (Fig. 1A). A strip film with a so-called “L-geometry” or “S-geometry” can morph into a torsional or twisted shape upon a change in the nematic order (Fig. 2). The nematic director of the two geometries changes smoothly by 90° along the thickness direction with the director at the midplane parallel to the long (L-geometry) or short (S-geometry) axis of the film50 (Fig. 2). Upon temperature change, the films twist around their central lines and form helicoids. When the width–thickness ratio of a sample exceeds a threshold value, the central line of the film curves into a helix and the strip forms a spiral ribbon.50–53 For a wider strip, spiral ribbons can even transform into tubules.8,54,55 Under the existence of the temperature gradient (or illumination gradient), the non-uniform shrinkage and extension of the tubule shape generate unbalanced forces and torques, which can provide the tubule with self-rolling motions.56–59 These motion dynamics can utilize environment interactions and physical intelligence, and can work as a new paradigm towards autonomous soft robots.7,60
 | ||
| Fig. 1 A flat LCE strip with a continuous and step-wise splay–bend director field. (A) Schematics of the deformation of a strip with splay–bend alignment. (B) A comparison of our simulations and theories.41 | ||
 | ||
| Fig. 2 Flat LCE strips with twist director fields. (A) Schematics of a strip with three kinds of twist alignments. The directors in the mid-layer (z direction) of D-geometry, S-geometry, and L-geometry are along the 45°-direction, the short axis, and the long axis, respectively. (B) A schematic showing the definition of helical pitch p and helical diameter d. (C) A comparison of simulation, experiment,50 and theory50 for a helicoid deformation of a 0.2 mm strip (narrow strip). (D) A comparison of simulation, experiment,50 and theory50 for a spiral ribbon deformation of a 0.76 mm strip (wide strip). | ||
Helicoid or spiral-shaped ribbons play many functional roles. Recent studies show they can (i) deliver compact torsional actuation, such as melt-extruded helical LCE spring contraction61 and function as miniature torsion motors and grippers,62 (ii) weave into fiber meshes to create multifunctional textiles that twist, lift, and bend on demand, offering architected artificial-muscle fabrics,30 and (iii) act as self-sensing elements: cholesteric helical ribbons shift the structural colour with strain or humidity, enabling colour-readout strain gauges and health monitoring in various systems.63 These demonstrated functions illustrate that helical LCEs provide a versatile platform for power-dense rotary actuation, intelligent soft robotics, and mechanochromic sensing well beyond the classic self-rolling showcase.
To the best of our knowledge, though existing studies have explored the effect of certain non-flat shapes of LCE films to some extent, a systematic and quantitative investigation of how different pre-shaped LCE strips deform remains largely unexplored. Comparing to flat LCE films, pre-shaped geometries have more morphing geometries and functional properties. For example, a pre-bent LCE with twist alignment was proposed for continuous and programmable jumps,64 showing the experimental realization and great application potential of pre-shaped structures. To explore a greater space of the shape formation of LCEs, in this work, we use continuum modelling to examine pre-shaped LCE strips and characterize their shape-morphing processes. Firstly, we validate our simulation method by comparing it with the existing theories of bending deformation,41 and then with the existing theory and experiments of LCE strip twisting into helices and spiral ribbons.50 After that, we provide systematic results of the shape formation process under temperature change. We consider two kinds of initial shapes, namely pre-bend and pre-twist; and we harness a twist alignment and a bend alignment as director alignments to induce two types of deformations. For pre-bend shapes, we investigate pre-bend along the short axis, along the long axis, and along an off-axis direction. We find that pre-bend along the short axis can be used to tune the state boundary between the helicoid state and spiral ribbon state; interestingly, a narrow strip with a pre-bend curvature is able to morph into a spiral ribbon. Pre-bending a strip along an off-axis direction results in a helical shape as the initial configuration. When the initial shape is flat, only very wide strips can form tubular structures, which are essential for the steady self-propulsion of LCE robots.8 However, our results challenge this limitation: we demonstrate that even a narrow strip can be transformed into a tubular shape. Furthermore, by fixing both ends of a pre-shaped (sine-shaped) strip, we observe tunable, anti-symmetric deformations. These findings suggest that pre-shaping offers a new strategy for programming 3D morphologies in LCE sheets upon activation, and provide valuable insights for designing shape-morphing LCE structures for diverse applications.
2 Methods and validation
2.1 Methods
Previously, several theoretical and simulation approaches have been used to investigate LCEs.65 Commonly used strategies to elucidate the physics of LCEs include but are not limited to finite element method,66–68 Monte Carlo method69,70 and molecular dynamics (MD).71,72 Our simulations use finite element modelling via Abaqus/Standard software. We perform 3D simulations using the C3D8 brick element (8-node 3D element). We apply implicit calculation and turn NIgeom on to account for the geometric nonlinearity. Structured meshing is adopted. We use a linear thermo-elastic material with a Young's modulus of 11 MPa and Poisson's ratio of 0.3.7,73Let Ω0 ⊂ R3 and Ω ⊂ R3 be the reference (initial) and the deformed (final) configuration, respectively. A material point in the undeformed state is ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) ,
, ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) ∈ Ω0. The deformation transforms
∈ Ω0. The deformation transforms ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) into
into ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) in the deformed state,
in the deformed state, ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ∈ Ω. Further, the deformation tensor is λ, the elements of which are defined as λij = ∂xi/∂Xj. LCEs are anisotropic due to the intrinsic nematic ordering. The director field in a nematic LCE can be represented by a double-headed unit vector
∈ Ω. Further, the deformation tensor is λ, the elements of which are defined as λij = ∂xi/∂Xj. LCEs are anisotropic due to the intrinsic nematic ordering. The director field in a nematic LCE can be represented by a double-headed unit vector ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) (
(![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ≡ −
≡ −![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ). The tensorial nematic order parameter Q represents the microstructure of the nematic, Qij = S(
). The tensorial nematic order parameter Q represents the microstructure of the nematic, Qij = S(![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) ninj − ½δij), where S is the scalar order parameter. We assume that when the external temperature changes, the order parameter S also varies while the director is kept fixed in the body frame. Parameter α is a coupling constant to account for the change of S in response to the change of temperature. Assuming that the director
ninj − ½δij), where S is the scalar order parameter. We assume that when the external temperature changes, the order parameter S also varies while the director is kept fixed in the body frame. Parameter α is a coupling constant to account for the change of S in response to the change of temperature. Assuming that the director ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) is along the z axis, the extensional strain along the director is
is along the z axis, the extensional strain along the director is  . The relationship between λzz and temperature T can be measured from the experiment and αS can be expressed empirically in terms of T:
. The relationship between λzz and temperature T can be measured from the experiment and αS can be expressed empirically in terms of T:
Except for sec 2.2 (the theoretical frameworks41,75 didn't specify thickness), we simply adopted the strip thickness t = 0.0352 mm reported by ref. 50 in all the simulations. This value has been proven to yield robust shape-morphing in experiments, so using this value we can easily compare with existing experiments and also make meaningful predictions for future experiments to confirm.
Physically, the choice makes sense because bending and torsional rigidities of a solid, thin ribbon scale as t3.76 Therefore, a sufficiently small t reduces both stiffnesses cubically, allowing the modest spontaneous strain of an LCE to drive the large twists and bends we target. Therefore, the thickness we choose is practical for its potential applications (e.g., actuation).
In the FEM, a perfect continuous director field cannot be achieved. We cannot apply a continuous director field in the FEM and our simulation more easily works with the discrete variation of the director field over the film thickness. Simulation results in Fig. 1(B) are from discrete director fields in the FEM. We did not simulate a continuous director field in our FEM simulation but instead, we compared it with a theoretical expression for the continuous director field.41 Layer-by-layer control is indeed challenging to achieve in the experiments. According to our literature search, methods like direct ink writing77 can match our discrete FEM alignment.
2.2 Benchmarking simple bend deformation
To validate our model, we first compare our results with the theory of weakly deformed LCEs.41,75 As shown in Fig. 1A, we consider a strip with a length of 15 mm, a width of 1.5 mm, and a thickness of 1 mm. A splay–bend nematic field with![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) = (cos
= (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(z), 0, sin
θ(z), 0, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(z)) varies from the bottom boundary (z = −h) to the top (z = h), where θ(z) is the angle that the director makes with the x-axis,
θ(z)) varies from the bottom boundary (z = −h) to the top (z = h), where θ(z) is the angle that the director makes with the x-axis,  . Upon a change in temperature, the total bending curvature along the long axis x becomes:41
. Upon a change in temperature, the total bending curvature along the long axis x becomes:41
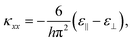 | (1) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) and ε⊥ is the strain perpendicular to
and ε⊥ is the strain perpendicular to ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) .
. ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) is the current strain and increases linearly from 0 to ε‖ along the x-axis. Fig. 1B shows the normalized thermal strain. For a bi-layer cantilever with the director
is the current strain and increases linearly from 0 to ε‖ along the x-axis. Fig. 1B shows the normalized thermal strain. For a bi-layer cantilever with the director ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) along the x-direction in the thickness interval (−h, 0) and along z within (0, h), the bending curvature becomes41
along the x-direction in the thickness interval (−h, 0) and along z within (0, h), the bending curvature becomes41
 | (2) |
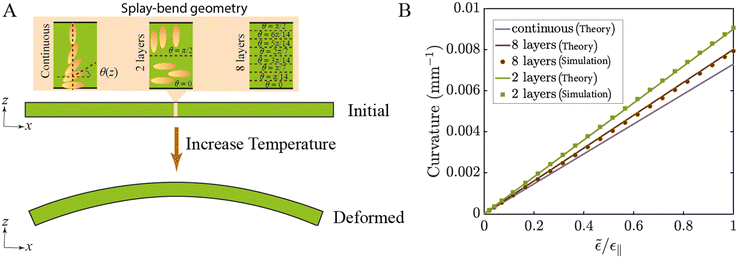
Given that our simulation more easily works with the discrete variation of the director field over the film thickness, we model a multi-layer strip, in which the director is uniform within a layer but varies from layer to layer to approximate the continuous splay–bend configuration. For an n-layer strip, the ith layer has 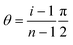 , i = 1, 2⋯n (Fig. 1A). Our n = 2 (bi-layer) and n = 8 simulation results agree well with theory (Fig. 1B). Interestingly, the bi-layer beam has the largest bending curvature, whereas an LCE beam with a continuous splay–bend director alignment has the smallest bending curvature. As we divide more layers along the z-axis (8 layers), the obtained bending curvature is closer to the continuous case in eqn (1).
, i = 1, 2⋯n (Fig. 1A). Our n = 2 (bi-layer) and n = 8 simulation results agree well with theory (Fig. 1B). Interestingly, the bi-layer beam has the largest bending curvature, whereas an LCE beam with a continuous splay–bend director alignment has the smallest bending curvature. As we divide more layers along the z-axis (8 layers), the obtained bending curvature is closer to the continuous case in eqn (1).
2.3 Benchmarking simple twist deformation
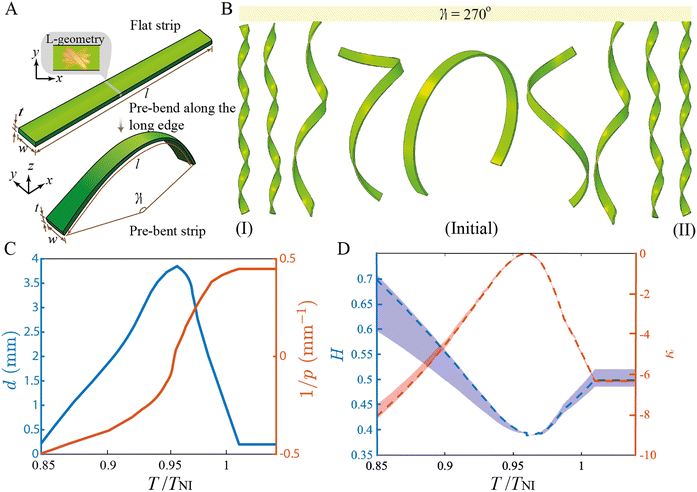
We further validate our simulations by comparing them to theories and experiments of LCEs with a twist director field across the film thickness (z) direction. As schematically shown in Fig. 2A, we consider three types of twist director fields: a D-geometry, where the director continuously rotates from the long-axis direction on one side of the film to the short-axis direction on the other side; an S-geometry, where the director points to the short-axis in the midplane of the film and points at a 45° angle with respect to the major axes on both sides of the film; and an L-geometry, where the director points to the long-axis in the midplane of the film and at a 45° angle relative to the major axes on both sides of the film. In all three cases, the director rotates by 90° across the z-direction. In the following studies, we fix the strip thickness at t = 0.0352 mm and the strip length at l = 6 mm, while investigating two strip widths: w = 0.23 mm and w = 0.76 mm.50 We set the initial temperature of the strip to T/TNI = 0.96.50Upon a change in temperature T, the D-geometry can lead to a bend deformation, similar to the splay–bend alignment. In what follows, we focus on the L- and S-geometry, for which a temperature-induced gradient in strain along the film thickness direction due to the twist of the director can give rise to an overall, reversible shape twist with respect to the z-direction. As shown in Fig. 2, the L- and S-geometry strips can swell or de-swell into either a helicoid shape or a spiral ribbon shape, depending on their width.50–53 In both cases, the configuration and the chirality of the deformed strip change with T. To characterize the deformed shape, we introduce p, the helical pitch for both shapes, and d, the diameter of the spiral ribbons (Fig. 2B). Following Sawa et al., we choose the sign of p to be negative and positive for the right- and left-handed configuration, respectively.50 During a cooling process, when T/TNI < 0.96, L-geometry strips become right-handed while S-geometry strips become left-handed (Fig. 2C). During a heating process as T/TNI > 0.96, this trend is reversed (Fig. 2C). Upon transition from a helicoid to a spiral ribbon, the diameter d jumps from 0 to a finite, maximum value, after which d gradually decreases (Fig. 2D). This is because the spiral ribbon, once formed, will roll into a more tubule-like structure as the strip twists more, rendering a decreasing diameter. There is also a good quantitative agreement between our simulation and the reported experiment by Sawa et al.50 as shown in Fig. 2C and D, further validating our simulation method. The L-geometry and S-geometry can both induce twist deformations but the deformations are not exactly the same: the L-geometry can wind more tightly.50 For conciseness and without loss of generality, we focus on the L-geometry configuration in the following discussion.
To further quantify the deformed shape of the strip, we measure its profiles of Gaussian curvature κ and mean curvature H. Specifically, we calculate κ = κ1κ2 and H = (κ1 + κ2)/2 of the middle layer of the strip, where κ1 and κ2 are its two main curvatures.78 As shown in Fig. 3A, the helicoid shape has a saddle-like negative Gaussian curvature and exhibits a vanishing mean curvature, and its central-line region has a more negative κ than the edge region, indicating that the temperature change induced internal stress is more localized in the central region. This also suggests that the shape-morphing of a helicoidal shape is primarily due to twist deformation. Note that the cooling shape, state-I at T/TNI = 0.85, and the heating shape, state-II at T/TNI = 1.05, with approximately the same temperature change |ΔT/|TNI ≈ 0.1 are not symmetric with respect to each other (Fig. 3A). This asymmetry is due to the fact that the change in the order parameter δS is not symmetric with respect to ΔT.50
For a wide strip (w > 0.3 mm), the initial helicoidal shape can transition into a spiral ribbon when the temperature change is beyond a certain threshold50 (Fig. 3B and C). The difference between the helicoid and the spiral ribbon is depicted in Fig. 3C: the central line of a spiral ribbon is a helical line with a nonzero diameter d, and the central line of a helicoid shape is roughly a straight line with d ≈ 0. In Fig. 3B, before the transition, the strip in the helicoid regime has a vanishing mean curvature H = 0, and a nonpositive Gaussian curvature κ. The dashed lines in Fig. 3B give the curvatures of the central line. After the strip transitions into a spiral ribbon, as T deviates from the original temperature, the Gaussian curvature κ of the central line region starts to increase, while κ on the edge region decreases. As a result, the spatial variation of κ also increases further. The mean curvature H also increases from zero after the transition as the strip is wound with a bending dominated deformation. The helical diameter d peaks at the transition and then keeps decreasing. The spatial pattern of the local curvature shows that the torsional deformation is concentrated near the center line region, and the Gaussian curvature exhibits a larger spatial variation than the mean curvature. These details will be potentially useful for the future design of relevant applications based on helicoids and spiral ribbons.
3 Pre-shapes and deformations
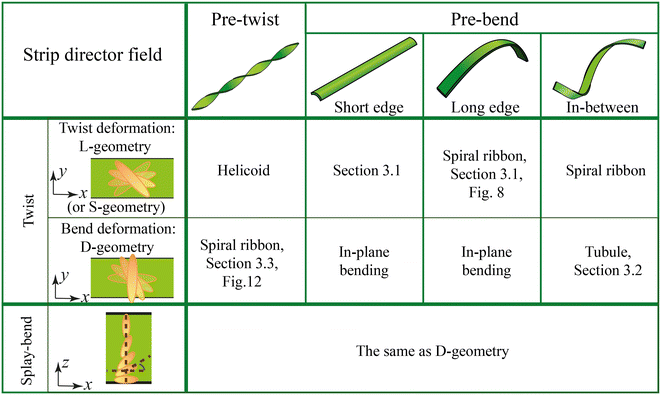
Next, we explore the principles of shape morphing of pre-shaped LCE strips. Table 1 gives a brief summary of how different pre-shapes (one type of pre-twist and three types of pre-bends) with different director fields (two types of twists and one type of splay–bend) along the sample thickness direction can give rise to different deformation modes.3.1 Pre-bend tunes the shape transition
We first focus on an L-geometry LCE strip with a pre-bend along its short axis (Fig. 4A). In this context, the parameter w represents the arc length, and the angle of the arc is denoted by γ. For an initially flat strip, γ = 0° and its width coincides with w. For a given temperature T, there exists a critical width wc, beyond which the strip can transition from the helicoid shape to the spiral ribbon shape.50 This critical width wc varies with temperature T. By minimizing the total elastic energy, the relationship reads .50 For flat strips narrower than 0.32 mm, the deformed strip remains in the helicoid state for the temperature range considered in this work, T/TNI ≥ 0.8. The solid lines in Fig. 4B represent the state boundaries between the helicoid and the spiral ribbon for initially flat strips reported in ref. 50.
.50 For flat strips narrower than 0.32 mm, the deformed strip remains in the helicoid state for the temperature range considered in this work, T/TNI ≥ 0.8. The solid lines in Fig. 4B represent the state boundaries between the helicoid and the spiral ribbon for initially flat strips reported in ref. 50.
The state boundaries of pre-bent strips from our simulations are presented as the two dashed lines in Fig. 4B. Clearly, some amount of pre-bending along the short axis can facilitate the state transition, especially for narrow strips. As T deviates from the initial value, narrow strips can first form a helicoid and then become a spiral ribbon. The transition happens earlier for strips with a larger pre-bend angle (γ = 60°) than those with a smaller pre-bend angle (γ = 45° and γ = 22.5°) (Fig. 4B). This can be understood by the fact that spiral ribbons have nonzero mean curvature H compared to helicoids (Fig. 3). Therefore, the pre-bend strip having nonzero H can favor spiral ribbon shapes against the helicoidal shape.
We further study the effect of the pre-bend angle γ (Fig. 4(A)) on a narrow strip (w = 0.2 mm) as shown in Fig. 5 and 6. For a small pre-bend angle, γ = 22.5°, state-I (T/TNI = 0.85) and state-II (T/TNI = 1.05) in Fig. 5A are both in the helicoid regime (d ≈ 0) and are similar to the flat strip shown in Fig. 3A. The only difference is the mean curvature (Fig. 5C), which increases from 0.75 to 1.18 (decreasing T) and 1.02 (increasing T), while that of a narrow flat strip remains zero (Fig. 3A). For γ = 45°, the transition from a helicoid to spiral ribbon occurs and the helical diameter d escalates at the transition points (Fig. 5B and D). Unlike d, the curvatures of the pre-bend strips change smoothly during the transition (Fig. 5D).
 | ||
| Fig. 6 The deformations of 0.2 mm strips with larger pre-bend angles along the short axis. (A) γ = 90°. (B) γ = 270°. State-I is for T/TNI = 0.85 and state-II is for T/TNI = 1.05. | ||
For larger pre-bend angles, γ = 90° and γ = 270°, the helicoid regime barely exists (Fig. 6). The trend of the mean curvature is mainly controlled by the initial curvature, and γ = 270° is the most curled with the largest mean curvature before the deformations (Fig. 6B). Among the four pre-bend angles, the γ = 90° strip shows the largest helical diameter at state-I and state-II. As the pre-bend angle of a 0.2 mm strip keeps increasing, the swelling process has a weaker effect on its change in diameter. The helical diameter of the γ = 270° strip is nearly constant, d ≈ 0.1 mm, and is independent of T due to the large barrier energy induced by the pre-curvature. The embedded elastic energy from the initial shape can be expressed using the Kirchhoff Rod model  , where Bt, Bb, and C are bending and torsional moduli, and κt, κb are two curvatures along the curve and orthogonal to the curve, respectively, and τ is the torsion.79,80 In the case of pre-bending along the short axis, the initial shape has τ = κt = 0, and a nonzero κb from pre-bending. For a large enough pre-bend angle (e.g., γ = 270°), the bending energy and curvature κb is large, and therefore the strip remains curled during the deformation with a nearly constant d as shown in Fig. 6B.
, where Bt, Bb, and C are bending and torsional moduli, and κt, κb are two curvatures along the curve and orthogonal to the curve, respectively, and τ is the torsion.79,80 In the case of pre-bending along the short axis, the initial shape has τ = κt = 0, and a nonzero κb from pre-bending. For a large enough pre-bend angle (e.g., γ = 270°), the bending energy and curvature κb is large, and therefore the strip remains curled during the deformation with a nearly constant d as shown in Fig. 6B.
Next, we study an LCE strip pre-bent along its long axis. To distinguish, we introduce γl as the pre-bend angle (Fig. 7A). The difference between the pre-bent long-axis and pre-bent short-axis is that under initial conditions, the central line is straight with d = 0 in the pre-bent short-axis scenario, but is curved with d ≠ 0 for the pre-bent long-axis scenario (Fig. 7B and C). The behaviors of the two curvatures are similar between the two pre-bent cases: as T deviates from its initial values, the Gaussian curvature κ will decrease from 0, while the mean curvature H increases (Fig. 7D).
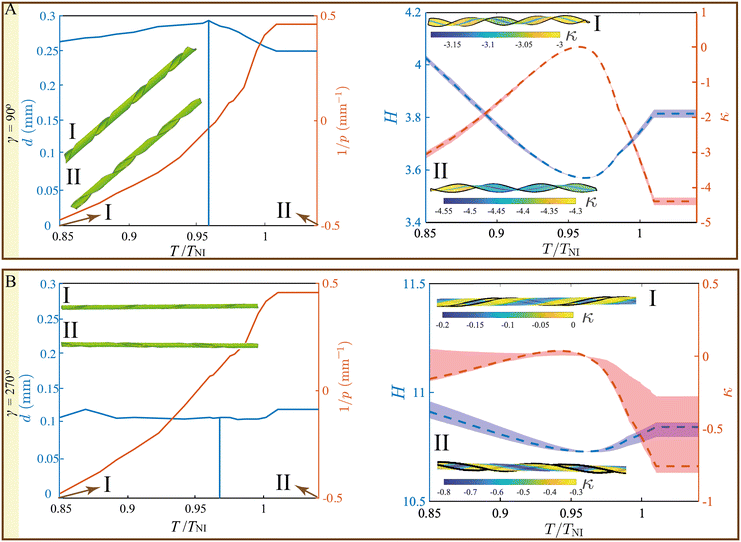
To compare the two types of pre-bending shapes more carefully, we further characterize the shape morphing process of a 0.4 mm strip during temperature variation in Fig. 8, including a flat strip (Fig. 2A), a strip pre-bent along its short axis (Fig. 3A, γ = 45°), and a strip with pre-bending along its long axis (Fig. 7A, γl = 45°). The three strips with the same width and director alignment share the identical amount of thermal-induced twist and therefore show the same evolving trend of the helical pitch p. The main difference among the three types of strips lies in the thermal behavior of the central line diameter d. For flat and short-axis pre-bent strips, d remains 0 in the vicinity of the initial temperature, indicating that the strip has a helicoidal shape. To trigger a transition from the helicoid to the spiral ribbon, a higher temperature change |ΔT| is required for flat strips than for short-axis pre-bent strips (Fig. 8A and B). For long-axis pre-bent strips, d decreases as T deviates from its initial value, and the shape is always a spiral ribbon (Fig. 8C). Comparing the change in d in the spiral ribbon regime between the two pre-bent strips, the long-axis pre-bent strip exhibits a much wider range of d, roughly spanning [1 mm, 8 mm) in the temperature range we have considered here (Fig. 8C). Whereas for the short-axis pre-bent strips, d covers a much narrower range, (0.35 mm, 0.5 mm] (Fig. 8B).
 | ||
| Fig. 8 The deformations of a 0.4 mm strip. (A) Flat strip. (B) Strip with pre-bend along the short axis (γ = 45°). (C) Strip with pre-bend along the long axis (γl = 45°). | ||
Comparing the mean curvature, H increases from 0 for flat strips but increases from ∼1.8 for short-axis pre-bent strips and increases from ∼0.1 for long-axis pre-bent strips (Fig. 8). Upon cooling, H increases continuously, with long-axis pre-bent strips exhibiting the largest increase compared to the other types of strips (Fig. 8C). Upon heating, H increases abruptly for flat strips (Fig. 8A), while continuously for the two types of pre-bent strips (Fig. 8B and C). Interestingly, short-axis pre-bent strips exhibit a larger change in H upon heating (Fig. 8B), which is in contrast to long-axis pre-bent strips, which exhibit a higher change in H upon cooling (Fig. 8C). All strips exhibit a continuous decrease from 0 in the Gaussian curvature κ during the temperature change. Among the three types of strips, flat strips exhibit the largest variation in κ (Fig. 8A). These detailed comparisons revealed by our simulation provide helpful insights into the interplay of the distorted director field and the pre-shape during thermal responses of LCEs.
3.2 Off-axis pre-bend and tubule shape
Besides pre-bending along the short-axis and along the long-axis, we also consider a strip pre-bent along an axis that is within the xy plane, making an angle Ψ with the x-axis. As shown in Fig. 9A, we pre-bend a flat strip along the dashed gray line direction, and obtain a spiral ribbon shape as the initial configuration. Let Ψ = 45° and the turning angle ω to be 2π (Fig. 9A). The inner side and outer side of the spiral ribbon are labeled. Note that the initial shape of the pre-bent spiral ribbon is different from the “imperfect” spiral ribbon shape formed after the temperature change, as the former has zero Gaussian curvature throughout the strip, whereas the latter has a negative Gaussian curvature as shown in Fig. 3C.Experimental results indicate that the helicoid shape cannot lead to a stable and sustained rolling motion of the strip, which can only occur when the sample is wide enough to form a tubule shape.8 In our simulation setup, with a fixed strip length l = 6 mm, the critical width for a flat strip to transform into a tubule is 1 mm, which happens at T/TNI = 1 (Fig. 9B). A tubule can only form when the strip width w satisfies w ∈ [1 mm, 1.5 mm] and cannot be wider, otherwise the shape becomes a 2D flat plate and cannot go through a global twisting. Generally speaking, it is trickier for the LCE strip to deform into a tubule than to form a helicoid or a spiral ribbon. Compared to flat strips, pre-bent strips can form a tubule shape with a narrower width and with a smaller temperature change (Fig. 9C)—this suggests the advantage of using pre-shape strips for the design of certain shape-morphing modes.
Next, we study the thermal behaviors of off-axis pre-bent strips of different widths. We focus on three widths: w = 0.2 mm, 0.4 mm, and 0.6 mm and measure their characteristic lengths d and p when the temperature changes from the initial value T/TNI = 0.96 (Fig. 10). Strip shapes at different temperatures for two wider w are also provided in Fig. 11. During cooling, the three strips behave similarly in terms of their pitch p, as they will de-wrap and stretch (Fig. 10A–C). This is because during cooling, the director field of the strip will impose an extension along the long-axis on the inner side and an extension along the short-axis on the outer side. However, their size d varies very differently. As temperature T/TNI drops from 0.96, the two thiner strips will first undergo a flip of side, as the wrapped strip turns inside out. This happens when d drops to 0. Upon further cooling, the strip will bend and d will start to increase correspondingly. For the thinnest strip, w = 0.2 mm, it can further wrap into a more compact spiral ribbon as the temperature continues to drop, as d starts to decrease when T/TNI ∼ 0.93 (Fig. 10A). For the thickest strip, w = 0.6 mm, it never flips its side (Fig. 11B).
 | ||
| Fig. 11 Snapshots of the morphing process of two wider strips with pre-bend along the Ψ = 45° axis. Temperature dependence of a 0.4 mm strip (A) and a 0.6 mm strip (B). | ||
The heating behaviors of the three strips are more similar to each other. A wider strip deforms into a tubule at a lower temperature than a narrower strip (Fig. 10D). For a not too large deformation, the geometry of the tubule dictates its helical diameter d and pitch d according to
3.3 Pre-twist
Next, we incorporate a pre-twist to an otherwise flat strip as its initial shape (Fig. 12). The strip is a right-handed twisted helicoid as its initial shape. We consider the D-geometry director alignment. We choose two colors to distinguish the two sides of the strip: the director![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) on the blue side and the director on the orange side are along the short axis and along the central line, respectively (Fig. 12A). Upon cooling, the strip extends along the director, and therefore the orange side will be stretched and appear on the outer side of the deformed ribbon shape (Fig. 12B). Conversely, as T is increased from the initial helicoid state, the orange side shrinks and appears on the inner side of the ribbon. Both states form right-handed spiral ribbons, and the transition is reversible. Therefore, it can potentially be utilized to design functional materials with two different sides81,82 or soft rollers that are suitable for two kinds of environments.7
on the blue side and the director on the orange side are along the short axis and along the central line, respectively (Fig. 12A). Upon cooling, the strip extends along the director, and therefore the orange side will be stretched and appear on the outer side of the deformed ribbon shape (Fig. 12B). Conversely, as T is increased from the initial helicoid state, the orange side shrinks and appears on the inner side of the ribbon. Both states form right-handed spiral ribbons, and the transition is reversible. Therefore, it can potentially be utilized to design functional materials with two different sides81,82 or soft rollers that are suitable for two kinds of environments.7
Twisting snap-through is attractive because the ribbon stores energy in both bending and torsion. The need to change handedness introduces extra metastable states, so the energy landscape contains more wells and higher barriers than that in pure bending snaps. This richer topology can deliver a larger work output, provide three or more stable shapes, and supply direct torque for rotary tasks such as latch-release grippers or jumping wheels. Preliminary demonstrations of twist-induced multistability in soft materials, such as PDMS–parylene bilayers39 and responsive LCE loops,80 confirm that the mechanism is experimentally accessible and not restricted to a single chemistry.
A full investigation would require dynamic finite-element analysis with rate-dependent LCE parameters plus high-speed experimental validation. These additions would shift the paper away from its current focus on quasi-static shape selection. We, therefore, leave the opportunity in the revised Discussion and reserve the detailed study for future work.
4 Boundary constraints
In the previous section, all the strips are free to deform. Here, we consider the effects of mechanical constraints. Specifically, we fix the positions of the two ends of a strip, with displacement vector components ux = uy = uz = 0 at x = 0 and L. Because any deformation will have difficulty emerging in such a constrained, flat strip, here we consider a pre-bent strip with a D-geometry director field. During the temperature change, the strip with a D-geometry will bend or de-bend. As schematically shown in Fig. 13A, the strip, facing in the z-direction, is extended in the x-direction with a one-period sinusoidal shape. We introduce h1 and h2 to represent the initial magnitude of bending in the +z and −z direction, respectively (Fig. 13A), and we keep h1 = h2 = h for the initial shape. Upon temperature change, the strip will re-shape, and their magnitudes of bending represented by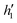 and
and  will deviate from the initial magnitudes (Fig. 13B).
will deviate from the initial magnitudes (Fig. 13B).
We keep the length s and the thickness t of the strip as constants, and simulate strips with different h values. The deformations in terms of  and
and  are shown in Fig. 13B. For a small bending amplitude, h = 0.25 mm, the strip becomes flat gradually as T increases; while the temperature decreases,
are shown in Fig. 13B. For a small bending amplitude, h = 0.25 mm, the strip becomes flat gradually as T increases; while the temperature decreases,  approaches zero and
approaches zero and  keeps increasing, which breaks the original symmetry (Fig. 13C). For strips with larger sine amplitudes, the strain from LCE transition is not enough to eliminate the pre-curvature (increasing T) or break the symmetry (decreasing T). The shape change could potentially be interpreted as information change and be used in the design of mechanical logic units.83
keeps increasing, which breaks the original symmetry (Fig. 13C). For strips with larger sine amplitudes, the strain from LCE transition is not enough to eliminate the pre-curvature (increasing T) or break the symmetry (decreasing T). The shape change could potentially be interpreted as information change and be used in the design of mechanical logic units.83
5 Discussion
In this work, we have explored the effects of initial-shape or pre-shape geometries on the deformations of an otherwise flat LCE strip. We consider three kinds of pre-bend geometries and a pre-twist geometry as the initial shapes. And we study how an L-geometry twist director field and a D-geometry splay–bend director field can induce nontrivial shape-morphing in various pre-shaped strips. A summary of all the explored scenarios is given in Table 1. Some trivial combinations of director field and pre-shape are not studied here. For example, if we consider a twist director field on a helical (twisted) strip, the two twisting modes will be superimposed and the eventual shape is still a helicoid, with a smaller or larger pitch than the initial state; similarly, if we incorporate a splay–bend director field (e.g., a D-geometry) to a pre-bend strip, we will obtain an enhanced or suppressed bent shape. Non-trivial deformations are found if we combine a twist director (L-geometry) in a pre-bend strip. Depending on the strip width and the change in the order parameter due to temperature variation, the strip can deform into a helicoid or a spiral ribbon (Fig. 4B). In contrast to a flat strip, a strip pre-bent along the short axis can transform from a helicoid to a spiral ribbon much more easily. For a strip pre-bent along an off-axis direction, it can deform into a tubule shape much easier than an initially flat strip. Different from designing target shapes in 3D using a 2D director field, our results provide new insights into designing morphing structures with responsive materials by using pre-shape as a useful tuning parameter. In this study, we don't consider any mechanical-induced director field variation, which is “soft elasticity”.15,84–88 Also, in this work, we focus on a single strip, and therefore exploring the collective motion arrays of pre-shaped LCE structures should also be of interest.89 Additionally, all shape-morphing processes are continuous, and any snap-through transformations can be studied in future work.31Data availability
All data and codes presented in this work are available upon reasonable request.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by the Guangdong Natural Science Foundation 2022A1515011186 and Hong Kong Research Grants Council via grant no. C6004-22Y. The authors would like to thank HKUST Fok Ying Tung Research Institute and National Supercomputing Center in Guangzhou Nansha Sub-center for providing high performance computational resources.References
- B. D. Texier, A. Ibarra and F. Melo, Phys. Rev. Lett., 2017, 119, 068003 CrossRef PubMed.
- W. Wang, C. Li, M. Cho and S.-H. Ahn, ACS Appl. Mater. Interfaces, 2018, 10, 10419–10427 CrossRef CAS PubMed.
- M. Wang, B.-P. Lin and H. Yang, Nat. Commun., 2016, 7, 13981 CrossRef CAS PubMed.
- F. Qiu, S. Fujita, R. Mhanna, L. Zhang, B. R. Simona and B. J. Nelson, Adv. Funct. Mater., 2015, 25, 1666–1671 CrossRef CAS.
- C. S. Haines, N. Li, G. M. Spinks, A. E. Aliev, J. Di and R. H. Baughman, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11709–11716 CrossRef CAS PubMed.
- S.-U. Kim, Y.-J. Lee, J. Liu, D. S. Kim, H. Wang and S. Yang, Nat. Mater., 2022, 21, 41–46 CrossRef CAS PubMed.
- Y. Zhao, Y. Chi, Y. Hong, Y. Li, S. Yang and J. Yin, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2200265119 CrossRef CAS PubMed.
- F. Zhai, Y. Feng, Z. Li, Y. Xie, J. Ge, H. Wang, W. Qiu and W. Feng, Matter, 2021, 4, 3313–3326 CrossRef CAS.
- X. Yang, M. Liu, B. Zhang, Z. Wang, T. Chen, Y. Zhou, Y. Chen, K. J. Hsia and Y. Wang, Matter, 2024, 7, 603–619 CrossRef.
- A. Sydney Gladman, E. A. Matsumoto, R. G. Nuzzo, L. Mahadevan and J. A. Lewis, Nat. Mater., 2016, 15, 413–418 CrossRef CAS PubMed.
- M. Zhang, Y. Lee, Z. Zheng, M. T. A. Khan, X. Lyu, J. Byun, H. Giessen and M. Sitti, Nat. Commun., 2023, 14, 8208 CrossRef CAS PubMed.
- Y. Chen, A. S. Kuenstler, R. C. Hayward and L. Jin, Soft Matter, 2022, 18, 4077–4089 RSC.
- L. Xue, K. Atli, C. Zhang, N. Hite, A. Srivastava, A. Leff, A. Wilson, D. Sharar, A. Elwany and R. Arroyave, et al., Acta Mater., 2022, 229, 117781 CrossRef CAS.
- A. Lendlein and O. E. Gould, Nat. Rev. Mater., 2019, 4, 116–133 CrossRef.
- M. Warner and E. M. Terentjev, Liquid Crystal Elastomers, Oxford University Press, 2007, vol. 120 Search PubMed.
- T. J. White and D. J. Broer, Nat. Mater., 2015, 14, 1087–1098 CrossRef CAS PubMed.
- M. Liu, L. Jin, S. Yang, Y. Wang, C. B. Murray and S. Yang, Adv. Mater., 2023, 35, 2208613 CrossRef CAS PubMed.
- Y. Yue, X. Changwei, W. Binglian, J. Lihua and H. Yongzhong, Int. J. Smart Nano Mater., 2011, 2, 245–260 CAS.
- L. Jin, Z. Zeng and Y. Huo, J. Mech. Phys. Solids, 2010, 58, 1907–1927 CrossRef CAS.
- J. Zhang, Y. Guo, W. Hu, R. H. Soon, Z. S. Davidson and M. Sitti, Adv. Mater., 2021, 33, 2006191 CrossRef CAS PubMed.
- Q. He, Z. Wang, Y. Wang, A. Minori, M. T. Tolley and S. Cai, Sci. Adv., 2019, 5, eaax5746 CrossRef CAS PubMed.
- Y. Yao, A. M. Wilborn, B. Lemaire, F. Trigka, F. Stricker, A. H. Weible, S. Li, R. K. Bennett, T. C. Cheung and A. Grinthal, et al., Science, 2024, 386, 1161–1168 CrossRef CAS PubMed.
- D. Mistry, M. Nikkhou, T. Raistrick, M. Hussain, E. I. Jull, D. L. Baker and H. F. Gleeson, Macromolecules, 2020, 53, 3709–3718 CrossRef CAS.
- S.-Y. Jeon, B. Shen, N. A. Traugutt, Z. Zhu, L. Fang, C. M. Yakacki, T. D. Nguyen and S. H. Kang, Adv. Mater., 2022, 34, 2200272 CrossRef CAS PubMed.
- Y. Wang, R. Yin, L. Jin, M. Liu, Y. Gao, J. Raney and S. Yang, Adv. Funct. Mater., 2023, 33, 2210614 CrossRef CAS.
- Z. Pei, Y. Yang, Q. Chen, E. M. Terentjev, Y. Wei and Y. Ji, Nat. Mater., 2014, 13, 36–41 CrossRef CAS PubMed.
- A. Kotikian, J. M. Morales, A. Lu, J. Mueller, Z. S. Davidson, J. W. Boley and J. A. Lewis, Adv. Mater., 2021, 33, 2101814 CrossRef CAS PubMed.
- J. Liu, Y. Gao, H. Wang, R. Poling-Skutvik, C. O. Osuji and S. Yang, Adv. Intell. Syst., 2020, 2, 1900163 CrossRef.
- Z.-Z. Nie, B. Zuo, M. Wang, S. Huang, X.-M. Chen, Z.-Y. Liu and H. Yang, Nat. Commun., 2021, 12, 2334 CrossRef CAS PubMed.
- H. Yang, X. Yin, C. Zhang, B. Chen, P. Sun and Y. Xu, Sci. Adv., 2025, 11, eads3058 CrossRef CAS PubMed.
- T. S. Hebner, K. Korner, C. N. Bowman, K. Bhattacharya and T. J. White, Sci. Adv., 2023, 9, eade1320 CrossRef PubMed.
- L. Wang, Z. Wei, Z. Xu, Q. Yu, Z. L. Wu, Z. Wang, J. Qian and R. Xiao, ACS Appl. Polym. Mater., 2023, 5, 7477–7484 CrossRef CAS.
- A. S. Kuenstler, H. Kim and R. C. Hayward, Adv. Mater., 2019, 31, 1901216 CrossRef PubMed.
- G. Vantomme, L. C. Elands, A. H. Gelebart, E. Meijer, A. Y. Pogromsky, H. Nijmeijer and D. J. Broer, Nat. Mater., 2021, 20, 1702–1706 CrossRef CAS PubMed.
- A. H. Gelebart, D. Jan Mulder, M. Varga, A. Konya, G. Vantomme, E. Meijer, R. L. Selinger and D. J. Broer, Nature, 2017, 546, 632–636 CrossRef CAS PubMed.
- S. J. Gerbode, J. R. Puzey, A. G. McCormick and L. Mahadevan, Science, 2012, 337, 1087–1091 CrossRef CAS PubMed.
- A. Goriely and M. Tabor, Phys. Rev. Lett., 1998, 80, 1564 CrossRef CAS.
- J. Liu, J. Huang, T. Su, K. Bertoldi and D. R. Clarke, PLoS One, 2014, 9, e93183 CrossRef PubMed.
- M. Tanaka, X. Wang, C. K. Mishra, J. Cai, J. Feng, R. D. Kamien and A. Yodh, Phys. Rev. E, 2022, 106, L012605 CrossRef CAS PubMed.
- T. Machon, G. P. Alexander, R. E. Goldstein and A. I. Pesci, Phys. Rev. Lett., 2016, 117, 017801 CrossRef PubMed.
- M. Warner, C. D. Modes and D. Corbett, Proc. R. Soc. A, 2010, 466, 2975–2989 CrossRef.
- T. H. Ware, M. E. McConney, J. J. Wie, V. P. Tondiglia and T. J. White, Science, 2015, 347, 982–984 CrossRef CAS PubMed.
- J. Chen, J. Jiang, J. Weber, V. Gimenez-Pinto and C. Peng, ACS Appl. Mater. Interfaces, 2023, 15, 4538–4548 CrossRef CAS PubMed.
- F. Feng, J. S. Biggins and M. Warner, Phys. Rev. E, 2020, 102, 013003 CrossRef CAS PubMed.
- H. Aharoni, Y. Xia, X. Zhang, R. D. Kamien and S. Yang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7206–7211 CrossRef CAS PubMed.
- D. Castro and H. Aharoni, Phys. Rev. Lett., 2023, 130, 178101 CrossRef CAS PubMed.
- C. Wei, Y. Zhou, B. Hsu and L. Jin, J. Mech. Phys. Solids, 2024, 183, 105522 CrossRef CAS.
- J. T. Waters, S. Li, Y. Yao, M. M. Lerch, M. Aizenberg, J. Aizenberg and A. C. Balazs, Sci. Adv., 2020, 6, eaay5349 CrossRef CAS PubMed.
- G. N. Mol, K. D. Harris, C. W. Bastiaansen and D. J. Broer, Adv. Funct. Mater., 2005, 15, 1155–1159 CrossRef CAS.
- Y. Sawa, F. Ye, K. Urayama, T. Takigawa, V. Gimenez-Pinto, R. L. Selinger and J. V. Selinger, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6364–6368 CrossRef CAS PubMed.
- Y. Sawa, K. Urayama, T. Takigawa, V. Gimenez-Pinto, B. L. Mbanga, F. Ye, J. V. Selinger and R. L. Selinger, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022502 CrossRef PubMed.
- S. Armon, E. Efrati, R. Kupferman and E. Sharon, Science, 2011, 333, 1726–1730 CrossRef CAS PubMed.
- R. Ghafouri and R. Bruinsma, Phys. Rev. Lett., 2005, 94, 138101 CrossRef PubMed.
- J. V. Selinger, M. S. Spector and J. M. Schnur, J. Phys. Chem. B, 2001, 105(30), 7157–7169 CrossRef CAS.
- L. Teresi and V. Varano, Soft Matter, 2013, 9, 3081–3088 RSC.
- C. Ahn, K. Li and S. Cai, ACS Appl. Mater. Interfaces, 2018, 10, 25689–25696 CrossRef CAS PubMed.
- X. Lu, S. Guo, X. Tong, H. Xia and Y. Zhao, Adv. Mater., 2017, 29, 1606467 CrossRef PubMed.
- J. J. Wie, M. R. Shankar and T. J. White, Nat. Commun., 2016, 7, 13260 CrossRef CAS PubMed.
- Z.-C. Jiang, Y.-Y. Xiao, R.-D. Cheng, J.-B. Hou and Y. Zhao, Chem. Mater., 2021, 33, 6541–6552 CrossRef CAS.
- F. Qi, Y. Li, Y. Hong, Y. Zhao, H. Qing and J. Yin, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2312680121 CrossRef CAS PubMed.
- M. C. Escobar and T. J. White, Adv. Mater., 2024, 36, 2401140 CrossRef CAS PubMed.
- D. S. Kim, Y.-J. Lee, Y. B. Kim, Y. Wang and S. Yang, Sci. Adv., 2023, 9, eadh5107 CrossRef CAS PubMed.
- Z. Zhang, C. Wang, Q. Wang, Y. Zhao and L. Shang, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2204113119 CrossRef CAS PubMed.
- J. Jeon, J.-C. Choi, H. Lee, W. Cho, K. Lee, J. G. Kim, J.-W. Lee, K.-I. Joo, M. Cho and H.-R. Kim, et al., Mater. Today, 2021, 49, 97–106 CrossRef CAS.
- M. Soltani, K. Raahemifar, A. Nokhosteen, F. M. Kashkooli and E. L. Zoudani, Polymers, 2021, 13, 1650 CrossRef CAS PubMed.
- A. Konya, V. Gimenez-Pinto and R. L. Selinger, Front. Mater., 2016, 24 Search PubMed.
- N. An, M. Li and J. Zhou, Smart Mater. Struct., 2015, 25, 015016 CrossRef.
- P. Plucinsky and K. Bhattacharya, J. Mech. Phys. Solids, 2017, 102, 125–150 CrossRef CAS.
- G. Skačej and C. Zannoni, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10193–10198 CrossRef PubMed.
- K. Osari and H. Koibuchi, Polymer, 2017, 114, 355–369 CrossRef CAS.
- J. K. Whitmer, T. F. Roberts, R. Shekhar, N. L. Abbott and J. J. De Pablo, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 87, 020502 CrossRef PubMed.
- P. Prathumrat, I. Sbarski, E. Hajizadeh and M. Nikzad, J. Appl. Phys., 2021, 129, 155101 CrossRef CAS.
- Z. Wang, Z. Wang, Y. Zheng, Q. He, Y. Wang and S. Cai, Sci. Adv., 2020, 6, eabc0034 CrossRef CAS PubMed.
- R. Bai and K. Bhattacharya, J. Mech. Phys. Solids, 2020, 144, 104115 CrossRef CAS.
- M. Warner, C. Modes and D. Corbett, Proc. R. Soc. A, 2010, 466, 3561–3578 CrossRef.
- L. D. Landau, L. Pitaevskii, A. M. Kosevich and E. M. Lifshitz, Theory of elasticity: volume 7, Elsevier, 2012, vol. 7 Search PubMed.
- J. Choi, Y. Choi, J.-H. Lee, M. C. Kim, S. Park, K. Hyun, K. M. Lee, T.-H. Yoon and S.-K. Ahn, Adv. Funct. Mater., 2024, 34, 2310658 CrossRef CAS.
- W. Klingenberg, A course in differential geometry, Springer Science & Business Media, 2013, vol. 51 Search PubMed.
- Y. Pomeau and B. Audoly, Elasticity and Geometry: From Hair Curls to the Non-linear Response of Shells, Oxford University Press, 2010 Search PubMed.
- Y. Zhao, Y. Hong, F. Qi, Y. Chi, H. Su and J. Yin, Adv. Mater., 2023, 35, 2207372 CrossRef CAS PubMed.
- G. Babakhanova, T. Turiv, Y. Guo, M. Hendrikx, Q.-H. Wei, A. P. Schenning, D. J. Broer and O. D. Lavrentovich, Nat. Commun., 2018, 9, 456 CrossRef PubMed.
- M. O. Astam, Y. Zhan, T. K. Slot and D. Liu, ACS Appl. Mater. Interfaces, 2022, 14, 22697–22705 CrossRef CAS PubMed.
- Y. Guo, J. Zhang, W. Hu, M. T. A. Khan and M. Sitti, Nat. Commun., 2021, 12, 5936 CrossRef CAS PubMed.
- S. Conti, A. DeSimone and G. Dolzmann, J. Mech. Phys. Solids, 2002, 50, 1431–1451 CrossRef CAS.
- X. Liang and D. Li, Front. Robot. AI, 2022, 9, 849516 CrossRef PubMed.
- L. A. Mihai and A. Goriely, MRS Bull., 2021, 46, 784–794 CrossRef CAS.
- D. Mistry, N. A. Traugutt, B. Sanborn, R. H. Volpe, L. Chatham, R. Zhou, B. Song, K. Yu, K. Long and C. M. Yakacki, Nat. Commun., 2021, 12, 6677 CrossRef CAS PubMed.
- H. Tokumoto, H. Zhou, A. Takebe, K. Kamitani, K. Kojio, A. Takahara, K. Bhattacharya and K. Urayama, Sci. Adv., 2021, 7, eabe9495 CrossRef CAS PubMed.
- S. Li, M. M. Lerch, J. T. Waters, B. Deng, R. S. Martens, Y. Yao, D. Y. Kim, K. Bertoldi, A. Grinthal and A. C. Balazs, et al., Nature, 2022, 605, 76–83 CrossRef CAS PubMed.
Footnote |
| † Present address: Department of Physics, University of Michigan, Ann Arbor, MI 48109, USA. |
| This journal is © The Royal Society of Chemistry 2025 |