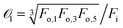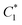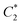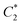Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evolution of adaptive force chains in reconfigurable granular metamaterials†
Sven Witthaus‡
 a,
Atoosa Parsa‡
a,
Atoosa Parsa‡ b,
Dong Wang
b,
Dong Wang a,
Nidhi Pashine
a,
Nidhi Pashine a,
Jerry Zhanga,
Arthur K. MacKeith
a,
Jerry Zhanga,
Arthur K. MacKeith a,
Mark D. Shattuck
a,
Mark D. Shattuck c,
Josh Bongardd,
Corey S. O’Hern
c,
Josh Bongardd,
Corey S. O’Hern ae and
Rebecca Kramer-Bottiglio
ae and
Rebecca Kramer-Bottiglio *a
*a
aDepartment of Mechanical Engineering, Yale University, 9 Hillhouse Ave., New Haven, CT 06511, USA. E-mail: rebecca.kramer@yale.edu
bDepartment of Biology, Tufts University, 200 Boston Ave., Medford, MA 02155, USA
cBenjamin Levich Institute and Physics Department, The City College of New York, New York 10031, NY, USA
dDepartment of Computer Science, University of Vermont, Innovation 428, Burlington, VT 05405, USA
eDepartment of Physics, Yale University, New Haven, CT 06520, USA
First published on 10th July 2025
Abstract
Under an externally applied load, granular packings form force chains that depend on the contact network and moduli of the grains. In this work, we investigate packings of variable modulus (VM) particles, where we can direct force chains by changing the Young's modulus of individual particles within the packing on demand. Each VM particle is made of a silicone shell that encapsulates a core made of a low-melting-point metallic alloy (Field's metal). By sending an electric current through a co-located copper heater, the Field's metal internal to each particle can be melted via Joule heating, which softens the particle. As the particle cools to room temperature, the alloy solidifies and the particle recovers its original modulus. To optimize the mechanical response of granular packings containing both soft and stiff particles, we employ an evolutionary algorithm coupled with discrete element method simulations to predict the patterns of particle moduli that will yield specific force outputs on the assembly boundaries. The predicted patterns of particle moduli from the simulations were realized in experiments using quasi-2D assemblies of VM particles and the force outputs on the assembly boundaries were measured using photoelastic techniques. These studies represent a step towards making robotic granular metamaterials that can dynamically adapt their mechanical properties in response to different environmental conditions or perform specific tasks on demand.
1 Introduction
Mechanical metamaterials process mechanical inputs, such as forces, pressures, or waves, to achieve programmable stiffness, shape transformations, and force propagation.1–3 Many current mechanical metamaterial approaches employ continuum solids or linkages/mechanisms with a fixed structure and therefore demonstrate only fixed responses. We are interested in mechanical metamaterials that can exhibit increased dynamic plasticity, enabling adaptation to different environmental inputs or task demands by reconfiguring their physical structure. Granular metamaterials—consisting of discrete, macroscale particles—offer an advantageous platform for such dynamic programmability, as individual particle properties can be tuned to achieve different bulk responses.4 For example, one can imagine a future granular metamaterial that uses changes in individual particle properties to route forces around a damaged region of the material thereby maintaining its function.Existing granular metamaterials most often incorporate ordered particle assemblies, as it is difficult to predict the material properties of disordered granular assemblies. Ordered granular metamaterials have been used for vibration mitigation,5–9 acoustic switches,10,11 energy absorption,12 elastic modulus and density tuning,13,14 and non-reciprocal behaviors.15 Most of these prior studies have confined their approach to granular systems with inert, rigid grains and fixed elastic moduli. In this work, we expand the parameter space by including variable modulus particles, thereby enabling access to a wider set of possible material responses.
In previous studies, we developed discrete element method (DEM) simulations to study the vibrational response of jammed packings composed of binary mixtures of spherical particles with different masses. For example, in one recent study,11 we showed that 2D and 3D mixed-mass granular assemblies can be used to either transmit or block vibrations with particular frequencies. Expanding on that result, we coupled evolutionary algorithms (EA) with DEM simulations to create more complex logic gates.16–18 Using similar granular systems, in this work we seek to control the transmission of force chains, in both simulations and experiments.
In general, granular packings are collections of macroscopic particles that are densely packed, forming contact networks through which interparticle forces are transmitted. It is well-known that a large fraction of the external load applied to granular packings is often carried by a small number of particles,19–24 resulting in the emergence of stable force chains.25 Due to the large number of degrees of freedom, nonlinear response, and out-of-equilibrium behavior of granular systems, force chain dynamics are challenging to predict analytically. However, there have been many computational studies of force chain networks, such as contact dynamics simulations,26 DEM simulations,27,28 random matrix theory, and statistical mechanics-based models,29 as well as experimental studies of force distributions.30–32 Previous studies have emphasized that individual particle properties, such as the elastic moduli and density, influence how forces propagate through granular assemblies.33 We will exploit this relationship by switching the elastic moduli of individual particles to achieve specific force outputs from selected particles.
We realize granular metamaterials with adaptable force chains using an assembly of variable modulus (VM) particles. While there are many potential approaches to particle modulus modulation, we adapt the approach previously used by Pashine, et al.34 to make variable stiffness bonds in an allosteric metamaterial. Our VM particles are fabricated by incorporating a low-melting-point alloy (Field's metal) in soft silicone shells. A VM particle possesses a larger modulus when the Field's metal core is solid (at low temperature) and a smaller modulus when the core is liquid (at high temperature).
Using discrete element method (DEM) simulations combined with evolutionary algorithms, we identify particle configurations that optimize specific force outputs on the boundaries of a granular assembly. These optimized configurations are then fabricated and tested in experiments, where we demonstrate that the force chain networks within the packing can be dynamically reconfigured by modulating the modulus of individual particles. To explore practical trade-offs, we implement a multi-objective optimization pipeline that simultaneously maximizes boundary force outputs and minimizes power consumption, based on the assumption that power is expended when switching particle stiffness between soft and stiff states. Across all cases studied, we find strong agreement between the simulation predictions and experimental measurements of output forces. The novelty of this work lies in the integration of three components: experiments with variable modulus particles, DEM simulations that quantitatively capture stiffness-dependent interactions, and evolutionary algorithms that discover particle arrangements producing optimal force networks consistent with experimental results. Taken together, these results represent a step toward dynamic granular metamaterials capable of adapting their mechanical responses to evolving environmental or task-specific demands.
2 Methods
To controllably modify the force chain network of a packing, we create a pipeline that takes a set of objectives (e.g., maximize the force between a specific particle and the boundary) and hardware constraints as inputs, and outputs the configuration of large- and small-modulus particles that best achieves the objectives. Our pipeline has several steps. First, we characterize the contact mechanics and interparticle force law of the VM particles. Second, we develop DEM simulations to represent the physical properties of the granular packings. Finally, we combine DEM simulations and evolutionary algorithms to identify the grain configurations that achieve the objectives (Fig. 1).The inverse design problem—designing particle configurations to match a desired force chain output—is an arduous task. Without a systematic methodology, we would have to evaluate an exponentially large number of configurations to decide which configuration gives the desired force output. While it is theoretically feasible to find packings for complex objectives analytically, this task is nontrivial given our nonlinear force model and inability to control the interparticle contacts that occur in granular packings. Therefore, we use DEM simulations coupled with an evolutionary algorithm to identify the optimal grain configurations. In particular, we implement a multi-objective optimization algorithm to search for solutions that satisfy the objectives, subject to experimental constraints. We can then make the grain configurations obtained from the optimization pipeline in experiments and evaluate their force networks, ensuring that the objectives have been met.
We focus on granular packings composed of monodisperse cylindrical particles (with diameter D) confined between two flat walls, such that their cylindrical axes are perpendicular to the walls, and arranged on a 2D triangular lattice. The experimental system is modeled in 2D as collection of monodipserse disks as shown in Fig. 1A. The packing consists of Nr = 5 rows, each with either 4 or 5 particles per row, yielding a total number of particles, N = 23. We index each particle p between 1 and N, increasing from left to right and from bottom to top in the packing, as shown in Fig. 1A. For a specific configuration denoted as C, we assign each grain with an elastic modulus chosen from one of two values: soft ksoft or stiff kstiff with ksoft < kstiff. We define the input force Fi as the total force applied downwards on the top boundary of the system (Fig. 1A) After applying Fi, we measure the output forces exerted on the boundary from the pth particle in the bottom row, Fo,p.
In the remainder of this section, we describe in detail the characterization of the Young's modulus of the particles and interparticle contact force law, the experimental setup, the DEM simulations, and the optimization approaches.
2.1 Experimental design
 | ||
| Fig. 2 Variable modulus (VM) particle characterization. (A) Illustration of the components of a VM particle (left) and an image of a fully assembled VM particle (right). Conductive wires (not shown) are connected to the leads of the copper heater. (B) Force F on VM particle from the two walls in the Instron plotted versus the symmetric displacement d of the walls (relative to the location of the walls at contact) in the soft (blue solid lines) and stiff (magenta solid lines) states. The dashed lines indicate fits to eqn (1) for the Hertzian contact law. Data for a particle with the same silicone geometry, but without Field's metal inside, is labeled as an “empty particle.” Shaded areas represent ±1 standard deviation from six trials. (C) Particle modulus k plotted as a function of temperature T. The melting temperature of the Field's metal is highlighted by the vertical dashed line. k for the “empty particle” is also indicated by the horizontal dashed line. | ||
Next, we describe measurements of the Young's modulus of the VM particles. We compress single VM particles between two steel walls using a material testing system (Instron™ 3365). We find that the relationship between the symmetric displacement d of the walls (relative to their location at contact with the particle) and the compressive force F is best fit by assuming a Hertzian contact law:36
 | (1) |
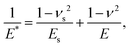 | (2) |
 | (3) |
 | (4) |
In Fig. 2C, we plot the dependence of k on the temperature T of the Field's metal. The particle modulus decreases rapidly when T > T0. We find ksoft ∼ 0.34 MPa for the soft state (T > T0) and kstiff ∼ 1 MPa for the stiff state (T < T0). Thus, the VM particle design possesses a three-fold change in modulus. ksoft is roughly 1.5 times the modulus of the empty silicone shell. For the empty silicone shell, we report k ≈ 0.2 MPa, which is below that for a solid silicone material (∼0.53 MPa). Also note that since the Field's metal becomes a liquid when heated above the melting temperature, an isolated Field's metal particle can in principle yield an infinite-fold modulus change between the liquid and solid states. The three-fold change for the VM particle modulus highlights the substantial contribution of the outer silicone shell to the VM particle modulus. Since the silicone shell encapsulates the metal core, compressive strains predominantly affect the silicone rather than the metal, reducing the modulus ratio between the stiff and soft states compared to the case where only the metal is compressed in the absence of the silicone shell.
We apply a uniform load Fi to the top layer of particles using the same materials testing system employed to characterize the moduli of the VM particles. The force propagates through the packing to create a particular force chain network that is a function of the positions of the particles and their individual moduli. Based on the locations of the stiff and soft particles, the load is transmitted differently to the bottom row of particles, exerting different amounts of force at various locations on the bottom boundary.
The assembly boundaries are made of a photoelastic material (ClearFlex™ 95) placed between two circular-crossed polarizers. We measure the output forces Fo,p on the bottom boundary by analyzing the stress-induced birefringence patterns.23,39,40 When the boundary is not under stress, no light passes through the polarizers. Any stress on the boundary rotates the direction of the incoming electric field, allowing light to pass through the polarizer and appear as a fringe pattern. Because different wavelengths of light will form different patterns on the photoelastic boundary, we use a filter to only observe one wavelength of light (λ = 530 nm).
To measure Fo,p, we consider the intensity Iout that occurs through the application of a point force Fo,p on an elastic half-plane through a polariscope.41,42 The light intensity Iout at any given point (x, y) within the half-plane is
 | (5) |
 | (6) |
Using eqn (5) and (6), we can construct an image for a given force on a half-plane. By comparing this image to the experimentally obtained image, we can fit for 2tKFo,p/λ using minimum chi-square estimation.41 This fit yields Fo,p to within a proportionality factor, 2tK/λ. However, we can eliminate the proportionality constant by summing all of the forces on the bottom boundary:  . See ESI,† S2 for more details.
. See ESI,† S2 for more details.
2.2 DEM simulations
We employ discrete element method (DEM) simulations in two dimensions that mimic the experimental setup. We assemble a collection of monodisperse, frictionless disks into a triangular lattice (see Fig. 1A). We apply a constant downward force Fi/(ksoftD2) = 0.01 to the top boundary. Each particle interacts with its neighbors and the walls, assuming purely repulsive Hertzian interactions, as in eqn (1). We integrate Newton's equations of motion for each disk with damping forces proportional to the particle velocities using a modified velocity-Verlet integration scheme until the net force on all disks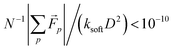 . Determining which disks are in contact allows us to construct the network of interparticle contacts, as shown in Fig. 1C. In ESI,† S3, we show that Fo,p is proportional to Fi over a broad range of Fi. Hence, the specific choice of Fi in the DEM simulations does not impact the optimal solutions predicted by the evolutionary algorithm, as long as Fi is sufficiently small.
. Determining which disks are in contact allows us to construct the network of interparticle contacts, as shown in Fig. 1C. In ESI,† S3, we show that Fo,p is proportional to Fi over a broad range of Fi. Hence, the specific choice of Fi in the DEM simulations does not impact the optimal solutions predicted by the evolutionary algorithm, as long as Fi is sufficiently small.
We note that there are some differences between the DEM simulations and the experiments. For example, the DEM simulations do not include particle–substrate and inter-particle friction. We mitigate the effects of friction by applying a thin layer of cornstarch over the surfaces of each VS particle in the experiments, thus decreasing the effective friction in the experiments. In addition, the particle sizes are slightly polydisperse (<2%) in the experiments, while the simulations assume monodisperse disks. Despite these differences, we find strong qualitative agreement between the results of the DEM simulations and the experiments.
2.3 Optimization setup
To solve the inverse design problem of finding particle configurations that achieve a desired output force pattern, we employ evolutionary algorithms (EAs) in our design pipeline (Fig. 1). EAs are a class of population-based gradient-free global optimization methods inspired by concepts from biology, genetics, and natural evolution.43 In the general case, the algorithm starts with a set of randomly generated solutions (called a population). In each subsequent optimization step (i.e., generation), possible solutions are evaluated using a fitness function. The solutions with the highest fitness are chosen to survive to the next generation and produce alternate solutions through a process of mutation and selection that can potentially create solutions with higher fitness. EAs have been useful in myriad problems in materials science,44 robotics,45 and data retrieval applications.46In this study, to find an optimal configuration of soft and stiff particles to achieve a desired force output, we utilize a particular EA called age-fitness Pareto optimization (AFPO).47,48 AFPO is a multi-objective evolutionary algorithm that balances the diversity of solutions with their fitness values, allowing for an extensive search in configuration space without converging to local optima in a rugged fitness landscape. When the objectives are not mutually exclusive and no explicit coupling is imposed during optimization, AFPO converges to a set of optimal solutions—commonly referred to as the Pareto front—rather than a single best solution. Note that AFPO can also be applied to single-objective optimization, in which case it does not produce a Pareto front, but instead converges to the single best solution. On the Pareto front, no solution is better than the others (and each solution optimizes the multiple objectives differently) unless additional trade-offs are specified.
To select a single best solution from the Pareto front, one can rank Pareto-front solutions with methods used for multiple criteria decision-making, such as the technique for order of preference by similarity to ideal solution (TOPSIS) method.49 TOPSIS implements trade-offs between objectives that oppose each other by assigning a weight vector W that indicates how much each given objective should be weighted while traversing the Pareto front. TOPSIS then chooses the solution with the shortest distance from the ideal solution and the greatest distance from the negative ideal (worst) solution. Note that TOPSIS is applied to the Pareto front only after it has been identified by the AFPO algorithm.
The AFPO algorithm has several components including a genome representation, a variation operator, and a fitness function. In this study, we used a direct encoding scheme for the genome, where the genotype is a binary string (0 for ksoft and 1 for kstiff) that represents the modulus values for all of the particles. The initial genotype is a string of N random bits, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (0,1). The variation operator is a bit-flip mutation with a given mutation probability. The bit-flip mutation changes the modulus of a particle from ksoft to kstiff or vice versa. We consider both single- and multi-objective fitness functions. Additional details concerning the implementation of the AFPO algorithm are provided in Table 1.
(0,1). The variation operator is a bit-flip mutation with a given mutation probability. The bit-flip mutation changes the modulus of a particle from ksoft to kstiff or vice versa. We consider both single- and multi-objective fitness functions. Additional details concerning the implementation of the AFPO algorithm are provided in Table 1.
We explore five optimization objectives as outlined in Table 1. In the feasibility check, we consider a single-objective optimization problem to maximize the force output from a single particle on the bottom row (Section 3.1). We then consider two other single-objective optimization problems to further test the efficacy of our optimization pipeline (cases I and II). In these two cases, the objective function is defined so that the force output from the odd- or even-numbered particles on the bottom boundary is maximized and has units of force before normalization (Section 3.2). In Secttion 3.3, we consider a multi-objective optimization problem (cases III and IV) where we can change from the optimal configuration in case I to that in case II (or vice versa) with an additional hardware constraint that limits the number of changes in the particle modulus as the second objective. The formulation of the objective functions and optimization results for each case are presented in the next section.
3 Results
3.1 Feasibility check: maximizing the output force from a single particle on the bottom row
To verify that the DEM simulations are sufficiently accurate and that the EA generates optimal solutions, we first study a simple case of maximizing the output force exerted by the middle particle in the bottom row on the boundary (Fo,3 in Fig. 3A). For this case, we define the objective function,
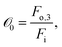 | (7) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 0. As shown in Fig. 3B, using EA, the optimal configuration emerges after ∼100 generations and has higher
0. As shown in Fig. 3B, using EA, the optimal configuration emerges after ∼100 generations and has higher ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 0 than that generated using a random search with over 5000 configurations (Fig. 3C).
0 than that generated using a random search with over 5000 configurations (Fig. 3C).
In Fig. 3D, we show that C* contains two lines of stiff particles stretching from the top corners to the central particle in the bottom row. This solution is intuitive, as larger forces will be carried by the stiffer particles. Thus, arranging stiff particles such that they form a connected path from the top to the bottom boundary without splitting will result in the largest force carried by the central bottom particle.
To validate the results obtained by the EA, we first construct the three configurations (best solution, random 1, and random 2) in the experiments (Fig. 3D) and measure Fo,3 as a function of Fi for each configuration. In Fig. 3E, we show that the output force Fo,3 is approximately linear with Fi for Fi > 4 N, which is consistent with the results from the DEM simulations in ESI,† S3. For Fi < 4 N, Fo,3 is nearly constant, which is caused by the low signal-to-noise values for the photoelastic material at small forces. We also note that the top plate provides comparable forces to each particle in the top row (e.g., ∼10 N/5 yields ∼2 N per particle) and these force magnitudes are similar to those used to measure the stiffness of the VM particles (∼1.5 N, Fig. 2B).
To de-emphasize the uncertainties of the photoelastic stress measurements at small Fo,3, we determine the objective function in the experiments, ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) exp3, as the slope of Fo,3 versus Fi (namely ∂Fo,3/∂Fi) for Fi > 4 N, instead of evaluating Fo,3/Fi at a given Fi. Note that ∂Fo,3/∂Fi can be different from Fo,3/Fi, and Fo,3/Fi can vary with Fi in the linear regime of the experimental curve. This is because Fo,3(Fi) has a non-zero intercept at Fi = 0, presumably due to errors in the photoelastic measurements.
exp3, as the slope of Fo,3 versus Fi (namely ∂Fo,3/∂Fi) for Fi > 4 N, instead of evaluating Fo,3/Fi at a given Fi. Note that ∂Fo,3/∂Fi can be different from Fo,3/Fi, and Fo,3/Fi can vary with Fi in the linear regime of the experimental curve. This is because Fo,3(Fi) has a non-zero intercept at Fi = 0, presumably due to errors in the photoelastic measurements.
As shown in Fig. 3E, the best solution (![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) exp0 ≈ 0.5) substantially outperforms the two random configurations (
exp0 ≈ 0.5) substantially outperforms the two random configurations (![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) exp0 ≈ 0.32 and 0.13 for random 1 and random 2, respectively).
exp0 ≈ 0.32 and 0.13 for random 1 and random 2, respectively).
We observe quantitative agreement for ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 0 between the experiments and DEM simulations for the best solution and random 1 configurations:
0 between the experiments and DEM simulations for the best solution and random 1 configurations: ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) sim0 ≈
sim0 ≈ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) exp0 ≈ 0.46 for the best solution and
exp0 ≈ 0.46 for the best solution and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) sim0 ≈
sim0 ≈ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) exp0 ≈ 0.28 for random 1. However,
exp0 ≈ 0.28 for random 1. However, ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) sim0 ≈ 0.27 for random 2 is approximately twice that measured in experiments. (Note that this discrepancy will not affect our results since the
sim0 ≈ 0.27 for random 2 is approximately twice that measured in experiments. (Note that this discrepancy will not affect our results since the ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) sim0 value for random 2 is much less than that for the best solution.) These results demonstrate our ability to experimentally construct configurations with maximal
sim0 value for random 2 is much less than that for the best solution.) These results demonstrate our ability to experimentally construct configurations with maximal ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 0 that have been predicted by EA.
0 that have been predicted by EA.
3.2 Maximizing force outputs from multiple particles
We next consider objective functions that yield configurations with maximal output forces from mutliple particles in the bottom row, instead of just one particle as described in Section 3.1. Specifically, we will consider the following two cases:• In case I, we seek a configuration 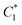 that maximizes the force outputs from the odd-numbered particles on the bottom row (Fig. 4A).
that maximizes the force outputs from the odd-numbered particles on the bottom row (Fig. 4A).
 | ||
Fig. 4 Assessment of the optimization for cases I and II. (A) For case I, we seek the optimal solution  that maximizes the output forces from the odd-numbered particles on the bottom row using the objective function that maximizes the output forces from the odd-numbered particles on the bottom row using the objective function ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 in eqn (8). (B) 1 in eqn (8). (B) ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 for the best solution and averaged over the whole population plotted versus the number of generations. The results are averaged over three independent trials with random initialization. (C) The probability distribution of 1 for the best solution and averaged over the whole population plotted versus the number of generations. The results are averaged over three independent trials with random initialization. (C) The probability distribution of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 for 5000 randomly generated configurations with vertical lines that indicate 1 for 5000 randomly generated configurations with vertical lines that indicate ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 for the average (blue dashed line) and best solution (red solid line) at G = 500. (D) We show one of the two optimal asymmetric solutions for 1 for the average (blue dashed line) and best solution (red solid line) at G = 500. (D) We show one of the two optimal asymmetric solutions for ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1, 1, 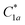 . The other optimal solution . The other optimal solution  is a mirror image of is a mirror image of  . We plot Fo,p versus the location p of the particles on the bottom row from the DEM simulations and experiments. The blue shading indicates the odd-numbered particles. (E) For case II, we seek the optimal solution . We plot Fo,p versus the location p of the particles on the bottom row from the DEM simulations and experiments. The blue shading indicates the odd-numbered particles. (E) For case II, we seek the optimal solution  that maximizes the output forces from the even-numbered particles on the bottom row using the objective function that maximizes the output forces from the even-numbered particles on the bottom row using the objective function ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 in eqn (9). (F) 2 in eqn (9). (F) ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 for the best solution and averaged over the whole population, plotted versus the number of generations. The results are averaged over three independent trials with random initialization. (G) The probability distribution of 2 for the best solution and averaged over the whole population, plotted versus the number of generations. The results are averaged over three independent trials with random initialization. (G) The probability distribution of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 for 5000 randomly generated configurations with vertical lines that indicate 2 for 5000 randomly generated configurations with vertical lines that indicate ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 for the average (blue dashed line) and best solution (red solid line) at G = 500. (H) 2 for the average (blue dashed line) and best solution (red solid line) at G = 500. (H)  is the optimal solution for is the optimal solution for ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2. We plot Fo,p versus p from the DEM simulations and experiments. The blue shading indicates the even-numbered particles. Fo,p/Fi is determined in experiments by measuring the slope of Fo,p versus Fi curve (namely, ∂Fo,p/∂Fi) in panels (D) and (H). 2. We plot Fo,p versus p from the DEM simulations and experiments. The blue shading indicates the even-numbered particles. Fo,p/Fi is determined in experiments by measuring the slope of Fo,p versus Fi curve (namely, ∂Fo,p/∂Fi) in panels (D) and (H). | ||
• In case II, we seek a configuration 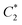 that maximizes the force outputs from the even-numbered particles on the bottom row (Fig. 4E).
that maximizes the force outputs from the even-numbered particles on the bottom row (Fig. 4E).
For case I, we define the objective function,
 | (8) |
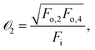 | (9) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 and
1 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 are normalized by the input force Fi. We defined
2 are normalized by the input force Fi. We defined ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 and
1 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 so that they have the same units—force—before normalizing by the input force Fi. For both cases I and II, we use the optimization pipeline described in Table 1. When calculating
2 so that they have the same units—force—before normalizing by the input force Fi. For both cases I and II, we use the optimization pipeline described in Table 1. When calculating ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 and
1 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 for the experiments, we assume that
2 for the experiments, we assume that ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) exp1 = ((∂Fo,1/∂Fi)(∂Fo,3/∂Fi)(∂Fo,5/∂Fi))1/3 and
exp1 = ((∂Fo,1/∂Fi)(∂Fo,3/∂Fi)(∂Fo,5/∂Fi))1/3 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) exp2 = ((∂Fo,2/∂Fi)(∂Fo,4/∂Fi))1/2.
exp2 = ((∂Fo,2/∂Fi)(∂Fo,4/∂Fi))1/2.
Similar to the case of the feasibility check, the optimal configuration  that maximizes
that maximizes ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 for case I emerges after ∼80 generations (Fig. 4B) and has a much larger
1 for case I emerges after ∼80 generations (Fig. 4B) and has a much larger ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 than that generated using a random search with over 5000 configurations (Fig. 4C).
1 than that generated using a random search with over 5000 configurations (Fig. 4C).  possesses lines of stiff particles that extend from the force input on the top row of particles to the odd-numbered particles in the bottom row (Fig. 4D), similar to the stiffness pattern in C*. Note that the stiffness pattern in
possesses lines of stiff particles that extend from the force input on the top row of particles to the odd-numbered particles in the bottom row (Fig. 4D), similar to the stiffness pattern in C*. Note that the stiffness pattern in  is not symmetric about the y-axis, hence there are two solutions:
is not symmetric about the y-axis, hence there are two solutions: 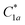 shown in Fig. 4D, and a mirror image of
shown in Fig. 4D, and a mirror image of  about the y-axis with different genome representations (Table 1), but the same
about the y-axis with different genome representations (Table 1), but the same ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1. In addition, in Fig. 4D we show that the Fo,p/Fi values in the experiments, which are determined by ∂Fo,p/∂Fi, are close to those predicted by the DEM simulations for all particles p. In addition, all odd-numbered particles have higher output forces than those for the even-numbered particles on the bottom row, which is consistent with maximizing
1. In addition, in Fig. 4D we show that the Fo,p/Fi values in the experiments, which are determined by ∂Fo,p/∂Fi, are close to those predicted by the DEM simulations for all particles p. In addition, all odd-numbered particles have higher output forces than those for the even-numbered particles on the bottom row, which is consistent with maximizing ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1.
1.
We observe similar results for cases I and II. We obtain the optimal configuration  that maximizes
that maximizes ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 after ∼80 generations (Fig. 4F). It has a much larger
2 after ∼80 generations (Fig. 4F). It has a much larger ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 than that generated using a random search (Fig. 4G).
2 than that generated using a random search (Fig. 4G). 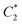 is symmetric about the y-axis and the lines of stiff particles are reflected at the side walls, which directs forces from the top plate to the even-numbered particles and avoids the propagation of large forces to the odd-numbered particles (Fig. 4H). We again find that Fo,p/Fi in the experiments are very close to those predicted by the DEM simulations for all p, as shown in Fig. 4H. In
is symmetric about the y-axis and the lines of stiff particles are reflected at the side walls, which directs forces from the top plate to the even-numbered particles and avoids the propagation of large forces to the odd-numbered particles (Fig. 4H). We again find that Fo,p/Fi in the experiments are very close to those predicted by the DEM simulations for all p, as shown in Fig. 4H. In  , all even-numbered particles have higher output forces than those for the odd-numbered particles on the bottom row, which is consistent with maximizing
, all even-numbered particles have higher output forces than those for the odd-numbered particles on the bottom row, which is consistent with maximizing ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2.
2.
3.3 Optimal solutions with two objectives
Given that there are different force outputs from the particles on the bottom row in , and
, and  , one can envision an application where the system needs to switch from
, one can envision an application where the system needs to switch from 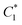 (large force outputs from odd-numbered particles) to
(large force outputs from odd-numbered particles) to  (large force outputs from even-numbered particles) or vice versa. The VM particles provide the capability to switch the packing from one configuration to another, i.e., by local heating, one can change k for each particle from soft to stiff and vice versa. In contrast, to switch from
(large force outputs from even-numbered particles) or vice versa. The VM particles provide the capability to switch the packing from one configuration to another, i.e., by local heating, one can change k for each particle from soft to stiff and vice versa. In contrast, to switch from 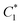 to
to  with inert particles, one would need to create
with inert particles, one would need to create  , disassemble it, and then build
, disassemble it, and then build 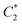 . In the movie in the ESI,† we show that using VM particles we can change the stiffness network from
. In the movie in the ESI,† we show that using VM particles we can change the stiffness network from 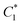 to
to 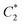 without disassembling the packing by changing the temperatures of the appropriate particles.
without disassembling the packing by changing the temperatures of the appropriate particles.
To change from  to
to  (and vice versa) requires Ns = 19 particle modulus changes. However, what if there is a hardware constraint for the VM particles where significant power is consumed to change the modulus, but not to maintain the particle modulus as soft or stiff? In this case, minimization of the power consumption corresponds to minimizing the number of switches in modulus between the two configurations and a multi-objective EA is required to identify the optimal solution.
(and vice versa) requires Ns = 19 particle modulus changes. However, what if there is a hardware constraint for the VM particles where significant power is consumed to change the modulus, but not to maintain the particle modulus as soft or stiff? In this case, minimization of the power consumption corresponds to minimizing the number of switches in modulus between the two configurations and a multi-objective EA is required to identify the optimal solution.
For case III, we consider the following multi-objective optimization problem. Starting from  , we seek to maximize
, we seek to maximize ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 and minimize
2 and minimize
 | (10) |
 is the number of particle modulus changes from
is the number of particle modulus changes from 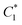 to C2, δ(x,y) = 1 when x = y and δ(x,y) = 0 when x ≠ y, and kC,p is the modulus of the pth particle in configuration C.
to C2, δ(x,y) = 1 when x = y and δ(x,y) = 0 when x ≠ y, and kC,p is the modulus of the pth particle in configuration C.
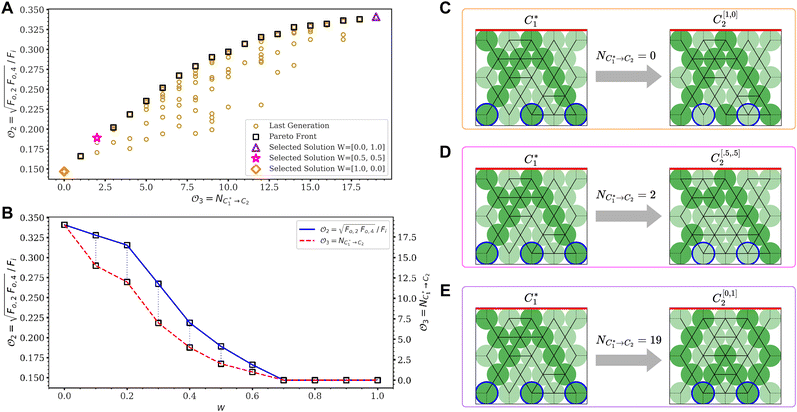
We ran the multi-objective optimization using AFPO with parameters outlined in Table 1. The algorithm converged to a Pareto front with Ns + 1 = 20 optimal solutions at G = 500, as shown in Fig. 5A. There is no “best” solution among the 20 solutions on the Pareto front if we do not consider trade-offs between maximizing ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 and minimizing
2 and minimizing ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 3. To implement trade-offs, we include a TOPSIS weight vector: W = [w,1 − w] with 0 ≤ w ≤ 1. The first and second components of W correspond to the weight for
3. To implement trade-offs, we include a TOPSIS weight vector: W = [w,1 − w] with 0 ≤ w ≤ 1. The first and second components of W correspond to the weight for ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 3 and
3 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2, respectively. We find that the best solution given by TOPSIS traverses the Pareto front from top-right to bottom-left in the
2, respectively. We find that the best solution given by TOPSIS traverses the Pareto front from top-right to bottom-left in the ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 3–
3–![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 plane. Namely,
2 plane. Namely, ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 3 and
3 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 decrease monotonically with increasing w, as shown in Fig. 5B. We also observe that the dependence of both
2 decrease monotonically with increasing w, as shown in Fig. 5B. We also observe that the dependence of both ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 3 and
3 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 on w on the Pareto front is non-linear.
2 on w on the Pareto front is non-linear.
Next, we present several examples of the best solutions selected by TOPSIS for different values of w. For instance, if we set w = 1, the best solution is  with no particle modulus changes (Fig. 5C). Similarly, if we set w = 0, only objective
with no particle modulus changes (Fig. 5C). Similarly, if we set w = 0, only objective ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2 is considered, and the best solution is
2 is considered, and the best solution is  (Fig. 5E). These two TOPSIS weight vectors have obvious solutions, and confirm that
(Fig. 5E). These two TOPSIS weight vectors have obvious solutions, and confirm that 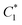 and
and  are on the Pareto front. However, if we set 0 < w < 1 (e.g., w = 0.5), the best solution is not
are on the Pareto front. However, if we set 0 < w < 1 (e.g., w = 0.5), the best solution is not  or
or  , and is instead a compromise between maximizing
, and is instead a compromise between maximizing ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 3 and minimizing
3 and minimizing ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2, as shown in Fig. 5D.
2, as shown in Fig. 5D.
For case IV, we consider the following multi-objective optimization problem. Starting from  , we seek to maximize
, we seek to maximize ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 and minimize
1 and minimize
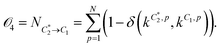 | (11) |
We again observe a Pareto front with Ns + 1 = 20 optimal solutions at G = 500, as shown in Fig. 6A. We implement a similar TOPSIS weight vector: W = [w,1 − w], with the first and second components corresponding to the weight for ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 4 and
4 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1, respectively. Similar to case III, we find that
1, respectively. Similar to case III, we find that ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 4 and
4 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 decrease monotonically with increasing w for the best solution given by TOPSIS, as shown in Fig. 6B. We again observe that the dependence of both
1 decrease monotonically with increasing w for the best solution given by TOPSIS, as shown in Fig. 6B. We again observe that the dependence of both ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 4 and
4 and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 on w on the Pareto front is non-linear. We also present several examples of the best solutions selected by TOPSIS for values of w. For instance, if we set w = 1, the best solution is
1 on w on the Pareto front is non-linear. We also present several examples of the best solutions selected by TOPSIS for values of w. For instance, if we set w = 1, the best solution is  with no particle modulus changes (Fig. 6C). Similarly, if we set w = 0, the best solution is
with no particle modulus changes (Fig. 6C). Similarly, if we set w = 0, the best solution is  , where only objective
, where only objective ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 1 is considered (Fig. 6E). If we set 0 < w < 1 (e.g., w = 0.5), the best solution is not
1 is considered (Fig. 6E). If we set 0 < w < 1 (e.g., w = 0.5), the best solution is not 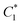 or
or  , and is instead a compromise between maximizing
, and is instead a compromise between maximizing ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 3 and minimizing
3 and minimizing ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) 2, as shown in Fig. 6D.
2, as shown in Fig. 6D.
4 Conclusions
In this article, we developed a pipeline that combines experiments using variable modulus (VM) particles, discrete element method (DEM) simulations, and evolutionary algorithms (EAs) to design granular packings with adaptive mechanical responses. Specifically, we use the pipeline to design granular packings composed of N = 23 same-sized VM particles arranged in a triangular lattice with different patterns of particle moduli that maximize the output forces from particles on the bottom row of the system. We realized VM particles in experiments by embedding a Field's metal core within a silicone shell. By running current through a resistive heater co-located with the Field's metal, we achieved a modulus ratio of kstiff/ksoft ∼ 3 when the Field's metal is heated above the melting temperature. The system boundaries were made of photoelastic material to enable measurements of the output forces. We characterized the inter-particle contact forces as a function of compressive strain in experiments to calibrate the inter-particle forces in the DEM simulations. We carried out evolutionary algorithms (EA) to identify the optimal configurations of soft and stiff particles for specific force outputs on the bottom boundary without enumerating all possible particle modulus combinations.We considered five optimization cases in this study. For the feasibility check, we found the configuration C* of particle moduli that maximizes the output force from the middle particle in the bottom row. In case I (case II), we identified the configuration  that maximizes the output forces from the odd-numbered (even-numbered) particles in the bottom row. In case III (case IV), we found the configuration C2 (C1) that maximizes the output forces from the even-numbered (odd-numbered) particles in the bottom row, while minimizing the number of particle modulus changes starting from
that maximizes the output forces from the odd-numbered (even-numbered) particles in the bottom row. In case III (case IV), we found the configuration C2 (C1) that maximizes the output forces from the even-numbered (odd-numbered) particles in the bottom row, while minimizing the number of particle modulus changes starting from 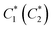 . The first three cases involve single-objective optimization, and the remaining two involve multi-objective optimization. We have shown that EA converges to the optimal solution for the cases involving single-objective optimization and a set of solutions on the Pareto front for the cases involving multi-objective optimization. We verify that the force outputs for the best solutions match in experiments and DEM simulations for the cases of single-objective optimization. We further show that we can identify the best solution in the cases of multi-objective optimization when trade-offs between the objectives are implemented using a TOPSIS weight vector. This study has demonstrated the ability to search efficiently through a large ensemble of granular packings for those that satisfy specific objectives concerning the mechanical response. Although there have been several numerical studies aimed at identifying optimal properties in granular packings using EA,11 few have validated the EA methods using experiments.44
. The first three cases involve single-objective optimization, and the remaining two involve multi-objective optimization. We have shown that EA converges to the optimal solution for the cases involving single-objective optimization and a set of solutions on the Pareto front for the cases involving multi-objective optimization. We verify that the force outputs for the best solutions match in experiments and DEM simulations for the cases of single-objective optimization. We further show that we can identify the best solution in the cases of multi-objective optimization when trade-offs between the objectives are implemented using a TOPSIS weight vector. This study has demonstrated the ability to search efficiently through a large ensemble of granular packings for those that satisfy specific objectives concerning the mechanical response. Although there have been several numerical studies aimed at identifying optimal properties in granular packings using EA,11 few have validated the EA methods using experiments.44
We envision several interesting directions for future studies. First, we can examine all of the solutions on the Pareto front in cases III and IV, implement the optimal solutions in experiments, and determine the power consumption when generating them. Second, our results can serve as a proof-of-concept for mechanical logic gates in granular materials, where continuous force values are discretized into binary inputs (“0” or “1”) and routed through different logic gate architectures. Previous work has shown logic capabilities within granular materials,50 but these studies relied on the embedded capabilities of the granular material rather than optimizing for a desired logic gate. Although no traditional form of logic has been investigated in the current study, we believe that the proposed pipeline can serve as a tool to optimize a material to perform logical operations. Third, the present study can be readily extended to bulk granular materials in three dimensions (3D). We anticipate that the greater number of contacts per particle in 3D packings will increase the complexity of the configurational search space for identifying optimal force networks.
The heterogeneity of force chain networks in granular packings is often controlled by positional disorder. Previous studies of force chain networks in granular materials have analyzed force propagation in disordered networks using methods from statistical physics and mathematics.29,51–54 In this work, we tuned the force chain networks through particle modulus variations (kstiff/ksoft ∼ 3) on a fixed triangular lattice, rather than through positional disorder. Although this modulus ratio is substantial and has allowed us to significantly vary the morphology of force chain networks, an optimized particle design can induce a more dramatic particle modulus ratio and thus more dramatic changes in the force chain networks in VM particle packings. To efficiently sample and quantify force chain networks, we implemented DEM simulations with a simplified contact model for VM particles and the system boundaries. However, the experimental system and the DEM simulations can have differing force outputs for some of the sub-optimal configurations. Increasing the complexity of the inter-particle contact model in the DEM simulations, e.g., using deformable particle simulations in 3D,55 can improve the agreement between the predicted and experimentally measured force outputs.
Author contributions
S. W.: methodology, validation, formal analysis, investigation, data curation, writing, review and editing, visualization, and project administration. A. P.: methodology, formal analysis, validation, writing, review and editing, and visualization. D. W.: methodology, formal analysis, writing, review and editing, and visualization. N. P.: methodology, investigation, supervision, review, and editing. J. Z.: methodology, formal analysis. A. K. M.: methodology. M. D. S.: investigation, resources. R. K.-B.: conceptualization, supervision, project administration, review and editing, resources, and funding acquisition. C. S. O.: conceptualization, supervision, project administration, review and editing, resources, and funding acquisition. J. B.: conceptualization, supervision, project administration, review and editing, resources, and funding acquisition.Conflicts of interest
There are no conflicts to declare.Data availability
We have deposited all relevant data for this paper in the repository https://github.com/AtoosaParsa/AdaptiveForceChains.Acknowledgements
This material is based upon work supported by the National Science Foundation under the Designing Materials to Revolutionize and Engineer our Future (DMREF) program (award no. 2118988).Notes and references
- C. Jiang, F. Rist, H. Wang, J. Wallner and H. Pottmann, Comput.-Aided Des., 2022, 143, 103146 CrossRef.
- W. Yang, Z.-M. Li, W. Shi, B.-H. Xie and M.-B. Yang, J. Mater. Sci., 2004, 39, 3269–3279 CrossRef CAS.
- Y. Wang, L. Li, D. Hofmann, J. Andrade and C. Daraio, Nature, 2021, 596, 238–243 CrossRef CAS PubMed.
- B. Jenett, C. Cameron, F. Tourlomousis, A. P. Rubio, M. Ochalek and N. Gershenfeld, Sci. Adv., 2020, 6, eabc9943 CrossRef PubMed.
- G. Gantzounis, M. Serra-Garcia, K. Homma, J. Mendoza and C. Daraio, J. Appl. Phys., 2013, 114, 093514 CrossRef.
- A. Leonard, L. Ponson and C. Daraio, J. Mech. Phys. Solids, 2014, 73, 103–117 CrossRef.
- L. Bonanomi, G. Theocharis and C. Daraio, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2015, 91, 033208 CrossRef PubMed.
- N. Nejadsadeghi, L. Placidi, M. Romeo and A. Misra, Mech. Res. Commun., 2019, 95, 96–103 CrossRef.
- E. Kim and J. Yang, Funct. Compos. Struct., 2019, 1, 012002 CrossRef CAS.
- F. Li, P. Anzel, J. Yang, P. G. Kevrekidis and C. Daraio, Nat. Commun., 2014, 5, 1–6 CrossRef.
- Q. Wu, C. Cui, T. Bertrand, M. D. Shattuck and C. S. O'Hern, Phys. Rev. E, 2019, 99, 062901 CrossRef CAS PubMed.
- K. Fu, Z. Zhao and L. Jin, Adv. Funct. Mater., 2019, 29, 1901258 CrossRef.
- M. A. Porter, P. G. Kevrekidis and C. Daraio, Phys. Today, 2015, 68, 44–50 CrossRef CAS.
- N. Nejadsadeghi and A. Misra, Int. J. Mech. Sci., 2019, 161, 105042 CrossRef.
- A. Merkel and J. Christensen, Commun. Phys., 2019, 2, 1–6 CrossRef.
- A. Parsa, D. Wang, C. S. O’Hern, M. D. Shattuck, R. Kramer-Bottiglio and J. Bongard, International Conference on the Applications of Evolutionary Computation (Part of EvoStar), 2022, pp. 93–109.
- A. Parsa, D. Wang, C. S. O’Hern, M. D. Shattuck, R. Kramer-Bottiglio and J. Bongard, Proceedings of the Genetic and Evolutionary Computation Conference, 2022, pp. 122–129.
- A. Parsa, S. Witthaus, N. Pashine, C. S. O’Hern, R. Kramer-Bottiglio and J. Bongard, Proceedings of the Genetic and Evolutionary Computation Conference, 2023, pp. 193–201.
- H. Herrmann, J. Hovi and S. Luding, Physics of Dry Granular Media, Springer, Netherlands, 2014 Search PubMed.
- H. M. Jaeger, S. R. Nagel and R. P. Behringer, Rev. Mod. Phys., 1996, 68, 1259–1273 CrossRef.
- R. Behringer, D. Howell, L. Kondic, S. Tennakoon and C. Veje, Phys. D, 1999, 133, 1–17 CrossRef.
- D. W. Howell, R. P. Behringer and C. T. Veje, Chaos, 1999, 9, 559–572 CrossRef PubMed.
- B. Utter and R. Behringer, Eur. Phys. J. E:Soft Matter Biol. Phys., 2004, 14, 373–380 CrossRef CAS PubMed.
- T. S. Majmudar and R. P. Behringer, Nature, 2005, 435, 1079–1082 CrossRef CAS PubMed.
- R. Behringer, H. Jaeger and S. Nagel, Chaos, 1999, 9, 509–510 CrossRef PubMed.
- F. Radjai, M. Jean, J.-J. Moreau and S. Roux, Phys. Rev. Lett., 1996, 77, 274–277 CrossRef CAS PubMed.
- S. Luding, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4720–4729 CrossRef CAS.
- J. F. Peters, M. Muthuswamy, J. Wibowo and A. Tordesillas, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2005, 72, 041307 CrossRef CAS PubMed.
- S. F. Edwards and D. V. Grinev, Granular Matter, 2003, 4, 147–153 CrossRef.
- A. H. Clark, A. J. Petersen, L. Kondic and R. P. Behringer, Phys. Rev. Lett., 2015, 114, 144502 CrossRef PubMed.
- L. Papadopoulos, J. G. Puckett, K. E. Daniels and D. S. Bassett, Phys. Rev. E, 2016, 94, 032908 CrossRef PubMed.
- D. Wang, J. Ren, J. A. Dijksman, H. Zheng and R. P. Behringer, Phys. Rev. Lett., 2018, 120, 208004 CrossRef CAS PubMed.
- C. S. Campbell, Powder Technol., 2006, 162, 208–229 CrossRef CAS.
- N. Pashine, A. M. Nasab and R. Kramer-Bottiglio, Soft Matter, 2023, 19, 1617–1623 RSC.
- W. Shan, T. Lu and C. Majidi, Smart Mater. Struct., 2013, 22, 085005 CrossRef CAS.
- M. J. Puttock and E. G. Thwaite, Elastic compression of spheres and cylinders at point and line contact, by M. J. Puttock and E. G. Thwaite, Commonwealth Scientific and Industrial Research Organization Melbourne, 1969, p. 64 Search PubMed.
- S. V. Franklin and M. D. Shattuck, Handbook of granular materials, CRC Press, 2016 Search PubMed.
- Y. Zhao, Y. Zhao, D. Wang, H. Zheng, B. Chakraborty and J. E. S. Socolar, Phys. Rev. X, 2022, 12, 031021 CAS.
- G. D. J. de Jong, in Étude photo-Élastique d'un empilement de disques, ed. R. J. Schotting, H. C. J. van Duijn and A. Verruijt, Springer, Netherlands, Dordrecht, 2006, pp. 148–161 Search PubMed.
- T. Wakabayashi, J. Phys. Soc. Jpn., 1950, 5, 383–385 CrossRef.
- A. Resnick, Contemp. Phys., 2016, 58, 1 Search PubMed.
- A. Flamant, C. R. Acad. Sci., 1892, 114, 1465–1468 Search PubMed.
- D. E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, Addison-Wesley Longman Publishing Co., Inc., USA, 1st edn, 1989 Search PubMed.
- M. Z. Miskin and H. M. Jaeger, Soft Matter, 2014, 10, 3708–3715 RSC.
- D. Shah, B. Yang, S. Kriegman, M. Levin, J. Bongard and R. Kramer-Bottiglio, Adv. Mater., 2021, 33, 2002882 CrossRef CAS PubMed.
- R. Chiong, T. Weise and Z. Michalewicz, Variants of evolutionary algorithms for real-world applications, Springer, 2012, vol. 2 Search PubMed.
- M. D. Schmidt and H. Lipson, Proceedings of the 12th annual conference on Genetic and evolutionary computation, 2010, pp. 543–544.
- M. Schmidt and H. Lipson, in Age-Fitness Pareto Optimization, ed. R. Riolo, T. McConaghy and E. Vladislavleva, Springer New York, New York, NY, 2011, pp. 129–146 Search PubMed.
- C.-L. Hwang, K. Yoon, C.-L. Hwang and K. Yoon, Multiple attribute decision making: methods and applications a state-of-the-art survey, 1981, pp. 58–191 Search PubMed.
- F. Li, P. Anzel, J. Yang, P. G. Kevrekidis and C. Daraio, Nat. Commun., 2014, 5, 5311 CrossRef CAS PubMed.
- M. Kramar, A. Goullet, L. Kondic and K. Mischaikow, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042207 CrossRef CAS PubMed.
- E. Stanifer, P. K. Morse, A. A. Middleton and M. L. Manning, Phys. Rev. E, 2018, 98, 042908 CrossRef CAS.
- M. Kramar, A. Goullet, L. Kondic and K. Mischaikow, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042207 CrossRef CAS PubMed.
- L. Kondic, A. Goullet, C. S. O'Hern, M. Kramar, K. Mischaikow and R. P. Behringer, Europhys. Lett., 2012, 97, 54001 CrossRef.
- D. Wang, J. D. Treado, A. Boromand, B. Norwick, M. P. Murrell, M. D. Shattuck and C. S. O’Hern, Soft Matter, 2021, 17, 9901–9915 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00965g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |



![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) )
)