Curvature-dependent propulsion of elastic flagella

Abstract

Soft robotic swimmers that can mimic the flagella-powered locomotion of micro-organisms are of significant interest in a broad range of applications. However, realising micro-organisms’ dexterity in soft robots remains challenging without an effective mechanism to achieve bidirectional propulsion in low Reynolds numbers. Here, inspired by recent theoretical studies that suggest the possibility of intrinsically curved elastic flagella to achieve bidirectional propulsion, we experimentally investigate the propulsion behaviour of elastic artificial flagella with uniform intrinsic curvature, actuated by transverse oscillations at Re < 0.1. Our results reveal that the flagella's curvature influences the propulsion direction and magnitude, suggesting a transition between positive and negative propulsion when the flagella's central angle in the stress-free state (θ₀) is between 60° and 90° at Sp = 1.5 and 1.8. We also investigate the relationship between the propulsion force and flagella oscillation with numerical simulations. These findings suggest the potential of on-demand curvature modulation during active oscillation to achieve bidirectional propulsion, enhancing the dexterity in flagella-driven artificial swimmers for a broad range of applications in microscale systems.

---

1. Introduction

Propulsion at the microscale often occurs at low Reynolds number (Re),¹ where Re = ρuL/μ ≪ 1 (ρ is the fluid density, u is the translational velocity, L is the contour length, and μ is the dynamic viscosity). At low Re, the inertia effect is negligible, the viscous effect dominates, and the governing equations become Stokes equations under incompressible and Newtonian assumptions. Importantly, as the equations of motion are time-reversible, propulsion must incorporate non-reciprocal motion.² One method to generate propulsion at low Re is by oscillating a slender elastic body,^2,3 as the body deformation is non-reciprocal, and the drag anisotropy on the slender body induces net propulsion.^4–6 Using these principles, micro-organisms such as Chlamydomonas achieve propulsion at low Re by actively oscillating flexible appendages called flagella.^5,7,8

Inspired by biological flagella, prior works have investigated the propulsion characteristics of elastic artificial flagella.^4,6,9–21 In contrast to the active internal torques that occur along the length of biological flagella during propulsion^8,22–24 and which have been used in previous micro-scale swimmers,^21,25,26 elastic artificial flagella are passive geometries that achieve propulsion due to interactions between fluid drag and flagella elasticity when actuated periodically at one end.⁴ Prior studies of elastic artificial flagella have largely focused on flagella with intrinsically straight profiles. For example, Wiggins and Goldstein studied the effect of flagella elasticity on locomotion with a focus on the deformations of the flagella during the motion;⁶ Yu et al. experimentally demonstrated propulsion by transverse periodic oscillation of a passive flexible filament;¹² and Peng et al. investigated the ability to increase propulsion by varying the flexibility along the filament.¹¹ However, straight flagella only exhibit positive propulsion (in the direction opposite to the wave propagation),³ which critically limits the functionalities that can be achieved. Bidirectional propulsion, or the ability to achieve both positive and negative propulsion, can enable advanced functionalities at the microscale by reversing flow in microfluidic devices, enhancing dexterity during microscale object manipulation^16,17 and reversing locomotion.^15,27,28

Intriguingly, recent studies have reported that bidirectional propulsion can be achieved by designing elastic artificial flagella with intrinsically curved profiles in the stress-free state.^14–16 For example, Namdeo et al. used a computational framework to demonstrate bidirectional propulsion with a ‘Y’-shaped swimmer actuated with transverse oscillations,¹⁶ where the swimming direction could be reversed by curving the two free ends. More recently, Liu et al. combined asymptotic theory and simulations to demonstrate the bidirectional propulsion of a swimmer that consisted of a spherical body and two symmetrical circular-arc profile filaments actuated with harmonic angular oscillations,¹⁵ where the propulsion direction depended on the filament's curvature. In another study, Liu et al. combined theory and simulations to demonstrate the bidirectional propulsion of filaments with cosinusoidal profiles that were actuated with transverse oscillation,¹⁴ where the propulsion direction could be changed by adjusting the sperm number (Sp = L(ξ_⊥ω/A)^1/4; L is the contour length, ξ_⊥ is the normal drag coefficient, ω is the oscillation frequency, and A is the filament's flexural rigidity). The authors noted that this relationship between Sp and propulsion direction could enable frequency-dependent bidirectional propulsion. Despite these impressive findings, the propulsion of elastic artificial flagella with intrinsic curvature that are periodically oscillated at one end has yet to be experimentally investigated.

This study investigates the propulsion of elastic artificial flagella with uniform intrinsic curvature at low Re (Re < 0.1). Section 2 describes the methods used in the low Re experiments and simulations. In Sections 3.1 and 3.2, we evaluate the effect of curvature and Sp on propulsion using experimental and simulation results. In Sections 3.3 and 3.4, we then investigate the time-varying force and the time-varying curvature of the flagella. Lastly, we conclude in Section 4 by summarizing our observations and providing a discussion on the implications of the results.

2. Materials and methods

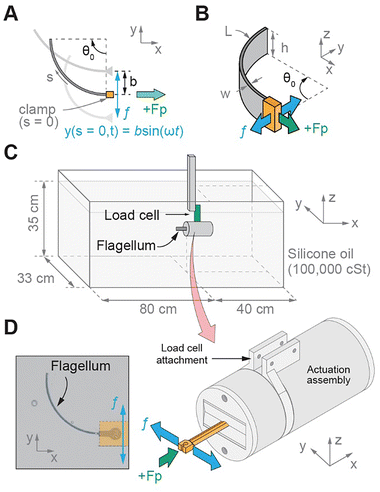
2.1 Experimental setup

To experimentally investigate the propulsion of elastic artificial flagella, we leverage 3D printing to fabricate flagella with uniform intrinsic curvature in the stress-free state and perform experiments in a macroscale setup at a low Re flow condition (Fig. 1). We build upon previous numerical and theoretical works that demonstrated bidirectional propulsion of elastic filaments with uniform intrinsic curvature that were angularly oscillated at one end,¹⁵ and elastic filaments with cosinusoidal intrinsic curvature that were transversely oscillated at one end.¹⁴ In this study, we design the flagella geometry with a uniform intrinsic curvature (Fig. 1(A) and (B)) that can, in principle, be modulated post-fabrication with an applied moment or internal strains (e.g., due to asymmetric shrinkage) based on Euler–Bernoulli beam theory.²⁹ Additionally, in contrast to the numerical and theoretical works that utilized filaments with circular cross-sections and restricted the filaments to planar deformations, we design the flagella with a rectangular cross-section at an aspect ratio of 10 : 1 (height : width) to decrease potential out-of-plane bending during oscillation (Fig. S1, ESI†).

Fig. 1 Experimentally measuring the propulsion of flagella with uniform intrinsic curvature. (A) The flagellum curvature is defined by the central angle in the stress-free state, θ₀. The clamped end is transversely oscillated at frequency f in the y-direction (b: amplitude), and the propulsive force Fp is measured in the x-direction (the direction of positive Fp is shown). (B) The flagellum is designed with a contour length L = 22 mm, width w = 0.5 mm, and height h = 5 mm. (C) Experiments are performed at the macroscale using an actuation assembly that is submerged in a tank of high-viscosity silicone oil. The Fp is measured with a load cell that connects the actuation assembly to a rigid frame. (D) The actuation assembly uses a Scotch Yoke mechanism to convert a motor's rotation to the transverse oscillation of the flagellum, where f is measured using the motor's encoder. In the schematics in (A)–(B), and in the image in (D), the flagellum has θ₀ = 90°.

The macro-scale experiments were performed in a glass tank (1.2 m length, 0.33 m width, 0.35 m oil depth) filled with high-viscosity silicone oil (PSF-100 000 cSt, Clearco) with a kinematic viscosity (ν) of 100 000 cSt and a density (ρ) of 977 kg m⁻³. Experimental Reynolds numbers were in the range of 0.01 (at 1.5 Hz and Sp = 1.5 with β = 0.25) to 0.05 (at 6.0 Hz and Sp = 2.1 with β = 0.25), where the translational velocity u = 2πfβL (the dimensionless amplitude β = b/L, where b is the oscillation amplitude). The actuated end of the flagellum was attached to an actuation assembly and was oriented to be centered in width and depth, and approximately 40 cm from the front wall (Fig. 1(C) and (D)). The actuation assembly was designed to perform transverse actuation using a geared DC motor (4863, Pololu) and a Scotch Yoke mechanism similar to a previous study.¹² In the experiments, f was controlled using the motor input voltage, and b was controlled using the Scotch Yoke geometry. As shown in Fig. 1(A) and (B), the flagellum was clamped at one end and transversely oscillated in the y-direction at frequency f. The propulsive force Fp was measured in the x-direction. The experiments were performed with β = 0.25. We focus on f = 1.5, 3.0, and 6.0 Hz due to simulation results for a flagellum with θ₀ = 90° (Fig. S2, ESI†). Specifically, we chose f = 3.0 Hz, as it was near the minimum 〈Fp〉. We chose f = 6.0 Hz, as the 〈Fp〉 was positive at approximately the same magnitude as the 〈Fp〉 at 3.0 Hz (Fig. S2, ESI†). We chose the lower bound of f = 1.5 Hz due to hardware limitations, as the motor would stall at lower speeds, and the upper bound of f = 6.0 Hz was near the upper limit for the motor speed. The chosen frequencies (1.5, 3.0, and 6.0 Hz) correspond to Sp values within the Sp range of negative propulsion in previous studies.^14,15

2.2 Data acquisition and processing

During oscillation, the time-varying propulsion force Fp was measured using a load cell (ANYLOAD 108AA-100g, Tacuna Systems; load cell specifications shown in the ESI†) attached to the top of the actuation assembly. The frequency f was measured with an encoder on the actuation motor. The load cell and encoder were powered by a calibrated power supply (2231A-30-3 CAL DU, Keithley), and measurements were acquired using a data acquisition system (USB-6353 DAQ, NI) and LabVIEW. The experimental data were post-processed (MATLAB, MathWorks) to calculate Fp and f for each oscillation. During postprocessing, the steady-state 〈Fp〉 and 〈f〉 were calculated using the respective values between oscillations 40 and 50 (Fig. S3, ESI†). To compensate for the nonzero forces from the actuation assembly with no flagellum attached, the Fp data were corrected using a second-order polynomial fit to the no-flagellum data (Fig. S4 and S5, ESI†). A second-order fit was chosen, as it was the lowest-order fit that best approximated the data (linear fit R = 0.9925, second-order fit R = 0.997). A camera (EOS R6, Canon) was mounted above the experiment to capture flagellum deformation during experiments at 120 fps.

2.3 Flagella fabrication

The flagella were fabricated by SLA 3D printing (Form3 and Form3+, FormLabs) with clear resin (FormLabs). After printing, the parts were washed (Form Wash, FormLabs) in isopropyl alcohol for 20 min and post-cured for 60 min at 60 °C (Form Cure, FormLabs) following procedures in the material datasheet, which reports the material's Young's modulus as E = 2.80 GPa. The flagella material was chosen to target the desired range of Sp. While the modulus is relatively high compared to many elastomers, the flagella remain flexible during the motion as the viscous forces dominate when Sp > 1.

2.4 Simulations

Three-dimensional numerical simulations were used to solve for the zero-Reynolds-number flow field and the fluid-structure interaction between the deformable solid body (i.e., flagellum) and the surrounding fluid flow. The simulations were performed using COMSOL Multiphysics 6.2. The incompressible, steady Stokes equations were solved using the finite-element method in COMSOL. In the simulation, the properties of the flagella and fluid remain consistent with the experimental setup, except that the flagella were positioned centrally within a fluid volume of 0.5 m length, 0.25 m depth, and 0.25 m width, with the wall far away to eliminate any wall effects. The computational meshes were generated in COMSOL with a physics-based fine mesh setting. Sample simulation domains illustrating the mesh design (Fig. S6, ESI†) show a close-up of the flagella with surrounding fluid. We locally refined the mesh to ensure we captured the complete physics near the flagella.

In the simulation setup, we imposed no-slip boundary conditions on the walls. We implemented a fluid-structure interaction Multiphysics node on the flagellum body to provide coupling on a boundary between a fluid and solid structure. The initial condition is stationary, and then we imposed a sine wave on the clamped end of the flagellum to simulate the experimental setup with an amplitude of b = βL. Simulations were performed for a range of frequency parameters, where f = 1.5, 3, and 6 Hz for θ₀ = 0°, 30°, 60°, 90°, 120°, 150°, and 180°. The 〈Fp〉 were calculated by taking the average of a spline fit to the x-component of the total traction on the flagellum exterior boundaries.

3. Results and discussion

3.1 Curvature-dependent propulsion

To investigate the effect of uniform intrinsic curvature on propulsion, we evaluate the propulsive force for designs with θ₀ between 0° and 180° at 〈f〉 ≈ 1.5 Hz, 3.0 Hz, and 6.0 Hz, which correspond to Sp = 1.5, 1.8, and 2.1, respectively (Fig. 2). The propulsive force is normalized by 〈Fp〉 at θ₀ = 0° to enable comparison across different 〈f〉. Based on numerical results in previous studies,^14,15 we hypothesized that the intrinsic curvature would change the magnitude and direction of the propulsive force.

Fig. 2 Curvature-dependent propulsion. (A) The propulsive force as a function of θ₀ and 〈f〉 for flagella with θ₀ between 0° and 180°, where is normalized by 〈Fp〉 at θ₀ = 0°. All designs have the same dimensions (L = 22 mm, h = 5 mm, w = 0.5 mm) and were actuated at three frequencies (〈f〉 = 1.52 ± 0.03, 3.03 ± 0.01, and 6.00 ± 0.03 Hz corresponding to Sp = 1.5, 1.8, and 2.1, respectively; error represents standard deviation across all experimental trials at each frequency) with β = 0.25. Experimental (solid) and simulation (open) data were acquired at each 〈f〉 and θ₀, where experimental error bars represent the standard deviation across 20 oscillations at steady state (10 oscillations each for two experiments at each frequency). (B) Illustrations show a top and three-dimensional view of each flagellum.

The experimental and simulation data in Fig. 2(A) demonstrate that the propulsion of the intrinsically curved flagella is curvature-dependent. To systematically discuss the results and compare the results with prior work, we will first discuss the general trends in the data, then focus on the transitions between positive and negative propulsion, and finally discuss the minimum .

The results in Fig. 2(A) show general agreement between the experimental and simulation results, where increasing θ₀ tends to decrease , with the highest rate of change between approximately θ₀ = 30° and 90°. The general agreement of the simulation and experimental results demonstrates that the macroscale experimental setup was capable of capturing some of the curvature-dependent propulsion characteristics of the flagella with uniform intrinsic curvature in the stress-free state. The results also show differences between the experiments and simulations, including in the regions of negative 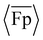. The differences between the experiments and simulations can be partially attributed to imperfections in the experimental setup (e.g., friction, clearance between parts, motor vibration) that lead to non-ideal actuation. The differences between the results are also influenced by differences in the geometrical setup (Fig. S7, ESI†).

Both the experimental and simulation results show that the transitions from positive to negative between θ₀ = 60° and 90°. Specifically, the experimental data transition between positive and negative at 〈f〉 ≈ 1.5 Hz (Sp = 1.5), while the simulation data transition at f = 1.5 Hz (Sp = 1.5) and f = 3.0 Hz (Sp = 1.8). Additional simulation results show that the transition between positive and negative propulsion occurs near θ₀ = 80° at 1.5 Hz and near θ₀ = 85° at 3.0 Hz (Fig. S8, ESI†). In comparison, Liu et al. reported negative propulsion when Sp < ∼3 for a flagellum with a cosine profile of one quarter wave under transverse oscillation, which qualitatively appears like a uniform intrinsic curvature profile with higher θ₀.¹⁴ The transition between positive and negative propulsion near θ₀ = 90° can be understood by using a reduced-order model in previous work¹⁴ that consisted of two rigid rods of equal length connected by a spring, with the second rod at an offset angle ϕ_I when the spring was undeflected. The reduced-order model was shown to predict negative propulsion when ϕ_I > 45°. In comparison, by modelling the present flagellum with uniform intrinsic curvature as a straight rod connecting the flagellum endpoints, the model would predict negative propulsion when θ₀ > 90° (θ₀ = 90° corresponds to ϕ_I = 45°; details in ESI†), which is relatively close to the transition in the experimental and simulation results between θ₀ = 60° and 90°. We anticipate that the transition point in the present results is lower than the θ₀ = 90° prediction, as the curved flagellum will exhibit more decrease in θ (i.e., straightening) than increase in θ due to the increased length perpendicular to the transverse oscillation when traveling in the positive y-direction.

The experimental and simulation results in Fig. 2(A) show that the minimum occurs at approximately θ₀ ≈ 120°. In comparison, Liu et al. indicated that increasing curvature caused a reversal in the total propulsive force direction with a local minimum 〈Fp〉 at κ_c ≈ 2.62, which corresponds to θ₀ = 150° (the intrinsic curvature κ_c = θ₀).¹⁵ The 30° difference in the local minimums of the previous report (which utilized angular oscillation at Sp = 2) and the present results (which utilized transverse oscillation at Sp = 1.5, 1.8, and 2.1) suggests that similar phenomena may influence the directionality of propulsion for both angular and transverse oscillation. One possible explanation for the 30° difference could be the differences in the force distribution across the flagellum for transverse and angular oscillation, as angular oscillation will have a higher velocity and force near the end of the flagellum due to the rotational motion.

The results in Fig. 2(A) suggest that the propulsion of future intrinsically curved flagella could be modulated on-demand by changing θ₀. For example, both the experimental and simulation results demonstrate that changing θ₀ between approximately 60° and 120° would cause a flagellum to transition between positive and negative 〈Fp〉 at 1.5 Hz (for more data showing the experimental results with negative Fp, see Fig. S9 and S10D, ESI†). Due to the constant curvature of a beam in pure bending,²⁹ the uniform intrinsic curvature of the flagella enables predictable curvature changes post-fabrication by inducing stress across the flagella's width. Building on this concept, future work could enable propulsion modulation by modulating the flagellum curvature with single-material constructs such as light-responsive polymers,¹⁶ or multi-layer constructs such as bimetallic strips³⁰ and anisotropic 3D printed materials.³¹

3.2 Sp-dependent propulsion

To investigate the effect of Sp on the propulsion of flagella with uniform intrinsic curvature, we performed experiments and simulations at 1.5, 3.0, and 6.0 Hz. The chosen frequencies correspond to Sp = 1.5, 1.8, and 2.1, respectively, which fall within the range of negative propulsion in previous studies. For instance, Liu et al. demonstrated negative propulsion below approximately Sp = 3 for a flagellum with a cosine profile of one quarter wave.¹⁴ In the same work, the authors predicted Sp-dependent negative propulsion below approximately Sp = 1.8 using a two-spring model.¹⁴ And, in a separate work, Liu et al. investigated negative propulsion at Sp = 2 using flagella with constant curvature profiles and circular cross-sections actuated by angular oscillation.¹⁵

The results in Fig. 2(A) and Fig. S11 (ESI†) demonstrate that the propulsion depends on Sp, where increasing Sp tends to increase . Specifically, the simulation data show that increasing Sp increases for each design across the studied Sp range, except for the flagellum with θ₀ = 180° (where appears relatively constant across the studied Sp range). The trend in the experimental results is less clear due to the relatively large error in the data. The simulation results agree with previous studies, which report that Sp tends to increase propulsion between Sp = 1.5 and 2.1.^14,15 We also note that a two-spring analytical model in previous work suggests that increasing Sp will ultimately cause the negative Fp to increase and become positive.¹⁴

The results in Fig. 2(A) and Fig. S11 (ESI†) suggest that the propulsion and the time-varying θ can be modulated by changing the oscillation frequency and the flagella's elastic modulus. Specifically, increasing f will increase Sp and thus tend to increase , while increasing E will decrease Sp and thus tend to decrease (as the flexural rigidity A = EI, where E is the elastic modulus and I is the area moment of inertia). As Sp is the ratio of viscous to elastic forces, increasing Sp will also increase the variation in θ during the oscillation. This implies that increasing f will increase Sp and increase the variation in θ during the oscillation, while increasing E will decrease the variation in θ during the oscillation.

3.3 Time-varying propulsion

To further investigate the negative propulsion, we examine the time-varying Fp across a representative oscillation from simulations at 1.5 Hz (Sp = 1.5; Fig. 3). Here, we choose to focus on data collected at 1.5 Hz, as this f resulted in negative propulsion with θ₀ = 120°. We hypothesized that the negative 〈Fp〉 would be due to increased effectiveness in the negative stroke of the oscillation. A comparison between the data in Fig. 3(A), however, shows that the negative stroke of the flagellum with θ₀ = 60° results in a lower minimum force (Fp_min ≈ −55 mN) than the flagellum with θ₀ = 120° (Fp_min ≈ −43 mN). This finding is surprising considering that the 〈Fp〉 for the flagellum with θ₀ = 60° is positive at 1.5 Hz (simulation: 3.53 mN, experiment: 2.01 ± 0.17 mN), while the 〈Fp〉 for the flagellum with θ₀ = 120° is negative at 1.5 Hz (simulation: −1.43 mN, experiment: −0.38 ± 0.22 mN). By comparing Fp across the entire oscillation, we see that the flagellum with θ₀ = 120° has a negative 〈Fp〉 primarily due to a decreased magnitude in the positive stroke, rather than from an increased magnitude in the negative stroke as hypothesized. In other words, these results suggest that negative propulsion may be more easily achieved by decreasing the effectiveness of the positive stroke during the oscillation of flagella that exhibit both positive and negative propulsion during the oscillation.

Fig. 3 Time-varying Fp from simulation data for flagella with θ₀ = 60° and 120° oscillating at 1.5 Hz (Sp = 1.5). (A) Time-varying Fp over approximately one oscillation. (B) Simulation images at the peak and trough of the oscillation, with snapshot times indicated. In the images, the thick black lines represent the flagella profiles, the contours represent the horizontal velocity of the fluid (i.e., parallel to the direction in which Fp is measured), and the black arrows show the streamlines. Text on the images also indicates the instantaneous central angle θ of the flagella.

3.4 Time-varying curvature

The simulation images in Fig. 3(B) and our observations during the experiments indicated that the flagella curvature varied during the oscillation. Changes in curvature during oscillation were anticipated, as the propulsion of elastic artificial flagella relies on interactions between the flagella's elasticity and the surrounding fluid. To quantify the time-varying curvature, we measured the instantaneous flagellum central angle (θ) in the macroscale experiments using image tracking on the experimental videos (Fig. 4). Here, we choose to focus on data collected at 1.5 Hz, as this f resulted in negative propulsion with θ₀ = 120°, and has the clearest images due to the lower translational velocity.

Fig. 4 Experimental data demonstrating the time-varying θ at 1.5 Hz (Sp = 1.5). (A) Time-varying θ across four representative oscillations at steady state for one flagellum at each θ₀. The θ was measured using image tracking on each frame in the experimental videos. (B) Experimental images at approximately 0%, 25%, 50%, 75%, and 100% of an oscillation for flagella with θ₀ = 120° (top row), 90° (middle row), and 60° (bottom row). To enable comparison between images, a red dashed line is overlaid on each image that shows the instantaneous profile at 0% of the oscillation.

The results in Fig. 4 include three notable characteristics: the θ varies periodically over time in a roughly sinusoidal manner, the average θ is approximately equal to θ₀ (i.e., [small theta, Greek, macron] ≈ θ₀), and the amplitude of θ decreases with increasing θ₀. First, the sinusoidal variation of θ was anticipated and can be attributed to the transverse oscillation of the clamped end of the flagella. Second, the observation of [small theta, Greek, macron] ≈ θ₀ was not unexpected, as a slender elastic body will intuitively bend in the direction opposite to the driven direction when in a viscous fluid. We suspect that slight deviations from [small theta, Greek, macron] = θ₀ (e.g., the higher [small theta, Greek, macron] for the flagellum designed with θ₀ = 90°) can be attributed to slight imperfections in the fabrication of the experimental flagella. Third, we attribute the decreasing amplitude of the time-varying θ with increasing θ₀ to a decreased deflection of curved cantilever beams under distributed loads and to changes in the fluid forces along the length of the flagella.

To compare the experimental results with simulations, we extract the profiles from the simulation and overlay the profiles onto the experimental images (Fig. S12, ESI†). A qualitative visual comparison between the experimental images and simulation profiles shows that the flagella deformations in the simulations agree closely with the flagella deformations in the experiments for flagella with θ₀ = 60° and 120°. Notably, the comparison shows that the experimental flagellum with θ₀ = 90° has more curvature (i.e., a higher θ) than in the simulation, which aligns with the data shown in Fig. 4(A), and suggests that the experimental flagellum with θ₀ = 90° could have more curvature than the design due to imperfections in the fabrication.

The results in Fig. 4 and Fig. S12 (ESI†) suggest that the time-varying θ likely influences 〈Fp〉 by changing the relative magnitudes of the normal and tangential components of propulsion in the x-direction. For flagella with uniform intrinsic curvature (θ₀ > 0), we suspect that the periodic variation in θ affects 〈Fp〉 by causing slight rotation of the drag-induced force vectors depending on the actuation direction. When the flagellum is actuated in the positive y-direction, θ decreases, which would cause the force vectors to rotate in the positive z-direction, causing a decrease in the magnitude of Fp in the x-direction (as ξ_⊥ > ξ_‖, where ξ_⊥ and ξ_‖ are the resistive force coefficients^5,32 in the perpendicular and parallel directions, respectively). On the other hand, when the flagellum is moving in the negative y-direction, θ increases, which would cause the force vectors to rotate in the negative z-direction, causing an increase in the magnitude of Fp. Future studies could investigate this hypothesis by building upon existing reduced-order models¹⁴ to account for the observed periodic variation in θ for flagella with uniform intrinsic curvature.

4. Conclusion

In this work, we studied the low Re (Re < 0.1) propulsion of elastic artificial flagella with uniform intrinsic curvature. First, we used macroscale experiments and three-dimensional numerical simulations to demonstrate that the time-averaged propulsion 〈Fp〉 is curvature dependent, with a transition between positive and negative propulsion when the central angle θ₀ is between 60° and 90° at 〈f〉 ≈ 1.5 Hz. Next, we demonstrated that Fp also depends on Sp. We then used simulation data of the time-varying Fp to observe that negative 〈Fp〉 at θ₀ = 120° is primarily due to a decrease in the effectiveness of the positive portion of the oscillation. Lastly, we investigated the time-varying curvature, which was shown to vary sinusoidally with [small theta, Greek, macron] ≈ θ₀.

We envision that future studies could leverage the curvature-dependent and Sp-dependent propulsion of intrinsically curved flagella shown in this work to achieve a variety of objectives, such as enhancing propulsion efficiency. These future developments could include methods to formally optimize designs for single or multiple objectives by incorporating FE simulations into numerical optimization algorithms.

The findings presented in this work suggest that flagella with uniform intrinsic curvature could achieve propulsion modulation, including bidirectional propulsion, by on-demand curvature modulation during active oscillation. Building on this concept, we envision that propulsion could be modulated in response to local environmental factors such as salinity, pH, temperature, and light, even without the need for external feedback or changes in externally controlled parameters (e.g., oscillation direction or frequency). For example, the stimuli-responsive curvature modulation could be achieved using a multi-layered construct of responsive materials with differing expansion coefficients, similar to a bimetallic strip. Autonomous propulsion modulation in response to environmental conditions is desirable to reduce the complexity of low Re flow control devices and artificial microscale swimmers. Moreover, such behaviour, which loosely resembles the biological locomotion of Chlamydomonas cells that have adapted to swim toward light,⁷ could be particularly advantageous where sensing and localization are challenging due to size or access constraints (e.g., within the human body).

This work considers a flagellum clamped at its driven end, consistent with prior work.¹⁴ The clamped end could be replicated in practice by using an actuation method that applies a counteracting torque at the driven end (e.g., using a uniform magnetic field) to maintain the driven end perpendicular to the transverse motion. Future work could extend the present results by investigating the propulsive force and motion of an unconstrained swimmer that more closely resembles biological organism locomotion^23,24 by accounting for the differences in the boundary conditions (e.g., force and torque-free at every instant). We suspect that an unconstrained swimmer would exhibit in-plane rotation due to the geometric asymmetry. One potential method to reduce this rotation could be to mirror the geometry across a plane perpendicular to the actuation direction.

Author contributions

Y. L. K., O. S. P., and T. E. G. conceived and planned the research. T. E. G., L. F. C., and S. L. performed experiments and collected data. J. T., S. L., E. D., and G. D. performed simulations and collected data. All authors analysed the data. T. E. G., J. T., and Y. L. K. prepared the manuscript with input from all authors.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

Y. L. K. is an inventor on multiple active patents describing 3D printing technologies, including active electronic materials and devices, and multifunctional hybrid devices and structures. Y. L. K. is also an inventor of gastric-resident systems, including gastric-resident electronics. All other authors declare no conflict of interest.

Acknowledgements

Y. L. K. acknowledges the support from the National Institutes of Health (NIH) NIBIB Trailblazer Award (grant no. R21-EB029563); NIH NIBIB R01 Award (grant no. R01-EB032959); Office of Naval Research Young Investigator Program Award (ONR YIP, N00014-23-1-2391), 3M Non-Tenured Faculty Award; CDMRP Discovery Award (HT9425-23-1-0041). O. S. P. acknowledges partial support from NSF under grant no. CBET-2323046 and CBET-2419945. Y. L. K. and O. S. P. acknowledge the National Science Foundation (NSF) under the Emerging Frontiers in Research and Innovation (EFRI) Program (grant no. EFRI 1830958).

References

1. E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601.
2. E. M. Purcell, Am. J. Phys., 1977, 45, 3–11.
3. G. I. Taylor, Proc. R. Soc. London, Ser. A, 1951, 209, 447–461.
4. E. Lauga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 041916.
5. J. Gray and G. J. Hancock, J. Exp. Biol., 1955, 32, 802–814.
6. C. H. Wiggins and R. E. Goldstein, Phys. Rev. Lett., 1997, 80, 3879–3882.
7. E. F. Smith, Mol. Biol. Cell, 2002, 13, 3303–3313.
8. I. H. Riedel-Kruse, A. Hilfinger, J. Howard and F. Jülicher, HFSP J., 2007, 1, 192–208.
9. I. S. M. Khalil, H. C. Dijkslag, L. Abelmann and S. Misra, Appl. Phys. Lett., 2014, 104, 223701.
10. Y. Xiao, J. Zhang, X. Zhao, B. Fang, L. Ma and N. Hao, Sens. Actuators, A, 2023, 361, 114592.
11. Z. Peng, G. J. Elfring and O. S. Pak, Soft Matter, 2017, 13, 2339–2347.
12. T. S. Yu, E. Lauga and A. E. Hosoi, Phys. Fluids, 2006, 18, 091701.
13. T. S. Singh, P. Singh and R. D. S. Yadava, Soft Matter, 2018, 14, 7748–7758.
14. Z. Liu, F. Qin and L. Zhu, Phys. Rev. Fluids, 2020, 5, 124101.
15. Z. Liu, F. Qin, L. Zhu, R. Yang and X. Luo, Phys. Fluids, 2020, 32, 041902.
16. S. Namdeo, S. N. Khaderi and P. R. Onck, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 043013.
17. S. Namdeo, S. N. Khaderi, J. M. J. den Toonder and P. R. Onck, Biomicrofluidics, 2011, 5, 034108.
18. S. Sudo, S. Segawa and T. Honda, J. Intell. Mater. Syst. Struct., 2006, 17, 729–736.
19. I. S. M. Khalil, A. F. Tabak, Y. Hamed, M. Tawakol, A. Klingner, N. E. Gohary, B. Mizaikoff and M. Sitti, IEEE Robot. Autom. Lett., 2018, 3, 1703–1710.
20. A. A. Evans and E. Lauga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041915.
21. V. Magdanz, I. S. M. Khalil, J. Simmchen, G. P. Furtado, S. Mohanty, J. Gebauer, H. Xu, A. Klingner, A. Aziz, M. Medina-Sánchez, O. G. Schmidt and S. Misra, Sci. Adv., 2020, 6, eaba5855.
22. I. R. Gibbons, J. Cell Biol., 1981, 91, 107s–124s.
23. C. Li, B. Chakrabarti, P. Castilla, A. Mahajan and D. Saintillan, Phys. Rev. Fluids, 2023, 8, 113102.
24. K. Y. Wan and R. E. Goldstein, Phys. Rev. Lett., 2018, 121, 058103.
25. R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862–865.
26. B. J. Williams, S. V. Anand, J. Rajagopalan and M. T. A. Saif, Nat. Commun., 2014, 5, 3081.
27. S. Mohanty, Q. Jin, G. P. Furtado, A. Ghosh, G. Pahapale, I. S. M. Khalil, D. H. Gracias and S. Misra, Adv. Intell. Syst., 2020, 2, 2000064.
28. A. Gürbüz, K. Qin, J. J. Abbott and O. S. Pak, Soft Matter, 2023, 19, 7100–7108.
29. O. A. Bauchau and J. I. Craig, in Structural analysis. Solid mechanics and its applications, ed. O. A. Bauchau and J. I. Craig, Springer, Dordrecht, 2009, vol. 163, pp. 173–221.
30. S. Timoshenko, J. Opt. Soc. Am., 1925, 233–255.
31. A. S. Gladman, E. A. Matsumoto, R. G. Nuzzo, L. Mahadevan and J. A. Lewis, Nat. Mater., 2016, 15, 413–418.
32. O. S. Pak and E. Lauga, in Fluid-Structure Interactions in Low-Reynolds-Number Flows, ed. C. Duprat and H. Stone, 2015, pp. 100–167.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01548g

‡ T. E. G. and L. F. C. contributed equally.

---