Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solvent-induced ion clusters generate long-ranged double-layer forces at high ionic strengths†
David
Ribar
 a,
Clifford E.
Woodward
b and
Jan
Forsman
a,
Clifford E.
Woodward
b and
Jan
Forsman
 *a
*a
aComputational Chemistry, Lund University, P.O. Box 124, S-221 00 Lund, Sweden. E-mail: jan.forsman@compchem.lu.se
bSchool of Physical, Environmental and Mathematical Sciences University College, University of New South Wales, ADFA Canberra ACT 2600, Australia
First published on 13th June 2025
Abstract
Recent experimental results by the surface force apparatus (SFA) have identified a dramatic deviation from previously established theories of simple electrolytes. This deviation, referred to as anomalous underscreening, suggests that the range of electrostatic interactions increase upon a further addition of salt, beyond some threshold concentration (usually about 1 M). In this theoretical work, we explore an extension of the restricted primitive model (RPM) wherein a short-ranged pair potential of mean force (sPMF) is added to the usual Coulombic interactions so as to mimic changes of the hydration as two ions approach one another. The strength of this potential is adjusted so that the modified RPM saturates at a realistic concentration level (within a range 4–7 M, typical to aqueous 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts). We utilise grand canonical simulations to establish surface forces predicted by the model and compare them directly with SFA data. We explore different sPMF models, which in all cases display significant clustering at concentrations above about 1 M. In these models, we find significant double-layer repulsion at separations that significantly exceed those expected from standard RPM predictions. We do not, however, observe an increase of the screening length with salt concentration, but rather that this screening length seemingly saturates at a (rather high) value. The simulated long-ranged interactions are shown to correlate with ion cluster formation, implicating the important role of accompanying cluster–cluster interactions. In particular, steric interactions between clusters (manifested in density–density correlations) are quite relevant in these systems.
1 salts). We utilise grand canonical simulations to establish surface forces predicted by the model and compare them directly with SFA data. We explore different sPMF models, which in all cases display significant clustering at concentrations above about 1 M. In these models, we find significant double-layer repulsion at separations that significantly exceed those expected from standard RPM predictions. We do not, however, observe an increase of the screening length with salt concentration, but rather that this screening length seemingly saturates at a (rather high) value. The simulated long-ranged interactions are shown to correlate with ion cluster formation, implicating the important role of accompanying cluster–cluster interactions. In particular, steric interactions between clusters (manifested in density–density correlations) are quite relevant in these systems.
1 Introduction
The theoretical study of interactions between large charged particles is important in almost all areas of colloid science.1–3 For some time there had been a general consensus that the behaviour of charged particles in aqueous solutions of monovalent (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) electrolytes could be described by so-called primitive models (PM), at least qualitatively. In these models the aqueous solvent is implicitly treated, only asserting itself via a uniform relative dielectric constant, εr. The ionic species, on the other hand, are explicitly accounted for as charged hard spheres. In a mean-field treatment that ignores ion–ion correlations, this description can be even further simplified by neglecting the hard core interactions between the background salt ions. Meanwhile, colloidal particles can be treated as charged surfaces. Assuming additive van der Waals forces (of quantum origin) between the surfaces results in the famous DLVO theory,4,5 which has proven very useful for the study of the stability of colloidal suspensions.
1) electrolytes could be described by so-called primitive models (PM), at least qualitatively. In these models the aqueous solvent is implicitly treated, only asserting itself via a uniform relative dielectric constant, εr. The ionic species, on the other hand, are explicitly accounted for as charged hard spheres. In a mean-field treatment that ignores ion–ion correlations, this description can be even further simplified by neglecting the hard core interactions between the background salt ions. Meanwhile, colloidal particles can be treated as charged surfaces. Assuming additive van der Waals forces (of quantum origin) between the surfaces results in the famous DLVO theory,4,5 which has proven very useful for the study of the stability of colloidal suspensions.
One generally finds that mean-field (MF) treatments of the PM predict that, at low electrolyte concentrations, the dominant non-quantum interaction between charged surfaces is electrostatic in origin and is exponential in form, with a range largely dictated by the Debye screening length, λD. This interaction arises from the direct forces between the charged surfaces that are screened by a counter-charge density sourced from the background salt. The Debye length measures the typical spatial length over which non-electroneutral fluctuations occur in the electrolyte solution. Structural variations in the overall density (rather than charge density) are also induced by the surfaces, but the forces that arise from this effect are usually negligible at large surface separations.6,7 The Debye length decreases with electrolyte concentration, c, according to,  . Corrections to MF theories require the inclusion of direct (short-ranged) ion correlations, which lead to minor modifications of the Debye length. For example, taking into account hard core interactions leads to an excluded volume corrected ‘effective’ value λeff, which is smaller than λD.6,8 The qualitative correctness of MF theories using the PM, and the role played by the Debye length, is reasonably well-supported at low electrolyte concentrations by experiments, as well as simulations.1
. Corrections to MF theories require the inclusion of direct (short-ranged) ion correlations, which lead to minor modifications of the Debye length. For example, taking into account hard core interactions leads to an excluded volume corrected ‘effective’ value λeff, which is smaller than λD.6,8 The qualitative correctness of MF theories using the PM, and the role played by the Debye length, is reasonably well-supported at low electrolyte concentrations by experiments, as well as simulations.1
MF theories break down at high concentration where the Debye length becomes small. In this regime, ion correlation corrections must be included to provide even a qualitative description of the PM. Such corrections predict that the surface interactions of electrostatic origin will switch from exponential to oscillatory, as the Debye length approaches the diameter scale of the salt particles. This is the so-called Kirkwood transition.9 This transition has been confirmed by simulations of the PM and is due to the monotonically decreasing (essentially exponential) ionic double-layer becoming unstable to the formation of charged layers by the electrolyte.10 In this regime, the non-electrostatic structural forces may compete with the electrostatic interactions for relative importance as both are oscillatory and of comparable range.6,7 However, recent experimental measurements using the surface force apparatus (SFA) have challenged this result.11–14 That is, instead of transitioning to an oscillatory function, the asymptotic interaction between charged surfaces remains exponential, but with a screening length that suddenly begins increasing (rather than decreasing) with concentration, eventually becoming significantly larger than the nominal Debye length. Surprisingly, this occurs even in aqueous 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt solutions, where it was generally believed that the PM should be reasonably reliable. This phenomenon has been described as anomalous underscreening. One consequence of this is that suspensions of like-charged colloids may remain stable at high ionic strength due to significant repulsive interactions at colloidal separations where the attractive van der Waals interactions remain small. This is counter to the predictions of traditional DLVO theory. Despite considerable theoretical efforts,15–21 there is at present no consensus as to the physical origin of interactions at such large inter-particle distances. One can find independent (non-SFA) experimental evidence for anomalous underscreening in literature.22–25 It should also be noted that there is at least one recent experimental work that does not support this phenomenon.26 Kumar et al. used an atomic force microscope to measure interactions between charged surfaces (mainly silica-silica) in aqueous salt solutions. They did not find any sign of anomalous underscreening, i.e. at high ionic strengths, the measured surface forces were quite short-ranged.
1 salt solutions, where it was generally believed that the PM should be reasonably reliable. This phenomenon has been described as anomalous underscreening. One consequence of this is that suspensions of like-charged colloids may remain stable at high ionic strength due to significant repulsive interactions at colloidal separations where the attractive van der Waals interactions remain small. This is counter to the predictions of traditional DLVO theory. Despite considerable theoretical efforts,15–21 there is at present no consensus as to the physical origin of interactions at such large inter-particle distances. One can find independent (non-SFA) experimental evidence for anomalous underscreening in literature.22–25 It should also be noted that there is at least one recent experimental work that does not support this phenomenon.26 Kumar et al. used an atomic force microscope to measure interactions between charged surfaces (mainly silica-silica) in aqueous salt solutions. They did not find any sign of anomalous underscreening, i.e. at high ionic strengths, the measured surface forces were quite short-ranged.
The formation of ionic clusters of low overall charge has been proposed as a possible mechanism for the putative increase in the Debye length observed in the underscreening concentration regime. Such a model implicitly assumes that the electrostatic interactions between the surfaces remains dominant and the formation of clusters will effectively reduce the concentration of screening charges.12,27 For this to be a feasible explanation, clustering needs to be sufficient to reduce the free charge concentration by a factor of up to ∼104. Recent simulations of the restricted primitive model (RPM), wherein ions have equal sizes, have investigated the degree of clustering that occurs in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte.21 That work also took into account dielectric saturation by allowing the relative dielectric constant of the solvent, εr, to become concentration-dependent. In particular εr decreased with c to account for the diminished dielectric response of rotationally constrained water molecules in the ionic hydration shells.28–34 It was seen that, while increased clustering was evident at high concentrations, and lower εr, it was not of a sufficient magnitude to explain anomalous underscreening.21 That is, the RPM (even accounting for dielectric saturation) would predict that forces between like-charged surfaces would be essentially completely screened by salt ions at the large distances where experiments still find a significant repulsion.
1 electrolyte.21 That work also took into account dielectric saturation by allowing the relative dielectric constant of the solvent, εr, to become concentration-dependent. In particular εr decreased with c to account for the diminished dielectric response of rotationally constrained water molecules in the ionic hydration shells.28–34 It was seen that, while increased clustering was evident at high concentrations, and lower εr, it was not of a sufficient magnitude to explain anomalous underscreening.21 That is, the RPM (even accounting for dielectric saturation) would predict that forces between like-charged surfaces would be essentially completely screened by salt ions at the large distances where experiments still find a significant repulsion.
This failure of the RPM led to a recent work35 in which we proposed a localised modification of the RPM by addition of an additional short-ranged potential of mean force (sPMF) between ions. The inclusion of the short-ranged potential induced significant ion clustering (as confirmed via simulations). In the present article, we study the consequences of the formed clusters on the interactions between two charged surfaces. These interactions are directly compared with experimental SFA data, and it is demonstrated that cluster formation indeed leads to remarkably long-ranged surface forces. We provide analyses of the separate contributions to the correlations in these systems in order to uncover the dominant physical mechanism leading to these long-ranged forces.
2 Model and methods
A weakness of the RPM is that it does not (with an aqueous solvent) saturate at reasonable concentrations. In this work, we explore the hypothesis that what the RPM is lacking is a short-ranged potential of mean force (sPMF), adjusted to induce solution instability at a concentration that is close to typical saturation values (4–7 M) for simple salts. While we do not have a detailed knowledge of this potential of mean force, it is plausibly a result of water restructuring as the ionic environment becomes crowded. In previous work,35 we took an approach whereby we assigned the sPMF a range of about one water diameter (3 Å). Since our simulations are based on Coulomb interactions, a convenient option was to increase the strength of the Coulomb interaction in this separation range. This is achieved by varying the dielectric constant using linear extrapolation from the bulk down to a smaller contact value. Of course, this choice of additional short-ranged interaction is not unique and in this paper we will consider different functional forms of the sPMF, including the model we used earlier.35 Due to its relatively narrow range, we will dub that model the “narrow” sPMF.2.1 The “narrow” sPMF, ϕn
As described above, the explicit form for this sPMF uses the following linear ramp function for the spatial variation of the dielectric constant, εr, within its range, | (1) |
With this choice for the dielectric factor, the sPMF between ions i and j of valency |Zi| = |Zj| = 1 (ϕijn) can be written as:
 | (2) |
For a given choice of d, we can tune εc to a value where the solution phase separates at a concentration typical of the saturation limit for an aqueous monovalent electrolyte solution (about 4–7 M, at room temperature). In practice, we chose d = 3 Å and εc = 23 where the solution is stable at 3.45 M, but will phase separate at a marginally smaller value for εc. Our rationale for choosing these values in given in ref. 35. We also consider d = 4 Å, in which case εc = 20 will give a similar stability. We will use this as the main model of investigation in this paper, including looking at the effect of salt concentration on the interaction between charged surfaces.
We will also perform a more limited study on a so-called “wide” version of an sPMF, where we will also explore other different combinations of attractions and repulsions between ionic species. The details of this interaction are given below.
2.2 The “wide” sPMF, ϕw
Here, we adopt a sPMF with the same cut-off (Δ) as ϕijn, but with a broader range over which it maintains a substantial strength. Specifically, we define it as, | (3) |
The overall qualitative difference between ϕn(r) and ϕw(r) is illustrated in Fig. 1. The total potential of mean force between ions i and j, ϕij(r) (separated a distance r) can thus be written as:
 | (4) |
2.3 Surface force simulation details
Our simulation system is comprised two parallel flat and uniformly charged surfaces, separated at a distance H, and extending infinitely along the x and y directions. We imagine these surfaces to be immersed in a salt solution. The bulk region external to the space between the surfaces is characterised by the electro-chemical potential and the bulk osmotic pressure, pb. A grand canonical simulation scheme ensured that the simulated fluid, contained between the surfaces, was in equilibrium with the bulk and that the surface charges were properly neutralised.36 The surface charge density was chosen to be σs = 1/70 ≈ −0.014336 e Å−2, which is a value typical to mica,37i.e. the surfaces used in SFA experiments. All simulations were performed at 298 K. Periodic boundary conditions were applied along the (x, y) directions, and the “charged sheet” method10 was adopted to account for long-ranged interactions. Cluster moves were implemented, leading to crucial improvements of the statistical performance. The internal (osmotic) pressure, p, acting transverse to the walls was evaluated from the average normal force across the walls, separated by the expected distance between Gibbs dividing (solid–fluid) surfaces, h ≡ H−d. Subtracting pb, we obtain the net pressure, pnet = p − pb. Integrating this pressure, and utilising the Derjaguin approximation | (5) |
The non-electrostatic ion–wall interaction was modelled by an analytic and purely repulsive wall potential. We explored two different choices, decaying as δ−4 and δ−6, respectively, where δ is the transverse distance between the ion and the wall. The first model was adopted when investigating the effect of salt concentration, using ϕn as the sPMF. One might argue that this softer choice amounts to a coarse-grained description of molecularly rough surfaces. In another part of this study, which explores the various choices for the sPMF in concentrated solutions (1.6–2 M), we chose the steeper wall, decaying as δ−6. This represents a better model for a molecularly smooth surface, such as mica. Details are provided in the ESI,† including a comparison between results obtained with either wall, for a given system. The ESI,† also contains a more thorough description of our model and simulation methods.
3 Results and discussion
Our results comprise two parts. In the first part, we evaluate how surface forces respond to salt concentration changes, using the “soft” wall (δ−4) description (see ESI†), and ϕn as the sPMF. The second part compares surface interactions at a high salt concentration, using various choices for the sPMF. In that part, we have employed the “steep” wall (δ−6) description, which arguably is a better choice for mica surfaces. On the other hand, as we discuss in the ESI,† the difference in wall softness essentially amounts to a small shift (about 3 Å) of the surface separation.3.1 Salt concentration effects, using ϕn
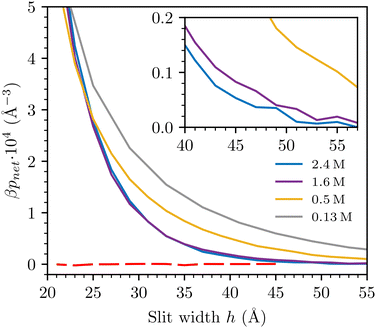
In previous work we performed simulations using the “narrow” ϕn potential as the sPMF in addition to the standard RPM interaction for bulk electrolyte solutions.35 We will denote this as the sRPM(ϕn) model The findings important to the current investigation can be summarised as follows:1. At low electrolyte concentration, charge–charge correlations displayed behaviours typical of classic MF theory, and the Debye length is the relevant length-scale.
2. At higher concentration (beyond 1 M) there was evidence of strong cluster formation, much larger than predicted by the RPM. Charge–charge correlations became short-ranged and oscillatory (the Kirkwood transition), while density–density correlations grew to become more dominant, displaying a monotonic decay, with a length-scale much longer than the Debye length.
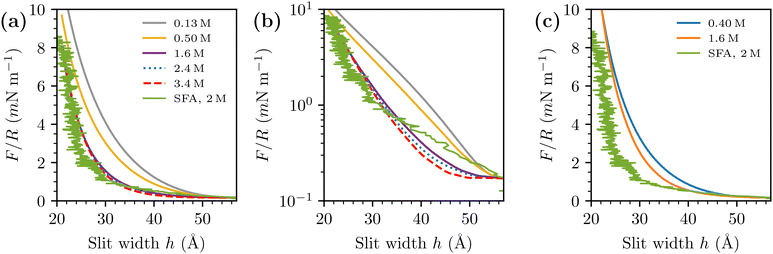 | ||
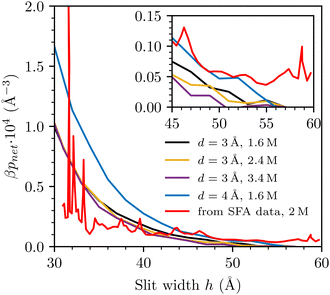
| Fig. 3 Simulated prediction of F/R, with d = 3 Å and d = 4 Å, at various salt concentrations, compared with SFA data with a 2 M NaCl(aq) solution, obtained from prof. Susan Perkin (data previously published in ref. 13). Simulated curves have been shifted to roughly match the SFA data, at the largest investigated separation. (a) d = 3 Å (linear scale). (b) d = 3 Å (log scale). (c) d = 4 Å (linear scale). | ||
For completeness, we include results obtained with a larger value for the hard-sphere diameter of the ions, d = 4 Å. Recall also that we chose εc = 20 at this diameter, as described in detail in ref. 35. Comparisons with raw SFA data are given in Fig. 3(c). We note that the difference between the interactions obtained at 0.40 M and 1.6 M is considerably smaller than we find by a similar comparison (0.50 M and 1.6 M), with d = 3 Å.
We also compare the simulated net pressures directly with a derivative of the experimentally observed free energies per unit area (taking into account an appropriate scaling factor), Fig. 4. In the latter case, we needed to smooth out the raw data by performing “running averages” prior to taking the derivative (via discrete difference). The extremely long-ranged tail found by the SFA is perhaps even more apparent in this presentation, and it appears to be an aspect of the experimental data that the sRPM(ϕn) is unable to reproduce.
In Fig. 5(b) we see how the mid plane values of the ion profiles gradually decreases towards the bulk concentration, but we note that a significant difference persists even at quite large surface separations.
We also investigated the correlations parallel the surface, focusing on the region at the mid plane. We computed lateral (2D) species resolved pair correlation functions (presented in detail in the ESI†) for low (0.13 M) and high (3.4 M) concentrations, for all slit widths under investigation. No evidence of a continuous solid phase was found in any of these systems indicating the absence of a frozen state. In order to further investigate the dominant correlations in our system, we computed the 2D charge–charge, hcc(ρ), and density–density, hnn(ρ), total correlation functions from the species resolved pair correlation functions.7 Note that the total correlation functions are related to the pair distribution functions via h(ρ) = g(ρ) − 1. For brevity, the explicit  dependence is omitted.
dependence is omitted.
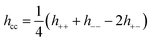 | (6) |
 | (7) |
 . The asymptotic behaviour of correlation functions, as r → ∞, is described by a Yukawa decay, or an oscillatory Yukawa decay7
. The asymptotic behaviour of correlation functions, as r → ∞, is described by a Yukawa decay, or an oscillatory Yukawa decay7 | (8) |
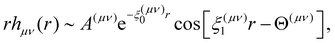 | (9) |
In order to complement the investigation of lateral correlation functions obtained at the mid plane, we present a comparison with bulk correlation functions on Fig. 7, computed with the method described in our previous work.35 We explicitly investigate three extreme cases: the smallest h = 21 Å surface separation, largest h = 57 Å, and a neutral wall h = 77 Å, by directly comparing with bulk correlation functions for a system of equal concentration. We plot all correlation functions on a linear scale on Fig. 7(a). We can observe a minimal difference between the full (h = 57 Å) and dashed (h = 77 Å neutral walls) lines, insert on Fig. 7(a). All of the correlations in the slit have amplitudes lower than the bulk. Fig. 7(b)–(d) demonstrate the similarity of the frequency correlation length 2π/ξ(cc)1 and decay correlation length 1/ξ(cc)0 between the bulk and slit systems. However, in both cases the amplitude of charge–charge correlations is smaller than the corresponding bulk value, demonstrated as a downwards shift on the y-axis. We also observe a slight phase shift between the bulk and slit system charge–charge correlations. The density–density correlations have a smaller decay correlation length for the short surface separation Fig. 7(b), and larger for the wider surface separation Fig. 7(c), when compared to the bulk values. In both cases, the amplitude is again smaller for the slit system. Fig. 7(d) demonstrates the correlation analysis for a wide surface separation with neutral walls. We can see that the difference between Fig. 7(c) and (d) is minimal, demonstrating that the charge of the surfaces has no effect on the lateral correlation decay at the mid plane at large surface separations. Importantly, the similarity of frequency and decay charge–charge correlation lengths between slit and bulk results at all surface separations (albeit with moderately large differences in amplitudes and a slight phase shift) demonstrate that the asymptotic behaviour lateral to the confining charged surfaces is dictated by bulk properties of the ionic fluid and not by the surfaces themselves. For completeness, the same analysis is also presented for the low concentration system in the ESI.† The ESI,† also contains illustrative configurational snapshots, at various separations, and bulk concentrations.
3.2 Comparison of different sPMF models at high salt concentrations
Here, we will compare results obtained with the sRPM(ϕn), and the sRPM(ϕw) models (where the latter uses the wider form of the sPMF in addition to the RPM interactions). Recall that with this latter model we have different combinations of attractions and repulsions between ionic species. To reiterate, they are denoted as, ϕw(a, r) (attractive +−, repulsive ++, −−), ϕw(a, a) (attractive +−, attractive ++, −−) and ϕw(a, 0) (attractive +−, no sPMF between ++ and −−). In all cases below, we have set d = 3 Å, and used the “steep” wall description. Bulk salt concentrations were adjusted (via the chemical potential) to lie in the regime 1.6–2 M.Net pressure curves in concentrated samples (1.6–2 M), for various choices of sPMF, are summarised in Fig. 8. A few important observations immediately emerge:
• The long-ranged pressures that are obtained with models in which the additional sPMF is attractive between unlike charges, and repulsive between like charges, is large. That is, the net pressures obtained from sRPM(ϕw(a, r)) are qualitatively similar to those of sRPM(ϕn). The sRPM(ϕw(a, r)) model generates a somewhat stronger repulsion, but the difference is small.
• The qualitative nature of the sPMF is quite important. Specifically, the sRPM(ϕw(a, a)) model only produces a short-ranged repulsive regime, outside of which we even note a weak attractive interaction. The sRPM(ϕw(a, 0)) model is an intermediate case, where the repulsion clearly extends further than with the pure RPM, but it is not as long-ranged as with ϕw(a, r) or ϕn.
• We do not observe any force oscillations in the investigated separation regime (irrespective of the chosen sPMF). SFA measurements11–13 have reported force “jumps”, indicative of such oscillations. On the other hand, such behaviours were not observed in a recent AFM26 study. It should be noted that possible oscillations due to solvent packing will be unaccounted for by our implicit solvent treatment.
It is also of interest to compare the cluster tendency displayed by some of our investigated models. On Fig. 9 we plot cluster probability distributions, Pc(Nc), for a range of different models. Here, Pc measures the probability for a cluster of size Nc. A cluster is defined such that an ion must be within a distance δc or less of at least one other ion within a cluster, in order to be a member of that cluster. We have set δc = d + 2 Å. These distributions were obtained from grand canonical slit simulations, where the chemical potential is adjusted so that the corresponding bulk solution has a concentration of about 1.8 M. The distributions are based on at least 100 different configurations, separated by 108 attempted moves to ensure statistical independence.
We note that the RPM approach does not generate large clusters, even if the (uniform) dielectric constant is set as low as 23. The sRPM:s, on the other hand, are able to produce quite large ion clusters. Interestingly enough, this is true also for the sRPM(ϕw(a, a)), even though we have seen that the corresponding surface forces are rather short-ranged. Nevertheless, the large cluster tail does not extend as far as with sRPM(ϕw(a, r)) or (in particular) sRPM(ϕn). Even so, these results imply that it is possibly not only the number of particles in each cluster that matters, but also the intrinsic structure of such clusters. This is supported by the long-ranged radial distribution tails that we observe with ϕn and ϕw(a, r), but not with ϕw(a, a) (see the ESI,† for details). In future work, we will scrutinise this further, making use of polymer classical density functional theory.
In graph (a) of Fig. 9 we also see that, as expected, very large clusters become improbable at short separations. It should be emphasised that this is not simply an effect of a diminishing number of ions within the simulation box in this regime. This is illustrated in the ESI,† where we find a very similar cluster probability distribution at short separations, but with an increased lateral (x, y) size of the simulation box.
Another interesting aspect is the average cluster charge, and how this varies with separation. We provide examples in Fig. 10. We note that the slopes of the curves, which provide the average net charge of an ion in a cluster, are similar between the models, but vary strongly with separation. At h = 21 Å, the slope is about +0.25e0, dropping to about +0.075e0 at h = 61 Å. The main reason is most likely a diminishing relative fraction of counterions, as the separation increases.
 | ||
| Fig. 10 The average net cluster charge, at two different separations, as obtained with the sRPM(ϕn), sRPM(ϕw(a, r)) and sRPM(ϕw(a, a)). | ||
4 Conclusion
In this article we have demonstrated that a modified RPM with an added short-ranged PMF, adjusted to provide the model more realistic saturation properties, produces surface forces in much better agreement with experiments than can be obtained with the RPM model itself. This is related to the increased prevalence of clusters, brought about by the added short-ranged solvent-induced potential, that we, in the initial part of this work (concentration dependence), chose to model by a locally enhanced electrostatic coupling. Density–density correlations appear to dominate at high salt concentrations. Thus, we hypothesise that the experimentally observed anomalous screening lengths originate from cluster correlations rather than simple ion correlations. One apparent failure of the sRPM(ϕn) is its inability to predict a growth in the interaction screening length with electrolyte concentration. This is possibly due to the lack of many-body contributions to the ion–ion interaction, which potentially leads to an underestimation of the effects from concentration on particle interactions. A future aim is to implement a simple many-body scheme which will provide some estimate of this effect.In the second part of this work, we established the qualitative nature of the sPMF is of crucial importance, even though its functional form is not. Our combined surface force and bulk solution cluster analyses suggest that the internal structure of the ion clusters may be as important as their average size. This will be investigated more closely in future work, employing classical polymer density functional theory.
Conflicts of interest
There are no conflicts to declare.Data availability
All generated data, as well as all codes used to generate these data, are freely available upon reasonable request.Acknowledgements
We thank professor Susan Perkin for sending us raw data from SFA measurements, as well as for fruitful discussions. Professors Sture Nordholm and Christian Holm are also acknowledged for enlightening discussions. J. F. acknowledges financial support by the Swedish Research Council, and computational resources by the Lund University computer cluster organisation, LUNARC.References
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 2nd edn, 1991 Search PubMed.
- F. A. Evans and H. Wennerström, The colloidal domain: where Physics, Chemistry, Biology and Technology meet, VCH Publishers, New York, 1994 Search PubMed.
- C. Holm, P. Kekicheff and R. Podgornik, Electrostatic Effects in Soft Matter and Biophysics, Kluwer Academic Publishers, Dordrecht, 2001 Search PubMed.
- B. V. Derjaguin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633–662 Search PubMed.
- E. J. W. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier Publishing Company Inc., Amsterdam, 1948 Search PubMed.
- P. Attard, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3604–3621 CrossRef CAS PubMed.
- R. Leote de Carvalho and R. Evans, Mol. Phys., 1994, 83, 619–654 CrossRef.
- J. Forsman, D. Ribar and C. E. Woodward, Phys. Chem. Chem. Phys., 2024, 26, 19921–19933 RSC.
- J. G. Kirkwood, Chem. Rev., 1936, 19, 275–307 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Chem. Phys., 1980, 73, 5807–5816 CrossRef CAS.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed.
- M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437 CrossRef CAS PubMed.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- G. R. Elliott, K. P. Gregory, H. Robertson, V. S. Craig, G. B. Webber, E. J. Wanless and A. J. Page, Chem. Phys. Lett., 2024, 843, 141190 CrossRef CAS.
- F. Coupette, A. A. Lee and A. Härtel, Phys. Rev. Lett., 2018, 121, 075501 CrossRef CAS PubMed.
- B. Rotenberg, O. Bernard and J.-P. Hansen, J. Phys.: Condens. Matter, 2018, 30, 054005 CrossRef PubMed.
- R. Kjellander, J. Chem. Phys., 2018, 148, 193701 CrossRef PubMed.
- S. W. Coles, C. Park, R. Nikam, M. Kanduc, J. Dzubiella and B. Rotenberg, J. Phys. Chem. B, 2020, 124, 1778–1786 CAS.
- J. Zeman, S. Kondrat and C. Holm, Chem. Commun., 2020, 56, 15635–15638 RSC.
- P. Cats, R. Evans, A. Härtel and R. van Roij, J. Chem. Phys., 2021, 154, 124504 CrossRef CAS PubMed.
- A. Härtel, M. Bültmann and F. Coupette, Phys. Rev. Lett., 2023, 130, 108202 CrossRef PubMed.
- P. Gaddam and W. Ducker, Langmuir, 2019, 35, 5719–5727 CrossRef CAS PubMed.
- H. Yuan, W. Deng, X. Zhu, G. Liu and V. S. J. Craig, Langmuir, 2022, 38, 6164–6173 CrossRef CAS PubMed.
- R. J. E. Reinertsen, S. Kewalramani, F. Jiménez-Ángeles, S. J. Weigand, M. J. Bedzyk and M. Olvera de la Cruz, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2316537121 CrossRef CAS PubMed.
- H. Robertson, G. R. Elliott, A. R. J. Nelson, A. P. Le Brun, G. B. Webber, S. W. Prescott, V. S. J. Craig, E. J. Wanless and J. D. Willott, Phys. Chem. Chem. Phys., 2023, 25, 24770–24782 RSC.
- S. Kumar, P. Cats, M. B. Alotaibi, S. C. Ayirala, A. A. Yousef, R. van Roij, I. Siretanu and F. Mugele, J. Colloid Interface Sci., 2022, 622, 819–827 CrossRef CAS PubMed.
- K. Ma, J. Forsman and C. E. Woodward, J. Chem. Phys., 2015, 142, 174704 CrossRef PubMed.
- J. B. Hasted, D. M. Ritson and C. H. Collie, J. Chem. Phys., 2004, 16, 1–21 CrossRef.
- J. de Souza, A. A. Kornyshev and M. Z. Bazant, J. Chem. Phys., 2022, 156, 244705 CrossRef CAS PubMed.
- B. Conway and S. Marshall, Aust. J. Chem., 1983, 36, 2145–2161 CrossRef CAS.
- D. J. Bonthuis, S. Gekle and R. R. Netz, Langmuir, 2012, 28, 7679–7694 CrossRef CAS PubMed.
- I. Danielewicz-Ferchmin, E. Banachowicz and A. Ferchmin, J. Mol. Liq., 2013, 187, 157–164 CrossRef CAS.
- R. M. Adar, T. Markovich, A. Levy, H. Orland and D. Andelman, J. Chem. Phys., 2018, 149, 054504 CrossRef PubMed.
- T. R. Underwood and I. C. Bourg, J. Phys. Chem. B, 2022, 126, 2688–2698 CrossRef CAS PubMed.
- D. Ribar, C. E. Woodward, S. Nordholm and J. Forsman, J. Phys. Chem. Lett., 2024, 15, 8326–8333 CrossRef CAS PubMed.
- S. Stenberg and J. Forsman, Langmuir, 2021, 37, 14360–14368 CrossRef CAS PubMed.
- A. R. Crothers, C. Li and C. Radke, Adv. Colloid Interface Sci., 2021, 288, 102335 CrossRef CAS PubMed.
- R. Evans, R. J. F. Leote de Carvalho, J. R. Henderson and D. C. Hoyle, J. Chem. Phys., 1994, 100, 591603 Search PubMed.
- L. Degreve and F. L. B. da Silva, J. Chem. Phys., 1999, 111, 5150–5156 CrossRef CAS.
- K. Komori and T. Terao, Chem. Phys. Lett., 2023, 825, 140627 CrossRef CAS.
- P. Auffinger, T. E. Cheatham and A. C. Vaiana, J. Chem. Theory Comput., 2007, 3, 1851–1859 CrossRef CAS PubMed.
- J. Tong, B. Peng, G. M. Kontogeorgis and X. Liang, J. Mol. Liq., 2023, 371, 121086 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00027k |
| This journal is © The Royal Society of Chemistry 2025 |