Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Turbulent-like flows in quasi two-dimensional dense suspensions of motile colloids†
Rui Luo a,
Alexey Snezhko
a,
Alexey Snezhko b and
Petia M. Vlahovska
b and
Petia M. Vlahovska *a
*a
aEngineering Sciences and Applied Mathematics, Northwestern University, Evanston, IL 60208, USA. E-mail: petia.vlahovska@northwestern.edu
bMaterials Science Division, Argonne National Laboratory, 9700 South Cass Avenue, Lemont, Illinois 60439, USA
First published on 2nd July 2025
Abstract
Dense bacterial suspensions exhibit turbulent-like flows at low Reynolds numbers, driven by the activity of the microswimmers. In this study, we develop a model system to examine these dynamics using motile colloids that mimic bacterial locomotion. The colloids are powered by the Quincke instability, which causes them to spontaneously roll in a random-walk pattern when exposed to a square-wave electric field. We experimentally investigate the flow dynamics in dense suspensions of these Quincke random walkers under quasi two-dimensional conditions, where the particle size is comparable to the gap between the electrodes. The results suggest a scaling regime in the energy spectrum ∼k−4 at high wavenumbers, observed consistently across activity levels and particle concentrations. We observe that velocity time correlations decay within a single period of the square-wave field, yet an anti-correlation appears between successive field applications, indicative of a dynamic structural memory of the ensemble.
1 Introduction
Swimming bacteria self-organize into macroscopic patterns such as swarms and dynamic clusters.1–7 At high concentrations, turbulent-like motion emerges characterized by erratic flows and transient vortices.8–14 Unlike the classical hydrodynamic turbulence, which is a high-Reynolds number, inertia-dominated phenomenon, bacterial turbulence occurs at very low Reynolds numbers, where inertia is negligible, and is driven by the active motion of the microswimmers.15 The energy spectrum in classical turbulence in two dimensions typically follows a power-law dependence on the wavenumber, E ∼ k−5/3, whereas for bacterial turbulence, different power laws have been reported.10,16–18Active turbulence has been observed in various living fluids such as sperm,20 microtubule-kinesin bundles (active nematics),21–23 and cell tissues.24,25 The phenomenon generated a lot of theoretical effort,10,11,26–42 to decipher how “activity engenders turbulence”.43 Recently, a universal scaling of E(k) ∼ k−4 has been predicted and validated for two-dimensional active nematics systems,44 and similar scaling has been observed in studies of bacterial turbulence transitioning from two-dimensional to three-dimensional flow, where such scaling is absent in purely two-dimensional conditions.18 However, experimental research in bacterial turbulence lags behind the theoretical advances due to the challenges to have well defined and controllable conditions e.g., particle density, speed (i.e., activity) and locomotion type, when working with living microswimmers.
Synthetic externally driven colloids offer an alternative platform for studying active turbulence.45–47 A promising model system to emulate bacterial flows is based on the Quincke rollers.48–52 Their motility is due to an electrohydrodynamic instability, which gives rise to a constant electric torque on the particles53 causing them to roll, if the particles are initially resting on the electrode. Quincke rollers exhibit a wide range of intricate collective behaviors.48,54–58 Temporal modulation of the rollers' activity through application of a square-wave electric field modifies the rollers persistence length resulting in even richer collective dynamics.19,59,60 By adjusting the durations of the pulses, τon, and their spacing, τoff, the trajectory of an isolated Quincke roller becomes a random walk, and the particle locomotion can be tuned to emulate various bacterial motility patterns.19 Populations of Quincke random walkers exhibit behaviors reminiscent of bacterial suspensions such as dynamic clustering in semi-dilute suspensions.19
Here, we employ dense suspensions of Quincke random walkers to gain insights into the turbulent-like flows of bacterial fluids. We consider suspensions confined between two parallel walls with spacing comparable to the colloid diameter, and experimentally measure spatial velocity correlations, structure functions, and kinetic energy spectra under varying concentrations of suspensions and activity, which is modulated by the applied field strength.
2 Experiment
Spherical polymethyl methacrylate (PMMA) spheres (Phosphorex) with a diameter of d = 100 μm are dispersed in a 0.15 mol L−1 AOT-hexadecane solution (conductivity σf = 2.2 × 10−8 S m). The experimental chamber consists of two 7.5 × 5 cm2 ITO-coated glass slides (Delta Technologies), separated by a ring-shaped Teflon tape with a thickness of 120 μm, see Fig. 1(a). The chamber is filled with the suspension solution. The particle motion and tracking is visualized using an inverted optical microscope (Zeiss) with 2× magnification mounted on a vibration isolation table (Kinetic Systems, Inc.). Videos were recorded at frame rates of 500 or 1000 frames per second by a high speed camera (Photron SA 1.1). The system is powered by a pre-designed pulsed electric field supplied by a high voltage amplifier (Matsusada) controlled by a function generator (Agilent Technologies 33521A). Particle tracking, flow field reconstruction and data analysis are carried out by means of particle image velocimetry (PIV) or particle tracking velocimetry (PTV) using open source Python codes (OpenPIV61 and Trackpy62) as well as custom codes (see ESI† for details). | ||
| Fig. 1 Turbulent-like flows in suspension of Quincke random walkers: (a) in a uniform direct current (DC) electric field E, free charges accumulate at the particle surface. Above the threshold for the Quincke instability, the induced electric dipole tilts and generates a net torque, causing the sphere to roll in a randomly chosen direction in the plane perpendicular to the applied field direction. (b) The rotation rate as well as the rolling speed, i.e., activity, of an individual Quincke roller increases with field strength. (c) Temporal modulation of the electric field in the form of a square-wave causes the particle to undergo a random walk19 (see ESI,† Movie S1), if τoff is much longer than the “particle memory” time τMW (the time required for complete depolarization). The mean-squared displacement (〈Δr2〉) of a single Quincke random walker is shown for E = 4.4 V mm−1, τon = 40 ms, and τoff = 20 ms, with the corresponding trajectory displayed in the inset. Scale bar: 1 mm. (d) Snapshot of the colloidal suspension (area fraction ϕ = 0.51) overlaid with the local density map (background color). Vortices (panel f) nucleate preferentially in high-density regions. (e) Particle trajectories, tracked using particle tracking velocimetry (PTV), during one period τon. (f) Vorticity computed based on the velocity field from particle imaging velocimetry (PIV). The red dashed line indicates the field of view, not a physical boundary. The experiment is conducted at E = 7.4 V μm−1, particle area fraction ϕ = 0.51. See ESI,† Movie S2. Movie S3 (ESI†) illustrates the flow for lower field strength and lower particle fraction (E = 2.8 V μm−1,ϕ = 0.27). | ||
When a constant voltage is applied across the ITO electrodes, the particles become polarized due to the accumulation of free charges at their interfaces, generating an induced electric dipole oriented antiparallel to the applied electric field. Beyond a critical field strength, the dipole loses its symmetric orientation, triggering what is known as the Quincke electrorotation63,64 and a particle rolls along the surface with a constant speed.48,65 In our system, the typical threshold voltage for the onset of electrorotation is Eq = 1.6 V μm−1 (Fig. 1(b)) and roller velocities (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) range from 4 mm s−1 to 35 mm s−1. The corresponding Reynolds number Re = ρf
) range from 4 mm s−1 to 35 mm s−1. The corresponding Reynolds number Re = ρf![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) d/2μf ranges from 0.07 to 0.6, (here ρf = 0.77 g cm−3 and μf = 4.3 × 10−3 Pa s are the fluid density and viscosity, respectively). While typical Reynolds numbers in bacterial suspensions are significantly lower, the viscous forces are still dominant in this overdamped system.
d/2μf ranges from 0.07 to 0.6, (here ρf = 0.77 g cm−3 and μf = 4.3 × 10−3 Pa s are the fluid density and viscosity, respectively). While typical Reynolds numbers in bacterial suspensions are significantly lower, the viscous forces are still dominant in this overdamped system.
When the electric field is pulsating, as shown in Fig. 1(c), the behavior of the roller changes. The roller “runs” while the field is on and stops when the field is turned off. Once the field is turned on again, the roller chooses a new random direction of rolling.19 In a dense suspension, the resulting flow is illustrated in Fig. 1(d–f). Notably the external electric field imposes that all rollers stop and turn simultaneously unlike the stochastic tumbling of individual bacteria in dilute suspensions. Nevertheless, the globally synchronized run-stop behavior actually resembles dense bacterial suspensions where bacteria synchronize the tumbling due to mechanical locking of flagella.66,67 This suggests that, although the microscopic triggering mechanisms differ (electric field vs. flagellar switching), the resulting active turbulent-like flow is robust to the specific details of the random walk, in particular the probability distribution of the run times. In our experiments, we vary the field magnitude E while maintaining fixed pulse durations τon = 40 ms and intervals τoff = 20 ms. The off-time is chosen to be much longer than the Maxwell–Wagner polarization relaxation time tMW = (εp + 2εf)/(σp + 2σf) ≈ 2 ms, to ensure that the roller executes an uncorrelated random walk. εp,f and σp,f are the permittivities and conductivities of the particle (p) and the suspending fluid (f), respectively. The experimental values used are εp = 3.2 × 10−11 F m−1, εf = 1.77 × 10−11 F m−1; σp = 1.0 × 10−17 S m, σf = 2.2 × 10−8 S m. τon sets the particle persistence length and it is chosen so that it is comparable to the collision time, which varies from 7 ms to 38 ms. The average collision time of the particles is estimated based on the average particle number density,  , where n is the number density of particles, d is the particle's diameter, and 〈|v|〉 is the average speed of the particles. The suspension is confined within a chamber bound by a ring-shaped Teflon tape (inner diameter 2.2 cm). To maintain the same gap between the electrodes in all experiments, we first fill the chamber with pure AOT-hexadecane solution before introducing approximately 40 mL of particle suspension at the chamber center. This protocol prevents particles from entering the space between the tape and the electrodes, which could disrupt electrode alignment. It establishes a central region of uniform particle density (1.6 cm diameter) surrounded by an outer region where the particle concentration decreases toward the chamber boundary. Over experimental timescales, we observe particle migration toward the boundary, though concentration variations in the field of view remain limited to less than 5% during measurement periods.
, where n is the number density of particles, d is the particle's diameter, and 〈|v|〉 is the average speed of the particles. The suspension is confined within a chamber bound by a ring-shaped Teflon tape (inner diameter 2.2 cm). To maintain the same gap between the electrodes in all experiments, we first fill the chamber with pure AOT-hexadecane solution before introducing approximately 40 mL of particle suspension at the chamber center. This protocol prevents particles from entering the space between the tape and the electrodes, which could disrupt electrode alignment. It establishes a central region of uniform particle density (1.6 cm diameter) surrounded by an outer region where the particle concentration decreases toward the chamber boundary. Over experimental timescales, we observe particle migration toward the boundary, though concentration variations in the field of view remain limited to less than 5% during measurement periods.
3 Results
3.1 Flow structure
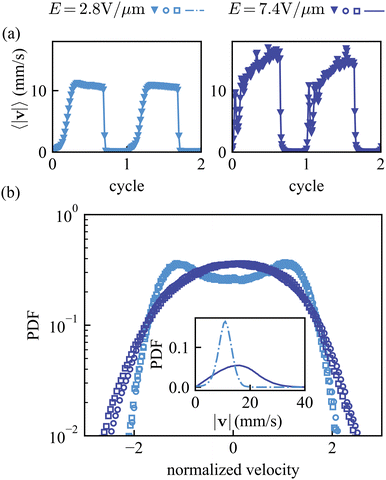
A unique feature of the Quincke random walkers is that when the field is on, they all run, and when the field is turned off, they all stop, see Fig. 2(a). At lower activity and particle fraction, E = 1.7Eq, ϕ = 0.27, the flow driven by the colloids reaches a steady state within one cycle while the field is on. However, higher activity and particle numbers, E = 4.6Eq, ϕ = 0.66, give rise to a more vigorous flow, which does not reach the steady state within the period of the applied electric field. The distinct flow development patterns observed in Fig. 2(a) arise primarily from particle inertia effects at elevated field strengths. For E = 7.4 V mm−1, rotation frequencies Ω ≈ 500 Hz as estimated from single roller measurement (Fig. 1(b)), yielding a rotational Reynolds number ReΩ = ρf(2πΩ)d2/(4μf) ≈ 1.4. This non-negligible inertia results in longer times to reach a steady velocity.65,68 Fig. 2(b) shows the velocity distribution for the experiments with low activity, low density (E = 1.7Eq, ϕ = 0.2) and higher activity, high density (E = 4.6Eq, ϕ = 0.6) systems. A bimodal structure of the PDF suggests that the particles are running with similar velocities; the sampling of the random velocity directions results in two peaks.69 At higher concentrations, the probability density function (PDF) approaches a Gaussian distribution with a single peak. This occurs because particles now experience multiple collisions within the same time interval between two consecutive frames, tfps, used to determine their velocities (τcol < tfps).To characterize the flow structure, we compute the velocity spatial correlation function
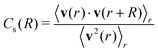 | (1) |
The transverse velocity structure function S⊥2(R) provides insight into vortex statistics.10,18 Defined as:
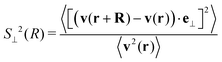 | (2) |
The vortex size distribution can be further investigated using the Okubo–Weiss (OW) parameter.32,44 The OW parameter is defined as
| OW = (∂xvx + ∂yvy)2 − 4(∂xvx)(∂yvy) + 4(∂xvy)(∂yvx). | (3) |
Regions with OW < 0 correspond to vortex regions. To analyze the vortex size distribution, we compute the histogram of the areas of connected vortex regions. This distribution, denoted as  , represents the normalized frequency of vortices with area a, where N(a) is the number of vortices of area a. We find that n(a) follows an exponential distribution, n(a) ∝ exp(−a/a*), where a* is the mean vortex area and
, represents the normalized frequency of vortices with area a, where N(a) is the number of vortices of area a. We find that n(a) follows an exponential distribution, n(a) ∝ exp(−a/a*), where a* is the mean vortex area and  is the mean vortex diameter. In Fig. 4 we demonstrate the vortex size distribution for two experimental conditions reported in the text. Their fitted dimensionless mean vortex diameters (DOW/d) are 4.3 and 6.1, where d is the particle diameter. These values are comparable to the mean vortex diameter extracted from the perpendicular structure function in Fig. 3(d).
is the mean vortex diameter. In Fig. 4 we demonstrate the vortex size distribution for two experimental conditions reported in the text. Their fitted dimensionless mean vortex diameters (DOW/d) are 4.3 and 6.1, where d is the particle diameter. These values are comparable to the mean vortex diameter extracted from the perpendicular structure function in Fig. 3(d).
 | ||
| Fig. 4 Vortex size distributions from two representative experiments (OW analysis), exhibiting exponential decay. | ||
3.2 Kinetic energy spectrum
We next examine how the kinetic energy E is distributed across different length scales for varying field strengths and particle concentrations. The energy spectrum, i.e., the energy of a vortex with size ∼1/k, E(k) is computed from the velocity field v(r,t) through the relation10,44,72–74
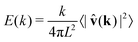 | (4) |
 is the Fourier transformation of velocity.
is the Fourier transformation of velocity.  is the total energy per unit mass of the system.
is the total energy per unit mass of the system.
Fig. 5 shows the energy spectra for our system, revealing two distinct scaling regimes that characterize the flow properties at different length scales across all experimental conditions. The spectrum exhibits a linear dependence E(k) ∼ k at small wavenumbers (k ≪ 1/Dv) indicating uncorrelated flow. This behavior can be understood through the Wiener–Khinchin relation,  where Cs(R) is the spatial velocity correlation function and 〈·〉θ denotes averaging over the azimuthal angle θ. The linear scaling indicates that the velocity correlations become negligible on length scales longer than Dv, causing the Fourier transform of the velocity correlation function to approach a constant at small k.
where Cs(R) is the spatial velocity correlation function and 〈·〉θ denotes averaging over the azimuthal angle θ. The linear scaling indicates that the velocity correlations become negligible on length scales longer than Dv, causing the Fourier transform of the velocity correlation function to approach a constant at small k.
Notably, at larger wavenumbers (k > 1/Dv), we find E(k) ∼ k−4 scaling, similar to observations in confined bacterial suspensions and 2D active nematics.18,32,44 The crossover between regimes occurs near k ≈ 1/Dv (Fig. 5(b and c)), where Dv is the average vortex size. The exponential vortex size distribution and k−4 scaling in the vortex-dominated regime appear across different confined active systems, suggesting common statistical properties of active turbulence under confinement.
3.3 Temporal memory effects
It was recently demonstrated60 that Quincke rollers in a globally correlated collective state (vortex) spontaneously develop structural positional ordering that “imprints” the chiral state of the system. Under a cessation and restoration of the activity facilitated by a pulsed field with both τon and τoff significantly larger than all relevant timescales, a global vortex alternates its chiral state with each activity cycle. This periodic response, despite the absence of memory at the level of individual particles, was attributed to a phenomenon referred to as collective or “structural memory”.60 To investigate whether a similar “memory” phenomenon occurs in our system under a pulsating field with shorter τon, we compute the temporal correlation function of the velocity field,
 | (5) |
 | (6) |
Here, the system is divided into a square grid. vi is the average velocity at the cell i; N is the total number of cells and 〈·〉t denotes the time average. Similarly, we compute the vorticity field ωi based on the velocity field and proceed to compute the vorticity temporal correlation function.
Within one cycle, see Fig. 6(a), the time correlation function decays to zero, indicating that at a fixed location, the flow field decorrelates from its initial state, likely due to the particle collisions. Nevertheless, when the time correlation function is computed between the pulses (stroboscopically- at fixed time within each period), the correlation functions exhibit clear non-negligible anti-correlations after one cycle (see Fig. 6(b)) indicative of the velocity and vorticity reversals in the ensemble during temporal activity cycling. This finding indicates that at the subsequent cycle, a vortex is likely to occur at the same location but with opposite direction of rotation. This behavior is attributed to structural memory, facilitated by local particle positional asymmetries in self-organized roller vortices.60 In our system under short activity pulses, local vortices do not coalesce into a giant vortex. Nonetheless, the formation of these locally correlated vortical states is the source of the anti-correlations in the system between the activity cycles. Only particles participating in local vortices contribute to the anti-correlations resulting in a correlation value significantly lower than −1 (as it is with a global vortex state60). The signature of the collective ensemble memory is robust and easily detectable. Over time (beyond 2 cycles) the correlations between the activity cycles are suppressed as the locations of vortices get randomized. The anti-correlation exhibits a non-monotonic dependence on particle concentration as structural memory gets suppressed with increased concentration, similarly to ref. 60 (see ESI† for details).
4 Conclusion
We have investigated active turbulence in a system of Quincke random walkers, a synthetic system which mimics the run-and-tumble behavior of bacteria. The Quincke random walkers provide a versatile experimental model of active matter to study the fundamental mechanisms of active turbulence. We observe that the kinetic energy spectra follow k−4 scaling, consistent with the observations in very confined bacterial suspensions.18 Our experiments indicate exponential vortex size distribution, which has been previously observed in active nematic turbulence and bacterial turbulence. In addition, the quasi-two-dimensional dense suspension of random walkers undergoing synchronized run-and-tumble behavior showed evidence of structural collective memory. Our findings highlight the importance of transient dynamic memory in the ensemble, both at the particle level and collective, in accessing unconventional self-organized states.Author contributions
PV and AS conceived the research. RL designed and carried out the experiments and analyzed the data. All authors discussed the results and wrote the paper.Conflicts of interest
There are no conflicts to declare.Data availability
Data for this article, including movies will be available at Research and Data Repository at https://arch.library.northwestern.edu.Acknowledgements
The research of R. L. and P. V. was supported by NSF-DMR award 2004926. The research of A. S. was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division.References
- M. F. Copeland and D. B. Weibel, Soft Matter, 2009, 5, 1174–1187 RSC.
- H. Zhang, A. Be’Er, R. S. Smith, E.-L. Florin and H. L. Swinney, Europhys. Lett., 2009, 87, 48011 CrossRef.
- H. P. Zhang, A. Be'er, E.-L. Florin and H. L. Swinney, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13626–13630 CrossRef CAS PubMed.
- X. Chen, X. Dong, A. Be'er, H. L. Swinney and H. Zhang, Phys. Rev. Lett., 2012, 108, 148101 CrossRef PubMed.
- X. Chen, X. Yang, M. Yang and H. Zhang, Europhys. Lett., 2015, 111, 54002 CrossRef.
- A. Be'er, B. Ilkanaiv, R. Gross, D. B. Kearns, S. Heidenreich, M. Baer and G. Ariel, Commun. Phys., 2020, 3, 66 CrossRef.
- I. S. Aranson, Rep. Prog. Phys., 2022, 85, 076601 CrossRef CAS PubMed.
- C. Dombrowski, L. Cisneros, S. Chatkaew, R. Goldstein and J. Kessler, Phys. Rev. Lett., 2004, 93, 098103 CrossRef PubMed.
- A. Sokolov, I. S. Aranson, J. O. Kessler and R. E. Goldstein, Phys. Rev. Lett., 2007, 98, 158102 CrossRef PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed.
- J. Dunkel, S. Heidenreich, K. Drescher, H. H. Wensink, M. Bär and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 228102 CrossRef PubMed.
- J. Gachelin, A. Rousselet, A. Lindner and E. Clement, New J. Phys., 2014, 16, 025003 CrossRef.
- S. Zhou, A. Sokolov, O. D. Lavrentovich and I. S. Aranson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1265–1270 CrossRef CAS PubMed.
- Y. Peng, Z. Liu and X. Cheng, Sci. Adv., 2021, 7, eabd1240 CrossRef CAS PubMed.
- R. Alert, J. Casademunt and J.-F. Joanny, Annu. Rev. Fluid Mech., 2022, 13, 143–170 Search PubMed.
- D. Saintillan and M. J. Shelley, J. R. Soc. Interface, 2012, 9, 571–585 CrossRef PubMed.
- Z. Liu, W. Zeng, X. Ma and X. Cheng, Soft Matter, 2021, 17, 10806–10817 RSC.
- D. Wei, Y. Yang, X. Wei, R. Golestanian, M. Li, F. Meng and Y. Peng, Adv. Sci., 2024, 2402643 CrossRef PubMed.
- H. Karani, G. E. Pradillo and P. M. Vlahovska, Phys. Rev. Lett., 2019, 123, 208002 CrossRef CAS PubMed.
- A. Creppy, O. Praud, X. Druart, P. L. Kohnke and F. Plourabou¥’e, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 032722 CrossRef PubMed.
- T. Sanchez, D. N. Chen, S. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431 CrossRef CAS PubMed.
- A. Opathalage, M. M. Norton, M. P. N. Juniper, B. Langeslay, S. A. Aghvami, S. Fraden and Z. Dogic, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4788–4797 CrossRef CAS PubMed.
- B. Martinez-Prat, J. Ignes-Mullol, J. Casademunt and F. Sagues, Nat. Phys., 2019, 15, 362 Search PubMed.
- C. Blanch-Mercader, V. Yashunsky, S. Garcia, G. Duclos, L. Giomi and P. Silberzan, Phys. Rev. Lett., 2018, 120, 208101 CrossRef CAS PubMed.
- S.-Z. Lin, W.-Y. Zhang, D. Bi, B. Li and X.-Q. Feng, Commun. Phys., 2021, 4, 21 CrossRef.
- R. Aditi Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef CAS PubMed.
- D. Saintillan and M. Shelley, Phys. Rev. Lett., 2007, 99, 058102 CrossRef PubMed.
- D. Saintillan and M. J. Shelley, J. R. Soc. Interface, 2012, 9, 571–585 CrossRef PubMed.
- D. Saintillan and M. J. Shelley, C. R. Phys., 2013, 14, 497–517 CrossRef CAS.
- J. Dunkel, S. Heidenreich, M. Br and R. E. Goldstein, New J. Phys., 2013, 15, 045016 CrossRef.
- V. Bratanov, F. Jenko and E. Frey, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 15048–15053 CrossRef CAS PubMed.
- L. Giomi, Phys. Rev. X, 2015, 5, 031003 Search PubMed.
- M. James, W. J. T. Bos and M. Wilczek, Phys. Rev. Fluids, 2018, 3, 061101 CrossRef.
- A. Doostmohammadi, J. Ignes-Mullol, J. M. Yeomans and F. Sagues, Nat. Commun., 2018, 9, 3246 CrossRef PubMed.
- M. Linkmann, G. Boffetta, M. C. Marchetti and B. Eckhardt, Phys. Rev. Lett., 2019, 122, 214503 CrossRef CAS PubMed.
- V. S. Škultéty, C. Nardini, J. Stenhammar, D. Marenduzzo and A. Morozov, Phys. Rev. X, 2020, 10, 031059 Search PubMed.
- M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Nat. Rev. Phys., 2020, 2, 181–199 CrossRef.
- K. Qi, E. Westphal, G. Gompper and R. G. Winkler, Commun. Phys., 2022, 5, 1–12 CrossRef.
- A. W. Zantop and H. Stark, Soft Matter, 2022, 18, 6179–6191 RSC.
- Y.-E. Keta, J. U. Klamser, R. L. Jack and L. Berthier, Phys. Rev. Lett., 2024, 132, 218301 CrossRef CAS PubMed.
- Q. Yang, M. Jiang, F. Picano and L. Zhu, Nat. Commun., 2024, 15, 2874 CrossRef CAS PubMed.
- S. Goh, E. Westphal, R. G. Winkler and G. Gompper, Phys. Rev. Res., 2025, 7, 013142 CrossRef CAS.
- S. Fraden, Nat. Phys., 2019, 15, 311–312 Search PubMed.
- B. Martínez-Prat, R. Alert, F. Meng, J. Ignés-Mullol, J.-F. Joanny, J. Casademunt, R. Golestanian and F. Sagués, Phys. Rev. X, 2021, 11, 031065 Search PubMed.
- D. Nishiguchi and M. Sano, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 052309 CrossRef PubMed.
- G. Kokot, S. Das, R. G. Winkler, G. Gompper, I. S. Aranson and A. Snezhko, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12870–12875 CrossRef CAS PubMed.
- J. Mecke, Y. Gao, C. A. Ramrez Medina, D. G. Aarts, G. Gompper and M. Ripoll, Commun. Phys., 2023, 6, 324 CrossRef.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- M. Driscoll and B. Delmotte, Curr. Opin. Colloid Interface Sci., 2019, 40, 42–57 CrossRef CAS.
- A. Boymelgreen, J. Schiffbauer, B. Khusid and G. Yossifon, Curr. Opin. Colloid Interface Sci., 2022, 101603 CrossRef CAS.
- N. M. Diwakar, G. Kunti, T. Miloh, G. Yossifon and O. D. Velev, Curr. Opin. Colloid Interface Sci., 2022, 101586 CrossRef CAS.
- K. J. Bishop, S. L. Biswal and B. Bharti, Annu. Rev. Chem. Biomol. Eng., 2023, 14, 1–30 CrossRef CAS PubMed.
- G. Quincke, Ann. Phys., 1896, 295, 417–486 CrossRef.
- A. Bricard, J.-B. Caussin, D. Das, C. Savoie, V. Chikkadi, K. Shitara, O. Chepizhko, F. Peruani, D. Saintillan and D. Bartolo, Nat. Commun., 2015, 6, 7470 CrossRef CAS PubMed.
- A. Chardac, S. Shankar, M. C. Marchetti and D. Bartolo, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018218118 CrossRef CAS PubMed.
- B. Zhang, A. Sokolov and A. Snezhko, Nat. Commun., 2020, 11, 4401 CrossRef CAS PubMed.
- B. Zhang, A. Snezhko and A. Sokolov, Phys. Rev. Lett., 2022, 128, 018004 CrossRef CAS PubMed.
- C. Jorge, A. Chardac, A. Poncet and D. Bartolo, Nat. Phys., 2024, 20, 303–309 Search PubMed.
- B. Zhang, H. Karani, P. M. Vlahovska and A. Snezhko, Soft Matter, 2021, 17, 4818–4825 RSC.
- B. Zhang, H. Yuan, A. Sokolov, M. O. De La Cruz and A. Snezhko, Nat. Phys., 2022, 18, 154–159 Search PubMed.
- A. Liberzon, T. Käufer, A. Bauer, P. Vennemann and E. Zimmer, OpenPIV/Openpiv-Python: OpenPIV-python v0.23.4, Zenodo, 2021 Search PubMed.
- D. B. Allan, T. Caswell, N. C. Keim, C. M. van der Wel and R. W. Verweij, Soft-Matter/Trackpy: V0.6.4, Zenodo, 2024 Search PubMed.
- E. Lemaire and L. Lobry, Physica A, 2002, 314, 663–671 CrossRef.
- T. B. Jones, IEEE Trans. Ind. Appl., 1984, 20, 845–849 Search PubMed.
- G. E. Pradillo, H. Karani and P. M. Vlahovska, Soft Matter, 2019, 15, 6564–6570 RSC.
- H. P. Zhang, A. Be'er, E.-L. Florin and H. L. Swinney, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13626–13630 CrossRef CAS PubMed.
- M. F. Copeland and D. B. Weibel, Soft Matter, 2009, 5, 1174–1187 RSC.
- Y. Wang, S. Canic, G. Kokot, A. Snezhko and I. S. Aranson, Phys. Rev. Fluids, 2019, 4, 013701 CrossRef.
- G. Kokot, A. Vilfan, A. Glatz and A. Snezhko, Soft Matter, 2019, 15, 3612–3619 RSC.
- B. Zhang, H. Yuan, A. Sokolov, M. O. De La Cruz and A. Snezhko, Nat. Phys., 2022, 18, 154–159 Search PubMed.
- J. Mecke, Y. Gao, G. Gompper and M. Ripoll, Commun. Phys., 2024, 7, 1–10 Search PubMed.
- R. H. Kraichnan and D. Montgomery, Rep. Prog. Phys., 1980, 43, 547 CrossRef CAS.
- G. Boffetta and R. E. Ecke, Annu. Rev. Fluid Mech., 2012,(44), 427–451 CrossRef.
- U. Frisch, Turbulence: The Legacy of A. N. Kolmogorov, Cambridge University Press, 1995 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00192g |
| This journal is © The Royal Society of Chemistry 2025 |