Open Access Article
Open Access ArticleBrownian dynamics simulation of the diffusion of rod-like nanoparticles in polymeric gels†
Mohammad-Reza
Rokhforouz
 a,
Don D.
Sin
b,
Sarah
Hedtrich
a,
Don D.
Sin
b,
Sarah
Hedtrich
 cde and
James J.
Feng
cde and
James J.
Feng
 *af
*af
aDepartment of Chemical and Biological Engineering, University of British Columbia, Vancouver, British Columbia, Canada. E-mail: james.feng@ubc.ca
bCentre for Heart Lung Innovation, University of British Columbia, Vancouver, British Columbia, Canada
cFaculty of Pharmaceutical Sciences, University of British Columbia, Vancouver, British Columbia, Canada
dSchool of Biomedical Engineering, University of British Columbia, Vancouver, British Columbia, Canada
eCenter of Biological Design, Berlin Institute of Health at Charité – Universitätsmedizin Berlin, Germany
fDepartment of Mathematics, University of British Columbia, Vancouver, British Columbia, Canada
First published on 9th June 2025
Abstract
Rod-like nanoparticles (RNPs) have been shown to diffuse faster than spherical ones in polymeric hydrogels, but the underlying physics is not well understood. We develop a 3D Brownian dynamics model to investigate this phenomenon, representing the gel as a random network of rigid fibers in water and incorporating both steric repulsion and adhesive interactions. In non-adhesive gels, RNP diffusivity increases monotonically with the aspect ratio while its hydrodynamic diameter is kept constant, in agreement with the predictions of an obstruction scaling (OS) model. However, our model predicts a much higher diffusivity than the OS model, by up to 5 times for higher aspect ratios. To rationalize this discrepancy, we demonstrate that RNPs experience a skewed pore-size distribution in favor of the larger pores; they spend more time in coarser regions of the gel than in denser regions. Moreover, the RNPs execute a meandering motion in the coarser regions with pronounced rotational and transverse diffusion. In contrast, in denser regions, restricted rotation results in predominantly longitudinal diffusion. This anisotropy in diffusion further elevates the translational diffusivity of RNPs. Our model also reveals a competition between the steric and adhesive interactions, where steric repulsion limits access to adhesion sites, and produces a diffusivity intermediate between the purely steric and purely adhesive cases. Overall, our results show an even greater advantage for RNPs, in terms of rapid diffusion in hydrogels, than previously anticipated by using the OS model.
1. Introduction
The diffusion of nanoparticles (NPs) in hydrogels (e.g., mucus) is determined not only by their size and surface chemistry, but also by their shape.1 It is known that the NPs should be smaller than the hydrogel's mesh size and possess a near-neutral charge for effective penetration into the gel.2 Inspired by the fact that the majority of microbial residents in the gastrointestinal tract are rod-shaped,3 rod-like NPs (RNPs) have emerged as an alternative to conventional spherical nanoparticles (SNPs). Yu et al.4 showed that 80 × 240 nm RNPs diffuse faster than their 80 nm spherical counterparts in intestinal mucus. Wang et al.5 captured the same trend and also showed that the diffusivity would fall again for overly long rods. Since then, experimental,6–12 theoretical,5 and computational12–16 investigations have been conducted to examine the underlying mechanisms responsible for the superiority of RNPs in penetrating hydrogels.In the literature, three protocols have been employed to examine the effects of the aspect ratio of RNPs. The d-protocol compares RNPs with the same minor-axis diameter but different lengths.4 The v-protocol compares RNPs with the same volume,14 and the hd-protocol compares RNPs with the same hydrodynamic diameter,5i.e., the diameter of a sphere possessing the same Stokes–Einstein diffusivity as the RNP in the solvent (see eqn (1) for details).
In non-adhesive gels, with steric repulsion only, our understanding of NP diffusion has come mostly from the obstruction-scaling (OS) model. Essentially, the model assumes that the obstacles reduce the NP diffusivity by a factor that is the probability of the NP encountering a polymer chain. By extending Ogston's OS model17 and conducting experiments, Wang et al.5 showed that in the d-protocol, longer rods with the same minor-axis diameter exhibit slower diffusion than shorter ones. This is essentially the same trend as that observed for diffusion in solvents;5,15 it is easily understood as the longer rods have greater volume that incurs larger drag. In the v-protocol14 and hd-protocol,5 however, the diffusivity increases with the aspect ratio. This increase is mainly because the longer rods have smaller cross-sections in either of these protocols, and thus encounter fewer polymer chains in the gel. Thus, the OS model suggests a mechanism for the high diffusivity of thin and long rods observed experimentally.
Adhesive gels feature non-steric interactions such as hydrophobic, van der Waals, and electrostatic forces, which are essential to the filtering capability of biopolymer gels like mucus.18 Among these, low-affinity hydrophobic interactions are particularly significant in driving adhesive behavior.19 Posing regularly spaced discrete adhesion sites, Wang et al.5 modeled the adhesive interaction with RNPs of different lengths. They uncovered an interesting non-monotonic trend for the diffusivity as a function of the RNP length in the d-protocols. Shorter RNPs tend to be captured by a single adhesive site. With increasing length, the RNP becomes increasingly susceptible to attraction toward a nearby site, which tends to dislodge it from the first site. Then the RNP moves quickly to the second adhesive site in a well-documented hopping diffusion.5,8 This tendency yields a local maximum in diffusivity for RNPs whose length matches the spacing between adhesive sites. Even longer rods can be trapped, simultaneously and more securely, by two adhesion sites. Thus, the diffusivity decreases with greater length. When the steric repulsion is superimposed on the adhesive interaction, the diffusivity–rod-length curve gets tilted downward for the d-protocol and upward for the hd-protocol, but the local maximum persists as a hallmark of the attraction to evenly spaced adhesive sites.5
Since steric repulsion is at work in both adhesive and non-adhesive gels, our understanding outlined in the above relies heavily on the obstruction-scaling representation of steric repulsion. But the OS model is a phenomenological model and is not based on first principles. Therefore, further evaluation through comparison with other methods, such as numerical simulations and experiments, is necessary. In this work, we employ the Brownian dynamics (BD) method to study the transport of RNPs in hydrogels, aiming to establish a fundamental understanding of the physics. Our results suggest that in non-adhesive gels, the OS model underestimates the diffusivity of RNPs by a large margin. In adhesive gels, steric repulsion can shield the RNP from adhesive sites, thus alleviating the effect that adhesion may have on the RNP diffusion, especially for longer rods. Thus, in either type of gel, rod-like nanoparticles may enjoy an even greater advantage in rapid diffusion than previously thought.
2. Methodology
2.1. Geometric setup
To simulate the diffusion of RNPs in the gel, we construct a system composed of straight rigid polymer fibers of negligible width and rigid NPs, with the water molecules implicitly reflected by the solvent viscosity. A random network of the fibers is generated in a periodic box with side length b, containing immobile fibers of length 2Lf. The fibers are randomly placed and oriented, creating a fibrous structure. The total number of fibers in the box is Nf, and the fiber density is υ = Nf/b3. Fig. 1(a) shows a schematic diagram of our simulation system. The box repeats periodically in all three dimensions such that the portion of the fibers sticking outside the box appear in it from the opposite side. Thus, the overall fiber density is maintained at the desired level. Note a simplification in our polymer network relative to a real polymer gel. Since the fibers have no thickness, they do not intersect, nor do they form physical crosslinks. Instead, the pore size is defined by the largest sphere that fits in a pore without contacting the fibers. More details will be given in Section 3.2.1.The RNP is a spherocylinder with caps on its two ends and an aspect ratio of λ = L/d. At the start of the simulation, the RNP is randomly placed in the fiber network without intersecting any fibers. As the volume fractions in typical applications of nanoparticles are below 2%,20 the RNPs remain in the dilute regime and do not interact with one another. Thus, we can deploy a single RNP in the periodic box and track its diffusion over a long period of time. We also include hundreds of different random realizations of the fiber network, and in each network configuration start from different initial positions and orientations of the RNP so as to construct a large ensemble of thousands of diffusive trajectories. The diffusivity to be presented will come from averages over long times and large ensembles. Fig. 1(b) and (c) illustrate the d- and hd-protocols for handling the aspect ratio, respectively. Since the hd- and v-protocols yield similar nanorods, we will no longer consider the v-protocol hereafter. The hydrodynamic diameter of the RNPs, dH, is calculated using the formula from Ortega and de la Torre.21 It represents the diameter of a sphere with the same solvent diffusivity as the nanorod, allowing us to obtain dH from the actual diameter (d) of the RNP:
 | (1) |
Unless otherwise noted, the parameters used in our simulations are based on those in Wang et al.5 and tabulated in Table 1. This allows for a direct comparison of our results with theirs. For the hydrodynamic diameter dH = 160 nm, eqn (1) gives us the length and diameter of the RNP as the aspect ratio λ changes, and such dimensions are given in Table S1 of the ESI.† The pore size distribution of the gel is given in Fig. S1 in the ESI.† According to Ogston,17 the average pore diameter of this network is  .
.
| Parameters | Value | Explanation |
|---|---|---|
| 2νLf | 16 × 1013 m−2 | Total fiber length per unit volume |
| 2Lf | 1 μm | Length of the fibers |
| d H | 160 nm | Hydrodynamic diameter of NPs |
2.2. Governing equations
The translational and rotational motions of the RNPs are governed by force and torque balances. Given the scale of the problem, inertia is neglected in our simulation. The influence of the solvent is implicitly considered via random Brownian and drag forces and torques.22 In our treatment of the Stokes drag force, we have neglected the hydrodynamic interaction between the RNP and the nearby polymer chains. Such interaction can potentially increase the drag on the RNP and reduce its diffusivity. But accounting for this effect would require a much more complex theoretical model.23,24 For an axisymmetric particle, the translational motion can be decomposed into the motion in the long axis direction and the motion in a direction normal to the long axis.25 According to Langevin's equation, the force and torque balances on a moving particle are | (2) |
 | (3) |
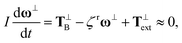 | (4) |
 | (5) |
 | (6) |
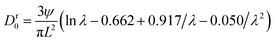 | (7) |
| ψ = kBT/μL | (8) |
The Brownian force components F‖B = F‖BΩ and F⊥B = F⊥1Be1 + F⊥2Be2, where e1 and e2 are two orthogonal unit vectors perpendicular to Ω, have the following stochastic characteristics:
| 〈F‖B(t)〉 = 0, 〈F‖B(t)F‖B(t′)〉 = 2ζ‖kBTδ(t − t′) | (9) |
| 〈F⊥1B(t)〉 = 〈F⊥2B(t)〉 = 0, 〈F⊥1B(t)F⊥1B(t′)〉 = 〈F⊥2B(t)F⊥2B(t′)〉 = 2ζ⊥kBTδ(t − t′) | (10) |
| 〈T⊥1B(t)〉 = 〈T⊥2B(t)〉 = 0, 〈T⊥1B(t)T⊥1B(t′)〉 = 〈T⊥2B(t)T⊥2B(t′)〉 = 2ζrkBTδ(t − t′) | (11) |
The discretization scheme of the governing equations is detailed in Section S2 of the ESI.†
2.3. Steric interaction
The steric effect is implemented using the Lennard-Jones (LJ) potential. We have also tested two others models to confirm that the specific details of the interaction potential or force do not significantly affect our results. The details of these models are given below. | (12) |
 | (13) |
| Trep = G × Frep | (14) |
2.4. Adhesive interactions
To capture the adhesive interaction between the RNP and the fiber network, we adapt the treatment of Wang et al.5 in one and three dimensions to the three-dimensional geometry of our Brownian dynamics simulation. Although multiple physical mechanisms can induce NP–gel adhesion, the modeling here is based on the physical picture of hydrophobic interactions with discrete sites on the polymer backbones. Other types of adhesive forces, e.g., electrostatic or van der Waals forces, can be easily incorporated through appropriate forms of the interaction potential below.31Following Wang et al.,5 we assume discrete adhesion sites on the fiber network. To describe the adhesion between one such site and a unit length of a nearby RNP, we adopt a Morse potential:
| U(x) = U0(e−2x/ρ − 2e−x/ρ) | (15) |
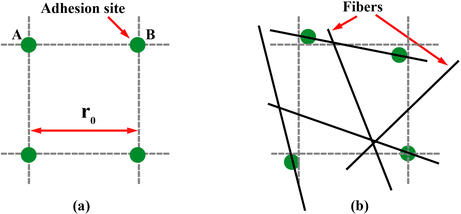
The main difference from Wang et al. adhesion model lies in the positioning of the adhesion sites on the 3D random fiber network. This is accomplished in two steps. First, we uniformly place the adhesion sites onto a regular cubic lattice inside the simulation box, with equal separation of r0 = 200 nm (Fig. 2(a)). This layout is identical to the 3D lattice employed by Wang et al.5 Second, we reposition the adhesion sites onto the random fiber network by shifting each site to the nearest point on the closest fiber (Fig. 2(b)). Thus, the adhesion sites all fall on the fibers but exhibit a roughly uniform spatial distribution. In a real gel, of course, the adhesion sites may not be uniform. Given our focus on the RNP shape, however, we will not probe the effects of the density and spatial heterogeneity of the adhesion sites.
Our numerical algorithm follows standard Brownian dynamics procedures. The temporal discretization scheme for integrating the Langevin equation is detailed in the ESI† (Section S2), as are the procedures for evaluating statistical quantities of interest, such as the mean square displacement (MSD) and the diffusivities, from the RNP trajectories (Section S4, ESI†).
3. Results & discussion
3.1. Validation of the model
To test the validity of our physical model and the accuracy of our numerical algorithm, we have simulated three simpler situations where a benchmark is available for comparison. First, we compute the translational and rotational diffusivities of nanorods of cross-sectional diameter d = 80 nm and various lengths in a pure solvent with μ = 1 cP, T = 300 K. Compared with the analytical relations of Tirado et al.27 (see eqn (5)–(8)), both show close agreement (Fig. 3(a) and (b)). This confirms that we have correctly implemented the discrete Brownian force in our model, and the numerical parameters used, including the time step Δt, number of particles P, total time of simulation, sampling protocols, ensure adequate resolution and accuracy in our code. We have previously tested these numerical parameters for SNPs in our previous work,2 and similar tests have been done for RNPs here. Details are not given for brevity. | ||
| Fig. 3 Comparison between our simulations and (a) and (b) analytical relations proposed by Tirado et al.27 in a pure solvent with μ = 1 cP, T = 300 K as a function of RNP aspect ratio (c) and (d) an existing BD study by Chen et al.29 under rod–rod interaction as a function of volume fraction where d = 5.6 nm and λ = 5, (e) Ogston's OS model17 in a non-adhesive random gel as a function of SNP size. In this model, 2Lf = 1 μm and ν = 1.6 × 1020 m−3. | ||
We further validate our model via Brownian dynamics simulation of Chen et al.29 of the interactions between RNPs with d = 5.6 nm and λ = 5. They are suspended in a quiescent liquid medium of viscosity μ = 1 cP, and their diffusion under a Brownian force is tracked in time for evaluating the translational and rotational diffusivities. To replicate their results, we employed Chen's model for the steric repulsion (eqn (13) and (14)). For volume concentration of up to 38%, our model accurately reproduces the literature data (Fig. 3(c) and (d)).
Finally, we reduce our model to account for the diffusion of SNPs, as Ogston17 has developed an OS model for such SNPs diffusing in a non-adhesive random polymer network. This model yields the following formula for the diffusivity of the SNP as a function of its diameter:
 | (16) |
As shown in Fig. 3(e), our results align well with Ogston's equation. Together, these three validations demonstrate that our model can accurately predict the diffusion of both RNPs and SNPs in non-adhesive gels.
3.2. Diffusion in non-adhesive gels: effect of aspect ratio
We study the diffusion of RNPs in random and non-adhesive gels by varying their aspect ratio in the hd-protocol. The main finding of this work is shown in Fig. 4 with the translational diffusivity as a function of the aspect ratio. Both our model, incorporating different repulsive potentials for steric interaction, and Wang's extended OS model5 show that the diffusivity of RNPs increases monotonically with the aspect ratio. This increase has been attributed to the cross-sectional area of the RNP:5 rods with a smaller λ have larger cross-sections which may impede their passage through the pores. Surprisingly, our BD model predicts much higher diffusivities compared to Wang's model, with the discrepancy becoming more pronounced as the RNPs become longer and thinner. As a check on our BD results using the LJ potential (eqn (12)), we have repeated the simulations using two alternative representations of the steric repulsion: the repulsive force of Chen et al.29 (eqn (13)) and the Monte Carlo scheme described in Section 2.3.3. All three results agree closely, with a much higher Dt than predicted by the OS model. We also numerically integrated Wang's model (eqn (6) and (7) in their paper) and successfully reproduced their reported results. Therefore, we conclude that the discrepancy is not due to errors. Rather it reflects substantive differences between the two models. | ||
| Fig. 4 Comparison between our simulations, employing different steric models, and Wang's OS model as a function of aspect ratio. The parameters used here are listed in Table 1. | ||
The OS model centers on the probability of the RNP overlapping a polymer chain if it were inserted into the gel at a randomly chosen centroid position and a random orientation. This probability is a purely geometric property, and can be calculated from the known location and orientation of all the polymer chains.5 More specifically, in a large ensemble of repeated random insertion of the RNP into the gel, one counts the percentage of the insertions with the RNP encountering no fiber. This probability p is then equated to the relative diffusivity Dg/D0 = p.
Our Brownian dynamics simulation tracks the continuous movement of the RNP through the pores of the network. Thus, the obstruction that it experiences from the polymer chains depends on its continuous trajectory and may well differ from that of an RNP repeatedly inserted into the gel, with no correlation of the RNP position and orientation from one trial to the next. More specifically, the diffusing RNP may linger in certain regions while speeding through other regions. It may even be excluded from certain pores. Fig. 5(a) and (b) compare the distribution of the RNP centroid for the successful insertions in the protocol of the OS model with that from diffusing RNPs in our Brownian dynamics simulation. In recording the location of successful RNP insertions without intersecting any fiber, panel (a) essentially presents a “negative” of the fiber density distribution or pore size distribution. Comparing the two plots, we notice similarities; in both cases, the RNP ends up more often in coarse regions with larger pores. But panel (b) is more spatially heterogeneous than (a), with the dark and blank areas more sharply delineated and separated from each other. Some regions with smaller pores, sparsely populated in (a), are not visited at all by the diffusing RNP in (b). The existence of such small “dead pores” implies that the RNP experiences a lower effective crowdedness than given by the overall fiber density. Equivalently, the difference between (a) and (b) suggests that the diffusing RNP lingers more in the coarser regions of the gel than the denser regions, thus amplifying the contrast between regions of low and high fiber density. Evidently, the diffusion trajectory samples a fiber distribution that is skewed from that experienced by a randomly inserted RNP. This qualitative observation is quantified in Fig. 5(c), which compares the distribution of nearest neighbor distances for the two models. In the BD simulation, the peak of the nearest-neighbor distance distribution occurs at a smaller value compared to the OS model, indicating a more compact particle distribution. In contrast, the OS model exhibits a longer tail towards larger distances, reflecting a sparser distribution of nanoparticles across the gel. Thus, the histogram provides numerical evidence for the amplified spatial heterogeneity seen in the BD simulation.
It turns out that the meandering mode occurs in coarser regions of the gel with larger pore sizes, and the directional mode in denser regions with smaller pore sizes. To demonstrate this, we enclosed the above trajectories in cuboids, in which the pore size and fiber crowdedness can be evaluated. To calculate the pore size, we follow a procedure adapted from Stylianopoulos et al.32 First, we randomly select a point inside the box that is not occupied by fibers. Then, we calculate the maximum diameter of a sphere centered at the selected point that does not touch any fiber. This is repeated over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points and the average is taken. The results reveal that the ensemble-averaged pore diameter is about 125 nm in the meandering mode and 100 nm in the longitudinal mode. These findings support the notion that the meandering and directional modes occurred in coarser and denser regions, respectively.
000 points and the average is taken. The results reveal that the ensemble-averaged pore diameter is about 125 nm in the meandering mode and 100 nm in the longitudinal mode. These findings support the notion that the meandering and directional modes occurred in coarser and denser regions, respectively.
Following Zhao et al.,14 we define a crowdedness number N to characterize the proximity of the fibers around the RNP. For this purpose, we discretize each fiber into nf equally spaced “beads”, and similarly the RNP into nr beads. This ad hoc segmentation is specific to this calculation and does not affect the BD model. We calculate a crowdedness number N(t) as follows:
 | (17) |
The implication is clear: the RNP spends more time in the coarser region of the gel while undergoing meandering diffusion and traverses the denser regions briefly in directional diffusion. Judging from the residence time, we clearly see a bias in how the RNP experiences the fiber network; it prefers to linger in the coarser regions with larger pores, and thus samples a pore-size distribution along its diffusive trajectory that is skewed in favor of larger pores. This provides quantitative support to the visual observations in Fig. 5. An immediate consequence of this observation is that the RNP will exhibit an overall translational diffusivity that corresponds to an effectively coarser gel with larger pores. This provides a plausible explanation for the discrepancy in Fig. 4; our BD simulation should indeed produce a higher Dt than that predicted by the OS model using the static pore size distribution.
In the coarser regions of the gel, the RNP can rotate more freely and have access to a wider range of directions for its diffusion. In contrast, in denser regions, their rotation and transverse diffusion are severely curtailed. As a consequence, the RNP is more liable to diffuse longitudinally, with little rotation or lateral translation. This distinction is illustrated by the cartoons of Fig. 7. As is well known, the longitudinal motion enjoys smaller viscous drag and faster diffusion. This is consistent with the previous observation that the RNP lingers in the coarser regions undergoing meandering diffusion, and rapidly traverses the denser regions in directional diffusion.
 | ||
| Fig. 7 Schematic illustration of (a) the meandering diffusion of nanorods in a coarser region of the gel, and (b) the directional diffusion in a denser region. | ||
To quantify the idea above, we compute a “local” translational and rotational diffusivity. At time t, we define the local mean squared displacement (LMSD) and the local translational diffusivity Dtl by tracing back M time steps:33
| LMSD(t) = 〈[(r(t) − r(t − MΔt))2]〉 | (18) |
 | (19) |
Similarly, the local rotational diffusivity Drl is defined as
 | (20) |
The local translational and rotational diffusivities, along with their corresponding distributions, are plotted in Fig. 8 for the trajectory shown in Fig. 6. The longitudinal motion features a higher translational diffusivity but a lower rotational diffusivity, while the opposite is true for the meandering motion. For example, the time- and ensemble-averaged translational diffusivity for the directional diffusion is 1.75 μm2 s−1, 2.3 times higher than that of the meandering diffusion (0.75 μm2 s−1). The trend is reversed for the rotational diffusivity: the meandering mode exhibits a higher average value of 181 s−1 compared to 123 s−1 for the directional mode. The same trend is demonstrated by the distributions of Dtl and Drl in Fig. 8(c) and (d). These histograms are obtained by sampling the diffusivity values from the 10 individual trajectories of Fig. 8(a) and (b), dividing the range of the diffusivity into 100 bins, and counting the occurrence in each bin as a percentage of the total counts over all the bins. Clearly, the meandering mode tends to have a lower Dtl and a higher Drl than the directional mode. The negative correlation between the rotational and translational diffusion (Fig. 8(e)) has a correlation coefficient
 | (21) |
 | ||
| Fig. 8 The evolution of (a) the local translational diffusivity Dtl and (b) the local rotational diffusivity Drl as a function of time for the trajectories shown in Fig. 6. (c) and (d) Histograms showing the corresponding distributions of the local translational and rotational diffusivities. (e) Scatter plot of Dtlversus Drl for the ensembled averaged data, with a linear regression showing the negative correlation: Dtl = −0.0034Drl + 1.7726. | ||
This forms an interesting contrast with the observation of a positive correlation by Xue et al.11 in a highly uniform gel. Our mechanism relies on spatial fluctuations of fiber concentration and pore size in our random gel, which are absent in their context.
In addition, we employ the local anisotropic diffusion parameter A(t), introduced by Zhao et al.,14 to characterize the anisotropy of diffusion:
 | (22) |
The OS model has long been the primary conceptual framework for understanding NP diffusion in polymer networks. However, our BD simulations have revealed its limitations: the OS model relies solely on the static geometry of the network and fails to account for the dynamic, continuous trajectories of diffusing NPs. For spherical NPs, this connectivity factor is largely negligible, and the OS model predicts SNP diffusivity with good accuracy (Fig. 3(e)). For rod-like NPs, however, the discrepancy is amplified by the anisotropy in diffusion, and grows with the aspect ratio (Fig. 4). This finding underscores the value of our work.
3.3. Comparison with experimental data
Can the discrepancy between our BD results and the prediction of the OS model be further assessed by comparison with experimental data? We find that quantitative comparison is hampered by a dearth of pertinent data, but qualitative ones can be made. Wang et al.5 conducted experiments on the diffusion of silica nanorods in 0.5 wt% hydroxyethyl cellulose (HEC) gel in water. This is a hydrophilic and non-ionic gel without hydrophobic regions, and a good model for a non-adhesive gel. We have chosen our model parameters to match the experimental system. The fiber length is set to 2Lf = 1 μm, a reasonable length in view of literature data.35 To estimate the fiber density (ν), we fitted the OS model to the experimental data at a single point: λ = 1, corresponding to an 80 nm SNP. This yields ν = 9.84 × 1020 m−3. In the OS model, the diffusivity depends only on the product vLf, rather than the individual values of v and Lf, as long as Lf is much longer than the pore sizes. We have tested different combinations of Lf and ν to ensure the robustness of our numerical parameters. The BD simulations produced essentially identical diffusivities across all combinations, confirming that the results are insensitive to the assumed fiber length Lf. Note that the ν chosen to compare with the experiments is more than six times that of Table 1 and Fig. 4.Using the extended OS and our BD model, we have computed the translational diffusivity for a range of λ values using the d-protocol, as the experiments were for a series of RNPs with the same cross-sectional diameter and increasing length. Fig. 9 compares the experimental data with predictions of both models. Both models capture the correct trend of Dt decreasing with λ in the d-protocol, but both underpredict Dt. Our model predicts a higher Dt that is closer to the experimental data over the entire λ range, except for the starting point at λ =1. This comparison, if not quantitatively conclusive, suggests that our model outperforms the OS model for RNPs. The higher diffusivity observed in the experiments can perhaps be attributed to the flexibility of both the nanorods and fibers in the experimental setup.36 Both models assume the rods and fibers to be rigid. Note that at λ = 1, the OS model is fitted to the experimental data to generate the model parameters. For such parameters, the BD model yields a slightly smaller Dt at λ = 1. Had we fitted that data point to our BD model, its predicted Dt would have been even closer to the experimental measurements for λ > 1.
 | ||
| Fig. 9 Comparison between Wang et al. experimental data5 and the predictions of their OS model and our BD model for different aspect ratio values. In this comparison, 2Lf = 1 μm and ν = 9.84 × 1020 m−3. | ||
3.4. Diffusion in adhesive gel
To understand the diffusion of RNPs under the combined effects of steric and adhesive interactions, it is convenient to first examine each interaction independently. Fig. 10 compares the RNP translational diffusivity in three scenarios, with steric repulsion only, adhesion only, and both effects simultaneously. The aspect ratio λ is varied according to the hd-protocol.RNP diffusion under purely steric interactions has been discussed in the previous section. Under purely adhesive interactions, the RNP exhibits the non-monotonic behavior that Wang et al.5 discovered. Short nanorods tend to be trapped by the attraction of a single adhesion site, while overly long ones can be captured and immobilized by simultaneous attraction of two adhesion sites. RNPs with an intermediate length comparable to the spacing between neighboring adhesion sites experience hopping diffusion at an elevated diffusivity. These observations align with the findings of Wang et al.5 In particular, the maximum occurs at λ = 2, at which the RNP length is 209.6 nm, close to the nominal spacing r0 = 200 nm between nearby adhesion sites.
To integrate both interactions into a single model, we adopt an approach different from that of Wang et al.5 They first determined the diffusivity under steric repulsion and subsequently used it as the baseline onto which the adhesive interaction was added. When the two were integrated, neither was affected by the other, and the two interactions were not coupled directly.
In our BD simulation, on the other hand, both steric and adhesive interactions are realized in the geometry of a random fiber network. The two are directly coupled in the sense that if steric repulsion keeps an RNP away from a fiber, that may directly hinder their adhesion. We take this to be a more realistic representation. Indeed, the diffusivity of Fig. 10 reflects a direct competition between steric repulsion and adhesive attraction. Dt is higher than the purely adhesive case but lower than the purely steric case, indicating a balancing effect between the two interactions. The steric repulsion, which accounts for the finite thickness of the RNP, tends to shield the adhesive sites and elevates RNP diffusivity well above that for the case with pure adhesion. In particular, the tendency of longer rods being captured by two or more adhesion sites simultaneously is largely obviated by the steric shielding. As a result, Dt increases monotonically with λ; the local maximum observed under pure adhesion has been overpowered.
It will be interesting to examine the coupling between the two mechanisms more generally, for other types of attractive potential and a range of parameter values for U0, ν and others, and perhaps for random distribution of adhesion sites on the polymer backbones. We leave such explorations to a separate endeavor.
4. Conclusions
In this work, we present Brownian dynamics simulations of rod-like nanoparticles (RNPs) diffusing in a random gel consisting of rigid fibers. Our observations show that in non-adhesive systems, RNP diffusivity increases monotonically with the RNP aspect ratio under the same hydrodynamic diameter. This trend is qualitatively similar to previous predictions of the obstruction-scaling (OS) model. Quantitatively, however, our model predicts a diffusivity considerably higher than the OS model prediction.We propose a new hypothesis to explain this discrepancy: a nanorod diffusing in a fibrous gel samples an effective pore-size distribution that differs from what the OS model assumes based on static geometry. We observe two modes of diffusion for RNPs in the networks: (a) the “meandering diffusion” occurs in coarser regions of the gel, characterized by lower translational diffusivity and higher rotational diffusivity; (b) the “longitudinal diffusion” occurs in denser regions, where tighter confinement by polymer chains limits RNP rotation and favors anisotropic diffusion along the long axis of the RNP, yielding lower rotational diffusivity and higher translational diffusivity. Moreover, the RNP spends considerably longer time in the meandering mode than the longitudinal mode. Effectively, therefore, the RNP samples preferably the coarser regions of the gel, and quickly traverses the denser regions by diffusing along its long axis. Both factors conspire to endow the long rods with superior diffusivity, much above what has previously been expected based on OS models. Our hypothesis has been supported by examining the average pore size in the gel surrounding either mode of diffusion, the number of close neighbors, and finally the anisotropic nature of the diffusion of rod-like NPs.
The above picture is counterintuitive, as one may expect NPs to linger in dense cages and to pass through coarse regions rapidly. The key to this puzzle is the anisotropic nature of the RNP diffusion, rooted in its shape anisotropy. Despite its great success for spherical NPs, the OS model turns out to be inaccurate for rod-like NPs. It estimates the obstruction by the polymer network solely from static geometry, disregarding the fact that in reality an NP has to trace out a continuous trajectory. In doing so, a rod-like NP experiences the hydrogel in a dynamic way that differs considerably from expectations based on the static geometry. We further assessed the discrepancy between the OS model predictions and our BD results by using experimental data. Our model shows better agreement with data than the extended OS model.
Furthermore, we have explored the interplay between steric and adhesive interactions. We demonstrate that it is essential to directly couple the two mechanisms, and that steric repulsion can shield certain adhesive sites, thereby diminishing the overall adhesion forces experienced by the RNP and resulting in a diffusivity that is intermediate between the purely steric and purely adhesive cases.
In examining the movement of the RNP through the network of rigid fibers, one may note a potential connection to reptation models for entangled polymers,37,38 and in particular the Doi theory for rod-like polymers.39 In a sense, the diffusive motion of the RNP in our context parallels that of a polymer reptating through a tube formed by entangled neighboring polymer chains; see Fig. 9.3 of Doi & Edwards.38 But there is a key difference, which is essentially the difference between a liquid and a gel. In the reptation models, the tube itself is constantly remodeling, thus giving rise to the flowability and viscoelasticity of the polymeric liquid. In the gel models, either with flexible polymers14 or rigid ones (our model), the polymer chains are cross-linked “permanently”, at least until yielding, and the medium remains an elastic solid permeated with liquid solvent.
We must point out a few simplifications in our model. First, we have neglected the flexibility of the polymer network. If the polymer chains can fluctuate and deform, they would allow the RNP more freedom in its diffusion, potentially increasing its diffusivity.6,14 To remedy this shortcoming, we may extend our description of the polymer network as composed of bead-spring chains, following earlier molecular dynamics models.6,14 Second, we have disregarded the hydrodynamic interaction (HI) between the RNP and the polymer chains. This could potentially increase the drag on the RNPs and reduce their diffusivity, especially when the RNP size is not much smaller than the pore size. Historically, HI has been accounted for via friction tensors originally developed for rigid spherical particles,23 and has been generalized to bead-spring models for polymer chains.24 This points to a method of adding HI to our RNP diffusion problem. Granted, the degree of complexity and magnitude of computation will be greatly augmented. Third, the spatial distribution of adhesion sites in real gels can differ from the roughly uniform distribution assumed in our model. Such spatial fluctuations may modify the long-time RNP diffusivity even if the overall density of adhesion sites is kept unchanged. Besides, we have not explored the effect of changing that density. Finally, polymeric fibers in real systems possess a finite thickness. Although our model is capable of accounting for finite-sized fibers, we performed all simulations with zero-thickness fibers in order to closely mimic the theoretical study of Wang et al.5 Incorporating finite fiber thickness would likely lead to reduced diffusivity, due to enhanced steric repulsion between the fibers and the diffusing particles. In light of the above limitations, our model should be viewed as a starting point for modeling diffusion of RNPs in realistic biological gels.
Thus, our Brownian model lays the groundwork for future extensions, e.g., to incorporate HI and network deformation. In spite of the above limitations, our simulations have provided deeper insights into the diffusion of rod-like nanoparticles in hydrogels, uncovering the role of anisotropic diffusion that can greatly boost the translational diffusivity of RNPs. Our findings can be leveraged to guide the design of nanoparticles optimized for targeted drug delivery through biopolymer gels like mucus.
Data availability
The computational methods for generating the numerical results, including the temporal discretization scheme, the statistical analysis of data and parameter evaluation, are described in the ESI.† The numerical code is available online: https://github.com/mrokhfrooz/BD_simulation_rodlike_nanoparticle_gels.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support from Mitacs Canada and Providence Healthcare (IT19059) and from the Natural Sciences and Engineering Research Council of Canada (Discovery Grant No. 2019-04162, 2024-03982 and Alliance International Grant No. 586462-23). They also extend their thanks to Joerg Rottler, Simcha Srebnik, Belal Tafech, and Jiuling Wang for fruitful discussions. This research was supported in part through the computational resources and services provided by Advanced Research Computing at the University of British Columbia.References
- D. Li, X. Li, J. Bai, Y. Liu, R. de Vries and Y. Li, Int. J. Biol. Macromol., 2021, 166, 401–408 CrossRef CAS PubMed
.
- B. Tafech, M. R. Rokhforouz, J. Leung, M. M. H. Sung, P. J. C. Lin, D. D. Sin, D. Lauster, S. Block, B. S. Quon, Y. Tam, P. Cullis, J. J. Feng and S. Hedtrich, Adv. Healthcare Mater., 2024, 13, 2304525 CrossRef CAS PubMed
.
- N. Zheng, J. Li, C. Xu, L. Xu, S. Li and L. Xu, Artif. Cells, Nanomed., Biotechnol., 2018, 46, 1132–1140 CrossRef CAS PubMed
.
- M. Yu, J. Wang, Y. Yang, C. Zhu, Q. Su, S. Guo, J. Sun, Y. Gan, X. Shi and H. Gao, Nano Lett., 2016, 16, 7176–7182 CrossRef CAS PubMed
.
- J. Wang, Y. Yang, M. Yu, G. Hu, Y. Gan, H. Gao and X. Shi, J. Mech. Phys. Solids, 2018, 112, 431–457 CrossRef CAS
.
- C. Bao, B. Liu, B. Li, J. Chai, L. Zhang, L. Jiao, D. Li, Z. Yu, F. Ren and X. Shi, Nano Lett., 2020, 20, 1352–1361 CrossRef CAS PubMed
.
- M. Guo, M. Wei, W. Li, M. Guo, C. Guo, M. Ma, Y. Wang, Z. Yang, M. Li and Q. Fu, J. Controlled Release, 2019, 307, 64–75 CrossRef CAS PubMed
.
- K. A. Rose, N. Gogotsi, J. H. Galarraga, J. A. Burdick, C. B. Murray, D. Lee and R. J. Composto, Macromolecules, 2022, 55, 8514–8523 CrossRef CAS
.
- A. Banerjee, J. Qi, R. Gogoi, J. Wong and S. Mitragotri, J. Controlled Release, 2016, 238, 176–185 CrossRef CAS PubMed
.
- W. Liu, L. Zhang, Z. Dong, K. Liu, H. He, Y. Lu, W. Wu and J. Qi, Nano Res., 2022, 15, 9243–9252 CrossRef CAS
.
- B. Xue, Y. Liu, Y. Tian and P. Yin, Nat. Commun., 2024, 15, 6502 CrossRef CAS PubMed
.
- X. Zhang, X. Dai, M. A. Habib, L. Gao, W. Chen, W. Wei, Z. Tang, X. Qi, X. Gong and L. Jiang, Nat. Commun., 2024, 15, 525 CrossRef CAS PubMed
.
- J. Wang and X. Shi, Acta Mech. Solida Sin., 2017, 30, 241–247 CrossRef
.
- B.-R. Zhao, B. Li and X. Shi, Nanoscale, 2021, 13, 17404–17416 RSC
.
- S.-J. Li, H.-J. Qian and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2018, 20, 20996–21007 RSC
.
- J. Wang, T. C. O’Connor, G. S. Grest, Y. Zheng, M. Rubinstein and T. Ge, Macromolecules, 2021, 54, 7051–7059 CrossRef CAS PubMed
.
- A. G. Ogston, Trans. Faraday Soc., 1958, 54, 1754–1757 RSC
.
- J. Hansing, C. Ciemer, W. K. Kim, X. Zhang, J. E. DeRouchey and R. R. Netz, Eur. Phys. J. E:Soft Matter Biol. Phys., 2016, 39, 1–13 CrossRef PubMed
.
- R. A. Cone, Adv. Drug Delivery Rev., 2009, 61, 75–85 CrossRef CAS PubMed
.
-
J. C. Berg, An introduction to interfaces and colloids: the bridge to nanoscience, World Scientific, 2010 Search PubMed
.
- A. Ortega and J. Garcıa de la Torre, J. Chem. Phys., 2003, 119, 9914–9919 CrossRef CAS
.
- A. Saadat and B. Khomami, J. Rheol., 2017, 61, 147–149 CrossRef CAS
.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352–1360 CrossRef CAS
.
- C.-C. Hsieh, L. Li and R. G. Larson, J. Non-Newtonian Fluid Mech., 2003, 113, 147–191 CrossRef CAS
.
-
A. Satoh, Modeling of magnetic particle suspensions for simulations, CRC Press, 2017 Search PubMed
.
- H. Löwen, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 1232 CrossRef PubMed
.
- M. M. Tirado, C. L. Martínez and J. G. De La Torre, J. Chem. Phys., 1984, 81, 2047–2052 CrossRef
.
- T. Kirchhoff, H. Löwen and R. Klein, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 5011 CrossRef CAS PubMed
.
- J.-Y. Chen, Z. Li, I. Szlufarska and D. J. Klingenberg, J. Rheol., 2021, 65, 273–288 CrossRef CAS
.
- M. T. Klann, A. Lapin and M. Reuss, Biophys. J., 2009, 96, 5122–5129 CrossRef CAS PubMed
.
- M. Quesada-Pérez and A. Martín-Molina, Adv. Colloid Interface Sci., 2021, 287, 102320 CrossRef PubMed
.
- T. Stylianopoulos, B. Diop-Frimpong, L. L. Munn and R. K. Jain, Biophys. J., 2010, 99, 3119–3128 CrossRef CAS PubMed
.
- D. Arcizet, B. Meier, E. Sackmann, J. O. Rädler and D. Heinrich, Phys. Rev. Lett., 2008, 101, 248103 CrossRef PubMed
.
- X. He, Y. Yang, Y. Han, C. Cao, Z. Zhang, L. Li, C. Xiao, H. Guo, L. Wang and L. Han, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2209260120 CrossRef CAS PubMed
.
- N. Arfin and H. B. Bohidar, Int. J. Biol. Macromol., 2012, 50, 759–767 CrossRef CAS PubMed
.
- M. Yu, L. Xu, F. Tian, Q. Su, N. Zheng, Y. Yang, J. Wang, A. Wang, C. Zhu and S. Guo, Nat. Commun., 2018, 9, 2607 CrossRef PubMed
.
- P.-G. De Gennes, J. Chem. Phys., 1971, 55, 572–579 CrossRef
.
-
M. Doi, S. F. Edwards and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, 1988, vol. 73 Search PubMed
.
- M. Doi, J. Polym. Sci., Polym. Phys. Ed., 1981, 19, 229–243 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00195a |
| This journal is © The Royal Society of Chemistry 2025 |