 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Long-range order in two-dimensional systems with fluctuating active stresses†
Yann-Edwin
Keta
 * and
Silke
Henkes
* and
Silke
Henkes
 *
*
Instituut-Lorentz for Theoretical Physics, Universiteit Leiden, 2333 CA Leiden, The Netherlands. E-mail: keta@lorentz.leidenuniv.nl; shenkes@lorentz.leidenuniv.nl
First published on 17th June 2025
Abstract
In two-dimensional tissues, such as developing germ layers, pair-wise forces (or active stresses) arise from the contractile activity of the cytoskeleton, with dissipation provided by the three-dimensional surroundings. We show analytically how these pair-wise stochastic forces, unlike the particle-wise independent fluctuating forces usually considered in active matter systems, produce conserved centre-of-mass dynamics and so are able to damp large-wavelength displacement fluctuations in elastic systems. A consequence of this is the stabilisation of long-range translational order in two dimensions, in clear violation of the celebrated Mermin–Wagner theorem, and the emergence of hyperuniformity with a structure factor S(q) ∼ q2 in the q → 0 limit. We then introduce two numerical cell tissue models which feature these pair-wise active forces. First a vertex model, in which the cell tissue is represented by a tiling of polygons where the edges represent cell junctions and with activity provided by stochastic junctional contractions. Second an active disk model, derived from active Brownian particles, but with pairs of equal and opposite stochastic forces between particles. We study the melting transition of these models and find a first-order phase transition between an ordered and a disordered phase in the disk model with active stresses. We confirm our analytical prediction of long-range order in both numerical models and show that hyperuniformity survives in the disordered phase, thus constituting a hidden order in our model tissue. Owing to the generality of this mechanism, we expect our results to be testable in living organisms, and to also apply to artificial systems with the same symmetry.
1 Introduction
Biological tissues are a paradigmatic active or living material, characterised by the competition between crowding effects and active driving. In in vitro epithelial cell layers, the focus of most models, activity arises primarily from cells crawling over the underlying solid substrate.1,2 This setup has motivated a number of minimal microscopic models of tissues, such as self-propelled particles3–6 and self-propelled Voronoi models.7–9 In these, the “self-propelled” qualifier indicates that a time-persistent and space-independent force acts on each degree of freedom (e.g. particle or Voronoi centre). However, in many developmental contexts such as avian10–12 and drosophila13 early development, the driving activity arises from cytoskeletal contractility,14–16 and the cells are surrounded by fluid that provides dissipation, but against which the tissue cannot exert active forces. These models therefore are not suitable here, and instead the active interactions within cell sheets need to be modelled as stochastic forces which act on pairs of degrees of freedom in an opposite manner, thus respecting action-reaction. Since the sum of these driving forces cancel, the dynamics they produce conserves the centre of mass, and should be regarded in continuum elastic formulation as deriving from the divergence of an active stress . We may then write for these overdamped systems
. We may then write for these overdamped systems | (1) |
![[D with combining low line]](https://www.rsc.org/images/entities/b_i_char_0044_0332.gif) el is a dynamical matrix17 describing elasticity (see Fig. 1(a)). More generally, one can envisage a full dissipation matrix
el is a dynamical matrix17 describing elasticity (see Fig. 1(a)). More generally, one can envisage a full dissipation matrix  that includes additional cell–cell terms, a point we will return to below.
that includes additional cell–cell terms, a point we will return to below.
 | ||
| Fig. 1 (a) Sketch of a two-dimensional continuous system with fluctuating active stress described by (1). (b) Vertex model with stochastic junction tension (jtVM). (c) Active Brownian particles with pair-wise propulsion forces (pABP). | ||
Recent studies within a field theoretical18 and a granular context19 have linked stochastic active stresses and the emergence of crystalline phases with long-range translational order and hyperuniform density fluctuations – fluctuations which vanish on large length scales. In the active matter context, long-range translational order and hyperuniformity have also been uncovered in systems with anti-alignment,20 chiral or non-reciprocal interactions,21–23 oscillatory driving forces,24 pulsating contractions,25 in systems of driven-dissipative hard spheres,26 as well as in active turbulence27 – see a recent review.28 However, a broader understanding together with a minimal model of these processes is lacking, and the link to the biological context has only very recently been made.25
It should be noted that within a continuum active fluid paradigm, eqn (1) with pair forces would belong to the well-understood class of dry or mixed dry-wet active nematics or active gels which have long been proposed as tissue models.29,30 The difference here is the active solid starting point with purely fluctuating activity, very unlike the typical active nematic state with moving defects. Moreover, we take microscopic order into account, allowing us to access translational and hexatic order parameters – see however31,32 for an intrinsically hexatic active fluid approach.
In this paper we first derive the active elastic theory of long-range correlations at linear order. We then show in two models of dense biological tissues how pair-wise fluctuating active forces stabilise long-range translational order. In addition, we show numerically that hyperuniformity is displayed both in the low-noise ordered solid and the large-noise disordered liquid. We contrast these results with simulations of analogous models with particle-wise fluctuating active forces where translational order is at most quasi-long-range with algebraically decreasing correlations33 and diverging structural fluctuations in the infinite size limit. The paper is organised as follows. In Section 2 we derive analytically the structural fluctuations of models described by (1). In Section 3 we introduce our models and perform the numerical study of their structural characteristics, including their melting transition. In Section 4 we gather our findings and discuss their future applications.
2 Long-range translational order and hyperuniformity
At thermal equilibrium, the Mermin–Wagner theorem indicates that there can be no spontaneous breaking of a continuous symmetry in dimensions d = 1, 2 at finite temperature.34 A consequence of this is that thermally induced long-range displacement fluctuations grow with system size in theses low dimensions, and long-range translational order is unachievable in the thermodynamic limit.35,36 Moving flocks however (almost certainly37) display true long-range polar orientational order,38 the first indication that activity allows for exceptions of this law.Structural fluctuations can be quantified through the counting of the number N(R) of particles in a volume Rd as a function of R. For typical disordered systems such as liquids, the variance Var(N;R) = 〈N(R)2〉 − 〈N(R)〉2 grows as Rd, while Var(N;R) ∼ Rd−1 in periodic crystals.39 Many active systems, in particular those which display flocking behaviours, were reported to display giant number fluctuations, in the sense that Var(N;R) grows faster than Rd.40–45 More recently, long-range translational order in two-dimensional active systems has been a subject of interest. Galliano et al. have shown how such order arises in a nonequilibrium particle model driven by pair-wise random displacements.46 Maire and Plati have derived this property in underdamped granular systems driven by a momentum-conserving noise,19 using an approach similar to the one detailed below. In both cases, long-range translational order is associated with hyperuniformity. This designates the anomalous vanishing of density fluctuations on large length scales,47 associated with a variance Var(N;R) which decreases slower than Rd, and is known to occur in systems with absorbing state transitions.48–50
In this section we derive, for a two-dimensional continuous elastic medium, the fluctuations of the displacement field at linear order. In a second part we show how these relate, in a discrete system, to the translational order correlation function and the scaling of the structure factor over large wavelengths.
2.1 Two-dimensional continuous medium
We introduce the Fourier transform in space and time of the displacement field | (2) |
 | (3) |
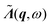 is the Fourier transform of the noise term
is the Fourier transform of the noise term | (4) |
We assume (i) that the Fourier transform of the dynamical matrix  can be decomposed as follows5
can be decomposed as follows5
 | (5) |
![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) = q/|q|, Ũ‖(q,ω) = (Ũ(q,ω)·
= q/|q|, Ũ‖(q,ω) = (Ũ(q,ω)·![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) )
)![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) and Ũ⊥(q,ω) = Ũ(q,t) − Ũ‖(q,ω) are respectively the longitudinal and transverse displacements in Fourier space, and B and μ are respectively the bulk and shear moduli.
and Ũ⊥(q,ω) = Ũ(q,t) − Ũ‖(q,ω) are respectively the longitudinal and transverse displacements in Fourier space, and B and μ are respectively the bulk and shear moduli.
We assume (ii) that the fluctuations of the active stress (4) follow18,19,51
| 〈λ(r,t)·λ(r′,t′)〉 = −σ2a2e−|t−t′|/τ∇2δ(r − r′), | (6) |
 | (7) |
We use (3), (5), and (7), to compute the equal-time displacement fluctuations in Fourier space (see ESI,† Section A, for a full derivation) and obtain
 | (8a) |
 and
and  . We compare this result to the case of a space-uncorrelated fluctuating force field with correlations 〈λ(r,t)·λ(r′,t′)〉 = f2a2e−|t−t′|/τδ(r − r′), for which the spectrum reads5
. We compare this result to the case of a space-uncorrelated fluctuating force field with correlations 〈λ(r,t)·λ(r′,t′)〉 = f2a2e−|t−t′|/τδ(r − r′), for which the spectrum reads5 | (8b) |
Spectrum (8a) importantly differs from (8b) by the absence of the factor 1/|q|2 which diverges on large length scales |q| → 0. This difference arises solely from the spectrum of stochastic forces (7) whose fluctuations vanish in the limit |q| → 0.
We define the variance of displacement for a square two-dimensional system of linear size L as
 | (9) |
 | (10a) |
 | (10b) |
2.2 Two-dimensional regular lattice
We just showed how two-dimensional systems with fluctuating active stresses have finite displacement fluctuations in the thermodynamic limit L → ∞. This motivates us to investigate structural fluctuations in discrete ordered systems. We then consider a system of N particles with displacements ui = ri − r0i from their equilibrium lattice points r0i. We highlight that the displacement spectra (8) follow the transformation from continuous to discrete Fourier space 〈ũ(q,t)·ũ(q′,t)*〉 → a4〈ũq(t)·ũq′(t)*〉, with the coarse-graining length , through the substitution rule δ(q − q′) → (Δq)−2δq,q′ with Δq = 2π/L the wavevector spacing.5
, through the substitution rule δ(q − q′) → (Δq)−2δq,q′ with Δq = 2π/L the wavevector spacing.5
We introduce the local hexatic orientational order parameter ψ6,i and the local translational order parameter ψq0,i in order to quantify structural order,33,54–56
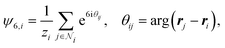 | (11) |
| ψq0,i = eiq0·(ri−r0), | (12) |
 is the ensemble of nearest neighbours of particle i and zi the coordination number of particle i, i.e. the number of particles in
is the ensemble of nearest neighbours of particle i and zi the coordination number of particle i, i.e. the number of particles in  , r0 is the position of one of the particles, and q0 is a reciprocal vector of the lattice. We infer the latter from the position of the maximum of the structure factor (16)S(q0) = maxq
, r0 is the position of one of the particles, and q0 is a reciprocal vector of the lattice. We infer the latter from the position of the maximum of the structure factor (16)S(q0) = maxq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(q).57
S(q).57
The translation by −r0 in (12) is chosen so that ψq0,i = 1 everywhere in a perfect crystal lattice (see Fig. 3). This works since for any vector v linking two lattice points, q0·v = 0 modulo 2π. As this simply corresponds to choosing a particular origin, it does not affect the correlations (14), only the argument of (12).
We quantify the global order parameter with the following ensemble averages (x = 6, q0)
 | (13) |
 | (14) |
The latter function, considering translational order, is related to the scalings (10) (see ESI,† Section C) as follows
 | (15a) |
 | (15b) |
These scalings show that, in the case a stochastic stress field, true long-range translational order is possible, as opposed to the quasi-long-range order in the case of a stochastic force field.
Finally, we define the structure factor58
 | (16) |
 | (17) |
This result relies on a Taylor expansion of the exponentials in (16), in the large-system-size and small-wavevector limits, and is consistent with previous derivations.59 Therefore, given the displacement spectra (8), we infer the following scalings for the structure factor (16)
 | (18a) |
 | (18b) |
In summary, we have presented three emerging properties for two-dimensional systems in the thermodynamic limit: finite displacement fluctuations with respect to the lattice positions (10a), long-range translational order (15a), and hyperuniformity (18a). We stress that these properties derive from considering a space-uncorrelated stochastic stress field rather than a force field: they rely on the driving fluctuations (here the active stress field) decaying on large wavelengths while competing against a dissipation mechanism acting independently on all individuals in the system. It is thus noteworthy that these properties would disappear if we included a white noise term in (1) (see ESI,† Section B.2) – such a term would be expected to counterbalance the white drag if the system were to follow the second fluctuation–dissipation theorem.60–62 We finally highlight that these properties are not affected if we include an additional viscosity-like cell–cell dissipation term (see ESI,† Section B.2), i.e. a full dissipation matrix  . This adds realism to cell models as it counterbalances the fluctuating stresses, and we can show that this modification as expected only affects the small-wavelength fluctuations.
. This adds realism to cell models as it counterbalances the fluctuating stresses, and we can show that this modification as expected only affects the small-wavelength fluctuations.
3 Tissue models with pair-wise stochastic forces
Our predictions were derived for harmonic systems with particles arranged in regular lattices, and so are potentially susceptible to renormalisation group flow to different exponents from nonlinear terms.18,50 In order to test the robustness of these predictions outside of the linear and ordered regime, as well as the applicability of these results, we introduce two numerical models suited for the description of dense cell tissues (see Fig. 1) and study their structural fluctuations.3.1 Model definitions
In Section 3.1.1, we introduce a model based on a polygonal tiling of the two-dimensional space, where each tile represents a single cell. This kind of model has been widely used to represent confluent cell sheets2,63,64 and allows to represent complex interactions, between cells and between cells and their substrate, as well as constraints on cell shapes. We highlight here two general classes of these models: Voronoi models7–9,65 where the tiling of cells is determined through a Voronoi tesselation from cell centres, and vertex models (VM)66–68 where cell corners (or vertices) are the degrees of freedom. The model we first introduce belongs to this second class.In Section 3.1.2, we introduce a model based on interacting disks. Despite such models lacking the possibility to represent accurate cell shapes and deformations, they have been applied with great success to understand mesoscale correlations in active tissues.5 Moreover, the simplicity of these models allow for the numerical simulation of the large systems needed to characterise large-wavelength fluctuations.
For both models studied here, we introduce the following overdamped equation of motion of their degrees of freedom (respectively cell vertices and disk centres), which is the discrete analogue of (1),
| ζṙμ = −∂rμUint + λactμ, | (19) |
 | (20) |
We introduce the following vertex model interaction potential65
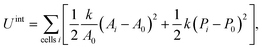 | (21) |
We consider active forces which are pair-wise or particle-wise, respectively (see Fig. 1(b) for a visual representation)
 | (22a) |
| λactμ = fu(θμ), | (22b) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θμ,sin
θμ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θμ), ν ∧ μ designates the vertices ν linked by an edge to vertex μ, Tμν is the tension of edge μν,
θμ), ν ∧ μ designates the vertices ν linked by an edge to vertex μ, Tμν is the tension of edge μν, ![[small script l]](https://www.rsc.org/images/entities/b_char_e146.gif) μν = rν − rμ and
μν = rν − rμ and  . These forces evolve stochastically: tensions Tμν follow an Ornstein–Uhlenbeck process69–72 and angles θμ diffuse similarly to self-propelled Voronoi models,8,9
. These forces evolve stochastically: tensions Tμν follow an Ornstein–Uhlenbeck process69–72 and angles θμ diffuse similarly to self-propelled Voronoi models,8,9 | (23a) |
 | (23b) |
We perform simulations of N cells with periodic boundary conditions. We define the unit length  , energy kA0 = 1, and time ζ/k = 1. Simulations are started from a regular hexagonal packing which satisfies cell areas Ai = A0. This implies that the area of the system is L2 = NA0. We enforce the shape index
, energy kA0 = 1, and time ζ/k = 1. Simulations are started from a regular hexagonal packing which satisfies cell areas Ai = A0. This implies that the area of the system is L2 = NA0. We enforce the shape index  such that in absence of forcing the regular hexagonal packing of cells is both rigid and force-free. We use τ = 5 for all data presented.
such that in absence of forcing the regular hexagonal packing of cells is both rigid and force-free. We use τ = 5 for all data presented.
This model is integrated using the MIT-licensed library cells.73
 | (24) |
We consider active forces which are pair-wise or particle-wise, respectively (see Fig. 1(c) for a visual representation)
 | (25a) |
| λactμ = fu(θμ), | (25b) |
 | (26) |
We perform simulations of N cells with periodic boundary conditions. We define the unit length D/2 = 1, energy k(D/2)2 = 1, and time ζ/k = 1. Except where noted, simulations are started from a regular hexagonal packing with packing fraction ϕ = Nπ(D/2)2/L2 = 1, corresponding to a thoroughly solid state. We use τ = 25 for all data presented.
This model is integrated using the GPL-licensed library SAMoS.75
3.2 Location and properties of the melting transition
We expect a disordered liquid phase at large stochastic force amplitude f, and an ordered solid phase at small f. While at equilibrium, it is expected that structural and dynamical characteristics coincide and so determine the phase of the system, we cannot exclude that out of equilibrium, structure and dynamics may indicate different phases (see e.g. the flowing crystals of ref. 76). We thus consider two structural characteristics, the global hexatic and translational order parameters Ψ6 and Ψq0(13), and a dynamical characteristics, the mean square displacement (MSD)77 | (27) |
 the position of the centre of mass at time t, to determine the phase of our models as a function of the force amplitudes.
the position of the centre of mass at time t, to determine the phase of our models as a function of the force amplitudes.
For both jtVM and pABP models there is, as the force amplitude is increased, a sharp simultaneous decrease in both translational and hexatic order (Fig. 2(a) and (b)). We thus observe a structurally ordered phase, in the jtVM model for f ≲ 0.03, and in the pABP model for f < 0.11. For the pABP model, dynamics is slow near the transition, and we have confirmed that configurations at f = 0.115 and f = 0.117 are disordered in steady-state by using long simulations of both ordered and disordered initial configurations.
 | ||
Fig. 2 (a) and (b) Global structural order parameters (13) – hexatic order parameter Ψ6 (blue open symbols) and translational order parameter Ψq0 (orange full symbols) – in steady state as functions of the stochastic force amplitude f. (c) and (d) Mean squared displacements as functions of time MSD(t) (27) in steady state for different stochastic force amplitudes f. Dashed lines are linear functions of time as guides to the eye. (a) and (c) Junctional tension vertex model (jtVM) with N = 108 cells and persistence time τ = 5. (b) and (d) Pair active Brownian particles (pABP) with N = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 particles and persistence time τ = 25. Identical markers between (a) and (c) and between (b) and (d) correspond to identical data sets. 384 particles and persistence time τ = 25. Identical markers between (a) and (c) and between (b) and (d) correspond to identical data sets. | ||
In Fig. 3, we plot configurations of the pABP model corresponding to the solid (a, b), the liquid (e, f), and a configuration at an intermediate value of f (c, d). The intermediate force amplitudes f = 0.112 and to a small extent f = 0.11 show phase coexistence at steady state after liquid bubbles slowly nucleate in the ordered solid (see ESI,† Videos S1 and S2).
 | ||
Fig. 3 Order and disorder for pair active Brownian particles (pABP). Visualisation of the argument of the local hexatic order parameter arg(ψ6,i) (11) (left column, (a), (c) and (e)), and the argument of the local translational order parameter arg(ψq0,i) (12) (right column, (b), (d) and (f)). (g) Shows different hexagonal packing orientations with the colour corresponding to the argument of the hexatic order parameter. Colours associated to the argument of the translational order parameter illustrate deviations from the regular lattice corresponding to ψq0: an ordered lattice should display arg(ψq0,i) = 0 everywhere. We used N = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 particles and persistence time τ = 25. Stochastic force amplitude is (a) and (b) f = 0.1, (c) and (d) f = 0.112, (e) and (f) f = 0.15. 384 particles and persistence time τ = 25. Stochastic force amplitude is (a) and (b) f = 0.1, (c) and (d) f = 0.112, (e) and (f) f = 0.15. | ||
This structural ordering partially coincides with a dynamical transition from a diffusing liquid state at large f, where correlations decay over times t ≳ τ, to an arrested solid state at small f as evidenced by the plateau in MSD (Fig. 2(c) and (d)). For the pABP model, we observe a narrow range f = 0.11–0.112 of very slow liquid dynamics while the system stays long range ordered while bubbles of disordered phase nucleate in the system. In the ESI† (Section E), we also show how the self-intermediate scattering function Fs(t) relaxes, and finally, we also provide the dynamical characteristics of the ABP model, for comparison.
The abrupt structural relaxation together with the equally abrupt transition in the MSD and the coexisting phase is indicative of a first-order melting transition in the pABP system. We now turn to our observations for the structural fluctuations.
3.3 Structural fluctuations
Deep in the solid phase, we expect our derivations for harmonic lattices to hold. We first compute the displacement variance 〈u2〉 for both models in the solid phase, with particle-wise and pair-wise stochastic forces, as a function of system size (Fig. 4(a) and (b)). These confirm our predictions (10). For systems with pair-wise stochastic forces, 〈u2〉 converges to a finite value at large N. In contrast, for systems with particle-wise stochastic forces, 〈u2〉 diverges as . We fit 〈u2〉(N) to a constant 〈u2〉σ∞ for models with pair-wise stochastic forces, and to
. We fit 〈u2〉(N) to a constant 〈u2〉σ∞ for models with pair-wise stochastic forces, and to  for models with particles-wise stochastic forces. We extract Cf ≈ 4.83 × 10−3 and 〈u2〉σ∞ ≈ 7.00 × 10−3 in the vertex model with self-propelled vertices and junction tensions respectively (Fig. 4(a)), and Cf ≈ 2.41 × 10−2 and 〈u2〉σ∞ ≈ 3.10 × 10−3 for active and pair active Brownian particles respectively (Fig. 4(b)). It is noteworthy that 〈u2〉 can be derived from the displacement spectra (8) (see ESI,† Section C).
for models with particles-wise stochastic forces. We extract Cf ≈ 4.83 × 10−3 and 〈u2〉σ∞ ≈ 7.00 × 10−3 in the vertex model with self-propelled vertices and junction tensions respectively (Fig. 4(a)), and Cf ≈ 2.41 × 10−2 and 〈u2〉σ∞ ≈ 3.10 × 10−3 for active and pair active Brownian particles respectively (Fig. 4(b)). It is noteworthy that 〈u2〉 can be derived from the displacement spectra (8) (see ESI,† Section C).
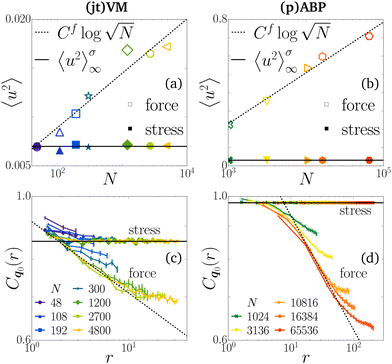 | ||
Fig. 4 (a) and (b) Displacement fluctuations 〈u2〉 (10) computed in steady state and plotted for (a) the vertex model with particle-based self-propulsion and junctional tension (jtVM), and (b) particle and pair active Brownian particles (pABP) as a function of the number of particles N. Full symbols represent models with pair-wise stochastic forces, which we fit to a constant 〈u2〉σ∞ (solid lines). In contrast, for models with particle-wise stochastic forces (plotted in open symbols), we fit to  (dashed lines). These plots are logarithmic on the x-axis and linear on the y-axis. (c) and (d) Translational order correlations Cq0(14) for the same data as in (a) and (b) with pair-wise models (full symbols) and particle-wise models (open symbols), together with our predictions for the large-distance scalings of the correlations (15): a constant (stress, solid lines) for pair-wise and an algebraic decay (force, dashed lines) for particle-wise stochastic forces. These plots are logarithmic on both axes. We used persistence time τ = 5 and force amplitude f = 0.02 for both vertex models (a) and (c) and persistence time τ = 25 and force amplitudes f = 0.1 and f = 0.05 for the pair-wise and particle-wise particle models respectively (b) and (d). Identical colours and markers between plots correspond to identical data sets. (dashed lines). These plots are logarithmic on the x-axis and linear on the y-axis. (c) and (d) Translational order correlations Cq0(14) for the same data as in (a) and (b) with pair-wise models (full symbols) and particle-wise models (open symbols), together with our predictions for the large-distance scalings of the correlations (15): a constant (stress, solid lines) for pair-wise and an algebraic decay (force, dashed lines) for particle-wise stochastic forces. These plots are logarithmic on both axes. We used persistence time τ = 5 and force amplitude f = 0.02 for both vertex models (a) and (c) and persistence time τ = 25 and force amplitudes f = 0.1 and f = 0.05 for the pair-wise and particle-wise particle models respectively (b) and (d). Identical colours and markers between plots correspond to identical data sets. | ||
Next, we compute the translational order correlation function Cq0 in the solid phase (Fig. 4(c) and (d)). We confirm that the solid phase of the models with pair-wise stochastic forces exhibits long-range translational order, with a large-distance correlation value deriving from the (finite) displacement variance. We observe, in the case of particle-wise stochastic forces, that correlations decay algebraically, consistently with quasi-long-range translational order.33 Our linear response predictions (15) fit this data if we use the values of Cf and 〈u2〉σ∞ determined from the system-size dependence of displacement fluctuations (Fig. 4(a) and (b)), as well as the measured reciprocal lattice vector squared norms |q0|2 ≈ 45.6 for the vertex model and |q0|2 ≈ 14.6 for the particle model. Therefore, we confirm that the exponent of this decay is directly related to the factor with which the displacement variance diverges (15b). We report the following exponents for the algebraic decay of the correlations Cq0 ∼ r−η in the case of systems with stochastic forces:  for disk ABPs and ηVM ≈ 0.110 for the self-propelled vertex model. Both exponents are below their expected upper limit of
for disk ABPs and ηVM ≈ 0.110 for the self-propelled vertex model. Both exponents are below their expected upper limit of  within the KTHNY theory, consistently with previous studies on self-propelled particles78 and unlike active particles with small amounts of polar alignment.33
within the KTHNY theory, consistently with previous studies on self-propelled particles78 and unlike active particles with small amounts of polar alignment.33
In Fig. 5 we compute the order correlation functions through the melting transition, using the largest system size N we have available. As shown in Fig. 5(a) and (b), the orientational order correlation function C6(r) in both ABP and pABP models shows long-range correlations in the solid phase and short-ranged correlations in the liquid phase. We observe indications of a power-law decay near the melting transition, and notably we find a significant drop between f = 0.11 and f = 0.112 for the pABP model, both liquids in the coexistence region. As shown in Fig. 5(c) and (d), the translational order correlation Cq0 has the same transition points, though in the solid phase the pABP has long range order while the ABP is power law (note the extended y range compared to Fig. 4(d)). We stress that regions with short-range structural order are rich in defects, as evidenced by coordination numbers zi ≠ 6, while regions with long-range structural order are exempt of these same defects (see ESI,† Section F), in accordance with the established understanding of the melting of two-dimensional solids.79 For the pABP model, we confirm thus that the diffusing liquid state corresponds to a molten state with short-range structural correlations, while the arrested solid state displays long-range structural order. At our current numerical resolution, in the pABP model, we do not see evidence of a hexatic phase8,78,80 with finite hexatic order and vanishing translational order, with the potential candidates f = 0.11–0.112 showing solid–liquid coexistence instead.
Finally, we compute the radially-averaged structure factor S(q) to test our predictions of hyperuniformity (16). We present results exclusively for the (p)ABP models because the large systems sizes needed to observe the large-wavelength decay of structural fluctuations are not yet attainable with our current vertex model algorithm. In Fig. 6, we plot the structure factor for particle-wise (a) and pair-wise (b) stochastic forces. In the former case, we observe that S(q) converges to a finite constant as q → 0, which is the expected behaviour for self-propelled particles systems at moderate activities away from spontaneous phase separation.81,82 In the latter case, we do observe the expected scaling S(q) ∼ q2 as q → 0 away from the order-to-disorder transition, which confirms that these systems are indeed hyperuniform. Most interestingly, we observe that this scaling applies not only in the solid phase at f ≤ 0.1, where our derivation is expected to hold, but also in the liquid phase at f ≥ 0.15. Therefore, despite this phase showing orientational and translational disorder on small length scales only (Fig. 3(e) and (f)), this measurement confirms that there is a “hidden order” on large length scales,39 which has also recently been observed in phase separating droplets.83 We also see that the scaling S(q) ∼ f2 of the continuum prediction works well in the deeply solid region. In both regions, we observe an apparent ∼qα scaling with α > 2 for some values of f. However, as we showed, large-wavelength relaxations are heavily suppressed for fluctuating active stresses, and relaxation to the true steady state of S(q) may occur only on an inordinately long time scale. Meanwhile, near the transition region where order and disorder coexist, on both sides, the system displays more complex, but not hyperuniform scaling of S(q).
 | ||
Fig. 6 Scaled structure factor S(q)/f2(16) defined as cylindrical average of S(q) over wavevectors q = (2πm/Lx,2πn/Ly) which satisfy |q| ∈ [q − δq/2,q + δq/2] with δq = 10−2 and divided by the square of the stochastic force amplitude f2. We plot the structure factor for different stochastic force amplitudes f in (a) for the particle model with particle-wise stochastic force (ABP), and in (b) for the particle model with pair-wise stochastic forces (pABP). We used N = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 or 65 384 or 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 particles, and persistence τ = 25. 536 particles, and persistence τ = 25. | ||
4 Discussion and conclusion
In this paper we first demonstrated how, within linear elasticity theory, two-dimensional active solids featuring fluctuating active stresses display finite displacement fluctuations 〈u2〉 in the thermodynamic limit N → ∞ (10), long-range translational order (15), and vanishing large-wavelength density fluctuations, i.e. hyperuniformity (18).These properties derive from, on the one hand, the absence of particle-wise white noise counterbalancing the instantaneous particle-wise friction, thus violating the second fluctuation–dissipation theorem,60–62 and on the other hand, the fluctuations of the driving force vanishing for large wavelengths (7).
Microscopically, these fluctuating active stresses take the form of pair-wise stochastic forces, forces which respect action-reaction rather than the more usual particle-wise active driving. We introduced two numerical models which incorporate these pair-wise stochastic forces: a vertex model with fluctuating junction tension (jtVM) and a particle-based model with pair-wise additive stochastic forces respecting action-reaction (pABP). We showed that all of our predictions held in both models. These models are built from widespread active matter models used to describe the physics of dense cell tissues, therefore we expect these results to shed light on both out-of-equilibrium ordering transitions as well as on structural fluctuations of living systems.
Since an ordered symmetry-broken phase is possible within our model, it is questionable if the two-step melting scenario of two-dimensional solid from the KTHNY theory applies here. This has been the subject of recent interest in the active matter community with several experimental systems being designed to address these questions.76,84,85 To the best of our current numerical efforts, we have not been able to identify a hexatic phase which would feature short-range translational order and quasi-long-range orientational order. Moreover we observe phase-separated configurations close to the transition (Fig. 3(c) and (d)) which indicate a first-order transition between a disordered liquid and an ordered solid as in three-dimensional equilibrium systems.
Our numerical results also show that disordered liquid states, outside the scope of linear elasticity theory, display hyperuniformity as well.21,25,26 Previously it was shown that force-balanced configurations (ground states of the potential energy) of Voronoi models of biological tissues have suppressed density fluctuations and are thus hyperuniform.86–88 In contrast, our pathway is more general as it is based on the symmetry of the active fluctuations and does not depend on the specific interaction potential. This outlines a larger class of active systems which encompasses non-motile active matter models, e.g. featuring pulsating contractions25 or state-dependent interaction potentials.89 Therefore we expect our results to be widely applicable.
We note that there is evidence of hyperuniform organisation in biological systems, e.g. cell nuclei in brain tumours90 or suspensions of algae.91 Further studies may explore if the mechanism we have described is exploited in cell tissues in order to suppress density fluctuations.
Conflicts of interest
There are no conflicts to declare.Data availability
All relevant data supporting the findings of this study are included in the manuscript and its ESI† and were generated using the free software libraries cells73 and SAMoS.75Acknowledgements
We wholeheartedly thank Henry Alston, Konstantinos Andreadis, Calvin Bakker, Arthur Hernandez, Sander Kammeraat, Juliane Klamser, Qun-Li Lei, Marko Popović, Jan Rozman, and Rastko Sknepnek for insightful discussions. We acknowledge fruitful discussions at the workshop “Computational Advances in Active Matter” held in December 2023 at the Lorentz Center in Leiden which we thank. SH would like to acknowledge the 2024 Active Solids KITP program, and this research was supported in part by grant NSF PHY-2309135 to the Kavli Institute for Theoretical Physics (KITP). This work was performed using the computational resources from Instituut-Lorentz and from the Academic Leiden Interdisciplinary Cluster Environment (ALICE) provided by Universiteit Leiden.Notes and references
- X. Trepat, M. R. Wasserman, T. E. Angelini, E. Millet, D. A. Weitz, J. P. Butler and J. J. Fredberg, Nat. Phys., 2009, 5, 426–430 Search PubMed.
- R. Alert and X. Trepat, Annu. Rev. Condens. Matter Phys., 2020, 11, 77–101 Search PubMed.
- A. P. Solon, M. E. Cates and J. Tailleur, Eur. Phys. J.: Spec. Top., 2015, 224, 1231–1262 Search PubMed.
- P. Romanczuk, M. Bär, W. Ebeling, B. Lindner and L. Schimansky-Geier, Eur. Phys. J.: Spec. Top., 2012, 202, 1–162 Search PubMed.
- S. Henkes, K. Kostanjevec, J. M. Collinson, R. Sknepnek and E. Bertin, Nat. Commun., 2020, 11, 1405 Search PubMed.
- D. Martin, J. O'Byrne, M. E. Cates, É. Fodor, C. Nardini, J. Tailleur and F. van Wijland, Phys. Rev. E, 2021, 103, 032607 CrossRef CAS PubMed.
- D. Bi, X. Yang, M. C. Marchetti and M. L. Manning, Phys. Rev. X, 2016, 6, 021011 Search PubMed.
- A. Pasupalak, L. Yan-Wei, R. Ni and M. Pica Ciamarra, Soft Matter, 2020, 16, 3914–3920 RSC.
- M.-Y. Li and Y.-W. Li, Phys. Rev. Res., 2024, 6, 033209 CrossRef CAS.
- E. Rozbicki, M. Chuai, A. I. Karjalainen, F. Song, H. M. Sang, R. Martin, H.-J. Knölker, M. P. MacDonald and C. J. Weijer, Nat. Cell Biol., 2015, 17, 397–408 CrossRef CAS PubMed.
- M. Saadaoui, D. Rocancourt, J. Roussel, F. Corson and J. Gros, Science, 2020, 367, 453–458 CrossRef CAS PubMed.
- R. Sknepnek, I. Djafer-Cherif, M. Chuai, C. Weijer and S. Henkes, eLife, 2023, 12, e79862 CrossRef CAS PubMed.
- F. Brauns, N. H. Claussen, M. F. Lefebvre, E. F. Wieschaus and B. I. Shraiman, eLife, 2024, 13, RP95521 CrossRef PubMed.
- D. Mizuno, C. Tardin, C. F. Schmidt and F. C. MacKintosh, Science, 2007, 315, 370–373 CrossRef CAS PubMed.
- F. C. MacKintosh and A. J. Levine, Phys. Rev. Lett., 2008, 100, 018104 CrossRef CAS PubMed.
- F. C. MacKintosh and C. F. Schmidt, Curr. Opin. Cell Biol., 2010, 22, 29–35 CrossRef CAS PubMed.
- W. van Saarloos, V. Vitelli and Z. Zeravcic, Soft Matter: Concepts, Phenomena, and Applications, Princeton University Press, Princeton, 2024 Search PubMed.
- H. Ikeda, Phys. Rev. E, 2023, 108, 064119 CrossRef CAS PubMed.
- R. Maire and A. Plati, J. Chem. Phys., 2024, 161, 054902 CrossRef CAS PubMed.
- H.-H. Boltz and T. Ihle, Hyperuniformity in Deterministic Anti-Aligning Active Matter, arXiv, 2024, arXiv:2402.19451 DOI:10.48550/arXiv.2402.19451.
- Q.-L. Lei, M. P. Ciamarra and R. Ni, Sci. Adv., 2019, 5, eaau7423 CrossRef PubMed.
- Y. Kuroda, T. Kawasaki and K. Miyazaki, Phys. Rev. Res., 2025, 7, L012048 CrossRef CAS.
- J. Chen, X. Lei, Y. Xiang, M. Duan, X. Peng and H. P. Zhang, Phys. Rev. Lett., 2024, 132, 118301 CrossRef CAS PubMed.
- H. Ikeda and Y. Kuroda, Phys. Rev. E, 2024, 110, 024140 CrossRef CAS PubMed.
- Z.-Q. Li, Q.-L. Lei and Y.-Q. Ma, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2421518122 CrossRef CAS PubMed.
- Q.-L. Lei and R. Ni, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 22983–22989 CrossRef CAS PubMed.
- R. Backofen, A. Y. A. Altawil, M. Salvalaglio and A. Voigt, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2320719121 CrossRef CAS PubMed.
- Y. Lei and R. Ni, J. Phys.: Condens. Matter, 2025, 37, 023004 CrossRef CAS PubMed.
- J. Prost, F. Jülicher and J.-F. Joanny, Nat. Phys., 2015, 11, 111–117 Search PubMed.
- A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Nat. Commun., 2018, 9, 3246 Search PubMed.
- J.-M. Armengol-Collado, L. N. Carenza, J. Eckert, D. Krommydas and L. Giomi, Nat. Phys., 2023, 19, 1773–1779 Search PubMed.
- J.-M. Armengol-Collado, L. N. Carenza and L. Giomi, eLife, 2024, 13, e86400 Search PubMed.
- X.-q Shi, F. Cheng and H. Chaté, Phys. Rev. Lett., 2023, 131, 108301 CrossRef CAS PubMed.
- B. I. Halperin, J. Stat. Phys., 2019, 175, 521–529 CrossRef.
- J. M. Kosterlitz, J. Phys.: Condens. Matter, 2016, 28, 481001 CrossRef CAS PubMed.
- B. Illing, S. Fritschi, H. Kaiser, C. L. Klix, G. Maret and P. Keim, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1856–1861 CrossRef CAS PubMed.
- B. Benvegnen, O. Granek, S. Ro, R. Yaacoby, H. Chaté, Y. Kafri, D. Mukamel, A. Solon and J. Tailleur, Phys. Rev. Lett., 2023, 131, 218301 CrossRef CAS PubMed.
- J. Toner and Y. Tu, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 4828–4858 CrossRef CAS.
- S. Torquato, Phys. Rep., 2018, 745, 1–95 CrossRef CAS.
- J. Toner, Y. Tu and S. Ramaswamy, Ann. Phys., 2005, 318, 170–244 CAS.
- H. Chaté, F. Ginelli and R. Montagne, Phys. Rev. Lett., 2006, 96, 180602 CrossRef PubMed.
- V. Narayan, S. Ramaswamy and N. Menon, Science, 2007, 317, 105–108 CrossRef CAS PubMed.
- J. Deseigne, O. Dauchot and H. Chaté, Phys. Rev. Lett., 2010, 105, 098001 CrossRef PubMed.
- H. P. Zhang, A. Be’er, E.-L. Florin and H. L. Swinney, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13626–13630 CrossRef CAS PubMed.
- S. Henkes, Y. Fily and M. C. Marchetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 040301 CrossRef PubMed.
- L. Galliano, M. E. Cates and L. Berthier, Phys. Rev. Lett., 2023, 131, 047101 CrossRef CAS PubMed.
- S. Torquato and F. H. Stillinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 041113 CrossRef PubMed.
- D. Hexner and D. Levine, Phys. Rev. Lett., 2017, 118, 020601 CrossRef PubMed.
- F. De Luca, X. Ma, C. Nardini and M. E. Cates, J. Phys.: Condens. Matter, 2024, 36, 405101 CrossRef CAS PubMed.
- A. Fernandez-Nieves, A. D. L. Cotte, D. Pearce, J. Nambisan, A. Levy and L. Giomi, Hyperuniform Active Matter, Research Square, 2024, preprint, rs-4292677 DOI:10.21203/rs.3.rs-4292677/v1.
- A. Cavagna, J. Cristín, I. Giardina and M. Veca, Phys. Rev. E, 2024, 109, 064136 CrossRef CAS PubMed.
- H. Peierls, Ann. Inst. Henri Poincare, 1935, 5, 177–222 Search PubMed.
- Y. Imry, Crit. Rev. Solid State Mater. Sci., 1979, 8, 157–174 CrossRef.
- D. R. Nelson and B. I. Halperin, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 2457–2484 CrossRef CAS.
- M. Kardar, Statistical Physics of Fields, Cambridge University Press, 1st edn, 2007 Search PubMed.
- M. Engel, J. A. Anderson, S. C. Glotzer, M. Isobe, E. P. Bernard and W. Krauth, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042134 CrossRef PubMed.
- Y.-W. Li and M. P. Ciamarra, Phys. Rev. E, 2019, 100, 062606 CrossRef PubMed.
- K. Binder and W. Kob, Glassy Materials and Disordered Solids: An Introduction to Their Statistical Mechanics, World Scientific Publishing Company, 2005 Search PubMed.
- J. Kim and S. Torquato, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 054105 CrossRef CAS.
- R. Kubo, Rep. Prog. Phys., 1966, 29, 255 CrossRef CAS.
- M. Doi and S. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1988 Search PubMed.
- J. Tóthová and V. Lisý, Eur. J. Phys., 2022, 43, 065103 CrossRef.
- R. Farhadifar, J.-C. Röper, B. Aigouy, S. Eaton and F. Jülicher, Curr. Biol., 2007, 17, 2095–2104 CrossRef CAS PubMed.
- A. G. Fletcher, M. Osterfield, R. E. Baker and S. Y. Shvartsman, Biophys. J., 2014, 106, 2291–2304 CrossRef CAS PubMed.
- D. L. Barton, S. Henkes, C. J. Weijer and R. Sknepnek, PLoS Comput. Biol., 2017, 13, e1005569 CrossRef PubMed.
- M. A. Spencer, Z. Jabeen and D. K. Lubensky, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 2 CrossRef PubMed.
- S. Tong, N. K. Singh, R. Sknepnek and A. Košmrlj, PLoS Comput. Biol., 2022, 18, e1010135 CrossRef CAS PubMed.
- S.-Z. Lin, M. Merkel and J.-F. Rupprecht, Phys. Rev. Lett., 2023, 130, 058202 CrossRef CAS PubMed.
- S. Curran, C. Strandkvist, J. Bathmann, M. De Gennes, A. Kabla, G. Salbreux and B. Baum, Dev. Cell, 2017, 43, 480–492.e6 CrossRef CAS PubMed.
- M. Krajnc, Soft Matter, 2020, 16, 3209–3215 RSC.
- C. Duclut, J. Paijmans, M. M. Inamdar, C. D. Modes and F. Jülicher, Cells Dev., 2021, 168, 203746 CrossRef CAS PubMed.
- T. Yamamoto, D. M. Sussman, T. Shibata and M. L. Manning, Soft Matter, 2022, 18, 2168–2175 RSC.
- Y.-E. Keta and S. Henkes, github.com/yketa/cells, GitHub repository, https://github.com/yketa/cells, MIT license.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- R. Sknepnek, S. Henkes, D. Barton and A. Das, github.com/sknepneklab/SAMoS, GitHub repository, https://github.com/sknepneklab/SAMoS, GPL license.
- G. Briand and O. Dauchot, Phys. Rev. Lett., 2016, 117, 098004 CrossRef CAS PubMed.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4626–4641 CrossRef CAS PubMed.
- J. U. Klamser, S. C. Kapfer and W. Krauth, Nat. Commun., 2018, 9, 5045 CrossRef PubMed.
- P. Digregorio, D. Levis, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Soft Matter, 2022, 18, 566–591 RSC.
- M. Durand and J. Heu, Phys. Rev. Lett., 2019, 123, 188001 CrossRef CAS PubMed.
- N. De Macedo Biniossek, H. Löwen, T. Voigtmann and F. Smallenburg, J. Phys.: Condens. Matter, 2018, 30, 074001 CrossRef CAS PubMed.
- A. R. Dulaney, S. A. Mallory and J. F. Brady, J. Chem. Phys., 2021, 154, 014902 CrossRef CAS PubMed.
- S. Wilken, A. Chaderjian and O. A. Saleh, Phys. Rev. X, 2023, 13, 031014 CAS.
- H. Massana-Cid, C. Maggi, N. Gnan, G. Frangipane and R. Di Leonardo, Nat. Commun., 2024, 15, 6574 CrossRef CAS PubMed.
- S. Das, M. Ciarchi, Z. Zhou, J. Yan, J. Zhang and R. Alert, Phys. Rev. X, 2024, 14, 031008 CAS.
- X. Li, A. Das and D. Bi, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6650–6655 CrossRef PubMed.
- Y. Zheng, Y.-W. Li and M. P. Ciamarra, Soft Matter, 2020, 16, 5942–5950 RSC.
- Y. Tang, X. Li and D. Bi, Tunable Hyperuniformity in Cellular Structures, arXiv, 2024, arXiv:2408.08976 DOI:10.48550/arXiv.2408.08976.
- H. Alston, A. O. Parry, R. Voituriez and T. Bertrand, Phys. Rev. E, 2022, 106, 034603 CrossRef CAS PubMed.
- Y. Jiao, H. Berman, T.-R. Kiehl and S. Torquato, PLoS One, 2011, 6, e27323 CrossRef CAS PubMed.
- M. Huang, W. Hu, S. Yang, Q.-X. Liu and H. P. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2100493118 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Derivations of displacement fluctuations in a continuous medium (Section A) and in a triangular lattice (Section B), the derivations of the scalings of the translational order correlation function (Section C) and the structure factor (Section D), and additional data for the dynamical transition (Section E), defects (Section F), and structure factor (Section G) in the active disk models. See DOI: https://doi.org/10.1039/d5sm00208g |
| This journal is © The Royal Society of Chemistry 2025 |

