Investigation of microgel monolayers with the colloidal probe technique: how concentration and temperature allow tuning the properties of a microgel coating

Abstract

Microgels are soft nanometer-sized polymer systems that show high potential as responsive functional coatings. Here, we report colloidal probe measurements with a silica particle and thermo-responsive PNIPAM-co-APMH microgels adsorbed to a solid substrate immersed in water at different surface concentrations and at different temperatures. We show that the increase in the microgel concentration allows for a higher deformation leading to an effective softer microgel monolayer. We attribute this to a lower lateral expansion of the microgel on the substrate leading to a higher protrusion of the soft microgel corona into the water phase. Further, it is shown that even a small number of charged functional groups significantly impacts the properties of the microgel coating. As the microgels collapse, the viscoelastic properties of the network change and the microgels become stiffer. Additionally, the surface charge density increases. Thus, adjusting the concentration of the microgels at the interface as well as the temperature allows controlling the viscoelastic properties of the monolayer as well as the steric and electrostatic interactions perpendicular to the interface.

---

1 Introduction

Microgels are nanometer- to micrometer-sized three-dimensional cross-linked polymer networks that swell in good solvents.^1,2 The possibility of controlling the microgel network architecture in combination with the microgel's size enables adjusting the microgel–solvent interactions and thus allows for the production of stimuli-responsive microgels.³ This induces not only a structural change of single microgels but also has an effect on the macroscopic properties of microgel systems, such as emulsion stabilization, the formation of colloidal crystals or flow behavior.^4–7 Poly-N-isopropylacrylamide (PNIPAM) based microgels belong to one of the most studied types of microgels, due to their thermo-responsiveness under physiological conditions combined with a wide variety of microgel architectures and a simple and scalable synthesis.^3,8,9 Their interfacial activity allows the production of highly stable emulsions which, due to their stimuli-responsiveness, can be broken on-demand.^10–13 This has a high potential in industrial processes to reduce e.g. energy consumption or catalyst leaching.^14–16 Additionally, their soft nature makes them ideal candidates for coatings in medical applications, where chemical functionalization combined with structural interfacial properties play a key role in e.g. promoting cell adhesion.¹⁷

There have been multiple studies describing the two-dimensional structure of microgel monolayers as a function of concentration and temperature both below and above the volume phase transition temperature (VPTT) attributing the rich phase behavior to the anisotropic structure of the microgels at the interface paired with a structural phase transition of the microgels at higher microgel concentration.^18,19 Further, it has been shown that the increase in concentration is accompanied by a structural change of the microgels orthogonal to the interface leading to a drastic increase in microgel volume fraction inside the water phase.^20,21

Although we have a good understanding of the structure of microgels at different interfaces, the interactions that determine the macroscopic properties of microgel–laden interfaces are barely understood.²² Considering that the increase in microgel concentration affects both the two and three-dimensional monolayer structure raises the question, how the structural changes affect the interactions of microgel with different species such as cells in medical coatings or other microgels in the case of emulsion stabilization.

The colloidal-probe technique is a suitable tool to distinguish changes in the interactions between a specific probe and a microgel monolayer which can be used on the one side to understand the interactions driving emulsion stabilization, and or to characterize the monolayers in terms of softness and interaction potentials. This has already been successfully applied to study e.g. microgel–cell interactions between E. coli bacteria and microgel monolayers or to probe the dynamic mechanical properties of the microgel corona.^23–25

In the following, we study the surface properties of microgel coatings in water by determining the interactions between a silica-particle and microgels at different concentrations as well as at temperatures below and above the VPTT. First, the interactions between a silica-particle and a single microgel are discussed, highlighting the effect of the heterogeneous network response of the swollen microgel. Then, the change in the attractive and repulsive interactions between a colloid and a microgel monolayer prepared with the Langmuir–Blodgett technique at different concentrations is addressed. We here focus on microgel monolayers at lower concentrations, at which the microgels interact with each other with their corona to form hexagonally packed monolayers. This shows that the structural change of the microgels leads to a stronger compression by the colloidal probe and also leads to enhanced long-range electrostatic attractions and stronger adhesion to the probe. While the higher deformation of the monolayer at higher concentrations can be seen as a softening of the monolayer, the changes in attractive interactions highlight the complex interplay between steric and Coulomb interactions of the microgel coating with its aqueous environment. Lastly, the stability of more densely packed microgel films is discussed.

2 Experimental

The investigated microgels are the same microgels as used by Bochenek et al.^19,22,26,27 A description of the synthesis alongside with the DLS and SANS data can be found in the ESI.†

2.1 Langmuir–Blodgett depositions

Langmuir–Blodgett depositions were performed with a custom-made Langmuir–Blodgett trough (KSV NIMA, Bioloin Scientific Oy, Finland) made of poly(oxyethylene) glycol with an approximate area of 402 cm². All depositions were performed at 20 °C at the air–water interface. Temperature control was ensured by a water bath connected to the trough. Before each deposition, the trough was cleaned extensively with ethanol and MilliQ-water in the given order. Rectangular glass coverslips (22 × 22 mm², VWR, No. 1.5) were used as a substrate. The substrates and the substrate holder were washed twice with isopropanol in an ultrasound bath for 15 min respectively after which the substrate was air-dried and treated in an ozone oven (UVC-1014, NanoBioAnalytics, Germany) for 15 min. The substrates were mounted to a dipper holder with an approx. 45° angle relative to the interface and immediately submerged into water. The surface pressure was recorded with a highly porous platinum Wilhelmy plate (perimeter = 39.24 mm, KSV NIMA, Biolin Scientific Oy, Finland). A microgel solution with a concentration of 2 mg mL⁻¹ in a mixture of 80 v/v% isopropanol and 20 v/v% water was spread drop-wise onto the interface. After an equilibration time of at least 60 minutes, the interface was compressed to a given surface pressure with a rate of 5.40 cm² min⁻¹. Subsequently, the dipper was started and the substrates were uplifted out of the interface with a constant velocity of 0.35 mm min⁻¹ while maintaining a constant surface pressure via a feedback loop with a maximum area rate change of 1.08 cm² min⁻¹.

2.2 AFM measurements

All atomic force microscope (AFM) measurements were performed on a dimension icon in closed loop operation (Veeco Instruments Inc., software Nanoscope 9.4 (Bruker Corporation)). The images were corrected using Gwyddion (version 2.61).²⁸

2.2.1 Langmuir–Blogett film characterization. The characterization of the microgel monolayers was carried out in the dry state. Images of the monolayers were recorded in tapping mode using OTESPA tips (NanoAndMore USA Corp., USA) with a nominal tip radius smaller than 7 nm, a nominal spring constant of 26 N m⁻¹ and a nominal resonance frequency of 300 kHz. Each monolayer was characterized by recording a total of at least 10 images at different positions within the accessible substrate area for the liquid AFM measurements with a scan size of 5 μm × 5 μm and a resolution of 512 × 512 pixels. Images were analyzed using a custom MATLAB script (version 9.13.0, 2022b) based on the work of Crocker et al.²⁹ to determine the average number of microgels per area (N_area) and the average nearest neighbour distance (NND) as published by Bochenek et al.¹⁹

2.3 Colloidal probe preparation

A micromanipulator (MMO-203, NARISHIGE CO. LTD, Japan) in combination with a light microscope was used to attach a silica sphere with a nominal diameter of 2 μm to cantilever D of an OP-N010 AFM Chip (Bruker Corporation) with a nominal spring constant of 0.06 N m⁻¹ and a nominal resonance frequency of 18 kHz using an epoxy resin (Araldite rapid). The cantilever was oxygen plasma treated for 5 minutes at 200 W and 1.4 mbar of oxygen pressure prior to the experiment and submerged into a 0.5 wt% polyvinylpyrrolidone (PVP) (10 kDa, Alfa Aesar) aqueous solution in order to reduce adhesion to the microgels. It was then rinsed with filtered bi-distilled water and used for the measurement immediately.

2.4 Force volume measurements

Liquid AFM measurements were conducted in force volume mode with a custom-built liquid cell equipped with a temperature controller (Model 335 Cryogenic Temperature Controller, Lake Shore Cryotronics). The liquid cell was rinsed with ethanol and dried with a bellow. A likewise cleaned 55 μm thick polyimide foil was placed under the glass substrate to tilt it away from the detector to prevent interference of the laser signal with the back-reflection from the glass substrate. The cantilever was calibrated in liquid at 27 °C using the thermal noise method. Therefore, the deflection sensitivity was averaged by recording at least ten force–distance curves at two different positions on a glass substrate which had been oxygen plasma treated as described for the colloidal probe. The probe was then retracted at least 1000 μm away from the surface and the power spectrum was recorded and fitted with the Nanoscope 9.4 software yielding the cantilever's spring constant.³⁰ All measurements were conducted at 27 and 40 °C with a trigger threshold of 4 nN at a constant tip velocity of 2 μm s⁻¹ adjusting the ramp size between 1000 and 1500 nm and the scan rate between 1 and 0.75 s⁻¹ accordingly if not stated otherwise.

3 Results and discussions

3.1 Colloid–microgel interactions on single microgels

For the force spectroscopy measurements PNIPAM microgels with N-(3-aminopropyl)methacrylamide hydrochloride (APMH) as co-monomer and 5% crosslinker concentration with a size of R_h,20°C = (150 ± 3) nm were chosen as they provide a good model system with a simple and up-scalable synthesis route resulting in a typical core-corona structure (compare Fig. S1 and S2, ESI†). The more crosslinked core and a less crosslinked corona is due to the reaction kinetics of the incorporation of the crosslinker during precipitation polymerization.^31–33 Furthermore, we used the identical microgel in various studies with respect to its bulk and interfacial properties.^19,22,26,27 The use of APMH as co-monomer not only allows for the post-functionalization of the microgels but also results in a slightly positively charged microgel network which promotes adhesion to the underlying glass substrate which itself carries a negative surface charge.^19,34–37

The complexity of the microgel architecture in combination with its finite size provides several experimental challenges including (i) the heterogeneous crosslinker density inside the microgel's polymer network which requires the use of force volume measurements with a reasonable resolution to depict the lateral and vertical variations in the microgels viscoelastic network response, (ii) the mixture of colloid–substrate interactions which, in addition to the network response, can include contribution form e.g. electrostatic interactions between the probe and the substrate, and (iii) the soft nature of the microgel requiring the consideration of e.g. hydrodynamic effects in the determination of the scan parameters.^2,26,38,39 Thus, in order to interpret the results for the colloid–monolayer interactions, the interactions between a colloid and a single microgel are discussed first.

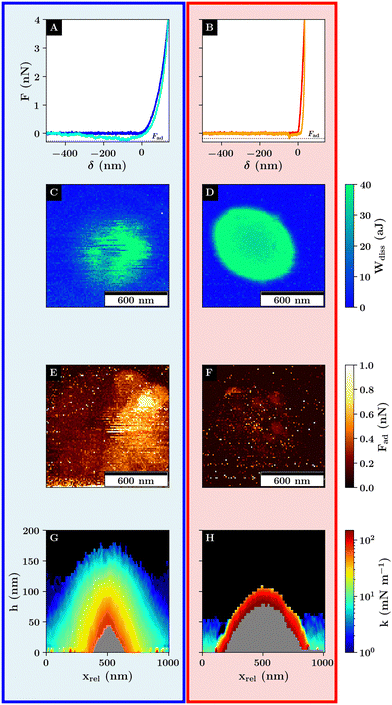
Due to the large probe size, the colloid can interact with more than one microgel during a single measurement. Thus, to ensure that the interactions between a single microgel and colloid are recorded, an overview scan was performed in force volume mode with adjusted scan parameters to ensure that the probe does not interact with any surrounding microgels (Fig. 1).

Fig. 1 Force volume measurement on a glass substrate with separated microgels recorded at 27 °C. (A) Height image and (B) corrected height image with a resolution of 52 × 52 px² and a scan size of 5 × 5 μm². The red square represents the scan area used to measure the single probe–microgel interactions. The measurement was performed with a ramp speed of 10 μm s⁻¹.

Here, the height image shows the topographical image represented by the measured height where the maximum force of 4 nN is applied (Fig. 1). The height image shows smaller 30 nm protrusions which correspond to the incompressible part of the microgel core (Fig. 1A). The corrected height includes the deformation of the sample based on the contact point determination of each curve (compare Fig. S6, ESI†). On the positions of the microgel cores, much larger structures are visible with a height of 180 nm (Fig. 1B). Further, a non-zero height of approx. 100 nm is measured where the colloid probes the non-coated substrate.

In Fig. 2A and B the corrected height image of the swollen and collapsed microgel in water recorded with the colloidal probe is shown. While the height images with the colloidal probe only show the laterally convoluted structure of the microgel as a consequence of the large probe radius, they yield information about their maximum height and the nature of the probe–substrate interactions. The colloidal probe measurement shows that the rehydrated microgels are four to six times larger with respect to their height of approx. 180 nm and 120 nm compared to the individual dried microgels due to the higher water content inside the microgel network (compare Fig. S4, ESI†).^40,41

Fig. 2 Corrected height images recorded at (A) 27 °C and (B) 40 °C. (C) Force–distance curves recorded on a glass substrate in close proximity to a microgel at 27 °C and 40 °C (light blue and light red) together with a force curve recorded on a bare glass substrate (black). (D) Force–distance curves recorded in the center of a single microgel at 27 °C (blue curve) and 40 °C (red curve). The z position representing the height h and the corrected h_corr are marked by striped blue and dotted red vertical lines following the same color coding as the curves. (E) Force-indentation curves of the same data as in D with the same color coding in log–log representation. The solid lines represent the fits according to eqn (1).

As for the overview scan in Fig. 1 the corrected height at the borders of the scan regions is not zero. A repulsive interaction between the clean glass substrate and the silica probe can be measured which is in the range of approx. 100 nm because the probe and the substrate carry a negative surface charge. This is shown for the calibration curve in Fig. 2C recorded on a clean glass substrate (black curve) in comparison to the glass curves recorded next to the microgel (light blue and beige curves). As the contact point is calculated from a shift in the probe–sample interactions with respect to the baseline, no distinction is made between the repulsive interactions from Coulomb and network interactions, resulting in an ambiguous transition from the probe–substrate to the probe–microgel interactions based on the corrected height image alone. However, depending on the lateral position of the force–distance curve measurement with respect to the position of the microgel, a change in the range of the repulsive interactions can be observed.

Here two regions in the corrected height images have to be distinguished where the probe is partially or not in contact with the microgels. The corrected height images show a transition in the change of height images from a homogeneous height at the edges of the scan region, due to the charge of the substrate, towards a systematic increase in height in the direction of the microgel apex due to the compression of the microgel network. The relative decrease of the corrected height in the direct vicinity of the microgel, which is more pronounced for the collapsed microgel, contains additional information about the nature of the probe–microgel interactions. The range of the repulsive interactions in this region is reduced, as indicated by the decrease in corrected height around the microgel (Fig. 2B). It suggests that the repulsive Coulomb interactions between the probe and the substrate in this area are inhibited. This is due to the positively charged microgel surface caused by the APMH co-monomer. It results in an effective screening of probe–substrate interactions as the attractive probe–microgel and the repulsive probe–substrate interactions partially cancel each other out (see Fig. 3).

Fig. 3 Sketch of the interactions between the probe and the microgel physiosorbed to the solid substrate. The negative surface charge of the probe and the substrate are represented by a blue edge and blue circles. The positive charge of the microgel network is represented by red spheres. The number of spheres does not represent the charge density of the respective system. The arrows represent the interactions between the probe and the microgel and the probe and the substrate. Arrows facing towards each other represent attractive interactions while arrows facing away from each other represent repulsive interactions. The interactions from left to right show the attractive van-der-Waals interactions between the probe and the network F_vdW, the repulsive interactions between the elastic microgel network and the probe F_network, the attractive Coulomb interactions between the negative surface charge of the probe and the positively charged APMH comonomer F_CI,+− and the repulsive Coulomb interactions between the negative surface charges of the probe and the substrate F_CI,−−.

At the outer edges of the scan area, where the probe is not in contact with the microgel, a second observation with respect to the repulsive probe–substrate interactions can be made which is represented in Fig. 2C. Similar to the probe–substrate interactions in close proximity to the microgel, the repulsive probe–substrate interactions further away from the microgel at the outer edges of the scan area (Fig. 2C light blue and beige curves) are also affected by the charge of the microgel resulting in an overall reduction in Coulomb interaction compared to the undisturbed probe–substrate interactions (Fig. 2C dark blue curve). However, unlike in the case close to the microgel, where the colloid–microgel interaction range is affected mainly by the microgel's surface charge, here the repulsive probe–substrate interactions are determined by the protrusion of the polymer network into the water phase resulting in a larger screening of the surface charge in case of the swollen microgel. Thus, the further protrusion of the microgel network into the water phase for the swollen microgel network has a larger effect on the screening of Coulomb interactions compared to the surface charge increase of the collapsed microgels. This shows that already at low microgel concentrations, way below the formation of a monolayer, the physical properties of an interface are affected over a larger area compared to the area covered by the microgel network.

The change in the repulsive interactions with the lateral position of the probe and the microgel thus demonstrates the complex nature of the charge interactions between the microgel and its environment because of the structural change of the microgel at different temperatures.

At the microgel's apex, the force curves show a steeper increase in force as a function the relative z-position, which is proportional to the deformation, above the VPTT (red curve) compared to the force curve below the VPTT (blue curve) (Fig. 2D). Thus, a reduction in the maximum indentation by approximately 70% can be observed which can be seen as a stiffening of the probe–microgel interactions. Additionally, the probe–microgel interactions display variances in the scaling behavior as a function of temperature (compare Fig. 2D and E) which is represented on the one hand by the slower increase in the repulsive force as a function of indentation below the VPTT (compare Fig. 2D) in combination with an increase in the slope of the curve in the respective logarithmic representation (compare Fig. 2E). Both curves show initial larger spreading of the data points below 100 pN in Fig. 2E which is caused by the background noise because of e.g. thermal fluctuations of the cantilever combined with an initial small contact area between the probe and the microgel resulting in a low repulsive interaction. However, the indentation range of this initial contact as well as the change in the scaling behavior is much more pronounced for the swollen microgel. This can be attributed to the fuzzy shell and the heterogeneous network architecture as a consequence of the swollen network, resulting in a slower increase of the elastic network response as a function of the indentation depth.

Unlike the contact point determination which is used for the generation of the corrected height image, the measurement of the dissipative energy is less susceptible to the microgel's charge as it is calculated from the hysteresis between the approach and retraction indicated by a small gap between the approach and retraction curves for d > 0 nm (Fig. 4A and B). This is, on the one hand, influenced by the viscoelastic properties of the underlying sample, and on the other hand, by the magnitude of the attractive probe sample interactions.³⁹ This results in negligible energy dissipation on a stiff substrate compared to the large energy dissipation resulting from the compression of the viscoelastic microgel. Thus, a more pronounced spatial transition of the dissipative energy can be observed allowing a more distinct differentiation between the probe–microgel and probe–substrate interactions (Fig. 4C and D).

Fig. 4 Different evaluations of force volume measurements on a single microgel recorded at 27 (left) and 40 °C (red, right). Example force-indentation curves (A) and (B), dissipative energy images (C) and (D), adhesion force images (E) and (F), and stiffness profiles (G) and (H). The black areas in the stiffness profiles indicate a lack of stiffness data because the probe is not in contact with the sample. The grey areas in the stiffness profile indicate a lack of stiffness data for the set trigger threshold of 4 nN because the sample is not further deformed. Profile in G is radially averaged. The measurements were recorded with a scan size of 1.2 by 1.2 μm² and a resolution of 96 × 96 pixels.

The images of the energy dissipation below the VPTT show a variation of the energy dissipation around the microgel apex with a gradual decrease of the energy dissipation towards the edges of the scan area represented by the higher energy dissipation around microgel's apex with more than 40 aJ compared to a dissipative energy of less than 20 aJ closer to the edges of the scan area. Further, the higher energy dissipation values above 20 aJ are rather spatially heterogeneous distributed. Additionally, the dissipative energy is spatially not correlated with the adhesion force representing the maximum force required to separate the probe and the sample (compare Fig. 4E and F). Thus, the energy dissipation can be related to the viscoelastic network response of the microgel.

The gradually decrease of the energy dissipation away from the microgel apex can be explained by the topography depicted by the corrected height images. As the probe compresses the network further away from the microgel's apex, less of the microgel network is compressed leading to a reduction in the energy dissipation. We attribute the heterogeneous distribution of energy dissipation around the microgel core (i) to smaller inhomogeneities in the network architecture as can be seen for dry microgels² and (ii) to different interactions between the probe and the sample which are difficult to predict for soft matter.⁴²

Despite the more homogeneous scaling behavior of the force curves in the collapsed state suggesting a more elastic response of the microgel, the total dissipative energy is much higher compared to the swollen state. Also, the indentation depth for the collapsed microgel is reduced in comparison to the swollen microgel (see Fig. S15, ESI†). Based on common contact models, we interpreted this as a reduction in the maximum contact area.³⁹ As the contact area for a fixed load is inversely proportional to the stress, the differences in the dissipative energy might be a consequence of the differences in the maximum stress acting on the sample. This is further supported by the slight toroidal shape depicted by the energy dissipation of the collapsed microgel. Considering the microgel's topography, the probe–microgel interactions away from the microgel apex can be viewed as a special case of indentation on an inclined surface resulting in a higher load on the microgel network compared to the measured load normal to the substrate interface (compare Fig. S7, ESI†).⁴³

Thus, the trends in the energy dissipation can be explained on the one hand by the loss of energy during the indentation of the swollen network, and on the other hand by the reduced contact area paired with an increase in stress for the collapsed microgel.

However, considering that the compression of the collapsed microgel is accompanied by a displacement of water in the network, the larger dissipative energy could also be related to the bad solvent conditions resulting in a slower network response during the retraction phase which would also lead to less energy recovery being measured. Probing the dynamic properties of the collapsed microgel is, however, beyond the scope of the current work.

The adhesion force above the VPTT is also reduced which supports the increase in energy dissipation due to the smaller contact area as the adhesion force also depends among others on the maximum contact area (Fig. 2C and D).⁴⁴ In addition, there exists a difference in the magnitude of the adhesion when comparing the left and right half of the image of adhesion force for the swollen microgel below the VPTT (Fig. 4E), which is similar to a scan directional effect. This is due to the experimental set-up and the topography of the scan area. The cantilever is tilted approx. 13° towards the interface to avoid a collision between the scan head and the substrate and to ensure that only the probe instead of the cantilever is in direct contact with the sample. This results in differences in the probe–microgel interaction during the upward-bending of the cantilever due to the differences in topography as the cantilever moves from a negative deflection back to no deflection towards or away from the microgel apex respectively (compare Fig. S8, ESI†).

The stiffness profiles of the swollen microgel show the network's high deformability. Unlike in the case of stiffness tomography using a sharp tip to probe the polymer density, the colloidal probe measurement determines the response of the polymer network.⁹ The change in magnitude of the contact stiffness is represented by the different colors associated with the topography of the interface. While the black area indicates no contact, the outer blue layer shows interactions with the fuzzy shell which shows high variances of the stiffness values, especially at the microgel's apex. This is due to the higher amounts of dangling chains contributing to the net interactions. Toward the outside, the profile widens as a transition from a probe–microgel contact to probe–substrate contact occurs. This is also visible based on the grey area, which indicates missing stiffness data because the trigger threshold has been reached. This maps the incompressible section of the sample which is on the one side determined by the direct contact with the stiff substrate represented by the flat section of the grey profile and on the other side by the incompressible microgel core in the center of the profiles (compare Fig. 4G).

As already shown by the force curves, the stiffness is much higher above the VPTT (Fig. 4). Thus, the stiffness is much higher in the initial and maximum indentation, and the microgel deformation is reduced as represented by a larger grey area compared to the colored area. Additionally, a sharp transition from high to very low stiffness values can be observed which shows a transition from the probe–microgel to probe–substrate interactions as discussed for the corrected height images (compare Fig. 2).

Unlike classical force mapping, the stiffness profiles allow for a better spatial correlation of neighbouring force–distance curves which allow to accurately depict the heterogeneous network response of the microgels which gradually increases closer to the microgel core for the swollen microgel.

So far, the transition from probe–substrate to probe–microgel interactions can not be determined precisely. A clear determination of this transition is relevant for a statistical analysis of the force volume measurements. As shown e.g. by the sharp transition in the stiffness for the collapsed microgel, the change from probe–microgel to probe–substrate interactions leads to a sharp transition of the shape of the force–distance curves resulting in differences of the stiffness values and consequently in a different scaling behavior of the force–distance curves. As has been shown before, parts of the force–distance curves for microgels can be modelled using a Hertzian contact model in order to describe small sections of deformation.^16,24,45,46 This is a good approximation as the scaling depicted in Fig. 2 for high deformations is in a first approximation constant. However, as the transition from the probe–substrate to the probe–microgel interactions is difficult to separate based on the scaling at low and high deformation alone, a function has to be chosen that describes the force–distance curves over the whole indentation range. Thus we use a Hertzian model with an additional exponential function to account for an increase in the elastic network response to describe the non-linearity depicted in Fig. 2C (see Fig. 5, compare eqn (1) and (2)).

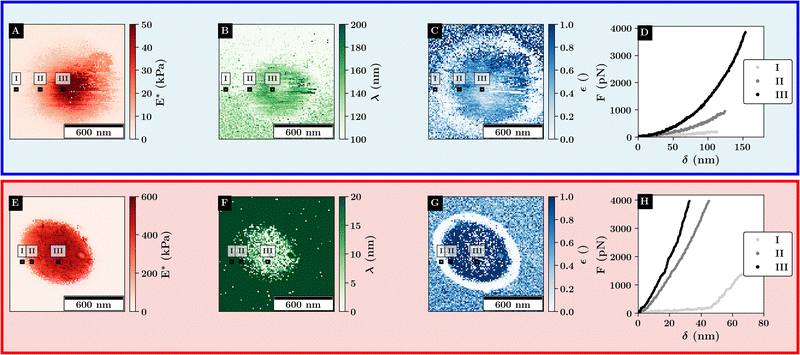Fig. 5 Fit results of the force curves scaling behavior according to eqn (1) for single microgels at 27 °C (top) and 40 °C (bottom). Example curves for the different regimes are marked with black rectangles. (A) and (E) Scaling factor at high indentation depth, (B) and (F) double the logistic functions midpoint. (C) and (G) Relative change in initial scaling relative to the final scaling. (D) and (H) Example curves at various positions relative to the microgel.

Here, E* describes the apparent complex modulus at high indentation depth, while the product of ε and E* corresponds to the apparent complex modulus at low indentation depth. λ accounts for a change in scaling from low to high indentation. The offset F_offset is used to account for a non-zero force at zero indentation due to, e.g., thermal noise. The function is heuristically determined based on the need for a simpler description of the variances between the different types of force–distance curves. A more detailed description of the choice for p(δ,ε,λ) is given in the ESI† (Discussion of the choice fit functions for the separation of force–distance curves). Briefly, rather than separating the force–distance curves into separate sections with respect to the deformation to fit a Hertzian model,¹⁶ an exponential increase in elasticity over a range λ is assumed which is described by the prefactor p(δ,λ,ε). p(δ,λ,ε) is normalized to 1 so that E* = E(δ_max) describes the scaling behavior at maximum indentation δ_max and 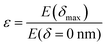maps the relative change in the scaling at low deformation with repsect to the maximum scaling factor E*. This ensures a clear separation of the force curves based on the comparison of the curve's scaling behavior at low and high deformation, respectively.

As depicted in Fig. 5A for the swollen monolayer, E* increases toward the microgel center, which is due to the core-corona structure resulting in a stiffer microgel core. While λ is mainly bound to the compression of the microgel, ε shows a ring-like structure where the outer diameter corresponds to the distance at which the microgel and colloid are no longer in contact. This indicates a change in the initial slope of the force–distance curves as ε describes the initial scaling behavior of the curve. Thus, the low ε region around the microgel reveals that the long-range repulsive interactions are dominated by the Coulomb interactions between the probe and the substrate, while the repulsive interactions at shorter distances to the microgel core are mainly determined by the probe–microgel interactions.

Above the VPTT, similar trends as for the stiffness profiles are observed. As the maximum stiffness is increased above the VPTT a large increase in the scaling behavior is observed with a maximum of around 50 kPa below the VPTT to more than 600 kPa. E* gradually decreases away from the microgel apex which aligns with the assumption that further outside more of the collapsed corona shell is compressed. This is in agreement with the observation that λ increases further away from the microgel apex. Like for the swollen microgel, ε shows the position where the probe and microgel are not in contact as indicated by the similar ring-like structure of low ε around the microgel. Further, the combination of small values for λ and high values of ε indicate that the contact close to the microgel center can be well approximated by a simple Hertz model.

This highlights, the polymer–particle duality of the microgel, where the swollen microgel behaves more like a heterogeneous network, while the collapsed microgel behaves more like a hard elastic particle.

3.2 Concentrated microgel monolayers

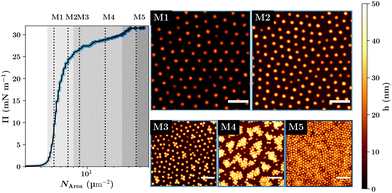
While the properties of the single microgels mainly determine the monolayer's properties, it is not enough to investigate single microgels at the interface. This is because the lateral constraint and the packing at the interface at high interfacial concentration influence the microgel's shape perpendicular to the interface.^19,21,47 Consequently, the different concentration regimes of the monolayer at the interface have to be investigated separately to get a full picture of the monolayer properties.

In Fig. 6, the structure of the deposited dry microgel monolayers for different surface pressures is shown. Here, the compression isotherm shows five distinct thermodynamic phases which are correlated with structural change of the monolayer formed on a solid substrate.^19,47 In phase (I) microgels are isolated and the surface pressure is zero. In phase (II) the surface pressure increases and the microgels start to form a homogeneous hexagonally packed film. Phase (III) shows a structural transition of the microgel film leading to the coexistence of two hexagonal packed phases with different lattice parameters. In phase (IV) again, a densely packed monodispers hexagonal-packed phase can be observed before the monolayer becomes unstable and multilayers start to form in phase (V). While the exact structure in the third compression regime can vary between different microgel systems based on e.g. size, charge or deposition technique, most systems show similar monolayer structures in the second and fourth compression regime.^48–53

Fig. 6 Compression isotherm of PNIPAM-co-APMH microgels at the air–water interface at 20 °C and AFM height images recorded by tapping mode at the solid–air interface of the prepared Langmuir–Blodgett films at five different surface pressures as indicated by the compression isotherm. Different shades of grey in the isotherm indicate the five thermodynamic phases. The white scale bar in the AFM height images is 1 μm in size.

In the following, the colloid–microgel interactions for the hexagonal-packed monolayer in the second compression regime are discussed first. The discussion is separated into different types of interactions, because for the monolayers, in addition to the temperature, also the effects of concentration and consequently the microgel–microgel distance are addressed. First, the attractive short- and long-range interactions are discussed as they contain the most information about the probe–monolayer interactions. Then, the repulsive probe–monolayer interactions are addressed which contain structural information about the microgel network and provide insights into the complex nature of the contact between the probe and multiple microgels at once. Finally, the energy dissipation is presented which contains additional information about the network viscoelasticity.

3.2.1 Attractive colloid–monolayer interactions. Microgel monolayers in the second concentration regime with a single hexagonal packing were measured at two different concentrations at (4.22 ± 0.12) μm⁻² (M1) and (6.10 ± 0.16) μm⁻² (M2) (compare Fig. 6 M1 and M2). This allows measuring the effect of the concentration and consequently the distance between neighbouring microgels on the monolayer properties.

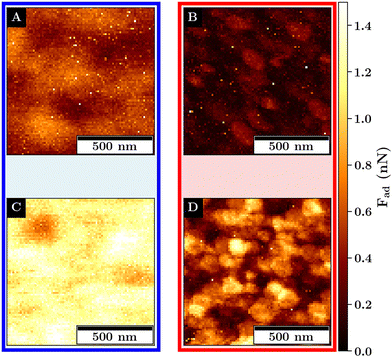
The adhesion force images for both monolayers below and above the VPTT are depicted in Fig. 7. Examples for force-indentation curves for each monolayers are displayed in Fig. S14 (ESI†).

Fig. 7 Images of the adhesion force F_ad on monolayers M1 (A) and (B) and M2 (C) and (D) recorded at 27 °C (left) and at 40 °C (right). Measurements were recorded with a scan size of 1 × 1 μm² and a resolution of 80 × 80 pixels.

Below the VPTT, at a lower concentration for M1, a structural variance in the adhesion force with respect to the position of the microgel is visible. Here, the adhesion force is reduced at the microgel apex and is increased at the position in between the microgels.

At a higher concentration, the adhesion force becomes spatially more homogeneous and overall increases from a maximum of about 1 nN to more than 1.5 nN.

The increase in adhesion force can be explained by the increase in the number of microgels that are in probe–microgel contact. In addition, an increase in the deformability can be observed from M1 to M2 (compare Fig. S15, ESI†). Assuming a similar shape of the deformed area between the probe and the monolayer for M1 and M2, a higher deformation is associated with a larger maximum contact area between the probe and the sample. A larger contact area results in more short-range attractive interaction and also explains the increase in the measured adhesion.

The larger deformation at a fixed load at a higher microgel concentration means that the monolayer effectively becomes easier to deform. This is unexpected as a distribution of load over more microgels should result in less deformation if the softness of the single microgel is not affected by the concentration change. Consequently, the softness of the single microgels at the interface for M1 must be reduced in comparison to M2.

The increase in deformation can be attributed to the lateral constrain of the microgel leading to an increase of the dimensions perpendicular to the interface as has been observed at e.g. the air–water interface and can be also observed for the dry monolayers (compare Fig. 6).²¹

Above the VPTT, the adhesion force for both monolayers is highly reduced in comparison to the swollen monolayers. This reduction in the adhesion force is accompanied by a reduction in the deformability of the interfaces (compare Fig. S15, ESI†). The adhesion maxima are close to the interstitial lattice spacings of the hexagonal packing. These adhesion maxima are represented by small dots which cover only a small area and abruptly decline which is in contrast to the swollen monolayer where a continuous change in the adhesion force is observed.

This can be explained by the topography of the interface allowing for contact with at least 3 microgels at the interstitial lattice spacings presumably maximizing the probe–microgel contact area compared to the indentation on the microgels apex where the distance to the next microgel is maximized and the contact area minimized.

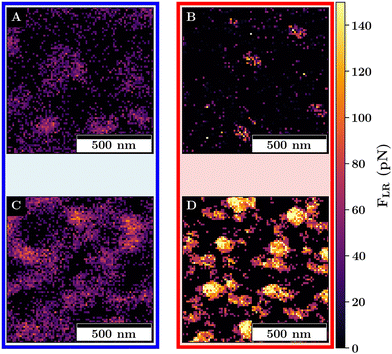
For both monolayers, jump-to-contacts (JTCs) are observed (compare Fig. 8).

Fig. 8 Images of the long-range attractive interaction F_LR on monolayers M1 (A) and (B) and M2 (C) and (D) recorded at 27 °C (left) and at 40 °C (right). Measurements were recorded with a scan size of 1 × 1 μm² and a resolution of 80 × 80 pixels.

The JTCs can be observed if a long-range attractive interaction between the probe and the sample occurs. This can cause an acceleration of the probe toward the sample, resulting in a negative force measured as the probe approaches the sample.⁵⁴ This is in the following referred to as long-range attractive interactions F_LR to distinguish it from the adhesion force.

While in the case of the swollen monolayers, the amount of JTCs is rather small for M1, the magnitude and number of the JTCs drastically increases for M2. Above the VPTT, the long-range attractive interactions for both monolayers increase in magnitude and show local maxima. As for the adhesion force, the maxima can be observed where the colloid probes the interstitial lattice spaces.

For both, the swollen and collapsed monolayers, the trends between M1 and M2 for the long-range attraction can be assigned to an increase of charge-density at the surface of the monolayer due to (i) a larger amount of microgels, (ii) the lower amount of APMH physiosorbed to the interface due to structural changes and (iii) because of the higher surface charge in the case of the collapsed microgel. Despite the amount of APMH is rather small, it has a large effect on the properties of the monolayer as determined by the colloidal probe. Thus, the influence of the charged groups becomes more important with increasing microgel concentration, and in the collapsed monolayer state (compare Fig. 9).

Fig. 9 Sketch of the interactions between the probe and the microgel physisorbed to the solid substrate. The negative surface charge of the probe and the substrate are represented by a blue edge and blue circles. The positive charge of the microgel network is represented by red spheres. On the left, the microgels are shown in the swollen state below the VPTT. On the right the microgels are shown in the collapsed state above the VPTT. The increase in charge density for the collapsed microgel is represented by a smaller distance between the charges in the microgel network.

3.2.2 Repulsive colloid–monolayer interactions. To visualize the repulsive probe–monolayer interactions, examples of stiffness profiles of both monolayers are shown in Fig. 10.

Fig. 10 Example stiffness profiles for monolayers M1 (A) and (B) and M2 (C) and (D). below (left) and above the VPTT (right). The black areas indicate a lack of stiffness data because the probe is not in contact with the sample. The grey areas indicate a lack of stiffness data for the set trigger threshold of 4 nN because the sample is not further deformed.

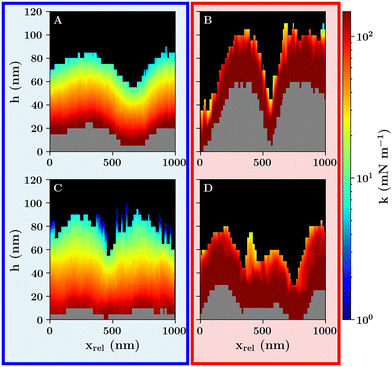
The stiffness profile of the swollen monolayer M1 shows a continuous increase in stiffness with respect to the deformation of the monolayer. This is represented by an increase in stiffness depicted by the transition from the black to the colored and the colored to the grey areas. In contrast, the swollen monolayer M2 depicts a different topography. The undeformed case, i.e., the transition from the black to the colored area is different compared to the topography at the maximum deformation, i.e., the transition of the colored to the grey area. Additionally, the shape of the stiffness profile of the swollen monolayer shows a higher indentation of the microgel at the microgel's apex for M2 (Fig. 10C) in comparison to M1 (Fig. 10A, compare Fig. S15, ESI†). The stiffness for low deformation is reduced at the microgel's apex as indicated by the thicker green and yellow areas representing a low stiffness which explains the higher total deformation.

Above the VPTT, the stiffness of both monolayers M1 and M2 are increased compared to the swollen monolayers. Here, the same structural changes can be observed related to the topography of the interface. At lower concentrations respective of larger microgel–microgel distances, the microgel's apex and the valley between microgel are partially resolved (Fig. 10B). At a higher concentration, in the case of M2, the valleys between the microgel's apices become less pronounced. Further, the stiffness at the microgel's apex is reduced as in the swollen state.

The change of the stiffness profile at the microgel's apex from M1 to M2 shows that microgel concentration affects the structure and consequently the network response of the microgels. This leads to a lower stiffness with increased concentration and consequently, a higher deformability of the monolayer which we interpret as a softening (Fig. 11).

Fig. 11 Sketch of the effect of distance between microgels d_microgel on the structure and elastic response of the microgel monolayer. The microgels protrude further into the water for M2 because of the smaller microgel–microgel distance. The effect on the stiffness is represented by a different shading of the microgels in the vertical direction.

We see that the monolayer is deformed stronger, despite the probe interacting with more microgels at the higher concentration at M2 as compared to M1. In other words, the compression at M2 is distributed over more microgels as compared to M1. This load distribution can be observed by the transition of the stiffness values from intermediate to high stiffness values represented by the orange and red areas for the swollen monolayer M2 (compare Fig. 10C). In the lateral direction, the height of this transition in stiffness shows local maxima and minima which can be explained by the compression of multiple microgels at once as more microgels contribute to the net repulsive interaction. This highlights the complex response of the monolayer. During an indentation process, multiple microgels contribute to the interactions at various states of compression in combination with the heterogeneous network response of the single microgel itself because of the core-corona architecture.

3.2.3 Energy dissipation for microgel monolayers. In the following, the images of the energy dissipation are discussed, which similar to the repulsive interactions, give information about the viscoelastic network response of the monolayer.

In Fig. 12 the images of the energy dissipation for M1 and M2 are depicted. Below the VPTT (Fig. 12A and C), both monolayers show a laterally homogeneous distribution of the energy dissipation. In the comparison of M1 to M2 the energy dissipation for the higher concentrated monolayer M2 is with W̃_diss = (24.30 ± 0.04) aJ increased compared to W̃_diss = (14.00 ± 0.15) aJ for M1 (compare Fig. S16A and C, ESI†). These results indicate that at higher microgel concentrations, the viscoelastic properties of the swollen monolayer change. This is in agreement with the results from the repulsive interactions.

Fig. 12 Images of the dissipative energy on monolayers M1 (A) and (B) and M2 (C) and (D) recorded at 27 °C (left) and at 40 °C (right). Measurements were recorded with a scan size of 1 × 1 μm² and a resolution of 80 × 80 pixels.

Above the VPTT (Fig. 12B and D), both monolayers show a pattern of the energy dissipation which can be described as faceted regions of higher energy dissipation separated by thin local minima of the energy dissipation. Unlike the case of the swollen monolayers, the average energy dissipation for both concentrations remains with W̃_diss = (24.3 ± 0.3) aJ for M1 and W̃_diss = (24.3 ± 0.3) aJ nearly the same (compare Fig. S16B and D, ESI†).

The appearance of a structured pattern in the image of the energy dissipation can be explained by the smaller deformation of the collapsed microgel. This leads to a smaller number of microgels in probe–microgel contact contributing to the net probe–monolayer interactions. Consequently, the monolayer response is probed more locally as compared to the swollen monolayer. Thus, the energy dissipation is more determined by the network response of a single microgel while for the swollen monolayers, the energy dissipation is averaged over more microgels.

In summary, the images of the energy dissipation show the magnitude of the dissipative energy changes with temperature for both microgel concentrations. The impact of the concentration on the dissipative energy on the monolayer properties is, however, significantly more pronounced for the swollen monolayers.

3.2.4 Colloidal–probe measurements in the third and fourth compression regime. Colloidal probe measurements at higher microgel concentrations did not allow for reproducible force volume measurements. This is because two types of measurements could be observed.

Firstly, some force–distance curves showed a steep increase in force at high indentation depth, similar to the measurements on a bare substrate for the single microgel. This indicates only a lower interfacial coverage with microgels compared to M1 and M2, as these curves were not observed for these monolayers.

Secondly, some measurements showed a drastic shift in the data trends with respect to the position on the substrate. This is shown in Fig. S23 (ESI†) for an image of the energy dissipation, displaying a drastic change in the magnitude of the energy dissipation from one pixel to the other. We attribute this behavior to the contamination of the colloidal probe with a microgel.

Both cases indicate the removal of microgels from the substrate as a consequence of the colloidal probe measurements. This leads to the conclusion that the adhesion to the probe exceeds the adhesion of the microgel to the substrate, which can be explained either by a reduction of the microgel's contact area with the substrate and or a larger contact area with the probe.

We conclude that the concentration significantly impacts the microgel film stability, in cases where external forces are applied to the interface. Consequently, to achieve good film stability either the microgel concentration should be kept low or additional surface modifications of the substrate should be applied to increase the adhesion of the microgel to the substrate.

Conclusions

In summary, we have shown how concentration and temperature affect the interaction potential between a silica probe and microgels. Various parameters contribute to changes in the response of the microgel's network. These effects play a key role in the design of functional microgel coatings as the sum of interactions mainly determines the coating's macroscopic properties.

For the force spectroscopy on a single microgel, a rather simple scaling law can be used to distinguish between the Coulomb and network interactions between the probe and the microgel and between the probe and the substrate. Additionally, the application of a scaling law well exemplifies the heterogeneous repulsive response of the microgel network which is due to its core-corona architecture.

Further, it could be shown that already a small number of charged functional groups can significantly impact the monolayer's properties leading to a change in long-range interactions. This effect becomes stronger as the microgel concentration and, with it, the number of functional groups increases. Additionally, the collapse of the microgels leads to a rearrangement of these functional groups within the microgel network which also leads to increased long-range interactions in comparison to the swollen monolayer.

Moreover, it could be shown that the concentration change impacts the microgel's network response. For the swollen monolayer, a higher deformation of the monolayer with a higher concentration was observed. We attribute this to the lateral constrain of the microgels at higher concentrations and a higher protrusion of the network into the aqueous phase which is in agreement with the behavior observed for the dry monolayers and the microgels absorbed to a liquid–air interface.^19,21,47 We interpret the higher deformability at higher concentrations as a softening of the monolayer. This highlights the interplay between the 2D and 3D structure and the viscoelastic properties of microgels at the interface.

At higher concentrations, where the microgels were further laterally constrained, the interactions with the colloidal probe systematically led to the removal of microgels from the substrate. From this, we conclude that the microgels stick less to the substrate which affects the structural stability of the monolayer when interacting with external matter.

These findings show that depending on the use case, several considerations have to be made for the design of functional coatings.

Firstly, the composition of the network and additional functional groups can significantly impact the long-range interactions which e.g. contribute to interactions between two monolayers and consequently affect emulsion stability.^55,56

Secondly, in medical applications where the interactions between cells and a coating depend, among others, on a combination of structure, softness, and the attractive interactions between the cell and the coating, the colloidal probe technique provides a highly sensitive and quantitative method to measure a microgel coatings properties.^57–63 This enables tuning the coating properties before performing complex cell assays. For the preparation of the microgel coating itself, the adjustment of interfacial concentration allows for a softer coating.

Lastly, in applications where the longevity of monolayer stability is of the outermost importance, such as in antifouling coatings, the interfacial coverage of the interface might need to be limited.⁶⁴

Further studies are needed to focus on the effect of network architecture and cross-linker concentrations which can impact the formation and behavior of a microgel film.^55,65 Additionally, while the Langmuir–Blodgett technique provides good control over the film structure, it is less used in commercial applications due to the lack of scalability compared to e.g. dip- or spin coating.⁶⁶ However, since the deposition itself can significantly impact film properties, a comparison of microgel–laden films with respect to the deposition technique might be necessary.^67–69

Author contributions

Timon Kratzenberg: investigation, data curation, formal analysis, software, validation, writing – original draft,  writing – review and editing; Simon Schog: software; Steffen Bochenek: investigation; M. Friederike Schulte: conceptualization, methodology; Walter Richtering: funding acquisition, conceptualization, supervision, writing – original draft,  writing – review and editing.

Data availability

Data are available at https://dx.doi.org/10.22000/zgtg8amdnqjq6mm6.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG) within SFB 985 “Functional Microgels and Microgel Systems” within project B8. This work contains data obtained from experiments performed at the KWS-2 instrument, operated by Jülich Centre for Neutron Science (JCNS) at the Heinz Maier-Leibnitz Zentrum (MLZ) in Garchingen, Germany.

Notes and references

1. F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140.
2. A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, Chem. Rev., 2022, 122, 11675–11700.
3. D. M. Zhilin and A. Pich, Chem. Teach. Int., 2021, 3, 155–167.
4. M. Destribats, M. Eyharts, V. Lapeyre, E. Sellier, I. Varga, V. Ravaine and V. Schmitt, Langmuir, 2014, 30, 1768–1777.
5. A. Scotti, U. Gasser, E. S. Herman, J. Han, A. Menzel, L. A. Lyon and A. Fernandez-Nieves, Phys. Rev. E, 2017, 96, 032609.
6. H. Senff and W. Richtering, Colloid Polym. Sci., 2000, 278, 830–840.
7. A. Scotti, M. Brugnoni, C. G. Lopez, S. Bochenek, J. J. Crassous and W. Richtering, Soft Matter, 2020, 16, 668–678.
8. R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33.
9. M. F. Schulte, E. Izak-Nau, S. Braun, A. Pich, W. Richtering and R. Göstl, Chem. Soc. Rev., 2022, 51, 2939–2956.
10. T. Ngai, S. H. Behrens and H. Auweter, Chem. Commun., 2005, 331–333.
11. B. Brugger, B. A. Rosen and W. Richtering, Langmuir, 2008, 24, 12202–12208.
12. B. Brugger, J. Vermant and W. Richtering, Phys. Chem. Chem. Phys., 2010, 12, 14573–14578.
13. M. Destribats, V. Lapeyre, M. Wolfs, E. Sellier, F. Leal-Calderon, V. Ravaine and V. Schmitt, Soft Matter, 2011, 7, 7689.
14. M.-H. Kwok, G. Sun and T. Ngai, Langmuir, 2019, 35, 4205–4217.
15. H. Monteillet, M. Workamp, X. Li, B. Schuur, J. M. Kleijn, F. A. M. Leermakers and J. Sprakel, Chem. Commun., 2014, 50, 12197–12200.
16. A. Aufderhorst-Roberts, D. Baker, R. J. Foster, O. Cayre, J. Mattsson and S. D. Connell, Nanoscale, 2018, 10, 16050–16061.
17. J. Riegert, A. Töpel, J. Schieren, R. Coryn, S. Dibenedetto, D. Braunmiller, K. Zajt, C. Schalla, S. Rütten, M. Zenke, A. Pich and A. Sechi, PLoS One, 2021, 16, e0257495.
18. J. Harrer, M. Rey, S. Ciarella, H. Löwen, L. M. C. Janssen and N. Vogel, Langmuir, 2019, 35, 10512–10521.
19. S. Bochenek, A. Scotti, W. Ogieglo, M. Á. Fernández-Rodríguez, M. F. Schulte, R. A. Gumerov, N. V. Bushuev, I. I. Potemkin, M. Wessling, L. Isa and W. Richtering, Langmuir, 2019, 35, 16780–16792.
20. S. Bochenek, F. Camerin, E. Zaccarelli, A. Maestro, M. M. Schmidt, W. Richtering and A. Scotti, Nat. Commun., 2022, 13, 3744.
21. Y. Gerelli, F. Camerin, S. Bochenek, M. M. Schmidt, A. Maestro, W. Richtering, E. Zaccarelli and A. Scotti, Soft Matter, 2024, 20, 3653–3665.
22. S. Bochenek, C. E. McNamee, M. Kappl, H.-J. Butt and W. Richtering, Phys. Chem. Chem. Phys., 2021, 23, 16754–16766.
23. S. M. Hashmi and E. R. Dufresne, Soft Matter, 2009, 5, 3682.
24. S. Backes and R. von Klitzing, Polymers, 2018, 10, 1–23.
25. D. Wilms, F. Schröer, T. J. Paul and S. Schmidt, Langmuir, 2020, 36, 12555–12562.
26. A. Scotti, S. Bochenek, M. Brugnoni, M. A. Fernandez-Rodriguez, M. F. Schulte, J. E. Houston, A. P. H. Gelissen, I. I. Potemkin, L. Isa and W. Richtering, Nat. Commun., 2019, 10, 1418.
27. S. Bochenek, A. Scotti and W. Richtering, Soft Matter, 2021, 17, 976–988.
28. D. Nečas and P. Klapetek, Open Phys., 2012, 10, 181–188.
29. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
30. J. te Riet, A. J. Katan, C. Rankl, S. W. Stahl, A. M. van Buul, I. Y. Phang, A. Gomez-Casado, P. Schön, J. W. Gerritsen, A. Cambi, A. E. Rowan, G. J. Vancso, P. Jonkheijm, J. Huskens, T. H. Oosterkamp, H. Gaub, P. Hinterdorfer, C. G. Figdor and S. Speller, Ultramicroscopy, 2011, 111, 1659–1669.
31. X. Wu, R. H. Pelton, A. E. Hamielec, D. R. Woods and W. McPhee, Colloid Polym. Sci., 1994, 272, 467–477.
32. M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206.
33. I. Berndt, J. S. Pedersen and W. Richtering, Angew. Chem., 2006, 45, 1737–1741.
34. X. Hu, Z. Tong and L. A. Lyon, Colloid Polym. Sci., 2010, 289, 333–339.
35. A. P. H. Gelissen, A. Oppermann, T. Caumanns, P. Hebbeker, S. K. Turnhoff, R. Tiwari, S. Eisold, U. Simon, Y. Lu, J. Mayer, W. Richtering, A. Walther and D. Wöll, Nano Lett., 2016, 16, 7295–7301.
36. R. K. Iler, The chemistry of silica: Solubility, polymerization, colloid and surface properties, and biochemistry, Wiley, New York, NY, 1979.
37. S. H. Behrens and D. G. Grier, J. Chem. Phys., 2001, 115, 6716–6721.
38. M. F. Schulte, S. Bochenek, M. Brugnoni, A. Scotti, A. Mourran and W. Richtering, Angew. Chem., Int. Ed., 2021, 60, 2280–2287.
39. H.-J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152.
40. T. Kyrey, J. Witte, J. Lutzki, M. Zamponi, S. Wellert and O. Holderer, Phys. Chem. Chem. Phys., 2021, 23, 14252–14259.
41. S. Schmidt, M. Zeiser, T. Hellweg, C. Duschl, A. Fery and H. Möhwald, Adv. Funct. Mater., 2010, 20, 3235–3243.
42. A. Leontev, L. Rozental and V. Freger, J. Colloid Interface Sci., 2023, 651, 464–476.
43. A. N. Ahmine, M. Bdiri, S. Féréol and R. Fodil, Sci. Rep., 2024, 14, 25869.
44. M. Kappl and H.-J. Butt, Part. Part. Syst. Charact., 2002, 19, 129.
45. A. Burmistrova, M. Richter, C. Uzum and R. V. Klitzing, Colloid Polym. Sci., 2011, 289, 613–624.
46. A. Burmistrova, M. Richter, M. Eisele, C. Üzüm and R. von Klitzing, Polymers, 2011, 3, 1575–1590.
47. M. Rey, M. Á. Fernández-Rodríguez, M. Steinacher, L. Scheidegger, K. Geisel, W. Richtering, T. M. Squires and L. Isa, Soft Matter, 2016, 12, 3545–3557.
48. M. Rey, X. Hou, J. S. J. Tang and N. Vogel, Soft Matter, 2017, 13, 8717–8727.
49. C. Picard, P. Garrigue, M.-C. Tatry, V. Lapeyre, S. Ravaine, V. Schmitt and V. Ravaine, Langmuir, 2017, 33, 7968–7981.
50. K. Kuk, V. Abgarjan, L. Gregel, Y. Zhou, V. Carrasco Fadanelli, I. Buttinoni and M. Karg, Soft Matter, 2023, 19, 175–188.
51. J. Vialetto, N. Nussbaum, J. Bergfreund, P. Fischer and L. Isa, J. Colloid Interface Sci., 2022, 608, 2584–2592.
52. D. Feller, M. Otten, M. S. Dimitriyev and M. Karg, Colloid Polym. Sci., 2024, 1–14.
53. M. M. Schmidt, S. Bochenek, A. A. Gavrilov, I. I. Potemkin and W. Richtering, Langmuir, 2020, 36, 11079–11093.
54. C. Yu and Z. Dai, J. Mech. Phys. Solids, 2024, 193, 105919.
55. M. Rey, J. Kolker, J. A. Richards, I. Malhotra, T. S. Glen, N. Y. D. Li, F. H. J. Laidlaw, D. Renggli, J. Vermant, A. B. Schofield, S. Fujii, H. Löwen and P. S. Clegg, Nat. Commun., 2023, 14, 6723.
56. A. V. Petrunin, S. Bochenek, W. Richtering and A. Scotti, Phys. Chem. Chem. Phys., 2023, 25, 2810–2820.
57. F. Chowdhury, S. Na, D. Li, Y.-C. Poh, T. S. Tanaka, F. Wang and N. Wang, Nat. Mater., 2010, 9, 82–88.
58. E. Fadeeva, A. Deiwick, B. Chichkov and S. Schlie-Wolter, Interface Focus, 2014, 4, 20130048.
59. X. Jia, J. Song, W. Lv, J. P. Hill, J. Nakanishi and K. Ariga, Nat. Commun., 2022, 13, 3110.
60. A. S. Caldwell, B. A. Aguado and K. S. Anseth, Adv. Funct. Mater., 2020, 30, 1907670.
61. Q. Sun, Y. Hou, Z. Chu and Q. Wei, Bioact. Mater., 2022, 10, 397–404.
62. X. Yao, R. Peng and J. Ding, Adv. Mater., 2013, 25, 5257–5286.
63. G. Huang, F. Li, X. Zhao, Y. Ma, Y. Li, M. Lin, G. Jin, T. J. Lu, G. M. Genin and F. Xu, Chem. Rev., 2017, 117, 12764–12850.
64. P. Saha, M. Santi, M. Emondts, H. Roth, K. Rahimi, J. Großkurth, R. Ganguly, M. Wessling, N. K. Singha and A. Pich, ACS Appl. Mater. Interfaces, 2020, 12, 58223–58238.
65. M. F. Schulte, A. Scotti, M. Brugnoni, S. Bochenek, A. Mourran and W. Richtering, Langmuir, 2019, 35, 14769–14781.
66. K. Ariga, Langmuir, 2020, 36, 7158–7180.
67. V. Nigro, E. Buratti, F. Limosani, R. Angelini, F. Dinelli, S. Franco, E. Nichelatti, M. Piccinini, M. A. Vincenti, R. M. Montereali and B. Ruzicka, Colloids Surf., A, 2023, 674, 131918.
68. E. Buratti, I. Sanzari, F. Dinelli, T. Prodromakis and M. Bertoldo, Polymers, 2020, 12, 1–19.
69. L. Hoppe Alvarez, A. A. Rudov, R. A. Gumerov, P. Lenssen, U. Simon, I. I. Potemkin and D. Wöll, Phys. Chem. Chem. Phys., 2021, 23, 4927–4934.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00237k

---