 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Droplet spreading in a wedge: a route to fluid rheology for power-law liquids†
Marcel Moura a,
Vanessa Kern
a,
Vanessa Kern b,
Knut Jørgen Måløy
b,
Knut Jørgen Måløy ac,
Andreas Carlson
ac,
Andreas Carlson bd and
Eirik G. Flekkøy
bd and
Eirik G. Flekkøy *ae
*ae
aPoreLab, The Njord Center, Department of Physics, University of Oslo, NO-0316 Oslo, Norway. E-mail: flekkoy@fys.uio.no
bDepartment of Mathematics, University of Oslo, NO-0316 Oslo, Norway
cPoreLab, Department of Geoscience and Petroleum, Norwegian University of Science and Technology, NO-7031 Trondheim, Norway
dDepartment of Medical Biochemistry and Biophysics, Umeå University, Umeå, Sweden
ePoreLab, Department of Chemistry, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway
First published on 7th July 2025
Abstract
Measuring the rheology of liquids typically requires precise control over shear rates and stresses. Here, we describe an alternative route for predicting the characteristic features of a power-law fluid by simply observing the capillary spreading dynamics of viscous droplets in a wedge-shaped geometry. In this confined setting, capillary and viscous forces interact to produce a spreading dynamics described by anomalous diffusion, a process where the front position grows as a power-law in time with an exponent that differs from the value 1/2 found in classical diffusion. We derive a nonlinear diffusion equation that captures this behavior, and we show that the diffusion exponent is directly related to the rheological exponent of the fluid. We verify this relationship by using both experiments and simulations for different power-law fluids. As the predictions are independent from flow-specific details, this approach provides a robust tool for inferring rheological properties from the spreading dynamics.
The spreading of droplets on solid surfaces is a ubiquitous phenomenon, observable in everyday events such as raindrops falling on a window, as well as in a variety of biological, geological, and physical systems. In these contexts, it can serve as a mechanism for delivering nutrients to living cells,1 oxidating substances to minerals,2 or forming fluid pathways within complex geometries.3,4 The spontanoeus spreading of fluids depends on the wetting properties and geometry of the medium through which it spreads.5–9 However, it also depends crucially on the rheology of the liquid, as is well known from the everyday application of non-Newtonian fluids, such as toothpaste, corn starch, paint, yogurt and shampoo. Controlling fluid rheology is also topical in industrial applications and in food science,10–17 where it covers everything from cooking recipes to consumer satisfaction.18 In this study, we show that the spreading dynamics of a droplet of a power-law liquid can be used to predict the fluid's rheological properties.
The rheology of a power-law fluid is characterized by the fact that the shear stress is given by a power of the strain rate. The spreading of such a liquid in a wedge-shaped geometry is anomalous in the sense that it is described in the same way as anomalous diffusion. Mathematically, it is captured by a non-linear diffusion equation that yields analytical solutions with a spreading rate which is given by an anomalous diffusion exponent.19–22 As an interesting by-product, we obtain a relationship between the exponent governing the rheology and the diffusion exponent. As this relationship depends only on the conservation of fluid mass and a non-linear Darcy law, which relates the volume flux to the pressure gradient, it is independent of other details of the flow structure. The rheological exponent may thus be obtained solely on the basis of the spontaneous (capillary driven) fluid motion, without any type of force- or shear-rate control, as needed in commercial rheometers.
The analysis and findings presented here complement the extensive literature on anomalous diffusion. Pattle23 noted, already in 1959, that the seepage of a liquid into a cloth or porous body could be described by a nonlinear diffusion equation, yielding sub-diffusive spreading of the fluid. In the 1980s, there was a large effort to understand the nature of anomalous diffusion, particularly in the context of transport in disordered and porous media. In porous media flows, strong confinement often gives rise to regimes where transport occurs through corners and thin films. In these cases, the balance between capillary and viscous forces plays a key role and can enable persistent, long-range transport5,24–27 such as when connecting otherwise disconnected fluid clusters.28–36 Our solution, which pertains to a viscous flow driven by capillarity as a droplet spreads in an idealized (sharp) wedge, see Fig. 1a, with a constant solid–liquid contact angle, may thus serve as a baseline model for more complex flow geometries.
A key finding in our study is the fact that the position of the tip of a droplet spreading in a wedge geometry scales with time as xtip ∝ tτ, where the exponent τ is directly linked to the rheological exponent n characterizing the power-law fluid. By contrast, when the spreading of a shear-thinning fluid happens in radial fashion on a plane,37,38 rather than along a corner line, the exponent governing the spreading rate has been shown to depend very weakly on the rheological exponent.38 Our theoretical prediction and measurements of the Newtonian spreading exponent τ ≈ 0.4 are consistent with the value τ ≈ 1/3 that has been measured for Newtonian flow of different liquids that imbibe along a corner from an infinite reservoir.39,40 This suggests that the hydrodynamics is strongly governed by the dynamics at the tip and less sensitive to the boundary condition where the fluid is supplied.
A droplet of a power-law fluid spreading in a wedge is characterized by the stress–strain relationship σ ∝ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n over a certain range of the strain rate
n over a certain range of the strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , which is frequently described by the Ostwald–de Waele model.13 The viscosity is then given by
, which is frequently described by the Ostwald–de Waele model.13 The viscosity is then given by
 | (1) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 is a reference strain rate at which the liquid is non-Newtonian. We shall take
0 is a reference strain rate at which the liquid is non-Newtonian. We shall take ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 10 s−1 for the fluids employed in this study (see the rheological characterization of the fluids in the ESI†). Many polymer melts and solutions exhibit a value of n in the range 0.3–0.7, depending upon the concentration and molecular weight of the polymer.41,42 Even smaller values of the power-law exponent (n = 0.1–0.15) are encountered with fine particle suspensions like kaolin-in-water, bentonite-in-water, etc. By using polyacrylamide solutions of different concentrations, Ansari et al.43 measured a range of power-law indices n = 0.26–0.47, which were obtained for shear rates in the range 10–1000 s−1. See also Jouenne and Levache44 for a comprehensive dataset on the rheology of acrylamide-based polymer solutions.
0 = 10 s−1 for the fluids employed in this study (see the rheological characterization of the fluids in the ESI†). Many polymer melts and solutions exhibit a value of n in the range 0.3–0.7, depending upon the concentration and molecular weight of the polymer.41,42 Even smaller values of the power-law exponent (n = 0.1–0.15) are encountered with fine particle suspensions like kaolin-in-water, bentonite-in-water, etc. By using polyacrylamide solutions of different concentrations, Ansari et al.43 measured a range of power-law indices n = 0.26–0.47, which were obtained for shear rates in the range 10–1000 s−1. See also Jouenne and Levache44 for a comprehensive dataset on the rheology of acrylamide-based polymer solutions.
We shall obtain a prediction for the height h(x, t) of a droplet of a power-law fluid when spreading along the wedge geometry, as shown in Fig. 1. Our power-law liquid wets the surface inside the wedge and spreads due to the capillary forces, as illustrated in Fig. 1a. Its shape is described by the height h(x, t). When the wetting angle Θ < (π − α)/2, α being the opening angle of the wedge (see Fig. 1b), the capillary pressure will be negative, and the minimal energy will be reached when the solid–liquid contact area is maximized. This occurs when the liquid spreads out as far as possible along the wedge. The negative capillary pressure drives the flow and increases in magnitude towards the tips of the drop as 1/h, since the radius of curvature of the liquid–air interface R ∝ h, see Fig. 1b. In Fig. 1c we show a snapshot of the experiment, where the red arrows denote the spreading direction. It is worth noting that in the experimental setup, the wedge is not perfectly sharp as in the idealized model. Instead, a small radius of curvature h0 exists along the bottom edge, see Fig. 1d. This curvature arises from the procedure employed to build the setup, which involves coating the glass slides that form the wedge walls with a PDMS film. Further details are provided in the ESI.†
In the ESI,† we show that the volumetric flow rate q across a surface normal to the corner line may be written
 | (2) |
 | (3) |
In order to obtain an analytical solution, our theoretical approach ignores: (1) the effects of gravity and inertia, (2) the finite initial droplet width and the interface curvature in the x-direction, (3) the cut-offs in shear rates where the non-Newtonian behavior becomes Newtonian, (4) the finite curvature of the corner geometry, and (5) dynamic variation of the contact angle Θ and pinning effects.
Approximating the contact angle by Θ = 20°, the curvature of the liquid interface 1/R sets the capillary pressure difference across this interface to be
 | (4) |
The relative magnitude of gravitational to capillary forces is estimated as the ratio between the hydrostatic pressure drop ρgh and the capillary pressure drop given in eqn (4). Ignoring the cosine term in this expression yields the ratio
 | (5) |
In order to estimate the relative importance of inertial forces, we calculate the Reynolds number for each experiment, that is, the ratio of the steady inertial and viscous terms of the Navier–Stokes equation. The quantity um represents a characteristic mean tip velocity, measured as the ratio xtip/t in the late-time regime of the experiment, where the scaling xtip ∝ tτ holds. While the actual velocity decreases over time, um serves as a useful reference for the typical velocity observed during the experiment. Calculating a relevant Reynolds number requires some care, as the viscous term ∝ ∇2u is dominated by the shear forces from the wall and thus governed by the width of the droplet, while the inertial term ∝ u·∇u is governed by variations along the flow and hence the droplet half-width xtip. As a result we define the relevant Reynolds number as
 | (6) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) tip, and Reynolds number Re. The threshold shear rate
tip, and Reynolds number Re. The threshold shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c, at which non-Newtonian behavior sets in, is shown in parentheses alongside
c, at which non-Newtonian behavior sets in, is shown in parentheses alongside ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) tip. The values of
tip. The values of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c are obtained from Fig. S1 (ESI), which also provides the corresponding kinematic viscosity values ν* = η/ρ. The Reynolds number is calculated as Re = umLeff/ν*, where the effective length Leff ≈ 10−5 m
c are obtained from Fig. S1 (ESI), which also provides the corresponding kinematic viscosity values ν* = η/ρ. The Reynolds number is calculated as Re = umLeff/ν*, where the effective length Leff ≈ 10−5 m
| XG [g L−1] | um [m s−1] | ν* [m2 s−1] | ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) tip ( tip (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c) [s−1] c) [s−1] |
Re |
|---|---|---|---|---|
| 0 | 1 × 10−2 | 5 × 10−6 | 70 (0) | 2 × 10−2 |
| 0.5 | 1 × 10−2 | 1 × 10−5 | 70 (3) | 1 × 10−2 |
| 1 | 6 × 10−3 | 4 × 10−5 | 40 (2) | 1 × 10−3 |
| 2 | 1 × 10−3 | 2 × 10−4 | 7 (0.8) | 5 × 10−5 |
| 3 | 5 × 10−5 | 2 × 10−3 | 0.35 (0.2) | 1 × 10−7 |
| 4 | 4 × 10−5 | 4 × 10−3 | 0.3 (0.1) | 1 × 10−7 |
| 6 | 2 × 10−5 | 2 × 10−2 | 0.15 (0.08) | 1 × 10−8 |
Assuming the fluids to be in the non-Newtonian regime is clearly not correct everywhere. Since the shear rate will be close to zero at x = 0, there will always be regions of slow Newtonian flow. However, since the capillary forces and viscous dissipation take on their maximum values at x = ±xtip, the spreading process is likely to be strongly dominated by the hydrodynamics right at the droplet tips. For that reason, we compare the shear rate there to the critical crossover shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c, where the rheology becomes Newtonian. Taking h0 to be the only relevant length scale for the flow at the tips, we estimate the tip shear rate as
c, where the rheology becomes Newtonian. Taking h0 to be the only relevant length scale for the flow at the tips, we estimate the tip shear rate as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) tip = um/(αh0/2). Table 1 shows the typical shear rate,
tip = um/(αh0/2). Table 1 shows the typical shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) tip, and how it compares with the crossover shear rates
tip, and how it compares with the crossover shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c obtained from Fig. S1 (ESI†). Note that in all cases
c obtained from Fig. S1 (ESI†). Note that in all cases ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) tip >
tip > ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c, although only by a small margin for the largest concentrations. We will include the influence of a finite corner curvature in our numerical solutions by setting the volumetric flow rate to q = 0 when h falls below a threshold h0, see Fig. 1d.
c, although only by a small margin for the largest concentrations. We will include the influence of a finite corner curvature in our numerical solutions by setting the volumetric flow rate to q = 0 when h falls below a threshold h0, see Fig. 1d.
It is the variations in h(x) that will cause a pressure gradient along the wedge, and we may invoke eqn (2) to get the mean flow. The cross-sectional area in the direction normal to x, A(x) ≈ (α/2)h2, and the amount of liquid volume is a conserved quantity, so that
 | (7) |
 | (8) |
 | (9) |
Since the solution A(x, t) is symmetric around x = 0, we will only consider x > 0, so that ∂P/∂x < 0. By taking the initial condition to be A(x, 0) = V0δ(x), where V0 is the droplet volume, we shall follow20 and seek a scaling solution of the form
 | (10) |
 | (11) |
This solution has the property that  In order to insert eqn (10) in eqn (8), we need the derivative, ∂A/∂t = (f′(t)/f(t)2)d(up)/du, which allows us to write eqn (8) in the form
In order to insert eqn (10) in eqn (8), we need the derivative, ∂A/∂t = (f′(t)/f(t)2)d(up)/du, which allows us to write eqn (8) in the form
 | (12) |
 | (13) |
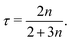 | (14) |
The p-part of eqn (12) takes the form, ((d/du)(p3/2−1/n(−dp/du)1/n) − λup) = 0, which may be integrated to give p3/2−1/n(−p′(u))1/n − λup = K. Since, by symmetry, p′(0) = 0 and p(0) must be finite, the integration constant K = 0, and the above equation may be rearranged to give pn/2−1p′ = λnun. This may be integrated to give
 | (15) |
 . Inserting this L-value in A(x, t) = p(u)/f(t), λ cancels out, and so we are free to choose λ =
. Inserting this L-value in A(x, t) = p(u)/f(t), λ cancels out, and so we are free to choose λ = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0/D0 in order to make
0/D0 in order to make
 | (16) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0)(V0/An)1/2)τ, where the dimension of u is m and that of p(u) is m2. Inserting λ in eqn (15) finally yields
0)(V0/An)1/2)τ, where the dimension of u is m and that of p(u) is m2. Inserting λ in eqn (15) finally yields
 | (17) |
Requiring that p(u) be real restricts this solution to the x-domain where Ln+1 − un+1 > 0, or |u| < L. Outside
 | (18) |
The fact that xtip ∝ tτ is a key result as it provides the link between the spreading rate and the diffusion exponent τ, and by eqn (14), the rheological exponent n. The τ = 0.4 value for n = 1 agrees with the result found by Hansen et al.,21 who solved eqn (8) in the special case of a Newtonian liquid. The τ-exponent is simply obtained by plotting the experimental xtip(t)-values on a log–log plot. Having obtained the τ and n-values from xtip(t) in this way, the scaling function f(t) is known and may be used to obtain a data collapse for the experimental values of A(x, t)f(t) versus x/f(t) as predicted by theory. With this experimental data collapse, fitting eqn (17) to the data using D0 as a fitting parameter gives D0. The rheological prefactor μ0 may then in principle be obtained by solving eqn (9) with respect to μ0 = η0![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0n−1 as
0n−1 as
 | (19) |
Also, since the analytic theory ignores the corner curvature h0, an experimentally measured value of h(x, t) (the distance from the curved corner to the meniscus) will be associated with an overestimated value of the capillary pressure that drives the flow. This will predict a faster overall spreading rate than what is actually observed. This effect thus has the opposite influence of the dynamic contact angle increasing above the static one, which will lead to a slower spreading. For these reasons μ0 cannot be obtained from eqn (19) unless Θdyn is measured independently and used instead of Θ, and the corner is made sufficiently sharp.
The mathematical model can be solved numerically, and the solutions provide testable predictions. To test these predictions, we design an experimental system consisting of two thin transparent plates, arranged at an angle α = 30° and securely held by a support mechanism (see Fig. 1). Standard microscope glass slides (dimensions 76 mm × 26 mm × 1 mm) were used. One critical experimental aspect was to ensure a high level of wettability with the wedge and minimize impurities that may affect the contact-line motion. As such, the plates were coated with a thin polymeric layer of PDMS, modified with a hydrophilic agent (methyl-terminated poly(dimethylsiloxane-b-ethylene oxide)). The coating was further treated with nitrogen plasma to enhance the wettability.49 We tested a range of different fluids, including mixtures of xanthan gum (XG)50 and water at varying concentrations, as well as a glycerol–water mixture to represent the Newtonian case. The XG concentration in water was systematically varied from 0.5 g L−1 to 6 g L−1. For further details about the coating procedure and fluids preparation, see the ESI.†
In the experiment the wedge's corner is not infinitely sharp, rather it has a radius of curvature h0 ≈ 0.6 mm due to the finite thickness of the PDMS coating, see Fig. 1d. To mimic the experiments, we solve eqn (7) numerically, introducing a Gaussian initial profile for h(x, t) and a cut-off corresponding to the corner curvature. This cut-off arises because the capillary pressure changes sign approximately at the point where h(x, t) becomes smaller than h0, see Fig. 1d. We set the radius of curvature h0 = 0.6 mm and the initial profile half-width w0 = 0.8 mm throughout in the numerical calculations, similar to the experiments. This may be represented mathematically by imposing q = 0 in eqn (7), where h(x, t) < h0. Eqn (8) can then be integrated numerically using centered spatial derivatives and an explicit first-order time stepping scheme.
Fig. 2a shows the temporal evolution of the droplet spread xtip, measured as half of the distance between the left and right tips of the droplet, marked in Fig. 1b, for seven experiments going from the Newtonian case (leftmost curve) to the most shear-thinning case (rightmost curve). Arbitrary horizontal shifts have been applied to the curves for better visualization. The linear range in the xtip plot allows the determination of τ by use of eqn (18). Fig. 2b shows a comparison between the measured τ-values against their theoretical predictions. The experimentally and numerically measured exponents are denoted τexp and τc, and the theoretical values τth are computed from eqn (14). The errorbars shown are due to the uncertainty in the fitting of the data from Fig. 2b. We notice that the experimental data tends to gather under the one-to-one τth-line. We attribute this divergence to the fact that in the experimental setup we do not have a sharp wedge. However, the numerically estimated exponents for which this finite curvature radius h0 is taken into account, agree with the experimental measurements from Fig. 2b within the error bar in these data, except for the smallest and largest τ-values.
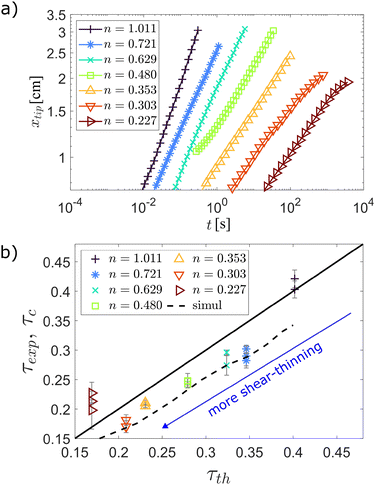 | ||
| Fig. 2 (a) Experimentally measured droplet spread xtip(t). The curves are shifted horizontally by arbitrary values to aid visualization. The leftmost curve corresponds to the Newtonian fluid, while the others are from XG fluids with XG concentrations of 0.5, 1, 2, 3, 4 and 6 g L−1 increasing from left to right. (b) Comparison between the experimental exponent τexp (symbols) and numerical exponent τc (dashed line), as well as the theoretical slopes τth computed from eqn (14) (full line). The numerical results take the finite corner curvature h0 = 0.6 mm and initial profile half-width w0 = 0.8 mm into account. The errorbars account for deviations from a perfect power-law fit from the data in (a). | ||
At the largest τ-value (the Newtonian case) the discrepancy is still moderate and may be linked to the difference in the Newtonian and non-Newtonian behavior near the contact line. On the other hand, the discrepancy at the smallest τ-value is likely caused by a departure from the non-Newtonian domain of the power-law fluid, which happens at sufficiently small shear rates. In the ESI,† we show how the numerical τ-values depend on h0 and converges to the analytical result as h0 → 0. Variations of the initial half-width w0 in the 0–2 mm range has less than a 1% effect on the τ-values as initial Gaussian profiles converge quickly to the profiles of eqn (17) (see ESI†).
Fig. 3a shows the experimental profiles h(x, t) for the spreading of a drop at a XG-concentration of 2 g L−1 and V0 = 19 mm3, while Fig. 3b shows the data collapse implied by eqn (10) and (11) outside the domain where the corner curvature introduces a cut-off. The numerical results capture this behavior, while also showing a close agreement between the analytic and numerical results in the central region. Note that the collapse also verifies the scaling xtip∝tτ while the agreement between the analytic and numerical results implies a very fast relaxation towards the analytical prediction.
 | ||
| Fig. 3 (a) Droplet profiles for an experiment with XG concentration of 2 g L−1 for 9 different times in the range t = 2.0–12.4 s shown in the colorbar. (b) The dots show the experimental values of A(x, t)f(t). The analytical result for the function p(u) of eqn (17) using the value n = 0.48 is plotted as a gray line, while the simulations that take the finite corner curvature h0 = 0.6 mm and initial profile half-width w0 = 0.8 mm, are shown for the initial and final times. The diffusion constant resulting from the data fit is D0 = 200 mm1/n s−1. | ||
For the experimental determination of the cross-sectional area A(x, t) employed in Fig. 3b, a correction due to the curvature radius h0 along the corner of the wedge is used so that the normalization 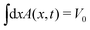 is verified. This is achieved by subtracting from the approximately triangular cross section of the ideal wedge a smaller triangular area that represents the empty region beneath the curved segment, see Fig. 1d. This correction is further described in the ESI.†
is verified. This is achieved by subtracting from the approximately triangular cross section of the ideal wedge a smaller triangular area that represents the empty region beneath the curved segment, see Fig. 1d. This correction is further described in the ESI.†
Having shown that the spontaneous spreading of a droplet of a power-law fluid in a wedge is governed by a non-linear diffusion equation, we have proceeded via an analytic solution of this equation to obtain the rheological exponents of several power-law fluids by simple experimental measurements. In classical (Fickian) diffusion, the position of the diffusing front grows in time as x ∝ t1/2. In our system, by contrast, the exponent differs from 1/2, a hallmark of anomalous diffusion. Specifically, the spreading follows xtip ∝ tτ, where τ was typically found to be smaller than 0.3 for the shear-thinning fluids tested (sub-diffusive behavior). The connection between the anomalous diffusion exponent τ and the fluid rheology exponent n is expressed in eqn (14), a key result of our work and the theoretical basis for our experiments.
In our corner geometry the τ-exponent depends sufficiently strongly on the rheological exponent n so as to make it experimentally possible to determine n from τ. The measured τ-values are in the range ∼0.16–0.42. By contrast, comparable experiments38 that study xanthan gum fluids spreading on a flat surface obtain τ values that are limited to the range ∼0.05–0.1. These values are too small, or too limited in range to allow for the determination of n. From a physical perspective this difference in sensitivity is likely linked to the difference in the nature of the driving forces between the two geometries: in a wedge of small opening angle the capillary pressure, which drives the flow, is negative and increases as 1/h as the film thins down towards the tip. On a flat surface (α = π), on the other hand, the driving mechanism is the moving contact line where the capillary pressure is set by some dynamic contact angle without a similar 1/h-increase. In a sharp corner the contact line motion is primarily normal to the flow direction, at least when |∂h/∂x| ≪ 1, while it is along the flow direction on a flat plane. In our theoretical description we have taken the capillary pressure to be governed by the curvature in the transverse direction, ignoring the smaller contribution due to the curvature in the flow direction. At the critical value α = π − 2Θ, the fluid surface has no curvature in the direction transverse to the flow. As α is increased past this critical value the capillary pressure due to this curvature changes sign. This signals the transition to a different flow regime, where the capillary pressure of the sharp corner geometry is replaced by a weaker pressure. In the case of spreading on a flat substrate, the pressure is entirely controlled by the curvature in the flow direction.
Carrying out the experiments for a range of different liquids, we have observed robust behavior in the sense that experimental artifacts like inertial effects, gravity, corner curvature, pinning effects, variability in the contact angle, and finally the crossover to Newtonian behavior at small shear rates, do not dominate in the end the measurements of the rheological exponent.
Conflicts of interest
There are no conflicts to declare.Data availability
Data for this article including experimental videos for the different power-law fluids employed are available at Zenodo at https://doi.org/10.5281/zenodo.15046745.Acknowledgements
We thank Alex Hansen, Per Arne Rikvold and Erika Eiser for helpful discussions during the execution of this project. This work was partly supported by the Research Council of Norway through its projects 262644 (Center of Excellence funding scheme), 324555 (Researcher Project for Young Talent) and 301138 (NANO2021 program).Notes and references
- E. Steudle and C. A. Peterson, J. Exp. Bot., 1998, 49, 775–788 CAS.
- Growth, Dissolution and Pattern Formation in Geosystems, ed. B. Jamtveit and P. Meakin, Kluwer, Dordrecht, 1999 Search PubMed.
- M. Tuller, D. Or and L. M. Dudley, Water Resour. Res., 1999, 35, 1949–1964 CrossRef.
- P. Meakin and A. M. Tartakovsky, Rev. Geophys., 2009, 47, RG3002 CrossRef.
- P. Concus and R. Finn, Proc. Natl. Acad. Sci. U. S. A., 1969, 63, 292–299 CrossRef CAS PubMed.
- A. Carlson, G. Bellani and G. Amberg, Phys. Rev. E, 2012, 85, 045302 CrossRef PubMed.
- P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef CAS.
- J. Van Hulle and N. Vandewalle, Soft Matter, 2023, 19, 4669–4675 RSC.
- J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid Mech., 2013, 45, 269–292 CrossRef.
- F. Irgens, Rheology and Non-Newtonian Fluids, Springer International Publishing, Cham, Switzerland, 2016 Search PubMed.
- E. Bingham, An Investigation of the Laws of Plastic Flow, U.S. Government Printing Office, 1917 Search PubMed.
- P. Coussot, J. Fluid Mech., 1999, 380, 363–376 CrossRef CAS.
- W. R. Schowalter, Mechanics of non-Newtonian fluids, Pergamon Press, London, England, 1978 Search PubMed.
- D. R. Heldman, D. B. Lund and C. M. Sabliov, Handbook of food engineering, CRC Press, Boca Raton, FL, 3rd edn, 2019 Search PubMed.
- T. Benezech and J. F. Maingonnat, J. Food Eng., 1994, 21, 447–472 CrossRef.
- P. Bertsch, L. Savorani and P. Fischer, ACS Omega, 2019, 4, 1103–1109 CrossRef CAS PubMed.
- G. Phillips and P. Williams, Handbook of Hydrocolloids, Elsevier Science, 2009 Search PubMed.
- A. Deblais, E. d Hollander, C. Boucon, A. E. Blok, B. Veltkamp, P. Voudouris, P. Versluis, H.-J. Kim, M. Mellema, M. Stieger, D. Bonn and K. P. Velikov, Nat. Commun., 2021, 12, 6328 CrossRef CAS PubMed.
- J.-P. Bouchaud and A. Georges, Elsevier Phys. Rep., 1990, 195, 127–293 CrossRef.
- E. G. Flekkøy, A. Hansen and B. Baldelli, Front. Phys., 2021, 9, 41 Search PubMed.
- A. Hansen, B.-S. Skagerstam and G. Tørå, Phys. Rev. E, 2011, 83, 056314 CrossRef PubMed.
- S. Gorthi, S. Meher, G. Biswas and P. Mondal, Proc. R. Soc. A, 2020, 476, 20200496 CrossRef.
- R. Pattle, Mechanics Appl. Math., 1959, 12, 407–409 CrossRef.
- M. Tuller and D. Or, Water Resour. Res., 2001, 37, 1257–1276 CrossRef.
- F. Hoogland, P. Lehmann, R. Mokso and D. Or, Water Resour. Res., 2016, 52, 8413–8436 CrossRef.
- M. Moura, E. G. Flekkøy, K. J. Måløy, G. Schäfer and R. Toussaint, Phys. Rev. Fluids, 2019, 4, 094102 CrossRef.
- P. Reis, M. Moura, G. Linga, P. A. Rikvold, R. Toussaint, E. G. Flekkøy and K. J. Måløy, Adv. Water Resour., 2023, 182, 104580 CrossRef.
- J. G. Savins, Ind. Eng. Chem., 1969, 61, 18–47 CrossRef CAS.
- W. J. Cannella, C. Huh and R. S. Seright, SPE Annual Technical Conference and Exhibition, 1988.
- T. Sochi and M. J. Blunt, J. Pet. Sci. Eng., 2008, 60, 105–124 CrossRef CAS.
- U. Eberhard, H. J. Seybold, E. Secchi, J. Jiménez-Martnez, P. A. Rühs, A. Ofner, J. S. Andrade, Jr and M. Holzner, Sci. Rep., 2020, 10, 11733 CrossRef CAS PubMed.
- N. M. Lima, J. Avendaño and M. S. Carvalho, J. Braz. Soc. Mech. Sci. Eng., 2022, 44, 144 CrossRef CAS.
- F. Lanza, A. Rosso, L. Talon and A. Hansen, Transport in Porous Media, 2022, 145, 245–269 CrossRef.
- S. An, M. Sahimi, T. Shende, M. Babaei and V. Niasar, Phys. Fluids, 2022, 34, 023105 CrossRef CAS.
- H. Fyhn, S. Sinha and A. Hansen, Front. Phys., 2023, 11, 1175426 CrossRef.
- L. Zhang, Z. Yang, Y. Méheust, I. Neuweiler, R. Hu and Y. Chen, Water Resources Res., 2023, 59, e2023WR034958 CrossRef.
- V. Starov, A. Tyatyushkin, M. Velarde and S. Zhdanov, J. Colloid. Interface Sci., 2003, 257, 284–290 CrossRef CAS PubMed.
- S. Rafai and D. Bonn, Physica A, 2005, 358, 58–67 CrossRef CAS.
- A. Ponomarenko, D. Queré and C. Clanet, J. Fluid Mech., 2011, 666, 146–154 CrossRef.
- R. Wijnhorst, T. C. de Goede, D. Bonn and N. Shahidzadeh, Langmuir, 2020, 36, 13784–13792 CrossRef CAS PubMed.
- Rheology of Complex Fluids, ed. A. P. Deshpande, J. M. Krishnan and P. B. S. Kumar, Springer, New York, 2010 Search PubMed.
- P. J. Carreau, Transact. Soc. Rheol., 1972, 16, 99–127 CrossRef CAS.
- S. Ansari, M. A. I. Rashid, P. R. Waghmare and D. S. Nobes, SN Appl. Sci., 2020, 2, 1787 CrossRef CAS.
- S. Jouenne and B. Levache, J. Rheol., 2020, 64, 1295–1313 CrossRef CAS.
- E. Guyon, J. P. Hulin, L. Petit and C. D. Mitescu, Physical Hydrodynamics, Oxford University Press, London, England, 2nd edn, 2014 Search PubMed.
- R. L. Hoffman, J. Colloid Interface Sci., 1975, 50, 228 CrossRef CAS.
- P. Sheng and M. Zhou, Phys. Rev. A, 1992, 45, 5694 CrossRef PubMed.
- M. Latva-Kokko and D. H. Rothman, Phys. Rev. Lett., 2007, 98, 254503 CrossRef CAS PubMed.
- S. H. Tan, N.-T. Nguyen, Y. C. Chua and T. G. Kang, Biomicrofluidics, 2010, 4, 32204 CrossRef PubMed.
- P. J. Whitcomb and C. W. Macosko, in Rheology of Xanthan Gum Solutions, American Chemical Society, 1977, pp. 160–173 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00286a |
| This journal is © The Royal Society of Chemistry 2025 |

