DOI:
10.1039/D5SM00340G
(Paper)
Soft Matter, 2025,
21, 5998-6011
Optimal first-passage times of active Brownian particles under stochastic resetting
Received
3rd April 2025
, Accepted 16th June 2025
First published on 10th July 2025
Abstract
We study the first-passage-time (FPT) properties of an active Brownian particle under stochastic resetting to its initial configuration, comprising its position and orientation, to reach an absorbing wall in two dimensions. We employ a renewal framework for the stochastic resetting process and use a perturbative approach for small Péclet numbers, measuring the relative importance of self-propulsion with respect to diffusion. This allows us to derive analytical expressions for the survival probability, the FPT probability density, and the associated low-order moments. Depending on their initial orientation, the minimal mean FPT for active particles to reach the boundary can both decrease and increase relative to the passive counterpart. The associated optimal resetting rates depend non-trivially on the initial distance to the boundary due to the intricate interplay of resetting, rotational Brownian noise, and active motion.
I. Introduction
Stochastic resetting is a relatively recent concept whereby a process is randomly reset to a predetermined state. Mainly introduced in the context of search processes with Brownian motion,1,2 this framework has been widely expanded to take into account other types of processes, such as Lévy flights,3–5 non-Poissonian waiting times,6–9 or partial,10,11 time-dependent,12 or random resetting mechanisms.13 Overall, stochastic resetting has proven to be a very fruitful research direction for the physics community with a variety of applications. The most common applications being algorithmics,14–17 chemical reactions,18–20 and animal foraging.21,22 In all of those applications, resetting prevents being trapped in a suboptimal state (e.g., resource- or reactant-depleted zone), and most importantly, expedites the search completion (food sources, reactants, or optima), thus improving performance when time constraints are imposed.
The question of FPT properties is particularly important in the context of biology, where the efficiency during foraging is a crucial part of a microorganism's ability to survive and achieve its biological purpose.23–29 Using biology as a model system, active agents have been engineered in the lab and extract energy from their environment to self-propel.30–34 Establishing a physical understanding of how fast these active colloids reach specific targets is an important aspect in their design for target-delivery and bioremediation applications.35–37 Because of the coupling between translational and rotational degrees of freedom, studying the FPT properties of active agents is arguably more difficult than the passive (Brownian) counterpart, but can also lead to a richer variety of results.38–44 In this paper, we study one of the paradigmatic models of active matter – the active Brownian particle (ABP) – comprising the effect of active motion, translational and rotational diffusion.45–49
It is well-established that resetting a passive tracer to its original position enables a stationary distribution and a finite mean FPT (MFPT) for reaching the target.1,50,51 Yet, the interplay of resetting with active motion has not yet been studied in the context of FPT statistics. In our recent work,52 relying on a perturbation analysis for low Péclet numbers, we find that the typical Brownian scaling of the survival probability S(t) ∝ t−1/2 is preserved, yet with a distinct prefactor depending on the agent's initial orientation. Even though the MFPT remains undefined, the median proves to be a robust metric, able to capture the new dynamics emerging from the rotational degree of freedom. Building upon our recent findings for the ABP and combining it with the typical renewal approach used for stochastic resetting,51 we study the interplay of resetting and self-propulsion. In particular, at the resetting event the agent is reset to its initial configuration, comprising its position and orientation. Our main results suggest that, owing to the strong dependence on the initial orientation, resetting in active motion can either increase or decrease the reset-enabled MFPT to reach the absorbing boundary in comparison to the passive case. Notably, we measure this directional bias through an anisotropy function and find that it becomes most pronounced when the initial distance to the wall is comparable to the distance traveled by the agent before being reset.
This paper is organized as follows: in Section II we first introduce our model. We then summarize the perturbative approach used to study the FPT statistics of an ABP without stochastic resetting and, using a renewal approach, we link the survival probabilities with and without stochastic resetting. This framework allows us to analytically compute various statistical indicators, including the MFPT, the median, and the skewness, and we finally resolve the full survival probability and FPT probability density, which we present in Section III. We summarize and conclude in Section IV.
II. Model
In this section, we outline the strategy employed to obtain the first-passage-time (FPT) statistics of an active Brownian particle (ABP), whose position and orientation are reset to their initial state at random times. We consider an ABP moving in a two-dimensional (2D) plane (O, x, z). The particle moves at a constant speed v along its instantaneous orientation e(ϑ(t)) = (sin(ϑ(t)), cos(ϑ(t))), where ϑ(t) denotes the polar angle [Fig. 1 (inset)]. The agent undergoes both random translational and rotational motion, characterized by their respective diffusion coefficients D and Drot. In addition, the instantaneous position r(t) and orientation ϑ(t) are randomly reset to the initial position r0 ≡ r(0) and orientation ϑ0 ≡ ϑ(0); the resetting events happen at times drawn from an exponential distribution ϕ(t) = λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λt) with rate λ (and mean time between resets 1/λ) (see Fig. 1). These processes are represented by the following set of stochastic equations:
exp(−λt) with rate λ (and mean time between resets 1/λ) (see Fig. 1). These processes are represented by the following set of stochastic equations:| |  | (1a) |
| |  | (1b) |
| | | r → r0 and ϑ → ϑ0 with T(t), | (1c) |
where η(t) and ξ(t) are independent Gaussian white noises of zero mean and delta-correlated variance, 〈ηi(t)ηj(t′)〉 = δijδ(t − t′) for i,j ∈ {1, 2} and 〈ξ(t)ξ(t′)〉 = δ(t − t′). Rescaling the position  with the particle's hydrodynamic radius a and the time t = τT with the diffusive time τ = a2/D, two non-dimensional numbers appear: Pe = va/D denotes the Péclet number, measuring the relative importance of active motion versus diffusion, and Λ = λτ is the reduced resetting rate, representing the prevalence of resetting events compared to the diffusive time scale. We further introduce γ = τDrot = 3/4, which follows from the Stokes–Einstein–Sutherland relation for a spherical particle. The latter lets us interpret the reduced resetting rate as a competition between resetting and rotational diffusion Λ = 3λ/4Drot.
with the particle's hydrodynamic radius a and the time t = τT with the diffusive time τ = a2/D, two non-dimensional numbers appear: Pe = va/D denotes the Péclet number, measuring the relative importance of active motion versus diffusion, and Λ = λτ is the reduced resetting rate, representing the prevalence of resetting events compared to the diffusive time scale. We further introduce γ = τDrot = 3/4, which follows from the Stokes–Einstein–Sutherland relation for a spherical particle. The latter lets us interpret the reduced resetting rate as a competition between resetting and rotational diffusion Λ = 3λ/4Drot.
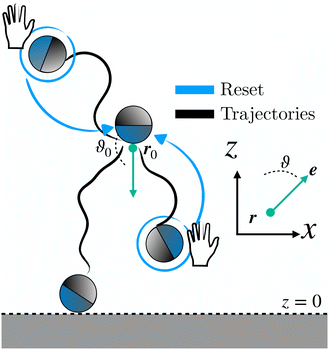 |
| | Fig. 1 Schematic of the motion of an ABP under stochastic resetting to its initial position r0 and orientation ϑ0 near an absorbing boundary at z = 0. The green dot and arrow represent the resetting position and orientation, respectively. The inset depicts the agent's position r and orientation ϑ. | |
A. Renewal framework
To make analytical progress, we rely on a renewal approach for the survival probability S(T|Z0,ϑ0), i.e. the probability that the agent, which has started at position Z0 with orientation ϑ0, has not yet reached the boundary at time T. Note that we have integrated over the X-direction due to the invariance in the direction parallel to the wall. For exponentially distributed resetting times ϕ(T) = Λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΛT), the survival probability follows:51
exp(−ΛT), the survival probability follows:51| | 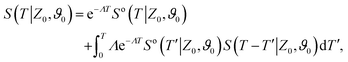 | (2) |
where So(T′|Z0,ϑ0) corresponds to the survival probability of an ABP in the absence of resetting. Eqn (2) is to be interpreted in the following way: the probability to survive up to time T is the sum of the probability to survive up to time T without any resetting event and the sum over the probabilities to survive up to time T′ given a reset at an earlier time T − T′. The survival probability provides access to the FPT probability density F(T|Z0,ϑ0), characterizing the distribution of times at which the agent reaches the wall:| |  | (3) |
To compute the survival probability we employ a Laplace transform T ↦ s| |  | (4) |
which allows us to readily obtain a closed-form solution| | 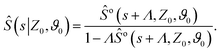 | (5) |
It then suffices to know Ŝo – the survival probability without resetting – to obtain the survival probability with resetting Ŝ in Laplace space.
The former quantity was the object of our previous work,52 where we have derived analytical expressions for So through a perturbation expansion for small Péclet numbers. While details of the perturbation expansion can be found in ref. 52 and Appendix A, we recapitulate the most important steps here. Starting from eqn (1a) and (1b), we first derive a (non-dimensional) Fokker–Planck equation for the probability density  of a particle to be at
of a particle to be at  with orientation ϑ at time T having started at
with orientation ϑ at time T having started at 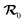 with orientation ϑ0 at T = 0:
with orientation ϑ0 at T = 0:
| | ∂T![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o = −Pe e·∇ o = −Pe e·∇![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o + γ∂ϑ2 o + γ∂ϑ2![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o + ∇2 o + ∇2![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o. o. | (6) |
Since the boundary is infinite in the
X direction, we further integrate out the
X component and arrive at
| | ∂T![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o = −Pe o = −Pe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑ)∂Z cos(ϑ)∂Z![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o + γ∂ϑ2 o + γ∂ϑ2![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o + ∂Z2 o + ∂Z2![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o, o, | (7) |
which is supplemented by the following initial and boundary conditions:
| | ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o(Z,ϑ,T = 0|Z0,ϑ0) = δ(Z − Z0)δ(ϑ − ϑ0), o(Z,ϑ,T = 0|Z0,ϑ0) = δ(Z − Z0)δ(ϑ − ϑ0), | (8a) |
| | ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o(Z = 0,ϑ,T|Z0,ϑ0) = 0 ∀T ∈ o(Z = 0,ϑ,T|Z0,ϑ0) = 0 ∀T ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +. +. | (8b) |
Next, we move to Laplace space (
s ↦
T) and thus
eqn (7) transforms to
| |  | (9) |
where the operator

is split into two components: the unperturbed operator

and the perturbation
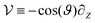
. Expanding the probability density in terms of the Péclet number
| |  | (10) |
and inserting it into
eqn (9), leads to a set of coupled equations for the perturbations [
eqn (A1a)–(A1c) in Appendix A]. Analytical expressions for
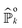
can be obtained iteratively and used as input for the survival probability
 via
via the relation
| |  | (11) |
Analytical predictions up to second order in the Pe number can be found in the Appendix A. Finally, inserting the small-Pe expansion of
Ŝo(
s|
Z0,
ϑ0) into
eqn (5) yields the survival probability in the presence of stochastic positional and orientational resetting
Ŝ(
s|
Z0,
ϑ0) and provides immediate access to the FPT probability density.
To further quantify the FPT properties, we are interested in the low-order moments of the first-passage times, which are accessible through the survival probability in Laplace space Ŝ. In particular, the n-th moment of the random variable FT associated with the FPT probability density can be obtained via
| | 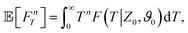 | (12a) |
| |  | (12b) |
| |  | (12c) |
where we have used the relation between
F(
T|
Z0,
ϑ0) and
S(
T|
Z0,
ϑ0) [
eqn (3)] and the properties of the Laplace transform.
B. Expansion in the Péclet number
Note that we can further expand the survival probability for small Pe,  [eqn (5)], and formally obtain the associated coefficients:
[eqn (5)], and formally obtain the associated coefficients:| |  | (13a) |
| | 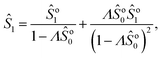 | (13b) |
| |  | (13c) |
which can be readily extended to higher orders. Using this result, the FPT probability density in Laplace space obeys| |  | (14) |
where the first two terms correspond to the FPT probability density of a Brownian particle under stochastic resetting and the sum encodes the effect of activity.
C. Brownian particle under stochastic resetting
Our framework allows recovering the well-established result for the survival probability of a passive Brownian particle under stochastic resetting as| |  | (15) |
Notably, we mentioned that introducing a resetting mechanism for a diffusive process establishes a finite mean first-passage time (MFPT). It reduces to| |  | (16) |
which represents the well-known MFPT for a diffusive particle under stochastic positional resetting.1 It diverges as ∝ Λ−1/2 for Λ → 0, thus approaching the behavior of a Brownian particle without resetting. Furthermore, it diverges as Λ → ∞, reflecting the particles that are constantly reset and never manage to reach the wall. Most importantly, for a fixed initial distance Z0, there exists an optimal resetting rate  that minimizes the MFPT, where Z* = 1.59362… is the unique solution of the transcendental equation:
that minimizes the MFPT, where Z* = 1.59362… is the unique solution of the transcendental equation:| |  | (17) |
This indicates that minimizing the MFPT far away from the wall requires resetting the agent less often.
III. Results
In what follows, we show our results for the active Brownian particle under stochastic resetting by expanding Ŝo up to the second order in the Péclet number. We discuss the mean first-passage times [Section III A], the optimal resetting rate [Section III B], the anisotropy of the process [Section III C], the survival probability and the probability density for the FPT [Section III D], as well as the skewness and the median of the FPTs [Section III E and F].
A. Mean first-passage time
We compute the mean first-passage time (MFPT) by following the strategy outlined in Section II A. Our theoretical prediction reveals that it becomes finite [eqn (B1) in Appendix B] within the limit of small Pe and depends strongly on the initial orientation ϑ0 and initial distance to the boundary z0. Let us first note that Fig. 2(A)–(C) show that our theoretical predictions are nicely corroborated by simulation results (see Appendix D for details). We further note that though our results may loose accuracy for Pe ≥ 1, we show in Appendix C that our perturbation approach remains valid for this parameter range and we observe very good agreement with simulations even at larger Péclet numbers.
 |
| | Fig. 2 (A)–(C) Mean first-passage time ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft] for three different initial angles ϑ0 as a function of the resetting rate Λ (with z0/a = 3) for different Péclet numbers Pe. Insets show the MFPT as a function of the initial distance z0 for several Λ and Pe = 0.5. (D)–(F) Ratio of the mean first-passage times of an active and passive Brownian particle at the optimal resetting rate [Ft] for three different initial angles ϑ0 as a function of the resetting rate Λ (with z0/a = 3) for different Péclet numbers Pe. Insets show the MFPT as a function of the initial distance z0 for several Λ and Pe = 0.5. (D)–(F) Ratio of the mean first-passage times of an active and passive Brownian particle at the optimal resetting rate  as a function of Pe and z0. Columns show results for particles (A) and (D) initially facing the wall, (B) and (E) initially facing against the wall, and (C) and (F) with initial angles drawn from a uniform distribution as a function of Pe and z0. Columns show results for particles (A) and (D) initially facing the wall, (B) and (E) initially facing against the wall, and (C) and (F) with initial angles drawn from a uniform distribution  . Solid lines and markers denote theory and simulations, respectively. The black lines in (A)–(C) correspond to the passive case with resetting rate ΛB = 1. . Solid lines and markers denote theory and simulations, respectively. The black lines in (A)–(C) correspond to the passive case with resetting rate ΛB = 1. | |
Importantly, we find that an agent initially facing the wall (ϑ = π) reaches it faster than an agent oriented away from the wall (ϑ = 0), which is in turn slower than a diffusive agent [Fig. 2(A) and (B)]. Assuming uniformly distributed initial angles leads to a slightly lower MFPT than the diffusive case [Fig. 2(C)]. Additionally, increasing activity through the Péclet number expedites and delays the arrival at the boundary for ϑ0 = π and ϑ0 = 0, respectively. This is explained by the fact that the distance the particle travels before reorienting (i.e., the persistence length) increases conjointly with activity, lp = v/Drot = aPe/γ, and that the agent's initial orientation is also reset in the process. Hence, a particle initially departing from (respectively moving towards) the wall at a higher velocity will reach the wall at later (respectively earlier) times even with resetting. Importantly, the divergence of the MFPT ∝ Λ−1/2 as Λ → 0 and for Λ → ∞ is preserved for an active particle, as resetting too often prevents ever reaching the wall and not resetting enough leads to the divergence as for a simple ABP. We can expect this scaling to change for higher activity, as persistent motion will dictate short-time dynamics.
The MFPTs further depend on the agent's initial distance z0 [Fig. 2(A)–(C) (insets)]. In particular, they increase linearly in z0 for short distances z0/a ≲ 1, in agreement with the passive case and irrespective of ϑ0 and Λ. Increasing Λ expedites the process for short initial distances z0/a ≲ 1. At large distances z0/a ≳ 1 the MFPTs diverge, which occurs earlier for small Λ. Thus, independent of the initial orientation ϑ0 resetting more frequently at short distances z0 is more efficient than at large z0. This can be rationalized as follows: when the time between resets becomes shorter than the time it takes the agents to reach the wall, it becomes impossible for particles to reach the wall and thus the MFPT diverges. Fixing the resetting rate for the passive case to Λ = 1 and comparing it to the active case with the same rate shows that at large z0 the active agent is always faster (ϑ0 = π,  ) or takes about an equal amount of time (ϑ0 = 0) to reach the wall.
) or takes about an equal amount of time (ϑ0 = 0) to reach the wall.
Our results demonstrate that the MFPTs exhibit a minimum as a function of Λ [Fig. 2(A)–(C)], which begs the question of the optimal MFPT ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft]* (and corresponding resetting rate Λ*) to accelerate absorption at the boundary. We begin this discussion by comparing
[Ft]* (and corresponding resetting rate Λ*) to accelerate absorption at the boundary. We begin this discussion by comparing ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft]* with its passive counterpart
[Ft]* with its passive counterpart  [Fig. 2(D)–(F)]. For low activity Pe ≲ 0.1, the active and passive cases are comparable,
[Fig. 2(D)–(F)]. For low activity Pe ≲ 0.1, the active and passive cases are comparable,  , and the initial angle remains unimportant. Deviations appear as Pe increases and approaches one, where agents initially oriented towards the wall always display a lower optimal MFPT. However, agents departing away from it exhibit a slightly more complex behavior: at short initial distances z0/a ≲ 3, they are naturally slower
, and the initial angle remains unimportant. Deviations appear as Pe increases and approaches one, where agents initially oriented towards the wall always display a lower optimal MFPT. However, agents departing away from it exhibit a slightly more complex behavior: at short initial distances z0/a ≲ 3, they are naturally slower 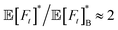 because of the persistent motion, but as z0/a → 10, rotational diffusion kicks in and allows agents to reorient and move persistently towards the boundary, which makes them faster than diffusive particles (see also inset of Fig. 2B). For the same reason, randomly initially oriented particles will reach the boundary faster when both activity and initial position are large enough.
because of the persistent motion, but as z0/a → 10, rotational diffusion kicks in and allows agents to reorient and move persistently towards the boundary, which makes them faster than diffusive particles (see also inset of Fig. 2B). For the same reason, randomly initially oriented particles will reach the boundary faster when both activity and initial position are large enough.
Overall, for particles facing the wall and randomly oriented particles, the optimal MFPT decreases as a function of Pe for any z0, while particles facing away from the wall exhibit an increase of their optimal MFPT with activity, except when the initial distance is sufficiently large, in which case this trend does not hold [Fig. 3].
 |
| | Fig. 3 Optimal MFPT ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft]* as a function of the Péclet number Pe for several initial distances z0/a. The solid lines correspond to ϑ0 = π, dashed lines to ϑ0 = 0 and dotted lines to an initial angle randomly chosen. [Ft]* as a function of the Péclet number Pe for several initial distances z0/a. The solid lines correspond to ϑ0 = π, dashed lines to ϑ0 = 0 and dotted lines to an initial angle randomly chosen. | |
B. Optimal resetting rate
Next, we are interested in what determines this optimal resetting rate and since trying to solve analytically for Λ* leads to a lengthy transcendental equation, we rather rely on numerics and compare it with the passive case  in Fig. 4. In agreement with our observation for the optimal MFPT, the initial angle appears irrelevant for small Pe ≲ 0.1, thus leading to
in Fig. 4. In agreement with our observation for the optimal MFPT, the initial angle appears irrelevant for small Pe ≲ 0.1, thus leading to  .
.
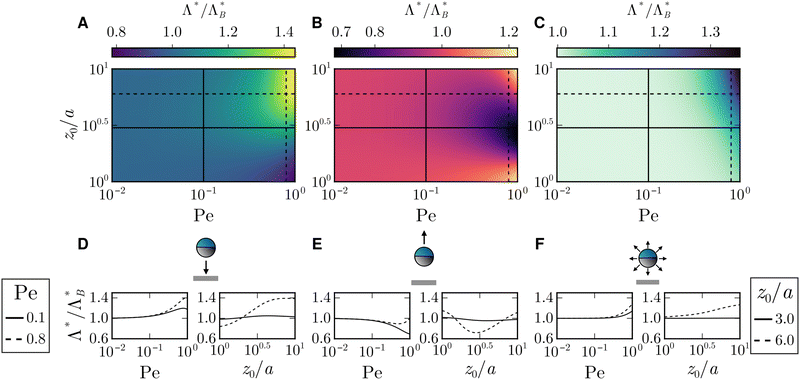 |
| | Fig. 4 (A)–(C) Ratio of the optimal resetting rate  for three different initial angles ϑ0 as a function of the Péclet number Pe and of the initial position z0/a. (D)–(F) Ratio for three different initial angles ϑ0 as a function of the Péclet number Pe and of the initial position z0/a. (D)–(F) Ratio  as function of Pe (respectively, z0/a) at fixed z0/a (respectively, Pe). Columns show results for particles (A) and (D) initially facing the wall, (B) and (E) initially facing against the wall, and (C) and (F) with initial angles drawn from a uniform distribution as function of Pe (respectively, z0/a) at fixed z0/a (respectively, Pe). Columns show results for particles (A) and (D) initially facing the wall, (B) and (E) initially facing against the wall, and (C) and (F) with initial angles drawn from a uniform distribution  . . | |
The optimal resetting rate Λ* for a particle facing the wall (ϑ0 = π) displays two behaviors depending on the initial distance: for z0/a ≃ 1 the optimal rate Λ* decreases with Péclet number, as letting the particle reach the boundary through persistent motion is the most effective strategy. In particular, resetting as often as in the passive case would take the particle away from the boundary and increase the FPT. However, at larger initial distances, Λ* becomes larger than the passive counterpart and increases with activity. Thus, active particles need to be reset more often as they can reorient due to rotational motion, which enables them to move away from the boundary. Furthermore,  displays a maximum (see first plot in Fig. 4D). The presence of this maximum can be understood by considering the length the agent moves in the z-direction before resetting
displays a maximum (see first plot in Fig. 4D). The presence of this maximum can be understood by considering the length the agent moves in the z-direction before resetting
| |  | (18) |
where 〈Δ
z(
t)〉 is the average displacement at time
t47| | 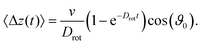 | (19) |
Eqn (18) represents the persistence length with a contribution of the resetting rate (
Drot →
Drot +
λ). Thus, as the resetting length and the initial distance become comparable
lR/
z0 ∼ 1, resetting too often becomes disadvantageous.
For a particle that is facing away from the boundary and for Pe close to one, we distinguish three cases: first, for z0/a ≃ 1, the particle needs to be reset more frequently because of the influence of ϑ0. In this regime, it is likely that the particle arrives at the wall through translational diffusion, while active motion takes it away. Second, for intermediate z0/a, resetting events need to be less frequent, to ultimately increase the chances of reorienting through rotational diffusion towards the wall and reaching it via active motion. Third and lastly, for z0/a ≃ 10, the agent requires more frequent resets, similar to the case of a particle initially facing the boundary.
Averaging out the effect of the initial orientation ϑ0 shows that an active particle, as a result of persistent motion, needs to be reset more frequently at larger initial distances and for higher Péclet numbers than the passive counterpart [Fig. 4F]. Interestingly Λ* seems to have no extremum when the initial angle is randomized, suggesting that resetting more frequently is always an advantage for the parameter range considered.
C. Anisotropy of the mean first-passage time
To further quantify the effect of the initial orientation we introduce the anisotropy function via| |  | (20) |
measuring the ratio of the MFPT given an initial position and orientation with the MFPT given the same initial position but with the diametrically opposed initial orientation. Fig. 5A indicates that the anisotropy for an agent initially oriented towards the wall (respectively opposite to the wall) is large at small initial distances z0/a ≲ 1 and is a decreasing function of Λ. This is due to the fact that at such distances, the particle initially oriented towards the wall should reach it almost immediately, which is hindered by a too frequent resetting mechanism. For z0/a ≳ 10, the anisotropy relaxes to  , independently of the resetting rate, as the memory of the initial orientation progressively decays for such large initial distances.
, independently of the resetting rate, as the memory of the initial orientation progressively decays for such large initial distances.
 |
| | Fig. 5 (A) Anisotropy 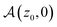 as a function of the initial position z0 for different resetting rates Λ. (B) and (C) Anisotropy as a function of the initial angle ϑ0 for different Λ and z0. The Péclet number is Pe = 0.4. as a function of the initial position z0 for different resetting rates Λ. (B) and (C) Anisotropy as a function of the initial angle ϑ0 for different Λ and z0. The Péclet number is Pe = 0.4. | |
At intermediate distances z0/a ≃ 1 the anisotropy exhibits a maximum for large enough resetting rates (Λ ≳ 0.1) which can be rationalized in the following way: at these distances, resetting events start to be prevalent and thus effectively rectify the trajectory of agents that started moving towards the wall but oriented away and the trajectory of agents that departed away from the wall but managed to reorient towards it through rotational diffusion, strengthening the discrepancy in their MFPTs. We further note that the maximum displaces towards the right with increasing resetting rate Λ, as the distance lR ∝ Pe/Λ traveled before resetting decreases with Λ.
We note that there is a point  where the anisotropy appears to be independent of the resetting rate. We anticipate that it corresponds to the distance when active motion starts to become comparable to translational diffusion. Comparing the length traveled through diffusion during time t (l2 = tD) with the length traveled using active motion (l = tv) leads to l = a/Pe, which predicts the disappearance of that point at larger Pe. This feature remains to be further studied for larger Péclet numbers that go beyond our perturbation limits.
where the anisotropy appears to be independent of the resetting rate. We anticipate that it corresponds to the distance when active motion starts to become comparable to translational diffusion. Comparing the length traveled through diffusion during time t (l2 = tD) with the length traveled using active motion (l = tv) leads to l = a/Pe, which predicts the disappearance of that point at larger Pe. This feature remains to be further studied for larger Péclet numbers that go beyond our perturbation limits.
Finally, we study how the anisotropy behaves as a function of the initial angle. It is maximal for ϑ0 = 0, 2π, since the median FPT of agents initially moving away from the wall is greater than that of agents going to the wall. Reciprocally, it is minimal for ϑ0 = π. Since translation diffusion plays a major role for small initial distances, the importance of the resetting rate is minimal [Fig. 5B] for small z0/a. As the initial distance gets larger, the particle takes more and more advantage of persistent motion and the anisotropy thus increases [Fig. 5C]. Most importantly, it becomes larger for increasing Λ, compared to smaller z0, where a reduced rate Λ produces the largest anisotropy. Thus the curves intersect at an intermediate distance 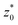 .
.
D. Survival probability and first-passage-time distribution
In the past section, we studied the MFPT, which gave us a quantitative answer to the question of “speed of completion”. We can now try to deepen our understanding by also computing the survival probability S(t|z0,ϑ0) and the FPT probability density function F(t|z0ϑ0). Fig. 6(A)–(C) shows an exponential decay for the survival probability, independently of the initial angle. Thus, resetting profoundly changes the power-law behavior ∼t−1/2 of a simple ABP at low Pe,52 which remains visible for times t/τ ≤ Λ−1, as resetting has not yet settled in [Fig. 6(A)–(C) (inset)]. The absence of this power-law tail is a sign that, unlike the non-resetting case, agents manage to reach the wall within a finite time due to the resets to their initial configuration.
 |
| | Fig. 6 Survival probability (A)–(C) and FPT probability density (D)–(F) as a function of time t for three different initial angles ϑ0: the particle is initially (A) facing the wall, (B) facing against the wall, and (C) randomly oriented with an angle drawn from a uniform distribution 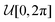 . Here, the initial position is z0/a = 3 and the Péclet number is Pe = 0.4. Solid lines and symbols denote theory and simulations for different resetting rates, respectively. The black lines represent the active case in the absence of resetting. The insets show a zoomed-in region of the plot containing them. The colored vertical lines represent the typical resetting times 1/Λ. . Here, the initial position is z0/a = 3 and the Péclet number is Pe = 0.4. Solid lines and symbols denote theory and simulations for different resetting rates, respectively. The black lines represent the active case in the absence of resetting. The insets show a zoomed-in region of the plot containing them. The colored vertical lines represent the typical resetting times 1/Λ. | |
As we resolve the distributions for distances larger than the agent's persistence length, z0/a = 3 ≳ lp/a, rotational diffusion plays an important role. Thus, the question of which survival distribution decays faster depending on Λ follows the same logic as for the optimal MFPT: resetting is an advantage if it resists departure from the wall without hindering reorientation towards it (ϑ0 = 0), while at the same time ensuring that there is enough time to reach it (ϑ0 = π). Furthermore, we note that the optimal resetting rate is Λ* ≈ 0.3 for all cases, which is reflected in the fact that the survival decays the fastest for Λ = 0.3.
We further comment on the behavior of the survival probability at large distances z0/a ≫ lp. In free space, it is well-established that at large times t ≳ 1/Drot an ABP enters an effective diffusive regime characterized by the effective diffusion coefficient
| |  | (21) |
We therefore suggest that an active particle, which starts far away from the boundary, reaches the wall through effective diffusion. Thus, its survival probability in this regime assumes the form of that of a Brownian particle in
eqn (15) by replacing the translational diffusivity
D by the effective diffusivity
Deff:
| |  | (22) |
In the time variable, the latter has the following asymptotic behavior
1| |  | (23) |
We observe that for Pe = 0.4, the survival probability at long times is well approximated by that of a passive agent under resetting performing effective diffusion [dotted lines in
Fig. 7]. The asymptotic prediction in
eqn (23) also nicely agrees with our findings, highlighting the exponential tails of the survival probability at long times. In our previous work,
52 we have demonstrated that the memory of the initial angle is never actually lost and that the amplitude of the tail of the survival probability in the absence of resetting depends non-trivially on the original orientation. Introducing the resetting smoothens this effect but deviations from the passive case are naturally expected to increase with the Péclet number.
 |
| | Fig. 7 Survival probability S(t|z0,ϑ0) of an active particle for different resetting rates Λ. The solid lines correspond to the perturbation theory, the dotted lines represent the prediction for the effective Brownian case [eqn (22)] and the dashed lines the associated asymptotic approximation [eqn (23)]. Here, the initial distance is z0/a = 30, the initial orientation is ϑ0 = π, and the Péclet number is Pe = 0.4. | |
Putting in parallel the survival probability with the FPT probability density [Fig. 6(D)–(F)] shows that a faster decay of S leads to a faster-decaying tail for F, where again no power-law F ∝ t−3/2 is present, as in the absence of resetting.52 Finally, we observe that even though the resetting mechanism annihilates the tail, increasing the rate causes the distribution to flatten and spread over at intermediate times 0.1 ≲ t/τ ≲ 100. Resetting the particle often enables situations where it reaches the wall after longer times due to the large number of resets. To expand on this observation, we compute another statistical quantity, the skewness.
E. Skewness of the distribution
Given the shape of the FPT probability density, we compute the skewness, measuring the asymmetry around the MFPT. The skewness is defined as the third standardized moment:| |  | (24) |
where we use eqn (12c) to obtain the moments. The results are summarized in Fig. 8A where we plot ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 3 as a function of Λ for several z0. We first note that the skewness is positive for all cases, indicating that the FPT distribution is right-skewed, or skewed towards the large arrival times, accounting for the agents that manage to reach the wall at later times t/τ ≫ 1. It also diverges for vanishing Λ, in accordance with the absence of moments for the non-resetting case. For a fixed z0/a, the skewness decreases when Λ increases, which is consistent with the observation that the FPT probability density for z0/a = 3 stretches over a broader range of times. If the particle is increasingly reset, it naturally requires more attempts and thus time to successfully reach the wall.
3 as a function of Λ for several z0. We first note that the skewness is positive for all cases, indicating that the FPT distribution is right-skewed, or skewed towards the large arrival times, accounting for the agents that manage to reach the wall at later times t/τ ≫ 1. It also diverges for vanishing Λ, in accordance with the absence of moments for the non-resetting case. For a fixed z0/a, the skewness decreases when Λ increases, which is consistent with the observation that the FPT probability density for z0/a = 3 stretches over a broader range of times. If the particle is increasingly reset, it naturally requires more attempts and thus time to successfully reach the wall.
 |
| | Fig. 8 (A) Skewness ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 3 as a function of the reduced resetting rate Λ for different initial positions z0 and (inset) as a function of z0 for different Λ. The Péclet number is Pe = 0.4 and initial orientation ϑ0 = π. Theory and simulations are shown with solid lines and markers, respectively. (B) Median T1/2 as a function of the initial position z0 for different reduced resetting rates Λ. The initial angle is ϑ0 = π and the Péclet number is Pe = 0.4. Theory and simulations are shown with solid lines and markers, respectively. The shaded gray corresponds to the simulation time limit. (inset) Shows the ratio of the MFPT and the median as a function of z0/a. 3 as a function of the reduced resetting rate Λ for different initial positions z0 and (inset) as a function of z0 for different Λ. The Péclet number is Pe = 0.4 and initial orientation ϑ0 = π. Theory and simulations are shown with solid lines and markers, respectively. (B) Median T1/2 as a function of the initial position z0 for different reduced resetting rates Λ. The initial angle is ϑ0 = π and the Péclet number is Pe = 0.4. Theory and simulations are shown with solid lines and markers, respectively. The shaded gray corresponds to the simulation time limit. (inset) Shows the ratio of the MFPT and the median as a function of z0/a. | |
Interestingly, the skewness converges to 2 when the initial position is large z0/a ≫ 1 (independently of Λ) or when the resetting rate is large Λ > 1 (independently of z0). Based on our analysis of the optimal MFPT and optimal resetting rate, we expect that the skewness should converge to that of the resetting effective Brownian case. Using eqn (24) with the leading-order term Ŝ0 provides the skewness of the FPT probability density of a Brownian particle under stochastic resetting
| |  | (25) |
which converges to 2 for
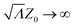
, thus explaining the behavior of the skewness for the FPT probability of an active agent.
F. Median of the first-passage time
For the sake of completeness we further compute the median T1/2, giving the value that splits the distribution into two equiprobable parts and defined as:| |  | (26) |
In the non-resetting case, where the MFPT is not defined, the median allowed us to give a quantitative answer to the question of the FPT,52 which we compare here to the resetting case. Fig. 8B displays the median T1/2 as a function of the initial position z0 for several rates Λ and for ϑ0 = π. In the case of no resetting and very low resetting rate Λ ≪ 1, the median grows quadratically with the initial distance T1/2 ∝ z02 (as the diffusive case). For increasing Λ, T1/2 starts to diverge at z0/a ≳ 10, as the positional resetting events are too frequent for the agent to ever reach the wall.
To further quantify the (a)symmetry of the distribution, we compare the ratio of the mean and the median in Fig. 8A (inset). At small initial distances z0/a ≲ 1, we first notice that for vanishing Λ, the ratio ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft]/T1/2 diverges since the MFPT itself diverges while the median remains defined. As the resetting rate increases,
[Ft]/T1/2 diverges since the MFPT itself diverges while the median remains defined. As the resetting rate increases, ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft]/T1/2 decreases due to the resetting process stabilizing the distribution. We finally note that even though both the median and the MFPT diverge at large z0/a, their ratio seems to eventually converge to a value slightly above one, independently of the resetting rate, which is consistent with the positive skewness studied in the previous section. Thus, this further emphasizes that the distribution remains asymmetric for any parameters considered here. (Let us finally note that the results remain qualitatively similar for different initial orientations.)
[Ft]/T1/2 decreases due to the resetting process stabilizing the distribution. We finally note that even though both the median and the MFPT diverge at large z0/a, their ratio seems to eventually converge to a value slightly above one, independently of the resetting rate, which is consistent with the positive skewness studied in the previous section. Thus, this further emphasizes that the distribution remains asymmetric for any parameters considered here. (Let us finally note that the results remain qualitatively similar for different initial orientations.)
IV. Conclusion
Here, we have studied the FPT properties of an ABP under stochastic resetting to its initial configuration. Employing a previously developed perturbative approach and a renewal framework, we compute exact expressions for the FPT probability density and several other statistical indicators such as the mean, skewness, and median. The main difference to the bare diffusive case is the additional initial orientation of the particle relative to the wall, which can make reaching the boundary slower or faster than a diffusive particle. By quantifying the optimal resetting rate our results demonstrate that active agents, which are relatively far away from the boundary, should be reset more frequently than passive ones to minimize their arrival time, as active motion can take them further away. We further discuss the effect of the initial orientation through an anisotropy function which becomes most pronounced when the initial distance is comparable to the distance the particle travels before it is reset.
The theory developed in this work is valid for small Péclet numbers and it is expected that the interplay of all processes changes for high activity. First insights along this line predict a t−1/4 scaling of the survival probability of highly persistent agents in the non-resetting case and for particles initially aligned parallel to the wall, highlighting the distinct physics that can arise in this limit.53 For instance, an agent departing away from the wall and swimming persistently at high Péclet number is unlikely to reach the wall and it would be interesting to see what the resetting mechanism changes in this case. While we have here integrated out the direction parallel to the wall, it would be interesting to explore where the particles hit the wall.
While we have considered the effect of simultaneous resetting of both the position and orientation, the behavior of only resetting the position or the orientation is important for identifying optimal resetting protocols in active systems. The process of resetting the particle's position while orientation diffuses depends on the relative importance of the resetting rate and the rotational diffusivity, Λ. Thus, in the regime of large rotational diffusivity Λ ≲ 1, this problem is expected to reduce to the situation, whereby the angle after each reset is chosen randomly. In the regime of low rotational diffusivity Λ ≳ 1, the initial orientation is expected to play a crucial role that needs to be further elucidated. Resetting of the orientation54 towards the wall will decrease the FPT, yet in this context considering the associated cost may be important.
Since the agent considered here is active, there are even more directions in which one can extend this work. Experimental realizations of positional stochastic resetting for passive particles have been achieved through different implementations55,56 and have yielded validation of the underlying theory. This is particularly relevant for our case, where the question of resetting a microscale active agent is experimentally not straightforward.57 Resetting is naturally associated with a thermodynamic cost58–62 and as these active agents are generally immersed in a fluidic environment they would also need to overcome an additional drag force and withstand shear-induced reorientations, not present in passive systems.63 Further experimental efforts may focus on designing efficient resetting protocols for microswimmers, guided by our theoretical predictions.
In the context of foraging and other target-search problems, stochastic resetting is often depicted as an advantageous search strategy56,64 but in a lot of situations agents are active and cannot be said to simply perform Brownian motion. One experimental example at the macroscale represents experiments on centimeter-sized, active robots, whose orientation is subject to resetting via light stimuli, providing potential insights into the optimal foraging and homing behaviors of animals.65 Unraveling the interplay of orientational and positional resetting in complex environments, including quenched disorder, boundaries,66,67 and external fields,68,69 is important for identifying optimal strategies of biological systems to find targets without being trapped in the environment. Furthermore, focusing on different swimming strategies that go beyond the paradigmatic active Brownian particle model, such as chiral motion,70 represents an exciting future research avenue.
Conflicts of interest
There are no conflicts to declare.
Data availability
Most data can be generated by using the formulas provided in the manuscript. The data that support the findings of this study are available upon reasonable request from the authors.
Appendices
The appendix contains a summary of the perturbative approach used to compute the propagator in the absence of resetting [Section A], the expression of the MFPT in the presence of resetting [Section B], a validation of the perturbative approach for intermediate Péclet numbers [Section C], and finally the details of our simulations [Section D].
A: Perturbative approach
In this section, we provide additional details regarding the approach we used for the FPT statistics of an ABP without stochastic resetting in ref. 52. Therefore, we insert the expansion in eqn (10) up to second order in the Péclet number into the Laplace transform of the Fokker–Planck equation [eqn (9)] to obtain a coupled set of equations that are solved iteratively:| |  | (A1a) |
| | 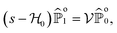 | (A1b) |
| |  | (A1c) |
The contribution of order i + 1 can be computed from the contribution of order i through:| | 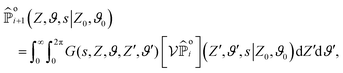 | (A2) |
where G denotes the Green's function solving eqn (A1a) with boundary condition G(s,Z = 0, ϑ, Z′, ϑ′) = 0. Computing G is done by first solving the equation for an unbounded domain (whose solution we denote by Gu) and subtracting the contribution of an image solution to impose the boundary condition:| |  | (A3) |
where p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2 = s + γl2. We further note that due to the symmetry of the coefficients, p
2 = s + γl2. We further note that due to the symmetry of the coefficients, p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = p−
= p−![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , there is no need to change the angular part of the image solution.
, there is no need to change the angular part of the image solution.
Each contribution to the survival probability is then obtained by marginalizing over the position:
| | 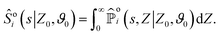 | (A4) |
The zeroth-order solution, corresponding to the survival probability of a passive particle, is
| |  | (A5) |
and the first- and second-order corrections read:
| |  | (A6) |
| | 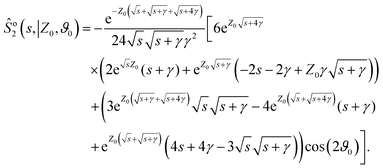 | (A7) |
Finally, the survival probability in Laplace space in the absence of resetting up to second order in the Péclet number is given by Ŝo = Ŝo0 + Pe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ŝo1 + Pe2
Ŝo1 + Pe2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ŝo2. The latter is inserted into eqn (5) in the main text to obtain the survival probability with resetting.
Ŝo2. The latter is inserted into eqn (5) in the main text to obtain the survival probability with resetting.
B: Analytical expression for the MFPT
The analytical expression of the MFPT of the ABP up to second order in the Péclet number in Laplace space reads| | 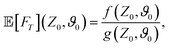 | (B1) |
where| |  | (B2a) |
| |  | (B2b) |
Expansion of the full expression up to second order in the Péclet number results in| | 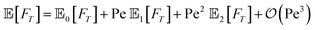 | (B3) |
with ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) 0[FT] =
0[FT] = ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [FT]B [eqn (16)] and the activity-induced contributions:
[FT]B [eqn (16)] and the activity-induced contributions:| |  | (B4a) |
| | 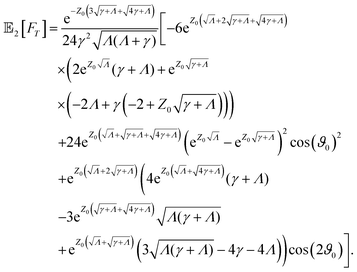 | (B4b) |
C: Validation of the perturbation approach
In ref. 52, we show how the contributions of the first- and second-order corrections affect the FPT statistics for a non-resetting particle, and give a recursive scheme to compute higher-order corrections. In particular, the second-order term captures the essential orientational degrees of freedom; higher-order corrections typically contribute negligibly to the statistics. This is why all our results are obtained by truncating the series expansion of Ŝo at the second-order in Pe. To check the range of validity of our perturbation approach for the computation of the MFPT, we also plot ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft] as a function of the Péclet number, Pe (i.e., our perturbation parameter). Our results shown in Fig. 9 indicate that, at least until a resetting rate Λ = 3, the theory provides good agreement with simulations up to Pe ≈ 1. It also remains valid up to Pe = 3 for the largest resetting rate Λ = 3, whereas discrepancies start to emerge as the resetting rate is lowered. This can be explained by considering that for Λ = 3, the length traveled by the particle before resetting is smaller than the persistence length lR/lp = γ/(Λ + γ) ≪ 1. Thus, the agent essentially reaches the wall without fully taking advantage of persistent motion. For lower resetting rates the effects of active motion can fully develop, leading to the observed discrepancies between theory and simulations.
[Ft] as a function of the Péclet number, Pe (i.e., our perturbation parameter). Our results shown in Fig. 9 indicate that, at least until a resetting rate Λ = 3, the theory provides good agreement with simulations up to Pe ≈ 1. It also remains valid up to Pe = 3 for the largest resetting rate Λ = 3, whereas discrepancies start to emerge as the resetting rate is lowered. This can be explained by considering that for Λ = 3, the length traveled by the particle before resetting is smaller than the persistence length lR/lp = γ/(Λ + γ) ≪ 1. Thus, the agent essentially reaches the wall without fully taking advantage of persistent motion. For lower resetting rates the effects of active motion can fully develop, leading to the observed discrepancies between theory and simulations.
 |
| | Fig. 9 MFPT ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft] as a function of the Péclet number Pe for several resetting rates Λ. Here, the initial distance is z0/a = 3 and the initial orientation ϑ0 is chosen randomly. Solid lines and symbols denote theory and simulations, respectively. Dashed lines correspond to the result given by eqn (B3). [Ft] as a function of the Péclet number Pe for several resetting rates Λ. Here, the initial distance is z0/a = 3 and the initial orientation ϑ0 is chosen randomly. Solid lines and symbols denote theory and simulations, respectively. Dashed lines correspond to the result given by eqn (B3). | |
In the same figure, we also plot as dashed lines the expansion of the MFPT given by eqn (B3) and see that it performs worse at larger Pe. Even though the expression given by eqn (B1) is exact up to second order in the Péclet number, it is a ratio and thus contains terms of mixed-order. Computing its series around zero naturally leads to truncating higher-order terms to approximate ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [FT]. Our results show that the agreement with numerics becomes considerably worse at Pe ≳ 1, which is why we use eqn (B1) throughout the manuscript.
[FT]. Our results show that the agreement with numerics becomes considerably worse at Pe ≳ 1, which is why we use eqn (B1) throughout the manuscript.
D: Computer simulations
To perform stochastic simulations, we discretize eqn (1a) and (1b) according to the Euler–Maruyama scheme:| |  | (D1a) |
| |  | (D1b) |
where Δt = 10−3τ is the time-step, Nt(0,1) and Nr(0,1) are independent, normally-distributed random variable with zero mean and unit variance. Furthermore, the statistics are obtained by simulating trajectories for 105 particles.
Acknowledgements
We gratefully acknowledge discussions with Thomas Franosch and Magali Le Goff. Open Access funding provided by the Max Planck Society.
References
- M. R. Evans and S. N. Majumdar, Diffusion with Stochastic Resetting, Phys. Rev. Lett., 2011, 106(16), 160601 CrossRef PubMed.
- J. Whitehouse, M. R. Evans and S. N. Majumdar, Effect of Partial Absorption on Diffusion with Resetting, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87(2), 022118 CrossRef PubMed.
- L. Kusmierz, S. N. Majumdar, S. Sabhapandit and G. Schehr, First Order Transition for the Optimal Search Time of Lévy Flights with Resetting, Phys. Rev. Lett., 2014, 113(22), 220602 CrossRef PubMed.
- L. Kuśmierz and E. Gudowska-Nowak, Optimal First-Arrival Times in Lévy Flights with Resetting, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(5), 052127 CrossRef PubMed.
- M. Radice and G. Cristadoro, Optimizing Leapover Lengths of Lévy Flights with Resetting, Phys. Rev. E, 2024, 110(2), L022103 CrossRef CAS PubMed.
- S. Eule and J. J. Metzger, Non-Equilibrium Steady States of Stochastic Processes with Intermittent Resetting, New J. Phys., 2016, 18(3), 033006 CrossRef.
- V. P. Shkilev, Continuous-Time Random Walk under Time-Dependent Resetting, Phys. Rev. E, 2017, 96(1), 012126 CrossRef CAS PubMed.
- C. Kurzthaler, Y. Zhao, N. Zhou, J. Schwarz-Linek, C. Devailly and J. Arlt,
et al., Characterization and Control of theRun-and-Tumble Dynamics of Escherichia coli, Phys. Rev. Lett., 2024, 132(3), 038302 CrossRef CAS PubMed.
- Y. Zhao, C. Kurzthaler, N. Zhou, J. Schwarz-Linek, C. Devailly and J. Arlt,
et al., Quantitative Characterization of Run-and-Tumble Statistics in Bulk Bacterial Suspensions, Phys. Rev. E, 2024, 109(1), 014612 CrossRef CAS PubMed.
- O. Tal-Friedman, Y. Roichman and S. Reuveni, Diffusion with Partial Resetting, Phys. Rev. E, 2022, 106(5), 054116 CrossRef CAS PubMed.
- M. Biroli, Y. Feld, A. K. Hartmann, S. N. Majumdar and G. Schehr, Resetting by Rescaling: Exact Results for a Diffusing Particle in One Dimension, Phys. Rev. E, 2024, 110(4), 044142 CrossRef CAS PubMed.
- A. Pal, A. Kundu and M. R. Evans, Diffusion under Time-Dependent Resetting, J. Phys. A: Math. Theor., 2016, 49(22), 225001 CrossRef.
- V. Méndez, R. Flaquer-Galmés and D. Campos, First-Passage Time of a Brownian Searcher with Stochastic Resetting to Random Positions, Phys. Rev. E, 2024, 109(4), 044134 CrossRef PubMed.
- M. Luby, A. Sinclair and D. Zuckerman, Optimal Speedup of Las Vegas Algorithms, Inf. Process. Lett., 1993, 47(4), 173–180 CrossRef.
- A. Montanari and R. Zecchina, Optimizing Searches via Rare Events, Phys. Rev. Lett., 2002, 88(17), 178701 CrossRef PubMed.
- O. Blumer, S. Reuveni and B. Hirshberg, Stochastic Resetting for Enhanced Sampling, J. Phys. Chem. Lett., 2022, 13(48), 11230–11236 CrossRef CAS PubMed.
- O. Blumer, S. Reuveni and B. Hirshberg, Combining Stochastic Resetting with Metadynamics to Speed-up Molecular Dynamics Simulations, Nat. Commun., 2024, 15(1), 240 CrossRef CAS PubMed.
- M. Coppey, O. Bénichou, R. Voituriez and M. Moreau, Kinetics of Target Site Localization of a Protein on DNA: A Stochastic Approach, Biophys. J., 2004, 87(3), 1640–1649 CrossRef CAS PubMed.
- J. Chmeliov, L. Valkunas, T. P. J. Krüger, C. Ilioaia and R. van Grondelle, Fluorescence Blinking of Single Major Light-Harvesting Complexes, New J. Phys., 2013, 15(8), 085007 CrossRef CAS.
- S. Ghosh, B. Mishra, A. B. Kolomeisky and D. Chowdhury, First-Passage Processes on a Filamentous Track in a Dense Traffic: Optimizing Diffusive Search for a Target in Crowding Conditions, J. Stat. Mech.: Theory Exp., 2018, 2018(12), 123209 CrossRef.
- O. Bénichou, M. Coppey, M. Moreau, P. H. Suet and R. Voituriez, Optimal Search Strategies for Hidden Targets, Phys. Rev. Lett., 2005, 94(19), 198101 CrossRef PubMed.
- O. Bénichou, C. Loverdo, M. Moreau and R. Voituriez, Intermittent Search Strategies, Rev. Mod. Phys., 2011, 83(1), 81–129 CrossRef.
- S. S. Suarez and A. A. Pacey, Sperm Transport in the Female Reproductive Tract, Hum. Reprod. Update, 2006, 12(1), 23–37 CrossRef CAS PubMed.
- E. Lauga and T. R. Powers, The Hydrodynamics of Swimming Microorganisms, Rep. Prog. Phys., 2009, 72(9), 096601 CrossRef.
-
The Physics of Foraging: An Introduction to Random Searches and Biological Encounters, ed. G. M. Viswanathan, Cambridge University Press, Cambridge, New York, 2011 Search PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Active Particles in Complex and Crowded Environments, Rev. Mod. Phys., 2016, 88(4), 045006 CrossRef.
-
E. Lauga, The Fluid Dynamics of Cell Motility, Cambridge Texts in Applied Mathematics, Cambridge University Press, Cambridge, 2020 Search PubMed.
-
Out-of-Equilibrium Soft Matter, ed. C. Kurzthaler, L. Gentile and H. A. Stone, The Royal Society of Chemistry, 1st edn, 2023 Search PubMed.
-
Target Search Problems, ed. D. Grebenkov, R. Metzler and G. Oshanin, Springer Nature Switzerland, Cham, 1st edn, 2024 Search PubMed.
- S. J. Ebbens and J. R. Howse, In Pursuit of Propulsion at the Nanoscale, Soft Matter, 2010, 6(4), 726–738 RSC.
- L. Baraban, M. Tasinkevych, M. N. Popescu, S. Sanchez, S. Dietrich and O. G. Schmidt, Transport of Cargo by Catalytic Janus Micro-Motors, Soft Matter, 2011, 8(1), 48–52 RSC.
- W. Gao, A. Uygun and J. Wang, Hydrogen-Bubble-Propelled Zinc-Based Microrockets in Strongly Acidic Media, J. Am. Chem. Soc., 2012, 134(2), 897–900 CrossRef CAS PubMed.
- S. J. Ebbens, Active Colloids: Progress and Challenges towards Realising Autonomous Applications, Curr. Opin. Colloid Interface Sci., 2016, 21, 14–23 CrossRef CAS.
- T. Robin, S. Reuveni and M. Urbakh, Single-Molecule Theory of Enzymatic Inhibition, Nat. Commun., 2018, 9(1), 779 CrossRef PubMed.
-
A. Aziz, D. Karnaushenko, N. Koukourakis, J. W. Czarske, O. G. Schmidt and M. Medina-Sánchez, Tracking of Magnetic Micromotors in Confined Channels Through Scattering Tissue. In: 2021 IEEE 15th International Conference on Nano/Molecular Medicine & Engineering (NANOMED), 2021, pp. 57–62.
-
A. Aziz, R. Nauber, A. S. Iglesias, L. M. Liz-Marzán, O. G. Schmidt and M. Medina-Sánchez, Imaging and Control of Nanomaterial-Decorated Micromotors. In: 2022 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), 2022, pp. 1–6.
- R. Nauber, S. R. Goudu, M. Goeckenjan, M. Bornhäuser, C. Ribeiro and M. Medina-Sánchez, Medical Microrobots in Reproductive Medicine from the Bench to the Clinic, Nat. Commun., 2023, 14(1), 728 CrossRef CAS PubMed.
- L. Angelani, R. Di Leonardo and M. Paoluzzi, First-Passage Time of Run-and-Tumble Particles, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37(7), 59 CrossRef PubMed.
- K. Malakar, V. Jemseena, A. Kundu, K. Vijay Kumar, S. Sabhapandit and S. N. Majumdar,
et al., Steady State, Relaxation and First-Passage Properties of a Run-and-Tumble Particle in One- Dimension, J. Stat. Mech.: Theory Exp., 2018, 2018(4), 043215 CrossRef.
- G. Tucci, A. Gambassi, S. N. Majumdar and G. Schehr, First-Passage Time of Run-and-Tumble Particles with Noninstantaneous Resetting, Phys. Rev. E, 2022, 106(4), 044127 CrossRef CAS PubMed.
- D. Vinod, A. G. Cherstvy, W. Wang, R. Metzler and I. M. Sokolov, Nonergodicity of Reset Geometric Brownian Motion, Phys. Rev. E, 2022, 105(1), L012106 CrossRef CAS PubMed.
- F. Di Trapani, T. Franosch and M. Caraglio, Active Brownian Particles in a Circular Disk with an Absorbing Boundary, Phys. Rev. E, 2023, 107(6), 064123 CrossRef CAS PubMed.
- M. Guéneau, S. N. Majumdar and G. Schehr, Optimal Mean First-Passage Time of a Run-and-Tumble Particle in a Class of One-Dimensional Confining Potentials, Europhys. Lett., 2024, 145(6), 61002 CrossRef.
- M. Guéneau, S. N. Majumdar and G. Schehr, Run-and-Tumble Particle in One-Dimensional Potentials: Mean First-Passage Time and Applications, Phys. Rev. E, 2025, 111(1), 014144 CrossRef PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Self-Motile Colloidal Particles: From Directed Propulsion to Random Walk, Phys. Rev. Lett., 2007, 99(4), 048102 CrossRef PubMed.
- P. Romanczuk, M. Bär, W. Ebeling, B. Lindner and L. Schimansky-Geier, Active Brownian Particles, Eur. Phys. J.: Spec. Top., 2012, 202(1), 1–162 CAS.
- B. ten Hagen, S. van Teeffelen and H. Löwen, Brownian Motion of a Self-Propelled Particle, J. Phys.: Condens. Matter, 2011, 23(19), 194119 CrossRef CAS PubMed.
- C. Kurzthaler, S. Leitmann and T. Franosch, Intermediate Scattering Function of an Anisotropic Active Brownian Particle, Sci. Rep., 2016, 6(1), 36702 CrossRef CAS PubMed.
- C. Kurzthaler, C. Devailly, J. Arlt, T. Franosch, W. C. K. Poon and V. A. Martinez,
et al., Probing the Spatiotemporal Dynamics of Catalytic Janus Particles with Single-Particle Tracking and Differential Dynamic Microscopy, Phys. Rev. Lett., 2018, 121(7), 078001 CrossRef CAS PubMed.
- J. Masoliver, Telegraphic Processes with Stochastic Resetting, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2019, 99(1), 012121 CrossRef CAS PubMed.
- M. R. Evans, S. N. Majumdar and G. Schehr, Stochastic Resetting and Applications, J. Phys. A: Math. Theor., 2020, 53(19), 193001 CrossRef.
- Y. Baouche, M. Le Goff, C. Kurzthaler and T. Franosch, First-Passage-Time Statistics of Active Brownian Particles: A Perturbative Approach, Phys. Rev. E, 2025, 111(5), 054113 CrossRef CAS PubMed.
- U. Basu, S. N. Majumdar, A. Rosso and G. Schehr, Active Brownian Motion in Two Dimensions, Phys. Rev. E, 2018, 98(6), 062121 CrossRef CAS.
- Y. Baouche, T. Franosch, M. Meiners and C. Kurzthaler, Active Brownian Particle under Stochastic Orientational Resetting, New J. Phys., 2024, 26(7), 073041 CrossRef.
- O. Tal-Friedman, A. Pal, A. Sekhon, S. Reuveni and Y. Roichman, Experimental Realization of Diffusion with Stochastic Resetting, J. Phys. Chem. Lett., 2020, 11(17), 7350–7355 CrossRef CAS PubMed.
- S. Gupta and A. M. Jayannavar, Stochastic Resetting: A (Very) Brief Review, Front. Phys., 2022, 10, 789097 CrossRef.
- I. Abdoli and A. Sharma, Stochastic Resetting of Active Brownian Particles with Lorentz Force, Soft Matter, 2021, 17(5), 1307–1316 RSC.
- J. Fuchs, S. Goldt and U. Seifert, Stochastic Thermodynamics of Resetting, Europhys. Lett., 2016, 113(6), 60009 CrossRef.
- D. M. Busiello, D. Gupta and A. Maritan, Entropy Production in Systems with Unidirectional Transitions, Phys. Rev. Res., 2020, 2(2), 023011 CrossRef CAS.
- P. S. Pal, A. Pal, H. Park and J. S. Lee, Thermodynamic Trade-off Relation for First Passage Time in Resetting Processes, Phys. Rev. E, 2023, 108(4), 044117 CrossRef CAS PubMed.
- J. C. Sunil, R. A. Blythe, M. R. Evans and S. N. Majumdar, The Cost of Stochastic Resetting, J. Phys. A: Math. Theor., 2023, 56(39), 395001 CrossRef.
- J. Q. Toledo-Marín and D. Boyer, First Passage Time and Information of a One-Dimensional Brownian Particle with Stochastic Resetting to Random Positions, Phys. A, 2023, 625, 129027 CrossRef.
- I. Abdoli, K. S. Olsen and H. Löwen, Shear-Driven Diffusion with Stochastic Resetting, Phys. Fluids, 2024, 36(11), 117151 CrossRef CAS.
- P. C. Bressloff, Search Processes with Stochastic Resetting and Multiple Targets, Phys. Rev. E, 2020, 102(2), 022115 CrossRef CAS PubMed.
- S. Paramanick, A. Biswas, H. Soni, A. Pal and N. Kumar, Uncovering Universal Characteristics of Homing Paths Using Foraging Robots, PRX Life, 2024, 2(3), 033007 CrossRef.
- E. Q. Z. Moen, K. S. Olsen, J. Rønning and L. Angheluta, Trapping of Active Brownian and Run-and-Tumble Particles: A First-Passage Time Approach, Phys. Rev. Res., 2022, 4(4), 043012 CrossRef CAS.
- G. Kumar Sar, A. Ray, D. Ghosh, C. Hens and A. Pal, Resetting-Mediated Navigation of an Active Brownian Searcher in a Homogeneous Topography, Soft Matter, 2023, 19(24), 4502–4518 RSC.
- B. Walter, G. Pruessner and G. Salbreux, First Passage Time Distribution of Active Thermal Particles in Potentials, Phys. Rev. Res., 2021, 3(1), 013075 CrossRef CAS.
- I. Abdoli, H. D. Vuijk, R. Wittmann, J. U. Sommer, J. M. Brader and A. Sharma, Stationary State in Brownian Systems with Lorentz Force, Phys. Rev. Res., 2020, 2(2), 023381 CrossRef CAS.
- K. S. Olsen and H. Löwen, Optimal Diffusion of Chiral Active Particles with Strategic Reorientations, Phys. Rev. E, 2024, 110(6), 064606 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a and
Christina
Kurzthaler
a and
Christina
Kurzthaler
 *abc
*abc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λt) with rate λ (and mean time between resets 1/λ) (see Fig. 1). These processes are represented by the following set of stochastic equations:
exp(−λt) with rate λ (and mean time between resets 1/λ) (see Fig. 1). These processes are represented by the following set of stochastic equations:

 with the particle's hydrodynamic radius a and the time t = τT with the diffusive time τ = a2/D, two non-dimensional numbers appear: Pe = va/D denotes the Péclet number, measuring the relative importance of active motion versus diffusion, and Λ = λτ is the reduced resetting rate, representing the prevalence of resetting events compared to the diffusive time scale. We further introduce γ = τDrot = 3/4, which follows from the Stokes–Einstein–Sutherland relation for a spherical particle. The latter lets us interpret the reduced resetting rate as a competition between resetting and rotational diffusion Λ = 3λ/4Drot.
with the particle's hydrodynamic radius a and the time t = τT with the diffusive time τ = a2/D, two non-dimensional numbers appear: Pe = va/D denotes the Péclet number, measuring the relative importance of active motion versus diffusion, and Λ = λτ is the reduced resetting rate, representing the prevalence of resetting events compared to the diffusive time scale. We further introduce γ = τDrot = 3/4, which follows from the Stokes–Einstein–Sutherland relation for a spherical particle. The latter lets us interpret the reduced resetting rate as a competition between resetting and rotational diffusion Λ = 3λ/4Drot.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΛT), the survival probability follows:51
exp(−ΛT), the survival probability follows:51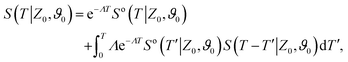


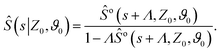
 of a particle to be at
of a particle to be at  with orientation ϑ at time T having started at
with orientation ϑ at time T having started at 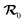 with orientation ϑ0 at T = 0:
with orientation ϑ0 at T = 0:![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o = −Pe e·∇
o = −Pe e·∇![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o + γ∂ϑ2
o + γ∂ϑ2![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o + ∇2
o + ∇2![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o.
o.![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o = −Pe
o = −Pe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑ)∂Z
cos(ϑ)∂Z![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o + γ∂ϑ2
o + γ∂ϑ2![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o + ∂Z2
o + ∂Z2![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o,
o,![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o(Z,ϑ,T = 0|Z0,ϑ0) = δ(Z − Z0)δ(ϑ − ϑ0),
o(Z,ϑ,T = 0|Z0,ϑ0) = δ(Z − Z0)δ(ϑ − ϑ0),![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) o(Z = 0,ϑ,T|Z0,ϑ0) = 0 ∀T ∈
o(Z = 0,ϑ,T|Z0,ϑ0) = 0 ∀T ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +.
+.
 is split into two components: the unperturbed operator
is split into two components: the unperturbed operator  and the perturbation
and the perturbation  . Expanding the probability density in terms of the Péclet number
. Expanding the probability density in terms of the Péclet number
 can be obtained iteratively and used as input for the survival probability
can be obtained iteratively and used as input for the survival probability  via the relation
via the relation
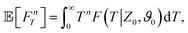


 [eqn (5)], and formally obtain the associated coefficients:
[eqn (5)], and formally obtain the associated coefficients:
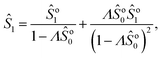




 that minimizes the MFPT, where Z* = 1.59362… is the unique solution of the transcendental equation:
that minimizes the MFPT, where Z* = 1.59362… is the unique solution of the transcendental equation:
 ) or takes about an equal amount of time (ϑ0 = 0) to reach the wall.
) or takes about an equal amount of time (ϑ0 = 0) to reach the wall.![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft]* (and corresponding resetting rate Λ*) to accelerate absorption at the boundary. We begin this discussion by comparing
[Ft]* (and corresponding resetting rate Λ*) to accelerate absorption at the boundary. We begin this discussion by comparing ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft]* with its passive counterpart
[Ft]* with its passive counterpart  [Fig. 2(D)–(F)]. For low activity Pe ≲ 0.1, the active and passive cases are comparable,
[Fig. 2(D)–(F)]. For low activity Pe ≲ 0.1, the active and passive cases are comparable,  , and the initial angle remains unimportant. Deviations appear as Pe increases and approaches one, where agents initially oriented towards the wall always display a lower optimal MFPT. However, agents departing away from it exhibit a slightly more complex behavior: at short initial distances z0/a ≲ 3, they are naturally slower
, and the initial angle remains unimportant. Deviations appear as Pe increases and approaches one, where agents initially oriented towards the wall always display a lower optimal MFPT. However, agents departing away from it exhibit a slightly more complex behavior: at short initial distances z0/a ≲ 3, they are naturally slower 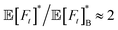 because of the persistent motion, but as z0/a → 10, rotational diffusion kicks in and allows agents to reorient and move persistently towards the boundary, which makes them faster than diffusive particles (see also inset of Fig. 2B). For the same reason, randomly initially oriented particles will reach the boundary faster when both activity and initial position are large enough.
because of the persistent motion, but as z0/a → 10, rotational diffusion kicks in and allows agents to reorient and move persistently towards the boundary, which makes them faster than diffusive particles (see also inset of Fig. 2B). For the same reason, randomly initially oriented particles will reach the boundary faster when both activity and initial position are large enough. in Fig. 4. In agreement with our observation for the optimal MFPT, the initial angle appears irrelevant for small Pe ≲ 0.1, thus leading to
in Fig. 4. In agreement with our observation for the optimal MFPT, the initial angle appears irrelevant for small Pe ≲ 0.1, thus leading to  .
.
 displays a maximum (see first plot in Fig. 4D). The presence of this maximum can be understood by considering the length the agent moves in the z-direction before resetting
displays a maximum (see first plot in Fig. 4D). The presence of this maximum can be understood by considering the length the agent moves in the z-direction before resetting
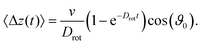

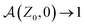 , independently of the resetting rate, as the memory of the initial orientation progressively decays for such large initial distances.
, independently of the resetting rate, as the memory of the initial orientation progressively decays for such large initial distances.
 where the anisotropy appears to be independent of the resetting rate. We anticipate that it corresponds to the distance when active motion starts to become comparable to translational diffusion. Comparing the length traveled through diffusion during time t (l2 = tD) with the length traveled using active motion (l = tv) leads to l = a/Pe, which predicts the disappearance of that point at larger Pe. This feature remains to be further studied for larger Péclet numbers that go beyond our perturbation limits.
where the anisotropy appears to be independent of the resetting rate. We anticipate that it corresponds to the distance when active motion starts to become comparable to translational diffusion. Comparing the length traveled through diffusion during time t (l2 = tD) with the length traveled using active motion (l = tv) leads to l = a/Pe, which predicts the disappearance of that point at larger Pe. This feature remains to be further studied for larger Péclet numbers that go beyond our perturbation limits.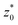 .
.




![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 3 as a function of Λ for several z0. We first note that the skewness is positive for all cases, indicating that the FPT distribution is right-skewed, or skewed towards the large arrival times, accounting for the agents that manage to reach the wall at later times t/τ ≫ 1. It also diverges for vanishing Λ, in accordance with the absence of moments for the non-resetting case. For a fixed z0/a, the skewness decreases when Λ increases, which is consistent with the observation that the FPT probability density for z0/a = 3 stretches over a broader range of times. If the particle is increasingly reset, it naturally requires more attempts and thus time to successfully reach the wall.
3 as a function of Λ for several z0. We first note that the skewness is positive for all cases, indicating that the FPT distribution is right-skewed, or skewed towards the large arrival times, accounting for the agents that manage to reach the wall at later times t/τ ≫ 1. It also diverges for vanishing Λ, in accordance with the absence of moments for the non-resetting case. For a fixed z0/a, the skewness decreases when Λ increases, which is consistent with the observation that the FPT probability density for z0/a = 3 stretches over a broader range of times. If the particle is increasingly reset, it naturally requires more attempts and thus time to successfully reach the wall.

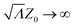 , thus explaining the behavior of the skewness for the FPT probability of an active agent.
, thus explaining the behavior of the skewness for the FPT probability of an active agent.

![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft]/T1/2 diverges since the MFPT itself diverges while the median remains defined. As the resetting rate increases,
[Ft]/T1/2 diverges since the MFPT itself diverges while the median remains defined. As the resetting rate increases, ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft]/T1/2 decreases due to the resetting process stabilizing the distribution. We finally note that even though both the median and the MFPT diverge at large z0/a, their ratio seems to eventually converge to a value slightly above one, independently of the resetting rate, which is consistent with the positive skewness studied in the previous section. Thus, this further emphasizes that the distribution remains asymmetric for any parameters considered here. (Let us finally note that the results remain qualitatively similar for different initial orientations.)
[Ft]/T1/2 decreases due to the resetting process stabilizing the distribution. We finally note that even though both the median and the MFPT diverge at large z0/a, their ratio seems to eventually converge to a value slightly above one, independently of the resetting rate, which is consistent with the positive skewness studied in the previous section. Thus, this further emphasizes that the distribution remains asymmetric for any parameters considered here. (Let us finally note that the results remain qualitatively similar for different initial orientations.)
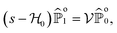

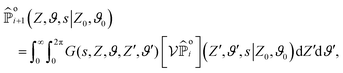

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2 = s + γl2. We further note that due to the symmetry of the coefficients, p
2 = s + γl2. We further note that due to the symmetry of the coefficients, p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = p−
= p−![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , there is no need to change the angular part of the image solution.
, there is no need to change the angular part of the image solution.
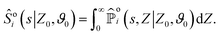


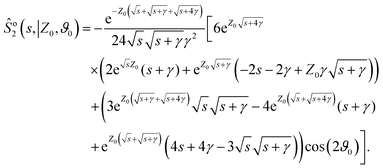
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ŝo1 + Pe2
Ŝo1 + Pe2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ŝo2. The latter is inserted into eqn (5) in the main text to obtain the survival probability with resetting.
Ŝo2. The latter is inserted into eqn (5) in the main text to obtain the survival probability with resetting.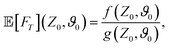


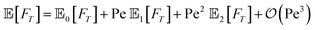
![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) 0[FT] =
0[FT] = ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [FT]B [eqn (16)] and the activity-induced contributions:
[FT]B [eqn (16)] and the activity-induced contributions:
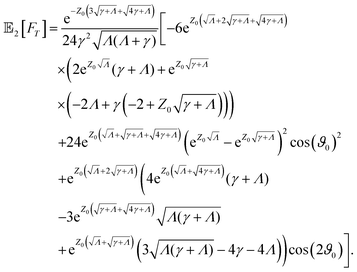
![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft] as a function of the Péclet number, Pe (i.e., our perturbation parameter). Our results shown in Fig. 9 indicate that, at least until a resetting rate Λ = 3, the theory provides good agreement with simulations up to Pe ≈ 1. It also remains valid up to Pe = 3 for the largest resetting rate Λ = 3, whereas discrepancies start to emerge as the resetting rate is lowered. This can be explained by considering that for Λ = 3, the length traveled by the particle before resetting is smaller than the persistence length lR/lp = γ/(Λ + γ) ≪ 1. Thus, the agent essentially reaches the wall without fully taking advantage of persistent motion. For lower resetting rates the effects of active motion can fully develop, leading to the observed discrepancies between theory and simulations.
[Ft] as a function of the Péclet number, Pe (i.e., our perturbation parameter). Our results shown in Fig. 9 indicate that, at least until a resetting rate Λ = 3, the theory provides good agreement with simulations up to Pe ≈ 1. It also remains valid up to Pe = 3 for the largest resetting rate Λ = 3, whereas discrepancies start to emerge as the resetting rate is lowered. This can be explained by considering that for Λ = 3, the length traveled by the particle before resetting is smaller than the persistence length lR/lp = γ/(Λ + γ) ≪ 1. Thus, the agent essentially reaches the wall without fully taking advantage of persistent motion. For lower resetting rates the effects of active motion can fully develop, leading to the observed discrepancies between theory and simulations.

![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [Ft] as a function of the Péclet number Pe for several resetting rates Λ. Here, the initial distance is z0/a = 3 and the initial orientation ϑ0 is chosen randomly. Solid lines and symbols denote theory and simulations, respectively. Dashed lines correspond to the result given by eqn (B3).
[Ft] as a function of the Péclet number Pe for several resetting rates Λ. Here, the initial distance is z0/a = 3 and the initial orientation ϑ0 is chosen randomly. Solid lines and symbols denote theory and simulations, respectively. Dashed lines correspond to the result given by eqn (B3).![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [FT]. Our results show that the agreement with numerics becomes considerably worse at Pe ≳ 1, which is why we use eqn (B1) throughout the manuscript.
[FT]. Our results show that the agreement with numerics becomes considerably worse at Pe ≳ 1, which is why we use eqn (B1) throughout the manuscript.