Depletion effect in an active chiral system

Abstract

We investigate the dynamics of ring-shaped chiral particles immersed in a monolayer of hard spherical beads, confined between two vertically vibrating plates. At high bead concentrations, we observe depletion-like attraction between the rings in both co-rotating and counter-rotating configurations, leading to the formation of a dimer. Notably, the range of this interaction extends over several bead diameters, in contrast to passive systems where interactions are typically limited to the particle size. More intriguingly, at low bead concentrations, the rings exhibit mutual repulsion in both cases, which we attribute to a localized high bead concentration between them—suggesting a mechanism opposite to conventional depletion interactions. Additionally, we examine the diffusive properties of dimerized rings and compare them with those of an isolated ring. While the angular diffusion of the dimer is significantly suppressed compared to that of a single ring, its translational diffusion remains nearly unchanged.

---

1. Introduction

Active systems, characterized by their inherently driven, non-equilibrium nature, have attracted significant attention due to their complex dynamics and unique properties, such as phase segregation,^1–6 pattern formation,^7–10 collective behaviors,^11–13 and phenomena like swarming, and vortex formation,^14–20 which distinguish them from passive systems. Physical systems composed of both active and passive particles exhibit intricate and diverse behaviors, particularly when both types play a pivotal role in the dynamics.^20–36 Here we are interested in the motion of the systems composed of chiral active entities. Chirality in active systems has been shown to give rise to novel phenomena, such as chiral edge currents, self-sorting, spontaneous flow reversal, and asymmetric cluster formation, among others,^37–51 motivating the exploration of systems composed of chiral active particles. We aim to advance the understanding of such systems by investigating the interaction of active chiral particles mediated by the surrounding spherical passive particles.

The interactions between active particles mediated by a passive medium have been studied in various contexts.^12,52,53 In vibrated granular systems, it has been observed that active granular rods tend to align due to flow-induced interactions within the bead medium, leading to emergent flocking dynamics.¹² Additionally, recent studies have shown that two motile rods attract each other at high bead concentrations, while at low bead concentrations, they exhibit repulsive interactions.⁵³ These findings highlight the crucial role of medium-mediated interactions in determining the collective behavior of active particles.^6,12 On the other hand, in the context of chirality, not much attention has been paid to such research problems. For magnetic spinners in a viscous fluid, the surrounding medium induces interactions that lead to repulsion when the spinners co-rotate and attraction when they counter-rotate. However, the addition of passive colloidal particles to the fluid reverses this interaction due to the elasticity introduced by the passive particles.⁵²

In this paper, we investigate the dynamics of hard chiral rings surrounded by hard spherical beads, confined between two vertically shaking plates (see Fig. 1a). Due to their chiral shape, the rings exhibit rotational motion in the xy-plane, with the direction of rotation determined by how they are placed between the plates. For the configuration shown in Fig. 1b, the rings rotate anti-clockwise, whereas for the configuration in Fig. 1c, they rotate clockwise. This behavior is clearly illustrated in the plot of ring orientation θ versus time t for both configurations, see Fig. 1d. The spherical beads, being isotropic, do not display any intrinsic rotational or directed motion. Instead, they move passively in the xy-plane when pushed by the rotating rings. We investigate how the presence of the bead medium modifies the interactions between the rings as the bead concentration is varied. Our results reveal that a depletion-type interaction, induced by the beads, governs the attractive and repulsive forces between the rings.

Fig. 1 (a) A schematic diagram of our system, consisting of chiral rings and spherical beads confined between two vertically shaking plates with frequency f and amplitude A, separated by a gap of width w. (b) and (c) Rings with different chiralities. Here, r_c is the radius of curvature, and the angle θ describes the orientation of the ring. (d) The angle θ vs. time t for the rings shown in (b) and (c), respectively, when confined between the vibrating plates without beads; we refer to them as anticlockwise and clockwise rings, respectively. (e) A pair of co-rotating rings and a pair of counter-rotating rings.

Our results can be summarized as follows: at high bead concentrations, we observe depletion-like attraction between the rings in both co-rotating and counter-rotating pairs of rings. Interestingly, the range of this interaction extends to several bead diameters, in contrast to passive depletion interaction where the interaction range is typically limited to the size of individual depletants. More strikingly, at low bead concentrations, the rings exhibit mutual repulsion in both cases, which we attribute to the high bead concentration localized between the rings—suggesting a mechanism opposite to conventional depletion interactions. Furthermore, we analyze the diffusive properties of the dimer formed by the rings at high bead concentrations and compare them to those of a single ring. The angular diffusion of the dimer is significantly reduced compared to that of an individual ring, whereas its translational diffusion remains nearly the same as that of a single ring.

The rest of the paper is organized as follows: In the next Section 2, we discuss the simulation details. In Section 3, we present the results. Finally, in Section 4, we provide a brief discussion and summarize our findings.

2. Simulation details

Our quasi-two-dimensional system, composed of a pair of chiral rings and spherical beads, is confined by perfectly rigid horizontal walls (see Fig. 1a). These walls, referred to as the lid (top wall) and the base (bottom wall), oscillate sinusoidally along the z-axis. Their time-dependent z-coordinates are given by A cos(2πft) for the base and A cos(2πft) + w for the lid, where A is the amplitude, f is the vibration frequency, and w is the gap between them. In the xy-plane, the simulation box is chosen to have a square shape with a side length of L = 86.85 mm, with periodic boundary conditions. The rigid body collisions between particles and between particles and the walls are treated as instantaneous events, which are modeled using an impulse-based rigid body collision model proposed by W. J. Stronge.^{5,12,13,53–55} The restitution and friction coefficients for various collisions are mentioned in Tables 1 and 2. Between any two collisions, a particle undergoes Newtonian rigid body motion. The nonspherical shapes of the rings pose several challenges and also slow down the simulation if one uses event-driven numerical simulation techniques.^56,57 Therefore, we opt for a time-driven simulation scheme⁵⁸ to obtain the trajectories of the system. The chiral rings are identical and consist of eighteen overlapping, equispaced spherical beads arranged along a circular arc with a radius r_c. For an anticlockwise ring, the radii of the beads increase linearly with their angular coordinate relative to the ring's center, starting from the smallest sphere and progressing to the largest sphere (see Fig. 1b). The clockwise ring is simply the mirror image of the anticlockwise ring, as shown in Fig. 1c. The radii of the smallest and largest spheres are set to 0.35 mm and 0.55 mm, respectively. The radius of the circular arc, r_c, is fixed at 1.09 mm, unless stated otherwise. The radius of the bead-like particles is taken to be 0.4 mm. To estimate the collision response, information about the inertia tensor of the particles is required. In our simulation, all particles are assumed to be solid, and the inertia tensor is calculated accordingly. The density ratio of the bead material to the ring material is set to 0.3, corresponding to brass and aluminum, respectively, as used in the experiments of Kumar et al.¹² The shaking frequency is f = 200 Hz, and the shaking strength, defined as Γ = Aω²/g, where ω = 2πf and g is the gravitational acceleration, is set to 7. The gap w is fixed at 1.2 mm. The VMD software⁵⁹ is used to visualize and capture snapshots of the system. This study explores the effect of medium concentration, measured in terms of the area fraction ϕ, defined aswhere N is the total number of spherical beads and A_b is the area occupied by the projection of a single bead onto the xy-plane.

Table 1 Friction and restitution coefficient, μ and e, for different collisions for rings

Collision	μ	e
Particle–base	0.03	0.1
Particle–lid	0.03	0.1
Particle–particle	0.05	0.3

---

Table 2 Friction and restitution coefficient, μ and e, for different collisions for beads

Collision	μ	e
Particle–base	0.0001	0.3
Particle–lid	0.0001	0.3
Particle–particle	0.05	0.3

---

3. Results

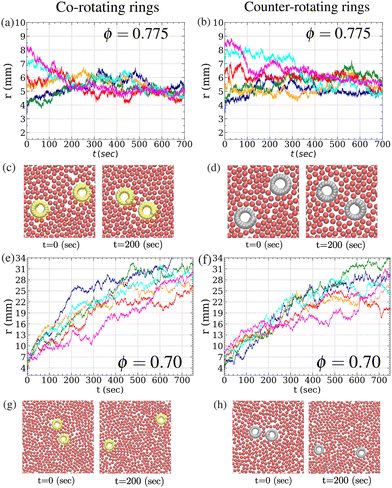
As discussed earlier, in the absence of the bead medium, the anti-clockwise ring rotates in the anti-clockwise direction, while the clockwise ring rotates in the clockwise direction, both with an average angular speed of 4.4 × 10⁻² rad s⁻¹. The orientation angle as a function of time for both types of rings is shown in Fig. 1d. We investigate the dynamical properties of ring pairs. Based on the chiralities of the rings, we examine the dynamics of two types of pairs: co-rotating pairs, in which both rings share the same chirality, and counter-rotating pairs, in which the rings have opposite chiralities (see Fig. 1e). Our results, obtained by systematically varying the area fraction ϕ of the bead medium and the initial separation distance r₀ between the rings, are as follows.

3.1. Temporal evolution of the inter-ring distance r

For each combination of (r₀, ϕ), we conduct 10 independent simulations to compute the average time-dependent distance r(t) between the rings. The simulations are carried out for both co-rotating and counter-rotating pairs. As shown in Fig. 2a, for ϕ = 0.775, the distance between the co-rotating rings saturates to approximately 5 mm, for all r₀ ≤ 8 mm (Movie S1, ESI†). This observation suggests that the rings repel each other at very short distances but attract when farther apart, forming a dimer with an average distance where a single chain of beads forms between the rings (see Fig. 2c). More remarkably, we found a similar behavior for the counter-rotating rings, although the distance r(t) exhibits larger fluctuations, and the steady-state value of r(t) is slightly larger than that for the co-rotating rings (see Fig. 2b, d, and Movie S2, ESI†). This contrasts with earlier studies of interactions between chiral particles, where counter-rotating particles were observed to repel each other.^35,52 The larger steady-state distance between the counter-rotating rings can be attributed to the compression and stress induced by the beads, which form a bridge between the rings, as observed in previous studies.⁵² In contrast to the behavior of co-rotating pairs, beads are pushed into the region between the rings in counter-rotating pairs, increasing the local pressure and driving the rings apart (see Fig. 3a and b). This results in an additional repulsive interaction between the rings. However, the mechanics responsible for the attraction between the rings counteracts this repulsion, allowing the counter-rotating pair to exhibit overall attractive behavior, albeit with larger average distance. Beyond r₀ = 8 mm, the attractive interaction weakens, and the rings fail to form a stable dimer. We do not perform simulations for ϕ > 0.775, as the system's dynamics freezes due to jamming. Within the range of simulation times explored, the dimer formed by the co-rotating rings remains intact. In contrast, the pair of counter-rotating rings is observed to dissociate in some cases due to an additional outward force caused by the inward bead flow discussed earlier.

Fig. 2 Ensemble-averaged inter-ring distance r(t) as a function of time for initial separations r₀ = 3, 4, 5, 6, 7, and 8 mm: (a) co-rotating rings with ϕ = 0.775, (b) counter-rotating rings with ϕ = 0.775, (e) co-rotating rings with ϕ = 0.70, and (f) counter-rotating rings with ϕ = 0.70. Snapshots from a single simulation at t = 0 s and t = 200 s: (c) co-rotating rings for r₀ = 8 mm with ϕ = 0.775, (d) counter-rotating rings for r₀ = 8 mm with ϕ = 0.775, (g) co-rotating rings for r₀ = 4 mm with ϕ = 0.70, and (h) counter-rotating rings for r₀ = 4 mm with ϕ = 0.70.

Fig. 3 (a) and (b) Schematic diagrams illustrating the direction of forces on the beads due to the rings for the co-rotating and counter-rotating pairs, respectively. (c) and (d) The time dependence of the average distance r(t) for co-rotating and counter-rotating rings, respectively, for different values of ϕ at r₀ = 3.0 mm. (e) Average distance over a 100-second window, measured from 400 seconds after the simulation starts, plotted as a function of ϕ for both co-rotating and counter-rotating pairs.

We conducted a similar study for ϕ = 0.70 and found that the rings in this case exhibit a strong tendency to repel each other (see Movies S3 and S4, ESI†). As shown in Fig. 2e–h, r(t) increases rapidly for all values of r₀ (≤8 mm) for both co-rotating and counter-rotating rings. A similar behavior has been observed for polar rods in a bead medium, which also exhibit mutual repulsion at low area fractions.⁵³

Fig. 3c and d display r(t) vs. t for co-rotating and counter-rotating rings, respectively, for different values of ϕ at r₀(t) = 3 mm. Clearly, in both cases, r(t) grows rapidly to large values for ϕ < 0.75, whereas it fluctuates around a mean value otherwise. As shown in Fig. 3e, the average of r(t) over 100 seconds, starting 400 seconds into the simulation, increases with ϕ. The formation of a dimer is observed for ϕ > 0.76.

3.2. Explanation for the interaction between rings

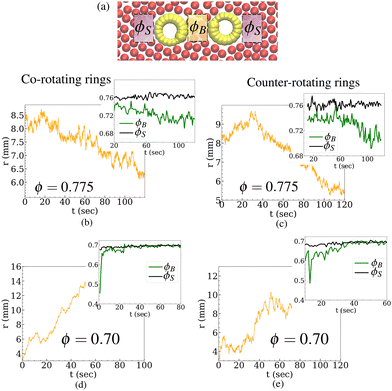
To understand the underlying mechanism of the interaction between the rings due to the beads, we examine how the local area fractions of the beads in the region between the rings and in the outer regions on both sides, denoted by ϕ_B(t) and ϕ_S(t), evolve as the rings repel or attract (see Fig. 4a). The inset of Fig. 4b shows that during a simulation of co-rotating rings at ϕ = 0.775 and r₀ = 8.0 mm, ϕ_B begins to decrease over time, while ϕ_S remains nearly constant. Consequently, the decreasing pressure exerted by the beads between the rings induces an overall attraction between them. This depletion-like interaction pulls the rings together, causing the distance between them to decrease (see Fig. 4b). A distinguishing feature of this attraction is that, unlike equilibrium depletion forces, the force acts over a range of 3–4 bead diameters, making it significantly longer-ranged than equilibrium depletion forces. This active depletion force arises due to the chiral motion of the rings, which is responsible for the reduction of the bead concentration between them. Notably, no interaction is observed between non-chiral rings (see Appendix (Fig. 8)). A similar trend in ϕ_B is also observed for counter-rotating rings; see Fig. 4c and its inset. We further examine the evolution of ϕ_B at ϕ = 0.70. As shown in the inset of Fig. 4d, for co-rotating rings at r₀ = 3.0 mm, ϕ_B increases over time, resulting in a rise in pressure between the rings. This leads to a greater outward force exerted by the beads between the rings, causing the distance between the rings to increase over time (see Fig. 4d). This effect, resulting in an effective repulsion between the rings, can be described as a reverse depletion effect, where the rising bead concentration between the rings induces repulsion. A similar trend is also observed for counter-rotating rings at ϕ = 0.70 (see Fig. 4e).

Fig. 4 (a) Schematic illustration highlighting the region between the rings and the surrounding side regions used to compute the local bead and sphere area fractions, ϕ_B and ϕ_S, respectively. (b)–(e) Time evolution of the inter-ring distance r(t) from single simulation runs, with insets showing the corresponding time dependence of ϕ_B and ϕ_S: (b) co-rotating rings at ϕ = 0.775 with initial separation r₀ = 8 mm, (c) counter-rotating rings at ϕ = 0.775 with r₀ = 8 mm, (d) co-rotating rings at ϕ = 0.70 with r₀ = 3 mm, and (e) counter-rotating rings at ϕ = 0.70 with r₀ = 3 mm.

3.3. Probability distribution of distance r

We now investigate the probability distribution P(r) of the center-to-center distance r between the rings, obtained from steady-state data of a trajectory lasting 3200 seconds. Fig. 5a presents P(r) for ϕ = 0.775, for both co-rotating and counter-rotating rings. The distribution exhibits three peaks, indicating three favorable configurations for the pair, and the peak heights decrease with increasing r. The peak positions are identical in both cases, suggesting that the favorable distance between the rings is independent of their relative chirality. The spacing between consecutive peaks and troughs is approximately 0.8 mm, which matches the diameter of the beads σ. This periodic behaviour suggests that the undulating distribution is closely tied to the structural arrangement of the bead medium. In contrast, for ϕ = 0.70, the steady-state probability distribution of the inter-ring distance increases with r, indicating a repulsive interaction between the rings (see Appendix (Fig. 9)).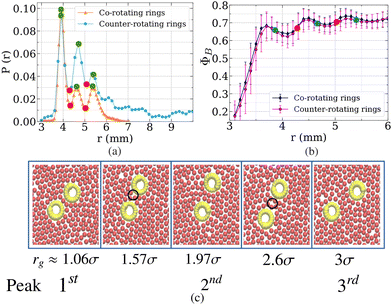

Fig. 5 (a) Probability distribution of the center-to-center inter-ring distance r for co-rotating and counter-rotating rings at ϕ = 0.775. (b) The local area fraction Φ_B of the beads in the region between the rings as a function of the distance r for co-rotating and counter-rotating rings (see Fig. 4a). (c) Snapshots of the co-rotating pair at various distances, including those corresponding to the first, second, and third peaks of the Φ_Bvs. r plots shown in (b).

To further understand this distribution, we plot the steady state time-average Φ_B of ϕ_B(t) as a function of the distance r between the rings for both co-rotating and counter-rotating cases (see Fig. 5b). The function ϕ_B exhibits three maxima corresponding to distances where the gap r_g between the rings satisfies r_g ≈ nσ, with n = 1, 2, 3. The underlying mechanism can be elucidated by analyzing the structural configurations at these distances, shown in Fig. 5c. At r_g = nσ, n-layered dense bead configurations form between the rings, resulting in peaks in the ϕ_Bvs. r plots.

We now justify the peaks in the probability distribution P(r). For a separation r = r_s at which the rings experience no net force from the surrounding beads and dΦ_B/dr < 0, an infinitesimal increase in r leads to a decrease in the local bead area fraction Φ_B. This reduction induces a depletion force that tends to restore r to r_s. Conversely, a decrease in r raises Φ_B, generating a reverse depletion force that again drives the system back toward r_s. This self-correcting mechanism stabilizes the inter-ring distance, and the probability distribution P(r) exhibits peaks at such stable separations. Such points are marked by green dots in Fig. 5a and b. In contrast, configurations with inter-ring separations r = r_u, where the net force vanishes but dΦ_B/dr > 0, are unstable. Here, an increase (decrease) in r results in a rise (fall) in Φ_B, which in turn amplifies the deviation from r_u, thereby destabilizing the configuration. These configurations lead to troughs in the P(r) vs. r plots which are indicated by red dots in Fig. 5a and b. For the counter-rotating pairs, the second peak is more pronounced compared to the co-rotating case, resulting in an overall increase in the average distance and its fluctuations for the counter-rotating pair, as shown in Fig. 2b. Again, this behavior can be attributed to the higher pressure due to the inward flow generated when the rings are counter-rotating, as discussed in Section 3.1.

3.4. Nonchiral nature of the dimer

An interesting feature of the dimer formed at high ϕ is that, unlike its constituent rings, it possesses no chirality. In Fig. 6a and b, we plot the distribution of the change in the orientation angle of the center-to-center direction of the dimer of co-rotating and counter-rotating rings, respectively, over one second for ϕ = 0.775. For both cases, the distribution is approximately symmetric around zero, indicating that the dimers have no chirality. For the sake of comparison, we have also plotted the distribution of the change in the orientation angle of the individual rings forming the dimer (see Fig. 6a and b). These distributions are shifted away from zero, confirming that the individual rings are chiral.

Fig. 6 (a) and (b) The probability distributions of the change Δθ in the orientation angle θ for the rings, and of the change Δθ_D in the direction from the center of one ring to the other ring of a dimer, for co-rotating and counter-rotating rings, respectively. (c) Mean square angular displacement for the orientations of a single ring and of the center-to-center direction of the dimers. (d) Mean square displacement for a single ring and for the centroid of the dimers. Here ϕ = 0.775.

3.5. Diffusive properties of the dimers

We now analyze the diffusive properties of the dimer formed by the rings. Fig. 6c illustrates the mean square angular displacement (MSAD) for a single ring and for both counter- and co-rotating dimers. The dimer's orientation is given by the direction joining the centers of the constituent rings (see inset of Fig. 6d). Clearly, the dimer's orientation diffuses less than that of a single ring. At large time scales, both the single ring and the dimer exhibit normal rotational diffusion. In contrast, at short time scales, both display superdiffusive rotational dynamics, with an MSD exponent below 2. We do not see any significant difference between the translational diffusive properties of the dimer and a single ring; Fig. 6d shows that the mean square displacement (MSD) of the dimer's center follows almost the same trend as the MSD of a single ring. At large time scales, both perform normal translational diffusion, whereas at short time scales they show superdiffusive behavior, with the MSD exponent remaining close to 3/2.

4. Discussion and conclusion

As far as we know, the interaction mediated by the granular medium between chiral particles has not been investigated previously. Aragones et al.⁵² explored the interaction between magnetic microspinners in a polystyrene colloidal medium. They reported that co-rotating chiral colloids attract each other, whereas counter-rotating colloids repel due to elastic forces arising from the surrounding colloidal particles. In contrast, our observations indicate attraction in both cases, suggesting that the interaction between the rings cannot be solely attributed to the elastic nature of the bead medium in our system. However, the same elastic forces are responsible for the attraction between two motile rods in a similar bead medium.⁵³ The chiral particles in our study exhibit a more intricate interaction mechanism. A locally reduced or increased bead concentration between the rings leads to attraction or repulsion, respectively, arising from a mechanism akin to the depletion effect. Moreover, the interaction is independent of the relative chirality of the particles and is instead influenced by the bead concentration. The notable feature of the depletion effect in our system is its range, which spans a few diameters of the spherical beads. This is in contrast to the equilibrium depletion attraction, where the interaction range typically corresponds to the depletant's diameter.^1,60 This is an intriguing observation, as the depletion effect offers a fundamental framework for understanding short-range interactions among colloidal particles, where solvent-mediated forces play a vital stabilizing role.^61,62 These forces, induced by the presence of the surrounding medium, significantly influence the collective dynamics of active systems, particularly in active–passive particle mixtures.^{19,24,32–34,46}

Remarkably, we also observe an oscillatory probability distribution of the inter-ring distance r when the rings attract each other, which is linked to the undulatory dependence on r of the bead concentration Φ_B between the rings. We stress that such undulations—arising from the structural arrangement of the medium particles—have also been reported in a system of two fixed hard walls suspended in a medium of hard active colloidal particles, where a comparable mechanism was found to govern the resultant force between the walls.³³ More recently, it was shown that for moving square-shaped passive objects in a similar system, repulsion was observed, which is reversed to attraction when the active particles exhibited chirality.⁶³

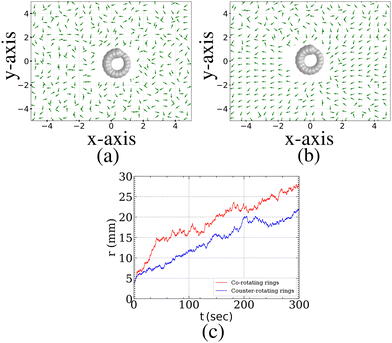
One natural question that arises from our observations is whether the velocity field around the ring contributes to the interactions observed in our system. Interestingly, we do not observe any significant structure in the velocity field surrounding the ring for Γ = 7 (see Fig. 7a). A plausible explanation is that the ring does not move rapidly enough to generate a sustained flow field, as the frictional forces resulting from collisions between the beads and the vibrating plates effectively suppress any such flow. However, when the shaking strength is increased to Γ = 9, the ring spins approximately 1.3 times faster. This enhanced rotational motion gives rise to an anisotropic velocity profile, as shown in Fig. 7b. The emergence of this flow profile is attributed to the ring's lack of full rotational symmetry. As a result of this flow profile, the rings exhibit mutual repulsion (see Fig. 7c and Movies S7 and S8, ESI†). This flow-induced repulsion is consistent with previous reports of repulsive interactions between motile rods.⁵³

Fig. 7 (a) and (b) The velocity field around a clockwise-spinning ring at Γ = 7 and Γ = 9, respectively. (c) Inter-ring separation as a function of time for co-rotating and counter-rotating rings at Γ = 9. Here, ϕ = 0.775.

In conclusion, we have studied the dynamics of pair of co-rotating and counter-rotating granular rings embedded in a monolayer of spherical beads, confined between vertically vibrating plates. For high bead concentrations, we observed depletion-like attraction between the rings in both cases. However, at low bead concentrations, the reverse depletion effect manifests, resulting in repulsion between the rings. Additionally, we examined the diffusive properties of the dimer formed by the rings and compared them with the dynamics of a single ring. Our findings provide new insights into the role of depletion interactions in active chiral systems and may have implications for self-assembly and pattern formation in driven granular and colloidal materials.

Conflicts of interest

There are no conflicts to declare.

Data availability

We performed the numerical simulations using our own custom-written numerical code, with all details provided in the paper. As it is a general-purpose code developed with significant effort, we prefer not to share it. Sharing the data on the cloud in terabytes is not feasible. However, we can provide the data upon request.

Appendix

Behavior of non-chiral rings in the medium and probability distribution of inter-ring separation at ϕ = 0.70.

Fig. 8 Time evolution of the distance between two rings at ϕ = 0.775 with an initial separation of r₀ = 3.0 mm for pairs of co-rotating chiral rings, counter-rotating chiral rings, and achiral rings. The distance between achiral rings remains nearly constant, indicating the absence of significant interactions between them.

Fig. 9 Probability distribution of the center-to-center inter-ring distance r for co-rotating and counter-rotating rings at ϕ = 0.70.

Acknowledgements

We sincerely thank the National Supercomputing Mission (NSM) for providing access to the computational resources of Param Himalaya at IIT Mandi, as well as the HPC facility at IIT Mandi.

References

1. Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702.
2. G. S. Redner, M. F. Hagan and A. Baskaran, Biophys. J., 2013, 104, 640a.
3. J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702.
4. R. Wittkowski, A. Tiribocchi, J. Stenhammar, R. J. Allen, D. Marenduzzo and M. E. Cates, Nat. Commun., 2014, 5, 4351.
5. N. Kumar, R. K. Gupta, H. Soni, S. Ramaswamy and A. Sood, Phys. Rev. E, 2019, 99, 032605.
6. R. Kant, R. K. Gupta, H. Soni, A. Sood and S. Ramaswamy, Phys. Rev. Lett., 2024, 133, 208301.
7. I. H. Riedel, K. Kruse and J. Howard, Science, 2005, 309, 300–303.
8. M. E. Cates, D. Marenduzzo, I. Pagonabarraga and J. Tailleur, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11715–11720.
9. F. D. Farrell, M. C. Marchetti, D. Marenduzzo and J. Tailleur, Phys. Rev. Lett., 2012, 108, 248101.
10. A. Sharma and H. Soni, Soft Matter, 2024, 20, 6608–6617.
11. A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98.
12. N. Kumar, H. Soni, S. Ramaswamy and A. Sood, Nat. Commun., 2014, 5, 4688.
13. H. Soni, N. Kumar, J. Nambisan, R. K. Gupta, A. Sood and S. Ramaswamy, Soft Matter, 2020, 16, 7210–7221.
14. N. C. Darnton, L. Turner, S. Rojevsky and H. C. Berg, Biophys. J., 2010, 98, 2082–2090.
15. Y. Wu, A. D. Kaiser, Y. Jiang and M. S. Alber, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1222–1227.
16. S.-N. Lin, W.-C. Lo and C.-J. Lo, Soft Matter, 2014, 10, 760–766.
17. J. L. Silverberg, M. Bierbaum, J. P. Sethna and I. Cohen, Phys. Rev. Lett., 2013, 110, 228701.
18. J.-F. Joanny and S. Ramaswamy, Nature, 2010, 467, 33–34.
19. T. Sanchez, D. T. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434.
20. D. F. Hinz, A. Panchenko, T.-Y. Kim and E. Fried, Soft Matter, 2014, 10, 9082–9089.
21. F. Kümmel, P. Shabestari, C. Lozano, G. Volpe and C. Bechinger, Soft Matter, 2015, 11, 6187–6191.
22. S. R. McCandlish, A. Baskaran and M. F. Hagan, Soft Matter, 2012, 8, 2527–2534.
23. W. Yang, V. Misko, K. Nelissen, M. Kong and F. Peeters, Soft Matter, 2012, 8, 5175–5179.
24. S. K. Das, S. A. Egorov, B. Trefz, P. Virnau and K. Binder, Phys. Rev. Lett., 2014, 112, 198301.
25. C. Tung, J. Harder, C. Valeriani and A. Cacciuto, Soft Matter, 2016, 12, 555–561.
26. J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 114, 018301.
27. Y.-S. Su, H.-C. Wang and I. Lin, Phys. Rev. E, 2015, 91, 030302.
28. X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017.
29. G. Grégoire, H. Chaté and Y. Tu, Phys. Rev. E, 2001, 64, 011902.
30. C. Valeriani, M. Li, J. Novosel, J. Arlt and D. Marenduzzo, Soft Matter, 2011, 7, 5228–5238.
31. Z. Lin, J.-L. Thiffeault and S. Childress, J. Fluid Mech., 2011, 669, 167–177.
32. L. Angelani, C. Maggi, M. Bernardini, A. Rizzo and R. Di Leonardo, Phys. Rev. Lett., 2011, 107, 138302.
33. R. Ni, M. A. Cohen Stuart and P. G. Bolhuis, Phys. Rev. Lett., 2015, 114, 018302.
34. J. Harder, S. Mallory, C. Tung, C. Valeriani and A. Cacciuto, J. Chem. Phys., 2014, 141, 194901.
35. J. L. Aragones, J. P. Steimel and A. Alexander-Katz, Soft Matter, 2019, 15, 3929–3937.
36. P. Dolai, A. Simha and S. Mishra, Soft Matter, 2018, 14, 6137–6145.
37. B. Liebchen and D. Levis, Europhys. Lett., 2022, 139, 67001.
38. H. C. Berg and L. Turner, Biophys. J., 1990, 58, 919–930.
39. W. R. DiLuzio, L. Turner, M. Mayer, P. Garstecki, D. B. Weibel, H. C. Berg and G. M. Whitesides, Nature, 2005, 435, 1271–1274.
40. D. Woolley, Reproduction, 2003, 126, 259–270.
41. B. Friedrich and F. Jülicher, New J. Phys., 2008, 10, 123025.
42. S. Nakata, Y. Iguchi, S. Ose, M. Kuboyama, T. Ishii and K. Yoshikawa, Langmuir, 1997, 13, 4454–4458.
43. F. Kümmel, B. Ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen and C. Bechinger, Phys. Rev. Lett., 2013, 110, 198302.
44. G. S. Redner, A. Baskaran and M. F. Hagan, Phys. Rev. E, 2013, 88, 012305.
45. A. Kaiser, K. Popowa and H. Löwen, Phys. Rev. E, 2015, 92, 012301.
46. J. Schwarz-Linek, C. Valeriani, A. Cacciuto, M. Cates, D. Marenduzzo, A. Morozov and W. Poon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4052–4057.
47. A. Cēbers, J. Magn. Magn. Mater., 2011, 323, 279–282.
48. F. Schmidt, B. Liebchen, H. Löwen and G. Volpe, J. Chem. Phys., 2019, 150, 094905.
49. X. Wang, Functional Soft Materials Designed Using Colloids and Interfaces at and Beyond Equilibrium, Cornell University, 2022.
50. P. Arora, A. Sood and R. Ganapathy, Sci. Adv., 2021, 7, eabd0331.
51. B. Ventejou, H. Chaté, R. Montagne and X.-Q. Shi, Phys. Rev. Lett., 2021, 127, 238001.
52. J. L. Aragones, J. P. Steimel and A. Alexander-Katz, Nat. Commun., 2016, 7, 11325.
53. R. K. Gupta, R. Kant, H. Soni, A. Sood and S. Ramaswamy, Phys. Rev. E, 2022, 105, 064602.
54. W. J. Stronge, J. Appl. Mech., 1994, 61, 605.
55. B. V. Mirtich, Impulse-based dynamic simulation of rigid body systems, University of California, Berkeley, 1996.
56. H. Soni, PhD thesis, Indian Institute of Science, Bangalore, 2015.
57. T. Pöschel and T. Schwager, Computational granular dynamics: models and algorithms, Springer Science & Business Media, 2005.
58. D. Frenkel, in Understanding Molecular Simulation, ed. D. Frenkel and B. Smit, 2002.
59. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
60. J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489–1499.
61. M. Doi, Soft Matter Physics, Oxford University Press, 2013.
62. S. Asakura and F. Oosawa, J. Polym. Sci., 1958, 33, 183–192.
63. C. H. Batton and G. M. Rotskoff, Soft Matter, 2024, 20, 4111–4126.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00361j

---