Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dispersions of weakly charged thermoresponsive microgels at high densities†‡
M. Hildebrandta,
D. Pham Thuya,
A. Domgansa,
A. Scotti b,
S. Prévost
b,
S. Prévost c,
M. Adhikarid,
J. Horbach
c,
M. Adhikarid,
J. Horbach d and
M. Karg§
d and
M. Karg§
 *a
*a
aInstitut für Physikalische Chemie I: Kolloide und Nanooptik, Heinrich-Heine-Universität Düsseldorf, Universitätsstraße 1, 40225 Düsseldorf, Germany
bDivision of Physical Chemistry, Lund University, SE-22100 Lund, Sweden
cInstitut Laue-Langevin – 71 avenue des Martyrs CS 20156, 38042 Grenoble Cedex 9, France
dInstitut für Theoretische Physik II: Weiche Materie, Heinrich-Heine-Universität Düsseldorf, Universitätsstraße 1, 40225 Düsseldorf, Germany
First published on 11th July 2025
Abstract
Poly-N-isopropylacrylamide-based microgels in aqueous dispersion exhibit a pronounced thermoresponse that allows to control their size and thus the volume fraction via temperature. Here, we study the phase behavior of aqueous dispersions of weakly charged microgels with small silica cores, employing different scattering techniques. From temperature- and concentration-dependent experiments in presence and absence of monovalent salt, we deduce phase diagrams. The central quantity to analyse the structure and thus the phase of the system is the static structure factor measured via small-angle scattering. As a reference, we also perform molecular dynamics computer simulations of systems of weakly charged particles, using a screened Coulomb (Yukawa) potential with a soft core to model the interactions between the microgels. For this model potential the phase diagram is known. By comparing structure factors determined by both experiment and simulation, we can assign the observed states of our soft model colloids to states in the Yukawa phase diagram.
1 Introduction
Microgels and nanogels are colloid-like objects with an internal polymer network structure that can host large amounts of solvent.1–3 They feature characteristics attributed to colloids, macromolecules and surfactants.4–9 Microgels are also known for their responsiveness towards external stimuli like pH, temperature and ionic strength, which depends on the polymer composition.3,10–13 First introduced by Pelton and Chibante,14 microgels based on poly-N-isopropylacrylamide (PNIPAM) are one of the most prominent examples of such responsive systems. In water, PNIPAM homopolymers exhibit a lower critical solution temperature (LCST) of approximately 32 °C.15,16 Because of this LCST, PNIPAM-based microgels respond to temperature with a volume phase transition (VPT) from a swollen state with large solvent contents to a collapsed state with significantly reduced solvent contents.17–20 In addition, typical PNIPAM-based microgels exhibit a gradient in crosslinking density, because the most often employed chemical crosslinker N,N′-methylenebisacrylamide (BIS) is consumed faster during synthesis, leading to a more crosslinked inner region and a rather undefined fuzzy-like surface structure with dangling polymer chains.21–23 Interestingly and despite their soft nature, microgels in dense packings can (self-)assemble into crystalline structures, whether in 2D at liquid interfaces24–29 or in 3D in bulk dispersion,30–39 similar to hard spheres.40A great advantage of responsive microgels is that, in contrast to hard spheres, the volume fraction of the particles can be influenced in situ, changing the respective external stimulus like temperature.41 This makes microgels an ideal model system to investigate crystallization processes and the phase behavior of soft colloidal objects. Therefore, the phase diagram of such systems can be expected to be complex, as the volume fraction, as well as the particle-to-particle interaction potential become a function of temperature and not only of particle number concentration.42 Despite microgels in dense packings were intensively investigated in the past, an experimentally recorded full, temperature-dependent phase diagram as function of the number density is not published by now.43,44 Receiving more experimental insight into the phase behavior of soft colloidal systems can also provide additional parameters for numerical simulations in the field of microgels.45 In order to investigate microgels in dense packings, small-angle scattering experiments can elucidate the overall structure of the system, provided by the structure factor S(q).31,46–48
This includes information about fluid and crystalline phases such as crystal structures or coexistence of fluid and crystalline regimes.41,47 The common challenge for the investigation of microgels in dense packings is to disentangle the form factor from the structure factor. In general, this is difficult for soft colloids, because the particle shape and thus the form factor can change depending on the packing density, respectively the volume fraction. Indeed, microgels can undergo the processes of deswelling, faceting and interpenetration.49–52 One approach to solve this issue is to make use of contrast variation methods in small-angle neutron scattering (SANS) and measure mixtures of deuterated and hydrogenated microgels in order to separately record the structure and form factor of the microgels at dense packing.53–56 By using small-angle X-ray scattering (SAXS), we have recently proposed that core–shell (CS) microgels with high scattering contrast cores that are significantly smaller than the total microgel dimensions, are ideally suited to determine (i) the number density, ρ, and (ii) S(q).38,41,47 Importantly, for sufficiently large shell-to-core size ratios, the cores are not expected to contribute to the phase behavior and thus the interactions of the CS microgels are comparable to that of classical microgels without cores over a broad range of packing fractions.57
Microgels are usually considered weakly charged when charges are only introduced by the used anionic or cationic radical initiator,58,59 like potassium or ammonium persulfate (PPS/APS) or 2,2′-azobis(2-methylpropionamidine) dihydrochloride (V50). In contrast, when chargeable comonomers are used in the synthesis, the resulting microgels are often considered as ionic microgels.11
Bergman et al.60 investigated the influence of charges on the morphology of P(NIPAM-co-acrylic acid) microgels by varying the charge density, making use of the pH-dependent degree of protonation of the carboxylic acid functionalities and the variation of ionic strength of the dispersion. In that work, distinct changes in the internal morphology of the microgels were found, accompanied by a reduction in size in response to an increase of ionic strength adjusted by monovalent salt (KCl). A recent study from Petrunin et al.61 on microgels in dense packings showed that charges can have a significant influence on the microgel response towards crowded environments. Weakly charged microgels undergo slight deswelling followed by faceting and deformation while ionic microgels show deswelling before interparticle contact.34,35 Zhou et al.58 studied the size of the counterion cloud that surrounds weakly charged microgels. Through SANS experiments the authors could show that the dimensions of the counterion cloud are similar to the total size of the microgels. Therefore, it was concluded that the counterion cloud is mostly located in the outer periphery of the microgel and will therefore significantly impact on the interaction potential. Electrostatic interactions play an important role in the stabilization of microgel dispersions.62 At lower temperatures, in the swollen state, microgels are stabilized by steric repulsion related to the fuzzy outer part of the polymer network and in addition electrostatic contributions associated with the presence of charges in the microgel. In the collapsed state, above the VPT temperature (VPTT), polymer–polymer interactions become favored, microgels behave more like homogeneous hard spheres and only the electrostatic contribution provides colloidal stability.22 When charges are screened at sufficiently high ionic strength, colloidal stability can be lost above the VPTT. Therefore, conducting a temperature-dependent experiment with screened charges of the microgels, especially at dense packings, requires a careful adjustment of the ionic strength in order to maintain colloidal stability over a broad range of temperatures and ρ.
Numerical simulations were used to elucidate the phase behavior and the microscopic interactions between the particles in the experimental microgel systems. A model potential that accurately describes the effective interactions between (weakly) like-charged colloidal particles in a dispersion with co- and counterions is the hard-core Yukawa (screened Coulomb) potential.63,64 The phase diagram for this model is known from previous simulation studies.65–68 In this work, we use this model as a reference to characterize the phase behavior of weakly charged microgels in dense packings. To this end, we perform molecular dynamics (MD) simulations of a hard-core Yukawa model (note that in our case, the hard core is modelled by an inverse power law potential with a large exponent, see below). From these simulations, we obtain the static structure factor along different paths in the vicinity of the fluid-FCC coexistence. By comparison of these structure factors to those from the experiment, we assign the measured states of the microgel system to states in the hard-core Yukawa phase diagram. Using this protocol, we can assign effective screening parameters to different states of the microgel system.
In the experiment, we prepared aqueous dispersions of weakly, negatively charged microgels in absence and presence of KCl as monovalent salt to adjust the ionic strength. Following our previous work, we make use of CS microgels with monodisperse, spherical silica nanoparticle (NP) cores and much larger, soft and thermoresponsive PNIPAM microgel shells.38 The CS microgels were investigated by SAXS, SANS and light scattering methods in dependence of temperature, ρ, and the absence/presence of salt. Synchrotron SAXS measurements well below the VPTT revealed crystalline samples above a critical ρ with values that depend on the ionic strength. Over a very broad range of ρ fluid-like behavior was found well above the VPTT, where the microgels are in their collapsed state. In combination with measurements by temperature-dependent Vis-NIR extinction spectroscopy, we were able to construct temperature- and ρ-dependent phase diagrams for the absence and presence of KCl. This work contributes to the fundamental understanding of soft colloids in dense packings with a particular focus on the role of electrostatic interactions.
2 Materials and methods
2.1 Chemicals
L-Arginine (PanReacAppliChem, ≥99%), cyclohexane (Fisher Scientific, analytical reagent grade), tetraethyl orthosilicate (TEOS, Sigma Aldrich, 98%), 3-(trimethoxysilyl)propyl methacrylate (MPS, Sigma Aldrich, 98%), N-isopropylacrylamide (NIPAM, TCI, >98%) N,N′-methylenebis(acrylamide) (BIS, Sigma-Aldrich, 99%), potassium persulfate (PPS, Sigma-Aldrich, 99.0%), potassium chloride (KCl, VWR chemicals, Reag. Ph. Eur.) and heavy water (D2O, Sigma Aldrich, 99.9%) were used as received without further purification.Water was always used in ultra-high purity provided by a Milli-Q system (Merck Millipore) with a resistivity of 18.2 MΩ cm.
2.2 Synthesis of CS microgels and sample preparation
For details on the synthesis of the CS microgels and the sample preparation, we refer to our previous work.38 Synchrotron SAXS experiments were performed with CS microgels dispersed in D2O, excluding the samples with volume fractions of 0.84, recorded at 40 °C, which were dispersed in H2O. No significant impact of the solvent on the swelling behavior of the CS microgels could be detected.38 CS microgel samples investigated by Vis-NIR absorbance spectroscopy were all dispersed in H2O. Dispersions of CS microgels at higher ionic strength were prepared with aqueous solutions of the monovalent and inert salt potassium chloride (KCl), using a concentration of 0.5 mM (Debye length at 25 °C: λD = 13.7 nm).Please note that a second batch of CS microgels (CS2) had to be synthesized to guarantee large enough quantities so that temperature-dependent phase diagrams could be recorded. Details on the microgel preparation, particle characterization and determination of the particle number concentration can be found in the ESI.‡
2.3 SANS
SANS experiments were performed on the D11 instrument at the Institut Laue-Langevin in France (Grenoble). The instrument was equipped with a multi-PSD 3He tube detector consisting of 256 tubes of 8 mm diameter and 1 m length, with 8 × 8 mm2 pixels and a cross-shaped sensitive area of 1.5 × 1.5 m2. The neutron wavelength was set to 0.6 nm and sample-to-detector distances of 1.7, 10.5 and 38.0 m were used to cover a large q-range up to 5 nm−1. Here, the instrumental resolution regarding q is based on the neutron beam width, the pixel size and the wavelength spread (Δλ/λ = 9% (FWHM)). Acquisition times were 120 s, 300 s and 900 s, respectively. Aqueous dispersions of CS microgel (0.45 wt% in D2O) were measured in cylindrical quartz glass cuvettes (Hellma, Germany, d = 1 mm). The recorded scattering data were reduced with Grasp V 9.20g.692.4 SAXS
Synchrotron SAXS experiments were conducted on the CoSAXS beamline at the MAX IV synchrotron in Sweden (Lund). An Eiger2 4 M detector with a sensitive area of 155.1 × 162.2 mm2 and total pixel sizes of 75 × 75 μm2 was used to record the scattering patterns. The energy of the X-ray beam was 12.4 keV for all performed experiments. The sample-to-detector distance was set to 11.04 m yielding an effective q-range of 0.01 nm−1 to 0.5 nm−1. CS microgel dispersions investigated at 20 °C were measured in 0.2 mm × 4.00 mm × 10 mm rectangular, flat-wall capillaries (VitroTubes), while the dispersions measured at 40 °C were prepared in 1 mm round capillaries (WJM Glas). The recorded detector images were radially averaged and background corrected for D2O.Additional SAXS measurements were performed on a Xeuss 2.0 (XENOCS). The instrument was equipped with a Pilatus3R 300 K detector possessing a sensitive area of 83.8 × 106.5 mm2 with total pixel sizes of 172 × 172 μm2. Here, the energy of the X-ray beam was 8.048 keV and the sample-to-detector distance was set to 1.2 m, resulting in an effective q-range of 0.03 nm−1 to 2 nm−1. The acquisition time was set to 3600 s and glassy carbon (1 mm) was used as reference to yield scattering intensities in absolute units.
CS microgel dispersions with mass contents of 10 wt% were measured in 1 mm round capillaries (WJM Glas). The resulting SAXS profiles were background corrected for the respective solvent.
The radially averaged scattering profiles were analyzed with the SasView software70 and the structure factors were fitted with SASfit (v0.94.12).71
2.5 Light scattering
Temperature-dependent DLS was performed with a Zetasizer Nano S from Malvern Panalytical, equipped with a laser of 633 nm wavelength. The scattered light was detected at an angle of 173°. Dilute dispersions (0.05 to 0.01 wt%) of CS microgels, filtered through a 5 μm syringe filter (PTFE, Carl Roth) were measured in semi-micro cuvettes (polymethylmethacrylate, VWR) at temperatures between 17 °C and 60 °C in 0.2 °C steps with equilibration times of 60 s after each step. Intensity-time autocorrelation functions were recorded in triplicate with acquisition times of 60 s. Hydrodynamic radii (Z-average) were determined by procedures provided by the instrument software. These involved cumulant analysis of the autocorrelation functions followed by application of the Stokes–Einstein equation to compute radii from translational diffusion coefficients.Static light scattering was measured on an angle-dependent 3D LS spectrometer (LS Instruments, Switzerland) equipped with a HeNe laser (632.8 nm). Measurements were performed in cylindrical glass cuvettes (10 × 75 mm, borosilicate, Fisher scientific), treated with 2% Hellmanex solution, followed by cleaning in an acetone fountain prior to use. CS microgel dispersions with mass contents of 0.01 wt% were filtered through a 5 μm syringe filter (PTFE, Carl Roth) and filled in glass cuvettes. The samples were placed in a temperature-controlled decalin bath (JULABO CF31, PT100 close to sample position). Measurements were performed at angles between 20° and 140° in 2° steps with acquisition times of 10 s.
2.6 Electrophoretic mobility
Temperature-dependent electrophoretic mobilities and respective zeta potentials of the CS microgels were determined with a Litesizer 500 (Anton Paar). CS microgel dispersions with mass contents of 0.05 wt% were filtered through a 5 μm syringe filter (PTFE, Carl Roth) and degassed in an ultrasonic bath for 600 s. The dispersions were filled into omega-cuvettes (Anton Paar) for zeta-potential measurements. The electrophoretic mobility was recorded at a voltage of 100 V and temperatures between 20 to 60 °C in 2 °C steps with equilibration times of 300 s.2.7 Transmission electron microscopy
Transmission electron microscopy (TEM) was conducted with a JEM-2100Plus (JEOL) operating in bright-field mode with an acceleration voltage of 80 kV. Dilute, aqueous dispersions of CS microgels were drop-casted on a carbon-coated copper grid (200 mesh, Electron Microscopy Science) and dried for several hours at ambient conditions.2.8 Absorbance spectroscopy
Vis-NIR spectroscopy was performed on a SPECORD S600 (Analytik Jena GmbH). Temperature-dependent measurements were conducted in a temperature-controlled sample changer at temperatures from 20 to 50 °C, in steps of 0.3 °C, with equilibration times of 720 s.2.9 Molecular dynamics simulation
Next we describe the details of the molecular dynamics (MD) simulation. The hard-core Yukawa potential is often used to model charged particles in an electrolyte solution.67 It is a repulsive pair potential, u(r), that describes the interaction between a pair of like-charged particles, separated by distance r, in the presence of the electrolyte solution. The charged particles in the electrolyte are not explicitly taken into account, but they are effectively described via an exponential function with a screening parameter κ (see below). Note that an explicit relation of κ with the salt concentration of the electrolyte is provided by the DLVO theory.72 We use a version of the potential function that has been proposed in ref. 68. According to this work, the function u(r) scaled by the inverse thermal energy β = 1/(kBT) (with kB the Boltzmann constant and T the temperature) is given by
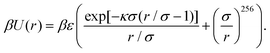 | (1) |
Here, the first term is a screened Coulomb potential with energy parameter ε and “interaction diameter” σ. The second term ∝ r−256 models the hard-core repulsion between the charged particles. As in ref. 68, we have kept βε = 81 and truncated the potential at rcut = 7.0σ.
We performed molecular dynamics (MD) simulations using LAMMPS.73 Applying periodic boundary conditions, we considered systems of N = 1000 particles at different values of κ and different densities 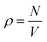 , with V = L3 the volume of the cubic box with linear dimension L. From the comparison of static structure factors from the simulation to those of the experiment (see below), we have determined the conversion of length unit to be σ = 139 nm. For κ = 5.1σ−1 (0.037 nm−1), simulations at the densities ρ = 0.0855σ−3 (3.18 × 1013 ml−1), 0.1105σ−3 (4.11 × 1013 ml−1), 0.1300σ−3 (4.84 × 1013 ml−1), 0.1500σ−3 (5.59 × 1013 ml−1), and 0.1711σ−3 (6.37 × 1013 ml−1) were done. Similarly, we also carried out simulations at the fixed density ρ = 0.1711σ−3 (6.37 × 1013 ml−1) for κ = 5.10σ−1 (3.70 × 10−2 nm−1), 7.10σ−1 (5.11 × 10−2 nm−1), 10.10σ−1 (7.27 × 10−2 nm−1), 12.10σ−1 (8.71 × 10−2 nm−1), and 15.10σ−1 (10.78 × 10−2 nm−1). The equations of motion were integrated using the velocity form of the Verlet algorithm with a time step of dt = 0.001τ, with
, with V = L3 the volume of the cubic box with linear dimension L. From the comparison of static structure factors from the simulation to those of the experiment (see below), we have determined the conversion of length unit to be σ = 139 nm. For κ = 5.1σ−1 (0.037 nm−1), simulations at the densities ρ = 0.0855σ−3 (3.18 × 1013 ml−1), 0.1105σ−3 (4.11 × 1013 ml−1), 0.1300σ−3 (4.84 × 1013 ml−1), 0.1500σ−3 (5.59 × 1013 ml−1), and 0.1711σ−3 (6.37 × 1013 ml−1) were done. Similarly, we also carried out simulations at the fixed density ρ = 0.1711σ−3 (6.37 × 1013 ml−1) for κ = 5.10σ−1 (3.70 × 10−2 nm−1), 7.10σ−1 (5.11 × 10−2 nm−1), 10.10σ−1 (7.27 × 10−2 nm−1), 12.10σ−1 (8.71 × 10−2 nm−1), and 15.10σ−1 (10.78 × 10−2 nm−1). The equations of motion were integrated using the velocity form of the Verlet algorithm with a time step of dt = 0.001τ, with 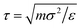 , setting the mass m to m = 1.0. The temperature was kept constant using a Nosé–Hoover thermostat.74,75 To compute the static structure factor S(q), to be defined below, from the MD simulation, at each of the considered values of ρ and κ we performed 10 independent runs, each with a total length of 300τ from which 100 equidistant configurations of the last 200τ were used for the computation of the structure factor. Thus, each structure factor at a given combination of ρ and κ was obtained from an average over 1000 configurations.
, setting the mass m to m = 1.0. The temperature was kept constant using a Nosé–Hoover thermostat.74,75 To compute the static structure factor S(q), to be defined below, from the MD simulation, at each of the considered values of ρ and κ we performed 10 independent runs, each with a total length of 300τ from which 100 equidistant configurations of the last 200τ were used for the computation of the structure factor. Thus, each structure factor at a given combination of ρ and κ was obtained from an average over 1000 configurations.
A (rough) phase diagram of the Yukawa model in the κ–ρ plane, as adapted from ref. 67 and 68, is shown in Fig. 1. Here, we have not indicated the coexistence between the three appearing phases fluid, FCC, and BCC, because all the first-order phase transitions between them exhibit a very narrow coexistence range with respect to density ρ and therefore the binodals in Fig. 1 are represented by a single line. The states at which the static structure factor is computed (see below) are marked by the symbols.
 | ||
| Fig. 1 Phase diagram of the hard-core Yukawa system, as adapted from ref. 67, without indicating the very narrow coexistence range between phases. The symbols correspond to the states where the simulations for the determination of the static structure factor are performed. | ||
In the simulation, the static structure factor S(q) can be directly computed from the particle coordinates ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) k (k = 1,…,N) via the definition
k (k = 1,…,N) via the definition
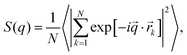 | (2) |
 (with
(with ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) ∈
∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 3) denotes the wave vector. Thus, the minimum absolute value of
3) denotes the wave vector. Thus, the minimum absolute value of ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) is given by
is given by  . Note that the static structure factor of a homogeneous fluid only depends on the absolute value q. For the crystalline phases, however, there is a vectorial dependence on the wave-vector
. Note that the static structure factor of a homogeneous fluid only depends on the absolute value q. For the crystalline phases, however, there is a vectorial dependence on the wave-vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) and the function S(q) corresponds to an average over all crystalline orientations.
and the function S(q) corresponds to an average over all crystalline orientations.
3 Results and discussion
3.1 Characterization in the dilute regime
CS microgels with monodipserse silica NPs of spherical shape were synthesized by seeded precipitation polymerization.38 The NP cores where chosen because (a) these serve as high contrast cores in the X-ray scattering experiments, (b) the seeded precipitation polymerization yields monodisperse microgels with total dimensions that can be tailored by the monomer feeding – at least to some extent – and thus microgel sizes can be optimized for the typically available q-range in small-angle scattering experiments, and (c) the cores are small with respect to the total microgel dimensions and thus should not contribute to the phase behavior unless ultrahigh densities are reached. During the polymerization charges are introduced to the microgel shell only through the anionic radical initiator. Thus, we consider these microgels as weakly charged in their shells in contrast to copolymer microgels with chargeable comonomers like acrylic acid.76 Furthermore, the resulting counterion cloud (K+) is expected to be localized at the fuzzy periphery of the microgel shells and therefore impacts on the microgel–microgel interactions.58 The successful encapsulation of single cores per each microgel is demonstrated by TEM images presented in Fig. S1 in the ESI.‡ Analysis of several TEM images yielded an average core radius of RTEM = 18 ± 2 nm. Throughout this work, we study and compare aqueous dispersions of the microgels in absence and presence of KCl. KCl was chosen as monovalent salt because it is chemically stable and does not show chaotropic properties according to the Hofmeister series.We begin with studying the influence of electrostatic contributions on microgel size and stability in the dilute regime. Fig. 2a shows the evolution of the hydrodynamic radii (Rh) with temperature for a salt-free sample (cKCl = 0 mM, blue) and a sample with cKCl = 0.5 mM (green). In both cases, we observe the typical VPT behavior known for PNIPAM-based microgels. From the swollen state at low temperatures we observe a continuous decrease in hydrodynamic dimensions. Until approximately 40 °C, both swelling curves overlap with only marginal differences in size. For example, at 17 °C we obtained Rh,0mM = 147 ± 1 nm and Rh,0.5mM = 145 ± 1 nm, respectively. Approaching the fully collapsed state at high temperatures, values of Rh are slightly smaller in presence of KCl than in the salt-free sample. We attribute this difference to the reduced ionic contribution to the osmotic pressure leading to slightly more pronounced deswelling. We want to note that these effects are minor in contrast to the expected changes for ionic copolymer microgels and higher ionic strength as for example studied in the work of Bergman et al.60 The VPTT was determined at 35 °C for both samples and thus is not influenced by the absence/presence of 0.5 mM salt. Using electrophoretic light scattering (ELS), we determined the electrophoretic mobilities (right axis in Fig. 2a). As expected we generally observe an increase in mobility with increasing temperature which is related to the increase in charge density in the microgel periphery as the microgel volume decreases, i.e. the microgels collapse. Both samples show very similar sigmoidal evolutions of the mobility with temperature despite a systematic offset of the sample with KCl towards significantly lower mobilities. The underlying decrease in charge density is attributed to the significantly reduced Debye length. In comparison to the VPTT from the DLS data, the inflection points of the electrophoretic mobilities are shifted to higher temperatures, which is in accordance with literature for PNIPAM-based microgels.11,59,77 We also computed zeta-potentials based on the electrophoretic mobilities using the Einstein–Smoluchowski relation. Respective data are shown in Fig. S2 in the ESI.‡ Importantly the ELS measurements reveal that at such rather low concentrations of salt of 0.5 mM (a) charges are already significantly screened, and (b) the concentration is still low enough that the microgels remain colloidally stable in dispersion, in particular above the VPTT. Therefore, we will use 0.5 mM KCl for samples with salt throughout this work.
 | ||
| Fig. 2 Characterization of CS microgels in the dilute state in absence (blue) and presence of KCl (green). (a) Temperature-dependent evolution of Rh (empty symbols) and electrophoretic mobility (filled symbols). (b) Normalized, generalized volume fraction ζ as a function of temperature. The data was normalized to ζ at 20 °C. (c) Scattering profiles from SAXS and SANS recorded at 20 °C (filled symbols) and 45 °C (empty symbols). Additional data points obtained from SLS were merged to the SANS profiles at low q (lighter color symbols, below 0.02 nm−1). The red lines correspond to form factor fits to the data. DLS and SAXS data at cKCl = 0 mM were adapted from our previous work.38 | ||
Fig. 2b shows the evolution of the generalized volume fraction ζgeneralized55 (normalized to the swollen state, 20 °C) with temperature. ζgeneralized was calculated from the DLS data (Rh) and using the particle number density ρ = 5.27 × 1012 mL−1 that was determined from a 1 wt% sample using the forward scattering of the cores measured by SAXS. Details on the determination of ρ and the calculation of ζ are given in the ESI‡ of our previous work.38 The data reveal that just by changes in temperature the volume fraction can be reduced by approximately 70%. This is ideal for studies of the phase behavior as we can probe a large range of volume fraction for individual samples with fixed ρ. As expected from the little difference in the swelling curves, also the profiles of ζ with temperature overlap nicely independent of the presence or absence of KCl. The form factor of the microgels was studied by combining SAXS, SANS and static light scattering (SLS) as shown in Fig. 2c. The solid lines correspond to the form factor fits to the data with a CS model with an exponentially decaying scattering length density (SLD) of the shell. This model was chosen to account for the gradient in the crosslinker distribution within the polymer network. The polydispersity of the CS microgels was taken into account by applying a Gaussian distribution to both the core and the shell. From the SAXS data at 20 °C we obtained a core radius Rcore = 18 ± 2 nm and a total radius of 138 ± 14 nm for the CS microgels, independent of the presence or absence of salt. The merged SLS (lighter colors) and SANS (darker colors) data at 20 °C required the addition of a Lorentzian term (Ornstein–Zernike (OZ) contribution) to the fitting model, due to the larger contrast of the PNIPAM shell compared the contrast situation in SAXS. The OZ contribution accounts for internal fluctuations of the polymer network.21,78 The SANS data reveal the first form factor minimum associated to the shell at approximately q = 0.04 nm−1, followed by additional form factor oscillations indicating the low polydispersity of the microgels. Despite the lower resolution as compared to the SAXS data, the SANS profiles still reveal contributions from the silica cores by a small increase in scattering intensity between q = 0.1 and 0.2 nm−1. The fits to the merged SLS and SANS data yielded a total radius of 138 ± 11 nm, again independent on the absence/presence of KCl. This value is in perfect agreement to the results from SAXS. All parameters obtained from the fits to the data are summarized in Tables S1 and S2 in the ESI.‡ Details on the SLDs and the theoretical differences in scattering amplitudes for the core with respect to shell are given in Table S3 in the ESI.‡ The merged SANS and SLS profiles recorded at 45 °C were fitted by a simple CS form factor model with homogeneous radial SLD profiles for core and shell (solid red lines) considering Gaussian polydispersities for the core and shell. The fits yielded a total radius of 88 ± 7 nm for the collapsed CS microgels, which is in good agreement with RSAXS(40 °C) = 90 ± 7 nm (Fig. S3 and Table S4 in the ESI‡). Furthermore, the scattering data at low q allowed for a Guinier analysis (Fig. S4 and Table S5 in the ESI‡). Radii of gyration (Rg) between 95 and 100 nm were found in the swollen state and radii of 70 to 75 nm in the collapsed state. Due to the gradient in the cross-linking density that is pronounced in the swollen state, it is common to compare the Rg/Rh ratio,79,80 which is approximately 0.67 for our CS microgels. This is in good agreement with literature for comparable microgels.57 Importantly, when comparing the measured scattering profiles from Fig. 2c we see almost no difference when comparing the salt-free samples to the ones containing KCl. In other words, neither from DLS that probes the total microgel dimensions, nor from the static scattering measurements that probe global as well as local characteristics, do we observe any significant differences for the microgel size and internal structure in presence or absence of salt in the dilute state. Also, the softness seems not to be affected significantly by the presence of 0.5 mM KCl because values of Rg/Rh deviate less than 5% for samples with and without salt (see ESI‡ for values of Rg and Rh).
3.2 Swollen core–shell microgels in dense packings
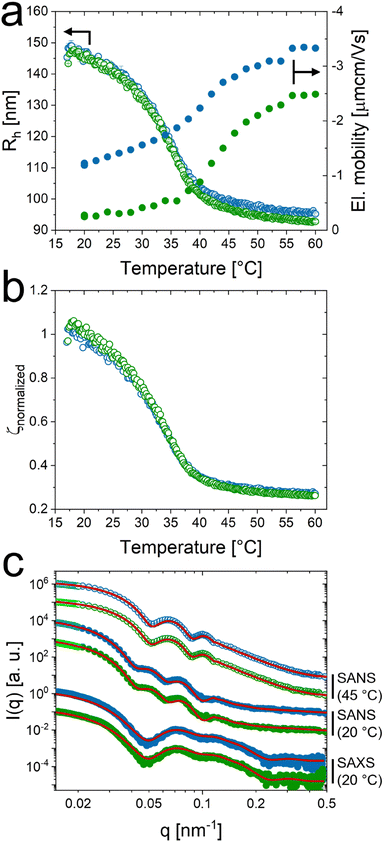
Fig. 3 shows 2D detector images from synchrotron-SAXS of samples with increasing volume fraction with and without salt. Scattering patterns recorded in the absence of salt were adapted from our previous work.38 The respective generalized volume fraction (ζ) of the CS microgels at a temperature of 20 °C are indicated in between the scattering patterns recorded without (top) and with (bottom) salt. As described before the generalized volume fraction was determined using the hydrodynamic size determined in dilute dispersion, i.e. under non-interacting conditions, and using the number density that linearly scales with the mass concentration. A comparison of ζ for cKCl = 0 mM and for cKCl = 0.5 mM at temperatures of 20 °C and 40 °C is given in Table S6 in the ESI.‡ At ζ = 0.42, both scattering patterns are dominated by a fluid-like structure factor (S(q)). When ζ is increased to 0.56, the sample in the salt-free state shows pronounced and narrow Bragg peaks of many diffraction orders indicating the crystalline state (solid) with pronounced long-range order. With salt we also observe an anisotropic scattering pattern with first Bragg peaks with significantly fewer diffraction orders and broader peak width as compared to the sample without salt. This indicates that the crystalline state at this ζ in presence of salt is only of short-range order. The reduced degree of order is a first hint that we might be close to the phase boundary. Upon further increase in ζ both, the salt-free and the salt containing samples are crystalline with pronounced Bragg peaks of many diffraction orders. The six-fold symmetry of the Bragg peaks indicates the alignment of hexagonally close packed planes of CS microgels parallel to the wall of the capillary.41,46,47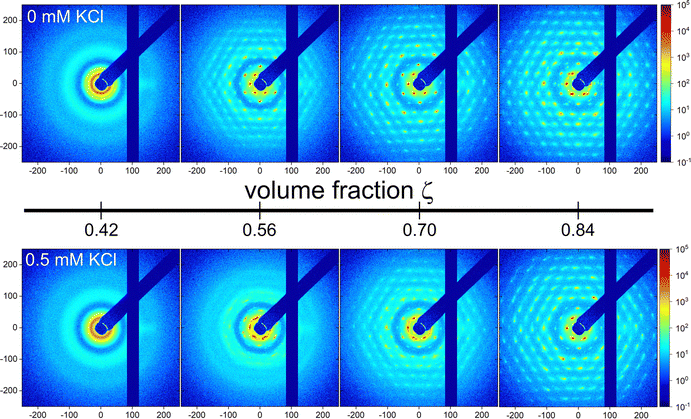 | ||
| Fig. 3 2D detector images from synchrotron-SAXS measurements of concentrated samples without (top) and with salt (bottom), increasing the generalized volume fraction ζ (20 °C) as indicated in the middle. The volume fraction was calculated based on number density ρ and Rh at 20 °C in the salt-free state. SAXS patterns (top) were adapted from our previous work.38 | ||
In addition to the scattering patterns recorded at 20 °C, Fig. S5 in the ESI‡ shows scattering patterns of CS microgel dispersions with the same values of ρ recorded at 40 °C, i.e., in the collapsed state of the microgels. Under these conditions all samples are in the fluid state as revealed by the isotropic scattering patterns.
Radially averaged SAXS profiles are shown in Fig. 4a. The profiles are determined by the structure factor (pronounced Bragg peaks) and form factor of the samples. The form factor minima at q = 0.25 nm−1 and 0.05 nm−1 are related to the SiO2 core and the shell, respectively. When ζ is increased, the form factor minimum related to the shell shifts towards higher q, which indicates a reduction in microgel size. This shrinking can be attributed to osmotic deswelling.35 As expected, the minima related to the form factor of the rigid cores remain unaffected by the increase in packing density. Because of the well-defined structure factor contribution with narrow Bragg peaks related to large crystalline domain sizes, we can still attempt to fit the form factors. For this, we used the same CS model with an exponentially decaying scattering contrast of the shell as in the dilute regime. The fits to the data shown as solid black lines in Fig. 4a describe the form factor oscillations very well for the high and mid q-range (q ≥ 0.04 nm−1). The respective fit parameters are listed in Tables S7 and S8 in the ESI.‡ Deviations between fits and experimental data at low q (q < 0.04 nm−1) are attributed to the structure factor contribution to scattering profiles. The fits reveal the already discussed decrease in total microgel radius with increasing ζ with values decreasing from 138 to 116 nm. This is accompanied by a more pronounced decline in the exponential decay of the shell.38 The lighter colors in Fig. 4 are associated to CS microgel dispersions with salt and the form factor oscillations are similar to oscillations observed from the CS microgels measured in absence of salt. This is proven by form factor analysis, where we cannot find differences within particle size or morphology depending on the KCl concentration. This indicates that the increase in ionic strength does not influence the osmotic deswelling of the CS microgels for the investigated conditions as already reported in the literature for classical PNIPAM microgels.35,52,58
With the modeled form factors, we are also able to extract the crystalline structure factors (S(q)crystal). This was done by dividing the scattering profiles by the modeled form factors. The extracted structure factors are shown in Fig. 4b, where the q-axis was normalized to the position of the first structure factor maximum  , related to a Bragg peak. Scattering profiles which do not possess a distinct Bragg peak related to the 100 crystal plane, were normalized on the 110 peak with respect to the ratio between 100 and 110 being 1.73.38 The sample with ζ = 0.42 and with salt (light orange), exhibits no Bragg peaks and the normalization was conducted similarly to the sample with the same ζ without salt. The normalization enables a direct comparison of the structure factors independent of ζ and the resulting changes in interparticle distance. Due to this, we can indicate the theoretical positions of the Bragg peaks as vertical black lines and relate the Bragg peaks to the respective Miller indices hkl, for a hexagonally close packed (hcp) crystal system.
, related to a Bragg peak. Scattering profiles which do not possess a distinct Bragg peak related to the 100 crystal plane, were normalized on the 110 peak with respect to the ratio between 100 and 110 being 1.73.38 The sample with ζ = 0.42 and with salt (light orange), exhibits no Bragg peaks and the normalization was conducted similarly to the sample with the same ζ without salt. The normalization enables a direct comparison of the structure factors independent of ζ and the resulting changes in interparticle distance. Due to this, we can indicate the theoretical positions of the Bragg peaks as vertical black lines and relate the Bragg peaks to the respective Miller indices hkl, for a hexagonally close packed (hcp) crystal system.
For details on the S(q) extraction, the normalization procedure and the determination of the crystal structure we refer to our previous work.38
At ζ = 0.42, the structure factor of the sample with salt (light orange) does not exhibit any crystalline contributions. Without salt the structure factor exhibits two Bragg peaks of weak intensity, indicating the the crystalline phase. This means that, without salt, the phase boundary between fluid and crystalline state should be close to ζ = 0.42.
At ζ = 0.56 the sample with salt shows fewer diffraction orders and less intense Bragg peaks compared to the sample without salt. This might indicate that the sample is close to the phase boundary between fluid and crystalline state. This is also reflected by the respective SAXS pattern in Fig. 3. We will address the phase boundaries in more detail later on in this work.
All extracted structure factors for ζ ≥ 0.56 possess distinct and sharp Bragg peaks, which match well to the theoretical peak positions for the hcp lattice.
With the known relation between the Bragg peaks and the respective Miller indices, we can extract the lattice constants of the colloidal crystals in dependence of ζ as shown in Fig. S6 in the ESI.‡ Lattice constants decreasing from 374 to 287 nm were obtained for increasing ζ. The addition of salt did not influence the lattice spacing (Table S9 in the ESI‡) significantly. We also performed Williamson–Hall analysis on the scattering data in order to extract the size of the coherently scattering domains of the colloidal crystals (Fig. S7 and Tables S10 and S11 in the ESI‡).81 Here, large domain sizes on the order of 2 to 4 μm were found (Fig. S8 in the ESI‡).
3.3 Collapsed core–shell microgels in dense packings
In addition to the scattering profiles recorded at 20 °C, where most of the investigated CS microgel samples were crystalline, we performed SAXS measurements at 40 °C, i.e., where the microgel shells are in the collapsed state. Thus, the volume fractions were significantly lower while the number concentrations for each sample were the same as in the previous experiments. The respective SAXS profiles are shown in Fig. 5a. For q > 0.05 nm−1, the scattering profiles are dominated by the form factor of the collapsed CS microgels with several pronounced intensity oscillations. In this region of q, all profiles look nearly identical. In other words, the form factors are independent of ζ and the presence/absence of salt in the collapsed state. This also implies that osmotic deswelling is not pronounced or is even absent in the collapsed state, at least for the investigated ρ. | ||
| Fig. 5 Synchrotron-SAXS data and structure factors of dense CS microgel samples at 40 °C. (a) Measured SAXS profiles and (b) structure factors extracted from the SAXS profiles of samples with ζ (20 °C) of 0.42 (orange), 0.56 (red), 0.70 (green) and 0.84 (blue). ζ was calculated based on Rh in the salt-free state. Filled symbols correspond to samples without KCl, empty symbols to samples with 0.5 mM KCl. (c) S(q) as a function of q for different densities at κ = 3.7 × 10−2 nm−1, as obtained from the simulation of the Yukawa model. Here, the values of ρ and κ correspond to the blue points in the phase diagram shown in Fig. 1. (d) Corresponding experimental data, where S(q) is measured for similar densities at a fixed salt concentration (= 0.50 mM). (e) S(q) is shown as a function of q for different concentrations at a given density ρ. Simulation data obtained at different values of κ, as shown in the legend. The values of ρ and κ used here correspond to the magenta points in the phase diagram shown in Fig. 1. (f) Experimental data where the density is fixed to ρ = 6.32 ml−1, for the two salt concentrations 0 mM and 0.5 mM. | ||
In the low q-regime, the scattering profiles show a pronounced structure factor contribution. In contrast to the form factor, the structure factors show clear differences between samples with and without salt. For samples in absence of salt (filled symbols) the structure factors are generally more pronounced and peak maxima can be clearly assigned. With increasing ζ the structure factor peak shifts to larger q corresponding to smaller center-to-center distances in real space (2π/q). For a detailed analysis, we extracted the structure factors, following the procedure recently reported by us.38 The extracted structure factors in Fig. 5b show a shift of the maxima towards higher q with increasing ζ. In addition, when comparing structure factors with similar ζ under conditions without and with salt it is noticeable that the maxima for the state with salt are slightly shifted towards higher q and that the structure factor is generally weaker.
The two “paths” in the phase diagrams for which we computed S(q) for the Yukawa model (cf. Fig. 1) have been selected for the comparison to the experimental data for S(q). We observed a good agreement of the shape of S(q) for ρ = 0.1711σ−3 and κ = 3.7 × 10−2 nm−1 from the simulation with that for ρ = 6.32 × 1013 ml−1 and 0.5 mM salt concentration from the experiment. From the comparison of the position of the first sharp diffraction peak (FSDP) of both structure factors, we inferred σ = 139 nm resulting in the number density ρ = 6.37 × 1013 ml−1 for the simulation which agrees within about 1% with experimental value of ρ = 6.32 × 1013 ml−1. As we shall see in the following, a similar agreement is also obtained for lower densities. Moreover, we can conclude that a salt concentration of 0.5 mM corresponds to a value of the screening parameter of about κ = 3.7 × 10−2 nm−1.
In Fig. 5c, S(q) is shown as a function of q for different ρ at the fixed value κ = 3.70 × 10−2 nm−1 of the screening parameter. The state points shown here are highlighted as blue triangles in the phase diagram, Fig. 1. At a constant value of κ we approach the fluid-FCC coexistence from below. As expected, we observe that the height of the FSDP of S(q) increases as the density increases, and the position of the FSDP shifts to larger q. A similar observation is found in the experiment, as shown in Fig. 5d. With increasing ρ, the peak height increases, and the position of the peak shifts to a larger value. Here, peak positions and densities are in fair agreement with those from the simulation.
Next, we investigate how S(q) changes with κ when the ρ is fixed. To this end, we consider the path in Fig. 1 that is marked by the open diamonds. In Fig. 5e, we show the corresponding S(q) for the different values of κ at the fixed density ρ = 6.37 × 1013 ml−1. We observe that the FSDP in S(q) becomes flatter with increasing κ, and its height decreases while shifting to larger values of q. We note that at κ = 3.7 × 10−2 nm−1, the stable phase is a crystalline FCC phase and thus, here, the structure factor represents a metastable fluid state. According to our data, at the density ρ = 6.37 × 1013 nm−1 the FSDP of the fluid structure factor at the melting point, i.e. around κ = 5.11 × 10−2 nm−1 (cf. Fig. 1) has an amplitude of about 1.8. Again the trends of the simulation data match well with the experiment, as shown in Fig. 5f, where two different structure factors at the density 6.32 × 1013 ml−1 are displayed for the salt concentrations 0 mM and 0.5 mM. Here, the FSDP of the structure factor for the salt-free case has an amplitude of about 2.4 and thus, for this state the structure factor represents a metastable fluid state. However, due to the difficulty of measuring the experimental structure factors accurately – particularly the peak height and the description at both low and high q-values – a direct fitting is not sufficiently reliable. Thus, we did not fit the data.
3.4 Solid–fluid transitions followed by spectroscopy
We now want to focus on temperature-induced fluid–solid transitions that rely on the changes in volume fraction for samples with fixed ρ.38 A time- and cost-efficient approach to do this is by using temperature-dependent extinction spectroscopy. The pronounced Bragg peaks in the VIS to IR region visible in the spectra of Fig. 6a indicate that the CS microgels crystallize at 20 °C, i.e. in their swollen state, over a broad range of volume fractions. This ‘solid’ state is observed for all samples independent of the addition of salt, except for the sample with ζ = 0.49 at 0.5 mM KCl. In Fig. 6a we see that, independent of cKCl, the Bragg peaks shift towards lower wavelength as ζ is increased. This is attributed to the decrease in lattice constant as ρ is increased. Additional spectra from all samples used for SAXS experiments at 20 °C and tables listing Bragg peak positions and lattice constants a, can be found in the ESI‡ in Fig. S9 and Tables S12 and S13.Vis-NIR spectra recorded from a dispersion of CS microgels with ζ = 0.70 (salt-free) at various temperatures are shown in Fig. 6b. At low temperatures, starting at 20 °C, the Bragg peak at 687 nm remains nearly unaffected until 31.1 °C, where the peak begins to shift towards lower wavelength and decreases in intensity. The peak disappears completely at 32.6 °C and higher (see also inset in Fig. 6b). Thus, the phase transition from crystalline (Bragg peak) to fluid (no Bragg peak) occurs in a temperature window as small as approximately 2 °C. Detailed information about the procedure of these measurements including temperature steps and equilibration times are given in the ESI‡ of our previous work.38 After the disappearance of the Bragg peak, the absorbance increases slightly until the temperature reaches 50 °C, the highest temperature in this experiment. This rise in absorbance as the microgels collapse in the fluid phase is related to the increase in light scattering intensity.22,82 To monitor the phase transition more quantitatively, we use the background corrected absorbance values at the maximum of the Bragg peak and follow its development with temperature. The background correction was used to consider only the coherent contribution to the absorbance at the Bragg peak position. In this way, the incoherent scattering background related to the light scattering of the CS microgels could be subtracted. Fig. 6c shows the evolution of the absorbance for the sample with ζ = 0.70 without (top) and with salt (bottom). The red triangles correspond to the heating cycle, while blue triangles refer to the cooling cycle. The green colored areas indicate the regions of the phase transition where the absorbance drops/rises significantly for the heating/cooling cycle. In the absence of salt, the nearly constant absorbances outside the phase transition region from the heating and cooling cycle overlap nicely. Small differences can only be observed in the phase transition region with a small hysteresis where recrystallization in the cooling cycle occurs a slightly lower temperatures than the melting during the heating cycle. Interestingly, in presence of salt the phase transition occurs at significantly lower temperatures, approximately 5 °C lower compared to the salt-free case. The decrease in the transition temperature, Ttransition is attributed to a reduction of the effective interaction radius of the CS microgels.
In Fig. 6d we compare the transition temperatures obtained from heating/cooling cycles as a function of ρ in the absence/presence of salt. For details on the determination of the transition temperatures we refer to our previous work.38 The respective temperature-dependent spectra and plots of the Bragg peak absorbance as function of temperature are given in the ESI,‡ Fig. S10 and S11. Generally, increasing ρ leads to an increase of Ttransition. This is expected because of the increase in ζ with ρ at given temperature. The denser the microgels are packed, i.e. the larger ζ, the more the microgels need to be deswollen to surpass the melting volume fraction where the transition to the fluid phase occurs. Values of Ttransition are generally higher for samples in the salt-free state (filled symbols) as compared to the state with salt (empty symbols). Since we know the respective CS microgel size (Rh, see Fig. 2a) at the respective Ttransition we can use ρ to calculate the critical volume fractions, ζtransition, where the phase transitions occur
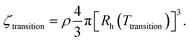 | (3) |
Fig. S13 in the ESI‡ shows ζtransition as function of the generalized volume fraction at 20 °C (ζ (20 °C)) resulting in an average ζtransition of 0.43 ± 0.03 in absence and 0.54 ± 0.02 in presence of salt. The addition of salt that is expected to further screen charges in the outer periphery of the CS microgels obviously leads to a reduction of the effective interaction radius of the microgels. This consequently shifts the critical volume fraction of the phase transition to higher values. In comparison to the transition volume fraction of hard spheres (Φ = 0.49), the CS microgels crystallize at lower volume fractions in the absence of salt. With salt, this volume fraction is drastically increased and above the value for hard spheres. This is again attributed to the reduction of the effective interaction radius of the microgels. Interestingly, melting and freezing volume fractions of PNIPAM-based microgels in literature are reported to be about 0.56 to 0.61.36,83 The microgels investigated in these studies were studied in absence of salt and had significantly lower degrees of cross-linking. The softness might influence the phase behavior and the critical volume fractions.84 The differences to our salt-free samples might also be related to a more complex ion cloud than for classical PNIPAM-based microgels without rigid cores.58 A zeta potential of −25 mV was determined for the pure silica NP cores and it is possible that the surface charge of the cores impacts the ion cloud of the microgels.
3.5 Temperature-dependent phase diagrams
Fig. 7 shows temperature-dependent phase diagrams for samples in absence (a) and presence of salt (b). These diagrams were constructed from results of temperature-dependent absorbance spectroscopy using small increments in ρ that required a second batch of CS microgels (CS2). More information can be found in the Experimental section and in the ESI‡ (Fig. S14, S15 and Tables S14–S18). Absorbance spectra of the CS2 microgel dispersions recorded at 20 °C as an example are shown in Fig. S16 in the ESI‡ including results from different steps of temperature annealing. For temperatures where Bragg peaks were detected, we assigned a crystalline (solid) state. This phase region is colored in light orange in Fig. 7. In contrast, a fluid-like phase was assigned when Bragg peaks were missing/disappeared (light blue areas). The transition region is colored in green and was determined from the respective temperature onsets of melting/recrystallization from heating/cooling cycles. This procedure is in agreement with our recently published work.38 More information can also be found in the ESI.‡ Generally, the phase diagrams reflect the swelling curves of the CS microgels (see Fig. 2a). The crystalline regime is small at low values of ρ and extends over increasing temperature ranges with increasing ρ. The crystalline regime is shifted to higher values of ρ when salt (0.5 mM KCl) is added as already discussed in the context of Fig. 6d. In presence of salt, we also find an overcrowded or jammed phase85 at very high ρ extending to temperatures reaching the VPTT of the microgels. The solid black lines correspond to the evolution of the average volume fractions of 0.39 ± 0.07 at cKCl = 0 mM and 0.52 ± 0.03 at cKCl = 0.5 mM where the phase transitions were observed (see Fig. S17 in the ESI‡). Although the two batches of CS microgels used in this work have slightly different core and shell dimensions, we want to highlight, that the average values for ζtransition are nearly the same for the two batches. This highlights the reproducibility of the synthesis and also the reliability of the analysis by temperature-dependent absorbance spectroscopy. Slight variations between the phase behavior of the two batches when comparing individual samples are most likely attributed to variations in sample preparation rather than differences between the microgels. In Fig. 7a (absence of salt) the transition region (green) fluctuates significantly between samples of different concentrations and sometimes extends over a few °C. In contrast, in Fig. 7b (presence of salt), the transition region shows a smooth evolution with increasing ρ with much smaller temperature ranges. Importantly, in presence of salt the phase boundary between fluid and solid state and the calculated transition temperatures based on the average ζtransition (black line) follow each other closely.The presented phase diagrams set the ground for more detailed studies on phase transitions in dense packings of soft and deformable microgels with temperature-dependent small-angle scattering. It is also shown that electrostatic interactions can have a pronounced influence on the phase behavior, even in the case of weakly charged colloidal systems.
4 Conclusions
We used weakly charged CS microgels to study the phase behavior of soft colloids without and with salt. The addition of 0.5 mM KCl to dispersions of the microgels resulted in a significant reduction of the electrophoretic mobility along with very minor changes in the hydrodynamic dimensions. Importantly, the colloidal stability was maintained even at temperatures well above the VPTT. This allowed for a direct comparison of the phase behavior in presence/absence of salt over a broad range of concentrations and temperatures. Complementary small-angle neutron and X-ray scattering data were used to study the form factor of the microgels in the dilute state. Dense samples were studied by synchrotron-SAXS revealing crystalline samples with extraordinary long-range order at 20 °C for sufficiently high packing fractions. Given the large number of Bragg peaks for most samples, we could prove that the microgels crystallize into hcp structures independent of the presence/absence of salt. However, the addition of salt induced a shift of the phase boundary between the fluid and crystalline phases towards higher volume fractions. In agreement with recent literature, the osmotic deswelling of the microgels was not affected by the presence of salt.35,52,58 In the collapsed state, above the volume phase transition temperature, the same samples showed pronounced fluid-like structure factors. The screening of charges in the outer periphery of the microgels due to the addition of salt was found to have a direct impact on the structure factors. The experimental findings were supported by molecular dynamics computer simulations with a screened Coulomb (Yukawa) potential.In order to screen a large set of number concentrations and temperatures, we used temperature-dependent absorbance spectroscopy to follow the melting and recrystallization of the samples. In this way, we could determine transition temperatures and temperature-dependent phase diagrams directly comparing conditions without and with salt. When 0.5 mM KCl is present, the crystalline phase is shifted to higher number densities while the temperature ranges of the phase transition region become much smaller than in the salt-free case. Furthermore, the transition region matches better to the transition curve that was calculated based on average critical volume fractions.
To the best of our knowledge temperature-dependent phase diagrams of weakly charged microgels under conditions without and with salt have not yet been presented in literature. Our work sets the ground for future studies on phase transitions in dense systems of soft colloids, for example using temperature-dependent synchrotron-SAXS. Our results suggest that studies on the phase behavior of weakly charged microgels are ideally performed under conditions with salt, i.e., in presence of low concentrations of salt that do not hamper the colloidal stability above the VPTT. In this case, we believe it will be of particular interest to study samples at high concentrations where we propose the jammed state. Quenching of samples with temperature jumps of different magnitudes might allow phase transitions from fluid to jammed or even from crystalline to jammed states and vice versa.
Conflicts of interest
There are no conflicts of interest to declare.Data availability
All data supporting the findings of this study are presented in the article and ESI.‡ Additional data are available from the corresponding author upon reasonable request.Acknowledgements
The authors acknowledge the German Research Foundation (DFG) and the state of NRW for funding the cryo-TEM (INST 208/749-1 FUGG) and Marius Otten from Heinrich Heine University Düsseldorf for his assistance with the operation and image recording. The authors thank the Center for Structural Studies (CSS) that is funded by the DFG (grant numbers 417919780 and INST 208/761-1 FUGG) for access to the SAXS instrument. A. S. acknowledges financial support from the Knut and Alice Wallenberg Foundation (Wallenberg Academy Fellows). J. H. and M. A. acknowledge the DFG for financial support in the framework of the project HO 2231/26-1. The authors acknowledge Déborah Feller (Heinrich Heine University Düsseldorf) for her assistance with the operation of the static light scattering setup. T. L. Wigger (Heinrich Heine University Düsseldorf) performed the data reduction from 2D detector images to enable the Williamson–Hall analysis. The authors thank the Institut Laue-Langevin for allocation of SANS beamtime on D11 (DOI: https://doi.org/10.5291/ILL-DATA.9-11-2027). A. V. Petrunin, T. Höfken, and P. Mota-Santiago helped with the SAXS measurements. The SAXS measurements were performed on the CoSAXS beamline at the MAX IV laboratory (Lund, Sweden) under the proposal 20220526. The research conducted at MAX IV, a Swedish national user facility, is supported by the Swedish Research council under contract 2018-07152, the Swedish Governmental Agency for Innovation Systems under contract 2018-04969, and Formas under contract 2019-02496. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Unions Horizon 2020 research and innovation program under the SINE2020 project, grant agreement no 654000. Data of this work were discussed and parts of this paper have been written at the Kavli Institute for Theoretical Physics (KITP), Santa Barbara (California) during the “Nanoparticle Assemblies: A New Form of Matter with Classical Structure and Quantum Function” programme. This research was supported in part by the National Science Foundation under Grant No. NSF PHY-1748958.Notes and references
- F. Scheffold, Nat. Commun., 2020, 11, 4315 CrossRef CAS PubMed.
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Langmuir, 2019, 35, 6231–6255 CrossRef CAS PubMed.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33 CrossRef CAS PubMed.
- A. S. J. Iyer and L. A. Lyon, Angew. Chem., 2009, 121, 4632–4636 CrossRef.
- K. Roger and J. J. Crassous, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2105530118 CrossRef CAS PubMed.
- A. Scotti, S. Bochenek, M. Brugnoni, M.-A. Fernandez-Rodriguez, M. F. Schulte, J. Houston, A. P. Gelissen, I. I. Potemkin, L. Isa and W. Richtering, Nat. Commun., 2019, 10, 1418 CrossRef CAS PubMed.
- M. Antonietti, W. Bremser and M. Schmidt, Macromolecules, 1990, 23, 3796–3805 CrossRef CAS.
- B. Brugger, B. A. Rosen and W. Richtering, Langmuir, 2008, 24, 12202–12208 CrossRef CAS PubMed.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- A. Pich, A. Tessier, V. Boyko, Y. Lu and H.-J. P. Adler, Macromolecules, 2006, 39, 7701–7707 CrossRef CAS.
- T. Hoare and R. Pelton, Langmuir, 2004, 20, 2123–2133 CrossRef CAS PubMed.
- M. Karg, I. Pastoriza-Santos, B. Rodriguez-Gonzalez, R. Von Klitzing, S. Wellert and T. Hellweg, Langmuir, 2008, 24, 6300–6306 CrossRef CAS PubMed.
- B. Wedel, Y. Hertle, O. Wrede, J. Bookhold and T. Hellweg, Polymers, 2016, 8, 162 CrossRef PubMed.
- R. H. Pelton and P. Chibante, Colloids Surf., 1986, 20, 247–256 CrossRef CAS.
- M. Heskins and J. E. Guillet, J. Macromol. Sci., Chem., 1968, 2, 1441–1455 CAS.
- A. Halperin, M. Kröger and F. M. Winnik, Angew. Chem., Int. Ed., 2015, 54, 15342–15367 CrossRef CAS PubMed.
- X. Shaulli, R. Rivas-Barbosa, M. J. Bergman, C. Zhang, N. Gnan, F. Scheffold and E. Zaccarelli, ACS Nano, 2023, 17, 2067–2078 CrossRef CAS PubMed.
- R. Pelton, J. Colloid Interface Sci., 2010, 348, 673–674 CrossRef CAS PubMed.
- C. G. Lopez and W. Richtering, Soft Matter, 2017, 13, 8271–8280 RSC.
- S. Marín-Aguilar and E. Zaccarelli, Predicting structure and swelling of microgels with different crosslinker concentrations combining machine-learning with numerical simulations, arXiv, 2025, preprint, arXiv:2502.07482 DOI:10.48550/arXiv.2502.07482.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed.
- E. Ponomareva, B. Tadgell, M. Hildebrandt, M. Krüsmann, S. Prévost, P. Mulvaney and M. Karg, Soft Matter, 2022, 18, 807–825 RSC.
- F. Scheffold, Soft Matter, 2024, 20, 8181–8184 RSC.
- L. Scheidegger, M. A. Fernandez-Rodriguez, K. Geisel, M. Zanini, R. Elnathan, W. Richtering and L. Isa, Phys. Chem. Chem. Phys., 2017, 19, 8671–8680 RSC.
- M. Rey, M. A. Fernandez-Rodriguez, M. Karg, L. Isa and N. Vogel, Acc. Chem. Res., 2020, 53, 414–424 CrossRef CAS PubMed.
- D. Feller and M. Karg, Soft Matter, 2022, 18, 6301–6312 RSC.
- K. Kuk, V. Abgarjan, L. Gregel, Y. Zhou, V. C. Fadanelli, I. Buttinoni and M. Karg, Soft Matter, 2023, 19, 175–188 RSC.
- Y. Zhou, J. J. Crassous and M. Karg, Langmuir, 2025, 41, 9274–9287 CrossRef CAS PubMed.
- A. Rubio-Andrés, D. Bastos-González and M. A. Fernandez-Rodriguez, J. Colloid Interface Sci., 2025, 688, 328–340 CrossRef PubMed.
- M. Karg, T. Hellweg and P. Mulvaney, Adv. Funct. Mater., 2011, 21, 4668–4676 CrossRef CAS.
- T. Hellweg, C. Dewhurst, E. Brückner, K. Kratz and W. Eimer, Colloid Polym. Sci., 2000, 278, 972–978 CrossRef CAS.
- L. A. Lyon, J. D. Debord, S. B. Debord, C. D. Jones, J. G. McGrath and M. J. Serpe, J. Phys. Chem. B, 2004, 108(50), 19099–19108 CrossRef CAS.
- T. Hellweg, C. D. Dewhurst, W. Eimer and K. Kratz, Langmuir, 2004, 20, 4330–4335 CrossRef CAS PubMed.
- M. Pelaez-Fernandez, A. Souslov, L. Lyon, P. Goldbart and A. Fernandez-Nieves, Phys. Rev. Lett., 2015, 114, 098303 CrossRef CAS PubMed.
- A. Scotti, U. Gasser, E. S. Herman, M. Pelaez-Fernandez, J. Han, A. Menzel, L. A. Lyon and A. Fernández-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5576–5581 CrossRef CAS PubMed.
- A. Scotti, U. Gasser, E. S. Herman, J. Han, A. Menzel, L. A. Lyon and A. Fernandez-Nieves, Phys. Rev. E, 2017, 96, 032609 CrossRef CAS PubMed.
- A. Scotti, A. R. Denton, M. Brugnoni, R. Schweins and W. Richtering, Phys. Rev. E, 2021, 103, 022612 CrossRef CAS PubMed.
- M. Hildebrandt, D. Pham Thuy, J. Kippenberger, T. L. Wigger, J. E. Houston, A. Scotti and M. Karg, Soft Matter, 2023, 19, 7122–7135 RSC.
- M. P. M. Schelling and J.-M. Meijer, Phys. Rev. E, 2024, 109, l062601 CrossRef CAS PubMed.
- P. N. Pusey and W. Van Megen, Nature, 1986, 320, 340–342 CrossRef CAS.
- D. Lapkin, N. Mukharamova, D. Assalauova, S. Dubinina, J. Stellhorn, F. Westermeier, S. Lazarev, M. Sprung, M. Karg and I. A. Vartanyants, et al., Soft Matter, 2022, 18, 1591–1602 RSC.
- D. Gottwald, C. N. Likos, G. Kahl and H. Löwen, Phys. Rev. Lett., 2004, 92, 068301 CrossRef CAS PubMed.
- J. Wu, B. Zhou and Z. Hu, Phys. Rev. Lett., 2003, 90, 048304 CrossRef PubMed.
- S. Nöjd, P. S. Mohanty, P. Bagheri, A. Yethiraj and P. Schurtenberger, Soft Matter, 2013, 9, 9199–9207 RSC.
- J. Ruiz-Franco, R. Rivas-Barbosa, M. A. Lara-Peña, J. R. Villanueva-Valencia, A. Licea-Claverie, E. Zaccarelli and M. Laurati, Soft Matter, 2023, 19, 3614–3628 RSC.
- U. Gasser and A. Fernandez-Nieves, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 81, 052401 CrossRef CAS PubMed.
- M. Hildebrandt, S. Lazarev, J. Pérez, I. A. Vartanyants, J.-M. Meijer and M. Karg, Macromolecules, 2022, 55, 2959–2969 CrossRef CAS.
- T. Eckert and W. Richtering, J. Chem. Phys., 2008, 129, 124902 CrossRef PubMed.
- G. M. Conley, P. Aebischer, S. Nöjd, P. Schurtenberger and F. Scheffold, Sci. Adv., 2017, 3, e1700969 CrossRef PubMed.
- A. Scotti, A. R. Denton, M. Brugnoni, J. E. Houston, R. Schweins, I. I. Potemkin and W. Richtering, Macromolecules, 2019, 52, 3995–4007 CrossRef CAS.
- T. Höfken, C. Strauch, S. Schneider and A. Scotti, Nano Lett., 2022, 22, 2412–2418 CrossRef PubMed.
- U. Gasser, A. Scotti and A. Fernandez-Nieves, Phys. Rev. E, 2019, 99, 042602 CrossRef CAS PubMed.
- U. Gasser, J. S. Hyatt, J.-J. Lietor-Santos, E. S. Herman, L. A. Lyon and A. Fernandez-Nieves, J. Chem. Phys., 2014, 141, 034901 CrossRef CAS PubMed.
- S. Nöjd, P. Holmqvist, N. Boon, M. Obiols-Rabasa, P. S. Mohanty, R. Schweins and P. Schurtenberger, Soft Matter, 2018, 14, 4150–4159 RSC.
- A. Scotti, Soft Matter, 2021, 17, 5548–5559 RSC.
- P. S. Mohanty, S. Nöjd, K. van Gruijthuijsen, J. J. Crassous, M. Obiols-Rabasa, R. Schweins, A. Stradner and P. Schurtenberger, Sci. Rep., 2017, 7, 1487 CrossRef PubMed.
- A. Rauh, N. Carl, R. Schweins and M. Karg, Langmuir, 2018, 34, 854–867 CrossRef CAS PubMed.
- B. Zhou, U. Gasser and A. Fernandez-Nieves, Nat. Commun., 2023, 14, 3827 CrossRef CAS PubMed.
- Y. Utashiro, M. Takiguchi and M. Satoh, Colloid Polym. Sci., 2017, 295, 45–52 CrossRef CAS.
- M. J. Bergman, J. S. Pedersen, P. Schurtenberger and N. Boon, Soft Matter, 2020, 16, 2786–2794 RSC.
- A. V. Petrunin, M. M. Schmidt, R. Schweins, J. E. Houston and A. Scotti, Langmuir, 2023, 39, 7530–7538 CrossRef CAS PubMed.
- L. K. Månsson, J. N. Immink, A. M. Mihut, P. Schurtenberger and J. J. Crassous, Faraday Discuss., 2015, 181, 49–69 RSC.
- B. Derjaguin and L. Landau, Prog. Surf. Sci., 1993, 43, 30–59 CrossRef.
- E. J. W. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids. The Interaction of Sol Particles Having an Electric Double Layer, Elsevier, Amsterdam, 1948 Search PubMed.
- E. J. Meijer and F. El Azhar, J. Chem. Phys., 1997, 106, 4678–4683 CrossRef CAS.
- F. El Azhar, M. Baus, J.-P. Ryckaert and E. J. Meijer, J. Chem. Phys., 2000, 112, 5121–5126 CrossRef CAS.
- A.-P. Hynninen and M. Dijkstra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021407 CrossRef PubMed.
- M. Eshraghi and J. Horbach, Soft Matter, 2018, 14, 4141–4149 RSC.
- C. D. Dewhurst, J. Appl. Crystallogr., 2023, 56, 1595–1609 CrossRef CAS PubMed.
- SasView, https://www.sasview.org/.
- J. Kohlbrecher and I. Breßler, Appl. Crystallogr., 2022, 55, 1677–1688 CrossRef PubMed.
- B. V. Derjaguin, Acta Phys. Chim. URSS, 1941, 14, 633 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- K. Kratz, T. Hellweg and W. Eimer, Colloids Surf., A, 2000, 170, 137–149 CrossRef CAS.
- E. Daly and B. R. Saunders, Phys. Chem. Chem. Phys., 2000, 2, 3187–3193 RSC.
- M. Shibayama, T. Tanaka and C. C. Han, J. Chem. Phys., 1992, 97, 6829–6841 CrossRef CAS.
- H. Senff and W. Richtering, Colloid Polym. Sci., 2000, 278, 830–840 CrossRef CAS.
- M. Cors, L. Wiehemeier, Y. Hertle, A. Feoktystov, F. Cousin, T. Hellweg and J. Oberdisse, Langmuir, 2018, 34, 15403–15415 CrossRef CAS PubMed.
- E. A. Sulyanova, A. Shabalin, A. V. Zozulya, J.-M. Meijer, D. Dzhigaev, O. Gorobtsov, R. P. Kurta, S. Lazarev, U. Lorenz, A. Singer, O. Yefanov, I. Zaluzhnyy, I. Besedin, M. Sprung, A. V. Petukhov and I. A. Vartanyantsothers, Langmuir, 2015, 31, 5274–5283 CrossRef CAS PubMed.
- B. Tadgell, E. Ponomareva, M. Karg and P. Mulvaney, J. Phys. Chem. C, 2022, 126, 15336–15347 CrossRef CAS.
- H. Senff and W. Richtering, J. Chem. Phys., 1999, 111, 1705–1711 CrossRef CAS.
- A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, Chem. Rev., 2022, 122, 11675–11700 CrossRef CAS PubMed.
- B. Sierra-Martin and A. Fernandez-Nieves, Soft Matter, 2012, 8, 4141–4150 RSC.
Footnotes |
| † This publication is in honor and remembrance of our friend and colleague Stefan U. Egelhaaf. |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00464k |
| § Present address: Institute of Chemistry, Physical Chemistry of Functional Polymers, Martin Luther University Halle-Wittenberg, 06120 Halle (Saale), Germany. E-mail: matthias.karg@chemie.uni-halle.de |
| This journal is © The Royal Society of Chemistry 2025 |