Open Access Article
Open Access ArticleJanssen effect in submerged granular columns
M. Aguilar-González a,
D. Maza
a,
D. Maza *b and
F. Pacheco-Vázquez
*b and
F. Pacheco-Vázquez *a
*a
aInstituto de Física, Benemérita Universidad Autónoma de Puebla, A. P. J-48, Puebla 72570, Mexico. E-mail: fpacheco.at.ifuap.buap.mx
bDepartamento de Física y Matemática Aplicada, Facultad de Ciencias, Universidad de Navarra, 31080 Pamplona, Spain
First published on 10th July 2025
Abstract
We experimentally study the effect of an interstitial liquid on pressure saturation in a confined granular column, specifically regarding the Janssen effect. First, we analyze the case of dry grains in a cylindrical container as a reference system. Then, the experiments are carried out in the same container filled with water, considering two scenarios: (i) when the grains are denser than water and sediment under gravity, and (ii) when the grains are less dense than water and rise to the surface due to buoyancy. In the first case, we observe a Janssen-like effect that depends on the particle density ratio to the liquid density. Stress saturation is evident when very dense particles are poured; however, this saturation nearly disappears for grains with a density similar to that of water. We describe these experimental observations using a Janssen-like approach that accounts for the hydrostatic stress introduced by the surrounding fluid. In the second scenario, a buoyancy-driven Janssen effect is found when the pressure is measured at the top of the column, and the model successfully accounts for this phenomenon. Importantly, these results demonstrate the significance of grain-to-grain stress transmission, even for granular columns suspended in a fluid.
1 Introduction
The Janssen effect is a distinctive feature of granular matter: when grains are deposited in a container, the network of contacts between the particles results in force chains that redistribute the stress of the granular column towards the sidewalls, causing the pressure at the bottom of the container to saturate as the level of the column increases.1–4 This ability of granular materials to self-distribute stresses via force chains differentiates them from conventional fluids and solids,5,6 making their study relevant in various fields of science and engineering. It becomes imperative in the industrial sector, where a large variety of raw materials are typically stored as grains in silos7 (only in 2024, the grain silo and storage market had a value of USD 1.7 billion, and it is expected to reach USD $2.3 billion in 2029, attributed to population growth, climate change concerns, food security, and other geopolitical factors8).Since Janssen's pioneering study of the eponymous phenomenon using seeds and dry grains,1 a continuum approach was used to derive the classical expression for the saturation of vertical stress (pressure) σz at a depth z, given by:
| σz = ρmgλ(1 − e−z/λ), | (1) |
All the former systems have in common that the interstitial fluid is air, which is negligible in the force distribution controlled by local dry contact between particles. Under this condition, we talk about dry granular systems. However, how is the Janssen effect modified when the grains are poured into a liquid? In an immersed granular material, additional factors such as buoyancy and hydrodynamic interactions come into play, and to the best of our knowledge, such a scenario has not been addressed. Indeed, the influence of hydrostatic pressure and granular redistribution has been considered in pressurized granular flows discharged from silos.32–35 Moreover, an analog effect at the colloidal scale was recently used to explain the solidification front of freezing suspensions.36 However, the Janssen effect was not quantified in such studies. Our research aims to examine the effect of the interstitial liquid (of density ρl) on the particle-contact-stress distribution and its influence on the pressure saturation. To that end, we implemented an experimental procedure to obtain precise and accurate measurements of the vertical pressure as the granular column forms in different scenarios, depending on the particle/liquid densities ratio, ρ/ρl. These scenarios range from the case where the grains quickly settle to the bottom of the container (case 1: ρ/ρl ≫ 1), to the case where the particles rise to the surface of the liquid (case 2: ρ/ρl ≪ 1). The results are accompanied by a model that can describe the different scenarios. For ρ/ρl > 1, the pressure at the bottom of the container results in a Janssen-like saturation plus the hydrostatic (linear) pressure of the liquid displaced by the sedimented particles. The saturation is rendered negligible under conditions of density matching. For ρ/ρl ≪ 1, the particles rise to the surface and agglomerate, producing force chains reverted in the vertical component. In the latter case, the buoyancy competing against gravity is the force redirected towards the sidewall. Consequently, a bouyancy-driven Janssen effect is quantified at the top of the granular column. By addressing these different situations, the present study contributes to a deeper understanding of the Janssen effect under submerged conditions. It expands its applicability to a broader range of practical and industrial contexts involving fluid-saturated granular materials, such as grain-washing processes, sediment transport, offshore drilling, and fracking.37–40
2 Case I: sedimented column (ρ/ρl > 1)
2.1 Experimental setup
A sketch of the apparatus used to characterize the Janssen effect for sedimented grains is presented in Fig. 1(a), and an actual photograph of the experimental system is shown in Fig. 1(b). It consists of two cylindrical concentric tubes made in transparent acrylic; the outer tube of internal diameter D = 57.3 mm and length l = 350 mm has a hermetic bottom and serves as a water reservoir; the inner tube of height h = 450 mm is used as an unbottomed silo to contain the granular column, with inner diameter Di = 44.0 mm and external diameter De = 50.3 mm. Thus, there is a 3.5 mm gap between the side walls of the concentric tubes. The internal tube is fixed vertically by an external support, while the base of the outer tube is screwed to a digital force sensor (Mark-10 DFG-355) with a maximum capacity of 25.0 N and a resolution of 0.2 N. The external tube-sensor system is mounted on a 1 m C-Beam linear actuator that can freely raise and lower the external container at a constant speed. This allows us to fill the tube with 600 ml of deionized water, then raise the system to leave an initial separation of 5.0 mm below the base of the inner fixed tube. Then, the force sensor is set to zero with the recipient exclusively containing water. At this step of the protocol, we ensured that the tubes do not touch by the absence of fluctuations in the force sensor signal when tapping the inner tube. After that, a mass M = 650 g of glass beads (diameter d = 300–500 μm, ρ = 2.5 g cm−3) is poured at a constant flow rate Φ ∼ 0.89 g s−1 from a funnel at the top of the inner tube. As the grains accumulate, the apparent mass, Mapp, measured at the bottom of the column, is registered with the force sensor as a function of time at a frequency of 10 Hz until all the granular material is discharged. The particle size and the flow rate were chosen to avoid air bubble trapping when the granular jet crosses the air water interface.41We conducted these experiments under two different water level conditions: (i) variable liquid level condition (VLL), where the water level was allowed to increase freely due to the volume displaced by the accumulated grains, and (ii) Constant liquid level condition (CLL) where the water level was kept constant by discharging the liquid displaced by the grains using a hose connected to an orifice in the lateral wall of the external container. The hose can be blocked or left open depending on the experimental configuration. The CLL condition is equivalent to performing the experiment with the setup submerged in a very large tank, where the water level would remain almost unperturbed during the filling process. Our setup allows the reproduction of such a situation without submerging the non-waterproof force sensor. Moreover, the setup feasibility was tested by filling the container without water to characterize the well-known pressure saturation in the case of dry granular systems. In what follows, primed symbols are used to differentiate the submerged case from the dry case.
2.2 Results
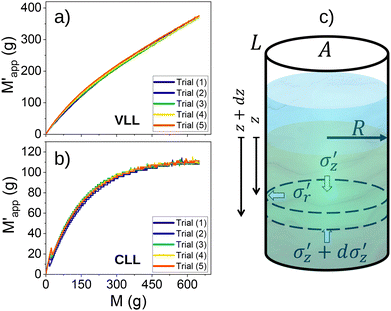
In the VLL experiments, the water level increases by approximately 11.5 cm when 650 g of glass beads are added to the liquid. Interestingly, we also noticed that the final height of the submerged granular column was H′ = 2.75 ± 0.3 cm, approximately 1.5 cm higher than the dry column formed with the same amount of grains, where H = 26.0 ± 0.3 cm, indicating a change in packing fraction η. Indeed, for submerged columns, we statistically estimated η′ = 0.62 ± 0.01 (in both VLL and CLL scenarios) while for the dry case η = 0.66 ± 0.01. This can be explained considering that the particles experience a larger viscous drag as they fall through the liquid, which decreases the collisional velocity of the particles and leads to a more porous granular column.For the VLL case, the resulting submerged mass 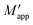 vs. the poured mass M is shown in Fig. 2(a) for five independent realizations. The plot shows a slight tendency to saturation at first, but then the data increases nearly linearly, which may be attributed to the combination of the pressure saturation due to the grains plus the linear contribution of the hydrostatic pressure. For the CLL state, see Fig. 2(b), Janssen-like saturation was observed; since the hydrostatic pressure remains constant, the pressure redistribution towards the walls must be the origin of the observed saturation. The reproducibility of the five experiments allowed by our experimental design is also remarkable.
vs. the poured mass M is shown in Fig. 2(a) for five independent realizations. The plot shows a slight tendency to saturation at first, but then the data increases nearly linearly, which may be attributed to the combination of the pressure saturation due to the grains plus the linear contribution of the hydrostatic pressure. For the CLL state, see Fig. 2(b), Janssen-like saturation was observed; since the hydrostatic pressure remains constant, the pressure redistribution towards the walls must be the origin of the observed saturation. The reproducibility of the five experiments allowed by our experimental design is also remarkable.
2.3 Continuum model for submerged granular columns
Based on the above observations, let us consider that the total vertical stress delivered by the liquid–grain mixture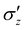 can be expressed as:
can be expressed as:
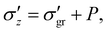 | (2) |
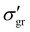 , regarding P, the hydrostatic (isotropic) pressure due to the liquid column.
, regarding P, the hydrostatic (isotropic) pressure due to the liquid column.
The differential equation that describes the conventional Janssen saturation for a dry medium confined in a cylindrical container of radius R reads as follows:4,42
 | (3) |
In order to describe the submerged case, let us consider an infinitesimal cylindrical slice of thickness dz and radius R of a mixture of particles immersed in water in a continuum medium approach (see Fig. 2(c)). In equilibrium conditions, the sum of the forces acting on the z-axis can be expressed as follows:
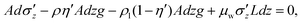 | (4) |
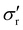 is the horizontal stress acting normal to the sidewall. In the left-hand side of eqn (4), the first term is the force due to the pressure difference above and below the slice. The second one is the weight of the granular medium within the slice, the third term represents the weight of the interstitial fluid, and the last term is the friction with the cylindrical wall of the slice of area Ldz, and perimeter L = 2πR. It is important to note that, based on the experimental results from rheological tests43 and studies on discharging submerged silos,44 the presence of the interstitial water does not alter significantly the effective friction coefficient μw between the submerged grains and the lateral wall. Thus, we can assume μw constant, but we must consider that the surrounding liquid could influence the stress redistribution factor κ′. For the dry case, Janssen's assumption states that σr is proportional to σz through the constant κ. In the submerged case, both the water and the grains exert a horizontal pressure on the walls; nevertheless, only the horizontal pressure exerted by the grains contributes to the friction, since the water exerts a net force equal to zero on the grains in the horizontal direction. Consequently, from eqn (2),
is the horizontal stress acting normal to the sidewall. In the left-hand side of eqn (4), the first term is the force due to the pressure difference above and below the slice. The second one is the weight of the granular medium within the slice, the third term represents the weight of the interstitial fluid, and the last term is the friction with the cylindrical wall of the slice of area Ldz, and perimeter L = 2πR. It is important to note that, based on the experimental results from rheological tests43 and studies on discharging submerged silos,44 the presence of the interstitial water does not alter significantly the effective friction coefficient μw between the submerged grains and the lateral wall. Thus, we can assume μw constant, but we must consider that the surrounding liquid could influence the stress redistribution factor κ′. For the dry case, Janssen's assumption states that σr is proportional to σz through the constant κ. In the submerged case, both the water and the grains exert a horizontal pressure on the walls; nevertheless, only the horizontal pressure exerted by the grains contributes to the friction, since the water exerts a net force equal to zero on the grains in the horizontal direction. Consequently, from eqn (2),  for the mixture (instead of
for the mixture (instead of  ). By substituting this assumption in eqn (4), the pressure in the submerged case can be integrated from:
). By substituting this assumption in eqn (4), the pressure in the submerged case can be integrated from:
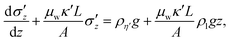 | (5) |
 . In the absence of liquid (ρl = 0), this expression reduces to the conventional Janssen model with η′ = η. Eqn (5) is a first-order non-homogeneous linear differential equation with solution:
. In the absence of liquid (ρl = 0), this expression reduces to the conventional Janssen model with η′ = η. Eqn (5) is a first-order non-homogeneous linear differential equation with solution:
 | (6) |
It is important to note that this equation represents the pressure at a depth z due to a static column of a homogeneous mixture of water and grains. In the actual experiment, the level of the granular column is different from the water level; thus, we must differentiate between the variable z appearing in the first and second terms of eqn (6); in the first term, z corresponds to the level of the column of grains submerged in water, while in the second term, z corresponds to the level of the water column. The above is valid because, in our VLL experiments, we initially had a container partially filled with water at a certain level. However, the initial pressure due to water was set to zero. If Δh represents the difference in water level before and after adding the grains, the equation describing the vertical stress evolution can be written in terms of a characteristic saturation length 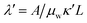 as:
as:
 | (7) |
Note the Janssen-like dependence of the first term, and that the last term represents the hydrostatic pressure due to the liquid displaced by the immersed grains. It should also be noted from eqn (6) that if the density of the particles is identical to that of water, the pressure contribution resulting from the grains is annulled and only the hydrostatic pressure would be measured.
A more convenient form to express eqn (7) is parameterizing the pressure with the apparent mass 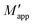 that is the data detected by the force sensor at the base of the system, and the height of the column with the mass added to the container M.29 This can be done by multiplying eqn (7) by A/g. After rearranging terms and denoting the liquid-to-grain density ratio as α = ρl/ρ, one obtains:
that is the data detected by the force sensor at the base of the system, and the height of the column with the mass added to the container M.29 This can be done by multiplying eqn (7) by A/g. After rearranging terms and denoting the liquid-to-grain density ratio as α = ρl/ρ, one obtains:
 | (8) |
Accordingly, for the dry case, eqn (1) can be written as:
| Mapp = M∞(1 − e−M/M∞), | (9) |
 and M∞ = λAηρ are the predicted asymptotic values of the apparent mass in each case. In the VLL case, it was confirmed that Δh measured at the end of the process coincided with the value expected from the volume displaced by the grains, confirming that there is no air entrainment durign the process. For the CLL condition, Δh = 0 in eqn (7). This condition implies that, in terms of mass, we are removing a quantity of liquid mass equal to αM from the container when we add M grams of grains. It is important to note that the VLL and CLL regimes are interconnected due to the assumption of linear stress superposition, as outlined in eqn (2). In the next section, we will experimentally verify the validity of this assumption.
and M∞ = λAηρ are the predicted asymptotic values of the apparent mass in each case. In the VLL case, it was confirmed that Δh measured at the end of the process coincided with the value expected from the volume displaced by the grains, confirming that there is no air entrainment durign the process. For the CLL condition, Δh = 0 in eqn (7). This condition implies that, in terms of mass, we are removing a quantity of liquid mass equal to αM from the container when we add M grams of grains. It is important to note that the VLL and CLL regimes are interconnected due to the assumption of linear stress superposition, as outlined in eqn (2). In the next section, we will experimentally verify the validity of this assumption.
2.4 Analysis: experiments vs. model
As a reference state, the Janssen effect was measured for the dry case using the same experimental apparatus as Fig. 1 but without liquid. The results are shown in Fig. 3(a). Remarkably, we obtained very reproducible results against expectations based on previous studies using dry particles.20 The complete set of data was fitted using eqn (9), yielding a saturation value of M∞ = 109 ± 1 g, as indicated by the horizontal black dashed line. | ||
Fig. 3 Apparent mass 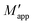 measured at the bottom of the container as a function of the added mass M for different scenarios: (a) dry case, (b) submerged case with a variable liquid level, and (c) submerged case with a constant liquid level and, variable level subtracted the displaced liquid mass, αM. The data represent the average of five independent trials, and the error bars indicate their standard deviation. The continuous lines illustrate the best fit according to eqn (8), and the horizontal dashed lines indicate the saturation values in each case. In panel (d), it is compared the normalized mass evolution (M/M∞) for both dry and submerged beads. It is important to note that the evolution of submerged particles occurs more slowly compared to that of the dry case. measured at the bottom of the container as a function of the added mass M for different scenarios: (a) dry case, (b) submerged case with a variable liquid level, and (c) submerged case with a constant liquid level and, variable level subtracted the displaced liquid mass, αM. The data represent the average of five independent trials, and the error bars indicate their standard deviation. The continuous lines illustrate the best fit according to eqn (8), and the horizontal dashed lines indicate the saturation values in each case. In panel (d), it is compared the normalized mass evolution (M/M∞) for both dry and submerged beads. It is important to note that the evolution of submerged particles occurs more slowly compared to that of the dry case. | ||
Let us now analyze the submerged cases. Fig. 3(b) and (c) show the averages of five independent experimental realizations (open symbols) of  vs. M′ previously depicted in Fig. 2(a) and (b), for the columns in the VLL and CLL states, respectively. Solid lines represent the fitting curves using eqn (8) with α = 0.39 for glass beads submerged in water, and
vs. M′ previously depicted in Fig. 2(a) and (b), for the columns in the VLL and CLL states, respectively. Solid lines represent the fitting curves using eqn (8) with α = 0.39 for glass beads submerged in water, and  as the only fitting parameter. We obtained an excellent fit of the experimental data for the VLL case (Fig. 3(b)) with
as the only fitting parameter. We obtained an excellent fit of the experimental data for the VLL case (Fig. 3(b)) with  . For the CLL condition, the linear term must be equal to zero, and then the data is fitted in Fig. 3(c), obtaining
. For the CLL condition, the linear term must be equal to zero, and then the data is fitted in Fig. 3(c), obtaining  , practically the same value as the one received in the VLL scenario. Both curves demonstrate that, indeed, for the VLL, we can separate the total pressure into two contributions: a granular-Janssen-like saturation and a hydrostatic component, as discussed in our model. Accordingly, subtracting the hydrostatic contribution, αM, from the VLL experimental data in Fig. 3(b) yields a result that is very similar to the CLL data in Fig. 3(c), supporting the validity of linear additivity introduced in eqn (2).
, practically the same value as the one received in the VLL scenario. Both curves demonstrate that, indeed, for the VLL, we can separate the total pressure into two contributions: a granular-Janssen-like saturation and a hydrostatic component, as discussed in our model. Accordingly, subtracting the hydrostatic contribution, αM, from the VLL experimental data in Fig. 3(b) yields a result that is very similar to the CLL data in Fig. 3(c), supporting the validity of linear additivity introduced in eqn (2).
More importantly, the comparison between eqn (8) and (9), indicates that submerged stress propagation cannot be treated as equivalent to a dry system with an “effective” grain mass reduced by buoyancy. The appearance of the factor (1 − α) in the exponential term results in a softer evolution of the submerged Janssen curve compared to the dry case, as illustrated in Fig. 3(d). We previously assumed that μw remains unchanged for submerged grains.43,44 Therefore, the source of the discrepancy lies in the influence of the interstitial fluid on the granular structure and its stress propagation through the lateral wall, which is accounted for by the κ factor. The interstitial fluid affects the spatial scale λ′, where the vertical stress must saturate. From the values of M∞, and  , we have λ = 4.3 ± 0.1 cm, and λ′ = 8.4 ± 0.1 cm; thus, the saturation length of the submerged material is approximately twice that of the dry case which as is usual is around 2 times the silo diameter. On the other hand, since
, we have λ = 4.3 ± 0.1 cm, and λ′ = 8.4 ± 0.1 cm; thus, the saturation length of the submerged material is approximately twice that of the dry case which as is usual is around 2 times the silo diameter. On the other hand, since  taking the corresponding values of packing fraction and mass saturation, we estimate κ′ ∼ 0.52κ. Considering that κ = D/(4μwλ), and assuming μw ∼ 0.5 for glass particles with acrylic,25 one estimates κ ∼ 0.5 and κ′ ∼ 0.26. This result shows that the proportion of stress redistributed towards the walls in the granular material is almost half that of the dry case due to the presence of interstitial liquid.
taking the corresponding values of packing fraction and mass saturation, we estimate κ′ ∼ 0.52κ. Considering that κ = D/(4μwλ), and assuming μw ∼ 0.5 for glass particles with acrylic,25 one estimates κ ∼ 0.5 and κ′ ∼ 0.26. This result shows that the proportion of stress redistributed towards the walls in the granular material is almost half that of the dry case due to the presence of interstitial liquid.
2.5 Effect of the particle-to-liquid density ratio
Eqn (8) indicates that the submerged Janssen effect is markedly affected by the liquid-to-grain density ratio α. Let us explore the behavior predicted by the model for the CLL and VLL scenarios. In Fig. 4(a) we plotted eqn (8) for different values of α considering the CLL case, in which the last term of the equation is zero. The softer saturation curves for the submerged cases with respect to the dry case (α = 0) indicate that, as the value of α increases, taller columns are required to reach saturation. The limit case α = 1 corresponds to particles suspended in water. As correctly predicted by the model, must be zero because the volume of liquid displaced by the particles is evacuated, and it is equivalent in mass to the added mass of material. On the other hand, Fig. 4(b) shows the results of eqn (8) for the VLL scenario. For particle density close to that of water (α ∼ 1), the first term of the equation becomes nearly zero and a linear dependence is predicted, with
must be zero because the volume of liquid displaced by the particles is evacuated, and it is equivalent in mass to the added mass of material. On the other hand, Fig. 4(b) shows the results of eqn (8) for the VLL scenario. For particle density close to that of water (α ∼ 1), the first term of the equation becomes nearly zero and a linear dependence is predicted, with  corresponding only to the hydrostatic pressure (red line). The Janssen-like term gets more importance as α decreases (blue and yellow lines). Finally, for densities markedly exceeding that of water (α ≪ 1), the saturation effect becomes notorious (green line).
corresponding only to the hydrostatic pressure (red line). The Janssen-like term gets more importance as α decreases (blue and yellow lines). Finally, for densities markedly exceeding that of water (α ≪ 1), the saturation effect becomes notorious (green line).
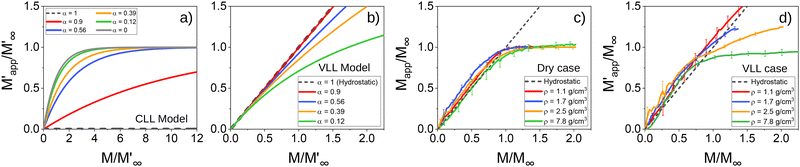 | ||
Fig. 4 (a) and (b) Model predictions using eqn (8) for the Janssen effect in submerged columns with grains of different densities, for (a) CLL and (b) VLL conditions. (c) and (d) Experimental determination of the Janssen effect for different material densities for (c) dry case and (d) submerged case (VLL). The hydrostatic dependence (dashed line) is included in each plot for reference. The plots are normalized with the saturation value 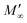 for the model prediction and M∞ for the experiments. for the model prediction and M∞ for the experiments. | ||
To experimentally verify the predictions of the model, we measured the apparent mass of submerged granular columns for particles of four different densities. Note in Fig. 4(a) that a wide range of  is required to observe the saturation in CLL conditions, which corresponds to extremely high columns, not accessible with our experimental setup. For that reason, the experiments were performed using the VLL scenario. Moreover, let us recall that the model is based on a continuum medium approach, and one can expect a better quantitative agreement with experiments using particles considerably smaller than the container diameter (as those used in Section 2). However, limited by our available laboratory supplies and the force sensor capacity, we used particles of millimetric size: plastic beads of two densities (ρ = 1.1 g cm−3 and ρ = 1.7 g cm−3, d = 6.0 mm), glass beads (ρ = 2.5 g cm−3, d = 4 mm), and steel spheres (ρ = 7.8 g cm−3, d = 3 mm).45 We poured the required mass to generate dry and submerged granular columns of approximately 30 cm high.
is required to observe the saturation in CLL conditions, which corresponds to extremely high columns, not accessible with our experimental setup. For that reason, the experiments were performed using the VLL scenario. Moreover, let us recall that the model is based on a continuum medium approach, and one can expect a better quantitative agreement with experiments using particles considerably smaller than the container diameter (as those used in Section 2). However, limited by our available laboratory supplies and the force sensor capacity, we used particles of millimetric size: plastic beads of two densities (ρ = 1.1 g cm−3 and ρ = 1.7 g cm−3, d = 6.0 mm), glass beads (ρ = 2.5 g cm−3, d = 4 mm), and steel spheres (ρ = 7.8 g cm−3, d = 3 mm).45 We poured the required mass to generate dry and submerged granular columns of approximately 30 cm high.
Fig. 4(c) shows the apparent mass for the case of dry particles as a function of the added mass depending on the density of the material. The mass saturation was evident in each case. The data was normalized by the observed saturation value M∞ of each material, allowing for the comparison of the degree of saturation of the curves despite the different material specifics. The fact that the particles were relatively large for the dimensions of the container (Di/dg ∼ 7–14) is reflected in a more abrupt saturation. Such ratio also generates values of Mapp > M in a particular range (data above the dashed line of slope 1) which has been reported as a reverse Janssen effect for dry particles deposited in narrow silos.26–28 Fig. 4(d) shows the corresponding results for the submerged particles (using VLL conditions). We cannot specifically know the asymptotic values  by fitting the experimental data because, for ρg ∼ ρl, it would require considerably higher columns for a reasonable estimate. Moreover, fitting would be a poor approach due to the sudden saturation caused by the particle size, which the continuum model does not capture. Nevertheless, based on the previous section, we can roughly assume that
by fitting the experimental data because, for ρg ∼ ρl, it would require considerably higher columns for a reasonable estimate. Moreover, fitting would be a poor approach due to the sudden saturation caused by the particle size, which the continuum model does not capture. Nevertheless, based on the previous section, we can roughly assume that  , and then normalize our experimental data for the submerged case with the values of M∞ obtained from the dry case. The normalized curves are shown in Fig. 4(d). One can notice a dominant hydrostatic effect when the density of the particles is close to the density of water. As we increase ρ, the slope of the linear region decreases, and a Janssen-like saturation is more evident. For particles much denser than water (steel spheres), the Janssen term largely dominates against the hydrostatic contribution, and the saturation becomes similar to the dry case. Despite the millimetric particle size, our experiments are qualitatively in remarkable agreement with our expectations from eqn (8). Notably, the results in Fig. 4(d) show a significant reverse Janssen effect under submerged conditions. This phenomenon cannot be adequately explained by the continuous approximation discussed in this study and will be examined in detail in future work.
, and then normalize our experimental data for the submerged case with the values of M∞ obtained from the dry case. The normalized curves are shown in Fig. 4(d). One can notice a dominant hydrostatic effect when the density of the particles is close to the density of water. As we increase ρ, the slope of the linear region decreases, and a Janssen-like saturation is more evident. For particles much denser than water (steel spheres), the Janssen term largely dominates against the hydrostatic contribution, and the saturation becomes similar to the dry case. Despite the millimetric particle size, our experiments are qualitatively in remarkable agreement with our expectations from eqn (8). Notably, the results in Fig. 4(d) show a significant reverse Janssen effect under submerged conditions. This phenomenon cannot be adequately explained by the continuous approximation discussed in this study and will be examined in detail in future work.
3 Case II: Buoyant granular column (ρ/ρl < 1)
In addition to examining cases where heavy particles are submerged in a liquid column, we also investigated the extreme scenario involving less dense particles than water. These lighter particles rise through the liquid due to buoyancy and accumulate at the water–air interface. This situation raises another question: can an inverted Janssen-like saturation be observed in a floating granular column? To explore this low-density regime, we adapted our experimental setup and the model described in eqn (8).3.1 Experimental setup
In these experiments, we used expanded polystyrene beads of average density ρp = 0.021 ± 0.002 g cm−3 and diameter ranging from 4 to 6 mm. This ultralight material is around 40 times less dense than water,46,47 thereby enabling a large buoyant force when the particles are submerged in water. We modified the experimental system as shown in Fig. 5 to measure the pressure at the top of the buoyant column of grains. Two transparent acrylic tubes of internal diameter Di = 44 mm and 35 cm length were connected using a 5 mm hydraulic PVC valve and sealed with silicone. The lower tube was hermetically closed at its bottom and filled with 6 g of particles through the valve, then the valve was almost closed to add distilled water until filling both tubes without allowing the flow of grains from the bottom to the upper tube. The lower tube works as a particle reservoir, while the upper tube receives the particles. The valve allows the flow of particles between the tubes and enables the regulation of a constant flow rate. In this case, a more accurate digital force sensor (Mark-10 DFG-355 with a maximum capacity of 1 N and a resolution of 0.002 N) was placed at the top of the upper tube, connected to a piston located 1 cm below the water surface to measure the buoyant force exerted by the grains trying to float towards the water–air interface. The diameter of the piston is two millimeters smaller than Di, leaving a gap of 1 mm that avoids contact between the piston and the sidewall of the tube and prevents the escape of particles from the system. In this way, there are no interfacial effects because the piston and the particles remain completely submerged. The force sensor is connected to a C-beam linear actuator that allows for the sensor to be freely raised and lowered, enabling the removal of the piston, plugging of the tube, and reversal of the system to recharge and repeat the experiment. To start the experiment, the sensor is tared to zero. Then, the valve is opened, and the particles begin to flow upward until they reach the piston. The sensor records the force exerted by the accumulation of particles at 10 readings per second.3.2 Results and analysis
Fig. 6(a) shows some snapshots of the upper container during the filling process. The particles start flowing close to the sidewall due to the valve's configuration and exhibit erratic rising trajectories with oscillations. This phenomenon is similar to the oscillation modes that appear when air bubbles rise close to a vertical wall.48 The oscillations promote the homogeneous accumulation of grains below the piston. We followed the trajectories of the first particles that rise when the valve is open, and the paths of five of them are plotted in Fig. 6(b). Due to the oscillatory motion, the particles reach a velocity ∼0.3 m s−1 (independently of the filling flow rate), considerably smaller than the terminal velocity predicted by the Stokes law, VT = (ρp − ρl)gdg2/18μl ∼ 3.5 m s−1. We estimate the flow rate using space-time montages built from side-view videos of the discharge (see Fig. 7(a)) where the upper white zone represents the accumulated particles, and the slope of the inclined region indicates a constant flow rate Φ = M/ΔT, where ΔT is the total time of discharge. | ||
Fig. 7 (a) Spatiotemporal evolution built from side-view videos taken at 250 fps of polystyrene particles rising through water and accumulated below the piston. (b) Mean stress saturation (obtained from five realizations) of polystyrene particles in dry conditions. (c)  vs. M of the submerged Janssen Effect for expanded polystyrene beads, the red dashed curve indicates the fitting obtained from eqn (10), with M∞ = 1.088 ± 0.0018. vs. M of the submerged Janssen Effect for expanded polystyrene beads, the red dashed curve indicates the fitting obtained from eqn (10), with M∞ = 1.088 ± 0.0018. | ||
For reference, we first quantified the normal Janssen effect under dry conditions for polystyrene particles deposited into a cylinder with Di = 44 mm, using the setup and procedure described in Section 2. It is important to note that electrostatic effects were almost suppressed by treating particles and the container whit an antistatic solution before the experiments. The results illustrating the relationship between Mapp and M are shown in Fig. 7(b). Indeed, a mass of 6 grams reaches a saturation value of only 2 grams. Still, an abrupt saturation is observed in the dry case, as expected for large particles deposited in narrow tubes.26,27 This saturation occurs (mainly) due to the relatively intricate structures adopted by this ultralight granular material. The same particles exhibit a softer Janssen-like saturation in considerably larger setups, as previously demonstrated using cylindrical containers with a diameter of 45 cm and a height of 3 m (ref. 46 and 47. In such large systems, the reverse Janssen effect was not observed.
In contrast, the saturation is softer despite the narrow tube when the same granular sample is analyzed under submerged conditions. Fig. 7(c) illustrates the force exerted by the particles on the piston, represented as the apparent mass Mapp measured by the sensor to the added mass of particles M, for three different flow rates. It is evident that the apparent mass increases smoothly until it reaches a certain saturation level and, notably, it is independent of the value of (Φ). Considering the buoyant force (Fb = ρlgVdis), and since all particles remain submerged, we have (Vdis = M/ρp). Therefore, the buoyant force can be expressed as ( ), which leads us to conclude that the effective mass supplied to the container will be (
), which leads us to conclude that the effective mass supplied to the container will be (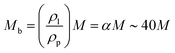 ), which is represented by the dashed straight line in Fig. 7(c). Thus, when 6 g of particles accumulate below the piston, the expected measured mass due to the buoyant force would be (40M = 240 g) in an unconstrained system. However, in the experiments, the apparent mass reaches a saturation value ∼72 g, i.e., only 12 times the actual mass of material. This suggests a buoyancy-driven Janssen effect in the floating granular column. Still, the container walls bear the buoyant stress rather than supporting the weight of the particles in this case.
), which is represented by the dashed straight line in Fig. 7(c). Thus, when 6 g of particles accumulate below the piston, the expected measured mass due to the buoyant force would be (40M = 240 g) in an unconstrained system. However, in the experiments, the apparent mass reaches a saturation value ∼72 g, i.e., only 12 times the actual mass of material. This suggests a buoyancy-driven Janssen effect in the floating granular column. Still, the container walls bear the buoyant stress rather than supporting the weight of the particles in this case.
We can use the eqn (8) to fit the experimental data, but in this situation, we suppress the linear term because the weight of the water column does not contribute to the force sensor reading. Moreover, we must invert the reference system because z = 0 is now at the bottom of the buoyant granular column. Thus, the equation describing the submerged case for particles less dense than water is:
 | (10) |
 . The red solid line in Fig. 7(c) represents the fitting curve of the average of 15 experiments (five per each value of Φ). From the fit, one obtains
. The red solid line in Fig. 7(c) represents the fitting curve of the average of 15 experiments (five per each value of Φ). From the fit, one obtains  and α = 41.3 ± 0.1, very similar to the values found in the experiments (
and α = 41.3 ± 0.1, very similar to the values found in the experiments ( and α = 40), corroborating that eqn (10) satisfies the limiting cases
and α = 40), corroborating that eqn (10) satisfies the limiting cases  when
when  , and
, and  for large values of M.
for large values of M.
The fact that the saturation in the submerged system is softer and better described by the continuum Janssen model than in the dry system (for the same particle size and tube diameter) reflects that the force chains are more stable against perturbations underwater, and that the floating granular column is more homogeneous. This occurs because the buoyancy force is significantly greater than the weight of the particles and can even slightly deform the expanded polystyrene beads, thereby strengthening the force chains. Note that the saturation curves in the submerged case are always below the dashed straight line and the effects of the narrow container are not detected (see Fig. 7(c)), in contrast to the dry case where Mapp > M in some interval before saturation (see Fig. 7(b)). We can hypothesize that, in the dry case, the collisions of incoming particles aid in the mobilization of the accumulated material, generating compressive frictional forces by the walls acting on the particles, that according to previous studies26,27 give rise to the reverse Janssen effect. This particle rearrangement is not possible when the buoyant forces are considerably dominant in floating columns, or for the higher densities in Fig. 4(c). A model that accounts for the effect of the interstitial liquid could be developed, starting from the approach recently introduced to explain the reverse Janssen effect for dry columns.27
4 Conclusions
We have experimentally investigated the Janssen effect in granular columns submerged in a liquid. Our findings demonstrate that the apparent weight of the column at the base of the container can be accurately described by a smooth saturation similar to the classical Janssen effect. When the liquid level is kept constant, the gradual evolution of stress at the bottom of the silo provides direct evidence of this effect. Conversely, when particles are added while maintaining the liquid volume, the free surface rises, and the stress at the bottom increases accordingly. The comparison between both evolutions confirms that as a first-order approximation, the lineal combination between granular and hydrostatic stresses adequately describes the stress exerted by the material at the silo base. Accordingly, we develop a continuous differential approach to derive the vertical stress at the bottom of the container, taking into account buoyant forces along with a linear hydrostatic term due to the liquid displaced by the added particles. Our model predicts the influence of the liquid-to-particle density ratio (ρl/ρp) on stress evolution, which we validated using particles of different densities. For (ρl/ρp ≪ 1), the saturation effect is predominant; however, as ρl/ρp approaches 1, the hydrostatic pressure becomes increasingly significant.Importantly, our experimental results highlight the critical scale κ introduced by Janssen, which accounts for the stress redirection effects observed. This scale is related to particle deposition, suggesting that its variation is connected to deposition dynamics. Hence, as the liquid environment determines the final particle arrangement responsible through its contact network of the stress redirection accounted by κ, the particle resulting configuration sets the typical spatial scale at which stress saturates. This scale increases by a factor of three in the experimental conditions explored in this work. We further explore this hypothesis by examining the extreme case where the particle density is lower than the surrounding liquid's (ρl/ρp ≫ 1). Even with this floating granular column, we observe a buoyant-Janssen-like saturation. This saturation aligns with the model introduced in eqn (8). Remarkably, Janssen dynamics do not adequately describe the vertical stress saturation for these lighter beads in a dry state. However, when a buoyant force drains the beads, a buoyant-Janssen-like saturation can effectively describe the stress acting on the top surface. This observation has significant implications for dispersion transport processes, similar to those explored in ref. 49, where an ensemble of suspended particles are pushed through a constriction.50 In a nutshell, our study highlights the various facets of pressure saturation in submerged granular media: (i) the Janssen effect (analogous to the dry case) with a strong dependence on the liquid–grain density ratio; (ii) the reverse Janssen effect in immersed columns; and (iii) a buoyancy-driven Janssen effect.
Author contributions
M. A.-G. and F. P.-V. designed and performed the experiments, derived the models, and analyzed the data. D. M. assisted with data analysis and interpretation of the results. M. A.-G. wrote the manuscript in consultation with F. P.-V. and D. M. All authors provided critical feedback and helped shape the research, analysis, and manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this study's findings can be downloaded from DOI 10.5281/zenodo.15471267.Acknowledgements
This research was financially supported by CONAHCyT, Mexico (now SECIHTI) and VIEP-BUAP projects 2024-2025. M. A. G. acknowledges PhD scholarship 1079091 (“Becas nacionales CONACyT 2023”). D. M. acknowledges Spanish project PID2023-146422NB-I00 MCIN/AEI/10.13039/501100011033, FEDER, UE for partial support.Notes and references
- H. Janssen, Vereins Eutscher Ingenieure Zeitschrift, 1895, vol. 39, pp. 1045–1049 Search PubMed.
- M. Sperl, Granular Matter, 2006, 8, 59–65 CrossRef.
- G. H. L. Hagen, Ann. Phys., 1839, 46, 423 CrossRef.
- B. P. Tighe and M. Sperl, Granular Matter, 2007, 9, 141–144 CrossRef.
- D. Agnès, M. Frédéric and R. Thierry, Powder Technol., 2018, 338, 993–1000 CrossRef.
- T. Cambau, J. Hure and J. Marthelot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022204 CrossRef PubMed.
- D. Schulze, in Powders and bulk solids: behavior, characterization, storage and flow Schulze, ed. Dietmar, 2014 Search PubMed.
- T. B. R. Company, 2025.
- L. Vanel, P. Claudin, J.-P. Bouchaud, M. Cates, E. Clément and J. Wittmer, Phys. Rev. Lett., 2000, 84, 1439 CrossRef CAS.
- Y.-Y. Liu, D.-L. Zhang, B.-B. Dai, J. Su, Y. Li and A. T. Yeung, Powder Technol., 2021, 381, 601–610 CrossRef CAS.
- R. Di Felice and C. Scapinello, Granular Matter, 2010, 12, 49–55 CrossRef.
- V. Ivchenko, Eur. J. Phys., 2023, 44, 025006 CrossRef.
- J. W. Landry, G. S. Grest and S. J. Plimpton, Powder Technol., 2004, 139, 233–239 CrossRef CAS.
- H. Zhao, X. An, Y. Wu and Q. Qian, Powder Technol., 2018, 323, 149–154 CrossRef CAS.
- C. Windows-Yule, S. Mühlbauer, L. T. Cisneros, P. Nair, V. Marzulli and T. Pöschel, Phys. Rev. E, 2019, 100, 022902 CrossRef CAS PubMed.
- E. B. Pitman, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 3170–3175 CrossRef CAS.
- M. Y. Karim and E. I. Corwin, Phys. Rev. Lett., 2014, 112, 188001 CrossRef PubMed.
- L. Vanel and E. Clément, Eur. Phys. J. B, 1999, 11, 525–533 CrossRef CAS.
- M. Tixier, O. Pitois and P. Mills, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 14, 241–247 CrossRef CAS PubMed.
- Y. Bertho, F. Giorgiutti-Dauphiné and J.-P. Hulin, Phys. Rev. Lett., 2003, 90, 144301 CrossRef PubMed.
- H. Pacheco-Martinez, H. J. van Gerner and J. C. Ruiz-Suárez, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 021303 CrossRef PubMed.
- F. Vivanco, J. Mercado, F. Santibáñez and F. Melo, Phys. Rev. E, 2016, 94, 022906 CrossRef.
- A. Ashour, T. Trittel, T. Börzsönyi and R. Stannarius, Phys. Rev. Fluids, 2017, 2, 123302 CrossRef.
- R. Tao, M. Wilson and E. R. Weeks, Phys. Rev. E, 2021, 104, 044909 CrossRef CAS.
- T. Pongó, V. Stiga, J. Török, S. Lévay, B. Szabó, R. Stannarius, R. Cruz-Hidalgo and T. Börzsönyi, New J. Phys., 2021, 23, 103036 CrossRef.
- I. Bratberg, K. Måløy and A. Hansen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 18, 245–252 CrossRef CAS PubMed.
- S. Mahajan, M. Tennenbaum, S. N. Pathak, D. Baxter, X. Fan, P. Padilla, C. Anderson, A. Fernandez-Nieves and M. Pica Ciamarra, Phys. Rev. Lett., 2020, 124, 128002 CrossRef CAS.
- S. Shah, A. M. M. Gomez, P. Jalali and L. Kondic, Phys. Rev. E, 2024, 110, 064901 CrossRef CAS PubMed.
- C. J. Anderson, P. A. Gibson and A. Fernandez-Nieves, Phys. Rev. E, 2022, 106, L012604 CrossRef CAS PubMed.
- L. Thorens, K. J. Måløy, M. Bourgoin and S. Santucci, Nat. Commun., 2021, 12, 2486 CrossRef CAS PubMed.
- M. Aguilar-González, L. Elizondo-Aguilera, Y. Dumaresq-Sobral and F. Pacheco-Vázquez, arXiv, 2025, preprint, arXiv:2507.08816 [cond-mat.soft] DOI:10.48550/arXiv.2507.08816.
- E. de Moraes Franklin and N. S. de Andrade, IV Journeys in Multiphase Flows, 2015, JEM-2015-0054, 23-27.
- A. M. Cervantes-Álvarez, S. Hidalgo-Caballero and F. Pacheco-Vázquez, Phys. Fluids, 2018, 30, 043302 CrossRef.
- D. Rodríguez-López, F. C. Pacheco-Sósol, L. F. Elizondo-Aguilera and F. Pacheco-Vázquez, Phys. Fluids, 2023, 35, 081702 CrossRef.
- M. V. Ferreyra, L. A. Pugnaloni and D. Maza, Phys. Rev. E, 2024, 109, L012901 CrossRef CAS PubMed.
- B. Saint-Michel, M. Georgelin, S. Deville and A. Pocheau, Soft Matter, 2018, 14, 9498–9510 RSC.
- J. Wang, G.-h Liu, J. Wang, X. Xu, Y. Shao, Q. Zhang, Y. Liu, L. Qi and H. Wang, Environ. Sci. Pollut. Res., 2021, 28, 43035–43049 CrossRef PubMed.
- C. Tao, B. G. Kutchko, E. Rosenbaum, W.-T. Wu and M. Massoudi, Energies, 2019, 12, 2604 CrossRef CAS.
- S. G. Vick, Planning, design, and analysis of tailings dams, BiTech Publishers Ltd., 1990 Search PubMed.
- J. Vincent, Coffee: Volume 2: Technology, Springer, 1987, pp. 1–33 Search PubMed.
- A. Cervantes-Álvarez, Y. Escobar-Ortega, A. Sauret and F. Pacheco-Vázquez, J. Colloid Interface Sci., 2020, 574, 285–292 CrossRef PubMed.
- P.-G. de Gennes, Rev. Mod. Phys., 1999, 71, S374 CrossRef.
- J. A. Dijksman, E. Wandersman, S. Slotterback, C. R. Berardi, W. D. Updegraff, M. van Hecke and W. Losert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 060301 CrossRef PubMed.
- J. Koivisto, M. Korhonen, M. Alava, C. P. Ortiz, D. J. Durian and A. Puisto, Soft Matter, 2017, 13, 7657–7664 RSC.
- For steep particles, we used an inner tube of D = 2.5 cm to obtain columns of 30 cm high, due to the maximum load limitation imposed by the force sensor.
- F. Pacheco-Vázquez, G. A. Caballero-Robledo, J. M. Solano-Altamirano, E. Altshuler, A. J. Batista-Leyva and J. C. Ruiz-Suárez, Phys. Rev. Lett., 2011, 106, 218001 CrossRef.
- L. A. López-Rodríguez and F. Pacheco-Vázquez, Phys. Rev. E, 2017, 96, 030901 CrossRef PubMed.
- Y. Zhang, S. Dabiri, K. Chen and Y. You, Int. J. Heat Fluid Flow, 2020, 85, 108649 CrossRef.
- M. Souzy, I. Zuriguel and A. Marin, Phys. Rev. E, 2020, 101, 060901 CrossRef CAS PubMed.
- E. Dressaire and A. Sauret, Soft Matter, 2017, 13, 37–48 RSC.
| This journal is © The Royal Society of Chemistry 2025 |