Temperature-dependent hysteresis effects in perovskite-based solar cells

Abstract

Staircase voltage sweep measurements were performed on a perovskite solar cell at 250 K, 300 K, and 360 K. Time-dependent photocurrent data reveal the complexity of the signal that cannot be described by a simple mono-exponential function, suggesting that multiple charging–discharging processes are responsible for the complex hysteresis behavior.

---

Organo-lead-halide perovskite (OHP) based solar cells were reported to achieve energy-to-electricity power conversion efficiency (PCE) as high as ∼19.3%,^1–8 which combined with reported methods for low-cost, flexibility, and large-area solar cell fabrication such as ultra-sonic spray-coating⁹ and printing technology,¹⁰ makes OHP cell technology amenable to scaling up to production levels.^2,5 The potential toxic effects of Pb have been discussed. Alternatives or solutions have been proposed, such as: Pb-free perovskite based solar cells, encapsulation, and Pb recycling.^11–14

Methylammonium (MA) lead iodide (CH₃NH₃PbI₃), the most commonly employed material in halide perovskite solar cells, was reported to have both a high absorption coefficient (direct bandgap of ∼1.55 eV) and high mobilities for electrons (7.5 cm² V⁻¹ s⁻¹) and holes (12.5–66 cm² V⁻¹ s⁻¹), resulting in long carrier diffusion lengths (100 nm to 1 μm).¹⁵ Although the amount of incorporated Cl is still under debate,¹⁶ mixed methylammonium-lead halide MAPbI_3−xCl_x is another type of halide perovskite reported with an even higher charge-carrier mobility (∼33 cm² V⁻¹ s⁻¹), resulting in carrier diffusion lengths of up to 3 μm.¹⁷ Despite all the superb properties, perovskite solar cells suffer from a strong hysteresis in current–voltage (I–V) measurements typically conducted under AM1.5G illumination.^18–20 Hysteresis in these cells is strongly influenced by the perovskite grain size and the structure of the underlying TiO₂ layer, which is used as an electron transport layer (ETL). Efforts now are concentrated on generating perovskite films with larger grain sizes to minimize the hysteresis.^4,19,21,22 In addition, the replacement of MA⁺ with cations that have a larger radius, such as formamidinium (NH₂CH=NH₂⁺, FA⁺)²³ and 5-ammoniumvaleric acid,¹⁰ have been reported to help reduce the hysteresis effects. The planar heterojunction architecture employing a compact-TiO₂ (c-TiO₂) layer is of particular interest due to its simple cell configuration. However, unlike cells with mesoporous-TiO₂ (m-TiO₂), in which the perovskite is scaffolded onto the mesoporous matrix, the hysteresis effects in planar heterojunction structure are usually strong.^18–20 Hysteresis effects in perovskite solar cells are generally associated with a high capacitance (of the order of mF cm⁻²) compared to Si cells (of the order of μF cm⁻²)^19,23–26 or other types of solar cells (as described further in the ESI†). This capacitance effect was hypothesized to be originated from (i) the ferroelectricity or the polarization of the perovskite layer; (ii) contact conductivity; (iii) diffusion of excess ions as interstitial defects; and/or (iv) the trapping/de-trapping of charge carriers.^18–20,27

In this work, we performed a series of staircase voltage sweep measurements^18–20 at three different temperatures (250 K, 300 K, and 360 K) to quantify the photocurrent transient behavior in a complete perovskite cell composed of FTO/c-TiO₂/perovskite/spiro-MeOTAD/Au where FTO stands for fluorine doped tin oxide. The hole-collection took place through the spiro-MeOTAD hole transport layer (HTL). Our photocurrent data suggest that multiple processes are responsible for the complex transient behavior. Furthermore, solar cell properties can be altered significantly by changes in the environmental conditions such as humidity and temperature.^28–31 Thus, device performance characterization of perovskite cells under various conditions is of paramount importance. Moreover, it can provide fundamental understanding of the charging–discharging processes in perovskite cells when studied in a controlled environment (temperature, humidity, and the gas environment).³¹ Temperature-dependent studies of steady-state I–V curves provide trends regarding the open-circuit voltage (V_oc), short-circuit current (I_sc), and fill factor (FF) electrical parameters as a function of temperature, shedding light on the physical processes taking place within the layers of perovskite solar cell. These results highlight the importance of establishing a protocol for the precise and artifact-free evaluation of perovskite solar cells.

The perovskite films in this work were prepared from MAI and PbCl₂ precursors according to a standard literature procedure reported elsewhere.^32–34 Sample preparation details are described in the ESI.† Sample characterization by X-ray diffraction (XRD) and scanning electron microscopy (SEM) is shown in Fig. 1. SEM reveals complete surface coverage and the formation of interconnected crystal domains. The determination of grain sizes was difficult based on those images. A film thickness of ∼380 nm was determined by a profilometer. XRD data showed the characteristic peaks at 14.1°, 28.5°, and 43.3° corresponding to the (110), (220), and (330) planes in the perovskite structure.³ The as-prepared sample was loaded into a variable temperature probe station chamber (Lake shore, CRX-6.5K) coupled with a pumping station (HiCube 80, Pfeiffer). The pressure inside the probe station was observed to vary between ∼2 × 10⁻⁶ and 4 × 10⁻⁵ Torr depending on the working temperature range (between 250 K and 360 K). Electrical signals from the probes contacting the FTO and Au electrodes were recorded using a semiconductor characterization system (4200-SCS, Keithley). The low-noise level (<1 pA) of our photocurrent data allowed us to unambiguously detect the different charge transport processes. It was difficult to couple a solar simulator with the probe station. Thus, light illumination on the perovskite samples was conducted using a tungsten halogen lamp. The relative light intensity of ∼9% compared to the standard AM1.5G was roughly estimated based on measurements on a reference Si solar cell. This light intensity was strong enough to induce hysteresis effects (photocurrent in the μA range) in perovskite solar cells during the current–voltage step (I–V_step) measurements. The perovskite cells were measured under vacuum conditions at three different temperatures (250 K, 300 K, and 360 K). The measurements under vacuum resulted in V_step curves with high stability. No influence of the pre-illumination step was observed in our studies.^20,30 It is most likely that the photodoping effect is inactive in our measurements because our samples were measured under vacuum, i.e., the influence of reactive gases such as O₂ and/or H₂O is minimal.^20,30,31

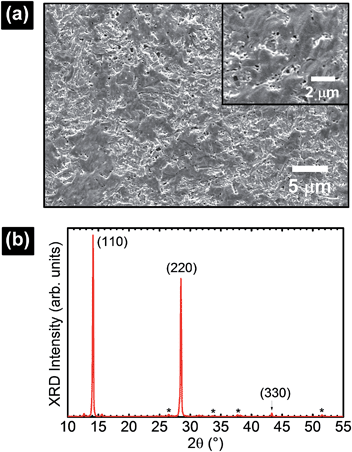Fig. 1 (a) SEM and (b) XRD characterization of the perovskite film formed from MAI and PbCl₂ precursors.

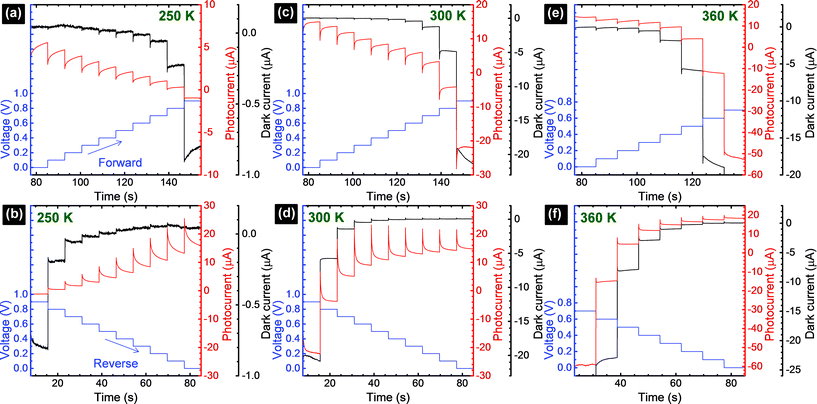
The I–V_step measurements were conducted at three different temperatures (250 K, 300 K, and 360 K) with V_step sweeping from −1 V to +1 V and from +1 V down to −1 V in steps of ±0.1 V (Fig. S3–S5†). To make a convention for this work, we set the voltage sweep starting from the negative to the positive voltage to be the forward scan direction, and the voltage starting from positive to negative to be the reverse scan direction. In the I–V quadrant where the solar cell outputs electrical power (Fig. 2), the photocurrent response shows transient behavior at all temperatures. Every time the voltage is increased or decreased by 0.1 V, a sharp initial (at t₀) jump in photocurrent is followed by the subsequent rise or decay. This time-dependent behavior was previously explained as being caused by capacitive currents in the perovskite solar cells.^18–20,23 Such capacitance effects were hypothesized to be originated from (i) ferroelectricity or polarization of the perovskite layer; (ii) contact conductivity; (iii) diffusion of excess ions as interstitial defects; and/or (iv) trapping/de-trapping of charge carriers.^18–20,27 The capacitive effect is enhanced under illumination conditions (photocurrent, Fig. 2) and shows a minimal influence under dark conditions (dark current, Fig. 2). It has been previously reported that lead halide perovskites (e.g., prepared from PbCl₂ and MAI precursors) show a giant dielectric constant (GDC) phenomenon with a low frequency dielectric constant of the order of ε ∼ 1000 in dark conditions.²⁵ More interestingly, under the illumination of one sun, ε was reported to increase by a factor of ∼1000. The origin of GDC and ε enhancement upon light illumination is still unclear at the moment,²⁵ but it has been proposed that it may originate from the ferroelectric response induced by the photogenerated carriers leading to the structural rearrangement of methylammonium ions (MA⁺).^20,25,27 As a consequence of this structural phase transition upon light illumination, charge transport is affected, and therefore enhanced photocurrent transients are produced within the perovskite film.^20,25,35 It is also found that at a lower temperature (250 K, Fig. 2a and b) and room temperature (300 K, Fig. 2c and d), the photocurrent transient period appears to be longer compared to that of a higher temperature (360 K, Fig. 2e and f). This may be related to the effects of capacitance at selective-contacts^25,36 and will be discussed in more detail later. Additional transient behavior, which was generally observed above the open circuit voltage,²⁰ including its effects on the photocurrent corresponding to an applied bias of 0.7 V at 360 K (Fig. 2e) will not be discussed because it is beyond the scope of this work.

Fig. 2 Photocurrent and dark current as a function of applied voltage using a staircase function generator. The voltage sweep from zero to positive voltage and from positive to zero are denoted as forward (a, c and e) and reverse (b, d and f), respectively. The 8 s long step delayed photocurrent responses are shown for three different temperatures: 250 K (a and b); 300 K (c and d); 360 K (e and f). The steep jumps observed in the current signals after each step-voltage are signatures of the capacitive effects in the device.

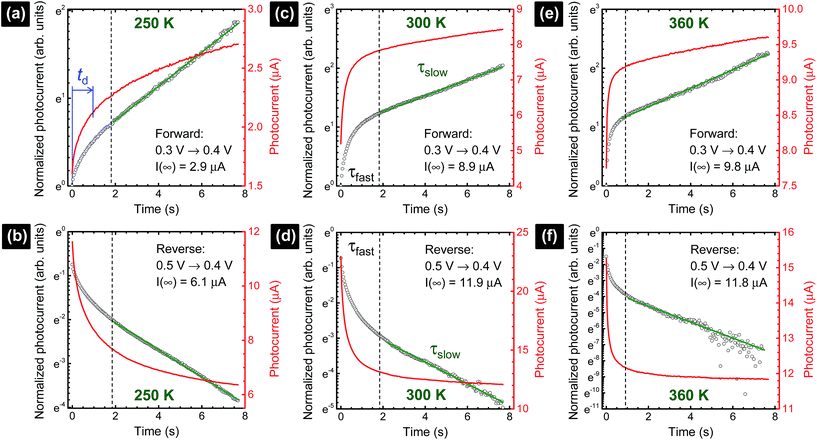
The photocurrent signals are modelled by using exponential functions. We observe that none of our raw data can be fitted with a mono-exponential function. Multi-exponential functions, eqn (1) and (2), with three terms (i = 0, 1, 2) are needed to reproduce the raw data, i.e., giving a reasonably low χ². The transient photovoltage decay technique is widely used to describe the physical processes of charge dynamics in solar cells. However, different descriptions for the transient signal are reported in the literature. For some perovskite solar cells, a mono-exponential function^37,38 was used, whereas for others, a bi-exponential function^23,39 was employed. This shows the complexity of the system under analysis, because the charging–discharging characteristics in the cell can be strongly influenced by the cell architecture and/or preparation conditions.²³ Considering the previously discussed capacitance factors²⁷ in perovskite solar cells, semi-logarithmic plots of time-dependent photocurrent signal as a response to the applied voltage step (Fig. 2) are expected to generate a straight line after subtracting the photocurrent under steady-state conditions (t → ∞).²⁰

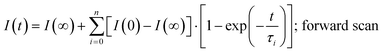where τ_i is the time constant of the system. Thus, as shown in the eqn (1) 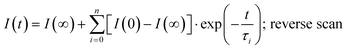and (2), any eventual straight line in the (forward scan) and (reverse scan) versus time plots will yield slopes with +1/τ and −1/τ values, respectively. The representative spectra are displayed in Fig. 3 for the cases of 0.3 V → 0.4 V (forward) and 0.5 V → 0.4 V (reverse) of applied voltage steps at three different temperatures. The complete set of individual I–V_step analyses obtained at different temperatures is described in the ESI (Fig. S6–S11†). The semi-logarithmic plots show at least two regimes with characteristic time decays. In the first time interval (t < ∼1.8 s for 250 K and 300 K and t < ∼1 s for 360 K, Fig. 3), after applying the voltage step, several fast charging–discharging processes (more than one because of the non-linearity observed in the semi-logarithmic plot) are inferred and designated as τ_fast. A quantitative description of this τ_fast (not a single time constant) is not possible from our experimental data because of the convolution of multi-exponential terms, eqn (1) and (2). However, considering the slowest process(es) in the first time interval, τ_fast is observed to decay faster at a high temperature (360 K) contributing less to hysteresis effects. A more elaborate equivalent circuit with RC components has been proposed by Dualeh et al.³⁹ and our data could be associated with (i) selective-contact resistance(s) and capacitance(s) within the FTO/c-TiO₂/perovskite/spiro-MeOTAD HTL/Au layers or (ii) due to the conduction of ion(s) within the perovskite film^18,20,39 and/or HTM (e.g., Li⁺ from Li-TFSI dopant^39,40) influenced by temperature. TiO₂ is a semiconductor material that manifests a size-dependent capacitive effect in this nanostructured form, showing enhanced chemical capacitance (C_μ); a smaller C_μ is expected for our c-TiO₂, but may still provide some influences on the charging–discharging processes.^26,29,36 In the second time interval (t > ∼1.8 s for 250 K and 300 K and t > ∼1 s for 360 K, Fig. 3), a linear regime prevails with the slowest decay time of the system designated as τ_slow. Based on previous descriptions, we attribute this slow process to the intrinsic ferroelectricity of the perovskite film.^{18–20,23,37} Least-square fitting method was applied on the second time interval of the experimental data to extract the τ_slow values. In the particular cases of applied voltage steps shown in Fig. 3, τ_slow = 5.15 ± 0.02 s (Fig. 3a) [and 3.25 ± 0.01 s (Fig. 3b)] at 250 K, 7.49 ± 0.03 s (Fig. 3c) [and 3.23 ± 0.03 s (Fig. 3d)] at 300 K, and 5.6 ± 0.2 s (Fig. 3e) [and 2.01 ± 0.04 s (Fig. 3f)] at 360 K were extracted from the fitted slopes in forward [and reverse bias]. A summary of the extracted τ_slow values for all solar cell working bias conditions (between 0 V and V_oc) are shown in Fig. 4 and tabulated in the ESI (Table S1†). Although a lower light intensity than that of AM1.5G was used in our experiments, the extracted values are still in good agreement with previously reported values ranging from seconds to hundreds of seconds.^18–20 It has been shown that the transient time period is strongly influenced by (i) the perovskite crystal size (e.g. larger crystallites led to shorter transient times) and (ii) the structural form of the underlying TiO₂ layer (e.g. the presence of mesoporous TiO₂ leads to shorter transient times than the case with only c-TiO₂).^19–21,26 Our SEM images (Fig. 1a) reveal that our perovskite films are composed of interconnected crystallites with smaller and larger grains fully covering the underlying c-TiO₂ layer. The determination of grain sizes is difficult based on the SEM images. No drastic variations in τ_slow were observed when the sample was held at three different temperatures of 250 K, 300 K, and 360 K. A slightly faster τ_slow of ∼2.5 s is observed when the sample is held at 360 K and the voltage is swept in the reverse direction (Fig. 4c). τ_slow is proportional to the perovskite capacitance, and therefore to the dielectric constant of the perovskite film. Temperature induced structural phase transitions in lead halide perovskite materials leading to variations in the dielectric constant, ε(T), have been previously reported.^{25,27,35,41–43} For example, in the particular case of CH₃NH₃PbI₃ crystals, a steep discontinuity of ε(T) at the orthorhombic → tetragonal phase transition (161.4 K) and a smooth ε(T) transition in the tetragonal → cubic phase (330.4 K) were reported.⁴² Although, the above description provides an idea of the phase transitions and expected relative ε(T) values as a function of temperature, a direct comparison with our perovskite material is not valid because our study was conducted on a thin film (∼380 nm) that differs significantly from the single crystal. In addition, the presence of Cl in our films might have had a significant influence on the structural phases and transition temperatures.^16,23,44,45 Based on the XRD results (Fig. 1b), our perovskite film exhibits an orthorhombic structure³ measured at room temperature and no large variations in the dielectric constants at temperatures of 250 K and 360 K can be inferred.⁴³ Note that the τ_slow values differ when the voltage is swept in the forward or reverse direction, suggesting a strong dependence on the applied voltage history (remnant polarization), which is consistent with ferroelectricity-influenced behavior.²⁷

Fig. 3 Semi-logarithmic plot of the photocurrent responses as a function of time after applying a voltage step at t = 0 (a, c and e) from 0.3 V → 0.4 V (forward) and (b, d and f) from 0.5 V → 0.4 V (reverse) at (a and b) 250 K, (c and d) 300 K, and (e and f) 360 K. The spectra show that multiple processes, designated as τ_fast and τ_slow, take place during the charging–discharging within a perovskite solar cell. The degree of hysteresis depends on the waiting period to measure the photocurrent after applying a voltage, i.e., the delay time (t_d).

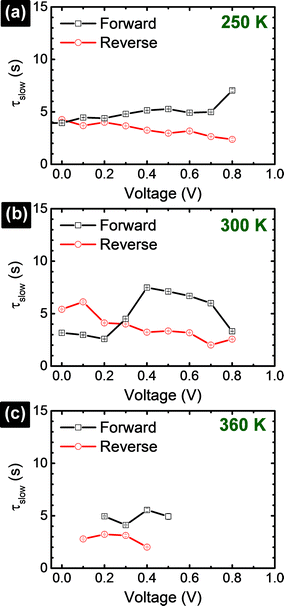Fig. 4 Extracted time-constants corresponding to the slowest process (τ_slow) observed in the semi-logarithmic plot of the transient part of the photocurrent response upon applied voltage.

Transient photocurrent response, as a consequence of capacitive effects in perovskite solar cells, has a strong influence on the shape of the I–V curves. Based on the time-dependent results shown in Fig. 2, we can deduce the I–V curves (Fig. 5) with the different delay times (t_d), as indicated in Fig. 3a. The I_sc, V_oc, and FF extracted from the I–V curves are summarized in the ESI (Table S2†). The I–V curve shapes are significantly influenced by the voltage sweep direction and t_d. Overall, low photocurrent and high photocurrent are measured in the forward and reverse directions, respectively, when t_d is small. Upon increasing t_d, a rise and decay in the photocurrent are observed in the forward and reverse scan directions, respectively, eventually reaching the steady-state photocurrent conditions, I(t_d → ∞). In the particular case of the cell measured at 300 K, a hump is observed at ∼0.5 V in the reverse direction (Fig. 5d) when the voltage is swept too fast (t_d ∼ 0–40 ms). This is an artifact of the solar cell measurement conditions because the photocurrent has not reached the steady-state value.^24,46 The delay time in Fig. 4 provides a lower bound for the solar cell photocurrent to attain its steady-state values. Considering that a perovskite solar cell is modelled with RC circuits,^{25,26,34,36,39} the time constant (τ = RC) characterizes the capacitor charging to ∼63% between the initial and final values (forward) and discharging down to ∼37% of the initial value (reverse). To reach a photocurrent level that is within 1% variation from the steady state, it takes a delay time of 5τ_slow, which is on the order of ∼30 s.^18–20 This is impractically long and new procedures are needed. At each temperature, comparing only the I–V curves corresponding to the steady-state conditions (t_d → ∞) in forward and reverse scans, we notice that none of the curves match each other exactly. A large discrepancy in the I_sc values between the forward and reverse I–V curves is noticed at low (250 K, Fig. 5a and b) and high temperatures (360 K, Fig. 5e and f) while the I_sc values are closely matched at 300 K^19,20 (Fig. 5c and d and Table S2†). For example, at 250 K, the steady-state I–V curves in the forward and reverse directions provide I_sc (V_oc and FF) values of 5.8 μA (0.84 V and 0.24) and 14.9 μA (0.90 V and 0.18), respectively. Meanwhile, at 300 K, the forward and reverse I_sc (V_oc and FF) values are 15.1 μA (0.77 V and 0.35) and 14.4 μA (0.77 V and 0.49), respectively. Finally, at 360 K, the forward and reverse I_sc (V_oc and FF) values are 14.2 μA (0.54 V and 0.51) and 18.3 μA (0.54 V and 0.49), respectively. Excess I⁻ or MA⁺ ions are proposed to be present as interstitial defects induced by photo-excitation and/or during sample preparation conditions. Under reverse bias with illumination, the negatively charged interstitial anions (I⁻) migrate to the c-TiO₂ layer and cations (MA⁺) towards the spiro-MeOTAD HTL. The ionic concentrations induce energy barriers for electrons and holes at their respective selective-contacts. Forward bias conditions drive these interstitial ions in the opposite direction. The difference in the redistribution of ions within the perovskite cell when operated under forward and reverse bias conditions can explain why the steady-state I–V curves measured in the forward and reverse scan directions (Fig. 5) do not match exactly. Accurate photovoltaic parameters (V_oc, I_sc, and FF) can only be analyzed if the I–V measurements are carried out under steady-state conditions.²⁰ Interestingly, V_oc decreases as the cell temperature is increased (Fig. S12†). In addition, the series resistance is significantly enhanced when the cell is held at 250 K. These trends may have the same origin as previously described in solid-state dye sensitized solar cells (ssDSCs)^28,40 and more recently highlighted by the strong influences of the selective contacts on the performance of perovskite solar cells.^36,47 Based on a systematic study varying the combinations of TiO₂ electron transport layer (E), perovskite (P), and spiro-MeOTAD hole transport layer (H) architectures (E/P/H, E/P, P/H, and P), impedance spectroscopy measurements by Juarez-Perez et al. showed that the photovoltaic parameters (I_sc, V_oc, and FF) are strongly affected by the hole selective contact.³⁶ Thus, the observed decrease in I_sc in our perovskite cell at low temperatures is possibly due to the decrease in the hole mobility of the organic spiro-MeOTAD HTM.^36,47 At the same time, the observed increase in FF at high temperatures (360 K) is consistent with the reduced series resistance due to the higher diffusion current.^36,47 In parallel, the charge-recombination rate is expected to increase with temperature, inducing an overall decrease in the charge density within the cell, which reduces V_oc.^36,47 Based on the quantitative analysis shown in Fig. 5, the major influence of temperature is on τ_fast processes (rather than on the τ_slow process), which may be associated with selective-contacts. Further investigation is needed to determine unambiguously the origin of τ_fast processes.

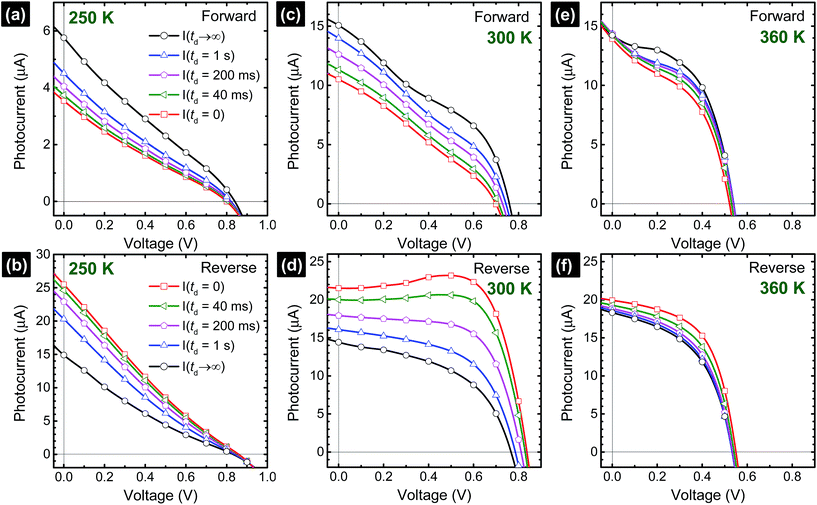Fig. 5 Photocurrent versus voltage curves composed from the time-dependent data shown in Fig. 2 considering the different delay times (t_d). The steady-state photocurrent values, I(t_d → ∞), were calculated from the semi-logarithmic plots.

Conclusions

In summary, staircase voltage sweep measurements at 250 K, 300 K, and 360 K conducted on a perovskite solar cell reveal a complex time-dependent photocurrent transient signal. Our photocurrent data suggest multiple charging–discharging processes take place within the perovskite cell. Semi-logarithmic plots of the photocurrent responses reveal a linear regime showing the slowest transient process (well-defined mono-exponential trend) with a time constant (τ_slow) of the order of seconds. This process was interpreted to have originated from the polarization response of the perovskite layer. Additional studies are needed to describe the convoluted τ_fast processes (multi-exponential terms), which had a stronger influence on the temperature. I–V curves under steady-state conditions were composed from the transient photocurrent data. The hysteresis effect was smaller at 360 K and higher at 300 K and 250 K. On the basis of our study, in order to compare the results from different laboratories, it is essential to establish a protocol for extracting hysteresis-free I–V curves on perovskite solar cells corresponding to steady-state conditions. The extrapolation method used in this work to extract the steady-state photocurrents is suggested as a possible method.

Acknowledgements

This work was financially supported by Okinawa Institute of Science and Technology Graduate University (OIST) in Japan.

Notes and references

1. H. Zhou, Q. Chen, G. Li, S. Luo, T.-b. Song, H.-S. Duan, Z. Hong, J. You, Y. Liu and Y. Yang, Science, 2014, 345, 542–546.
2. O. Malinkiewicz, A. Yella, Y. H. Lee, G. M. Espallargas, M. Graetzel, M. K. Nazeeruddin and H. J. Bolink, Nat. Photonics, 2014, 8, 128–132.
3. M. Z. Liu, M. B. Johnston and H. J. Snaith, Nature, 2013, 501, 395–398.
4. N. J. Jeon, J. H. Noh, Y. C. Kim, W. S. Yang, S. Ryu and S. I. Seok, Nat. Mater., 2014, 13, 897–903.
5. K. Wojciechowski, M. Saliba, T. Leijtens, A. Abate and H. J. Snaith, Energy Environ. Sci., 2014, 7, 1142–1147.
6. M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647.
7. National Renewable Energy Laboratory (NREL), http://www.nrel.gov/ncpv/images/efficiency_chart.jpg.
8. L. K. Ono, S. Wang, Y. Kato, S. R. Raga and Y. Qi, Energy Environ. Sci., 2014 10.1039/c4ee02539c.
9. A. T. Barrows, A. J. Pearson, C. K. Kwak, A. D. F. Dunbar, A. R. Buckley and D. G. Lidzey, Energy Environ. Sci., 2014, 7, 2944–2950.
10. A. Mei, X. Li, L. Liu, Z. Ku, T. Liu, Y. Rong, M. Xu, M. Hu, J. Chen, Y. Yang, M. Grätzel and H. Han, Science, 2014, 345, 295–298.
11. N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A.-A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 3061–3068.
12. F. Hao, C. C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Nat. Photonics, 2014, 8, 489–494.
13. M. H. Kumar, S. Dharani, W. L. Leong, P. P. Boix, R. R. Prabhakar, T. Baikie, C. Shi, H. Ding, R. Ramesh, M. Asta, M. Graetzel, S. G. Mhaisalkar and N. Mathews, Adv. Mater., 2014, 26, 7122–7127.
14. P.-Y. Chen, J. Qi, M. T. Klug, X. Dang, P. T. Hammond and A. M. Belcher, Energy Environ. Sci., 2014, 7, 3659–3665.
15. M. Gratzel, Nat. Mater., 2014, 13, 838–842.
16. H. Yu, F. Wang, F. Xie, W. Li, J. Chen and N. Zhao, Adv. Funct. Mater., 2014 DOI:10.1002/adfm.201401872.
17. C. Wehrenfennig, M. Z. Liu, H. J. Snaith, M. B. Johnston and L. M. Herz, Energy Environ. Sci., 2014, 7, 2269–2275.
18. H. J. Snaith, A. Abate, J. M. Ball, G. E. Eperon, T. Leijtens, N. K. Noel, S. D. Stranks, J. T.-W. Wang, K. Wojciechowski and W. Zhang, J. Phys. Chem. Lett., 2014, 5, 1511–1515.
19. H.-S. Kim and N.-G. Park, J. Phys. Chem. Lett., 2014, 5, 2927–2934.
20. E. L. Unger, E. T. Hoke, C. D. Bailie, W. H. Nguyen, A. R. Bowring, T. Heumuller, M. G. Christoforo and M. D. McGehee, Energy Environ. Sci., 2014, 7, 3690–3698.
21. Z. Xiao, Q. Dong, C. Bi, Y. Shao, Y. Yuan and J. Huang, Adv. Mater., 2014, 26, 6503–6509.
22. C.-W. Chen, H.-W. Kang, S.-Y. Hsiao, P.-F. Yang, K.-M. Chiang and H.-W. Lin, Adv. Mater., 2014, 26, 6647–6652.
23. R. S. Sanchez, V. Gonzalez-Pedro, J.-W. Lee, N.-G. Park, Y. S. Kang, I. Mora-Sero and J. Bisquert, J. Phys. Chem. Lett., 2014, 5, 2357–2363.
24. H. M. Tian, J. Y. Zhang, X. Y. Wang, T. Yu and Z. G. Zou, Measurement, 2011, 44, 1551–1555.
25. E. J. Juarez-Perez, R. S. Sanchez, L. Badia, G. Garcia-Belmonte, Y. S. Kang, I. Mora-Sero and J. Bisquert, J. Phys. Chem. Lett., 2014, 5, 2390–2394.
26. H. S. Kim, I. Mora-Sero, V. Gonzalez-Pedro, F. Fabregat-Santiago, E. J. Juarez-Perez, N. G. Park and J. Bisquert, Nat. Commun., 2013, 4, 2242.
27. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038.
28. H. J. Snaith, L. Schmidt-Mende, M. Gratzel and M. Chiesa, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045306.
29. S. R. Raga and F. Fabregat-Santiago, Phys. Chem. Chem. Phys., 2013, 15, 2328–2336.
30. U. B. Cappel, T. Daeneke and U. Bach, Nano Lett., 2012, 12, 4925–4931.
31. L. K. Ono, P. Schulz, J. J. Endres, G. O. Nikiforov, Y. Kato, A. Kahn and Y. Qi, J. Phys. Chem. Lett., 2014, 5, 1374–1379.
32. G. E. Eperon, V. M. Burlakov, P. Docampo, A. Goriely and H. J. Snaith, Adv. Funct. Mater., 2014, 24, 151–157.
33. E. Edri, S. Kirmayer, A. Henning, S. Mukhopadhyay, K. Gartsman, Y. Rosenwaks, G. Hodes and D. Cahen, Nano Lett., 2014, 14, 1000–1004.
34. V. Gonzalez-Pedro, E. J. Juarez-Perez, W.-S. Arsyad, E. M. Barea, F. Fabregat-Santiago, I. Mora-Sero and J. Bisquert, Nano Lett., 2014, 14, 888–893.
35. J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590.
36. E. J. Juarez-Perez, M. Wuβler, F. Fabregat-Santiago, K. Lakus-Wollny, E. Mankel, T. Mayer, W. Jaegermann and I. Mora-Sero, J. Phys. Chem. Lett., 2014, 5, 680–685.
37. D. Q. Bi, L. Yang, G. Boschloo, A. Hagfeldt and E. M. J. Johansson, J. Phys. Chem. Lett., 2013, 4, 1532–1536.
38. Y. Zhao, A. M. Nardes and K. Zhu, J. Phys. Chem. Lett., 2014, 5, 490–494.
39. A. Dualeh, T. Moehl, N. Tétreault, J. Teuscher, P. Gao, M. K. Nazeeruddin and M. Grätzel, ACS Nano, 2014, 8, 362–373.
40. H. J. Snaith, S. M. Zakeeruddin, L. Schmidt-Mende, C. Klein and M. Gratzel, Angew. Chem., Int. Ed., 2005, 44, 6413–6417.
41. J. M. Frost, K. T. Butler and A. Walsh, APL Mater., 2014, 2, 081506.
42. N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1992, 53, 935–939.
43. T. Baikie, Y. N. Fang, J. M. Kadro, M. Schreyer, F. X. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628–5641.
44. S. Colella, E. Mosconi, P. Fedeli, A. Listorti, F. Gazza, F. Orlandi, P. Ferro, T. Besagni, A. Rizzo, G. Calestani, G. Gigli, F. De Angelis and R. Mosca, Chem. Mater., 2013, 25, 4613–4618.
45. B. Suarez, V. Gonzalez-Pedro, T. S. Ripolles, R. S. Sanchez, L. Otero and I. Mora-Sero, J. Phys. Chem. Lett., 2014, 5, 1628–1635.
46. H. Tian, L. Liu, B. Liu, S. Yuan, X. Wang, Y. Wang, T. Yu and Z. Zou, J. Phys. D: Appl. Phys., 2009, 42, 045109.
47. F. Fabregat-Santiago, G. Garcia-Belmonte, I. Mora-Sero and J. Bisquert, Phys. Chem. Chem. Phys., 2011, 13, 9083–9118.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental section, semi-logarithmic plots of photocurrents, and tabulated time constants and I_sc, V_oc, and FF as a function of temperature. See DOI: 10.1039/c4ta04969a

---