Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles molecular dynamics simulation of the Ca2UO2(CO3)3 complex in water†
Chad
Priest
,
Ziqi
Tian
and
De-en
Jiang
*
Department of Chemistry, University California, Riverside, California 92521, USA. E-mail: de-en.jiang@ucr.edu
First published on 22nd January 2016
Abstract
Recent experiments have shown that the neutral Ca2UO2(CO3)3 complex is the dominant species of uranium in many uranyl-containing streams. However, the structure and solvation of such a species in water has not been investigated from first principles. Herein we present a first principles molecular dynamics perspective of the Ca2UO2(CO3)3 complex in water based on density functional theory and Born–Oppenheimer approximation. We find that the Ca2UO2(CO3)3 complex is very stable in our simulation timeframe for three different concentrations considered and that the key distances from our simulation are in good agreement with the experimental data from extended X-ray absorption fine structure (EXAFS) spectroscopy. More important, we find that the two Ca ions bind differently in the complex, as a result of the hydrogen-bonding network around the whole complex. This finding invites confirmation from time-resolved EXAFS and has implications in understanding the dissociative equilibrium of the Ca2UO2(CO3)3 complex in water.
Introduction
The concentration of uranium in seawater is very minute at about 3.3 ppb, but the large mass of seawater contains about 4.5 billion metric tons of uranium.1 Mining uranium from seawater can provide an ideal sustainable alternative to current uranium mining methods (open pit, underground, and leaching) that create much environmental concern. In addition, extraction from seawater can provide a price ceiling for uranium that is of strategic importance in evaluating the economics of long-term supply of uranium for nuclear energy.2,3Much research has been focused on the development of selective methods for mining uranium in seawater. Currently, the most viable method is utilizing an amidoxime-functionalized polymer sorbent known as poly(acrylamidoxime) fibers.1–6 However, to make the uranium extraction from seawater economically viable, sorbent performance in terms of uranium uptake and uranium/vanadium selectivity needs to be further improved.1,7 To design a better ligand and sorbent for uranium extraction, it is necessary to understand the fundamentals about uranium speciation in seawater.
In aqueous solution, uranium exists as the stable oxocation with an oxidation state of U(VI), called uranyl – UO22+. Early work has focused on prying into the prominent equilibrium species bound to the uranyl complex in seawater8 and suggested the anionic [UO2(CO3)3]4− complex to be the dominant species in seawater. However, over the past two decades experimental data has shifted the consensus to cation-balanced complexes.9–13 Concentrations of magnesium (Mg2+) and calcium (Ca2+) in seawater are overwhelmingly larger than the concentration of U(VI), so the ternary Ca–UO2–CO3 or Mg–UO2–CO3 exists predominately in seawater. The complexation of Ca2+ with [UO2(CO3)3]4− has been validated experimentally by Bernhard et al.10 and Kelly et al.11 with extended X-ray absorption fine structure (EXAFS) spectroscopy. Most recently, Rao et al.13 examined the thermodynamics of uranium in seawater and the complexation between Ca/Mg and [UO2(CO3)3]4−. They concluded that in seawater pH (8.2) Ca2UO2(CO3)3 accounts for 58% of the total uranium in the solution while CaUO2(CO3)32− and MgUO2(CO3)32− account for 18% each and [UO2(CO3)3]4− accounts for only 6%.13 In addition, Rao et al. studied the binding of U(VI) with various types of ligands and the subsequent leaching process.14–19 In addition, the stability constant for the speciation of calcium is larger than magnesium.13
On the theoretical and computational side, work has been done on the binding of UO22+ with ligands using a cluster model18,20–23 and on the structure and dynamics of [UO2(CO3)3]4− in aqueous environment using molecular dynamics (MD) simulations.24–27 Hofer et al. examined the structure and dynamics of [UO2(CO3)3]4− in water using quantum mechanical charge field molecular dynamics (QMCF-MD).24,25 Kerisit et al. investigated the structure and dynamics of Ca2UO2(CO3)3 in aqueous solution with classical MD simulations based on non-polarizable force fields.26 Given the highly charged nature of Ca2+ ions and [UO2(CO3)3]4−, polarization may be important in describing the interaction between Ca2+ ions and [UO2(CO3)3]4− and between the complex and the water molecules. First principles MD at the electronic structure would be desirable, as the polarization effect is taken into account automatically. However, no such work has been done on Ca2UO2(CO3)3 in aqueous solution, to the best of our knowledge.
The present work seeks to describe the structure and solvation of Ca2UO2(CO3)3 in water using first principles MD based on density functional theory (DFT-MD for short) for the first time. Our goal is to provide a fundamental baseline understanding of the structure and solvation of Ca2UO2(CO3)3 in water in terms of Ca–UO2(CO3)3 and Ca–water interactions. The other goal is to compare DFT-MD simulations with the previous EXAFS data and classical MD simulations.
Computational methods
First-principles molecular dynamics simulations based on density functional theory (DFT-MD) and Born–Oppenheimer approximation were carried out using the Vienna ab initio simulation package with plane wave basis and periodic boundary conditions.28,29 The Kohn–Sham equations are solved with the all-electron projected augmented wave (PAW) method.30,31 We have chosen the Perdew–Burke–Ernzerhof (PBE) functional of the generalized-gradient approximation (GGA) for electron exchange and correlation.32 PBE is one of the most popular GGA functionals, providing a balanced description for diverse molecules and materials, instead of being designed for a special class of molecules or interactions. In the case of liquid water, it has been shown that the PBE functional can describe well the peak positions in the radial distribution functions of gOO and gOH for the liquid structure of water but it overestimates the peak heights, in comparison with the experiment, leading to over-structuring.33,34 Using hybrid functionals together with van der Waals interactions can soften the water structure, giving a better agreement with the experiment. But hybrid functionals are usually about two orders of magnitude more expensive than a pure DFT method such as GGA-PBE. We think that PBE is a reasonable choice in balancing accuracy and efficiency. In the ESI,† we provide an orbital-resolved local density of states for the U atom (Fig. S1†) from a snapshot of the Ca2UO2(CO3)3 complex in water to show that the bonding picture from the PBE functional is consistent with previous theoretical studies.35,36The MD calculations were carried out at 298 K in a canonical NVT ensemble for a periodic cubic box that contains one Ca2UO2(CO3)3 complex in a fixed number of water molecules. Three concentrations were examined: 0.53 M, 0.42 M, and 0.36 M, corresponding to one Ca2UO2(CO3)3 complex in a periodic box containing 100, 125, and 150 water molecules, respectively; the corresponding simulation box sizes and densities are also compared in Table 1. Here we note that since there is only one complex in the simulation box for the three concentrations, this approach cannot probe the correlations between complexes but serves more to test the potential presence of size artifacts. We determined the densities from constant-pressure classical MD simulations using force-field parameters from a previous study.26 The temperature was kept constant via a Nose–Hoover thermostat. A Verlet algorithm was used to integrate Newton's equation of motion with a time step of 1 femtosecond. After equilibration at 298 K for 15 ps, another 15 ps of production run was followed. Graphical visualization and analysis of the liquid structure packing of the uranium complex was examined with VMD.37
| Concentration (M) | Water molecules | Simulation box size (Å) | Density (g cm−3) |
|---|---|---|---|
| 0.36 | 150 | 17.5 | 1.13 |
| 0.42 | 125 | 16.7 | 1.14 |
| 0.53 | 100 | 15.7 | 1.21 |
Results and discussion
Interaction between calcium and carbonate
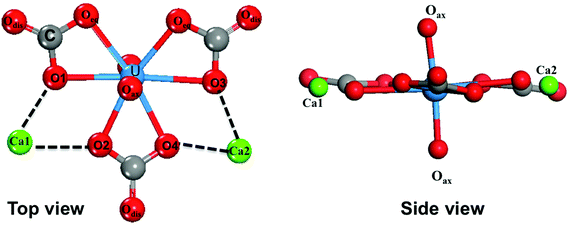
The most important structural feature of the Ca2UO2(CO3)3 species is the binding between the two Ca ions and the [UO2(CO3)3]4− ion. This interaction is mediated by the carbonate groups. As shown in Fig. 1, the three carbonate groups bind to the uranyl group on the equatorial plane in a bidentate mode; this structural model has been established from the crystal structure of the naturally occurring mineral Liebigite [Ca2UO2)(CO3)3·11H2O],38 fitting of the EXAFS data,10,11 and quantum mechanical modeling.20 There are three different oxygens in the uranium complex: the two axial oxygens (Oax) triple-bonded to U in the uranyl structure,35 six equatorial carbonate oxygens (Oeq) that are bonded to U, and three distal carbonate oxygens (Odis) not directly interacting with U. The two Ca2+ ions bind to the carbonate groups on the same plane; each Ca2+ ion binds to two equatorial oxygen atoms from two neighboring carbonate groups. In our DFT-MD simulations, interaction of the Ca ions to the [UO2(CO3)3]4− complex was monitored by the four Ca–Oeq distances (dashed lines in Fig. 1): Ca1–O1, Ca1–O2, Ca2–O3, and Ca2–O4.We placed an initial structure of the uranium complex as shown in Fig. 1 into a periodic water box at a concentration of 0.53 M. After equilibration at 298 K, a production run of 15 ps was used for statistical analysis. Fig. 2 shows the four Ca–Oeq distances during the 15 ps production trajectory. One can see that Ca1–O1 and Ca1–O2 distances exhibit fluctuations around 2.45–2.50 Å (Fig. 2a), while Ca2–O3 and Ca2–O4 around 2.35–2.40 Å (Fig. 2b). So in our simulation timeframe, the Ca2UO2(CO3)3 complex is very stable and maintains steady Ca–Oeq distances about 2.45 Å with a standard deviation of about 0.12 Å. Another important observation is that there exists asymmetry between the two Ca ions: Ca2 binds to [UO2(CO3)3]4− stronger than Ca1, as evidenced by the shorter average Ca2–Oeq distance (2.37 Å; Fig. 2b) than Ca1–Oeq (2.47 Å; Fig. 2a). Here we note that initially, we placed the Ca2UO2(CO3)3 complex randomly inside a water box. To test the robustness of the asymmetric structure, we tried several different initial configurations of water solvation around the Ca2UO2(CO3)3 complex and found that they always equilibrated to the asymmetric configuration after about 5 ps.
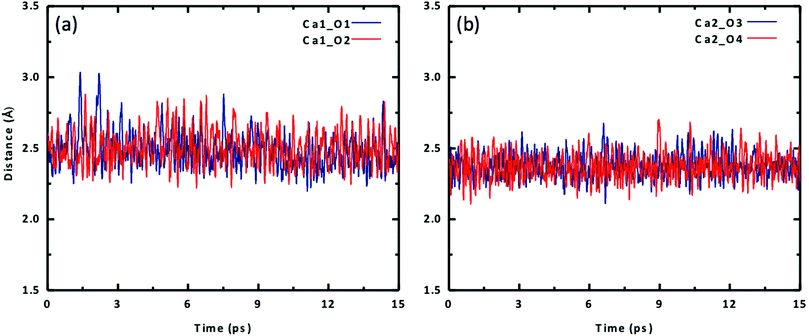 | ||
| Fig. 2 Change of Ca–O distances with time for the Ca2UO2(CO3)3 complex in water (0.53 M): (a) Ca1–O1 and Ca1–O2; (b) Ca2–O3 and Ca2–O4. See Fig. 1 for atom labels. | ||
To further examine the difference between the two Ca ions, we plot the radial distribution function (RDF) of carbonate Oeq atoms around each of the two Ca ions in Fig. 3. One can see that the stronger binding Ca2+ has a narrower and higher Oeq distribution (Fig. 3b), while the weaker Ca2+ has a broader and lower Oeq distribution (Fig. 3a). In addition, there is a slight difference between the two Oeq atoms binding to each Ca2+. For Ca1, Ca1–O1 is slightly shorter than Ca1–O2; for Ca2, Ca2–O4 is slightly shorter than Ca2–O3.
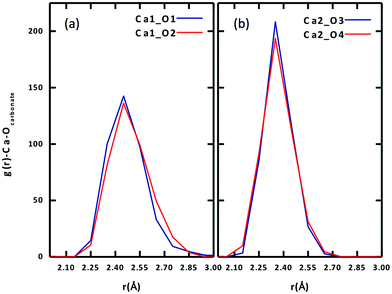 | ||
| Fig. 3 Radial distribution functions of equatorial carbonate oxygen (Oeq) around each Ca ion of the Ca2UO2(CO3)3 complex in water (0.53 M): (a) Ca1; (b) Ca2. See Fig. 1 for atom labels. | ||
To confirm the stability of the Ca2UO2(CO3)3 complex and the asymmetry of the two Ca2+ ions, we further simulated two lower concentrations (0.42 M and 0.36 M) and arrived at the same conclusions. The Ca2UO2(CO3)3 complex in the two lower concentrations is also stable in our simulation time frame, as shown by the steady maintaining of the binding of the two Ca2+ ions with the [UO2(CO3)3]4− complex. More interestingly, we found that the asymmetry between the two Ca2+ ions also persists in the two lower concentrations, indicating that this is likely an intrinsic feature of the Ca2UO2(CO3)3 complex in water. Fig. 4 displays the four Ca–Oeq distances as a function of the U concentration. Both the asymmetry between the two Ca2+ ions and the small difference between the two Oeq atoms for each Ca2+ ion are evident.
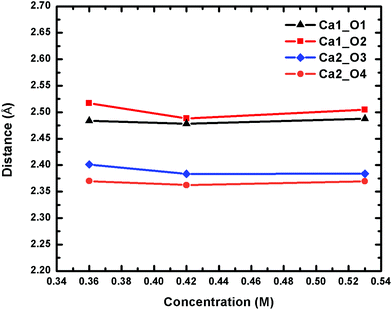 | ||
| Fig. 4 Change of the four Ca–Oeq distances of the Ca2UO2(CO3)3 complex in water at three different concentrations. See Fig. 1 for atom labels. The distances are averages over 15 ps trajectories; the standard deviations for each data point are shown in Fig. S2 of the ESI.† | ||
Interaction between calcium and water
The interaction between calcium and carbonate in the Ca2UO2(CO3)3 complex is the most important information that we obtained from our DFT-MD simulations. The asymmetry between the two Ca2+ ions must be closely related to the water molecules around the Ca2UO2(CO3)3 complex. We now analyze the interaction between the two Ca2+ ions and the water molecules. Fig. 5 shows radial distribution functions (RDFs) of oxygen atoms from the water molecules around the two Ca2+ ions both separately and together. One can see that the solvation shell around Ca1 has an average Ca–Owater distance of 2.45 Å (with a standard deviation of 0.12 Å) and the integrated RDF (with a cutoff at 3.0 Å) gives the coordination number of five; in other words, there are five molecules around Ca1 in addition to the two Oeq atoms from two carbonate groups. On the other hand, Ca2 has four water molecules in the solvation shell with an average Ca–Owater distance of 2.35 Å (with a standard deviation of 0.09 Å). So together, the average coordination number of the two Ca2+ ions is 4.5 in terms of water molecules. We further examined the RDF of water oxygens around Ca2+ ions for the two lower concentrations and found the same trend of five water molecules around Ca1 and four water molecules around Ca2. In comparison, previous classical MD simulations predicted that both calcium ions have five water molecules in the first hydration shell,26 similar to the case of Ca1 in our simulation.Solvation environments of the two calcium ions
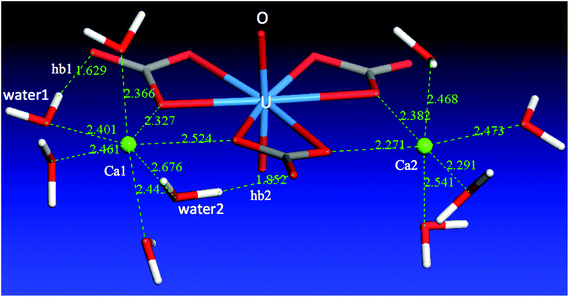
From the above discussion of the Ca2UO2(CO3)3 complex in water, we can clearly see that the difference between the two Ca ions is reflected in both the Ca–carbonate and the Ca–water interactions. The two interactions are in fact correlated: Ca1 has weaker binding with the [UO2(CO3)3]4− complex, five molecules in the solvation shell, and a total of seven coordination bonds; Ca2 has stronger binding with the [UO2(CO3)3]4− complex, four molecules in the solvation shell, and a total of six coordination bonds. Ca2 has a tighter solvation shell, so both average Ca2–Owater and Ca2–Ocarbonate distances are shorter than Ca1–Owater and Ca1–Ocarbonate distances, respectively.What causes the asymmetry of binding and solvation between the two Ca ions in the Ca2UO2(CO3)3 complex? To answer this question, we analyzed the solvation environment of the complex from the views of Ca–carbonate, Ca–water, and carbonate–water interactions together, as shown in Fig. 6. One can see that there are three water molecules in the equatorial plane coordinating to Ca1, instead of two in the case of Ca2. The reason why Ca1 can have one more water molecule in the equatorial plane is that two of the three water molecules (water1 and water2 in Fig. 6) are interacting with both Ca1 and the carbonates. From Fig. 6, one can see that both water1 and water2 form hydrogen bonding (hb1 and hb2) with the two distal oxygen atoms of the two carbonate groups. These two hydrogen bonds pull water1 and water2 closer to the Ca2UO2(CO3)3 complex, thereby leaving space for a third water molecule to enter the equatorial plane. In other words, it is the hydrogen-bonding network around the Ca2UO2(CO3)3 complex that leads to the difference in solvation and binding between the two Ca ions. We further examined the two lower concentrations and found the same solvation environment around the Ca2UO2(CO3)3 complex that confirmed the role of the hydrogen-bonding network in differentiating the two Ca ions in the Ca2UO2(CO3)3 complex.
To further explain the asymmetry between the two Ca ions, we show a schematic drawing (Fig. 7) of the equatorial plane around U. One can see that Ca1 is coordinated by both water1 (W1) and water2 (W2), while W1 is hydrogen bonded to O5 of carbonate1 (C1) and W2 is hydrogen bonded to O6 of carbonate2 (C2). As a result, the hydrogen bonding pulls the two carbonate groups closer (indicated by the two black arrows), so Ca1 is “squeezed” a little further away from O1 and O2. On the other hand, the O3–U–O4 angle becomes wider (indicated by the red double arrow), thereby allowing Ca2 to come closer to O3 and O4. Another way to think about this is via carbonate1. If Ca1 and Ca2 were symmetric in binding, the hydrogen bonding around carbonate1 (C1) would be symmetric. But as shown in Fig. 7, the hydrogen bonding around carbonate1 is asymmetric that eventually leads to the asymmetry in binding between Ca1 and Ca2.
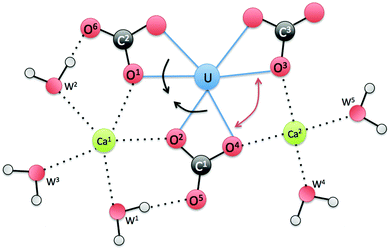 | ||
| Fig. 7 A schematic view of the equatorial plane around U for the Ca2UO2(CO3)3 complex in water. W stands for water. | ||
Solvation environments of the whole complex
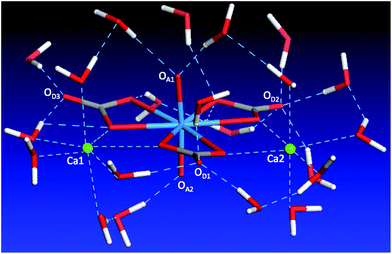
The discussion above shows the importance of the hydrogen-bonding network in dictating the complex geometry. To further analyze this network, we examined the first solvation shell of the whole complex, namely, the water molecules in direct interaction with the complex. Since we have analyzed the water solvation around the two Ca ions, here we focus our discussion on the carbonate and uranyl oxygens. One can see from Fig. 8 that the top uranyl oxygen (OA1) has two water molecules hydrogen-bonded to it, while the bottom uranyl oxygen (OA2) has one. Moreover, one can see strong solvation of the carbonate distal oxygens by water: OD1 is hydrogen-bonded by three water molecules, OD2 by four, OD3 by two. In addition, the two carbonate equatorial oxygens not interacting with the Ca ions are also solvated by water. Together with the water molecules around the two Ca ions, we found that there are 21 molecules in the first solvation shell. This large solvation shell indicates the necessity of using the explicit solvation model to address the structure, thermodynamics, and chemistry of the aqueous Ca2UO2(CO3)3 complex.Ca–U distances
Besides speciation studies based on thermodynamics,10,12,13 the most direct characterization of the Ca2UO2(CO3)3 complex in water has been EXAFS studies of the coordination shells around the central U atom.10,11 Since the Ca–U distance is a key piece of information available from fitting the EXAFS spectra, we examined in detail the Ca–U distances for the Ca2UO2(CO3)3 complex in water. Fig. 9 shows the RDF of Ca ions around the U atom at three different concentrations. One can see that the asymmetry between the two Ca ions is also reflected in the Ca–U distances: the stronger-binding Ca2 is about 4.05 Å away from U and has a narrower distribution of the Ca2–U distance (standard deviation: 0.10 Å), while the weaker-binding Ca1 is about 4.15 Å away from U and has a broader distribution of the Ca1–U distance (standard deviation: 0.12 Å). In addition, the three concentrations show very consistent distributions of Ca–U distances (Fig. 9).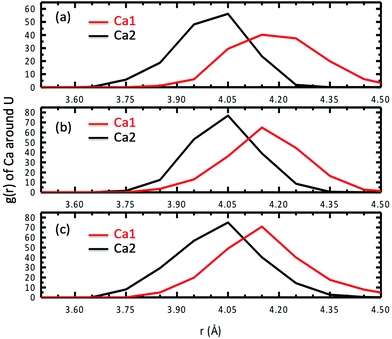 | ||
| Fig. 9 Radial distribution functions of Ca ions around the U atom for three different concentrations of Ca2UO2(CO3)3 in water: (a) 0.53; (b) 0.42; (c) 0.36 M. | ||
Comparison with the literature
To our knowledge, the present study is the first DFT-MD simulation of the Ca2UO2(CO3)3 complex in water. It would be very informative to compare the present DFT-MD results with previous experiments and molecular-mechanical MD simulations (MM-MD) based on empirical force fields. For comparison with the experiment, we focus mainly on the liquid-phase EXAFS analysis on the structure of the Ca2UO2(CO3)3 complex from Kelly et al.11 and Bernhard et al.10 In the model fitting of the EXAFS spectra, they assumed that the two U–Ca distances are the same. To directly compare with their data, we therefore computed the total RDF of Ca ions around U and obtained an average Ca–U distance of about 4.07 Å at the peak of the RDF. Table 2 compares our DFT-MD simulation with the EXAFS data (EXAFS-1 from Kelly et al.11 and EXAFS-2 from Bernhard et al.10) and the MM-MD simulations26,39 for the key distances, including the U–Ca distance. One can see that the DFT-MD results are in good agreement with experiment. Our U–Ca distance is closer to the value from Kelly et al. (4.02 Å) than the one from Bernhard et al. (3.94 Å). Compared with the MM-MD simulation from Kerisit and Liu (MM-MD-1),26 our DFT-MD simulation gives a U–Odis distance much closer to the experiment. Compared with the MM-MD simulation from Doudou et al. (MM-MD-2),39 our DFT-MD simulation yields a U–Ca distance in better agreement with the experiment.| Method | U–Oeq | U–Oax | U–Odis | U–Ca | U–C | Ref. |
|---|---|---|---|---|---|---|
| a Present work (p.w.) for the concentration of 0.36 M: the distances are the peak positions in the radial distribution functions; the error bars are the standard deviations of the distances averaged over 15 ps trajectories. b A modified force field for calcite was used for the carbonate ion (ref. 39). c The AMBER GAFF force field was used for the carbonate ion (ref. 39). n/a: not provided in the reference. | ||||||
| DFT-MDa | 2.45 ± 0.12 | 1.85 ± 0.04 | 4.15 ± 0.14 | 4.07 ± 0.15 | 2.85 ± 0.10 | p.w. |
| EXAFS-1 | 2.45 ± 0.01 | 1.78 ± 0.01 | 4.11 ± 0.07 | 4.02 ± 0.02 | 2.89 ± 0.01 | 11 |
| EXAFS-2 | 2.44 ± 0.07 | 1.81 ± 0.03 | 4.22 ± 0.04 | 3.94 ± 0.09 | 2.90 ± 0.02 | 10 |
| MM-MD-1 | 2.43 | 1.83 | 3.97 | 4.00 | 2.88 | 26 |
| MM-MD-2ib | 2.41 | n/a | n/a | 4.12 | n/a | 39 |
| MM-MD-2iic | 2.41 | n/a | n/a | 4.18–4.84 | n/a | 39 |
Implications of the present findings
As we discussed above, a key finding from the present DFT-MD simulation is the asymmetry between the two Ca ions in the Ca2UO2(CO3)3 complex. A key issue here is whether and how often the two Ca ions can switch their bonding environments, namely, from Ca1-weak binding/Ca2-strong binding to Ca1-strong binding/Ca2-weak binding. Such switching will be closely related to water exchange in the first solvation shell of the Ca ions. In our limited simulation timeframe (∼50 ps), we did not observe such switching. This implies that our brute-force DFT-MD is unlikely to address this issue due to its limited accessible timescale that is too short in comparison with the timescale of such switching. We are currently pursuing two lines of research to address this issue that will be published in the near future: (a) DFT-MD coupled with metadynamics to estimate the free-energy profile of such switching; (b) classical MD based on force fields to increase the timescale to about ∼100 ns.Despite the limited timescale of the present DFT-MD simulation, our finding of the asymmetry between the two Ca ions in the aqueous Ca2UO2(CO3)3 complex in the timescale of 10 to 100 ps may be confirmed by time-resolved EXAFS that can measure the variation in bond length in ps timescale.40 Here we suggest an experiment to use time-resolved EXAFS to measure the Ca–U distances of the aqueous Ca2UO2(CO3)3 complex at ps snapshots. Another implication from our finding concerns dissociation of Ca2UO2(CO3)3 to CaUO2(CO3)32−. Rao et al. found that in seawater conditions, Ca2UO2(CO3)3 and CaUO2(CO3)32− account for 58% and 18% of total U(VI), respectively.13 In other words, Ca2UO2(CO3)3 is in equilibrium with CaUO2(CO3)32− and free Ca2+ in seawater. Our finding suggests that Ca1 is much more likely to break away from Ca2UO2(CO3)3 than Ca2, to form CaUO2(CO3)32−. This information will be useful for studies of the mechanism of Ca2UO2(CO3)3 dissociation with or without an attacking ligand. We plan to also use DFT-MD coupled with metadynamics to examine the free-energy profile of the dissociation mechanism. We suspect that there may exist some intermediate states of the Ca2UO2(CO3)3 complex before it becomes [CaUO2(CO3)3]2− and free Ca2+. For example, one likely configuration can have one Ca ion coordinating to one equatorial and one distal oxygen from the same carbonate group, while the other Ca ion coordinates “normally” to two equatorial oxygens of two different carbonate groups.
Conclusion
We have simulated the neutral Ca2UO2(CO3)3 complex in water using first principles molecular dynamics based on density functional theory (DFT-MD). Three concentrations (0.53, 0.42, and 0.36 M) feasible to DFT-MD simulations were examined. In the accessible timescale (∼30 ps), we found that the structure of the Ca2UO2(CO3)3 complex is very stable where the two Ca ions bind to the carbonate groups on the same equatorial plane. We found that one Ca ion binds to the center UO2(CO3)34− anion more stronger than the other Ca ion. This asymmetry of binding between the two Ca ions is reflected in several aspects: the stronger binding Ca has shorter Ca–Ocarbonate bonds, shorter Ca–U distance, and four coordinating water molecules, while the weaker binding Ca has longer Ca–Ocarbonate bonds, longer Ca–U distance, and five coordinating water molecules. This finding suggests that using time-resolved EXAFS spectra may confirm the asymmetry in binding of the two Ca ions in the aqueous Ca2UO2(CO3)3 complex, since our DFT-MD simulation shows in general good agreement in terms of key distances with the EXAFS experiments.Acknowledgements
This research was supported by the US-DOE Office of Nuclear Energy – Nuclear Energy University Programs (Grant No. DE-NE0008397).Notes and references
- J. Kim, C. Tsouris, R. T. Mayes, Y. Oyola, T. Saito, C. J. Janke, S. Dai, E. Schneider and D. Sachde, Sep. Sci. Technol., 2013, 48, 367–387 CrossRef CAS.
- J. Kim, C. Tsouris, Y. Oyola, C. J. Janke, R. T. Mayes, S. Dai, G. Gill, L. J. Kuo, J. Wood, K. Y. Choe, E. Schneider and H. Lindner, Ind. Eng. Chem. Res., 2014, 53, 6076–6083 CrossRef CAS.
- S. Das, W. P. Liao, M. Flicker Byers, C. Tsouris, C. J. Janke, R. T. Mayes, E. Schneider, L. J. Kuo, J. R. Wood, G. A. Gill and S. Dai, Ind. Eng. Chem. Res., 2015 DOI:10.1021/acs.iecr.5b03210.
- T. Kago, A. Goto, K. Kusakabe and S. Morooka, Ind. Eng. Chem. Res., 1992, 31, 204–209 CrossRef CAS.
- A. Katakai, N. Seko, T. Kawakami, K. Saito and T. Sugo, J. Atom. Energy Soc. Jpn., 1998, 40, 878–880 CrossRef CAS.
- N. Seko, A. Katakai, S. Hasegawa, M. Tamada, N. Kasai, H. Takeda, T. Sugo and K. Saito, Nucl. Technol., 2003, 144, 274–278 CAS.
- S. P. Kelley, P. S. Barber, P. H. K. Mullins and R. D. Rogers, Chem. Commun., 2014, 50, 12504–12507 RSC.
- J. W. Morse, P. M. Shanbhag, A. Saito and G. R. Choppin, Chem. Geol., 1984, 42, 85–99 CrossRef CAS.
- G. Bernhard, G. Geipel, V. Brendler and H. Nitsche, Radiochim. Acta, 1996, 74, 87–91 CrossRef CAS.
- G. Bernhard, G. Geipel, T. Reich, V. Brendler, S. Amayri and H. Nitsche, Radiochim. Acta, 2001, 89, 511–518 CrossRef CAS.
- S. D. Kelly, K. M. Kemner and S. C. Brooks, Geochim. Cosmochim. Acta, 2007, 71, 821–834 CrossRef CAS.
- J. Y. Lee and J. I. Yun, Dalton Trans., 2013, 42, 9862–9869 RSC.
- F. Endrizzi and L. F. Rao, Chem. – Eur. J., 2014, 20, 14499–14506 CrossRef CAS PubMed.
- P. Di Bernardo, P. L. Zanonato, F. Benetollo, A. Melchior, M. Tolazzi and L. F. Rao, Inorg. Chem., 2012, 51, 9045–9055 CrossRef CAS PubMed.
- G. X. Tian, S. J. Teat and L. F. Rao, Dalton Trans., 2013, 42, 5690–5696 RSC.
- C. Xu, G. X. Tian, S. J. Teat and L. F. Rao, Inorg. Chem., 2013, 52, 2750–2756 CrossRef CAS PubMed.
- H. B. Pan, W. S. Liao, C. M. Wai, Y. Oyola, C. J. Janke, G. X. Tian and L. F. Rao, Dalton Trans., 2014, 43, 10713–10718 RSC.
- X. Q. Sun, G. X. Tian, C. Xu, L. F. Rao, S. Vukovic, S. O. Kang and B. P. Hay, Dalton Trans., 2014, 43, 551–557 RSC.
- C. J. Leggett and L. F. Rao, Polyhedron, 2015, 95, 54–59 CrossRef CAS.
- J. D. Kubicki, G. P. Halada, P. Jha and B. L. Phillips, Chem. Cent. J., 2009, 3, 10 CrossRef PubMed.
- S. Vukovic, L. A. Watson, S. O. Kang, R. Custelcean and B. P. Hay, Inorg. Chem., 2012, 51, 3855–3859 CrossRef CAS PubMed.
- S. Vukovic and B. P. Hay, Inorg. Chem., 2013, 52, 7805–7810 CrossRef CAS PubMed.
- C. W. Abney, S. B. Liu and W. B. Lin, J. Phys. Chem. A, 2013, 117, 11558–11565 CrossRef CAS PubMed.
- A. O. Tirler, A. K. H. Weiss and T. S. Hofer, J. Phys. Chem. B, 2013, 117, 16174–16187 CrossRef CAS PubMed.
- A. O. Tirler and T. S. Hofer, J. Phys. Chem. B, 2014, 118, 12938–12951 CrossRef CAS PubMed.
- S. Kerisit and C. X. Liu, Geochim. Cosmochim. Acta, 2010, 74, 4937–4952 CrossRef CAS.
- S. Kerisit and C. X. Liu, J. Phys. Chem. A, 2013, 117, 6421–6432 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- R. A. DiStasio, B. Santra, Z. F. Li, X. F. Wu and R. Car, J. Chem. Phys., 2014, 141, 084502 CrossRef PubMed.
- K. Forster-Tonigold and A. Gross, J. Chem. Phys., 2014, 141, 064501 CrossRef PubMed.
- R. G. Denning, J. Phys. Chem. A, 2007, 111, 4125–4143 CrossRef CAS PubMed.
- N. Kaltsoyannis, Inorg. Chem., 2000, 39, 6009–6017 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS.
- K. Mereiter, Tscher. Miner. Petrog., 1982, 30, 277–288 CrossRef.
- S. Doudou, K. Arumugam, D. J. Vaughan, F. R. Livens and N. A. Burton, Phys. Chem. Chem. Phys., 2011, 13, 11402–11411 RSC.
- J. Chen, H. Zhang and P. M. Rentzepis, J. Phys. Chem. A, 2010, 114, 2751–2756 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5dt04576b |
| This journal is © The Royal Society of Chemistry 2016 |