Noble metal plasmonic nanostructure related chromisms
Chao
Zhang
,
Ling-Dong
Sun
* and
Chun-Hua
Yan
*
Beijing National Laboratory for Molecular Sciences, State Key Laboratory of Rare Earth Materials Chemistry and Applications, PKU-HKU Joint Laboratory in Rare Earth Materials and Bioinorganic Chemistry, Peking University, Beijing 100871, China. E-mail: sun@pku.edu.cn; yan@pku.edu.cn; Fax: +86-10-62754179; Tel: +86-10-62754179
First published on 8th December 2015
Abstract
Chromism focuses on the phenomena of color change, and the studies in the related area have conventionally been centered on organic dyes. In recent decades, noble metal nanostructures, featured with rich optical properties arising from their characteristic localized surface plasmon resonances, have emerged as an alternative family of color-rendering agents, and have therefore been introducing new trends into the research realm of chromisms. Here in this review we summarize the related studies on noble metal plasmonic nanostructure related chromisms, which are sorted into four major categories, namely, solvatochromism, sorptiochromism, aggregachromism and chronochromism. For each category, the basic principles (some with comparison to those for dye-related systems) are delineated, followed with examples illustrating the performances and utilizations of representative systems. Of note, we put particular emphasis on the category of chronochromism, which, in our opinion, has not received as much deserved attention yet promises great potential in practical applications. In the final section, we discuss the challenges that plasmonic nanostructures are currently facing, and outlook the opportunities that may emerge in the near future.
1. Introduction
Human beings assimilate information everyday using our five basic senses, namely, sight, hearing, smell, taste and touch. Among all sorts of information being perceived, color is probably the most conspicuous one, for being directly discernible by the naked eye. Therefore, a change in color is arguably the most intuitively detectable signal to report the occurrence of a particular event, or to convey specific information coded therein. Examples can be found both in nature and in human world, to name a few, the ripening process of blackberries (Rubus fruticosus) during which their color changes from green to red and to dark purple, the appearance of iridescent blue rings on the venomous blue-ringed octopuses (Hapalochlaena lunulata) when they are agitated, and the traffic lights that regulate our daily traffic.The term “chromism” is coined by scientists to refer to the phenomena where a compound or material, usually upon the application of a certain external stimulus, undergoes a change in color (often reversible, but not in all the cases).1 The stimulus origin can be physical (like light, heat and mechanical forces) or chemical (like ions, gases and solvents); thereby, chromic phenomena can be classified into a number of categories, like photochromism,2 thermochromism,3,4 mechanochromism,5–9 vapochromism,10 and solvatochromism.11 Some chromophores like squaraine dyes exhibit a color change when they form aggregates (dimers and higher oligomers), thus constituting good examples of “aggregachromism”.12 And particularly, the term “chronochromism” denotes the processes where a system changes its color with respect to the passage of time.1 It should be noted that these categories do not cover all chromic phenomena; also, there may also be some overlap between different categories of chromisms.
Besides classifying according to the nature of stimuli, there exists an alternative classification manner. By the pathway how the color change is effected, chromic phenomena can be sorted into direct and indirect chromisms.1 For indirect chromisms, the applied stimulus does not instantly result in the color change, but rather induces variation in a certain intermediate index (physical or chemical) that would in turn lead to the color change. Therefore, it can be seen that indirect chromisms could be realized by the reconfiguration of direct chromisms. This is of great technological importance because by judicious design and engineering, direct chromic systems can be reconfigured to respond to stimuli that they are not innately sensitive to, and therefore immensely extend their practical applicability.
For chromism, coloring agents are always at the central position. Conventionally, the colorants of interest are predominantly organic dyes, particularly in solution chemistry. Benefiting from their highly variable molecular structures, organic dyes exhibit a wide spectrum of colors, which are usually synthetically adjustable. Therefore, a major part of chromism-related studies thus far have been focused on the dye family. However, the inherent instability of organic dyes makes them susceptible to a number of common factors, such as light, heat and atmospheric oxygen, which oftentimes leads to irreversible degradation, and undermines the robustness of relevant materials. As a result, scientists have been looking for alternative chromophores that are as color-rendering as organic dyes, but with superior performances, in particular, improved stability against environmental factors. And plasmonic noble metal nanostructures,13–24 which during the past few decades have witnessed an explosion of research interest, constitute a promising candidate family.
Metal nanostructures are known for their ability to support localized surface plasmon resonance (LSPR), that is, the collective oscillation of their conduction band electrons.13–15 The LSPR behavior enables the metal nanostructures to absorb and scatter light near their resonance frequencies. And when the surface plasmon resonates near the visible range of the electromagnetic spectrum, the metal nanoparticles (MNPs) would exhibit light extinction (absorption and scattering, collectively), and are then colored.
Therefore, the physics underlying the color rendering effect of metal nanostructures is quite different from that of organic dyes (that is, electronic excitation between molecular orbitals). This endows plasmonic nanostructures with a wealth of distinguished optical properties. Some previous results showed that, for MNPs, their extinction cross sections are typically larger than their physical cross sections, quite contrary to the cases for dye molecules, implying that MNPs are able to interact with electromagnetic irradiation that is even outside their physical boundaries.21 This particular capability confers on MNPs generally high extinction coefficients. Their mass-specific extinction cross sections are typically on the same order of magnitudes with those of commercialized dyes.15,21 When normalized by the amount of substance, the molar extinction coefficients of MNPs are commonly in the range of 108–1010 L mol−1 cm−1 (per mole of NPs), in contrast to 103–105 L mol−1 cm−1 typically for conventional organic chromophores.25 Therefore, as far as the chromogenic effect is concerned, plasmonic nanostructures give comparable (or even better) performances with respect to organic dyes. Besides, for noble metal NPs, the superior stability, low toxicity and relatively simple chemistry in preparation and functionalization also promise great potential in a broad range of practical applications, such as surface-enhanced spectroscopy,21,26–32 sunlight harvesting,33–37 light-assisted catalysis,24,38–40 optical storage41,42 and optical sensors.43–45
Currently, the plasmonic MNPs that are most extensively and intensively studied are gold and silver nanostructures, by virtue of their suitable resonance frequencies, inert chemical nature and well established preparation protocols (such as lithographical fabrication, seed-mediated growth, and thermolysis in high-boiling-point solvent). Besides gold and silver, other metals, such as palladium,46–49 copper50–53 and aluminium,54–56 also exhibit interesting LSPR properties; however, there are considerably fewer reports on these systems, probably owing to their chemical instability (for example, copper is susceptible to oxidation), or their unsatisfactory spectral properties (for palladium and aluminium, the resonance wavelengths are normally in the ultraviolet region).
The LSPR properties of metal nanostructures are dependent on several factors, which are discussed as follows. (i) The chemical composition. Gold nanospheres with a diameter less than 50 nm usually give a LSPR peak around 520 nm and thus a red color (dispersed in water),15 while for silver nanospheres with comparable sizes, the LSPR maximum is located near 420 nm, and the corresponding colloidal solution appears yellow.57 Aluminum, in comparison, resonates in the ultraviolet region.54 (ii) The particle size. For example, a recent study shows that for spherical gold NPs with diameters ranging from 24 nm to 221 nm, the dipolar plasmon resonance modes exhibit a systematic red shift in peak wavelength from roughly 520 nm to 810 nm; meanwhile, for NPs with larger sizes, high-order plasmon resonance modes become more prominent. Therefore, the colloidal solutions of these gold NP samples display successive colors ranging from red to violet to yellow.58 (iii) The particle shape. Altering the particle shape is probably the most feasible and effective way to tune the LSPR properties of metal nanostructures. In contrast to highly symmetrical nanospheres, particles with anisotropic geometries offer richer plasmonic modes. For instance, gold nanorods display two LSPR peaks, respectively ascribed to the transverse and longitudinal plasmon resonances; the position of the latter resides at the longer wavelength end, and is continuously tunable by synthetically altering the MNP's aspect ratio. Plenty of other shapes have also been prepared and studied, such as cubes,59 wires,60 plates,61 as well as cages.62 (iv) The surrounding environment. The LSPR maxima are also sensitive to MNPs’ local microenvironments, most importantly, the dispersing medium (solvents or polymer matrixes), and surface status (stabilizing agents, adsorbed species, and oxidation layer). (v) The aggregation manner. When brought in close vicinity (usually tens of nanometers and less), the electron oscillation in neighboring individual MNPs would interact with each other, leading to plasmonic coupling and new plasmonic bands.15 Therefore, the aggregation from separate MNPs, as well as the disintegration of MNP aggregates, is always accompanied by changes in LSPR properties.
From the above discussion it can be seen that the optical properties of metal nanostructures are sensitive to a number of factors that are foreign to organic dyes. And therefore, the rational manipulation of these factors would effectively regulate the LSPR behaviors, thus forming the basis of noble metal plasmonic nanostructure related chromisms.
2. Noble metal plasmonic nanostructure related chromisms
In this section we will summarize and discuss noble metal plasmonic nanostructure related chromisms, which are sorted into four major categories, namely, solvatochromism, sorptiochromism, aggregachromism and chronochromism. In addition, related miscellaneous chromisms will also be briefly discussed. Wherever we see proper, comparison with dye-related systems will be made. Also, it should be noted that, as the reports on relevant fields are quite abundant, and there already exist a number of comprehensive reviewing articles that partially overlap with the topics discussed below,13–15,44 here we do not attempt to deliver an exhaustive overview, but rather would select the most representative and systematic examples to demonstrate the very essence of each specific category. In particular, the area of chronochromism, to the best of our knowledge, has not received much deserved scientific interest and research scrutiny from the academic community. Therefore here in this review, we will put particular emphasis on this topic by elaborating upon the underlying mathematical and chemical principles, and present relevant examples with important practical applications.A. Solvatochromism
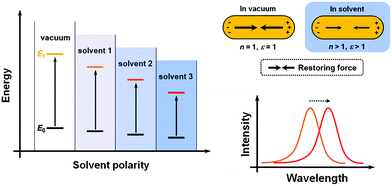
Conventionally, the term “solvatochromism” describes the phenomena that the absorption maximum of certain dye molecules shifts in different solvents. This is due to the change in solvation energy that stabilizes the electronic states of the dye molecules when the properties of the solvents vary. It is known that the absorption of organic dyes arises from the electronic transitions from the ground state (E0) and excited state (usually the first excited state, E1), and the absorption maximum is determined by the energy gap between E0 and E1 (Fig. 1A). When the effect of solvation is considered, the energy of both E0 and E1 would be lowered than in a vacuum, but usually not equally lowered. For a wealth of dye molecules, their E1 configurations have larger dipole moments than the E0, therefore, as the solvent polarity increases, E1 becomes more stabilized than E0, thus reducing the energy gap, and the absorption peak shifts towards the red end. These phenomena form the subcategory of positive solvatochromism. And conversely, certain dye molecules with an E0 configuration more polar than E1 display negative solvatochromism, meaning that their absorption peaks shift to the blue end in solvents with higher polarity. Therefore, it can be seen that the solvatochromism in conventional dye systems is dependent upon the polarity of the solvents.For plasmonic MNPs, the mechanism of solvatochromism is fundamentally different. As mentioned before, the extinction of MNPs arises from the plasmon resonance, which is the periodic oscillation of free electron cloud against the metal crystal lattice. In excited MNPs, the oscillation leads to a displacement between the centers of positive and negative charges, which in turn produces a Coulombic restoring force (Fig. 1B). As dictated by Coulomb's law, the intensity of restoring force is dependent on the dielectric constant ε of the environmental medium. When the solvent does not show significant absorption near the LSPR wavelengths, the dielectric constant of the solvent is equal to the square of the refractive index (RI) n. When the RI of the solvent increases, the Coulombic restoring force is reduced, the plasmon resonance frequency is then lowered, and the LSPR wavelength shows a red shift. Therefore, the solvatochromism for plasmonic nanostructures is dependent on the dielectric constant (ε), and in turn, the RI (n) of the solvents.
Such a particular mechanism of solvatochromism for MNPs forms the basis of a number of applications, most prominently, detecting and sensing specific target molecules. The detection limit is clearly dependent on the MNP's sensitivity to the RI of the solvents. Therefore, a major task in this research field is to explore metal nanostructures with different compositions, sizes and shapes, to assess their solvatochromic performances, and to screen for those nanostructures with higher sensitivities.
For MNPs, their solvatochromic features can be quantitatively characterized in two ways. One is to measure the extinction (or transmission) spectrum of NPs dispersed in solution (or deposited on transparent substrates). This method can be conducted on a common spectrometer, and thus is relatively simple, fast and inexpensive. However, the information obtained in this manner results from the ensemble behavior of MNPs. Therefore, the nanostructures being sampled are required to be highly monodispersed, that is, with uniform size and shape. The other method is to measure the dark-field scattering of each single particle, usually immobilized on a substrate.63 This method allows the nanostructures to be individually addressed, enabling higher spatial resolution, larger multiplexing capacity as well as miniaturization. However, the measurement is conducted on relatively advanced instruments (i.e., dark-field scattering microscope/spectrometer), and the nanostructures being investigated are required be large enough in size so as to give detectable scattering signals.
The RI sensitivity of MNPs is usually expressed by wavelength shift per RIU (refractive index unit). Experimentally, the RI sensitivity of a particular sample is obtained by recording the LSPR peak wavelength in solvents of different nature. The spectral shift can be plotted against the RI values, which generally shows a roughly linear dependence, and the slope then corresponds to the RI sensitivity, with the unit of nm RIU−1. Another important parameter commonly used to characterize the solvatochromic performances is the figure of merit (FOM), which is defined as the RI index divided by the full width at half maximum (FWHM) of the extinction band. Nanostructures with high FOM values are preferred in application because a tiny change in the RI would result in more discernible spectral shifts and larger intensity variations at a specified wavelength.
Several characteristics of MNPs would influence their solvatochromic performances, including shape, size and chemical composition. Wang et al. conducted a series of systematic investigations on these topics, and summarized the effects of these characteristics.63–66 The shape effect dictates that gold nanostructures with higher symmetries (such as spheres, cubes) generally have lower RI sensitivities than those with lower symmetries (such as rods, bipyramids); for gold nanorods (and nanobipyramids) of similar diameters, those with larger aspect ratios (and therefore longer longitudinal plasmon wavelengths) possess higher RI sensitivities; and for nanostructures displaying similar plasmon wavelengths, those with sharp apexes (like bipyramids) show superior RI sensitivities and FOMs to those with relatively dull vertexes (like rods).64 Size-specific studies revealed that for nanorods with similar aspect ratios and plasmon peak wavelengths, particles with a larger size exhibit higher RI sensitivities than the smaller ones.65 As for the composition effect, the authors compared gold and silver nanocubes with the same geometry and similar size and plasmon wavelengths, and found that silver is more than twice as sensitive to the RI as gold; they also compared gold nanobars with gold/silver core/shell nanobars, and concluded that the latter gives better performances than the former in both RI sensitivity and FOM.66
Recently, Shen et al. demonstrated a plasmonic sensing platform with exceptional performances.67 Arrays consisting of submicrometer gold mushrooms were lithographically fabricated (Fig. 2). Benefiting from a narrow band (with a FWHM around 10 nm) in the near-infrared region as well as a high RI sensitivity (around 1010 nm RIU−1), the sensing platform presented a FOM value as high as 108, comparable to the upper limit of commercially available sensors constructed based on propagating surface plasmon resonances.
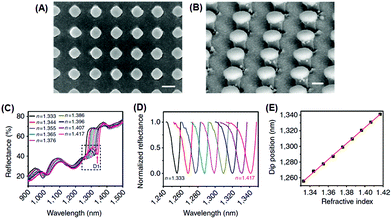 | ||
| Fig. 2 Sensing platform comprising gold mushroom arrays. (A, B) Scanning electron microscopy images of gold mushroom arrays. (C) Reflectance spectra of gold mushroom arrays immersed in solutions with varying refractive indexes (n). (D) Spectral profiles for D1 after normalization. (E) The linear correlation between the dip wavelength and the refractive index (reprinted with permission from ref. 67). | ||
Besides using spectral shifts, there are also alternative methods to assess the solvatochromic behaviors of plasmonic nanostructures. Notably, Huang et al. employed the tricolor RGB (red, green and blue) system to code the scattering signals of gold NPs on substrates (Fig. 3).68 When the solvent was changed from water to oil, the green dots in the dark-field scattering image visibly turned yellow, and the corresponding RGB analysis of the scattering light revealed a distinctly decreased green component and increased red components, confirming the validity and feasibility of this protocol. The authors claimed that this method is simpler to achieve, and may allow for larger multiplexing capacity in high-throughput analysis.
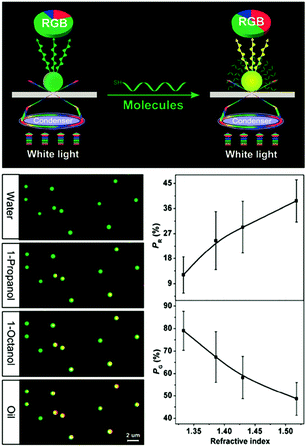 | ||
| Fig. 3 (Top) Schematic illustration of the dark-field scattering signal interpreted into tricolor RGB values. (Bottom left) Scattering images of gold NPs immersed in solvents with different refractive indexes, showing the green dots for water gradually turned yellow. (Bottom right) Results of RGB analysis showing that as the refractive index of the surrounding solvent increases, the red component (PR) increases while the green component (PG) decreases. (Reprinted with permission from ref. 68.) | ||
B. Sorptiochromism
Sorptiochromism refers to the phenomena of spectral shift resulting from certain species adsorbed (physically or chemically) on the MNP surface. For those adsorbed molecules that are transparent around the plasmon resonance wavelengths, the sorptiochromism follows basically the same principles as in solvatochromism discussed in the previous section. Therefore, in this respect, sorptiochromism can be regarded as a particular subcategory of solvatochromism. This property can be used to detect certain species that possess strong affinity to the metal particle surfaces, including thiols,69 as well as biomolecules like antigens70–73 and proteins.74,75In certain cases, the adsorbates (i.e., dye molecules) are strongly absorptive near the LSPR wavelengths. In this scenario, the interactions between MNPs and the adsorbed dyes would be more complex. As both the MNPs and the dyes under light excitation can be idealized as dipoles (plasmonic dipoles for the former, and molecular dipoles for the latter), and they have similar resonance frequencies, there may emerge strong plasmonic–molecular resonance coupling, which could significantly alter the absorption properties of both the MNPs and the dye molecules. The underlying principles have been well discussed in the previous literature,31 therefore here in this section we will be more focused on the phenomenological results of the resonance coupling.
Wang et al. employed a positively-charged water-soluble HITC dye (CAS no. 16595-48-5, with absorption maximum at 734 nm) as the adsorbate molecule, which was electrostatically immobilized onto the surface of negatively-charged gold nanorods via a layer-by-layer assembly method.76 Using gold nanorods with different longitudinal LSPR wavelengths (varying from 570 nm to 870 nm), they found that after HITC adsorption, the extinction spectral profiles of the nanorods were remarkably altered in both peak wavelength and intensity. In particular, the nanorod sample with a LSPR wavelength around 740 nm displayed the largest spectral shift, indicating that the plasmonic–molecular resonance coupling maximizes when the two components have similar resonance frequencies. Likewise, Jensen et al. fabricated similar hybrid nanostructures using gold nanorods and another organic dye (2,2′-dimethyl-8-phenyl-5,6,5′,6′-dibenzoithiacarbocyanine chloride).77 The gold nanorods and dye molecules had very similar resonance wavelengths (692 nm and 693 nm, respectively). They studied the effect on molecular resonance by systematically varying the concentration of the dye molecules and thus the nanorod-to-dye ratio, and found that the plasmon splitting in the resultant hybrid nanostructures increases in a linear manner with respect to the square root of the absorbance of the molecular layer. Similar results have been reported amply in the literature.78–81
The plasmonic–molecular resonance coupling can be readily reconfigured into indirect sorptiochromic systems, when stimuli-responsive chromophores are employed as the surface-bound molecular component. Wang et al. reported a light-controlled resonance-coupling-based plasmon switch fabricated with gold nanorods and a photochromic spirooxazine dye (1,3-dihydro-1,3,3-trimethylspiro[2H-indole-2,3′-[3H]naphtha[2,1-b][1,4]oxazine]).82 The dye in its closed-ring form is thermodynamically stable, and displays no typical absorption in the visible region; when illuminated with UV light, the dye transforms into its open-ring isomer, which shows an absorption peak at 620 nm. Employing gold nanorods with similar LSPR wavelengths, the authors obtained a reversible single-nanorod plasmon switch, with a maximal modulation depth of 7.2 dB at 634 nm in the dark-field scattering spectrum. Recently, the same research group presented a new plasmon switch comprising gold nanorods as the core and a semiconducting polyaniline polymer as the shell layer.83 Embedded in microfluidic chips, the hybrid nanostructures were subjected to acidic and basic solution environments, which could reversibly tune the conductivity of polyaniline by proton doping and dedoping, and therefore alter the absorption properties of the shell layer. With an optimized thickness of the polyaniline shell, the hybrid nanostructures exhibited a scattering peak shift as large as 100 nm, and a maximized modulation depth of 10 dB (Fig. 4). As the polyaniline polymer is also electroactive, the authors claimed that this plasmon switch may find applications in electro-controlled smart windows.
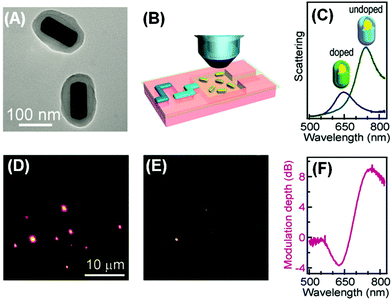 | ||
| Fig. 4 Gold nanorod/polyaniline core/shell nanostructures as resonance-coupling-based plasmon switches. (A) Transmission electron microscopy image of the core/shell nanostructures. (B) Schematic illustration of core/shell nanostructures embedded in a microfluidic chip for optical measurement. (C) Dark-field scattering spectrum for a representative nanostructure before and after proton doping. (D, E) Dark-field scattering photographs observed before and after proton doping, respectively. (F) Modulation depth of the plasmon switch. (Reprinted with permission from ref. 83.) | ||
C. Aggregachromism
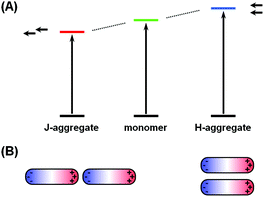
The phenomena of aggregachromism have been well documented and discussed for dye-related systems. When dye molecules form aggregates (dimers, trimers and higher oligomers), the electronic interaction between neighboring chromophores would alter the energy levels of molecular orbitals, resulting in spectral shifts. This can be interpreted using the dipole models. Fig. 5A shows a simplified illustrative explanation, in which two dye molecules, each idealized as a dipole, form dimers with two distinct configurations. When the two dipoles are aligned head-to-tail, this configuration (known as J-aggregate) stabilizes the energy levels owing to Coulombic attraction, and thus decreases the energy gap, resulting in a red-shift of the absorption maximum. In contrast, when the two dipoles are coupled side-by-side (H-aggregate), the energy levels become destabilized owing to Coulombic repulsion, increasing the energy gap and blue-shifting the absorption maximum.The cases for plasmonic nanostructures are somewhat similar, at least phenomenologically. Fig. 5B shows ideal examples of nanorod dimers. If the two nanorods are paired in an end-to-end manner, meaning the aggregation axis is parallel to the longitudinal axis, the longitudinal plasmon would resonate to longer-wavelength excitations due to plasmonic coupling, leading to a red-shift of the LSPR peak, just like that for J-aggregates of dye molecules; if the nanorods form a side-by-side dimer, like in H-aggregates, the LSPR wavelength would shift to the blue end.
Chen et al. presented a series of elegant studies regarding the monomers, dimers, trimers and higher oligomers of gold nanospheres.84,85 Clusters assembled from gold nanospheres were encapsulated with polymers, and subjected to density gradient centrifugation. Dimer and trimer samples were thus purified with good selectivity (95% and 81%, respectively), allowing for spectroscopic studies of nearly-pure dimers and trimers, rather than a mixed ensemble.
Regarding the anisotropic assembly manners of gold nanorods, an excellent example has been demonstrated by Xu et al.86 In their study, they employed gold nanorods to build H- and J-aggregates as sensing motifs, and exploited the chromic response resulting from plasmonic coupling to detect a pervasive environmental toxin, namely MC-LR (Fig. 6). In the first step, a portion of gold nanorods were functionalized with MC-LR antibodies, and another portion functionalized with MC-LR-OVA, an analogue antigen to MC-LR. Using different strategies, the functional groups could be attached preferentially on the sides or at the ends of nanorods. When mixed, driven by antigen–antibody affinity, ladder-like H-aggregates would be formed for the side-functionalized nanorods, and chain-like J-aggregates for the end-functionalized nanorods. When the toxin MC-LR was introduced, aggregates disassembled back into individual nanorods, restoring the characteristic extinction profiles of well-dispersed nanorods. The extinction spectra clearly show, during the disintegration of H-aggregates, the longitudinal LSPR peak displaying a continuous red-shift; while for J-aggregates, the LSPR peak was blue-shifted after disintegration. By calibrating the spectral responses, the detection limit was estimated to be 0.6 ng mL−1 for the H-aggregate mode, and even lower (0.03 ng mL−1) for the J-aggregate mode, far surpassing the standard (1 ng mL−1) required by World Health Organization (WHO). Such a high detection sensitivity clearly benefits from the ultrahigh extinction coefficient of plasmonic nanocrystals.
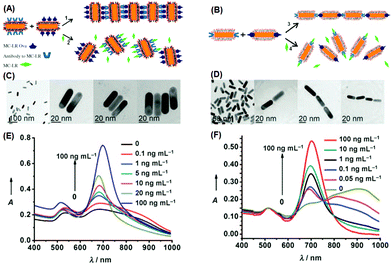 | ||
| Fig. 6 (A, B) Schematic illustration of assembling gold nanorods into side-by-side and end-to-end aggregates, respectively. (C, D) Corresponding transmission electron microscopy images of individually dispersed nanorods and assembled ones. (E, F) Extinction spectra when nanorod aggregates disassembled. (Reprinted with permission from ref. 86.) | ||
From the above example, it can be seen that by judiciously incorporating suitable stimuli-sensitive entities as the surface functional units, the aggregachromism of plasmonic MNPs can be readily reconfigured into indirect chromisms. This avenue can immensely broaden the applicability of aggregachromism and the susceptibilities of MNPs. To date, plasmonic nanostructures have been reconfigured and endowed with responsiveness to a number of external stimuli, including temperature, light, mechanical force, and a diverse range of (bio)chemical agents like acid/base, metal ions, peptides, and oligonucleotides.
Li et al. employed a temperature sensitive polymer, namely poly(N-isopropylacrylamide) (PPA), to functionalize gold nanospheres.87 PPA in aqueous solution has a low critical solution temperature (LCST) typically ranging from 30 °C to 45 °C. The polymer is hydrophilic below the LCST, and becomes hydrophobic and insoluble above the temperature. The polymer chain was functionalized with a thiol tail, and tethered to the surface of gold nanospheres. The afforded gold–PPA hybrid nanostructures are then also endowed with thermosensitivity. A transition temperature Tt of 28.4 °C was found for the colloidal solution, below which the gold nanospheres are well-dispersed, displaying a characteristic red color; when the temperature went above Tt, the nanospheres form aggregates owing to reduced solubility, resulting in an opaque yet stable colloid with a violet color. The clear–opaque transition could be modulated in a reversible on/off manner by running several heating–cooling cycles. The authors claimed that these thermosensitive gold NPs could potentially be used to fabricate smart windows that autonomously alter their transmittance in response to temperature changes during day and night. Similarly, Tenhu et al. adopted the thermally responsive diblock copolymer poly(methacrylic acid)-block-poly(N-isopropylacrylamide) (PMAA-b-PNIPAM) as the surface functional layer for gold NPs, and also observed moderate temperature-dependent optical responses of aggregates.88 And most recently, Hayward et al. prepared gold NPs capped with poly(styrene-r-2-vinylpyridine) [P(S-r-2VP)], and then loaded the NPs into a poly(styrene-r-4-vinyl phenol) [P(S-r-4VPh)] matrix.89 Owing to the strong hydrogen bonding between the surface ligands and the matrix at room temperature, gold NPs were well dispersed in the composite film even at high loading ratios. The author found that annealing at high temperatures (typically 200 °C) would weaken the hydrogen bonds, promoting the formation of NP aggregates and broadening the extinction bands; annealing at a lower temperature (typically 120 °C) would restore the initial dispersion state, revealing a good switching reversibility.
Klajn et al. grafted photoswitchable azobenzene ligands on a series of MNPs, including Au, Ag, Pd and Pt.90 The NPs, dispersed in toluene, were treated with an azobenzene dithiol (ADT) agent. Upon ultraviolet (UV) irradiation, the thermodynamically favored trans isomers of ADT transformed into cis isomers, accompanied by an increase in the electric dipole moment from 0 to 4.4 debye. The dipole–dipole interaction would then drive individual NPs to aggregate, forming internally cross-linked superspheres with diameters varying roughly from 50 nm to 300 nm (Fig. 7A). The authors demonstrated that for gold NPs, the solutions with different ADT/NP ratios could display varying final colors including red, purple, violet and blue (Fig. 7B). The authors further assembled these deformable superspheres into macroscopic structures that are plastic and moldable against substrates with arbitrary shapes. Employing an azobenzene monothiol instead, they managed to reversibly modulate the aggregation process.91 Under UV light, functionalized gold (and silver) NPs would coalesce into larger superspheres, which could then slowly break down back into free NPs. Both heat and visible light irradiation was found to help accelerate the disintegration process. Therefore, the color change accompanying the photo-induced aggregation process could be switched with full reversibility. Liu et al. conjugated water-soluble gold NPs with photochromic spiropyran groups through hydrophilic bridges with a thiol tail.92 UV light could trigger the isomerization of spiropyran ligands from an inert spiro-form to the active mero-form. When Cu2+ ions are introduced into the colloidal solution, mero-ligands would complex with Cu2+ ions, pulling the gold NPs to form aggregates and thus changing the solution color from red to purple. Using UV light, Cu2+, Fe3+ and EDTA as input signals, the authors built a series of logic gates including AND, OR and INHIBIT based on the responses in extinction spectra. The operation was also proved reversible using alternating UV and visible irradiation, implying the resettability of the afforded logic gates.
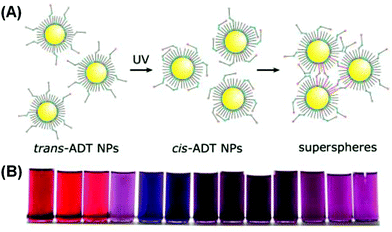 | ||
| Fig. 7 (A) Schematic illustration of UV-induced assembly of gold NPs mediated by ADT ligands. (B) Photographs of solutions with different gold NP/ADT ratios after UV irradiation. (Reprinted with permission from ref. 90.) | ||
D. Chronochromism
The term “chronochromism” describes the processes where a system changes its color with respect to the passage of time.1 Clearly, a chronochromic system is designed and constructed on the basis of concerns on the kinetics of involved reactions, rather than the mechanism itself of the chromism. All chronochromic systems are examples of indirect chromisms; and technically, all chromic phenomena are chronochromic, because they all require a certain period of time (either short or long) to proceed. However, most of the reported chronochromic systems exploit slow reactions that cover a temporal duration typically of minutes, hours, days and even months. This is because, as can be seen later, chronochromism is commonly used to translate time-related information into color change, in other words, to report time using a signal that is visual and intuitive.From the perspective of applications, apart from direct indication of time passage, chronochromic systems are usually employed for two other purposes: (i) self-destruction, and (ii) real-time mimicking and indication of some particular dynamic processes.
Self-erasing inks are classic examples of chronochromism. Most recently, Sheng et al. incorporated into paper substrates a series of hydrochromic dyes that isomerize in the presence of water, and demonstrated a new rewritable paper that is even compatible to common desktop printers (Fig. 8A).94 After water evaporation, the colored dye isomers gradually change to the initial colorless form, and the printed texts vanish within roughly a day at ambient temperature and humidity. Mild heating would accelerate the process, with the text self-erased in 30 s at 70 °C. Liu et al. also reported self-erasing recording media by loading their photo-induced aggregating gold–azobenzene hybrid NPs into organogel films.92 When illuminated with UV light, the hybrid NPs would coalesce into aggregates and change the film's color; with the UV light off, aggregates slowly would disassemble, restoring the original color. The self-erasing process could speed up on heat or visible light irradiation (Fig. 8B). The authors claimed this paper can be potentially used to store confidential and temporary information, or for self-expiring purposes like bus tickets.
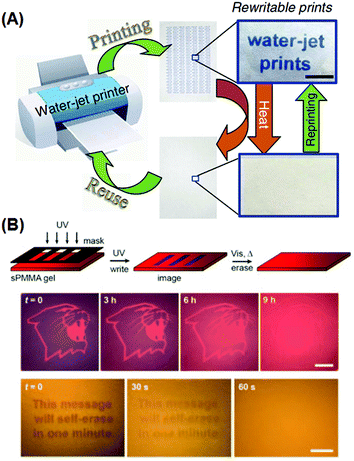 | ||
| Fig. 8 Rewritable and self-erasing recording media employing chronochromism. (A) Schematic illustration of the printing–reusing cycle with photographs of the paper after printing (right top) and after self-erasing (right bottom) using a water-jet printer. (B) Schematic illustration of the write–erasing cycle, and photographs of patterns showing the self-erasing processes at different rates. (Reprinted with permission from ref. 94 and 91.) | ||
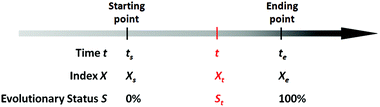
There exists quite a number of dynamic processes in daily life that concerns people, like the spoilage of foods (owing to microbial growth or chemical deterioration), the corrosion of metals, the aging of rubber products, the wearing of machinery, the degradation of chemical agents (owing to oxidation, deliquescence, decomposition, etc.), and the development of chronic diseases of human beings owing to long-term exposure to hazards. In these dynamic processes, time is a fundamental factor that determines how far these processes have evolved. Mathematically, for a specific evolving event, we can always find a particular variable X (which is associated with the evolving process) as an index, so that the evolution process of this event can be expressed by the process function below:
| X = f(t) | (1) |
| R = (te − ts)−1 | (2) |
Based on the definition of the kinetic rate, we can also define another parameter termed as evolutionary status (denoted as S), which is defined as:
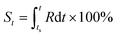 | (3) |
From this definition, it can be easily deduced that when t = ts, S = 0%, and when t = te, S = 100% (Scheme 1). Obviously, for those dynamic processes mentioned above, people are always interested in how far they have evolved, which can be described by the evolutionary status S.
As can be seen in eqn (3), the value of S is dictated by the integral of the kinetic rate R over the time interval [ts, t]. For most dynamic processes, the kinetic rate is dependent on (and sensitive to) one or multiple environmental factors that the system of interest is exposed to; for example, the growth rate of microorganisms in foods is dependent primarily on temperature, and the corrosion rate of metal is dependent on temperature and humidity (in addition to other environmental factors such as the partial pressure of oxygen and carbon dioxide). Therefore, eqn (3) can be rewritten as:
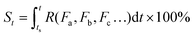 | (4) |
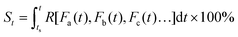 | (5) |
Eqn (5) implies that in order to calculate the value of St, one needs to know the entire history that the sample of interest has experienced, and how each of the environmental factors has varied during the history (Fa(t), Fb(t), Fc(t)⋯), which is rather complex and practically often impossible.
Fortunately, sometimes people do not necessarily have to resort to eqn (5) to determine the evolutionary status; for some dynamic processes, certain particular indexes that are intrinsic and easily perceivable in the system of interest could be employed for estimation, because these indexes are (roughly) correlated to and indicative of the value of S. For example, during the ripening process of strawberries, the color goes from pale green to bright red, which indicates that the fruits have become edible; and during the aging process of bananas, the appearance of brown freckles indicates the fruits are about to go bad. However, for a majority of evolution processes (for instance, the deterioration of canned foods, pharmaceuticals and vaccines), there is hardly any intrinsic and easily perceivable variable available as the indicative index. Therefore, extrinsic indicators (preferably chronochromic) can be designed and employed to mimic the target evolution process and to manifest the approximate value of evolutionary status S, which is proved as follows.
First, we need to know the prerequisite to which one dynamic process (in the system of interest) can be correlated to another one (in the extrinsic indicator). It can be easily proved mathematically that, two process functions, namely, X = f(t) and X′ = g(t), can always be correlated as long as they are both monotonic (as shown in Scheme 2):
∵X = f(t) and X′ = g(t) are both monotonic within the time interval [0, t].
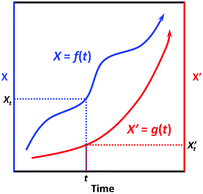 | ||
| Scheme 2 Illustration of the correlatability between two monotonic process functions, namely, X = f(t) and X′ = g(t). | ||
∴ For X′ = g(t), due to its monotonicity, there always exists its inverse function t = g−1(X′).
∴ We then have X = f(t) = f[g−1(X′)] = h(X′).
∴ Conversely, we also have X′ = g[f−1(X)] = h−1(X).
This result indicates that given the only prerequisite that both process functions are monotonic, each specific X value is correlated to a specific X’ value, and vice versa (Scheme 2); in other words, the two processes can always be correlated via a bijective function X = h(X′). Interestingly, most dynamic processes that people are concerned with can be regarded as monotonic, like microbial growth, freshness degradation, and quality loss; also, most chemical reactions are also monotonic, as they generally evolve unidirectionally from non-equilibrated states towards equilibrated ones. Therefore, given a series of specified conditions (all environmental factors remain constant over time), we can devise an indicator based on a (slow) chemical reaction process X′ = g(t) to indicate the target process X = f(t); with the correlation function X = h(X′) established, one can always tell the value of X based on the value of X’.
The above conclusion is obtained on a condition that all environmental factors are kept constant over the entire duration. For practical use, the variation of environmental factors over time needs to be taken into consideration. Hereafter, we choose temperature as a representative environmental factor for further discussion.
Now suppose we have the two monotonic evolution processes X = f(t) and X′ = g(t), for which temperature is the only environmental factor that affects their kinetic rates R and R’.
| R = R(T) and R′ = R′(T) | (6) |
When the environmental temperature is kept constant T = T1 (that is, under isothermal conditions), it can be easily deduced according to Scheme 3A that X = fT1(t) and X′ = gT1(t) can always be correlated, and the correlation function at T1 can be written as:
| X = hT1(X′) and X′ = hT1−1(X′) | (7) |
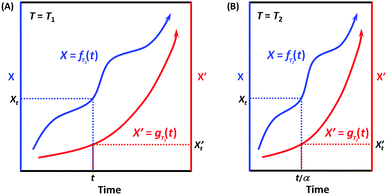 | ||
| Scheme 3 Illustration of the correlatability between two monotonic process functions, namely, X = f(t) and X′ = g(t), when (A) T = T1 and (B) T = T2. | ||
When the environmental temperature changes to an arbitrary T2, now X = fT2(t) (Scheme 3B). Assuming that the temperature change only alters the kinetic rate R, and RT2/RT1 = α, then we have:
| fT2(t) = fT1(αt) and fT1(t) = fT2(t/α) | (8) |
Analogously, for X’ now X′ = gT2(t). Assuming that the temperature change only alters the kinetic rate R’, and R′T2/R′T1 = α′, then we have:
| gT2(t) = gT1(α′t) and gT1(t) = gT2(t/α′) | (9) |
If for the two processes, their kinetic rates R and R’ are equally accelerated (or decelerated) when temperature changes from T1 to T2, that is, α = α′, which means that the two processes have the same apparent activation energy Ea = E′a (or in general, the same sensitivity on the environmental factor T), then we have:
| X = fT2(t) = fT1(αt) and X′ = gT2(t) = gT1(αt) | (10) |
Therefore, it can be easily deduced that:
| X = hT2(X′) = hT1(X′) and X′ = hT2−1(X) = hT1−1(X) | (11) |
| hT2(X′) = hT1(X′) and hT2−1(X) = hT1−1(X) | (12) |
| Ea = E′a or R(T) = R′(T) | (13) |
Eqn (13) implies that as long as they are under the same (arbitrary) temperature, the two processes would have the same kinetic rates, which means that in principle, we can use the latter process X′ = g(t) to mimic the former X = f(t).
The above conclusion serves as the underlying principle of an important niche application, namely, time–temperature indicators (TTI).95 TTIs are designed to indicate the real-time quality of perishable products. Perishable products are known to degrade over time owing to inherent physical/chemical/microbial deterioration processes, the rate of which is dependent on the environmental temperature. Therefore, most perishable products are recommended to be stored at low temperature so as to prolong their shelf lives. However, during the supply chain (from manufacturers to transporters, dealers and to consumers), the perishables might be unduly exposed to hazardously high temperatures, which could result in unexpected spoilage. TTIs are invented to address such issues caused by the fluctuations in temperature history. For a target perishable product, a TTI with (ideally) the same kinetic features (both kinetic rate R and apparent activation energy Ea) could be programmed and formulated. Attached to the perishable product from the very beginning, the TTI undergoes the same temperature history, mimics the deterioration in perishables, and therefore indicate the real-time quality. TTI represents a major technological trend in active and intelligent packaging, and finds application in the advanced quality control of perishables like foods, pharmaceuticals and vaccines.
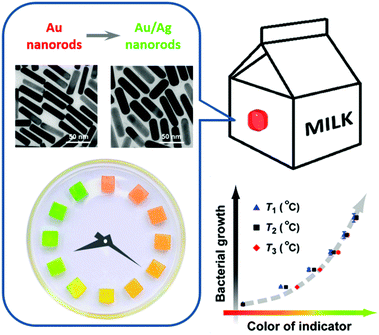
During the past few decades, there have been reports on TTIs constructed on the basis of various physicochemical reactions, such as enzymatic hydrolysis and polymerization.95 In recent years, noble metal nanostructures, by virtue of their vibrant and readily tunable optical properties and relatively low cost, have also been incorporated as the functioning agents in TTIs. Xia et al. reported in 2010 a silver-nanoplate-based TTI model.96 The as-synthesized silver triangular nanoplates undergo spontaneous shape transformation into round nanoplates, accompanied by a color change from cyan to blue, violet, magenta, and orange. The authors studied the cumulative effect of shape transformation and color change at different temperatures, and found that the kinetics of this particular reaction could not be easily programmed. Our research group presented a kinetically tunable TTI based on the overgrowth of the silver shell on gold nanorods.97 In the presence of AgNO3 and the reducing agent ascorbic acid, gold nanorods in aqueous solution spontaneously evolve into gold/silver core/shell nanorods, during which the solution changes its color from an initial red to orange, yellow, and green (Fig. 9). More importantly, the kinetic rate and apparent activation energy of silver overgrowth can be continuously and readily tuned in a broad range, simply by modifying the recipe (for example, adjusting the pH values, introducing additive agents). Using E. coli as a target system, we demonstrated the validity of the TTI by synchronizing at multiple temperatures the TTI color evolution with E. coli growth, and establishing a temperature-independent correlation between the TTI color and the microbial population.
There also exist chronochromic indicators that concern environmental factors other than temperature. For instance, Mills et al. presented an UV indicator that incorporates a photoacid and a pH-sensitive colorimetric indicator.98 The color-change kinetics could be tuned by introducing different amounts of alkali. When used as a skin patch, the UV indicator is expected to show warnings of the approach of erythema. It can be foreseen that noble metal nanostructures may also find utility in this regard, for example, to indicate long-term exposure to hazardous conditions like H2S and formaldehyde.
E. Miscellaneous chromisms
There also exist plenty of other processes that involve an alteration in the size, shape, composition, surrounding microenvironment and aggregation manners of noble metal nanostructures, which would in turn lead to a change in plasmon resonance and optical properties. For example, anisotropic oxidation of gold nanorods using Au(III) species would result in a decreased aspect ratio, and hence a blue shift of the longitudinal LSPR band, accompanied by a series of color changes;99 selective overgrowth in the transverse direction of gold nanorods would have a similar effect.100 Epitaxial growth of foreign metals on MNPs would afford bimetallic nanostructures, for example, Au/Pd, Au/Ag, Pd/Ag nanostructures;47,97,101–105 during the overgrowth process a continuous color change can usually be observed. Galvanic replacement of silver nanocubes with Au(III) species would afford gold nanocages;62,106–109 the corresponding changes in both composition and particle shape also give a systematic color change. Employing the sensitivity of some noble metals to certain gases, several research teams have constructed gasochromic sensors. For instance, Au–Pd heterostructures give spectral responses when exposed to H2 gas because Pd tends to adsorb H2.110–114 Ag-based nanostructures show a red shift in the LSPR wavelength when exposed to H2S or S2− owing to sulfidation; such nanostructures have been used to detect H2S species in living organisms.115–117 In addition, Chen et al. exploited the distinct color change during the overgrowth of the silver shell on gold nanorods, and successfully designed a colorimetric sensor for ascorbic acid with a detection limit of 49 nM.1183. Conclusions and outlook
Noble metal nanostructures, benefiting from their characteristic LSPR properties, commonly possess extraordinarily high extinction coefficients, and consequently are able to render intense colors at relatively low concentrations. We have done some simple estimations, which show that for a colloidal solution with an optical density around 1 cm−1 at a specific wavelength (in the visible region), the concentrations of noble metals therein are typically in the range of 1–100 μg mL−1, promising a satisfactorily low cost and good affordability. The chromism of plasmonic nanostructures, in particular, the aggregachromism and chronochromism, can present distinctly altered spectral profiles, with peak wavelengths significantly shifted (typically not less than 50 nm, and in some cases, even over 100 nm) and extinction intensities significantly altered, and therefore conveying high-contrast macroscopic color changes that are directly discernible by the naked eye, and thus readily enabling qualitative and even semi-quantitative analyses. These merits generally guarantee a high indication sensitivity while ideally circumventing the necessity of complex analytical instruments, and thereby lay only minimal training requirements on the common end-users, well meeting the ASSURED criteria (Affordable, Sensitive, Specific, User-friendly, Rapid and robust, Equipment-free and Deliverable to end-users) proposed by World Health Organization in 2006,119 which have been acknowledged as a general benchmark for a wide range of detecting, indicating and sensing applications.Although scientists have made plentiful achievements using noble metal plasmonic nanostructures to design, construct and fabricate chromic materials with important potential applications, there still remain a number of issues yet to be addressed in both fundamental and practical aspects. Some detailed description is listed as follows.
(I) Despite the superiorities of noble metal nanostructures discussed above, currently it still seems impractical to use these nanoparticles as an alternative or substitute to conventional dyes in modern industries, mostly because the preparation of metal nanostructures has been known to have notoriously low reproducibility.120,121 The nucleation–growth process of metal nanostructures is highly sensitive to the experimental conditions, and the obtained products generally show batch-to-batch differences. Therefore, a better and deepened understanding on the synthetic mechanisms is yet to be established. In addition, an improved protocol that allows for continuous, reproducible synthesis and purification on an industrially relevant scale is yet to be developed.
(II) Among the several categories of chromism summarized in this review, solvatochromism (and sorptiochromism) generally employs metal nanostructures with plasmonic bands in the NIR region, due to their relatively high sensitivities to refractive indexes; plasmonic bands in the visible range typically exhibit less pronounced spectral changes in both wavelength shifting and signal intensity, which, in most cases, necessitates spectrometers for even qualitative investigations. Therefore, metal nanostructures with directly visible solvatochromic/sorptiochromic responses are yet to be explored.
(III) Aggregachromism, limited by its inherent mechanism, can only be realized on nanoparticles with certain mobility, which are usually dispersed in colloidal solution, thus not quite conducive to practical application. Nonetheless, the colloidal dispersion of metal nanostructures could be solidified without essentially hampering their aggregachromic performances, for example, by taking the form of polymers, hydrogels/organogels and by deposition on flexible substrates like paper strips.122
(IV) The reusability of relevant materials constitutes another major concern, which put forward particular demands on the reversibility of chromism. These demands imply that for the design of related materials, the mechanism governing their chromic performances are, on the nanoscopic level, preferred to be mild supramolecular interactions, rather than strong and rigid covalent/metallic bonds.
(V) As far as material manipulation and device setup are concerned, physical stimuli are generally favored over chemical stimuli, because the latter require specific input channels, and usually result in dilution of the functioning agents as well as accumulation of wastes. In contrast, physical stimuli (like light, heat and mechanical forces) are “cleaner” as they only introduce energy flows to the working system, promising simple operation procedures and neat device setup. In particular, self-evolving materials, represented by chronochromic materials here in this review, commonly require no stimulating signals at all; once deployed, they can work autonomously and reliably with little or even no human supervision. This newly emerging family represents an important direction in material design and engineering, and deserves particular attention from both the academic and industrial communities.
Acknowledgements
The authors acknowledge the funding from NSFC (No. 21371011, 21331001, and 21321001) and MOST of China (No. 2014CB643800).References
- P. Bamfield and M. G. Hutchings, Chromic Phenomena: Technological Applications of Colour Chemistry, RSC Publishing, U.K., 2nd edn, 2010 Search PubMed.
- G. H. Brown, Photochromism, Wiley-Interscience, New York, 1971 Search PubMed.
- A. Seeboth and D. Lötzsch, Thermochromic Phenomena in Polymers, Smithers Papra Technology Limited, U.K., 2008 Search PubMed.
- A. Seeboth, D. Lötzsch, R. Ruhmann and O. Muehling, Chem. Rev., 2014, 114, 3037 CrossRef CAS PubMed.
- M. M. Caruso, D. A. Davis, Q. Shen, S. A. Odom, N. R. Sottos and S. R. White, et al. , Chem. Rev., 2009, 109, 5755 CrossRef CAS PubMed.
- F. Ciardelli, G. Ruggeri and A. Pucci, Chem. Soc. Rev., 2013, 42, 857 RSC.
- D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough and S. L. Potisek, Nature, 2009, 459, 68 CrossRef CAS PubMed.
- H. Ito, T. Saito, N. Oshima, N. Kitamura, S. Ishizaka and Y. Hinatsu, et al. , J. Am. Chem. Soc., 2008, 130, 10044 CrossRef CAS PubMed.
- K. Nagura, S. Saito, H. Yusa, H. Yamawaki, H. Fujihisa and H. Sato, et al. , J. Am. Chem. Soc., 2013, 135, 10322 CrossRef CAS PubMed.
- O. S. Venger, Chem. Rev., 2013, 113, 3686 CrossRef PubMed.
- V. I. Minkin, Chem. Rev., 2004, 104, 2751 CrossRef CAS PubMed.
- E. Arunkumar and A. Ajayaghosh, J. Am. Chem. Soc., 2005, 127, 3156 CrossRef CAS PubMed.
- J. Pérez-Juste, I. Pastoriza-Santos, L. M. Liz-Marzán and P. Mulvaney, Coord. Chem. Rev., 2005, 249, 1870 CrossRef.
- M. Hu, J. Y. Chen, Z.-Y. Li, L. Au, G. V. Hartland and X. D. Li, et al. , Chem. Soc. Rev., 2006, 35, 1084 RSC.
- S. K. Ghosh and T. Pal, Chem. Rev., 2007, 107, 4797 CrossRef CAS PubMed.
- M. Grzelczak, J. Pérez-Juste, P. Mulvaney and L. M. Liz-Marzán, Chem. Soc. Rev., 2008, 37, 1783 RSC.
- A. R. Tao, S. Habas and P. D. Yang, Small, 2008, 4, 310 CrossRef CAS.
- P. K. Jain, X. H. Huang, I. H. El-Sayed and M. A. El-Sayed, Acc. Chem. Res., 2008, 41, 1578 CrossRef CAS PubMed.
- X. M. Lu, M. Rycenga, S. E. Skrabalak, B. Wiley and Y. N. Xia, Annu. Rev. Phys. Chem., 2009, 60, 167 CrossRef CAS PubMed.
- M. Rycenga, C. M. Cobley, J. Zeng, W. Y. Li, C. H. Moran and Q. Zhang, et al. , Chem. Rev., 2011, 111, 3669 CrossRef CAS PubMed.
- T. Ming, H. Chen, R. Jiang, Q. Li and J. Wang, J. Phys. Chem. Lett., 2012, 3, 191 CrossRef CAS.
- H. Chen, L. Shao, Q. Li and J. Wang, Chem. Soc. Rev., 2013, 42, 2679 RSC.
- L. M. Liz-Marzán, C. J. Murphy and J. Wang, Chem. Soc. Rev., 2014, 43, 3820 RSC.
- G. Baffou and R. Quidant, Chem. Soc. Rev., 2014, 43, 3898 RSC.
- R. Jiang, S. Cheng, L. Shao, Q. Ruan and J. Wang, J. Phys. Chem. C, 2013, 117, 8909 CAS.
- A. J. Haes, C. L. Haynes, A. D. McFarland, G. C. Schatz, R. P. Van Duyne and S. L. Zou, MRS Bull., 2005, 30, 368 CrossRef CAS.
- L. Brus, Acc. Chem. Res., 2008, 41, 1742 CrossRef CAS PubMed.
- S. Lal, N. K. Grady, J. Kundu, C. S. Levin, J. B. Lassiter and N. J. Halas, Chem. Soc. Rev., 2008, 37, 898 RSC.
- X.-M. Qian and S. M. Nie, Chem. Soc. Rev., 2008, 37, 912 RSC.
- N. P. W. Pieczonka and R. F. Aroca, Chem. Soc. Rev., 2008, 37, 946 RSC.
- H. Chen, T. Ming, L. Zhao, F. Wang, L.-D. Sun and J. Wang, et al. , Nano Today, 2010, 5, 494 CrossRef CAS.
- J. F. Li, Y. F. Huang, Y. Ding, Z. L. Yang, S. B. Li and X. S. Zhou, et al. , Nature, 2010, 464, 392 CrossRef CAS PubMed.
- S. D. Standridge, G. C. Schatz and J. T. Hupp, J. Am. Chem. Soc., 2009, 131, 8407 CrossRef CAS PubMed.
- H. Nakanishi, K. J. M. Bishop, B. Kowalczyk, A. Nitzan, E. A. Weiss and K. V. Tretiakov, Nature, 2009, 460, 371 CrossRef CAS PubMed.
- A. Aubry, D. Y. Lei, A. I. Fernández-Domínguez, Y. Sonnefraud, S. A. Maier and J. B. Pendry, Nano Lett., 2010, 10, 2574 CrossRef CAS PubMed.
- J.-L. Wu, F.-C. Chen, Y.-S. Hsiao, F.-C. Chien, P. L. Chen and C.-H. Kuo, et al. , ACS Nano, 2011, 5, 959 CrossRef CAS PubMed.
- M. D. Brown, T. Suteewong, R. S. S. Kumar, V. D'Innocenzo, A. Petrozza and M. M. Lee, et al. , Nano Lett., 2011, 11, 438 CrossRef CAS PubMed.
- D. B. Ingram and S. Linic, J. Am. Chem. Soc., 2011, 133, 5202 CrossRef CAS PubMed.
- S. K. Cushings, J. T. Li, F. K. Meng, T. R. Senty, S. Suri and M. J. Zhi, et al. , J. Am. Chem. Soc., 2012, 134, 15033 CrossRef PubMed.
- F. Wang, C. Li, H. Chen, R. Jiang, L.-D. Sun and Q. Li, et al. , J. Am. Chem. Soc., 2013, 135, 5588 CrossRef CAS PubMed.
- J. W. M. Chon, C. Bullen, P. Zijlstra and M. Gu, Adv. Funct. Mater., 2007, 17, 875 CrossRef CAS.
- P. Zijlstra, J. W. M. Chon and M. Gu, Nature, 2009, 459, 410 CrossRef CAS PubMed.
- J. N. Anker, W. P. Hall, O. Lyandres, N. C. Shah, J. Zhao and R. P. Van Duyne, Nat. Mater., 2008, 7, 442 CrossRef CAS PubMed.
- B. Sepúlveda, P. C. Angelomé, L. M. Lechuga and L. M. Liz-Marzán, Nano Today, 2009, 4, 244 CrossRef.
- N. Liu, M. L. Tang, M. Hentschel, H. Giessen and A. P. Alivisatos, Nat. Mater., 2011, 10, 631 CrossRef CAS PubMed.
- X. Q. Huang, S. H. Tang, X. L. Mu, Y. Dai, G. X. Chen and Z. Y. Zhou, et al. , Nat. Nanotechnol., 2011, 6, 28 CrossRef CAS PubMed.
- X. Q. Huang, S. H. Tang, B. J. Liu, B. Ren and N. F. Zheng, Adv. Mater., 2011, 23, 3420 CrossRef CAS PubMed.
- L. Nie, M. Chen, X. Sun, P. Rong, N. F. Zheng and X. Chen, Nanoscale, 2014, 6, 1271 RSC.
- J.-W. Xiao, S.-X. Fan, F. Wang, L.-D. Sun, X.-Y. Zheng and C.-H. Yan, Nanoscale, 2014, 6, 4345 RSC.
- G. H. Chan, J. Zhao, E. M. Hicks, G. C. Schatz and R. P. Van Duyne, Nano Lett., 2007, 7, 1947 CrossRef CAS.
- R. He, Y.-C. Wang, X. Wang, Z. Wang, G. Liu and W. Zhou, et al. , Nat. Commun., 2014, 5, 4327 CAS.
- V. G. Kravets, J. Jalil, Y.-J. Kim, D. Ansell, D. E. Aznakayeva and B. Thackray, et al. , Sci. Rep., 2014, 4, 5517 CAS.
- Q.-C. Sun, Y. Ding, S. M. Goodman, H. H. Funke and P. Nagpal, Nanoscale, 2014, 6, 12450 RSC.
- M. W. Knight, L. Liu, Y. Wang, L. Brown, S. Mukherjee and N. S. King, et al. , Nano Lett., 2012, 12, 6000 CrossRef CAS PubMed.
- G. Maidecchi, G. Gonella, R. P. Zaccaria, R. Moroni, L. Anghinolfi and A. Giglia, et al. , ACS Nano, 2013, 7, 5834 CrossRef CAS PubMed.
- M. W. Knight, N. S. King, L. Liu, H. O. Everitt, P. Nordlander and N. J. Halas, ACS Nano, 2014, 8, 834 CrossRef CAS PubMed.
- R. J. Stokes, A. Macaskill, P. J. Lundahl, W. E. Smith, K. Faulds and D. Graham, Small, 2007, 3, 1593 CrossRef CAS PubMed.
- Q. Ruan, L. Shao, Y. Shu, J. Wang and H. Wu, Adv. Opt. Mater., 2014, 2, 65 CrossRef.
- S. H. Im, Y. T. Lee, B. Wiley and Y. Xia, Angew. Chem., Int. Ed., 2005, 44, 2154 CrossRef CAS PubMed.
- Z. Huo, C.-K. Tsung, W. Huang, X. Zhang and P. Yang, Nano Lett., 2008, 8, 2041 CrossRef CAS PubMed.
- J. Xie, J. Y. Lee and D. I. C. Wang, J. Phys. Chem. C, 2007, 111, 10226 CAS.
- S. E. Skrabalak, J. Chen, Y. Sun, X. Lu, L. Au, C. M. Cobley and Y. Xia, Acc. Chem. Res., 2008, 41, 1587 CrossRef CAS PubMed.
- L. Shao, Q. Ruan, R. Jiang and J. Wang, Small, 2014, 10, 802 CrossRef CAS PubMed.
- H. Chen, X. Kou, Z. Yang, W. Ni and J. Wang, Langmuir, 2008, 24, 5233 CrossRef CAS PubMed.
- H. Chen, L. Shao, K. C. Woo, T. Ming, H.-Q. Lin and J. Wang, J. Phys. Chem. C, 2009, 113, 17691 CAS.
- Y. H. Lee, H. Chen, Q.-H. Xu and J. Wang, J. Phys. Chem. C, 2011, 115, 7997 CAS.
- Y. Shen, J. Zhou, T. Liu, Y. Tao, R. Jiang and M. Liu, et al. , Nat. Commun., 2013, 4, 2381 Search PubMed.
- Y. Liu, J. Ling and C. Z. Huang, Chem. Commun., 2011, 47, 8121 RSC.
- L. J. Sherry, R. C. Jin, C. A. Mirkin, G. C. Schatz and R. P. Van Duyne, Nano Lett., 2006, 6, 2060 CrossRef CAS PubMed.
- D. A. Gish, F. Nsiah, M. T. McDermott and M. J. Brett, Anal. Chem., 2007, 79, 4228 CrossRef CAS PubMed.
- C. X. Yu and J. Irudayaraj, Biophys. J., 2007, 93, 3684 CrossRef CAS PubMed.
- C. X. Yu and J. Irudayaraj, Anal. Chem., 2007, 79, 572 CrossRef CAS PubMed.
- K. M. Mayer, S. Lee, H. W. Liao, B. C. Rostro, A. Fuentes and P. T. Scully, et al. , ACS Nano, 2008, 2, 687 CrossRef CAS PubMed.
- S. M. Marinakos, S. H. Chen and A. Chilkoti, Anal. Chem., 2007, 79, 5278 CrossRef CAS PubMed.
- G. J. Nusz, S. M. Marinakos, A. C. Curry, A. Dahlin, F. Höök and A. Wax, et al. , Anal. Chem., 2008, 80, 984 CrossRef CAS PubMed.
- W. Ni, Z. Yang, H. Chen, L. Li and J. Wang, J. Am. Chem. Soc., 2008, 130, 6692 CrossRef CAS PubMed.
- B. K. Juluri, M. Lu, Y. B. Zheng, T. J. Huang and L. Jensen, J. Phys. Chem. C, 2009, 113, 18499 CAS.
- Y. B. Zheng, B. Kiraly, S. Cheunkar, T. J. Huang and P. S. Weiss, Nano Lett., 2011, 11, 2061 CrossRef CAS PubMed.
- T. Schwartz, J. A. Hutchison, C. Genet and T. W. Ebbesen, Phys. Rev. Lett., 2011, 106, 196405 CrossRef CAS PubMed.
- H. Chen, L. Shao, K. C. Woo, J. Wang and H.-Q. Lin, J. Phys. Chem. C, 2012, 116, 14088 CAS.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592 CrossRef CAS PubMed.
- T. Ming, L. Zhao, M. Xiao and J. Wang, Small, 2010, 6, 2514 CrossRef CAS PubMed.
- N. Jiang, L. Shao and J. Wang, Adv. Mater., 2014, 26, 3282 CrossRef CAS PubMed.
- G. Chen, Y. Wang, L. H. Tan, M. Yang, L. S. Tan and Y. Chen, et al. , J. Am. Chem. Soc., 2009, 131, 4218 CrossRef CAS PubMed.
- G. Chen, Y. Wang, M. Yang, J. Xu, S. J. Goh and M. Pan, et al. , J. Am. Chem. Soc., 2010, 132, 3644 CrossRef CAS PubMed.
- L. Wang, Y. Zhu, L. Xu, W. Chen, H. Kuang and L. Liu, et al. , Angew. Chem., Int. Ed., 2010, 49, 5472 CrossRef CAS PubMed.
- M. Q. Zhu, L. Q. Wang, G. J. Exarhos and A. D. Q. Li, J. Am. Chem. Soc., 2004, 126, 2656 CrossRef CAS PubMed.
- M. Nuopponen and H. Tenhu, Langmuir, 2007, 23, 5352 CrossRef CAS PubMed.
- K. Heo, C. Miesch, T. Emrick and R. C. Hayward, Nano Lett., 2013, 13, 5297 CrossRef CAS PubMed.
- R. Klajn, K. J. M. Bishop, M. Fialkowski, M. Paszewski, C. J. Campbell and T. P. Gray, et al. , Science, 2007, 316, 261 CrossRef CAS PubMed.
- R. Klajn, P. J. Wesson, K. J. M. Bishop and B. A. Grzybowski, Angew. Chem., Int. Ed., 2009, 48, 7035 CrossRef CAS PubMed.
- D. Liu, W. Chen, K. Sun, K. Deng, W. Zhang and Z. Wang, Angew. Chem., Int. Ed., 2011, 50, 4103 CrossRef CAS PubMed.
- M. D. Hager, P. Greil, C. Leyens, S. van der Zwang and U. S. Schubert, Adv. Mater., 2010, 22, 5424 CrossRef CAS PubMed.
- L. Sheng, M. Li, S. Zhu, H. Li, G. Xi and Y.-G. Li, et al. , Nat. Commun., 2014, 5, 3044 Search PubMed.
- G. L. Robertson, Food Packaging: Principles and Practice, Taylor & Francis, Boca Raton, 3rd edn, 2013 Search PubMed.
- J. Zeng, S. Roberts and Y. Xia, Chem. – Eur. J., 2010, 16, 12559 CrossRef CAS PubMed.
- C. Zhang, A.-X. Yin, R. Jiang, J. Rong, L. Dong and T. Zhao, et al. , ACS Nano, 2013, 7, 4561 CrossRef CAS PubMed.
- A. Mills, K. McDiarmid, M. McFarlane and P. Grosshans, Chem. Commun., 2009, 1345 RSC.
- C.-K. Tsung, X. Kou, Q. Shi, J. Zhang, M. H. Yeung and J. Wang, et al. , J. Am. Chem. Soc., 2006, 128, 5352 CrossRef CAS PubMed.
- X. Kou, S. Zhang, Z. Yang, C.-K. Tsung, G. D. Stucky and L.-D. Sun, et al. , J. Am. Chem. Soc., 2007, 129, 6402 CrossRef CAS PubMed.
- F. Wang, L.-D. Sun, W. Feng, H. Chen, M. H. Yeung and J. Wang, et al. , Small, 2010, 6, 2566 CrossRef CAS PubMed.
- Q. Li, R. Jiang, T. Ming, C. Fang and J. Wang, Nanoscale, 2012, 4, 7070 RSC.
- Y. Okuno, K. Nishioka, A. Kiya, N. Nakashima, A. Ishibashi and Y. Niidome, et al. , Nanoscale, 2010, 2, 1489 RSC.
- R. Jiang, H. Chen, L. Shao, Q. Li and J. Wang, Adv. Mater., 2012, 24, OP200 CAS.
- C. J. DeSantis, R. G. Weiner, A. Radmilovic, M. M. Bower and S. E. Skrabalak, J. Phys. Chem. Lett., 2013, 4, 3072 CrossRef CAS.
- S. E. Skabalak, L. Au, X. Li and Y. Xia, Nat. Protoc., 2007, 2, 2182 CrossRef PubMed.
- Y. Xia, W. Li, C. M. Cobley, J. Chen, X. Xia and Q. Zhang, et al. , Acc. Chem. Res., 2011, 44, 914 CrossRef CAS PubMed.
- W. Xiong, D. Sikdar, M. Walsh, K. J. Si, Y. Tang and Y. Chen, et al. , Chem. Commun., 2013, 49, 9630 RSC.
- X. Xia and Y. Xia, Front. Phys., 2014, 9, 378 CrossRef.
- N. Liu, M. L. Tang, M. Hentschel, H. Giessen and A. P. Alivisatos, Nat. Mater., 2011, 10, 631 CrossRef CAS PubMed.
- M. L. Tang, N. Liu, J. A. Dionne and A. P. Alivisatos, J. Am. Chem. Soc., 2011, 133, 13220 CrossRef CAS PubMed.
- T. Shegai, P. Johansson, C. Langhammer and M. Käll, Nano Lett., 2012, 12, 2464 CrossRef CAS PubMed.
- C.-Y. Chiu and M. H. Huang, Angew. Chem., Int. Ed., 2013, 52, 12709 CrossRef CAS PubMed.
- R. Jiang, F. Qin, Q. Ruan, J. Wang and C. Jin, Adv. Funct. Mater., 2014, 24, 7328 CrossRef CAS.
- J. Zeng, J. Tao, D. Su, Y. Zhu, D. Qin and Y. Xia, Nano Lett., 2011, 11, 3010 CrossRef CAS PubMed.
- B. Xiong, R. Zhou, J. Hao, Y. Jia, Y. He and E. S. Yeung, Nat. Commun., 2012, 4, 1708 CrossRef PubMed.
- C. Fang, Y. H. Lee, L. Shao, R. Jiang, J. Wang and Q.-H. Xu, ACS Nano, 2013, 7, 9354 CrossRef CAS PubMed.
- G. Wang, Z. Chen and L. Chen, Nanoscale, 2011, 3, 1756 RSC.
- P. W. Peeling, K. K. Holmes, D. Mabey and A. Ronald, Sex. Transm. Infect., 2006, 82, v1 CrossRef PubMed.
- M. L. Personick and C. A. Mirkin, J. Am. Chem. Soc., 2013, 135, 18238 CrossRef CAS PubMed.
- Y. Xia, Angew. Chem., Int. Ed., 2014, 53, 12268 CAS.
- D. D. Liana, B. Raguse, J. J. Gooding and E. Chow, Sensors, 2012, 12, 11505 CrossRef CAS PubMed.
| This journal is © the Partner Organisations 2016 |